Metamagneto em Campos Magnéticos Uniforme e Aleatório

Dissertação de Mestrado

Metamagneto em Campos Magnéticos

Uniforme e Aleatório

Antonio Weizenmann

Dissertação de Mestrado

Metamagneto em Campos Magnéticos

Uniforme e Aleatório

Antonio Weizenmann

Dissertação apresentada ao Departamento de Pós-graduação em Física da Universidade Federal do Ceará

como parte dos requesitos para obtenção do grau de Mestre em Física Estatística.

Orientador

Aos meus pais,

Agradecimentos

Quero agradecer ao Prof. Dr. Alberto Sebastião de Arruda, meu orientador, por suas inúmeras sugestões e constante suporte durante a elaboração do trabalho. Sua amizade e caráter tornaram muito mais humano este trabalho que poderia ser puramente catedrático.

Também sou muito grato aos professores Dr. Josué Mendes Filho, Dr. Gil de Aquino Farias, Dr. Raimundo Nogueira da Costa Filho, Dr. José Soares Andrade Júnior, Dr. Uriel Medeiros Costa, Dr. Newton Theophilo de Oliveira, Dr. Murilo Pereira de Almeida, que, de diversas formas, me auxiliaram durante o Curso de Mestrado. As suas críticas, sugestões e mesmo o companheirismo e a amizade, facilitaram muito a realização do curso e do presente trabalho.

Não é possível deixar de agradecer a todos da Coordenação do Curso e do Departa-mento, que sempre me apoiaram e realizaram seu trabalho com presteza.

Aos colegas, devo gratidão pela amizade e a oportunidade de realizar trabalhos em grupo, abrindo os horizontes do conhecimento e da compreensão nas coisas que só deles podemos aprender.

Aos amigos, em especial Euzenil, Jean, Daniel, Arian, Teldo e Rosa, Hulk e Rose, Eduardo e Fabiana, Ricardo e Karen, agradeço pela atenção, solidariedade, lealdade mesmo nos momentos de dificuldade.

À minha família, sou grato pelo apoio incondicional às escolhas que tenho feito. Ao meu pai, Laurindo, que me serve como exemplo de coragem e determinação; minha mãe, Antonieta, da qual aprendi as mais importantes lições; aos meus irmãos, Laerte, Sidnei e Ari, dos quais me orgulho por ser o irmão mais novo, podendo assim espelhar-me em suas virtudes e diferenças, que se complementam de forma peculiar.

À mulher de minha vida, Sally, agradeço o companheirismo, a paciência e o amor, que me motivam a cada instante.

Fortaleza, Ceará Antonio Weizenmann

Resumo

Abstract

Sumário

Agradecimentos . . . ii

Resumo . . . iii

Abstract . . . iv

Introdução 1 1 Fenômenos Críticos 8 1.1 Transições de Fases . . . 8

1.2 Modelos para Sistemas Magnéticos . . . 18

1.2.1 A Função de Partição . . . 18

1.2.2 Médias . . . 19

1.2.3 Modelo de Ising . . . 20

1.2.4 Modelo de Heisenberg . . . 22

1.3 Resolução do Modelo de Ising . . . 23

1.3.1 Resolução Exata em Uma Dimensão . . . 23

1.3.2 Solução Exata em Uma Dimensão na Presença de um Campo . . . 26

1.3.3 Aproximação de Campo Médio para o Modelo de Ising . . . 30

2 Metamagneto em Campo Uniforme e Aleatório 32 2.1 Introdução . . . 32

2.2 Definição do Modelo . . . 35

2.3 Equações do Campo Médio . . . 35

3 Resultados e Discussões 50

4 Conclusões 58

4.1 Introdução . . . 58 4.2 Principais Resultados . . . 59 4.3 Perspectivas Futuras . . . 62

Lista de Figuras

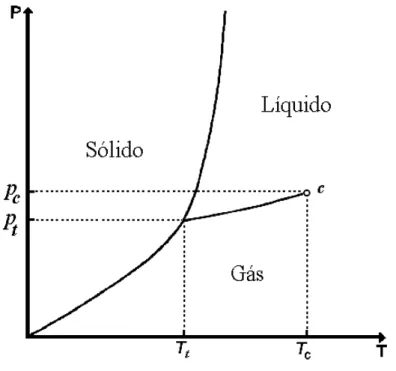
1.1 Diagrama de fases de um fluido simples, em termos da pressão contra temperatura. As linhas cheias indicam transições de primeira ordem e o ponto crítico c uma transição de segunda ordem. No ponto triplo (pt, Tt)

há uma coexistência de três fases. . . 10 1.2 Projeção da equação de estado no plano p versus ρ. . . 11

1.3 Projeção da equação de estado no plano ρ versus T. . . 11

1.4 Esboço do modelo de gás de rede em várias temperaturas. Cada célula indica que há uma molécula ocupando esse volume. O comprimento de correlação (ξ) indica o diâmetro de um cluster ou célula. . . 13

1.5 Diagrama de fases no plano campo aplicado contra a temperatura para um sistema ferromagnético uniaxial simples. A linha de coexistência é dada porH = 0 com T < T c. . . 14

1.6 Parâmetro de ordem (magnetização espontânea) em função da tempera-tura para um ferromagneto uniaxial simples. . . 14 1.7 Isoterma do ferromagneto uniaxial simples (magnetizaçãomversus campo

magnético H). . . 15

1.8 Dados obtidos por Guggenheim em 1945 para a curva de coexistência de oito fluidos diferentes (as densidades e as temperaturas são divididas pelos valores no ponto crítico). . . 17 1.9 Rede linear com N sítios com energia de interação Ji e spin S. O índicei

2.1 Rede bidimensional regular com spins Si = ±1. Observe que a rede

pode ser dividida em duas sub-redes interpenetrantes equivalentes, onde os primeiros vizinhos estão na outra sub-rede e os segundos vizinhos estão na mesma sub-rede. A energia de interação entre os primeiros vizinhos é

−J e a interação entre os segundos vizinhos é J′_{. . . . 36}

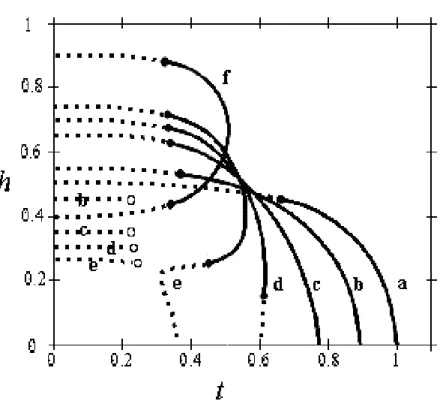
3.1 Diagrama de fases no plano h₋t para uma distribuição de probabilidade

bimodal com (a) ha = 0; (b) ha = 0,3; (c) ha = 0,4; (d) ha = 0,45; (e)

ha = 0,49 e (f) ha = 0,65. As linhas simples representam transições

con-tínuas ou de segunda ordem. As linhas pontilhadas representam transições de primeira ordem. Os círculos cheios são pontos tricríticos. Os círculos vazios são pontos críticos. . . 52 3.2 Diagrama de fases no plano h₋t para uma distribuição de probabilidade

trimodal ondep= 1,0 equivale ao caso puro, com ha= 0. . . 54

3.3 Diagrama de fases no plano h₋t para uma distribuição de probabilidade

trimodal com p = 0,8. As linhas representam transições contínuas ou de

segunda ordem. Os círculos são pontos tricríticos. . . 55 3.4 Diagrama de fases no plano h₋ t, com diversos valores para o campo

aleatóriohapara uma distribuição de probabilidade trimodal comp= 0,5.

Introdução

Modelo de Ising para 4 Spins

Magnetismo

Os fenômenos magnéticos são largamente utilizados no desenvolvimento de novas tecnologias, desde sistemas de geração e distribuição de energia (hidrelétricas, entre ou-tros), a sistemas de conversão eletromecânica (eletrodomésticos, automóveis), eletrônicos e de telecomunicações, transdutores, sensoriamento, prospecção geológica, informática, automação industrial até a medicina e a engenharia biomédica. Isto só foi possível com o entendimento dos fenômenos magnéticos, e com a descoberta de novos materi-ais magnéticos. Fenômenos estes que são rigorosamente descritos pela mecânica quântica e pela mecânica estatística, mas que podem ser compreendidos em uma primeira análise utilizando-se uma abordagem macroscópica, possibilitando assim a aplicação de conceitos de física clássica. Embora o magnetismo não receba a ênfase necessária no ensino médio, está muito presente em nossa vida. Pois desde o ímã que colocamos na porta geladeira até a memória (HD-hard disk) do computador, ou mesmo as fitas cassete que utilizamos para armazenar as nossas músicas preferidas, utilizam fenômenos e materiais magnéticos. A palavra magnetismo está associada ao fenômeno pelo qual um ente tem o poder de atrair e influenciar outro ente. Sua origem está ligada ao nome de uma cidade da região da antiga Turquia, que era rica em minério de ferro, a Magnésia. Provavelmente foram os gregos, quem primeiro refletiram sobre as propriedades da magnetita (F e2O4). Este

um imã aponta aproximadamente para o pólo norte do planeta. Dos filósofos naturais que estudaram magnetismo, o mais famoso é William Gilbert de Colchester (1544-1603), chamado de “Pai do Magnetismo”, pois sistematizou as especulações sobre o assunto. Vinte anos à frente de Sir Francis Bacon, foi um firme defensor do que nós chamamos hoje de método experimental. De Magnete foi sua obra-prima, dezessete anos do seu

trabalho registrado, contendo todos os seus resultados. Nesta foi reunido todo o conhe-cimento sobre magnetismo digno de confiança de seu tempo, junto com suas maiores contribuições. Entre outros experimentos, foram reproduzidos aqueles executados três séculos antes por Peregrinus com a magnetita esférica que foi chamada de terrella (pe-quena terra), pois Gilbert a idealizou como sendo um modelo atual da Terra e assim foi o primeiro a afirmar que a Terra é um ímã, ou seja, possui um campo magnético próprio. Os fenômenos magnéticos passaram a ser melhor modelados, a partir do século XIX, com a descoberta de sua correlação com a eletricidade. Em 1820, Oersted descobriu que uma corrente elétrica passando por um fio também produzia efeito magnético, mudando a ori-entação da agulha de uma bússola. Posteriormente, Ampère formulou a lei que relaciona o campo magnético gerado com a intensidade de corrente no fio e em 1831, Faraday e Henry, descobriram que um campo magnético variável induzia uma corrente elétrica em um circuito. Após a descoberta dos efeitos magnéticos das correntes, foi sugerido por Ampère, que a magnetização de meios materiais (ímãs permanentes) deveriam se originar de correntes microscópicas, que foram denominadas correntes de Ampère. Assim todos os fenômenos magnéticos seriam gerados por correntes, da mesma forma que todos os efeitos elétricos são gerados pelos portadores de carga (elétron).

Fases Magnéticas

Podemos classificar as diversas fases magnéticas de acordo com a origem microscópica de sua magnetização e de suas interações internas. Os principais tipos de fases magnéticas são o Diamagnetismo, Paramagnetismo, Ferromagnetismo, Antiferromagnetismo, entre outros. A seguir vamos discutir estes, utilizando uma abordagem macroscópica para que se tenha uma idéia dos diferentes tipos de comportamento magnético.

Diamagnetismo

Diamagnetismo em geral corresponde ao tipo mais fraco de resposta magnética de um sistema, caracterizado por susceptibilidade negativa e da ordem de χm ∼ 10−5 (SI)

(o fato deste valor ser negativo é justificado pela Lei de Lenz: esta é uma lei que diz que um circuito submetido a um campo magnético externo variável, cria um campo contrário opondo-se a variação deste campo externo). O seu efeito é diminuir o módulo do campo no interior do material. Está presente em todos os materiais, ou seja, todo material é diamagnético, mas isto só é observado quando não existem outros tipos de comportamento magnéticos superpostos. Nos materiais diamagnéticos os átomos têm momento angular total nulo, ou seja, não possuem momento de dipolo magnético intrínseco, ele é induzido pelo campo magnético externo.

Paramagnetismo

Paramagnetismo é o fenômeno que ocorre em materiais que possuem momentos mag-néticos intrínsecos não interagentes entre si. Na ausência de campo magnético nestes materiais a magnetização é nula. A aplicação de um campo externo tenderá a alinhar os dipolos na direção do campo magnético, pois esta configuração é energeticamente favore-cida. Por isso, os materiais paramagnéticos têm susceptibilidade magnética positiva, com ordem de grandeza entre105 _e103_{(SI). A tendência ao alinhamento encontra oposição na}

agitação térmica, assim a susceptibilidade paramagnética deve depender da temperatura (T), diminuindo quando esta aumenta. Alguns materiais paramagnéticos são os metais

elementos dos actinídeos, entre outros. O paramagnetismo pode ter diferentes origens, dois aspectos são freqüentemente usados para determinar a origem do paramagnetismo: a magnitude deχe a dependência da susceptibilidade com a temperatura (χ(T)). Para o

paramagnetismo de Curie, existe uma interação que tenta alinhar os momentos magnéti-cos nos átomos com o campo magnético. A dependência com a temperatura é resultado da competição entre a tendência que alinha os momentos paralelos ao campo e a tendên-cia da agitação térmica em romper este alinhamento. A dependêntendên-cia de 1/χ com T é

linear. Quando uma pequena interação entre os momentos magnéticos de diferentes áto-mos é adicionada a interação com campo magnético aplicado, teáto-mos o paramagnetismo de Curie-Weiss. Esta interação entre os momentos (interação de troca) pode ajudar a alinhar momentos adjacentes na mesma direção ou pode ajudar a alinhar a vizinhança na direção oposta. Outra forma de paramagnetismo é o de Pauli, que é observado em metais e é devido ao fato dos elétrons de condução terem momentos magnéticos que podem ser alinhados com o campo aplicado (a banda de condução é separada em duas com aplicação do campo, uma com elétrons de spin1/2e outra com elétrons de spin ₋1/2, o momento

magnético resultante dessas bandas tem a direção do campo, caracterizando o paramag-netismo). Uma característica do paramagnetismo de Pauli é que χ é aproximadamente

independente da temperatura e em muitos casos tem valor muito pequeno.

Ferromagnetismo

Alguns elementos do grupo de transição, como o ferro, níquel e cobalto puros ou em ligas com outros elementos, apresentam uma alta magnetização espontânea abaixo da temperatura de Curie (TC). Essa alta magnetização nos materiais ferromagnéticos

mas do tratamento (térmico, magnético) a que este foi submetido, ou seja, de sua história anterior. Por isso, costumam-se dizer que os materiais ferromagnéticos possuem memória ou uma função memória χ(H).

Antiferromagnetismo

O antiferromagnetismo, assim como o ferromagnetismo, é originado pela interação entre os spins, mas esta tende a alinhar os momentos magnéticos (spin) em direções opostas, assim os momentos vizinhos se cancelam mutuamente. O comportamento da magnetização em função do campo é semelhante a de um paramagneto, mas as origens deste comportamento para um antiferromagneto são totalmente diferentes, pois este é um estado ordenado de longo alcance, enquanto o paramagnetismo é um estado desordenado. Os momentos magnéticos são alinhados em uma configuração alternada.

Um bom exemplo de antiferromagneto é o cromo.

Neste trabalho é usada a aproximação de campo médio, via princípio variacional de Bogoliubov, para estudar o diagrama de fases de um metamagneto de Ising em um campo magnético uniforme e aleatório. Este sistema tem despertado o interesse de muitos autores [2], pois ele pode ser utilizado como modelo protótipo do modelo de Ising em campo aleatório.

Nesta dissertação, os assuntos serão abordados de acordo com o seguinte esquema: No Capítulo 1, é realizada uma discussão geral sobre “Transições de Fases e Fenômenos Críticos” [3], onde é dada ênfase a sistema magnético, em especial ao modelo de Ising para o qual são apresentadas duas soluções diferentes [2, 3, 4] para a versão unidimensional. Este Capítulo é finalizado com uma solução aproximada (campo médio, versão de Bragg-Williams) do modelo de Ising em uma, duas e três dimensões, uma vez que até agora não há solução exata para o caso tridimensional e levando em conta que a solução exata para bidimensional é muito longa e complicada.

experi-mentalmente em antiferromagnetos com ligações misturadas ou com diluições de sítios. É de grande interesse investigar a existência de um ponto tricrítico. Dependendo da escolha da distribuição do campo aleatório, a aproximação de campo médio origina um ponto tricrítico (que está presente para uma distribuição simétrica bimodal, mas não ocorre no caso da forma gaussiana). Neste Capítulo foram desenvolvidas as equações de estado e energia livre via um estudo de campo médio, associado com a expansão de Landau, para estudar o diagrama de fases.

Capítulo 1

Fenômenos Críticos

1.1

Transições de Fases

A existência da vida na Terra está ligada diretamente à existência da água. O planeta, com aproximadamente dois terços de sua superfície coberta por essa substância, é um fascinante sistema termodinâmico acoplado a fontes externas de energia, interagindo permanentemente com a sua vizinhança. A temperatura de sua superfície permite que a água assuma as fases (ou estados) sólida, líquida e gasosa, gerando ciclos como o que propicia a chuva.

A mudança nas fases da água pode ser obtida variando-se apropriadamente a pressão e a temperatura. Tal transformação, denominada de mudança ou transição de fase, também pode ser observada macroscopicamente em outras substâncias. Pode-se dizer de forma geral que uma transição de fase caracteriza-se pela mudança brusca em certa propriedade físicas do sistema considerado. A propriedade observada, portanto, é o parâmetro que define a transição.

Desse modo, em outros sistemas físicos, como os sistemas magnéticos e as ligas binárias, por exemplo, ao observarmos grandezas como a magnetização, percebemos que eles exibem transições de fase. Em substâncias ferromagnéticas existe magnetização espontânea quando sua temperatura é menor que uma dada temperatura, denominada de temperatura de Curie (Tc). Acima desta temperatura crítica a substância torna-se

mag-nético externo. Na fase paramagnética os momentos de dipolo magmag-néticos atômicos da substância orientam-se aleatoriamente enquanto que, na fase ferromagnética, há uma orientação preferencial desses dipolos. Por esta razão a fase paramagnética (ferromag-nética) é também chamada de fase desordenada (ordenada) [10]. Na fase desordenada a simetria de orientação dos dipolos magnéticos atômicos é maior que aquela exibida na fase ordenada. Conseqüentemente, diz-se que na temperatura crítica de transição ocorre uma quebra espontânea de simetria no sistema.

Um estado de equilíbrio de um sistema termodinâmico é descrito por uma equação, chamada de equação de estado. Ela uma é função do tipo f = f(x1, x2, x3,· · ·xN),

de vários parâmetros xi, que podem ser intensivos e/ou extensivos. Cada estado está

associado com um valor determinado de cada um dos parâmetros. A mudança em um valor de um dos parâmetros corresponde à mudanças nos valores dos outros parâmetros, assim o sistema passa para um outro estado de equilíbrio.

Para um fluido tem-se a chamada equação de estado, que é uma relação funcional do tipoF(p, ρ, T) = 0, envolvendo a pressão (p), a densidade (ρ) e a temperatura do sistema

(T). Essa equação define no espaço gerado pelas variáveis(p, ρ, T), uma superfície, cujos

pontos representam estados de equilíbrio do sistema. Para melhor compreender essa superfície é conveniente considerar as suas projeções nos planos p₋T, p₋ρ e ρ₋T.

A Figura (1.1) exibe a projeção da superfície no plano p₋T. Note que as fases sólida

e gasosa estão em equilíbrio ao longo da curva de sublimação. De forma semelhante, as fases sólida e líquida estão em equilíbrio ao longo da curva de fusão, assim como, as fases líquida e gasosa encontram-se em equilíbrio ao longo da curva de transição líquido-vapor (curva de pressão de líquido-vapor). A última curva, acima mencionada, apresenta uma inclinação positiva, uma vez que a temperatura de transição cresce com o aumento da pressão e, sobre ela, líquido e vapor coexistem sem distinção. Observa-se que essa linha não se estende indefinidamente, terminando num ponto denominado ponto crítico, com coordenadas (pc, ρc, Tc). Essas coordenadas são, respectivamente, a pressão, a densidade

Figura 1.1: Diagrama de fases de um fluido simples, em termos da pressão contra tem-peratura. As linhas cheias indicam transições de primeira ordem e o ponto crítico cuma transição de segunda ordem. No ponto triplo (pt, Tt) há uma coexistência de três fases.

entre fase líquida e a fase gasosa.

O fato da curva de pressão de vapor terminar num ponto crítico foi descoberto no século XIX por Andrews (1869) [3]. Antes dessa época acreditava-se que determinados gases eram permanentes, ou seja, não se condensavam por maior que fosse a pressão neles aplicada. Certamente esse trabalho de compressão era realizado acima da temperatura crítica Tc, contrariando a condição de que, para obter gotículas da fase condensada, é

necessário comprimir o gás abaixo da temperatura críticaTc. Para a água temos (pc= 218

atm, Tc= 647 K) enquanto que, para o gás hélio, temos (pc = 2,25atm, Tc= 5,2 K).

É também interessante considerar as projeções da equação de estado F(p, ρ, T) nos planos p₋ρ e ρ₋T, conforme pode ser visto nas Figuras (1.2) e (1.3). Nessas figuras

observa-se que, em baixas temperaturas há uma diferença significativa entre as densidades do gás (ρG) e do líquido (ρL). Contudo, à medida que a temperatura cresce a diferença

ρL−ρG decresce anulando-se na temperatura críticaTc. O fato de existir uma quantidade

comum associado aos pontos críticos de uma ampla variedade de sistemas físicos. Tal fato permite a introdução do conceito de parâmetro de ordem do sistema. Portanto, na fase de maior simetria do sistema (fase desordenada) o parâmetro de ordem assume um valor nulo enquanto que, na fase de menor simetria do sistema (fase ordenada) esse parâmetro torna-se diferentes de zero. Para a transição líquido-vapor o parâmetro de ordem é definido como sendo a diferençaρL -ρG enquanto que, num material com

carac-terísticas ferromagnéticas, atribui-se à magnetização espontânea o papel de parâmetro de ordem do sistema.

Figura 1.2: Projeção da equação de estado no plano pversus ρ.

Um outro aspecto importante está associado à forma das isotermas que podem ainda ser vistas na Figura (1.2). No regime de altas temperaturas, T _≫ Tc, o fluido pode

ser descrito em termos de um conjunto de partículas não interagentes. Neste caso, a lei do gás ideal pode ser aplicada e as isotermas ficam bem representadas por linhas retas, definidas pela equação p = ρ kBT

m onde, kB é a constante de Boltzmann e m a massa da

molécula. Essas isotermas adquirem uma curvatura à medida que T _→Tc, exibindo, em

T =Tc, um ponto de inflexão. Tal fato pode ser visto como sendo uma manifestação da

interação entre as moléculas constituintes do fluido.

A transição líquido-vapor pode ainda ser discutida no contexto de um modelo bastante simples, o chamado gás de rede. Para isso supõe-se que o fluido esteja contido em um volume macroscópicoV e, que possa ser subdividido em células microscópicas, de volume v. Tal volume v é da mesma ordem do tamanho médio das moléculas que compõem o

fluido (aproximadamente5Å). O número de moléculas,N, na região gasosa é tal queV _≫ N v. No modelo de gás de rede o comprimento de correlação ξ, pode ser definido como

o diâmetro médio dos clusters de moléculas na rede. Um cluster é um agrupamento de

sítios, no caso, moléculas, com as mesmas características. Assim, em altas temperaturas, isto é, para T _≫ Tc, há poucas moléculas vizinhas, necessárias para formação de gotas

(clusters). Tal situação é representada no reticulado visto na Figura (1.4) em (T _≫ Tc)

no qual, ξ _≪ L, com L indicando o comprimento característico do sistema considerado.

À medida que T _→ Tc as “gotas” crescem em dimensão, ou seja, ξ cresce atingindo o

seu valor máximo ξ = L, em T = Tc, conforme está representado nos reticulados da

Figura (1.4) em(T _→Tc)e(T =Tc). Vale ressaltar que no ponto crítico o sistema ainda

não encontra-se completamente ordenado uma vez que, para T _≫ Tc, o parâmetro de

ordem ρL−ρG = 0. Evidentemente o sistema estará completamente ordenado, isto é,

perfeitamente compactado apenas em T = 0. Portanto a Figura (1.4)(T =Tc)deve ser

interpretada como uma pequena porção de um grande sistema. Deve-se ainda observar que, apesar de ρL−ρG = 0 para T ≫ Tc, existe um considerável grau de ordenamento

no sistema. Esse fato é refletido no grande tamanho dosclusters (ξ). Este tipo de ordem

que ocorre para T _≫Tc(onde ρL−ρG = 0 ) é freqüentemente chamado de ordenamento

de ordenamento de longo alcance.

Figura 1.4: Esboço do modelo de gás de rede em várias temperaturas. Cada célula indica que há uma molécula ocupando esse volume. O comprimento de correlação (ξ) indica o diâmetro de um cluster ou célula.

O espalhamento de luz é uma das técnicas mais importantes para se obter informações a respeito do ponto crítico de um fluido. A partir desta técnica, é possível acompa-nhar experimentalmente um fluido até uma região bastante próxima a seu ponto crítico. Quando a dimensão lateral das gotas for da mesma ordem do comprimento de onda (λ) da luz incidente sobre o fluido, a radiação será fortemente espalhada. Tal fenômeno é conhecido como opalescência crítica. Em temperaturas acima de Tc o fluido exibe

uma única fase. Neste caso as flutuações são desprezíveis, não ocorrendo um apreciável espalhamento da luz incidente. Na medida em queT se aproxima deTcocorre um grande

aumento nas flutuações (comξ crescendo até tornar-se da ordem deλ) o comprimento de

Por razões didáticas, a analogia entre sistemas magnéticos e fluidos é bastante útil. Aplicando-se, por exemplo, uma pressão p a um fluido, a sua densidade ρ cresce. De

forma semelhante, aplicando-se um campo magnético H a um ferromagneto observa-se

que a sua magnetização m cresce. Assim, em um certo sentido, H é análogo a pe m aρ

e a equação de estado magnético é dada por uma função do tipo g(H, m, T) = 0. Essa

equação descreve uma superfície correspondendo aos estados de equilíbrio do sistema ferromagnético uniaxial simples, cujos diagramas de fase estão mostrados nas Figuras (1.5, 1.6 e 1.7).

Figura 1.5: Diagrama de fases no plano campo aplicado contra a temperatura para um sistema ferromagnético uniaxial simples. A linha de coexistência é dada por H = 0 com

T < T c.

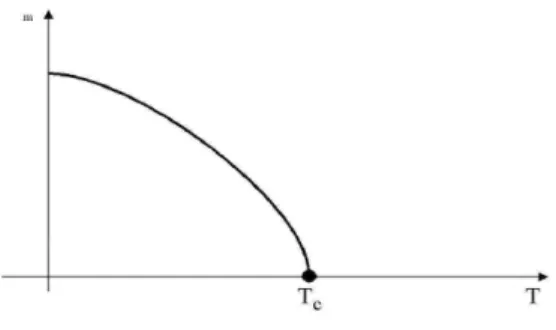
Figura 1.6: Parâmetro de ordem (magnetização espontânea) em função da temperatura para um ferromagneto uniaxial simples.

Figura 1.7: Isoterma do ferromagneto uniaxial simples (magnetização m versus campo

magnético H).

ferro-1 (“spins up”) e ferro-2 (“spins down”), correspondente à H= 0 eT < Tc. No caso

de um fluido, tal situação é análoga ao diagrama de fases no plano pversusT. Na Figura

(1.6) vê-se que a magnetização espontânea anula-se acima de Tc, tal qual ocorre com a

diferença ρL−ρG, no caso de um fluido simples. Finalmente, na Figura (1.7)

observa-se que a evolução da magnetização espontânea em função do campo externo aplicado é muito semelhante ao comportamento de ρ no plano p versus ρ em um fluido simples,

conforme pode ser visto na Figura (1.2).

As primeiras idéias sobre transição de fase remontam ao século XIX [10], sendo van der Waals um dos pioneiros a apresentar contribuições relevantes nessa área. van der Waals propôs pela primeira vez, como parte de sua tese de doutorado, uma teoria que descrevia com sucesso a continuidade dos estados líquido e gasoso da matéria. Nela estavam previstos a condensação e a existência de um ponto crítico, em sistemas fluidos. Publicada em 1873 essa teoria permanece ainda hoje como importante referência na análise do comportamento crítico de fluidos. Além disso, no início do século XX, Pierre Curie propôs uma teoria fenomenológica sobre a transição ferromagnética, posteriormente desenvolvida por Pierre Weiss. A teoria Curie-Weiss apresentava muitos aspectos em comum com a teoria de van der Waals, sendo ambas hoje conhecidas como teorias clássicas das transições de fase ou teorias de campo médio.

nas vizinhanças desse ponto. Um comportamento semelhante é também observado no caso da susceptibilidade magnética de um ferromagneto, próximo a temperatura crítica de transição. Esta divergência assintótica, observada nas vizinhanças do ponto, crítico pode ser caracterizada por meio de um expoente crítico. Esse comportamento peculiar na região crítica, de sistemas tão diferentes como um fluido e um sistema magnético, nos leva à idéia de universalidade. Esta é a palavra utilizada para caracterizar essa corres-pondência de comportamento entre os diferentes sistemas. Outras propriedades termo-dinâmicas pertinentes a fluidos e a sistemas magnéticos exibem divergências assintóticas nas vizinhanças do ponto crítico, podendo também ser caracterizadas através de uma coleção de expoentes críticos.

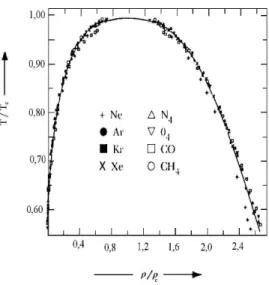
O centro da teoria dos fenômenos críticos refere-se aos expoentes críticos, que são parâmetros que caracterizam as propriedades termodinâmicas de um sistema nas proxi-midades da região crítica. Dimensão, simetria do parâmetro de ordem e a dinâmica das interações são os fatores responsáveis pelo comportamento físico do sistema. A principal idéia sobre esses expoentes, ampara-se nas evidências experimentais, uma vez que eles não dependem do material ou do sistema específico e sim, da dimensão do sistema. Alguns desses expoentes podem ser introduzidos a partir do clássico diagrama de Guggenheim [10], conforme está exibido na Figura (1.8). Este diagrama, obtido em 1945, mostra a dependência deρL-ρG com a temperatura para diferentes fluidos simples:

N e, Ar, Xe, Kr, CO, O4, N4, CH4.

A teoria de van der Waals, essencialmente uma teoria de campo médio, predizia que a linha vista na Figura (1.8) deveria ter uma forma quadrática. Entretanto, os dados referentes aos oito diferentes fluidos presentes na curva de coexistência se ajustam a uma linha cúbica. Portanto, no contexto da teoria de campo médio a razão ρ/ρc, nas

vizinhanças do ponto crítico, segue a seguinte lei de potência: ρ

ρc ∼(Tc−T)

1/2 _enquanto

que, experimentalmente é observado que: ρ

ρc ∼ (Tc−T)

1/3_{. De forma correspondente, o}

comportamento assintótico do parâmetro de ordem (magnetização espontânea) para um sistema magnético, segundo a teoria de campo médio é: M _∼(Tc−T)1/2 enquanto que,

experimentalmente é observado que: M _∼(Tc−T)1/3. Em geral o expoente crítico para o

Figura 1.8: Dados obtidos por Guggenheim em 1945 para a curva de coexistência de oito fluidos diferentes (as densidades e as temperaturas são divididas pelos valores no ponto crítico).

em=ρL−ρG(fluidos). Um aspecto interessante é que para diversos materiais o valor de

β é praticamente o mesmo por exemplo: Fe (Tc = 1044K, β = 0,34), Ni (Tc = 631,6K,

β = 0,33). Para todos os gases presentes no diagrama de Guggenheim obtém-se que

β _∼ 1₃. Valores típicos de β estão na faixa entre(0,31₋0,34).

A susceptibilidade magnética a campo nulo(h= 0), definida comoχ= (∂m

∂h)T diverge

quando T _→ Tc de acordo com a lei de potência, caracterizada pelos expoentes críticos

γ e γ′_{: χ ∼C}

+(T −Tc)−γ, para T > Tc e χ ∼ C−(Tc−T)−γ

′

, para T < Tc. Observa-se

que γ =γ′ _{porém, as constantes de proporcionalidade C}

+, C− são diferentes. Em geral os expoentes γ e γ′ _{estão entre 1,2 e 1,4, por exemplo, para (Fe, Ni, Gd) γ = γ}′ ₌ 1,33_≃ 4/3. No caso de fluidos a grandeza análoga a χ é a chamada compressibilidade

isotérmica definida por KT = 1_ρ(∂ρ_∂p)T. Nas vizinhanças do ponto crítico quando T →Tc

esta quantidade(KT)é governada pela seguinte lei de potência: KT ∼(Tc−T)−γ,T > Tc

onde, de acordo com a teoria de van der Waals, o expoente críticoγ = 1. Este valor difere

dos resultados experimentais que estimam o expoente críticoγcom valores variando entre

1,2e 1,4[10]. Para o CO2 e o Xe, γ =γ′ = 1,2.

T =Tc, caracterizada pelos expoentes críticos α e α

′

com c_∼(T ₋Tc)−α para T > Tc e

c_∼(Tc−T)−α

′

para T < Tc. Onde α =α′ ≃0. Para F e e N i, α=α′ = 0,12. No caso

de fluidos o calor específico a volume constante cV próximo de Tc comporta-se com a lei

de potência cV ∼(T −Tc)−α para T > Tc e cV ∼(Tc−T)−α

′

para T < Tc. Para o CO2

observa-se que α =α′ _{= 1/8 = 0,125 enquanto que para o Xe,α =α}′ _{= 0,08.}

A coleção de expoentes críticos obtidos para fluidos ou sistemas magnéticos via teoria de campo médio são chamados de expoentes clássicos. Estes expoentes exibem uma com-pleta universalidade, isto é, observa-se que esses expoentes críticos são aproximadamente os mesmos para diversos tipos de materiais, que vão desde fluidos até cristais ferromag-néticos. Por outro lado, dados experimentais e diversos resultados teóricos indicam a existência de classes de universalidade caracterizadas por expoentes críticos que estão em franco desacordo com o conjunto de expoentes clássicos. Atualmente é sabido que apenas alguns fatores são imprescindíveis na determinação dos expoentes críticos: (i) a dimensionalidade dos sistemas físicos, (ii) a dimensionalidade do parâmetro de ordem e o (iii) alcance das interações microscópicas no sistema de interesse físico.

1.2

Modelos para Sistemas Magnéticos

1.2.1

A Função de Partição

A Física Estatística no Equilíbrio está baseada na idéia de uma função de partição

Z, que possui todas as informações essenciais do sistema. O símbolo Z vem da palavra

alemãZustandsumme, que quer dizer “soma sobre todos os estados”. A forma geral dessa

função para um sistema clássico é

Z =X e−H/kBT

. (1.1)

O símbolo _H representa a Hamiltoniana do sistema e é a função que descreve como se comporta a energia do sistema, T é a temperatura e kB a constante de Boltzmann. A

A função de partição só é conhecida de forma exata para alguns sistemas bastante simples ou muito pequenos.

Quando conhecemos a função de partição podemos determinar a probabilidade Pi de

encontrar o sistema no estado i da seguinte forma:

Pi =

e−Hi/kBT

Z , (1.2)

onde _Hi é a Hamiltoniana do sistema quando este se encontra no estado i.

Também, a partir da função de partição, podemos determinar a energia livre

F =₋kB lnZ (1.3)

e, a partir da energia livre, podemos calcular todas as outras quantidades termodinâmicas. A Equação (1.3) é a conexão entre a Termodinâmica e a Física Estatística. A entropia na Mecânica Estatística é definida como

S =₋kB lnP , (1.4)

onde P é a probabilidade que um estado tem de ocorrer. Podemos escrever a entropia em termos da energia livre da seguinte forma:

S=₋

µ

∂F ∂T

¶

V,N

, (1.5)

onde os índicesV, N, indicam que V (o volume do sistema) e N (o número de partículas

do sistema) permanecem constantes.

Para determinar a energia interna do sistema (U) fazemos

U =₋T2

µ

∂(F/T)

∂T

¶

V,N

. (1.6)

1.2.2

Médias

O que se espera de modelos, como o de Ising [4], é a determinação de características macroscópicas como a magnetização. Em geral essas características são determinadas a partir de médias sobre propriedades microscópicas. A média de uma grandeza mi-croscópica A é calculada da seguinte forma:

hA_i=

P

i A e−H

i/kBT

de modo que a magnetização, para o modelo de Ising, pode ser escrita como

M =_hσii=

P

i σie−H

i/kBT

Z . (1.8)

A partir da magnetização podemos escrever a susceptibilidade (χ) como

χ= ∂M

∂H , (1.9)

onde H é uma campo aplicado ao sistema (como na Equação (1.11)).

O objetivo da Física Estatística é descrever as propriedades termodinâmicas de um sistema através das suas propriedades microscópicas. Para alcançar este objetivo é necessária a utilização de modelos que possam descrever da melhor forma possível um sistema real.

A seguir apresentaremos o modelo de Ising [4] e modelo de Heisenberg [11]. Estes são os modelos de maior importância no estudo de materiais magnéticos.

1.2.3

Modelo de Ising

Em 1923, Wilhelm Lenz propôs ao seu aluno de doutorado, Ernest Ising, um modelo bastante simples. Nesse modelo, um spin Si tem apenas dois estados possíveis: “para

cima” ou “para baixo”, que são representados matematicamente por +1 e ₋1, respec-tivamente. Podemos, como é convencional, organizar os spins em redes de 1, 2, 3 ou outra dimensão d qualquer. Em 1925, Ising publicou a solução exata para uma cadeia

linear (d= 1). Em 1944, Lars Onsager produziu uma solução analítica para o modelo de

Ising em uma rede quadrada (d = 2), com condições de contorno periódicas sem campo

aplicado [12]. Até hoje, nenhuma solução exata para duas dimensões com campo e para três dimensões foi publicada.

A energia associada a uma configuração de spins neste modelo é dada por

H=₋J X

i,i+1

SiSi+1 (1.10)

onde i e i+ 1 são primeiros vizinhos na rede. J indica o valor da interação entre o

spin do sítio i e o spin do sítio i + 1. Vendo os spins como momentos magnéticos

antiferromagnética. No caso do ferromagnetismo o estado fundamental (de mais baixa energia) é aquele em que os spins estão alinhados, isto é, todos para cima ou todos para baixo. No antiferromagnetismo, o estado fundamental é aquele em que os spins estão anti-paralelos, isto é, cada spin tende a se manter no sentido oposto ao dos primeiros vizinhos.

A equação acima, portanto, possui esta simetria interessante: se virarmos todos os spins, seu valor continuará o mesmo. A introdução de um campo magnético externo H

quebra esta simetria,

H=₋J X

i,i+1

SiSi+1−H

X

i

Si (1.11)

restando, entretanto, a simetria para o caso em que o sinal (sentido) do campo também seja invertido.

A agitação térmica influencia no sistema de spins de Ising de modo que à temperatura bastante baixa (kBT ≪J, sendo kB a constante de Boltzmann) este terá um valor baixo

na energia, spins alinhados e uma magnetização elevada. Já à temperaturas altas, os spins estarão apontando em direções aleatórias, o sistema terá elevada energia e não apresentará magnetização líquida a nível macroscópico. Se baixarmos a temperatura gradualmente, encontraremos um ponto crítico de temperatura onde ocorre uma transição de fase no sistema. Essa transição consiste em passar da fase desordenada (paramagnética, de altas temperaturas) para a fase ordenada (ferromagnética, de baixa temperatura). Esta temperatura crítica é comumente chamada de temperatura de Curie.

Na solução exata para d= 1, Ising mostrou que o modelo não apresenta transição de

fase a nenhuma temperatura, exceto T = 0. Deste modo, a magnetização decresce lenta

e continuamente com o aumento da temperatura. A susceptibilidade χ = ∂M_∂T é finita a qualquer temperatura T. Aqui, M é a magnetização. Não há divergência tanto no calor

específico quanto na susceptibilidade.

Todos os dados do parágrafo anterior, entretanto, são considerados incorretos do ponto de vista da Teoria da Aproximação de Campo Médio, que indica a existência de uma transição não-trivial (em T ₆= 0). Este problema colocou em dúvida a idéia

fenômenos de transição de fase. Pode-se argumentar que a transição de fase que não aparece na solução de Ising é um artifício da aproximação de campo médio. Quando Onsager, como já dissemos, resolveu o modelo de Ising em duas dimensões, deu fim ao dilema. Isto porque para d = 2, o modelo apresenta uma transição de fase de segunda

ordem, caracterizada por singularidades na função de partição com divergências no calor específico, susceptibilidade e comprimento de correlação. A temperatura de transição é dada por kBT /J = 2/ln(1 +

√

2).

Desde a última metade do século XX, o Modelo de Ising tem sido intensivamente estudado, sendo que o modelo com interações entre os primeiros vizinhos em uma rede quadrada tem um papel especial, pois o conhecimento exato da energia, magnetização espontânea e das correlações a campo zero, leva ao conhecimento exato dos expoentes críticos, que são valores que obedecem à característica de universalidade. É digno de nota que os expoentes críticos são conhecidos para apenas poucos modelos. O valor dos expoentes críticos na solução de Onsager [12], são

α= 0, β = 1/8 e γ = 7/4. (1.12)

O modelo de Ising tem sido muito utilizado por ser um modelo bastante simples e ainda assim apresenta aproximações a muitas propriedades de sistemas reais.

1.2.4

Modelo de Heisenberg

O modelo de Heisenberg [11] foi introduzido em 1928 e pode ser visto como uma generalização do modelo de Ising. A Hamiltoniana do modelo de Heisenberg é

H =₋J X

i,j

~σi·~σj . (1.13)

~σi é um vetor unitário que, diferentemente de Si do modelo de Ising, não está limitado

a uma direção e dois sentidos, mas pode assumir qualquer direção e sentido nas três dimensões.

A esta Hamiltoniana também pode ser acrescentado um campo H,

H=₋J X

i,j

~σi·~σj −H

X

i

que, neste caso, atua na direção do eixo z.

Este modelo, como apresentado acima, é uma aproximação extremamente realista ao caso quântico para temperaturas próximas a Tc [13, 14, 15]. Já para domínios de

baixas temperaturas ele não é uma boa aproximação (também em se tratando do caso quântico) [3].

1.3

Resolução do Modelo de Ising

1.3.1

Resolução Exata em Uma Dimensão

Provavelmente a solução mais simples para sistemas de interação de muitos corpos é modelo de Ising para uma dimensão (ou cadeia linear) na ausência de um campo externo [3]. Este sistema corresponde a um caso particular do modelo clássico de Heisen-berg, que é utilizado para o caso de três dimensões.

Consideremos uma cadeia ou rede linear com N sítios, Figura (1.9), para a qual

✉ ✉ ✉ ✉ ✉ ✉ ✉

✻ ✻ ✻ ✻ ✻ ✻ ✻ _✲

✲ ✛

J

S

S

S

. . .

S

Figura 1.9: Rede linear com N sítios com energia de interação Ji e spin S. O índice i

indica que a energia pode ter várias magnitudes.

poderemos obter a função de correlação diretamente da função de partição, sendo útil considerar que a energia de interação (J) entre os primeiros vizinhos pode assumir

magnitudes arbitrárias. Deste modo, a Hamiltoniana que descreve o modelo de Ising é:

H=₋

N−1

X

onde os spins Si são vetores unitários unidimensionais e que podem assumir apenas os

valores discretos+1e₋1. Ji é a energia de interação entre os spins localizados nos sítios

i e i+ 1. Note que apesar da somatória ser feita de i= 1 até N ₋1, temos N sítios na

rede, pois quando i=N ₋1 teremosSi+1 =SN.

O objetivo de nossos cálculos é obter, de forma fechada, a função de partição

ZN ≡ZN(J1, J2, J3, . . . , JN−1) = 1

X

S1=−1

1

X

S2=−1

. . .

1

X

SN=−1

exp

Ã_N−1 X

i=1

JiSiSi+1

!

(1.16)

onde _Ji ≡ βJi ≡ _kJBiT é um termo de energia de troca e não possui dimensão. kB é a

constante de Boltzmann eT a temperatura absoluta. As N somatórias se estendem sobre

as 2N _{configurações de estado possíveis para o sistema.}

O método de solução é calcular o efeito da adição de um spin a mais no fim da cadeia. Isto é, pretendemos expressar a função de partição para a rede extensa,ZN+1, em termos

da função de partição para a rede original ZN. Tendo feito isso, teremos uma relação de

recorrência com a qual poderemos encontrar a solução. Da Equação (1.16) fazemos:

ZN+1 = 1

X

S1=−1

1

X

S2=−1

. . .

1

X

SN=−1

exp

Ã_N−1 X

i=1

JiSiSi+1

! ₁

X

SN+1=−1

exp(_JNSNSN+1)

(1.17)

Observe que agora a última somatória da equação acima, (1.17), é:

1

X

SN+1=−1

exp(_JNSNSN+1) =eJNSN +e−JNSN = 2cosh(JNSN) (1.18)

A função cosseno hiperbólico é positiva para qualquer valor real, o que nos leva a perceber que o segundo termo da equação (1.18) não depende de SN já que os valores

possíveis para SN são +1 e −1, ou seja,cosh(+JN) = cosh(−JN). Então

ZN+1 =ZN2 cosh(JN) (1.19)

e como ocorre o mesmo com as outras somatórias e exponenciais para todos os2N _estados

possíveis, resulta que

Agora é fácil ver que Z1 = 2, sendo Z1 é exatamente a função de partição para um

sistema simples de apenas um spin, de modo que a “soma sobre os estados” é simplesmente o “número de estados”. Substituindo ZN+1 e Z1 na equação anterior (Equação 1.20)

teremos

ZN2 cosh(JN) = 2.2N(coshJ1coshJ2coshJ3. . .coshJN) (1.21)

Eliminando os termos repetidos teremos, de forma clara:

ZN = 2N(coshJ1coshJ2. . . coshJ(N−1)) (1.22)

que pode ser reescrita assim:

ZN = 2N

(N−1)

Y

i=1

(cosh_Ji). (1.23)

No caso uniforme, ou seja quando quaisquer dois spins tiverem sua energia de interação constante e igual a J, (Ji =J), teremos:

ZN = 2Ncosh(N−1)J (1.24)

ou, de forma ainda mais explícita

ZN = 2Ncosh(N−1)

J kBT

. (1.25)

Voltemos agora para expressão mais geral da função de partição,

ZN = 2N

(N−1)

Y

i=1

(cosh_Ji), (1.26)

cuja forma nos sugere uma relação com a ordem da temperatura TC. Por esta razão

vamos calcular a função de correlação entre dois spins

Γk(r)≡ hSkSk+ri=ZN−1

X

{S}

SkSk+r exp

Ã_N−1 X

i=1

JiSiSi+1

!

(1.27)

onde a somatória P

{S}SkSk+r é feita sobre todos os 2N estados, S representa os spins

cujo valor é dado em unidades de uma rede constante. A função de correlação para o primeiro vizinho é simplesmente Γk(1), o que satisfaz a relação

ZNΓk(1) =

X

{S}

SkSk+1 exp

Ã_N−1 X

i=1

JiSiSi+1

!

= ∂

∂_Jk

X

{S} exp

Ã_N−1 X

i=1

JiSiSi+1

!

(1.28)

Claramente o argumento que nos levou a equação acima pode ser generalizado para um

r arbitrário, resultando em

ZNΓk(r) =

∂ ∂_Jk

∂ ∂_Jk+1

. . . ∂ ∂_Jk+r−1

ZN (1.29)

com isso, podemos obter, a partir da diferenciação da equação geral para ZN, o seguinte

resultado:

Γk(1) =tangh(Jk) (1.30)

e

Γk(r) = (tanghJk)(tanghJk+1). . .(tanghJk+r−1) =

r

Y

i=1

tangh_Jk+i−1 (1.31)

que é simplesmente o produto das funções de correlação entre os primeiros vizinhos. Para um caso uniforme, esta equação se reduz a

Γk(r) = hSkSk+ri=tanghrJ (1.32)

ou, mais explicitamente,

Γk(r) = hSkSk+ri=tanghr

µ

J kBT

¶

(1.33)

que se mostra independente do sítio k.

1.3.2

Solução Exata em Uma Dimensão na Presença de um

Campo

Para este caso o modelo de Ising pode ser escrito como

H=₋J

N

X

i=1

SiSi+1−H

N

X

i=1

ondeSi eSj são as variáveis de spin, J é a energia devido a uma interação entre os sítios

representados pelas variáveis de spin, H é um campo externo aplicado ao sistema.

Como já vimos em (1.2.3), as variáveis de spin podem ter interpretações diversas de acordo com a situação do problema. A solução para o modelo de Ising é possível através de uma função de partição canônica

Z =X

{Si}

exp(₋β_H) (1.35)

ondeP

{Si} é uma somatória de todas as variáveis de spin sobre a expressão exponencial,

que resulta na agregação de todos os estados (soma dos estados do sistema).

Isso nos permite obter, no limite termodinâmico, a energia livre de Gibbs do sistema:

g = g(T, H) = lim

N→∞ 1

βN lnZN (1.36)

Vamos começar escrevendo então a função de partição

ZN =

X

{Si}

exp " βJ N X i=1

SiSi+1+βH

N X i=1 Si # (1.37)

usando a notação K =βJ e L=βH e escrevendo o segundo termo de uma forma mais

simétrica, teremos:

ZN =

X

{Si}

exp " K N X i=1

SiSi+1+

L

2

N

X

i=1

Si+Si+1

#

(1.38)

Por mera conveniência, vamos adotar condições periódicas de contorno SN+1 = S1. Se

ex+y _{= e}x_ey_{, podemos escrever a parte exponencial da função acima como um produto}

de exponenciais:

e[KPNi=1SiSi+1]_e[

L

2

PN

i=1Si+Si+1] (1.39)

ou, de forma ainda mais explícita:

eKS1S2_eKS2S3_...eKSNSN+1_e

L

2(S1+S2)e

L

2(S2+S3)...e

L

2(SN+SN+1) (1.40)

Obtemos assim uma produtória, que vamos representar por

N

Y

T(Si, Si+1) = exp

"

K

N

X

SiSi+1+

L

2

N

X

Si+Si+1

#

de modo que a Equação 1.38 possa ser escrita de forma simplificada:

ZN =

X

{Si}

N

Y

i=1

T (SiSi+1). (1.42)

Observe agora que cada fator da produtória

T (SiSi+1) =exp

"

K

N

X

i=1

SiSi+1+

L

2

N

X

i=1

Si +Si+1

#

pode assumir quatro valores, pois Si±1 eSi+1±1, independentemente do valor de i.

eK(1·1)+L2·(1+1) =eK+L

eK(1·−1)+L2·(1−1) =e−K

eK(−1·1)+L2·(−1+1)=e−K

eK(−1·−1)+L2·(−1−1) =eK−L

Se colocarmos estes valores em forma de matriz,

T=





T(+,+) T(+,₋)

T(₋,+) T(₋,₋)



= 



eK+L _e−K

e−K _eK−L



 (1.43)

onde Té a matriz transferência, podemos notar que a produtória da Equação 1.42 pode

ser representada como um produto de N matrizes 2 x 2 idênticas. Por conseguinte, se

diagonalizarmos esta matriz, a Equação 1.42 como um todo, pode ser interpretada como o traço (T r), ou seja, a soma dos elementos da diagonal principal, do produto de N

matrizes (de transferência) idênticas,

ZN =T r(T)N. (1.44)

Aplicando a equação secular (T ₋λI = 0), onde I é uma matriz identidade, podemos

encontrar as raízes a partir de uma matriz diagonalizada D:

ZN =T r(D)N = λN1 +λN2 (1.45)

onde as raízes λ1 eλ2 são

λ1,2 =

1 2

¡

eK+L_+eK−L¢

± 1

2

p

ou

λ1,2 =eKcosh(L)±

p

e2K_cosh2_{L−2senh(2K) (1.47)}

É fácil perceber que esses autovalores são sempre positivos e queλ1>λ2, exceto no ponto

trivial T =H= 0. A campo nulo essas expressões ficam mais simples,

λ1 = 2 cosh K ≥λ2 = 2senh K , (1.48)

com a degenerescência (λ1 =λ2) no limite K →0(ou seja, T →0).

Para obter a energia livre no limite termodinâmico, é conveniente escrever

ZN =λN1

"

1 +

µ

λ1

λ2

¶N#

(1.49)

Como λ2 < λ1, temos o limite

g(T, H) = lim

N→∞

·

−_βN1 lnZN

¸

(1.50) fazendo com que na Equação 1.49 tenhamos

µ

λ1

λ2

¶N

→0 (1.51)

e daí:

g(T, H) =₋1

βlnλ1 (1.52)

ou seja,

g(T, H) = ₋1

βln

n

eβJcosh(βH) +pe2βJ_cosh2_{(βH)−2senh(2βJ)}o _(1.53)

que é uma função analítica, de onde vêm todas as propriedades termodinâmicas do sis-tema.

A magnetização por spin, por exemplo, é dada por

m=₋

µ

∂g ∂H

¶

T

(1.54) onde:

m = _p senh(βH)

senh2_{(βH) +exp(−4βJ)} (1.55)

que se anula para H= 0, servindo apenas para a explicação do paramagnetismo e não o

1.3.3

Aproximação de Campo Médio para o Modelo de Ising

Sendo, para um modelo de spin 1/2 (S =_±1),N+ o número de spins para cima eN− o número de spins para baixo, temos

N =N+ + N− (1.56)

e

N m =N+ − N− (1.57)

onde m é a magnetização adimensional. Conhecendo N+ e N−, podemos calcular a

entropia total

S =kBlnΩ, (1.58)

sendo que Ωé o número de estados, o que pode ser rescrito com sendo

S =kBln

N!

N+!N−!

(1.59)

ou ainda

S =kBln

N!

¡_{N+N m}

2

¢

!¡_{N−N m}

2

¢

! (1.60)

Levando em conta a simetria translacional do problema, a energia interna numa rede hipercúbica d-dimensional será dada por

U =_hHi=₋J d N_hSiSji −H N m. (1.61)

Portanto, a energia livre magnética por spin, com o vínculo interno representado pela magnetização fixa, é dada pela expressão

g_hT, H;m_i = 1

N(U −T S) (1.62)

= ₋Jd_hSiSji −Hm−

kBT

N ln

N!

¡_{N+N m}

2

¢

!¡_{N−N m}

2

¢

Até esse ponto não há nenhuma aproximação. O problema reside na dificuldade para calcular as correlações de dois pontos em termos de T,H e m.

A aproximação de Bragg-Williams consiste em desprezar as flutuações nas funções de correlação, fazendo a aproximação

hSiSji ≈ hSiihSji=m2. (1.63)

Escrevendo uma expansão de Stirling para os fatoriais e utilizando essa aproximação para as correlações, obtemos no limite termodinâmico a energia livre de Bragg-Williams por spin,

g_BW(T, H;m) = ₋ Jdm2 ₋Hm₋ 1

βln2 (1.64)

+ 1

2β [(1 +m)ln(1 +m) + (1−m)ln(1−m)]

Para remover o vínculo interno a fim de obter a energia livre termodinâmica, basta minimizar g_BW em relação a m. Assim, temos

∂g_BW

∂m =−2Jdm−H+

1 2β ln

1 +m

1₋m = 0 (1.65)

de onde vem a equação de Curie-Weiss,

m=tanh(β2Jdm+βH), (1.66)

onde o parâmetro fenomenológicoλé identificado como o produto 2dJ, prevendo-se uma

transição mesmo no caso unidimensional. Embora esse resultado esteja completamente errado, esperam-se melhores previsões à medida que a dimensionalidade do sistema au-mente.

A energia livre de Bragg-Williams, dada pela Equação (1.65) também pode ser escrita na forma

g_BW(T, H;m) =₋Jdm2₋Hm₋ 1

β ln2 +

1

β

Z ¡

tanh−1m¢

dm (1.67)

que permite uma identificação imediata com a função g_BW(T, H;m), obtida a partir da

Capítulo 2

Metamagneto em Campo Uniforme e

Aleatório

2.1

Introdução

Em 1932, L. Néel, propôs a primeira teoria do antiferromagnetismo [16] para explicar as anomalias nas medidas da susceptibilidade em M n e Cr. Estas medidas implicavam

em uma temperatura de Curie negativa para a susceptibilidade χ _∼ 1

T−Tc no modelo

de Curie-Weiss para explicar este comportamento anômalo, Néel foi obrigado a con-siderar que cada um dos momentos magnéticos se localizavam em pontos de uma rede composta por duas sub-redes equivalentes, onde cada uma delas experimentavam cam-pos internos proporcionais, porém ocam-postos. Assim, na então teoria do campo molecular Weiss-Néel, a temperatura negativa de Curie indicava um alinhamento antiparalelo dos momentos magnéticos dessas substâncias. Esta teoria (Weiss-Néel) previa uma transição, da fase paramagnética para uma fase antiferromagnética, em uma temperatura crítica (₋Tc=TN), posteriormente chamada de temperatura de Néel. Quase duas décadas mais

tarde, em 1949, foi verificado experimentalmente, através da difração de nêutrons [17], que o alinhamento dos momentos magnéticos que ocorre nesses materiais realmente é o antiparalelo. A transição paramagnética-antiferromagnética é de segunda ordem.

função decrescente do campo magnético, assim o ponto de Néel torna-se uma linha de Néel no plano T ₋H.

Na maioria dos materiais antiferromagnéticos, o efeito de um campo magnético ex-terno suficientemente forte é o de levar a uma nova transição de fase, isto é, a fase antiferromagnética (momentos magnéticos antiparalelos entre si, porém perpendiculares ao campo externo) torna-se spin-flop (momentos magnéticos alinhados antiparalelamente entre si, porém perpendiculares ao campo externo) [6, 19, 20, 21, 22, 23]. Mais tarde, uma grande quantidade de trabalhos chegaram a um completo diagrama de fase para os materiais antiferromagnéticos. Uma completa visão histórica do antiferromagnetismo pode ser visto nos trabalhos de Nagamiya et al [24] e de Jacobs et al [25].

Por outro lado, existem duas classes de materiais (sólidos) antiferromagnetos anisotrópi-cos. A primeira, tais comoF eCl2 (cloreto ferroso), F eBr2 (brometo ferroso),N i(N O3)2·

2H2O (nitrato de níquel di-hidratado), DAG(Dysprosium Aluminium Garnet), possuem

uma estrutura de camadas alternadas com uma fraca interação antiferromagnética entre as camadas e uma forte interação ferromagnética intra-camada.

A segunda é composta de substâncias ferromagnéticas ou antiferromagnéticas que apresentam um comportamento não ortodoxo. Estas duas classes de materiais são os hoje conhecidos como “metamagnetos”. A origem da nomenclatura “metamagneto” foi inicialmente utilizada por Kramers [26] para caracterizar alguns sólidos que apresentavam um comportamento não ortodoxo, isto é, sólidos que ora apresentavam comportamento de um ferromagneto, ora de antiferromagneto. Alguns autores [2, 26] utilizam o termo “metamagneto” para especificar sistemas magnéticos do tipo Ising com interação antifer-romagnética entre os spins primeiros vizinhos e interação ferantifer-romagnética entre os spins segundos vizinhos, formando um sólido com duas sub-redes entrelaçadas.

Os primeiros estudos teóricos dos metamagnetos tiveram seu início com as teorias fenomenológicas de Landau nos anos de 1930. Sauer [27] e Garret [28] consideraram a teoria de campo médio para o modelo de Ising com uma escolha conveniente dos sinais e dos valores das interações de primeiros e de segundos vizinhos.

antiferromagnético entre os spins das camadas adjacentes. Um outro modo de pensar um cristal metamagnético é considerar um cristal cúbico com os acoplamentos entre os primeiros vizinhos como sendo de caráter antiferromagnético e os acoplamentos entre os segundos vizinhos como sendo ferromagnéticos.

Em um campo externo nulo, um metamagneto comporta-se como um antiferromag-neto de Ising. A correspondente transição de fase antiferromagnética é de segunda ordem para um campo magnético suficientemente baixo. No entanto, para campos suficiente-mente grandes, a ordem desta transição muda de segunda para primeira ordem em um ponto tricrítico, cujas propriedades tem sido largamente estudadas nos últimos anos [26]. Neste Capítulo estamos interessados em estudar o comportamento tricrítico de um metamagneto em um campo magnético externo uniforme e em um campo aleatório. Os problemas envolvendo o modelo de Ising em um campo aleatório tem sido uma fonte de pesquisa nesses últimos vinte anos [5, 6, 7, 8, 9]. Sistemas deste tipo têm sido realizados experimentalmente em antiferromagnetos com ligações misturadas ou com diluições de sítios. É de grande interesse investigar a existência de um ponto tricrítico e a exata relação para o antiferromagneto diluído em um campo uniforme. Dependendo da escolha da distribuição do campo aleatório, a aproximação de campo médio origina um ponto tricrítico (que está presente para uma distribuição simétrica bimodal, mas não ocorre no caso da forma gaussiana). Com base no teorema central do limite, alguns argumentos podem ser usados para dar suporte à relevância física da distribuição Gaussiana (o ponto tricrítico produzido com a função bimodal, existe apenas como um mero artifício da aproximação de campo médio).

A prova da equivalência entre o ferromagneto de Ising em um campo aleatório e um antiferromagneto diluído em um campo uniforme é baseada nos argumentos do grupo de renormalização que pode ser aplicado a campos fracos. Na aproximação de campo médio (ou o equivalente e com solução exata do modelo com interações de alcance infinito), isto é possível estabelecendo um mapeamento completo entre os parâmetros do ferromagneto de Ising em um campo aleatório e o antiferromagneto ou metamagneto de Ising diluídos, em um campo uniforme.

dis-tribuição simétrica da função bimodal para a diluição arbitrária, incluindo o caso puro, onde não há diluição. Simulações numéricas e experimentos indicam que a transição de primeira ordem é destruída quando a diluição é acrescentada, de modo que nenhum efeito é previsto pelo cálculo de campo médio.

2.2

Definição do Modelo

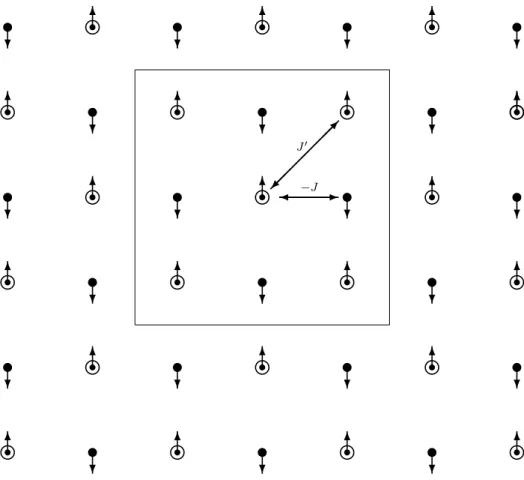
Consideremos uma rede regular de n sítios, como na Figura 2.1, com spins de Ising Si =±1 em cada sítio, isto pode ser dividido em duas sub-redes equivalentes

interpene-trantes,A eB [26]. Os z spins , primeiros vizinhos (nn), onde z é o número de primeiros

vizinhos, de um dado spin, estão localizados na outra sub-rede, enquanto os z′ _spins, segundos vizinhos (nnn), estão todos na mesma sub-rede. A Hamiltoniana do sistema é

dado por:

H=JX

nn

SiSj−J′

X

nnn

SiSj −

X

i

(H+Ha)Si (2.1)

ondeJ é a constante de acoplamento entre os spins primeiros vizinhos (nn), a somatória

P

nn é sobre todos os pares de spins nn, J′ é a constante de acoplamento entre os spins

segundos vizinhos (nnn), a somatória P

nnn é sobre todos os pares de spins nnn, H é

a intensidade do campo magnético uniforme externo, e Ha é a intensidade do campo

aleatório local. Assumimos, neste trabalho, que as interações entre os primeiros vizinhos

nn são antiferromagnéticas (J > 0), as interações entre os segundos vizinhos nnn são

ferromagnéticas (J′ _{≥0) e que os campos aleatórios locaisH}

a não estão correlacionados.

Ainda que seja possível considerar sub-rede dependente da distribuição de probabilidade, neste trabalho usamos a mesma probabilidade para cada sítio.

2.3

Equações do Campo Médio

s ✉ s ✉ s ✉ s

✉ s ✉ s ✉ s ✉

s ✉ s ✉ s ✉ s

✉ s ✉ s ✉ s ✉

s ✉ s ✉ s ✉ s

✉ s ✉ s ✉ s ✉

✻ ✻ ✻ ✻

✻ ✻ ✻

✻ ✻ ✻ ✻

✻ ✻¡_{✛ ✲}

¡¡ ¡¡✒ ¡ ¡ ¡ ¡ ¡ ✠ −J

J′

✻

✻ ✻ ✻ ✻

✻ ✻ ✻

✻

❄ ❄ ❄

❄ ❄ ❄ ❄

❄ ❄ ❄

❄ ❄ ❄ ❄

❄ ❄ ❄

❄ ❄ ❄ ❄

❤ ❤ ❤ ❤

❤ ❤ ❤

❤ ❤ ❤ ❤

❤ ❤ ❤

❤ ❤ ❤ ❤

❤ ❤ ❤

❤

Figura 2.1: Rede bidimensional regular com spins Si = ±1. Observe que a rede pode

ser dividida em duas sub-redes interpenetrantes equivalentes, onde os primeiros vizinhos estão na outra sub-rede e os segundos vizinhos estão na mesma sub-rede. A energia de interação entre os primeiros vizinhos é ₋J e a interação entre os segundos vizinhos é J′_.

1D, 2D, etc.). Podemos, entretanto, obter uma solução aproximada usando os princípios variacionais, sendo um deles baseado na desigualdade de Bogoliubov [3].

Considerando que a partir da Hamiltoniana _H não conseguimos escrever a função de partição Z, essa desigualdade parte da definição de uma Hamiltoniana tentativa _Ht, da

qual se conhece a solução exata. Escrevemos então a diferença

V =_{H − H}t (2.2)

e a função de partição da Hamiltoniana tentativa,

Zt=

X

{S}

e−βHt

Uma média térmica, escrita em função da Hamiltoniana tentativa, será

hA_it =

P

{S}A e−βH

t

Zt

. (2.4)

Vamos escrever uma função de partição em relação a V:

ZV =

X

{S}

e−βV (2.5)

Podemos notar que

Zt

­

e−βV®

=X

{S}

e−βV_e−βHt (2.6)

ou seja,

Z =Zt

­

e−βV®

. (2.7)

Usando a relação matemática

ex _≥1 +x+ x

2

2! +· · · (2.8) e sabendo que

hx2_i>_hx_i2, (2.9)

podemos escrever:

­

e−βV®

=

¿

1₋βV + β

2_V2

2! +· · ·

À

(2.10)

­

e−βV®

= 1₋β_hV_i+ β

2_hV2_i

2! +· · · (2.11)

e−βhVi = 1₋β_hV_i+β

2_hVi2

2! +· · · (2.12) de onde tiramos a inequação

­

e−βV®

≥e−βhVi. (2.13)

Multiplicando por Zt e usando as relações (2.7) e (2.2), teremos:

Z _≥Zt e−βhH−Hti, (2.14)

da qual, tomando o logaritmo natural de ambos os termos, escrevemos a energia livre:

onde F é a energia livre de Helmholtz, _H é a Hamiltoniana que se quer estudar e _Ht é a

Hamiltoniana tentativa, da qual conhecemos a solução exata, _h. . ._iav representa a média

da distribuição do campo aleatório e _h. . ._it é a média térmica com respeito à Ht.

Neste trabalho usaremos a Hamiltoniana tentativa não interagente,

Ht=−

X

i

(H+Ha)Si−ηA

X

i∈A

Si−ηB

X

i∈B

Si (2.16)

onde ηA e ηB são os parâmetros variacionais sendo que a Hamiltoniana pode ser escrita

para a sub-rede A como:

HtA=−

X

i

(H+Ha)Si−ηA

X

i∈A

Si (2.17)

e para a sub-rede B:

HtB =−

X

i

(H+Ha)Si−ηB

X

i∈B

Si (2.18)

Vamos escrever a energia livre em relação à Hamiltoniana tentativa para cada uma das sub-redes

hFtiav =hFtAiav+hFtBiav (2.19)

A função de partição canônica (Zustandsumme), isto é, a soma do fator de Boltzmann sobre todos os estados, é dada por

Z =T r e−βHt (2.20)

onde β _{≡ KB}1_T, sendo KB a constante de Boltzmann, T a temperatura absoluta eT r é o

traço realizado sobre _Ht e que pode ser escrita para as redes A e B como

ZA=T r e−βHtA ; ZB =T r e−βHtB (2.21)

substituindo o valor de Ht para Si =±1,

Z′A =eβ(H+Ha+ηA)+e−β(H+Ha+ηA) (2.22)

Onde Z′ _{é a função de partição para os estados de apenas um spin (+1 ou −1). Usando} a definição:

ex_+e−x

2 ≡coshx (2.24)

teremos

Z′A= 2coshβ(H+Ha+ηA) ; Z′B = 2coshβ(H+Ha+ηB) (2.25)

onde Z′

A é a função de partição para um spin da sub-redeA, Z′B é a função de partição

para um spin da sub-rede B e cada spin possui apenas dois estados possíveis (S = +1 e

S =₋1).

Somos levados, portanto, a fazer

ZA= (Z′A)

N

2 ; Z

B = (Z′B)

N

2 (2.26)

onde N representa todos os spins da rede (sub-rede A + sub-rede B). Pela conexão com

a termodinâmica, temos que a energia livre para cada sub-rede é:

FtA =−KBT ln ZA ; FtB =−KBT ln ZB (2.27)

SubstituindoZA eZB como na Equação (2.26).

FtA =−

KBT N

2 ln 2coshβ(H+Ha+ηA) (2.28)

FtB =−

KBT N

2 ln 2coshβ(H+Ha+ηB) (2.29)

obtemos então a solução para a Equação (2.15)

hFti=−

N

2βhln 2coshβ(H+Ha+ηA)i − N

2βhln 2coshβ(H+Ha+ηB)i (2.30)

Para calcular hhH − Htitiav, vamos escrever

hhH − Htitiav = J

X

nn

hSiSji −J′

X

nnn

hSiSji −

X

i

(H+Ha)hSii

+ X(H+Ha)hSii+ηA

X

hSii+ηB

X