Propriedades termodinˆ
amicas do oscilador
de Dirac e algumas contribui¸
c˜
oes da fun¸c˜
ao
theta de Jacobi
Propriedades termodinˆ
amicas do oscilador
de Dirac e algumas contribui¸
c˜
oes da fun¸c˜
ao
theta de Jacobi
Tese submetida `a Coordena¸c˜ao do Curso de P´os-Gradua¸c˜ao em F´ısica, da Universidade Federal do Cear´a, como requisito parcial para a obten¸c˜ao do grau de Doutor em F´ısica
Orientador:
Ricardo Renan Landim de Carvalho
universidade federal do ceara - Departamento de F´ısica
Fortaleza
Propriedades termodinˆ
amicas do oscilador
de Dirac e algumas contribui¸
c˜
oes da fun¸c˜
ao
theta de Jacobi
Tese submetida `a Coordena¸c˜ao do Curso de P´os-Gradua¸c˜ao em F´ısica, da Universidade Federal do Cear´a, como requisito parcial para a obten¸c˜ao do grau de Doutor em F´ısica
Aprovada em 12 de julho de 2007
BANCA EXAMINADORA
Prof. Dr. Ricardo Renan Landim de Carvalho (Orientador)
Universidade Federal do Cear´a - UFC
Prof. Dr. Antonio Soares de Castro Universidade Estadual Paulista -
UNESP-Guaratinguet´a
Prof. Dr. Carlos Alberto Santos de Almeida Universidade Federal do Cear´a - UFC
Prof. Dr. Kleiton do Carmo Mendes Universidade Estadual do Cear´a - UECE
Prof. Dr. M´arcio Andr´e de Melo Gomes Centro Federal de Educa¸c˜ao Tecnol´ogica do Cear´a
Primeiramente, agrade¸co a minha esposa, Maria Eniana A. Gomes Pacheco e ao meu filho Enio Henrique Gomes Pachecoˆ , cujas presen¸cas neste trabalho s˜ao t˜ao sublimes e imprescind´ıveis que somente eu posso compreender. N˜ao existe manifesta¸c˜ao ling¨u´ıstica capaz de se quer representar esta influˆencia, contida em cada id´eia deste tra-balho, redigida ou n˜ao.
Iguais sentimentos valem para os meus pais, Maria de Lourdes Gomes Pacheco
e Francisco Jo˜ao Pacheco, aos quais serei eternamente grato, sobretudo pela opor-tunidade de viver e por todo o sacrif´ıcio a que se dispuseram para que eu chegasse at´e aqui.
Agrade¸co `a minha querida irm˜a,Mara Renata Gomes Pacheco, e aos meus irm˜aos
Jo˜ao Alfredo Gomes Pacheco eLuis Gustavo Gomes Pacheco.
Ao professor Ricardo Renan Landim de Carvalho, pela paciˆencia, dedica¸c˜ao e amizade dispensadas ao longo deste trabalho.
Ao professor Jos´e Soares de Andrade J´unior, coordenador do curso de p´os-gradua¸c˜ao em F´ısica e ao professor Josu´e Mendes Filho, vice-coordenador do curso de p´os-gradua¸c˜ao em F´ısica.
Agrade¸co a todos os professores do departamento de F´ısica-UFC, em especial aoJos´e de Arimat´eia, aoJos´e Ramos, aoCleuton Freire, aoMurilo PereiraeJos´e Evan-gelista.
Ao Abra˜ao Cefas, pela amizade e pelas inumer´aveis situa¸c˜oes em que se prontificou a me ajudar.
Aos amigos do GTQC-UFC-Lassco: Francisco Wagner, Wilami Cruz, Carlos Alex, Roberto Maluf, Ivan Jardim, Geov´a Maciel, Hiroshi, Hudson, Victor Hugo eAristeu Rosendo.
Agrade¸co aos amigos(as) professores(as) da UECE: Luciana Ang´elica S. Nunes,
Makarius O. Tahim, Kleiton do Carmo, Luis Gonzaga R. Filho e `aquele que sempre vestir´a a camisa ueceana, professorC´elio Rodrigues Muniz.
Aos amigos professores da UFBA: Paulo Baqueiro, Luis Gustavo, Ronaldo Pe-sente, Evanildo Cardoso e Angelo Manieroˆ
Ao amigo Jo˜ao Cosme Reinaldo in memoriam . Ao CNPq, pelo suporte financeiro.
INTRODUC¸ ˜AO p. 10
1 ALGUMAS DEFINIC¸ ˜OES DO OSCILADOR DE DIRAC p. 13
1.1 Introdu¸c˜ao . . . p. 13
1.2 Auto-solu¸c˜oes do oscilador de Dirac . . . p. 14
1.3 O termo de intera¸c˜ao do oscilador de Dirac . . . p. 17
2 PROPRIEDADES TERMODIN ˆAMICAS DO OSCILADOR DE DIRAC
UNIDIMENSIONAL p. 19
2.1 Introdu¸c˜ao . . . p. 19
2.2 A fun¸c˜ao de parti¸c˜ao do oscilador de Dirac . . . p. 19
2.3 Estudo da fun¸c˜ao de parti¸c˜ao do oscilador de Dirac para altas temperaturas p. 20
2.4 Obtendo da fun¸c˜ao de parti¸c˜ao pelo uso da f´ormula de integra¸c˜ao de
Euler-Maclaurin . . . p. 24
2.5 An´alise n´umerica das quantidades termodinˆamicas do oscilador hamˆonico
e do oscilador de Dirac unidimensional . . . p. 25
2.6 Oscilador de Dirac unidimensional na presen¸ca do termo de comprimento
m´ınimo . . . p. 29
3 PROPRIEDADES TERMODIN ˆAMICAS DO OSCILADOR DE DIRAC
TRIDIMENSIONAL p. 31
3.1 Introdu¸c˜ao . . . p. 31
3.2 A fun¸c˜ao de parti¸c˜ao e o calor espec´ıfico do oscilador de Dirac 3D . . . p. 31
4.1 Introdu¸c˜ao . . . p. 42
4.2 Propriedades termodinˆamicas do po¸co infinito . . . p. 44
4.3 Propriedades termodinˆamicas de um po¸co de potencial infinito usando a
fun¸c˜ao theta de Jacobi . . . p. 46
4.3.1 A fun¸c˜ao theta de Jacobi . . . p. 46
4.4 Fun¸c˜ao theta de Jacobi e o po¸co de potencial . . . p. 47
CONCLUS ˜AO p. 50
Apˆendice . . . p. 50
Apˆendice A -- A equa¸c˜ao de Dirac p. 51
A.1 A equa¸c˜ao . . . p. 51
A.2 Solu¸c˜ao da equa¸c˜ao de Dirac para part´ıcula livre . . . p. 53
Apˆendice B -- Teste de convergˆencia de s´eries infinitas p. 58
B.1 O teste da raz˜ao . . . p. 58
B.2 O teste da integral . . . p. 58
B.3 O teste da compara¸c˜ao . . . p. 59
B.4 A s´erieP∞
n=0e−
√
an+bβ . . . . p. 59
Apˆendice C -- Rela¸c˜oes e constantes f´ısicas ´uteis p. 61
C.1 Quantidades termodinˆamicas . . . p. 61
C.2 Constantes f´ısicas . . . p. 61
C.3 Rela¸c˜oes da m´etrica e derivadas . . . p. 61
C.4 Matrizes de Dirac . . . p. 62
C.5 Matrizes de Pauli . . . p. 62
INTRODUC
¸ ˜
AO
O nome oscilador de Dirac foi primeiramente introduzido por M. Moshinsky and A. Szczepaniak em (1), onde eles simplesmente trocaram na equa¸c˜ao de Dirac o momento
para o caso do oscilador de Dirac. Quesne em (28) analisaram o oscilador de Dirac com a rela¸c˜ao de incerteza na posi¸c˜ao. B. Mirza em (29) estudou o oscilador de Dirac e a equa¸c˜ao de Klein-Gordon no espa¸co n˜ao-comutativo. M. Moshinsky e outros em (30) apresentaram a supersimetria e a super´algebra para um sistema de dois corpos com a intera¸c˜ao do oscilador de Dirac.
Al´em dos trabalhos citados acima, ainda temos na literatura v´arios artigos que anali-sam as solu¸c˜oes e as propriedades do oscilador de Dirac, mas at´e o ano de 2003, ainda n˜ao se falava do oscilador de Dirac relacionado com temperatura. Foi ent˜ao que come¸camos a estudar o oscilador de Dirac em uma dimens˜ao no banho t´ermico (31). Neste trabalho, utilizando a fun¸c˜ao de parti¸c˜ao calculada somente para os valores de energia positiva do os-cilador de Dirac, encontramos as propriedades termodinˆamicas; todas estas propriedades ser˜ao mostradas nesta tese. No ano de 2006 (32) analisou o oscilador de Dirac unidimen-sional na presen¸ca do comprimento m´ınimo. No c´alculo das propriedades estat´ısticas do oscilador de Dirac, ele chegou ao resultado que obtivemos em (31) com o acr´escimo de mais um termo na express˜ao da fun¸c˜ao de parti¸c˜ao e do calor espec´ıfico. Assim percebe-mos que ainda poder´ıapercebe-mos tratar de modelos relativ´ısticos com temperatura. Resolvepercebe-mos ent˜ao dar continuidade ao trabalho fazendo uma estudo das propriedades termodinˆamicas do oscilador de Dirac, mas agora estudando o caso tridimensional. No caso tridimensional, os estados fisicamente aceit´aveis s˜ao os de energias positivas e com degenerescˆencia finita. Resultados anal´ıticos e num´ericos interessantes foram obtidos com este estudo e ser˜ao mostrados no cap´ıtulo 3.
Depois surgiu a id´eia de estudar alguns sistemas quˆanticos simples relacionados com temperatura. No primeiro sistema utilizamos uma heteroestrutura simples, tipo po¸co quˆantico para estudarmos suas propriedades termodinˆamicas. De in´ıcio, para estudarmos quantidades termodinˆamicas temos que estabelecer a fun¸c˜ao de parti¸c˜ao para encontrar as outras quantidades. Quando encontramos a fun¸c˜ao de parti¸c˜ao de um po¸co infinito, observamos que esta possu´ıa a mesma forma da fun¸c˜ao theta de Jacobi. Isso nos deixou particularmente interessados pelo fato de podermos usar as propriedades da fun¸c˜ao theta de Jacobi para o nosso problema da heteroestrutura tipo po¸co e assim estudarmos com mais detalhes as quantidades termodinˆamicas.
1
ALGUMAS DEFINIC
¸ ˜
OES DO
OSCILADOR DE DIRAC
1.1
Introdu¸c˜
ao
O oscilador harmˆonico possui v´arias aplica¸c˜oes na mecˆanica quˆantica n˜ao-relativ´ıstica cujas equa¸c˜oes podem ser resolvidas exatamente. Isso deve-se ao fato de que a hamilto-niana ´e quadr´atica no momento e na coordenada espacial.
Como a equa¸c˜ao de Dirac ´e linear no momento, procurou-se obter um modelo an´alogo ao oscilador harmˆonico na mecˆanica quˆantica relativ´ıstica. Com isso surgiu o oscilador de Dirac analizado em (1). A equa¸c˜ao do movimento desse oscilador ´e obtida fazendo uma substitui¸c˜ao na hamiltoniana da equa¸c˜ao (A.2), que ´e dita ser uma substitui¸c˜ao n˜ao-m´ınima e definida como:
p →p−ımωβr, (1.1)
onde m´e a massa da part´ıcula e ω ´e a freq¨uˆencia do oscilador, assim (A.2) fica1:
ı∂ψ
∂t =Hψ = [α·(p−ımωβr) +mβ]ψ. (1.2)
Como podemos observar na equa¸c˜ao (1.2) apesar de (1.1) n˜ao ser hermitiana, a matrizα permite que o hamiltoniano seja. A matrizβ faz com que a equa¸c˜ao (1.1) seja covariante de Lorentz como analisada em (33).
Para fazer uma compara¸c˜ao entre o oscilador harmˆonico n˜ao-relativ´ıstico e oscilador de Dirac, inicialmente tomemos o quadrado do hamiltoniano de (A.2), ou seja:
H2 = [α·(p−ımωβr) +mβ]2. (1.3)
Fazendo algumas manipula¸c˜oes chegaremos na equa¸c˜ao abaixo:
onde
L =r×p S= (~
2)σ, (1.5)
s˜ao o momento angular orbital e o spin, respectivamente.
De (1.4) podemos observar que o quadrado do hamiltoniano fica sendo a intera¸c˜ao do oscilador harmˆonico somado com um termo de spin-´orbita acoplado, ou seja, o oscilador de Dirac pode ser visto como sendo uma raiz quadrada do oscilador harmˆonico linear n˜ao-relativ´ıstico. O hamiltoniano ao quadrado possui somente termos comutantes com a matrizβ. Esses operadores s˜ao chamados de operadores pares.
Para mostrarmos que o momento angular total ´e conservado no caso do oscilador de Dirac, basta definir o momento angular total como sendo J = L+ σ
2. Inicialmente
notamos que o hamiltoniano n˜ao comuta separadamente com L e σ respectivamente, ou seja:
[L, H] =ı(α×p)−mω(r×α)β (1.6)
[σ
2, H] =−ı(α×p) +mω(r×α)β, (1.7) onde [A, B] = AB −BA. Mas se tomarmos a express˜ao completa de J, temos que o momento angular total ´e conservado, ou seja:
[J, H] = 0. (1.8)
1.2
Auto-solu¸c˜
oes do oscilador de Dirac
Nesta se¸c˜ao calcularemos o espectro de energia do oscilador de Dirac. Como vimos na primeira se¸c˜ao, o momento angular ´e conservado em nosso sistema, pois o momento angular total J comuta com H. A regra de soma do momento angular ´e definida como
=ℓ±12, onde´e o n´umero quˆantico de momento angular total eℓ´e o n´umero quˆantico orbital. A paridade ´e utilizada em nosso sistema para classificar as autofun¸c˜oes da energia. Como a paridade das autofun¸c˜oes de energia ´e definida como sendo (−1)ℓ, temos, portanto:
ǫ= (
+1 se a paridade (−1)+1 2
−1 se a paridade (−1)−1 2
, (1.9)
onde, nos dois casos, temos ℓ=+ ǫ2.
auto-fun¸c˜oes da energia em duas partes, ou seja, na parte radial e na parte angular, de acordo com o valor deǫ (34). Assim a solu¸c˜ao da equa¸c˜ao (1.2) ser´a:
Ψ(~r, t) = 1
r
Ã
F(r)y±
mℓ(θ, φ)
ıG(r)ymℓ∓ ′(θ, φ)
!
exp(−ıEt), (1.10)
onde ymℓ± e ymℓ∓ ′ s˜ao os harmˆonicos esf´ericos espinoriais. Eles s˜ao definidos como:
y±
mℓ(θ, φ) =
q
ℓ±m+1 2
2ℓ+1 Yℓ,m−1 2(θ, φ)
± q
ℓ∓m+1 2
2ℓ+1 Yℓ,m+1 2(θ, φ)
, (1.11)
ondeYℓ,m−1
2 eYℓ,m+ 1
2 s˜ao os harmˆonicos esf´ericos. O operador paridade ´e definido em (34)
como:
P =eıϕγ0,
onde eıϕ ´e um fator de fase n˜ao observ´avel, escolhido como sendo ±1 ou ±ı, assim P
´e proporcional a β = γ0. As paridades dos harmˆonicos esf´ericos espinoriais devem ser
opostas, isto ´e, paraℓ =+ ǫ
2 temosℓ
′
=− ǫ
2. Desta maneira, ficamos com:
(+ 1 2)(+
1
2 +ǫ) = ℓ(ℓ+ 1) (1.12)
e
(+1 2)(+
1
2−ǫ) = ℓ
′
(ℓ′ + 1), (1.13)
assim temos que o quadrado do momento angular satisfaz:
L2 = (+1 2)(+
1
2+ǫβ). (1.14)
Da equa¸c˜ao (1.14) e usando as rela¸c˜oes abaixo:
J2 =L2+ 2S·L+3
4
J2 =(+ 1), (1.15)
temos:
(+ 1) = (+ 1 2)(+
1
2 +ǫβ) + 2S·L+ 3 4 −2S·L=ǫβ+ ǫβ
2 + 1
S·L=−ǫβ 2 −
ǫβ
4 − 1 4
S·L=−1
4ǫ(2+ 1)β− 1
Observemos que a express˜ao (1.16) ´e independente de r, ou seja, no espectro de energia o acoplamento ´e constante. Usando a rela¸c˜ao entre o quadrado do momento linear e o quadrado do momento angular (34) temos:
E2−m2 =− d
2
dr2 +
(+1 2)(+
1 2 +ǫβ)
r2 +m
2ω2r2+mω[ǫ(2+ 1)
−β]. (1.17)
Observemos que na equa¸c˜ao (1.17) o termo E2−m2 ´e uma soma entre a parte radial
da equa¸c˜ao de um oscilador n˜ao-relativ´ıstico e o termo abaixo:
mω[ǫ(2+ 1)−β].
O espectro de energia do oscilador de Dirac ´e dado pela soma do espectro de energia do oscilador harmˆonico n˜ao-relativ´ıstico e o termo constante acima, ou seja:
E2−m2 = 2mEn+mω[ǫ(2+ 1)−β], (1.18)
onde En = ~ω(N + 23) para N = 0,1,2, .... O n´umero quˆantico principal ´e dado por
N = 2n+ℓ. Assim o espectro de energia ´e dado, como em (19), por
E+=
p
mω[2(N + 1) +ǫ(2+ 1)] +m2, (1.19)
para os estados de energia positiva e
E−=− p
mω[2(N + 2) +ǫ(2+ 1)] +m2, (1.20)
1.3
O termo de intera¸c˜
ao do oscilador de Dirac
Nesta se¸c˜ao, como j´a feito nas referˆencias (2, 16), mostraremos que o hamiltoniano do oscilador de Dirac ´e resultado da intera¸c˜ao do momento magn´etico anˆomalo de uma part´ıcula acoplado ao campo el´etrico produzido por uma esfera carregada. Inicialmente consideremos uma esfera diel´etrica de raio R uniformemente carregada. Dentro da esfera o campo el´etrico varia com o raio na forma E = −λr; j´a o campo magn´etico ´e nulo em qualquer lugar, ou seja,B =0.
Calculando o potencial eletromagn´etico Aµ associado ao campo magn´etico est´atico,
usandoA0 = 0 e A =λtr, temos:
Aµ =λ(0, tr). (1.21) Para escrever a express˜ao acima na forma covariante de Lorentz, usamos o fato de o campo eletromagn´etico ser invariante de gauge. Assim basta escolhermos a fun¸c˜ao de gauge apropriada, ou seja:
Λ =−λ 4
µ
tr2+t
3
3 ¶
. (1.22)
Usando a rela¸c˜ao A′µ =Aµ−∂µΛ e pela defini¸c˜ao da derivada covariante como em (35)
temos que o novo potencial ser´a dado por:
A′µ = λ 4(t
2+r2,2tr). (1.23)
Usando agora o quadrivetor uµ=mω(1,0) podemos ver que o termo de intera¸c˜ao da
equa¸c˜ao (1.2) pode ser dado na forma:
ımωα·r=σµνxµuν, (1.24)
assim, a equa¸c˜ao (1.2) pode ser escrita na forma covariante:
·
γµpµ−m+ (
κe
4m)σ
µνF µν
¸
= 0, (1.25)
Aµ= λ
4[2(u.x)x
µ
−x2uµ], (1.26) onde o tensor eletromagn´etico pode ser dado como sendo:
Fµν =λ(uµxν −uνxµ). (1.27)
Quando substitu´ımos a equa¸c˜ao (1.27) para o campo eletromagn´etico no termo de in-tera¸c˜ao da express˜ao (1.25) temos:
κe
4mσµνF
µν = κe
2mλ(ıα·r). (1.28)
Multiplicando (1.28) pela matrizβ, n´os encontraremos o termo de intera¸c˜ao do oscilador de Dirac. Ent˜ao podemos ver que o hamiltoniano do oscilador de Dirac pode ser dado pelo acoplamento n˜ao-m´ınimo:
p →p− ı
2meκλrβ, (1.29)
onde λ= 2meκ2ω , ou seja:
2
PROPRIEDADES
TERMODIN ˆ
AMICAS DO
OSCILADOR DE DIRAC
UNIDIMENSIONAL
2.1
Introdu¸c˜
ao
Neste cap´ıtulo estudaremos o oscilador de Dirac unidimensional num banho t´ermico. Consideraremos o oscilador em equil´ıbrio com um reservat´orio de calor a uma dada tem-peraturaT. Com o espectro de energia positiva do oscilador, poderemos encontrar o fator de Boltzmann dado por exp(−Eβ) onde E´e a energia eβ = kT1 ; assim procedendo, poder-emos encontrar as quantidades termodinˆamicas, a saber, a fun¸c˜ao de parti¸c˜ao, a energia m´edia e o calor espec´ıfico. Em seguida, iremos comparar com os resultados obtidos com o caso do oscilador harmˆonico n˜ao-relativ´ıstico.
2.2
A fun¸c˜
ao de parti¸c˜
ao do oscilador de Dirac
Inicialmente para o oscilador harmˆonico n˜ao-relativ´ıstico em uma dimens˜ao, de acordo com a Mˆecanica Quˆantica, os n´ıveis de energia s˜ao n˜ao-degenerados e dados por:
En= (n+
1
2)~ω. (2.1)
A fun¸c˜ao de parti¸c˜ao (36) neste caso ´e dada por
Z = X
estados
exp(−Enβ), (2.2)
ou ainda,
Z = X
estados
exp[−β(n+ 1
2)~ω] = exp(−β ~ω
2 ) ∞ X
n=0
A probabilidade do oscilador harmˆonico n˜ao-relativ´ıstico unidimensional ter autoval-ores de energia (n+12)~ω, no equil´ıbrio t´ermico, ´e dada por:
Pn=
exp[−β(n+1 2)~ω]
Z . (2.4)
Assim, a energia m´edia do oscilador harmˆonico n˜ao-relativ´ıstico ´e:
U =X
n=0
PnEn =
P (n+ 1
2)~ωexp[−β(n+ 1 2)~ω]
P
exp[−β(n+ 1 2)~ω]
. (2.5)
Depois de algumas considera¸c˜oes podemos simplificar a equa¸c˜ao acima tornando-se:
U = 1 2~ω+
~ω
eβ~ω
−1. (2.6)
Para o caso relativ´ıstico unidimensional ´e importante destacar que estamos con-siderando a troca de energia entre o banho t´ermico e um sistema de uma part´ıcula. Considerando tamb´em, que os estados de energias positivas e negativas n˜ao se misturam devido a estabilidade do mar de Dirac (19), iremos considerar somente os estados de energia positiva, ou seja:
E =p2mω~(n+ 1) +m2, (2.7)
onde o termo de spin ´orbita n˜ao est´a presente. Assim a fun¸c˜ao de parti¸c˜ao do oscilador de Dirac ser´a dada por:
Z = X
estados
exp[−p(2(n+ 1)m~ω+m2)β], (2.8)
e a energia m´edia ser´a:
U = P∞
n=0
p
(2(n+ 1)m~ω+m2) exp[−p
(2(n+ 1)m~ω+m2)β]
P∞
n=0exp[−
p
(2(n+ 1)m~ω+m2)β] . (2.9)
2.3
Estudo da fun¸c˜
ao de parti¸c˜
ao do oscilador de
Dirac para altas temperaturas
Inicialmente iremos considerar a fun¸c˜ao de parti¸c˜ao do oscilador harmˆonico n˜ao-relativ´ıstico como definido em (2.3), ou seja :
Z =e−β~2ω
∞ X
n=0
e−nβ~ω
Usando unidades naturais,~=ω= 1 e considerando que β seja muito pequeno, o termo
e−β2 ≃1, assim a equa¸c˜ao acima fica:
Z = ∞ X
n=0
e−nβ. (2.11)
Para altas temperaturas, ou seja, paraβ ≪1, a fun¸c˜ao de parti¸c˜ao do oscilador harmˆonico n˜ao-relativ´ıstico pode ser escrita como:
Z = 1
1−e−β ≃
1 β + 1 2. ou seja, ∞ X n=0
e−nβ ≃ 1 β +
1
2. (2.12)
Considere a seguinte integral
I = Z ∞
0
e−βxdx=
−e −βx β ∞ 0 = 1 β (2.13)
Usando a regra dos trap´ezios, a integral acima pode ser aproximada por :
S = (1 +e−
β)
2 +
(e−β +e−2β)
2 +· · ·
S =−1 2 +
∞ X
n=0
e−nβ. (2.14)
Para o casoβ ≪1, usando (2.12) temos:
S =−1 2 + 1 2 + 1 β = 1
β. (2.15)
Ou seja, para altas temperaturas, o valor da integral (2.13), ´e equivalente a soma dos trap´ezios dada por (2.15).
Se agora considerarmos o caso relativ´ıstico, partindo da fun¸c˜ao de parti¸c˜ao dada por (2.8), temos:
Z = ∞ X
n=0
e−√2(n+1)m~ω+m2β
. (2.16)
Z = ∞ X
n=0
e−√an+bβ, (2.17)
onde a= 2m~ω eb =m2+ 2m~ω. Agora considerando a integral,
I(β) = Z ∞
0
e−√ax+bβdx, (2.18) e fazendo uma mudan¸ca de vari´aveis, temos:
I(β) = 2
a
Z ∞ √
b
e−yβydy. (2.19)
A integral acima pode ser facilmente calculada
I(β) = 2
a
µ −∂β∂
Z ∞ √
b
e−yβdy
¶
, (2.20)
resultando ent˜ao:
I(β) = 2
aβ2e
−√bβ(1 +β√b). (2.21)
Considerando agora a regra dos trap´ezios, a integral dada por (2.18) pode ser aproximada por:
S = e
−√bβ+e−√a+bβ
2 +
e−√a+bβ+e−√2a+bβ
2 +· · ·
S = e −√bβ
2 +e
−√a+bβ+e−√2a+bβ+
· · · (2.22)
ainda podemos reescrever a rela¸c˜ao acima como:
S = e −√bβ
2 −e
−√bβ+e−√bβ+e−√a+bβ+
· · · (2.23)
Ou seja:
S=−e− √
bβ
2 +Z. (2.24)
Podemos ent˜ao dizer que, para altas temperaturas, o resultado da integral dada pela equa¸c˜ao (2.21) ´e equivalente `a soma dos trap´ezios em (2.24), ou seja:
−e− √
bβ
2 +Z ≃ 2
aβ2e
Assim, a fun¸c˜ao de parti¸c˜ao do oscilador de Dirac no limite de altas temperaturas ´e dada pela express˜ao abaixo:
Z ≃ e−
√
bβ
2 + 2
aβ2e
−√bβ(1 +β√b) (2.26)
ou ainda:
Z ≃e−√bβ
µ
2(1 +β√b)
aβ2 +
1 2
¶
(2.27)
.
Para altas temperaturas o termo 1 2e−
√
bβ da equa¸c˜ao acima pode ser desprezado, assim
nossa fun¸c˜ao de parti¸c˜ao pode ser escrita simplesmente como:
Z = 2(1 +β √
b)
aβ2 . (2.28)
Agora calculando a energia m´edia temos:
U =−1
Z ∂Z
∂β, (2.29)
onde Z ´e dado na equa¸c˜ao (2.28).
Ap´os alguns c´alculos alg´ebricos e fazendo β = 1
kT ondeT ´e a temperatura, temos que
a equa¸c˜ao acima fica:
U = 2T + √
b
1 + √Tb . (2.30)
Para altos valores de T, a equa¸c˜ao acima fica simplesmente como:
U ≃2kT. (2.31)
Assim o calor espec´ıfico do oscilador de Dirac para altas temperaturas ser´a dado por:
c≃ ∂U¯
∂T ≃2k. (2.32)
2.4
Obtendo da fun¸c˜
ao de parti¸c˜
ao pelo uso da f´
ormula
de integra¸c˜
ao de Euler-Maclaurin
O resultado obtido na se¸c˜ao anterior pode ainda ser mostrado de uma forma ainda mais elegante, usando a f´ormula de integra¸c˜ao de Euler-Maclaurin. Como sabemos a fun¸c˜ao f(x) = exp(−√ax+bβ) ´e uma fun¸c˜ao monotonicamente decrescente e temos que a integral correspondente ser´a
I(β) = Z ∞
0
e−√ax+bβdx= 2
aβ2e
−√bβ(1 +β√b), (2.33)
assim a fun¸c˜ao de parti¸c˜ao ser´a convergente. Usando a f´ormula de Euler-Maclaurin
∞ X
n=0
f(n) = 1
2f(0) + Z ∞
0
f(x)dx−
∞ X
p=1
1
(2p)!B2pf
(2p−1)(0) +... (2.34)
onde B2p s˜ao os n´umeros de Bernoulli, B2 = 1/6, B4 =−1/30, .... Eles s˜ao definidos pela
s´erie
t et−1 =
∞ X
n=0
Bn
tn
n!. (2.35)
Ent˜ao a fun¸c˜ao de parti¸c˜ao pode ser escrita como:
Z = 1 2 +
2
aβ2(1 +β
√
b)−e√bβ
∞ X
p=1
B2p
(2p)!f
(2p−1)(0) +... (2.36)
Na equa¸c˜ao acima considerando p variando at´e 2 somente , temos que
e√bβ
2
X
p=1
B2p
(2p)!f
(2p−1)(0) =
1 24 β a √ b − 1 1920
β a3
b5/2 −
1 1920
β2a3
b2 −
1 5760
β3a3
b3/2 . (2.37)
Mas, como estamos interessados em analisar a fun¸c˜ao de parti¸c˜ao para altas tempera turas; assim paraβ <<1 todos os termos da soma acima ser˜ao pequenos em compara¸c˜ao com o termo 2(1 +β√b)/aβ2. Portanto a fun¸c˜ao de parti¸c˜ao ser´a:
Z ≃ 2
aβ2, (2.38)
U =−∂lnZ
∂β ≃2kT, (2.39)
C ≃ ∂U
∂T ≃2k. (2.40)
2.5
An´
alise n´
umerica das quantidades termodinˆ
amicas
do oscilador hamˆ
onico e do oscilador de Dirac
unidimensional
Como podemos observar, torna-se invi´avel calcularmos anal´ıticamente a soma da equa¸c˜ao (2.9), e mais complicado ainda deriv´a-la para encontrar o calor espec´ıfico do os-cilador de Dirac. Ent˜ao iremos fazer uma an´alise n´umerica das quantidades termodinˆamicas para podermos comparar os dois osciladores.
Inicialmente usamos as energias do oscilador harmˆonico n˜ao-relativ´ıstico e do oscilador de Dirac, obtivemos a energia m´edia e calor espec´ıfico de ambos.
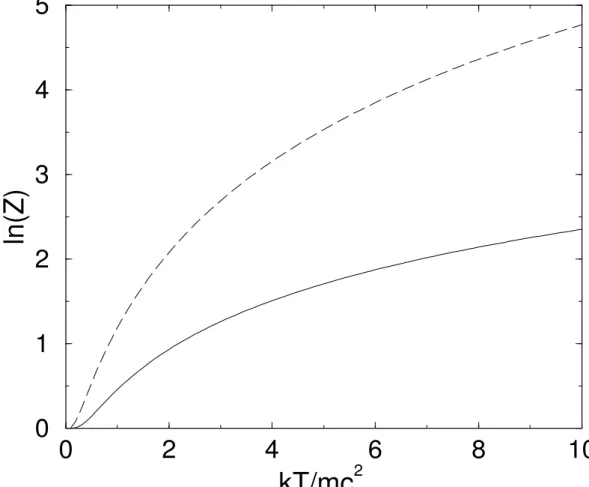
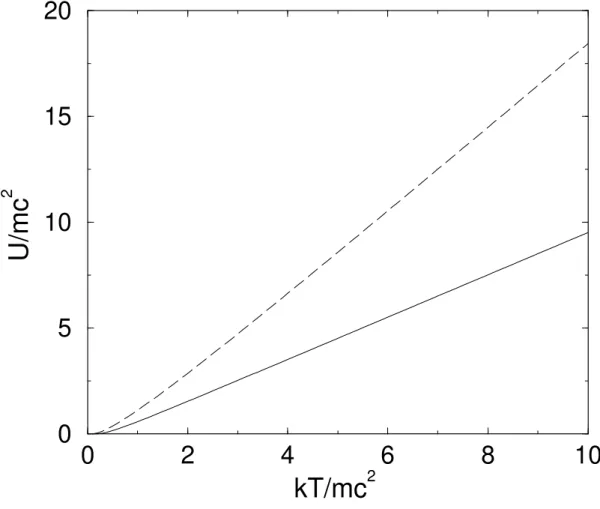
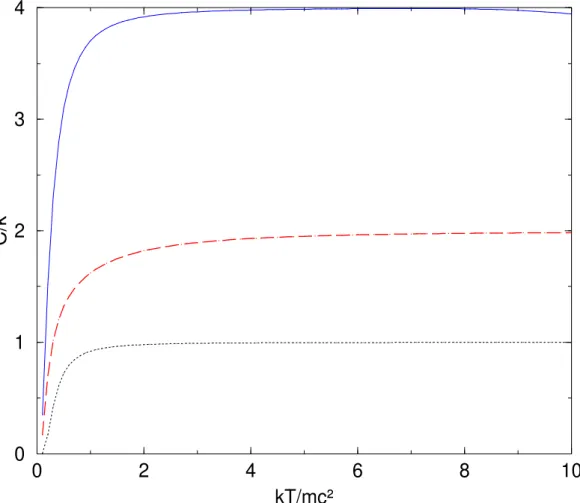
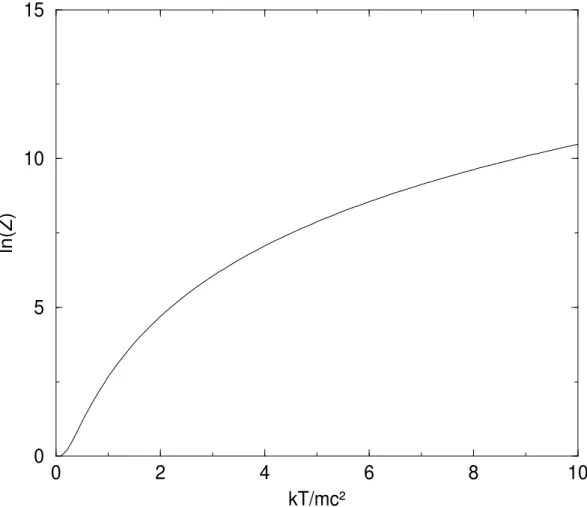
Como podemos observar nas figuras 1 e 2, as curvas para a energia livre de Helmholtz e energia m´edia possuem as mesmas caracter´ısticas, com os valores obtidos pelo oscilador de Dirac maiores que os de Schr¨odinger, com uma pequena diferen¸ca da ordem de 1/2~ω.
0
2
4
6
8
10
kT/mc
20
1
2
3
4
5
ln(Z)
0
2
4
6
8
10
kT/mc
20
5
10
15
20
U/mc
2
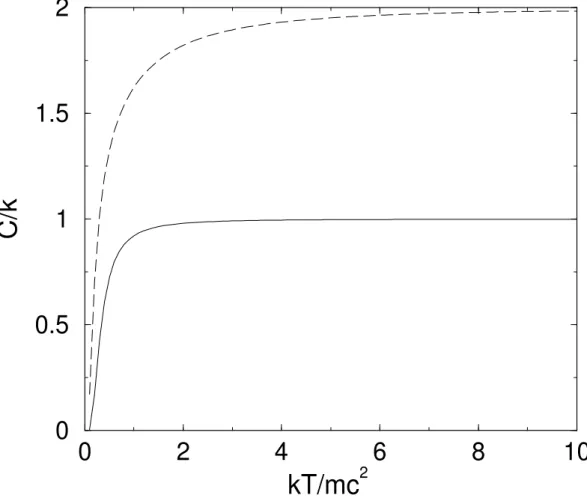
0
2
4
6
8
10
kT/mc
20
0.5
1
1.5
2
C/k
2.6
Oscilador de Dirac unidimensional na presen¸ca
do termo de comprimento m´ınimo
Depois que obtivemos os resultados do estudo das quantidades termodinˆamicas do oscilador de Dirac unidimensional, recentemente Nouicer (32), usando a representa¸c˜ao dos espa¸cos-momento, obteve a energia e as propriedades termodinˆamicas do oscilador de Dirac unidimensional na presen¸ca do termo de comprimento m´ınimo dado por
(△x)min =~
p
β, (2.41)
onde β ´e um parˆametro de deforma¸c˜ao da rela¸c˜ao de comuta¸c˜ao modificada
[x, p] =ı~(1 +βp2) (2.42)
O espectro de energia positiva do oscilador de Dirac unidimensional, para valores pequenos deβ, ´e dado por
En =mc2
r
1 + 2n~ω
mc2
"
1 + β~
2ω2
2c2
n2
1 + 2n~ω
mc2
#
(2.43)
Observemos que o segundo termo da express˜ao acima representa a corre¸c˜ao adequada na presen¸ca do termo de comprimento m´ınimo, onden2 est´a relacionado ao confinamento.
A fun¸c˜ao de parti¸c˜ao do oscilador de Dirac, para uma temperatura T, na presen¸ca do comprimento m´ınimo ´e dada por:
Zβ′ =
∞ X
0
exp(−β′mc2
r
1 + βω
2~2n2
c2 +
2nω~
mc2 ), (2.44)
onde β′
= 1
kT.
No regime de altas temperaturas a express˜ao acima fica:
Zβ′ ≃
(kT)2
~ωmc2 −
3β(kT)4
~ωmc4 (2.45)
A energia m´edia ´e dada por:
U ≃2kT
· 1−3
µ
△X)min
lth
¶2¸
e o calor espec´ıfico ´e dado por:
c≃2k
· 1−9
µ
△X)min
lth
¶2¸
. (2.47)
3
PROPRIEDADES
TERMODIN ˆ
AMICAS DO
OSCILADOR DE DIRAC
TRIDIMENSIONAL
3.1
Introdu¸c˜
ao
Depois dos resultados obtidos em (31) para o caso unidimensional, ainda nos restava explorar o caso tridimensional. De in´ıcio achavamos que talvez esse caso fosse um pouco complicado devido o problema da degenerescˆencia dos estados, mas resolvemos encontrar uma maneira que nos pudesse fornecer um resultado significativo. Ent˜ao reescrevemos o espectro de energia do oscilador de Dirac 3D, de forma que conseguinos tratar com o problema da degenerescˆencia para ent˜ao come¸car calcular a fun¸c˜ao de parti¸c˜ao. Ent˜ao, neste cap´ıtulo irei apresentar os resultados anal´ıticos para as quantidades termodinˆamicas (fun¸c˜ao de parti¸c˜ao, energia m´edia e calor espec´ıfico) do oscilador de Dirac tridimensional e mostraremos tamb´em uma an´alise n´umerica da fun¸c˜ao de parti¸c˜ao do caso em 3 dimens˜oes
1.
3.2
A fun¸c˜
ao de parti¸c˜
ao e o calor espec´ıfico do
os-cilador de Dirac 3D
Como vimos no primeiro cap´ıtulo, o espectro de energia positiva do oscilador de Dirac ´e dado por:
E+=
p
mω[2(N + 1) +ǫ(2+ 1)] +m2. (3.1)
Naquele momento n˜ao consideramos os termos de spin, uma vez que estav´amos interessa-dos apenas no caso unidimensional. Agora temos que levar em considera¸c˜ao o momento
angular total e o n´umero quˆantico orbital. De acordo com (1) ´e observado a existˆencia de degenerescˆencia quando tratamos do oscilador de Dirac em 3 dimens˜oes. Dependendo da paridade do sistema, temos duas possibilidades (1):
(mc2)−1(E2
nlj−m2c4) =
~ω[2(N −j) + 1] se l=j−1/2,
~ω[2(N +j) + 3] se l=j+ 1/2.
(3.2)
Na equa¸c˜ao acima, temos casos de degenerescˆencia infinita e finita respectivamente. Con-siderando somente o caso de degenerescˆencia finita, uma vez que n˜ao podemos construir representa¸c˜oes do grupo de Lorentz com estados de degenerescˆencia infinita, a equa¸c˜ao acima pode ainda ser escrita como em (20), assim
Enlj =mc2
p
ξA+ 1, (3.3)
ondeA= 2(N+j)+3 eξ= ~
mc2. Agora para o estudo das quantidades termodinˆamicas
do oscilador de Dirac tridimensional, vamos inicialmente redefinir a express˜ao de A, em fun¸c˜ao de uma nova constante que chamaremos de ς, e definida como ς = N +l, onde
N, l∈N. Dessa forma temos que A= 2(ς + 1).
Ent˜ao agora podemos escrever a fun¸c˜ao de parti¸c˜ao do oscilador de Dirac tridimen-sional, para uma temperaturaT:
Z =e√bβ
∞ X
ς=0
(ς + 1)e−√aς+bβ (3.4)
onde a= 2~mωc2 e b=m2c4+ 2~ωmc2
Analisando a convergˆencia da fun¸c˜ao de parti¸c˜ao, observamos que a fun¸c˜ao f(x) = (x+ 1)e−√ax+bβ monotonicamente convergente e corresponde a integral
I(β) = Z ∞
0
(x+ 1)e−√ax+bβdx (3.5)
que ´e convergente.
Para calcular o somat´orio da equa¸c˜ao (3.4), podemos utilizar a f´ormula de Euler-MacLaurin
∞ X
n=0
f(n) = 1
2f(0) + Z ∞
0
f(x)dx−
∞ X
p=1
1
(2p)!B2pf
(2p−1)(0) +..., (3.6)
s´erie
t et−1 =
∞ X
n=0
Bn
tn
n!. (3.7)
O primeiro termo da expans˜ao acima tomado em n = 0 ´e dado por 12e−√bβ. Para
encontrarmos o segundo termo, temos que calcular a integral dada por (3.5), ou seja:
I(β) = Z ∞
0
(x+ 1)e−√ax+bβdx. (3.8)
Fazendou2 =ax+b, a integral acima resulta em:
I = 2
a2
·Z ∞ √
b
u3e−uβdu+ (a−b) Z ∞
√
b
e−uβudu
¸
, (3.9)
observemos que, a primeira integral2 acima n˜ao ´e trivial quanto a segunda integral, cuja
solu¸c˜ao ´e dada por:
e−√bβ
β2 (1 +β)
Notemos que a solu¸c˜ao da primeira integral ´e encontrada quando derivamos parcialmente a raz˜ao
− ∂
3
∂β3
e−√bβ
β ,
ou seja
− ∂
3
∂β3
e−√bβ
β =
e−√bβ
β2
· 6
β2 +
6√b
β + 3b+βb √
b
¸
.
Assim a solu¸c˜ao da integral dada pela equa¸c˜ao (3.9) ´e dada por:
I = 2e −√bβ
a2β2 =
· 6
β2 +
6√b
β + 3b+βb √
b+a+βa−b−βb
¸
. (3.10)
Ent˜ao agora resta somente calcular o terceiro termo da expans˜ao dada em (3.6). Considerando apenas p variando de 1 a 2, temos que calcular a derivada de terceira ordem da fun¸c˜ao f(x) = (x+ 1)e−√ax+bβ.
Agora que j´a conhecemos os trˆes termos da expans˜ao de Euler-MacLaurin, podemos substitu´ı-los na fun¸c˜ao de parti¸c˜ao (3.4). Uma vez realizado esse procedimento, chegamos ent˜ao finalmente a express˜ao da fun¸c˜ao de parti¸c˜ao do oscilador de Dirac tridimensional, ou seja:
Z = 1 2 + 2 a2 · 6
β4 +
6√b β3 +
a−b β2 +
a−b
β +
3 +b√b β
¸ +
− 1 12−
a3β3
5760√b3 +
a2β2
1440b − a3β2
2880b2 +
a3β2
5760b +
+a
2β2
2880 +
a2β
2880√b3 +
a3β
5760√b3 −
a2β
1440√b + aβ
24√b. (3.11)
Como no caso unidimensional, agora vamos fazer um estudo para altas temperaturas, ou seja para T → ∞. Dessa forma, podemos observar que no regime de altas temperat-uras, os termos que resultaram do terceiro termo da expans˜ao de Euler-MacLaurin ser˜ao todos desconsiderados, uma vez que β → 0. Ent˜ao da fun¸c˜ao de parti¸c˜ao acima restar´a apenas os termos resultantes da integral dada em (3.9), ou seja:
Z = 1 2 +
2
a2
· 6
β4 +
6√b β3 +
a−b β2 +
a−b
β +
3 +b√b β
¸ − 1
12. (3.12)
Podemos assim considerar que na express˜ao acima o termo da ordem de β4 ´e muito
maior em compara¸c˜ao com os demais. Logo a fun¸c˜ao de parti¸c˜ao pode ser finalmente escrita como:
Z ≃ 12
a2β4. (3.13)
A equa¸c˜ao acima pode ser encontrada, de uma forma mais simples, basta considerar o somat´orio da fun¸c˜ao f(n) = (n+ 1)e−√an+bβ, ou seja
∞ X
n=0
= (n+ 1)e−√an+bβ (3.14)
O somat´orio acima pode ser aproximado por trap´ezios
S = e− √
bβ+ 2e−√a+bβ
2 +
2e−√a+bβ+ 3e−√2a+bβ
2 +· · ·
ainda podemos reescrever a equa¸c˜ao acima como:
S =−e− √
bβ
2 +e
−√bβ+ 2e−√bβ+ 3e−√2a+bβ+
· · · (3.15)
Ou seja:
S=−e− √
bβ
A equa¸c˜ao acima ser´a igual ao resultado da integral (3.8), logo:
−e −√bβ
2 +Z ≃
2e−√bβ
a2β2
· 6
β2 +
6√b
β +· · · ,
considerando valores pequenos de β, ou seja altas temperaturas, temos:
Z ≃ 12
a2β4 (3.17)
o que mais uma vez comprova a exatid˜ao do nosso resultado.
Continuando a obten¸c˜ao das quantidades termodinˆamicas, a energia m´edia ´e obtida atrav´es da express˜ao:
U =− ∂
∂βlnZ. (3.18)
Tomando
lnZ =ln12−ln(a2β4)
ent˜ao a energia m´edia pode ser escrita como:
U =− ∂
∂βlnZ ≃4kT. (3.19)
E por ´ultimo podemos encontrar o calor espec´ıfico, que pode ser escrito como:
c≃ ∂U
∂T ≃4k. (3.20)
Esse resultado mostra que para altas temperaturas, a energia m´edia e o calor espec´ıfico do oscilador de Dirac tridimensional ´e o dobro do obtido para o caso unidimensional.
3.3
Resultados n´
umericos do oscilador de Dirac 3D
para o caso de degenerescˆ
encia finita
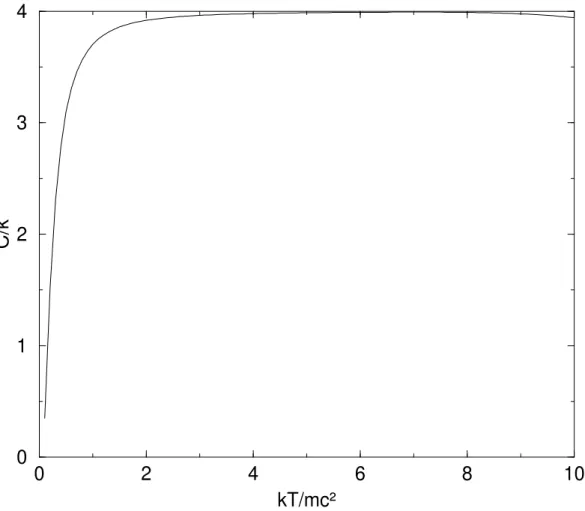
Depois dos resultados anal´ıticos obtidos na se¸c˜ao anterior, resolvemos fazer uma an´alise n´umerica das quantidades termodinˆamicas do oscilador de Dirac tridimensional.
0
2
4
6
8
10
kT/mc²
0
10
20
30
40
U/mc²
Figura 4: A energia m´edia do oscilador de Dirac tridimensional em fun¸c˜ao da temperatura, onde consideramos~ω/mc2 = 1.
0
2
4
6
8
10
kT/mc²
0
1
2
3
4
C/k
0
2
4
6
8
10
kT/mc²
0
10
20
30
40
U/mc²
0
2
4
6
8
10
kT/mc²
0
1
2
3
4
C/k
0
2
4
6
8
10
kT/mc²
0
5
10
15
ln(Z)
0
2
4
6
8
10
KT/mc²
0
5
10
15
ln(Z)
4
PROPRIEDADES
TERMODIN ˆ
AMICAS DO
POC
¸ O INFINITO E A
RELAC
¸ ˜
AO COM A FUNC
¸ ˜
AO
THETA DE JACOBI
4.1
Introdu¸c˜
ao
Neste cap´ıtulo iremos analisar as propriedades termodinˆamicas de heteroestrutura simples, tipo o po¸co de potencial quadrado. Inicialmente gostaria de esclarecer um pouco mais sobre as heteroestruturas.
Em 1950 a id´eia de se utilizar filmes finos para estudar os efeitos de confinamento era bastante difundido, e a principal estrutura estudada eram os filmes de semi-metais depositados a v´acuo sobre substratos de mica.
Nesta ´epoca muitas previs˜oes existiam, como o tunelamento ressonante, mas as t´ecnicas experimentais do momento n˜ao favoreciam aos pesquisadores para que pudessem desen-volver filmes de qualidade para poder esclarecer tais efeitos.
Com o surgimento das t´ecnicas de crescimento epitaxial, tamb´em conhecida como Molecular Beam Epitaxi, come¸caram inserir camadas de alguns angstr¨ons de espessura de semicondutores de gap menor sobre substratos de gap maior, restrigindo o movimento dos el´etrons a apenas duas dire¸c˜oes, garantindo assim uma interface perfeita. Com isso os fenˆomenos de confinamento previstos puderam ser verificados e muitas outras id´eias foram experimentados.
O primeiro deles ´e composto por duas camadas de um semicondutor qualquer separadas por uma terceira camada de um semicondutor distinto, de gap menor, cuja fun¸c˜ao ´e prover aos el´etrons uma regi˜ao na qual a energia potencial do g´as bidimensional de el´etrons seja menor que em qualquer outra regi˜ao do material e, portanto, mantˆe-los ali confinados. Antes do advento das heteroestruturas, os po¸cos-quˆanticos n˜ao passavam de estruturas t´eoricas cuja ´unica fun¸c˜ao era ilustrar as equa¸c˜oes da Mecˆanica Quˆantica. Hoje eles s˜ao utilizados na confec¸c˜ao de v´arios dispositivos optoeletrˆonico de alta performance como os lasers e fotodetectores.
4.2
Propriedades termodinˆ
amicas do po¸co infinito
Vamos considerar inicialmente uma part´ıcula de massa m confinada em po¸co infinito com o potencial dado por
V =
0 se 0< x < a,
∞ x > ae x <0.
(4.1)
Escrevendo o hamiltoniano como sendo
H =T +V =p2(2m)−1+V(x), (4.2)
a equa¸c˜ao de Schr¨odinger ser´a dada por:
(−~
2
2m ∂2
∂x2 +V)ψ(x) =Eψ(x). (4.3)
A equa¸c˜ao acima pode ainda ser escrita como
∂2
∂x2ψ(x) +
2mE
~2 ψ(x) = 0. (4.4)
que ´e uma equa¸c˜ao diferencial linear de 2aordem com coeficientes constantes, cuja solu¸c˜ao
geral ´e:
ψ(x) =c1eıkx+c2e−ıkx, (4.5)
onde k = q2mE
~2 . Aplicando agora as condi¸c˜oes de contorno ψ(x) = 0 para x = 0 ou
x=a, pois a fun¸c˜ao de onda ψ(x) deve desaparecer fora da caixa, temos:
ψ(0) =c1 +c2,
ψ(a) =c1eıka+c2e−ıka;
ψ(0) = 0 =⇒c1 =−c2,
ent˜ao:
ψ(a) = 0 =⇒c1eıka−c1eıka = 0 =⇒c1(eıka−e−ıka) = 0,
ou ainda
Assim podemos escrever:
ψ(x) = c1(eıkx−e−ıkx).
Calculando a derivada primeira e segunda da express˜ao acima e substituindo na equa¸c˜ao 4.4, encontraremos:
c1k2(eıkx+e−ıkx) + 2mE~−2c1(eıkx−e−ıkx) = 0.
Agora explicitando o valor de E, temos que as energias dos estados quˆanticos s˜ao dadas por:
En =
n2π2~2
2ma2 , n= 1,2, ... (4.6)
Como estamos interessados em estudar as quantidades termodinˆamicas do po¸co de potencial quadrado, temos que encontrar inicialmente a fun¸c˜ao de parti¸c˜ao do sistema.
A fun¸c˜ao de parti¸c˜ao de um sistema no banho t´ermico ´e obtida pela express˜ao,
Z = ∞ X
n=0
e−Enβ, (4.7)
onde β = 1/kT, e k ´e a constante de Boltzmann. Usando (4.6) e desconsiderando o valorn= 0, correspondente ao estado de energia igual a zero na equa¸c˜ao (4.7), podemos escrever a fun¸c˜ao de parti¸c˜ao como:
Z = ∞ X
n=1
e−Enβ = ∞ X
1
en2π2~2/2ma2
. (4.8)
4.3
Propriedades termodinˆ
amicas de um po¸co de
po-tencial infinito usando a fun¸c˜
ao theta de Jacobi
4.3.1
A fun¸c˜
ao theta de Jacobi
Nos ´ultimos anos v´arios artigos foram publicados usando a fun¸c˜ao theta de Jacobi tanto na ´area de Matem´atica como em F´ısica. Alguns deles destacam-se por suas formas de apresentarem as propriedades e as aplica¸c˜oes da fun¸c˜ao theta de Jacobi. Em partic-ular, (38) estudou as propriedades el´ıpticas da fun¸c˜ao de Jacobi envolvendo expans˜oes trigonom´etricas da fun¸c˜ao theta. Alguns sistemas quˆanticos simples s˜ao analisados nu-mericamente por (39) e (40), onde utilizam uma propriedade da fun¸c˜ao theta de Jacobi para tratar condensa¸c˜ao de Bose-Einstein com v´ortices.
A fun¸c˜ao theta Cl´assica est´a historicamente ligada `a teoria dos n´umeros, e definida como (41)
v(z) = ∞ X
n=−∞
eiπn2
z, Im(z)>0, (4.9)
que ´e convergente paraIm(z)>0 e satisfaz a rela¸c˜ao
v(z+ 2) =v(z)
e
v
µ −1
z
¶
=√−izv(z).
Agora tomandoz =it em (4.9) temos que
θ(t) =X
n∈Z e−πn2t
, t >0, (4.10)
que ´e a fun¸c˜ao theta de Jacobi, ondeθ(t) satisfaz a chamada f´ormula de invers˜ao de Jacobi
θ(t) = √1 tθ
µ 1
t
¶
, t >0,√t >0. (4.11)
A equa¸c˜ao acima ´e tamb´em chamada de equa¸c˜ao funcional da fun¸c˜ao theta.
termicamente nas extremidades, resulta na equa¸c˜ao funcional da fun¸c˜ao theta.
Na pr´oxima se¸c˜ao iremos aplicar a fun¸c˜ao theta de Jacobi para analisar as quantidades termodinˆamicas de um po¸co de potencial.
4.4
Fun¸
c˜
ao theta de Jacobi e o po¸co de potencial
Quando estudamos a fun¸c˜ao theta de Jacobi percebemos que ela possui a mesma forma da fun¸c˜ao de parti¸c˜ao (4.8) da se¸c˜ao anterior. Ou seja, da fun¸c˜ao Theta de Jacobi:
θ(x) = ∞ X
n=−∞
e−n2πx= 2 ∞ X
n=1
e−n2πx+ 1, (4.12)
temos que o segundo membro ´e a fun¸c˜ao de parti¸c˜ao (4.8), a menos de uma constante. Observemos que a fun¸c˜ao de parti¸c˜ao pode ainda ser escrita como:
Z(T) = θ(
T0
T )−1
2 , (4.13)
onde T0 = π
~2
2ma2k ´e uma temperatura caracter´ıstica que depende da largura do po¸co.
Usando a propriedade (4.11) e a rela¸c˜ao (4.13) podemos escrever:
Z
µ
T0
α
¶
= Z(√αT0)
α +
1−√α
2√α , (4.14)
ondeα´e um fator de escala. Observemos na express˜ao acima que se conhecermos a fun¸c˜ao de parti¸c˜ao para uma temperatura T0
α, ent˜ao poderemos encontrar a fun¸c˜ao de parti¸c˜ao
para uma temperatura αT0. Este ´e um resultado interessante pelo fato de podermos
encontrar todas as propriedades termodinˆamicas do sistema usando somente a fun¸c˜ao de parti¸c˜ao. Ent˜ao, num procedimento experimental, quando precisamos medir o calor espec´ıfico para uma temperatura T1, n´os n˜ao precisaremos medir o calor espec´ıfico para
uma temperatura T = T02
T1, uma vez conhecendo a temperatura T0. Esta propriedade da
fun¸c˜ao theta de Jacobi, nos permite ainda relacionar a energia m´edia com a fun¸c˜ao de parti¸c˜ao. Derivando a express˜ao anterior (4.14), em rela¸c˜ao aα, temos:
−Z′
µ
T0
α
¶
T0
α2 =
Z′(αT0)
√
α .T0+Z(αT0).
µ
−12α−3/2
¶ +
µ
−14α−3/2
¶
. (4.15)
Fazendoα= 1, chegamos na rela¸c˜ao
Z′(T0)T0 =
1 8 +
Z(T0)
A express˜ao acima ainda pode ser escrita em fun¸c˜ao da energia m´edia, ou seja, usando a defini¸c˜ao da energia m´edia, temos:
U = P
nEne−Enβ
Z , (4.17)
podemos ainda escrever
Z′(T)T = 1
kT
X
n
Ene−Enβ =β
X
n
Ene−Enβ, (4.18)
ent˜ao:
Z′
(T)T
Z =βU. (4.19)
Usando a rela¸c˜ao (4.16) , chegamos na equa¸c˜ao:
1 8Z(T0)
+1 4 =
U(T0)
kT0
(4.20)
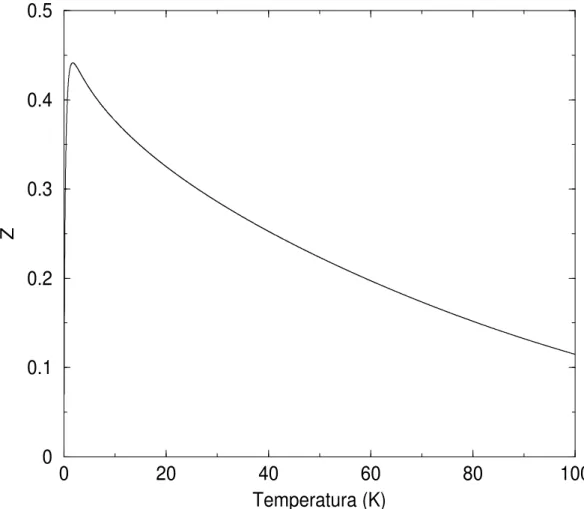
Fazendo um estudo num´erico da fun¸c˜ao de parti¸c˜ao de um po¸co infinito usando a express˜ao dado por (4.13) e adotando os valores de~,k, da massa do el´etronm dados no apˆendice, a temperatura caracter´ıstica ser´a dada porT0 = 5.49x10−14/a2, assim:
a(˚A) T0(K)
100 549 200 137 300 61
O gr´afico da figura 8 nos mostra a fun¸c˜ao de parti¸c˜ao de um po¸co infinito de 183˚Ade largura em fun¸c˜ao da temperatura. Neste gr´afico a temperatura varia de 0 a 100K.
0
20
40
60
80
100
Temperatura (K)
0
0.1
0.2
0.3
0.4
0.5
Z
CONCLUS ˜
AO
Acreditamos ter estabelecido nesta tese um estudo anal´ıtico e num´erico das quanti-dades termodinˆamicas do oscilador de Dirac. No primeiro momento fizemos um trata-mento anal´ıtico do caso unidimensional que nos confirmou os resultados num´ericos j´a obtidos no ano de 2001. As quantidades termodinˆamicas do oscilador de Dirac em uma dimens˜ao ´e o dobro do obtido no caso do oscilador harmˆonico quˆantico n˜ao-relativ´ıstico. Uma vez esclarecido o caso unidimensional, partimos para o caso tridimensional, agora com uma complexidade maior, pois tratamos de considerar o espectro de energia com o termo de spin-´orbita que resulta nos casos de degenerescˆencia finita e infinita. Os resultados anal´ıticos e num´ericos mostraram que para o caso tridimensional com de-generescˆencia finita, os valores das quantidades termodinˆamicas do oscilador de Dirac s˜ao exatamente o dobro do caso unidimensional, considerando altas temperaturas. Neste trabalho tamb´em estabelecemos uma rela¸c˜ao entre a fun¸c˜ao theta de Jacobi e as quanti-dades termodinˆamicas de um po¸co de potencial infinito, mostrando que poderemos ainda futuramente, calcular as quantidades termodinˆamicas de um po¸co de potencial finito que s˜ao bastante utilizados na simula¸c˜ao das heteroestruturas semicondutoras.
Em s´ıntese:
• Nosso principal resultado foi mostrar que o calor espec´ıfico de um oscilador de Dirac tridimensional com degenerescˆencia finita ´e o dobro do calor espec´ıfico do oscilador de Dirac unidimensional e quatro vezes maior que o calor espec´ıfico do oscilador harmˆonico quˆantico n˜ao-relativ´ıstico quando estamos num sistema de altas temperaturas.
• Os resultados encontrados nos deixam uma perspectiva de poder construir uma rede de osciladores de Dirac em um banho t´ermico e tamb´em tamb´em estabelecer as quantidades termodinˆamicas em altas dimens˜oes.
APˆ
ENDICE A -- A equa¸c˜
ao de Dirac
A equa¸c˜ao de Dirac ´e uma equa¸c˜ao relativ´ıstica que descreve part´ıculas de spin 1/2, como el´etrons e quarks; uma caracter´ıstica dessas part´ıculas ´e que elas possuem dois graus de liberdade. Part´ıculas de spin 0 s˜ao descritas pela equa¸c˜ao relativ´ıstica de Klein-Gordon.
A.1
A equa¸c˜
ao
A equa¸c˜ao de Klein-Gordon na forma de duas componentes ´e escrita como
ı~∂
∂tψ =Hψ. (A.1)
Enquanto esta equa¸c˜ao ´e de primeira ordem na derivada temporal, o hamiltoniano de Klein-Gordon ´e de segunda ordem na derivada espacial e portanto n˜ao temos equivalˆencia nas coordenadas espacial e temporal. Al´em disso, como na teoria de Klein-Gordon a densidade de probabilidade n˜ao ´e positiva definida, logo o hamiltoniano da equa¸c˜ao de Klein-Gordon de duas componentes n˜ao ´e hermitiano. Finalmente a covariˆancia dessa equa¸c˜ao somente se manifesta na forma da equa¸c˜ao de uma componente. Sendo assim, surgem as seguintes perguntas: existe uma equa¸c˜ao relativ´ıstica que seja de primeira ordem na derivada temporal e que as coordenadas espaciais e temporais manifestem-se simetricamente? E que a densidade de probabilidade seja positiva definida (implicando que o hamiltoniano seja hermitiano)? E que manifeste covariˆancia de Lorentz? Estas perguntas nos levam diretamente `a equa¸c˜ao de Dirac.
Esta equa¸c˜ao deve ter a seguinte forma:
ı~∂
∂tΨ =HΨ = (cα·p+βmc
2)Ψ, (A.2)
onde α e β s˜ao matrizes hermitianas e p = −ı~∇. A rela¸c˜ao energia-momento surge naturalmente, usando a energia como E→ı~∂
equa¸c˜ao (A.2), ou seja,
−~2 ∂
2
∂t2Ψ = ı~
∂
∂t(cα·p+βmc
2)Ψ, (A.3)
ou ainda
−~2 ∂
2
∂t2Ψ = (cα·p+βmc
2)2Ψ = (p2c2+m2c4)Ψ. (A.4)
Podemos ainda escrever:
(αipi+βm)2 =β2m2+(αi)2(pi)2+{β, αi}mpi+
1
2{αi, αj}i6=jp
ipj =X
ı
(pı)2+m2, (A.5)
onde {A, B} = AB+BA ´e o anticomutador dos operadores A e B. A equa¸c˜ao acima ´e v´alida se, e somente se,
{αi, β}={αi, αj}= 0
β2 =α2
i = 1.
Uma representa¸c˜ao destas matrizes ´e dada por
αi =
"
0 σi
σi 0
#
, β =
"
1 0
0 −1
#
, (A.6)
onde σi s˜ao as matrizes de Pauli
σ1 =
" 0 1 1 0
#
, σ2 =
"
0 −ı
ı 0
#
, σ3 =
"
1 0 0 −1
#
.
A equa¸c˜ao de Dirac ainda pode ser escrita na forma covariante. Usando as matrizes
γµ, onde γµ = (β, βα
i), encontraremos a forma covariante da equa¸c˜ao de Dirac, que ser´a
dada por:
(ı~γµ ∂
∂xµ −mc)Ψ = 0. (A.7)
Para construirmos a lei diferencial de conserva¸c˜ao da corrente, inicialmente escrevendo (A.1) na seguinte forma
ı~∂Ψ
∂t = ·~ c ı µ ˆ α1 ∂
∂x1 + ˆα2
∂
∂x2 + ˆα3
∂ ∂x3
¶
+βmc2
¸
Ψ =HΨ, (A.8)
e definindo a fun¸c˜ao de onda conjugada hermitiana Ψ† = (Ψ∗
multi-plicar a equa¸c˜ao (A.8) por Ψ† pelo lado esquerdo, ou seja,
ı~Ψ†∂Ψ
∂t =
~c
ı Σ
3
k=1Ψ†αk
∂
∂xkΨ +mc
2Ψ†βΨ. (A.9)
Al´em disso, com a forma hermitiana conjugada das matrizes αı eβ
−ı~∂Ψ †
∂t =−
~c
ı Σ
3
k=1
∂Ψ†
∂xkα
†
k+mc
2Ψ†β†, (A.10)
multiplicando (A.10) pela direita por Ψ e considerando a hermiticidade das matrizes de Dirac, ou seja (α†i =αi, β† =β), temos:
−ı~∂Ψ †
∂t Ψ =−
~c
ı Σ
3
k=1
∂Ψ†
∂xkαkΨ +mc
2Ψ†βΨ. (A.11)
Agora subtraindo (A.11) de (A.9) temos:
ı~∂(Ψ †Ψ) ∂t = ~c ı Σ 3 k=1
∂(Ψ†α
kΨ)
∂xk , (A.12)
ou ainda
∂ρ
∂t +∇ ·j= 0,
onde ρ = Ψ†Ψ = P4
µ=1Ψ∗µΨµ ´e a densidade de probabilidade positiva definida e k =
cΨ†αkΨ ou j=cΨ†αΨ ´e a densidade de corrente.
A.2
Solu¸c˜
ao da equa¸c˜
ao de Dirac para part´ıcula livre
A equa¸c˜ao de Dirac pode ser escrita como:
ı~∂Ψ
∂t = ˆHΨ = (cα·p+mc
2βˆ)Ψ. (A.13)
Para os estados estacion´arios, se utilizarmos o Ansatz
Ψ(x, t) =ψ(x)e−~ıεt, (A.14)
assim,
εψ((x)) =Hψ(x). (A.15)
componentesϕ e χ temos: ψ = ψ1 ψ2 ψ3 ψ4 = Ã ϕ χ ! , (A.16)
ondeχ= Ã
ψ3
ψ4
! eϕ =
Ã
ψ1
ψ2
!
. Usando as matrizes de Dirac (A.6) e (A.15), podemos escrever: ε à ϕ χ ! =c à 0 σ σ 0 ! ·p à ϕ χ !
+m2c2
Ã
1 0
0 −1
! Ã ϕ χ ! , ou
εϕ=cσ·pχ+mc2ϕ
εχ =cσ·pϕ−mc2χ. (A.17)
Organizando as equa¸c˜oes acima e considerando o operadorp sendo o autovalor p e que
à ϕ χ ! = à ϕ0 χ0 ! exp[(ı
~)p·x], (A.18)
temos:
(ε−m0c2)1ϕ0−cσ·pχ0 = 0
−cσ·pϕ0 + (ε+m0c2)1χ0 = 0. (A.19)
Considerando que o determinante da matriz dos coeficientes de (A.19) seja zero, ou seja, a equa¸c˜ao (A.17) possui solu¸c˜ao n˜ao-nula, temos:
¯ ¯ ¯ ¯ ¯
(ε−m0c2)1 −cσ·p
−cσ·p (ε+m0c2)1
¯ ¯ ¯ ¯ ¯
= 0, (A.20)
assim
(ε2−m20c4)1−c2(σ·p)(σ·p) = 0. (A.21)
Usando o fato que (σ·p)2 =p2, temos que a rela¸c˜ao energia-momento (A.21) fornece:
ε2 =m2
Considerando ε=±Ep temos:
Ep =c
q
p2+m2
0c2, (A.22)
onde os sinais + ou −deε descrevem as duas solu¸c˜oes da equa¸c˜ao de Dirac. Da equa¸c˜ao (A.19) podemos encontrar o valor deχ0, assim:
χ0 =
c(σ·p)
m0c2+ε
ϕ0. (A.23)
Se considerarmos ϕ0 na forma
ϕ0 =U =
"
U1
U2
#
, (A.24)
e a normaliza¸c˜ao
U†U =U∗
1U1+U2∗U2 = 1
onde U1 e U2 s˜ao n´umeros complexos, e usando (A.14) e (A.18) teremos o conjunto
completo de solu¸c˜oes livres positivas e negativas da equa¸c˜ao de Dirac como sendo:
Ψ(x, t) = N (√2π~)3
"
U
c(σ·p)
m0c2+λEpU #
exp[ı(p·x−λEpt)/~], (A.25)
onde λ=±1 e ε=λEp.
A constante N pode ser determinada pela condi¸c˜ao de ortonormaliza¸c˜ao
Z
Ψ†pλ(x, t)Ψp′λ′(x, t)d3x=δλλ′δ(p−p ′
portanto,
N2(U†U +U†c2(σ·p)(σ·p) (mc2+λE
p)2
U) = 1
N2(1 + c
2p2
(mc2+λE
p)2
) = 1
N =
s
(mc2+λE
p)2
(mc2+λE
p)2+c2p2
N =
s
(mc2+λE
p)2
(m2c4+c2p2) + 2mc2λE
p+Ep2
N =
s
(mc2+λE
p)2
2(mc2+λE
p)λEp
N =
s
mc2 +λE
p
2λEp
. (A.27)
O espectro de εpλ = λEp, correspondendo aos autovalores da fun¸c˜ao Ψpλ(x,t). Do
mesmo modo que na equa¸c˜ao de Klein-Gordon, temos autovalores de energia positiva e negativa. Considerando que todos os estados de (A.25) s˜ao autofun¸c˜oes do momento, ou seja:
ˆ
pΨpλ =pΨpλ(x, t), (A.28)
para todo p temos duas diferentes solu¸c˜oes, uma dada por λ = 1(ε = Ep) e outra λ =
−1(ε=−Ep).
De acordo com (43), o operador helicidade ˆΛs ´e definido como:
ˆ Λs =
~ 2
1 0 0 0 0 −1 0 0 0 0 1 0 0 0 0 −1
= ˆSz, (A.29)
e pode ser usado para classificar os estados de uma part´ıcula livre. Os autovalores s˜ao ±~
2 e os autovetores de ˆΛs s˜ao:
" u1 0 # , "
u−1
0 # , " 0 u1 # , " 0
u−1
#
, (A.30)
com
u1 =
" 1 0
#
, u−1 =
" 0 1
#
Assim a propaga¸c˜ao de onda livre de Dirac na dire¸c˜ao z ´e denotada por Ψpz,λ,sz e escrita como:
Ψp,λ,+1/2 =
1 √
2π~ s
mc2+λE
p
2λEp
à 1 0 !
cσzp
mc2+λE
p à 1 0 !
exp[ı(pz−λEpt)/~]. (A.31)
e
Ψp,λ,−1/2 =
1 √
2π~ s
mc2+λE
p
2λEp
à 0 1 !
cσzp
mc2+λE
p à 0 1 !
APˆ
ENDICE B -- Teste de convergˆ
encia de
s´
eries infinitas
Existem v´arios testes para estudar a convergˆencia ou divergˆencia de uma s´erie. Al-gumas vezes ao se aplicar um teste para uma determinada s´erie, este n˜ao ´e adequado, ou n˜ao nos leva `a conclus˜ao alguma e assim sendo teremos que utilizar um outro teste. Aqui vamos resumir os principais testes de convergˆencia para s´eries infinitas.
B.1
O teste da raz˜
ao
Seja P+∞
n=1un uma s´erie infinita dada para todo un n˜ao-nulo. Ent˜ao:
i) se limn→∞|un+1|/|un|=L <1, a s´erie ´e absolutamente convergente;
ii) se limn→∞|un+1|/|un| = L > 1, ou se limn→∞|un+1|/|un| = +∞, a s´erie dada ´e
divergente.
iii) se limn→∞|un+1|/|un| = 1, nenhuma conclus˜ao quanto `a convergˆencia pode ser
tirada do teste, devendo assim utilizar-se outro teste.
B.2
O teste da integral
Seja f uma fun¸c˜ao cont´ınua, decrescente e com valores positivos para todo x ≥ 1. Ent˜ao, a s´erie infinita:
∞ X
n=1
f(n) = f(1) +f(2) +f(3) +· · ·+f(n) +· · ·
ser´a convergente se a integral impr´opria
Z +∞
1
existir, e ser´a divergente se
lim
b→∞ Z b
1
f(x)dx= +∞
B.3
O teste da compara¸c˜
ao
Seja P+∞
n=1un uma s´erie de termos positivos.
i) se P+∞
n=1vn for uma s´erie convergente de termos positivos j´a conhecida e un ≤ vn
para todon inteiro positivo, ent˜ao P+∞
n=1un ser´a convergente.
ii) se P+∞
n=1wn for uma s´erie divergente de termos positivos j´a conhecida e un ≥ vn
para todon inteiro positivo, ent˜ao P+∞
n=1un ser´a divergente.
Existem outros testes que podem ser utilizados como citados em (44).
B.4
A s´
erie
P
∞n=0
e
−√
an+bβ
A s´erie fun¸c˜ao de parti¸c˜ao do oscilador de Dirac unidimensional ´e do tipo: ∞
X
n=0
e−√an+bβ (B.1)
Iremos agora estudar a convergˆencia da s´erie acima. Iniciemos nosso estudo pela s´erie P∞
n=0e−
√
nβ. Aplicando o teste da raz˜ao temos:
an+1 =e−
√
n+1β
an =e−
√
nβ (B.2)
assim calculando:
lim
n→∞|an+1|/|an|= limn→∞
e−√n+1β
e−√nβ = limn→∞e
− 1 √n+√
n+1β =e0 = 1 (B.3)
logo n˜ao podemos afirmar nada sobre a convergˆencia da s´erie. Ent˜ao aplicaremos o teste da integral. Basta verificar a existˆencia da integral impr´opria:
Z ∞
0
e−√xdx (B.4)
Fazendo uma mudan¸ca de vari´avel
a equa¸c˜ao acima fica:
I = 2 Z ∞
0
e−yydy (B.5)
Agora integrando por partes temos:
I = 2 µ
e−yy
∞
0
− Z ∞
0
e−ydy
¶
= 2 (B.6)
Logo a integral existe e a s´erie ´e convergente. Agora usando o m´etodo da integral para a s´erie P∞
n=0e−
√
an+bβ, verificamos que a integral resulta em:
I = Z ∞
0
e−√an+bβdn (B.7)
Fazendo uma mudan¸ca de vari´avel temos:
an+b=y2 , adn= 2ydy
logo (B.7) fica:
I = 2
a
Z ∞
0
e−yydy
I = 2
aeβ (B.8)
APˆ
ENDICE C -- Rela¸c˜
oes e constantes
f´ısicas ´
uteis
C.1
Quantidades termodinˆ
amicas
Fun¸c˜ao de parti¸c˜ao:
Z =X
n
e−EnkT (C.1)
onde En´e a energia do sistema.
Energia m´edia:
U = 1
Z
X
n
Ene−
En
kT =−1
Z ∂Z ∂β =−
∂lnZ
∂β , (C.2)
onde Z ´e dado por (C.1) e β = kT1 . Calor espec´ıfico:
c= ∂U
∂T (C.3)
C.2
Constantes f´ısicas
Constante de Plank:
~= 1,054573.10−34J.s= 6,582122.10−16eV.s
Constante de Boltzmann:
k = 8,617385.10−5eV /K = 1,3181.10−23J/K
C.3
Rela¸c˜
oes da m´
etrica e derivadas
∂µ≡ ∂ ∂xµ =
µ
∂ ∂t,−∇
¶
Derivada contravariante:
∂µ≡ ∂x∂µ = µ
∂ ∂t,∇
¶
C.4
Matrizes de Dirac
γ0 =
"
1 0
0 −1
#
e γi =
"
0 σi
−σi 0
#
,
As matrizes de Dirac satisfazem a rela¸c˜ao:
{γµ, γν}=γµγν+γνγµ= 2gµν (C.4)
C.5
Matrizes de Pauli
σ1 =
" 0 1 1 0
#
, σ2 =
"
0 −ı
ı 0
#
, σ3 =
"
1 0 0 −1
#
.
C.6
Rela¸c˜
ao ´
util
Z ∞ √
b
une−uβdu=e−β√b
3
X
k=0
3!
k! (√b)k