Controle H-infinito não linear e a equação de Hamilton Jacobi-Isaacs

(1)

CONTROLE

H∞

N ˜

AO LINEAR E A EQUAC

¸ ˜

AO DE

HAMILTON-JACOBI-ISAACS

(2)

CONTROLE

H∞

N ˜

AO LINEAR E A EQUAC

¸ ˜

AO DE

HAMILTON-JACOBI-ISAACS

Tese apresentada à Escola Politécnica da Universidade de São Paulo para obten¸cão do t´ıtulo de Doutor em Engenharia Elétrica

´

Area de Concentra¸c˜ao: Engenharia de Sistemas

Orientador:

Prof. Dr. Roberto Moura Sales

(3)

things; it will improve your theories. If you find that

you’re spending almost all your time on practice,

start turning some attention to theoretical things; it

will improve your practice.

(4)

O objetivo desta tese é investigar aspectos práticos que facilitem a aplica¸cão da teoria de controle H∞ não linear em projetos de sistemas de controle. A primeira

contribui¸cão deste trabalho é a proposta do uso de fun¸cões pondera¸cão com dinâmica no projeto de controladores H∞ não lineares. Essas fun¸cões são usadas no projeto de

controladoresH∞ lineares para rejei¸cão de perturba¸cões, ru´ıdos, atenua¸cão de erro de

rastreamento, dentre outras especifica¸cões. O maior obstáculo para aplica¸cão prática da teoria de controle H∞ não linear é a dificuldade para resolver simultaneamente as

duas equa¸cões de Hamilton-Jacobi-Isaacs relacionadas ao problema de realimenta¸cão de estados e inje¸cão da sa´ıda. Não há métodos sistemáticos para resolver essas duas equa¸cões diferenciais parciais não lineares, equivalentes às equa¸cões de Riccati da te-oria de controle H∞ linear. A segunda contribui¸cão desta tese é um método para

obter a inje¸cão da sa´ıda transformando a equa¸cão de Hamilton-Jacobi-Isaacs em uma seqüência de equa¸cões diferenciais parciais lineares, que são resolvidas usando o método de Galerkin. Controladores H∞ não lineares para um sistema de levita¸cão magnética

são obtidos usando o método clássico de expansão em série de Taylor e o método de proposto para compara¸cão.

Palavras-chave: Controle H∞ não linear, fun¸cões pondera¸cão, realimenta¸cão da

(5)

The purpose of this thesis is to investigate practical aspects to facilitate the ap-plication of nonlinear H∞ theory in control systems design. Firstly, it is shown that

dynamic weighting functions can be used to improve the performance and robustness of the nonlinearH∞controller such as in the design of H∞ controllers for linear plants.

The biggest bottleneck to the practical applications of nonlinear H∞ control theory

has been the difficulty in solving the Hamilton-Jacobi-Isaacs equations associated with the design of a state feedback and an output injection gain. There is no systematic numerical approach for solving this first order, nonlinear partial differential equations, which reduces to Riccati equations in the linear context. In this work, successive ap-proximation and Galerkin apap-proximation methods are combined to derive an algorithm that produces an output injection gain. Design of nonlinear H∞ controllers obtained

by the well established Taylor approximation and by the proposed Galerkin approxi-mation method applied to a magnetic levitation system are presented for comparison purposes.

Keywords: Nonlinear H∞ control, Weighting functions, Output feedback,

(6)

2.1 Sistema em malha fechada com fun¸c˜ao pondera¸c˜ao . . . 22

3.1 Proje¸c˜ao de um vetor do R3 _noR2 _{. . . .} ₃₄

4.1 Sistema de levita¸c˜ao magn´etica . . . 58

4.2 Sistema em malha fechada com fun¸c˜oes pondera¸c˜ao . . . 61

4.3 Fun¸c˜oes pondera¸c˜ao . . . 62

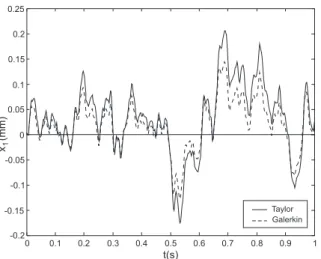
4.4 Rejei¸cão de ru´ıdo e perturba¸cão do sistema sem e com fun¸cões pondera¸cão 64 4.5 Posi¸cão, velocidade e a¸cão de controle para sistema com inje¸cão da sa´ıda obtida por expansão em série de Taylor e ASG . . . 66

4.6 Rejei¸cão de ru´ıdo para sistema com inje¸cão da sa´ıda obtida por expansão em série de Taylor e ASG . . . 67

4.7 Resposta a uma perturba¸c˜ao do tipo impulso na for¸ca de levita¸c˜ao . . . 68

4.8 Efeito do dom´ınio de estabilidade sobre a resposta . . . 69

(7)

η Mapa suave η: Ξ×Rp _→Rν _{. . . 8}

γ Ganho L2. . . 9

Al(Ω) Conjunto de leis de controle admiss´ıveis para o problema de controle ótimo não linear com fun¸cão penaliza¸cão l e região de estabilidade Ω . . . 50

P(Φ,Ω) Conjunto de todas as combina¸c˜oes lineares dos elementos em Φ que convergem ponto a ponto a cada x∈Ω . . . 51

C− _{Semiplano esquerdo do plano complexo . . . 14}

Ω Regi˜ao de estabilidade . . . 30

Φ Conjunto de fun¸c˜oes usadas como base para aproxima¸c˜ao de Galerkin . . . 51

φv Base de fun¸c˜oes para realimenta¸c˜ao de estado . . . 36

φw Base de fun¸c˜oes para realimenta¸c˜ao da sa´ıda . . . 40

σ(M) Conjunto de autovalores da matriz M. . . 14

θ Mapa suave η: Ξ×Rp _→_Rm_{. . . 8}

Ξ Vizinhan¸ca da origem em Rν_{. . . 8}

ξ Vetor estado estimado em Rν _{. . . 8}

A Matriz Rn×n_{. . . 13}

(8)

C1 Matriz Rn×s. . . 13

C2 Matriz Rn×p. . . 20

cv coeficientes da aproxima¸c˜ao de Galerkin para VN. . . 36

cw coeficientes da aproxima¸c˜ao de Galerkin para WN. . . 40

D2 Matriz Rp×r. . . 15

D11 Matriz Rr×s. . . 20

D12 Matriz Rm×s. . . 20

D21 Matriz Rr×p. . . 20

F Mapa suave Rn_×_Rr_×_Rm _→_Rn_{. . . 8}

f Mapa Rn _→_Rn_{. . . 13}

F(t) For¸ca magn´etica . . . 58

fd For¸ca de perturba¸c˜ao . . . 58

G Inje¸c˜ao da sa´ıda . . . 17

g Acelera¸c˜ao da gravidade . . . 58

g1 Mapa Rn →Rn. . . 13

g2 Mapa Rn →Rn. . . 13

H Fun¸c˜ao Hamiltoniana do estado . . . 10

H∗ Hamiltoniana para w∗ e u∗. . . 11

h1 Mapa Rn →Rs. . . 13

h2 Vetor em Rp. . . 18

(9)

K Fun¸c˜ao Hamiltoniana da sa´ıda . . . 14

k Constante do mancal magn´etico . . . 58

k11 Matriz Rr×s. . . 18

k12 Matriz Rm×s. . . 18

k21 Matriz Rr×p. . . 18

L Matriz de realimenta¸c˜ao de estados Rm×n_{. . . 13}

l Fun¸cão penaliza¸cão para controlador ótimo não linear . . . 50

m massa do corpo levitado . . . 58

P Solu¸c˜ao da EAR do estado . . . 26

Q Solu¸c˜ao da EAR da sa´ıda . . . 26

s taxa de suprimento . . . 9

u vetor de entrada de controle em Rm_{. . . 8}

u∗ Controle que minimiza a Hamiltoniana H. . . 10

V Fun¸c˜ao armazenamento do estado . . . 9

Va Fun¸c˜ao armazenamento dispon´ıvel . . . 44

VN Aproxima¸c˜ao de ordem N para a fun¸c˜ao armazenamento . . . 34

W Fun¸c˜ao armazenamento da sa´ıda . . . 16

w Vetor de entrada ex´ogena em Rr_{. . . 8}

W(s) Fun¸c˜ao pondera¸c˜ao . . . 22

w∗ Perturba¸c˜ao que maxima a Hamiltoniana H . . . 10

(10)

WN Aproxima¸c˜ao de ordem N da fun¸c˜ao armazenamento da sa´ıda . . . 40

w∗∗ Vetor w que maximiza a HamitonianaK. . . 16

x Vetor de estado em Rn_{. . . 8}

Y Mapa suave Rn_×Rr _→Rp_{. . . 8}

y vetor de sa´ıda em Rp _{. . . 8}

y∗ Vetor y que minimiza a Hamiltoniana K. . . 15

Z Mapa suave Rn_×_Rm _→_Rs_{. . . 8}

(11)

ASG Aproxima¸c˜ao Sucessiva de Galerkin . . . 4

CTMSP Centro Tecnol´ogico da Marinha em S˜ao Paulo . . . 57

DHJI Desigualdade de Hamilton-Jacobi-Isaacs . . . 12

DOV Dom´ınio de validade . . . 44

EAR Equa¸c˜ao Alg´ebrica de Riccati . . . 1

EDP Equa¸c˜ao Diferencial Parcial . . . 3

EHJB Equa¸c˜ao de Hamilton-Jacobi-Bellman . . . 3

EHJI Equa¸c˜ao de Hamilton-Jacobi-Isaacs . . . 2

EHJIG Equa¸c˜ao de Hamilton-Jacobi-Isaacs Generalizada . . . 4

LMI Desigualdade Matricial Linear. . . 4

(12)

1 Introdu¸c˜ao 1

1.1 Revis˜ao bibliogr´afica . . . 1

1.2 Objetivo . . . 4

1.3 Contribui¸c˜oes do trabalho . . . 5

1.4 Estrutura do texto . . . 6

2 Controle H∞ n˜ao linear 7 2.1 Introdu¸c˜ao . . . 7

2.2 Controle H∞ n˜ao linear via realimenta¸c˜ao de estados . . . 9

2.2.1 Realimenta¸c˜ao de estados para sistema n˜ao linear afim . . . 12

2.3 Controle H∞ n˜ao linear via realimenta¸c˜ao da sa´ıda . . . 14

2.3.1 Uma condi¸c˜ao necess´aria . . . 14

2.3.2 Realimenta¸c˜ao da sa´ıda . . . 16

2.3.3 Realimenta¸c˜ao da sa´ıda para sistema n˜ao linear afim . . . 18

2.4 Inclusão de fun¸cões pondera¸cão com dinâmica no projeto de controle H∞ não linear . . . 21

2.5 Solu¸cão das EHJI por expansão em série de Taylor . . . 23

2.5.1 Realimenta¸c˜ao de estados . . . 24

(13)

3.1 Introdu¸c˜ao . . . 28

3.2 Aproxima¸c˜ao sucessiva . . . 28

3.3 M´etodo de Galerkin . . . 33

3.4 Convergência do método de aproxima¸cões sucessivas . . . 43

3.5 Convergˆencia do M´etodo de Galerkin . . . 49

3.5.1 Problema de controle ´otimo n˜ao linear . . . 50

3.5.2 Problema de controle H∞ não linear por realimenta¸cão de estados 53 3.5.3 Problema de controle H∞ não linear por realimenta¸cão da sa´ıda 54 4 Controle H∞ não linear de sistema de levita¸cão magnética 57 4.1 Introdu¸cão . . . 57

4.2 Modelo não linear do sistema de levita¸cão magnética . . . 57

4.3 Projeto do controlador H∞ n˜ao linear . . . 60

4.3.1 Realimenta¸c˜ao dos estados . . . 60

4.4 Inclusão de fun¸cões pondera¸cão . . . 61

4.5 Aproxima¸c˜ao sucessiva de Galerkin para a EHJI . . . 64

(14)

(15)

Introdu¸

c˜

ao

1.1 Revis˜

ao bibliogr´

afica

A norma H∞ desempenha um importante papel no estudo e an´alise da teoria de

controle robusto desde sua formula¸cão original por Zames (1981) empregando métodos no dom´ınio da freqüência. Solu¸cões no dom´ınio do tempo foram rigorosamente deriva-das por Doyle et al. (1989) para sistemas lineares e estão relacionaderiva-das com a existência de solu¸cões de Equa¸cões Algébricas de Riccati (EAR). Posteriormente o problema de controleH∞foi formulado como um jogo diferencial de duas pessoas e soma zero (Ba¸sar

e Bernhard, 1990).

A contrapartida n˜ao linear da teoria de controleH∞come¸cou a ser desenvolvida a

partir das importantes contribui¸c˜oes de Ball e Helton (1989), Ba¸sar e Bernhard (1990) e van der Schaft (1991). Apesar da norma H∞ ser definida como uma norma para

matrizes de transferˆencia, no dom´ınio do tempo, nada mais ´e que a normaL2 induzida

(da entrada no tempo para sa´ıda no tempo com estado inicial nulo). Van der Schaft (1991) mostrou que a solu¸cão do problema de controleH∞não linear por realimenta¸cão

de estados pode ser obtida da solu¸cão de um tipo de equa¸cão de Hamilton-Jacobi, a equa¸cão (ou desigualdade) de Hamilton-Jacobi-Isaacs (EHJI), que é a versão não linear da EAR do problema de controle H∞ para sistemas lineares. Van der Schaft (1992)

mostrou que se o problema de controleH∞para a planta linearizada tem solu¸c˜ao, ent˜ao

(16)

O problema de controle H∞ n˜ao linear por realimenta¸c˜ao da sa´ıda foi tratado

por, dentre outros, Isidori e Astolfi (1992), Ball, Helton e Walker (1993), van der Schaft (1993), Isidori (1994), Isidori e Kang (1995) e James e Baras (1995). Em parti-cular, Isidori e Astolfi (1992) apresentam um conjunto de condi¸cões suficientes para a solu¸cão do problema de atenua¸cão local de perturba¸cões no caso de realimenta¸cão da sa´ıda para sistemas modelados por equa¸cões que são afins tanto no controle quanto na perturba¸cão. Ball, Helton e Walker (1993) apresentam resultados relacionados à ne-cessidade das condi¸cões propostas por Isidori e Astolfi (1992) e mostram a nene-cessidade da existência de solu¸cão de uma EHJI, que é a versão não linear da EAR associada com o problema de controle H∞ por realimenta¸cão da sa´ıda para sistemas lineares.

Além disso, mostram que as solu¸cão das EHJIs relacionadas aos problemas de rea-limenta¸cão de estado e inje¸cão da sa´ıda obedecem uma condi¸cão de desacoplamento que, novamente, é totalmente análoga à condi¸cão de desacoplamento existente entre as solu¸cões das EARs no caso de sistemas lineares. Ball, Helton e Walker (1993) verifi-cam, portanto, um princ´ıpio da separa¸cão na teoria de controleH∞não linear. Isidori e

Kang (1995) apresentam condi¸cões necessárias para existência de solu¸cão do problema de realimenta¸cão da sa´ıda para sistemas não lineares não necessariamente afins nas entradas.

Devido `as analogias entre a teoria de controle H∞ linear e n˜ao linear, alguns

trabalhos procuram estender resultados existentes do caso linear para o contexto não linear. Por exemplo, Fromion, Monaco e Normand-Cyrot (2001) mostram como normas incrementais ponderadas podem ser usadas para atingir, em um contexto não linear, requisitos básicos de estabilidade robusta, atenua¸cão de perturba¸cão e comportamento de estado permanente para sistemas lineares com parâmetros variantes, obtendo con-troladores dependentes dos parâmetros (ganho escalonado). A formula¸cão do problema de controleH∞não linear nesse trabalho, no entanto, é diferente da formula¸cão clássica

de van der Schaft (1991, 1992) que é tratada nessa tese. Su, Anderson e Brinsmead (2002) usam integrador para rejei¸cão de perturba¸cão constante no projeto de contro-ladores H∞ não lineares. Algo semelhante já havia sido proposto para o projeto de

controladoresH∞ lineares.

(17)

desenvol-vida, a solu¸cão das EHJIs permanecem como um desafio e é o maior obstáculo para aplica¸cão prática da teoria (Lu e Doyle, 1995; Beard e McLain, 1998; Aliyu, 2003; Abu-Khalaf, Lewis e Huang, 2006a,b). A EHJI é uma equa¸cão diferencial parcial (EDP) não linear de primeira ordem imposs´ıvel de ser resolvida para um caso geral e muito dif´ıcil ser resolvida para sistemas não lineares espec´ıficos. Como essa equa¸cão é muito dif´ıcil de ser resolvida analiticamente, vários métodos numéricos sistemáticos tem sido propostos para resolvê-la.

A expansão em série de Taylor foi o primeiro método usado para aproximar as solu¸cões da EHJI e é o mais usado para objetivos práticos. Esse método foi primeiro aplicado para a solu¸cão da equa¸cão de Hamilton-Jacobi-Belman (EHJB) proveniente do problema de controle ótimo não linear (Lukes, 1969). Van der Schaft (1992) foi o primeiro a propor a expansão em série de Taylor para solu¸cão da EHJI. Alguns traba-lhos apresentam a solu¸cão aproximada por série de Taylor de sistemas como aviões de combate (Kang, De e Isidori, 1992), manipuladores robóticos (Yazdanpanah, Khora-sani e Patel, 1998) e levitador magnético (Sinha e Pechev, 2004). Huang e Lin (1995) propõem um procedimento sistemático para encontrar a aproxima¸cão por série de Tay-lor da solu¸cão da EHJI para realimenta¸cão de estados. A dificuldade em resolver o problema aumenta conforme aumenta a ordem do termo da aproxima¸cão e é dif´ıcil garantir estabilidade para um número finito de termos da série. Apesar de estudarem a região de estabilidade da realimenta¸cão de estados obtida por aproxima¸cão por série de Taylor, não é poss´ıvel determiná-la a prio

A região de estabilidade da lei de controle aproximada é limitada pela região de convergência da série de Taylor e é melhor estudada em Yazdanpanah, Khorasani e Patel (1999). Esta região é imposs´ıvel determinar a priori. (Beard e McLain, 1998).

(18)

Esse procedimento leva a um sistema de equa¸cões diferenciais parciais que podem ser resolvidas pelo método das caracter´ısticas. Lu e Doyle (1995) e Patpong et al. (1996) analisam a possibilidade de caracterizar o problema de controle H∞ não linear como

um problema convexo e apresentam solu¸cões em termos de desigualdades matriciais não lineares (NLMIs), que são desigualdades matriciais lineares (LMIs) dependentes do estado. Contudo, não há garantia de existência de solu¸cões através desse método.

Beard e McLain (1998) combinam o método de aproxima¸cões sucessivas e o método de aproxima¸cão de Galerkin para obter um algoritmo que produz realimenta¸cões de estado estabilizantes com regiões de estabilidade bem conhecidas. Enquanto o método de aproxima¸cões sucessivas reduz a EHJI em uma seqüência de EDPs lineares, chamadas Equa¸cões de Hamilton-Jacobi-Isaacs Generalizadas (EHJIG), o método de Galerkin é usado para aproximá-las. Esse método será chamado, assim como em (Be-ard e McLain, 1998), Aproxima¸cão Sucessiva de Galerkin (ASG). Apesar desse método exigir o cálculo de integrais cujo número cresce exponencialmente com a ordem do sistema, a estrutura do algoritmo proposto diminui significativamente a quantidade de cálculos. O método de Galerkin assume que a solu¸cão da EHJIG pode ser expressa como uma soma infinita de fun¸cões base. A escolha dessa base não é trivial e exige conhecimento do sistema onde o método será aplicado. No entanto, uma boa escolha da base pode fornecer controladores com boa performance. Abu-Khalaf, Lewis e Hu-ang (2006a) combinam o método de aproxima¸cões sucessivas com redes neurais para obter a realimenta¸cão de estados para o problema de controle ótimo e controleH∞não

lineares.

1.2 Objetivo

O objetivo deste estudo é investigar aspectos práticos que facilitem a aplica¸cão da teoria de controleH∞ não linear em projetos de sistemas de controle. Tal necessidade

(19)

1.3 Contribui¸

c˜

oes do trabalho

A primeira contribui¸cão desta tese é mostrar que fun¸cões pondera¸cão, assim como no contexto do controleH∞ linear, podem ser usadas para melhorar a performance do

controlador H∞ n˜ao linear. Se o problema de controle H∞ linear incluindo fun¸c˜oes

pondera¸cão na planta é solúvel, é poss´ıvel mostrar que o problema de controleH∞não

linear para a planta não linear incluindo as fun¸cões pondera¸cão usadas no projeto linear também é solúvel.

A segunda contribui¸cão desta tese é estender o método de aproxima¸cão suces-siva de Galerkin para resolver de um modo sistemático o problema de realimenta¸cão da sa´ıda. De todos os métodos anteriormente citados para resolver a EHJI, apenas o método de aproxima¸cão por série de Taylor tem sido aplicado no problema de re-alimenta¸cão da sa´ıda e não há um procedimento sistemático como no caso da reali-menta¸cão de estados (Huang e Lin, 1995), o que dificulta a implereali-menta¸cão computa-cional do método. Abu-Khalaf, Lewis e Huang (2006b) provaram a convergência do método de aproxima¸cões sucessivas para aproximar a solu¸cão da EHIJ e Beard, Sari-dis e Wen (1997) provaram a convergência do método de Galerkin para a solu¸cão da EHJB do problema de controle ótimo não linear via realimenta¸cão de estados. Nesta tese será provada a convergência do método de aproxima¸cões sucessivas para a EHIJ do problema de realimenta¸cão da sa´ıda e será provada a convergência do método de Galerkin para aproxima¸cão da solu¸cão da EHIJ dos problemas de controle H∞ não

linear via realimenta¸c˜ao de estado e de sa´ıda.

(20)

1.4 Estrutura do texto

Este trabalho est´a organizado da seguinte forma.

No cap´ıtulo 2 são apresentados os principais resultados da teoria de controle H∞ não linear. É mostrado que fun¸cões pondera¸cão podem ser usadas no projeto de

controladores H∞ não lineares, assim como é feito no contexto linear. Finalmente é

mostrado o método clássico de solu¸cão das EHJIs, a expansão em série de Taylor.

No cap´ıtulo 3 é apresentado o método de aproxima¸cão sucessiva de Galerkin para realimenta¸cão de estados proposto por Beard e McLain (1998). É desenvolvido um procedimento para solu¸cão da EHJI associada ao problema de realimenta¸cão da sa´ıda usando o método de aproxima¸cão sucessiva de Galerkin. A convergência do algoritmo proposto é provada.

No cap´ıtulo 4 os resultados obtidos nesta tese são aplicados a um sistema de levita¸cão magnética. Primeiramente é mostrada a vantagem do uso de fun¸cões pon-dera¸cão no projeto do controladorH∞ não linear. Depois as EHJIs referentes aos

pro-blemas de realimenta¸cão de estados e de realimenta¸cão da sa´ıda são resolvidas usando o algoritmo de aproxima¸cão sucessiva de Galerkin, desenvolvido no cap´ıtulo 3.

(21)

Controle

H

_∞

n˜

ao linear

2.1 Introdu¸

c˜

ao

O controle H∞ n˜ao linear resulta da teoria da dissipatividade para sistemas n˜ao

lineares e da teoria de controle H∞ linear. Esta conex˜ao entre a teoria da

dissipa-tividade, que foi desenvolvida no come¸co da d´ecada de 1970, e a teoria de controle H∞ linear, apareceu no final da d´ecada de 1980 e atingiu algum n´ıvel de maturidade

no in´ıcio da década de 1990. Neste cap´ıtulo são apresentados os resultados mais im-portantes da teoria de controleH∞ não linear.

Os resultados da teoria de controle H∞ n˜ao linear usados neste trabalho foram

propostos por van der Schaft (1991, 1992) para realimenta¸cão de estados e por Isidori e Astolfi (1992) e Isidori e Kang (1995) para realimenta¸cão da sa´ıda. Inicialmente serão mostrados resultados para sistemas não lineares em uma forma mais geral, como em Isidori e Kang (1995) e depois para sistemas não lineares afins, como em van der Schaft (1991, 1992) e Isidori e Astolfi (1992).

Considere um sistema n˜ao linear modelado pelas equa¸c˜oes na forma

˙

x=F(x, w, u), z =Z(x, u), y=Y(x, w).

(2.1)

(22)

uma vizinhan¸ca X da origem em Rn _com _{entrada de controle} _u _∈ _Rm _{e sujeita a um}

conjunto de entradas ex´ogenas w ∈ Rr _{que inclui} _{perturba¸c˜}_oes _{(a serem rejeitadas)} e/ou referˆencias (a serem rastreadas). Admite-se que s≥m.

A segunda equa¸c˜ao define uma vari´avel penalidade z ∈ Rs_{, que pode incluir}

um erro de rastreamento assim como um custo da entrada u necess´aria para atingir o objetivo do sistema de controle.

A terceira equa¸cão define um conjunto devariáveis medidas y∈Rp_{, que também}

são fun¸cões do estado da planta xe da entrada exógena w. Admite-se que p≤r.

Os mapeamentos F(x, w, u), Z(x, u) e Y(x, w) s˜ao mapeamentos suaves (isto ´e, mapeamentos de classe Ck _{para algum} _k _{suficientemente grande) definidos em uma}

vizinhan¸ca da origem em Rn _×_Rr _× _Rm_{. ´}_{E assumido tamb´em que} _F_(0,_0,_{0) = 0,}

Z(0,0) = 0 e Y(0,0) = 0.

A lei de controle para (2.1) será provida por um controlador, que processa a variável medida y, gera uma entrada de controle apropriada u, e é modelado por equa¸cões na forma

˙

ξ=η(ξ, y),

u=θ(ξ, y), (2.2)

onde ξ é definida em uma vizinhan¸ca Ξ da origem em Rν _e _η _{: Ξ}_× Rp _→ Rν _e θ: Ξ×Rp _→_Rm _{são fun¸cões suaves, satisfazendo} _η(0,_{0) = 0 e}_θ(0,_{0) = 0.}

O objetivo do controle é duplo: alcan¸car a estabilidade em malha fechada e atenuar a influência da entrada exógenawna variável penalidadez. A propriedade de atenua¸cão de perturba¸cão em um sistema não linear pode ser caracterizada da seguinte forma (Willems, 1972; van der Schaft, 1992; Ball, Helton e Walker, 1993). Um sistema não linear

˙

x=f(x, u),

y=h(x), (2.3)

´e localmente dissipativo perto de (x, u) = (0,0), com respeito `a uma dada taxa de

(23)

n˜ao negativa exceto em x= 0, tal que

∂V

∂xf(x, u)−s(u, h(x))≤0,

para todo (x, u) em uma vizinhan¸ca de (0,0).

Se (2.3) for localmente assintoticamente estável (na origem) e localmente dissi-pativa com respeito à taxa de suprimentos(u, y) =γ2_k_u_k2_{− k}_y_k2_{, então sua sa´ıda para}

qualquer entrada suficientemente pequena, a partir do estado inicialx(0) = 0, satisfaz

0≤V(x(t))≤

Z t

0

(γ2ku(s)k2− ky(s)k2)ds,

para todot >0. Como conseq¨uˆencia, (2.3) tem ganho L2 menor ou igual aγ.

A seguir, será tratado o problema de encontrar um controlador que proporcione um sistema em malha fechada (2.1) – (2.2) localmente assintoticamente estável e lo-calmente dissipativo com respeito à taxa de suprimentos(w, z) =γ2_k_w_k2_{− k}_z_k2_{. Esse}

problema será chamado de problema de controle H∞ não linear. Primeiro será

anali-sada a situa¸cão em que todos os estados estão dispon´ıveis para realimenta¸cão. Depois será analisado o caso de realimenta¸cão da sa´ıda.

2.2 Controle

H

∞

n˜

ao linear via realimenta¸

c˜

ao de

estados

Como apontado por v´arios autores (veja, por exemplo, Ball, Helton e Walker (1993) e Ba¸sar e Bernhard (1990)), o problema de encontrar uma lei de controle da forma u=α(x) gerando um sistema em malha fechada

˙

x=F(x, w, α(x)),

z =Z(x, α(x)), (2.4)

localmente dissipativo com respeito `a taxa de suprimentos(w, z) =γ2_k_w_k2_−k_z_k2_{, pode}

(24)

norma da entrada de u e maximizada norma da entradaw.

A fun¸cão Hamiltoniana associada com o jogo em questão é uma fun¸cão H : Rn_×_Rn_×_Rr_×_Rm _→_R_{definida como}

H(x, p, w, u) =pT_F_{(x, w, u) +}_k_{Z(x, u)}_k2 ₋_γ2_k_w_k2_. _(2.5)

Suponha que a planta (2.1) satisfa¸ca `a seguinte hip´otese.

Hip´otese 2.1. O mapa penalidade Z(x, u) ´e tal que a matriz

D1 =

∂Z ∂u(0,0)

tem postom.

Então é fácil ver que em uma vizinhan¸ca do ponto (x, p, w, u) = (0,0,0,0), a fun¸cão H(x, p, u, w) tem ponto de sela local único em (w, u) para cada (x, p). Mais precisamente, existem fun¸cões suaves w∗(x, p) e u∗(x, p) únicas, definidas em uma

vi-zinhan¸ca de (0,0), satisfazendo

∂H

∂w(x, p, w∗(x, p), u∗(x, p)) = 0, ∂H

∂u(x, p, w∗(x, p), u∗(x, p)) = 0,

w∗(0,0) = 0,

u∗(0,0) = 0,

e tais que

H(x, p, w, u∗(x, p))≤H(x, p, w∗(x, p), u∗(x, p))≤H(x, p, w∗(x, p), u) (2.6)

(25)





−2γ2_I ₀

0 2DT

1D1



,

onde DT

1D1 ´e positiva definida por hip´otese (D1 tem postom).

Seja agora V : Rn _→ _R _{uma fun¸c˜ao suave, definida em uma vizinhan¸ca} _U _de

x= 0 e tal queV(0) = 0 e Vx(0) = 0, defina

H∗(x, p) = H(x, p, w∗(x, p), u∗(x, p)),

α1 =w∗(x, VxT(x)),

α2 =u∗(x, V_xT(x)),

(2.7)

e observe que (2.6), em particular, implica

H(x, VxT(x), w, α2(x))≤H∗(x, VxT(x)).

Agora, suponha que a fun¸cãoV(x) é não negativa (casoV(0) = 0, tem-seVx(0) =

0) e considere a desigualdade

H∗(x, VxT(x))≤0 (2.8)

satisfeita para todox em uma vizinhan¸ca de zero. Ent˜ao fa¸ca α(x) =α2(x) em (2.4).

Isto faz o sistema em malha fechada satisfazer

Vx(x)F(x, w, α2(x)) +kZ(x, α2(x))k2−γ2kwk2 ≤0,

que ´e um sistema que, em uma vizinhan¸ca de (x, w) = (0,0), tem a propriedade de dissipatividade satisfeita.

A desigualdade (2.8) é chamada desigualdade de Hamilton-Jacobi-Isaacs (DHJI). SeV(x) é positiva definida e uma hipótese adicional apropriada é satisfeita, pode ser provado que a lei de controleu=α2(x) é também localmente assintoticamente

(26)

Hip´otese 2.2. Qualquer trajet´oria limitadax(t) do sistema

˙

x(t) = F(x(t),0, u(t))

satisfazendo

Z(x(t), u(t)) = 0

para todot >0, ´e tal que lim

t→0x(t) = 0.

Proposi¸cão 2.1 (Isidori e Kang (1995)). Considere que o sistema (2.1) e as hipóteses 2.1 e 2.2 sejam satisfeitas. Suponha que exista uma fun¸cão suave positiva definida V(x), localmente definida em uma vizinhan¸ca dex= 0 e tal que V(0) = 0, que satisfaz a DHJI (2.8). Então a lei de controleu=α2(x) resolve o problema de atenua¸cão local

de perturba¸c˜ao com estabilidade interna.

Observa¸cão 2.1. Apesar de haver interesse em solu¸cões não negativas de (2.8), o pro-blema será restrito a encontrar solu¸cões da equa¸cão de Hamilton-Jacobi-Isaacs (EHJI):

H∗(x, VxT(x)) = 0, V(0) = 0, Vx(0) = 0.

Note que a condi¸cão extraVx(0) = 0 é automaticamente satisfeita seV é não negativa.

2.2.1 Realimenta¸

c˜

ao de estados para sistema n˜

ao linear afim

Considere um sistema n˜ao linear na seguinte forma

˙

x=f(x) +g1(x)w+g2(x)u,

z =





h1(x)

u



,

(2.9)

onde x∈ Rn_, _u_∈ _Rm_, _w_∈ _Rr_, _z _∈_Rs_, _{f(0) = 0 e} _h

1(0) = 0. A solu¸c˜ao do problema

(27)

Teorema 2.1 (van der Schaft (1992)). Considere o sistema n˜ao linear dado por (2.9) com γ >0. Suponha que exista uma solu¸c˜ao suave V(x)≥0 para a DHJI

∂V(x)

∂x f(x) + 1 2

∂V(x) ∂x

·

1

γ2g1(x)g

T

1(x)−g2(x)g2T(x)

¸

∂VT_(x)

∂x +

1 2h

T

1(x)h1(x)≤0,

(2.10)

com V(0) = 0. Ent˜ao a realimenta¸c˜ao de estados

u=−gT

2(x)

∂VT_(x)

∂x (2.11)

tem ganhoL2 menor ou igual a γ.

Teorema 2.2 (van der Schaft (1992, 1993)). Considere o sistema (2.9) linearizado

˙¯

x=Ax¯+B1w¯+B2u,¯

¯ z =





C1x¯

¯ u



,

onde ¯x ∈ Rn_{, ¯}_u _∈ _Rm_{, ¯}_w _∈ _Rr_{, ¯}_z _∈_Rs_, _A ₌ _∂f_(x)/∂x_|

x=0, B1 =g1(0), B2 = g2(0) e

C1 =∂h(x)/∂x|x=0.

Assuma que (A, C1) seja detectável. As seguintes afirma¸cões são equivalentes

i) Existe uma realimenta¸c˜ao linear de estados

¯ u=L¯x

tal que o sistema em malha fechada ´e assintoticamente est´avel e tem ganho L2 <

γ (isto ´e, o problema de controle H∞ linear via realimenta¸c˜ao de estados tem

solu¸c˜ao).

ii) Existe uma solu¸cão simétrica X =XT _≥_{0 para a Equa¸cão algébrica de Riccati}

(EAR)

AT_X₊_XA₊_X µ

1 γ2B1B

T

1 −B2B2T

¶

X+CT

(28)

satisfazendo tamb´em

σ

µ

A−B2B2TX+

1 γ2B1B

T

1X

¶

X ⊂C−_,

onde σ(M) representa o conjunto de autovalores da matrizM eC− _corresponde

ao semiplano esquerdo do plano complexo.

iii) Existe uma vizinhan¸ca W ⊂ M da origem e uma realimenta¸c˜ao n˜ao linear de estados

u=α(x), α(0) = 0,

definida em W, tal que A +B2L, com L = ∂α(x)/∂x|x=0 ´e assintoticamente

est´avel e o sistema (2.9) em malha fechada tem, localmente em W, ganhoL2 < γ

(isto é, o problema de controle H∞ não linear via realimenta¸cão de estados é

sol´uvel em W).

2.3 Controle

H

∞

n˜

ao linear via realimenta¸

c˜

ao da

sa´ıda

Se somente a sa´ıda y estiver dispon´ıvel para realimenta¸cão, o estado pode ser estimado por um observador. Nesta se¸cão, serão apresentadas as condi¸cões que devem ser satisfeitas para que a planta com o controlador baseado em observador tenha ganho L2 ≤0.

2.3.1 Uma condi¸

c˜

ao necess´

aria

Considere a fun¸c˜ao Hamiltoniana K :Rn_×_Rn_×_Rr_×_Rp _→_R _{definida como}

K(x, p, w, y) =pT_F_{(x, w,}₀₎₋_yT_Y_{(x, w) +}_k_Z_(x,₀₎_k2₋_γ2_k_w_k2 _(2.12)

(29)

Hip´otese 2.3. O mapeamento Y(x, w) ´e tal que a matriz

D2 =

∂Y ∂w(0,0)

tem postop.

Como

µ

∂2_K_{(x, p, w, y)}

∂w2

¶

(x,p,w,y)=(0,0,0,0)

=−2γ2I,

existe uma fun¸c˜ao suave ˆw(x, p, y), definida em uma vizinhan¸ca de (0,0,0) tal que

µ

∂K(x, p, w, y) ∂w

¶

w= ˆw(x,p,y)

= 0, w(0,ˆ 0,0) = 0.

Além disso, é fácil verificar que

µ

∂2_{K(x, p,}_{w(x, p, y), y)}_ˆ

∂y2

¶

(x,p,y)=(0,0,0)

= 1 2γ2D2D

T

2.

Assim, existe uma fun¸c˜ao suave y∗(x, p), definida em uma vizinhan¸ca de (0,0) tal que

µ

∂K(x, p,w(x, p, y), y)ˆ ∂y

¶

y=y∗(x,p)

= 0, y∗(0,0) = 0.

Por constru¸c˜ao,

K(x, p, w, y)≤K(x, p,w(x, p, y), y)ˆ

para todo (x, p, w, y) em uma vizinhan¸ca (0,0,0,0) e

K(x, p,w(x, p, y), yˆ )≤K(x, p,w(x, p, yˆ ∗(x, p)), y∗(x, p))

para todo (x, p, y) em uma vizinhan¸ca de (0,0,0).

(30)

w∗∗(x, p) = ˆw(x, p, y∗(x, p)).

As fun¸c˜oes w∗∗(x, p) e y∗(x, p) assim definidas podem ser usadas para

expres-sar uma condi¸cão necessária para o problema de atenua¸cão de perturba¸cão via reali-menta¸cão da sa´ıda.

Teorema 2.3 (Isidori e Kang (1995)). Considere o sistema (2.1) e suponha que a hipótese 2.3 seja satisfeita. Suponha que o problema de atenua¸cão local de perturba¸cão seja resolvido por uma lei de controle

˙

ξ =η(ξ, y), u=θ(ξ),

e sejaU(x, ξ) uma fun¸c˜ao suave definida positiva satisfazendo

[ Ux(x, ξ) Uξ(x, ξ) ] 



F(x, w, θ(ξ)) η(ξ, Y(x, w))



+kZ(x, θ(ξ))k2−γ2kwk2 ≤0

para todo (x, ξ, w) em uma vizinhan¸ca de (0,0,0). Assim, a fun¸c˜ao positiva definida W(x) = U(x,0) satisfaz

K(x, WT

x (x), w∗∗(x, W_xT(x)), y∗(x, W_xT(x))) ≤0

para todox na vizinhan¸ca de zero.

2.3.2 Realimenta¸

c˜

ao da sa´ıda

Teorema 2.4 (Isidori e Kang (1995)). Considere o sistema (2.1) e suponha que

i) As hip´oteses 2.1, 2.2 e 2.3 forem satisfeitas,

(31)

iii) A desigualdade

K(x, WxT(x), w∗∗(x, WxT(x)), y∗(x, WxT(x)))−H∗(x, VxT(x))<0

tiver solu¸c˜ao suave W(x) >0, definida em uma vizinhan¸ca de x = 0, W(0) = 0 e positiva para x6= 0,

iv) W(x)−V(x)>0 para todo x6= 0,

v) A matriz Hessiana de

K(x, WT

x (x), w∗∗(x, WxT(x)), y∗(x, WxT(x)))−H∗(x, VxT(x))

for n˜ao singular em x= 0 e a equa¸c˜ao

(Wx(x)−Vx(x))G(x) = y∗T(x, W

T

x(x)) (2.13)

tiver uma solu¸c˜ao suave G(x),

então o problema de atenua¸cão local de perturba¸cão com estabilidade interna é resol-vido pela realimenta¸cão da sa´ıda

˙

ξ=F(ξ, α1(ξ), α2(ξ))−G(ξ)(y−Y(ξ, α1(ξ))),

u=α2(ξ),

onde α1(x),α2(x) e G(x) s˜ao escolhidos como em (2.7) e (2.13).

Observa¸c˜ao 2.2. Como apontado por Isidori e Kang (1995), o ganho do observador G(x) que ´e definido implicitamente em (2.13) pode ser calculado extraindo-se xT _de

Wx(x)−Vx(x) e deyT∗(x, W

T x(x)):

G(x) = L−1_(x)R 1(x),

(32)

Wx(x)−Vx(x) = xTL(x),

yT

∗(x, W

T

x(x)) =xTR1(x).

Observa¸c˜ao 2.3. Os sinaisw∗∗(x, WxT(x)) ey∗(x, WxT(x)) podem ser interpretados da

seguinte forma. Como visto na se¸c˜ao 2.3.1, w∗∗ maximiza a Hamiltoniana K enquanto

y∗ a minimiza. A interpreta¸cão, portanto, é similar para o caso de realimenta¸cão de

estado: w∗∗é o pior caso da entrada exógena que tenta aumentar a norma da variável

controladaz. O sinal de controle n˜ao ´e mais u mas y∗, que estabiliza a planta e reduz

a influˆencia de w em z pela inje¸c˜ao da sa´ıda.

2.3.3 Realimenta¸

c˜

ao da sa´ıda para sistema n˜

ao linear afim

´

E assumido que o sistema n˜ao linear esteja na seguinte forma afim

˙

z =h1(x) +k11w+k12u,

y =h2(x) +k21(x)w,

(2.14)

onde x∈Rn_,_u_∈_Rm_, _w_∈_Rr_,_z _∈_Rs _e_y _∈_Rp_.

Primeiramente é necessário apresentar a no¸cão de detectatibilidade.

Defini¸cão 2.1. Suponha f(0) = 0 e h1(0). O par (f, h1) é localmente detectável se

existir uma vizinhan¸caU do pontox= 0 tal que, sex(t) for qualquer curva integral de ˙

x=f(x) satisfazendox(0) ∈U, ent˜aoh1(x(t)) ´e definida para todot≥0 eh1(x(t)) = 0

para todot≥0 implica lim

t→0x(t) = 0.

O seguinte teorema apresenta a solu¸c˜ao do problema de realimenta¸c˜ao da sa´ıda para um sistema afim.

Teorema 2.5 (Isidori e Astolfi (1992)). Para o sistema dado por (2.14), suponha que

H1) O par (f, h1) ´e localmente detect´avel,

(33)

Vxf(x) +hT₁(x)h1(x) +γ2αT1(x)α1−αT2(x)α2 = 0, (2.15)

onde

α1(x) = ₂_γ12g₁T(x)VxT(x),

α2(x) =−1₂gT2(x)VxT(x),

H3) Exista uma matriz G, n×p, tal que o equil´ıbrio ξ = 0 do sistema

˙

ξ =f(ξ) +g1(ξ)α1(ξ)−Gh2(ξ)

´e localmente assintoticamente est´avel,

H4) Exista uma fun¸c˜ao suave semidefinida positiva W(x, ξ), localmente definida em uma vizinhan¸ca da origem de Rn_×_Rn _{e tal que}_W_{(0, ξ)}_>_{0 para todo}_ξ₆_{= 0 que}

resolve a EHJI

( Wx Wξ )fe(x, ξ) +hTe(x, ξ)he(x, ξ) +γ2ΦT(x, ξ)Φ(x, ξ) = 0, (2.16)

onde

fe(x, ξ) = 



f(x) +g1(x)α1(x) +g2(x)α2(x)

f(ξ) +g1(ξ)α1(ξ) +g2(ξ)α2(ξ) +G(h2(x)−h2(ξ))



,

he(x, ξ) =α2(ξ)−α2(x),

Φ(x, ξ) = ₂_γ12(Wxg1(x) +WξGk21(x))T.

Então o problema de atenua¸cão de perturba¸cão com estabilidade interna é resolvido pela realimenta¸cão da sa´ıda

˙

ξ=f(ξ) +g1(ξ)α1(ξ) +g2(ξ)α2(ξ) +G(y−h2(ξ)),

u=α2(ξ).

(34)

Observa¸cão 2.4. Para simplificar a análise e resultar em expressões mais simples para o controlador foi assumido no último teorema que as matrizes da planta (2.14) satis-fazem as seguintes condi¸cões, que são as versões não lineares das condi¸cões assumidas por Doyle et al. (1989):

k11(x) = 0,

hT

1(x)k12(x) = 0,

kT

12(x)k12(x) =I,

k21(x)gT1(x) = 0,

kT

21(x)k21(x) =I.

(2.18)

Proposi¸c˜ao 2.2 (Isidori e Astolfi (1992); van der Schaft (1993)). Suponha que o sistema (2.14) seja linear, dado por

˙

x=Ax+B1w+B2u,

z =C1x+D11w+D12u,

y =C2x+D21w,

e assuma as seguintes hip´oteses

L1) O par (A, B1) ´e estabiliz´avel.

L2) O par A, C1 ´e detect´avel.

L3) Existe uma solu¸c˜ao sim´etrica definida positiva X da EAR

AT_X₊_XA₊_CT

1C1−XB2B2TX+

1

γ2XB1B

T

1X = 0. (2.19)

L4) Existe uma solu¸c˜ao sim´etrica definida positiva Y da EAR

Y AT ₊_AY ₊_B

1B1T −Y C2TC2Y +

1 γ2Y C

T

1 C1Y = 0. (2.20)

L5) ρ(XY)< γ2_.

(35)

G=ZCT

2,

V(x) = xT_Xx,

W(x, ξ) =γ2_(x₋_ξ)T_Z−1_(x₋_ξ),

onde

Z =Y

µ

I− 1

γ2XY

¶−1

.

A EHJI (2.16) é solúvel sob as condi¸cões da proposi¸cão a seguir.

Proposi¸cão 2.3 (Isidori e Astolfi (1992)). Suponha que o sistema é não linear e sua aproxima¸cão linear na origem (x, w, u) = (0,0,0) satisfaz as hipóteses L3), L4), L5 e

L3*) A matriz A + 1

γ2B1B1TX − B2B2TX tem todos os autovalores com parte real

negativa;

L4*) A matriz A + 1

γ2Y H1TH1 − Y H2TH2 tem todos os autovalores com parte real

negativa.

Suponha o controlador

˙

ξ = (A+B1F1+B2F2−GH2)ξ+Gy

u = F2ξ

(2.21)

onde F1 = (1/γ2)B1TX, F2 =−B2TX eG=ZH2T é controlável e observável. Então as

hipóteses H2)–H4) do teorema 2.5 são válidas, comG dado como na proposi¸cão 2.2.

2.4 Inclus˜

ao de fun¸

c˜

oes pondera¸

c˜

ao com dinˆ

amica

no projeto de controle

H

∞

n˜

ao linear

A vari´avel penalidade z inclui todas as sa´ıdas f´ısicas ou cuja norma L2 ´e

de-sej´avel ser minimizada. No contexto do controle H∞ linear, as vari´aveis penalidade

(36)

fun¸cões com dinâmica. Isso permite que, por exemplo, o erro de rastreamento, esfor¸co de controle, caracter´ısticas de sensibilidade e de robustez via resposta em freqüência, atinjam critérios pré-estabelecidos. Critérios para sele¸cão dessas fun¸cões podem ser encontrados, por exemplo, em Zhou e Doyle (1998). Para controladores H∞ não

line-ares essas variáveis penalidade recebem ganhos estáticos. Nesta tese é mostrado que fun¸cões pondera¸cão com dinâmicas também podem ser usadas no projeto de controla-dores H∞ não lineares. A vantagem de seu uso será mostrado através de um exemplo

de sistema de levita¸c˜ao magn´etica.

Considere um sistema n˜ao linear na forma afim

˙

xp =fp(xp) +gp1(xp)w+gp2(xp)u,

y=hp2(xp) +kp21(xp)w.

Considere, por exemplo, uma fun¸cão pondera¸cão linear com dinâmica W1(s) (veja

figura 2.1) com a seguinte descri¸c˜ao de estados

u

Controlador

Planta z

w

y W (s)₂

W (s)₁ 1

z₂

Figura 2.1: Sistema em malha fechada com fun¸c˜ao pondera¸c˜ao

˙

xw1 =Aw1xw+Bw1y=Aw1xw +Bw1hp2(xp) +Bw1kp21(xp)w,

z1 =Cw1xw.

Note que Aw1, Bw1 e Cw1 s˜ao matrizes constantes. Al´em disso, por simplicidade,

considere que a entradau seja ponderada pela matriz constante W2

(37)

Combinando a planta com as fun¸c˜oes pondera¸c˜ao, tem-se

˙

z =h1(x) +k11(x)w+k12(x)u,

y=h2(x) +k21(x)u,

(2.22) onde x=   xp

xw1



, f(x) = 



fp(xp)

Aw1xw+Bw1hp2(xp) 

,

g1(x) =





gp1(xp)

Bw1kp21(xp) 

, g2(x) =





gp2(xp)

0  , z =   z1 z2 

, h₁(x) = 



Cw1xw

0



, k₁₁(x) = 



0 0



, k₁₂(x) =   0 W2  ,

h2(x) =hp2(xp), k21(x) = kp21(xp).

Suponha que para o sistema (2.22) linearizado exista um controlador H∞ linear.

Então, de acordo com o teorema 2.2 e a proposi¸cão 2.2, existe um controladorH∞não

linear para o sistema (2.22). Em outras palavras, se as EARs (2.19) e (2.20) têm solu¸cão para o sistema linearizado, então as EHJIs (2.15) e (2.16) também têm solu¸cão em uma vizinhan¸ca de x∈Rn_.

2.5 Solu¸

c˜

ao das EHJI por expans˜

ao em s´

erie de

Taylor

(38)

(1992), Huang e Lin (1995), Yazdanpanah, Khorasani e Patel (1998), Tsiotras, Corless e Rotea (1998) e Sinha e Pechev (2004).

A expansão em série de Taylor, em geral, não converge monotonicamente. É dif´ıcil garantir estabilidade quando a série é truncada em um número finito de termos. Além disso, a região de estabilidade da lei de controle aproximada é limitada pela região de convergência da série. Essa região é imposs´ıvel de ser determinada a priori.

2.5.1 Realimenta¸

c˜

ao de estados

Se a fun¸c˜ao armazenamentoV(x) e sua derivadaVx(x) forem expandidas em s´erie

de Taylor em torno da origem, ter˜ao a forma

V(x) = V(2)(x) +V(3)(x) +. . .=

∞

X

k=1

V(k+1)(x), Vx(x) = Vx(2)(x) +Vx(3)(x) +. . .=

∞

X

k=1

V(k+1)

x (x).

Assim, a lei de controleu∗(x) que minimiza a Hamiltoniana e a entrada ex´ogenaw∗(x)

que a maximiza podem ser expressas como

u∗(x) = u(1)∗ (x) +u

(2)

∗ (x) +. . .= ∞

X

k=1

u(∗k)(x),

w∗(x) = w(1)∗ (x) +w

(2)

∗ (x) +. . .= ∞

X

k=1

w(k)

∗ (x),

onde o sobre-escrito indica a ordem do termo da expans˜ao em s´erie de Taylor.

Aproxima¸c˜ao de primeira ordem: O problema de controle H∞ linear

Para o sistema linearizado

˙

x=Ax+B1w+B2u,

z =C1x+D11w+D12u,

(39)

a solu¸cão do problema de controleH∞é bem conhecida (Doyle et al., 1989). A fun¸cão

armazenamento ´e dada por

V(2)(x) =xTP x.

Com esta fun¸c˜ao armazenamento, as aproxima¸c˜oes de primeira ordem para w∗ e u∗

ficam

w∗(1) = _γ12B1TP x,

u(1)∗ (x) = −B₂TP x.

(2.23)

A EHJI (2.15) se reduz `a seguinte EAR

AT_P ₊_{P A}₊_P µ

1 γ2B1B

T

1 −B2BT2

¶

P +CT

1 C1 = 0. (2.24)

Esta EAR e a lei de controle correspondem `a solu¸c˜ao do problema de controleH∞linear.

Aproxima¸c˜oes de ordem superior

Com a planta linearizada, a dinˆamica da planta pode ser reescrita como

˙

x=Ax+B1w+B2u+f(x, w, u),

com taxa de suprimento s(w, z)

zTz−γ2wTw=C₁TC1+uTu−γ2wTw+g(x, w, u).

O termo de ordem m,V(m)_{(x), de} _V_{(x) e termos de ordem superior de}_w

∗ eu∗ podem

ser determinados recursivamente por

Vx(m) µ

A+ 1 γ2B1B

T

1P −B2B2TP

¶

= [−Vx(B1w∗ +B2u∗−Vxf(x, w∗, u∗)

(40)

w∗(k)= ₂_γ12 ³

BT

1VxT + ∂f ∂w T

(x, w∗, u∗)VxT + ∂g ∂w

T

(x, w∗, u∗)

´(k)

, k = 2,3, . . .

u(∗k)=−1₂

³

BT

2VxT + ∂f ∂u T

(x, w∗, u∗)VxT + ∂g ∂u T

(x, w∗, u∗)

´(k)

.

(2.25)

2.5.2 Realimenta¸

c˜

ao da sa´ıda

Para resolver a EHJI (2.16) referente ao problema de realimenta¸cão da sa´ıda, a fun¸cão armazenamentoW(x) pode ser expandida em série de Taylor como

W(x) =

∞

X

k=1

W(k)(x). (2.26)

Aproxima¸c˜ao de primeira ordem

A fun¸c˜ao armazenamento ´e dada por

W(x) = xTQx. (2.27)

O problema ´e reduzido a resolver a EHJI (2.16) para a matrizRdesconhecida (R =RT_,

R >0). O m´aximo da Hamiltoniana (2.12) fica

ˆ

w(x, WT

x ) =

1 2γ2(2B

T

1Rx−D21Y(x, WxT)), (2.28)

e o m´ınimo fica

y∗(x, Wx) = 2(D21B1TRx+γ2C2x). (2.29)

Substituindo (2.27), (2.28) e (2.29) em (2.16), a EHJI pode ser reescrita como uma EAR da forma

AQQ+QAQ+QBQQ+CQ= 0. (2.30)

(41)

AQ = A−B1D21T C2,

BQ =

1 γ2(B1B

T

1 −B1B1T),

CQ = C₁TC1−H∗.

A inje¸c˜ao da sa´ıdaG´e dada por

(Q−P)G=D21B1TR+γ2C2, (2.31)

onde P é solu¸cão de (2.24) eQé a solu¸cão de (2.30).

Aproxima¸c˜oes de ordem superior

Substituindo a aproxima¸cão em série de Taylor da fun¸cão armazenamento (2.26) na EHJI (2.16) podem ser obtidas as seguintes expressões que permitem o cálculo recursivo deW(x) e w∗∗

Wx(m)(Ax+B1w∗∗(1)−GC2x) = [−WxB1w∗∗−Wxf(x, w∗∗,0) +y∗T(x, W

T

x)Y(x, w∗∗) +

γ2wT∗∗w∗∗−g(x, w∗∗,0) +H(x, VxT, w∗, u∗)](m),

m = 3,4, . . .

w∗∗(x, WxT) =

1 2γ2 =

µ

∂g

∂w(x, w,0)−y

T∂Y

∂w(x, w) +Wx ∂F

∂w(x, w,0)

¶T¯

¯ ¯ ¯ ¯

(k)

w=w∗∗(x,WxT)

,

(42)

Aproxima¸

c˜

ao sucessiva de Galerkin

para o controle

H

_∞

n˜

ao linear

3.1 Introdu¸

c˜

ao

Neste cap´ıtulo será apresentado o método chamado de aproxima¸cão sucessiva de Galerkin (ASG) para solu¸cão da EHJI. Esse algoritmo combina o método de apro-xima¸cões sucessivas, que transforma a EHJI em uma seqüência de EDPs lineares, com o método de Galerkin, que aproxima a solu¸cão dessa seqüência de EDPs. Beard e McLain (1998) usam este método para resolver a EHJI referente ao problema de con-trole H∞ não linear via realimenta¸cão de estados e aqui é aplicado para resolver o

problema de controle H∞ n˜ao linear via realimenta¸c˜ao da sa´ıda. Este algoritmo,

jun-tamente com sua prova de convergência são as principais contribui¸cões desta tese.

3.2 Aproxima¸

c˜

ao sucessiva

(43)

calcu-lar sucessivamente o controle sub-ótimo para sistemas lineares com performance não quadrática. Haussler (1963) estendeu a idéia para sistemas não lineares e mostrou que o método poderia prover simultaneamente barreiras inferiores e superiores na deriva¸cão do controle sub-ótimo a partir do controle ótimo.

O método das aproxima¸cões sucessivas recebeu pela primeira vez uma funda-menta¸cão teórica por Saridis e Lee (1979). Os autores usam aproxima¸cão sucessiva para propor um algoritmo que melhora a perfomance de um controle inicial estabi-lizante. É mostrado que o método converge monotonamente para a solu¸cão ótima, isto é, para a solu¸cão da EHJB. O algoritmo foi posteriormente estendido para siste-mas não lineares estocáticos por Saridis e Wang (1994). Wise e Sedwick (1994) usam aproxima¸cões sucessivas pela primeira vez na EHJI relativa ao problema de controle H∞ via realimenta¸cão de estados para transformá-la em uma série de EDPs lineares.

Bertsekas (1976) mostra que o algoritmo de aproxima¸cões sucessivas é uma contra¸cão em um espa¸co completo e portanto, tem solu¸cão única. Além disso, neste trabalho são derivadas barreiras expl´ıcitas da sub-otimalidade a cada itera¸cão. A principal dificul-dade em todos estes trabalhos é resolver a EHJB e assim, o método não é aplicado em sistemas reais.

3.2.1 Realimenta¸

c˜

ao de estados

A EHJI (2.10) para uma lei de controle estabilizante inicialu(0)_{e uma perturba¸c˜ao}

w(0) _{pode ser reescrita como}

∂V(0)

∂x

T

(f+g1w(0)+g2u(0)) +hT1h1+ku(0)k2−γ2kw(0)k2 = 0,

que ´e linear emV(0)_{. Para melhorar a performance da lei de controle} _u(0)_{, ´e encontrada}

u(1) _{que minimiza a Hamiltoniana (2.5) e} _w(0) _{que a maximiza}

u(1) = −1

2g

T

2

∂V(0)

∂x ,

w(1) = 1 2γ2g

T

1

∂V(0)

(44)

Se para um dadoi, V(i+1)_{(x) =}_V(i)_{(x), ent˜ao} _V(i+1)_{(x) =} _V∗_{(x). Da´ı}

∂V∗

∂x

T

(f +g1w∗+g2u∗) +hT1h1+ku∗k2−γ2kw∗k2 = 0,

com

u∗

= −1

2g

T

2

∂V∗

∂x , w∗

= 1 2γ2g

T

1

∂V∗

∂x .

Escrevendo a EHJI desta forma deixa claro que a fonte de não linearidade está em u e w, que dependem do valor da fun¸cão V. Para reduzir a EHJI a uma seqüência de equa¸cões diferenciais parciais, devem ser usadas duas itera¸cões simultâneas da apro-xima¸cão sucessiva. O algoritmo é listado a seguir

Algoritmo 3.1. Sejau(0) _{uma lei de controle estabilizante inicial para o sistema (2.9)}

(w= 0) com regi˜ao de estabilidade Ω.

Parai= 0,1,2,3, . . .

Fa¸ca w(i,0) _{= 0}

Para j = 0,1,2,3, . . .

Resolva para V(i,j) _de

∂V(i,j)

∂x (f +g1w

(i,j)₊_g

2u(i,j)) +hT1h1+ku(i)k2−γ2kw(i,j)k2 = 0

Atualize a perturba¸c˜ao

w(i,j+1) ₌ 1 2γ2g₁T∂V

(i,j)

∂x

Fim

Atualize o controle

u(i+1) ₌₋1 2g

T

2 ∂V

(i,j) ∂x

Fim

Esta itera¸c˜ao tem uma interpreta¸c˜ao da teoria de jogos. Dado um controle u(i)

(45)

pode suportar. Depois que esta perturba¸cão de pior caso é encontrada, o controle é atualizado para melhorar a performance do sistema para esta perturba¸cão.

A essência do algoritmo 3.1 é reduzir a EHJI a uma seqüência infinita de equa¸cões diferenciais parciais lineares da forma

∂V ∂x

T

(f +g1w+g2u) +hT1h1+kuk2−γ2kwk2 = 0,

ondeuew são fun¸cões conhecidas dex. Beard e McLain (1998) chamam essa equa¸cão de Equa¸cão de Hamilton-Jacobi-Isaacs Generalizada (EHJIG), também conhecida como pré Hamiltoniana. Essa equa¸cão é dif´ıcil de ser resolvida analiticamente. Na se¸cão 3.3.1 será usado o método de Galerkin para aproximar essa equa¸cão.

3.2.2 Realimenta¸

c˜

ao da sa´ıda

Para o problema de realimenta¸c˜ao da sa´ıda, considere a seguinte fun¸c˜ao Hamil-toniana

K(x, p, w, y) = pT_F_{(x, w,}₀₎₋_yT_Y_{(x, w) +}_ZT_(x,_0)Z(x,₀₎₋_γ2_wT_w

= pT_{(f(x) +}_g

1(x)w)−yT(h2(x) +k21w) +hT1(x)h1(x)−γ2wTw

= pT_f_{(x) +}_pT_g

1(x)w−yTh2(x)−yTk21(x)w+hT1(x)h1(x)−γ2wTw.

A última expressão é a pré-Hamiltoniana do problema. No ponto de sela, tem-se

∂K

∂w(x, p, w, y)

¯ ¯ ¯ ¯_w

= ˆw(x,p,y)

=g₁Tp−k₂₁T (x)y−2γ2wˆ = 0 ⇒

ˆ

w(x, p, y) = 1 2γ2(g

T

(46)

K(x, p,w, y) =ˆ pT_(f_{(x) +}_g

1(x)₂1_γ2(g1T(x)p−k21T (x)y))

−yT_(h

2(x) +k21₂1_γ2(g₁T(x)p−kT₂₁(x)y)) +hT₁(x)h1(x)

−γ2 1

2γ2(pTg1(x)−yTk21(x))₂_γ12(gT1(x)p−k21T(x)y)

=pT_{f(x) +} 1 2γ2p

T_g

1(x)g1T(x)p− 2γ12p

T_g

1(x)kT21(x)y−yTh2(x)

−₂_γ12yTk21(x)g1T(x)p+21γ2k21(x)k21T (x)y+hT1(x)h1(x)− ₄1_γ2pTg1(x)g1T(x)p

+₄1_γ2p

T_g

1(x)k21T(x)y+ 41γ2y

T_k

21(x)g1T(x)p− 41γ2y

T_k

21(x)kT21(x)y

=pT_{f(x) +} 1

4γ2pTg1(x)g1T(x)p−yTh2(x) + ₄1_γ2yTy+hT1(x)h1(x),

∂K

∂y (x, p,w, y)ˆ

¯ ¯ ¯ ¯

y=y∗(x,p)

=−h2(x) +

1

2γ2y∗(x, p) = 0 ⇒ y∗(x, p) = 2γ 2_h

2(x),

w∗∗(x, p) = ˆw(x, p, y∗(x, p)) =

1 2γ2g

T

1(x)p−k

T

21(x)h2(x).

Adotandop=Wx(x), tem-se

y∗(x, Wx(x)) = 2γ2h2(x), (3.1)

w∗∗(x, Wx(x)) =

1 2γ2g

T

1(x)Wx(x)−k21T(x)h2(x). (3.2)

Para esse ponto, a Hamiltoniana pode ser escrita como

K(x, Wx(x), w∗∗(x, Wx(x)), y∗(x, Wx(x))) =WxT(x)F(x, w∗∗(x, Wx(x)),0)

−yT

∗(x, Wx(x))Y(x, w∗∗(x, Wx(x))) +ZT(x,0)Z(x,0)

−γ2_wT

∗∗(x, Wx(x))w∗∗(x, Wx(x))

=WT

x(x)(f(x) +g1(x)w∗∗(x, Wx(x)))−yT∗(h2(x) +k21w∗∗(x, Wx(x))) +hT₁(x)h1(x)

−γ2_wT

∗∗(x, Wx(x))w∗∗(x, Wx(x)).

Para resolver o problema de controle H∞ n˜ao linear via realimenta¸c˜ao da sa´ıda, a

seguinte DHJI deve ser satisfeita

(47)

com

W(x)>0 e Wx(x)−Vx(x)>0, ∀x6= 0.

Algoritmo 3.2. Sejaw uma entrada ex´ogena com regi˜ao de estabilidade Ω

Parai= 0,1,2,3, . . .

Resolva para W(i) _de

Wxf+Wxg1w(i)−yTh2−yTk21w(i)+hT1h1−γ2kw(i)k2−H∗ = 0

Atualize a perturba¸c˜ao

w(i+1) ₌ 1 2γ2g

T

1Wx−k21T h2

Fim

3.3 M´

etodo de Galerkin

A seguir será apresentado brevemente o método de aproxima¸cão de Galerkin. Para um tratamento mais rigoroso e completo veja, por exemplo, Guenther e Lee (1988), Celia e Gray (1992) ou Fletcher (1984). A idéia básica por trás do método de Galerkin é a proje¸cão linear. Suponha que é dado um vetor arbitrário v ∈ R3 _{e que}

deseja-se aproximar este vetor como uma combina¸c˜ao linear de dois vetores linearmente independentes emR2_{, isto ´e, deseja-se encontrar} _c

i,i= 1,2, tal que

ˆ

v ≈c1xˆ1+c2xˆ2,

como ´e poss´ıvel ver na figura 3.1.

Para encontrar os coeficientes ci, o vetorv ´e projetado nos vetores ˆxi, obtendo o

seguinte sistema linear





hv,xˆ1i

hv,xˆ2i



=





hxˆ1,xˆ1i hxˆ2,xˆ1i

hxˆ1,xˆ2i hxˆ2,xˆ2i



 



c1

c2



(48)

x

1

x

2

x

3

v

v^

c

1

c

2

c

3

Figura 3.1: Proje¸c˜ao de um vetor do R3 _no R2

onde o operador proje¸c˜ao ´e o produto interno em R3_{. A matriz que multiplica os}

coeficientes é chamada matriz Gramiana dos vetores xi’s e é invert´ıvel se os xi’s são

linearmente independentes. Os coeficientes s˜ao encontrados pela invers˜ao da matriz Gramiana.

O método de Galerkin é uma extensão dessa idéia para o espa¸co de fun¸cões. Dada uma equa¸cão diferencialLV +η= 0, onde Lé um operador linear e ηestá na imagem de L, a solu¸cão V é assumida pertencer ao espa¸co gerado pela combina¸cão linear de um conjunto de fun¸cões linearmente independentes span{φj}∞j=1, isto é,

V(x) =

∞

X

j=1

cjφj(x).

Como há um número infinito de cj, a série deve ser truncada para formar uma

apro-xima¸c˜ao paraV

VN(x) = N X

j=1

cjφj(x).

Quando VN é substitu´ıdo na equa¸cão diferencial o erro obtido é

erro =LVN +η.

(49)

herro, φji= 0, j = 1, . . . , N,

onde o operador proje¸c˜ao ´e o produto interno em um espa¸co de Hilbert apropriado.

O método de Galerkin será usado para aproximar a solu¸cão da EHJIG em um conjunto compacto Ω. É assumido que é poss´ıvel selecionar um conjunto{φj}∞j=1, onde

φj(0) = 0 de fun¸c˜oes (n˜ao necessariamente linearmente independentes) em Ω em que

V(i) _{é combina¸cão linear dessas fun¸cões para todo} _x_∈_{Ω, onde} _V(i) _{resolve a EHJIG.}

´

E procurada uma solu¸c˜ao aproximada V_N(i), para a equa¸c˜aoH(V(i)_{, u}(i)_{, w}(i)_{) = 0,}

tal que

V_N(i)(x) =

N X

j=1

c(ji)φj(x).

A substitui¸c˜ao dessa express˜ao na EHJIG resulta em um erro

erro =H

Ã _N

X

j=1

c(_ji)φj, u(i), w(i) !

.

Os coeficientesc(ji) s˜ao determinados igualando a zero a proje¸c˜ao do erro em uma base

finita{φj}Nj=1, ∀x∈Ω

*

H

Ã _N

X

j=1

c(_ji)φj, u(i), w(i) !

, φn +

Ω

= 0, n = 1, . . . , N,

onde o produto interno ´e definido como

hf, giΩ =

Z

Ω

f(x)g(x)dx.

3.3.1 Realimenta¸

c˜

ao de estados

(50)

(1998). Assuma queu: Ω→Rm _{´e uma lei de controle que estabiliza assintoticamente}

o sistema (2.9) em um conjunto compacto Ω. Assuma tamb´em que o conjunto{φ(vj)}∞j=1

é uma base completa para o dom´ınio da EHJI (2.10). Uma solu¸cão aproximada desta equa¸cão pode ser dada por

VN(x) = N X

j=1

c(vj)φ( j)

v (x),

onde os coeficientes devem satisfazer a equa¸c˜ao

Z

Ω

H(x, VT

x (x), w, u)φldx= 0,

Z

Ω



 

∂³PN_j₌₁c(vj)φ(vj) ´T

∂x (f+g1w+g2u) +h

T

1h1+kuk2−γ2kwk2





φldx= 0,

Z Ω   Ã _N X j=1

c(vj)

∂φ(vj)

∂x

!T

(f +g1w+g2u) +hT1h1+kuk2−γ2kwk2



φldx= 0. (3.4)

Definindo cv = [ c(1)v . . . c(vN) ]T, φv(x) = [ φ(1)v . . . φ(vN) ] e

∇φv(x) = [ ∂φ(1)v /∂x . . . ∂φ(vN)/∂x ], a equa¸c˜ao (3.4) pode ser reescrita como Z

Ω

£

cTv∇φv(f+g1w+g2u) +hT1h1+kuk2−γ2kwk2

¤

φvdx= 0,

cT v

Z

Ω

∇φv(f +g1w+g2u)φvdx=− Z

Ω

(hT

1h1+kuk2−γ2kwk2)φvdx, ·Z

Ω

φv(f +g1w+g2u)T∇φTvdx ¸

cv =− Z

Ω

φv(hT₁h1+kuk2−γ2kwk2)dx,

£¡R

Ωφvf

T_∇_φT

vdx

¢

+¡R

Ωφvw

T_gT

1∇φTvdx ¢

+¡R

Ωφvu

T_gT

2∇φTvdx ¢¤

cv =

−R

Ωφvh

T

1h1dx−

R

Ωφvkuk2dx+γ2

R

(51)

(A1+A2(w) +A3(u))cv =b1+b2(w) +b3(u),

onde A1, b1, n˜ao dependem nem do controle u e nem da entrada ex´ogena w. Assim,

dadosuew, a EHJI pode ser aproximada resolvendo integrais e invertendo uma matriz.

As integrais A2(w), A3(u), b2(w) e b3(u) n˜ao precisam ser recalculadas a cada

passo do algoritmo. Usando a fun¸c˜ao VN para calcular e atualizar o controle u e a

entrada ex´ogenaw, tem-se

w= 1 2γ2g

T

1

∂VN

∂x = 1 2γ2g

T

1

N X

j=1

c(vj)

∂φ(vj)

∂x = 1 2γ2g

T

1∇φ

T vcv,

u=−1

2g

T

2

∂VN

∂x =− 1 2g T 2 N X j=1

c(vj)

∂φ(vj)

∂x =− 1 2g

T

2∇φ

T

vcv. (3.5)

Para encontrar um valor aproximado parauew, as integraisA2(w),A3(u),b2(w)

eb3(u) devem ser calculadas, mas

A2(w) =

Z

Ω

φvwTg1T∇φTvdx=

1 2γ2

Z

Ω

φvcTv∇φvg1gT1∇φTvdx

= 1 2γ2

N X

j=1

c(j)

v Z

Ω

φv

∂φ(vj)

∂x

T

g1gT1∇φTvdx=

1 2γ2

N X

j=1

c(j)

v G

(j) 1 ,

A3(u) =

Z

Ω

φvuTgT2∇φTvdx=

1 2

Z

Ω

φvcTv∇φvg2g2T∇φTvdx

= 1 2

N X

j=1

c(j)

v Z

Ω

φv

∂φ(vj)

∂x

T

g2g2T∇φTvdx=

1 2

N X

j=1

c(j)

v G

(j) 2 ,

b2(w) =

Z

Ω

φvwTwdx=

1 4γ2

Z

Ω

φvcTv∇φvg1gT1∇φ

T

vcvdx

= 1 4γ2

N X

j=1

c(vj) Z

Ω

φv

∂φ(vj)

∂x

T

g1gT1∇φ

T

vdxcv =

1 4γ2

N X

j=1

c(vj)G

(52)

b3(u) =

Z

Ω

φvuTudx=

1 4

Z

Ω

φvcTv∇φvg2g2T∇φTvcvdx

= 1 4

N X

j=1

c(j)

v Z

Ω

φv

∂φ(vj)

∂x

T

g2g2T∇φTvdxcv =

1 4

N X

j=1

c(j)

v G

(j) 2 cv.

Assim, tem-se

µ

A1+

1 2γ2A2(c

(n)

v )−

1 2A3(c

(n)

v )

¶

c(vn+1) =−b1+

1 4γ2b2(c

(n)

v )−

1 4b3(c

(n)

v ),

A1 =

R

Ωφvf

T_∇_φT

vdx, A2(cv) = N X

j=1

c(vj)G

(j)

1 , A3(cv) = N X

j=1

c(vj)G

(j) 2 ,

b1 =

R

Ωφvh

T

1h1dx b2(cv) = N X

j=1

c(j)

v G

(j)

1 cv, b3 =

N X

j=1

c(j)

v G

(j) 2 cv,

G(₁j)=

Z

Ω

φv

∂φ(vj)

∂x

T

g1g1T∇φTvdx, G

(j) 2 =

Z

Ω

φv

∂φ(vj)

∂x

T

g2g2T∇φTvdx,

e, portanto, os coeficientescv ficam fora das integrais eA2(w),A3(u),b2(w) eb3(u)

po-dem ser calculadas iterativamente a partir das matrizes{G(₁j)}N

j=1e{G

(j)

2 }Nj=1calculadas

previamente.

A aproxima¸c˜ao de Galerkin para a EHJI pode ser combinada com o algoritmo 3.1 para produzir o algoritmo a seguir para calcular uma aproxima¸c˜ao para a EHJI.

Algoritmo 3.3. Sejau(0) uma lei de controle estabilizante inicial ew= 0. Pr´e calcule as integraisA1, A3(u(0)), b1, b3(u(0)), {G(1j)}Nj=1 e{G

(j) 2 }Nj=1.

Parai= 0,1,2,3, . . .

Se i= 0

A(i) ₌_A

1+A3(u(0))

b(i)₌₋_b

1−b3(u(0))

(53)

A(i) ₌_A

1− 1₂PNk=1c (i−1)

v (k)G(₂k)