Aula 8 – Teorema de Tales

Aula 8 – Teorema de Tales

Objetivos

• Apresentar o Teorema de Tales.

• Preparar o estudo de semelhan¸ca de triˆangulos.

Introdu¸

c˜

ao

O objetivo central desta Aula 8 ´e provar o Teorema de Tales. Pela primeira vez neste curso aparece uma id´eia nova envolvida nos argumentos t´ecnicos que usaremos para a prova desse Teorema. ´E a id´eia de limite ou convergˆencia de n´umeros reais. Pela sua importˆancia na matem´atica, e pelo papel fundamental que representam, estas id´eias deveriam ser estudadas e maturadas desde o jardim de infˆancia. Pode-se dizer que grande parte da Matem´atica trata de conjuntos, estruturas nos conjuntos e fun¸c˜oes entre conjuntos que preservam estas estruturas. A abordagem que expressa estes assuntos ´e a convergˆencia e o limite.

Mas voltemos ao nosso ch˜ao de f´abrica, nossa pedreira, ap´os estas di-vaga¸c˜oes.

Nota:

No texto, desta aula, estamos usando nota¸c˜oes do tipoAB_{= 2 para significar} que a medida do segmento AB_{´e 2. Isto ´e estamos} substituindo a nota¸c˜ao mais pesadam₍AB_{) = 2. Do} mesmo modo escrevemos DM=M Npara expressar que os segmentos tem a mesma medida.

Como tudo em matem´atica, para chegar ao nosso objetivo temos toda uma seq¨uˆencia de tijolinhos ou cap´ıtulos a serem preenchidos, preparados, at´e o ato final, que ´e a prova do Teorema. Por isso, Matem´atica n˜ao ´e como novelas de televis˜ao: se vocˆe perde um cap´ıtulo, possivelmente perde a conex˜ao com a trama e pode correr o risco de torcer pelo vil˜ao!

Vamos ao nosso primeiro tijolinho. Nesta proposi¸c˜ao e nas seguintes, as propriedades que conhecemos sobre paralelogramos ser˜ao muito utilizadas.

Proposi¸c˜ao 16

Sejam trˆes retas paralelasm, nercortadas por retas transversaisset. Sejam

A, B, C eE, F, G os pontos de interse¸c˜ao de s et, respectivamente, com as retas m, ne r. Se AB =BC ent˜ao EF =F G(veja figura 141).

t s

A

B

C

E

F

G

m

n

r

Prova:

Se t ´e paralela a s n˜ao precisamos provar nada, porque nesta situa¸c˜ao

ABF E e BCGF seriam paralelogramos (lados opostos paralelos). Isto ga-rantiria que AB = EF e BC =F G. Como AB =BC, todos os segmentos seriam iguais. Em particularBC =F G.

Vamos supor ent˜ao que t n˜ao ´e paralela as. Construimos pelos pontos

E e F as retas t1 e t2, respectivamente, ambas paralelas a s. Veja a figura 142.

t s

A

B

C

E

F

G

m

n

r H

I

L t

1 t2

Fig. 142:

H, I eF, Ls˜ao os pontos de interse¸c˜ao det1 et2 com ne r, respectiva-mente.

A conclus˜ao agora ´e conseq¨uˆencia direta da seguinte congruˆencia de triˆangulos:

EHF ≡F LG

Antes de continuar, interrompa a leitura, examine a figura 142 com suas propriedades, pegue um papel para rascunho e tente antecipadamente responder a duas quest˜oes:

- Qual caso de congruˆencia garanteEHF ≡F LG?

- Por que a congruˆencia encerra a prova da proposi¸c˜ao?

Insista numa resposta sua... encontrou alguma pista... use propriedades de paralelas e transversais... releia os argumentos at´e aqui desenvolvidos... lute um pouco com as duas quest˜oes propostas... se passaram 15 minutos e vocˆe n˜ao avan¸cou venha conosco no caminho da resposta!

A congruˆencia EHF ≡F LG´e garantida pelo caso A.L.A.

De fato, ABHE ´e paralelogramo (lados paralelos) e ent˜ao AB =HE. Tamb´em BCIH e HILF s˜ao paralelogramos e ent˜ao BC = HI = F L. Conclus˜ao: O lado L que aparece no caso A.L.A. est´a garantido, pois

Tamb´em, usandon er como paralelas etcomo transversal encontramos que

ˆ

F GL=EF Hˆ (ˆangulos correspondentes)

Tamb´em, usando t1 e t2 como paralelas e t como transversal encontramos que

ˆ

LF G=HEFˆ (ˆangulos correspondentes).

Ora, a soma dos ˆangulos internos de um triˆangulo ´e 180◦_{. Com dois ˆangulos}

coincidindo em medidas, o terceiro tamb´em coincidir´a. Isto ´e,

EHFˆ =FLG.ˆ

Portanto a congruˆencia vale pelo caso A.L.A.

Est´a respondida a primeira quest˜ao.

Vamos `a segunda quest˜ao: por que a congruˆenciaEHF ≡F LGencerra a prova? Pedimos que vocˆe leia o enunciado da proposi¸c˜ao de novo para ver que a conclus˜ao salta aos olhos!

Ora EHF ≡F LG⇒EF =F G, onde quer´ıamos chegar.

Vamos agora explorar o resultado que acabamos de provar para tirarmos uma importante consequˆencia.

- Vocˆe sabe o que ´e um feixe de paralelas no plano?

Um feixe de paralelas ´e um conjunto de retas do plano onde quaisquer duas delas s˜ao paralelas. O conjunto de retas formando o feixe deve possuir no m´ınimo duas retas, podendo ter um n´umero finito ou mesmo infinito de retas.

Na figura 143 abaixo representamos um feixe de paralelas com 5 retas.

Fig. 143: .

Corol´ario 1

Considere um feixe de paralelas no plano, contendo um n´umero finito de retas e duas retas transversaiss et intersectando o feixe. Se a transversal s

determina segmentos consecutivos de mesmo comprimento, o mesmo ocorrer´a com os segmentos consecutivos determinados no feixe pela reta transversalt.

Corol´ario: ´E uma proposi¸c˜ao obtida como conseq¨uˆencia direta de outra proposi¸c˜ao

Prova:

Na figura 144, representamos um feixe com 4 retas. Vamos provar o resultado neste caso.

t s

E F G

m n r A

B C

p

D H

Fig. 144: .

O enunciado garante que AB = BC = CD e pede para provar que

EF =F G=GH. ´

E evidente que o resultado ´e verdadeiro, basta usar a proposi¸c˜ao 16 duas vezes. Primeiro, considerando as retas r, me n para concluir que

AB=BC ⇒EF =F G;

e em seguida usar as retasm, nep, para concluir que ´e verdadeira a seguinte implica¸c˜ao:

BC =CD ⇒F G=GH.

- Vocˆe j´a percebeu que chegamos, n˜ao?

A partir de agora talvez estejamos malhando em ferro frio, tudo est´a dito e mais nada se acrescenta. Mas vamos l´a!

As duas conclus˜oes acima reunidas mostram que

AB =BC =CD ⇒EF =F G=GH.

Apesar da prova ter sido feita para um feixe com 4 retas, ´e evidente que vale para 52 ou 52 milh˜oes de retas, ou um n´umero qualquer n ∈ N _de

Mais uma vez, recordamos que nosso objetivo central nesta aula ´e pro-var o Teorema de Tales (se tiver curiosidade leia o enunciado no texto adi-ante). ´E um resultado muito importante, ferramenta de primeira linha, que abre muita portas. No entanto quero convidar vocˆe a refletir sobre um argu-mento crucial que aparecer´a na prova do Teorema de Tales.

Em primeiro lugar considere on n´umeros naturais N _{= {0,1,2, ...}, os}

quais podem ser representados sobre a parte positiva da reta real R_{. A reta} R_{´e onde representamos todos os n´umeros reais. veja figura 145 .}

0 1 2 n n+1

x

R

Fig. 145:

Na parte positiva da reta real R_{, est˜ao localizados todos os n´umeros}

reais positivos.

Temos a seguinte propriedade: “dado um n´umero realx >0, existe um n´umero natural n, tal quen > x ”.

Esta propriedade ´e chamada de “Princ´ıpio Arquimediano” em home-nagem ao grande matem´atico e engenheiro grego Arquimedes (s´ec IV a.C.)

Usando o Princ´ıpio Arquimediano como base, pe¸co para vocˆe pensar sobre a seguinte pergunta.

Considere um n´umero real B que possui duas propriedades:

• B ≥0

• B < 1

n, para todo n´umero natural n >0.

- Quem ´e o n´umero B?

Reflita um pouco sobre as propriedades de B. S˜ao duas camisas de for¸ca obrigando B a revelar sua identidade, seu lugar na reta real R_{, figura}

145. Releia a pergunta e insista numa resposta sua...

Vocˆe respondeu corretamente se cravou B = 0.

De fato, ´e a ´unica alternativa para o DNA deB. Por que?

Em primeiro lugar B ≥ 0. Vamos provar que a suposi¸c˜ao B > 0 ´e absurda e nos leva a contradi¸c˜oes, deixando-nos como ´unica alternativa

B = 0.

De fato, seB >0 ent˜ao 1

B >0 e pelo Princ´ıpio Arquimediano existe um

n´umero natural n >0, tal que n > 1

B. Como tratamos com n´umeros

positi-vos, podemos inverter as posi¸c˜oes dos n´umeros para concluir que

Este resultado diz que existe um n´umero natural n, para o qual a se-gunda propriedade deB n˜ao ´e satisfeita. Esta contradi¸c˜ao mostra queB >0 n˜ao ´e poss´ıvel. LogoB = 0.

Vamos, sem mais delongas ao n´umero principal de nosso espet´aculo, aquele pelo qual pagamos o ingresso:

Teorema de Tales

Sejam trˆes retas paralelasr, men cortadas pelas retas transversaiss

et. Suponha queA, B, C eE, F, Gsejam os pontos de interse¸c˜ao das retas s e t com r, m e n, respectivamente (veja figura 146). Nestas condi¸c˜oes

AB BC =

EF F G. Vocˆe sabia que...

O nome de Tales est´a associado com um n´umero de teoremas em Geometria: 1. Um c´ırculo ´e bissectado por um diˆametro 2. Os ˆangulos da base de um triˆangulo is´osceles s˜ao iguais 3. ˆAngulos opostos pelo v´ertice s˜ao iguais 4. Caso L.A.A. de congruˆencia 5. Dado um triˆanguloABC_, inscrito em um semic´ırculo, o ˆangulo oposto ao lado que est´a sobre o diˆametro ´e reto. 6. A soma dos ˆangulos internos de um triˆangulo ´e 180o

. Todos esses teoremas eram conhecidos pelos eg´ıpcios e babilˆonios. A raz˜ao pela qual eles est˜ao associados a Tales ´e porque ele foi o primeiro a oferecer provas para esses teoremas.

t s A B C E F G m n r Fig. 146: Prova:

Vamos provar uma forma equivalente da igualdade enunciada. Note que

AB BC =

EF

F G ⇔

BC AB =

F G

EF ⇔

BC

AB + 1 = F G EF + 1

⇔ BC+AB

AB =

F G+EF EF

⇔ AC

AB = EG EF.

Ent˜ao para efeito da prova do teorema ´e suficiente mostrar que

AC AB =

EG EF.

Agora vamos soltar uma frase que merece aten¸c˜ao:

“Suponha que este processo permitiu que coloc´assemos n pontos sobre

AB e at´em pontos sobreAC, com m > n”. ˆ

Epa, a frase acima guarda mist´erios! O que queremos dizer? Vamos com calma.

Vocˆe sabia que...

Por volta do ano 600 a.C., o s´abio grego Tales de Mileto fez uma viagem ao Egito. O fara´o j´a conhecia sua fama de grande matem´atico. Ouvira dizer at´e que Tales era capaz de uma incr´ıvel fa¸canha: podia calcular a altura de uma constru¸c˜ao, por maior que fosse, sem precisar subir nela. Por ordem do monarca, alguns matem´aticos eg´ıpcios foram ao encontro do visitante e pediram-lhe que calculasse a altura de uma das pirˆamides. Tales ouviu-os com aten¸c˜ao e se dispˆos a atendˆe-los imediatamente. J´a no deserto, pr´oximo `a pirˆamide, o s´abio fincou no ch˜ao uma vara, na vertical.

Observando a posi¸c˜ao da sombra, Tales deitou a vara no ch˜ao, a partir do ponto em que foi fincada, marcando na areia o tamanho do seu

comprimento. Depois, voltou a vara `a posi¸c˜ao vertical. -Vamos esperar alguns instantes, disse ele. Daqui a pouco poderei dar a resposta. Ficaram todos ali, observando a sombra que a vara projetava. Num determinado momento, a sombra ficou exatamente do comprimento da vara. Tales disse ent˜ao aos eg´ıpcios: -V˜ao depressa at´e a pirˆamide, me¸cam sua sombra e acrescentem ao resultado a medida da metade do lado da base. Essa soma ´e a altura exata da pirˆamide. Como Tales descobriu isso? Tales usousemelhan¸ca de triˆangulos. Esse assunto estudaremos mais tarde.

Primeiro a frase quer dizer que se damos nome aos pontos consecuti-vos, por exemplo P1, P2, ..., Pn sobre AB, quer dizer que AP1 ´e o primeiro

segmento de AB e Pn₋1Pn ´e o ´ultimo segmento de AB. Neste casoPn =B.

A coisa foi constru´ıda para se ajustar perfeitamente sobre AB. No en-tanto, prosseguindo com os pontos agora Pn+1, Pn+2, ... em BC, ocorre um

fenˆomeno. Ou o ´ultimo ponto, que estamos chamando Pm, coincide com C,

ou ele est´a antes de C. Qualquer que seja o caso o pr´oximo ponto Pm₊₁

estaria fora deAC (veja a figura 147).

Tra¸camos agora retas paralelas a r, men e passando pelos pontos que definimos sobre o segmento AC. Estas retas formam com r, m e n um feixe de paralelas e determinam sobre EF e EG segmentos de reta de mesmo comprimento.

Denomine por ˜U o comprimento de cada um desses segmentos.

Ent˜ao podemos escrever que

• AB=nU, EF =nU˜

• mU ≤AC <(m+ 1)U, mU˜ ≤EG <(m+ 1) ˜U

Dividindo e cancelando os termos U e ˜U, encontramos que,

m n ≤

AC AB <

m+ 1

n e

m n ≤

EG EF <

m+ 1

n (1)

Represente na reta real R_{, os n´umeros} m

n e

m+ 1

n . e os n´umeros AC AB e EG EF. m n m+1 n AB AC EF EG R Fig. 148:

A figura 148 e tamb´em as desigualdades mostram que AC

AB e EG EF s˜ao

n´umeros que pertencem ao intervalo

m n,

m+ 1

n

⊂ R_{. Isto significa que a}

distˆancia entre AC

AB e EG

EF ´e menor que a amplitude do intervalo.

Em outras palavras

AC AB − EG EF <

m+ 1

n −

m n =

1

n.

Note que a desigualdade acima poderia ter sido deduzida diretamente de (1).

Preferimos a explica¸c˜ao acima de natureza mais geom´etrica.

Ora a desigualdade acima diz AC

AB − EG EF = 0

Logo AC

AB = EG

EF, como almejamos provar.

Proposi¸c˜ao 17

O segmento que une os pontos m´edios de dois lados de um triˆangulo ´e paralelo ao terceiro lado e tem medade de seu comprimento.

Prova:

SejaABC um triˆangulo e sejamM eN os pontos m´edios dos ladosAB

eAC respectivamente. Trace o segmento M N, como na figura 149.

N

C B

A

M

Fig. 149: Proposi¸c˜ao 17.

Queremos provar que as retas←−→M N e←→BCs˜ao paralelas, e quem(M N) =

m₍BC₎

2 . Para isso, vamos construir um quadril´atero da seguinte forma: na reta

←−→

M N marcamos um ponto D tal que M esteja entre D e N, e DM ≡M N, e ligamos D a B (veja figura 150). Vamos mostrar que DN CB ´e um para-lelogramo.

A

M _N

B C

D

Fig. 150: Prova da proposi¸c˜ao 17.

Como os ˆangulos DM Bc e NM Ac s˜ao congruentes (por serem opostos pelo v´ertice), segue de L.A.L. que AM N ≡ BM D. Como conseq¨uˆencia, temosAN Mb ≡BDMb e AN ≡BD, como indicado na figura 151.

A

M

N

B C

D

A reta ←→DN ´e transversal `as retas ←→DB e ←→N C, formando um par de ˆangulos alternos internos congruentes, que s˜ao AN Db e BDNb . Segue da proposi¸c˜ao 9, da aula 5, que as retas ←→DB e ←→N C s˜ao paralelas. O qua-dril´atero DN CB possui assim um par de lados opostos paralelos e congru-entes: DB e N C.

Pela proposi¸c˜ao 12, da aula 6, podemos concluir que DN CB ´e um paralelogramo. Por esse fato, DN e BC tamb´em s˜ao paralelos e, segundo a proposi¸c˜ao 11, da aula 6, congruentes. Finalmente, podemos concluir da´ı queM N ´e paralelo a BC e tem metade de seu comprimento.

Q.E.D.

Resumo

Nesta aula vocˆe aprendeu...

• A propor¸c˜ao entre segmentos determinados por transversais cortando feixes de paralelas, s´o depende do feixe de paralelas e n˜ao da posi¸c˜ao da transversal.

• Que o segmento que une os pontos m´edios de dois lados de um triˆangulo ´e paralelo ao terceiro lado e tem metade do seu comprimento.

Exerc´ıcios

1. (Constru¸c˜ao da paralela.) Sejam r uma reta e P um ponto n˜ao pertencente a r. Sabemos que existe uma ´unica reta s passando por

P e que ´e paralela a r. O objetivo deste exerc´ıcio ´e provar como se pode obter a retasusando-se apenas r´egua (sem marca¸c˜ao de medida) e compasso. Para isso, trace trˆes c´ırculos, sempre com o mesmo raio: o primeiro com centro em P, determinando um ponto A na reta r; o segundo com centro emA, determinando um pontoB na mesma reta, e o terceiro com centro emB, determinando um pontoCsobre o primeiro c´ırculo (veja figura 152).

r s P

A B

C

2. Divis˜ao de segmentos em partes iguais. O objetivo deste exerc´ıcio ´e indicar um m´etodo para que vocˆe possa permite dividir, usando apenas r´egua (sem marca¸c˜ao) e compasso, um dado segmento em um n´umero qualquer de segmentos congruentes.

Constru¸c˜ao:

Suponha que desejemos dividir o segmento AB da figura 153 em sete partes iguais.

A B

Fig. 153: SegmentoAB.

Para isso, vamos tra¸car uma semi-reta−→AC de forma que o ˆanguloCABb

seja agudo (essa condi¸c˜ao n˜ao ´e decisiva, mas torna o desenho mais f´acil). Sobre a semi-reta −→AC, tra¸camos os pontos D1, D2, . . ., D7 de modo queAD1 ≡D1D2 ≡. . .≡D6D7. Isso pode ser feito marcando-se um ponto D1 e usando o compasso para transportar o segmento AD1

para a semi-reta ←−→D1C, e assim sucessivamente, como na figura 154. O tamanho de AD1 n˜ao ´e importante.

A E₁ E₂ E₃ E₄ E₅ E₆ B

D1 D

D

2 3

D₄ D5

D

D C

6 7

Fig. 154: Divis˜ao deAB_{em 7 partes iguais.}

3. Prove que os pontos m´edios dos lados de um quadril´atero qualquer formam um paralelogramo.

4. Na figura 155 temos: m(AB) = 4cm,m(BC) = 6cm, m(AC) = 8cm,

m(DC) = 3cm, F D//BC e DE//AB. Determine as medidas dos lados de F DEB.

A

D

C F

B

E

5. Na figura 156, ABC ´e is´osceles de baseBC,M ´e o ponto m´edio deBC,

M P//AC eM Q//AB. Prove que AP M Q´e um losango.

A

Q P

B M C

Fig. 156: Exerc´ıcio 5.

6. Na figura 157, BM ≡ M C, AF ≡ F B e F D//BC. Prove que E ´e o ponto m´edio deF D.

A

B C

D E

F

M

Fig. 157: Exerc´ıcio 6.

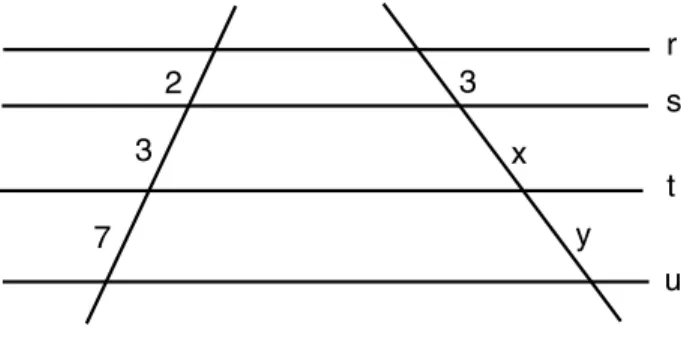
7. Determine x e y na figura 158, sabendo quer, s, t eu s˜ao paralelas.

2

3

3

x

r

s

y u

t

7

8. Na figura 159, EADˆ ≡DACˆ .

A

B

C D

2 3

4 x

E

Fig. 159: Exerc´ıcio 8.

Usando apenas o teorema de Tales, determine x.

9. (ITA-1989) Considere um quadril´atero ABCD cujas diagonais AC e

BD medem, respectivamente, 5cm e 6cm. Se R, S, T e U s˜ao os pontos m´edios dos lados do quadril´atero dado, determine o per´ımetro do quadril´atero RST U.

10. (U.C. Salvador, 1992)

Sejam

P: o conjunto dos retˆangulos

Q: o conjunto dos quadrados

L: o conjunto dos losangos

A figura que melhor representa as rela¸c˜oes existentes entre eles ´e:

L Q P

(a)

L P

Q

(b)

L P

Q

(c)

L

P Q

(d)

L Q

P

(e)