Universidade de Cabo Verde

(1)

Universidade de Cabo Verde

Departamento Ciˆencia & Tecnologia

Texto teórico de Análise Matemática III

Prof. Narciso Resende Gomes

Ano lectivo: 2012/2013

(2)

Referˆ

encias

[1] A. Breda e J. Costa,Cálculo com fun¸cões de várias variáveis. McGraw Hill-Portugal, Lisboa, 1996.

[2] E. Lima, An´alise Real - Vol. 2. Rio de Janeiro, Brasil, 2004.

[3] H. Bertolossi, Cálculo diferencial a várias variáveis. Edi¸cões Loyola e editora PUC-Rio, São Paulo, Brasil, 2002.

[4] S. Lang, Calculus of Several Variables. Adison-Wesley, 1973.

[5] T. Apostol, C´alculo (Vol. 2). Editora Revert´e, 1996.

(3)

1 Fun¸

c˜

oes a v´

arias vari´

aveis reais

Defini¸c˜ao 1: Uma aplica¸c˜aof :_{D ⊆}_Rn_→

Rm, comm >1, denomina-sefun¸cão vectorial de várias variáveis reais. Quando m = 1, isto é, f : Rn → R chamamos a fun¸cão de fun¸cão escalar de várias variáveis reais ou simplesmente fun¸cão de várias variáveis reais. Assim, uma fun¸cão de n (maior que 1) variáveis reais definida em _D é uma correspondência que a cada x _{= (}_x₁_{, x}₂_{, . . . , x}_n₎ _{∈ D} _{associa um e um só n´}_{umero real} y=f(x1, x2, . . . , xn). Abreviamente escreve-se

f :_{D ⊆}Rn→R

x_{= (}_x₁_{, x}₂_{, . . . , x}_n₎_7→_f₍_x₁_{, x}₂_{, . . . , x}_n₎

ou

f :_{D ⊆} Rn→R

x_7→_f₍x₎_.

O dom´ınio de f é _D. O contradom´ınio de f é conjunto dos valores que f toma em R, isto é,

{f(x1, x2, . . . , xn) : (x1, x2, . . . , xn)∈ D} ∈R.

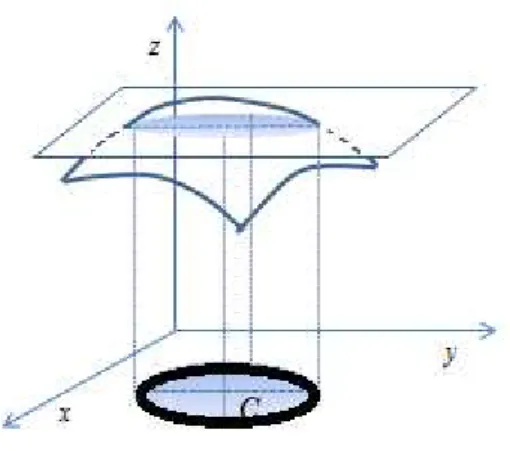
Ogr´afico def ´e o subconjunto de Rn+1

{(x1, x2, . . . , xn, f(x1, x2, . . . , xn)) : (x1, x2, . . . , xn)∈ D}.

Fig. 1: Fun¸c˜ao real de duas vari´aveis reais, z =f(x, y)_∈_R, com (x, y)_{∈ D ⊆}_R2_.

Observa¸cão 1: Em R2 e R3 é usual usarem-se as nota¸cões z = f(x, y) e w = f(x, y, z) em vez de f(x1, x2) e f(x1, x2, x3), respectivamente.

Exemplo 1: O gráfico da fun¸cão constante z =f(x, y) =k é um plano paralelo ao plano

xy.

Exemplo 2: Seja f uma fun¸c˜ao real de duas vari´aveis reais definida por z = f(x, y) =

x2₊_y2_. _{O dom´ınio}_D _de_f _´e_R2 _{e o contradom´ınio} _D′ _´e_R+

0 e o gr´afico ´e

{(x, y, x2+y2) : (x, y)_∈R2}=_{(x, y, z)_∈R3 : (x, y)_∈R2ez =x2+y2._}

(4)

Fig. 2: z =f(x, y) =x2₊_y2_.

1.1 Curvas de n´ıvel

Defini¸cão 2: Considere-se a fun¸cão real de duas variáveis

f :_{D ⊆} Rn→R

(x, y)_7→f(x, y).

Parakpertencente ao contradom´ınio def, acurva de n´ıvel de f de valorké a projeçcão ortogonal sobre o plano xy, de interseçcão do plano da equa¸cão z =k com o gráfico de

f, isto ´e, com a superf´ıcie da equa¸c˜aoz =f(x, y).

Analiticamente a curva de n´ıvel def de valork ´e _{(x, y)_{∈ D} :f(x, y) =k_}.

(5)

´

E por vezes útil recorrer a curva de n´ıvel da fun¸cão que numa imagem a duas dimensões permitem obter informa¸cão sobre o gráfico da fun¸cão.

Exemplo 3: Seja f(x, y) = x2₊_y2_. _{O contradom´ınio de} _f _´e _R+

0. Para k ∈ R+0, a curva

de n´ıvel de f de valor k ´e:

• O ponto (0,0), sek = 0.

• A circunferˆencia do plano xy de centro (0,0) e raio √k, se k >0.

Fig. 4: f(x, y) = k ou circunferˆencia de centro (0,0,0) e raio √k.

Observa¸cão 2: Analogamente definem-se as superf´ıcies de n´ıvel de uma fun¸cão de três variáveis reais, ou seja,

f :_{D ⊆} R3 →R

(x, y, z)_7→f(x, y, z).

para k pertencente ao contradom´ınio de f, a superf´ıcie de n´ıvel de f de valor k ´e

{(x, y, z)_{∈ D} :f(x, y, z) =k_}.

Exemplo 4: Seja

f :_{D ⊆}R3 →R

(x, y, z)_7→x2+y2+z2.

O contradom´ınio de f ´e R+0. Para k ∈ R+0, a superf´ıcie de n´ıvel de f de valor k ´e

{(x, y, z)_{∈ D} :x2 ₊_y2 ₊_z2 ₌_k_}_,_{ou seja:}

• O ponto (0,0,0), se k = 0.

(6)

Fig. 5: f(x, y, z) = k ou superf´ıcie esf´erica de centro (0,0,0).

2 No¸

c˜

ao de limite

Defini¸c˜ao 3: Sejam

f :_{D ⊆}Rn →R

x_7→_f₍x₎

ea_{= (}_a₁_{, a}₂_{, . . . , a}_n_{) um ponto de acumula¸c˜ao de} _D_e _L_∈_R_. _{Diz-se que}_L_{´e o} _limite_de f quando x_{tende para} a_ou _limite _de _f _{no ponto} a_{, e escreve-se}

lim

x→a

f(x_{) =} _L _ou _lim

(x1,...,xn)→(a1,...,an)

f(x1, x2, . . . , xn) = L,

se _∀ǫ >0,_∃δ >0 tal que

0<_||x₋a_||_{< δ}_∧x_{∈ D \ {}a_}

⇒ |f(x₎₋_L_|_{< ǫ.}

Equivalentemente, temos

∀ǫ >0,_∃δ >0 :x_{∈ D \ {}a_{} ∩ B}₍a_{, δ}₎_⇒_f₍x₎_{∈ B}₍_{L, ǫ}₎_.

Exemplo 5: Considere-se a fun¸cão real de duas variáveis reais e cuja expressão anal´ıtica éf(x, y) = _x22x_+y32.

O dom´ınio de f é_D = R2\ {(0,0)_}. O ponto (0,0) não pertence a _D mas é um ponto de acumula¸cão de_D. Verifica-se ainda que existe o limite de f quando (x, y) tende para (0,0) e que esse limite é zero.

Sejaǫ >0 qualquer. Pretende-se provar que existe δ >0 verificando 0_{≤ ||}(x, y)₋(0,0)_||< δ_∧(x, y)_∈_R2_{\ {}₍₀_,₀₎_{} ⇒ |}_f₍_{x, y}₎₋₀_|_{< ǫ.}

Uma vez que, para (x, y)_∈R2\ {(0,0)_},x2 _≤_x2₊_y2_{, tem-se que} x

2 x2_+y2

≤1 e portanto

|f(x, y)_|= 2_|x_| x

2 x2_+y2

≤2|x| ≤2 p

x2₊_y2 _{= 2}_||₍_{x, y}₎₋₍₀_,₀₎_||_.

Assim, para todoǫ, existe δ = ₂ǫ >0 e assim,

lim

(x,y)→(0,0)

2x3

x2 ₊_y2 = 0.

Proposi¸cão 1: (Unicidade de limite) O limite duma fun¸cão num ponto quando existe é ´

(7)

Algumas desigualdades

No processo de verifica¸c˜ao de limite, podemos, caso necess´ario, utilizar as desigual-dades seguintes:

• |x_{| ≤}p

x2₊_y2

• |y_{| ≤}px2₊_y2

• |xy_{| ≤ |}x_||y_{| ≤} 1₂(x2₊_y2₎

• |x_±y_{| ≤ |}x_|+_|y_{| ≤}2px2₊_y2

• |x3₋_y3_{| ≤}₍_x2₊_y2₎3/2

Exemplo 6: Seja f(x, y) = k uma fun¸c˜ao constante, ent˜ao, para todo (a, b)_∈_R2_,

lim

(x,y)→(a,b)k =k.

Temos que _|f(x, y)₋k_|=_|k₋k_|= 0. Assim, dado ǫ >0 e tomandoδ >0 qualquer,

0_{≤ ||}(x, y)₋(a, b)_||< δ _{⇒ |}f(x, y)₋k_|< ǫ.

Logo,

lim

(x,y)→(a,b)f(x, y) =(x,y)lim→(a,b)k =k.

Proposi¸cão 2: Sejam f e g duas fun¸cões reais den variáveis reais de dom´ınios_Df e Dg,

respectivamente. Seja aindaλ um escalar:

• A soma de f e g ´e a fun¸c˜ao

f+g :_Df ∩ Dg ⊆Rn→R

x_7→_f₍x_{) +}_g₍x₎_.

• Oproduto deλ pela fun¸cão f é a fun¸cão

λf :_Df ⊆Rn →R

x_7→_λf₍x₎_.

• Oproduto def eg ´e a fun¸c˜ao

f g :_Df ∩ Dg ⊆Rn→R

x_7→_f₍x₎_g₍x₎_.

• Oquociente def e g ´e a fun¸c˜ao

f

g :{x∈ Df ∩ Dg :g(x)6= 0} ⊆R

n

→R

x_7→ f(x) g(x₎.

Proposi¸c˜ao 3: (Lei do enquadramento) Sejam as fun¸c˜oes f, g eh de_{D ∈}Rn em R. Seja

a_{um ponto de acumula¸c˜ao de}_D_{e tais que}_L_∈_R_{tais que lim}

x→a

g(x_{) =} _L_{e lim}

x→a

h(x_{) =}_L.

Se existe uma vizinhan¸ca _V deL tal que para qualquer x_{∈ V ∩ D}_{, se tem}

g(x)_≤f(x)_≤h(x),

ent˜ao lim

x→a

(8)

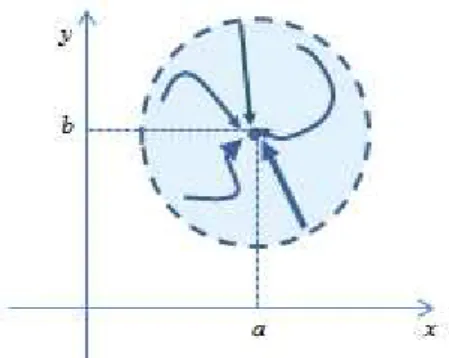
Fig. 6: Várias direçcões para se chegar ao ponto (a, b).

Defini¸c˜ao 4: Sejam f : _{D ⊆} _Rn _→

R, _C um subconjunto de _D e a _{um ponto de}

acu-mula¸c˜ao de _C. Diz-se que b ´e o limite de f relativo1 a _C quando x tende para a, e representa-se

lim

x→a∧x∈C

f(x) = b

se o limite da restri¸c˜ao de f a_C quando x_{tende para} a_´e_b_.

Pode verificar a existência de limite def relativo a um certo subconjunto do dom´ınio, sem que exista o limite da fun¸cão nesse ponto. Este facto pode ser verificado no exemplo que se segue onde revela-se particularmente útil para provar que não existe _{limite de}

uma determinada fun¸c˜ao num ponto.

Exemplo 7: Seja a fun¸c˜ao definida em_D =_{(x, y)_∈R2 :y₆=₋x2_} _por

f(x, y) = y−x

2

y+x2.

A fun¸cão f não tem limite quando (x, y) tende para (0,0). De facto, se considerarmos (x, y) a tender para (0,0) segundo a direçcão do eixo OX, tem-se que

lim

(x,y)→(0,0)∧y=0f(x, y) = limx→0f(x,0) = limx→0

0₋x2

0 +x2 =−1.

Segundo a direc¸c˜ao do eixo OY, tem-se

lim

(x,y)→(0,0)∧x=0f(x, y) = limx→0f(0, y) = limy→0

y₋0

y+ 0 = 1.

Conclui-se, assim, que limite n˜ao existe considerando que os limites relativos s˜ao dife-rentes.

1_Sendo_f _{uma fun¸c˜}_{ao definida em}_D_e_C _{um subconjunto de} _D_{, `}_{a fun¸c˜}_{ao definida em}_C _{que a cada}

(9)

2.1.1 Limites iterados

Observa¸cão 3: Sejax_∈_Rn_com _n_{= 2. Os limites direccionais na origem na direçcão do}

eixo OX e na direçcão do eixo OY, respectivamente, são chamados limites iterados ou limites sucessivos. Ainda, o cálculo de limite iterado é equivalente a seguinte:

lim

(x,y)→(a,b)f(x, y) = limx→a limy→bf(x, y)

=l1 e,

lim

(x,y)→(a,b)f(x, y) = limy→b xlim→af(x, y)

=l2.

2.1.2 Limites direccionais

No caso de o caminho seja uma recta não vertical de declive m que passa por ponto (a, b) e a equa¸cão da familia de rectas é dada por

y=b+m(x₋a), m_∈R.

O limite a calcular ´e

lim

(x,y)→(a,b)f(x, y) = (x,y)→(a,b)lim∧y=b+m(x−a)f(x, y) = limx→af(x, b+m(x−a)) = L.

No caso de o caminho seja uma parábola de eixo vertical que passa por ponto (a, b) e a equa¸cão das familias de parábolas é dada por

y=b+m(x₋a)2, m _∈R.

Neste caso, o limite a calcular ´e

lim

(x,y)→(a,b)f(x, y) = (x,y)→(a,b)∧limy=b+m(x−a)2f(x, y) = lim_x_→_af(x, b+m(x−a)

2_{) =}_L.

Observa¸c˜ao 4: Quando o limite depende do declive da rectam, concluimos que n˜ao existe limite no ponto (a, b).

Observa¸c˜ao 5: Conv´em, portanto, salientar que:

1. No caso de obtermos limites relativos diferentes (sucessivos ou direccionais) pode-mos concluir que a fun¸c˜ao n˜ao possui limite quando (x, y)_→(a, b).

2. No entanto, não podemos concluir que existe limite pelo facto dos limites relativos serem iguais, pois pode haver um caminho que dê um limite diferente. Para concluirmos acerca da existência de limite, e na impossibilidade de estudarmos todos os caminhos poss´ıveis por serem infinitos, teremos que recorrer à defini¸cão de limite.

Exemplo 8: O limite sucessivo da fun¸c˜ao f(x, y) = x_x+y−y22 pode ser determinado

lim

(x,y)→(0,0)f(x, y) =(x,y)lim→(0,0)

x₋y2

x+y2 = lim_x_→₀

lim

y→0

x₋y2

x+y2

= lim

y→0

x x = 1.

lim

(x,y)→(0,0)f(x, y) =(x,y)lim→(0,0)

x₋y2

x+y2 = lim_y_→₀

lim

x→0

x₋y2

x+y2

= lim

x→0

−y2

y2 =−1.

(10)

limite. Apliquemos, ent˜ao, os limites direccionais. Consideremos a rectay=b+m(x₋a), com (a, b) = (0,0). Assim,y=mx e portanto:

lim

x→0f(x, mx) = limx→0

x(mx)3

x2_{+ (}_mx₎6 = lim_x_→₀

m3_x4

x2₊_m6_x6 = lim_x_→₀

m3_x4

x2_{(1 +}_m6_x4₎ = lim_x_→₀

m3_x2

1 +m6_x4 = lim_x_→₀

0 1 = 0.

Como os limites direccionais são também iguais e iguais a zero, nada se pode concluir. No entanto, se o limite existir terá que ser obrigatoriamente zero (uma vez que o limite quando existe é único). Vejamos que não existe limite.

Fa¸camos, por exemplo, (x, y) = (0,0) atrav´es da linha y =√3

x, temos:

lim

x→0f(x, 3

√

x) = lim

x→0

x(√3

x)3

x2_{+ (}√3

x = limx→0

x2

x2₊_x2 = lim_x_→₀

x2

2x2 =

1 2.

Ent˜ao, obtivemos um limite relativo diferente de zero, podemos concluir que n˜ao existe limite no ponto (0,0).

Exerc´ıcio 1: Estude, quanto ao limite no ponto (0,0), a fun¸c˜ao f(x, y) = _x2xy_+y2.

2.1.3 Limites direccionais - caso geral

Teorema 2.1: Sejaf : X _⊆ Rn → R e a _∈ _X′_. _{Se lim}

x→af(

x_{) =} _b_{, ent˜ao para qualquer}

vector u_∈_Rn _com u₆_{= 0, temos que:}

lim

t→0f(

a₊_tu_{) =}_b, _com_t_∈_R_.

Note que o rec´ıproco nem sempre ´e verdadeiro. E portanto, podemos aplicar o teorema anterior.

Exemplo 10: Confirmemos que n˜ao existe limite def(x, y, z) = _x3 xyz +y3

+z3 quando (x, y, z)→

(0,0,0).

Neste caso, n˜ao aplicaremos os limites sucessivos vistos para o caso de R2, iremos aplicar directamente o teorema anterior, que consiste na generaliza¸c˜ao do conceito de limite direccional.

Sejam u_{= (}_u₁_{, u}₂_{, u}₃₎_∈_R3 _e _t_∈_R_{, com} u₆_{= (0}_,₀_,₀₎_.

Portanto,a₊_tu_{= (0}_,₀_,_{0) +}_t₍_u₁_{, u}₂_{, u}₃_{) = (}_tu₁_{, tu}₂_{, tu}₃₎_._{Consequentemente, temos}

lim

t→0f(tu1, tu2, tu3) =

tu1tu2tu3

t3_u3

1+t3u32+t3u33

= lim

t→0

t3_u 1u2u3

t3₍_u3

1+u32+u33)

= lim

t→0

u1u2u3

u3

1+u32+u33

.

Concluimos assim, que não existe limite, pois para vectores diferentes, u _∈ R3, obtemos valores diferentes. Por exemplo, u _{= (1}_,₁_,_{0), o limite é 0 e para o caso} u_{= (1}_,₁_,_{1), o limite é} 1

(11)

Exerc´ıcio 2: Utilize o caso geral do limite direccional para averiguar se a fun¸c˜ao seguinte tem limite na origem

f(x, y) =

xy

x2

−y2, (x, y)6= (0,0)

0, (x, y) = (0,0).

2.2 Continuidade

Defini¸c˜ao 5: Sejam

f :_{D ⊆}Rn→R

x_7→_f₍x₎

uma fun¸cão de n variáveis reais e a _{= (}_a₁_{, a}₂_{, . . . , a}_n_{) um ponto de acumula¸cão de} _D_,

diz-se que f ´e cont´ınua em a _{se existir limite de} _f _em a _{e esse limite for igual a} _f₍a_),

ou seja, a fun¸c˜ao f ´e cont´ınua ema_{∈ D} _sse

∀ǫ >0,_∃δ >0,

||x₋a_||_{< δ}_∧x_{∈ D}

⇒ |f(x₎₋_f₍a₎_|_{< ǫ.}

Observa¸cão 6: Uma fun¸cão é dita cont´ınua em um conjunto _D quando for cont´ınua em todos os pontos de _D.

Proposi¸cão 4: Sejam f e g duas fun¸cões reais den variáveis reais de dom´ınios_Df e Dg,

respectivamente. Suponha que f e g são cont´ınuas em a_{∈ D}_f _{∩ D}_g_. _{Então as fun¸cões} f+g,f g são cont´ınuas ema_._{Ainda, se}_g₍_a₎₆_{= 0 também a fun¸cão} f

g ´e tamb´em cont´ınua

em a_.

Exemplo 11: Seja a fun¸c˜ao

f(x, y) = x

2₊_y2

x4₊_y4

´e uma fun¸c˜ao racional e portanto, cont´ınua no seu dom´ınio R2\ {(0,0)_}.

f(x, y) = (

xy2 2(x2

+y2

), (x, y)6= (0,0)

0, (x, y) = (0,0).

é uma fun¸cão cont´ınua emR2\{(0,0)_},considerando que a soma, o produto e o quociente de fun¸cões cont´ınuas, são fun¸cões cont´ınuas. O limite lim

(x,y)→(0,0)f(x, y) = 0 ef(0,0) = 0,

então a fun¸cão é cont´ınua no ponto (0,0). Conclui-se assim que a fun¸cão é cont´ınua em

R2.

g(x, y) = (

xy2 2(x2

+y2

), (x, y)6= (0,0)

1, (x, y) = (0,0).

Verificamos que nos pontos (x, y)₆=_{(0,0)_},a fun¸c˜ao ´e cont´ınua. O limite lim

(x,y)→(0,0)f(x, y) =

(12)

Particularmente em R2 tem-se

• (a, b)_{∈ D}/ f e existir lim

(x,y)→(a,b)f(x, y).

Sendo f prolong´avel por continuidade no ponto (a, b), a fun¸c˜ao f∗_, _{prolongamento} _de_f

por continuidade no ponto (a, b), ´e definida por

f∗(x, y) = (

f(x, y), se (x, y)_{∈ D}f

lim

(x,y)→(a,b)f(x, y), se (x, y) = (a, b).

f(x, y) = xy

2

2(x2₊_y2₎

´e uma fun¸c˜ao racional e portanto, cont´ınua no seu dom´ınio _R2_{\ {}₍₀_,₀₎_}_. _Averiguemos

se h´eprolong´avel por continuidade ao ponto (0,0).

Provemos, por defini¸c˜ao, que o seu limite quando (x, y) tende para (0,0) ´e nulo. Pretende-se demonstrar que

∀ǫ >0,_∃δ >0 : (x, y)_∈R2\ {(0,0)_{} ∧}px2₊_y2 _{< δ} _⇒

xy2

2(x2₊_y2₎ < ǫ. Como xy2 2(x2 +y2 )

= _2(x|x2|y2 +y2

), x

2 _≤ _x2₊_y2 _e _y2 _≤ _x2₊_y2 _{e ainda} _|_x_{| ≤} √_x2 _≤p

x2₊_y2

e _|y_{| ≤}p

y2 _≤p

x2₊_y2_,

pelo que xy2

2(x2₊_y2₎ ≤

(x2₊_y2₎p

x2₊_y2

2(x2₊_y2₎ = p

x2₊_y2

2 .

Considerando δ = 2ǫ, tem-se ent˜ao que, quando px2₊_y2 _{< δ} _{com (}_{x, y}₎₆_{= (0}_,₀₎_,

xy2

2(x2₊_y2₎ ≤

p

x2₊_y2

2 <

δ

2 =ǫ.

Assim, a fun¸c˜ao tem limite no ponto (0,0) sendo prolong´avel por continuidade a esse ponto.

Exerc´ıcio 4: Averigue se a fun¸c˜ao

f(x, y) = (

2x3

−y3

x2_+y2 , (x, y)6= (0,0)

0, (x, y) = (0,0).