TC - Newton e Leibniz, Os Pais do Cálculo.pdf

U

NIVERSIDADE

C

ATÓLICA

P

ORTUGUESA

História da Matemática

Newton e Leibniz

(Pré-versão)

Susana Gorete Monteiro Almeida

2

INTRODUÇÃO

Para se realizar um estudo completo sobre as origens, desenvolvimento e consequências do Cálculo, era necessário uma pesquisa muito extensa e cujo resultado final seria, sem dúvida, um texto longo. Assim o intuito deste trabalho é o de uma apresentação geral que contenha alguns factos importantes que permeiam os acontecimentos históricos relacionados com a construção desta poderosa ferramenta da matemática, que é o Cálculo.

Na Roma antiga, etimologicamente a palavra calculus significava uma pequena pedra ou seixo utilizado para a contagem e jogo, e o verbo latino calculare significava figurar, computar, calcular, contar. Hoje o Cálculo é um sistema de métodos para resolver problemas quantitativos de natureza particular, como no cálculo das probabilidades, no cálculo de variações, etc. O cálculo abordado agora, é às vezes chamado O Cálculo, para distingui-lo de todos os outros cálculos subordinados.

Por vezes é referido que o Cálculo foi inventado por esses dois grandes génios matemáticos do século XVII, Newton e Leibniz. Mas, na verdade o Cálculo é o produto de um longo processo evolutivo que começou na Grécia Antiga e continuou no século XIX. Newton e Leibniz foram homens verdadeiramente notáveis e as suas contribuições foram de uma importância decisiva, tendo o trabalho destes continuado após o seu desaparecimento. Problemas semelhantes estavam presentes nas mentes de muitos cientistas europeus do século XVII, onde cada um colaborou consideravelmente com engenhosos métodos de resolução de problemas.

O Nascimento do Cálculo

As contribuições dos matemáticos para o nascimento do Cálculo são inúmeras. Muitos deles, mesmo que de forma imprecisa ou não rigorosa, já utilizavam conceitos do Cálculo para resolver vários problemas, tais como Cavalieri, Barrow, Fermat e Kepler. Nesse tempo ainda não havia uma sistematização, no sentido de uma construção logicamente estruturada. A união das partes conhecidas e utilizadas até então, aliada ao desenvolvimento e aperfeiçoamento das técnicas, aconteceu com Newton e Leibniz que deram origem aos fundamentos mais importantes do Cálculo: as Derivadas e os Integrais.

O Cálculo pode ser dividido em duas partes: uma relacionada às derivadas ou Cálculo Diferencial e outra parte relacionada aos integrais, ou Cálculo Integral.

Cálculo Diferencial

O aparecimento e o desenvolvimento do Cálculo Diferencial estão ambos estreitamente ligados à questão das tangentes. Desde a época dos Gregos antigos, já se conhecia a recta tangente como sendo uma recta que intercepta uma curva num único ponto, generalizando a situação observada no caso da circunferência.

Arquimedes e também Apolônio utilizavam métodos geométricos, que diferiam entre si, para a determinação de tangentes, parábolas, elipses e hipérboles. Vários outros métodos para resolver o problema de encontrar a tangente a uma curva num ponto foram desenvolvidos ao longo da história.

Na realidade, após os Gregos, o interesse por tangentes a curvas reapareceu no século XVII, como parte do desenvolvimento da geometria analítica. Como as equações eram então utilizadas para descrever curvas, a quantidade e variedade de curvas estudadas aumentou bastante em comparação àquelas conhecidas na época clássica. A introdução de símbolos algébricos como uma ferramenta para estudar a geometria das curvas também contribuiu para o desenvolvimento do conceito de derivada. Com o tempo, o tratamento tornou-se mais algébrico e menos geométrico, proporcionando um contínuo progresso no desenvolvimento dos conceitos de função, derivada, integral e outros tantos tópicos relacionados ao Cálculo.

Destacando Pierre de Fermat, este elaborou um método algébrico para determinar os máximos e os mínimos de uma função. Ele encontrava geometricamente os pontos onde a recta tangente ao gráfico tinha inclinação zero, ou seja, procurava os pontos em que o coeficiente angular da recta tangente era nulo. Escreveu a Descartes explicando o seu método que é basicamente utilizado ainda hoje. Na realidade, devido a esse trabalho, que estava intimamente relacionado com as derivadas, Lagrange afirmou considerar Fermat o inventor do Cálculo.

A questão de encontrar a tangente a uma curva é, historicamente, de especial importância, pois, ao que parece, foi o que Newton pensou quando teve uma perspicácia sobre como utilizar tangentes para estudar o movimento dos planetas. O método para a determinação foi desenvolvido pelo antecessor de Newton, Isaac Barrow, e consistia no limite de uma corda com os pontos aproximando-se entre si.

4 O estudo do movimento dos corpos havia começado de maneira sistemática com Galileu. Entretanto ele estudara o movimento geometricamente, utilizando as proposições de Euclides e as propriedades das cónicas de Apolônio para chegar a relações entre distância, velocidade e aceleração, que, hoje em dia, são aplicações básicas da derivada.

Vários matemáticos estavam, nessa altura, a estudar problemas relacionados com o movimento. Torricelli e Barrow consideraram o problema do movimento com velocidades variadas. Já se sabia que a taxa de variação pontual — derivada — do deslocamento era a velocidade e que a operação inversa da velocidade era o deslocamento. Isso mostra que já existia uma certa noção da operação inversa da derivada, sendo que, a ideia de que o integral era inverso da derivada era familiar a Barrow.

Para Newton, o movimento era a base fundamental para o estudo das curvas e de outras questões relacionadas com o Cálculo. Newton escreveu o seu tratado sobre

fluxions em 1666. Nele considerava uma partícula, descrevendo uma curva com duas linhas que se movimentavam e que representavam o sistema de coordenadas. A velocidade horizontal e a velocidade vertical eram as fluxões de x e y associadas ao fluxo do tempo. Os fluentes eram x e y. Em linguagem moderna, seria a derivada de

x em relação ao tempo, ou simplesmente x

( )

t e analogamente, a derivada de y em relação ao tempo ou ainda y

( )

t .

Tanto os nomes quanto as notações de Newton foram deixadas de lado ao longo dos anos, prevalecendo a notação criada por Leibniz. Saliente-se que, é ainda bastante utilizada pelos físicos quando a derivada em questão é em relação ao tempo e é dada a função deslocamento x=x

( )

t ; nesse caso, será a velocidade e a aceleração. Embora Newton tenha desenvolvido e revisto o seu Cálculo entre 1666 e 1671, nada foi publicado até 1736, tendo apenas mostrado os seus manuscritos para alguns colegas e amigos.

Entretanto Leibniz, em 1672, enquanto vivia em Paris, encontrou-se com Huygens e com ele aprendeu e obteve muitos conselhos que constituíram um forte impulso para que viesse a desenvolver o seu Cálculo Diferencial e Integral. Nesse período, ele estabeleceu contacto com muitos outros matemáticos respeitados da Royal Society . Dentre eles destaca-se Barrow e assim Leibniz teve acesso aos seus trabalhos e estabeleceu um longo período de correspondências.

O Cálculo Diferencial de Leibniz tinha uma fundamentação bem diferente do de Newton. Leibniz não estudou o movimento para chegar aos conceitos de derivada e integral. Ele pensou nas variáveis x e y como grandezas que variavam por uma sucessão de valores infinitamente pequenos. Introduziu dx e dy como a diferença entre esses valores sucessivos. Embora Leibniz não tenha usado como definição de derivada, ele sabia que representava o coeficiente angular da tangente.

Há um capítulo especial na história do Cálculo: uma longa e quase sempre inescrupulosa disputa entre Newton e Leibniz sobre quem havia "criado" o Cálculo. Ambos não pouparam acusações picantes para descrever o outro e os seus feitos e geraram uma discussão acalorada no meio científico da época sobre quem seria a mais importante autoridade no Cálculo. Apesar das diferenças, tanto Newton quanto Leibniz reconheceram até certo ponto a importância do "adversário". Leibniz disse um dia: “Considerando a Matemática desde o início do mundo até a época de Newton, o que ele fez é sem dúvida a melhor metade”. Newton, por sua vez, na primeira edição do

6

Issac Newton

Os grandes avanços na matemática e na ciência são quase sempre construídos pelo trabalho de muitos homens que contribuem pouco a pouco durante centenas de anos. Issac Newton foi um desses Homens. Na história do Cálculo, Newton foi um homem astuto o suficiente para distinguir as ideias válidas dos seus antecessores, imaginativo o suficiente para transformar as contribuições existentes em novos pressupostos e audaz o suficiente para construir um plano de mestre para dar o passo culminante e definitivo.

Newton nasceu na pequena aldeia de Woolsthorpe, Inglaterra, onde a sua mãe tratava da quinta deixada pelo marido, que morreu dois meses antes de Newton nascer. Frequentou as escolas locais pautadas de baixos níveis de sucesso escolar, e enquanto jovem não mostrou qualquer instinto especial, à excepção de um interesse por aparelhos mecânicos. Tendo passado os exames de admissão com uma insuficiência em geometria euclidiana, entrou na Universidade Trinity College of Cambridge em 1661, e o seu estudo decorreu de forma tranquila e discreta. Uma altura houve em que Newton quase mudava do seu curso de filosofia (ramo cientifico) para direito. Recebendo aparentemente pouco estimulo da parte dos professores, excepto possivelmente de Barrow, Newton tomou contacto com a Géométrie de Descartes tal como com os trabalhos de Copérnio, Kepler, Galileu, Wallis, e Barrow por si próprio.

Mesmo após Newton ter acabado a sua licenciatura, a universidade fechou devido a uma peste que se espalhou por Londres. Ele abandonou Cambridge e passou os anos de 1665 e 1666 no seio calmo da família em Woolsthorpe. Foi lá que Newton iniciou o seu grande trabalho de Mecânica, Matemática e Óptica.

Nesta altura, ele deu-se conta de que a lei do quadrado inverso da gravidade, um conceito avançado por outros, incluindo Kepler por volta de 1612, era um conceito chave para uma ciência abrangente de mecânica; ele desenvolveu um método geral de tratar os problemas do Cálculo; e através de experiências com a luz, ele fez a descoberta do século. Descobriu que a luz branca, tal como a luz do sol é realmente composta de todas as cores desde o violeta ao vermelho, Tendo Newton dito mais tarde, “Tudo isto, foi descoberto nos dois anos de peste de 1665 e 1666, pois nestes anos eu encontrava-me no auge da minha idade para invenções , e interessava-encontrava-me mais pela matemática e filosofia como nunca até então”.

Newton não se pronunciou acerca destas descobertas e regressou a Cambridge em 1667, para fazer o mestrado onde foi eleito membro do corpo directivo da Universidade de Cambridge. Em 1669 Isaac Barrow reformou-se do ensino e Newton foi convidado para o substituir como professor de matemática no Lucasian. Aparentemente, Newton não foi bem sucedido como professor, uma vez que poucos alunos frequentavam as suas aulas e o material apresentado também não era muito motivador , tal como afirmavam os seus colegas. Apenas Barrow, e mais tarde, o astrónomo Edmond Halley reconheceram sua grandeza e encorajaram-no.

publicar mais um trabalho sobre a luz, que continha a sua ideia que a luz era um raio de partículas — a Teoria Corpuscular da Luz. Novamente foi desgastado por uma tempestade de critica tendo sido inclusivamente acusado por outros de estas ideias já terem sido descobertas. Nesta altura, Newton resolveu que os seus resultados só seriam publicados após a sua morte. Ainda assim, ele chegou a publicar trabalhos e vários livros famosos tais como Principia,Opticks eArithmetica Universalis.

A partir de 1665 Newton aplicou a lei da gravidade ao movimento planetário; nesta área os trabalhos de Huygens e Hook influenciaram-no consideravelmente. Em 1684 o seu amigo Halley impulsionou-o para que publicasse os seus resultados, mas para além da sua relutância em publicar, faltavam-lhe ainda evidências de que a atracção gravitacional exercida por uma esfera sólida age como se a massa da esfera estivesse concentrada no centro. Ele escreveu numa carta a Halley em Junho 1686, que até 1685, ele suspeitou que esta teoria era falsa. Neste mesmo ano, ele mostrou que uma esfera cuja densidade varie apenas na distância para o centro, atrai de facto uma partícula externa, como se a massa da esfera estivesse concentrada no seu centro, e concordou em publicar este trabalho.

Halley prestou auxilio editorial a Newton a partir de então e pagava as publicações. Em 1687 surgiu a primeira edição de Philosophiae Naturalis Principia Mathematica (The Mathematical Principles of Natural Philosophy). Foram publicadas mais duas edições subsequentes, uma em 1713, e outra em 1726, a segunda edição continha melhorias. Apesar de este livro ter brindado Newton com muita fama, o seu entendimento tornava-se algo difícil. Ele comentou com um amigo que o tinha tornado propositadamente difícil “para evitar ver o seu trabalho ser criticado por pessoas que têm conhecimentos superficiais na área da Matemática”. Newton procurou desta forma evitar a critica de que os seus anteriores trabalhos sobre a luz tinham sido alvos.

Newton era também um grande químico. Apesar de não haver grandes descobertas associadas ao seu trabalho nesta área, temos que ter em conta que na química dava apenas os primeiros passos nesta altura. Newton defendia como correcto, o pressuposto de tentar explicar os fenómenos químicos em termos de partículas elementares, e ele tinha também um conhecimento profundo no que respeita à química experimental. Na obra Philosophical Transactions of the Royal Society de 1701, ele publicou um trabalho acerca do calor e que contém a sua famosa lei do arrefecimento. Apesar de Newton ter lido os trabalhos de alguns alquimistas, ele não aceitava as suas ideias místicas e obscuras. As propriedades químicas e físicas dos corpos podiam, defendia Newton, ser contáveis em termos de dimensão, forma, e movimento das suas partículas elementares Ele rejeitava as forças ocultas dos alquimistas, tal como a simpatia, antipatia, congruidade e atracção.

Além do seu trabalho em mecânica celestial, Newton fez ainda experiências sobre a acção de amortecimento do movimento do pêndulo das mais variadas formas, sobre a queda de esferas no ar e na água, e ainda sobre a corrente de água vinda de jactos. Tal como todos os teóricos do seu tempo, Newton construiu todo o seu equipamento. Ele construiu dois telescópios reflectores, fez a liga de metal para as estruturas, moldou as estruturas do telescópio, fez a montagem e poliu as lentes.

Após ter estado ao serviço do ensino durante 35 anos, Newton sofreu uma depressão e ficou com um esgotamento nervoso. Ele decidiu desistir da pesquisa, e em 1665 aceitou tornar-se guardião da British Mint em Londres.

Tornou-se presidente da Royal Society em 1703, um trabalho que levou até à sua morte; ele foi nomeado Cavaleiro em 1705.

8 que o apoio religioso era o principal valor do seu trabalho cientifico, e ele era de facto um teólogo letrado, apesar de nunca ter sido ordenado. Newton considerava que a pesquisa cientifica era dura e monótona, mas apaixonou-se por ela porque ela era a prova do trabalho de Deus.

Gottfried Wilhelm Leibniz

Apesar das suas contribuições terem sido bem diferentes, o homem que ao lado de Newton contribuiu para a construção do Cálculo, foi Gottfried Wilhelm Leibniz. Leibniz nasceu em Leipzig em 1646, estudou direito e, logo após ter defendido a sua tese sobre a lógica, adquiriu um bacharelato em Filosofia. Em 1666, escreveu a tese De Arte Combinatoria, um trabalho acerca do método de raciocínio; trabalho este, que contribuiu para o seu doutoramento em Filosofia na Universidade de Altdorf e para comprovar a sua aptidão para o ensino.

Durante os anos de 1670 e 1671, Leibniz escreveu os seus primeiros trabalhos sobre mecânica, e por volta de 1671, produziu a sua máquina de calcular. Leibniz assegurou um trabalho como embaixador do Elector de Mainz e em Março de 1672 foi para Paris numa missão política. Esta visita fez com que Leibniz estabelecesse contacto com muitos matemáticos e cientistas, nomeadamente Huygens, e fez também com que o seu interesse pela Matemática disparasse. Apesar de ter lido pouco sobre o assunto, e ter escrito o trabalho de 1666, Leibniz afirmou não ter tomado conhecimento com a Matemática até 1672.

Em 1673 Leibniz foi para Londres e conheceu mais matemáticos e cientistas, incluindo Henry Oldenburg, que na altura era secretário da Royal Society de Londres. À medida que ganhava a vida como diplomata, Leibniz aprofundava cada vez mais os seus conhecimentos em Matemática lendo Descartes e Pascal. Em 1776, Leibniz foi nomeado bibliotecário e membro do Conselho do Elector em Hanover. Vinte e quatro anos depois, o Elector (eleitor) de Brandenburgo convidou Leibniz para trabalhar para ele em Berlim. Ao mesmo tempo que se encontrava envolvido em manobras políticas de todo o tipo, Leibniz trabalhou em muitas áreas, e as suas actividades paralelas abrangiam um grande campo.

Para além de ser um diplomata, Leibniz era um filósofo, advogado, historiador, filologista, e um geólogo pioneiro. Ele desenvolveu trabalhos importantes nas áreas da lógica, mecânica, óptica, matemática, hidrostática, pneumática, ciência náutica, e máquinas calculadoras. Apesar da sua profissão ser a jurisprudência, o seu trabalho na área da matemática e filosofia está entre os melhores que o mundo já produziu.

Leibniz manteve contacto por meio de cartas com pessoas dos locais mais longínquos como a China e Ceylon. Ele tentou incessantemente reconciliar as fés católica e protestante. Foi Leibniz quem propôs, em 1669 que se fundasse uma Academia Alemã de Ciência, acabando por ser organizada em 1700 a Academia de Berlim. A sua recomendação inicial, foi que fosse criada uma sociedade para fazer invenções de mecânica e descobertas em química e fisiologia que fossem úteis à humanidade; Leibniz queria que o conhecimento fosse aplicado. Ele apelidava as universidades de “monásticas” e acusava-as de possuíam a aprendizagem mas de não a colocarem em prática e que estavam absorvidas em insignificâncias. Em vez disto, Leibniz defendia a urgência de perseguir o conhecimento real – matemática, física, geografia, química, anatomia, botânica, zoologia, e história. Para Leibniz as habilidades de um artesão e do homem prático, eram mais valorizadas do que as subtilezas aprendidas pelos letrados.

10 lado, era entendida pela mais comum das pessoas, e podia ajudar a desenvolver a clareza do pensamento e a intensidade do raciocínio.

Leibniz publicou trabalhos sobre o Cálculo a partir de 1684,contudo, muitos dos seus resultados, tal como o desenvolvimento das suas ideias, estão contidos em centenas de páginas de notas feitas a partir de 1673, mas nunca publicados por ele. Estas notas, tal como é de esperar, saltam de um tema para outro e contêm exemplos de mudança, à medida que o pensamento de Leibniz se ia desenvolvendo. Algumas, são apenas ideias que lhe ocorriam quando estava a ler um livro ou artigos de Gregory de St. Vincent, Fermat, Pascal, Descartes e Barrow, ou apenas tentativas de projectar os pensamentos destes, na sua própria aproximação do Cálculo.

Em 1714, Leibniz escreveu Historia et Origo Calculi Differentialis, no qual ele faz um relato do desenvolvimento da sua própria forma de pensar. Todavia, isto foi feito muitos anos após Leibniz ter desenvolvido o seu trabalho, e na visão da fraca memória humana, e do grande impacto que ele causou nessa época, a sua história pode não ser a mais fiel. Uma vez que o seu propósito era defender-se de uma acusação de plágio, Leibniz pode ter distorcido, inconscientemente o relato da origem das suas ideias.

A obra de Issac Newton

Em 1669 Newton fez circular entre os seus amigos um monografo intitulado De Analysi per Aequationes Numero Terminorum Infinitas (On Analysis by Means of Equations with an Infinite Number of Terms), sendo publicado apenas em 1711. Neste trabalho, Newton supôs que a área z ( figura 1), sob a curva é dada por :

(1) _z=_axm

onde mé integral ou uma fracção. Newton designava um infinitésimo aumento em x de “o momento de x”, e indica-o por o. A área limitada pela curva, o eixo dos xx, o eixo dos yy, e a ordenada de x+o,é indicada por Newton por z+oy, sendo oyo momento da área. Depois,

(2) z+oy=a

(

x+o

)

m

Figura 1

Ele aplica o Teorema Binomial ao segundo membro, obtendo uma série infinita quando m é fraccionário, a (1) subtrai (2) divide por o, omite os termos que contêm o

e obtém,

1 .

= m

x ma y

Portanto, na linguagem corrente, a taxa de variação da área em qualquer valor de

x ,é o valor y da curva nesse valor de x. Contrariamente, se a curva é 1

.

=_maxm

y

a área sob ela é

m

ax

z= .

12 a diferenciação, é o que nós agora designamos de Teorema Fundamental do Cálculo. Apesar de ser já conhecido em casos especiais, e ter sido obscuramente previsto pelos antecessores de Newton, ele considerava-o geral. Ele aplicou o método para obter a área sob muitas curvas e para resolver outros problemas que pudessem ser formulados como adições.

Após ter mostrado que a derivada da área é o valor y, e afirmado que o contrário também é verdade, Newton formulou a regra: “Se o valor y é a soma dos termos, então a área é a soma das áreas que resultam de cada um dos termos”. Em termos modernos, o integral indefinido de uma soma de funções, é a soma dos integrais das funções separadas.

A sua seguinte contribuição no monografo, estava mais relacionada com o seu uso de séries infinitas. Para integrar

(

b x

)

a y

+

= 2 , dividiu a2 por b+x e obteve

... 4 3 2 3 2 2 2 2 2 + + = b x a b x a b x a b a y

Tendo obtido estas séries infinitas, Newton encontra o integral, integrando termo a termo, de tal forma que a área seja,

... 4 3 2 4 4 2 3 3 2 2 2 2 2 + + b x a b x a b x a b x a

Newton proferiu que alguns dos termos iniciais das suas séries infinitas são demasiado exactos para qualquer utilização, de forma que estabeleceu que b fosse igual a x repetido algumas vezes.

De igual forma, para integrar

(

2

)

1 1

x y

+

= ele utiliza a expansão binomial para escrever,

... 1 2 + 4 6 + 8

= x x x x y

e integra termo a termo. Newton nota que, se y for

(

1

)

1 2 +

= x

y , então pela expansão binomial iria obter-se,

... 8 6 4

2 + +

= x x x x y

e agora pode integrar termo a termo.

Newton chama a atenção para o facto de, quando o valor de x é demasiado pequeno, é a primeira expansão que deve ser utilizada, mas quando o valor de x é maior, é a segunda expansão que deve ser utilizada. Portanto, Newton estava ciente de que aquilo que designamos por convergência, tem um papel importante, mas não tinha uma noção precisa disso. Newton deu-se conta de que tinha expandido a integração termo a termo às séries infinitas, e afirma na obra De Analysi:

Mortais cujo poder do raciocínio está confinado a estreitos limites; não conseguimos expressar nem conceber todos os Termos destas Equações, para saber daí exactamente as quantidades que queremos”.

Ao longo da sua abordagem ao Cálculo, Newton utilizou aquilo a que se pode designar de Método dos Infinitésimos. Nele os momentos são quantidades infinitamente pequenas, indivisíveis ou infinitésimas. A lógica das teorias de Newton não é clara. Ele próprio diz na sua obra que o seu método é “laconicamente explicado e não claramente demonstrado”.

Newton expôs uma segunda vez as suas ideias de forma mais extensiva e definitiva na obra Methodus Fluxionum et Serierum Infinitarum, escrito em 1671 e publicado em 1736. Neste trabalho, Newton diz considerar as variáveis como sendo geradas pelo movimento continuo de pontos, linhas e planos, e não como agregados estéticos de elementos infinitésimos, tal como havia considerado no seu anterior trabalho. Newton designava agora uma quantidade variável por fluente e a sua taxa de variação de fluxo. A sua notação é x e y para os fluxos e x e y para os fluentes. O fluxo de x é x,o fluxo de x é x e assim sucessivamente.

Neste seu segundo trabalho, Newton expõe de forma mais clara o problema fundamental do Cálculo: “Dada a relação entre dois fluentes, tem que encontrar-se a relação entre os seus fluxos e o inverso”. As duas variáveis cuja relação é aqui apresentada, podem representar quaisquer quantidades.

Contudo, Newton considerou que elas mudam com o tempo, apesar de ele sublinhar que isto pode não acontecer. Se o for um intervalo infinitamente pequeno de tempo, então xo e yo são os incrementos indefinidamente pequenos em x e y ou os momentos de x e y. Para encontrar a relação entre y e x sendo, por exemplo, o fluente y= xn. Newton em primeiro lugar forma,

(

)

n

o x x o y

y+ = +

e depois prossegue como no seu primeiro trabalho. Ele desenvolve o lado direito utilizando o teorema binomial, subtrai _y=_xn_{, divide por o, omite todos os termos que}

contenham o e obtém,

x nx y= n 1 .

Em notação moderna, este resultado pode ser traduzido por

dt dx nx dt

dy _{n 1}

=

e uma vez que

dt dx dt dy dx dy

= , Newton ao encontrar a relação (razão) (ratio) de

dt dy

para

dt dx

ou y para x encontrou

dx dy

.

O método dos fluxos não é essencialmente diferente daquele mencionado na obra De Analysi, nem o rigor é maior. Newton deixa cair por terra termos como xxo e

o x o x

x (ele escreve x3oo_{),pois estes são infinitamente pequenos comparados com o}

14 Contudo, o seu ponto de vista na obra Method of Fluxions é de certa forma diferente. Os momentos xo e yo mudam com o tempo o, enquanto que no primeiro trabalho, os momentos eram pedaços fixos de x e z. Esta nova visão segue o rasto mais dinâmico de Galileu, enquanto que a visão mais antiga seguia a linha do pensamento estático e indivisível de Cavalieri. A mudança serviu apenas, como diz Newton, para remover o rigor da doutrina dos indivisíveis. Para além do mais, x e y, que são os fluxos ou derivadas no que respeita ao tempo de x e y, nunca estão verdadeiramente definidas; este problema central deixa de existir.

Dada a relação entre x e y, encontrar a relação entre x e y é mais difícil do que meramente integrar uma função de x. Newton trata vários tipos:

(1) quandox, y e x ou y estão presentes; (2) quando x, y,x e y estão presentes;

(3) quando x, y,z e os fluentes estão presentes.

O primeiro tipo é o mais fácil e, em notação moderna, resolve-se por f

( )

x dx

dy

= .

Newton trata o segundo tipo da seguinte forma:

xy x y x x

y

+ + +

= 2

3 1

e resolve-o través de um processo de aproximação sucessivo. Newton começa por 2

3

1 x x

x

y _{= +}

como uma primeira aproximação, obtém y como função de x, de seguida introduz o valor de y no lado direito da equação original e continua o processo. Newton descreve como procedeu, mas não justifica. O terceiro tipo é estudado por Newton como: 2x z+yx=0 Newton assume a relação entre x e y, diz que x= y2, de forma a que x=2yy Então a equação torna-se 4yy z yy2 =0, da qual ele obtém

z y y + =

3 2

3 2

Portanto, se o terceiro tipo é visto como sendo uma equação diferencial parcial, Newton apenas obtém um integral particular.

Newton deu-se conta de que tinha apresentado um método geral no seu trabalho. Numa carta a John Collins, datada do dia 10 de Dezembro de 1672, ele expõe o seu método e dá um exemplo:

“ Esta é uma conclusão particular de um método geral, que se estende por si próprio sem quaisquer cálculos complicados, não apenas destinado ao desenho de tangentes de linhas curvas, geométricas ou mecânicas...mas também para resolver outros tipos de problemas obscuros como a curvatura, áreas, comprimentos, centros de gravidade de curvas, ets; também não é ... limitado a equações livres de quantidades irracionais. Este método eu misturei-o com aquele que serve para trabalhar equações, reduzindo-as a séries infinitas. “

Newton enfatizava o uso de séries infinitas, porque através delas ele podia tratar funções tais como

(

₁+_x

)

32_{, enquanto que os seus antecessores haviam sido algo} limitados no que respeita ao todo das funções algébricas racionais.

abandonado os infinitésimos ou quantidades infinitamente pequenas. Newton critica agora o abandono de termos envolvendo o e afirma,

“Em matemática o mais mínimo erro não pode ser negligenciado...eu considero as quantidades matemáticas neste campo, não sendo constituídas por partes muito pequenas, mas como sendo descritas por um movimento contínuo. As linhas são descritas e geradas não pela aposição das partes, mas pelo movimento contínuo de pontos; superfícies pelo movimento de linhas; sólidos pelo movimento de superfícies; ângulos pela rotação dos lados; porções de tempo por fluxos contínuos...

Fluxos são, como quisermos, incrementos de fluentes gerados em tempos, iguais e o mais pequenos possível, e para falar com rigor, são o primeiro ratio (proporção) dos incrementos nascentes. Mas podem ser expressos por quaisquer linhas, que são algo proporcionais a eles. “

O novo conceito de Newton, o método do primeiro e do último ratio (proporção) é equivalente a isto. Ele considera a função _y=_xn_{. Para encontrar o fluxo de y ou} n

x ,

Newton deixa que x“flua” e se torne x+o. Então xn traduz-se por

(

)

...

2

2 2 2

1+ +

+ =

+ n n n n

x o n n nox x

o x

Os acréscimos de x e y, nomeadamente o e ... 2

2 2 2

1+ n +

n

x o n n

nox estão

para cada um deles como (dividindo ambos por o),

1 para ...

2

2 2

1₊ n ₊

n

ox n n nx

“Que os incrementos desapareçam e que a sua última relação seja; 1 para nxn 1.

16 Newton fez também uma interpretação geométrica.

Figura 2

Considerando os dados da figura 2, e supondo que bc se move para BC de tal forma que c coincide com C. Então o triângulo curvilíneo CEc é “na sua última forma” similar ao triângulo CET, e os seus lados “evanescentes” serão proporcionais a

CE, ET, e CT. Portanto, os fluxos das quantidades AB, BC e AC são, no último ratio (proporção) dos seus incrementos evanescentes, proporcionais aos lados do triângulo

CET ou do triângulo VBC.

A primeira publicação de Newton envolvendo o seu Cálculo é a grande

Mathematical Principles of Natural Philosophy.. No que diz respeito à noção de Cálculo, de fluxo, ou como dizemos, de derivada, Newton faz várias afirmações. Ele rejeita infinitésimos ou quantidades indivisíveis, e defende “quantidades divisíveis evanescentes”, quantidades estas, que podem ser infinitamente diminuídas.

Na primeira e terceira edições da obra Principia, Newton afirma que: “Ratios (proporções) definitivas, nas quais as quantidades se desvanecem, não são, rigorosamente falando, ratios (proporções) de quantidades definitivas, mas sim limites dos quais, as ratios (proporções) destas quantidades, decrescendo sem limite, se aproximam, e que , apesar de elas se poderem aproximar mais do que qualquer outra diferença, nunca a poderão ultrapassar, nem alcançar antes das quantidades terem decrescido indefinidamente”.

Esta foi a declaração mais clara que Newton alguma fez acerca do significado da sua última ratio (proporção). A propósito da citação anterior, Newton também afirmou: “A expressão “última velocidade” refere-se à velocidade através da qual um corpo é movido, nem antes de chegar ao seu último lugar, quando o movimento cessa, nem depois; mas no preciso momento em que chega...e de igual forma, a expressão “a última ratio de quantidades evanescentes”, refere-se à proporção de quantidades, não antes de se terem desvanecido, nem depois, mas àquela (quantidade) com a qual elas se desvanecem”.

para além daqueles que conseguiu “traduzir” em geometria. Uma das razões pela qual Newton recorreu à geometria, foi porque acreditava que desta forma os seus resultados iriam tornar-se mais compreensíveis aos seus contemporâneos. Outro motivo para isto, é que Newton admirava imensamente o trabalho que Huygens fez com a geometria e esperava igualá-lo. Nestas provas geométricas Newton utiliza os processos básicos do Cálculo.Portanto, a área sob uma curva é considerada essencialmente como o limite da soma dos rectângulos mais próximos, tal como acontece actualmente no Cálculo. Contudo, em vez de calcular tais áreas, Newton utilizou este conceito para comparar áreas sob diferentes curvas.

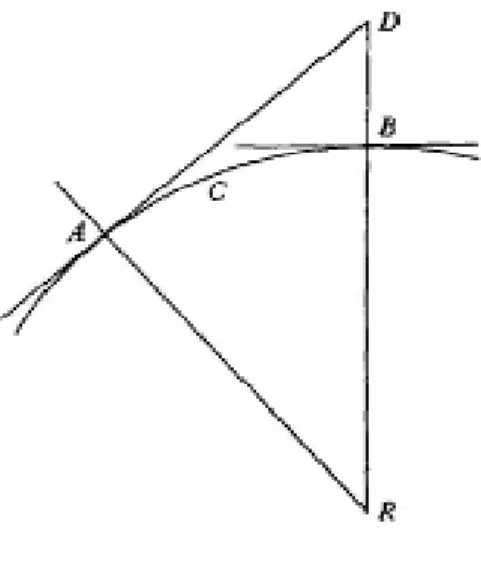
Newton prova que, e observando-se a figura 4, quando AR e BR são as perpendiculares às tangentes em AeBdo arco ACB, a última ratio ( proporção), quando

Bse aproxima e coincide com A, de qualquer das duas quantidades AB, arco ABC e AD, é 1. Newton também prova que , quando B se aproxima e coincide com A, a razão entre os triângulos RAB, RACD e RAD será 1.

Da mesma forma e analisando a figura 5, sendo BD e CE perpendiculares a AE

(que não é necessariamente a tangente do arco ABC em A), quando BeCse aproximam e coincidem com a última proporção das áreas ACE e ABD, estas irão ser iguais à última proporção de AE2 para AD2.

Figura 4 Figura 5

A obra Principia contém uma abundância de resultados e alguns dos quais deve-se ter em consideração. Apesar de o livro deve-ser devotado à Mecânica Celestial, teve uma grande importância para a História da Matemática, não apenas devido ao facto do trabalho que Newton desenvolveu sobre o Cálculo ter sido motivado em grande parte pelo seu interesse preferencial pelos problemas tratados nesta área, mas porque

18

A obra de Leibniz

O seu cálculo infinitesimal é também uma notável obra no que respeita à notação e terminologia. Elas são ainda hoje usadas, até mesmo para enunciar e discutir os resultados dos matemáticos que o antecederam.

A sua primeira época criativa coincide com a sua permanência em Paris (1672 a 1676) onde começou a estudar Geometria e em que a sua inspiração remonta ao trabalho realizado com somas e diferenças, o que o levou a considerar a possibilidade de somar “séries infinitas”.

Em 1673 Leibniz estava consciente da importância do problema directo e inverso de encontrar tangentes de curvas, estando também bem certo, de que o método inverso era o equivalente a encontrar áreas e volumes através do método da soma.

O desenvolvimento algo sistemático das suas ideias começa com as suas notas de 1675. Contudo, parece ser de grande ajuda, a fim de entender a sua forma de pensar, ter em atenção que na sua obra De Arte Combinatoria, Leibniz considerou sequências de números, primeiras diferenças, segundas diferenças, e diferenças de várias sequências. Portanto, para a sequência de quadrados,

,... 36 , 25 , 16 , 9 , 4 , 1 , 0 as primeiras diferenças são,

,... 11 , 9 , 7 , 5 , 3 , 1 e as segundas diferenças são,

,... 2 , 2 , 2 , 2 , 2 , 2

Leibniz notou o ausência das segundas diferenças para a sequência de números naturais, das terceiras diferenças para a sequência de quadrados, e assim

sucessivamente.

Leibniz também observou que, se a sequência inicial começar por 0, a soma das primeiras diferenças é o último termo da sequência.

Para relacionar estes factos com o Cálculo, Leibniz teve que pensar na sequência de números enquanto valores de y de uma função e a diferença entre qualquer dos dois, como a diferença dos dois valores y mais próximos. Inicialmente, Leibniz pensou em

x como representando a ordem do termo na sequência e em y como representando o valor desse termo.

A quantidade dx, que ele frequentemente escreve como a, é então 1 porque é a diferença da ordem dos dois termos sucessivos, e dy é a actual diferença nos valores dos dois termos sucessivos. Depois, utilizando omn. como abreviatura do Latim omnia, que significa soma e utilizar l por dy, Leibniz conclui que omn.l= y, porque omn.lé a soma das primeiras diferenças de uma sequência cujos termos começam por 0, dando como resultado o último termo. Contudo, omn.yl apresenta um novo problema. Leibniz obtém o resultado de que omn.yl é

2 2

y

Figura 1

Logo, tal como mostra a figura 1, a área do triângulo ABC é a soma de yl e é também

2 2

y

. Leibniz diz: “Linhas rectas que aumentam do nada, cada uma delas multiplicadas pelo seu elemento de aumento correspondente, formam um triângulo”.

De seguida, Leibniz lutou contra várias dificuldades. Teve que fazer a transição para uma série discreta de valores para o caso onde dy e dxsão incrementos de uma função arbitrária yde x. Uma vez que Leibniz ainda estava ligado às sequências, onde

x é a ordem do termo, o seu a ou dx era 1, tendo a sido inserido e omitido livremente. Quando Leibniz fez a transição para dy e dx de qualquer função,a já não era 1. Contudo, enquanto ainda lutava contra a noção de soma, Leibniz ignorou este facto.

Mas, num manuscrito do dia 29 de Outubro,1675, Leibniz começa com (1)

a l l omn omn yl

omn. = . .

cuja lógica se mantém, porque y é ele próprio omn.l.Aqui Leibniz divide l por a

para preservar dimensões. Leibniz diz que (1) mantém -se, independentemente do que l

possa ser. Mas, tal como vimos em relação á imagem 17.17,

(2)

2 .

2

y yl omn =

Por isso, a partir de (1) e (2),

a l l omn omn y

. . 2

2

20 Em notação moderna, Leibniz mostrou que,

{ }

= = dx dy y dx dy dy y 2 2

e afirma que este resultado é admirável.

Outro teorema do, mesmo tipo, que Leibniz derivou de um raciocínio geométrico, é (3) omn.xl =xomn.l omn.omn.l

onde l é a diferença em valores de dois termos sucessivos de uma sequência e x é o número do termo. Para nós esta equação é,

=xy ydx xdy

Agora Leibniz deixa que lem (3) seja x, e obtém,

x omn omn x xomn x

omn. 2 = . . .

Mas omn. , éx

2 2

x

( ele mostrou que

2 .

2

y yl

omn = ). Assim,

2 . 2 . 2 2 2 x omn x x x omn =

Transpondo o último termo, Leibniz obtém,

3 . 3 2 x x omn =

Neste manuscrito do dia 29 de Outubro de 1675, Leibniz decidiu escrever , em vez de omn.,por forma que,

l omn

l= . e

2 2

x x=

O símbolo é um alongamento para significar “soma”.

Leibniz, cedo se apercebeu que, provavelmente por ter estudado o trabalho de Barrow, a diferenciação e integração enquanto soma, têm que ser processos inversos e assim a área quando diferenciada, tem que dar um comprimento. Do mesmo modo, no mesmo manuscrito do dia 29 de Outubro, Leibniz afirma: “Dado l e a sua relação com

x para encontrar l. Supondo que l =ya e

d ya

l= . Então à medida que vai aumentando, d vai diminuindo as suas dimensões. Mas significa uma soma, e

d,uma diferença. Dado y podemos sempre encontrar

d y

ou l,ou seja, a diferença dos

Por exemplo, da equação

3 3 2

3a l c l

c =

podemos obter a equação,

d a

l c l c

3 3 2

3

= “.

Neste trabalho, Leibniz parece estar a explorar as operações de e de d e conclui que eles são inversos. Finalmente dá-se conta de que não aumenta a sua dimensão, nem d a diminui, porque é realmente a soma de rectângulos, e portanto, a soma de áreas. Prontamente Leibniz reconheceu que, para passar de dy para y, tinha que formar a diferença dos yy, ou então tomar o diferencial de y. Leibniz diz, “Mas significa uma soma e d uma diferença”. Isto pode ter sido uma introdução mais tardia. Desta forma, algumas semanas depois, a fim de passar de y para dy, ele troca, dividindo por d para obter o diferencial de y e escreve dy.

Até este ponto, Leibniz tinha estado a pensar nos valores de y enquanto valores dos termos de uma sequência, e em x, normalmente como a ordem destes termos, mas agora, neste trabalho Leibniz afirma: “Todos estes teoremas são verdadeiros para séries nas quais as diferenças de termos geram para os próprios termos uma relação que é menor do que qualquer quantidade aplicável” Ora,

y dy

, pode ser menor do que qualquer quantidade aplicável.

Num manuscrito datado do dia 11 de Novembro de 1675, intitulado “Examples of Inverse Methods of Tangents”, Leibniz utiliza para a soma e

d x

para a diferença. Ele então afirma que

d x

é dx, a diferença de dois valores de x consecutivos , mas aparentemente aqui dx é uma unidade igual e constante.

A partir de argumentos pouco claros, tais como o anterior, Leibniz considerava

a integração como um processo somatório que é inverso da diferenciação. Esta ideia está também patente nos trabalhos de Newton e Barrow, que obtinham áreas por um processo de anti-diferenciação. Mas é a primeira vez que é enunciada, e por Leibniz, como uma relação entre a soma e a diferenciação. Apesar desta afirmação, Leibniz não estava certo de como obter uma área, e de uma maneira geral pode traduzir-se por

22 diferença entre esta soma e a verdadeira área sob a curva podia ser omitida, e noutras alturas como a soma de valores ordinários ou valores de y.

Este último conceito de área era comum, especialmente entre os teóricos que defendiam a teoria dos indivisíveis, que consideravam que a última unidade da área e que os valores de y eram o mesmo

No que diz respeito à diferenciação, mesmo após ter reconhecido que dy e dx

podem ser quantidades arbitrárias pequenas, Leibniz teve ainda que ultrapassar a principal dificuldade, de que a relação

dx dy

não é exactamente a derivada, pelo menos como se conhece actualmente.

Leibniz baseou o seu argumento no triângulo característico, que Pascal e Barrow também utilizaram.

Figura 2

Este triângulo, que se pode observar na figura 2, é formado por dy, dxe pela linha PQ, a qual Leibniz designou por a curva entre P e Q e parte da tangente em T.

Apesar de Leibniz falar deste triângulo como sendo infinitamente pequeno, ele mantém, contudo, que este triângulo é semelhante a um triângulo delimitado, nomeadamente, o triângulo STU formado pela subtangente SU, a ordenada em T, e o comprimento da tangente ST. Uma vez que dy e dx são elementos fixos, a sua relação tem um significado delimitado. De facto, Leibniz usa o argumento que, de triângulos semelhantes PRQ e STU, resulta

SU TU dx dy

= .

Ainda no manuscrito do dia 11 de Novembro 1675, Leibniz mostrou como podia resolver um problema delimitado. Ele procura a curva, cuja subnormal é inversamente proporcional à ordenada. Na figura 2, a normal é TV e a subnormal p é UV. Da semelhança dos triângulos PRQ eTUV, Leibniz obtém,

y p dx dy

=

ou, da mesma forma,

dy y dx

Mas a curva tem a propriedade,

y b p=

onde b é proporcionalmente constante. Desta forma,

dy b y dx 2 = Logo, = dy b y dx 2 ou b y x 3 3 =

Leibniz também resolveu outros problemas inversos de tangentes. Num jornal do dia 26 de Junho do ano 1676, Leibniz apercebe-se que o melhor método de encontrar tangentes é encontrar

dx dy

, onde dy, e dx são diferenças e

dx dy

é o quociente. Leibniz ignora dx.dxe potências mais elevados de dx.

Em redor de Novembro de 1676, Leibniz já é capaz de formular regras gerais, tais como, dxn =nxn 1dx para integrais e n fraccionadoe

+ = + 1 1 n x x n n

, e afirma: “O raciocínio é geral, e não depende das progressões dos xx “ Aqui x ainda significa a ordem dos termos de uma sequência

No dia 11 de Julho de 1677, Leibniz já estava capaz de formular as regras correctas para o diferencial da soma, diferença, produto, quociente de duas funções, potências e raízes, mas não existiam provas. No manuscrito do dia 11 de Novembro de 1675, Leibniz tinha-se debatido com d

( )

uv e

v u

d , e pensou que d

( )

uv =dudv.

Em 1680, dx tornou-se a diferença de abcissas e dy a diferença nas ordenadas. Leibniz diz:

“...agora estes valores,dx e dy, são considerados infinitamente pequenos, ou, como dois pontos na curva que são compreendidos como uma distância à parte, que é menor do que qualquer outro comprimento”. Leibniz designa dy de “incremento momentâneo” em y, conforme a ordenada se move ao longo do eixo dos xx. Mas PQ,

na figura 2 ainda é considerado como sendo parte de uma linha recta. É “um elemento da curva, ou um lado de um polígono de ângulo infinito que está em vez da curva. ...”

Leibniz continua a utilizar a forma diferencial habitual. Assim, se

24 Leibniz também ilustrou que as diferenças são o oposto das somas. Assim, para encontrar a área sob uma curva ,como mostra a figura 3, Leibniz considera a soma dos rectângulos e afirma que podemos omitir os restantes “triângulos, uma vez que estes são infinitamente pequenos comparados aos rectângulos… assim I, representa no meu Cálculo, a área da figura por ydx ….”

Figura 3

Apesar das anteriores declarações, de que dx e dy são pequenas diferenças, Leibniz ainda fala de sequências. Ele diz que “Diferenças e somas são os inversos um do outro, o que por assim dizer, a soma das diferenças de uma sequência é um termo da sequência , e Ienumera o primeiro por dx=x, e o último por d x=dx”. De facto, num manuscrito escrito depois de 1684, Leibniz diz que o seu método de infinitésimos tornou-se bastante conhecido como o Cálculo das Diferenças.

A primeira publicação de Leibniz sobre o Cálculo é em Acta Eruditorum de 1684. Neste trabalho, o significado de dx e dy ainda não é claro. Leibniz considera dx

como uma qualquer quantidade arbitrária e dy, observando a figura 3, é definida por:

subtg y dx dy

=

Esta definição de dy prevê uma expressão para a subtangente; assim a definição não está completa. Para além disto, a definição de tangente de Leibniz como sendo uma linha que junta dois pontos infinitamente próximos, não é satisfatória.

Leibniz também expõe neste trabalho as leis que ele obteve em 1667 para o diferencial da soma, produto e cociente de duas funções, e a regra para encontrard

( )

xn . Neste último caso, Leibniz esboça a prova para o integral quando n é positivo, mas diz que esta regra é válida para qualquer valor de n.Para as outras regras Leibniz não dá quaisquer provas.

Leibniz também tentou encontrar um significado para d y onde corresponde a qualquer número real.

Relativamente à notação, Leibniz trabalhou arduamente para alcançar o ideal. Os seus dx,dy e

dx dy

são, sem dúvida, exemplos da sua excepcional notação. Ele introduziu a notação para logx, dn para o diferencial de ordem n, entre outros exemplos.

26

Comparação entre o trabalho de Newton e de Leibniz

Newton e Leibniz têm que ser elogiados por verem o Cálculo como um método novo e geral, aplicável a muitos tipos de funções. Após o seu trabalho, o Cálculo não foi mais considerado um apêndice e uma extensão da geometria Grega, mas sim uma ciência independente capaz de tratar uma vasta gama de problemas.

Ambos também transformaram o Cálculo numa função aritmética, ou seja, baseado em conceitos algébricos. As técnicas e os exemplos algébricos de Newton e Leibniz, não só se tornaram numa ferramenta mais real do que a geometria, como também permitiram o tratamento de problemas físicos e geométricos. Uma grande mudança desde o início até ao final do século dezassete, foi a transformação do Cálculo numa função da álgebra. Isto é comparável com o que Vieta fez com a teoria das equações, e Descartes e Fermat com a geometria.

A terceira contribuição vital que Leibniz e Newton partilharam, foi a simplificação à anti-diferenciação, a determinação de áreas, volumes, e outros problemas que eram anteriormente calculados por meio de somas. Portanto, os quatro principais problemas – média, tangentes, máxima e mínima, e soma - foram reduzidos a diferenciações e anti-diferenciações.

Com Newton, a obtenção dum fluente a partir da sua fluxão, corresponde à primitivação – integral indefinido – e assim calcula áreas e volumes. Para Leibniz, o integral é uma soma infinita de diferenciais – integral definido –, que acaba também, por ser calculado por anti-diferenciação. Ambos assentam, assim, na relação inversa entre problemas de “quadratura” e de “tangente”.

A principal distinção entre o trabalho destes dois homens é que Newton utilizava os incrementos infinitamente pequenos em x e emy, como forma de determinar o fluxo, ou seja, a derivada. Era essencialmente o limite da razão dos incrementos, à medida que eles se iam tornando cada vez mais pequenos. Por outro lado, Leibniz lidava directamente com incrementos infinitamente pequenos em x e em y, ou seja, com diferenciais, e determinou a relação entre eles. Esta diferença reflecte a orientação para a Física de Newton , na qual um conceito como a velocidade é central, e demonstra também a preocupação filosófica de Leibniz com as partículas fixas, que ele chamava de mónadas. Como consequência, Newton resolveu os problemas da área e volume pensando inteiramente em termos da taxa de variação. Para ele a diferenciação era básica; este processo e o seu inverso resolvia todos os problemas do Cálculo, e de facto a utilização da soma para obter uma área, um volume, ou um centro de gravidade, raramente aparece no seu trabalho. Leibniz, por outro lado, pensou primeiramente em termos de soma, apesar de estas somas serem, obviamente, avaliadas pela anti-diferenciação.

reduzidas às funções logarítmicas e circulares, e desafiou Newton a determinar, através do uso de séries se Gregory estava ou não correcto. Newton respondeu que através do uso de séries, ele podia decidir se algumas integrações podiam ser alcançadas em termos finitos, mas não adiantou qualquer critério. Novamente numa carta de 1712, a John Bernoulli, Leibniz contrariou a expansão de funções em série, e afirmou que o Cálculo devia servir para reduzir os seus resultados a quadraturas (integrações), sempre que necessário, quadraturas envolvendo funções transcendentes.

28

A Controvérsia sobre a Prioridade

Nada do trabalho de Newton sobre o Cálculofoi publicado de 1687, apesar de ele ter comunicado os seus resultados a amigos durante os anos de 1665 a 1687. Em particular, ele enviou o seu tratado De Analysi em 1669 a Barrow, que o enviou por sua vez a John Collins. Leibniz visitou Paris em 1672 e Londres em 1673, e comunicou com algumas pessoas que conheciam o trabalho de Newton. Contudo, não publicou os seus trabalhos sobre o Cálculo até 1684. Apesar de se levantar aqui a questão de Leibniz conhecer ou não os detalhes do trabalho de Newton, Leibniz foi acusado de plágio. Contudo, as investigações efectuadas muito tempo após a sua morte mostraram que Leibniz foi um inventor independente das maiores e mais importante ideias sobre o Cálculo, apesar de Newton ter desenvolvido também muito trabalho antes de Leibniz. Ambos devem muito a Barrow, apesar de que Barrow utilizava métodos geométricos quase de forma exclusiva. O significado da controvérsia não está em apurar quem era o vencedor, mas sim no facto de os matemáticos serem tendenciosos. Os matemáticos continentais, em particular os irmãos Bernoulli, tendiam para o lado de Leibniz enquanto que os matemáticos ingleses defendiam Newton. Os dois grupos tornaram-se desagradáveis e até amargos entre si. John Bernoulli foi tão longe como ridicularizar e caluniar os matemáticos ingleses.

Como resultado, os matemáticos ingleses e os continentais cessaram a sua troca de ideias. Porque o maior trabalho de Newton, e a sua primeira publicação sobre o Cálculo, Principia, utilizou métodos geométricos, os ingleses continuaram a utilizar principalmente a geometria durante pelo menos cem anos após a sua morte. Os continentais tomaram os métodos analíticos de Leibniz expandindo-os e melhorando-os. Isto provou ser mais efectivo; pois não apenas os matemáticos ingleses ficaram para trás, como também os matemáticos continentais se viram privados de dar a sua contribuição acerca do trabalho que as mentes brilhantes haviam desenvolvido.