Grupo de renormalização na aproximação de potencial local para o modelo O(N) de Heisenberg...

(1)

Grupo de Renormaliza¸c˜

ao na Aproxima¸c˜

ao de

Potencial Local para o Modelo

O(N

)

de Heisenberg

Hier´

arquico: Trajet´

oria Cr´ıtica e Somabilidade da

Expans˜

ao

1/N

William Remo Pedroso Conti

Orientador: Prof. Dr. Domingos Humberto Urbano Marchetti

Tese de Doutorado

apresentada ao Instituto de F´ısica da Universidade de S˜ao Paulo

para a obten¸c˜ao do t´ıtulo de Doutor em Ciˆencias.

Banca Examinadora:

Prof. Dr. Carlos Eugˆenio Imbassahy Carneiro - IFUSP Prof. Dr. Gast˜ao de Almeida Braga - UFMG

Prof. Dr. Jo˜ao Carlos Alves Barata - IFUSP Prof. Dr. Paulo Domingos Cordaro - IMEUSP

Prof. Dr. Silvio Roberto de Azevedo Salinas (presidente) - IFUSP

(2)

(3)

`

A minha amada fam´ılia - Sra. Maria Cristina Pedroso Conti, Sr. Leonildo Remo Conti, Thiago Vin´ıcius Pedroso Conti e Mayara Cristina Pedroso Conti - pelo apoio e incentivo.

Ao meu orientador, Prof. Dr. Domingos Humberto Urbano Marchetti, pelo modo como

conduziu meus passos; por toda sua aten¸c˜ao, em todos os momentos deste projeto; pela conﬁan¸ca em mim depositada.

Ao Prof. Dr. Silvio Roberto de Azevedo Salinas, que aceitou ﬁcar por mim respons´avel

nos meus ´ultimos meses de doutorado, por conta da viagem de meu orientador.

Aos meus amigos do Grupo de Mecˆanica Estat´ıstica, meus companheiros de caminhada.

`

As secret´arias e funcion´arios do Departamento de F´ısica Geral, pelo suporte e prestivi-dade.

`

A Funda¸cão de Amparo à Pesquisa do Estado de São Paulo (FAPESP), pelo apoio

(4)

(5)

Na aproxima¸cão de potencial local (L_↓1) a transforma¸cão de grupo de renormaliza¸cão para o modelo O(N) de Heisenberg hierárquico na criticalidade (sistema à temperatura inversa cr´ıtica βc(N, d)) é descrita pela equa¸cão

u(tN) =

2

Nxu

(N)

xx +u(xN)−2x u(xN)

2

−(d+ 2)xu(xN)+du(N)−u(xN)(t,0),

sendo que a condi¸cão inicial definida pelo modelo é dada por

u(N)(0, x) =₋1

N ln

"

Γ(N/2)

i√βxN/2N/2−1JN/2−1

ipβxN

#

.

O objetivo deste trabalho é investigar a somabilidade da série formal em potências de 1/N da equa¸cão de evolu¸cão satisfeita por u(xN)(t, x) quando o sistema encontra-se na

criticalidade (β =βc(N, d)). Considerando a fun¸c˜ao inversa v(N)₍_{t, p}_{) = (}_u(N)

x )−1(t, p),

mostramos que na criticalidade a s´erie formal

ˆ

v(N)(t, p) =

∞

X

i=0

v[i](t, p) (2/N)i

´e s-Gevrey, para todo p ﬁxo pertencente ao disco fechado centrado em p = ₋1 e raio

ς (denotado por Dς(−1)), com s > 2 e 0 < ς < 1/2. Mostramos tamb´em que a s´erie

formal

ˆ

u(_xN)(0, x) =

∞

X

i=0

fi(x) (2/N)i

(6)

(7)

In the local potential approximation (L_↓ 1) the renormalization group transformation for the hierarchical O(N) Heisenberg model at criticality (system at inverse critical temperature βc(N, d)) is given by the evolution equation

u(tN) =

2

Nxu

(N)

2

−(d+ 2)xu(xN)+du(N)−u(xN)(t,0),

and the initial condition deﬁned by the model is given by

u(N)(0, x) =₋1

N ln

"

Γ(N/2)

i√βxN/2N/2−1JN/2−1

ipβxN

#

.

The main goal of this work is to investigate the summability of the formal power series (in 1/N) solution of the evolution equation satisﬁed by u(xN)(t, x) when the system is at

criticality (β = βc(N, d)). Considering the inverse function v(N)₍_{t, p}_{) = (}_u(N)

x )−1(t, p),

we show that at criticality the formal series

ˆ

v(N)(t, p) =

∞

X

i=0

v[i](t, p) (2/N)i

iss-Gevrey, for every ﬁxedpin the closed disc centered atp=₋1 and radiusς (denoted by Dς(−1)), where s >2 and 0< ς <1/2. We also show that the formal series

ˆ

u(xN)(0, x) =

∞

X

i=0

fi(x) (2/N)i

(8)

(9)

1 Motiva¸c˜oes e Resultados 12

2 Trajet´oria Discreta: Resumo 31

2.1 O Modelo O(N) de Heisenberg Hier´arquico . . . 31

2.2 Transforma¸c˜ao de Grupo de Renormaliza¸c˜ao . . . 39

2.3 A Aproxima¸c˜ao de Potencial Local (L_↓1) . . . 58

3 Defini¸cões e Ferramentas 64 3.1 Teoria de Somabilidade: Defini¸cões . . . 64

3.2 Normas e Estimativas . . . 67

3.3 Ingredientes Chave . . . 72

3.4 Propriedades deg(ε, w) a Partir das Propriedades de f(ε, z) =g−1₍_{ε, z}_{) . 79} 4 Estudo da Condi¸c˜ao Inicial 88 4.1 A Classe P das Fun¸c˜oes de Pick . . . 88

4.2 Raio de Univalˆencia . . . 96

4.3 1-Somabilidade na Dire¸c˜ao θ= 0 . . . 102

4.3.1 A EDO Satisfeita por u(ε,0, x) = u(N)₍₀_{, x}_{) . . . 103}

4.3.2 Série de Potências na Variável x . . . 105

4.3.3 Série de Potências na Variável ε = 2/N . . . 108

4.3.4 S´erie Assint´otica . . . 112

4.3.5 Concluindo a Se¸c˜ao: o Teorema . . . 118

5 O Caso t >0 na Criticalidade 120 5.1 Transformada de Legendre de u(ε, t, x) =u(N)₍_{t, x}_{) com Respeito a} _x _{. . 120}

(10)

5.2.1 Equa¸c˜ao Satisfeita por Cada Coeﬁciente v[i]₍_{t, p}_{) . . . 124}

5.2.2 A Criticalidade . . . 129 5.2.3 Existência de uma Única Solu¸cão v[i]₍_{t, p}_{) na Criticalidade . . . . 130}

5.2.4 Estimativas de Gevrey para _|v[i]₍_{t, p}₎_|_{na Criticalidade . . . 139}

5.3 S´erie Assint´otica . . . 148

6 Conclus˜oes e Coment´arios Finais 149

A Apˆendices 152

(11)

(12)

Motiva¸c˜

oes e Resultados

A aproxima¸cão de potencial local é uma versão de escala cont´ınua para uma trans-forma¸cão de grupo de renormaliza¸cão. Como dito por Zumbach em [51], essa é a mais simples “boa aproxima¸cão” do grupo de renormaliza¸cão, entendendo por “boa

aproxima¸cão” aquela que é suficientemente simples para que possamos lidar com ela, e suficientemente sofisticada para que contenha a essência f´ısica do problema.

No ano de 1987, em um trabalho seminal, Felder [17] estudou a versão de escala cont´ınua do modelo hierárquico de Dyson [14]. Ela é dada pela equa¸cão diferencial parcial

ψt= 1 2ψyy −

1 2(ψy)

2

− d−₂ 2yψy+dψ, (1.0.1)

que descreve o fluxo do potencial efetivo ψ(t, y) (ψ(t, y) =₋lnσ(t, y), comσ(t, y) uma medida de probabilidade) na escala e−t_{como fun¸cão do campo (variável de spin)} _y_∈_R_,

(13)

Na aproxima¸cão de potencial local os pontos fixos da transforma¸cão de grupo de re-normaliza¸cão devem ser identificados com solu¸cões globalmente estacionárias de (1.0.1). Assim, o problema de encontrar pontos fixos na aproxima¸cão de potencial local se reduz

ao estudo de solu¸cões globais (definidas para todo y) da seguinte equa¸cão diferencial ordinária:

ψ′′₋(ψ′)2₋(d₋2)yψ′+ 2dψ= 0. (1.0.2)

O que Felder mostra é que, além do ponto fixo gaussiano (também chamado de ponto fixo trivial) ψgauss₍_y_{) = 0 e do ponto fixo de altas temperaturas} _ψat₍_y_{) =} _y2 ₋ ₁_/d_,

a equa¸cão (1.0.1) possui solu¸cões globalmente estacionárias não-triviais ψ∗

2n(y) com a

forma de n potenciais do “tipo po¸co” para 2< d < dn= 2 + 2/(n₋1),n= 2,3, . . .. A estabilidade local dos pontos fixos triviais e algumas propriedades dinâmicas da equa¸cão de evolu¸cão correspondente ao sistema de spins de N-componentes foram estudadas anal´ıtica e numericamente por Zumbach [51]. Em [37], Lima refinou o estudo de Felder para o dom´ınio de dimensões d _≥ 3. Após isso, pouca aten¸cão foi dada à equa¸cão (1.0.1), sendo que um dos principais obstáculos aos avan¸cos está no fato de o espa¸co de configura¸cão RN _{× · · · ×}RN ₌RN.n _de_n _{spins ser não-compacto.}

No ano de 2005 iniciamos nossos estudos sobre o modelo O(N) de Heisenberg hierárquico. Inicialmente, como parte de um estudo preliminar ao projeto de mes-trado, estendemos e complementamos para esse modelo os resultados obtidos por Kunz e Zumbach [34]: mostramos em [8] a convergência da energia livre e da fun¸cão

gera-triz do modelo O(N) de Heisenberg hierárquico para as do modelo esférico hierárquico quando os limites n _{→ ∞} (limite termodinâmico) eN _{→ ∞} são tomados, independen-temente da ordem de tais limites. Para tanto, utilizamos uma adapta¸cão do método empregado por Kac e Thompson [28], além do já citado artigo [34] de Kunz e Zumbach,

e uma generaliza¸cão (L > 1 e d _≥ 1) da defini¸cão de positividade por reflexão para o laplaceano hierárquico encontrada em [49]. Devemos destacar que tais resultados valem para qualquer β < βc; eles não incluem a criticalidade (β = βc). Além da extensão acima apontada, mostramos em [8] que o modelo esférico hierárquico exibe transi¸cão de

fase para d >2.

(14)

criticalidade, o que requer a implementa¸cão do grupo de renormaliza¸cão. Visando um entendimento mais claro e profundo de algumas questões, optamos por trabalhar com o grupo de renormaliza¸cão na aproxima¸cão de potencial local. O estudo do modelo esférico

hierárquico na criticalidade foi feito entre os anos de 2006 e 2008, resultando no artigo [41] e na disserta¸cão de mestrado [7]. O presente projeto de pesquisa dá continuidade às investiga¸cões realizadas no mestrado, sendo o modelo O(N) de Heisenberg hierárquico na criticalidade o nosso foco. Nossos estudos têm contribu´ıdo em algumas dire¸cões, que

ser˜ao explicitadas ao longo deste cap´ıtulo t˜ao logo o contexto em que aparecem e os conceitos envolvidos sejam introduzidos.

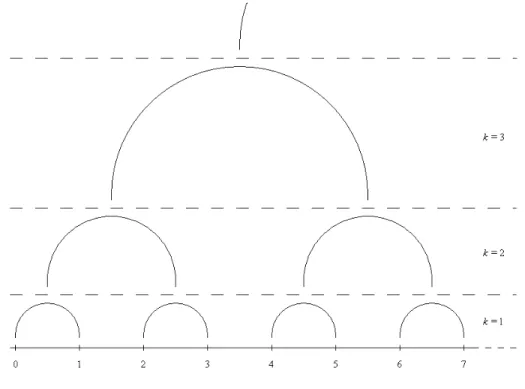
O Modelo O(N) de Heisenberg Hier´arquico. Dados os inteiros L, K e d, com

L, K >1 ed_≥1, seja

ΛK ={0,1, . . . , LK−1}d⊂Zd

uma rede finita hipercúbicad-dimensional de cardinalidade_|ΛK|=LKd=n. Pormodelo O(N) de Heisenberg hierárquico entende-se o modelo que associa a cada vértice de ΛK

uma vari´avel de spin cl´assica y que assume valores sobre a esfera de raio√βN em RN_,

com β o inverso da temperatura. Essas variáveis sãodependentes segundo uma matriz de acoplamento ferromagnética chamada matriz de intera¸cão hierárquica (JH). Trata-se de uma matriz n _×n real simétrica, positiva e positiva definida, que não obedece invariância por transla¸cão nem alcance finito, e cuja forma quadrática é dada por

(s, JHs)Rn = K

X

k=1

L−2k X r∈ΛK−k

(Bks)2_r

(Bks)r =

1

Ldk/2

X

j∈Λk

sLk_r₊_j,

com (r, s)Rn =

X

i∈ΛK

risi. Vê-se assim que as variáveis de spin interagem segundo uma estrutura de blocos: a cada hierarquia são formados blocos de Ld _{variáveis de spin da}

hierarquia anterior, de tal maneira que na hierarquia k tem-se a rede ΛK−k de

(15)

Posto isso, temos que o modelo O(N) de Heisenberg hierárquico é definido pela medida de equil´ıbrio (medida de Gibbs) O(N) invariante

dν_n(N)(y) = 1

Zn(N)

exp

−1₂Un(y)

Y

i∈ΛK

dσ₀(N)(yi),

sendo que ydenota um elemento do espa¸co de conﬁgura¸c˜ao Ωn=RN×· · ·×RN =RN.n;

Un(y) =−(L−1)(y,(JH ⊗IN)y)Ωn,

com (x,y)Ωn =

X

i∈ΛK

xi_·yi= X

i∈ΛK N

X

q=1

x(_iq)y_i(q) eIN a matriz identidade de ordem N;

dσ(₀N)(y) = 1

SN βN

δ_|y_{| −}pβN dNy (1.0.3)

´e a medida “a priori” uniforme sobre a esfera N-dimensional de raio√βN eSN

βN a ´area

da superf´ıcie dessa esfera.

Transforma¸cão de Grupo de Renormaliza¸cão. Seja σ_k(N)(y) a distribui¸cão “a priori” da variável soma

X_k(N) = √ 1

m1+2/d

X

i∈Λk

yi, (1.0.4)

com m = _|Λk| = Lkd. Se M denota o espa¸co das distribui¸c˜oes “a priori” (medidas

de probabilidade) em RN _{invariantes por transforma¸c˜oes ortogonais} _O₍_N_{), o modelo}

hier´arquico permite estabelecer, em raz˜ao da estrutura auto-similar da energia _Un(y),

um mapa discreto _R:_{M → M} (vide Proposi¸c˜ao 2.2.1):

σ_k(N)(y) = 1

Cke

(L−1)|y|2_/₂

σ(_kN₋)₁ _{∗ · · · ∗}σ_k(N₋)₁

| {z }

Ld₋_termos

(L1+d/2y) (1.0.5)

(16)

ρ_∗η(y) =

Z

RN

ρ(y₋y′)dη(y′)

e Ck uma normaliza¸cão que garante que σ(_kN) é uma medida de probabilidade. A convolu¸cão de Ld _{medidas “a priori” da hierarquia anterior decorre do fato que}

X_k(N) =L−(1+d/2)(X_k(₋N₁)+. . .+X_k(N₋)₁

| {z }

Ld₋_termos

),

lembrando que σ_k(N₋)₁(y) é a distribui¸cão da variável X_k(N₋)₁; o termo e(L−1)|y|2_/₂

vem da energia (termo de intera¸cão), e portanto traz a informa¸cão de que as variáveis de spin são dependentes (vide Observa¸cão 2.2.2).

Sendo nσ_k(N)(y;β)o∞

k=0 uma fam´ılia de trajet´orias parametrizada pelo inverso da

temperatura β, e βc atemperatura inversa cr´ıtica, o propósito do projeto é investigar a convergência (y= (y(1)_{, . . . , y}(N)₎_∈_RN₎

lim

k→∞σ

(N)

k (y;βc) =σgauss(y) =

1

(2(L+ 1)π)N/2

Z y(1)

−∞ · · ·

Z y(N)

−∞

e−2(L1+1)|y′|2_dN_y′

da trajet´oria cr´ıticanσ_k(N)(y;βc)o∞

k=1 para a distribui¸c˜ao gaussiana σ

gauss₍_y_{) quando se}

parte da condi¸c˜ao inicial deﬁnida pelo modelo (integrando-se (1.0.3))

σ(₀N)(y) =

(

0 se _|y_|<√βN

1 se _|y_{| ≥}√βN

eN é muito grande; em outras palavras, estabelecer o Teorema Central do Limite para o modeloO(N) de Heisenberg hierárquico na criticalidade paraN suficientemente grande. Note que σgauss₍_y_{) é um ponto fixo do mapa (1.0.5), chamado de ponto fixo} _gaussiano

ou ponto ﬁxo trivial.

(17)

global dessa equa¸cão tem sido empregada - vide [25] e [49], e mais recentemente nossa contribui¸cão [41]. Essas referências estão alinhadas com a seguinte dire¸cão:

Dire¸cão 1.0.1 (Análise Global das Trajetórias) Estudo da trajetória do grupo de renormaliza¸cão partindo da condi¸cão inicial definida pelo modelo. Em especial, estudo da trajetória cr´ıtica (quando β = βc) - os modelos a serem tratados exibem transi¸cão de fase, existindo assim uma temperatura inversa cr´ıtica βc (que depende da dimensão

espacial em que o modelo é definido) que separa comportamentos distintos do sistema. Devemos enfatizar que a determina¸cão da superf´ıcie cr´ıtica por um único parâmetro (a temperatura) é bastante complicada, mesmo quando se investiga as trajetórias na vizinhan¸ca de um ponto fixo, vizinhan¸ca essa que, em geral, não contém a condi¸cão

inicial original do modelo. O objetivo aqui é estabelecer critérios para determinar a trajetória cr´ıtica mesmo partindo de uma condi¸cão inicial distante do ponto fixo.

Teorema de Lee-Yang. Seja dνn(y) a medida de Gibbs (medida de equil´ıbrio) de

um sistema ferromagn´etico cl´assico de _|Λ_|=n spins, comy = (y1, . . . , yn) um elemento

do espa¸co de configura¸cão Ωn =R×· · ·×R=Rn, e consideremos a fun¸cão caracter´ıstica

(transformada de Fourier) dessa medida

Φn(z;β) =

Z

Ωn

exp_{i(z,y)Ωn}dνn(y),

com z = (z1, . . . , zn) a vari´avel conjugada. Segundo Lee e Yang, as propriedades de

equil´ıbrio termodinâmico do sistema são regidas pela distribui¸cão dos zeros (zeros de Lee-Yang) de

ϕn(x;β) := Φn(z, . . . , z;β), x=−|z|2. (1.0.6)

No artigo [40] de 1952 Lee e Yang calculam, por uma analogia com a eletrost´atica, a densidade de zeros do modelo de Ising unidimensional e derivam, a partir dessa, a

(18)

equil´ıbrio do modelo s˜ao determinadas a partir da densidade (distribui¸c˜ao emp´ırica) dos zeros de (1.0.6).

Em 1974 Newman [44] formulou esse problema da determina¸c˜ao dos zeros de Lee-Yang da seguinte maneira: se ϕn(x; 0) possui zeros sobre a reta real, ent˜ao ϕn(x;β)

mant´em os zeros sobre R _para _{β >} ₀ _{e todo} _n_{, e esses zeros possivelmente se adensam}

no limite n _{→ ∞} - essa questão do adensamento somente foi levada em considera¸cão por De Coninck [11], e será explicada mais adiante (vide páginas 26 e 27).

Teorema de Lee-Yang e o Modelo O(N) de Heisenberg Hier´arquico. As

fun¸cões termodinâmicas do modelo O(N) de Heisenberg hierárquico dependem das variáveis macroscópicas X_k(N) (1.0.3). Para esse modelo temos a seguinte rela¸cão

Φ(_mN)

z

√

m1+2/d , . . . , z

√

m1+2/d

=

Z

Ωm

exp_{iz_·X_k(N)_}dν_m(N)(y) =

Z

RN

exp_{iz_·y_}dσ_k(N)(y) =φ(_kN)(z),

comdνm(N)(y) a medida de Gibbs para um bloco dem=Lkdspins eσ_k(N)(y) a distribui¸c˜ao

“a priori” da variável soma X_k(N). Para um estudo do modelo à luz do Teorema de Lee-Yang é portanto suficiente que se conhe¸ca os zeros da fun¸cão caracter´ıstica φ(_kN)(z),

k = 0,1,2, . . ., quando escrita como fun¸c˜ao de_−|z_|2_{. Deﬁne-se nesse contexto a chamada}

propriedade de Lee-Yang (vide Deﬁni¸c˜ao 2.2.8): diz-se que uma medida de probabilidade

σ em RN _{invariante por transforma¸c˜oes ortogonais} _O₍_N₎ _{possui a propriedade de}

Lee-Yang se sua fun¸c˜ao caracter´ıstica φ(z) =RRNexp{iz·y}dσ(y) = ϕ(x), com x=−|z|2,

´e tal que possui a representa¸c˜ao

ϕ(x) = exp (λx)

∞

Y

n=1

1 + x

γn

, (1.0.7)

com λ _≥0 e _{−γn, n_≥1_} n´umeros reais n˜ao-positivos tais que ₋γn+1 ≤ −γn ≤0 para

todo n = 1,2,3, . . .e

∞

X

n=1

γn−1 <∞; em outras palavras, ϕ(x) pertence `a classe

(19)

sendo _L a classe das fun¸cões inteiras de Laguerre (vide Defini¸cão 2.2.7) - tal classe é formada por polinômios que possuem somente zeros reais não-positivos, bem como os limites uniformes desses polinômios sobre subconjuntos compactos de C_.

Convergência da Seqüêncianσ_k(N)(y;βc)o∞

k=1. A abordagem apresentada neste

pro-jeto, bem como nos trabalhos de Kozitsky [32] e Watanabe [49], envolve t´ecnicas de

grupo de renormaliza¸cão, segundo as quais a convergência mencionada é investigada seguindo-se a trajetória cr´ıticanφ(_kN)(z;βc)

o∞

k=1 das fun¸c˜oes caracter´ısticas das medidas

n

σ_k(N)(y;βc)o∞

k=1, partindo-se de alguma condi¸c˜ao inicial. Em termos deφ (N)

k (z), (1.0.5)

ﬁca (vide Proposi¸c˜ao 2.2.4)

φ(_kN)(z) = 1

Nk

exp

−(L−₂ 1)∆ φ_k(N₋)₁(L−(1+d/2)z)L

d

, (1.0.8)

sendo ∆ = ∂2_/∂z2

1 +· · ·+ ∂2/∂zN2 o operador laplaceano N-dimensional e Nk uma

normaliza¸c˜ao tal que φ(_kN)(0) = 1 para todo k. Note que

φgauss(z) =

Z

RN

exp_{iz_·y_}dσgauss(y) =e−L+12 |z|2

´e o ponto ﬁxo gaussiano (ou trivial) de (1.0.8).

Um ingrediente chave no estudo da seq¨uˆencia nφ(_kN)(z;βc)o∞

k=1 gerada por (1.0.8)

decorre do seguinte resultado (vide referˆencia [29]): sejaLd _{um inteiro e} _χ _{uma medida}

de probabilidade que possui a propriedade de Lee-Yang; se χ é tomada como condi¸cão inicial para o mapa (1.0.5), então σ_k(N)(y), para todo k = 1,2,3, . . ., também possui a propriedade de Lee-Yang. Pela defini¸cão de propriedade de Lee-Yang, esse teorema nos diz que se

h(z) =

Z

RN

exp_{iz_·y_}dχ(y) =g(x),

com g(x) pertencente à classe _L(1)_{, é tomada como condi¸cão inicial para (1.0.8), então}

para todo k = 1,2,3, . . .tem-se que

φ(_kN)(z) =

Z

RN

(20)

com ϕ(_kN)(x) pertencente `a classe _L(1)_{. Agora, para essa classe de fun¸c˜oes existem}

algumas desigualdades devidas `a Newman (vide Teorema 6 de [44]): partindo da

repre-senta¸c˜ao (1.0.7) temos que

ϕ(_kN)(x) = exp

∞

X

j=1

ν_j,k(N)xj

!

com

ν₁(N_,k)=λ(_kN)+

∞

X

n=1

(γ_n,k(N))−1 e ν_j,k(N) = (−1)

j+1

j

∞

X

n=1

(γ_n,k(N))−j (j _≥2),

sendo que essa expansão é válida para todo _|x_|< γ₁(N_,k); o teorema de Newman diz que

0_≤(₋1)j+1jν_j,k(N) _≤₋2ν₂(N_,k)j/2, j _≥3. (1.0.9)

Se ao longo de uma trajet´orianϕ(_kN)(x)o∞

k=1 o coeﬁcienteν (N)

2,k convergir para zero, ent˜ao

todos coeficientes de ordem superiorν_j,k(N),j _≥3, convergem igualmente para zero. Nesse caso ter´ıamos a convergência ϕ(_kN)(x)_−→eν1(N,∞)x (isto é, φ(N)

k (z)−→e

−ν(₁N_,_∞)|z|2 ).

Apresentados esses fatos, vejamos as contribui¸c˜oes de Kozitsky e Watanabe:

Em [32], Kozitsky estabelece o Teorema Central do Limite para o modelo O(N) de Heisenberg hier´arquico na criticalidade (φ(_kN)(z;βc) _→ φgauss₍_z_{)) para todo} _N _≥ _0,

4< d <_∞, Ld _≥_{2 um inteiro, partindo de uma condi¸c˜ao inicial}_h₍_z_{) =}_g₍_x_{) com} _g₍_x₎

pertencente a uma subclasse de _L(1) _{que depende de} _d _{(vide Defini¸cão 2.2.17). Como já}

explicado, o fato de se ter Ld _{um inteiro garante que a propriedade de Lee-Yang ´e}

pre-servada e, conseqüentemente, tem-se à disposi¸cão a desigualdade (1.0.9) para o controle da convergência dos cumulantes (vide Comentário 2.2.13). Um ponto importante escla-recido nesse artigo é o seguinte: a convergência da seqüência de fun¸cões caracter´ısticas

n

φ(_kN)(z;β)o∞

k=1 para o ponto ﬁxo gaussiano ocorre somente se β = βc; se β > βc, a

seqüência diverge; se β < βc, a seqüência converge para a fun¸cão identicamente igual a 1 (note que 1 é um ponto fixo de (1.0.8)).

(21)

(note a inclus˜ao de d = 4), Ld _{= 2, partindo da fun¸c˜ao caracter´ıstica da medida “a}

priori” dσ₀(N)(y) (vide (1.0.3))

φ(₀N)(z) =

Z

RN

exp_{iz_·y_}dσ₀(N)(y)

= _√ Γ(N/2)

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_|, (1.0.10)

que éa condi¸cão inicial definida pelo próprio modelo - se_{±αn,N/2−1, n≥1}denotam os

zeros positivos e negativos deJN/2−1(ξ) (fun¸c˜ao de Bessel de ordemN/2−1), mostramos

na Proposi¸˜ao 2.2.9 que ϕ(₀N)(x) (φ₀(N)(z) escrita em termos de x = _−|z_|2_{) possui a}

representa¸c˜ao

ϕ(₀N)(x) =

∞

Y

n=1



1 + _α2 x

n,N/2−1

βN



, (1.0.11)

e portanto ϕ(₀N) _{∈ L}(1)_{. Para controlar a trajet´oria} _O₍_N_{), que parte de muito longe}

do ponto fixo gaussiano, Watanabe utiliza a trajetória exatamente solúvel O(_∞) jun-tamente com dois ingredientes válidos para Ld _{inteiro: o fato de o mapa preservar a}

propriedade de Lee-Yang (e por conseguinte podemos fazer uso da desigualdade (1.0.9)), e a propriedade de positividade por reflexão (o que permite o emprego de um resultado devido a Kupiainen [35] sobre a expansão 1/N, e que garante a convergência uniforme da trajetória O(N) para a trajetória O(_∞) - vide Comentário 2.2.20).

A Aproxima¸c˜ao de Potencial Local (L _↓ 1). Embora a transforma¸c˜ao (1.0.8)

seja discreta, em ambos os artigos ([32] e [49]) parte da dinâmica é evolu´ıda através da equa¸cão do calor. O presente trabalho diferencia-se desses dois pela utiliza¸cão da

chamada aproxima¸cão de potencial local: definindo a fun¸cão

U(t, z) =₋lnφ(_kN)(z)

(22)

t =klnL,

toma-se conjuntamente os limites k _{→ ∞} e L _↓ 1 de tal maneira que klnL per-mane¸ca fixo em um número real positivo t. Com tal procedimento, a órbita discreta

n

−lnφ(_kN)(z)o∞

k=0 torna-se cont´ınua, e a dinˆamica passa a ser gerada pela seguinte

equa¸c˜ao (vide Proposi¸c˜ao 2.3.1):

Ut =−

1

2 ∆U − |Uz|

2

− d+ 2

2 z·Uz+dU + 1

2 ∆U − |Uz|

2

z=0, (1.0.12)

t _∈R₊ _e_z _∈RN_{, com condi¸c˜ao inicial}

U(0, z) =₋ln

"

Γ(N/2) √

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_|

#

(1.0.13)

- U(0, z) =₋lnφ(₀N)(z), comφ(₀N)(z) dada por (1.0.10). O último termo no lado direito de (1.0.12) garante que U(t,0) = 0 para todo t _≥ 0 - note que essa propriedade é satisfeita pela condi¸cão inicial, já queφ(₀N)(0) = 1. Essa equa¸cão de evolu¸cão descreve a transforma¸cão de grupo de renormaliza¸cão do modelo O(N) de Heisenberg hierárquico em um espa¸co de dimensão d a uma temperatura inversa β: ela determina a fun¸cão caracter´ıstica φ(N)₍_{t, z}_{) = exp (}₋_U₍_{t, z}_{)) da distribui¸cão da variável de spin de bloco na}

escala t. Note que

Ugauss(z) = lim

L↓1{−lnφ

gauss₍_z₎

}=_|z_|2

A fun¸cão inicial (1.0.13) depende de_|z_|e a simetria esférica é preservada por (1.0.12). Logo, é conveniente e suficiente que trabalhemos com a variável radialx=_−|z_|2_{. Desse}

fato, e levando em conta que queremos tomar N para infinito, definimos a fun¸cão ade-quadamente escalada em N

u(N)(t, x) = 1

NU(t,

√

(23)

Em termos desse, (1.0.12)-(1.0.13) ﬁcam (vide Proposi¸c˜ao 2.3.3)

u(tN)=

2

Nxu

(N)

2

−(d+ 2)xu(_xN)+du(N)₋u(_xN)(t,0), (1.0.14)

aqui denominada de Eu(N)_{, com}

u(N)₍₀_{, x}_{) =}₋1

N ln

"

Γ(N/2)

i√βxN/2N/2−1JN/2−1

ipβxN

#

. (1.0.15)

O ´ultimo termo em (1.0.14) garante que u(N)₍_t,_{0) = 0 para todo}_t_≥_{0. Note que}

ugauss(x) = 1

NU

gauss₍√_{N z}_{) =}

−x

O problema de valor inicial (1.0.14)-(1.0.15) ´e o ponto de partida de nossos estudos.

Nosso objetivo pode ser enunciado da seguinte maneira: fixado β na temperatura in-versa cr´ıtica βc = βc(d, N), mostrar que a trajet´oria cr´ıtica _{u(N)₍_{t, x}₎_{, t} _≥ ₀_{, β} ₌ _βc_}

permanece sobre uma variedade est´avel e converge para o ponto fixo gaussiano ugauss₍_x₎

quando t _{→ ∞} (limite termodinâmico) se N é suficientemente grande e 4 _≤ d < _∞. Devemos enfatizar que em decorrência do fato que no limite L _↓ 1 a propriedade de Lee-Yang e a propriedade de positividade por reflexão deixam de valer, um método inteiramente novo tem sido desenvolvido em nossas análises.

O Caso N =_∞. Assim como no programa de Watanabe [49], tamb´em devemos lidar

com a trajet´oria cr´ıtica no limite N _{→ ∞}- quando N =_∞ o modelo recebe o nome de

modelo esf´erico hier´arquico (vide [8]). O estudo desse caso foi realizado entre os anos

de 2006 e 2008, e deu origem ao artigo [41] e à disserta¸cão de mestrado [7]. Embora tenhamo-nos concentrado no casod= 4, todos os resultados são válidos para 4_≤d <_∞. O principal teorema diz que a trajetória cr´ıtica (exatamente solúvel)

(24)

u(∞)(0, x) = lim

N→∞u

(N)₍₀_{, x}_{) =}

Z x

0

−β

1 +√1 + 4βx′ dx ′_,

permanece sobre uma variedade est´avel e converge para o ponto ﬁxo gaussianougauss₍_x₎

quandot_{→ ∞}. Embora tenhamos usado a expressão “exatamente solúvel”, (1.0.16) não foi estudada diretamente, mas pela trajetória cr´ıtica _{v(∞)₍_{t, p}₎_{, t} _≥₀_{, β} ₌_βc_{(4) = 4}_}_,

sendo v(∞)₍_{t, p}_{) =} _w(∞)

p (t, p) e

w(∞)(t, p) = max

x (xp−u

(∞)₍_{t, x}_{)) = ¯}_xp

−u(∞)(t,x¯)

a transformada de Legendre de u(∞)₍_{t, x}_{) com respeito `a vari´avel} _x_{. Trabalhar com}

v(∞)₍_{t, p}_{) mostrou-se bastante vantajoso. Um dos pontos que merece destaque ´e a}

de-termina¸c˜ao da temperatura inversa cr´ıtica a partir da EDP satisfeita por v(∞)₍_{t, p}₎1_:

para d >2 qualquer

βc(d) = 2d

d₋2.

Como já foi dito na Dire¸cão 1.0.1, detectar a superf´ıcie cr´ıtica em uma transforma¸cão de

grupo de renormaliza¸c˜ao ´e uma tarefa bastante dif´ıcil, mesmo na vizinhan¸ca deugauss₍_x_).

Vale lembrarmos que o método utilizado para modelos hierárquicos é devido a Bleher-Sinai. Outro ponto que merece destaque é o fato de o estudo de v(∞)₍_{t, p}_{) do ponto}

de vista da teoria geométrica de fun¸cões permitir a descri¸cão precisa da dinâmica das

singularidades de u(x∞)(t, x). Essa investiga¸cão diz respeito à seguinte dire¸cão:

Dire¸cão 1.0.2 (Solu¸cões no Plano Complexo) Extensão da solu¸cão da equa¸cão a

derivadas parciais para o plano complexo com o prop´osito de estudar a evolu¸c˜ao de suas singularidades, cortes e zeros. Nesse panorama, temos interesse em saber se a classe

P das fun¸cões de Pick é preservada - trata-se de fun¸cões f(x) anal´ıticas no semi-plano superior H _{que apresentam parte imaginária positiva se o argumento está em} H_{, isto é,}

ℑm(f) _≥0 se _ℑm(x) >0. A referida classe de fun¸c˜oes ´e suficientemente abrangente,

1_{Até ent˜}_{ao a temperatura inversa cr´ıtica tinha sido encontrada pelo método assintótico de Kac}

(25)

incluindo fun¸cões meromorfas (isto é, possuem zeros e pólos) e fun¸cões que possuem cortes sobre o eixo real.

A classe P aparece no estudo da condi¸c˜ao inicial u(xN)(0, x) =

r

β

4x

iJN/2(i√βxN)

JN/2−1(i√βxN)

:

pela deﬁni¸c˜ao de u(N)₍_{t, x}_{) e por (1.0.11) segue que}

u(_xN)(0, x) = d

dx

−_N1 lnϕ(₀N)(Nx)

= ₋ 1

N

∞

X

n=1

1

α2

n,N/2−1

βN2 +x

,

que é a representa¸cão de uma fun¸cão meromorfa com pólos de massa 1/N localizados em {−α2

n,N/2−1/(βN2), n ≥ 1} - os zeros de ϕ (N)

0 (Nx) passam a ser os p´olos de u (N)

x (0, x).

Mostramos que a seqüência de condi¸cões iniciais (u(xN)(0, x))N≥3, bem como seu limite

u(_x∞)(0, x) = lim

N→∞u

(N)

x (0, x) = − β

1 +√1 + 4βx,

pertencem à classe P - a interpreta¸cão que fizemos é que no limite N _{→ ∞} os pólos de u(xN)(0, x) se adensam, formando o corte apresentado poru(x∞)(0, x). Para essa classe

existe uma representa¸c˜ao integral canˆonica; para u(x∞)(0, x) comβ =βc(4) = 4 temos

u(_x∞)(0, x) =

Z +∞ −∞

1

λ₋xdµ

(∞)₍_λ₎_,

com

dµ(∞)(λ) = 4

π

p

16(₋λ)₋1 16(₋λ) dλ

uma medida de Borel positiva absolutamente cont´ınua com respeito `a medida de Le-besgue dλ, suportada sobre o intervalo (_−∞,₋1/16) (o corte de u(x∞)(0, x)).

Com essas constata¸cões, a pergunta seguinte foi: a classe P das fun¸cões de Pick é preservada pela dinâmica de u(x∞)(t, x)? A resposta encontra foi positiva, e demos a

(26)

u(_x∞)(t, x) =₋1 +

Z +∞ −∞

1

λ₋x −

1

λ₋1/2

dµ(∞)(t, λ), (1.0.17)

sendo que o modo de se determinar a medidadµ(∞)₍_{t, λ}_{) =}_ρ₍_{t, λ}₎_dλ_{´e o mesmo da}

repre-senta¸cão integral canônica. Essa medida é uma medida de Borel positiva absolutamente

cont´ınua com respeito `a medida de Lebesgue dλ, suportada sobre Σ(t) = (_−∞, x†₍_t_)),

o corte de u(x∞)(t, x). Mostramos que x†(t) é uma fun¸cão monótona decrescente de t,

com x†_{(0) =}₋₁_/_{16 e lim}

t→∞x†(t) =−∞; desse limite temos a informa¸c˜ao que o corte

é expelido para o infinito negativo no limite t _{→ ∞}. Assim, o suporte Σ(t) vai para o conjunto vazio quando t _{→ ∞}, de modo que a integral da representa¸cão converge para 0 uniformemente em todo compactoK _∈H_{. Em outras palavras,}_ux₍_{t, x}_{) converge para}

a fun¸c˜ao inteira ugauss

x (x)≡ −1 no limite (termodinˆamico) t → ∞.

Por ﬁm, lembrando que φ(N)₍_{t, z}_{) = exp (}₋_U₍_{t, z}_{)) e fazendo}_ϕ(N)₍_{t, x}_{) =}_φ(N)₍_{t, z}_),

deparamo-nos com a seguinte quest˜ao: a fun¸c˜ao

exp ₋u(∞)(t, x)= lim

N→∞ ϕ

(N)₍_{t, Nx}₎1/N

´e a transformada de Fourier de uma medida positiva em R_{? Nesse contexto ´e}

impor-tante o conceito de distribui¸c˜oes de probabilidade infinitamente divis´ıveis. Tal quest˜ao

contribui na seguinte dire¸c˜ao:

Dire¸c˜ao 1.0.3 (Divisibilidade Infinita) Uma distribui¸c˜ao de probabilidade sobreR₊

é dita ser infinitamente divis´ıvel se, e somente se, para todo número natural N sua transformada de Laplace (ou Fourier) elevada a 1/N é a transformada de Laplace (ou Fourier) de uma distribui¸cão de probabilidade. A fun¸cão caracter´ıstica (transformada de Fourier da medida de probabilidade) de uma distribui¸cão infinitamente divis´ıvel é

(27)

uma rela¸cão entre energia livre e o logaritmo de uma fun¸cão caracter´ıstica infinitamente divis´ıvel, válida inclusive no limite termodinâmico. Essa rela¸cão (como demonstramos para o modelo esférico hierárquico - vide [7] ou [41]) é preservada pela dinâmica de

grupo de renormaliza¸cão e pode ser expressa em termos da teoria da representa¸cão das fun¸cões de Pick.

Para respondermos a nossa questão lan¸camos mão do seguinte teorema, encontrado na Se¸cão 7 do Cap´ıtulo XIII do livro “An Introduction to Probability Theory and Its Applications”, Vol. 2, 2a

¯ edi¸c˜ao, Wiley, New York (1971), de William Feller (vide p´agina

450, Teorema 1):

Teorema 1.0.4 Uma fun¸cão f(x) é a transformada de Laplace de uma distribui¸cão de probabilidade infinitamente divis´ıvel sobre R₊ _{se, e somente se,} _f₍_x_{) =} _e−h(x) _com

h(0+_{) = 0} _e ₍₋₁₎mdmh′(x)

dxm ≥0 para x∈R+ e todo m= 0,1,2, . . ..

A nossa conclusão é que F(t, x) = exp +u(∞)₍_{t, x}₎ _{é a transformada de Laplace de}

uma distribui¸c˜ao de probabilidade inﬁnitamente divis´ıvel sobre R₊_{, haja vista que:}

(i) u(∞)₍_t,_{0) = 0 para todo}_t _≥_{0 (vide coment´ario abaixo de (1.0.14)-(1.0.15));}

(ii) ´e poss´ıvel veriﬁcar que₋u(x∞)(t, x)≥0 para todo t ≥0 ex∈R+;

(iii) pela representa¸c˜ao (1.0.17) (lembrando que a medida ´e positiva) segue que

(₋1)m∂m−u

(∞)

x (t, x) ∂xm =

Z +∞ −∞

m!

(x₋λ)m+1 dµ

(∞)₍_{t, λ}₎_≥₀

para todo t _≥ 0, x _∈ (x†₍_t₎_,_∞_{) (e em particular em} _R

+, pois x†(t) ≤ −1/16) e

m = 1,2,3, . . ..

O Caso N >> 1 Finito. Sobre (1.0.14), trata-se de uma equa¸cão não-linear que apresenta o termo 1/N na frente do termo de derivada segunda. A equa¸cão com N

(28)

[39] entre tantas outras, as quais tratam da chamada somabilidade de séries formais; em especial, a primeira citada trata do estudo da somabilidade de séries formais que satisfazem uma dada EDO, EDO essa que apresenta uma perturba¸cão singular. Tais

questões estão alinhadas com a seguinte dire¸cão:

Dire¸cão 1.0.5 (Somabilidade da Série Formal em 2/N) Através de um método de somabilidade, transformar a série formal em ε = 2/N da solu¸cão da equa¸cão de grupo de renormaliza¸cão, aqui estendida para um setor do plano complexo, na única

solu¸cão anal´ıtica. Como discutido na introdu¸cão do artigo [4], um método de somabi-lidade pode ser visto como um mapa linear _S definido sobre algum espa¸co vetorial X

de séries; tomaremos séries formais de potências na variável complexa ε. A cada série formal dessas, _S associa uma soma generalizada, que para séries de potências em ε

devem ser fun¸cões holomorfas nessa variável. Para ser útil em aplica¸cões a equa¸cões diferenciais, o operador _S deve ter algumas propriedades:

• O espa¸coX deve conter todas as séries de potências convergentes, e_S deve mapear cada série convergente em sua soma natural.

• O espa¸co linear X deve ser uma álgebra diferencial; isto é, para cada série de potências emX, sua derivada formal deve também pertencer aX, e para quaisquer duas séries de potências em X, o produto delas deve também estar em X.

• O operador _S deve ser um homomorfismo de ´algebras diferenciais; assim, deve ser n˜ao apenas linear, mas deve mapear produtos em produtos, e derivadas em derivadas.

• Para qualquer série formal de potências fˆ_∈X, a fun¸cão _Sfˆdeve ser holomorfa em algum dom´ınio setorial S, e assintótica a fˆquando ε _→0 em S.

Uma variante da chamada somabilidade de Borel preenche todos esses requisitos - vide [1] e [4].

Como foi dito acima, a fun¸cão obtida pelo método de somabilidade é holomorfa em algum dom´ınio setorial S, sendo que a unicidade dessa fun¸cão é garantida se o setor S

tiver uma abertura ampla; além disso, a fun¸cão holomorfa obtida é assintótica à série

(29)

Conte´udo desta Tese

O presente trabalho é destinado ao estudo da condi¸cão inicial u(xN)(0, x) e da fun¸cão v(N)₍_{t, p}_{) para} _{t >} _{0, sendo} _v(N)₍_{t, p}_{) a fun¸cão inversa de} _u(N)

x (t, x) com respeito `a

variável x, no que diz respeito à somabilidade de suas séries formais em potências de 2/N - a razão de estudarmos v(N)₍_{t, p}_{), e não} _u(N)

x (t, x), para t > 0 ser´a elucidada

posteriormente. Ao longo deste trabalho adotaremos a nota¸c˜ao ε = 2/N, sendo que

ε sempre pertencer´a a um setor do plano complexo. Quando utilizarmos a vari´avel ε, passaremos a escrever u(xN)(t, x) e v(N)(t, p) respectivamente comoux(ε, t, x) e v(ε, t, p).

O Cap´ıtulo 2 é formado por três se¸cões. Na Se¸cão 2.1 definimos o modelo O(N) de Heisenberg hierárquico: definimos de modo cuidadoso a intera¸cão hierárquica e a medida de Gibbs do modelo. Fazendo uso da estrutura da energia hierárquica, achamos

na Se¸cão 2.2 uma rela¸cão recursiva para a chamada medida “a priori” e, a partir dessa, uma rela¸cão recursiva para a transformada de Fourier da medida “a priori”. É pela fun¸cão caracter´ıstica da medida que se faz ponte com a teoria de Lee-Yang. Com esse próposito definimos propriedade de Lee-Yang. Para fechar essa se¸cão expomos parte de

um artigo de Kozitsky, além de fazermos um comentário sobre um trabalho de Watanabe. A Se¸cão 2.3, que encerra o primeiro cap´ıtulo, trata da chamadaaproxima¸cão de potencial local, e somos levados a uma equa¸cão a derivadas parciais para um potencial associado às fun¸cões caracter´ısticas acima mencionadas.

No Cap´ıtulo 3 apresentamos algumas defini¸cões, um teorema básico e importante,

e algumas ferramentas que serão de extrema importância neste trabalho. Basicamente, seguimos o Parágrafo 1 de [39]. Também apresentamos nosso primeiro teorema (Teorema 3.4.1): ele trata das propriedades que podem ser inferidas para uma fun¸cão g(ε, w) a partir das propriedades verificadas para sua inversa com respeito à variável w,f(ε, z) =

g−1₍_{ε, z}_{). Mais especiﬁcamente, as propriedades de ser anal´ıtica em} _S _×_D _{e Gevrey}

ordems assintoticamente expansiva emS,S um setor e Dum disco do plano complexo. De todas as referências com as quais tivemos contato, nenhuma trata dessa questão. Entretanto, em nossos estudos, esse problema de se obter informa¸cões deg(ε, w) a partir de f(ε, z) = g−1₍_{ε, z}_{) aparece naturalmente: queremos estudar a fun¸cão} _ux₍_{ε, t, x}_);

(30)

de trabalhar com v(ε, t, p), que como já foi dito no parágrafo acima, é a inversa de

ux(ε, t, x) com respeito à variávelx. Assim sendo, nossa estratégia é que, encerradas as investiga¸cões sobre a fun¸cão v(ε, t, p), evoquemos o Teorema 3.4.1 e tiremos conclusões sobre a fun¸cãoux(ε, t, x). Como julgamos que esse teorema é interessante por si, estamos organizando-o em um artigo ([9]).

O Cap´ıtulo 4 é devotado à condi¸cão inicial ux(ε,0, x), e o Cap´ıtulo 5 à v(ε, t, p), que corresponde ao caso t >0. Maiores detalhes serão dados no in´ıcio desses cap´ıtulos.

Um ponto que merece destaque, apresentado no Cap´ıtulo 5, é a questão de se en-contrar a superf´ıcie cr´ıtica fixando o parâmetro β: essa é abordada ordem a ordem em

ε. Considerando a s´erie (formal)

β(ε) =

∞

X

i=0

βiεi,

damos um crit´erio para se determinar o valor cr´ıtico βi =βc[i](d) na i-´esima ordem.

Uma contribui¸cão técnica muito importante deste trabalho diz respeito ao controle de crescimento do módulo de derivadas de ordem superior de composi¸cões utilizando indu¸cão: aqui reunimos duas ferramentas pouco conhecidas, a saber,

(a) os coeﬁcientes Cl=Al!λ_/l2_{, que satisfazem (3.3.3) e (3.3.4) (aprendemos em [50])}

(b) a f´ormula de Scott (3.3.15) para a derivada de ordem superior de composi¸c˜oes (aprendemos em [18]),

para formar uma ferramenta inteiramente nova e bastante poderosa. O item (a), por satisfazer as rela¸cões citadas, é adequado para controlarconvolu¸cões; devemos enfatizar que nessa tecnologia o fator 1/l2 _{é de fundamental importância. Com respeito ao item}

(b), esse se mostra adequado ao uso do item (a) por apresentar um termo de convolu¸cões, diferentemente de outras fórmulas para a derivada de ordem superior de composi¸cões,

como por exemplo a f´ormula de Fa`a di Bruno.

(31)

Trajet´

oria Discreta: Resumo

2.1 O Modelo

O(N

)

de Heisenberg Hier´

arquico

Por um postulado devido a Gibbs, a termodinâmica de um sistema de spins é derivada de uma distribui¸cão de probabilidade definida sobre o espa¸co de configura¸cão, denominada

medida de equil´ıbrio oumedida de Gibbs.

Para o modeloO(N) de Heisenbergferromagnético considerado sobre uma rede finita ΛK ⊂Zd de cardinalidade |ΛK|=n essa medida é dada por

dν_n(N)(y) = 1

Zn(N)

exp

−1₂(y, Ay)Ωn

Y

i∈ΛK

dσ0(N)(yi). (2.1.1)

Nesta express˜ao,

Z(N)

n =

Z

Ωn

exp

−1

2(y, Ay)Ωn

Y

i∈ΛK

dσ(₀N)(yi) (2.1.2)

é a chamada fun¸cão de parti¸cão, uma normaliza¸cão necessária para que dνn(N)(y) seja

uma medida de probabilidade; y denota um elemento do espa¸co de conﬁgura¸c˜ao Ωn =

RN _{× · · · ×}RN ₌RN.n_{; (}_x_,_y₎_Ω

n ´e o produto interno sobre Ωn

(x,y)Ωn =

X

i∈ΛK

xi_·yi= X

i∈ΛK N

X

q=1

(32)

dσ₀(N)(y) = 1

SN βN

δ_|y_{| −}pβNdNy (2.1.4)

´e a medida “a priori” uniforme sobre a esfera N-dimensional

ΣN_βN =

(

y_∈RN _:_|_y_|2 ₌

N

X

q=1

(y(q))2 =βN

)

(2.1.5)

de raio √βN, com β o inverso da temperatura e

SN βN =

Z

RN

δ_|y_{| −}pβN dN_y₌ 2π

N/2 √_βNN−1

Γ(N/2) (2.1.6)

a ´area da superf´ıcie da esfera ΣN

βN. No modelo O(N) de Heisenberg associamos a cada

vérticei_∈ΛK umavariável de spin clássicayique assume valores sobre a esfera unitária

em RN_{. Entretanto, para os prop´ositos de nosso estudo, ´e conveniente que se tenha}

yi_∈ RN_{. Assim sendo introduzimos, na medida “a priori”, o v´ınculo (2.1.5). Tamb´em}

por conveniˆencia escolhemos o raio √βN1 _{ao raio unit´ario. Quanto ao acoplamento}

entre as vari´aveis de spin yi, este ´e expresso pela matriz A= [Aij] presente na energia

Un(y) = (y, Ay)Ωn (2.1.7)

associada à configura¸cão y, sendo A=₋J _⊗IN com IN a matriz identidade de ordem

N e J = [Jij] uma matriz n_×n de intera¸c˜ao ferromagn´etica:

Jij _≥0 _∀i,j _∈ΛK. (2.1.8)

O nosso interesse está na chamada intera¸cão hierárquica, que será definida a seguir. Por uma questão de completeza, fa¸camos:

1_{Note que pela mudan¸ca de vari´}_avel_y_→√_β_y_{o parˆ}_ametro_β_{passa a ser escrito no termo exponencial}

(33)

C´alculo da ´Area da Superf´ıcie de uma Esfera N-dimensional

(a) de Raio Unitário: é conveniente que se passe para coordenadas esféricas

generali-zadas; o jacobiano ´e dado por

dNy=rN−1(sinθ1)N−2(sinθ2)N−3· · ·sinθN−2dr dθ1dθ2· · ·dθN−1, (2.1.9)

com 0_≤r =_|y_|<_∞,

0_≤θ1, θ2, . . . , θN−2 ≤π

e

0_≤θN−1 ≤2π.

Para se chegar `a igualdade

S₁N =

Z π

0

(sinθ1)N−2dθ1

Z π

0

(sinθ2)N−3dθ2· · ·

Z π

0

sinθN−2dθN−2

Z 2π

0

dθN−1

= 2π

N/2

Γ(N/2), (2.1.10)

pode-se utilizar a integral gaussiana

Z

RN

e−|y|2dNy =

Z

R

e−y2dy

N

=πN/2, (2.1.11)

pois essa tamb´em ´e igual a

Z

RN

e−|y|2dNy = S₁N

Z ∞

0

rN−1e−r2dr

= S₁N1

2

Z ∞

0

tN/2−1e−tdt

= S₁NΓ(N/2)

(34)

(b) de Raio R: de (2.1.9) temos que

S_RN2 =RN−1S₁N, (2.1.13)

de onde se conclui, juntamente com (2.1.10), a equa¸c˜ao (2.1.6).

A Matriz de Intera¸c˜ao Hier´arquica. Dados os inteirosL,K ed,L, K >1 ed_≥1, seja para cada m= 1,2, . . . , K

Λm ={0,1, . . . , Lm−1}d ⊂Zd (2.1.14)

a rede ﬁnita hiperc´ubica d-dimensional de cardinalidade _|Λm| = Lmd. Seja u ∈ R|Λm|

um vetor que associa a cada vértice i = (i1, . . . , id) de Λm uma variável real ui, e v _∈R|Λm−1| _{um vetor que associa a cada vértice} _r _{= (}_r

1, . . . , rd) de Λm−1 uma vari´avel

real vr. Deﬁnimos o operador de bloco B :R|Λm|_→_R|Λm−1| _por

Bu =v (2.1.15)

tal que a componente r desse vetor ´e dada por

vr = (Bu)r=

1

Ld/2

X

j∈Λ1

uLr+j. (2.1.16)

Seu adjunto B∗ _:_R|Λm−1|_→R|Λm|

(w, Bu)R|Λm−1| = (B

∗_{w, u}₎

R|Λm| (2.1.17)

com respeito ao produto interno (w, u)R|Λm| =

X

i∈Λm

wiui´e

B∗v =u (2.1.18)

(35)

uLr+j = (B∗v)Lr+j =

1

Ld/2vr ∀j ∈Λ1. (2.1.19)

Introduzimos assim as no¸cões de bloco e hierarquia à rede ΛK: a cada vértice r de

ΛK−k−1 associamos um bloco de Ld v´ertices de ΛK−k, a saber, todos os elementos de

{Lr1, . . . , Lr1+L−1} × · · · × {Lrd, . . . , Lrd+L−1}; (2.1.20)

os vértices i _∈ΛK−k são denominadosvértices da hierarquia k e os r ∈ΛK−k−1 vértices

da k+ 1-ésima hierarquia; i_∈ΛK são vértices da hierarquia zero, e na K-ésima

hierar-quia há somente um único vértice Λ0 ={0}. Se u e v denotam configura¸cões de spins,

dado um vértice r dak+ 1-ésima hierarquia, a opera¸cão realizada pelo operador B é a de somar todas as variáveis de spin uida hierarquia k associadas ar, e normalizar pela raiz quadrada do tamanho do bloco (Ld_{). Quanto a}_B∗_{, transforma a variável de spin de}

bloco vr da k+ 1-´esima hierarquia em Ld _{vari´aveis de spin da hierarquia} _k_{, atribuindo}

a cada uma delas o mesmo valor.

Utilizando os operadores B e B∗ _{deﬁnimos, sobre} _R|ΛK|_{, a} _{matriz de intera¸c˜ao}

hier´arquica JH:

JH =

K

X

k=1

L−2k(B∗)kBk. (2.1.21)

Bk ₌_BB_{· · ·}_B

| {z }

k−vezes

é a aplica¸cão sucessiva de B, e portanto Bk _:_R|ΛK|_→_R|ΛK−k|_{; o ´ındice} k indica a hierarquia. Assim, o número máximo de hierarquias que se tem em ΛK éK.

Defini¸c˜ao 2.1.1 (Matriz Positiva e Positiva Definida) Uma matriz M = [Mij]

n_×n real ´e dita ser positiva se

Mij >0 _∀i, j, (2.1.22)

(36)

(u, Mu)Rn >0 (2.1.23)

para todo vetor n˜ao nulo u_∈Rn_.

Proposi¸cão 2.1.2 JH é uma matriz LKd_×_LKd _{real simétrica positiva e positiva}

defi-nida.

Para demonstrarmos esta proposi¸cão é necessária a defini¸cão de distância hierárquica: consideremos uma seqüência (θ1, . . . ,θK) de vetoresθk ∈ {0,1, . . . , L−1}dtal que, para

cada vértice i = (i1, . . . , id)∈ΛK, temos uma única expansão na baseLd-nária

i=

K

X

k=1

θkLk−1. (2.1.24)

O vetor θk indica a posi¸cão do vértice i dentro do bloco, ao qual pertence, da k-ésima

hierarquia. A t´ıtulo de esclarecimento, consideremos o exemplo mostrado pela Figura 2.1, em que L= 2 e d= 1.

(37)

O vértice i= 3 possui a expansão binária (1,1,0,0, . . . ,0): dentro do bloco da primeira hierarquia ele ocupa a posi¸cão θ1 = 1; dentro do bloco da segunda hierarquia, a posi¸cão

θ2 = 1; dentro do bloco da terceira hierarquia, a posi¸c˜aoθ3 = 0; e assim sucessivamente.

Ao vértice i= 4 está associada a expansão (0,0,1,0,0, . . . ,0).

Defini¸cão 2.1.3 (Distância Hierárquica) Seja(θ1, . . . ,θK)a expansão Ld-nária do

vértice i_∈ΛK, e (θ′1, . . . ,θ′K) a do vértice j ∈ΛK. A distância hierárquica entre i e j

´e definida por

distL(i,j) =

(

Lk(i,j) _se _i₆₌_j

0 se i=j , (2.1.25)

sendo k(i,j) = max_{l _{∈ {}0,1, . . . , K_}:θl 6=θ′l} a menor hierarquia k que faz com que

i e j sejam cobertos por um mesmo bloco de tamanho Lkd.

Peguemos como exemplo os s´ıtios 3 e 4 da Figura 2.1, cujas expansões binárias já conhe-cemos: k(3,4) = 3; logo dist2(3,4) = 23 = 8, apesar de serem vizinhos próximos.

Observa¸cão 2.1.4 Note que a distância hierárquica não é estacionária com respeito a qualquer transla¸cão a _∈ Zd_{, isto é, em geral} _distL₍_i₊_a_,_j ₊_a₎ ₆₌ _distL₍_i_,_j₎_{. Além}

disso, a desigualdade distL(i,j) > _|i₋j_| ´e sempre satisfeita, com _|i₋j_| a distˆancia euclidiana entre os s´ıtios.

Estamos agora em posi¸c˜ao de demonstrar a Proposi¸c˜ao 2.1.2:

Demonstra¸c˜ao. Seja δi_∈R|ΛK| um vetor cujas componentes ul s˜ao nulas exceto para

l =i, com l,i_∈ΛK:

(δi)l=

(

0 se l₆=i

1 se l=i . (2.1.26)

(38)

(JH)ij = (δi, JHδj)R|ΛK|

=

K

X

k=1

L−2k(δi,(B∗)kBkδj)R|ΛK|

=

K

X

k=1

L−2k(Bkδi, Bkδj)R|ΛK−k|. (2.1.27)

Para i₆=j

(Bkδi, Bkδj)R|ΛK−k| =

(

0 se k < k(i,j)

L−dk _se _k_≥_k₍_i_,_j₎ , (2.1.28)

e para i=j temos que (Bk_{δi, B}k_δj₎

R|ΛK−k| =L−dk para todo k. Desta maneira

(JH)ij =

(

L−(d+2)k(i,j)₋_L−(d+2)(K+1) ₁₋_L−(d+2)−1 _se _i₆₌_j

L−(d+2)₋_L−(d+2)(K+1) ₁₋_L−(d+2)−1 _se _i₌_j . (2.1.29)

Uma vez que k(i,j) = k(j,i), e (JH)ij > 0 e real para quaisquer i e j da rede ΛK,

temos que JH ´e uma matriz real sim´etrica positiva.

Seja agora s _∈ R|ΛK| um vetor qualquer n˜ao nulo e que associa a cada v´ertice _i de

ΛK uma variável real si, er = (r1, . . . , rd). Então a forma quadrática associada aJH é

(s, JHs)R|ΛK| = K

X

k=1

L−2k(s,(B∗)kBks)R|ΛK|

=

K

X

k=1

L−2k(Bks, Bks)R|ΛK−k|

=

K

X

k=1

L−2k X r∈ΛK−k

(Bks)2_r >0, (2.1.30)

(39)

(Bks)r =

1

Ldk/2

X

j∈Λk

sLk_r₊_j. (2.1.31)

Assim, JH ´e uma matriz positiva deﬁnida.

Pela Proposi¸cão 2.1.2 a matriz de intera¸cão hierárquica JH, definida por (2.1.21), é uma matriz de intera¸cão ferromagnética (vide (2.1.8)). Em vista desse fato, temos:

Defini¸cão 2.1.5 O modelo O(N) de Heisenberg hierárquico é definido pela medida de Gibbs (2.1.1) com energia de intera¸cão ferromagnética

Un(y) = (y, Ay)Ωn =−(L−1)(y,(JH ⊗IN)y)Ωn, (2.1.32)

sendo n=_|ΛK|=LKd. O fator (L−1)é acrescentado para garantir, no limite em que L_↓1, a convergência do laplaceano hierárquico para o laplaceano hierárquico cont´ınuo, como pode ser visto em [8].

2.2 Transforma¸c˜

ao de Grupo de Renormaliza¸c˜

ao

Comecemos esta se¸c˜ao por notar a estrutura da energia hier´arquica _ULKd(y):

ULKd(y) = −(L−1) K

X

m=1

L−2m((Bm_⊗IN)y,(Bm⊗IN)y)Ω_L(K−m)d

= L−2_UL(K−1)d(y[1])−(L−1)L−2

X

r∈ΛK−1

yr[1]

2, (2.2.1)

que é a energia hierárquica normalizada porL−2 _{de uma configura¸cão de spins de bloco} y[1] _{= (}_B_⊗_IN₎_y_{da primeira hierarquia sobre a rede Λ}

K−1, somada `a energia de intera¸c˜ao

das L(K−1)d _{vari´aveis de spin de bloco} _y[1]

r = ((B ⊗IN)y)r da primeira hierarquia. De

(40)

ULKd(y) =L−2kU_L(K−k)d(y[k])−(L−1)L−2k

X

r∈ΛK−k

y[_rk]2, (2.2.2)

com y[k] = (Bk _⊗_IN₎_y _{a configura¸cão de spins de bloco da} _k_{-ésima hierarquia. ´}_E

justamente esta caracter´ıstica da energia hier´arquica que permite a implementa¸c˜ao do

grupo de renormaliza¸c˜ao mais facilmente.

Rela¸cão de Recorrência. O nosso interesse está na evolu¸cão, com o aumento da hierarquia k, da distribui¸cão da variável soma

X_k,Nγ = _√ 1

mγ/d

X

i∈Λk

yi, (2.2.3)

com m=_|Λk|=Lkd. Deﬁnimos com essa ﬁnalidade a medida “a priori” σ(kN) associada

`a escala k pela seguinte equa¸c˜ao:

Z

Ω_LKd

δL−(γ−2d)k(Bk⊗IN)_y′−_y

dν_L(NKd)(y′) =

= 1

Z_L(N(K)−k)d

expn₋cγ,k

2 UL(K−k)d(y)

o Y

i∈ΛK−k

dσ_k(N)(yi); (2.2.4)

integramos a medida (2.1.1) sobre o espa¸co de configura¸cão mantendo a configura¸cão de spins de bloco da k-ésima hierarquia fixa - (2.2.4) é uma medida marginal sobre Ω_L(K−k)d. O fator γ pode assumir o valor d+ 2 ou d, introduzido a fim de se incluir ou

não a normaliza¸cão L−k_{, presente em (2.2.2), à variável de bloco; assim,}

cγ,k =

(

1 se γ =d+ 2

L−2k se γ =d . (2.2.5)

(41)

Estabeleceremos agora uma rela¸c˜ao recursiva para as medidas “a priori”:

Proposi¸c˜ao 2.2.1 As medidas “a priori” associadas a escalas consecutivas relacionam-se por

σ_k(N)(y) = 1

Cke

cγ,k(L−1)|y|2_/₂

σ_k(N₋)₁_{∗ · · · ∗}σ_k(N₋)₁

| {z }

Ld₋_termos

(Lγ/2y) (2.2.6)

com condi¸c˜ao inicial

σ0(N)(y) =

(

0 se _|y_|<√βN

1 se _|y_{| ≥}√βN , (2.2.7)

sendo que _∗ denota o produto de convolu¸c˜ao

ρ_∗η(y) =

Z

RN

ρ(y₋y′)dη(y′), (2.2.8)

e Ck uma normaliza¸c˜ao que garante que σ_k(N) ´e uma medida de probabilidade.

Demonstra¸cão. Sendo (2.2.4) uma medida marginal, podemos obtê-la pela integra¸cão da medida de Gibbs

1

Z_L(N(K)−(k−1))d

expn₋cγ,k−1

2 UL(K−(k−1))d(y

′₎o Y

i∈ΛK−(k−1)

dσ_k(N₋)₁(y_i′) (2.2.9)

sobre o espa¸co de configura¸cão Ω_L(K−(k−1))d mantendo-se fixa a configura¸cão de spins de

bloco normalizada L−(γ−2d)(B⊗IN)y′∈Ω

L(K−k)d. Para isso precisamos de uma rela¸c˜ao

entre as energias _UL(K−(k−1))d(y′) e U_L(K−k)d((B ⊗IN)y′) an´aloga `a (2.2.1); trocando K

por K₋(k₋1) em (2.2.1):

UL(K−(k−1))d(y′) = L−2U_L(K−k)d((B ⊗IN)y′)

−(L₋1)L−2 X r∈ΛK−k

((B_⊗IN)y′₎

r

2

(42)

Note que

L−(γ−2d)((B⊗IN)_y′)

r =

1

L(γ−2d) 1

Ld/2

X

j∈Λ1

y′_Lr₊j

= 1

Lγ/2

X

j∈Λ1

y_Lr′ ₊_j. (2.2.11)

Utilizando a seguinte decomposi¸c˜ao e nota¸c˜ao

δL−(γ−2d)(B ⊗IN)_y′−_y

= Y

r∈ΛK−k

δL−(γ−2d)((B⊗IN)_y′)

r−yr

= Y

r∈ΛK−k

δ(.r), (2.2.12)

temos ent˜ao

Z

Ω_L(K−(k−1))d

δL−(γ−2d)(B⊗IN)y′−y

×(2.2.9) =

=

Z

Ω_L(K−k)d

Z

Ω_Ld

Y

r∈ΛK−k

(

ecγ,k−1(L−1)L−2|((B⊗IN)y′)r|2/2_δ₍_.r₎ Y

j∈Λ1

dσ_k(N₋)₁(y′

Lr+j)

)

×

× 1

Z_L(N(K)−(k−1))d

exp

−cγ,k−1L

−2

2 UL(K−k)d((B⊗IN)y ′₎

= 1

Z_L(N(K)−k)d

expn₋cγ,k

2 UL(K−k)d(y)

o Y

r∈ΛK−k

1

Cke

cγ,k(L−1)|yr|2/2_d₍_σ(N)

k−1 ∗ · · · ∗σ (N)

k−1

| {z }

Ld₋_termos

)(Lγ/2_yr_);

(2.2.13)

Ld _{termos porque a cardinalidade de Λ}

1 ´e Ld. Para concluirmos (2.2.6) devemos

(43)

Quanto à condi¸cão inicial (2.2.7), essa é a fun¸cão distribui¸cão

Z y(1)

−∞ · · ·

Z y(N)

−∞

dσ₀(N)(y′) y′ _∈RN _(2.2.14)

associada `a medida “a priori” inicial (2.1.4).

Observa¸cão 2.2.2 Pela mudan¸ca de variável y _→ √βy em (2.1.1) (lembrar da nota de rodapé 1, página 32), (2.2.6) passa a ser escrita

σ_k(N)(y) = 1

Ck

eβcγ,k(L−1)|y|2/2_σ(N)

k−1∗ · · · ∗σ (N)

k−1

| {z }

Ld₋_termos

(Lγ/2y)

com condi¸c˜ao inicial

σ₀(N)(y) =

(

0 se _|y_|<√N

1 se _|y_{| ≥}√N .

No limite de altas temperaturas (β _→ 0+_{) temos apenas a convolu¸c˜ao de} _Ld _medidas

“a priori”. Isto está em pleno acordo com o fato que nesse limite as variáveis de spin comportam-se como variáveis aleatórias independentes (não há acoplamento).

Observa¸c˜ao 2.2.3 Se _M denota o espa¸co das medidas “a priori” em RN _invariantes

por transforma¸c˜oes ortogonais O(N), (2.2.6) define um mapa _R:_{M → M}

σ_k(N) =_Rσ_k(N₋)₁,

e a cole¸c˜ao nσ_k(N)(y)oK

(44)

Rela¸cão de Recorrência Dual. Consideremos agora a fun¸cão caracter´ıstica da me-dida “a priori” associada à escala k

φ(_kN)(z) =

Z

RN

exp_{iz_·y_}dσ(_kN)(y). (2.2.15)

Proposi¸cão 2.2.4 A medida “a priori” φ(_kN)(z) obedece a rela¸cão de recorrência

φ(_kN)(z) = 1

Nk exp

−cγ,k(L₂−1)∆ φ_k(N₋)₁(L−γ/2z)L

d

(2.2.16)

com

φ(₀N)(z) = _√ Γ(N/2)

βN_|z_|/2N/2−1JN/2−1

p

βN_|z_|, (2.2.17)

sendo ∆ =∂2_/∂z2

1+· · ·+∂2/∂zN2 o operador laplaceanoN-dimensional, Jν(ξ)a fun¸c˜ao

de Bessel de ordem ν, Γ(n) a fun¸c˜ao gama de Euler, e Nk uma normaliza¸c˜ao tal que

φ(_kN)(0) = 1.

Demonstra¸c˜ao. Por (2.2.6), ignorando o fator Ck, temos que

φ(_kN)(z) =

Z

RN

exp_{iz_·y_}ecγ,k(L−1)|y|2/2_d₍_σ(N)

k−1∗ · · · ∗σ (N)

k−1

| {z }

Ld₋_termos

)(Lγ/2y). (2.2.18)

Uma vez que o laplaceano atua somente na vari´avel z

eiz·yecγ,k(L−1)|y|2/2 =

∞

X

n=0

1

n!

cγ,k(L₋1) 2

n

(_|y_|)2neiz·y

=

∞

X

n=0

1

n!

cγ,k(L₋1) 2

n

(∆)n (i2₎n e

iz·y

= exp

−cγ,k(L₂−1)∆