Teoria de correção de erros quânticos durante operações lógicas e medidas de diagnóstico...

(1)

UNIVERSIDADE DE SÃO PAULO

INSTITUTO DE FÍSICA DE SÃO CARLOS

Leonardo Andreta de Castro

Teoria de correção de erros quânticos durante operações lógicas e medidas

de diagnóstico de duração finita

(2)

(3)

Leonardo Andreta de Castro

Teoria de correção de erros quânticos durante operações lógicas

e medidas de diagnóstico de duração finita

Dissertação apresentada ao Programa de Pós-Graduação em Física do Instituto de Física de São Carlos da Universidade de São Paulo, para obtenção do título de Mestre em Ciências. Área de concentração: Física Básica

Orientador: Prof. Dr. Reginaldo de Jesus Napolitano

Versão corrigida

(original se encontra disponível na Unidade que aloja o Programa)

(4)

AUTORIZO A REPRODUÇÃO E DIVULGAÇÃO TOTAL OU PARCIAL DESTE TRABALHO, POR QUALQUER MEIO CONVENCIONAL OU ELETRÔNICO, PARA FINS DE ESTUDO E PESQUISA, DESDE QUE CITADA A FONTE.

Ficha catalográfica elaborada pelo Serviço de Biblioteca e Informação do IFSC com os dados fornecidos pelo autor

de Castro, Leonardo Andreta

Teoria de correção de erros quânticos durante operações lógicas e medidas de diagnóstico de duração finita/ Leonardo Andreta de Castro; orientador Reginaldo de Jesus Napolitano - versão corrigida – São Carlos, 2012.

143 p.

Dissertação (Mestrado – Programa de Pós-graduação em Física Básica) - Instituto de Física de São Carlos, Universidade de São Paulo, 2012.

(5)

(6)

(7)

AGRADECIMENTOS

Ao Prof. Dr. Reginaldo de Jesus Napolitano, por haver me acolhido, muitos anos atrás, nessa empreitada da computação quântica; pelo apoio prestado na solução das mais difíceis equações; e pelas discussões sobre os mais bizarros aspectos do mundo microscópico.

A Carlos Alexandre Brasil, por ser pioneiro, desenvolvendo as teorias nas quais me refugiaria depois; por sua ajuda na interminável batalha contra o LATEX; e por sua insistência em levar-me às distantes paragens do meridião.

A Paulo Eduardo Marques Furtado de Mendonça, pelas sugestões e histórias durante os quase periódicos encontros de quinta-feira.

Aos companheiros de sala, Diego Paiva Pires, Guilherme Nery Prata e Guilherme da Costa Pereira Innocentini, ao nosso lado durante as horas mais escuras.

(8)

(9)

“I love deadlines.

(10)

(11)

RESUMO

DE CASTRO, L. A.Teoria de correção de erros quânticos durante operações lógicas e medidas de diagnóstico de duração finita. 2012. 143p. Dissertação (Mestrado em Ciências) - Instituto de Física de São Carlos, Universidade de São Paulo, 2012.

Neste trabalho, estudamos a teoria quântica de correção de erros, um dos principais métodos de prevenção de perda de informação num computador quântico. Este método, porém, normalmente é estudado considerando-se condições ideais em que a atuação das portas lógicas que constituem o algoritmo quântico não interfere com o tipo de erro que o sistema sofre. Além disso, as medidas de síndrome empregadas no método tradicional são consideradas instantâneas. Nossos objetivos neste trabalho serão avaliar como a alteração dessas duas suposições modificaria o processo de correção de erros. Com relação ao primeiro objetivo, verificamos que, para erros causados por ambientes externos, a atuação de uma porta lógica simultânea ao ruído pode gerar erros que, a princípio, podem não ser corrigíveis pelo código empregado. Propomos em seguida um método de correção a pequenos passos que pode ser usado para tornar desprezíveis os erros incorrigíveis, além de poder ser usado para reduzir a probabilidade de erros corrigíveis. Para o segundo objetivo, estudamos primeiro como medidas de tempo finito afetam a descoerência de apenas um qubit, concluindo que esse tipo de medida pode na verdade proteger o estado que está sendo medido. Motivados por isso, mostramos que, em certos casos, medidas de síndrome finitas realizadas conjuntamente ao ruído são capazes de proteger o estado dos qubits contra os erros mais eficientemente do que se as medidas fossem realizadas instantaneamente ao fim do processo.

(12)

(13)

ABSTRACT

DE CASTRO, L. A. Quantum error-correction theory during logical gates and finite-time syndrome measurements. 2012. 143p. Dissertação (Mestrado em Ciências) - Instituto de Física de São Carlos, Universidade de São Paulo, 2012.

In this work, we study the theory of quantum error correction, one of the main methods of preventing loss of information in a quantum computer. This method, however, is normally studied under ideal conditions in which the operation of the quantum gates that constitute the quantum algorithm do not interefere with the kind of error the system undergoes. Moreover, the syndrome measurements employed in the traditional method are considered instantaneous. Our aims with this work are to evaluate how altering these two suppositions would modify the quantum error correction process. In respect with the first objective, we verify that, for errors caused by external environments, the action of a logical gate simultaneously to the noise can provoke errors that, in principle, may not be correctable by the code employed. We subsequently propose a short-step correction method that can be used to render negligible the uncorrectable errors, besides being capable of reducing the probability of occurrence of correctable errors. For the second objective, we first study how finite-time measurements affect the decoherence of a single qubit, concluding that this kind of measurement can actually protect the state under scrutiny. Motivated by that, we demonstrate, that, in certain cases, finite syndrome measurements performed concurrently with the noise are capable of protecting more efficiently the state of the qubits against errors than if the measurements had been performed instantaneously at the the end of the process.

(14)

(15)

LISTA DE FIGURAS

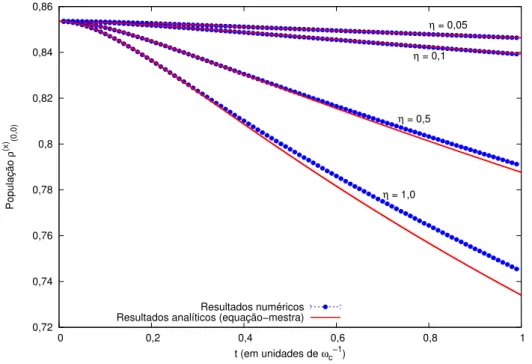
Figura 5.1 – Comparação da evolução temporal da população para diferentes valores do acoplamento com o ambiente, η. Conforme η aumenta, vemos um crescimento também na taxa da variação da população. Todas as curvas calculadas comλ= 2ωc1/2. . . 94

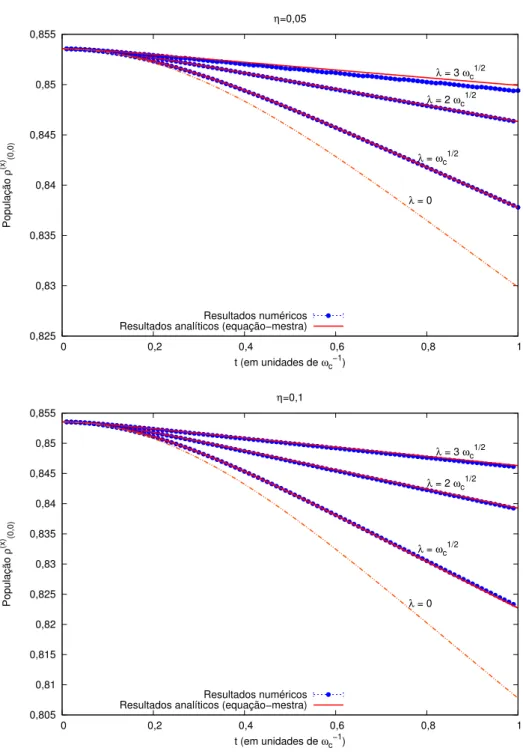
Figura 5.2 – Comparação da evolução temporal das populações, na base em que a medida anticomutante é realizada, para diversas intensidades de medida e dois valores fracos para a interação com o ambiente. . . 97 Figura 5.3 – Comparação da evolução temporal das populações, na base em que a

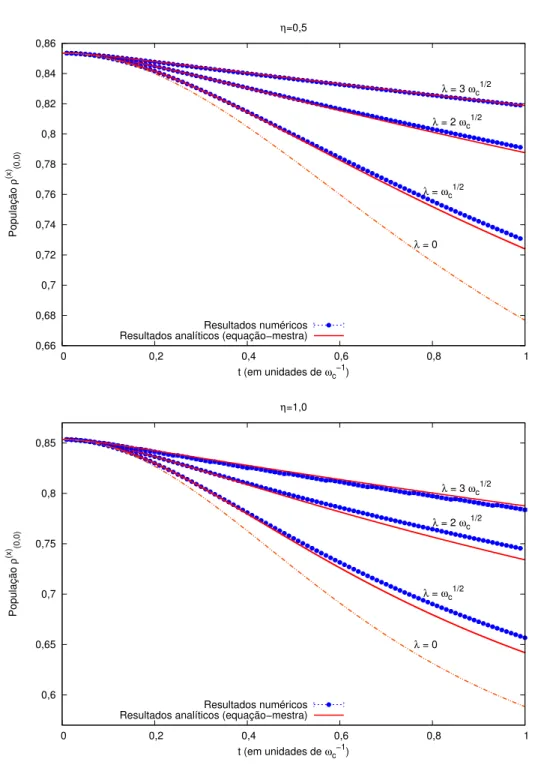
medida anticomutante é realizada, para diversas intensidades de medida e dois valores fortes para a interação com o ambiente. . . 98 Figura 5.4 – Comparação da evolução temporal da parte imaginária da coerência, na

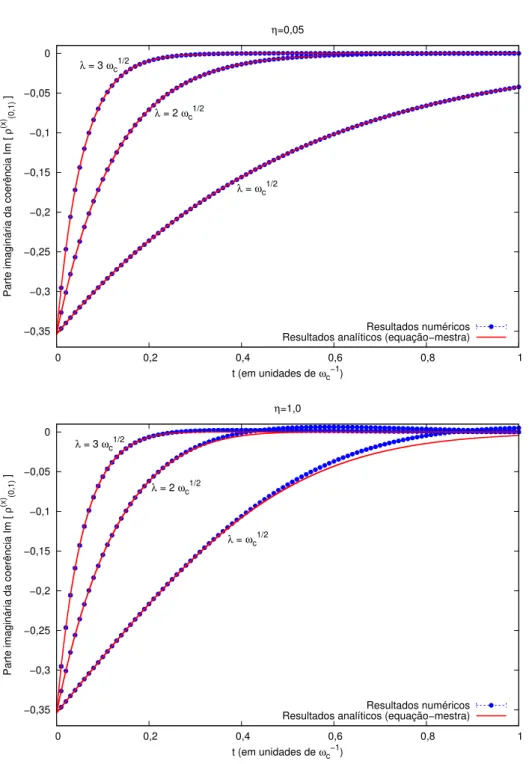
base em que a medida anticomutante é realizada, para diversas intensidades de medida e dois valores, um forte e outro fraco, para a interação com o ambiente. . . 99

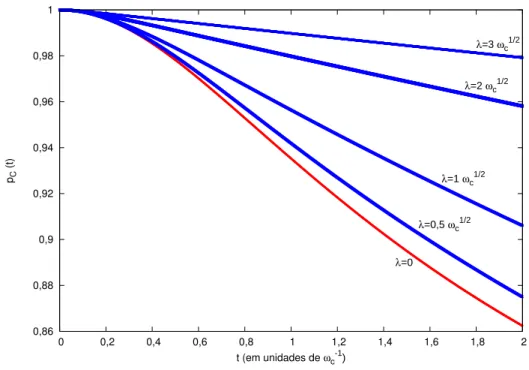
Figura 6.1 – Evolução temporal da probabilidade de encontrar-se o sistema dentro do subespaço do código, pC(t), em função do tempo, medido em unidades do inverso da frequência de corte, ωc. Em todas as curvas, escolhemos o

(16)

(17)

LISTA DE TABELAS

Tabela 3.1 – Resultados da medida de síndrome para cada tipo de erro. Repare que apenas quaisquer duas colunas são necessárias para determinar-se o erro ocorrido. . . 54

Tabela 6.1 – Resultado da expressão fi,r,j(1−fi,r,k), presente na exponencial, em

(18)

(19)

SUMÁRIO

Introdução 19

1 Introdução à computação quântica 21

1.1 Informação quântica . . . 21

1.2 Portas lógicas quânticas . . . 24

1.3 Emaranhamento . . . 27

1.4 Ambientes bosônicos . . . 28

1.5 Estados coerentes e operadores de deslocamento . . . 30

2 Sistemas quânticos abertos 35 2.1 Equação de von Neumann . . . 35

2.2 Operadores de Kraus . . . 37

2.3 Equação de Lindblad . . . 39

2.4 Perturbações . . . 42

2.5 Equação-mestra híbrida . . . 46

3 Teoria de correção de erros quânticos 51 3.1 Código de correção de um erro de fase . . . 52

3.2 Dinâmica de um canal com ruído de fase . . . 55

3.3 Densidade espectral ôhmica . . . 58

4 Correção a passos curtos 59 4.1 Fundamentos matemáticos . . . 60

4.2 O método . . . 62

4.3 Construção das portas lógicas . . . 64

4.4 Aplicação ao código de três qubits . . . 66

5 Efeitos protetivos de medidas de tempo finito 71 5.1 Soluções exatas . . . 71

5.2 Soluções da equação-mestra . . . 75

5.2.1 Caso comutativo . . . 78

5.2.2 Caso anticomutativo . . . 81

5.3 Método numérico: operador partido ao meio . . . 86

5.3.1 Densidade espectral ôhmica . . . 91

(20)

6 Correção contínua de erros 101

6.1 Aplicação a códigos estabilizados . . . 101

6.2 Aplicação a erros de fase . . . 107

6.3 Caso do código de dois qubits . . . 110

6.4 Simulações numéricas . . . 114

Conclusões e perspectivas 116 REFERÊNCIAS 119 Apêndice A Cálculo dos traços do ambiente 123 A.1 Valor esperado do número de bósons . . . 123

A.2 Traço do ruído de fase . . . 124

A.3 Traço para o algoritmo . . . 126

Apêndice B Lema de Hadamard 131 Apêndice C Identidade de Snider 133 C.1 Fórmula para operadores . . . 133

C.2 Fórmula para superoperadores . . . 134

Apêndice D Listagem de programa 137

(21)

19

Introdução

A teoria quântica, desenvolvida nos início do século XX, representou uma revolução para a ciência, revelando aspectos inusitados do comportamento do universo. Apesar de já estabelecida nos anos 1920, foi só no final do século passado que a mecânica quântica passou a despertar interesse para a construção de computadores (1). Percebeu-se, pela primeira vez, que poderia haver tarefas que a matéria quântica seria capaz de executar com mais eficiência que os bits clássicos, levando à emergência do estudo da computação quântica.

A principal razão para a maior eficiência da computação quântica encontra-se no fato de que um sistema quântico de dois níveis é capaz de estar em qualquer de uma infinidade de superposições de estados, enquanto que os sistemas clássicos equivalentes só podem se encontrar num ou noutro. Isso permite a realização de cômputos de forma distinta dos computadores clássicos, já que a superposição de estados permite o chamado paralelismo quântico: operações em estados clássicos distintos podem ser feitas simultaneamente no mesmo sistema quântico, que pode estar em vários estados ao mesmo.

O paralelismo, porém, não se trata de uma panaceia. A natureza do fenômeno da medida na teoria quântica significa que os resultados dessas diferentes operações não estarão todos disponíveis para leitura ao final do algoritmo. Assim, é necessária certa criatividade para que a informação requerida possa ser extraída com grande probabilidade ao final da computação.

As primeiras indicações de que isso seria possível ocorreram na década de 1980 e início da década de 1990, quando Deutsch e Josza mostraram (2), com seu algoritmo das caixas pretas, uma situação simples em que um computador quântico daria uma resposta mais rapidamente que qualquer computador clássico. Essa demonstração, porém, apenas ilustrava essa possibilidade, mas não apresentava nenhuma aplicação prática. Alguns anos depois, com o algoritmo de Shor (3), concluiu-se que computadores quânticos poderiam ter uma utilidade muito real na solução de problemas insolúveis eficientemente em seus equivalentes clássicos.

(22)

20

que poderia destruir os preciosos estados quânticos que carregam os resultados dos algoritmos (4). Diversos esquemas foram propostos para a superação deste obstáculo, entre eles aquele que nos irá interessar neste trabalho: a teoria da correção de erros (5, 6). Este esquema consiste em se codificar os estados lógicos em um conjunto maior de estados físicos, de forma que haja uma redundância de informação que possa ser usada, após os erros ocorrerem, para recuperar o estado original.

Este método, porém, é normalmente empregado com algumas simplificações. Primeiro, não se considera que a atuação simultânea das portas lógicas ao ruído é capaz de alterar o tipo de erro que ocorre (7–9). Segundo, considera-se que as medidas ocorrem instantaneamente, o que, apesar de constituir a hipótese padrão da mecânica quântica (10), pode ser substituído pela mais interessante formulação da medida como um processo dinâmico que dura um tempo finito. Nosso objetivo neste trabalho é, portanto, substituir essas suposições pelas ideias de que os pares erro e porta lógica ou erro e medida são processos dinâmicos que podem interferir entre si, observando quais serão as consequências de sua ação simultânea.

(23)

21

Capítulo 1 Introdução à computação

quântica

Neste capítulo, veremos os conceitos fundamentais de computação quântica necessários para a compreensão deste trabalho. Escrito com o intuito de permitir o entendimento do neófito, este capítulo pressupõe do leitor apenas um conhecimento de cálculo e álgebra linear. Aqueles que já estiverem familiarizados com computação quântica poderão facilmente compreender o restante da dissertação sem o auxílio deste capítulo, desde que conheçam também a segunda quantização e os estados coerentes, apresentados nas duas últimas seções.

1.1 Informação quântica

Qualquer sistema isolado, na mecânica quântica, pode ser descrito por um vetor de estado (10), também conhecido como função de onda quando projetado numa base de uma variável contínua, como posição ou momento. O vetor de estado encapsula toda a informação que temos sobre o sistema, e o ato de obter-se tais informações de um sistema quântico, transportando-as para o ambiente clássico onde podemos analisá-ltransportando-as, é chamado de medida. Dessa forma, transportando-as funções de onda são dadas em termos dos resultados de possíveis medidas sobre o sistema que elas representam.

Suponhamos que uma certa medida possa ter uma série de resultados distintos: r0, r1, r2, . . ..

Por uma questão de simplicidade que se encaixa no espírito dos problemas que trataremos nesta dissertação, vamos supor que esses resultados são discretos, mas podem ser infinitos. Para representar o estado de um sistema quântico logo após uma medida que determine-o como sendo

(24)

22 Capítulo 1. Introdução à computação quântica

de estado correspondendo a todos os possíveis resultados de uma certa medida é uma base do chamado espaço de Hilbert, que representaremos pelo símbolo _H.

Um espaço vetorial não contém apenas os vetores que pertencem à base, mas também combinações lineares deles. Assim, anteriormente à medida, quando o seu estado ainda não está bem determinado, o sistema pode estar numa combinação de diversos estados clássicos diferentes, o que chamamos de superposição. Tal fenômeno é popularmente ilustrado no exemplo do gato de Schrödinger (11), no qual o felino epônimo está num estado que mistura a vida e a morte. No exemplo que usamos acima, um estado geral do sistema que pode ser medido com os valoresr0, r1, r2, . . . será:

|ψ_i=

∞

X

n=0

cn|rni, (1.1)

onde os cn são coeficientes complexos. O valor destes não é aleatório: a probabilidade de

encontrar o sistema no estado |rni é proporcional ao valor do módulo quadrado do coeficiente

que multiplica tal vetor de estado.

A medida desta variável é representada pelo operador cujos autovetores são aqueles da base, e os autovalores correspondentes são os resultados possíveis da medida, que neste caso representaremos porR:

R_|rni=rn|rni. (1.2)

Desde que a base{|rni}seja ortonormal (o que se representa em notação de Dirac porhrn|rmi=

δn,m), o elemento de matrizhψ|R|ψirepresenta o valor esperado de uma medidaRde um sistema

inicialmente no estado|ψ_i:

hψ_|R_|ψ_i=X

n

rn|cn|2 =hRi, (1.3)

desde que o vetor de estado |ψ_i seja também normalizado, ou seja,hψ_|ψ_i= 1, o que equivale a:

X

n

|cn|2 = 1. (1.4)

Como afirmamos acima, ao término de uma medida que resulte em rn, o estado do sistema

torna-se _|rni. Vemos, portanto, que a medida na mecânica quântica é um processo que envolve

(25)

1.1. Informação quântica 23

uma superposição a um estado bem definido classicamente. A compreensão da medida como um processo em que, devido à interação com um ambiente externo, o sistema perde seu estado de superposição, será a que usaremos para modelá-la como um processo contínuo.

A evolução temporal de processos que não envolvem medidas não requer uma interpretação probabilística. Pelo contrário, ela pode ser representada por um operador de evolução temporal

U(t) que atua sobre os vetores de estado, levando-os a um resultado final específico:

|ψ(t)_i=U(t)_|ψ(0)_i. (1.5)

Os vetores de estado têm sua evolução regida pela equação de Schrödinger, que é apresentada como um postulado desprovido de necessidade de demonstração, e que aqui escreveremos em termos do operador evolução temporalU(t):

d

dtU(t) =− i

~H(t)U(t), (1.6)

ondeH(t)é o hamiltoniano, a observável das energias. Em alguns trabalhos da área, escolhe-se

as unidades de forma que~_{= 1}(12), com o propósito de eliminar esta constante das expressões.

Aqui, sempre escreveremos~explicitamente.

A partir da equação de Schrödinger, é simples provar que a evolução é unitária, isto é, que ela é reversível pela aplicação do conjugado U†(t). Para comprovarmos isso, primeiro confirmemos

que a unitariedade é verdadeira para o instantet= 0. De fato, nesse instante a evolução temporal

é igual à identidade e, portanto,

U(0)U†(0) =U†(0)U(0) = 1. (1.7)

Agora, multipliquemos a equação de Schrödinger (1.6) pela esquerda porU†(t) e somemos com o conjugado da mesma equação multiplicado à direita porU(t). Da soma resulta que:

d dt

h

U†(t)U(t)i=₋i ~U

†₍_t₎_H₍_t₎_U₍_t_{) +} i

~U

†₍_t₎_H₍_t₎_U₍_t_{) = 0}_. _(1.8)

Assim, como o valor deU†₍_t₎_U₍_t₎_{não varia com o tempo, a evolução temporal deve permanecer} unitária para todos os instantes, conforme queríamos demonstrar.

(26)

informação não se perca durante o processamento, isto é, eles devem ser reversíveis. Excetuam-se, é claro, as situações em que medidas são realizadas.

1.2 Portas lógicas quânticas

A computação quântica, assim como as formas mais difundidas de computação clássica, trabalha com o armazenamento de informações em objetos que podem assumir estados discretos. Assim como classicamente existe o bit como unidade mínima de informação, em computação quântica define-se o qubit como qualquer sistema que pode ser medido em apenas dois estados distintos (13). Representaremos tais estados por |0_i e |1_i, cada um com uma representação matricial correspondente:

|0_i=˙

  

1

0

 

, |1i=˙   

0

1

 

. (1.9)

Assim como na computação clássica as operações são realizadas sobre os bits através de sua passagem por portas lógicas como NOT, AND ou XOR, num esquema usual de computação quântica chamamos de porta lógica o processo durante o qual permite-se que o sistema evolua sob a atuação de um certo hamiltoniano durante um período adequado de tempo. Para apenas um qubit, as opções de portas lógicas retringem-se àquelas que podem ser representadas como matrizes2_×2. É, portanto, útil decompô-la numa base do espaço dessas matrizes, que consistirá de quatro elementos. Para formar essa base, empregaremos as três matrizes de Pauli:

σx≡

  

0 1

1 0

 

, σy ≡   

0 ₋i

i 0

 

, σz ≡   

1 0

0 ₋1

 

, (1.10)

que, combinadas com a identidade, podem formar qualquer matriz 2_×2. De fato, todas as

matrizes de Pauli apresentam traço (soma dos elementos da diagonal principal) nulo. Por isso, se definirmos o produto interno entre duas matrizesAeBcomo a operaçãoTr_{A†B_}, concluiremos

que elas são ortogonais:

(27)

1.2. Portas lógicas quânticas 25

onde substituímos cada um dos índicesx, y, zpelos número1,2,3, como faremos recorrentemente

neste trabalho.

As matrizes de Pauli são utilizadas extensivamente neste trabalho, de forma que é necessário reconhecer algumas de suas propriedades importantes. Primeiro, elas, em conjunto com a identidade, são fechadas ao produto matricial, formando um grupo (convenientemente referido como grupo de Pauli):

σrσs=δr,s+iεr,s,tσt. (1.12)

Dessa propriedade do produto, segue-se que a seguinte relação de comutação:

[σr, σs] = 2iεr,s,tσt. (1.13)

Finalmente, muitas vezes nos referiremos a tais matrizes por um vetor tridimensional que as inclua,σ:

σ≡σ_xˆx+σ_yˆy+σ_zˆz. (1.14)

Com esse vetor, podemos obter a seguinte identidade:

(mˆ _·σ) (nˆ·σ) = (mˆ ·nˆ) +i(mˆ ×nˆ)·σ, (1.15)

que pode ser usada duas vezes para escrever:

(mˆ _·σ) (nˆ·σ) (mˆ ·σ) = (mˆ ·nˆ) (mˆ ·σ) +i[(mˆ ×ˆn)·σ] (mˆ ·σ)

= (mˆ _·nˆ) (mˆ _·σ) +i(mˆ ×nˆ)·mˆ −[(mˆ ×nˆ)×mˆ]·σ. (1.16)

Comomˆ _×nˆ é perpendicular amˆ, a expressão (1.16) perde o segundo termo do lado direito. Além disso, comomˆ _·mˆ = 1, teremos:

(mˆ _·σ) (ˆn·σ) (mˆ ·σ) = 2 (mˆ ·nˆ) (mˆ ·σ)−(nˆ·σ). (1.17)

É claro que não é necessário expressar os estados do sistema apenas em termos da base_|0_i e

(28)

base de autovetores deσx:

|0_i_x _≡ _√1

2(|0i+|1i), (1.18)

|1_i_x _≡ _√1

2(|0i − |1i). (1.19)

Pode-se obter a nova base a partir da original com a aplicação da chamada porta de Hadamard. Esta é definida conforme:

H= _√1

2(σz+σx), (1.20)

de forma que:

H_|0_i = _|0_i_x, (1.21)

H_|1_i = _|1_i_x, (1.22)

H_|0_i_x = _|0_i, (1.23)

H_|1_i_x = _|1_i. (1.24)

Em (1.20), vemos que a porta de Hadamard pode ser expressa como combinação linear de identidades e matrizes de Pauli, assim como, aliás, qualquer operador que atue somente sobre um qubit. Além dessas combinações, que chamamos de rotações, para a criação de um circuito quântico qualquer é necessário o emprego de mais uma porta lógica quântica que permita atuar sobre dois qubits. Para esses casos, ordinariamente escolhe-se a porta lógica CNOT, que, conforme o nome, atua como uma porta lógica NOT (σx, em nossa notação) sobre um dos qubits

(chamado qubit alvo) apenas quando o valor do qubit de controle for_|1_i. Escolhendo o primeiro

(29)

1.3. Emaranhamento 27

UCNOT|0i ⊗ |0i = |0i ⊗ |0i, (1.25)

UCNOT|0i ⊗ |1i = |0i ⊗ |1i, (1.26)

UCNOT|1i ⊗ |0i = |1i ⊗ |1i, (1.27)

UCNOT|1i ⊗ |1i = |1i ⊗ |0i, (1.28)

onde o significado preciso do símbolo_⊗, que separa os estados dos dois qubits, será explicado na próxima seção.

1.3 Emaranhamento

Na nossa descrição de computadores quânticos, não bastará descrever qubits isolados. Precisaremos tratá-los como partes de sistemas maiores, que podem tanto envolver outros qubits quanto objetos de natureza diferente. Para descrevê-los, emprega-se o produto tensorial, que transforma dois espaços de Hilbert que contêm bases que podem ser medidas independentemente por um espaço total que combina todos os possíveis resultados das duas medidas. Assim, se _HA e HB são dois espaços de Hilbert cujas bases são {|φii_A} e |φji_B ,

respectivamente, então o espaço de Hilbert que resulta do produto tensorial _HA⊗ HB conterá

todas as combinações lineares da base composta de todos os possíveis|ϕi,ji:

|ϕi,ji ≡ |φiiA⊗ |φji_B. (1.29)

Um estado qualquer no espaço de Hilbert HA⊗ HB pode ser expresso como:

|ψ_i=X

i,j

ci,j|ϕi,ji=

X

i,j

ci,j |φiiA⊗ |φji_B. (1.30)

(30)

|ψ_i= X

i

ci|ψiiA

!

⊗

 X

j

dj|ψji_B



. (1.31)

O emaranhamento ocorre justamente quando tal separação não é possível, de forma que medidas realizadas em HA afetam aquelas que serão realizadas em HB. Essa é uma propriedade da

matéria quântica sem análogo na clássica, notada na década de 1930 por Erwin Schrödinger (14), inspirado pelo paradoxo de Einstein-Podolsky-Rosen (15), que alertava justamente para o fato de que, na mecânica quântica, uma medida em uma partícula pode afetar imediatamente uma partícula distante.

Pela definição da porta CNOT dada nas equações de (1.25), (1.26), (1.27) e (1.28), essa porta não parece satisfazer a condição necessária de emaranhamento de (1.30). Isso é apenas uma questão de aplicá-la ao estado inicial apropriado. Por exemplo:

UCNOT

1

√

2(|0i+|1i)⊗ |0i= 1

√

2(|0i ⊗ |0i+|1i ⊗ |1i), (1.32)

certamente é um estado emaranhado.

O emaranhamento é um recurso importante para a informação quântica, já que permite estabelecer relações entre os estados de qubits mais fortes do que aquelas que podem ser obtidas com bits clássicos. Porém, neste trabalho nos concentraremos principalmente nos efeitos detrimentais que podem haver quando o qubit se emaranha com um ambiente externo. Isto altera o estado do qubit, que já não poderá ser descrito independentemente, acarretando em falhas na computação. O objetivo deste trabalho é estudar métodos que permitam-nos contornar tais falhas, de forma a corrigir tais erros. Na próxima seção, veremos como modelam-se os ambientes que poremos em contato com os qubits.

1.4 Ambientes bosônicos

(31)

1.4. Ambientes bosônicos 29

Primeiramente, o espaço de Hilbert do ambiente (que simbolizaremos por _HA, de forma a

distingui-lo do espaço do sistema sob estudo,_HS) é, na verdade, composto pelo produto tensorial

de infinitos espaços, cada um caracterizado por uma frequênciaωk. Cada um desses espaços de

Hilbert tem uma base de estados infinita, mas discreta. Os autoestados do hamiltoniano, que formam a chamada base de Fock, serão identificados pelo índicen, de forma que on-ésimo estado,

|n_i_k, terá energia correspondente ~_ω_k_n. Ou seja, se _H_A é o hamiltoniano do ambiente,

HA|ni_k=~ωkn|nik. (1.33)

Para manipular esses estados, empregaremos os operadores de criação a†_k e aniquilação ak.

Estes são definidos para levar de um estado da base de Fock aos seus vizinhos de índices, somando ou subtraindo 1:

a†_k_|n_i_k = √n+ 1_|n_i_k, (1.34)

ak|nik =

√

n_|n₋1_i_k. (1.35)

Vê-se que, se atua sobre o chamado estado de vácuo,_|0_i_k, o operador aniquilação não produz

um estado_|−1_i_k, mas apenas o vetor nulo, devido à presença do fator√0. Nota-se ainda que os

estados da base de Fock são autovetores das combinaçõesa†_kak e aka†k, como se pode deduzir de

suas combinações:

aka†_k|ni_k = (n+ 1)|ni_k, (1.36)

a†_kak|nik = n|nik. (1.37)

Finalmente, da subtração dessas duas definições operacionais, obtém-se a relação de comutação:

h

ak, a†_ℓ

i

=δk,ℓ, (1.38)

de onde o delta de Kronecker justifica-se pelo fato de que operadores que atuam sobre diferentes espaços de Hilbert sempre comutam entre si.

(32)

conseguimos construir um hamiltoniano para o ambiente:

HA=

X

k

~_ω_k_a†

kak. (1.39)

Trabalhamos até aqui com a base de Fock, mas é claro que não precisamos lidar exclusivamente com a base de autovetores do hamiltoniano. Na verdade, muitas vezes é útil trabalhar com uma base alternativa, como veremos na próxima seção.

1.5 Estados coerentes e operadores de deslocamento

Chamamos de estados coerentes os autovetores do operador destruição. Não é difícil expressar um estado coerente |α_i_k em termos da base de Fock, basta resolver a equação de autovalores:

a_|α_i_k=α_|α_i_k, _|α_i_k =

∞

X

n=0

cn|ni_k. (1.40)

Substituindo a expressão para _|α_i_k em termos da base de Fock e igualando os coeficientes que

multiplicam os mesmos vetores dos dois lados, obtemos a fórmula de recorrência:

√

n+ 1cn+1=αcn, (1.41)

que, iterativamente, permite expressar qualquer dos coeficientes em termos de c0:

cn= α n

√

n!c0. (1.42)

Empregando-se a expansão da exponencial em série de potências, pode-se escrever o estado coerente também da forma:

|α_i_k=e−|α|2/2

∞

X

n=0

αn

√

n!|nik, (1.43)

onde a constantec0 foi escolhida de forma a normalizar o vetor de estado.

(33)

1.5. Estados coerentes e operadores de deslocamento 31

hβ_|α_i_k=e−(|α|2+|β|2)/2+αβ∗. (1.44)

É interessante notar que a passagem para a representação de interação só adiciona uma fase ao estado coerente:

e−iHAt_|_α_i

k=e−iωka

†

kakt_|_α_i

k =

e−iωkt_α

k. (1.45)

Sendo essa uma base de autoestados contínua, qualquer vetor de estados expresso nela deve ser escrito com o auxílio de uma integral:

|ψ_i=

Z

C

d2α f(α)_|α_i_k. (1.46) Além disso, a relação de completeza não é escrita tão trivialmente quanto numa base em que os vetores sejam ortonormais. De fato, se escrevermos simplesmente:

Z

C

d2α _|α_i_k_hα_|_k=

∞

X

m,n=0 Z

C

d2α e−|α|2(α∗)mαn |m√ikhn|

m!n! , (1.47)

vemos que a relação de completeza na base de Fock ainda não está evidente. Para encontrá-la, devemos fazer a integração em α, para a qual é necessário primeiro dividir a variável complexa

em seu módulor e o argumento θ, de forma que:

α=reiθ. (1.48)

Com as novas variáveis a integral dupla torna-se:

Z

C

d2α e−|α|2(α∗)mαn=

Z ∞

0

dr re−r2rm+n

Z 2π

0

dθ eiθ(m−n). (1.49)

A integral emθequivale à delta de Dirac 2πδm,n, de forma que na verdade temos

Z

C

d2α e−|α|2(α∗)mαn= 2πδm,n

Z ∞

0

dr e−r2r2m+1. (1.50) Mudando a variável da integral restante paraw=r2, encontramos uma função gama, que pode

(34)

Z

C

d2α e−|α|2(α∗)mαn=πδm,n

Z ∞

0

dw e−wwm=πδm,n(m+ 1)!. (1.51)

Portanto, obtém-se:

Z

C

d2α _|α_i_k_hα_|_k =π

∞

X

m=0

|m_i_k_hm_|_k, (1.52)

o que signica que a relação de completeza escreve-se com o acréscimo de um π−1 multiplicando

a integral:

1

π

Z

C

d2α _|α_i_k_hα_|_k = 1. (1.53) A mais importante consequência deste resultado é que o traço tomado na base de estados coerentes terá que ser normalizado por π. Provamos isso adicionando a relação de completeza (1.53) a um traço tomado na base de Fock:

Trk{X}=

∞

X

n=0

hn_|_kX_|n_i_k= 1

π

∞

X

n=0

hn_|_kX

Z

C

d2α _|α_i_k_hα_|n_i_k, (1.54) e invertendo a ordem dos elementos de matriz, de forma que a relação de completeza na base de Fock fique explícita:

Trk{X}=

1

π

Z

C

d2α

∞

X

n=0

hα_|n_i_k_hn_|_kX_|α_i_k = 1

π

Z

C

d2α _hα_|_kX_|α_i_k. (1.55)

Tendo definido os estados coerentes, passemos à definição dos operadores deslocamento, que levam um estado coerente a outro, através da adição de um deslocamentoα. Assim, um operador de deslocamentoD(α) age no estado de vácuo conforme:

D(α)_|0_i_k=_|α_i_k. (1.56) Um operador que atua dessa forma é facilmente construído a partir da definição de um estado coerente e dos operadores de criação:

|α_i_k=

"

e−|α|2/2

∞ X n=0 αn n!

a†n

#

|0_i_k=e−|α|2/2eαa†_|0_i_k. (1.57)

(35)

1.5. Estados coerentes e operadores de deslocamento 33

só o primeiro termo da expansão em série de potências do operador exponencial, proporcional à identidade, produz efeito não-nulo sobre o estado _|0_i_k. Usando-se adicionalmente a relação

de comutação entre os operadores criação e aniquilação (1.38), pode-se usar a expansão de Zassenhaus (18) para escrever o operador deslocamento como:

D(α) =e(αa†−α∗a)=eαa†e−α∗ae[a†,a]|α|2/2. (1.58)

A adição do termo de aniquilação, que poderia parecer arbitrária, na verdade permite que o deslocamento satisfaça:

D(₋α) =D†(α). (1.59)

Usando a mesma expansão de Zassenhaus, podemos expandir uma combinação de dois deslocamentos:

D(α+α0) =e(αa

†₋_α∗_a₎₊₍_α

0a†−α∗₀a) ₌_D₍_α₎_D₍_α

0)e−(αα

∗

0−α∗α0)/2. (1.60)

Daí, fica claro que tais operadores produzem não apenas um deslocamento num estado coerente qualquer_|α0ik, mas também adicionam uma certa fase:

D(α)_|α0ik=D(α)D(α0)|0ik=e(αα

∗

0−α∗α0)/2_|_α

0+αik. (1.61)

Finalmente, podemos empregar esse operador para criar um operador aniquilação cujos autovalores estejam deslocados de um valorα. Para isso aplicamos:

D†(α)aD(α)_|α0ik= (α0+α)|α0ik, (1.62)

o que pode ser empregado inclusive em exponenciais, como a expansão em série revela:

ea+α =D†(α)eaD(α). (1.63)

O último resultado (1.63) será necessário no Apêndice A para o cálculo de traços com a utilização de estados coerentes.

(36)

(37)

35

Capítulo 2 Sistemas quânticos abertos

Desde o princípio da computação quântica, sabe-se que uma descrição realista de um computador quântico deve levar em conta não apenas os qubits, mas também as interações acidentais que estes têm com um ambiente externo gerando resultados inesperados com os quais precisamos lidar (4).

A descrição dos sistemas abertos é obtida adicionando-se um espaço de Hilbert para o ambiente bosônico,HA, ao espaço já reservado ao sistema de qubits, HS. O espaço de Hilbert

total, obtido com o produto tensorial dos dois estados originais, deverá ser empregado nas equações que utilizaremos para descrever a dinâmica do sistema, já que o sistema total é isolado, e, portanto, evolui unitariamente e deterministicamente de acordo com a equação de Schrödinger. A diferença é que o ambiente será descartado ao final, de forma que a evolução de apenas o sistema que nos interessa,_HS, não será mais unitária, mas probabilística.

2.1 Equação de von Neumann

Em situações como essa, o sistema S emaranha-se com o ambiente A. A evolução unitária dos dois permite que o estado total de ambos possa ser descrito em termos de um vetor de estado bem determinado. Porém, o fato de os dois estarem emaranhados impede que o estado do sistema isoladamente seja passível de ser descrito da mesma forma. Pelo contrário, haverá mais de uma função de onda capaz de ser associada com o sistema de interesse, como pode ser visto se tentarmos separar um estado emaranhado como (1.30).

Por isso, descreveremos o estado do sistema através do operador densidade, que permite a descrição tanto de estados puros (representáveis por vetores estado) ou misturas, que representam

(38)

36 Capítulo 2. Sistemas quânticos abertos

um associado com uma probabilidade pi:

ρ=X

i

pi|ψii hψi|,

X

i

pi = 1. (2.1)

O valor esperado da medida de um sistema descrito por um operador densidade, portanto, será dado pela operação de traço:

X

i

pihRii =

X

i

hψi|piR|ψii= Tr

( X

i

pi|ψii hψi|R

)

= Tr_{ρR_}. (2.2)

Pela definição, a soma dos elementos da diagonal da representação matricial de um operador densidade é sempre igual a 1, o que equivale a dizer que o traço é unitário:

Tr_{ρ_}=X

i

pihψi|ψii= 1. (2.3)

Os elementos da diagonal principal, numa certa base, são as chamadas populações, enquanto que os elementos fora dela são as coerências. Como estados do tipo |ψii hψi|, escolhida a base

apropriada, só contêm termos na diagonal, vemos que a superposição está relacionada com as coerências. Por isso, o processo de medida estará relacionado com a perda do valor dessas coerências.

A evolução de um sistema isolado deste tipo é dada pela equação de von Neumann, derivada diretamente da equação de Schrödinger (1.6), sujeitando os vetores de estado da definição (2.1) à sua equação de evolução apropriada:

d

dtρ(t) =− i

~[H(t), ρ(t)]. (2.4)

A solução de tal equação é bastante simples. Dado que o operador evolução temporal do sistema é U(t), a evolução é certamente escrita como:

ρ(t) =U(t)ρ(0)U†(t). (2.5)

(39)

2.2. Operadores de Kraus 37

quânticos quanto pelas medidas.

A obtenção de tal informação é feita pelo procedimento de traço parcial, no qual os graus de liberdade que não pertencem ao sistema de interesse são descartados. Ao final dela, obtemos um operador que descreve apenas o sistema em consideração, como se tivéssemos considerado apenas a evolução dele desde o princípio. Sendo _|φji_A uma base do espaço de Hilbert do ambiente

HA, o traço parcial é obtido através de:

ρS = TrA{ρSA}=

X

j

hφj|_AρSA|φji_A. (2.6)

O operador resultante,ρS, chamado de operador densidade reduzido, representa apenas o estado

da parte do sistema que é relevante para este estudo.

2.2 Operadores de Kraus

Enquanto que a evolução de um sistema isolado sempre pode ser descrita através da aplicação de um operador unitário (1.5), a evolução de um sistema aberto pode ser descrita pela generalização direta desses operadores, chamados de operadores de Kraus. A demonstração de sua origem é deveras simples. Primeiro, consideramos o sistema completo, formado pelo espaço de Hilbert total _HS ⊗ HA, que evolui unitariamente segundo o operador

de evolução temporalU(t):

ρSA(t) =U(t)ρSA(0)U†(t). (2.7)

Tomando o traço parcial (2.6), encontramos a evolução apenas do sistema, que não pode mais ser descrita em termos tão simples:

ρS(t) = TrA

n

U(t)ρSA(0)U†(t)

o

. (2.8)

Desde que o sistema seja inicialmente separável do ambiente, como nos casos que trataremos neste trabalho (já que, por hipótese, o sistema só começa a emaranhar-se com o ambiente em

(40)

ρSA(0) =ρS(0)⊗

X

i

pi|ψiiAhψi|A. (2.9)

Dessa forma, escolhendo uma base completa {|φji_A}, o traço parcial pode ser expresso

conforme:

ρS(t) =

X

i,j

pihφj|_AU(t)|ψii_AρS(0)hψi|_AU†(t)|φji_A. (2.10)

Definindo os operadores de Kraus como:

Ei,j(t)≡√pihφj|_AU(t)|ψii_A, (2.11)

a evolução completa do sistema pode ser expressa em termos deles:

ρS(t) =

X

i,j

Ei,j(t)ρS(0)Ei,j† (t). (2.12)

É importante notar que os operadores de Kraus satisfazem a seguinte propriedade, obtida a partir de sua definição (2.11) e equivalente à unitariedade dos operadores de evolução temporal:

X

i,j

E_i,j† (t)Ei,j(t) =

X

i

pihψi|AU†(t)

 X

j

|φji_Ahφj|_A



U(t)|ψ_ii_A

= X

i

pihψi|AU†(t)U(t)|ψiiA

= X

i

pihψi|ψii_A

= X

i

pi

= 1. (2.13)

(41)

2.3. Equação de Lindblad 39

2.3 Equação de Lindblad

A equação de Lindblad é uma equação diferencial para o operador densidade reduzidoρS(t),

equivalente à função que a equação de von Neumann desempenha para o operador densidade totalρSA(t), mas que emprega a aproximação markoviana para simplificar a evolução do sistema.

Sabendo que a evolução de tais sistemas é dada pelos operadores de Kraus acima, podemos obter a equação diferencial a partir deles. A demonstração abaixo é semelhante à encontrada em (17).

Os operadores que atuam no sistema certamente podem ser expressos como elementos de um espaço vetorial, assim como os vetores de estado pertencem ao espaço de Hilbert. Nesse espaço, denominado espaço de Liouville, definimos o produto interno como sendo o traço tomado sobre o operador e seu hermitiano conjugado, de forma que uma base ortonormal{Fi}de operadores

satisfaz:

TrS

n

FiF_j†

o

=δi,j. (2.14)

Em termos dessa base independente do tempo, expressam-se os operadores de Kraus conforme:

Ei(t) =

X

j

ci,j(t)Fj, (2.15)

de forma que, o que era uma dependência temporal sobre operadores agora torna-se de escalares:

ρS(t) =

X

k

X

r,s

ck,r(t)c∗k,s(t)

FrρS(0)Fs†. (2.16)

Suponhamos que um dos elementos do conjunto ortonormal é proporcional à identidade. Vamos representá-lo pelo índice0, e dá-lo uma constante de normalização α, tal que:

α−1 = TrS{1}, (2.17)

(42)

ρS(t) = |α|2

X

k

ck,0(t)c∗k,0(t)

ρS(0) +α

X

s6=0 X

k

ck,0(t)c∗k,s(t)

ρS(0)Fs†

+α∗X

r6=0 X

k

ck,r(t)c∗k,0(t)

FrρS(0) +

X

r,s6=0 X

k

ck,r(t)c∗k,s(t)

FrρS(0)Fs†. (2.18)

O diferencial da equação de Lindblad é que ela usa a aproximação markoviana: a evolução da matriz densidade reduzida só depende de seu estado presente, ignorando a sua evolução em momentos anteriores. Isso quer dizer que podemos tratar a evolução do sistema como se a variação do instante t ao instante t+ ∆t fosse a mesma que regesse a evolução inicial até ∆t.

Nesse caso,

ρS(t+ ∆t) =

X

k

Ek(∆t)ρS(t)E_k†(∆t). (2.19)

A derivada temporal da matriz densidade reduzida é dada por:

d

dtρS(t) = lim∆t→0

ρS(t+ ∆t)−ρS(t)

∆t , (2.20)

o que, usando tanto a aproximação markoviana quanto a expressão em termos da base _{Fi},

torna-se:

d

dtρS(t) = ∆limt→0

|α_|2_d

0,0(∆t)−1

∆t ρS(t) + lim∆t→0α X

s6=0

d0,s(∆t)

∆t ρS(t)F

†

s

+ lim

∆t→0α

∗X

r6=0

dr,0(∆t)

∆t FrρS(t) + lim∆t→0 X

r,s6=0

dr,s(∆t)

∆t FrρS(t)F

†

s, (2.21)

onde substituímos os escalaresck,r(∆t) por:

dr,s(t)≡

X

k

ck,r(t)c∗k,s(t). (2.22)

Se expandirmos essa nova função em termos de uma série de potências no tempo, encontraremos, se impusermos o respeito das condições iniciais:

(43)

2.3. Equação de Lindblad 41

o que leva ao seguinte valor da derivada:

d

dtρS(t) =|α|

2_d(1)

0,0ρS(t) +α

X

s6=0

d(1)₀_,sρS(t)Fs†+α∗

X

r6=0

d(1)_r,₀FrρS(t) +

X

r,s6=0

d(1)_r,sFrρS(t)Fs†. (2.24)

Se definirmos os operadores:

G _≡ |α|

2

2 ∗d

(1) 0,0+

 α∗X

r6=0

d(1)_r,₀Fr+α

X

s6=0

d(1)₀_,sF_s†

 ,

H _≡ i~

 α∗X

r6=0

d(1)_r,₀Fr−α

X

s6=0

d(1)₀_,sF_s†

 ,

(2.25)

podemos representar a evolução temporal por meio de um comutador e um anticomutador:

d

dtρS(t) =− i

~[H, ρS(t)] +{G, ρS(t)}+

X

r,s6=0

d(1)_r,sFrρS(t)Fs†. (2.26)

Como o traço do operador densidade deve permanecer constante e igual a um, encontramos a condição: TrS    

2G+ X

r,s6=0

d(1)_r,sF_s†Fr

 ρS(t)

  

= 0, (2.27)

que é válida para qualquerρS(t) apenas se tivermos:

G=₋1 2

X

r,s6=0

d(1)_r,sF_s†Fr, (2.28)

de forma que a equação diferencial torna-se:

d

dtρS(t) =− i

~[H, ρS(t)] +

X

r,s6=0

d(1)_r,s

F_s†ρS(t)Fr−

1 2

n

F_s†Fr, ρS(t)

o

. (2.29)

Como só fixamos um elemento da base_{Fi}, ao qual impusemos uma proporcionalidade com

a identidade, temos bastante liberdade para a escolha dos demais operadoresFr. Escolhendo-os

(44)

d

dtρS(t) =− i

~[H, ρS(t)] +

X

r

F_r†ρS(t)Fr−

1 2

n

F_r†Fr, ρS(t)

o

. (2.30)

É importante lembrar que a equação de Lindblad é uma generalização para sistemas abertos da evolução markoviana típica de operadores densidade de sistemas fechados. Portanto, ela deve ser capaz de recuperar a equação de von Neumann para uma escolha adequada dos operadores de Lindblad {Fr}. Dessa forma, é natural identificar o operador H com o hamiltoniano do

sistema isolado, conforme a própria notação escolhida sugere. Por essa razão, o primeiro termo do lado direito da equação (2.30) é denotado de liouvilliano, enquanto o segundo representa o lindbladiano. Nos cálculos subsequentes, representaremos o primeiro por Le o segundo por M:

d

dtρS(t) =LρS(t) +MρS(t). (2.31)

É importante lembrar que, devido à forma da equação de Lindblad (2.30), o lindbladiano e o liouvilliano não são meros operadores, mas sim superoperadores, já que eles incluem comutadores ou anticomutadores, ou seja, são operadores que atuam sobre operadores.

Neste trabalho, a equação de Lindblad será empregada para representar a evolução de medidas finitas ruidosas. O termo lindbladiano _M, markoviano, será usado para representar a medida, atuando somente no sistema, enquanto o termo não-markoviano_Lé empregado para representar o ruído, incluindo, portanto, termos que atuam também no ambiente.

A modelagem da medida é simples: substituímos um único operador de Lindblad Fr pela

observável que queremos medir multiplicada por uma constante real λ, que encapsula a

intensidade da medida. Como veremos nos capítulos 5 e 6, isso fará com que as coerências na base dessa medida vão a zero, como é esperado da medida de uma observável. Para mais de uma medida simultânea, como necessitaremos no capítulo 6, vamos simplesmente adicionar quantos lindbladianos necessitarmos.

2.4 Perturbações

Nestes problemas, estamos sempre considerando que o sistema S modifica-se principalmente

(45)

2.4. Perturbações 43

sua interação com o ambiente A. Assim, se dividirmos o hamiltoniano em termos que atuam

individualmente em cada um dos espaços de Hilbert, que chamaremos deHS eHA, e um termo

de interação que atua nos dois, que denotamos por Hint, devemos sempre poder escrever este

último como multiplicado por um número pequenoη:

H=HS+HA+ηHint. (2.32)

Sendo esse termoηrealmente pequeno, podemos escrever o estado do sistema como uma expansão em séries de potências dele, desprezando aqueles de maior ordem. Normalmente, estes são conservados até segunda ordem:

ρ(t) =ρ(0)(t) +ηρ(1)(t) +η2ρ(2)(t) +O(η3). (2.33)

Esta é, portanto, uma teoria de perturbação dependente do tempo adaptada ao nosso problema, que envolve operadores densidade e que será expressa em termos de operadores de evolução temporal, ou seja, das portas lógicas às quais nossos qubits estarão sujeitos.

Expandindo a evolução temporal numa série de potências da intensidade da perturbação, encontramos:

U(t) =US(t)UA(t)

"

1 +

∞

X

k=1

ηkCk(t)

#

, (2.34)

onde osUS(t)eUA(t)são evoluções devidas apenas aos hamiltonianosHSeHA, isoladamente. A

condição de unitariedade do operador densidade nos permite escrever os hermitianos conjugados dosCk(t):

C_k†(t) =₋Ck(t)− k−1 X

j=1

Cj(t)C_k†₋_j(t). (2.35)

Até a segunda ordem, que contém os termos que nos interessam, osCk(t) são:

C₁†(t) = ₋C1(t),

C₂†(t) = C1(t)C1(t)−C2(t). (2.36)

(46)

ρSA(t) = US(t)UA(t)ρSA(0) +η[C1(t), ρSA(0)]−η2[C1(t), ρSA(0)C1(t)] +η2[C2(t), ρSA(0)]

×U_S†(t)U_A†(t) +O(η3). (2.37)

A dificuldade restante é obter os operadoresCk(t). A partir de sua definição na equação (2.34),

podemos obter cada um deles pela derivada:

Ck(t) =US†(t)U

†

A(t)

1

k!

∂k ∂ηkU(t)

η=0 . (2.38)

O valor de cada uma das derivadas parciais pode ser determinado através do emprego da identidade de Snider (C.5). Com auxílio desta conclui-se que:

C1(t) = −

i

~

Z t

0

dt′ U_S†(t′)HI(t′)US(t′) (2.39)

C2(t) =

1

2[C1(t)]

2

−₂1_~₂

Z t

0

dt′

Z t′

0

dt′′hU_S†(t′)HI(t′)US(t′), US†(t′′)HI(t′′)US(t′′)

i

,(2.40)

onde empregamos o hamiltoniano na representação de interaçãoHI(t)≡U_A†(t)HintUA(t).

De posse das expressões para os dois primeiros Ck(t), tomamos o traço parcial sobre ρSA(t),

já que estamos interessados apenas no operador densidade reduzido do ambiente:

ρS(t) = US(t)

ρS(0)−

i

~η

Z t

0

dt′ U_S†(t′)TrAHI(t′)ρA(0) US(t′), ρS(0)

+η 2 ~2 Z t 0

dt′

Z t

0

dt′′U_S†(t′)TrA

n

HI(t′)US(t′)ρSA(0)U_S†(t′′)HI(t′′)

o

US(t′′)

−1₂η

2

~2 Z t

0

dt′

Z t

0

dt′′TrA

nn

U_S†(t′)HI(t′)US(t′)U_S†(t′′)HI(t′′)US(t′′), ρSA(0)

oo

−1₂η

2

~2 Z t

0

dt′

Z t′

0

dt′′ TrA

nhh

U_S†(t′)HI(t′)US(t′), US†(t′′)HI(t′′)US(t′′)

i

, ρSA(0)

io)

×U_S†(t) +O(η3), (2.41)

(47)

2.4. Perturbações 45

ρSA(0) =ρS(0)⊗ρA(0). (2.42)

Usualmente faz-se a hipótese de que TrA{HI(t′)ρA(0)} = 0, (17) para que os termos de

primeira ordem na perturbação se anulem. Isso é especialmente válido para os casos em que o ambiente é modelado como um banho bosônico, em cujo caso o hamiltoniano de interação geralmente pode ser escrito como uma soma de termos que incluem apenas um operador de criação ou de destruição atuando sobre o ambiente. Como o valor esperado de qualquer um desses operadores sempre se anula

TrA{aρA(0)}= TrA

n

a†ρA(0)

o

= 0, (2.43)

desde que suponhamos o ambiente inicialmente num estado térmico:

ρA(0) =

1

Ze

−βHA_, _Z _{= Tr}

A

n

e−βHA

o

, (2.44)

o traço do hamiltoniano com a matriz densidade também se anula, levando ao desaparecimento dos termos de primeira ordem, conforme o esperado. Vamos aproveitar esse ponto para também incorporar a evolução devida à porta lógica à interação, definindo um novo hamiltoniano de interação _H˜_I₍_t₎ _≡ _U†

S(t)HI(t)US(t), e um operador densidade na representação de interação

˜

ρS(t) =U_S†(t)ρS(t)US(t):

˜

ρS(t) = ρS(0) +

η2

~2 Z t

0

dt′

Z t

0

dt′′TrA

n

˜

HI(t′)ρA(0)ρS(0) ˜HI(t′′)

o

−1₂η

2

~2 Z t

0

dt′

Z t

0

dt′′ nTrA

n

˜

HI(t′) ˜HI(t′′)ρA(0)

o

, ρS(0)

o

−1₂η

2

~2

Z t

0

dt′

Z t′

0

dt′′ hTrA

nh

˜

HI(t′),H˜I(t′′)

i

ρA(0)

o

, ρS(0)

i

+O(η3). (2.45)

Tomando a primeira derivada temporal da expressão (2.45), encontramos a seguinte equação diferencial:

d

dtρ˜S(t) =− η2

~2 Z t

0

dt′TrA

nh

˜

HI(t),

h

˜

HI(t′), ρA(0)ρS(0)

iio

(48)

que, em conjunto com a aproximação ρ˜S(t) = ρS(0) +O(η2) e com a incorporação dos η aos

hamiltonianos de interação, nos dá a equação-mestra de Redfield (19), válida para pequenos valores de η:

d

dtρ˜S(t) =−

1 ~2

Z t

0

dt′TrA

nh

˜

HI(t),

h

˜

HI(t′), ρA(0)˜ρS(t)

iio

. (2.47)

A equação-mestra, como a sua derivação nos mostra, dá a evolução aproximada do sistema para situações de interação fraca. Apesar de não usarmos a equação de Redfield diretamente nesta dissertação, sua derivação correta ilustra como este método perturbativo funciona e servirá de ponto de partida para a derivação da equação-mestra híbrida, esta utilizada para o cálculo aproximado da evolução das medidas ruidosas.

2.5 Equação-mestra híbrida

Agora que já vimos como derivar a equação-mestra a partir da equação de von Neumann (2.4), vamos ver como ela pode ser derivada de uma equação de Lindblad (2.30), necessária para nossa descrição de uma medida ruidosa. Isso será feito pela substituição, no procedimento anterior, dos operadores hamiltoniano e de evolução temporal por superoperadores equivalentes. Assim, se originalmente o operador evolução temporal obedecia uma equação diferencial derivada da equação de Schrödinger, a evolução do operador densidade total ρSA(t) agora será dada por

um superoperador U(t):

ρSA(t) =U(t)ρSA(0), (2.48)

que deverá satisfazer a equação diferencial:

d

dtU(t) = [L+M]U(t), (2.49)

(49)

2.5. Equação-mestra híbrida 47

Novamente considerando a interação entre o ambiente e o sistema como fraca e proporcional a um número pequenoη, podemos expandir o superoperador de evolução temporal numa série

de potências deη:

U(t) =_U0(t) "

1 +

∞

X

k=1

ηk_Ck(t)

#

. (2.50)

onde _U0(t) representa a evolução temporal no caso em que não há interação sistema-ambiente,

ou seja, quando η = 0. Analogamente ao procedimento da seção anterior, podemos encontrar

expressões para os Ck(t):

Ck(t) =U0(−t)

1

k!

∂k

∂ηkU(t)

η=0 . (2.51)

De posse dessa expressão e da fórmula de Snider para superoperadores (C.11), derivada no Apêndice C, encontramos os dois primeiros desses_Ck(t):

C1(t) = Z t

0

dt′ _U0(−t′)

∂_L ∂ηU0(t

′₎_, _(2.52)

C2(t) =

1 2[C1(t)]

2₊ 1

2

Z t

0

dt′

Z t′

0

dt′′

U0(−t′)

∂_L ∂ηU0(t

′₎

U0(−t′′)

∂_L ∂ηU0(t

′′₎

−1₂

Z t

0

dt′

Z t′

0

dt′′

U0(−t′)U0(t′′)

∂_L ∂ηU0(−t

′′₎∂L

∂ηU0(t

′₎

. (2.53)

Conhecidas tais funções, tomamos a derivada e o traço parcial da expressão (2.48), de forma a obtermos uma equação diferencial aproximada para a evolução da matriz densidade reduzida:

d

dtρS(t) = TrA

d

dtU0(t)ρSA(0)

+ TrA

η_U0(t)

d

dtC1(t)ρSA(0)

+TrA

η2_U0(t)

d

dtC2(t)ρSA(0)

+O(η3). (2.54)

(50)

d

dtC1(t) = U0(−t) ∂_L

∂ηU0(t), (2.55)

d

dtC2(t) =

1 2

Z t

0

dt′ _U0(−t′)∂L

∂ηU0(t

′₎

U0(−t)∂L

∂ηU0(t)

+_U0(−t)

∂_L ∂ηU0(t)

Z t

0

dt′ _U0(−t′)

∂_L ∂ηU0(t

′₎

−1

2U0(−t)

Z t

0

dt′_U0(t′)

∂_L ∂ηU0(−t

′₎

∂_L

∂ηU0(t). (2.56)

Usando a propriedade U(t1)U(t2) =U(t1+t2), válida pois estes não passam de exponenciais

de superoperadores multiplicados pelo tempo, podemos mudar de variável de integração de t′

parat₋t′, de forma que encontraremos a igualdade:

U0(−t) Z t

0

dt′ _U0(t′)

∂_L ∂ηU0(−t

′₎

=

Z t

0

dt′ _U0(−t′)

∂_L ∂ηU0(t

′₎

U0(−t). (2.57)

Portanto, a derivada deC2(t) simplifica-se para:

d

dtC2(t) =U0(−t) ∂_L ∂ηU0(t)

Z t

0

dt′ _U0(−t′)

∂_L ∂ηU0(t

′₎

. (2.58)

Substituindo essas duas derivadas na equação diferencial, encontramos:

d

dtρS(t) = TrA

d

dtU0(t)ρSA(0)

+ηTrA

∂_L

∂ηU0(t)ρSA(0)

+η2TrA

∂_L ∂ηU0(t)

Z t

0

dt′ _U0(−t′)

∂_L ∂ηU0(t

′₎

ρSA(0)

+O(η3). (2.59)

Agora torna-se conveniente abrir o liouvilliano explicitamente nas partes que agem no sistema, no ambiente, e no termo de interação proporcional a η, de forma que sua derivada será:

∂_L ∂ηρ=−

i

~

∂

∂η[HA+HS+ηHint, ρ] =− i

~[Hint, ρ]. (2.60)

Já o superoperador U0(t) pode ser expresso da forma:

U0(t)ρ=e−iHAt/~eStρeiHAt/~, (2.61)

(51)

2.5. Equação-mestra híbrida 49

hamiltonianoHS e o lindbladiano de medida M:

Sρ_{≡ −}i

~[HS, ρ] +Mρ. (2.62)

Substituindo esses resultados na equação diferencial, encontramos:

d

dtρS(t) = TrA

n

(_L+_M)_η₌₀_U0(t)ρSA(0)

o

−η

2

~2TrA

Hint,U0(t) Z t

0

dt′ _U0(−t′)

Hint,U0(t′)ρSA(0)

+O(η3).(2.63)

Empregando o hamiltoniano da representação de interação HI(t) ≡ eiHAt/~Hinte−iHAt/~,

encontramos:

d

dtρS(t) = e

St_Tr A

n

(_L+_M)_η₌₀ρSA(0)

o

−η

2

~2 Z t

0

dt′ TrA

nh

HI(t), eS(t−t

′₎h

HI(t′), eSt

′

ρSA(0)

iio

+O(η3). (2.64)

De acordo com a definição de S, teremos:

ρS(t)ρA(0) = TrA{ρSA(t)}ρA(0)

= TrA{U0(t)ρSA(0)}ρA(0) +O(η)

= TrAeStρSA(0) ρA(0) +O(η)

= eStρSA(0) +O(η) (2.65)

Além disso, comoTrA{[HA, ρSA(0)]}= 0, e pela mesma consideração que descartou o termo

de primeira ordem na equação de Redfield, encontramos:

d

dtρS(t) =SρS(t)−

1 ~2

Z t

0

dt′TrA

nh

HI(t), eS(t−t

′₎h

HI(t′), e−S(t−t

′₎

ρS(t)ρA(0)

iio

, (2.66)

onde já descartamos os termos de ordem maior e incorporamos os parâmetrosηaos hamiltonianos

(52)

Como geralmente escolhemos ρA(0)no estado térmico (2.44), temos [ρA(0), e±iHAt/~] = 0, o

que podemos empregar para reescrever a equação diferencial conforme:

d

1 ~2

Z t

0

dt′ TrA

nh

HI(t−t′), eS(t−t

′₎h

HI(0), e−S(t−t

′₎

ρS(t)ρA(0)

iio

. (2.67)

Mudando a variável de integração para τ =t₋t′, encontramos uma fórmula mais simples:

d

1 ~2

Z t

0

dτ TrAHI(τ), eSτHI(0), e−SτρS(t)ρA(0) . (2.68)

(53)

51

Capítulo 3 Teoria de correção de erros

quânticos

Diversas formas de superar as dificuldades impostas pelas incorreções que podem surgir durante a computação quântica foram sugeridas desde a década de 1990 (5, 22). A correção de erros especificamente adapta a teoria clássica de códigos – com suas origens remontando aos primeiros computadores clássicos, em 1950 (21) – para o contexto quântico, de forma a permitir a recuperação do estado original do sistema após o erro já haver ocorrido.

Assim como no caso clássico, a teoria quântica de correção de erros emprega medidas de síndrome (ou diagnóstico) para determinar que erro ocorreu, para, após isso, aplicar-se uma medida de correção que leva o sistema ao seu estado original. Os correspodentes quânticos dos efeitos clássicos, porém, apresentam certas dificuldades. Em primeiro lugar, as medidas de síndrome devem ser feitas com cuidado para não revelar a informação guardada pelos qubits, pois uma perda do estado de superposição arruinaria a computação. A única solução é que as medidas de síndrome meçam apenas o erro, e não o estado do sistema.

Outra questão é que os erros quânticos podem ser muito mais complexos do que os erros clássicos. Classicamente, um bit pode sofrer apenas uma modificação, a mudança para um valor oposto, também chamada debit flip. Esse processo é equivalente à aplicação da matriz de Pauli

σx. Quanticamente, um qubit pode receber qualquer rotação, expressa pela exponencial do

produto de um vetor qualquer pelo vetor das matrizes de Pauli (1.14), o que sempre pode ser decomposto numa combinação linear das três matrizes de Pauli e a identidade. Assim, além do caso em que não há erros, representado pela identidade, há três erros linearmente independentes que podem ocorrer com cada qubit:

(ˆu_·σ)|ψi=u_xσ_x|ψi+u_yσ_y|ψi+u_zσ_z|ψi. (3.1)

(54)

52 Capítulo 3. Teoria de correção de erros quânticos

superposição, é resolvido pela redundância de informação, obtida codificando cada estado de k

qubits lógicos em n > k de qubits físicos. Os estados propriamente codificados formarão um

subespaço de dimensão2k, menor do que o total de2n dimensões do espaço de Hilbert total dos

qubits_HS. Chamaremos tal subespaço de código, C.

As medidas de síndrome efetivamente nos dizem se o sistema está dentro do subespaço do código. Para lidar com a multiplicidade de erros possíveis, que é o segundo problema enfrentado pela teoria de correção de erros quânticos, cada código deve ser projetado de forma que os erros que ele possa corrigir levem os estados do sistema para fora do subespaço do código. Assim, a tarefa da síndrome torna-se determinar em que subespaço do espaço de Hilbert total se está. Se estiver dentro do código, o estado não sofreu nenhum erro; se não estiver, a medida deve ser capaz de identificar que erro ocorreu através da localização do estado dentro de HS, para que o

procedimento de correção adequado possa ser aplicado.

Para identificar os estados do código, empregaremos o subescrito L, que representa o fato de que o estado referido é um estado lógico, em oposição ao estado físico equivalente. Usaremos o mesmo índice para indicar portas lógicas que façam o mesmo papel que as portas físicas equivalentes. Assim, se um estado físico_|ψ_i sofre a ação de uma operaçãoU até tornar-se_|ψ′_i:

U_|ψ_i=ψ′, (3.2)

os seus equivalentes lógicos, se propriamente construídos, atuarão conforme:

UL|ψi_L=ψ′_L. (3.3)

Na próxima seção, veremos como construir um código simples de correção de erros, além de mostrar como constroem-se as portas lógicas que sobre ele devem operar.