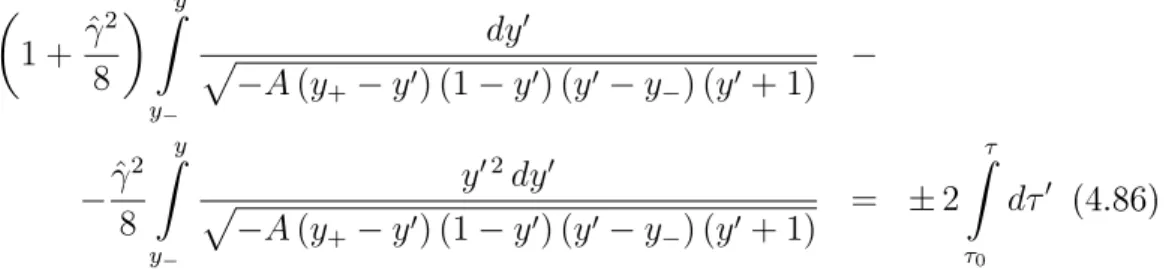Cordas em espaços deformados

Universidade de São Paulo

Instituto de Física

Cordas em espaços deformados

Sergio Augusto Jardino Filho

Orientador: Prof. Dr. Victor de Oliveira Rivelles

Tese apresentada ao Instituto de Física da

Universidade de São Paulo para a obtenção

do título de Doutor em Ciências.

Comissão examinadora:

Prof. Dr. Victor de Oliveira Rivelles (IFUSP) Prof. Dr. Dmitry Vasilevich (UFABC)

Prof. Dr. Nathan Jacob Berkovits (IFT/UNESP) Prof. Dr. Ricardo Ivan Medina Bascur (UNIFEI) Prof. Dr. Henrique Boschi Filho (UFRJ)

Resumo

Nesta tese foram estudadas congurações de cordas em movimentos de rotação e de oscilação no âmbito da correspondência AdS/CF T. Estas cordas movimentam-se nos espaços AdS5 ×S5, de Lunin e Maldacena, R1,9 e R1,9 deformado. Para

o caso da corda em rotação, determinou-se a existência do mágnon gigante e da corda farpada. Para o caso da corda oscilante, foram encontradas as soluções das equações de movimento clássicas e determinada a energia. Também calculamos explicitamente o número de supercargas preservadas para os espaços AdS5 ×S5 e

para R1,9 deformado.

Abstract

In this thesis we studied rotating and oscillating strings under the AdS/CF T cor-respondence. These strings move in the AdS5 ×S5, Lunin and Maldacena, R1,9

and deformedR1,9 spaces. In the case of the rotating string, the giant magnon and

the spiky string were determined. In the case of the oscillating string, we found the solutions fo the classical equations of motion and the energy. We also explicitly calculated the number of preserved supercharges for the AdS5 ×S5and deformed

Sumário

1 Introdução 5

2 Teorias de supergravidade 9

2.1 Modelo AdS5×S5 . . . 9

2.2 Modelo de Lunin e Maldacena . . . 11

2.2.1 Introdução . . . 11

2.2.2 Deformação de R1,9 . . . 16

2.2.3 Deformação de AdS5×S5 . . . 18

2.3 Supersimetria e espaços curvos . . . 19

2.3.1 Supersimetria em AdS5×S5 . . . 21

2.3.2 Supersimetria em R1,9 deformado . . . 21

3 Cordas em espaços não-deformados 24 3.1 Introdução . . . 24

3.2 Corda em rotação . . . 28

3.2.1 Rotações com velocidades angulares idênticas . . . 30

3.2.2 Rotações com velocidades angulares diferentes . . . 31

3.2.3 Corda com ansatz de Bobev e Rashkov . . . 36

3.3 Corda oscilante . . . 39

3.3.1 Corda oscilante no espaço plano . . . 39

3.3.2 Corda oscilante na esfera de AdS5×S5 . . . 40

4 Cordas em espaços deformados 47 4.1 O efeito da deformação . . . 47

4.2 Corda no espaço R1,9 . . . 50

4.3 Cordas em rotação . . . 52

4.4 Corda com anzatz de Bobev e Rashkov . . . 53

4.5 Cordas oscilantes . . . 56

4.5.1 Corda oscilante no espaço plano deformado . . . 56

4.5.2 Corda oscilante na esfera de AdS5×S5 deformado . . . 61

SUMÁRIO 4

Conclusão 68

Apêndice 70

A. Símbolos e convenções . . . 70

B. Parametrizações . . . 71

C. Dinâmica do modelo de Lunin e Maldacena . . . 72

Capítulo 1

Introdução

A teoria de cordas [1] é uma candidata a unicar as interações conhecidas, isto é, a gravitação, a força eletrofraca e a força nuclear forte. Esta teoria propõe que todas as partículas e todas as interações podem ser obtidas da vibração de uma corda. Apesar desta teoria não ter resultados experimentais que permitam conrmar ou refutar esta hipótese, o seu desenvolvimento do ponto de vista teórico prossegue. Dentre estes desenvolvimentos teóricos da teoria de cordas, destaca-se a sua relação com teorias de calibre. Este relacionamento começou com a dualidade anti-de Sit-ter/teoria de campos conforme (AdS/CF T) [2], que propõe que a teoria de cordas no espaço AdS5×S5 em D = 10 dimensões, é dual, ou equivalente, a uma teoria

de calibre de super-Yang Mills (SYM ) emD= 4 dimensões, com grupo de simetria

U(N) e com N = 4 supersimetrias. Segundo esta dualidade, o espectro de energia

da teoria de cordas é igual ao espectro do operador de dilatação de operadores inva-riantes de calibre da teoria de SYM. Entretanto, a quantização da teoria de cordas em AdS5 ×S5 não é totalmente conhecida, e portanto não conhecemos

completa-mente seu espectro de energia. O mesmo ocorre para a teoria de SY M, onde o espectro do operador de dilatação também não é totalmente conhecido. Este fato inviabiliza a comparação completa dos espectros das teorias, e portanto uma prova rigorosa da correspondência AdS/CF T. Esta correspondência pode ser estendida para teorias de cordas e de calibre diferentes das da proposta inicial da correspon-dência AdS/CF T [3]. Nestes casos, temos uma generalização da correspondência AdS/CF T como uma dualidade entre uma teoria de cordas e uma teoria de calibre. Algumas pesquisas buscam encontrar teorias de cordas e de calibre duais com poucas supersimetrias [4]. Como o modelo padrão de partículas elementares não é supersimétrico, teorias com pouca supersimetria apresentam maiores possibilidades de aplicação em fenomenologia que as muito supersimétricas. As teorias de Mal-dacena e Núñez [5] e de Lunin e MalMal-dacena [6] são representativas desta linha de pesquisa. No caso da teoria de Lunin e Maldacena, é feita uma transformação na

CAPÍTULO 1. INTRODUÇÃO 6 geometria deAdS5×S5, em que a esferaS5 é deformada. Analogamente, a teoria de

calibre dual à solução de Lunin e Maldacena é uma deformação da teoria de SY M dual aAdS5×S5.

Um caso especíco da dualidade se estabelece entre uma teoria de calibre e cordas em movimento de rotação [7]. Os operadores invariantes de calibre neste caso contêm um produto de campos escalares. Se estes campos escalares,e.g.Φe Ξ

forem representados como um valor determinado de spin, tal que

|· · ·ΦΦΞΦΦΦ_{· · · i → |· · · ↑↑↓↑↑↑ · · · i},

os operadores invariantes de calibre são interpretados como cadeias de spin. Ope-radores de calibre onde todos os campos escalares são idênticos são interpretados como cadeias de spin ferromagnéticas, onde todos os spins têm a mesma orientação. Estes operadores são duais a cordas em movimento de rotação [8]. Entretanto, uma cadeia na qual existem ambas as orientações para o spin, sendo uma em pequena quantidade, também foi proposta. Os spins em pequena quantidade são impurezas da cadeia ferromagnética chamadas de mágnons. No setor de cordas, o mágnon da teoria de calibre foi identicado com uma corda na esfera deAdS5×S5. Nesta corda

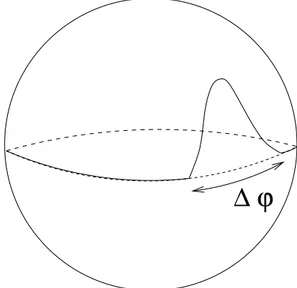
existe uma deformação chamada de mágnon gigante [9]. A largura da deformação é chamada ângulo de décit. Um esboço do mágnon gigante encontra-se na Figura 1.1.

∆ ϕ

Figura 1.1: Mágnon gigante e ângulo de décit∆ϕ.

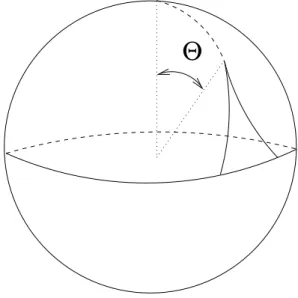
CAPÍTULO 1. INTRODUÇÃO 7 do pico, como no caso do do mágnon gigante. O fato desta quantidade ser innita indica que a corda está innitamente enrolada ao longo da direção. A corda farpada tem picos cuja altura é medida pelo ângulo polar da esfera. Uma representação de uma corda farpada com um único pico de altura Θestá mostrada na Figura 1.2.

Θ

Figura 1.2: Corda farpada com pico de altura Θ.

A energia e os momentos obedecem uma prescrição estrita como no caso do mágnon gigante. Entretanto, seu setor de calibre ainda não é compreendido. Considera-se que as cordas farpadas sejam duais a uma teoria de calibre com férmions descritos pelo modelo de Hubbard, [11] mas esta é uma questão aberta.

Além da rotação, outros tipos de movimento, como a oscilação, foram pesqui-sados em diversas teorias de cordas. Podemos citar os casos de cordas que se mo-vimentam nos espaços de AdS5 ×S5 [12, 13, 14, 16, 17, 18, 19, 20, 21], de

Malda-cena e Núñez [22], de Lunin e MaldaMalda-cena [23, 24, 25, 26, 27, 28, 29] e AdS4×CP3

[30, 31, 32, 33, 34]. Uma interpolação entre uma corda oscilante e uma corda farpada é a corda helicoidal [35]. Nestes estudos, a dinâmica clássica de cordas é estudada e diferentes procedimentos de quantização são propostos.

Nesta tese estudamos a corda tanto do ponto de vista clássico como quântico. Analisamos o efeito da deformação geométrica sobre as os resultados conhecidos. Isto pode ser visualizado tanto na solução das equações de movimento como na energia da corda. Assim, apresentamos um resumo de resultados da literatura para cordas em rotação e oscilação. A seguir, analisamos o caso de uma corda em oscilação em

R1,9 com e sem deformação. Também analisamos aspectos da corda oscilante no

espaçoAdS5×S5 deformado. A organização da tese é a seguinte:

No capítulo 2 zemos uma revisão da correspondência teoria de cordas/teoria de calibre para os espaços AdS5 ×S5 e AdS5 ×S5 deformado segundo o método

CAPÍTULO 1. INTRODUÇÃO 8 descrito. Também descrevemos como deformar o espaçoR1,9 pelo mesmo o método.

Na seção 2.3.2, determinamos explicitamente o número de supersimetrias existente nas soluções de AdS5 × S5 e R1,9 deformado. Utilizamos a equação de Killing

espinorial para calcular explicitamente o número de supersimetrias preservadas em

R1,9 deformado.

No capítulo 3 revisamos soluções clássicas de cordas em movimento de rotação e de oscilação na esfera do espaço AdS5×S5 e no espaço R1,9. Também revisamos

a existência do mágnon gigante e da corda farpada nestes casos. Apresentamos a solução clássica da corda oscilante em R1,9 na seção 3.3.2.

No capítulo 4 estudamos o efeito da deformação em várias situações. Na seção 4.1 construímos explicitamente uma esferaS2 _{deformada. Na seção 4.2 analisamos}

o movimento de cordas no espaço R1,9 deformado e mostramos que ele pode exibir

mágnons e cordas farpadas. Nas seções 4.3 e 4.4 zemos uma revisão para cordas em rotação, para o mágnon gigante e para a corda farpada em AdS5×S5 deformado.

Na seção 4.5 derivamos as soluções clássicas da corda oscilante emR1,9 e_AdS5×S5

deformados e também calculamos suas energias.

Uma breve conclusão encerra esta tese no capítulo 5. Nos apêndices estão reu-nidas as convenções, as parametrizações deAdS5 eS5, e as equações de movimento

Capítulo 2

Teorias de supergravidade

2.1 Modelo

AdS

×

S

Nesta seção obtemos a soluçãoAdS5×S5 da supergravidade IIB. Para atingir este

objetivo, partimos de uma solução de supergravidade [4] que contém a métrica, o dílatonΦ constante e o campo F5 de uxo constante dada por

ds2 = H−12

3 ηαβdxαdxβ +H

1 2

3δijdxidxj

eΦ = 1 (2.1)

F5 = dH3−1∧dx0∧dx1∧dx2∧dx3 +∗

¡

dH−1

3 ∧dx0∧dx1∧dx2∧dx3

¢

,

onde, sendor =r(xα_{) uma coordenada radial, temos que}

H3 = 1 +

R4

r4,

os demais campos da que em geral compõem a supergravidadeIIB [37] são identi-camente nulos, R é uma constante de integração, α, β = 0, . . . , 3, e i, j = 4, ..., 9. Esta solução descreve N 3-branas como um sub-espaço conformalmente plano de 3 + 1dimensões e um sub-espaço transverso de seis dimensões conformalmente

eu-clidiano. Para diferentes soluções da teoria da supergravidade, pode haver diferentes dimensões na brana. Em geral, branas p-dimensionais são chamadasp-branas.

Analisemos o comportamento desta solução em certos limites da cordenada r. Se r À R, H3 → 1 e a métrica se torna minkowskiana. Por outro lado, para

r¿R, H3 → R 4

r4 e a métrica, depois da substituição z = R 2

r , torna-se a métrica de

AdS5×S5,

ds2 = R

2

z2

¡

ηαβdxαdxβ+dz2

¢

+R2dΩ2₅. (2.2) Notamos que os raios da esfera e do espaço AdS5 têm o mesmo valor, R.

A princípio, esta solução não está relacionada com a teoria de cordas, pois foi

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 10 obtida de maneira independente. Contudo, sabe-se que a supergravidade é o limite de baixas energias da teoria de cordas. Esta solução tem, então, uma interpretação em termos da teoria de cordas. Para estabelecer a conexão entre uma solução de supergravidade do tipop-brana e a teoria de cordas, utiliza-se o conceito de D-brana. As branas de Dirichlet, D-branas ou ainda Dp-branas [38, 39, 40] são introduzidas na teoria de cordas quando condições de contorno de Dirichlet, ou condições de extremidades xas, são impostas para cordas abertas. Até então, as condições de contorno para estas cordas eram somente as de Neumann, onde as extremidades da corda estão livres. A utilização de condições de Dirichlet exige um objeto onde a extremidade da corda esteja xa. Este objeto é uma D-brana. Mais especicamente, uma Dp-brana é um hiperplano(p+ 1)-dimensional, comp <9, imerso num

espaço-tempo(9+1)-dimensional onde as extremidades de cordas abertas estão xas. Estas

extremidades obedecem condições de Neumann nas p coordenadas da D-brana e condições de Dirichlet nas9−pcoordenadas transversais. Assume-se que D-branas ep-branas são o mesmo objeto, e assim, para o caso acima, a3-brana será identicada

com uma D3-brana.

Como admitimos que p-branas e D-branas são idênticas, é necessário considerar o campo de calibre existente no volume-mundo da D-brana e que não está presente na teoria da supergravidade. No espaço plano, a dinâmica de baixas energias de N D-branas superpostas gera uma teoria de calibre de super-Yang Mills, SYM, com grupo de calibre U(N). A identicação entre D-branas e p-branas exige que as simetrias da teoria de supergravidade e da teoria de SYM sejam idênticas. O grupo de isometria deAdS5×S5 éSO(2, 4)×SO(6). Estes grupos podem ser encontrados

em N = 4 SYM : a simetria SO(2,4) corresponde ao grupo de simetria conforme e

SO(6) ao grupo de simetria R. Também é feita a identicação de suas constantes

de acoplamento na forma

g_{Y M}2 = 4πgs, R4 = 4πgsN α′2, (2.3)

onde gs é a constante de acoplamento da teoria de cordas, α′ = ℓ2s, onde ℓs é o

comprimento da corda e gY M é a constante de acoplamento de SYM. Em virtude

destas simetrias em comum e da igualdade das constantes de acoplamento, a corres-pondência AdS/CF T [36] pode ser expressa como: a teoria de cordas do tipo IIB na geometria AdS5 ×S5, com dílaton constante, campo F5 de uxo constante igual

a N e demais campos identicamente nulos é dual, ou equivalente, à teoria de calibre de super-Yang Mills com N = 4 supersimetrias em D = 4 dimensões e grupo de

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 11

2.2 Modelo de Lunin e Maldacena

2.2.1 Introdução

Nesta seção apresentamos solução de Lunin e Maldacena [6] para a teoria da super-gravidade. Antes disso, porém, vamos descrever brevemente a sua teoria de calibre dual. Esta é uma teoria de SYM conforme em D = 4 dimensões, com N = 1

supersimetria, grupo de calibre U(N) e uma simetria global U(1) ×U(1). Nesta

teoria, o produto de dois campos f e g no potencial da lagrangiana foi modicado, ou deformado, de acordo com

f ∗g ≡ eiπβQ[1fQ

2]

g_{f g,} (2.4)

onde β = γ −iκ é o parâmetro complexo de deformação, Qi

f é a i-ésima carga

U(1) associada ao campo f e fg é a multiplicação usual. Esta teoria é chamada

de beta deformada [41, 42]. A deformação (2.4) introduz fases em alguns termos da lagrangiana. Se considerarmos β real, o parâmetro de deformação da teoria é simplesmente γ.

Devido à correspondência AdS/CF T, a teoria de supergravidade em AdS5×S5

também sofre uma modicação em virtude da deformação. O objetivo é encontrar esta solução de supergravidade deformada. O meio de alcançar este objetivo é explorar a simetria globalSL(2, R_)×SL(2,R₎da supergravidade, que é semelhante

à simetriaU(1)×U(1)de SYM. O grupo de simetriaSL(2, R₎possui dois geradores:

uma inversão e uma translação. Se atuarem sobre um objetoτ, os geradores do grupo são

τ → 1

τ e τ →τ +γ, (2.5) onde γ ∈ R. Os geradores (2.5) levam a um caso partiular da transformação para

SL(2, R₎

τγ =

τ

1 +γτ. (2.6)

A transformação SL(2, R₎ pode ser interpretada sicamente em teoria de cordas.

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 12 o inverso do outro. Como a transformação (2.6) é formada por uma inversão, seguida por uma translação e por outra inversão, estas três operações representam, na teoria de cordas, uma transformação da dualidade T, uma mudança de coordenadas e outra dualidade T. Esta transformação é referida na literatura como TsT.

O objeto τ e a transformação (2.6) serão usados para gerar uma nova solução de supergravidade a partir de AdS5 ×S5. Para alcançar este objetivo, a simetria

global U(1)×U(1) da teoria de calibre, que é também o grupo de simetria de um

toro T2_{, deve estar presente na supergravidade. A teoria de supergravidade IIB}

com coordenadas identicáveis com as de um toro tem suas soluções relacionadas de acordo com a simetria SL(2, R₎ [44]. O parâmetro _τ, sobre o qual a simetria

SL(2, R₎atua para gerar uma nova solução, é denido por [6]

τ =B12+i√g, (2.7)

onde g é o determinante da métrica do toro e B12 uma componente do campo de

Kalb-Ramond. O fatorγ de (2.6) é identicado com o parâmetro de deformação da teoria de calibre (2.4). Observa-se que τ0 = τ em (2.6), e assim espera-se que ao

tomarγ = 0 numa solução transformada a solução não-deformada seja recuperada.

Iremos agora utilizar a simetria SL(2,R₎ na forma (2.6) sobre o parâmetro _τ

denido por (2.7) para gerar soluções de supergravidade deformadas a partir de soluções conhecidas. Como ilustração deste procedimento, tomemos o espaço eucli-dianoR4 parametrizado em termos de coordenadas toroidais _{(ρ1, ρ2,, ϕ1, ϕ2)}, onde

ϕ1, ϕ2 ∈[0, 2π] e ρ1, ρ2 ∈[0,∞). A métrica deste espaço é

ds2 =dρ2₁+dρ2₂+ρ₁2dϕ2₁+ρ2₂dϕ2₂. (2.8) ComoB12= 0, (2.7) leva a τ =iρ1ρ2. E de (2.6), chega-se a

τγ =

γρ2 1ρ22

1 +γ2_ρ2 1ρ22

+i ρ1ρ2

1 +γ2_ρ2 1ρ22

. (2.9)

Esta transformação implica que B12, inicialmente nulo, tornou-se

B12 =

γρ2 1ρ22

1 +γ2_ρ2 1ρ22

, (2.10)

e a raiz quadrada do determinante do setor toroidal da métrica, inicialmente √g =

ρ1ρ2, tornou-se

√

g = ρ1ρ2 1 +γ2_ρ2

1ρ22

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 13 de maneira que podemos reescrever a métrica na forma

ds2 = dρ2₁+dρ2₂+ 1 1 +γ2_ρ2

1ρ22

¡

ρ2₁dϕ2₁+ρ2₂dϕ2₂¢

. (2.12)

A métrica (2.12) contém uma deformação parametrizada por γ, que reduz-se à mé-trica plana emγ = 0. Porém, a transformação sobreτ não somente altera a métrica e gera um campoB12, o dílaton também é modicado. Contudo, os resultados (2.10)

e (2.11) não permitem deduzir a sua forma nal após a transformação. Isto pode ser determinado pela aplicação direta da transformação TsT. Duas teorias de super-gravidade que estejam relacionadas por dualidade T têm seus campos relacionados através das regras de Buscher [4, 43],

g′11=

1

g11

, e2Φ′ = e

2Φ

g11

, gµ′1 =

Bµ1

g11

, Bµ′1 =

gµ1

g11 (2.13)

g′

µν =gµν −

g2

µ1 −Bν21

g11 e

B′

µν =Bµν −

B[µ1gν]1

g11

,

onde µe ν são índices das coordenadas espaciais. Para R4, a dualidade atuará em

ds2 = ρ2₁dϕ2₁+ρ2₂dϕ2₂, (2.14) logo µ= 1,2. Utilizando (2.13) sobre ϕ2 com ϕ1 xo, de (2.14) obtemos

g′

11=

1

ρ2 1

, g′

12 = 0, g22′ =ρ12, B12′ = 0 e e2Φ ′

= e

Φ0

ρ2 1

. (2.15) Faz-se agora a translação

ϕ1 →ϕ2+γϕ1,

que produz a métrica

ds2 = ρ2₁dϕ2₁+ 2γρ2₁dϕ1dϕ2+

1 +γ2_ρ2 1ρ22

ρ2 2

dϕ2₂.

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 14

e2Φ ₌ e2Φ0

1 +γ2_ρ2 1ρ22

. (2.16)

A métrica (2.12), o campo de Kalb-Ramond (2.10) e o dílaton (2.16) constituem a solução deformada para a métrica R4. Evidentemente, este procedimento não

garante que a solução encontrada tenha uma teoria de calibre dual. Em todo caso, ela permite gerar uma nova solução de supergravidade onde for possível encontrar uma simetriaU(1)×U(1) na métrica.

Antes de aplicar este procedimento para soluções em dez dimensões, é importante salientar que existem duas formas de escrever o elemento de linha em teoria de cordas: as representações de Einstein e de cordas, relacionadas por

ds2_Einstein = e−Φ2ds2

Cordas, (2.17)

ondeΦé o dílaton. O procedimento apresentado paraR4 e para os casos que seguem

estão denidos para métricas na representação de cordas.

Para encontrar a solução AdS5×S5 deformada por meio deste procedimento, é

preciso tratar, além da métrica, do campo tensorial F5. Para gerar esta solução, é

necessário uma solução de supergravidade que apresente a simetria toroidalU(1)_×

U(1). Uma solução com estas propriedades é conhecida [45]

ds2_IIB = F

"

(Dϕ1−C Dϕ2)2

√

∆ +

√

∆(Dϕ2)2

#

+ e

2φ

3

F13

gµνdxµdxν (2.18)

B2 = B12Dϕ1∧Dϕ2+ (B1µDϕ1+B2µDϕ2)∧dxµ−

− 1

2A

κ

µBκνdxµ∧dxν +

1 2˜bµνdx

µ_dxν

e2Φ _{= e}2φ

C0 = χ

C2 = C12Dϕ1∧Dϕ2+ (C1µDϕ1+C2µDϕ2)∧dxµ−

− 1

2A

κ

µCκνdxµ∧dxν+

1 2c˜µνdx

µ_∧dxν

C4 = −

1 2

³

˜

dµν+B12˜cµν −²κλBκµCλν−B12AκµCκν

´

dxµ∧dxν ∧Dϕ1∧Dϕ2+

+ 1

6

h

Cµνλ+ 3

³

˜_{bµν +A}1

µB1ν −A2µB2ν

´

C1λ

i

dxµ∧dxν ∧dxλ∧Dϕ1+

+ dµµ′_νν′dxµ∧dxµ ′

∧dxν _∧dxν′+ ˆdµνκdxµ∧dxν ∧dxκ∧Dϕ2,

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 15 autodual com relação à atuação do operador de Hodge, ou∗d4 =d4. O procedimento

de deformação de Lunin e de Maldacena pode ser entendido como identicar a simetria U(1) _×U(1) na solução (2.18) e aplicar a seqüência de transformações

TsT representada pela atuação de SL(2, R₎ em _τ. Para deformar uma solução de

supergravidade, esta deverá ser escrita de maneira a identicar seus campos com os de (2.18). Depois que isto for feito, basta substituir os campos identicados na solução transformada. Para transformar (2.18), é preciso considerar que esta solução possui uma simetria SL(3, R_{) ⊃ SL(2,} R₎. Ou seja, a transformação TsT

atua sobre a métrica e SL(3, R₎ atua sobre matrizes contruídas com os campos.

Dene-se então a matriz

M = h hT _(2.19)

onde

hT =



 

e−φ3F− 1

3 0 0

0 e−φ_3F2_{3 0}

0 0 e23φF−

1 3



 



 

1 B12 0

0 1 0

χ χB12−C12 1





. (2.20)

M se transforma segundo

M _→ΛMΛT (2.21)

para Λ_∈SL(3, R_).Dene-se também

Wµν =



 

˜

cµν

˜

dµν

˜_bµν





, (2.22)

que transforma-se com um vetor de 3 componentes por Wµν → ΛWµν. O dílaton

e as formas diferenciais são feitas iguais a zero, exceto _d˜_{µν e dµµ′νν′. É importante}

destacar que _d˜_{µν é não-nulo apenas para a aplicação de Wµν → ΛWµν. Os demais}

escalares e a métrica permanecem inalterados. Os campos remanescentes são

C0 = χ (2.23)

C4 = dµµ′_νν′dxµ∧dxµ ′

∧dxν _∧dxν′.

Esta escolha _d˜_{µν e dµµ}′_νν′ não-nulos de permite que F₅ = dC₄ seja auto-dual se

escrita como

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 16 Aplicamos agora as transformações (2.21) sobre a matriz M e Wµν → ΛWµν sobre

o vetorWµν utilizando a matriz

Λ =



 

1 γ 0

0 1 0

0 σ 1





, (2.25)

cujo parâmetro σ permite restringir a simetria SL(3, R₎ a _SL(2, R₎ quando_{σ = 0}.

A matriz (2.25) em (2.19) leva a

h′T ₌

    1 √

GHF13 0 0

0 √GF23 0

0 0 √HF−13

      

1 γF2_{G 0}

0 1 0

γσF2

H σ F2

H 1





. (2.26)

A comparação de (2.20) com (2.26) leva aos novos campos

B₁₂′ = γF2G, C₁₂′ =−σF2G, χ′ =γσF

2

H, F

′ _{=F G}√_H,(2.27)

e2φ′

=GH2_{, G}−1 _{= 1 + (γ}2_+σ2_)F2 _{e H}′ _{= 1 +σ}2_F2_,

que compõem a solução transformada

ds2 = F GH1/2

"

(Dϕ1−C Dϕ2)2

√

∆ +

√

∆(Dϕ2)2

#

+

√

H F13

gµνdxµdxν (2.28)

e2φ′ = H2G χ = γσF

2

H

B2 = γF2G Dϕ1∧Dϕ2+

σ

2d˜µνdx

ν _∧dxµ

C2 = −σF2G Dϕ1∧Dϕ2+

γ

2d˜µνdx

ν _∧dxµ

F5 = F˜5+∗F˜5.

Esta é a solução de Lunin e Maldacena obtida para (2.18). Veremos agora alguns casos de aplicação deste procedimento para gerar de soluções deformadas.

2.2.2 Deformação de

R

Aplicaremos o procedimento da seção anterior para o espaço plano em dez dimensões [6]. Com o uso das coordenadas angulares ϕ1, ϕ2 eψ ∈ [0, 2π] e ri ∈ [0, ∞] para

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 17

ds2 = ηµνdxµdxν +

3

X

i=1

¡

dr2_i +r2_idφ2_i¢

(2.29)

onde µ= 0, 1, 2, 3, e

φ1 =ψ−ϕ1, φ2 =ψ+ϕ1+ϕ2, φ3 =ψ−ϕ2, (2.30)

pode ser parametrizada como

ds2 = ηµνdxµdxν +

3

X

i=1

dr2_i + (r₂2+r2₃)2

µ

Dϕ1+

r2 2

r2 2 +r32

Dϕ2

¶2

+

+ g0

r2 2 +r32

(Dϕ2)2+ 9

r2 1r22r32

g0

dψ2, (2.31)

onde

Dϕ1 =dϕ1−dψ+ 3

r2 1r22

g0

dψ , Dϕ2 =dϕ2−dψ+ 3

r2 2r23

g0

dψ,

eg0 =r12r22+r22r32+r12r23 . A comparação de (2.29) com (2.18) fornece

ηµν =

e23φ

F13

gµν, ηrr=

e23φ

F13

grr, 9

r2 1r22r32

g0

= e

2φ

3

F13

gψψ, (2.32)

C =₋ r

2 2

r2 2 +r23

, g0 r2

2+r23

=F√∆, r₂2+r₃2 = √F

∆

o que permite concluir que

F2 =g0 e ∆ =

g0

(r2₂+r2 3)2

. (2.33)

Ao substituir (2.33) em (2.28) e fazer σ= 0, obtemos

B′

12=γF2G, C12′ = 0, χ′ = 0, F′ =F G

√

H, (2.34) e2Φ′ =GH2 H = 1 e G−1 _{= 1 +γ}2_F2_.

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 18

ds2 = ηµνdxµdxν +

3

X

i=1

¡

dr2_i +Gr2_idφ2_i¢

+γ2r2₁r₂2r2₃G

à ₃ X

i=1

dφi

!2

(2.35) B2 = R2γG

¡

r₁2r2₂dφ1∧dφ2+r22r32dφ2∧dφ3−r12r23dφ1∧dφ3

¢

e2Φ = G, G−1 _{= 1 +γ}2_g 0.

Nesta solução, como no caso de R4_{, surgem o campo de Kalb-Ramond e o dílaton,}

que não estavam presentes inicialmente. Também observa-se que fazer γ = 0 em

(2.35) recupera a solução não deformada (2.29), como esperado.

2.2.3 Deformação de

AdS

×

S

Tomemos a solução de AdS5×S5

ds2 = R

2

z2(ηαβdx

α_dxβ _+dz2_{) +R}2_dΩ2

5; α, β = 0, ...3 (2.36)

Φ = Φ0

F5 = dH3−1∧dx0∧dx1∧dx2∧dx3 +∗

¡

dH−1

3 ∧dx0∧dx1∧dx2∧dx3

¢

,

onde

H3 =

z4

R4, R

4 _{= 4πg}

sN ℓ4s e Φ0 =constante.

Para estabelecer a comparação com a solução não-deformada (2.18), a esfera S5 _de

(2.36) será escrita com as coordenadas ϕ1, ϕ2eψ ∈[0, 2π]eα, β ∈[0, π], de forma

a evidenciar a simetria U(1)×U(1)

dΩ2₅ = dα2+sen2α dθ2+ 36sen

2_2αsen2_2θ

4 cos2_α+sen2_αsen2_2θdψ

2_{+ (2.37)}

+ sen2α(dϕ1+ cos2θ dϕ2+ cos 2θ dψ)2+

+ 4 cos

2_α+sen2_αsen2_2θ

4

µ

dϕ2+ 2sen

2_αsen2_{2θ−2 cos}2_α

4 cos2_α+sen2_αsen2_2θdψ

¶2

.

Esta maneira de escrever a esfera permite uma comparação direta dos dois últimos termos de (2.37) com o primeiro de (2.18). Além disso, denem-se variáveis as φi=1,2,3 tais como (2.30) e µi=1,2,3 ∈ [0,1] sujeitas ao vínculo Pµ2i = 1. Assim, a

comparação dos termos, como a feita para o espaço R1,9, levará à solução de Lunin

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 19

ds2 = R2



ds2_AdS5 +

3

X

i=1

(dµ2_i +Gµ2_idφi) + ˆγ2µ21µ22µ23G

à ₃ X

i=1

dφi

!2

 (2.38)

B2 = ˆγR2G

¡

µ2₁µ2₂dφ1∧dφ2+µ22µ32dφ2∧dφ3−µ12µ23dφ1∧dφ3

¢

e2Φ = e2Φ0G

C2 = −48π Nˆγ ω1∧dψ

C4 = 16π N(ω4+G dω1∧dφ1 ∧dφ2∧dφ3),

onde

G−1 = 1 + ˆγ2¡

µ21µ22+µ22µ23+µ21µ23

¢

, (2.39)

3

X

i=1

µ2i = 1, γˆ=R2γ e R4 = 4πeΦ0N.

Nas fórmulas acima,

dω1 =sen3αcosαsenθcosθdα∧dθ e ωAdS5 =dω4.

As formas diferenciais de Ramond-Ramond (RR) tais queF3 =dC2 eF5 =dC4 são

F3 = −4ˆγe−Φ0R2µ2µ3dµ2∧dµ3∧ 3

X

i=1

dφi (2.40)

F5 =

4R4_e−Φ0

(x4₎2 dx

0 _∧dx1_∧dx2_∧dx3_∧dx4₊

+ 4R4Gµ2µ3dµ2 ∧dµ3∧dφ1∧dφ2∧dφ3.

Observa-se que, seγˆ= 0, recupera-se a soluçãoAdS5×S5com todos os seus campos

originais.

2.3 Supersimetria e espaços curvos

Para obter o setor bosônico de uma solução clássica da teoria de supergravidade, os férmions do espectro, o gravitinoΨµ e o dilatino λ, são tomados iguais a zero. Isto

signica que as suas transformações de supersimetria são nulas, ou seja,

δΨµ = 0 (2.41)

δλ = 0.

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 20 na solução. Para que uma solução da teoria de supergravidade preserve alguma su-persimetria, é necessário que as transformações do gravitino e do dilatino se anulem não trivialmente, ou seja, sem que o espinor de Killing² seja identicamente nulo. A transformação do gravitino é a equação mais importante para a contagem de super-simetrias de uma solução da teoria de supergravidade, e é conhecida por equação de Killing espinorial. Esta transformação é a derivada covariante de um espinor à qual são adicionados outros termos além da conexão de spin. Simplicadamente,

δΨµ=Dµ²= (∂µ+ Ωµ)², (2.42)

onde² é um espinor que parametriza a transformação de supersimetria e Ωµ é uma

conexão generalizada que depende tanto da conexão de spin como dos campos ten-soriais da supergravidade. Resolver a equação (2.42) é equivalente diagonalizar um operador. Para isso, esta precisa ser escrita como

(∂µ+λµI)² = 0, (2.43)

onde λµ é o autovalor associado à matriz Ωµ e I é a matriz identidade. Podemos

considerar (2.42) como uma derivada generalizada ou supercovariante. Para resolver a equação δΨµ = 0, é preciso determinar tanto a expressão funcional como a base

vetorial de ². Porém, para a contagem das supersimetrias, basta a determinação da dimensão da base vetorial para ². Isto pode ser feito através da resolução di-reta da equação de Killing espinorial, mas também é possível fazer a contagem das supersimetrias a partir das condições de integrabilidade de equação de Killing espi-norial. As condições de integrabilidade são denidas analogamente ao caso de uma variedade diferenciável, em que o comutador de duas derivadas covariantes dene a curvatura do espaço. O comutador de duas derivadas supercovariantes gera uma curvatura generalizada, ou supercurvatura

D[µDν]²=RµνabΓab =

¡

∂[µΩν]+ Ω[µΩν]

¢

²= 0, (2.44) sendo os índices gregos para o espaço-tempo e os latinos para o espaço tangente,

Γab _{o produto antisimetrizado de duas matrizes de Dirac no espaço-tangente de}

dez dimensões eRµνab um tensor covariantizado obtido do comutador de derivadas

supercovariantes. A resolução das equações (2.44) determina um espaço vetorial cuja base é constituída pelos espinores de Killing ² e cuja dimensão é o número de supercargas preservadas. Uma outra maneira de determinar o número de supersi-metrias é através do grupo de simetria da conexão generalizadaΩµ, chamado grupo

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 21 preservadas e o grupo de holonomia, de maneira que, dado o grupo de holonomia, determina-se o número de supersimetrias. Este método, contudo, não será explorado nesta tese. Vejamos então dois exemplos de contagem de supersimetrias através da determinação da dimensão da base vetorial do espinor de Killing.

2.3.1 Supersimetria em

AdS

×

S

A transformação de supersimetria para o gravitino de AdS5 × S5 no quadro de

Einstein [48] é

δΨµ=

µ

∂µ+

1 4 6ωµ−

i

1926Fµ

¶

², (2.45)

onde

6ωµ = ωµabΓab e 6Fµ =FµabcdΓabcd.

Tomemos por exemplo o caso µ = t. Nesta situação, a única conexão não nula é ωt04 = 1_z, e a componente da forma RR relevante éFt1234 = 4_z.Feitas as substituições

em δΨµ= 0, chegamos a

∂t²+

1 2z

¡

Γ0 ₋iΓ1Γ2Γ3¢

Γ4²= 0. (2.46) Em analogia a (2.43), o autovalor do segundo termo de (2.46) é λt = 0 e portanto

qualquer espinor constante de 32 componentes satisfaz a equação. O mesmo se aplica a todas as outras nove coordenadas. Ou seja, o número de supercargas nesta solução é 32, e isto signica que todas as supersimetrias possíveis são preservadas. O mesmo resultado pode ser obtido através da condição de integrabilidade (2.44)

1

2RµνabΓ

a_Γb_²+ i

8

µ

∂[µFν]abcdΓaΓbΓcΓd+

1

4ω[ν abFµ]cdef

£

ΓaΓb, ΓcΓdΓeΓf¤ ¶

²₋

− 1

64FµabcdFνef gh

£

ΓaΓbΓcΓd, ΓeΓfΓgΓh¤

²= 0,

(2.47) sendo Rµνab o tensor de Riemann. A equação (2.47) fornece a mesma informação

obtida da equação de Killing (2.46), porém mais laboriosamente.

2.3.2 Supersimetria em

R

deformado

Este caso é um pouco mais complicado que o anterior, dada a existência do campo anti-simétrico de Kalb-Ramond, B2. A transformação do gravitino no quadro de

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 22

δΨµ =

Ã

∂µ+

1 46ωµ−

1

86Hµσ3+

eΦ

16

X

n=1,...5

1

(2n₋1)!6F2n−1ΓµPn

!

² (2.48)

onde

Pn = σ1para npar,

Pn = iσ2 para nímpar,

σi são matrizes de Pauli e 6Hµ = HµabΓab. O espinor ² tem 32 componentes e é

dividido em duas partes de 16 componentes para que as matrizes de Pauli atuem, ou seja, ² = Ã ²1 ²2 ! ,

onde²i=1,2 têm 16 componentes. Para resolver a equação (2.48), utilizamos as

coor-denadas

(xµ, ya) = ©

(x0, y0), (xi, yi), (r1, y4), (r2, y5),

(r3, y6), (φ1, y7), (φ2, y8), (φ3, y9)

ª

,

onde as coordenadasxµ_{são do espaço-tempo,y}a_{são do espaço tangente ei= 1, 2, 3.}

A métrica (2.35) permite escrever a seguinte tetrada para o setor não diagonal



 

eφ1 7 e

φ1 8 e

φ1 9

eφ2 7 e

φ2 8 e

φ2 9

eφ3 7 e φ3 8 e φ3 9   =    1

r1 γr2 −γr3

−γr1 _r1₂ γr3

γr1 −γr2 _r1₃





. (2.49)

A 3-forma e a conexão de spin podem ser escritas como

1 2



 

H478 H479 H489

H578 H579 H589

H678 H679 H689

   =   

ωr178 ωr179 ωr189

ωr278 ωr279 ωr289

ωr378 ωr379 ωr389





= (2.50)

=



 

γr2(1 +γr32)G −γr3(1−γr22)G 0

γr1(1−γr32)G 0 γr3(1 +γr21)G

0 ₋γr1(1 +γr22)G γr2(1−γr21)G



 .

CAPÍTULO 2. TEORIAS DE SUPERGRAVIDADE 23

µ

1

4RµνabΓ

ab

− 1

8∂[µ 6Hν]σ3− 1

16ω[µ6Hν]σ3+ 1

646H[µ6Hν]

¶

² = 0. (2.51) Esta é uma equação de autovalores, e como as equações são longas e cremos que não iluminam a copreensão do resultado, não as escreveremos. A única situação onde há uma solução onde o espinor está restrito a um espaço vetorial de dimensão menor que 32 ocorre para µ=ri e ν=φj. Neste caso, o espaço vetorial do espinor

Capítulo 3

Cordas em espaços não-deformados

3.1 Introdução

Comos discutido na seção 2.1, a correspondência AdS/CF T arma que a teoria de cordas IIB em AdS5 ×S5 é equivalente, ou dual, à teoria de SYM em D = 4

dimensões e comN = 4 supersimetrias. O espectro de energia da teoria de cordas é

igual ao espectro do operador de dilatação para operadores invariantes de calibre de SYM. Esta correspondência também se baseia, dentre outros fatos, que os estados

|Ski da teoria de cordas são duais aos operadores OK da teoria de SYM e que os

parâmetros das teorias estão relacionados por

gs =

g2

Y M

4π e λ=

R4

α′2,

onde R é o raio de AdS5 ×S5, α′2 = ℓs com ℓs o comprimento da corda, gs é a

constante de acoplamento da teoria de cordas, gY M é a constante de acoplamento

de SYM e N é a ordem do grupo da simetria de calibre de SYM. O parâmetro λ = g2

Y M N de `t Hooft [50] deve ser usado na expansão perturbativa da teoria de

calibre.

No limite de baixas energias da teoria de cordas, ou seja, na teoria de supergra-vidade emAdS5×S5, a curvatura do espaço é pequena e o raio do espaço AdS5×S5

é grande. Isto é,λ_À1 e não pode ser utilizado como parâmetro de expansão para

uma série perturbativa na teoria de calibre. Neste regime, o espectro do operador de dilatação de SYM pode ser obtido da teoria de cordas dual.

Por outro lado, a teoria de SYM é uma teoria de campos conforme e esta simetria tem um operador de dilatação associado. O autovalor∆é a dimensão do operador,

dada por

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 25

∆ = ∆0+ ∆K,

onde∆0 é a dimensão clássica do operador e∆K é a dimensão anômala, esta última

correspondente à correção quântica do valor clássico. A correspondência entre os espectros das teorias duais equivale à igualdade entre a energia Ek dos estados |Ski

da teoria de cordas e a dimensão anômala ∆K dos operadores de dilatação de uma

teoria de calibre conforme [7]. Explicitamente,∆K(λ, N) =Ek(R

2

α′, gs).

No limite planar [51], em que N → ∞, o operador dilatação assume a forma de

uma hamiltoniana de uma cadeia de operadores de spin [7]. Se o operador dilatação no limite planar é interpretado como uma hamiltoniana, a dimensão anômala neste limite é interpretada como a energia da cadeia de spins. Além disso, como a hamil-toniana atua sobre cadeias de spin, os operadores de teoria de calibre OK, onde o

operador dilatação atua, podem ser visualizados como cadeias de spins. A hamil-toniana que atua sobre uma cadeia de spins é diagonalizada, por exemplo, usando o método do ansatz de Bethe algébrico [8], e está fora do escopo desta tese. Um operador de SYM escrito como

OK ≡trZJ, (3.1)

comJ campos escalares complexos Z, é visualizado como uma cadeia de spin ferro-magnética, onde todos os spins, representados por Z, têm a mesma orientação. Para o caso em queJ é grande, a dimensão anômala é [7]

∆n=J+ 2

r

1 + λn

2

J2 , (3.2)

onde n _∈ R. O operador (3.1) é o caso mais simples possível, mas não é o único

conhecido. A introdução de um segundo campo possibilita duas orientações para o spin. Um operador deste tipo é

Op ∼

X

l

eilp(· · ·ZZW Z· · ·), (3.3) onde l é a posição do campo W no operador e p_∈R.

Estes resultados da teoria de calibre têm, através da correspondênciaAdS/CF T, uma interpretação em termos de teoria de cordas. A teoria de calibre de SYM em D= 4 dimensões e N = 4 supersimetrias é dual a uma teoria onde a corda realiza

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 26 a

J, N _{→ ∞} com J

2

N =constante. (3.4) A geometria observada por uma corda nestas condições é a de uma onda plana gravitacional, que é o limite de Penrose deAdS5×S5. Neste espaço, a quantização

da corda livre é possível no calibre do cone de luz [52], resultado que reproduz a expressão (3.2) obtido na teoria de calibre.

A correspondência entre cordas em movimento e operadores de SYM análogos a cadeias de spin foi explorada em operadores diferentes de (3.1). Pequenas variações nesta cadeia geram correções na dimensão anômala que também são observadas na energia da corda, pois estas quantidades são iguais. Para um número de camposW muito inferior ao de Z, temos uma cadeia formada por Z dopada com W, que é a impureza da cadeia. A dimensão anômala associada a (3.3) nessas condições é uma correção da dimensão anômala da cadeia pura (3.1). A soma sobre as posições de W permite que o operador represente uma cadeia cujas impurezas propagam-se em movimento uniforme com momento p. Estas impurezas são chamadas mágnons e possuem, a relação de dispersão [53],

E₋J =

r

1 + λ

π2sen2

p

2. (3.5)

No limite em que é λ grande, a relação de dispersão (3.5) é obedecida também na teoria de cordas dual. Neste caso, temos cordas que giram rapidamente e satisfazem a prescrição de Hofman e Maldacena

E, J _{→ ∞}, λ=g_{Y M}2 N =xo, p=xo e E₋J =xo (3.6)

Os mágnons da teoria de calibre têm como dual deformações que se deslocam ao longo da corda em rotação. Estas deformações se deslocam ao longo do comprimento de uma corda extendida sobre uma dimensão compacta e são chamados de mágnons gigantes [9]. Assim, (3.6) é a condição a ser observada para determinar se uma solução clássica de cordas em movimento apresenta a existência de mágnons gigantes. É importante salientar que E −J é um valor nito e não nulo. Se a relação de dispersão da teoria de cordas é E−J = 0com E, J → ∞, esta teoria não conterá

mágnons gigantes. O operador da teoria de calibre dual é (3.1).

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 27 descrição dual para operadores

O =tr¡

Dl1

+Φ1· · · D+lnΦn

¢

, (3.7)

onde li é o número de derivadas covariantes D+ sobre os campos escalares Φi, com

i = 1, . . . , n e o índice + signica que a coordenada correspondente está escrita

em coordenadas do cone de luz, x_± = 1/√2(x0 ±x1). Se li À n ≥ 1 haverá n

pontos singulares sobre a corda dual ao operador (3.7). Estes pontos singulares estão localizados nas extremidades de picos, ou farpas, da corda. Os operadores do tipo (3.7) foram identicados com cordas que se movimentam no espaçoAdS5. Para

cordas que se movimentam na esfera de AdS5 ×S5, a interpretação em termos de

teoria de campos não é clara [23], mas existem hipóteses que consideram o setor de calibre em termos de férmions livres num modelo de Hubbard [11]. Apesar da denição da teoria de calibre dual a uma corda farpada na esfera deAdS5×S5ser um

problema aberto, existe uma prescrição para uma corda mono-farpada innitamente enrolada numa coordenada da esfera. A corda está no equador e o pico aponta para o pólo da esfera. A energia da corda satisfaz a relação [23]

E₋

√

λ

2π∆φ=

√

λ π

³π

2 −θ

´

com E, ∆φ_{→ ∞}, (3.8) onde o ângulo θ é a direção polar de um sistema esférico de coordenadas e fornece a altura do pico da corda e∆φ é o ângulo de décit. O momento angular para uma corda farpada em S3 _{é dado por [24]}

J1 =

r

J2 2 +

λ

π2 cos2θ. (3.9)

Para estudar a dinâmica de cordas em movimento utiliza-se uma ação para gerar as equações de movimento. A ação da teoria de cordas pode ser obtida por analogia com a ação de uma partícula livre

S = −m

Z

ds (3.10)

onde ds = p

−g_µνdXµ_dXν, com _{µ = 0}, . . . , D, é a trajetória da partícula num

espaço-tempo (D+ 1)-dimensional de métrica gµν e coordenadas Xµ. Se uma

par-tícula descreve uma linha ao deslocar-se no espaço tempo, uma corda varre uma superfície, e então generaliza-se (3.10) para uma superfície (1 + 1)-dimensional, a

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 28

SN G = −T

Z

dτ dσ√₋h, (3.11) é conhecida como ação de Nambu e Goto. Em (3.11) T é uma constante necessária para que a ação seja adimensional e será interpretada como a tensão na corda. O radicando hé o determinante da métrica sobre a folha-mundo, tal que

h = dethab, hab =gµν∂aXµ∂bXν e a, b= 1, 2.

A ação de Nambu e Goto pode ser reescrita de maneira a eliminar a raiz quadrada e gerar a ação de Polyakov

SP =−

T

2

Z

dτ dσ√₋hhabgµν∂aXµ∂bXν. (3.12)

A nulidade do traço do tensor energia momento gera a partir de (3.12) os vínculos de Virasoro

gµν∂τXµ∂σXν = 0 (3.13)

gµν(∂τXµ∂τXν+∂σXµ∂σXν) = 0.

Finalmente, é preciso acoplar à ação de Polyakov o campo de Kalb-Ramond,Bµν

e a forma mais geral para (3.12) é

SP = −

T

2

Z

dσdτ√₋h¡

habgµν∂aXµ∂bXν−²abBµν∂aXµ∂bXν

¢

. (3.14)

onde ²ab _{é um tensor antisimétrico tal que ²}12_{= 1 e²}11_=²22_{= 0.}

3.2 Corda em rotação

Nesta seção será abordado o caso discutido por Frolov e Tseytlin [14, 15] e resumida por Plefka [7], no qual uma corda realiza um movimento de rotação no setor esférico S5 _{de AdS}

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 29

t = κτ (3.15)

ρ = 0

θ = π/2

ψ = ψ(σ)

φ1 = ω1τ

φ2 = 0

φ3 = ω3τ.

onde κ é constante, θ, ψ ∈ [0, π/2] e φi=1,2,3 ∈ [0, 2π] são as coordenadas de S5 e

ρ é a coordenada radial de AdS5. A escolha de ρ = 0torna desnecessária a escolha

de um ansatz para as demais coordenadas de AdS5 como pode ser visto em (B.11).

Nesta conguração, a única coordenada a ser determinada éψ, a qual dene a forma da corda. A ação de Polyakov (3.14) com Bµν = 0, se torna

I0 =−

√

λ

4π

Z

dσdτ³t˙2+ψ′2

−cos2ψφ˙2₁₋sen2ψφ˙2₃´, (3.16)

sendo_φ˙_{i =∂τφi. Antes de discutir a dinâmica decorrente de (3.16), vejamos as suas}

duas simetrias. A primeira é

ψ → ±ψ±nπ; n∈Z (3.17)

e a segunda,

ψ _{→ ±}ψ_±π/2 e φ1 ↔φ3. (3.18)

Estes resultados serão úteis para a discussão das soluções das equações de movi-mento. Determinadas as simetrias, vejamos a equação de movimento paraψ obtida da variação da ação (3.16), que é

ψ′′_{+senψcosψ(ω}2

3 −ω12) = 0, (3.19)

onde ψ′ _=∂

σψ. Somente um dos vínculos de Virasoro (C.6) para a proposta (3.15)

é não trivial,

−κ2_+ψ′2_+ω2

1cos2ψ+ω23sen2ψ = 0. (3.20)

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 30 (3.19) e pela equação de vínculo (3.20), vamos calcular as quantidades conservadas da corda em rotação. A energia E e os momentaJi são obtidos de

E = ∂L

∂t˙ (3.21)

Ji = −

∂L ∂φ˙i

.

De acordo com a ação (3.16), obtemos

E =

√

λ

2πκ

2π

Z

0

dσ (3.22)

J1 = ω1

√

λ

2π

2π

Z

0

dσcos2ψ (3.23)

J3 = ω3

√

λ

2π

2π

Z

0

dσsen2_{ψ. (3.24)}

As quantidades (3.23) e (3.24) permitem estabelecer a relação

√

λ= J1

ω1

+ J3

ω3

. (3.25)

A equação (3.19) mostra que existem dois casos a serem considerados para a corda girante (3.15). No primeiro, a mesma velocidade angular é idêntica para ambos os eixos de rotação, e no segundo estas são diferentes. Estes casos são discutidos nas seções (3.2.1) e (3.2.2).

3.2.1 Rotações com velocidades angulares idênticas

Neste caso, as velocidades angulares nas coordenadasφi=1,3 são iguais, ouω1 =ω3 =

ω, e a equação para ψ será

ψ′′ _{= 0. (3.26)}

A solução de (3.26) é, evidentemente,

ψ =P σ+Q, (3.27)

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 31 periodicidade

ψ(σ+ 2π) =ψ(σ) + 2nπ, n_∈N_. (3.28)

obtemos que a corda é circular e dánvoltas na coordenadaψ. Esta condição admite xarP =n eQ= 0. A primeira identicação decorre da possibilidade de múltiplos

enrolamentos da corda sobre a direção ψ. A segunda se justica pela equivalência dos pontos da corda, ou seja, sempre é possível escolher um ponto arbitrário da corda como a origem da coordenada σ. Com ψ =nσ, o vínculo de Virasoro (3.20) implica em

κ2 =n2+ω2. (3.29) As equações (3.29) e (3.25) permitem calcular a relação de dispersão para a corda circular

E = 2J

r

1 + n

2_λ

4J2. (3.30)

onde J =J1 =J3 é o momento angular da corda.

3.2.2 Rotações com velocidades angulares diferentes

ψ′′_{+senψcosψ(ω}2

3 −ω12) = 0. (3.31)

Através da substituição ψ′′_=ψ′_∂

ψψ′, podemos integrar (3.31), obtendo

ψ′2+ω₁2cos2ψ +ω₃2sen2ψ =A, (3.32) sendo A a constante de integração. O vínculo (3.20) impõe A = κ2_{, e então a}

equação a ser resolvida é

ψ′2 _=κ2

−ω₁2₋(ω2₃₋ω₁2)sen2ψ. (3.33) Ambos os lados de (3.33) devem ser quantidades reais e positivas, de acordo com os valores das constantesκ2_{, ω}2

1 e ω23. Para classicar as regiões do domínio de ψ onde

ψ′2 _{≥0, denamos o parâmero}

q= κ

2_−ω2 1

ω2 3 −ω12

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 32 Consideram-se os casos em que q > 1 e q _≤ 1. Se q > 1, ψ′2 _{em (3.33) é}

estrita-mente positivo ou estritaestrita-mente negativo. O caso positivo signica que a corda pode estar em qualquer ponto do domínio de ψ, e portanto a corda é circular. No caso estritamente negativo, não existem valores de ψ que tornem o membro direito de (3.33) positivo, e portanto ψ′ _{é imaginário puro e sem interpretação física.}

Por outro lado, se q ≤ 1 o domínio de ψ contém regiões onde ψ′2 _{é positivo e}

onde ψ′2 _{é negativo. Os valores de ψ onde ψ}′2 _{se anula são os pontos extremos}

do intervalo. A região entre os pontos extremos do intervalo, onde ψ′2 _{≥ 0, será}

considerada para a pesquisa de soluções físicas. Como esta exigência não se cumpre em todo o domínio de ψ, a circunferência em torno desta coordenada não pode ser completada sem violar a exigência de realidade paraψ′_{. Portanto a corda não é}

circular, mas está dobrada sobre a região ondeψ′2 _{≥0. Esta classicação preliminar}

em termos de q pode ser detalhada em termos de κ e ωi=1,3. Veremos que os casos

estão divididos em corda cicular, corda dobrada e casos não-físicos. Vejamos cada um deles.

Será mais fácil analisar as possibilidades através da representação gráca das regiões de positividade deψ′2_{. Para isso, seja}

ψ′2 =κ2 −ω₁2−(ω2₃ −ω₁2)x2. (3.35) O gráco da equação (3.35) corresponde ao de (3.33) para x ∈[−1, 1]. As relações entre as constantes e o respectivo esboço do gráco paraψ′2 _são:

a. Corda circular a1. κ2 _{> ω}2

3 > ω12

-2 -1 1 2 x

y

PSfrag replacements x

(ψ′₎2

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 33

-1 -0.5 0.5 1 x y

PSfrag replacements x

(ψ′₎2

b. Corda dobrada b1. ω2

3 ≥κ2 > ω21

-1 -0.5 0.5 1 x y

PSfrag replacements x

(ψ′₎2

b2. ω2

1 > κ2 ≥ω23

-1 -0.5 0.5 1 x y

PSfrag replacements x

(ψ′₎2

c. Casos não-físicos c1. ω2

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 34

-1.5 -1 -0.5 0.5 1 1.5 x y

PSfrag replacements x

(ψ′₎2

c2. ω2

3 > ω12 > κ2

-2 -1 1 2 x

y

PSfrag replacements x

(ψ′₎2

Utilizamos agora as simetrias (3.17) e (3.18) para determinar as situações sica-mente equivalentes. A troca de índices, tal que ω1 ↔ω3, leva o caso a1 no caso a2.

Esta troca, acompanhada da translação ψ _→ψ _±π/2, é a simetria (3.18) da ação.

O efeito da aplicação desta simetria sobre a solução da corda circular é intercambiar as velocidades angulares entre as coordenadas sem alterar a sua forma.

No caso b1, que representa a corda dobrada, a região deψ′2 _{positivo vale tanto}

para ψ no intervalo ψ ∈ [ψ0, −ψ0] como para ψ ∈ [π −ψ0, π +ψ0]. Da mesma

forma, o caso b2 é válido tanto paraψ ∈[ψ0, π−ψ0]como paraψ ∈[π+ψ0, −ψ0].

Aparentemente é possivel a existência de duas cordas em cada caso. Porém, uma das simetrias da ação é ψ → ±ψ ± π, de maneira que os dois intervalos onde a

solução é possível estão relacionados. Logo, existe uma única corda para cado caso. Finalmente, os casos b1 e b2 estão relacionados pela simetria (3.18), que muda a posição da corda emψ e troca a velocidade angular dos eixos de rotação sem alterar a forma da corda. Assim, temos somente dois casos, a corda circular e a corda dobrada. Para calcular a energia e os momenta, reescrevemos (3.33) como

dσ = p dψ

κ2_−ω2

1−(ω32−ω21)sen2ψ

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 35 A relação (3.36) substituída em (3.22) permite escrever a energia e os momenta em termos de integrais elípticas. As denições e os respectivos resultados das integrações a serem usados na seqüência foram obtidos em Byrd e Friedman [54]. As denições das integrais elípticas utilizadas estão resumidas no Apêndice D.

a. Corda circular

De (3.22), encontramos

E = 2

√

λ π

κ

p

κ2_−ω2 1

K(k) (3.37)

J1 =

2√λ π

ω1

ω2 3 −ω12

1

p

κ2_−ω2 1

£¡

κ2−ω₁2¢

E(k)−¡

κ2−ω2₃¢

K(k)¤

J3 =

2√λ π

ω3

ω2 3 −ω12

q

κ2_−ω2

1[K(k)−E(k)],

onde k = qω23−ω21

κ2_−ω2

1 < 1 e K(k) e E(k) são integrais elípticas completas de primeira

e segunda espécies. No caso da corda circular, podemos classicar os parâmetros em duas possibilidades, κ2 _{> ω}2

3 > ω12 ou ω12 > ω32 > κ2. A primeira gera a corda

circular, como visto na gura a1. A segunda possibilidade é um caso não-físico.

b. Corda dobrada

Para a corda dobrada, os resultados são

E = 2

√ λ π κ p ω2 3−ω12

K(senψ0) (3.38)

J1 =

2√λ π

ω1

p

ω2 3−ω12

E(senψ0)

J3 =

2√λ π

ω3

p

ω2 3−ω12

[K(senψ0)−E(senψ0)],

onde

sen2_ψ 0 =

κ2_−ω2 1

ω2 3 −ω21

. (3.39)

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 36 assumem os seguintes valores:

E, J3 → ∞ (3.40)

J1 → ω1

√

λ E₋J3 =

ω3

ω1

J1

Contudo, este resultado não satisfaz todos os requisitos da prescrição de Hofman e Maldacena (3.6). O ângulo de décit para os casos considerados é sempre nulo, e portanto não é possível encontar um mágnon gigante.

3.2.3 Corda com ansatz de Bobev e Rashkov

Uma corda em rotação na esfera deAdS5×S5 pode apresentar um mágnon gigante,

como visto na seção anterior. Entretanto, existem outras situações onde mágnons gigantes e também cordas farpadas podem ser encontrados. Estas possibilidades foram estudadas em diversos trabalhos [19, 23, 24, 25, 26, 27]. Nesta seção, apre-sentamos os resultados obtidos por Bobev e Rashkov [23], que estudaram o caso dos espaços AdS5 ×S5 e de Lunin e Maldacena. Obtemos as equações de movimento

para AdS5×S5 fazendo γˆ2 = 0 em (C.9), (C.10), (C.11), (C.12) e (C.13), que

des-crevem o modelo deformado de Lunin e Maldacena. Para um ansatz onde φ3 = 0 e

ψ = 0, as equações de movimento são

∂a(sen2θ∂aφ1) = 0 (3.41)

∂a(cos2θ∂aφ2) = 0 (3.42)

2∂a∂aθ−(sen2θ)θ∂aφ1∂aφ1−(cos2θ)θ∂aφ2∂aφ2 = 0 (3.43)

onde a= 1, 2. Os vínculos de Virasoro são

−∂τt∂σt+∂τθ∂σθ+sen2θ∂τφ1∂σφ1+ cos2θ∂τφ2∂σφ2 = 0 (3.44)

−(∂τt)2−(∂σt)2+ (∂τθ)2+ (∂σθ)2 + (3.45)

+sen2_θ£

(∂τφ1)2+ (∂σφ1)2

¤

+ cos2_θ£

(∂τφ2)2+ (∂σφ2)2

¤

= 0.

Nesta situação, Bobev e Rashkov utilizaram o ansatz adicional

t =κτ, θ =θ(y), φi=1,2 =ωiτ + ˜φi(y), (3.46)

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 37

−ω1β(sen2θ)y + (α2−β2)(sen2θφ˜1, y)y = 0, (3.47)

onde os índices y indicam derivada nesta variável. Esta equação pode ser imediata-mente integrada, e a equação paraφ2 idem. Assim,

˜

φ1y =

1

α2_−β2

µ

ω1β+

A sen2_θ

¶

(3.48)

˜

φ2y =

1

α2_−β2

µ

ω2β−+

B

cos2_θ

¶

onde A e B são constantes de integração. A equação de movimento para a coorde-nada θ é obtida da soma dos vínculos (3.44) e (3.45). Substituem-se as expressões (3.48) a esta soma para obter

θ2y =

1 (α2_−β2₎2

· ¡

α2+β2¢

κ2− A

2

sen2_θ −

B2

cos2_θ− (3.49)

− α2¡

ω2₁sen2θ+ω₂2cos2θ¢¤

Este resultado pode ser obtido também da integração direta da equação de movi-mento para θ (3.43). A substituição de (3.48) na diferença das equações de vínculo (3.44) e (3.45) permite relacionar as constantes de integração aos demais parâmetros

ω1A+ω2B+κβ = 0. (3.50)

Podemos agora calcular as cargas

E = 2T κ

α

θ1

Z

θ0

dθ

θy (3.51)

J1 =

2T α θ1 Z θ0 dθ θysen

2_θ(ω

1+βφ˜1y)

J2 =

2T α θ1 Z θ0 dθ θy

cos2θ(ω2+βφ˜2y).

Seφ2 = 0, o movimento está restrito a S2 e as equações a serem resolvidas são

˜

φ1y =

β α2_−β2

ω1

sen2_θ(sen 2_θ−t2

1) (3.52)

θy =

αω1

α2_−β2

1 sinθ

q

(sen2_θ−t2

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 38 onde

t2 1 =

κ2

ω2 1

e t2 0 =

β2_κ2

α2_ω2 1

.

O radicando de (3.53) deve ser positivo, e θ_∈[0, π/2] não assume necessariamente

todos os valores do seu domínio. As possibilidades são: 1. t2

0, t21 > 1, onde o radicando é sempre negativo, e não há nenhum caso

sicamente interessante. 2. t2

0 ≤ 1, t21 > 1, ou vice-versa. Neste caso o radicando é positivo para

θ _∈[θL, π−θL]ou paraθ ∈[−θL, θL], sendo θL=arcsent0 o ponto onde

o radicando se anula. 3. t2

0, t21 ≤1, onde o radicando será positivo paraθ ∈[θL, θM],onde senθL =

t0 e senθM =t1.

Estudemos o caso 3, tal como feito em [23]. Faremos t = senθ, t0 = senθ0 e

t1 =senθ1. Substituímos (3.52) e (3.53) em (3.51) para encontrar a energia E(k) e

o momento angularJ1(k)

E(k) = 2T κ

ω1

α2_−β2

α2

K(k)

cosθ0 (3.54)

J1(k) =

α2_−β2_sen2_θ 1

α2 _−β2

E(k)

senθ1 −

2Tcosθ0, sendo k2 =

cos2_θ

0−cos2θ1

cos2_θ 0

.

Nesta situação, se θ1 =π/2, obtemos que

E−J1 = 2T cosθ0 (3.55)

J1, E → ∞

Este resultado mostra que a prescrição de Hofman e Maldacena (3.6) é satisfeita, e portanto temos um mágnon gigante. Também é possível encontrar cordas farpadas. Para isso, calculamos o ângulo de décit∆φ1 num instante determinado de tempo,

ou seja, ondedτ = 0. Nestas condições de acordo com (3.46), dφ1 =dφ˜1, portanto

∆φ1 =

b

Z

a

dφ1 =

b

Z

a

dyφ˜1y = 2

Z θ1

θ0

dθ θy

˜

φ1y. (3.56)

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 39

∆φ1 =

2β α

1 cosθ1

·

K(k)₋ 1 cos2_θ

0

E(k)

¸

, (3.57)

onde k2 ₌ cos2_θ

1−cos2θ0

cos2_θ1 e E(k) é a integral elíptica completa. Se θ0 = π/2, (3.57)

diverge. Este resultado permite construir as quantidades

J1 =

√

λ

π cosθ1 (3.58) E₋T∆φ1 =

√

λ π

³π

2 −θ1

´

. (3.59)

Ou seja, a energia E e o enrolamento da corda∆φ1 são divergentes, mas mantêm a

relação (3.59) nita. Além disso, o momentoJ1também é nito. Estes fatos

demon-stram que, no limite θ0 =π/2, obtém-se a corda farpada. Os mesmos resultados de

corda farpada e mágnon gigante podem ser obtidos para o caso 2.

3.3 Corda oscilante

Esta solução consiste de uma corda cuja oscilação ocorre numa ou mais coordenadas. Na primeira proposta formulada [16], a pulsação ocorre numa única coordenada, porém a pulsação simultânea em mais coordenadas foi trabalhada, por exemplo, em [17, 18]. Cordas em pulsação e rotação foram estudadas em [19, 20, 21]. Nesta seção, estudaremos cordas oscilantes de acordo com [16].

3.3.1 Corda oscilante no espaço plano

O movimento da corda se dá no setor do espaço R1,9 de métrica

ds2 =₋dt2+dr2+r2dθ2. (3.60) A dinâmica da corda será descrita com as coordenadas

t = τ (3.61)

r = r(τ)

θ = mσ,

onde m é o número de voltas da corda na coordenada θ. A ação de Polyakov para este ansatz é

S=₋

√

λ

4π

Z

dσdτ( ˙t2_−r˙2_+θ′2_),

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 40

¨

r+rm2 = 0. (3.62) O vínculo de Virasoro para o movimento é

˙

r2+r2m2 = 1.

A equação de movimento na coordenada r caracteriza classicamente um oscilador. Para quantizar o movimento, é mais conveniente utilizar a ação de Nambu e Goto,

S =₋ 1 2πα′

Z

dσdτq₋det(∂aXµ∂bXµ), (3.63)

pois ela encerra toda a dinâmica do sistema, sem a necessidade de vínculos. Depois de substituído o ansatz (3.61) para as coordenadas, a ação (3.63) se torna

S =₋ m 2πα′

Z

dσdτ r√1₋r˙2_. (3.64)

O momento canônico da coordenada r, será

Πr=

m α′

rr˙

√

1₋r˙2, (3.65)

e a hamiltoniana,H = Πrr˙−L ,

H =

r

Π2

r+

m2_r2

α′2 . (3.66)

A hamiltonianaH2 _{descreve um oscilador harmônico radial, cuja energia quantizada}

é

E_n2 = (2n+ 1)2m

α′ . (3.67)

3.3.2 Corda oscilante na esfera de

AdS

×

S

O setor relevante da métrica é

ds2 =₋R2¡

−cosh2ρ dt2+dρ2+dθ2+sen2θ dφ2¢

, (3.68) e a ação de Polyakov,

A= T 2

Z

dτ dσ¡

−cosh2ρ∂at∂at+∂aρ∂aρ+∂aθ∂aθ+sen2θ∂aψ∂aψ

¢

CAPÍTULO 3. CORDAS EM ESPAÇOS NÃO-DEFORMADOS 41 gera as seguintes equações de movimento

∂a(coshρ ∂at) = 0 (3.70)

∂a∂aρ+

1 2(cosh

2_ρ)

ρ∂at∂at = 0 (3.71)

∂a∂aθ−

1 2(sen

2_θ)

θ∂aψ∂aψ = 0. (3.72)

Propõe-se o ansatz

t=τ ρ=ρ(τ) θ =θ(τ) ψ =mσ. (3.73) A corda está localizada ao longo de ψ _∈ [0,2π], e o seu enrolamento nesta direção

pode ser múltiplo. A oscilação ocorre em θ ∈ [0, π/2]. A coordenada radial do

espaço AdS5, ρ ∈ [0,∞) também terá, a princípio, dependência temporal. Porém,

a equação de movimento (3.70) implica queρ deve ser constante. Isso signica que, no calibre temporal escolhido, a oscilação nesta coordenada não é visível. A solução clássica pode ser encontrada no calibre

˙

t = 1

coshρ, (3.74)

onde a oscilação na coordenada ρ é vericada [55]. Em todo caso, a dependência temporal em ρ é mantida para detectar possíveis utuações quânticas. Assim, a única equação para evolução temporal clássica, após o uso do vínculo

−cosh2ρ+ ˙ρ2+ ˙θ2+sen2θψ′2 _{= 0 (3.75)}

será

˙

θ2 = cosh2ρ−m2sen2θ. (3.76)

Esta equação permite solução em termos de integrais elípticas, de maneira que

F

µ

θ, m

coshρ

¶

= coshρ(τ₋τ0) ; coshρ > m(3.77)

F

µ

arcsen

µ

m

coshρsenθ

¶

, coshρ m

¶

= m

coshρ(τ −τ0) ; coshρ < m, onde τ0 é a constante de integração. A integral elíptica F(ϕ, k) é uma função