Existência de soluções estacionárias estáveis para equações de reação-difusão com condição de fronteira de Neumann não-linear: condições necessárias e condições suficientes.

(1)

CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE P ÓS-GRADUAÇ ÃO EM MATEM ÁTICA

Existˆ

encia de solu¸c˜

oes estacion´

arias est´

aveis

para equa¸c˜

oes de rea¸c˜

ao-difus˜

ao com condi¸c˜

ao

de fronteira de Neumann n˜

ao-linear: condi¸c˜

oes

necess´

arias e condi¸c˜

oes suficientes

Renato Jos´e de Moura

(2)

CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE P ÓS-GRADUAÇ ÃO EM MATEM ÁTICA

Existˆ

encia de solu¸c˜

oes estacion´

arias est´

aveis

para equa¸c˜

oes de rea¸c˜

ao-difus˜

ao com condi¸c˜

ao

de fronteira de Neumann n˜

ao-linear: condi¸c˜

oes

necess´

arias e condi¸c˜

oes suficientes

Renato Jos´e de Moura

Orientador: Prof. Dr. Arnaldo Simal do Nascimento

Tese apresentada ao Programa de Pós-Gradua¸cão em Matemática da UFS-Car como parte dos requisitos para obten¸cão do t´ıtulo de Doutor em Matemática

(3)

Ficha catalográfica elaborada pelo DePT da Biblioteca Comunitária/UFSCar

M453es

Moura, Renato José de.

Existência de soluções estacionárias estáveis para equações de reação-difusão com condição de fronteira de Neumann não-linear: condições necessárias e condições suficientes / Renato José de Moura. -- São Carlos : UFSCar, 2005.

133 p.

Tese (Doutorado) -- Universidade Federal de São Carlos, 2004.

1. Equações diferenciais parciais não-lineares. 2. Equações de reação e difusão (matemática). 3. Gama-convergência. 4. Equilíbrios estáveis não-constantes. 5. Sistemas dinâmicos. I. Título.

(4)

(5)

Como fazemos para encontr´a-lo?

Quem sabe est´a mais perto do que imaginamos...”

(6)

Agradecimentos

`

A Deus, pelo dom da vida e a Espiritualidade que nunca me desamparou. Ao Programa de Pós-Gradua¸cão em Matemática e ao Departamento de Mate-mática da Universidade Federal de São Carlos, pela oportunidade de realiza¸cão deste trabalho.

Ao Prof. Dr. Arnaldo Simal do Nascimento, pela pronta disposi¸cão na ori-enta¸cão deste trabalho e principalmente a amizade e a oriori-enta¸cão para minha vida.

Aos professores do Departamento de Matem´atica da UFSCar, pela minha forma¸c˜ao e as amizades conquistadas.

`

A CAPES, pelo apoio ﬁnanceiro. `

A Prof. Dra. Neus Cònsul Porras, da Universitat Politècnica de Catalunya, pela indica¸cão do artigo sobre a Gama-convergência, necessário ao Cap´ıtulo 2. Ao Prof. Dr. Antônio Luiz Pereira, pelas sugestões oportunas e corre¸cões a este trabalho.

Aos membros da banca de defesa pública, Prof. Dr. Djairo Guedes de Figuei-redo, Prof. Dr. Antônio Luiz Pereira, Prof. Dr. Marcos Montenegro e Prof. Dr. Hildebrando Munhoz Rodrigues, pelas cr´ıticas e sugestões a este trabalho. Aos membros da banca de qualifica¸cão, Prof. Dr. Ruidival dos Santos Filho e Profa. Dra. Janete Crema, pelas cr´ıticas e sugestões a este trabalho.

Ao Prof. Dr. Gerson Petronilho, meu orientador de mestrado, o qual tenho grande apre¸co e estima. Um exemplo a ser seguido.

(7)

`

As secretárias Célia e Irma, pela amizade e disposi¸cão em sempre nos atender de imediato.

Aos amigos da p´os, pelos momentos e discuss˜oes salutares. Aos familiares que me fortaleceram com seus incentivos.

Aos amigos do Coral São Carlos, por aceitarem minhas “desafina¸cões”. Aos amigos Dimas e Kalé, cujos la¸cos de amizade (além dos cabelos brancos e barriga) se acentuaram em nós nesses últimos anos.

`

A Adriana (uma das pessoas mais importantes em minha vida), por ter me ensinado a “crescer” não só na Matemática mas principalmente como pessoa. Aos amigos Yashiro, Ivan, Jean, Dalton, Harumi e Daisy, pela amizade, apren-dizagem e a oportunidade de crescermos juntos.

`

A minha nova fam´ılia, Octac´ılio, Vera, Elson, Elenise e Pércio, São e Lú (que você nos guie e nos fortale¸ca onde quer que esteja), por me acolherem. Que Deus sempre os ilumine.

(8)

Resumo

(9)

Abstract

(10)

Sum´

ario

1 Introdu¸c˜ao 10

2 Existência de padrões: uma abordagem via Γ-convergência 19

2.1 Apresenta¸c˜ao do problema . . . 19

2.2 Resultados preliminares . . . 23

2.2.1 Medida de Hausdorﬀ e Aplica¸c˜oes Lipschitz . . . 23

2.2.2 Fun¸c˜oes de varia¸c˜ao limitada . . . 24

2.2.3 Conjuntos de per´ımetro ﬁnito . . . 25

2.2.4 Um resumo sobre a Γ-convergˆencia dos funcionais . . . . 27

2.3 O Teorema de De Giorgi . . . 29

2.4 M´ınimos locais isolados dos Γ-limites . . . 33

2.5 Existˆencia de Padr˜oes . . . 45

3 O papel da condi¸cão de igualdade de área na forma¸cão de camadas de transi¸cão interna e superficial 50 3.1 Apresenta¸cão do problema . . . 50

3.2 Hipóteses e defini¸cões . . . 51

3.3 Desenvolvimento de camadas de transi¸c˜ao . . . 54

3.4 Decorrˆencias . . . 67

4 A influência da geometria do dom´ınio na existência de padrões 71 4.1 Apresenta¸cão do problema . . . 71

4.2 Convexidade do dom´ınio: uma condi¸c˜ao necess´aria . . . 72

(11)

5 Existência de padrões: caso espacialmente heterogêneo 81

5.1 Apresenta¸c˜ao do problema . . . 81

5.2 Resultados preliminares . . . 83

5.2.1 Formula¸c˜ao abstrata . . . 84

5.2.2 Existˆencia e regularidade das solu¸c˜oes . . . 85

5.2.3 Propriedades do funcional energia . . . 87

5.3 Conjunto invariante . . . 89

5.4 Estabilidade . . . 94

5.5 Condi¸cões suficientes para a existência de padrões . . . 103

5.5.1 Difusibilidade n˜ao-constante . . . 103

5.5.2 Difusibilidade constante . . . 106

A Uma observa¸cão sobre a Γ-convergência 111 A.1 Γ-Convergência . . . 112

A.1.1 Resultados utilizados . . . 114

A.1.2 Demonstra¸c˜ao do Teorema A.1 . . . 117

(12)

Cap´ıtulo 1

Introdu¸c˜

ao

Neste trabalho estudamos alguns problemas de rea¸cão-difusão com condi¸cão de fronteira de Neumann não-linear e que na sua forma mais geral pode ser escrito como

(P)

          

∂u

∂t = div(a(x)∇u) +f(x, u), (t, x)∈IR

+

×Ω

a(x)∂u

∂ν =g(x, u), (t, x)∈IR

+

×∂Ω u(0, x) = u0(x), x∈Ω,

sendo que Ω _⊂ IRN, N _≥ 2, ´e um dom´ınio limitado com ∂Ω suﬁcientemente regular, ∂

∂ν denota a derivada na dire¸cão normal unitária exterior a ∂Ω. As fun¸cões f(x, u) : Ω_×IR_→IR eg(x, u) :∂Ω_×IR_→IR são suaves e satisfazem algumas condi¸cões de crescimento.

Tais problemas matemáticos servem como modelos fenomenológicos para os conhecidos problemas de rea¸cão-difusão com a propriedade adicional da existência do termo de rea¸cão não-linear na fronteira do dom´ınio. A presen¸ca de tal termo justifica-se, por exemplo, pela presen¸ca de um catalizador agindo na fronteira do dom´ınio. Veja [13, 23].

A existência de solu¸cões estacionárias estáveis não constantes, que por uma questão de brevidade na nota¸cão denominamos por padrões (terminolo-gia esta utilizada em genética populacional), tem sido muito estudada nas ´

(13)

de rea¸c˜ao-difus˜ao dadas por (P). Citamos, entre outros trabalhos, [24, 10, 7, 29, 11, 13].

Motivados por estes trabalhos, uma das questões que norteia nossa investiga¸cão é encontrar condi¸cões envolvendo os termosa(x), f eg,bem como a geometria de Ω,que garantam a existência, assim como a não existência, de padrões para (P).

Lembramos que solu¸cões estacionárias (equil´ıbrios) para o problema (P) são solu¸cões da equa¸cão el´ıptica semi-linear dada por

(Q)

  

div(a(x)_∇u) +f(x, u) = 0, x_∈Ω a(x)∂u

∂ν =g(x, u), x∈∂Ω.

Uma condi¸cão importante para a existência (ou inexistência) de pa-drões para (P) quando a(x) é constante, f(x, u) = f(u) e g = 0 (isto é, não há rea¸cão na fronteira do dom´ınio), foi mostrada nos trabalhos [24, 10]: se Ω é um dom´ınio convexo então (P) não admite padrões. Este resultado também foi mostrado em [11] quando Ω é uma bola de IRN, com g(x, u) = g(u) na fronteira e f = 0 no interior. É importante ressaltar que a demonstra¸cão da autora é diferente das demonstra¸cões de [24] e de [10].

Baseando-se nos trabalhos de [24, 10], mostramos no Cap´ıtulo 4 que se a(x) é constante, f(x, u) = f(u), g(x, u) = g(u) e Ω é um dom´ınio suave, limitado econvexo, então não existem padrõespara o problema (P). Este resultado generaliza os casos acima citados.

Portanto uma pergunta natural que surge é: se Ω não é convexo então (P) sempre possui padrões? Em outras palavras, a não-convexidade também é uma condi¸cão suficiente para a existência de padrões?

A resposta em geral é negativa. Por exemplo, em [24] o autor provou, entre outros resultados, que se Ω é um anel, a(x) é constante e g = 0 então (P) não possui padrões.

(14)

• a(x) constante, f(x, u) = f(u), g(x, u) = b(x)g(u), com f, g fun¸cões suaves e ambas com exatamente três ra´ızes α < 0< β, e b uma fun¸cão suave e estritamente positiva,

então (P) admite padrões desde que Ω seja formado por dois subconjuntos disjuntos e conexos ligados por um estreito canal, e a fun¸cão b, quando for não-constante, satisfa¸ca algumas propriedades, como por exemplo, ser sufi-cientemente grande na fronteira destes subconjuntos. Este tipo de dom´ınio é chamado de “dumbbell” ou “halter” (ou mesmo “osso-de-cachorro”).

Esta particularidade sobre o dom´ınio, que é necessária para a ex-istência de padrões, foi observada inicialmente em [24], o qual estabeleceu, sob determinadas condi¸cões da fun¸cão de rea¸cão e dom´ınios tipo “dumbbell”, que é poss´ıvel encontrarmos padrões para o problema

    

∂u

∂t = ∆u+cf(u), (x, t)∈Ω×IR

+

∂u

∂ν = 0, (x, t)∈∂Ω×IR

+_,

sendo quec´e uma constante positiva.

Em [13] temos um outro modelo, agora com a condi¸c˜ao n˜ao-linear na

fronteira _

   

∂u

∂t = ∆u, (x, t)∈Ω×IR

+

∂u

∂ν =cg(u), (x, t)∈∂Ω×IR

+_,

comcuma constante positiva. Entretanto este problema não envolve a rea¸cão no dom´ınio e tem difusão constante. A autora mostrou que se o dom´ınio também for do tipo “dumbbell”, cuja geometria tem a dependência expl´ıcita da constante c, então pode existir padrões para esse problema dependendo de algumas condi¸cões técnicas sobre a fun¸cãog.

(15)

fun¸c˜ao de difusibilidadea(x) para que o problema

    

ut= div(a(x)∇u) +f(u), Ω×IR+

∂u

∂ν = 0, ∂Ω×IR

+_,

admita padrões mesmo para dom´ınios convexos. Provaram que se a fun¸cão a(x) assumir valores suficientemente pequenos em torno de uma superf´ıcie suave sem bordo em Ω,então o problema acima apresenta padrões. Motivados por estes trabalhos, também no Cap´ıtulo 5, exibimos condi¸cões sobre a(x), quando esta for não-constante, para que (P) admita a existência de padrões para o caso em que f(x, u) =f(u) e g(x, u) =b(x)g(u).

Basicamente todos estes trabalhos, [13, 29, 7], (e o que apresentamos no Cap´ıtulo 5) utilizam uma técnica envolvendo a existência de um conjunto in-variante para o sistema dinâmico gerado pela equa¸cão parabólica do problema (P). Esse conjunto, sob hipóteses adequadas, contém equil´ıbrios não-constantes e mostra-se, via lineariza¸cão em torno destes equil´ıbrios, que o espectro do o-perador linearizado é formado por uma seqüência não-positiva de auto-valores. Com resultados clássicos tem-se a estabilidade.

Atualmente vários trabalhos têm abordado a questão da existência de padrões para equa¸cões (ou mesmo para sistemas de equa¸cões) de rea¸cão-difusão com pequenos parâmetros dados na forma

    

∂u ∂t =ε

2_div(_a

∇u) +f(x, u), (t, x)_∈IR+_×Ω ε2a(x)∂u

∂ν =g(x, u), (t, x)∈IR

+

×∂Ω.

(16)

condi¸c˜ao g _≡ 0, f(x, u) = k(x)f(u) vetorial, e tamb´em a e k estritamente positivas, de classeC2_.

Em [6] os autores demonstraram a existência de padrões para este problema com um pequeno parâmetro ε, a(x) _≡ 1, f _≡ 0 e a condi¸cão não-linear na fronteira é dada por g(x, u) =u(1₋u)(c(x)₋u), com 0 < c < 1 e algumas condi¸cões técnicas. A abordagem neste caso não envolve técnicas de Γ-convergência.

Através da abordagem via Γ-convergência, apresentamos novas con-tribui¸cões à existência de padrões para equa¸cões de rea¸cão-difusão com condi-¸cões não-lineares no dom´ınio e na fronteira dadas por

(Pε)

            

∂u ∂t =ε

2_∆_u₊_f₍_u₎_, ₍_{t, x}₎

∈IR+_×Ω ε∂u

∂ν =δεg(u), (t, x)∈IR

+

×∂Ω u(0, x) = u0(x), x∈Ω,

sendo que Ω_⊂IR3 é um dom´ınio suave e as fun¸cõesf e g satisfazem algumas condi¸cões de crescimento e suavidade e ambas com ra´ızes α < 0< β. ε é um parâmetro pequeno e δε satisfaz δε ≥ 1, lim

ε→0εlnδε = k, com 0 ≤ k < ∞,

hip´otese esta que ´e crucial neste trabalho. Por exemplo, se δε = ε−n, n ∈ IN,

ent˜aok = 0.

Para encontrarmos solu¸cões estacionárias de (Pε),é suficiente mostrar

a existˆencia de m´ınimos locais para os funcionais deﬁnidos em H1_{(Ω) por}

Eε(u) =ε

Z

Ω|∇

u_|2dx+ 1 ε

Z

Ω

F(u)dx+δε

Z

∂Ω

G(T u)d_HN−1,

sendo que T u é o tra¸co da fun¸cão u, _HN−1 _{é a medida de Hausdorff}

(N ₋ 1)-dimensional, e os potenciais F e G, primitivas de f e g respecti-vamente, são não-negativos e possuem apenas duas ra´ızes denotadas por α e β.Os pontos cr´ıticos de_Eεtambém são pontos cr´ıticos dos funcionaisEε=εEε,

para cada ε > 0 fixado. E estes são os funcionais energia cujas equa¸cões de Euler-Lagrange são dados por (Pε).

Para este ﬁm, calculamos o Γ-limite de _Eε (em um espa¸co de Banach

(17)

E0, que ´e essencialmente um problema geom´etrico. E ao demonstrarmos a

existˆencia de um m´ınimo local isolado para_E0,temos a existˆencia de m´ınimos

locais para os correspondentes funcionais_Eε,garantidos por um teorema de De

Giorgi (veja [14]) adaptado à forma variacional. Em outras palavras, o teorema garante que se o problema limite (no sentido de Γ-convergência) possuir um m´ınimo local isoladou0 então o funcional original também possui um m´ınimo

localuε em uma vizinhan¸ca de u0 (para uma certa topologia).

Entretanto, encontrar m´ınimos locais isolados para _E0 n˜ao ´e

trivi-al, embora muitas vezes sua identifica¸cão seja intuitivamente óbvia. Tanto que nos trabalhos [21, 27] os autores lograram êxito apenas para dom´ınios Ω_⊂IR2.Como nosso problema está colocado em Ω_⊂IR3,tivemos que encon-trar uma nova demonstra¸cão para este caso, a qual apresentamos no Cap´ıtulo 2. Ressaltamos que esta demonstra¸cão é diferente daquelas elaboradas pe-los autores citados e tudo indica que pode ser estendida para dom´ınios N -dimensionais,N _≥3.

Diversos autores (veja [3, 25, 26, 30, 37]) com diferentes interesses, estudaram o comportamento, quandoε_→0,dos funcionais_Eεdescritos acima,

com varias escalas δε adotadas na fronteira. O estudo destes funcionais tem

importância também, por exemplo, para descrever modelos de Cahn-Hillard para fluidos que assumem duas fases distintas.

Em [25, 37], os autores estudaram o caso em que δε = 0, ou seja,

nenhum termo de rea¸cão na fronteira foi levado em considera¸cão. Em [25] o autor demonstrou também que cada seqüencia (uε) ⊂ H1(Ω), com Eε(uε)

uniformemente limitado, é relativamente compacta em L1(Ω) e cada ponto de acumula¸cão u, pertence ao espa¸co BV(Ω,_{α, β_}), espa¸co das fun¸cões de varia¸cão total limitada que assumem somente os valores_{α, β_}em quase todos os pontos de Ω. Além disso uε tem transi¸cão de fase α para a fase β em uma

superf´ıcie Su ⊂Ω, a qual separa as fases {u=α} e {u=β}. A energia limite

(18)

neste caso ´e o funcional penalizado

E0(u) =

  

σ_HN−1₍_S

u), se u∈BV(Ω,{α, β})

+_∞, se u_∈L1_(Ω)_\_BV_(Ω_,_{_{α, β}_}₎_,

com σ = 2

Z β α

p

F(ξ)dξ. E este funcional, a menos da constante σ, é o co-nhecido funcional área da geometria diferencial, mas agora definido no espa¸co BV(Ω,_{α, β_}).

Esta an´alise foi estendida em [26] para δε = 1, com G sendo uma

fun¸c˜ao positiva qualquer. Nesse trabalho, Modica observou que os tra¸cos dos minimizantes uε, denotados por T uε, convergiam para uma nova fun¸c˜ao v

definida em∂Ω. Ocorre que tal fun¸cão é constante sobre o tra¸co de cada fase,

{T u = α_} e _{T u = β_}, mas pode diferir de T u. Isto contribuiu para que surgisse uma densidade adicional na fronteira de Ω no problema limite.

A partir desta observa¸c˜ao, em [3] os autores consideraram o caso em queδε → ∞,quandoε→0,assumindo ainda que o potencialGcontinha duas

ra´ızes distintas _{α′_{, β}′_} _satisfazendo _α′ _≤ _{α < β} _≤ _β′ _{e Ω} _⊂ _IR3_. _Mostraram

tamb´em que os tra¸cosT uεconvergiam para uma fun¸c˜aovque assume os valores

α′ eβ′ qtp em∂Ω.Além disso eles demonstraram que quando a escala adotada δε satisfaz a rela¸cão: εlogδε → k quando ε →0; com 0 < k < ∞, então uma

nova concentra¸c˜ao de energia surge ao longo da curva Sv ⊂∂Ω que separa as

fases na fronteira _{v =α′_} e _{v =β′_}.

Esses fatos sobre a nova vari´avel na fronteira do dom´ınio, observados por [26, 3], permite-nos estudar a Γ-convergˆencia no espa¸co L1_(Ω)_×_L1₍_∂_Ω)_.

Para isso reescrevemos os funcionais_Eε da seguinte forma

Eε(u, v) =

  

Eε(u), se u∈H1(Ω) ev =T u

+_∞, caso contr´ario em L1_(Ω)_×_L1₍_∂_Ω)_.

Com isso obtemos que o funcional Γ-limite ´e dado por

E0(u, v) =

  

Φ(u, v), (u, v)_∈BV(∂Ω,_{α, β_})_×BV(∂Ω,_{α′_{, β}′_}₎

(19)

sendo que Φ(u, v) ´e deﬁnido por

Φ(u, v) =σ_H2(Su) +

Z

∂Ω|

h(T u)₋h(v)_|d_H2+c_H1(Sv),

com c= (β

′₋_α′₎2

π k e h(t) = 2

Z t

0

p

F(ξ)dξ.

Este funcional apresenta as caracter´ısticas das observa¸c˜oes feitas por [26, 3], como observado acima.

´

E importante ressaltar que uma leitura cuidadosa nas demonstra¸cões de [3] permitiu-nos verificar que a mesma demonstra¸cão da Γ-convergência, quando k > 0, também vale para o caso em que k = 0, e mais ainda, para dom´ınios N-dimensionais, N _≥ 3. Neste caso não temos a contribui¸cão do termo c_H1₍_S

v) no funcional Φ, o que nos remete `a observa¸c˜ao de [26] sobre o

termo adicional na fronteira, que ´e o segundo valor do lado direito no funcional Φ. Colocamos estes resultados no Apˆendice A.

Uma outra propriedade importante que tem sido estudada nos últimos anos sobre as solu¸cões estacionárias do problema (Pε), ou mesmo para

proble-mas mais gerais de equa¸cões de rea¸cão-difusão deste tipo, proble-mas com condi¸cões de fronteira de Neumann homogêneas (g _≡0), é sob que condi¸cões estas solu¸cões desenvolvem camadas de transi¸cão interna. Tanto quanto sabemos, tal inves-tiga¸cão teve in´ıcio com o trabalho [28], no qual foi provado que a conhecida condi¸cão de igualdade de área constitui na realidade uma condi¸cão necessária para a forma¸cão de camadas de transi¸cão interna.

Neste sentido, no Cap´ıtulo 3, estabelecemos condi¸cões necessárias para que uma fam´ılia de solu¸cões de

(Qε)

  

εdiv(a(x)_∇vε) +f(x, vε) = 0, x∈Ω

εa(x)∂vε

∂n_b =g(x, vε), x∈ ∂Ω,

(20)

para uma fam´ılia de solu¸c˜oes de (Qε) desenvolver camadas de transi¸c˜ao

in-terna e superficial é que tenhamos a condi¸cão de área paraf e para g, isto é,

Rβ

α f = 0 =

Rβ α g.

A questão da forma¸cão de camadas internas de transi¸cão, está rela-cionada à convergência das solu¸cões para fun¸cões que assumem apenas dois valores, a saber as ra´ızes das fun¸cões f e g (veja Defini¸cão 3.1).

Em [28] o autor estudou este problema quandog _≡0 e demonstrou, em particular, que a condi¸cão necessária para que uma fam´ılia de solu¸cões de (Qε)

desenvolva camadas de transi¸cão interna, quandof(x, u) = f(u),é a condi¸cão de área para a fun¸cão f R_αβf = 0. Nesse trabalho o autor considerou a convergência uniforme em compactos K _⊂ (Ω_\S), sendo S a superf´ıcie que separa as fases _{u = α_} e _{u = β_} em Ω. Essa convergência em princ´ıpio pode substituir a convergência em L1_(Ω)_, _{pois como demonstrado em [9], se}

{vε}é uma seqüência de m´ınimos locais para certas classes de funcionais (por

exemplo, Eε acima com δε = 0) e vε converge em L1(Ω), quando ε →0, para

uma fun¸cão cujos valores são as ra´ızes de f, então a convergência é uniforme em compactos K _⊂(Ω_\S).

Em [32] os autores também estudam condi¸cões para a forma¸cão de camadas de transi¸cão internas.

Como exemplo de uma fam´ılia de solu¸cões que desenvolvem camadas de transi¸cão interna e superficial, no sentido da defini¸cão do presente trabalho, temos as solu¸cões estacionárias de (Pε) obtidas no Cap´ıtulo 2. E uma das

(21)

Cap´ıtulo 2

Existˆ

encia de padr˜

oes: uma

abordagem via

_Γ

-convergˆ

encia

2.1 Apresenta¸c˜

ao do problema

Atualmente, muito dos problemas relacionados às equa¸cões de rea¸cão-difusão não-lineares não envolvem o termo de rea¸cão na fronteira. Neste cap´ı-tulo o objetivo será encontrarmos padrões para a seguinte fam´ılia de equa¸cões de rea¸cão-difusão com condi¸cão de Neumann não-linear:

            

∂u ∂t =ε

2_∆_u₊_f₍_u₎_, ₍_{t, x}₎

∈IR+_×Ω ε∂u

∂ν =δεg(u), (t, x)∈IR

+

×∂Ω u(0, x) =u0(x), x∈Ω.

(2.1)

O dom´ınio Ω _⊂ IRN, N _≥ 3, ´e simplesmente conexo e de classe C2_{, ν} _{´e o}

vetor normal, unitário e exterior a ∂Ω. As fun¸cões f e g são ambas de classe C1_(IR_,_{IR) e satisfazem:}

(f0) f(l) = 0 =g(l),∀l ∈ {α,0, β}(´unicas) e α <0< β.

(22)

(f2) Existem constantesC >0, t0 >max{|α|, β}, r, s, σf eσg tais que

|f(t)_|,_|g(t)_{| ≥}C_|t_|, _{∀ |}t_|> t0.

|f(t)_{| ≤}r+s_|t_|σf_, ₁_≤_σ

f <

N + 2 N ₋2 ∀t,

|g(t)_{| ≤}r+s_|t_|σg_, ₁_≤_σ

g <

N

N ₋2 ∀t. (f3)

Z β α

f = 0 =

Z β α

g (condi¸c˜ao de ´area). (f4) lim

ε→0εlnδε =k, com 0≤k < ∞ eδε ≥1.

Inicialmente lembramos que as solu¸cões estacionárias de (2.1) são solu¸cões da fam´ılia de equa¸cões el´ıpticas semi-lineares dadas por

  

ε2∆u+f(u) = 0, x_∈Ω, ε∂u

∂ν =δεg(u), x∈∂Ω.

(2.2)

Sabe-se, pela hip´otese (f1), que as solu¸c˜oes constantes u=α e u=β

são solu¸cões estáveis do problema (2.1). Além disso, cada solu¸cão uε de (2.2)

satisfaz α_≤uε ≤β,gra¸cas ao princ´ıpio do m´aximo.

Assim nosso objetivo é encontrar solu¸cões estacionárias não-constantes (veja Teorema 2.9, Se¸cão 2.5) e em seguida verificar a estabilidade. E para mostrarmos a existência dessas solu¸cões, é suficiente encontrarmos, para cada 0 < ε _≤ ε0 dado, um m´ınimo local do funcional energia, definido em H1(Ω)

por

Eε(u) =

ε2

2

Z

Ω|∇

u_|2dx+

Z

Ω

F(u)dx+εδε

Z

∂Ω

G(u)d_HN−1, (2.3) sendo que

F(u) =₋

Z u α

f(ξ)dξ e G(u) =₋

Z u α

g(τ)dτ, (2.4) cuja equa¸cão de Euler-Lagrange é a equa¸cão (2.2). Os pontos cr´ıticos desse funcional são solu¸cões fracas de (2.2), isto é, são as fun¸cõesu_∈H1_{(Ω) tais que}

ε2

Z

Ω∇

u_∇ϕ dx₋

Z

Ω

f(u)ϕ dx₋εδε

Z

∂Ω

(23)

para cada ϕ_∈H1_(Ω)_.

Devido a regularidade das fun¸cõesf eg, usamos argumentos padrões (por exemplo “bootstrap”) para estas solu¸cões fracas e garantimos que são solu¸cões clássicas de (2.2), isto é, estão no espa¸co C2_(Ω)_∩_C1_(Ω)_.

Para obtermos m´ınimos de Eε usamos como ferramenta um teorema

de De Giorgi (Se¸cão 2.4, Teorema 2.7), adaptado à forma variacional, o qual afirma que se encontrarmos um m´ınimo local isolado u0 para o funcional E0

(veja 2.6), que ´e o Γ-limite, quandoε _→0,dos funcionais_Eε =

2

εEεpenalizados (veja 2.5), ent˜ao pr´oximo de u0 (em uma certa topologia) existem m´ınimos

locais dos correspondentes funcionais _Eε, que por sua vez s˜ao m´ınimos de Eε.

A estabilidade decorre dos resultados apresentados no Cap´ıtulo 5. Uma análise da hipótese (f4) permite-nos estudar a equa¸cão (2.2) com

a mesma escala, ou escalas diferentes, de difusibilidade no dom´ınio e na fron-teira. Por exemplo, seδε =ε−1 temos a mesma difusibilidade no dom´ınio e na

fronteira; mas δε = ε−n, com n ≥ 0 e n 6= 1, s˜ao casos em que as

difusibili-dades são diferentes, como pode ser observado na equa¸cão (2.2). Todos estes exemplos satisfazem a rela¸cão lim

ε→0εlnδε= 0.

Podemos tamb´em escolher, por exemplo, escalas da forma δε = ek/ε,

com k >0. Neste caso temos lim

ε→0εlnδε=k.

Entretanto n˜ao nos foi poss´ıvel abordar o caso em queδε =ε−n, n <0,

embora tenhamos lim

ε→0εlnδε = 0. A justificativa para isso é que no cálculo da

Γ-convergência dos funcionais _Eε, quando k = 0, é necessário que εlnδε seja

positivo. E se δε =ε−n, n <0, por exemplo, isto n˜ao se veriﬁca quando ε for

muito pequeno. ´

E importante ressaltar que (f3) constitui-se na condi¸c˜ao necess´aria

para a existência de uma fam´ılia de solu¸cões estacionárias de (2.1) que desen-volvem camadas de transi¸cão interna e superficial (veja Defini¸cão 3.1), quando ε_→0. A demonstra¸cão da condi¸cão necessária está feita no Cap´ıtulo 3.

(24)

garantem que o funcional Eε esteja bem deﬁnido e que os potenciais F e G

sejam do tipo “double-well” (ou po¸co-duplo), respectivamente, cuja deﬁni¸c˜ao damos a seguir.

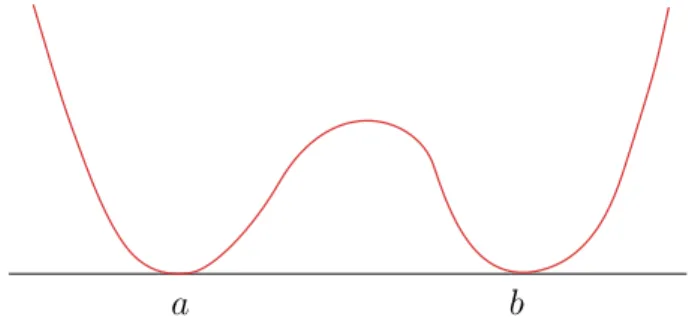
Dizemos que um potencialU ´e do tipo “double-well” (ou po¸co-duplo) seU : IR_→IR, ´e de classeC2 _{e satisfaz as seguintes propriedades:}

(i)U _≥0;

(ii) U tem exatamente duas ra´ızes, a e b, com a < b; (iii) U′₍_a_{) = 0 =}_U′₍_b₎_{, U}′′₍_a₎_>₀_{, U}′′₍_b₎_>_0;

(iv) c1|t|p1 ≤ U(t)≤ c2|t|p2, para certas constantes ci >0, pi ≥2 (i = 1,2) e

|t_{| ≥}t0, com t0 suﬁcientemente grande.

Veja abaixo uma ilustra¸c˜ao de como deve ser o comportamento destes potenciais.

a b

Figura 2.1: Ilustra¸c˜ao de um potencial do tipo “double-well”.

A condi¸cão sobre os potenciaisF eGserem do tipo po¸co-duplo é essen-cial para garantir uma determinada compacidade das solu¸cões encontradas. Esta compacidade é uma das hipóteses do Teorema 2.7 na Se¸cão 2.3. Veja o Apêndice A para maiores detalhes.

(25)

na Se¸cão 2.3 apresentamos um teorema de De Giorgi para obtermos, sob de-terminadas condi¸cões, a existência de m´ınimos locais para a fam´ılia de fun-cionais definidas por (2.3). Uma hipótese essencial para esse teorema de De Giorgi é a existência de um m´ınimo local isolado para um determinado fun-cional Γ₋limite, e que na Se¸cão 2.4 mostramos sua existência. Encerramos o cap´ıtulo com a Se¸cão 2.5 na qual todos os resultados em conjunto demonstra a existência dos padrões desejados.

2.2 Resultados preliminares

A seguir apresentamos um resumo de alguns resultados considerados importantes para a leitura deste cap´ıtulo. Não há demonstra¸cão dos resultados nesta se¸cão, mas sugerimos ao leitor o local para consulta destes e outros resultados relacionados.

2.2.1 Medida de Hausdorff e Aplica¸c˜

oes Lipschitz

SejaA_⊂IRN,0_≤s <_∞. Deﬁna

Hsδ(A) = inf

( _∞ X

j=1

α(s)

diamCj

2

s

:A_⊂

∞

[

j=1

Cj,diamCj ≤δ

)

,

em que

α(s) = π

s/2

Γ(s

2 + 1)

.

Aqui Γ(s) =

Z ∞

0

e−xxs−1dx, (0< s <_∞),´e a usual fun¸c˜ao gama.

Defini¸cão 2.1 Para cada subconjuntoA _⊂IRN como acima, definimos _Hs, a medida de Hausdorff s-dimensional em IRN por

Hs(A) = lim

δ→0H

s

δ(A) = sup δ>0 H

s δ(A).

Teorema 2.1 _Hs _{´e uma medida de Borel regular para cada} ₀_≤_{s <}_∞_.

(26)

Defini¸cão 2.2 Uma fun¸cãof : IRn_→IRm é chamada Lipschitz se existe uma constante C tal que

|f(x)₋f(y)_{| ≤}C_|x₋y_|,

para cada x, y _∈IRn. Al´em disso deﬁnimos

Lip(f) = sup

|f(x)₋f(y)_|

|x₋y_| :x, y ∈IR

n_{, x}

6

=y

Teorema 2.2 Sejam f : IRn _→IRm uma fun¸c˜ao Lipschitz, A _⊂IRn, 0_≤ s <

∞. Ent˜ao

Hs(f(A))_≤(Lip(f))s_Hs(A).

Demonstra¸c˜ao: [16] p. 75.

Corolário 2.1 Suponhamos que n > k. Sejam P : IRn _→ IRk, a fun¸cão proje¸cão, A_⊂IRn e 0_≤s <_∞. Então

Hs(P(A))_{≤ H}s(A).

Demonstra¸c˜ao: Lip(P) = 1.

2.2.2 Fun¸c˜

oes de varia¸c˜

ao limitada

Defini¸cão 2.3 Sejam Ω_⊂IRN, um conjunto aberto e limitado, e f _∈ L1(Ω). f é dita ser de varia¸cão limitada se

Z

Ω|∇

f_|def= sup

Z

Ω

fdivϕ dx:ϕ_∈C∞

0 (Ω; IRN),|ϕ| ≤1

<_∞.

Observa¸cão 2.1 Se f tem varia¸cão limitada, o gradiente de f, _∇f, no sen-tido das distribui¸cões, define uma medida de Radon. Esta medida, também

denotada por _k∇f_k, ´e uma medida de varia¸c˜ao e

k∇f_k(Ω)def=

Z

Ω|∇

f_|

(27)

Defini¸cão 2.4 Definimos o conjunto BV(Ω) como sendo o conjunto das fun-¸cões f _∈ L1(Ω) de varia¸cão limitada. E BV(Ω) munido com a norma

kf_k_BV_(Ω) =_kf_k_L1_(Ω)+k∇fk(Ω)

´e um espa¸co de Banach.

Teorema 2.3 (Semi-continuidade inferior)Seja Ω_⊂IRN,um conjunto aberto e seja_{fj}j∈IN⊂BV(Ω) uma seqüência de fun¸cões tal que fj →f em L1loc(Ω).

Ent˜ao

Z

Ω|∇

f_{| ≤}lim inf

j→∞

Z

Ω|∇

fj|.

Teorema 2.4 Seja Ω_⊂IRN, um conjunto aberto e limitado com fronteira de Lipschitz. Seja _{fj}j∈IN ⊂ BV(Ω) uma seqüência limitada. Então existe uma

subseq¨uˆencia _{fjk}k∈IN ⊂ {fj}j∈IN e f ∈ BV(Ω) tal que fjk → f em L

1_(Ω)_.

Em outras palavras BV(Ω) ֒_→L1(Ω) compactamente.

Observa¸cão 2.2 Existem outras propriedades importantes envolvendo as fun-¸cões de varia¸cão limitada. E uma delas é a existência do operador tra¸co

T :BV(Ω)_−→L1(∂Ω),

que é um operador linear e limitado. Para os nossos propósitos não há neces-sidade de maiores detalhes.

2.2.3 Conjuntos de per´ımetro finito

(28)

Defini¸cão 2.5 SejamE _⊂IRN um conjunto de Borel e Ω_⊂IRN um conjunto aberto. O per´ımetro de E em Ωé definido como

PerΩE def

= sup

Z

Ω

χ

Edivϕ dx:ϕ∈C

∞

0 (Ω; IRN),|ϕ| ≤1

=

Z

Ω|∇

χ E|,

sendo que χ_E ´e a fun¸c˜ao caracter´ıstica do conjunto E.

Se um conjunto de BorelE tem per´ımetro ﬁnito, ou seja, PerΩE <∞,

para cada conjunto limitado Ω,entãoEé chamado de conjunto de Cacciopoli. Destacamos algumas propriedades sobre conjuntos de per´ımetro finito:

(1) Se Ω =A_∪B, com A_∩B = /,❡ ent˜ao

PerΩA = PerΩB.

(2) SeE ´e um conjunto com fronteira suave (de classeC1_{) ent˜ao}

PerΩE =HN−1(∂E∩Ω).

(3) Cada conjunto de Cacciopoli limitadoEpode ser aproximado por seq¨uˆencia de conjuntosEj, de classeC2, tais que

Z

Ω|

χ

Ej −χE|dx→0,

Z

Ω|∇

χ Ej| →

Z

Ω|∇

χ_E_|;

HN−1(∂Ej∩∂Ω) = 0,

para j suﬁcientemente grande. Veja [37] Lema 1, ou [18] p. 22.

Defini¸c˜ao 2.6 Seja E um conjunto de per´ımetro ﬁnito e consideremos a me-dida _k∇χ_E_k. Dizemos que um ponto x_∈ ∂E, pertence a fronteira reduzida de

E, ∂∗_E, _se

(i)

Z

B(x,r)|∇

χ_E_|>0, para cada r >0;

(ii) lim

r→0

Z

B(x,r)

νEdk∇χ_Ek

Z

B(x,r)|∇

χ_E_|

=νE(x);

(29)

Teorema 2.5 Seja E um conjunto de Cacciopoli. Ent˜ao

(i) ∂∗E =

∞

[

i=1

Ci∪K,

sendo que Ci s˜ao superf´ıcies compactas, de classe C1, e HN−1(K) = 0;

(ii) PerΩE =HN−1(∂∗E∩Ω);

(iii) ∂∗_E ₌_∂E.

Demonstra¸c˜ao: [18] p. 54 ou [16] p. 205.

Observa¸c˜ao 2.3 Se ∂E ´e uma superf´ıcie de classeC1_, _{temos que} _∂∗_E ₌_∂E

e, conseqüentemente,νE(x) é o vetor normal unitário interno à ∂E em x.

Definimos o espa¸co BV(Ω,_{α, β_}) como o conjunto das fun¸cões u _∈ BV(Ω) que assumem apenas os valores αeβ qtp em Ω. Analogamente defini-mos BV(∂Ω,_{α, β_}).Por uma questão de brevidade na nota¸cão em todo este trabalho usamos I def= _{α, β_}.

Para cada u _∈ BV(Ω, I), o conjunto _{x _∈ Ω : u(x) = β_} é um conjunto de per´ımetro finito. Definimos Su

def

= ∂∗_{x _∈ Ω : u(x) = β_{} ∩}Ω. Assim PerΩ{x∈Ω :u(x) = β}=HN−1(Su).

Não é dif´ıcil verificarmos que a varia¸cão total deu satisfaz

k∇u_k(Ω) =

Z

Ω|∇

u_|= (β₋α)_HN−1(Su).

A defini¸cão deSv para v ∈BV(∂Ω, I) é análoga.

(30)

Consideremos o espa¸co IL1 _{= IL}1_(Ω_{, ∂}_Ω) def₌ _L1_(Ω) _×_L1₍_∂_{Ω) com a}

seguinte norma

k(u, v)_k_IL1

def

= _ku_kL1_(Ω)+kvk_L1₍_∂_Ω).

Ent˜ao (IL1_,_{k · k}

IL1) ´e um espa¸co de Banach.

Deﬁnimos_Eε,E0 : IL1 →IR∪ {∞} por

Eε(u, v) =

  

2

εEε(u) se u∈H

1_{(Ω) e} _v ₌_{T u,}

+_∞caso contr´ario em IL1_,

(2.5)

com Eε deﬁnido por (2.3) e

E0(u, v) =

  

Φ(u, v), (u, v)_∈BV(Ω, I)_×BV(∂Ω, I)

+_∞, caso contr´ario em IL1_, (2.6)

sendo que Φ(u, v) ´e deﬁnido por

Φ(u, v) =σ_H2(Su) +

Z

∂Ω|

h(T u)₋h(v)_|d_H2+c_H1(Sv), (2.7)

com c= (β

′₋_α′₎2

π k, h(t) = 2

Z t

0

p

2F(ξ)dξ e σ=_|h(β)₋h(α)_|

Teorema 2.6 Se Ω_⊂ IR3 e k >0 ent˜ao _Eε Γ-converge (em IL1) para o

fun-cional _E0.

Demonstra¸c˜ao: [3].

Uma leitura cuidadosa de [3] permite-nos verificar que este teorema sobre a Γ-convergência dos funcionais definidos em (2.5), quando lim

ε→0εlnδε=

k >0,tamb´em vale para o caso em que lim

ε→0εlnδε=k = 0 e, mais ainda, para

dom´ınios N-dimensionais, N _≥ 3 (veja Teorema A.1). Neste caso o Γ-limite dos funcionais _Eε ´e o funcionalE0 com

Φ(u, v) = σ_HN−1(Su) +

Z

∂Ω|

h(T u)₋h(v)_|d_HN−1.

(31)

2.3 O Teorema de De Giorgi

Enunciamos e provamos aqui uma versão variacional de um teorema de De Giorgi. Este teorema é responsável, sob determinadas hipóteses, pela existência de m´ınimos locais para a fam´ılia de funcionais definidas por (2.5). Como conseqüência, na Se¸cão 2.5 usaremos estes resultados para encontrarmos os padrões desejados.

Teorema 2.7 Seja Ω_⊂IR3 um dom´ınio limitado com fronteira suave. Sejam

Eε e E0 deﬁnidos por (2.5) e (2.6), respectivamente, com k ≥ 0. Suponhamos

que sejam satisfeitas as seguintes condi¸c˜oes

(i)Existem constantes C >0 e d _∈IR tais que F(t)_≥C_|t_|p ₋d, com p_≥2. (ii)A fam´ılia de funcionais_{Eε}εΓ-converge, em IL1(Ω, ∂Ω),para o funcional

E0,

(iii) _{Eε}ε ´e equicoerciva, isto ´e, para cada {(uε, vε)}0<ε≤ε0 ⊂ IL

1_(Ω_{, ∂}_Ω)

sa-tisfazendo _Eε(uε, vε)≤M, para todo 0 < ε ≤ε0, {(uε, vε)}0<ε≤ε0 ´e

com-pacta em IL1_(Ω_{, ∂}_Ω)_.

Se (u0, v0) é um m´ınimo local isolado de E0, então existe uma seqüencia

{(uεj, vεj)}, com εj →0, tal que (uεj, vεj)´e um m´ınimo local de Eεj e

k(uεj, vεj)−(u0, v0)kIL1

εj→0

−→0. (2.8)

Para a demonstra¸c˜ao deste teorema necessitamos do seguinte

Lema 2.1 Seja_Eεdeﬁnido por (2.5). Suponhamos que existamC >0ed∈IR

tais que F(t)_≥C_|t_|p₋_d, _com _p_≥₂_. _{Ent˜ao para cada} _{δ >}₀ _e _{ε >}₀_, _existe

(uε, vε)∈Bδ(u0, v0)def= (u, v) :k(u, v)−(u0, v0)k_IL1 ≤δ

satisfazendo

(32)

Demonstra¸c˜ao: Fixe δ >0 e ε >0.Como _Eε≥0, existe M ≥0 tal que

M = inf_{Eε(u, v) : (u, v)∈Bδ}.

Como H1_{(Ω) ´e denso em} _L1_(Ω)_{, M <} _∞_. _Seja _{₍_u

i, vi)}_i_∈_IN uma seq¨uencia

minimizante, isto ´e, lim

i→∞Eε(ui, vi) =M.

Logo existec >0 tal que ε

Z

Ω|∇

ui|2dx+

2 ε

Z

Ω

F(ui)dx+ 2δε

Z

∂Ω

G(T ui)dH2 ≤c, (2.9)

evi =T ui pela defini¸cão deEε. De (2.9) e das nossas hipóteses sobreF temos

C

Z

Ω|

ui|pdx−d|Ω| ≤

Z

Ω

F(ui)dx≤εc=ec.

Logo

kuikp_Lp_(Ω)≤ec, ∀i.

Como p_≥ 2, pela desigualdade (2.9) segue que (ui) é uma seqüência

limitada em H1_(Ω)_. _{Logo existe} _u

ε ∈ H1(Ω) e uma subseq¨uˆencia de (ui)

(de-notada ainda por (ui)) tal que

ui ⇀ uε em H1(Ω), ui →uε em L2(Ω).

Al´em disso, pelas propriedades sobre o operador tra¸co obtemos tamb´em T ui ⇀ T uε em H1/2(∂Ω), T ui →T uε =vε em L2(∂Ω).

Uma vez queL2 _⊂_L1_,_{existe uma nova subseq¨}_{uˆencia de (}_u

i), denotada

tamb´em por (ui), tal que ui(x) → uε(x) qtp em Ω e T ui(y) → vε(y) qtp em

∂Ω. Pela continuidade de F e G vem que F(ui(x)) → F(uε(x)) qtp em Ω e

G(T ui(y))→G(vε(y)) qtp em∂Ω. Aplicando o Lema de Fatou obtemos

Z

Ω

F(uε(x))dx≤lim inf i→∞

Z

Ω

F(ui(x))dx

Z

∂Ω

G(vε(y))dH2 ≤lim inf i→∞

Z

∂Ω

G(T ui(y))dH2.

(2.10)

Da teoria cl´assica sobre funcionais tipo energia sabe-se que W :H1_(Ω)_→_{IR deﬁnido por}

W(u) =

Z

Ω|∇

(33)

´e fracamente semicont´ınuo inferiormente em H1_(Ω)_._{Disto obtemos que}

Z

Ω|∇

uε|2dx≤lim inf i→∞

Z

Ω|∇

ui|2dx. (2.11)

Logo, de (2.10) e (2.11)

Eε(uε, vε) =ε

Z

Ω|∇

uε|2dx+

2 ε

Z

Ω

F(uε)dx+ 2δε

Z

∂Ω

G(vε)dH2

≤lim inf

i→∞ ε

Z

Ω|∇

ui|2dx+ lim inf i→∞

2 ε

Z

Ω

F(ui), dx+ lim inf i→∞ 2δε

Z

∂Ω

G(T ui)dH2

≤lim inf

i→∞

ε

Z

Ω|∇

ui|2dx+

2 ε

Z

Ω

F(ui), dx+ 2δε

Z

∂Ω

G(T ui)dH2

= lim inf

i→∞ Eε(ui, vi) = M.

Pelo fato de Bδ ser um subconjunto fechado de IL1 e (ui, T ui) → (uε, vε) em

IL1_, _{conclu´ımos que (}_u

ε, vε)∈Bδ e ´e um m´ınimo deEε em Bδ.

Em vista deste lema podemos elaborar a

Demonstra¸c˜ao do Teorema 2.7: Seja (u0, v0) um m´ınimo local isolado de

E0 em Bδ(u0, v0), para algum δ >0. Como Eε Γ-converge para E0, existe uma

seq¨uencia_{(aεj, bεj)} ⊂IL

1 _{tal que (}_a

εj, bεj)→(u0, v0) em IL

1 _e

lim

j→∞Eεj(aεj, bεj) =E0(u0, v0). (2.12)

Pelo Lema 2.1, existe uma seq¨uencia_{(uεj, vεj)} ⊂IL

1 _{de m´ınimos de}

Eεj em Bδ(u0, v0).

Paraj suﬁcientemente grande temos que (aεj, bεj)∈Bδ(u0, v0).Assim, como (uεj, vεj) ´e m´ınimo em Bδ(u0, v0), segue que

Eεj(uεj, vεj)≤ Eεj(aεj, bεj), (2.13) implicando que_{Eεj(uεj, vεj)} é uma seqüencia limitada, já que {Eεj(aεj, bεj)} o é (pois é convergente).

Por outro lado, segue de (2.13) e (2.12) que para qualquer subseq¨uˆencia (εjk)⊂(εj) vale que

lim inf

k→∞ Eεjk(uεjk, vεjk) ≤ lim infk→∞ Eεjk(aεjk, bεjk) = limk→∞Eεjk(aεjk, bεjk)

(34)

Afirmamos que (uεj, vεj) está no interior de Bδ(u0, v0). Em outras palavras, (uεj, vεj) é um m´ınimo local de Eεj.

Suponhamos o contrário. Então existe uma subseqüência (mas usamos a mesma nota¸cão)_{(uεj, vεj)⊂IL

1_} _{tal que}

k(uεj, vεj)−(u0, v0)kIL1 =δ. (2.15) Como _{Eεj(uεj, vεj)} é limitada e por hipótese {Eεj} é equicoerciva, segue que _{(uεj, vεj)}é compacta em IL

1_. _{Logo existe uma nova subsequencia}

{(uε_jk, vε_jk)} de {(uεj, vεj)}e (u, v)∈IL

1 _{tais que}

(uε_jk, vε_jk) k→∞

−→ (u, v)

em IL1_.

Portanto de (2.15) vem que

k(u, v)₋(u0, v0)k_IL1 =δ.

Pela Γ-convergˆencia de_{Eεj} e (2.14) conclu´ımos que

E0(u, v)≤lim inf

k→∞ Eεjk(uεjk, vεjk) = E0(u0, v0),

o que contradiz com o fato de (u0, v0) ser m´ınimo local isolado.

Para mostrarmos (2.8), o procedimento é o mesmo. Suponha, por absurdo, que (2.8) não se verifica. Entao existe γ > 0 e uma subseqüência

{(uε_jk, vε_jk)} ⊂ {(uεj, vεj)} tal que

0< γ _{≤ k}(uεj, vεj)−(u0, v0)kIL1 ≤δ.

Como a seqüência _{Eε_jk(uε_jk, vε_jk)} é limitada e equicoerciva,

encon-tramos uma nova subseq¨uˆencia (e supomos ser a mesma) _{(uε_jk, vε_jk)} ⊂IL1 e

(u, v)_∈IL1 _{tais que (}_u

ε_jk, vε_jk)→(u, v) em IL1, e, assim,

0< γ _{≤ k}(u, v)₋(u0, v0)k_IL1 ≤δ.

(35)

A Γ-convergˆencia de _Eε e por (2.14) nos d´a

E0(u, v)≤lim inf

k→∞ Eεjk(uεjk, vεjk) = E0(u0, v0),

e isto contradiz o fato de (u0, v0) ser m´ınimo local isolado. Conclu´ımos assim

o teorema.

Observa¸cão 2.4 E importante ressaltarmos que a mesma demonstra¸cão desse´ teorema vale para dom´ınios N₋dimensionais e também para outras fam´ılias de funcionais, quando satisfeitas as hipóteses.

A seguir apresentamos um resultado que é a principal contribui¸cão deste cap´ıtulo, que é a existência de um m´ınimo local isolado para o Γ₋limite, condi¸cão imprescind´ıvel para utilizarmos o Teorema 2.7 na Se¸cão 2.5.

2.4 M´ınimos locais isolados dos

_Γ

-limites

A partir de agora consideramos Ω _⊂ IR3, um dom´ınio limitado com fronteira de classeC2 _{e simplesmente conexo.}

Suponhamos que existam _{O ⊂} Ω, h > 0 e θ : (₋h, h) _→ IR, uma fun¸c˜ao de classeC2_,_{tais que}_θ _{tenha um m´ınimo absoluto em 0, com}_θ₍₀₎ _>₀_,

e que ∂Ω_∩ ∂_O seja uma superf´ıcie de revolu¸cão (em torno do eixo z, por exemplo) gerada pelo gráfico deθ.Veja abaixo uma ilustra¸cão para um dom´ınio satisfazendo estas hipóteses.

(36)

Sejam

S def= _{(x, y,0) :x2₊_y2 _{< θ}2₍₀₎_}

Cdef= _{(x, y,0) :x2₊_y2 ₌_θ2₍₀₎_}_. (2.16)

Suponha, sem perda de generalidade que_O =_Oα∪ S ∪ Oβ,sendo que

Oα ={(x, y, z)∈Ω : 0< z < h}e Oβ ={(x, y, z)∈Ω :−h < z < 0}.

Como o conjunto Ω_{\ S} é formado por duas componentes conexas, defina Ωα como uma destas componentes e a qual contém o conjunto Oα.

Analogamente para Ωβ. Assim Ω = Ωα∪ S ∪Ωβ.

Deﬁna tamb´em Mα =∂Ωα∩∂Ω\C, Mβ =∂Ωβ ∩∂Ω\C e

u0 =αχΩα +βχΩβ, v0 =αχMα +βχMβ. (2.17) Em vista das considera¸c˜oes acima temos os seguintes resultados que se constituem na principal contribui¸c˜ao deste cap´ıtulo.

Teorema 2.8 Seja

E0(u) =

  

σ_H2₍_S

u), se u∈BV(Ω, I)

+_∞, se u_∈L1_(Ω)_\_BV_(Ω_{, I}₎_.

Então u0, definido em (2.17), é um m´ınimo L1-local isolado para o funcional

E0.

Corolário 2.2 Se 0 _≤k < _∞, então (u0, v0), dado por (2.17), é um m´ınimo

IL1_{-local isolado para o funcional deﬁnido por} _{(2.6), com Φ deﬁnida por (2.7).}

Observa¸cão 2.5 Não é dif´ıcil verificar que tanto u0 quanto v0 são fun¸cões

pertencentes aos espa¸cos BV(Ω, I) e BV(∂Ω, I) respectivamente. Pois pela defini¸cão, Su0 =S eSv0 =C. Além disso o tra¸co de u0 satisfaz T u0 =v0.

Observa¸cão 2.6 Sempre que mencionarmosu_∈BV(Ω, I) ouv _∈BV(∂Ω, I), consideramos u e v como sendo constantes em cada componente conexa de Ω_\Su e ∂Ω\Sv, respectivamente. Não há perda de generalidade nisso, pois

(37)

Demonstra¸cão do Teorema 2.8: Relembremos a defini¸cão de m´ınimo local isolado (m.l.i.), a qual deve ser observada a topologia envolvida. Uma fun¸cão u0 ∈L1(Ω) é um m.l.i. para o funcional E0 se existeδ >0 tal que ∀u∈L1(Ω)

satisfazendo 0<_ku₋u0kL1_(Ω) < δ, implicaE₀(u)> E₀(u₀).

Se u _∈ L1_(Ω)_\_BV_(Ω_{, I}_{) ent˜ao} _E

0(u) = ∞ > E0(u0). Se u = β (ou

u=α) qtp em Ω, ent˜aoE0(u) = 0. Portanto, u ´e um m´ınimo global.

Logo nosso trabalho resume-se em mostrar queu0 ´e um m´ınimo local

de E0 para toda u ∈ BV(Ω, I) satisfazendo 0 < |{x ∈ Ω : u(x) = β}| < |Ω|,

sendo _{| · |}a medida de Lebesgue em IR3.

Afirmamos que é suficiente mostrar que _H2₍_S₎ _< _H2₍_S

u) para cada

u_∈BV(_O, I) tal que 0<_ku₋u0kL1₍_O₎ < δ,para algum δ >0.

De fato, suponhamos que exista δ > 0 satisfazendo estas rela¸c˜oes. Como_ku₋u0kL1_(Ω) ≥ ku−u₀k_L1₍_O₎,seu∈BV(Ω, I) e 0<ku−u₀k_L1_(Ω) < δ

ent˜ao

E0(u0) = σH2(S)< σH2(Su_|O) =σPerO({x∈ O:u(x) =β})

≤ σPerΩ({x∈Ω :u(x) =β}) = σH2(Su) =E0(u).

Apresentamos a seguir uma mudan¸ca de variáveis que transforma o conjunto_Oem um cilindro circular reto_C.Esta mudan¸ca, descrita mais abaixo, faz com que a fun¸cãoθ,a qual determina a concavidade local do bordo, tenha grande influência no resultado desejado.

Das nossas hip´oteses podemos escrever

∂Ω_∩∂_O=_{(θ(z) cost, θ(z)sent, z),0_≤t <2π,₋h < z < h_} (2.18)

para algumh >0.

Consideremos a transforma¸c˜ao Λ :_{O → C} deﬁnida por

Λ(x, y, z) = θ(0) θ(z)

1/2

x,

θ(0) θ(z)

1/2

y, z

!

.

(38)

C2_,_{e que}

|JΛ(x, y, z)_|= θ(0) θ(z) e

JΛ−1(x, y, z)= θ(z)

θ(0) ≥1, ∀(x, y, z)∈ C, pois 0 ´e um m´ınimo absoluto para θ.

Note que vale a rela¸c˜ao Λ(_S) =_S e, portanto,

H2(_S) =_H2(Su0), (2.19)

sendo queu0 =u0◦Λ−1 =αχCα +βχCβ, na qual

Cα

def

= Λ(_Oα) = {(x, y, z)∈ C : 0< z < h}

Cβ

def

= Λ(_Oβ) ={(x, y, z)∈ C :−h < z <0}.

Para cadau_∈BV(_C, I),denotamos

Cu

α ={x∈ C :u(x) =α}

Cu

β ={x∈ C :u(x) = β}.

(2.20)

Sabemos que Su é uma superf´ıcie retificável e disto conclu´ımos que

´e formada por componentes conexas disjuntas, as quais denotamos por V_βj, e assim,

Su =

[

j

V_βj. (2.21)

Como estamos interessados em m´ınimos n˜ao-triviais, consideramos apenas as fun¸c˜oes u_∈BV(_C, I), satisfazendo 0<_|Cu

α|<|C|.

SejaP : IR3 _→IR2 a proje¸c˜ao ortogonal. Identiﬁcamos IR2 com IR2_×

{0_}. Com isso temos P(x, y, z) = (x, y,0).Logo _{S ⊂} P(IR3).

Dada u _∈ BV(_C, I), Su necessariamente satisfaz uma das seguintes

propriedades:

(i) existe uma componente conexaVβ deSu tal que P(Vβ) = S;

(ii) n˜ao existe nenhuma componente conexa Vβ de Su tal que P(Vβ) =S.

Suponhamos que u _∈ BV(_C, I) satisfaz (i) e que Su tem uma ´unica

(39)

e V2

β, com H2(Vβi)>0 (i= 1,2) e uma delas satisﬁzer (i), digamosVβ1, ent˜ao

pelo Corol´ario 2.1 ter´ıamos

H2(Su) = H2(Vβ1) +H2(Vβ2)≥ H2(P(Vβ1)) +H2(Vβ2)

≥ H2(_S) +_H2(V_β2)>_H2(_S). (2.22) Abaixo temos uma ilustra¸c˜ao em IR2 de um poss´ıvel caso.

xx xx xx xx xxxxxx xxxxxx xxx xx xx xx xx xx xx xx xx xx xx xx xx xxx xxx xxx xxx xxxx xxxx x x x x x x x xxxxxx xxxxxx xxxxxx xxxxxxxxxx xxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxx xxxx xxxx xxxx xxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxx xxxx xxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xx xx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxxxx xxxxxxx xxxxxxx xxxxxx xxxxxx xxxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxx x x x xx xx xx xxxx xxxx xxxxx xxxxx xxxxx xxxxxxx xxxxxxx xxxxxxx xxxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxxxxx xxx xxx xxx xxxxxxx xxxxxxx xxxxxxx xxxxxxx xxxxxxxxxxxxx xxxxxxxxxxxxx xxxxxxxxxxxxx xxxxxxxxxxxxx xxxxxxxxxxxxx xxxx xxxx xxxx xxxx xxxxx xxxxx xxxxx xxxxx xxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx xxxxxxxxxxxxxxx x x xxx xxx xxx x xxxx xxxx xxxx x x x x xxxxxxx xxxxxxx xxxxxxx xxxxxxx xxxxxxx xxx xxx xxx

v =β v =α S

Suponhamos que tenhamos escolhidoδ > 0. Seu_∈BV(_C, I), satisfaz (i) e se

0<_ku₋u0kL1₍_C₎ < δ, (2.23)

ent˜ao_H2₍_S

u\ S)>0.

Com efeito, como por hip´otese

0<_ku₋u0kL1₍_C₎= (β−α)|C_α∩ C_βu|+|C_β ∩ C_αu| ,

ent˜ao _|Cα ∩ Cβu| > 0 ou |Cβ ∩ Cαu| > 0, necessariamente. Em ambos os casos

devemos ter que_H2₍_S

u\ S)>0.

Assim existe um conjuntoWu ⊂Su tal queWu∩S = /❡eH2(Wu)>0.

Suponhamos, sem perda de generalidade, queWu ⊂ Cα. Logo existez0 >0 tal

quez0 = inf{z: (x, y, z)∈Wu}. Pelas hip´oteses da fun¸c˜ao θ temos que

|JΛ−1_|= θ(z)

θ(0) >1,∀z : (x, y, z)∈Wu. (2.24) Temos

ku₋u0kL1₍_O₎ =

Z

O|

u₋u0|dx=

Z

C|

(40)

Portanto, para qualqueru_∈BV(_O, I) tal que 0<_ku₋u0kL1₍_O₎ < δ,

se u = u _◦Λ−1 _{satisfaz (i), ent˜ao por (2.25), (2.24) e pelo Corol´ario 2.1,}

respectivamente, vem que

H2(Su) =

Z

Su

d_H2 =

Z

Su θ(z) θ(0)dH

2 ₌

Z

Su\W θ(z) θ(0)dH

2₊

Z

W

θ(z) θ(0) dH

2

>

Z

Su\W

d_H2+

Z

W

d_H2 =_H2(Su)≥ H2(P(Su)) =H2(S). (2.26)

Note que, para u=u_◦Λ−1_, _{sempre vale} _H2₍

Su)≥ H2(Su).

Seja u _∈ BV(_C, I) tal que Su satisfaz (ii). Para cada componente

conexa Vβ de Su, com H2(Vβ) > 0, existe uma regi˜ao interna, digamos Ri,

contida em _C, satisfazendo _|Ri| > 0, tal que u assume o valor α ou β (ou

ambos) e que ∂Ri∩ C ⊇Vβ, com a igualdade no caso em queRi n˜ao contenha

outra componente conexaVβdeSu.Esta regi˜ao interna ´e uma das componentes

conexas de_{C \}Su.Veja abaixo uma ilustra¸c˜ao de um poss´ıvel caso em IR2 desta

situa¸c˜ao. xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx

v =β _R

i v =α

S

Admita que cada componente conexaVβ deSu tenha uma ´unica regi˜ao

interna Ri. Não há perda de generalidade com esta suposi¸cão, como pode ser

visto mais adiante.

Como_S´e de classeC∞_,_H2₍_S_{) coincide com a ´area de}_S_._{Da geometria}

elementar e das nossas hip´oteses sobre_C temos

|Cα|=|Cβ|=H2(S)·h. (2.27)

Aﬁrmamos que se u _∈ BV(_C, I) satisfaz (ii) e (2.23), com δ_≤ (β−α)

4 H

2₍

(41)

De fato, seja u_∈BV(_C, I) satisfazendo estas hip´oteses. Ent˜ao

0<

Z

C|

< (β−α)

4 H

2₍

S)_·h,

sendo que_Cu

α , Cβu foram deﬁnidos em (2.20). Portanto

max_|Cα∩ Cβu|,|Cβ∩ Cαu| <

1 4H

2₍

S)_·h. (2.28)

Disto observamos que n˜ao pode ocorrer nenhum dos seguintes casos:

Cαu ⊂ Cβ ou Cβu ⊂ Cα, pois isto implicaria que Cαu ∩ Cβ = Cβ ou Cβu∩ Cα = Cα,

respectivamente, contradizendo (2.28). Veja a ﬁgura ilustrativa.

xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxx xxxx xxxx xxxx xxxx Cu α Cu β Cβ Cα xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxx xxxxx xxxxx xxxxx xxxxx Cu β Cβ Cα S Cu β ∩Cβ

Figura 2.3: Do lado esquerdo um caso que não pode ocorrer devido a hipótese (2.28). Do lado direito o conjunto _Cβ ∩ Cβu contido em uma região interna Ri.

Agora, pelas hip´oteses sobre u devemos ter ent˜ao _Cα∩ Cαu ou Cβ∩ Cβu

contido em uma ou mais regi˜oes internas Ri, ou que uma delas seja uma das

regi˜oes internas. Suponhamos, por simplicidade, que seja _Cβ ∩ Cβu. O mesmo

argumento se aplica para_Cα∩ Cαu (veja ﬁgura acima).

Não é dif´ıcil verificarmos que _Cβ = (Cβ ∩ Cβu)∪(Cβ∩ Cαu)∪(∂Cβu∩ Cβ),

sendo que_|∂_Cu

β ∩ Cβ|= 0.

Como_|Cβ|=H2(S)·h, de (2.28) e desta ´ultima observa¸c˜ao segue que

|Cβ ∩ Cβu| ≥

3 4H

2₍

S)_·h.

Como anteriormente, consideremos a fun¸cão proje¸cão ortogonal P. Afirmamos que _H2(P(_Cβ ∩ Cβu))>

1 2H

2₍

(42)

Com efeito, seja

Σdef= (x, y, z)_{∈ C} : (x, y,0)_∈P(_Cβ ∩ Cβu),−h < z <0 .

Para cada (x, y, z)_{∈ C}β ∩ Cβu temos −h < z <0.

ComoP(x, y, z) = (x, y,0)_∈P(_Cβ∩ Cβu),segue que (x, y, z)∈Σ.Logo

Cβ ∩ Cβu ⊂Σ e assim |Cβ∩ Cβu| ≤ |Σ|.

Mas_|Σ_|=_H2(P(_Cβ∩ Cβu))·h. Logo

H2(P(_Cβ ∩ Cβu))·h≥ |Cβ ∩ Cβu| ≥

3 4H

2₍

S)_·h > 1 2H

2₍

S)_·h, donde conclu´ımos que

H2(P(_Cβ ∩ Cβu))>

1 2H

2₍

S).

Como_C_βu _{⊃ C}β ∩ Cβu e P(Su)⊇P(Cβu)⊃P(Cβ∩ Cβu),vem que

H2(P(Su))>

1 2H

2₍

S).

Para concluir a aﬁrma¸c˜ao basta mostrarmos que

H2(P(Su))≤

1 2H

2₍_S

u).

Fa¸camos isto mostrando, para cada componente conexaVβ deSu, que

H2(P(Vβ))≤

1 2H

2₍_V

β), (2.29)

pois como Su =

[

j

V_βj (com uni˜ao disjunta) e _H2(Su) =

X

j

H2(V_βj), o resul-tado segue uma vez que P(Su) =

[

j

P(V_βj). Se _H2₍_V

β) = 0, ent˜ao H2(P(Vβ)) = 0, pelo Corol´ario 2.1 e, assim, a

desigualdade (2.29) se veriﬁca imediatamente.

SejaVβ uma componente conexa deSu,comH2(Vβ)>0,eRi a regi˜ao

interna envolvida por Vβ.

Sejam M, m:P(Vβ)→IR deﬁnidas por

M(Y) = maxz : (x, y, z)_∈P−1₍_Y₎_∩_R

i

m(Y) = minz : (x, y, z)_∈P−1₍_Y₎_∩_R