DOI: http://dx.doi.org/10.1590/1806-9126-RBEF-2018-0252 Licença Creative Commons
Um passeio por várias álgebras na descrição do momento
angular
A walk through multiple algebras in the description of the moment angular
Emerson Dionísio Belançon
*1, Samuel da Silva
21Universidade Federal de Mato Grosso, Departamento de Matemática, Instituto de Ciências Exatas e Naturais, Rondonópolis, MT, Brasil
2Universidade Estadual Paulista, Faculdade de Engenharia de Ilha Solteira, Departamento de Engenharia Mecânica, Ilha Solteira, SP, Brasil
Recebido em 01 de Setembro, 2018. Revisado em 28 de Setembro, 2018. Aceito em 01 de Outubro, 2018. A forma mais comum de definir matematicamente o momento angular é através da operação de produto vetorial como definido por Josiah Willard Gibbs e ao mesmo tempo por Oliver Heaviside. Neste sentido, a contribuição deste artigo é mostrar que a definição do momento angular também pode ser feita usando outros sistemas algébricos existentes e menos conhecidos da maioria dos estudantes, como a álgebra de Hamilton, a álgebra de Grassmann e a álgebra geométrica de Clifford. Por fim, realizamos uma comparação crítica entre estas definições e o seus significados.
Palavras-chave:momento angular, álgebra, quatérnion, vetores, multivetores, Hamilton, Grassmann, Clifford.
The most common way to mathematically define the angular moment is through the vector product operation as defined by Josiah Willard Gibbs and at the same time by Oliver Heaviside. This way, the contribution of this article is to show that the definition of angular moment can also be made using other algebraic systems existing and less known to most students, such as Hamilton algebra, Grassmann algebra and Clifford geometric algebra. Finally, we make a critical comparison between these definitions and their meanings.
Keywords:angular moment, algebra, quaternion, vectors, multivectors, Hamilton, Grassmann, Clifford.
1. Introdução
O momento angular é uma grandeza associada a um objeto que executa um movimento de rotação em torno de um ponto fixo, sendo uma das principais grandezas tanto na física clássica quanto moderna, podendo ser observado em diversas situações, por exemplo, Lekner [1] mostra que os pulsos sonoros transportam momento an-gular e são conservados quando o amortecimento e o espalhamento viscosos são desprezados. Nessa mesma li-nha Wunenburger, Lozano e Brasselet [2] realizaram uma demonstração experimental da troca de momento angu-lar orbital entre som e matéria medida por um processo de espalhamento quiral não dissipativo. Na mecânica quântica, Singh e Mobed [3] afirmam que a curvatura do espaço-tempo local pode contribuir de forma não tri-vial para as propriedades do momento angular orbital já em [4] há uma discussão de novos resultados sobre a conversão spin-orbital do momento angular orbital da luz e em [5], um estudo experimental mostra a reconstru-ção do spin e do momento angular orbital da luz após distorção em amplitude, fase e estado de polarização.
Apesar do momento angular ter uma expressão apa-rentemente simples muitos estudantes encontram
difi-*Endereço de correspondência: edbelancon@ufmt.br.
culdades quando iniciam o estudo de rotação de sólidos. Essas dificuldades estão relacionadas diretamente com o conceito de momento angular e a velocidade angular. Uma das causas destas dificuldades são conceituais e deve-se ao fato de que as leis que governam a translação e rotação são semelhantes [6, 7]. Por outro lado, vários experimentos podem ser feitos para que os alunos possam visualizar e demonstrar o momento angular [8–10] ou a conservação do momento angular [11–14]. Aliado a isto, a própria descrição matemática do momento angular, dependendo do sistema álgebrico usado pode dificultar ou facilitar o entendimento dos signficados e a precisão deste conceito aos estudantes.
Na primeira seção é feito uma sucinta revisão dos principais conceitos para definir a álgebra vetorial de Gibbs-Heaviside. Logo após, é colocado uma descrição detalhada do momento angular frisando os conceitos que serão usados para uma melhor compreensão da sua descrição com as outras álgebras partindo da criação histórica de cada uma delas e como se interpreta o con-ceito de produto entre vetores. No final, apresenta-se uma comparação crítica do momento angular escrito nes-tas quatro álgebras apontando a melhor forma para sua representação matemática e uso prático em problemas da física.
2. A Álgebra Vetorial
Por volta de 1883, Josiah Willard Gibbs fez uma
aná-lise da Álgebra de Grassmann assim como a álgebra de Hamilton [20] e pôde simplificá-las de forma consi-derável. Gibbs apresentou seus estudos sob a forma de notas de aula que utilizava junto aos seus alunos [21] que posteriormente foi publicada em forma de livro [22]. Ao mesmo tempo, Oliver Heaviside, chegou a resultados semelhantes ao de Gibbs, de forma independente, mas nunca escreveu um tratado formal sobre análise vetorial. Os resultados desenvolvidos sobre vetores foram introdu-zidos em seus artigos sobre eletromagnetismo que depois foram reunidos em dois volumes chamadosElectrical Pa-pers [23]. Estes acontecimentos marcam o nascimento da chamada álgebra vetorial conhecida também como
álgebra de Gibbs-Heaviside.
Nesta álgebra os elementos existentes são escalares e os vetores. Os vetores se dividem em duas classes: osvetores polares, ou simplesmente vetores, que possuem direção e sentido natural e osvetores axiaisoupseudovetores1 que possuem direção e sentido convencionados pela regra da mão direita (ou regra de Fleming2) [24] na operação de produto vetorial entre eles. A definição da álgebra vetorial pode ser encontrada em uma vasta lista de livros básicos de geometria [25,26].
Para definir os elementos desta álgebra toma-se o es-paço euclidiano tridimensionalR3 e uma base ortonor-mal B = {ˆe1,ˆe2,eˆ3} neste espaço. Assim, a
represen-tação de um vetor w ∈ R3 é dada simplesmente por w=xeˆ1+yˆe2+zˆe3 comx, y, z∈R. O módulo de um
vetor é dado por
|w|=px2+y2+z2.
Gibbs, ao mesmo tempo que Heaviside, definiram dois produtos entre estes elementos. Sejamw,u∈R3 eαo
menor ângulo entre eles. Paraα6= 0,weudefinem um plano e o produto escalar entre eles, representado por w·u, é um número real definido por
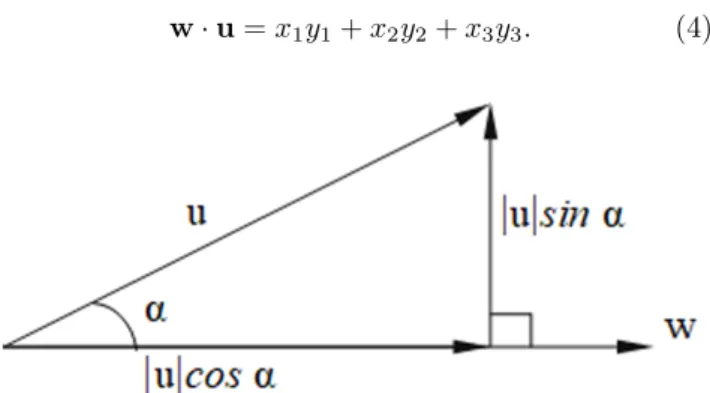
w·u=|w||u|cosα.
1Os adjetivos polares e axiais foram introduzidos por Woldemar
Voigt em 1896.
2Criada originalmente pelo físico John Ambrose Fleming
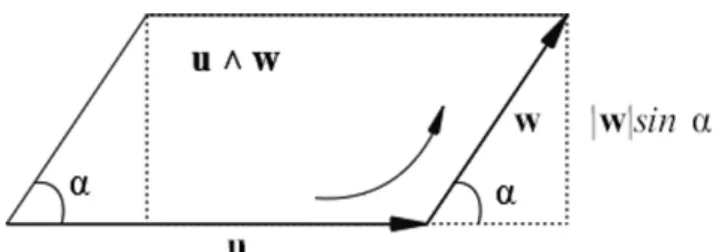
A interpretação geométrica desse produto pode ser vista como a multiplicação do módulo dewcom módulo da componente deuque tem mesma direção dewcomo ilustrado na figura (1). Esse produto está relacionado com comprimento uma vez que ele amplia/reduz o com-primento de um dos vetores. Segue que o produto escalar é comutativo mas não associativo e satisfaz as seguintes relações entre os vetores da baseB
ˆ
ei·eˆi= 1 para i= 1,2,3 ˆ
ei·eˆj = ˆej·ˆei= 0 para i6=j. (1)
Já oproduto vetorial entre esses vetores, representado porw×u, é um vetor definido por
w×u=|w||u|sinαˆn,
onde ˆn é um vetor unitário cujo sentido é normal ao
plano formado porw eue direção satisfazendo a regra da mão direita e com módulo dado por
|w×u|=|w||u|sinα. (2)
A interpretação geométrica do módulo desse produto pode ser vista como a multiplicação do módulo de w com módulo da componente deuque é perpendicular a direção de w, também ilustrado na figura (1). Esse produto está relacionado com o valor da área do parale-logramo formado por esses vetores já que a componente perpendicular é a altura deste paralelogramo.
Segue que o produto vetorial, por sua vez, não é comu-tativo e nem associativo e satisfaz as seguintes relações entre os vetores da baseB
ˆ
ei׈ei= 0 para i= 1,2ou3 ˆ
ei׈ej=εijkˆek para i6=j6=k. (3)
sendoεijk= 1seijk= 123,231ou312(permutação
cí-clica) ouεijk=−1seijk= 213,132ou321(permutação
acíclica) o que dá origem a conhecida regra mnemônica da mão direita.
Com isso, dado os vetores w = x1ˆe1+x2ˆe2+x3eˆ3
eu =y1eˆ1+y2ˆe2+y3ˆe3 segue das relações (1), (3) e
das propriedades associativa e distributiva dos números reais as expressões conhecidas para os produtos escalar e vetorial, respectivamente
w·u=x1y1+x2y2+x3y3. (4)
w×u = (x2y3−x3y2)ˆe1+ (x3y1−x1y3)ˆe2
+ (x1y2−x2y1)ˆe3. (5)
Em qualquer livro de física, por exemplo [27,28], pode-se encontrar a definição do momento angular de uma partícula usando o conceito anterior de produto vetorial. Com esta álgebra o momento angular de uma partícula de massam, denotado porH, com relação ao pontoO movendo-se com velocidade vé calculado como
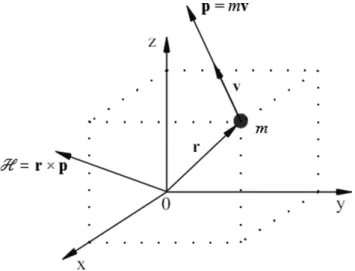
H =r×p=m(r×v) (6)
sendoro vetor com origem no pontoO até a posição da
partícula e p=mvé o momento linear desta partícula. Decorre que o momento angular é normal ao plano for-mado pelos vetoresrep. Geometricamente, o momento angular pode ser representado como o expresso na figura (2).
Se um vetor posição ér=r1eˆ1+r2eˆ2+r3eˆ3e um vetor
velocidade év=v1eˆ1+v2ˆe2+v3eˆ3, segue da equação
(5) que a representação algébrica do momento angular será
H = m[(r2v3−r3v2)ˆe1+ (r3v1−r1v3)ˆe2
+ (r1v2−r2v1)ˆe3] (7)
que é a forma padrão com que a totalidade dos estudan-tes tem contato com a definição do momento angular. Porém, como abordamos neste artigo, outras formas me-nos conhecidas do grande público podem ser usadas para descrever o mesmo conceito físico do momento angular.
3. A Álgebra de Hamilton
Bem antes dos trabalhos de Gibbs e Heaviside, Wil-liam Rowan Hamilton construiu no século XIX um novo conjunto de objetos com propriedades semelhantes aos números complexos tentando generaliza-los para o espaço tridimensional com uma estrutura fechada. Esses novos objetos com quatro componentes sendo uma escalar e
Figura 2: Representação geométrica dos momentos linear e angular
três unidades imaginárias foi por ele denominado quatér-nions e publicado no livroElements of quaternions [29] em 1843. Com este formalismo, as regras válidas para
os números complexos eram satisfeitas, com a única di-ferença de que o produto entre quatérnions não é uma operação comutativa.
O conjunto dos quatérnions, denotado porH, satisfaz as propriedades de espaço vetorial sobre o corpo dos números reais. Um quatérnion pode ser representado, conforme Kuipers [30], por
e
q=q0+q1i+q2j+q3k,
sendoq0, q1, q2 eq3∈Ros componentes deeqei,jekas
unidades imaginárias que satisfazem as seguintes relações fundamentais
i2=j2=k2=−1
ij=k=−ji jk=i=−kj ki=j=−ik.
(8)
Um quatérnioneqpossui uma parte real, chamada por
Hamilton de parte escalar, denotada por S(eq) = q0 e
uma parte imaginária, conhecida como parte vetorial ou simplesmentevetor, denotada porV(qe) =q1i+q2j+q3k.
Assim, um quatérnion pode ser escrito simplesmente comoeq=S(qe) +V(eq). SeV(qe) = 0, entãoqe=S(eq)é um
número real; agora seS(qe) = 0, entãoeq=V(qe)é dito um
quatérnion puro (vetor). Hamilton também definiu o pro-duto entre quatérnions utilizando as regras dos números complexos e alguns relações fundamentais, descritas pelas equações (8) envolvendo as unidades imaginárias. Aqui será considerado o caso particular de quatérnions puros que se mostram suficientes para a definição do momento angular. Dados os quatérnionsqe= 0+w=x1i+x2j+x3k
e pe= 0 +u= y1i+y2j+y3k, o produto entre eles é
dado por
e
qpe=wu = −(x1y1+x2y2+x3y3)
+ (x2y3−x3y2)i+ (x3y1−x1y3)j
+ (x1y2−x2y1)k
(9)
O espaço vetorial realHequipado com o produto entre quatérnions é dito uma álgebra, denominada álgebra de Hamilton. A álgebra de Hamilton é associativa em relação ao produto mas não é comutativa que claramente pode ser visto nas relações (8), porém é uma álgebra fechada. Como o objetivo é escrever o momento angular será considerado o vetor posiçãore o vetor velocidadevcomo quatérnions puros da formaer= 0 +r=r1i+r2j+r3k
eev= 0 +v=v1i+v2j+v3k.
significado diferente. Assim, o produto entre quatérnions puro é dado pela expressão
e
rve=rv = −(r1v1+r2v2+r3v3)
+ (r2v3−r3v2)i+ (r3v1−r1v3)j
+ (r1v2−r2v1)k
(10)
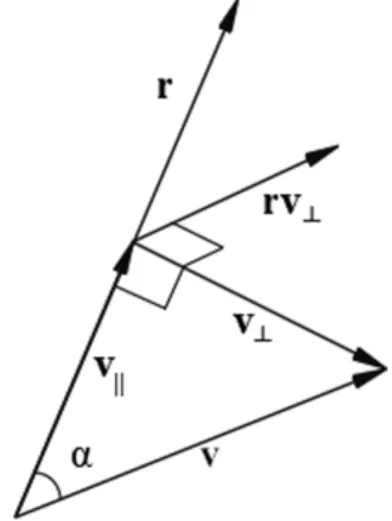
O produto de dois quatérnions puros tem como resul-tado a estrutura de um quatérnion geral (parte escalar e vetorial). A interpretação geométrica desse produto via rotações no espaço só foi feito por Hamilton em 1844
com o artigo [31]. Inicialmente Hamilton decompôsvnos vetoresvk ev⊥ ondevk é a projeção devna direção de
rev⊥ é a projeção devem uma direção perpendicular
àr, como ilustrado na figura (3).
Admitindo que a multiplicação entre vetores é distri-butiva, Hamilton obteve
e
rev=rv=r(vk+v⊥) =rvk+rv⊥ (11)
e definiu os produtos parciais rvk e rv⊥ da seguinte
maneira:
• rvk é um escalar dado pelo produto dos
compri-mentos dos vetoresrevk, antecedido por um sinal
negativo se estes possuem o mesmo sentido ou por sinal positivo, se possuem sentido contrário. • rv⊥ é um vetor cujo comprimento é o produto dos
comprimentos de rev⊥ cuja direção é
perpendi-cular a ambos.
Pode-se observar na equação (10) que a parte vetorial tem a mesma estrutura que a equação (7), além disso, de acordo com a interpretação geométrica de Hamilton, a parte vetorial deste resultado descreve a mesma grandeza da equação (7) já que possuem mesmo módulo, direção e sentido. Portanto, o momento angular pode ser consi-derado como a parte vetorial do produto entre os dois quatérnionsereev, isto é,H =m[V(erev)].
Figura 3:Representação geométrica de Hamilton.
4. A Álgebra de Grassmann
Com a descoberta de Hamilton outros pesquisadores se interessaram em pesquisar novos objetos matemáticos, entre eles, Hermann Günther Grassmann teve importân-cia fundamental. O primeiro volume do principal trabalho de Grassmann foi apresentado em1843, na forma
ma-nuscrita, com o nome deDie Lineale Ausdehnungslehre3 e publicada em1844[32]. Neste trabralho, Grassmann
propôs representar as grandezas físicas por objetos geo-métricos ao invés de números. Estes objetos seriam como retas orientadas, fragmentos de plano orientados, cubos orientados, etc. Pode-se dizer que foi exatamente neste ponto que surgiu o conceito de objetos vetoriais, como é conhecido hoje. O trabalho de Grassmann foi, sem dúvida, excepcional, entretanto, o seu trabalho era por demais complexo para a época em que foi publicado, e poucos foram os que o entenderam e deram importância na época.
A álgebra de Grassmann pode ser construída a partir de aplicações lineares alternadas ou a partir do quociente de alguma álgebra tensorial. Porém, nosso objetivo é sa-ber como calcular o produto entre vetores para descrever o momento angular. Sendo assim, será colocado apenas as principais definições sem entrar em conceitos mais gerais. O leitor interessado pode consultar as referências [19,33] para detalhes aprofundados.
Dado um tensor na formav1⊗v2⊗...⊗vp, em que
vi com i= 1, ..., psão vetores de um espaço vetorial V
sobre o corpo dos reaisRe⊗denota o produto tensorial, pode-se definir ooperador alternador, denotado por Alt, como segue
Alt(v1⊗v2⊗...⊗vp) =
1
p!
X
σ∈Sp
ε(σ)vσ(1)⊗vσ(2)⊗...⊗vσ(p), (12)
ondeSpé o conjunto de todas as permutações possíveis
eε(σ) = 1, se o número de permutações feitas for par, e
ε(σ) =−1, se o número de permutações feitas for ímpar.
Nestas condições, um p-vetores, denotado porAp, é um
tensor contravariante4de ordemp(ou gradep) alternado
Ap =Alt(v1⊗v2⊗...⊗vp), (13)
ondev1,v2, ...,vp ∈V.
Denota-se porVp
(V) o conjunto dos p-vetores. Tal
conjunto possui a estrutura de espaço vetorial. É possível definir um produto entre elementos desses espaços. Sejam
Ap ∈V p
(V)um p-vetor e Bq ∈V q
(V) um q-vetor. O
produto exterior é dado por
∧: Vp(V)×Vq(V) −→ Vp+q(V)
Ap∧Bq 7−→ Alt(Ap⊗Bq), (14)
3A Teoria das Extensões Lineares
4São tensores do tipo (p,q) - por exemplo um vetor é um tensor
este produto também é conhecido como cunha ou de Grassmann e é associativo.
Das equações (12) e (14) pode-se calcular o produto exterior de dois vetoresweu
w∧u= 1
2(w⊗u−u⊗w) (15)
claramente é possível concluir que o produto exterior é não comutativo.
Assumindo o espaço euclidiano tridimensionalV =R3 e uma base ortonormal B={ˆe1,eˆ2,eˆ3}, conclui-se que
os vetores deB satisfazem as seguintes relações
ˆ
ei∧ˆei= 0 para i= 1,2,3 ˆ
ei∧ˆej=−ˆej∧eˆi para i6=j. (16)
Além disso, pode-se construir quatro espaços vetoriais a partirR3, isto é, parap= 0, ...,3têm-seV0(R3) =R espaço dos escalares,V1
(R3) =R3 espaço dos 1-vetores (ou vetores),V2
(R3)espaço dos 2-vetores (ou bivetores),
V3
(R3)espaço dos 3-vetores (ou trivetores).
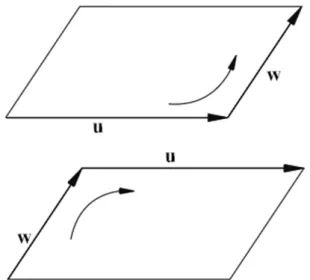
Os escalares e vetores são os velhos conhecidos da ál-gebra vetorial, mas os bivetor e trivetor são os objetos que diferenciam a álgebra de Grassmann uma vez que estes estão relacionados com área e volume que não en-contram correspondentes na álgebra de Gibbs-Heaviside. Uma base para o espaço dos bivetores é dado por todas as permutações da forma eˆi ∧eˆj dos elementos de B
que são linearmente independentes. Um conjunto dessas permutações é dado por{ˆe1∧eˆ2,ˆe1∧eˆ3,ˆe2∧ˆe3}. Assim,
um bivetor pode ser escrito, algebricamente, na forma
A2=a12eˆ1∧eˆ2+a13eˆ1∧eˆ3+a23ˆe2∧eˆ3
e, geometricamente, pode ser representado como um fragmento de plano orientado gerado por dois vetores ordenados, conforme a figura (4).
Já uma base para o espaço dos trivetores é qualquer permutação da forma ˆei∧eˆj∧eˆk. Assim, um trivetor
Figura 4:Representação geométrica das duas orientações possí-veis para um bivetor.
pode ser escrito, algebricamente, na forma
A3=a123ˆe1∧ˆe2∧eˆ3
e, geometricamente, pode ser representado como um volume orientado, conforme a figura (5).
Ao aplicar o produto exterior em um p-vetor e um q-vetor, equação (14), o resultado é ump+q-vetor que não
pertence ao espaçoVp
(V)e nem ao espaçoVq(V). Para
resolver o problema do não fechamento deste produto, pode-se considerar a soma direta dos quatros espaços vetoriais construídos a partir deR3, isto é,
^
(R3) =
3
M
p=0
p
^
(R3)
no qual é fechado em relação ao produto exterior. Este es-paço é denominadoespaço multivetorial e cada elemento arbitrárioA∈V(R3)é chamado demultivetor e pode
ser escrito de maneira geral como
A = a0+a1eˆ1+a2ˆe2+a3eˆ3+a12ˆe1∧eˆ2
= +a13eˆ1∧eˆ3+a23ˆe2∧eˆ3+a123eˆ1∧ˆe2∧eˆ3.
Tal espaço dotado do produto exterior é denominado
álgebra exterior do espaço vetorialR3. Em muitos textos é considerado a álgebra exterior e a álgebra de Grassmann como sinônimos, porém existe uma distinção entre as duas estruturas, a álgebra de Grassmann é a álgebra exterior equipado com uma generalização de um funcional linear
g : V ×V → R para o espaço vetorial V(V). Como
o interesse é no produto entre dois vetores, o produto exterior é calculado de forma análoga na álgebra de Grassmann e não vamos adentrar no rigor das definições, que podem ser encontradas em lingua portuguesa em [19]. O módulo de um bivetor pode ser dado como a área do paralelogramo formado pelo produto exterior entre dois vetores, isto é
|u∧w|=|u||w|sinα (17)
com a interpretação geométrica descrita na figura (6). Pode-se definir um produto métrico, denominado con-tração à esquerda,5entrep-vetores equivalente ao produto escalar quando restrito à vetores.
Figura 5:Representação geométrica do trivetoru∧w∧t.
5Pode-se definir a contração à direita de forma anóloga e denotada
por⌊. A contração também é muitas vezes denominada de produto
Figura 6:Representação geométrica do módulo de um bivetor.
⌋: Vp(R3)×Vq(R3) −→ Vq−p(R3)
Ap⌋Bq 7−→ Cq−p
Este produto não é associativo e só é simétrico sep=q
porém satisfaz as seguintes propriedades: i) α⌋Ap=αAp;
ii) u⌋w=u·w;
iii) u⌋(Bq∧Ck) = (u⌋Bq)∧Ck+ (−1)qBq∧(u⌋Ck);
iv) (Ap∧Bq)⌋Ck=Ap⌋(Bq⌋Ck).
ondeαé um escalar,uewsão vetores eAp,Bq,Ck um
p-vetor umq-vetor e umk-vetor respectivamente.
Com isto, defini-se uma operação denominada duali-dade ou como em [19] isomorfismo quase-Hodge como segue
⋆: Vp(R3) −→ V3−p(R3)
⋆Ap 7−→ −Ap⌋I3 (18)
onde I3 representa um trivetor simples unitário, isto é,
I3= ˆe1∧ˆe2∧eˆ3 denominado como pseudoescalar.
Por exemplo, para calcular o dual do bivetor A2 =
ˆ
e1∧eˆ2 deve ser aplicado, além da definição (18), as
propriedades da contração, ou seja,
⋆A2 = −(ˆe1∧eˆ2)⌋(ˆe1∧ˆe2∧ˆe3)
= −{ˆe1⌋(ˆe2⌋(ˆe1∧(ˆe2∧eˆ3)))} (iv)
= −{ˆe1⌋(ˆe2⌋eˆ1)∧(ˆe2∧eˆ3)
−eˆ1∧(ˆe2⌋(ˆe2∧ˆe3))} (iii)
= −{ˆe1⌋(ˆe2⌋eˆ1)∧(ˆe2∧eˆ3)
−eˆ1∧[(ˆe2⌋eˆ2)∧eˆ3−eˆ3∧(ˆe2⌋eˆ1)]} (iii)
= −{ˆe1⌋(−eˆ1∧ˆe3)} (ii)
= −{−eˆ1⌋ˆe1∧eˆ3+ ˆe1∧(ˆe1⌋eˆ3)} (iii)
= −{−eˆ3}= ˆe3 (ii)
Com isso, a representação dos vetores posição r e velocidade v no espaço multivetorial V(R3) pode ser
escritos da seguinte formar=r1ˆe1+r2eˆ2+r3ˆe3ev=
v1eˆ1+v2eˆ2+v3eˆ3. Segue do produto exterior entre vetores,
(15), que
r∧v= 1
2(r⊗v−v⊗r). (19)
Desenvolvendo os termos
r⊗v = r1v1eˆ1∧ˆe1+r1v2eˆ1∧eˆ2+r1v3ˆe1∧eˆ3
+ r2v1ˆe2∧ˆe1+r2v2eˆ2∧eˆ2+r2v3ˆe2∧eˆ3
+ r3v1ˆe3∧ˆe1+r3v2eˆ3∧eˆ2+r3v3ˆe3∧eˆ3
v⊗r = v1r1eˆ1∧ˆe1+v1r2eˆ1∧eˆ2+v1r3ˆe1∧eˆ3
+ v2r1ˆe2∧ˆe1+v2r2eˆ2∧eˆ2+v2r3ˆe2∧eˆ3
+ v3r1ˆe3∧ˆe1+v3r2eˆ3∧eˆ2+v3r3ˆe3∧eˆ3
e aplicando as relações (16) nestes termos e substituindo o resultado em (19) tem-se finalmente
r∧v = (r1v2−r2v1)ˆe1∧eˆ2+ (r1v3−r3v1)ˆe1∧eˆ3
+ (r2v3−r3v2)ˆe2∧eˆ3
(20)
Mesmo sabendo que o produto entre vetores na álgebra de Grassmann resulta em um bivetor que por sua vez está relacionado com área assim como o momento angular isto não é suficiente para dizer que ambos representam a mesma grandeza. Além disto, a comparação das equa-ções (20) e (7) não podem ser feita pois possuem grades diferentes. Mas com a operação de dualidade é possível encontrar um representante do bivetorr∧vno espaço dos vetores para tal comparação. Desta forma,
⋆(r∧v) = (r2v3−r3v2)ˆe1+ (r3v1−r1v3)ˆe2
+ (r1v2−r2v1)ˆe3=r×v.
Por outro lado, o bivetorr∧ve o vetorr×vpossuem o mesmo módulo, conforme as equações (2) e (17). Assim o momento angular é o dual deste bivetor, isto é,H =
m[⋆(r∧v)].
5. A Álgebra Geométrica de Clifford
Em1878William Kingdon Clifford publicou um artigo noAmerican Journal of Mathematics intituladoApplications of Grassmann’s extensive algebra[34] apresentando uma nova estrutura matemática que ele denominouálgebra geométrica, mas que hoje também costuma ser conhecida como Álgebra de Clifford. O que Clifford fez foi sintetizar duas estruturas matemáticas aparentemente dissociadas: os quatérnions de Hamilton e a álgebra de extensão de Grassmann, mas por infelicidade o seu trabalho tampouco ganhou a devida atenção na época, sobretudo por causa de sua morte prematura que contribuiu para que seu trabalho caísse no esquecimento por algumas décadas.
Seu trabalho começou a ressurgir e ganhar maior im-portância a partir do final do século XX por ações do Prof. David Hestenes. Com esta visão mais abrangente da estru-tura desta álgebra, verificou-se que a álgebra geométrica poderia ser usada como forma de unificar várias áreas da mecânica quântica e as aplicações nos mais variados temas e áreas contribuíram para uma grande e impor-tante gama de trabalhos publicados recentemente [35–51]. Desde então, este assunto tem ganhado crescente impor-tância. Além disto na descrição do momento angular, pode-se observar de forma clara, como a álgebra geomé-trica consegue em uma única estrutura unificar o seu conceito matemático e físico de forma clara, exata e concisa.
será descrito detalhes das diversas formas de introduzir tal álgebra.
SupomosV um espaço vetorial sobreRequipado com uma forma bilinear simétricag, Auma álgebra associ-ativa com unidade 1A e ainda γ uma aplicação linear
γ:V → A. Umaálgebra de Clifford é o par(A, γ)para
o espaço quadrático(V, g)quandoAé gerada como uma álgebra por {γ(u)|u∈V} comγ satisfazendo
γ(u)γ(w) +γ(w)γ(u) = 2g(u,w)1A, (21)
para todou,w∈V. Denotamos essa álgebra porCℓ(V, g).
Oproduto geométrico(ou Clifford) entre dois vetores u,w∈V é dado por
γ(u)γ(w) =γ(g(u,w)) +γ(u∧w). (22)
O produto geométrico entre dois vetores pode ser visto como uma composição entre duas partes: a primeira é a imagem dentro deCℓ(V, g)da contração deusobrewe a segunda parte é a imagem dentro deCℓ(V, g)do produto
exterior.
Existe um isomorfismo de espaço vetorial entre a álge-bra de Clifford e a álgeálge-bra de Grassmann e portanto o espaço de CliffordCℓ(V, g)possui uma estrutura
multive-torial. Desta forma, os elementos da álgebra de Clifford são denominados também de multivetores. Nesta seção também será considerado um sistema euclidiano tridi-mensional, isto é V = R3, e uma base ortonormal re-presentada por B = {eˆ1,eˆ2,ˆe3}, neste caso a álgebra
de Clifford é denotadaCℓ3. A relação (21) aplicada aos
elementos dessa base pode ser escrita como
ˆ
eiˆei= 1 para i= 1,2,3 ˆ
eiˆej=−ˆejˆei para i6=j. (23)
O produto de Clifford, dado pela equação (22), entre vetores pode ser reescrito como
uw=u·w+u∧w. (24)
Dentro da álgebra de Clifford também é possível definir a operação de dualidade e será denotado por ⋆. Esta
operação é análoga à chamada dualidade de Hodge dentro do cálculo com formas diferenciais [52]. Dado um p-vetor
Ap ∈V(R3), comp= 0, ...,3, seu dual é definido como
sendo
⋆Ap= (−1)
p(p−1) 2 ApI
onde Irepresenta um trivetor simples unitário, isto é, I= ˆe1ˆe2eˆ3 denominado como pseudoescalar.
Um resultado importante obtido usando dualidade é, dados dois vetores u,w ∈ V(R3) pode-se relacionar o
produto vetorial com o produto exterior
u×w=⋆(u∧w) =−(u∧w)I. (25)
sendo que a figura (7) mostra a interpretação geométrica desta relação.
Já a representação dos vetores posiçãor e velocidade vno espaço multivetorialV(R3)é da formar=r1eˆ1+
r2eˆ2+r3eˆ3ev=v1eˆ1+v2ˆe2+v3ˆe3.
Calculando os produtos escalar e exterior e substi-tuindo na equação (24) obtém-se a expressão do produto geométrico
rv = r·v+r∧v
rv = (r1v1+r2v2+r3v3)
+ (r1v2−r2v1)ˆe1∧eˆ2+ (r1v3−r3v1)ˆe1∧eˆ3
+ (r2v3−r3v2)ˆe2∧eˆ3
(26)
Observa-se que ao aplicar a equação (24) nos elementos da base, tem-se
ˆ
eiˆej= ˆei·eˆj+ ˆei∧ˆej,
e da relação (1) que
ˆ
eiˆej= ˆei∧ˆej.
Logo a equação (26) pode ser reescrita da forma rv = (r1v1+r2v2+r3v3)
+ (r1v2−r2v1)ˆe1eˆ2+ (r1v3−r3v1)ˆe1eˆ3
+ (r2v3−r3v2)ˆe2eˆ3
(27)
Pode-se ver claramente na equação (27) que aparece o bivetor dado pelo produto exterior escrito em termos do produto geométrico. Esse bivetor representa, como já foi visto na seção anterior, de maneira mais precisa o mo-mento angular poisH está associada com área ao invés de comprimento e os bivetores possuem naturalmente esta característica. Outra forma de ver isto é calcular o vetor momento angular através da operação de dualidade
(25), isto é,
r×v=−(r∧v)I
e uma característica importante desta operação é que seu resultado não muda o sinal perante uma inversão espacial qua é a mesma característica do produto vetorial. A beleza do produto geométrico é que contém todas as informações entre os vetoresrev: a relação métrica e a relação vetorial.
6. Conclusão
Heaviside usou o eletromagnetismo como incentivo para elaborar seu produto vetorial na descrição das equações
de Maxwell, obtendo uma praticidade operacional no tratamento destas equações. Porém, com as novas te-orias físicas deve-se descrever com maior exatidão tais grandezas. Neste cenário, vale observar que o momento angular é uma grandeza que não atua ao longo de uma reta, mas sim normal a um plano. Logo da forma que é definido via álgebra vetorial, não é a melhor maneira de representá-lo. Na álgebra de Hamilton a parte veto-rial da equação (10) representa, tanto algebricamente, quanto geometricamente, o momento angular descrito na álgebra vetorial. Porém, matematicamente, também não é a forma mais efetiva de representá-lo conforme mostramos neste artigo. Já na álgebra de Grassmann o produto entre dois vetores tem como resultado um bivetor, dado pela equação (15), que descreve natural-mente uma área orientada e possui a mesma estrutura , bastando aplicar o isomorfismo de Hodge para chegar a isto, além de possuir o mesmo módulo que a equa-ção (7). Desta forma, um bivetor é a melhor maneira de representar matematicamente a grandeza física mo-mento angular. Por outro lado, na álgebra geométrica de Clifford, o resultado do produto geométrico, além de ter o bivetor, que descreve a relação vetorial, possuí também um escalar, que descreve a relação métrica, unificando duas operações em um produto. Isto torna esta álgebra a mais completa para descrever a complexidade de diversas grandezas físicas importantes não só para físicos, como também engenheiros. Esta álgebra é mais geral e engloba todas as outras. Os autores em [19] mostram diversas representações da álgebra dos números complexos,Cℓ0,1,
da álgebra dos quatérnions,Cℓ0,2 e uma construção da
álgebra de Grassmann a partir do produto geométrico, uma vez que ambos possuem a mesma estrutura multi-vetorial. Vale ressaltar também que a álgebra vetorial só vale para espaços de dimensão três, enquanto a álgebra de Hamilton é válida para espaços de dimensão até qua-tro, por outro lado, as álgebras de Grassmann e Clifford são válidas para espaços de qualquer dimensão.
Agradecimentos
Os autores gostariam de agradecer ao apoio financeiro do CNPq dos Processos 404463/2016-9 e 307520/2016-1. O primeiro autor também gostaria de agradecer ao Departamento de Matemática da Universidade Federal do Mato Grosso, Campus de Rondonópolis, por ter con-cedido afastamento para o curso de pós-graduação na UNESP - Ilha Solteira. Os autores também agradecem os comentários e sugestões pertinentes do árbitro da Revista Brasileira de Ensino de Física e do Editor.
Referências
[1] J. Lekner, Journal of Physics: Condensed Matter 18, 6149 (2006).
[2] R. Wunenburger, J.I.V. Lozano e E. Brasselet, New Journal of Physics17, 103022 (2015).
[3] D. Singh e N. Mobed, Classical and Quantum Gravity
28, 105024 (2011).
[4] L. Marrucci, E. Karimi, S. Slussarenko, B. Piccirillo, E. Santamato, E. Nagali e F. Sciarrino, Journal of Optics
13, 64001 (2011).
[5] V. Garcés-Chávez, D. McGloin, M.D. Summers, A. Fernandez-Nieves, G.C. Spalding, G. Cristobal e K. Dho-lakia, Journal of Optics A: Pure and Applied Optics6, S235 (2004).
[6] J.P. Silva e J.M. Tavares, American Journal of Physics
75, 53 (2007).
[7] S.J. Robinson, Physics Education49, 144 (2014). [8] T.J. Hendrickson, American Journal of Physics33, iii
(1965).
[9] S. Datta, American Journal of Physics46, 1190 (1978). [10] J. Lindén, Physics Education53, 23004 (2017). [11] R.M. Sutton, American Journal of Physics 26, 580
(1958).
[12] R.B. Prigo e M. Reading, American Journal of Physics
45, 636 (1977).
[13] T.M. Kalotas e A.R. Lee, American Journal of Physics
58, 80 (1990).
[14] L.J. Pellizza, M.G. Mayochi, L.C. Brazzano e S.E. Pe-drosa, American Journal of Physics83, 1019 (2015). [15] G.S. Krishnaswami e S. Sachdev, Resonance 21, 529
(2016).
[16] J. Vaz Jr., Revista Brasileira de Ensino de Física22, 5 (2000).
[17] F. Brackx, R. Delanghe e F. Sommen, Pitman Books Limited76, 308 (1982).
[18] J. Vaz Jr., Revista Brasileira de Ensino de Física19, 234 (1997).
[19] J. Vaz e R. Rocha Jr.,Algebras de Clifford e Espinores
(Editora Livraria da Física, São Paulo, 2012).
[20] M.J. Crowe,A history of vector analysis: The evolution of the idea of a vectorial system(Notre Dame University Press, London, 1967).
[21] J.W. Gibbs,Elements of vector analysis: arranged for the use of students in physics(Tuttle, Morehouse & Taylor, New Haven, 1884).
[22] J.W. Gibbs,The scientific papers of Josiah Willard Gibbs
(Dover, New York, 1961).
[23] O. Heaviside,Electrical Papers(Chelsea Publishing Com-pany, New York, 1970).
[24] S. Verma,Ideias Geniais. Os principais teoremas, teorias, leis e princípios científicos de todos os tempos(Editora Gutenberg, Belo Horizonte, 2011).
[25] I.D. Camargo e P. Boulos,Geometria analítica: um tra-tamento vetorial(Editora Pearson Education, São Paulo, 2005).
[26] P. Winterle,Vetores e geometria analítica(Editora Pe-arson Makron Books, São Paulo, 2014).
[27] J. Walker,Fundamentos de Física(Editora LTC, Rio de Janeiro, 2016).
[28] H.M. Nussenzveig, Curso de Física Básica: Mecânica
(Editora Edgard Blucher, São Paulo, 2013).
[29] W.R. Hamilton,Elements of quaternions(Chelsea Pu-blishing Company, New York, 1969).
[31] W.R. Hamilton, inProceedings of the Royal Irish Aca-demy, Dublin, 1847 (Royal Irish Academy, Dublin, 1847). [32] H.G. Grassmann,Die Lineale Ausdehnungslehre(Otto
Wigand, Leipzig, 1844).
[33] E.L. Lima, Álgebra Exterior (IMPA, Rio de Janeiro, 2009).
[34] W.K. Clifford, American Journal of Mathematics1, 350 (1878).
[35] D. Hestenes e A.N. Lasenby,Space-time algebra, (Gordon and Breach, New York, 1966).
[36] D. Hestenes, Journal of Mathematical Physics 8, 798 (1967).
[37] D. Hestenes, Journal of Mathematical Physics15, 1768 (1974).
[38] D. Hestenes, Foundations of Physics12, 153 (1982). [39] D. Hestenes e G. Sobczyk,Clifford algebra to geometric
calculus: a unified language for mathematics and physics
(D. Reidel Publishing Company, Dordrecht, 1984). [40] D. Hestenes, Foundations of Physics15, 63 (1985). [41] D. Hestenes, in:Clifford Algebras and their Applications
in Mathematical Physics, editado por J.S.R. Chisholm e A.K. Common (Springer, Dordrecht, 1986), v. 183, p. 321.
[42] D. Hestenes, New foundations for classical mechanics
(Kluwer Academic Publishers, Dordrecht, 1986). [43] D. Hestenes, in:Clifford Algebras and their Applications
in Mathematical Physics, editado por F. Brackx, R. De-langhe e H. Serras (Springer, Dordrecht, 1993), v. 55, p. 269.
[44] D. Hestenes, Advances in Applied Clifford Algebras7, 97, (1997).
[45] D. Hestenes, in:Clifford Algebras and their Applications in Mathematical Physics, editado por V. Dietrich, K. Habetha e G. Jank (Springer, Dordrecht, 1998), v. 94, p. 129.
[46] D. Hestenes, in:Geometric Algebra with Applications in Science and Engineering, editado por E.B. Corrochano e G. Sobczyk, (Birkhäuser, Boston, 2001), p. 3. [47] D. Hestenes, Foundations of Physics35, 903 (2005). [48] D. Hestenes e J.W. Holt, Journal of Mathematical
Phy-sics48, 23514 (2007).
[49] D. Hestenes, in:Geometric Algebra Computing,editado por E. Bayro-Corrochano e G. Scheuermann (Springer, London, 2010), p.3.
[50] D. Hestenes, Advances in Applied Clifford Algebras24, 257 (2014).
[51] D. Hestenes, Advances in Applied Clifford Algebras27, 351, (2017).