Cap5 Espaco de Estados Discreto

(1)

Capítulo 5

5 Espaço de Estados Discreto

A representação em forma de Matrizes de Estado é um das principais ferramentas de simulação de sistemas, e elas são formuladas diretamente no domínio em tempo contínuo ou discreto e não envolvem transformações para Laplace ou transformada Z.

5.1 Introdução à formulação de estado

Considerando um sistema massa-mola-amortecedor na forma, )

t ( u ) t ( ky ) t ( y c ) t ( y

m&& + & + =

Que pode ser reescrito como,

m ) t ( u ) t ( y ) t ( y 2 ) t (

y& + ζω_n& +ω2_n =

&

Definindo uma variável como,

) t ( y ) t ( x ) t ( y ) t (

x₁ = ⇒ &₁ = &

Definindo uma outra variável como,

) t ( y ) t ( x ) t ( x ) t ( y ) t (

x₂ = & = &₁ ⇒ &₂ =&&

Substituindo na equação original e deixando somente uma variável com a derivada temporal, então,

m ) t ( u ) t ( x ) t ( x 2 ) t (

x 2 ₁

n 2

n

2 + ζω +ω =

&

Agora, escrevendo um sistema na seguinte forma,

) t ( u m / 1

0

) t ( x

2 0 1

) t ( x

2 1

n 2

1

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢

⎣ ⎡

ζω − ω − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ & &

Ainda está faltando a resposta y(t) do sistema, que é dada por,

[

]

{ }

0u(t)

) t ( x

) t ( x 0 1 ) t ( y

2 1 ₊

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ =

Que pode ser escrito da seguinte maneira, ) t ( Du ) t ( Cx ) t ( y

) t ( Bu ) t ( Ax ) t ( x

+ =

&

(2)

5.2 Nomenclatura de Espaço de Estados

Vetor de estado x(t) é o vetor de ordem n que contém todos os estados. Vetor de saída y(t) é o vetor de ordem m que contém todas as respostas. Vetor de entrada u(t) é o vetor de ordem r que contém todas as entradas.

Matriz de estado A é a matriz de ordem n×n que contém os autovalores e os autovetores do sistema.

Matriz de entrada B é a matriz de ordem n×r da entrada. Matriz de saída C é a matriz de ordem m×n da saída.

Matriz de transmissão direta D é matriz de ordem m×r que correlaciona diretamente a entrada com a saída.

Então,

{ }

[ ]

{ }

[ ]

{ }

m1

[ ]

m n

{ }

n1

[ ]

m r

{ }

r 1 1 r r n 1 n n n 1 n

) t ( u D )

t ( x C )

t ( y

) t ( u B )

t ( x A )

t ( x

× ×

×

× ×

×

+ =

&

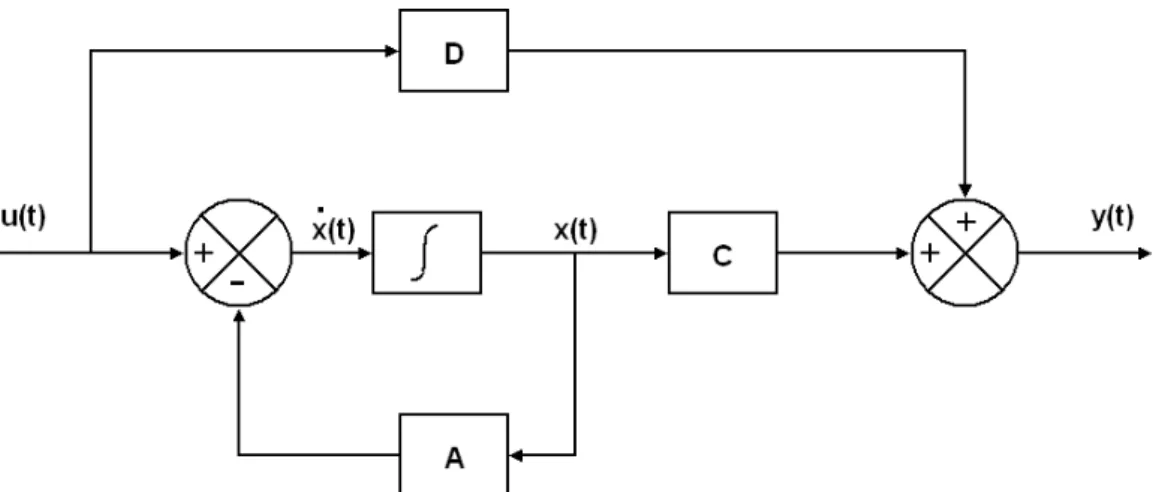
A representação em diagramas de bloco do sistema acima é dada por,

Figura 5.1: Representação em diagrama de blocos para tempo contínuo.

5.3 Representação de Espaço de Estados discretos

A formulação de espaço de estados discretos é dado por, )

k ( Du ) k ( Cx ) k ( y

) k ( Hu ) k ( Gx ) 1 k ( x

+ =

+

Nota-se que as matrizes C e D não mudaram, significando que são as mesmas matrizes para sistemas em tempo contínuo.

Agora, supondo um sistema discreto cuja função de transferência é dada por, n

n 1

1

n n 1

1 0

z a z

a 1

z b z

b b ) z ( U

) z ( Y

− −

+ + +

=

L L

Esta FT pode ser representada de várias maneiras em espaço de estados, pois a formulação de estado não é única.

(3)

A forma canônica controlável é dada por,

) k ( u

1 0 0 0

) k ( x

a a

1 0

0 0

0 1

0 0

1 0

) 1 k ( x

n 1 n

2 1

1 2

n 1 n n n

1 n

2 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

+

⎪ ⎪ ⎪

⎭ ⎪⎪ ⎪

⎬ ⎫

⎪ ⎪ ⎪

⎩ ⎪⎪ ⎪

⎨ ⎧

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

− −

− − =

⎪ ⎪ ⎪

⎭ ⎪⎪ ⎪

⎬ ⎫

⎪ ⎪ ⎪

⎩ ⎪⎪ ⎪

⎨ ⎧

+ + + +

− −

−

− M

M

L L

M O M

M M

L L

M

[

]

b u(k)

) k ( x

b a b b

a b b a b ) k (

y ₀

n 2 1

0 1 1 0

1 n 1 n 0 n

n +

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

− −

−

= ₋ ₋

M L

Se a matriz G for uma matriz de posto cheio, isto é, o determinante é diferente de zero, o sistema é controlável, caso contrário, significa que pelo menos 1 dos estados não é controlável. A controlabilidade significa que o sistema pode ser alterado de qualquer estado para qualquer estado em um período de tempo finito.

5.3.2 Forma Canônica Observável

A forma canônica observável é dada por,

) k ( u

b a b

) k ( x

a 1 0

0

a 0 0

0

a 0

0 1

a 0

0 0

) 1 k ( x

0 1 1

0 2 2

0 1 n 1 n

0 n n

n 1 n

2 1

1 2 1 n

n

n 1 n

2 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

− − − −

+

⎪ ⎪ ⎪

⎭ ⎪⎪ ⎪

⎬ ⎫

⎪ ⎪ ⎪

⎩ ⎪⎪ ⎪

⎨ ⎧

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

− − −

−

=

⎪ ⎪ ⎪

⎭ ⎪⎪ ⎪

⎬ ⎫

⎪ ⎪ ⎪

⎩ ⎪⎪ ⎪

⎨ ⎧

+ + + +

− −

−

M M

L L

M O M M M

L L

M

[

]

b u(k)

) k ( x

1 0

0 ) k (

y ₀

n 2 1

+

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

=

M L

Para o sistema ser completamente observável, a matriz G deve ser uma matriz de posto cheio. A observabilidade significa que todos os estados do sistema podem ser observados ou medidos.

5.3.3 Forma Canônica Diagonal

Expandindo a FT em frações parciais tal que,

n n

2 2

1 1 0

p z

c p

z c p z

c b ) z ( U

) z ( Y

− + − + − +

= L

(4)

) k ( u

1 1 1

) k ( x

p 0

0 0

0 p

0

0 0

p

) 1 k ( x

n 2 1

n 2

1

n 2 1

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

+

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

+ + +

M M

L M O M

L L

M

[

]

b u(k)

) k ( x

c c

c ) k (

y ₀

n 2 1

n 2

1 +

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

=

M L

onde pi representa os pólos do sistema.

5.3.4 Forma Canônica de Jordan

A forma canônica de jordan é usada quando se deseja representar o sistema na forma diagonal mas existem pólos repetidos. Supondo que o pólo p1 é repetido m vezes,

então,

) k ( u

1 1 __ 1 0 0

) k ( x

_______ ) k ( x

) k ( x

p 0

0 p

] 0 [

p 0

0 0

0 1

p 0

0 0

1 p

) 1 k ( x

_______ ) 1 k ( x

) 1 k ( x

n 1 m m 2 1

n 1

m 1 1

1

n 1 m m 2 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

+

⎪ ⎪ ⎪ ⎪ ⎪ ⎪

⎭ ⎪⎪ ⎪ ⎪ ⎪ ⎪

⎬ ⎫

⎪ ⎪ ⎪ ⎪ ⎪ ⎪

⎩ ⎪⎪ ⎪ ⎪ ⎪ ⎪

⎨ ⎧

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

⎪ ⎪ ⎪ ⎪ ⎪ ⎪

⎭ ⎪⎪ ⎪ ⎪ ⎪ ⎪

⎬ ⎫

⎪ ⎪ ⎪ ⎪ ⎪ ⎪

⎩ ⎪⎪ ⎪ ⎪ ⎪ ⎪

⎨ ⎧

+ + + + +

+ +

+

M M

L M O M

L L

M O M M M

L L

M M

[

]

b u(k)

) k ( x

c c

c ) k (

y ₀

n 2 1

n 2

1 +

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

=

M L

5.3.5 Não unicidade das matrizes de estado

A representação de estado não é única, isto é, para um mesmo sistema na forma de função de transferência pode haver várias representações de estado. Por exemplo, supondo que um sistema seja observável e controlável, definições que serão apresentada mais à frente, então haverá uma representação na forma canônica controlável e observável.

Para exemplificar, supondo o sistema na seguinte forma de estado, )

k ( Du ) k ( Cx ) k ( y

) k ( Hu ) k ( Gx ) 1 k ( x

+ =

+

(5)

) k ( xˆ P ) k (

x =

onde a matriz P é de ordem n×n, mesma ordem da matriz G. Então, )

k ( Du ) k ( xˆ CP ) k ( y

) k ( Hu ) k ( xˆ GP ) 1 k ( xˆ P

+ =

+

Que pode ser reescrito como,

) k ( Du ) k ( xˆ CP ) k ( y

) k ( Hu P ) k ( xˆ GP P ) 1 k (

xˆ 1 1

+ =

+ − −

Agora definindo,

GP P

Gˆ = −1 , Cˆ =CP e Hˆ =P−1H Então,

) k ( Du ) k ( xˆ Cˆ ) k ( y

) k ( u Hˆ ) k ( xˆ Gˆ ) 1 k ( xˆ

+ =

+

Que é exatamente da mesma forma que o sistema original. Se a matriz P for a matriz dos autovetores da matriz G, então o sistema será diagonalizado, caso isso não seja possível, a matriz resultante será a matriz de Jordan.

5.4 Simulando um sistema na forma de estado discreto

Nesta parte, supõe-se que o sistema seja linear e invariante no tempo na forma, )

k ( Du ) k ( Cx ) k ( y

) k ( Hu ) k ( Gx ) 1 k ( x

+ =

+

Pegando apenas os estados do sistema, para o instante inicial têm-se, )

0 ( Hu ) 0 ( Gx ) 1 (

x = +

Para o instante seguinte,

(

Gx(0) Hu(0)

)

Hu(1) G x(0) GHu(0) Hu(1) G

) 1 ( Hu ) 1 ( Gx ) 2 (

x = + = + + = 2 + +

Para o instante seguinte,

(

)

) 2 ( Hu ) 1 ( GHu )

0 ( Hu G ) 0 ( x G

) 2 ( Hu ) 1 ( Hu ) 0 ( GHu )

0 ( x G G ) 2 ( Hu ) 2 ( Gx ) 3 ( x

2 3

2

+ +

+ =

= +

+ +

= +

=

Fazendo isso para k instantes,

∑

−

= − − +

= k 1

0 j

1 j k k

) j ( Hu G

) 0 ( x G ) k (

x k = 1, 2, 3 ...

Substituindo este resultado em y(k),

) k ( Du ) j ( Hu G

) 0 ( x G C ) k ( y

1 k

0 j

1 j k

k +

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

+

=

∑

−

= − −

k = 1, 2, 3 ...

5.5 Passando de Matrizes de Estado para FT

Supõe-se o sistema na forma,

) k ( Du ) k ( Cx ) k ( y

) k ( Hu ) k ( Gx ) 1 k ( x

+ =

+

(6)

) z ( DU ) z ( CX ) z ( Y

) z ( HU ) z ( GX ) 0 ( zx ) z ( zX

+ =

−

Supondo condições iniciais nulas,

(

zI G

)

X(z) HU(z) X(z)

(

zI G

)

HU(z) )

z ( HU ) z ( GX ) z (

zX = + ⇒ − = ⇒ = − −1

Substituindo em Y(z),

(

zI G

)

HU(z) DU(z)

[

C

(

zI G

)

H D

]

U(z) C

) z (

Y = − −1 + = − −1 +

Como a função de transferência pulsada é a relação dada por Y(z)/U(z),

(

zI G

)

H D

C ) z ( U

) z (

Y ₌ ₋ −1 ₊

Observe que se Y(z)/U(z) é uma matriz m×r.

5.6 Discretização de Matrizes de Estado Contínuas

Em se tratando de sistemas em tempo discreto, pode-se converter diretamente de matrizes de estado contínuas para matrizes de estado discretas. Porem é necessário fazer uma revisão de matrizes antes de mostrar o processo de discretização.

Em se tratando de matrizes há alguns cuidados a serem tomados e algumas definições a serem compreendidas. Começando com,

∑

∞

= = + +

+ +

+ =

0 k

k k k

k 2

2 At

! k

t A t

A ! k

1 t

A ! 2 1 At I

e L L

Diferenciando esta solução em relação ao tempo, para isso a derivada é feita termo a termo, encontra-se,

A e Ae e

dt

d _At _At _At

= =

Agora, três relações importantes,

I e eAt −At =

(A B)t At Bt

e e

e + = se AB = BA

(A B)t At Bt

e e

e + ≠ se AB ≠ BA

Agora, obtendo a resposta para matrizes de estado contínuas, isto é, )

t ( Bu ) t ( Ax ) t (

x& = + Que pode ser reescrita como,

) t ( Bu ) t ( Ax ) t (

x& − = Agora pré-multiplicando por e-At,

[

]

(

e x(t)

)

e Bu(t) dt

d ) t ( Ax ) t ( x

e−At & − = −At = −At Integrando1 de 0 a t,

∫

τ τ

=

− − τ

− t

0 A At

d ) ( Bu e ) 0 ( x ) t ( x e

Que pode ser rearranjada como,

( )

∫

τ τ

+

= t −τ

0 t A At

d ) ( Bu e

) 0 ( x e ) t ( x

A equação acima representa a solução para um sistema na forma de estado contínuo. Para a solução completa, basta substituir os estados x(t) em,

1

(7)

) t ( Du ) t ( Cx ) t (

y = +

Para fazer o mesmo para um sistema discreto, tem-se que,

) kT ( Hu ) kT ( Gx ) T ) 1 k (( x )

t ( Bu ) t ( Ax ) t (

x& = + ⇒ + = +

Para que possa ser utilizada a solução de um sistema contínuo para encontrar a solução de um sistema discreto, assume-se que a entrada u(t) entre um período e outro de amostragem é constante, isto é, que há um ZOH, então,

) kT ( u ) t (

u = kT ≤ t < kT+T Então, a solução,

( )

∫

τ τ

+

= t −τ

0 t A At

d ) ( Bu e

) 0 ( x e ) t ( x

Para o tempo kT,

∫

τ τ

+

= kT − τ

0 A AkT AkT

d ) ( Bu e e ) 0 ( x e ) kT ( x

Para o tempo (k+1)T,

( +) ₊ (( +) )( +

_∫

) − τ _τ _τ

=

+ k 1T

0 A T

1 k A T

1 k A

d ) ( Bu e e

) 0 ( x e ) T ) 1 k (( x

Agora fazendo,

( ) ( ) (( ) ) ( )

⎥ ⎦ ⎤ ⎢

⎣ ⎡

τ τ +

− τ τ +

= −

+ + +

∫

+ −τ kT

∫

−τ

0 kT A AkT

AT T

1 k

0

T 1 k A T

1 k A AT

d ) ( Bu e

) 0 ( x e e d ) ( Bu e

) 0 ( x e ) kT ( x e ) T ) 1 k (( x

Simplificando2,

( )

(

)

( ) ( )

∫

+ τ − +

τ − +

τ − + +

τ τ +

=

τ τ −

τ τ +

− +

= +

T 1 k

kT A T 1 k A AT

kT

0 A AkT AT T

1 k

0 A T 1 k A AkT

AT T 1 k A AT

d ) ( Bu e e

) kT ( x e

d ) ( Bu e e e d ) ( Bu e e

) 0 ( x e e e

) kT ( x e ) T ) 1 k (( x

Supondo agora o ZOH, então, o tempo entre kT e (k+1)T pode ser substituído por 0 e T dentro da integral, pois o que vai variar é apenas u(τ) que é considerado constante. Então,

∫

τ τ

+ =

+ T − τ

0 A AT

AT_x₍_kT₎ _e _e _Bu₍ ₎_d e

) T ) 1 k (( x

Aplicando a transformação de variável onde λ = T-τ,

∫

λ λ

+ =

+ T λ

0 A

AT_x₍_kT₎ _e _Bu₍ ₎_d e

) T ) 1 k (( x

Que representa a solução da equação de estado discreta na forma, )

kT ( Hu ) kT ( Gx ) T ) 1 k ((

x + = +

Que neste caso, tem-se que para encontrar estas matrizes discretas, necessariamente,

AT e

G= e H e d B T

0 A

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

λ =

_∫

λ

Pelas equações acima, verifica-se claramente que as matrizes discretas são dependentes do tempo de amostragem.

2

(8)

A solução para y(kT) é dada simplesmente por, ) kT ( Du ) kT ( Cx ) kT (

y = +

Se a matriz A for não singular, então

(

e I

) (

B e I

)

A B A

B d e

H 1 AT AT 1

T

0

Aλ = − − = − −

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

λ =

∫

Exemplo 5.1: Considerando o sistema abaixo, encontrar a representação de estado discreto e a expressão para função de transferência discreta para T = 1 s.

2 1 2

2 2

a s a s

b s

2 s

1 )

2 s ( s

1 )

s ( G

+ + = + = + =

Solução: O primeiro passo é encontrar uma representação de estado para o sistema, utilizando a forma canônica controlável,

[

]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ =

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢

⎣ ⎡

− = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧

) t ( x

) t ( x 0 1 ) t ( y

) k ( u 1 0 ) t ( x

) t ( x 2 0

1 0 ) t ( x

) t ( x

2 1

& &

Como foi visto, para as matrizes discretas têm-se3,

(

)

⎥ ⎦ ⎤ ⎢

⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢

⎢ ⎣

⎡ ₋

= =

− −

1353 . 0 0

4323 . 0 1 e

0

e 1 2 1 1 e

G

T 2

T 2 AT

Outra forma de encontrar a matriz G é fazendo,

[ ]

(

)

(

)

⎥ ⎥ ⎥ ⎥ ⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎣ ⎡

+ + =

−

= −

2 s

1 0

2 s s

1 s 1 A

sI e

L At 1

Cuja transformada de laplace inversa é dada por,

(

)

(

)

⎥ ⎥ ⎦ ⎤ ⎢

⎢ ⎣

⎡ ₋

= ⎥ ⎥ ⎥ ⎥ ⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎣ ⎡

+ + =

− − −

t 2

t 2 1

At

e 0

e 1 2 1 1 2

s 1 0

2 s s

1 s 1 L e

Então,

(

)

(

)

(

)

⎥⎦

⎤ ⎢

⎣ ⎡ = ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

−

⎟⎟ ⎠ ⎞ ⎜⎜

⎝

⎛ ₊ −

= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

−

⎟⎟ ⎠ ⎞ ⎜⎜

⎝

⎛ ₊ −

=

= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜

⎜ ⎝ ⎛

λ ⎥ ⎥ ⎦ ⎤ ⎢

⎢ ⎣

⎡ ₋

= ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

λ =

− −

λ −

λ − λ

∫

4323 . 0

2838 . 0 e

1 2 1

2 1 e T 2 1 1 0 e

1 2 1 0

2 1 e T 2 1 T

1 0 d e

0

e 1 2 1 1 B

d e H

T 2 T 2

T

0 2

2 T

0 A

Desta forma, o sistema discreto na forma de matrizes de estado é dado por,

3

∑

∞

=

= + +

+ +

+ =

0 k

k k k

k 2

2 At

! k

t A t

A ! k 1 t

A ! 2 1 At I

(9)

[

]

⎭ ⎬ ⎫ ⎩

⎨ ⎧ =

⎥ ⎦ ⎤ ⎢

⎣ ⎡ + ⎭ ⎬ ⎫ ⎩

⎨ ⎧ ⎥ ⎦ ⎤ ⎢

⎣ ⎡ = ⎭ ⎬ ⎫ ⎩

⎨ ⎧

+ +

) k ( x

) k ( x 0 1 ) k ( y

) k ( u 4323 . 0

2838 . 0 ) k ( x

) k ( x 1353 . 0 0

4323 . 0 1 ) 1 k ( x

) 1 k ( x

2 1

Para a representação em FT discreta,

(

)

[

]

1353 . 0 z 1353 . 1 z

1485 . 0 z 2838 . 0 0 4323 . 0

2838 . 0 1353 . 0 0

4323 . 0 1 1 0

0 1 z 0 1

D H G zI C ) z ( G ) z ( U

) z ( Y

2 1

1

− −

+ =

+ ⎥ ⎦ ⎤ ⎢

⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

⎥ ⎦ ⎤ ⎢

⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ =

+ −

= =

− −

O mesmo problema pode ser resolvido utilizando o Matlab,

clear all;close all;clc

% Planta contínua

num=1; % numerador

den=[conv([0 0 1],[1 2 0])]; % denominador % Transformando para matrizes de Estado

[A,B,C,D]=tf2ss(num,den)

% discretizando as matrizes

T=1;

[G,H]=c2d(A,B,T)

% voltando para TF discreta

[numd,dend]=ss2tf(G,H,C,D)

Observe que neste caso, as matrizes de estado não estão na forma canônica, mas o resultado em Função de Transferência deve ser exatamente o mesmo.

5.7 Exercícios Resolvidos

Exemplo 5.2: Para o sistema abaixo, converter para matrizes de estado discretas utilizando o Matlab,

10 s 6325 . 10 s 6325 . 1 s

2 s )

s ( G

2

3 + + +

+ =

clear all;close all;clc

% denifindo os dados da planta

T=0.1; num=[1 2];

den=conv([1 2*0.1*sqrt(10) 10],[1 1]);

% Funções de Transferencia

Gs=tf(num,den) % planta contínua

Gz=c2d(Gs,T) % planta discreta % Matrizes de Estado

(10)

MEs=ss(A,B,C,D) % empacotando

MEz=c2d(MEs,T) % Matrizes de estado discreta

Exemplo 5.3: Para uma suspensão ativa representando ¼ de veículo, escrever as matrizes de estado contínuas supondo que o distúrbio da via seja w(t).

Neste caso, as matrizes que regem o comportamento dinâmico do sistema são dadas por,

Massa Suspensa,

(

x x

)

k

(

x x

)

u(t) c

x

m_S&&_S + _S &_S− &_N + _S _S− _N =

Masssa Não-Suspensa,

(

x x

)

k

(

x x

)

k x k w(t) u(t) c

x

m_N&&_N + _S &_N −&_S + _S _N − _S + _P _N = _P − Que na forma matricial fica,

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− =

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ −

− +

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢

⎣ ⎡ −

− +

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢

⎣ ⎡

) t ( u ) t ( w k

) t ( u

x x

k k k

k k

x x

c c

x x

m 0

0 m

p P

S

P S S

S S

P S

S S

P S

N S

& & &

Este caso representa um sistema MIMO, duas entradas e duas saídas. Definindo as variáveis de estado iniciando pelos deslocamentos,

S 1 S

1 x x x

x = ⇒ & = & e x₂ =x_N ⇒ x&₂ =x&_N Para as velocidades,

S 1 3 x x

x = & =&& e x₄ =x&₂ =&x&_N

Com as definições acima, as equações de estado são dadas por, 3

1 x x& =

4 2 x

x& =

(

)

(

)

S 2

1 S S 4 3 S S 3

m ) t ( u x x m

k x x m

c

x& =− − − − +

(

)

(

)

u(t)

m 1 ) t ( w m

k x m

k x x m

c x

N N

P 2 N P 1 2 N S 3 4 N S

4 =− − − − − + −

&

Que na forma matricial fica,

(

)

⎭

⎬ ⎫ ⎩ ⎨ ⎧

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

− +

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

− +

−

− −

=

⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧

w u

m k m

1 0 m

1

0 0

x x x x

m c m

c m

k k m

k

m c m

c m

k m

k

1 0

0 0

0 1

0 0

x x x x

N P

N S

4 3 2 1

N S

N P S

N S

S S

4 3 2 1

& & & &

(11)

)} t ( F { )} t ( X ]{ K [ )} t ( X ]{ C [ )} t ( X ]{ M

[ && + & + =

Sendo que o vetor de estado,

{

}

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ = ) t ( X ) t ( X ) t ( X _&

E as matrizes de estado,

{ }

U

F ] M [ ] 0 [ X C ] M [ K ] M [ I ] 0 [

X ₁ ₁ ₁ _⎥

⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − = ₋ ₋ ₋ &

A resposta do sistema deve ser dado pelo que se deseja medir, supondo que seja necessário medir os deslocamentos e velocidades,

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ w u 0 0 0 0 0 0 0 0 x x x x 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 y y y y 4 3 2 1 4 3 2 1

Caso seje necessário medir apenas o deslocamento da massa suspensa,

{ }

[

]

[

]

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = w u 0 0 x x x x 0 0 0 1 y 4 3 2 1 1

Exemplo 5.4:Para o sistema abaixo, encontrar as matrizes de estado.

As equações de movimento na forma matricial são dadas por,

⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ + − + − + = ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − − + − − + ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 3 3 3 2 2 2 1 1 3 2 1 3 2 3 3 2 1 2 2 1 3 2 1 3 2 1 u F u u F u u F x x x k k k 0 k k k k 0 k k x x x m 0 0 0 m 0 0 0 m & & & & & &

Portanto, as matrizes de estado podem ser dadas como,

⎪ ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − + ⎪ ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + − + − − = ⎪ ⎪ ⎪ ⎪ ⎭ ⎪⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎪ ⎨ ⎧ 3 2 1 3 2 1 3 3 2 2 2 1 1 1 6 5 4 3 2 1 3 3 2 3 3 2 3 2 2 1 2 2 1 2 1 1 6 5 4 3 2 1 u u u F F F m 1 0 0 m 1 0 0 m 1 m 1 0 0 m 1 0 0 m 1 m 1 0 0 m

10 0 0 0 0 0