It consists of a short overview of the "topological recursion", a relation that appears in the asymptotic expansion of. The purpose of this short article is just a small glimpse of the rapidly developing mathematics of these invariants. Ln) be the hyperbolic volume (called the "Weil-Petersson volume" [2], see fig. 1) of the moduli-spaceMg,n of genusg bor-.
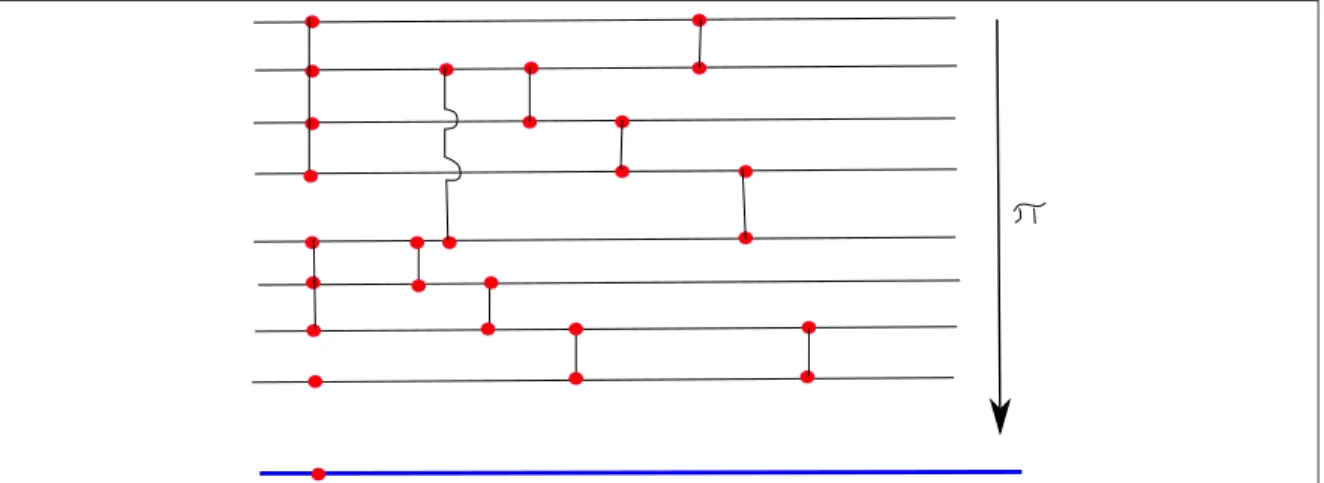
The 3g−3 +n lengths of the glued boundaries and the 3g−3 +n glue angles are called the Fenchel Nielsen coordinates. Topologically, a branched cover is the data of the cover transformations (a permutation of skins) at each branch point, which requires that one of the. A branched covering (Σ, π) of the Riemann sphere CP1, is the data of a Riemann surfaceΣ, and an analytic mapπ: Σ→CP1 of some measure.
Again, this theorem is an illustration of the universal "topological recursion", which we shall see below. The connected components of Σ\G are called faces, they are surrounded by edges and vertices of the graph.

Introductory remark: Invariants in Geometry
Random Matrices
The purpose of this section is to recall how topological recursion (which is primarily a geometric notion) was first discovered from the study of large random matrices, and then happened to have a much wider scope in a geometric setting. For example, the equilibrium measure for the eigenvalues of a Gaussian random matrix is the famous "Wigner semicircle". Another famous example is the "Markenko-Pastur Law", for the singular values of the Gaussian random matrix anM× N with variance σ2. where a and b are zeros of the square root term).
Around 2004 it was observed that the knowledge of the equilibrium measure is sufficient to recover the asymptotic expansion of any expectation value and all orders in the asymptotic expansion. In other words, if S is the planar algebraic curve of the equilibrium measure, then all correlation functions are obtained only as universal functions of S. Under "good assumptions" on the measure dµ, the partition function has a large N asymptotic expansion of the form.
For example, F1(S) is (up to some extra factors beyond the scope of this introductory review, see [1]) the log of the determinant of a canonical Laplacian on S. It was also discovered that there are also universal functionals ωg,n : S 7→ ωg,n(S) which calculates the gth order in the large N expansion of the joint probability of n−eigenvalues (more precisely the cumulants of correlations of n resolvents). Therefore, for random matrices, there exists some functional ωg,n (and we call Fg = ωg,0) that calculates all correlation functions from the geometry of the spectral curve alone.
Eventually, this means that knowing S (which is the large N equilibrium density of eigenvalues) allows recovery of all correlation functions of the random matrix law, i.e. since the functions ωg,n that give the expected values are universal and do not require anything other than curves S, we can try to apply these functionals ωg,n to any arbitrary algebraic curve, regardless of whether this algebraic curve S was connected to laws of random matrices or not. In a sense, topological recursion defines a "pseudo-random matrix law" associated with any plane curve S.
As we will see, topological recursion uses only local properties of the curve (residues) and thus extends analytically to curves that are not necessarily algebraic.
Link with Mirror symmetry
We will call them the "symbolic invariants of S" or the "TR (topological recursion) invariants" of S. The equilibrium spectral curve of a pseudo-random matrix (or more precisely its Stielje transform), is an analytic function y = f(x), defined on a Riemann surface with a complex structure. The probability law of the pseudo-random matrix, i.e. the spectral curve, may depend on several parameters ˆt= (ˆt1,ˆt2,.
Deformations of the probability law induce deformations of the spectral curve and especially deformations of its complex structure. One is often interested in studying how the amplitudes depend on the parameters and thus unravel the complex structure of the modulus space. Mirror symmetry is the claim that an A-model is dual to a B-model and vice versa, and there exists a "mirror map" t7→ˆt like that.
One of the problems of mirror symmetry is identifying which spectral curve to associate with an enumeration geometry problem, i.e. Usually the spectral curve is a very simple and natural geometric object from the point of view of the A model. It is typically the "most likely form" of the objects counted in the A model, in some "major limit".
This is the case for random matrices, the spectral curve is the large size limit of the eigenvalue density. Another example occurs with counting plane distributions, where the spectral curve is the shape of the limiting plane distribution (often called polar circle). But unfortunately there is no general recipe of how to find the spectral curve mirror of a given A model.
-Lakkoofsota walqaxxaamuraa sagalee y2 =x Wg,n=P. Ln) y= sin (2π4π√x) Lakkoofsota HurwitzHg(μ) ye−y = ex Maatiriksii tasaa: babal’ina asimptootikii y= 2iπρeq(x) faankishiniiwwan walqabsiisaa.
Some applications of symplectic invariants
Toric Calabi-Yau Gromov-Witten mirror curve invariants H(ex,ey) = 0 Knot theory Jones polynomial A polynomialA(ex,ey) = 0. The idea of the proof of [16, 17] is that the recursive structure of the topological recursion can be coded as graphs (see def. 4.5 below), so the ωg,n( ˆX) can be written as the sum of weighted graphs. Those graphs, except for some combinatorial manipulations, coincidentally coincide with the localization graphs of Gromov-Witten invariants [70, 71].
The sign variety K is the locus of eigenvalues of the holonomies of the planar connection SL(2) on the complement of knots S3\K. The Jones polynomial JN(q)∈C[q] depends on N (denoting the representation) and is a polynomial of the variable q. Conjecture: A Jones knot polynomial is a set in ~ whose coefficients are the principal symplectic invariants of its A-polynomial.
If true (which is of course expected), this conjecture would be an extension of the famous 'Volume conjecture' and imply a new understanding of what Jones polynomials are, in particular that Jones polynomials are Tau functions of some integrable systems.
Spectral curves
In other words, the invariants are always well-defined, but they have several properties if, in addition, the Riemann surface has structure, for example if it is connected and/or compact, and for example if B is globally meromorphic.
Definition by recursion (B-model side)
The definition gives a special role to p1, but the result of the sum of residues is in fact symmetric in allpi's, it can be proved by recursion [1]. In fact, branch points of higher order ra > 2 can be obtained by taking a limit of several simple branch points that merge smoothly. It was proved in [26] that the limit of the definition with simple branches, indeed converges to that of.
For specialists, higher order branch points correspond to structures not necessarily semisimple Frobenius manifolds in the Givental formalism. The definition of F1 and F0 is given in [1], but we will not write it in this short review.
Definition as graphs
There are k unarrowed edges that go from a vertex to a leaf, and g unarrowed edges that connect two inner vertices. Two inner vertices can only be connected by an unarrowed edge if one is older than the other along the tree. If an edge with arrow and an inner edge without arrow come from a vertex, then the edge with arrow is the left child.
This rule only applies when the non-arrow edge connects this vertex to one of its descendants (not one of its parents). Kap(p, q) (4.12) where the order of taking the residuals is by following the arrows from leaves to root (deeper vertices are integrated first). Those graphs are simply a notation for the previous recursive definition, they are simply a convenient mnemonic rewriting.
This graphical notation is very convenient, is a good support for intuition and is very useful for proving some theorems.
A-model side definition
BGavM(agvv,n)v (4.23) where M(a)g,n are #{a} copies of Mg,n labeled by the branch points a, and BGa the classification space of the local Galois group Ga at the branch point a , and BGaMg,n is determined by the Chen-Ruan cohomology of C3/Ga. Then, we define the following tautological classes on the cohomology ring of the modulo space Mg,n(a). Proof idea: Using the graphical definition def.4.5 of theog,n, with a recombination of vertices of the same color, find that ωg,n can be written as a sum over the graphs of a Wick theorem where the edge weights are ˆBa ,k;b,l and it remains to calculate the weights of the vertices.
Since vertices are independent of the ˆBa,k;b,l, they can be found from the case that all ˆBa,k;b,l disappear, and when there is only one branch point. Then the Baker-Akhiezer function. converted into a vector by choosing pi ∈ C the preimages of a point x ∈ C0 from the base through the projection map. 6.10) where Lq is a Higgs field whose spectral curve is C (the eigenvalues of Lq are independent of q, only the eigenvectors depend on q). The spectral curve is the so-called A polynomial of the node, it is also called the character variant of the node.
The number of branched coverings of the sphere with torus and faces of higher genera. The Laplace transform of the cut-and-join equation and the Bouchard-Marino conjecture on Hurwitz numbers. Orantin, "Computation of open Grom-Witten invariants for Calabi-Yau toric triples by topological recursion, a proof of the BKMP conjecture," arXiv:1205.1103v1 [math-ph].
Murakami, SL2(C) Chern-Simons theory and the asymptotic behavior of the colored Jones polynomial, Lett. Hikami, the generalized volume conjecture and A polynomials: the Neumann-Zagier potential function as a classical limit of the partition function. 54] I.Krichever “The τ-function of Whitham's universal hierarchy, matrix models and topological field theories”, Commun.Pure Appl.Math.
Sorkin, “Spectral curve of Eynard-Orantin recursion via Laplace transform,” arXiv:1202.1159v1 [math.AG]. Enumerative geometry of stable mappings with Lagrangian boundary conditions and multiple disc covers. Mumford, “Towards an enumerative geometry of the moduli space of curves”, in Arithmetic and Geometry (M Artin, J. Tate, editors), vol.