Un développement de cette méthode permet d'étendre la modélisation de la propagation des ondes acoustiques à l'échelle des quartiers [70]. Dans le cadre de l'étude de la propagation acoustique, l'approche unidirectionnelle consiste à considérer la propagation des ondes selon une direction de propagation privilégiée.
Généralités sur les équations paraboliques
- Formulation de l’équation parabolique petit angle
- Décomposition de l’équation de Helmholtz
- Splitting de l’équation d’onde conduisant aux équations paraboliques petit
- Equation parabolique grand angle
- Conclusion
La première partie présente l'approximation unidirectionnelle de l'équation des ondes sous forme d'équations paraboliques. L'équation parabolique aux petits angles (1.3) peut être déterminée à l'aide du système de décomposition de l'équation d'onde (1.7).
Formulation multimodale de la propagation acoustique unidirectionnelle
- Généralités sur la méthode multimodale en guide de section variable
- Décomposition du champ de pression
- Approximation unidirectionnelle
- Conclusion
Une deuxième forme de l’équation multimodale unidirectionnelle est proposée à partir de la forme finale de la décomposition des équations d’onde (1.34). Cela donne lieu à un développement asymptotique de la solution de l’équation des ondes sous forme de série de Bremmer, mais en deux dimensions.
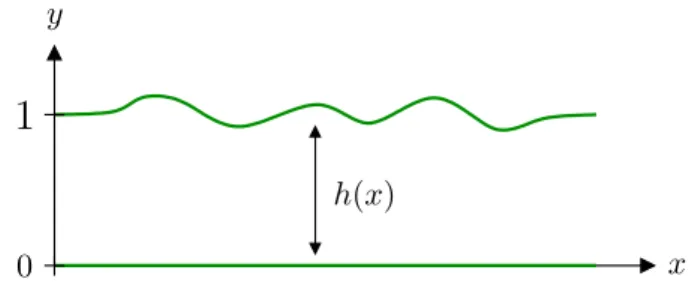
Projection de l’équation d’onde sur les modes transverses
Modified parabolic equation method
- Formulation
- Boundary condition
- Numerical scheme
Validation of the modified parabolic equation
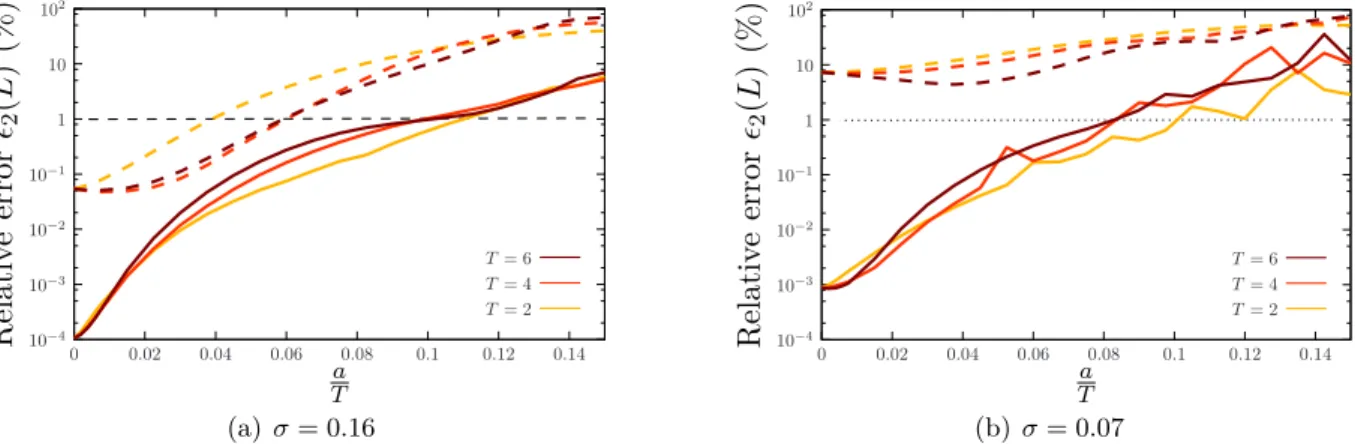
Range of validity
From these results it also appears that the maximum slope a/T can be an important parameter to estimate the limit of the validity range of the method. The geometry of the irregular part is randomly generated using polynomial functions, where the maximum slope is fixed toa/T = 0.1.

Conclusion
3.4 – Représentation de la résolution numérique de l'équation parabolique 3D par la méthode des directions alternatives (exemple pour M = 3). Pour modéliser une variation brusque de la largeur d'une rue, la méthode de résolution de l'équation parabolique tridimensionnelle est associée à une approximation de Kirchhoff. De manière plus quantitative, la figure 5.8 présente l'évolution de l'erreur relative ǫ1 sur le champ de pression en fonction de la séquence d'évolution de la série.
Cette partie traite de la décomposition du champ de pression en série de Bremmer à l'intérieur d'un guide d'onde irrégulier. Cela correspond pour chaque ordre de la série à la moitié des composantes du champ de pression (voir Fig. 5.12). Par définition, l'approximation unidirectionnelle en fin de guide ne peut pas présenter une erreur plus importante que la reconstruction du champ de pression jusqu'à l'ordre 1.
Dans le cadre de la propagation acoustique en milieu urbain, une méthode de résolution de l'équation parabolique tridimensionnelle a été présentée. La forme complète de l'équation multimodale unidirectionnelle a été présentée comme une reconstruction partielle de la série de Bremmer. A partir de l’ordre 1, certains composants de la série ne sont pas pris en compte.
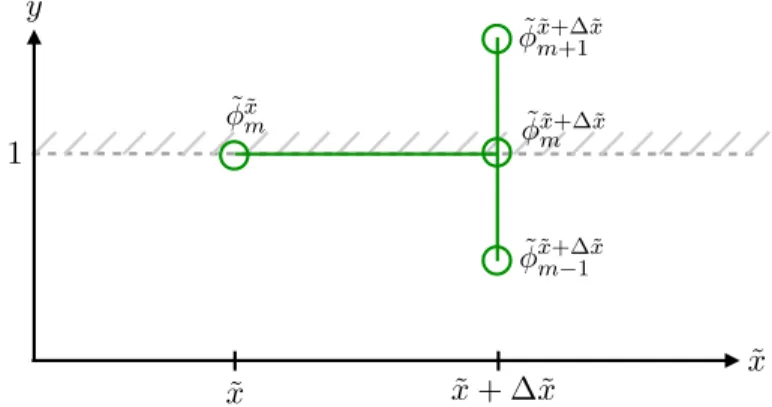
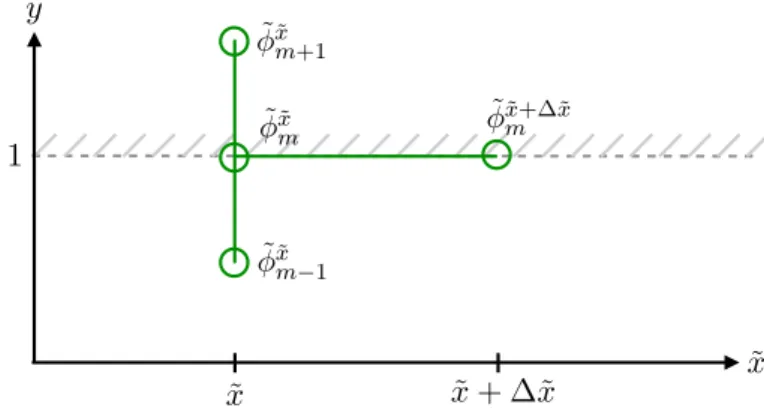
Finite Difference implementation of the boundary condition
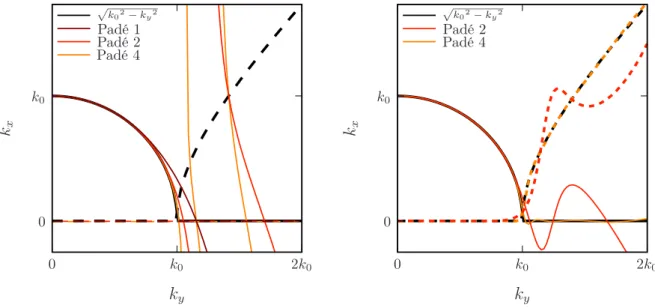
Rotation angles in the complex plane for complex Padé coefficients
Formulation d’une équation parabolique 3D en guide d’ondes ouvert
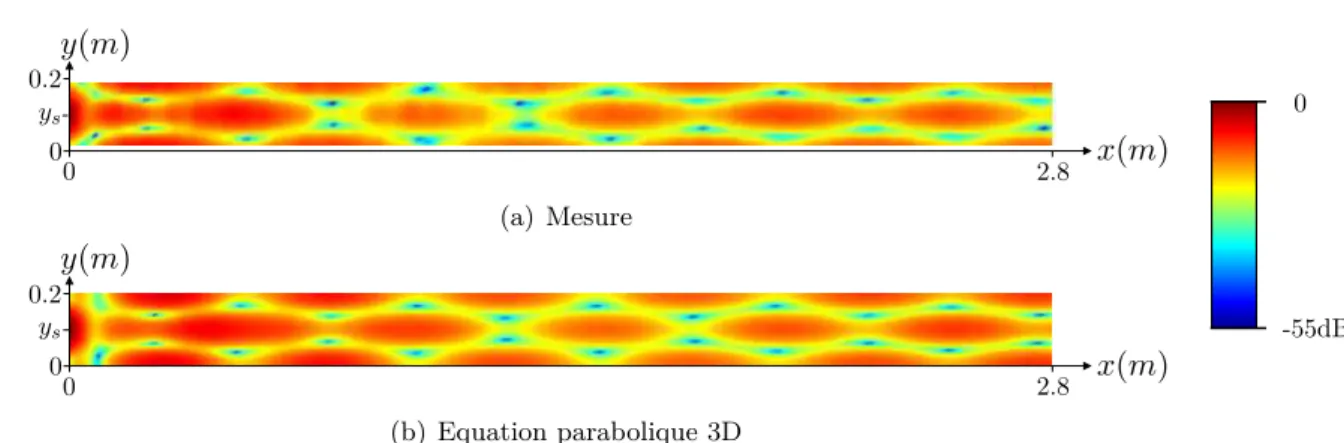
3.5 – Représentation de la décomposition du domaine numérique transverse imposée par la méthode des directions alternées. Pour cela, une cartographie du champ de pression transversal à l'entrée de la rue est systématiquement mesurée pour chaque configuration du modèle. Pour une rue de dimensions Ly = 0,2 m et Lz = 0,3 m, la Figure 3.10(a) présente la cartographie du champ de pression transversal mesuré à l'entrée de la rue.
Pour l'exemple de la Figure 3.10, cette approche ne semble pas fausser l'interpolation du champ de pression mesuré. La figure 3.11 présente les cartes des niveaux de pression mesurés et simulés au sein de la rue dans un planxy.
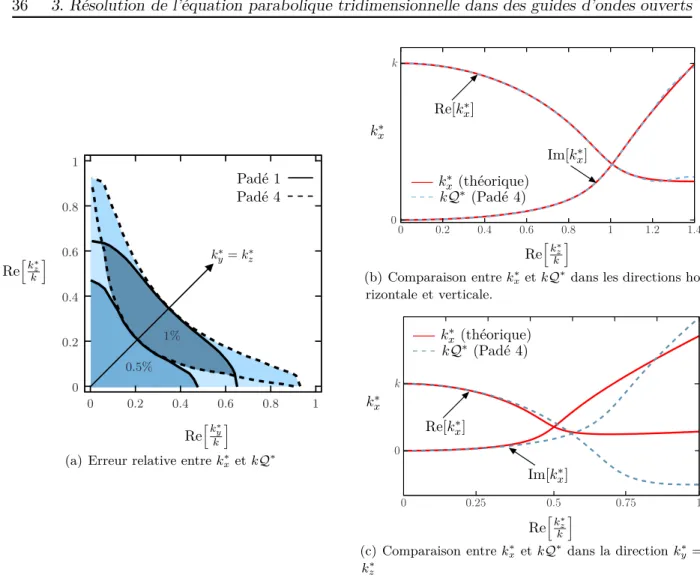
Conclusion
3.14 – Comparaison à 2500 Hz entre mesure et simulation du niveau de pression et de l'intensité acoustique Iy dans l'axe de la source (ys= 10 cm et zs= 7 cm). Les comparaisons qui viennent d'être présentées entre données expérimentales et simulations permettent de souligner la validité de la méthode de résolution de l'équation parabolique tridimensionnelle. Tant au niveau de la localisation des interférences qu'au niveau de la réduction de l'intensité acoustique intégrée, les tendances prédites par la simulation décrivent assez fidèlement la propagation des ondes acoustiques pour les exemples évoqués précédemment.
La principale limitation de la méthode réside dans la séparation des opérateurs transversaux, ce qui limite la validité de l'équation parabolique tridimensionnelle. Le développement de l'opérateur transversal à un ordre supérieur [12, 21] permet de s'affranchir de cette limitation au détriment de la complexité du schéma numérique et de l'augmentation du coût numérique de la méthode.
Variation brusque de la section du guide d’ondes
- Approximation de Kirchhoff
- Validation par comparaison avec des résultats expérimentaux
- Conclusion
3.18 – Comparaison à 2500 Hz entre mesure et simulation pour le niveau de pression et pour l'intensité acoustique Iy à l'axe source (ys= 10cm etzs= 7cm), la discontinuité du tronçon correspond à une modification de 25% de la largeur de la route. Dans ce cas, le saut de section correspond à une modification de 25 % de la largeur de la route. 3.17(a)) sont dus à des ondes de rétroaction créées par des changements soudains de la largeur de la route.
3.20 – Comparaison à 2500 Hz entre mesure et simulation du niveau de pression et de l'intensité acoustique Iy dans l'axe de la source (ys = 10cm et zs = 7cm), la discontinuité de section correspond à une variation de 50% de la largeur du rue. Comme le montrent les figures 3.19(a) et 3.19(b), la validité de l'approche unidirectionnelle en amont de la discontinuité est discutable.
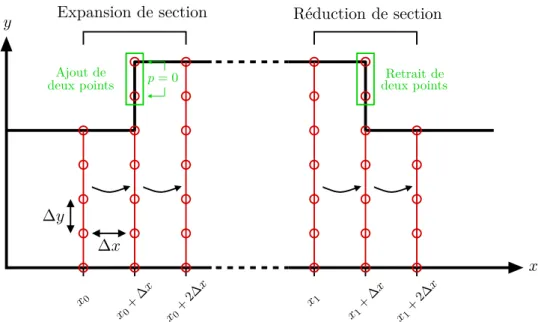
Variation continue de la section du guide d’ondes
- Formulation de l’équation parabolique 3D modifiée
- Modification de la méthode de résolution de l’équation parabolique 3D
- Application de la méthode
- Conclusion
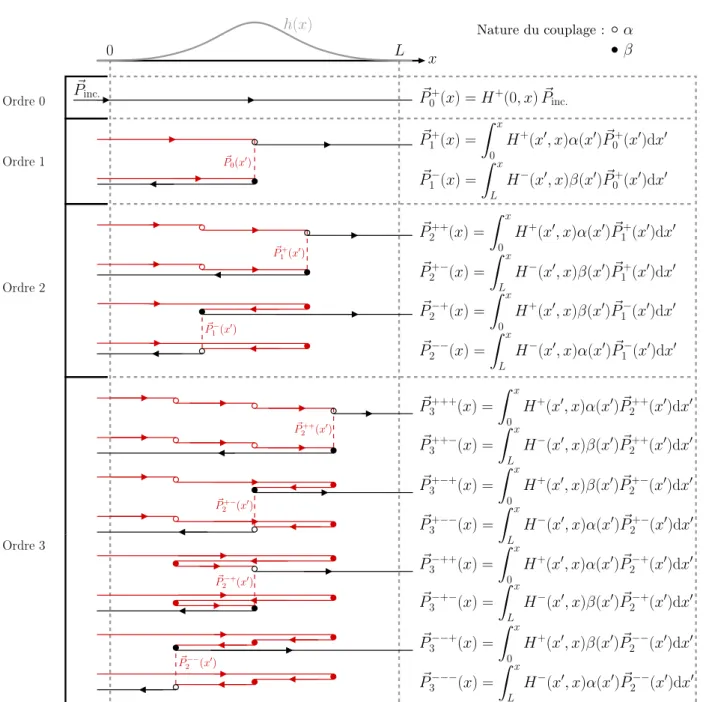
5.12 – Représentation de la décomposition du champ de pression en série de Bremmer pour une onde incidente se propageant dans le sens de x croissant. Une erreur significative est affichée entre la solution de référence et l'ordre 0 de la série. Il en est de même pour l'approximation unidirectionnelle, qui se rapproche ici de l'ordre 2 de la reconstruction du champ de pression à la sortie du conducteur.
5.20(b)) et pour une condition de plan d'incidence, l'approximation unidirectionnelle se rapproche du troisième ordre de reconstruction du champ de pression, tandis que pour. Une reconstruction séquentielle du champ de pression a mis en évidence les contributions particulières des différents rangs de la série Bremmer.
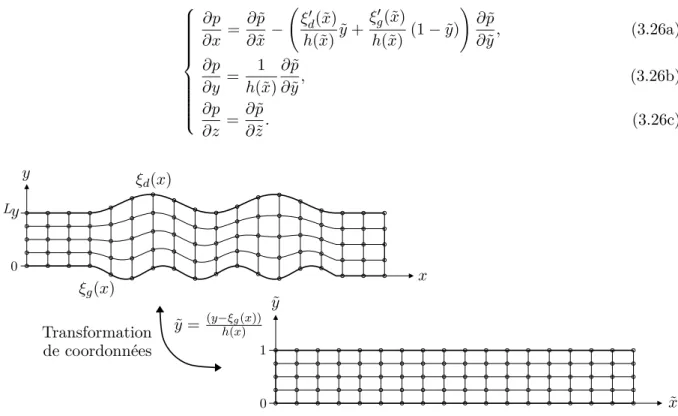
Intégration des PML dans la discrétisation par différences finies de l’équa-
Multimodal admittance method
- Coupled mode equations
- Numerical integration
An incident wave propagates from the left side of the region of interest (x ∈[0, L]) and the waveguide is assumed to be uniform and semi-infinite downstream of this region. The medium filling the waveguide is homogeneous and invisible, with sound speed c0, such that the pressure field p is solution of the Helmholtz equation. 73, 74] This problem is solved by first calculating the admittance matrix Y, defined by Q~ =Y ~P, along the waveguide.
First, the Riccati equation (4.8) is integrated from the output of the region of interest (with the initial value Y(L) = iΓ, indicating that no backward wave propagates downstream) to its input (x = 0). Without loss of generality, we assume that the waveguide axis is dictated by a constant step size ∆x >0.
One-way approximation
Accuracy of the one-way method for coarse discretization
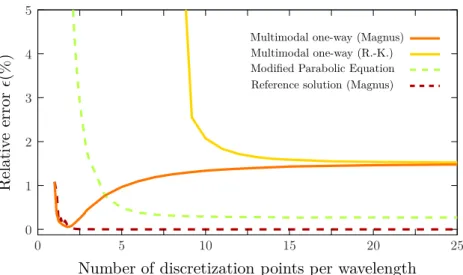
4.2 – Convergence of the multimodal one-way method, measured by the relative error ǫ(Eq. 4.20), as a function of the number of discretization points per wavelength. It appears that the choice of the numerical scheme does not matter when computing the multimodal one-way solution, although computing the reference solution with either one numerical scheme or the other gives comparable results. If both the fourth-order Runge-Kutta and second-order Magnus scheme errors tend towards the same asymptotic limit as the discretization is refined, then, contrary to the expected behavior, the Magnus scheme gives better results as the mesh becomes coarser. 4.19) appears to be a rough approximation of the original problem (the value of the asymptotic limit is relatively high, especially compared to the solution of the modified parabolic equation [26]), the error is almost zero for a discretization at two points per wavelength, regardless of the wavelength or magnitude (height and lengthT) of the cosine irregularity (Fig. 4.4).
The first one corresponds to a waveguide with arbitrary and weak variations of the cross-section (using polynomial functions to obtain a randomly generated geometry). 4.4 – The relative deviation ǫ (color contour plot) between the multimodal one-way method calculated with a Magnus scheme and the reference solution, as a function of the wavelength and geometry parameters and T, has a minimum at two discretization points per wavelength, regardless of these parameters .
One-dimensional analytical solutions
It follows that since in the configurations we are interested in (non-reflective initial condition and weakly varying cross section), |Y| is of the order of k, the term refers to the impedance in Eqs. In the multimodal case, E2 is a matrix rather than a scalar function, but it still reaches a minimum near λ/∆x = 2, in the same way as in the scalar case. However, in practice, especially in the multimodal case, neither the approximate method nor the exact multimodal access method yields relevant results in such a coarse discretization.
4.7 – Function kE2 (see equation 4.25) as a function of the number of discretization points per wavelength, for three different values of the small parameter ε=−h′/2hk.
Conclusion
- Méthode multimodale pour les guides avec discontinuités de section
- Utilisation des matrices de diffusion pour la décomposition du champ de
- Multidiffusion dans un créneau
- Convergence de la série
- Sens de propagation des modes couplés
- Conclusion
De même, la contribution de la partie réfléchie du champ de pression peut être exprimée. Si l'on ajoute la contribution de la première réflexion (p1) à l'approximation unidirectionnelle, on voit que le champ de pression résultant (Figure 5.6 - Carte du module de pression en fonction de l'ordre d'évolution, k/π= 2,5, a = 0,31 et T = 3 est le mode plan d'onde incidente se propageant dans le sens de x croissant.
5.8 – Convergence de la série, k/π et a sont variables, T = 3 et l'onde incidente est un mode plat se propageant dans le sens de x croissant. Il s’avère que la contribution majoritaire des modes P~0 permet une bonne approximation du champ de pression en aval de la discontinuité.
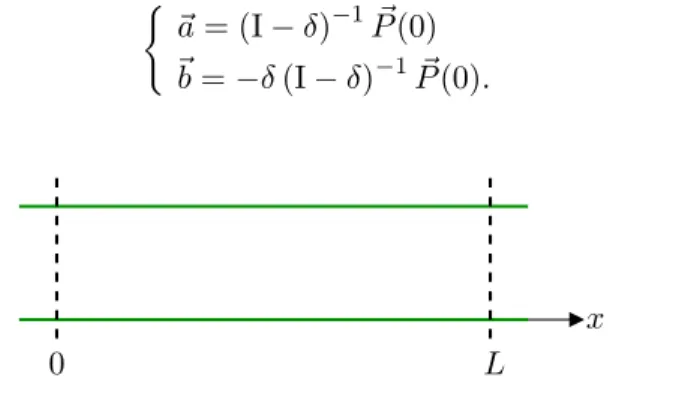
Série de Bremmer dans des guides d’ondes bidimensionnels à variation de section
- Décomposition en ordres : introduction
- Décomposition en ordres : résolution itérative
- Méthode de résolution numérique
- Approximation unidirectionnelle
- Reconstruction du champ de pression jusqu’à un ordre donné
- Modélisation du champ de pression transmis à travers un guide d’ondes
Pour le même exemple, la figure 5.16 montre la répartition du champ de pression dans la série de Bremmer pour les deux premières lignes de la série. 5.17(a)) compare les amplitudes des modes de propagation résultant de la reconstruction du champ de pression jusqu'à un ordre de développement donné (noté d). 5.17(b)) présente une comparaison entre les amplitudes des composantes de l’approximation unidirectionnelle et celle de la solution de référence.
5.17 –(a) : Amplitudes des modes résultant de la reconstruction du champ de pression jusqu'à l'ordre d ; (b) : Comparaison entre les amplitudes des modes de la solution de référence et les amplitudes des modes de l'approximation unidirectionnelle (notée 1w). 5.18 – Erreur relativeǫ2d(L) en fonction de la longueur de l'irrégularité L10, comparaison entre l'approximation unidirectionnelle et la reconstruction du champ de pression jusqu'à un ordre de grandeur d, (mode événement 1, a= 0,075, η= 4,5 et L = 9). 5.22 – Erreur relative ǫ2d(L) en fonction de la hauteur de l'irrégularité a, comparaison entre l'approximation unidirectionnelle et la reconstruction du champ de pression jusqu'à un ordre de grandeur d, (mode événementiel 1, ν = 2, η= 1,5 et L = 3).
Dans certains cas cependant, l'approche unidirectionnelle a permis d'obtenir une estimation du champ de pression émis qui pourrait correspondre à une reconstruction de la séquence à l'ordre 2.