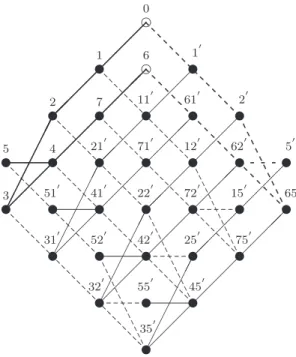
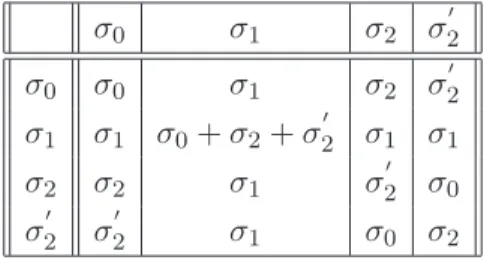
Le problème de la classification des fonctions de partition des théories conformes su(n) dans différents environnements se réduit donc à la détermination de l'ensemble de ces matrices. Le chapitre 3 est consacré à la présentation d'une certaine réalisation de l'algèbre des symétries quantiques dans Ocneanu.
Th´eories conformes : une introduction
- Importance des sym´etries
- Transformations conformes
- OPE des champs
- Alg`ebre de Virasoro et repr´esentations V i
Corollaire classique Dans la transformation infiniminale générale (1.4), la variation d'action (S7→S+δS) est donnée par. Connaître l'OPE des champs présents dans le système est d'une grande utilité : il permet de réduire progressivement le calcul des fonctions de corrélation en N points à celui en 2 points.
Th´eories conformes rationelles : RCFT
- Alg`ebre de fusion
- Unitarit´e et irr´eductibilit´e de V i
- Mod`eles minimaux
- Mod`eles b g-WZWN
- Propri´et´es modulaires des caract`eres χ i et formule de Verlinde
Par conséquent, les matrices Ni forment une représentation fidèle de l'algèbre de fusion. Une généralisation de la notion de représentations irréductibles d'une algèbre de Lie simple g est fournie par la notion de représentations intégrables.
Invariance modulaire, conditions aux bord et lignes de d´efaut
- Mod`eles d´efinis sur le tore
- Fonctions de partition invariante modulaire
- Conditions au bord
- Lignes de d´efauts et fonctions de partition g´en´eralis´ees
Les matrices toriques généralisées Wxy (qui définissent les fonctions de partition à deux droites fractionnaires) sont alors obtenues à partir de la connaissance des matrices toriques Wx et des coefficients de structure Oxyz (négatifs non entiers) de l'algèbre d'Ocneanu. Les conditions de compatibilité [79] impliquent qu'elles forment une représentation de l'algèbre Oc(G) (généralement de dimension différente).
Classifications et graphes
- Mod`eles c su(2)
- Mod`eles minimaux
- Mod`eles c su(n), n ≥ 3 et mod`eles minimaux g´en´eralis´es
- Quelques d´efinitions
- Graphes bi-orient´es et leur classification
- Chemins essentiels sur un graphe
La classification des modèles minimaux (c < 1) est complétée [11], et suit également une classification de type ADE : à chaque fonction de partition invariante modulaire correspond un couple de diagrammes de Dynkin (A, G). Modèles su(3)c Suite à une approche combinatoire de la recherche d'invariants modulairesM, la classification des modèles csu(3) a été obtenue par Gannon en 1994 [44].

La big`ebre de Hopf faible B (G)
- Endomorphismes gradu´es de chemins essentiels
- Big`ebre faible B (G) : construction abstraite
- Equations pentagonales
- Projecteurs minimaux centraux π i et ̟ x et graphes A (G) et Oc(G) . 47
Alors la composante (i+1, b) de la matriceEa est le nombre de chemins essentiels de longueur reliant le sommetv au sommetvb. Le produit ◦ des éléments de la base de B correspond alors au produit des unités de la matrice : eξξ′(i)◦eηη′(j) =δij δξ′η eξη′(i).
Une construction explicite
Cas A 3
On obtient alors la représentation matricielle d'un élément ξ ⊗ξ′ pour la loi ⊙ dans le bloc x1. De manière condensée, on peut écrire la représentation (◦)-matrice des éléments ξξ′ comme
Graphes G du type ADE et g´en´eralisations
D'une part, cette réalisation permet d'obtenir un algorithme très simple pour le calcul des différents coefficients qui définissent les fonctions de distribution généralisées du modèle conforme csu(2) associé au graphe G. D'autre part, cette réalisation se prête naturellement à la généralisation à cassu(n), n ≥3, ce qui nous a permis de définir le graphe d'Ocneanu et l'algèbreOc (G) pour quelques exemples choisis de types su(3) et d'obtenir ainsi les fonctions de partition généralisées associées à ces exemples.
D´efinitions
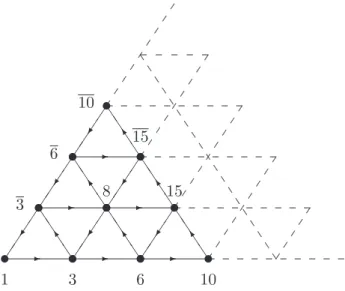
Le résultat de cette décomposition peut être encodé dans le graphe A∞ de SU(2) illustré sur la Fig.3.1. Si les représentations 3 et 3 sont combinées, le graphe correspondant à la tensorialisation avec 3 est obtenu en inversant le sens des arcs du graphe correspondant à 3.
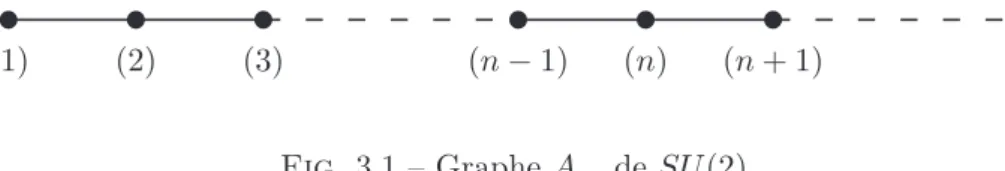
Alg`ebre de graphe et matrices N i
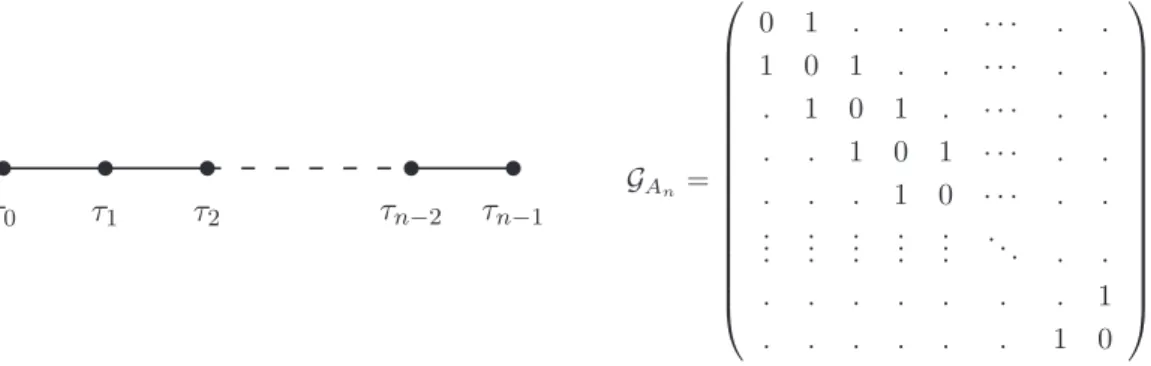
En imposant l'associativité, on construit pas à pas la table de multiplication de l'algèbre de graphes An. Ils forment l'algèbre matricielle du graphe An et fournissent une représentation plausible de l'algèbre de graphe An.
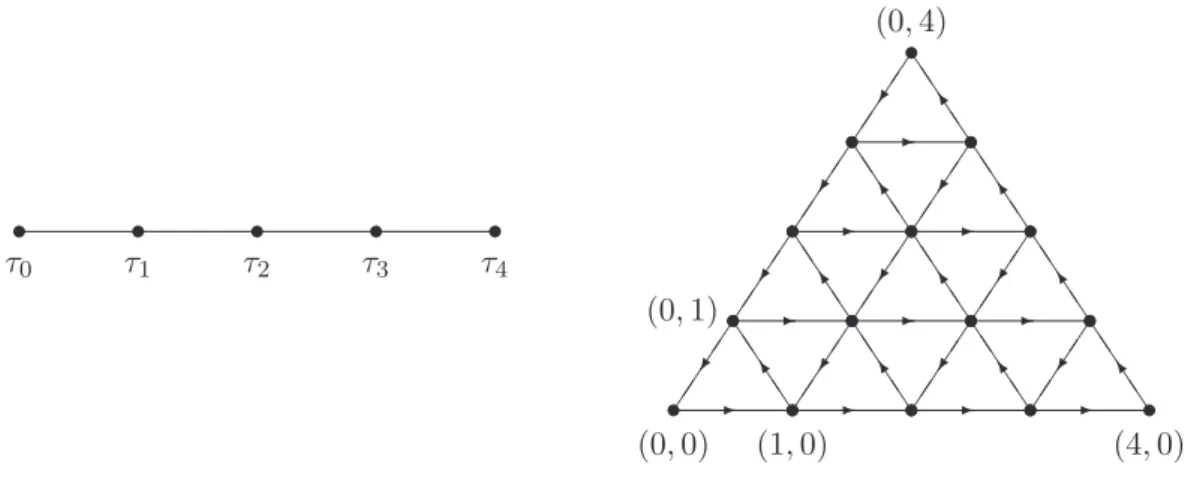
Par conséquent, la matrice qui diagonalise les matrices Ni est l'analogue quantique de la table de caractères. Dans le cas de SU(2)k, la matrice T est donnée en (3.9) et l'exposant modulaire pour le sommet τi est déterminé par la quantité ˆT donnée par.
Historique et d´efinitions
On peut reformuler cette correspondance en disant qu'il y a une action des irreps de SU(2) sur les irreps de Γ : on écrit que bΓ est un module sur dSU(2). Nous avons une correspondance biunivoque entre les sous-groupes finis de SU(2) (diagrammes ADE(1)) et leur analogue quantique (diagrammes ADE).
Alg`ebre de graphe
Pour D2n+1 et E7 il est impossible d'obtenir une algèbre commutative et associative, avec des coefficients de structure entiers non négatifs [73] (pour le cas E7 une algèbre existe, mais avec des coefficients de structure négatifs). Dans le cas de graphes possédant une autofusion, on peut donner une réalisation matricielle de leur algèbre de graphes.
Les sommets τi (i κ−2) du graphe A(G) forment un espace vectoriel sur lequel on peut définir la multiplication : on obtient l'algèbre du graphe A(G). Ils généralisent ces constructions aux cas de SU(n)ℓ : les matrices Fi codant l'opération de A(G) sur V(G) donnent une représentation d'une algèbre de fusion.
Graphes d’Ocneanu Oc(G)
D´efinition
Cependant, notre réalisation de l'algèbre d'Ocneanu se prête naturellement à une généralisation aux cas SU(n)ℓ. Nous prenons comme données initiales les graphes d'Ocneanu Oc(G) du modèle ADE publié dans [67].
R´ealisation alg´ebrique de Oc(G)
Pour les cas où l'algèbre d'Ocneanu est commutative (An, E6, E8) on obtient la réalisation suivante de Oc(G). L'algèbre Oc(D2n+1) est obtenue en diviseur (à l'aide d'une application) du produit tensoriel de l'algèbre A (de même nombre de Coxeter).
V (G) comme module sur Oc(G) : matrices S x
L'algèbre de graphes de type II d'Ocneanu consiste en l'algèbre de graphes H, où H est un graphe de type I appelé « graphe parent » de G [79]. On obtient Oc(E7) = D10⊗ρD10, où la torsion exceptionnelle ρ est déterminée par les propriétés modulaires du graphe A17.
Relations entre A (G) et Oc(G)
Fonctions de partition
L'élément F1 est le générateur de l'algèbre de fusion et correspond à la matrice adjacente d'un graphe : ainsi le graphe ADE est apparu formellement dans les fonctions de partition de classification des modèles csu(2). Les fonctions de partition des modèles de type II sont obtenues à partir de celles de type I par une procédure de torsion.
L'action est bien définie et permet d'obtenir des formules compactes pour les expressions des fonctions de partition invariantes modulaires et généralisées. Nous restaurons ainsi la classification de Cappelli-Itzykson-Zuber et donnons des formules pour les expressions des fonctions de partition à une et deux fractions de tous les modèles su(2).c.
Relations de compatibilit´e alg´ebrique
Ni = (Ni)jk sont les matrices qui représentent l'algèbre du graphe A(G). Une base de l'algèbre d'Ocneanu de E7 est donnée par les 17 éléments suivants.
Calculs des cas c su(2)
Les cas A n
Pour tous les cas An, l'algèbre des graphes est entièrement déterminée par les données du graphe. Les matrices de fusion Ni qui forment la représentation matricielle de l'algèbre de graphes Ans sont obtenues par la formule d'induction tronquée de SU(2).
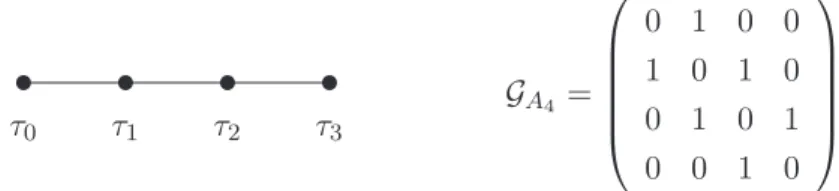
Le cas E 6
Les matrices essentielles Ea((Ea)ib= (Fi)ab) ont 11 lignes (notées par les sommetsτi de A11) et 6 colonnes (notées par les sommetsσb de E6). Matrices toriques généralisées L'action de A11 sur Oc(E6) est codée par les matrices Wxy.

Le cas E 8
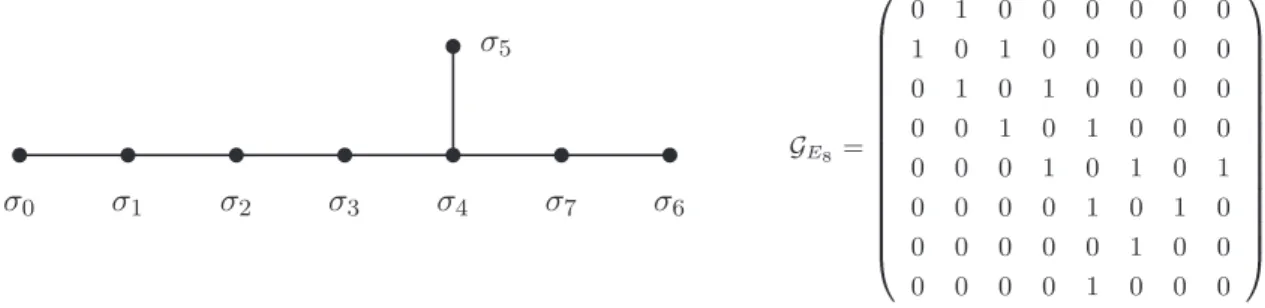
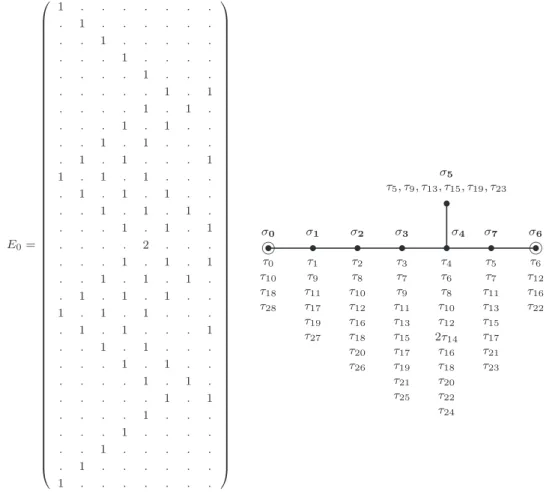
Les matrices essentielles Ea ((Ea)ib= (Fi)ab) ont 29 lignes (notées par les sommets τ de A29) et 8 colonnes (notées par les sommets σ de E8). La fonction de partition invariante modulaire de E8 est diagonale en fonction des caractères étendus ˆχa.
Les cas D 2n
Algèbre d'Ocneanu On serait tenté de définir l'algèbre d'Ocneanu D4 par D4⊗JD4. La non-commutativité de l'algèbre d'Ocneanu D4 se manifeste par la présence du coefficient 2 dans l'invariant modulaire M (et donc dans la fonction de partition correspondante).
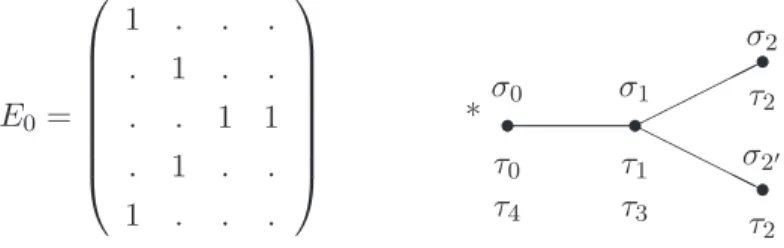
Les cas D 2n+1
La multiplication avec ces générateurs est codée par le graphe d'Ocneanu D5 présenté sur la figure 1. Les matrices de fusion Ni et Fi codant l'opération de A4n−1 sur D2n+1 sont obtenues comme d'habitude.

Le cas E 7
Le graphe D10 a aussi la même norme que A17 et E7 : nous verrons que l'algèbre d'Ocneanu de E7. Les éléments a engendrent une sous-algèbre de Oc(E7), isomorphe à l'algèbre de graphes D10.
Quelques exemples du cas su(3)
Le cas E 5
Matrices toriques et fonctions de partition généralisées Les matrices toriques généralisées sont définies par l'opération de A5 sur Oc(E5). Les autres matrices Wxy sont calculées de la même manière, et les matrices toriques généralisées E5 sont obtenues par.

Le cas E 9
En connaissant le graphe d'Ocneanu de D2n, nous avons réussi à donner une réalisation de l'algèbre d'Ocneanu. Cependant, notons que l'identité de Oc(E9) est 00⊗ 00, et nous pouvons calculer la fonction de partition associée à ce point.
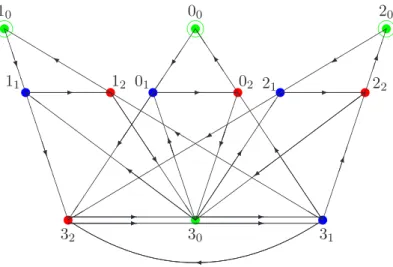
Le cas E 21
Les modèles minimaux (« ordinaires ») – construits par irréps de l'algèbre de Virasoro – sont apparentés aux modèles csu(2). Peut-on définir une matrice R pour l'algèbre de Hopf faible et obtenir une équation de Yang-Baxter (généralisée).
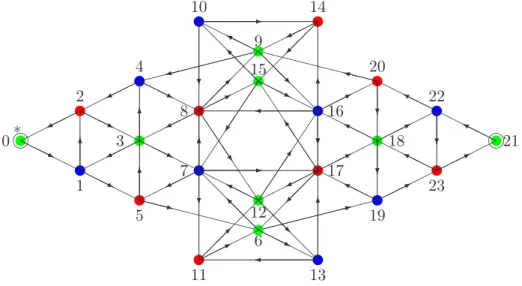
Le groupe SU (2) classique
En utilisant l'associativité ⊗ et en effectuant des calculs dans l'espace virtuel des représentations (c'est-à-dire en autorisant des signes négatifs dans l'étape intermédiaire des calculs), on peut calculer la décomposition (i)⊗ (j) à partir des données (B.2).
Formulation matricielle et graphe A ∞
En général, on peut coder en matrice le résultat de la décomposition (B.1) : pour chaque irrep (i), introduisons une matrice carrée infinieNitelle, où (Ni)jk =Nijk. Les autres matrices Ni sont obtenues à partir de la connaissance de N1 et N2 par la formule d'induction pour SU(2).
Un fait remarquable est que cette matrice S, correctement ordonnée, représente la table de caractères de Γ [61, 57]. Ces graphes codent la décomposition du produit tensoriel (2)⊗(σi), où (2) est la représentation fondamentale induite de SU(2).
Exemple : le groupe binaire octah´edrique O et le graphe E 7 (1)
L'algèbre Uq(sl(2)) est l'algèbre engendrée par les éléments {K, K−1, X±} vérifiant les relations suivantes. On peut donc voir l'algèbre de Hecke comme une déformation de l'algèbre du groupe des permutations.
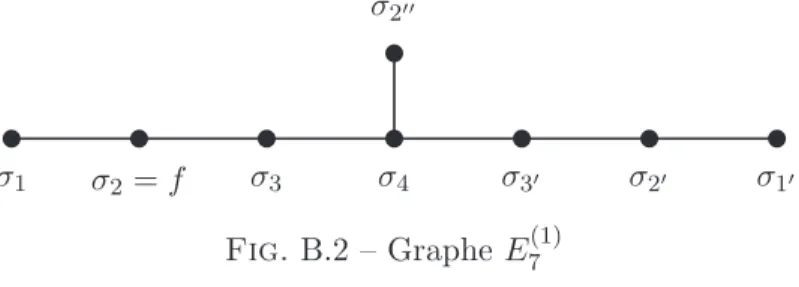
Correspondance de McKay quantique et graphes ADE
Le groupe quantique U q (sl(2))
Alors F unq(SL(2)) est l'algèbre des transformations de coordonnées, de déterminant égal à 1, qui préserve la relation (B.9). Les relations définissant la structure de l'algèbre de Hopf de Funq(SL(2)) sont, bien sûr, définies sur ses générateurs. F unq(SL(2)) et Uq( sl(2)) sont duales (suivant la notion de dualité introduite par M Takeushi [84]) au sens où il existe une forme bilinéaire h , i → C, appariement appelé, qui relie leurs structures.
On peut maintenant résumer les définitions de l'algèbre et de la coalgèbre : Définition 15 Une algèbre est un triplet (A, µ, η), où A est un espace vectoriel, et. Définition 17 Le produit tensoriel de deux algèbres A1 et A2 est une algèbre dont l'espace vectoriel est le produit tensoriel des espaces vectoriels de A1 et A2, et dont le produit µ′ : (A⊗A) ⊗(A⊗A)−→A ⊗ A est une application linéaire telle que.
Alg`ebre de Hopf faible
Une bialgèbre à antipode est une bialgèbre de Hopf, communément appelée algèbre de Hopf.
Divers
- Le cas A 4
- Le cas E 6
- Le cas E 8
- Le cas D 4
- Le cas D 6
- Le cas D 5
- Le cas E 7
Jusqu'ici nous n'avons fait que reformuler la définition de l'algèbre de Hecke Hn(q). L'algèbre de Temperley-Lieb Tn(τ) est l'algèbre associative uniforme engendrée par n générateurs (1, e1, e2, . . . , et-1) qui vérifient les relations suivantes.
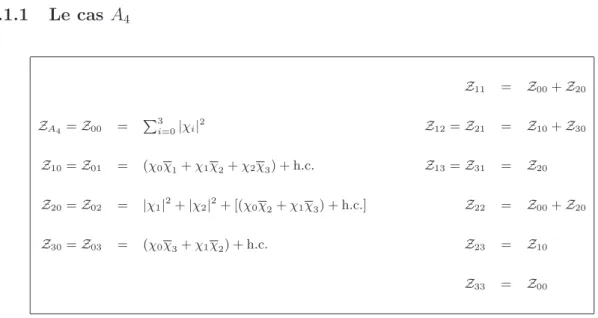
Schieber, Twisted partition functions for ADE boundary conformal field theories and Ocneanu algebra of quantum symmetries, J. Ostrik, On a q analog of the McKay correspondence and the ADE classification of slb2 conformal field theories, Adv.