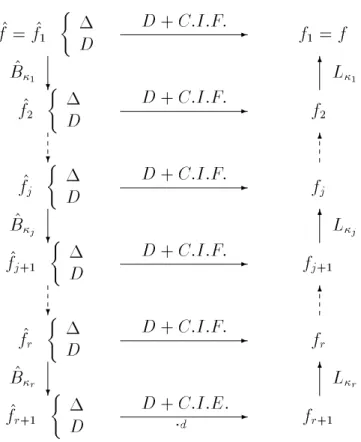Considérant les équations de q-différence [6], nous sommes amenés à trouver pour s;s02 IR l'espaceCl [[x]]q ;s;s0 (resp.Cl [[x]](q ;s ;s0 )) formel seriesPn0anxn dont les coefficients ont un incrément de type. Les théorèmes d'indice pour les opérateurs à coefficients polynomiaux s'étendent par dualité et par passage à l'infini. Le bon espace des séries formelles stables par l'action de Cl [;qx] est celui de la série q-factorielle généralisée Pn0,q(x++n+1),q(x) ou 2Cl (,q est la fonction Gamma q -similaire).
Operateurs a indice
Espaces Gevrey generalises
C'est pourquoi il faut introduire de nouveaux espaces, que nous définissons par analogie avec les espaces précédents.
Il faut donc introduire de nouveaux espaces, que l'on définit par analogie avec les espaces précédents. idem pour les espaces de Beurling).
Theoremes d'indices et de comparaison
- Operateurs etudies
Espaces de Banach
Pour le calcul des indices possibles, nous reviendrons à l'étude des opérateurs dans les espaces de Banach, afin d'appliquer des théorèmes connus. donc compact) et image proche. Remarque : En fait, la propriété qui nous intéressera sera le caractère compact de cette application, moins fort que le caractère nucléaire ; cela suffira pour utiliser des arguments de perturbation compacts.
Theoremes d'indices
Theoreme d'indice dans lC fxg
Soit j0 le plus petit des indices tels qu'il existe un i avec ai;j0 non identiquement nul. On note r = fx = jxj r g et Bi(r) les fonctions de classe Ci sur r et les fonctions holomorphes sur l'ouvert _r. Pour établir le théorème d'indice dans lCfxg, nous établissons le théorème suivant, puis nous utilisons l'argument limite inductif classique.
L'operateur L : lC fxg , ! lC fxg est a indice, d'indice egal a
Theoremes de comparaison
Interpretation des theoremes d'indices 1. Polygone de Newton
Traduction des theoremes d'indices en fonction du polygone de Newton
Les valeurs extraordinaires sont les réels s pour lesquels les guides de pente (cas . jqj> 1) ou de pente (cas jqj< 1) rencontrent le polygone de Newton après un segment ou une demi-droite. Si s exceptionnel et s0 exceptionnel : (q ;s;s0) =,k2(;0) On laisse au lecteur le soin d'établir un théorème analogue pour L de la forme (1). Démonstration : C'est nécessaire et il savait qu'il n'y a pas de valeurs exceptionnelles s > 0, ni de valeurs exceptionnelles s0 > 0 par rapport à s= 0.
Equations a coecients polynomiaux
- Dualite topologique
Une condition nécessaire et suffisante pour que toutes les solutions de l'équation L( ^f) =g soient convergentes est que le polygone de Newton soit de la forme .
Etude a l'inni
Theoremes d'indices
2 IR, d'indice égal à ,k() si s n'est pas exceptionnel, ,k(;0) si s est exceptionnel et si s0 n'est pas exceptionnel, ,k1(;0) si s est exceptionnel et si s0 est extraordinaire . 2 IR, d'indice égal à ,k() si s n'est pas exceptionnel, ,k(;0) si s est exceptionnel et si s0 n'est pas exceptionnel, ,k2(;0) si s est exceptionnel et si s0 est extraordinaire .
Soit L un operateur a coecients polynomiaux du type
Estimations de croissance
A l’inverse, supposons que la fonction entière f(x) admet comme évolution asymptotique Pn0anxn2Cl [[x]]q ;s;s0, ce qui signifie qu’il existe C et A >0 tels que.
Preliminaires
- La fonction Gamma q -analogue
- La q -integrale
Transformee q -Mellin formelle
- Transformee q -Mellin formelle d'un operateur
Preuve de propriété 3.2.2 : Il est sûr de montrer pour tout 2lC, pour allk;j 2IN, que k
Avec les notations de la denition 3.2.1, la transformee q -Mellin formelle d'une serie formelle de q -factorielles generalisees est la serie formelle
- Indice dans lC ~ q [[ t ]]
- Indices dans les espaces q -Gevrey
Solutions series de q -factorielles formelles 1. Polygone de Newton
- Caracterisation q -Gevrey des series de q -factorielles solutions
Nous devons définir un polygone de Newton pour les opérateurs de différence à coefficients polynomiaux en qx. Il est en fait confondu avec ce que nous avions nié précédemment pour les opérateurs avec des p-diences considérées comme agissant sur ~Cl q[[t]]. Par définition, Pl(q) est le polygone de Newton inférieur de q, Pu(q) est le polygone de Newton supérieur et P(q) est le polygone de Newton de q.
Alors f^q q-Gevrey est d'ordre 0 ou il existe un réel unique s>0 tel que f^q est q-Gevrey d'ordre optimal s. Remarque : On dit qu'une suite q-Gevrey d'ordre s est optimale s'il n'existe pas de réel s0 < s tel que cette suite q-Gevrey soit d'ordre s0.
Theoremes d'indices (series de q -factorielles) 1. Indices formels
- Indices q -Gevrey
Transformee de q -Laplace formelle 1. Denitions
- Solutions formelles
- La k -sommabilite et la multisommabilite
- Methode des transformees de Laplace iterees (W. Balser)
- Polyn^omes d'Ore
Balser recommande un processus mathématique explicite pour obtenir la somme d'une série formelle multisommable dans le cas général [1,2,4]. La séquence formelle ^f est k- sommable dans la direction d s'il existe un secteur S = S(d;;) d'ouverture > k sommable dans la direction d s'il existe un secteur S = S(d; ; ) ouverture > k. Une séquence formelle est (k1;:::;kr)-sommable si elle est (k1;:::;kr)-sommable dans toutes les directions sauf dans un certain nombre de directions (modulo 2), appelées directions singulières.
Puisque la séquence ^f(xei) est également k-sommable dans la direction d+, elle est également k-sommable dans la direction d. Une série formelle ^f(x) est k-sommable dans la direction d si sa transformée borélienne formelle ^ = ^Bk( ^f) est d'ordre k (refusée dans la direction d si sa transformée borélienne formelle ^ = ^Bk ( ^ f ) d'ordre k (nié par ^Bk(x)(t) = t,k=,(k)) est convergent et si sa somme se développe analytiquement en une fonction holomorphe et a une croissance d'ordre au plus exponentielle. Balser [1 , 2, 4] la méthode de calcul de la somme du type multisommable est basée sur le principe des transformations itérées de Laplace (et itérées de Borel) et dérive de la proposition suivante.
Pour calculer la somme d'une série sommée formelle ^f(x) (1;:::;r),iL nous procédons comme suit. L'algorithme formel calcule les transformées formelles de Borel d'ordre rationnel j et produit une équation différentielle à partir de laquelle chaque série formelle ^fj est résolue pour j = 2;:::;r+ 1. La fonction fj+1 a été précédemment calculée par la même méthode. sauf pour le dernier niveau pour lequel les conditions initiales à partir desquelles le développement analytique est effectué peuvent être lues directement à partir des coefficients de la série formelle convergente ^fr +1 et sont donc exactes.
La transformée de Mellin d'un opérateur écrit sous la troisième forme (resp. la quatrième forme) est l'opérateur différentiel Pri=0Pql=0i;lil (resp.
Outils formels
- Denition du concept de serie formelle
- Passage d'une equation aux dierences a une equation dierentielle puis a un systeme dierentiel
- Scindage d'une serie formelle
- Transformee de Borel formelle
- Transformees de Borel iterees
- L'exemple de Ramis-Sibuya
On aurait donc pu aussi définir la série formelle par des équations aux différences de la forme. Passage d'une équation différentielle à une équation différentielle puis à un système différentiel un système différentiel. Il reste donc à déterminer une équation différentielle satisfaite par une série formelle définie par une équation aux différences.
La transformée formelle de Borel du plan d'une série formelle ^f(x) =Pj0ajxj, représentée par l'équation aux différences. La présence de la fonction nous empêche de définir la séquence (aj=,(j=)) par une équation aux différences polynomiales. Il nous reste donc à donner un algorithme qui permette de passer formellement d'une équation aux différences de forme.
Nous n'appliquons donc pas l'algorithme de Balser à la série formelle ^f(x) elle-même, mais à chacune des sous-séries. Le diagramme suivant décrit la transformation formelle de Borel appliquée à une série formelle (1;:::;r), iL sommable (11 = 1). Soit ^f(x) une série de solutions formelles d'une équation différentielle à coefficients polynomiaux dont le polygone de Newton a deux pentes k1 > k2 > 0.
La deuxième étape consiste à diviser chaque série formelle ^q(x) en 2 sous-séries, puis des transformations ~B1 sont effectuées.
Prolongement analytique
- Transformees de Laplace iterees
- Localisation des singularites
- Prolongement analytique
- Logiciel Compas
Par conséquent, ces outils formels donnent des directions spéciales possibles et nous permettent d'optimiser les chemins d'intégration des transformées de Laplace. L'extension analytique le long d'un chemin j constitue le problème numérique central de l'algorithme de Balser. Il est donc impossible de calculer j+1(t) près de l'origine, sauf par la méthode des transformées de Laplace itératives elles-mêmes.
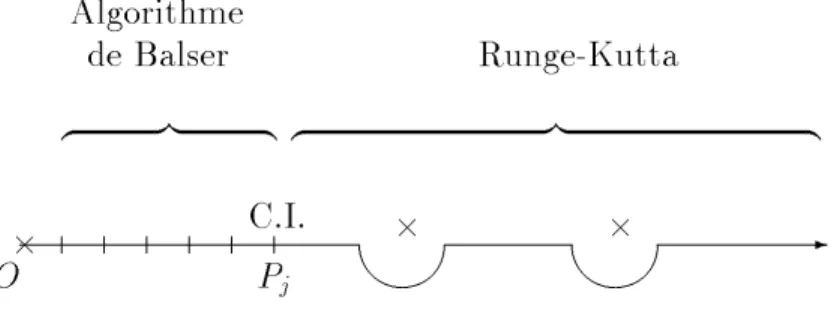
Mais pour calculer j+1(t) sur les abscisses définies par les formules de quadrature, nous devons utiliser une méthode numérique efficace pour effectuer l'extension analytique. Ainsi, à chaque niveau, l'extension analytique se fait de la même manière : de l'origine au point Pj, on utilise récursivement la méthode des transformées de Laplace répétées ; au-delà de Pj, nous utilisons une autre méthode. Celle que nous utilisons est la méthode Runge-Kutta à partir des conditions initiales (exactement à l'origine O pour le dernier niveau, numériquement à Pj pour les autres).
Si l'ordre de l'équation différentielle dont ^j+1(t) est la solution est grand, d'ordre 7 ou 8 pour ^r +1(t) par exemple, et si le rayon de convergence de la série est petit ( par exemple 0:25), la longueur du pas d'intégration utilisée dans la méthode Runge-Kutta doit être choisie très petite. La multisummation (méthode Balser) est intégrée à Compas et est utilisée comme méthode analytique d'extension. Pour calculer les transformées de Laplace répétées et donc la somme d'une série, il nous faut 89.
Par exemple, si la méthode est de type Séries, le développement analytique se fait en appelant l'algorithme de Balser.

Implantation
- AutoDer
- PowerSeries
- Contenu algorithmique
- CreatePowerSeries
- Coherent?
- Coecients
- Exemple de 2 -sommabilite
- Exemple de Ramis-Sibuya
Ce n'est pas exactement une transformée de Borel, mais l'application qui a ^f(x) =Pj0ajxj associe une série formelle. Record(abscisse : Sheet CF, somme : Sheet CF) analytic( ^f;) calcule le développement analytique de la chaîne depuis l'origine, le long du chemin. Si l'on connaît les valeurs des transformations de Borel en abscisse en quadrature et les poids correspondants, on peut ainsi calculer les dérivées dans n'importe quel ordre de la somme.
Le calcul de la somme et de la dérivée d'une série sommable (1;:::;r),iL suit le schéma suivant. Le développement d'une série (1;:::;r), qui peut être sommée le long d'un chemin, se fait de la manière suivante. Si la méthode de calcul associée au chemin élémentaire est de type série, le calcul de la somme se fait de manière récursive (calcul des transformées de Borel en sous-série, etc.).
Les directions uniques pour résumer la série de solutions formelles de l'équation de Ramis-Sibuya sont les directions 2 + 2l (l 2ZZ). Les résultats que nous avons obtenus pour la série d'Euler et la série formelle 2-sommables sont bons. Le logiciel dans son état actuel permettra le déploiement et le test de ces méthodes dans le contexte général de la multisommation.
Thomann, Problèmes algorithmiques posés par la multisummation, Spring Day of the PRC Math-Info (1990).
Ce résultat se généralise au complexe q, 0 < jqj < 1, en définissant l'abscisse de convergence d'une série de Newtonq analogue à inff0 2IR=la série converge pour<(xlogq)>0logjqjg. Si f^ est une série de formules convergentes, ++ analyticpath( .. f;ch) calcule l'extension analytique de ++ la somme le long du chemin ch en utilisant la méthode Runge-Kutta. Calcul de la somme d'une série multisommable le long du chemin ch, +++ les points où la somme est calculée sont équidistants +++ sur chaque chemin élémentaire.
Calcul de la somme d'une séquence multisomable iL le long du chemin +++ ch, où sont les points auxquels la somme est calculée. Calcule les dérivées successives de la somme, où le développement ++ de chacune de ses sous-séquences est connu.