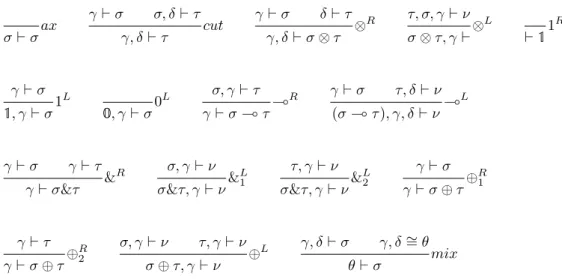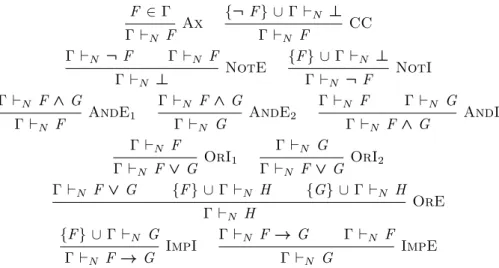The TYPES meetings are a forum for presenting new and ongoing work in all aspects of type theory and its applications, particularly in formalized and computer-aided reasoning and computer programming. The TYPES areas of interest include, but are not limited to: foundations of type theory and constructive mathematics; applications of type theory; depending on entered programming;.
Intuitionistic Multiplicative-Additive Linear Logic
Guillaume Allais
1 Introduction
To be able to use type theory to formally study the metatheory of the programming languages whose type system includes notions of linearity, we need to have a good representation of such constraints. In each case, the premises correspond to arguments (usually called parameters and indices for types) and the conclusion shows the name of the constructor.
2 The Calculus of Raw Terms
Indeed, the use of large quantification in the definition of the ST monad essentially rests on impredicativity. However, it is important to keep in mind the distinction between different types of objects.

3 Linear Typing Rules
Usage Annotations
In the same vein, rather than deploying the available resources in the appropriate subroutines, we consider the term verified in a given context, to which usage notes are added. Type checking) is then inferring (or verifying) the type of an expression, but also marking the resources consumed by the expression in question and returning the residues that gave their name to that document.
Typing as Consumption Annotation
- Typing de Bruijn indices
- Typing Terms
The same will be true for INFER, CHECK, and PATTERN, meaning that writing down a writable program can be seen as either writing a raw expression or the writing derivation associated with it, depending on the author's intent. The input relation for INFER is typed in a way similar to that for VAR: in both cases the type is inferred.

4 Framing
They rely on the previous lemmas to, when faced with a rule with multiple premises and residual threads, generate the proof of inclusion (Lemma 18) and use it to partition the proof of consumption equivalence (Lemma 17:3) and distribute it appropriately in the induction hypotheses. Returning to the type derivation for de Bruijn index 1 in Example 8, we can use the Framing theorem to transport the proof that Γ·fτ·fσ`vs z∈τΓ·sτ·fσ.
5 Weakening
It is given by a simple structural induction of the terms themselves, using copyto go under binders. Now that we know that attenuation is compatible with the typical relations, let's study substitution.

6 Substituting
If not, the typing environment carries a typing derivation for the term intended to be substituted for this variable. The proof by mutual structural induction on the tic derivations relies heavily on the fact that these tic relations enjoy the frame property of matching the .
7 Functionality
8 Typechecking
The proof proceeds by mutual induction on the raw terms, using inversion lemmas to reject the impossible cases, using auxiliary lemmas showing that type checking of VARs and PATTERNS can also be determined and strongly depend on the functionality of the different relationships. One of the advantages of having a formal proof of a theorem in Agda is that the theorem actually has computational content and can be run: the proof is a decision procedure.
9 Equivalence to ILL
A Sequent Calculus for Intuitionistic Linear Logic
For example, we can check that the search procedure succeeds in finding the swapTyped derivation that we wrote down as Example 13.
Soundness
The eliminators in our language are translated using ILL'scut along with left rules.
Completeness
10 Related Work
If we focus on the applications, it is not proven that it is stable under substitution or that the type-testing process will always pass. In that context, it is indeed crucial to retain the ability to talk about a resource even if it has already been consumed.
11 Conclusion
This system can handle multiplicatives, additives, and is even extended to dual intuitionistic linear logic [7] to accommodate values that can be doubled. Another interesting question is whether these resource annotations can be used to develop a fully formalized proof-finding procedure for intuitionistic linear logic.
A Fully-expanded Typing Derivation for swap
Andrej Dudenhefner
Jakob Rehof
The result presented here includes two motivational aspects that distinguish it from existing work (see [20] for an overview). First, similar to Bokov [6], we explore the lower end of the Linial-Post spectrum, whereas existing work focuses on classical or superintuitionistic calculi that often have rich type syntax, e.g.
2 Preliminaries
- Simply Typed Lambda Calculus
- Simply Typed Combinatory Logic
- Hilbert-Style Calculus
- Post Correspondence Problem
The axiom σ is principal if there exists a λ-term of M in β-normal form such that σ is the principal type of M in the simply typed λ-calculus. As an immediate consequence, the following slight restriction of the problem, where vi6=wi, is also undecidable.
We aim to show undecidability of the recognition of main axiomatizations of the calculus a→b→aby reduction from PCP. While the former approach requires an equality test for arbitrarily large structures as a final operation (the coding of which appears problematic in terms of main axioms), the final operation of the latter approach can be bounded.
PCP Reduction
J Let us define∈N∪ {∞}(cf. pcp_reduction.min_special) either as the smallest size of a combinatorial term that can be typified in Γ by σ→σ→σ, or as∞if no such term exists. Finally, we can prove the following key lemma 26 (cf. pcp_reduction.aba_iff_pcp_set), which connects the membership of (v1, w1) in some PCPn and the derivation possibility a→b→af|Γ|.
Principality of Axioms |Γ|
Similarly, for the primary resident of σz, we must ensure that the primary type of the first suffix argumentpair from the given words. Interestingly, the above main implementation of the given axioms makes more computational sense than simply preserving an argument.
Seeing |Γ| as an intuitive axiomatization of the corresponding PCP instance, this provides an additional twist to the Curry–Howard isomorphism. J As a result of the above syntactic characterization with Lemma 27 of the formulas derived from a → b → a, it is solvable in linear time if for a given formula σ we have σ ∈ [{a→b→a}]H . Gl) J As a side note, the above proof of Lemma 28 implies that the set of minimal proofs from the axioms{σ1→σ1,. One reason why knowing the axiomatizations of a→aanda→b→bis is trivial is that the set of minimal proofs in the corresponding calculus is finite, which is not the case fora→b→a. Recursive undecidability of deducibility, Tarski completeness and independence of axioms Propositional calculus problems. Herman Geuvers For the standard intuitionistic connections, the general elimination rules are quite close to ours, but. Many of the general elimination rules, for example for∧, appear naturally as a consequence of our approach to deriving the rules from the truth table. From the rules in the truth table of A → B/C with a 1 we get the following four introductory rules: J We can now prove the correctness of the interpretation of intuitionistic propositional logic intotonand logic. Here we can reduce to one of the following derivations of Γ`D, which shows that the detour conversion process is not Kerk-Rosser. Aj spans all statements that have a 1 in the truth table of c0;Ai spans everything. When reducing terms for ∨ and ∧, the elimination is always removed at each step. Given the permutation convertibility as defined in Definition 25, we add the reduction rules for the related terms as follows. The translation of a −→a step in the optimized calculus translates to a (possibly multistep) −→a step in the original calculusλC. We translate the parallel∧ elimination rule of Definition 44 by defining it in terms of the optimized terms for∧ of Example 39. We ignore the rest of the proof as it adds a lot of notational overhead, so we just write forhtiρ. In case (1), ql[yl:=sj]∈Dby the assumption and the induction hypothesis. A) as a saturated set and the induction hypothesis. The idea is to contract an inner redex of highest rank of a term inb-normal form. By induction hypothesis,qi·Φ[s, sk ;λy.r]gfor some normal form with all redexes of lower rank. We can also say a little more about the transformation of derivatives in these systems themselves: the bypass transformation is strongly normalizing, the permutational transformation is strongly normalizing, and we can also conclude that the combined transformation is weakly normalizing. The reductions for the optimized rules of Definition 36, the parallel ∧-elimination rule of Definition 44, the standard →-introduction of Definition 47, and the traditional elimination rule of Definition 50 are weakly normalizing. J. is done in [12] in their “uniform calculation”) explaining the entry rules in terms of the elimination rules. From our research, we would propose the following as an appropriate system for intuitionistic logic with "parallel rules of elimination" that follow Prawitz's inversion principle [15]. Rodolphe Lepigre This (ordinary) part of the type system provides the basic principles of reasoning, which are used to structure evidence. The second component is an automatic decision-making procedure for the equational theory of language. Previous work on the language Disclaimer: the aim of this paper A more interesting example, which cannot be written without a control operator, will be given in Section 4. From a computational point of view, the manipulation of continuation using control operators can be understood as "cheating". Another example of extension for a preexisting type can be obtained by defining the type red-black trees as a subtype of binary trees. More precisely, a red-black tree can be represented as a tree whose nodes have an extra color field. This can be done in a more systematic way with a syntax that requires the user to provide the intended stack type definition. It is possible to define a dot projection operation to access abstract types, so that it is possible for writestack_impl.stack to refer to the stacks type. Note that we need to provide at least a type annotation for the system to know what to instantiate the existential with. On the other hand, it is possible to call a lemma by calling the corresponding function. They are also type-checked in that order, and the corresponding equations are added to the context one after the other as a side effect of the type-checking. In this case, the equation corresponding to the conclusion of the used lemma is added directly to the context. Note that no addition to the system is needed to support such annotations, they are only syntactic sugar. It produces a vector whose length is the sum of the lengths of its two arguments. Thanks to the Curry-like nature of our system, the dimensions of the argument vectors do not need to be specified as arguments. Intuitively, this will allow us to reason about the oddness (or equality) of a given input stream number on a case-by-case basis. Indeed, at most 2 x n elements of the input stream must be considered to construct the result. Although PML2 is unable to prove the conclusion of mccarthy91's commented version, we can give the following alternative (but equivalent) definition. We can then write check and prove the termination of the original version of the McCarthy 91 function as follows. Clearly, the completeness proof corresponding to a given function has a similar structure to the definition of the function itself. It is currently not possible to officially verify proofs produced by PML2 in another system. Although it is possible to use classical logic to prove that a program meets its specification, the underlying programming language is not efficient. Finally, it is also possible to reason about ML programs (including efficient ones) by compiling them down to higher-order formulas [4, 5], which can then be manipulated using an external prover such as Coq [23]. Julius Michaelis Related Work 2 Isabelle Notation 3 Formulas and Their Semantics The proof of the admissibility of the cut rule is by induction on the cut formula as in [48]. A generalization of the last two facts (with variables for empty lists) is followed by an induction to the computation of sc. 5 Translating Between Proof Systems We proved this both by the completeness result of Section 4.2, compactness and attenuation, and by the compactness, SC completeness result of Section 4.1 and (4) of Section 5. After splitting the set notion into two distinct sets of clauses based on whether {k¬v} ∪C ∈ S, we can use the two weakening lemmas (5,6) and resolution to complete the proof. The idea for this trick is borrowed from Gallier [15], but the details of the proofs differ (cf. [26]). Doing so requires a series of auxiliary lemmas with laborious proofs to convert deductions of Γ ⇒L to deductions of Γ0 ⇒L, where Γ0 is a variant of Γ such that er_cnf holds for all elements of Γ0. A Toy Resolution Prover Craig Interpolation via Substitution Our formalization of this proof corresponds very closely to Fitting's proof, and we do not wish to repeat it here. The proof of this is constructed automatically after dealing with the minor differences between sets and multisets. Thieman et al. 's formalization IsaFoR/CeTA [46] of large parts of the rewriting theory (starting with [47]) shows that the dream of a unified formalization of logic is achievable and ideally the two efforts will one day be connected. 29 Tobias Nipkow, Lawrence Paulson and Markus Wenzel.Isabelle/HOL — A Proof Assistant for Higher-Order Logic, volume 2283 of LNCS. In univalent type theory (UTT), also known as homotopy type theory (HoTT), these problems are solved by taking a different approach to the statement of the univalence axiom. For example, verifying the univalence axiom in a model of type theory can be a difficult task. To show sef is an equivalence, it suffices to show sef is a bi-invertible map [15, Section 4.3]. For the proper inverse we take gunchanged and note that we know f(g(y)) =y for all y:Y(x, x0) by assumption. For the forward direction, we know from Theorem 4.1 that axioms (1) to (3) allow us to construct a termua:UAi. Axioms (1)-(5) for a universe Ui are together logically equivalent to the correct univalence axiom for Ui. We work in the theory of internal type topos of cubic sets wherever possible, but this approach has its limitations. We have seen that we can easily satisfy axioms (1) and (2) in the cubic set model. J Compare this result with Theorem 3.5, where we saw that naive univalence with an arithmetic rule is logically equivalent to the correct univalence axiom. If this is the case, we have fst◦(coerceunit) :{A:U} →A→A, which is not equal to the identity function. Constructive Type Theory Another important term used in this paper is the family of setoids indexed by a setoid. An equivalent definition is obtained by considering A as a discrete E-category A# (whose objects are elements of |A| and whose hom-setoids are Hom(a, b) = (a=Ab,∼) with p∼q always true ) and B as a functor from this category to the E category of setoids. This uses only terms defined below.). There are several possibilities, but the one corresponding to the fibers{f−1(a)}a∈A of the extension function f :B→Abetween setoids is a notion of family that is irrelevant to the proof. The Cartesian product Π(A, F) of the family F : Fam(A) consists of pairs f = (|f|,extf), wheref : (Πx:|A|)|F(x)|and extf is a proof object that proves that|f|is extensional, i.e. An interesting question now is whether we can impose an equality of objects on an E-category compatible with composition, in order to obtain an HF-category. In classical category theory, any category can be equipped with isomorphism as equality of objects (see comment above). Consider the group Z2 as a single object, a skeletal precategory: let N1 be the basic set and Hom(0,0) = N2 with 0 as unit and ◦ as addition. In short, the notion of a univalent category is too restrictive to cover many known examples.6 Conclusion
Tonny Hurkens
Related work and contribution of the paper
2 Deriving constructive natural deduction rules from truth tables
Three larger examples
3 Convertibilities and conversion
4 The Curry-Howard isomorphism
5 Extending the Curry-Howard isomorphism to definable rules
6 Normalization
Strong Normalization of the detour conversion
Weak Normalization of conversion
Corollaries of normalization
7 Conclusion and Further work
1 Introduction: joining programming and proving
Program verification principles
2 Functional programming in PML 2
Control operator and classical logic
Non-coercive subtyping
Toward the encoding of a module system
3 Verification of ML programs
3.1 (Un)typed quantification and unary natural numbers
Building up an equational context
Detailed proofs using type annotations
Mixing proofs and programs
4 Programs extracted from classical proofs
5 Termination and internal totality proofs
6 Future work
7 Similar systems
Tobias Nipkow
4 Proof Systems 4.1 Sequent Calculus
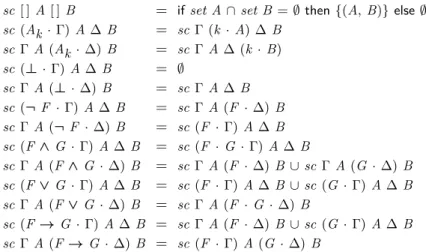
6 Compactness
7 Resolution
Soundness and Completeness
A Translation Between SC and Resolution
8 Craig Interpolation
9 The Model Existence Theorem
10 Conclusion
Andrew M. Pitts
3 Voevodsky’s Univalence Axiom
4 A new set of axioms
5 Applications in models of type theory
Example: the CCHM model of univalent type theory
6 An application to an open problem in type theory
Erik Palmgren
2 Categories in standard type theory
3 E-categories and H-categories in standard type theory
4 E-categories are proper generalizations of H-categories
5 Categories in Univalent Type Theory