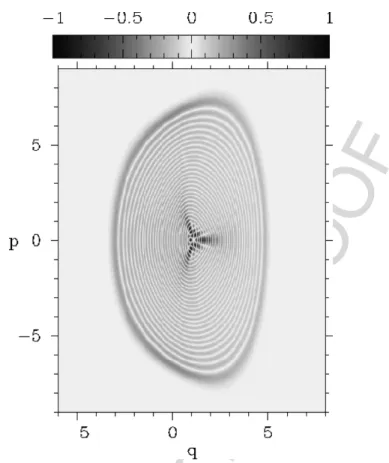
Each point in phase space fully explains the state of the classical system evolving along a trajectory. For this reason, its description in terms of the classical concept of phase space seems reckless. HL, i.e. the tensor product of the factor Hilbert spaces describing each degree of freedom.
UNCORRECTED PROOF
Semiclassical Quantum States
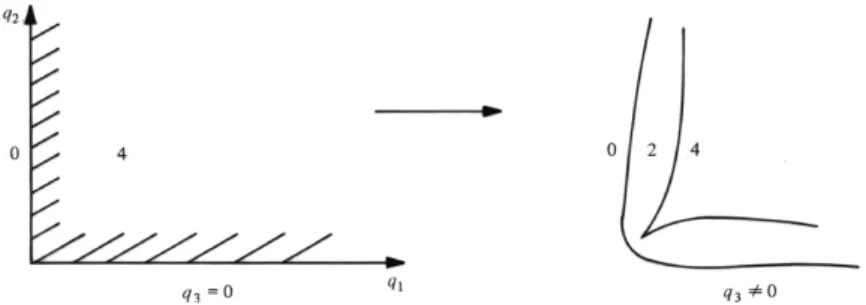
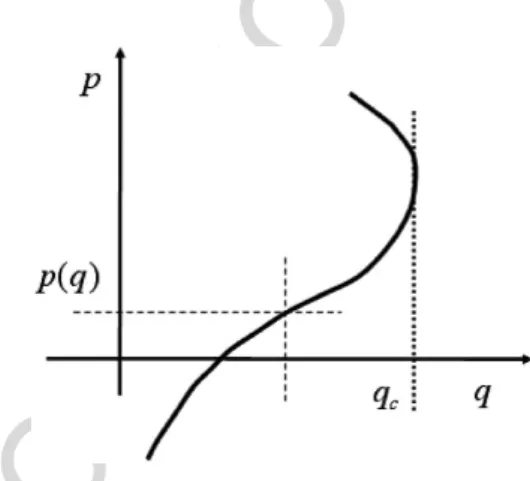
However, the smoothness of the evolution implies that the topology of the surface must be preserved (be it planar, torus, or, in the middle, cylindrical). There are four possibilities for the rectangle unfolding topology, shown in Fig. For L > 1, we can take the Fourier transform for a subset of the degrees of freedom.
Operator Representations and Double Phase Space
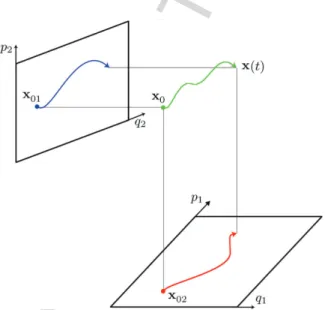
The semiclassical limit for a complex phase space is not as transparent as the real theory treated here. Thus, we can consider γ± as projections of the curve Γ defined on the (2L)-dimensional surface, ΛC, which specifies the canonical transformation, within the dual (4L)-dimensional phase space, X = (P, Q). In the case that both surfaces are tori, we get a double phase space torus, τ =τ−⊗τ+, as if we had doubled the number of degrees of freedom.
However, we can consider the rotation π/2, q+ → p+, p+ → −q+, the multiple of the identity inx−, as an example of the canonical transformation in the two-phase space: X →X. Note that |Q is a first example of an operator basis corresponding to a set of parallel Lagrangian planes in two-phase space, which, however, have internal coordinates that can be independently identified with a phase space. Here we will have to discover the unpleasant situation that the canonical coordinate in two-phase space is y, but the geometrically meaningful variable in one-phase space is ξ, the chord of the trajectory, in the case of continuous evolution.
The chord representation is therefore a second example of a representation of operators in terms of an operator basis that can be uniquely identified to a phase space. Indeed, each chord corresponds to a Lagrangian surface in dual phase space and thus a particular uniform translation in single phase space. What was missing was simply the identification of each of these different phase spaces with a specific foliation of Lagrange planes in dual phase space.
This is the case of the Weyl representation for each observable that classically corresponds to a smooth classical function of points in the phase space [17].
The Wigner Function and the Chord Function
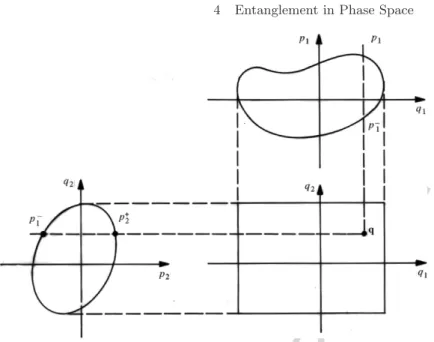
Then it is clear that the expansion of the chord function at the origin is given by a quadratic form. All these planes are Lagrangian, so it follows that the projection of the Wigner function onto any Lagrangian plane in phase space is a probability distribution for the corresponding variable. Reconstruction of the Wigner function from a suitable set of these marginal distributions is known as quantum tomography.
In fact, we obtain [32] by inserting the above expression in the definition of the phase space correlation. Yet the loss of the phase information inC(ξ), but contained in the chord function, seems to suggest that these are necessary conditions, whereas the full sufficient condition for purity is ˆρ2=ρ, which is expressed in the chord. representation' as [33]. The chord function is simply a rescaling of the Wigner function if the midpoint is at the origin.
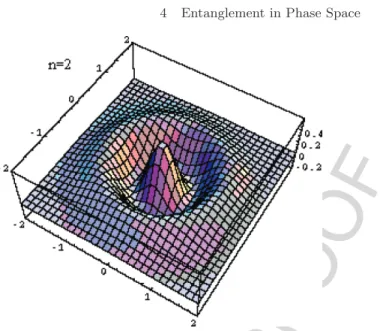
Fock states, |n, i.e. the excited states of the harmonic oscillator, also have reflection symmetry with respect to the origin. No matter how classic the appearance of the Wigner function is (i.e. it can be smooth and positive), it is always completely quantum in terms of parity measures. The adaptation of the Wigner function for finite Hilbert spaces is of particular interest to quantum computing and quantum information theory.
Thus, we must first face a choice of topology in which to compact the phase space.
The Partial Trace: Sections and Projections
For example, in the case of the cat state (4.102) with smallη, they are found in the shallow negative regions where|W+(x)| is exponentially small. It follows that a representation in terms of the restricted translation operators, T'ξ1, would not be complete. In the case of the chord function we have to take care of the normalization, which depends on the number of degrees of freedom.
These relations can be interpreted in terms of average values of the basis operators, i.e. R'x=R'x1 R'x2andT'ξ= T'ξ1T'ξ2. Expanding this to first order results in the linear entropy of a partial trace of the full density operator. But it is a simple consequence of , the invariance of the quantum correlations with respect to Fourier transforms for a pure state, that.
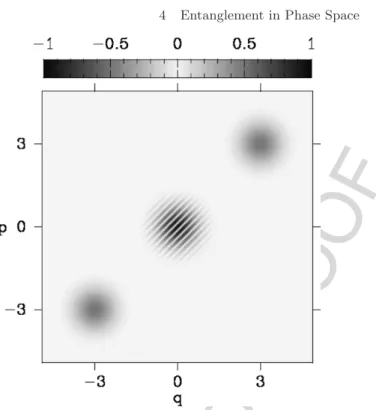
The invariance of the partial traces with respect to local transformations carries over to the aforementioned measures of entanglement. In terms of Husimi functions (4.108), it is obvious to describe entanglement in terms of the Wehrl entropy (4.109) for the reduced density operator. To conclude this section, let's now study another kind of projection of the Wigner function.
It is then shown that the same simultaneity introduced in terms of partial trace can be expressed as the sum of conditional probabilities for measurements on any component.
Generating a Classical Entanglement
To obtain a violation of the CHSH inequality, we must choose pairs of observable values for each component that do not commute. The correlation for a given choice of observable data from each pair can still be calculated from the probabilities in the respective Lagrangian plane, but we must use different planes in each of the four correlations. If the overall Wigner function generating all these densities has negative regions, the CHSH inequality may be violated, as discussed in the next section.
The point is that the measurements are restricted to the projection operators for the factor states in the Schmidt basis.
The EPR State
Entanglement and Decoherence
The usual view is that the environment is somewhere outside, but it may just as well consist of internal degrees of freedom for the center of mass (CM) of a large system of particles. Exchanges between large-scale motion and internal variables lead to macroscopic energy dissipation as well as quantum state decoherence for the CM. Let us consider the simplest possible example of CM decoherence, due to its interweaving with internal variables.
It is noteworthy that positivity is not a necessary ingredient for the proof of the central limit theorem: In the case of identical quadratically integrable pure-state Wigner functions, Tegmark and Shapiro [69] show that convergence to a Gaussian again results. Thus, the entanglement of the center of mass with its surroundings is invariant in this simple case. The averages of the moments resulting from the different evolutions of many Wigner functions lead to a progressive loss of purity for the CM.
The operators of Lindblad L'j account for the non-unitarity of evolution, that is, they take the part of merging with the environment. The derivation of the Markovian approximation in the context of quantum optics (damped harmonic oscillator) was first performed by Agarwal [74], but this is all in the language of complex phase space. It is remarkable that the Wigner function becomes positive after a time that depends only on the parameters of the Lindblad equation, regardless of the pure initial state [72, 75].
This allows an interpretation of the Gaussian smoothing as originating in the multiple small contributions envisioned in the central limit theorem.
A Semiclassical Picture of Entanglement
Viewed in two-phase space, there must always be pairs of chords of the double torus emanating from each center, x. Therefore, in the case of the Wigner function, we take the cosine phase as half the area between the torus and its reflection at the center x [22], which coincides with the area between the torus and the chord [84. , 85] (see also [86]). Viewed in single-phase space, the Caustic of the Wigner function arises from the union of the torus chords as their center, x, moves.
Similarly, the caustics of the chord function are the loci of ξ, such that Tξ(τψ) is tangent to τψ. For example, the accumulation at the center of the Wigner function for the Fock state is a caustic. It turns out that the double folding surfaces of the Wigner caustics meeting along the torus do not unfold in the manner shown in Fig.
A pair of leaves of a double torus are joined on the identity plane along this curve or torus. The large amplitude of fluctuations of the Wigner function near the quantized curve is due to this caustic. Taking into account the change of sign, p−→ −p−, in the definition of the dual phase space, we find that it must be the Hamiltonian of the dual phase space. 4.159).
Explicit formulas for the semiclassical evolution of the Wigner function are given in [91, 92], while the evolving operation of the chord function is presented in [93].

This classically corresponds to driving Hamilton's equations backwards in two-phase space; eg, in the example of Sect. This is always possible in quantum mechanics because one can always specify a unitary transformation in the entire Hilbert space which transforms any given state into another state and we can choose the latter as a product state. It remains to be seen whether this particular type of entangled state has any application in quantum information theory.
Many of the ideas and results presented here arose in the context of a fruitful collaboration with Olivier Brodier in CBPF. Raul Vallejos, Marcos Saraceno and Pedro Rios also played important roles in the developments I have outlined here. Hannay: Geometry of two-dimensional tori in phase space: Projections, cuts and the Wigner function, Ann.
Davidovich: Method for Direct Measurement of Wigner Function in QED Cavity and Ion Traps, Phys. Haroche: Direct measurement of the Wigner function of a one-photon focal state in a cavity, Phys. In: New Techniques and Ideas in Quantum Measurement Theory (New York Academy of Sciences, New York 1986).
Ozorio de Almeida: The Wigner function for two-dimensional tori: uniform approximation and projections, Ann.