Modelos de sobrevivência com fração de cura e omissão nas covariáveis

(1)

MODELOS DE SOBREVIVˆ

ENCIA COM

FRA ¸

C ˜

AO DE CURA E

OMISS ˜

AO NAS COVARI ´

AVEIS

Renata Santana Fonseca

Disserta¸cão apresentada ao Corpo Docente do Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıs-tica - CCET - UFRN, como requisito parcial para obten¸cão do t´ıtulo de Mestre em Matemática Aplicada e Estat´ıstica.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica Orientador: Profa _Dra _{Dione Maria Valen¸ca}

(2)

(3)

Modelos de Sobrevivˆencia com Fra¸c˜

ao de Cura e

Omiss˜

ao nas Covari´

aveis

Este exemplar corresponde à reda¸cão final da disserta¸cão devidamente corrigida, defendida por Renata Santana Fonseca e aprovada pela comissão julgadora.

Natal, mar¸co de 2009

BANCA EXAMINADORA:

Profa _Dra _{Dione Maria Valen¸ca (orientadora) - DEST - UFRN}

Profa _Dra _{Jeanete Alves Moreira - DEST - UFRN}

Prof. Dr. Dami˜ao N´obrega da Silva - DEST - UFRN

Profa _Dra _{Silvia Maria de Freitas - DEMA - UFC}

(4)

Dedicat´

oria

Dedico este trabalho a todos aqueles que choraram saudades junto comigo.

(5)

Agradecimentos

Tudo é do Pai, toda Honra e toda Glória, é dele a vitória alcan¸cada em minha vida.

Agrade¸co à minha orientadora, Dione pela orienta¸cão, paciência e por ter me mostrado o prazer de se fazer um trabalho como este.

Tenho muito que agradecer aos meus pais, Antonio e Edneide pelos valores trans-mitidos em todo o percurso da minha vida e pelo apoio incondicional em todas as horas.

Ao meu eterno amigo, companheiro e, mais do que nunca, grande amor, Gilmar pela compreensão, enorme paciência e dedica¸cão que me foram mostrados ao longo destes dois anos.

Meus irmãos, Liu, Nando e Bia, sobrinha, Pam, cunhados, Tom e Jú e amigas C´ıntia, Nivea, Mar´ılia, Mariese e Relva, obrigada pelos momentos de descontra¸cão em Salvador, boas recargas de ânimo pra continuar a jornada.

Aos amigos de Natal. Allan, Cec´ılio, Manassés, Patr´ıcia e Renatinha. Sem vocês eu não seria nada, não teria chegado até o fim. Obrigada pelo apoio nas horas em que pensava em desistir, pelas poucas, porém gostosas farras que fizemos e pela ver-dadeira amizade. Com vocês aprendi muito sobre convivência e respeito, mas não posso esquecer de pedir desculpas pelas grosserias.

Aos professores da UFRN, Dami˜ao, Jeanete, Pledson, Carla e Paulo pela recep-tividade, pelos conselhos, dicas e principalmente por acreditarem no meu potencial e me incentivarem a continuar com os estudos.

Aos colegas do PPGMAE, Hermes, pela enciclopédia que carrega e sempre tem uma resposta pra todas as perguntas, Lenilson, Neto, Daniel, Tatiana, Enai, Camila, Aparecida e Moisés pelos consolos, pelas solu¸cões de exerc´ıcios e programas.

Ao secretário Rafael e ex-secretário Paulo pela disposi¸cão em ajudar e esclarecer dúvidas, e a todos os funcionários do CCET.

(6)

Ao professor Heleno Bolfarine pela sugest˜ao do tema. `

A Cristiane Fernandes (Cris), a primeira pessoa que conheci em Natal, que mesmo sem saber quem eu era, me orientou e ajudou nos primeiros dias.

E `a CAPES pelo apoio financeiro.

(7)

Resumo

Neste trabalho estudamos o modelo de sobrevivência com fra¸cão de cura proposto por Yakovlev et al. (1993) que possui uma estrutura de riscos competitivos. Covariá-veis são introduzidas para modelar o número médio de riscos e permitimos que algumas destas covariáveis apresentem omissão. Consideramos apenas os casos em que as cova-riáveis omissas são categóricas e as estimativas dos parâmetros são obtidas através do algoritmo EM ponderado. Apresentamos uma série de simula¸cões para confrontar as estimativas obtidas através deste método com as obtidas quando se exclui do banco de dados as observa¸cões que apresentam omissão, conhecida como análise de casos comple-tos. Avaliamos também através de simula¸cões, o impacto na estimativa dos parâmetros quando aumenta-se o percentual de curados e de censura entre indiv´ıduos não curados. Um conjunto de dados reais referentes ao tempo até a conclusão do curso de estat´ıstica na Universidade Federal do Rio Grande do Norte é utilizado para ilustrar o método.

Palavras - chave: Análise de Sobrevivência; Fra¸cão de cura; variáveis omissas;

(8)

Abstract

In this work we study the survival cure rate model proposed by Yakovlev (1993) that are considered in a competing risk setting. Covariates are introduced for modeling the cure rate and we allow some covariates to have missing values. We consider only the cases by which the missing covariates are categorical and implement the EM algorithm via the method of weights for maximum likelihood estimation. We present a Monte Carlo simulation experiment to compare the properties of the estimators based on this method with those estimators under the complete case scenario. We also evaluate, in this experiment, the impact in the parameter estimates when we increase the proportion of immune and censored individuals among the not immune one. We demonstrate the proposed methodology with a real data set involving the time until the graduation for the undergraduate course of Statistics of the Universidade Federal do Rio Grande do Norte.

(9)

Sum´

ario

1 Introdu¸c˜ao 1

1.1 Conceitos básicos de análise de sobrevivência . . . 1

1.2 Fra¸c˜ao de cura . . . 4

1.3 O Problema de dados omissos . . . 7

1.3.1 Mecanismos de omiss˜ao . . . 9

1.4 Objetivos . . . 10

1.5 Estrutura da disserta¸c˜ao . . . 11

2 Modelo com Fra¸c˜ao de Cura 12 2.1 Formula¸c˜ao do modelo . . . 12

2.2 Fun¸c˜ao de verossimilhan¸ca . . . 15

2.3 Modelo param´etrico Weibull . . . 18

3 Modelo com Fra¸cão de Cura e Omissão nas Covariáveis 21 3.1 Estima¸cão de máxima verossimilhan¸ca via algoritmo EM . . . 21

3.1.1 Algoritmo EM ponderado . . . 23

3.1.2 Modelando a distribui¸c˜ao das covari´aveis . . . 27

4 Estudo de Simula¸c˜ao 29 4.1 Obten¸c˜ao dos dados simulados . . . 29

4.2 Resultados para os dados simulados . . . 32

4.2.1 Resultados para amostras completamente observadas . . . 32

(10)

4.2.2 Efeito das omiss˜oes nas estimativas dos parˆametros . . . 34

5 Aplica¸c˜ao 43

5.1 Ajuste do modelo aos dados de evas˜ao escolar . . . 43

6 Considera¸c˜oes Finais 48

6.1 Conclus˜ao . . . 48 6.2 Pesquisas futuras . . . 49

A Obten¸c˜ao da Fun¸c˜ao de Verossimilhan¸ca 51

A.1 Verossimilhan¸ca . . . 51 A.2 Verossimilhan¸ca marginal . . . 53

B Aspectos Computacionais 55

(11)

Cap´ıtulo 1

Introdu¸

c˜

ao

Neste trabalho abordamos aspectos teóricos, computacionais e aplicados de análise estat´ıstica para modelar dados de sobrevivência extra´ıdos de uma popula¸cão na qual uma parcela dos indiv´ıduos está imune à ocorrência do evento (ou são conside-rados cuconside-rados). Além disso, estudamos um procedimento para tratar a ocorrência de omissão em covariáveis.

Faremos neste cap´ıtulo, uma breve introdu¸cão aos conceitos básicos de análise de sobrevivência, à modelagem para dados com fra¸cão de cura e ao problema de dados omissos, seguida de uma revisão bibliográfica com algumas propostas encontradas na literatura para tratar de dados com tais caracter´ısticas.

1.1 Conceitos b´

asicos de an´

alise de sobrevivˆ

encia

A análise de sobrevivência é um conjunto de técnicas estat´ısticas que servem para analisar dados correspondentes ao tempo até ocorrência de determinado evento; como, por exemplo, o tempo até a morte ou o tempo até a cura de um paciente, ou ainda, o tempo até a falha de um equipamento eletrônico.

Estes métodos foram originalmente designados para estudos de mortalidade, ex-plicando, portanto, o nome “sobrevivência”. No entanto, a aplicabilidade destas técni-cas se estende a diversas áreas do conhecimento. Na engenharia, onde recebe o nome

(12)

1.1 Conceitos básicos de análise de sobrevivência 2

de “confiabilidade”, busca-se estudar o tempo até a falha de um equipamento, na crimi-nologia o interesse pode ser o tempo até um ex-detento reincidir no crime, na educa¸cão, o tempo até a conclusão de um curso. Na literatura refere-se a este tempo comotempo de falha.

Seja T uma variável aleatória cont´ınua não negativa representando o tempo de vida, f(t) a sua correspondente fun¸cão densidade eF(t) a fun¸cão distribui¸cão acumu-lada. Em análise de sobrevivência, existe um especial interessse na probabilidade de um indiv´ıduo sobreviver pelo menos até o tempot, conhecida como fun¸cão de sobrevivência que é dada por

S(t) =P(T > t) =

∞

t

f(u)du= 1₋F(t), para t >0. (1.1)

Esta é uma fun¸cão monótona decrescente com as seguintes propriedades:

(i) S(0) = 1;

(ii) lim

t→∞S(t) = 0.

Fun¸cões de sobrevivência que não satisfazem à propriedade (ii) são denominadas fun¸cões de sobrevivência impróprias ou com fra¸cão de cura, ou ainda de longa dura¸cão (Rodrigues, Cancho, & Castro 2008) e são objeto de estudo desta disserta¸cão.

Outra fun¸cão de interesse na análise de sobrevivência é a fun¸cão risco, que es-pecifica a taxa de falha instantânea no tempot, definida como

h(t) = lim Δt→0+

P(t < T _≤t+ Δt_|T > t)

Δt (1.2)

As fun¸cões de densidade, de sobrevivência e de risco são matematicamente rela-cionadas. Assim, conhecendo uma delas pode-se obter as outras através das seguintes rela¸cões:

h(t) =₋dlogS(t)

dt =

f(t)

S(t), (1.3)

f(t) =₋dS(t)

(13)

1.1 Conceitos básicos de análise de sobrevivência 3

Uma propriedade da fun¸c˜ao risco que define uma importante classe de modelos ´e a proporcionalidade dos riscos, ou seja, para duas unidades observacionais distintas i

e j, a razão entre os riscoshi(t)/hj(t) =k, sendo k constante para todo tempo t. Por exemplo, se k = 3 , dizemos que o risco (de falha) do indiv´ıduo i é três vezes o risco do indiv´ıduo j em todo o per´ıodo de acompanhamento. Um modelo cuja fun¸cão risco satisfaz esta condi¸cão é chamado de modelo de riscos porporcionais.

A principal caracter´ıstica de dados de sobrevivência é a presen¸ca de censura, que é uma observa¸cão parcial da resposta (tempo de falha). Isto ocorre devido a perda de acompanhamento do indiv´ıduo, seja porque o paciente morreu de causa diferente da estudada, mudou de cidade, ou porque, ao final do estudo, o evento não foi observado. Sem a presen¸ca de censura, as técnicas estat´ısticas clássicas, como análise de regressão e planejamento de experimento, poderiam ser utilizadas na análise deste tipo de dados, provavelmente usando uma transforma¸cão para a resposta. No entanto, se houver censuras, tais técnicas não podem ser utilizadas (Colosimo & Giolo 2006). Neste caso, sabe-se que o tempo entre o in´ıcio do estudo e a ocorrência do evento é maior do que o observado, o que caracteriza censura à direita. No entanto, o tempo durante o qual o indiv´ıduo esteve em observa¸cão é aproveitado. Dentre os mecanismos de censura existentes podemos citar:

• acensura tipo Iem que experimento ´e realizado em um per´ıodo de tempo

pr´e-fixado, de forma que o tempo de vida do indiv´ıduo ´e conhecido apenas se ocorrer antes do final do estudo;

• a censura tipo II em que o estudo ´e realizado at´e que o evento ocorra um

n´umero pr´e-estabelecido de vezes e

• a censura aletória, que é a mais freqüente em estudos reais, caracteriza-se

(14)

1.2 Fra¸c˜ao de cura 4

variáveis aleatórias. Quando a distribui¸cão da censura não envolve parâmetros de interesse ao estudo, dizemos que a censura é não infomativa.

1.2 Fra¸

c˜

ao de cura

Em modelos tradicionais de tempos de falha, assume-se que em dado momento o evento de interesse irá ocorrer para todos os indiv´ıduos observados após um espa¸co de tempo razoável, isto é, todos os indiv´ıduos estão em risco durante a realiza¸cão do estudo.

No entanto, em determinados experimentos, alguns indiv´ıduos podem nunca apre-sentar o evento pois estão curados ou são consideradosimunes ao evento. Se, por exem-plo, o evento de interesse é a recorrência de determinado tipo de câncer, após aplica¸cão de tratamentos, uma parte dos indiv´ıduos em estudo pode não apresentar o retorno da doen¸ca (da´ı a denomina¸cão “fra¸cão de cura”). Dados com estas caracter´ısticas podem surgir em outros contextos. Por exemplo, em estudos na área de criminologia um pos-s´ıvel evento de interesse é o tempo até um ex-detento reincidir no crime, entretanto, alguns deles estarão reabilitados e não apresentarão tal evento. Na demografia, em estudos sobre tempo até o divórcio, alguns casais podem nunca experimentar o evento. Modelar estes dados ignorando a existência de uma parcela de curados ou imunes na popula¸cão pode conduzir o pesquisador a conclusões distorcidas, ao passo que quando esta caracter´ıstica é incorporada no modelo, pode-se saber, por exemplo, qual tratamento resulta em uma maior propor¸cão de curados, ou que tratamento é mais eficiente para determinado perfil de paciente.

(15)

pela experiˆencia do pesquisador.

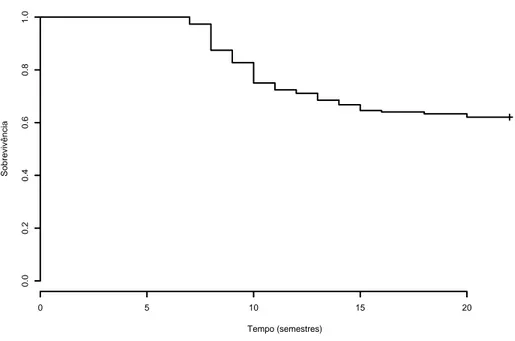
A presen¸ca de imunes na popula¸cão pode ser identificada através do gráfico da fun¸cão de sobrevivência emp´ırica conhecida como Kaplan-Meier ou estimador produto-limite (Kaplan & Meier 1958). Se a cauda direita apresenta um n´ıvel aproximadamente constante e estritamente maior do que zero durante um per´ıodo de tempo razoável, caracterizando uma fun¸cão de sobrevivência imprópria (fun¸cão que não converge para zero a medida que o tempo cresce), há ind´ıcios da presen¸ca de imunes.

A Figura 1.1 mostra a curva de sobrevivência estimada para um conjunto de dados reais referente ao tempo até a conclusão do curso de gradua¸cão em Estat´ıstica da UFRN. Observa-se que a cauda direita alcan¸ca um patamar acima de zero por um per´ıodo considerável, o que retrata o comportamento de uma fun¸cão de sobrevivência imprópria.

0 5 10 15 20

0.0

0.2

0.4

0.6

0.8

1.0

Tempo (semestres)

Sobrevivência

Figura 1.1: Fun¸cão de Sobrevivência estimada para os dados de tempo até a conclusão do curso de gradua¸cão em Estat´ıstica da UFRN no per´ıodo de 1997 a 2004. Amostra com n= 414 alunos.

(16)

da popula¸cão não curada e outra é dada por uma distribui¸cão degenerada com tempos infinitos para os imunes (Boag 1949; Berkson & Gage 1952). Neste modelo, conhecido como modelo de mistura padrão, é assumido que uma fra¸cão π (0< π < 1) da popu-la¸cão está curada, e a restante 1₋π, não está curada. Utilizando uma parti¸cão em imunes (I) e não imunes (NI), comP(I) =πeP(NI) = 1₋πa fun¸cão de sobrevivência para a popula¸cão, denotada por Spop(t) para este modelo, é dada por

Spop(t) = P(T > t)

= P(T > t_|I)P(I) +P(T > t_|NI)P(NI)

= π+ (1₋π)S∗(t), (1.5)

em que P(T > t_|NI) = S∗₍_t_{) denota a fun¸cão de sobrevivência para a popula¸cão não}

imune e P(T > t_|I) = 1 para todot >0.

Algumas desvantagens deste modelo são apontadas por Chen, Ibrahim, & Sinha (1999). Na presen¸ca de covariáveis relacionadas com o parâmetro π, o modelo de mis-tura padrão não possui a propriedade de riscos proporcionais. Além disso, no contexto bayesiano, as distribui¸cões a priori não informativas impróprias implicam, em geral, em distribui¸cões a posteriori impróprias.

Neste trabalho, discutimos um modelo alternativo com estrutura de riscos com-petitivos1 _{proposto por Yakovlev et al. (1993) e Chen, Ibrahim, & Sinha (1999), que é} referido em Rodrigues, Cancho, & Castro (2008) comomodelo de tempo de promo¸cão. Este modelo supera tais desvantagens e será descrito com detalhes no Cap´ıtulo 2.

Modelos de sobrevivência com fra¸cão de cura têm sido extensivamente discutidos e aplicados a dados reais na literatura estat´ıstica por vários autores nos últimos anos. Técnicas bayesianas para estima¸cão dos parâmetros do modelo de tempo de promo¸cão são dadas em Ibrahim, Chen, & Sinha (2001). Utilizando o modelo de tempo de promo¸cão, Zaider et al. (2001) estudam o efeito de diferentes doses de radia¸cão sobre a fra¸cão de curados em pacientes com câncer de próstata. A proposta de Yin & Ibrahim

1

(17)

1.3 O Problema de dados omissos 7

(2005) consiste em uma classe de modelos que naturalmente liga uma fam´ılia de fun¸cões de sobrevivência próprias e imprópras. Um modelo unificado, que inclui o modelo de mistura padrão e o modelo de tempo de promo¸cão como dois casos especiais, é discutido em Rodrigues & Louzada-Neto (2006). O modelo de tempo de promo¸cão foi estendido por Mizoi (2007) para a situa¸cão em que há erro de medi¸cão nas covariáveis. Uma abordagem semiparamétrica que permite utilizar dados correlacionados no modelo de mistura padrão é discutida em Peng et al. (2007). Um teste para avaliar a suficiência do tempo de acompanhamento em uma ampla classe de modelos de fra¸cão de cura foi proposto por Klebanov & Yakovlev (2007).

A inclusão de informa¸cões concomitantes no modelo de fra¸cão de cura é de grande importância para descrever a heterogeneidade da popula¸cão. Unidades com caracter´ıs-ticas diferentes certamente apresentarão tempos de sobrevida e chance de cura dife-rentes. Contudo, algumas destas informa¸cões podem não ser observadas para todos os indiv´ıduos, resultando em algumas lacunas na matriz de dados. Na próxima se¸cão, descrevemos o problema e caracter´ısticas importantes em dados com omissões nas co-variáveis.

1.3 O Problema de dados omissos

A presen¸ca de omissão em covariáveis é um problema frequente na análise es-tat´ıstica e pode ser causada por diversos fatores, como por exemplo, a recusa de um indiv´ıduo a fornecer alguma informa¸cão ou a morte de um paciente antes de realizar todos os exames. Em um experimento industrial, algumas covariáveis podem não ser observadas em equipamentos quebrados devido a causas não relacionadas ao processo experimental.

(18)

percentual de dados omissos, pode causar perda de informa¸cão e resultar em estimativas tendenciosas e ineficientes. Portanto, é importante o desenvolvimento de métodos que incorporem os dados omissos nas análises. Uma revisão sobre os métodos existentes para ajustar modelos de regressão utilizando este tipo de dado é abordada em Little (1992), que destaca maior eficiência dos métodos de imputa¸cão múltipla.

Muitas propostas vêm sendo discutidas para tratar dados omissos em diversos con-textos. Diversas técnicas para análise de dados que apresentam omissão são abordadas por Roderick, Little, & Rubin (1987). Quando as covariáveis omissas são categóricas, Ibrahim (1990) propõem utilizar o algoritmo EM ponderado (Dempster et al. 1977) para obter estimativas dos parâmetros em modelos lineares generalizados. Esta técnica foi extendida por Ibrahim, Chen, & Lipsitz (1999) para covariáveis cont´ınuas ou mistas (cont´ınuas e categóricas), em que é implementada a versão Monte Carlo do algoritmo EM (Tanner 1996). O algoritmoEM ponderado é descrito em detalhes por Horton & Laird (1999) que, por meio de exemplos, ilustram sua aplica¸cão discutindo vantagens e limita¸cões. Na área de sobrevivência, modelos com fra¸cão de cura, efeitos aleatórios permitindo omissão não-ignorável nas covariáveis é discutido por Herring & Ibrahim (2002).

(19)

1.3.1 Mecanismos de omiss˜

ao

Para analisar dados omissos deve-se levar em conta o processo que causa as omissões, conhecido como mecanismos de omissão, originalmente descritos em Rubin (1976). Em particular, é necessário considerar se a omissão nas covariáveis está rela-cionada com as variáveis no conjunto de dados.

Seja X a matrix de covariáveis, T o vetor de tempos até a falha e C o vetor de tempos de censura. Se houver omissão, pode-se particionar a matriz de covariáveis X

em (Xobs,Xmis), em queXmis é uma matriz de covariáveis com omissão e Xobs é uma matriz de covariáveis completamente observadas.

Considere que, para a j-ésima covariável,j = 1, . . . , p, tem-se a variável aleatória indicadora de omissão Rj, que vale 1 se Xj é omissa e 0 caso contrário.

O mecanismo de omissão é caracterizado pela distribui¸cão condicional deRj dado (X,T,C), digamos P(Rj|X,T,C;τ), sendoτ um vetor de parâmetros desconhecidos. Se as omissões não dependem dos valores de (X,T,C), omissos ou observados, isto é, se

P(Rj =rj|X,T,C,τ) = P(Rj =rj|τ),

os dados são classificados como MCAR (missing completely at random). Em outras palavras, supor que os dados são MCAR significa supor que os indiv´ıduos com dados omissos têm o mesmo perfil que os indiv´ıduos completamente observados. Se, por exemplo, um indiv´ıduo entrou tardiamente no estudo e não realiza todos os exames antes de findar o per´ıodo de observa¸cão, esta suposi¸cão é adequada.

O mecanismo conhecido por omissão aleatória ou MAR (missing at random) supõe que as probabilidades condicionais de omissão dependem apenas do que é obser-vado, isto é

P(Rj =rj|X,T,C,τ) =P(Rj =rj|Xobs,T,C,τ).

(20)

1.4 Objetivos 10

todos os exames, indicando que a omissão está relacionada aos tempos de falha, então, o mecanismo de omissão aparentemente é MAR.

Se as probabilidades condicionais de omissão dependem também das quantidades não observadas e não podem ser completamente explicadas pelos dados observados, a omissão é chamada não aleatória (missing not at random) - MNAR ou não ignorável. Em termos de probabilidade, o mecanismo MNAR pode ser representado comoP(Rj =

rj|X,T,C,τ) e n˜ao pode ser simplificada. ´

E importante salientar que ao excluir as observa¸cões omissas, pressupõe-se que a omissão é do tipo MCAR, ou seja, que os indiv´ıduos com covariáveis completamente observadas constituem uma subamostra aleatória da amostra original, o que não é razoável na maioria das circunstâncias.

1.4 Objetivos

O objetivo deste trabalho é implementar um procedimento de estima¸cão dos parâmetros do modelo com fra¸cão de cura em que algumas observa¸cões apresentam omissão em pelo menos uma das covariáveis. A proposta de Chen & Ibrahim (2001) consiste em implementar a versão Monte Carlo do algoritmo EM, permitindo que as covariáveis sejam cont´ınuas, categóricas ou mistas. Nossa proposta difere desta pois utilizamos uma verossimilhan¸ca marginal, que elimina as variáveis latentes, simplifi-cando o uso do algoritmo EM, que será empregado para imputar somente os dados omissos. Além disso, consideramos apenas os casos em que as covariáveis omissas são categóricas, assim, podemos utilizar o algoritmoEM ponderado proposto por Ibrahim (1990).

(21)

1.5 Estrutura da disserta¸c˜ao 11

indiv´ıduos não imunes em amostras completamente observadas e amostras com omis-são, bem como o quanto o percentual de dados omissos pode interferir nos resultados das análises.

1.5 Estrutura da disserta¸

c˜

ao

(22)

Cap´ıtulo 2

Modelo com Fra¸

c˜

ao de Cura

Neste cap´ıtulo, descrevemos a formula¸cão do modelo com fra¸cão de cura proposto por Yakovlev et al. (1993), bem como as fun¸cões de verossimilhan¸ca e verossimilhan¸ca marginal associadas, supondo que os tempos de promo¸cão seguem uma distribui¸cão Weibull.

2.1 Formula¸

c˜

ao do modelo

SejaM uma variável aleatória (v.a.) representando o número de causas ou riscos de ocorrência de um particular evento de interesse. É assumido queM tem distribui¸cão

P oisson(θ). Dado M =m, sejam Zj, j = 1, . . . , m, variáveis aleatórias cont´ınuas não negativas, independentes e identicamente distribu´ıdas com fun¸cão distribui¸cão acumu-lada F(_·) = 1₋S(_·) e independentes de M, representando o tempo de ocorrência do evento devido à j-ésima causa ou risco, ou o tempo de promo¸cão do evento. O tempo até a ocorrência do evento de interesse é definido como Y = min_{Zj; 0_≤j _≤M_}

comP (Z0 =∞) = 1, pois se M = 0 não existem causas ou riscos para a ocorrência do evento de interesse. As variáveisM eZj são variáveis latentes, ou seja, não observáveis eY é uma v.a. observável que pode ser censurada à direita. Para este modelo a fun¸cão

(23)

2.1 Formula¸c˜ao do modelo 13

de sobrevivência para a popula¸cão é dada por

Sp(y) = P(Y > y) =Pmin_{Z0, Z1, ..., ZM}> y

,

que usando a lei da probabilidade total (Magalh˜aes, 2006; p. 29) pode ser escrita como

Sp(y) =

∞

k=0

Pmin_{Z0, Z1, ..., ZM}> y|M =k

P (M =k)

= P(Z0 > y)P(M = 0) +

∞

k=1

Pmin_{Z1, . . . , Zk}> y

_θk

k!e

−θ

= e−θ₊

∞

k=1

PZ1 > y, ..., Zk > y

_θk

k!e

−θ_,

poisP(Z0 > y) = 1, para todo y. Agora, dadoM =k, parak = 1, . . . ,∞, as variáveis aleatóriasZj,j = 1, . . . , M são independentes e identicamente distribu´ıdas com fun¸cão de sobrevivênciaS(y), então, segue que

Sp(y) = e−θ₊

∞

k=1

S(y)kθ k

k!e

−θ

= e−θ

∞

k=0

S(y)kθk

k! = e−θ_eθS(y)

= exp [₋θ(1₋S(y))],

e portanto,

Sp(y) = exp [₋θF(y)], (2.1)

em queF(y), a fun¸cão de distribui¸cão acumulada deZj,j = 1. . . , M é uma fun¸cão de distribui¸cão própria. Consequentemente,

lim

(24)

2.1 Formula¸c˜ao do modelo 14

ou seja, Sp(y) é uma fun¸cão de sobrevivência imprópria e exp(₋θ) = P(M = 0) representa a fra¸cão de cura induzida pelo modelo.

Pode-se observar que à medida que θ cresce, a fra¸cão de cura, exp(₋θ) decresce, o que é bastante intuitivo, já que θ é o valor esperado para a variável latente M, que representa o número de causas ou riscos de ocorrência do evento. Consequentemente, o indiv´ıduo que apresenta um elevado número de causas para ocorrência do evento terá baixa fra¸cão de cura. O raioc´ınio para θ decrescente é análogo.

Através das rela¸cões entre as fun¸cões de sobrevivência, risco e densidade, dadas em (1.3) e (1.4), é poss´ıvel obter a fun¸cão de densidade correspondente a (2.1) como sendo

fp(y) = θf(y) exp_{−θF(y)_}, y >0, (2.2)

com f(y) = dF(y)/dy uma fun¸cão densidade própria. A fun¸cão risco (taxa de falha instantânea) para a popula¸cão é

hp(y) = fp(y)

Sp(y) =θf(y). (2.3)

Quando relacionamos covariáveis ao parâmetro θ, a fun¸cão risco em (2.3) possui uma estrutura de riscos proporcionais, que é uma propriedade desejável na análise de sobrevivência. Isto ocorre devido à suposi¸cão de que a variável latente M, que repre-senta o número de riscos ou causas para a ocorrência do evento, segue uma distribui¸cão de Poisson (Rodrigues, Cancho, & Castro 2008).

A fun¸cão de sobrevivência para a popula¸cão não curada é dada por

S∗(y) = P(Y > y_|M _≥1) = P(Y > y, M ≥1)

P(M _≥1)

= exp{−θF(y)} −exp(−θ)

1₋exp(₋θ) . (2.4)

(25)

2.2 Fun¸c˜ao de verossimilhan¸ca 15

de promo¸cão através da rela¸cão

Sp(y) = exp(₋θ) + [1₋exp(₋θ)]S∗(y),

em que S∗₍_y_{) é dada por (2.4) e a fra¸cão de cura é} _π _{= exp(}₋_θ_{). Isto mostra que}

o modelo (2.1) pode ser escrito como o modelo de mistura padrão com uma fam´ılia espec´ıfica de fun¸cões de sobrevivência S∗₍_y_{) dada em (2.4).}

2.2 Fun¸

c˜

ao de verossimilhan¸

ca

Considere uma amostra aleatória denindiv´ıduos de uma determinada popula¸cão. Define-se portanto, as seguintes variáveis:

• Mi - variável latente representando o número de causas para a ocorrência do evento no i-ésimo indiv´ıduo, com Mi ∼P oisson(θi), i= 1, . . . , n;

• Zij são os tempos, não observáveis, até a ocorrência do evento devido à j-ésima causa ou risco, com j = 1, . . . , Mi para o i-ésimo indiv´ıduo, com fun¸cão dis-tribui¸cão acumulada F(_·|λ) = 1₋S(_·|λ) que não depende de Mi, sendo λ um vetor de parâmetros desconhecidos;

• yi = min{Ti, Ci} , tempo de falha observado, com Ti = min{Zij; 0≤j ≤Mi} e

Ci tempo de censura do i-´esimo indiv´ıduo;

• δi - indicador de censura, com δi igual a 1, seTi ≤Ci, e igual a zero, se Ti > Ci;

• x′

i = (xi1, ..., xip) vetor p-dimensional de covari´aveis associado ao i-´esimo indiv´ı-duo;

Considere os vetores n-dimensionais

(26)

δ = (δ1, δ2, . . . , δn)′

M= (M1, M2, . . . , Mn)′, e a matriz de covari´aveis de dimens˜ao n_×p

X=

⎛

⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝

x′

1

x′

2 ...

x′

n

⎞

⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠

,

denotamos o conjunto dos dados completos (que inclui os dados observados e as vari´a-veis latentes) por_Dc = (n,y,δ,M,X) e os dados observados porD= (n,y,δ,X).

Covariáveis são introduzidas no parâmetro θ através da rela¸cão θ _≡ θ(x′β) = exp(x′β), com β = (β1, ..., βp)′ representando o vetor de coeficientes de regressão, de maneira que a fra¸cão de cura para o indiv´ıduo i é

π(xi) = exp(₋θi) = exp_{−exp(x′iβ)}. (2.5) Denotando a densidade conjunta de (yi, δi, Mi) por

f(yi, δi, Mi) = f(yi, δi|Mi)f(Mi),

temos, conforme mostrado em (A.1), que

f(yi, δi|Mi) =S(yi|λ)Mi−δi[Mif(yi|λ)] δi

, (2.6)

e portanto,

f(yi, δi, Mi) =S(yi|λ)Mi−δi[Mif(yi|λ)]δi

e−θ_θMi

Mi! .

Sendo φ= (β′,λ′)′ _{o vetor de parˆametros desconhecidos, a fun¸c˜ao de}

(27)

L(φ;_Dc) =

_n

i=1

S(yi|λ)Mi−δi[Mif(yi|λ)]δi

×exp

_n

i=1

[Mix′iβ−ln(Mi!)−exp(x

′

iβ)]

. (2.7)

O logar´ıtmo da fun¸c˜ao de verossimilhan¸ca ´e

ℓ(φ;_Dc) = logL(φ;_Dc) =

n

i=1

[(Mi−δi) lnS(yi|λ) +δilnMi+δilnf(yi|λ)] +

n

i=1

′

iβ)]. (2.8)

Visto que (2.8) não é observável, já que depende das variáveis latentes Mi, i = 1, . . . , n, pode-se trabalhar com o logar´ıtmo da fun¸cão de verossimilhan¸ca marginal, que pode ser obtida fazendo-se o somatório nas variáveis Mi. Como mostrado no Apêndice A.2, a verossimilhan¸ca marginal é dada por

L(φ;_D) = n

i=1

[x′iβf(yi|λ)] δi

exp₋exp(x′iβ)

1₋S(yi|λ)

, (2.9)

e o logar´ıtmo da fun¸c˜ao de verossimilhan¸ca marginal ´e

ℓ(φ;_D) = n

i=1

δi(x′iβ+ lnf(yi|λ))−exp(x′iβ)

1₋S(yi|λ)

. (2.10)

(28)

2.3 Modelo param´etrico Weibull 18

(2008).

Para grandes amostras, o estimador de m´axima verossimilhan¸ca ˆφ´e tal que √

n( ˆφ₋φ) ˙_∼ N0,_I−1(φ) em que _I(φ) ´e a matriz de informa¸c˜ao de Fisher dada por

I(φ) = ₋E[¨ℓ(φ)] com

¨

ℓ(φ) = ∂

2_ℓ₍_φ_;_D₎

∂φ∂φ′ .

Como o cálculo de _I(φ) não é poss´ıvel devido à presen¸ca de censuras, pode-se utilizar a matriz ₋ℓ¨(φ) avaliada emφ= ˆφque é uma estimativa consistente de _I(φ), conhecida como matriz de informa¸cão observada que será denotada aqui por _Iobs( ˆφ). Assim, pode-se realizar inferências, como intervalos de confian¸ca e testes de hipóteses, para os parâmetros de interesse.

2.3 Modelo param´

etrico Weibull

Suponha agora que os tempos de promo¸cãoZijsão independentes e identicamente distribu´ıdos (i.i.d.) e seguem uma distribui¸cão Weibull com parâmetros λ = (ρ, γ)′_,

j = 1, . . . , Mi, i = 1, . . . , n, com densidade f(z) = ρzρ−1_exp(_γ ₋_zρ_eγ_{) e fun¸cão de} sobrevivênciaS(z) = exp(₋zρ_eγ_{). Neste caso, o logar´ıtmo da fun¸cão de verossimilhan¸ca} dos dados completos em (2.8) será dada por

ℓ(φ;_Dc) = n

i=1

−Miyρie γ₊_δ

iln(Miρyiρ−1e γ₎

+ n

i=1

′

(29)

O logar´ıtmo da verossimilhan¸ca marginal em (2.10) toma a forma

ℓ(φ;_D) = n

i=1

δi

x_i′β+γ+ ln(ρy_iρ−1)₋y_iρeγ −

n

i=1

exp(x′iβ) [1−exp(−y ρ ie

γ_)]_. _(2.12)

Para o modelo (2.12), a matriz de informa¸c˜ao observada, _Iobs( ˆφ), fica

Iobs( ˆφ) =

⎛ ⎜ ⎜ ⎜ ⎝ ¨

ℓββ _ℓ¨βρ _ℓ¨βγ ¨

ℓρρ _ℓ¨ργ ¨ ℓγγ ⎞ ⎟ ⎟ ⎟ ⎠

φ= ˆφ

(2.13)

sendo as submatrizes com elementos

¨

ℓββ_k,l = ∂

2_ℓ₍_φ_;_D₎

∂βl∂βk =₋

n

i=1

xilxikexp(x′iβ) [1−exp(−y ρ ie

γ_)]_, _{l, k}_{= 1}_{, . . . , p,}

¨

ℓβ_lρ = ∂

2_ℓ₍_φ_;_D₎

∂βl∂ρ

=₋ n

i=1

xilyiρe

γ_ln(_y_{i) exp(}_x′

iβ−y ρ ie

γ₎_, _l_{= 1}_{, . . . , p,}

¨

ℓβ_lγ = ∂

2_ℓ₍_φ_;_D₎

∂βl∂γ

=₋ n

i=1

xily ρ ie

γ

exp(x′iβ−y ρ ie

γ

), l= 1, . . . , p,

¨

ℓρρ = ∂

2_ℓ₍_φ_;_D₎

∂ρ∂ρ =−

n

i=1

δi

ρ2 +y ρ ie

γ

(ln(yi))2δi+ exp(x′iβ−y ρ ie

γ

) [1₋yρie γ

],

¨

ℓργ = ∂

2_ℓ₍_φ_;_D₎

∂ρ∂γ =−

n

i=1

yiρe γ

ln(yi)δi+ exp(x′iβ−y ρ ie

γ

) [1₋yρie γ

],

¨

ℓγγ ₌ ∂2ℓ(φ;D)

∂γ∂γ =−

n

i=1

y_iρeγ_δ

i+ exp(x′iβ−y ρ ie

γ_{) [1}

−yρ_ieγ_]_.

Testes estat´ısticos podem ser realizados para o vetor de parˆametros β, sendo

λ= (ρ, γ) tratados como parˆametros de perturba¸c˜ao.

Considere as hip´oteses H0 :β =β0 versus H1 :β =β0 e seja ˜λ a estimativa de

(30)

λ para β=β0 fixado. Então, a estat´ıstica da razão de verossimilhan¸cas é dada por

ξRV =−2

ℓ(β₀,λ˜,_D)₋ℓ(φˆ,_D),

(31)

Cap´ıtulo 3

Modelo com Fra¸

c˜

ao de Cura e

Omiss˜

ao nas Covari´

aveis

Neste cap´ıtulo descrevemos o procedimento de estima¸cão dos parâmetros e erros padrão para o modelo com fra¸cão de cura na situa¸cão em que algumas covariáveis categóricas não são observadas para todos os indiv´ıduos na amostra. Apresentamos a verossimilhan¸ca marginal (com respeito às variáveis latentes) sob a suposi¸cão de que o mecanismo gerador das omissões é MAR e o algoritmo EM ponderado será utilizado para imputar valores para as covariávieis omissas.

3.1 Estima¸

c˜

ao de m´

axima verossimilhan¸

ca via

algo-ritmo EM

Suponhamos que o mecanismo gerador da omissão é do tipo MAR, ou seja, a omissão não depende dos valores omissos, mas talvez dependa dos valores observa-dos. Assumimos também que os tempos de falha e censura são sempre observaobserva-dos. Neste caso, é necessário considerar um modelo paramétrico para as covariáveis omis-sas, p(xi;α), em que α é um vetor de parâmetros desconhecidos, vistos aqui como parâmetros de perturba¸cão, pois nosso principal interesse é realizar inferências sobre o

(32)

3.1 Estima¸c˜ao de m´axima verossimilhan¸ca via algoritmo EM 22

vetor de coeficientes de regress˜ao do modelo, β.

Considere que, para a i-´esima unidade amostral, ´e poss´ıvel particionar o vetor

xi em xi = (x′mis,i, x′obs,i)′ com xmis,i um vetor de dimens˜ao qi de covari´aveis omissas e

xobs,i um vetor de dimens˜ao p−qi de covari´aveis completamente observadas.

Seja agora_Dobs = (n,y,δ,Xobs) o conjunto de dados observados, comXobs a ma-triz de covari´aveis observadas eψ = (β′,λ′,α′)′_{, o vetor de parˆametros desconhecidos.}

Então o logar´ıtmo da fun¸cão de verossimilhan¸ca dos dados completos é dada por

ℓ(ψ;_Dc) = n

i=1

[(Mi −δi) lnS(yi|λ) +δilnMi+δilnf(yi|λ)] +

n

i=1

[Mix′iβ−ln(Mi!)−exp(x′iβ)] +

n

i=1

ln[p(xi;α)] = ℓ(φ;_Dc) +

n

i=1

ln[p(xi;α)] (3.1)

Para eliminar as variáveis latentes efetua-se o somatório em (3.1) sobre todos os valores poss´ıveis de Mi, de forma análoga ao caso sem omissão, e assim obtém-se

ℓ(ψ;_D) = n

i=1

[δi(x′iβ+ lnf(yi|λ))−exp(x′iβ) (1−S(yi|λ))] + n

i=1

ln[p(xi;α)] = ℓ(φ;_D) +

n

i=1

ln[p(xi;α)]. (3.2)

O logar´ıtmo da fun¸cão de verossimilhan¸ca em (3.2) pode ser maximizado através do algoritmo EM que é um procedimento iterativo composto de dois passos a cada itera¸cão: o passo E (Expectation) e o passo M (Maximization), por isso, o algoritmo foi chamado Algoritmo EM por Dempster et al. (1977) e é uma poderosa ferramenta para obter estimativas de máxima verossimilhan¸ca quando existem covariáveis não observáveis (latentes) ou omissas.

(33)

da-3.1 Estima¸c˜ao de m´axima verossimilhan¸ca via algoritmo EM 23

dos evidentemente incompletos (dados omissos, distribui¸cões truncadas, observa¸cões censuradas ou truncadas), mas também uma ampla variedade de problemas onde a falta de dados não é natural ou evidente. A desvantagem do algoritmoEM é que sua taxa de convergência pode ser extremamente lenta quando existe uma grande fra¸cão de informa¸cão omissa. Nesta disserta¸cão, o algoritmo EM é utilizado para encontrar estimativas de máxima verossimilhan¸ca quando covariáveis não são observadas para todos indiv´ıduos.

Consideramos ψ(k) = (β′(k),λ′(k),α′(k))′ _{as estimativas de} _ψ _na _k_-´esima

iter-a¸cão do algoritmo. Para os dados referentes à i-ésima observa¸cão, os dados sem as variáveis latentes são representados por _Di = (yi, δi, xi), e os dados observados por Dobs,i = (yi, δi, xobs,i). No passo E, calcula-se a esperan¸ca condicional de ℓ(ψ|Di) dado a estimativa atualψ(k) e os dados observados_Dobs,i, parai= 1, . . . , n. Denotando essa esperan¸ca por Qi(ψ_|ψ(k)), o passo E para a i-ésima observa¸cão na k-ésima itera¸cão pode ser escrito como

Qi(ψ_|ψ(k)) =Eℓ(ψ,_Di)_|Dobs,i,ψ(k)

(3.3)

A seguir, descrevemos a obten¸cão deQi(ψ_|ψ(k)) para covariáveis omissas categóri-cas utilizando o algorimoEM ponderado.

3.1.1 Algoritmo

_EM

ponderado

No caso em que as covariáveis omissas são todas categóricas, uma técnica útil para obter etimativas de máxima verossimilhan¸ca é o algoritmo EM ponderado, proposto por Ibrahim (1990) que é descrito em detalhes em Horton & Laird (1999).

(34)

o valor x(j)_mis,i s˜ao os pesos denotados porw(k)_ij , sendo

wij(k)=p(x (j)

mis,i|xobs,i, yi, δi,ψ(k)) =

L(ψ(k);_D(j)i )f(x (j) i |α(k)) J

j=1

L(ψ(k);_D_i(j))f(x(j)_i _|α(k))

, (3.4)

Para tornar mais clara a obten¸cão de Qi(ψ_|ψ(k)), vamos reportar o cálculo de uma esperan¸ca condicional. Considerando V uma variável aleatória discreta e U uma variável aleatória qualquer, a esperan¸ca de V dadoU é dada por

E[V_|U] = j

vjp(vj|u). (3.5)

Agora, fazendo V =ℓ(ψ,_Di(j)) e U = (Dobs,i,ψ(k)) tem-se

Qi(ψ_|ψ(k)) =E[V_|U] = j

vjp(vj|u) = J

j=1

ℓ(ψ,_D_i(j))w(k)_ij .

Assim, para o modelo com fra¸cão de cura, e considerando o logar´ıtmo da fun¸cão de verossimilhan¸ca em (3.2), o passoE para a i-ésima observa¸cão assume a forma

Qi(ψ_|ψ(k)) = J

j=1

w(k)_ij δi

ln [f(yi|λ)] +x(j

′₎ i β − J j=1

w(k)ij exp(x (j′₎

i β) [1−S(yi|λ)] +

J

j=1

wij(k)ln

p(x(j)i |α)

= Q1i(β,λ_|ψ(k)) +Q2i(α_|ψ(k)) (3.6) sendo,Q1i(β,λ_|ψ(k)) =

J

j=1

w(k)_ij δi

ln [f(yi|λ)] +x(j

′₎

i β

−exp(x(j_i ′)β) [1₋S(yi|λ)]

e Q2i(α_|ψ(k)) = J

j=1

w(k)ij ln

p(x(j)i |α)

(35)

Note que J

j=1

w(k)ij = 1, para todo k e i, e que se todas as covari´aveis para o

i-ésimo indiv´ıduo são observadas, então w_ij(k) = 1. A expressão (3.6) pode ser escrita como a soma entre Q1i(β,λ_|ψ(k)) e Q2i(α_|ψ(k)), sendo que a primeira não envolve o parâmetro α e a segunda não envolve os parâmetros β e λ. Assim, na etapa de maximiza¸cão (passo M) podemos maximizá-las separadamente com respeito a (β,λ) e α, respectivamente.

O passo E para todas as observa¸c˜oes ´e portanto dado por

Q(ψ_|ψ(k)) = n

i=1

Q1i(β,λ_|ψ(k)) + n

i=1

Q2i(α_|ψ(k))

= Q1(β,λ|ψ(k)) +Q2(α|ψ(k)). (3.7) O passo M consiste na maximiza¸cão de (3.7) com respeito a ψ, que pode ser feita através de um método iterativo, como Newton-Raphson. A fun¸cão Q(ψ_|ψ(k)) é atualizada usando a estimativa atual ψ(k+1), e o algoritmo é repetido até que seja satisfeito um critério de parada estabelecido. Adotamos aqui, como critério a condi¸cão

ψ(k+1)−ψ(k) < ε

com ψ(k) = (β′(k),λ′(k),α′(k)

)′ _e _{ε >} _{0 em que} _||_a₋_b_|| _{denota a distˆancia Euclidiana}

entre os pontos a eb.

Para ilustrar a implementa¸cão do algoritmoEM ponderado, adaptamos um exem-plo dado em Horton & Laird (1999). Considere um conjunto de dados hipotético com duas covariáveis dicotômicas (x1, x2), a resposta (y) e a variável incadora de falha (δ). A Tabela 3.1 mostra os dados com algumas observa¸cões omissas e a Tabela 3.2 exibe os correspondentes dados aumentados, em que wij(k) são os pesos estimados para o indiv´ıduo i na k-ésima itera¸cão. Por exemplo, w₃₁(k) = P(x2 = 0|x1 = δ = 1, y =

y3,ψ(k)) e w(k)31 +w (k) 32 = 1.

(36)

Tabela 3.1: Conjunto de dados original (hipot´etico).

i y δ x1 x2

1 y1 0 0 0 2 y2 0 0 1 3 y3 1 1 -4 y4 1 0 1 5 y5 0 -

-Tabela 3.2: Conjunto de dados aumentados.

i y δ x1 x2 w(k)

1 y1 0 0 0 1 2 y2 0 0 1 1 3 y3 1 1 0 w(k)31 3 y3 1 1 1 w(k)32 4 y4 1 0 1 1 5 y5 0 0 0 w(k)51 5 y5 0 0 1 w(k)52 5 y5 0 1 0 w(k)53 5 y5 0 1 1 w(k)54

que ´e baseado no vetor gradiente (matriz de primeiras derivadas parciais) e na matriz Hessiana (matriz de segundas derivadas) de Q(ψ_|ψ(k)).

Sejam o vetor gradiente e a matriz Hessiana deQi(ψ_|ψ(k)), respectivamente dados por

˙

Qi( ˆψ) = ∂Qi(ψ_∂_β|ψ(k))′ ∂Qi(ψ_∂_λ|ψ(k))′ ∂Qi(_∂ψ_α|ψ(k))′

′

,

¨

Qi( ˆψ) =

⎡

⎢ ⎢ ⎢ ⎣

∂2_Qi(_ψ_|_ψ(k)₎

∂β∂β′

∂2_Qi(_ψ_|_ψ(k)₎

∂β∂λ

∂2_Qi(_ψ_|_ψ(k)₎

∂β∂α

∂2_Qi(_ψ_|_ψ(k)₎

∂λ∂λ′

∂2_Qi(_ψ_|_ψ(k)₎

∂λ∂α

∂2_Qi(_ψ_|_ψ(k)₎

∂α∂α′ ⎤

⎥ ⎥ ⎥ ⎦

,

de acordo com Louis (1982), a matriz de informa¸c˜ao observada ´e dada por

ILouis( ˆψ) = n

i=1

(37)

Se as covariáveis omissas são categóricas tem-se que

Eℓ˙( ˆψ,_Di) ˙ℓ( ˆψ,_Di)′ = J

j=1

w(k)_ij ℓ˙( ˆψ,_D(j)_i ) ˙ℓ( ˆψ,_D_i(j))′,

assim, a equa¸c˜ao (3.8) assume a forma

ILouis( ˆψ) = n

i=1

−Q¨i( ˆψ) + J

j=1

wij(k)ℓ˙( ˆψ,D (j)

i ) ˙ℓ( ˆψ,D (j)

i )′−Q˙i( ˆψ) ˙Qi( ˆψ)′

. (3.9)

Deste modo, a variância asssintótica de ˆψ é dada por

V ar( ˆψ) =_ILouis( ˆψ)−1

então, pode-se realizar inferências sobre o vetor de parâmetros β.

3.1.2 Modelando a distribui¸

c˜

ao das covari´

aveis

(38)

condicionais unidimensionais da seguinte forma

p(xi1, ..., xip|α) = p(xip|xi1, ..., xi(p−1),αp)...p(xi2|xi1,α2)p(xi1|α1) (3.10) em que αj é um vetor de parâmetros para a j-ésima distribui¸cão condicional, α = (α′₁,α′₂, . . . ,α′_p)′_{. ´}_{E importante ressaltar que a equa¸cão (3.10) precisa ser especificada}

apenas para as covari´aveis omissas.

Se as covariáveis omissas são todas categóricas dicotômicas, uma sequência de modelos log´ısticos (ou liga¸cões probito e complemento log-log) podem ser modelados para cadap(xij|xi1, ..., xi(j−1),αj),j = 1, . . . , p. Para covariáveis categóricas com mais de dois n´ıveis, podemos considerar um modelo log´ıstico multinomial (Agresti 2002). Se as covariáveis consistem de contagem, é poss´ıvel modelarp(xij|xi1, ..., xi(j−1),αj) como um modelo de regressão Poisson.

(39)

Cap´ıtulo 4

Estudo de Simula¸

c˜

ao

Neste cap´ıtulo apresentamos estudos de simula¸cão para comparar propriedades do estimador de máxima verossimilhan¸ca sob o modelo de fra¸cão de cura e omissão nas covariáveis pela análise de casos completos e pela imputa¸cão dos dados faltantes com o algoritmoEM. Para este estudo, utilizamos o ambiente R (versão 2.7.2).

Como a metodologia mais comumente empregada na prática é a análise de casos completos, nosso principal objetivo aqui é comparar as estimativas obtidas por este método com as estimativas de máxima verossimilhan¸ca obtidas através do algoritmo EM. Investigamos também as propriedades assintóticas das estimativas de máxima ve-rossimilhan¸ca para o modelo com fra¸cão de cura quando as amostras são completamente observadas.

4.1 Obten¸

c˜

ao dos dados simulados

Consideramos uma situa¸cão com três covariáveis associadas a cada indiv´ıduo (x1, x2, x3). Para i = 1, . . . , n, assumimos para cada i que (xi1, xi2) são sempre obser-vadas, sendo xi1 e xi2 independentes, com valores xi1 obtidos por amostragem i.i.d. da distribui¸cão normal padrão e xi2 obtidos por amostragem i.i.d. da distribui¸cão de Bernoulli com probabilidade de sucesso 0,6 e que xi3 pode ser omissa. Consideramos que, dado xi1 e xi2, a covariável com omissão xi3 tem distribui¸cão de Bernoulli com

(40)

4.1 Obten¸c˜ao dos dados simulados 30

parˆametroαi, ent˜ao

p(xi3|xi1, xi2, αi) =αixi3(1−αi) 1−xi3

com xi1 ∈R, xi2 = 0,1 e xi3 = 0,1 sendo

αi =

exp(α1xi1+α2xi2) 1 + exp(α1xi1+α2xi2)

,

com α = (α1, α2) = (−0,5; 1) e as distribui¸c˜oes condicionais s˜ao independentes para cada i.

Para cada indiv´ıduo foram gerados valores para Mi como uma amostra i.i.d. da distribui¸cão de Poisson com média θi = exp(x′iβ), representando o número de riscos para a ocorrência do evento, com β = (β1, β2, β3). O valor fixado para o vetor β determina o percentual de indiv´ıduos com mi = 0, ou seja, o percentual de imunes na amostra.

Para cada indiv´ıduo n˜ao imune, (mi > 0), foram geradas amostras de tamanho

mi para Zij ∼W eibull(ρ, γ), com ρ= 2 eγ =−2 log 4. Assim, os tempos de falha s˜ao

ti = min{zij;j = 1, . . . , mi}.

Geramos também censuras aleatórias a partir de uma distribui¸cão uniforme no intervalo (0, u), sendo que a mudan¸ca no valor de u afeta a propor¸cão de censuras na amostra. Consideramos aqui a propor¸cão de censuras calculada com respeito ao total de indiv´ıduos sujeitos ao evento, com o intuito de avaliar separadamente o efeito do aumento da propor¸cão de censuras entre não curados e de imunes na estima¸cão dos parâmetros. Assim, considerando os eventos: A _≡ curados; ¯A _≡ não curados e

B _≡ censurados ou imunes. A propor¸cão de censura entre não imunes utilizada nesta simula¸cão (denotada pc1) representa a frequência relativa de B dado ¯A, ou seja,

pc1 =

n´umero de indiv´ıduos em B_∩A¯

n´umero de indiv´ıduos em ¯A ,

(41)

4.1 Obten¸c˜ao dos dados simulados 31

´e interpretado simplesmente como a propor¸c˜ao de censuras, pode ser representado por

pc2 =

n´umero de indiv´ıduos em B

n´umero de indiv´ıduos na popula¸c˜ao.

Denotando por π a propor¸c˜ao de imunes, pode-se verificar, pelo uso de pro-priedades de frequencia relativa, a seguinte rela¸c˜ao entre estas duas quantidades:

pc2 =pc1(1−π) +π. (4.1)

Os tempos observados ser˜ao yi = min{ti, ci} e, associado a cada tempo, tem-se

δi = 1 seti ≤ci e δi = 0 seti > ci.

Os dados omissos para xi3 foram gerados com um mecanismo de omissão que não depende dexi3, e portanto, os dados são MAR, sendo que mecanismo de omissão dos dados pode ser ignorado na estima¸cão dos parâmetros. Para simular omissão, adaptamos a idéia de Ibrahim, Chen, & Lipsitz (1999). A variável indicadora de omissão foi especificada como descrito na Se¸cão 1.3.1, sendori3 = 0 se a variávelxi3é observada eri3 = 1 se xi3 é omissa, i= 1, . . . , n. A distribui¸cão assumida para ri3 é dada por

P(Ri3 =r|Dobs, τ) =τir(1−τi) 1−r_,

com

τi =

exp(τ30+τ31xi1+τ32xi2+τ33yi+τ34δi) 1 + exp(τ30+τ31xi1+τ32xi2+τ33yi+τ34δi)

e o valor considerado para o vetor τ3 = (τ30, τ31, τ32, τ33, τ34)′ controla o percentual de omiss˜ao na amostra.

(42)

4.2 Resultados para os dados simulados 32

4.2 Resultados para os dados simulados

Nesta se¸cão apresentamos os resultados obtidos para amostras simuladas em diferentes situa¸cões. A Tabela 4.1 resume os casos considerados nas simula¸cões:

Tabela 4.1: Situa¸c˜oes consideradas para simula¸c˜ao.

Caso Omiss˜ao % Imunes % Censura Tamanho da Amostra Se¸c˜ao 1

sem variando 0 variando 4.2.1

2 variando variando ﬁxo (n= 300)

3

com variando 0 ﬁxo (n= 300) 4.2.2

4 ﬁxo (45%) variando ﬁxo (n= 300)

4.2.1 Resultados para amostras completamente observadas

A partir da Tabela 4.2 observamos que, para amostras moderadas (n = 50) não apresentando omissão nas covariáveis nem censuras entre os não imunes (caso 1), as estimativas dos parâmetros apresentam vieses, especialmente no parâmetro γ, para diferentes propor¸cões de imunes (10%, 45% e 65%), no entanto, aumentando-se o tamanho da amostra este problema é aparentemente sanado.

Na Tabela 4.3, que mostra os resultados para amostras em que as covariáveis não apresentam omissão mas apresentam censura entre os não imunes (caso 2), podemos ver que o percentual de censuras na amostra, afeta sensivelmente as estimativas dos parâmetros. Observamos vieses e erros quadráticos médios acentuados nas estimativas dos parâmetros quando o percentual de censuras é alto (50%). Por exemplo, na Tabela 4.2 para 65% de imunes (que, na prática, aparecem no conjunto de dados como ob-serva¸cões censuradas) todos os parâmetros são bem estimados. No entanto, a Tabela 4.3 mostra que, em uma situa¸cão similar, quando o percentual de imunes é de 45% e o percentual de censuras entre os não imunes é de 30%, o que resulta em um percentual de censuras entre imunes e não imunes de aproximadamente 62%1_{, as estimativas para} os parâmetros β2 eγ apresentam viés acentuado.

1

Com base na rela¸c˜ao (4.1), tem-se na Tabela 4.3 que com pc1 = 0,3 e π = 0,45 obtem-se

(43)

Tabela 4.2: Estimativas (média), erros-padrão (EP) e raiz dos erros quadráticos médios (REQM) dos parâmetros em 1500 réplicas considerando amostras sem omissão e sem censura entre os não imunes, variando o tamanho da amostra e o percentual de imunes.

10% de imunes

Parˆametro n= 50 n= 150 n= 300

média EP REQM média EP REQM média EP REQM

β1= 2.0 2.154 0.3202 0.3552 2.050 0.1635 0.1709 2.021 0.1119 0.1139

β2= 3.0 3.219 0.5261 0.5697 3.064 0.2768 0.2840 3.033 0.1774 0.1804

β3= 2.0 2.145 0.4352 0.4589 2.046 0.2230 0.2276 2.019 0.1531 0.1543

ρ= 2.0 2.149 0.2535 0.2915 2.041 0.1311 0.1374 2.019 0.0905 0.0924

γ=−2.8 -2.962 0.5232 0.5565 -2.830 0.2735 0.2795 -2.799 0.1846 0.1865 45% de imunes

β1= 1.5 1.634 0.3444 0.3691 1.547 0.1698 0.1763 1.519 0.1185 0.1200

β2=−1.5 -1.608 0.4807 0.4927 -1.534 0.2710 0.2731 -1.514 0.1813 0.1818

β3= 1.0 1.095 0.4210 0.4315 1.031 0.2224 0.2247 1.012 0.1570 0.1575

ρ= 2.0 2.161 0.3453 0.3812 2.048 0.1783 0.1847 2.019 0.1221 0.1235

γ=−2.8 -3.001 0.5395 0.5887 -2.854 0.2856 0.2970 -2.804 0.2004 0.2029 65% de imunes

β1=−0.5 -0.511 0.3261 0.3263 -0.503 0.1719 0.1719 -0.497 0.1426 0.1426

β2=−1.5 -1.605 0.6953 0.7033 -1.516 0.4078 0.4081 -1.490 0.3467 0.3470

β3=−0.2 -0.201 0.5495 0.5495 -0.220 0.3003 0.3009 -0.213 0.2590 0.2594

ρ= 2.0 2.189 0.5322 0.5648 2.047 0.2911 0.2948 2.022 0.2595 0.2604

γ=−2.8 -3.054 0.8098 0.8574 -2.851 0.4355 0.4426 -2.813 0.3993 0.4014

Tabela 4.3: Estimativas (média), erros-padrão (EP) e raiz dos erros quadráticos médios (REQM) dos parâmetros em 1500 réplicas, amostras de tamanhon= 300 sem omissão nas covariáveis, variando o percentual de censura entre os não imunes e de imunes.

10% de imunes

Parˆametro 10% de censura 30% de censura 50% de censura

β1= 2.0 2.023 0.1203 0.1224 2.027 0.1311 0.1339 2.127 0.1660 0.2092

β2= 3.0 2.979 0.1937 0.1948 2.935 0.2364 0.2453 3.363 0.3584 0.5099

β3= 2.0 1.948 0.1667 0.1746 1.840 0.1895 0.2481 2.097 0.2656 0.2826

ρ= 2.0 2.028 0.0956 0.0996 2.024 0.1083 0.1108 1.944 0.1351 0.1463

γ=−2.8 -2.690 0.2065 0.2222 -2.573 0.2587 0.3269 -3.357 0.4063 0.7119 45% de imunes

β1= 1.5 1.529 0.1184 0.1219 1.505 0.1370 0.1371 1.686 0.1816 0.2598

β2=−1.5 -1.587 0.1847 0.2041 -1.765 0.1967 0.3302 -1.779 0.2626 0.3830

β3= 1.0 0.939 0.1583 0.1697 0.727 0.1687 0.3211 1.025 0.3082 0.3092

ρ= 2.0 2.040 0.1258 0.1320 2.167 0.1516 0.2258 1.815 0.2168 0.2852

γ=−2.8 -2.729 0.1984 0.2032 -2.502 0.2238 0.3510 -2.914 0.3898 0.4144 65% de imunes

β1=−0.5 -0.523 0.1088 0.1111 -0.531 0.1235 0.1274 -0.557 0.1353 0.1468

β2=−1.5 -1.600 0.2221 0.2434 -1.722 0.2391 0.3264 -1.973 0.2892 0.5545

β3=−0.2 -0.303 0.1721 0.2006 -0.446 0.1925 0.3122 -0.749 0.2063 0.5868

ρ= 2.0 2.024 0.1587 0.1606 2.061 0.1842 0.1941 2.240 0.2563 0.3512

(44)

4.2.2 Efeito das omiss˜

oes nas estimativas dos parˆ

ametros

Analisando a Tabela 4.4, que mostra os resultados para o caso 3, observa-se que as estimativas dos parâmetros obtidas através do algoritmo EM, em geral, apresentam com desempenho, mesmo quando o percentual de omissão é alto. O mesmo não é observado para as estimativas obtidas com a análise de casos completos (ACC), que apresentam vicios crescentes de acordo o percentual de omissão. Observa-se também que as estimativas obtidas com ACC são ainda piores quando o percentual de imunes é médio ou alto (45% e 60%).

A Tabela 4.5 mostra que, na presen¸ca de censura para não imunes (caso 4), o algoritmo EM, em geral, não apresenta bom desempenho quanto à estimativa dos parâmetros. No entanto, as estimativas referentes à análise de casos completos apre-sentam resultados muito piores e grandes vieses para todos os parâmetros envolvidos no modelo, mesmo quando os percentuais de omissão e de censura são baixos.

Mesmo para o caso sem omissão, foram obtidos resultados insatisfatórios quanto à estimativa dos parâmetros na presen¸ca de censura entre os não imunes. Portanto, os vieses encontrados nas estimativas obtidas através do algoritmo EM na Tabela 4.5 podem ser devido à presen¸ca de censuras e não a dados omissos.

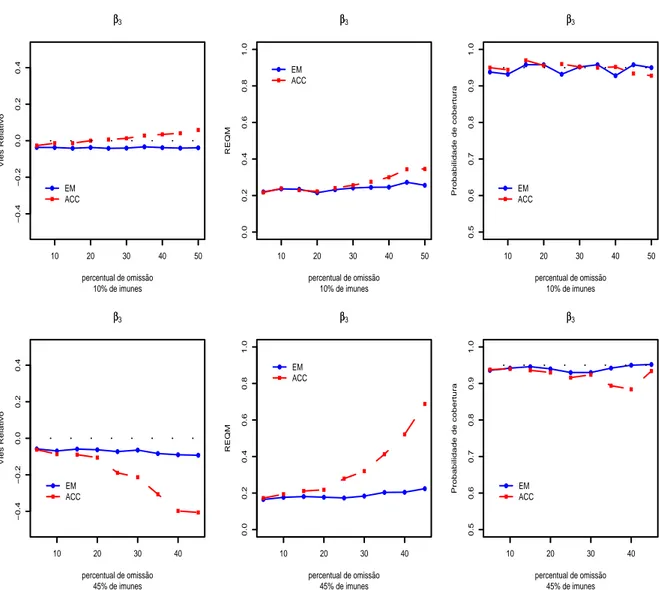
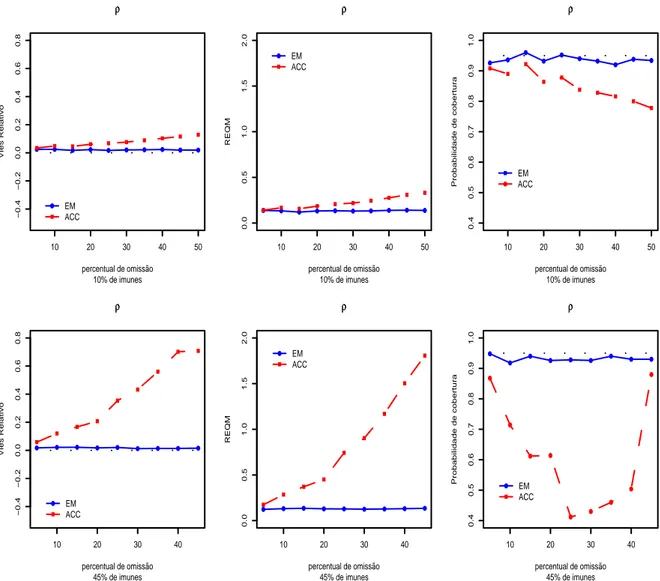
Para visualizar o efeito das omissões nas estimativas dos parâmetros, na ra´ız quadrada dos erros quadráticos médios e nas probabilidades de cobertura2 _{a um n´ıvel} nominal de 95%, variamos o percentual de dados omissos entre 5 e 50%. Os resultados são mostrados nas Figuras (4.1), (4.2), (4.3), (4.4) e (4.5). Podemos ver que, para os parâmetros β1, ρ e γ, o uso do algoritmo EM resulta em vieses relativos3 _bem próximos de zero, erros quadráticos médios constantes em fun¸cão do percentual de omissão e probabilidades de cobertura próximas ao valor nominal de 95%, enquanto o método ACC fornece vieses e erros quadráticos médios crescentes em fun¸cão do percentual de omissão e probabilidades de cobertura insatisfatórias, principalmente

2

Probabilidade de cobertura: Percentual de intervalos de confian¸ca que contém o verdadeiro valor do parâmetro.

3

(45)

Tabela 4.4: Estimativas (média), erros-padrão (EP) e raiz dos erros quadráticos médios (REQM) dos parâmetros em 1500 réplicas, amostras de tamanho n= 300 sem censura entre não imunes, variando o percentual de omissão e de imunes.

10% de imunes

Parâmetro Método 15 % de omissão 30% de omissão 50% de omissão

β1= 2.0 EM 2.020 0.1164 0.1180 2.030 0.1280 0.1314 2.026 0.1416 0.1440

ACC 2.169 0.1269 0.2112 2.018 0.1590 0.1599 1.969 0.2082 0.2105

β2= 3.0 EM 3.033 0.1839 0.1869 3.037 0.2051 0.2083 3.027 0.2081 0.2099

ACC 3.108 0.1970 0.2244 3.134 0.2468 0.2807 3.179 0.2940 0.3440

β3= 2.0 EM 2.020 0.1624 0.1636 2.029 0.1715 0.1739 2.038 0.1868 0.1907

ACC 2.079 0.1689 0.1864 2.068 0.1956 0.2070 2.060 0.2404 0.2477

ρ= 2.0 EM 2.018 0.0932 0.0949 2.027 0.0964 0.0999 2.024 0.1009 0.1037 ACC 2.082 0.1024 0.1311 2.104 0.1181 0.1575 2.173 0.1520 0.2305

γ=−2.8 EM -2.800 0.1948 0.1967 -2.809 0.2082 0.2115 -2.808 0.2150 0.2179 ACC -2.979 0.2048 0.2907 -3.004 0.2365 0.3309 -3.191 0.2796 0.5028

α1=−0.5 EM -0.509 0.1406 0.1409 0.508 0.1676 0.1678 -0.506 0.1890 0.1891

ACC - - -

-α2= 1.0 EM 1.015 0.1856 0.1862 1.030 0.2092 0.2113 1.019 0.2444 0.2452

ACC - - -

-45% de imunes

β1= 1.5 EM 1.524 0.1185 0.1210 1.526 0.1206 0.1232 1.521 0.1320 0.1337

ACC 1.535 0.1399 0.1441 1.288 0.1864 0.2820 0.977 0.4977 0.7222

β2=−1.5 EM -1.531 0.1788 0.1815 -1.524 0.1924 0.1939 -1.535 0.2300 0.2327

ACC -1.635 0.1985 0.2398 -1.707 0.2567 0.3301 -2.060 1.1000 1.2344

β3= 1.0 EM

1.024 0.1575 0.1593 1.016 0.1749 0.1756 1.143 1.3709 1.3783 ACC 1.010 0.16941 0.1697 0.855 0.2263 0.2687 0.873 1.5335 1.5387

ρ= 2.0 EM 2.031 0.1150 0.1191 2.029 0.1216 0.1250 2.020 0.1463 0.1476 ACC 2.104 0.1355 0.1708 2.810 0.2671 0.8529 2.542 1.8625 1.9398

γ=−2.8 EM -2.821 0.1896 0.1957 -2.810 0.1978 0.2014 -2.923 1.3629 1.3713 ACC -2.998 0.2216 0.3164 -4.355 0.4059 1.6332 -6.579 2.6387 4.6316

α1=−0.5 EM -0.510 0.1518 0.1521 -0.517 0.1882 0.1890 -0.514 0.2316 0.2321

ACC - - -

-α2= 1.0 EM 1.003 0.1781 0.1781 1.014 0.1988 0.1992 1.022 0.2437 0.2447

ACC - - -

-65% de imunes

β1=−0.5 EM

-0.506 0.1075 0.1077 -0.511 0.1099 0.1105 -0.513 0.1146 0.1153 ACC -0.881 0.1617 0.4139 -1.128 0.2727 0.6843 -0.118 0.5238 0.6486

β2=−1.5 EM

-1.526 0.2160 0.2175 -1.526 0.2187 0.2202 -1.525 0.2365 0.2378 ACC -1.827 0.2956 0.4411 -2.064 0.5273 0.7717 -2.247 1.2015 1.4150

β3=−0.2 EM -0.190 0.1892 0.1895 -0.198 0.2000 0.2000 -0.233 0.7143 0.7150

ACC -0.621 0.2586 0.4942 -0.858 0.6418 0.9185 -1.013 1.0366 1.3173

ρ= 2.0 EM 2.027 0.1542 0.1566 2.035 0.1571 0.1609 2.035 0.1504 0.1543 ACC 2.657 0.3441 0.7412 2.621 1.1807 1.3339 1.909 0.9150 0.9195

γ=−2.8 EM -2.809 0.2511 0.2537 -2.826 0.2531 0.2587 -2.818 0.2497 0.2538 ACC -4.243 0.5275 1.5620 -5.446 1.1924 2.9274 -3.715 0.9534 1.3402

α1=−0.5 EM

-0.509 0.1473 0.1476 -0.505 0.1596 0.1596 -0.514 0.2156 0.2160

ACC - - -

-α2= 1.0 EM

1.006 0.1887 0.1888 1.021 0.1922 0.1933 1.010 0.2711 0.2713

(46)

-4.2 Resultados para os dados simulados 36

Tabela 4.5: Estimativas (média), erros-padrão (EP) e raiz dos erros quadráticos médios (REQM) dos parâmetros em 1500 réplicas, amostras de tamanho n = 300 sem censura entre os não imunes, com 45% de imunes e variando o percentual de censura e de omissão.

10% de censura

Parâmetro Método 15 % de omissão 30% de omissão 50% de omissão

β1= 1.5 EM

1.516 0.1144 0.1155 1.511 0.1181 0.1186 1.512 0.1176 0.1182 ACC 1.669 0.1443 0.2219 1.817 0.1737 0.3613 1.778 0.2033 0.3441

β2=−1.5 EM

-1.586 0.2106 0.2274 -1.580 0.2068 0.2217 -1.579 0.2196 0.2333 ACC -1.740 0.2417 0.3408 -1.920 0.2771 0.5033 -1.997 0.3236 0.5927

β3= 1.0 EM 0.897 0.1501 0.1820 0.894 0.1541 0.1873 0.891 0.1711 0.2031

ACC 0.859 0.1702 0.2212 0.685 0.1959 0.3706 0.647 0.2287 0.4205

ρ= 2.0 EM 2.045 0.1182 0.1266 2.042 0.1227 0.1298 2.044 0.1155 0.1235 ACC 2.316 0.1596 0.3538 2.193 0.1779 0.2627 2.148 0.2049 0.2529

γ=−2.8 EM -2.708 0.1902 0.2008 -2.704 0.1948 0.2064 -2.703 0.1977 0.2096 ACC -3.282 0.2460 0.6245 -3.224 0.2942 0.5391 -3.060 0.3489 0.4520

α1=−0.5 EM

-0.511 0.1509 0.1514 -0.497 0.1479 0.1479 -0.499 0.1772 0.1772

ACC - - -

-α2= 1.0 EM

1.007 0.2408 0.2409 0.984 0.2478 0.2484 0.978 0.2845 0.2854

ACC - - -

-30% de censura

β1= 1.5 EM 1.503 0.1314 0.1314 1.491 0.1330 0.1333 1.456 0.1030 0.1121

ACC 1.672 0.1533 0.2305 1.927 0.2370 0.4881 2.364 0.5565 1.0278

β2=−1.5 EM -1.737 0.2081 0.3150 -1.698 0.2204 0.2962 -1.604 0.1832 0.2106

ACC -1.895 0.2334 0.4584 -2.320 0.3270 0.8823 -2.779 0.8282 1.5237

β3= 1.0 EM 0.735 0.1773 0.3186 0.693 0.2049 0.3692 0.582 0.1899 0.4594

ACC 0.726 0.1905 0.3341 0.555 0.2741 0.5231 0.499 0.9670 1.0891

ρ= 2.0 EM 2.140 0.1474 0.2029 2.130 0.1483 0.1974 2.092 0.1111 0.1442 ACC 2.390 0.1864 0.4326 2.573 0.2955 0.6448 2.723 1.4720 1.6400

γ=−2.8 EM -2.519 0.2198 0.3354 -2.491 0.2241 0.3596 -2.419 0.1687 0.3921 ACC -2.997 0.2624 0.3449 -3.547 0.4467 0.8937 -5.589 1.2442 3.0785

α1=−0.5 EM -0.510 0.1438 0.1442 -0.523 0.1651 0.1666 -0.581 0.1624 0.1813

ACC - - -

-α2= 1.0 EM 0.972 0.1790 0.1812 0.906 0.1980 0.2192 0.792 0.1778 0.2736

(47)

-4.2 Resultados para os dados simulados 37

para os parˆametros β1 eρ.

O parâmetro β2 é bem estimado pelo algoritmo EM para amostras com pe-queno percentual de imunes (10%), mas quando o percentual de imunes é maior (45%), observa-se um pequeno viés que permanece constante em fun¸cão do percentual de omis-são. Quando o método utilizado é a ACC, observa-se que as estimativas, bem como probabilidade de cobertura pioram com o aumento do percentual de omissão.

Curiosamente, os resultados obtidos com os dois métodos para o parâmetro β3, que é o coeficiente associado à covariável omissa, são equivalentes para o caso em que há 10% de imunes na amostra. No entanto, apesar do viés relativo para a estimativa ACC estar sempre mais próximo de zero, do que as estimativasEM, pode-se notar que esta quantidade apresenta uma tendência crescente com o aumento do percentual de omissão. Além disso, os vieses observados com a ACC é negativo quando o percentual de omissão é de no máximo 15% e positivo para percentuais de omissão maior do que 15%, enquanto o algoritmo EM apresenta vieses sempre negativos. Quando o percentual de imunes é de 45%, as estimativas EM apresentam viés acentuado, porém constante, enquanto as estimativas ACC apresentam vieses muito maiores e crescentes segundo o percentual de omissão.

(48)

● ● ● ● ● ● ● ● ● ●

10 20 30 40 50

−0.4 −0.2 0.0 0.2 0.4 ββ1

10% de imunes percentual de omissão

Viés Relativo

● EM

ACC ● ●

● ● ● ● ● ● ● ●

10 20 30 40 50

0.0 0.2 0.4 0.6 0.8 1.0 ββ1

REQM ● EM ACC ● ● ● ● ● ● ● ● ● ●

10 20 30 40 50

0.5 0.6 0.7 0.8 0.9 1.0 ββ1

Probabilidade de cobertura ● EM

ACC

● ● ● ● ● ● ● ● ●

10 20 30 40

−0.4 −0.2 0.0 0.2 0.4 ββ1

Viés Relativo

● _EM

ACC

● ● ● ● ● ● ● ● ●

10 20 30 40

0.0 0.2 0.4 0.6 0.8 1.0 ββ1

REQM ● _EM ACC ● ● ● ● ● ● ● ● ●

10 20 30 40

0.5 0.6 0.7 0.8 0.9 1.0 ββ1

Probabilidade de cobertura ● EM

ACC

(49)

● ● ● ● ● ● ● ● ● ●

10 20 30 40 50

−0.4 −0.2 0.0 0.2 0.4 ββ2

Viés Relativo ● EM ACC ● ● ● ● ● ● ● ● ● ●

10 20 30 40 50

0.0 0.2 0.4 0.6 0.8 1.0 ββ2

REQM

● EM ACC

10 20 30 40 50

0.5 0.6 0.7 0.8 0.9 1.0 ββ2

Probabilidade de cobertura

● ● ● ● ● ● ● ● ● ● ● EM ACC ● ● ● ● ● ● ● ● ●

10 20 30 40

−0.4 −0.2 0.0 0.2 0.4 ββ2

Viés Relativo

● _EM

ACC ● ●

●

● ● ● ● ● ●

10 20 30 40

0.0 0.2 0.4 0.6 0.8 1.0 ββ2

REQM

● _EM

ACC

10 20 30 40

0.5 0.6 0.7 0.8 0.9 1.0 ββ2

Probabilidade de cobertura

●

● ● ●

● ● ● ● ●

● _EM

ACC