UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXATAS E DA TERRA DEPARTAMENTO DE INFORMÁTICA E MATEMÁTICA
APLICADA
PROGRAMA DE PÓS-GRADUAÇÃO EM SISTEMAS E COMPUTAÇÃO
MESTRADO ACADÊMICO EM SISTEMAS E COMPUTAÇÃO
O Problema do Hiker Dice em Tabuleiro Compacto: Um estudo
algorítmico
Elder Gonçalves Pereira
Elder Gonçalves Pereira
O Problema do Hiker Dice em Tabuleiro Compacto: Um estudo
algorítmico
Dissertação apresentada à Universidade Federal do Rio Grande do Norte, como requisito parcial para a obtenção do título de Mestre em Sistemas e Computação, Área de Concentração: Algoritmos Experimentais.
PPgSC – Programa de Pós-Graduação em Sistemas e Computação DIMAp – Departamento de Informática e Matemática Aplicada
CCET – Centro de Ciências Exatas e da Terra UFRN – Universidade Federal do Rio Grande do Norte
Orientador
Prof. Dr. Marco César Goldbarg
Catalogação da Publicação na Fonte. UFRN / SISBI / Biblioteca Setorial Centro de Ciências Exatas e da Terra – CCET.
Pereira, Elder Gonçalves.
O problema do Hiker Dice em tabuleiro compacto: um estudo algorítmico/ Elder Gonçalves Pereira. - Natal, 2014.
111 f.: il.
Orientador: Prof. Dr. Marco César Goldbarg
Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Sistemas e Computação.
1. Algoritmos – Dissertação. 2. Hiker Dice – Dissertação. 3. Algoritmo exato – Dissertação. 4. Algoritmos heurísticos – Dissertação. I. Goldbag, Marco César. II. Título.
Dissertação, sob o título O Problema do HIker Dice em Tabuleiro compacto: Um Estudo Algorítmico à banca examinadora como requisito parcial para obtenção do título de Mestre em Sistemas e Computação da Universidade Federal do Rio Grande do Norte
BANCA EXAMINADORA
____________________________________________ Prof. Dr. Marco Cesar Goldbarg (Orientador)
Centro de Ciências Exatas e da Terra
Departamento de Informática e Matemática Aplicada UFRN
____________________________________________ Profa. Dra. Elizabeth Ferreira Gouvea
Centro de Ciências Exatas e da Terra
Departamento de Informática e Matemática Aplicada UFRN
_____________________________________________ Profa. Dra. Iloneide Carlos de Oliveira Ramos
Examinadora externa ao Programa Departamento de Estatística
UFRN
____________________________________________ Prof. Dr. Henrique Pacca Loureiro Luna
Examinador externo ao Programa UFAL - Universidade Federal de Alagoas
____________________________________________ Profa. Dra. Myriam Regattieri De Biase da Silva Delgado
Examinadora externa ao Programa
UTFPR - Universidade Tecnológica Federal do Paraná
RESUMO
O Hiker Dice foi um jogo proposto recentemente em um software projetado por Mara Kuzmich e Leonardo Goldbarg. No jogo um dado é responsável pela construção de uma trilha sobre um tabuleiro n x m. O dado ao visitar uma célula do tabuleiro imprime (marca) a face que entra em contato com a superfície. O jogo apresenta o “Problema do Caminho Hamiltoniano Simples Máximo Hiker Dice (CHS-HiDi) em Tabuleiros Compactos de ordem N”, esse problema é então caracterizado por buscar um caminho hamiltoniano que maximize a soma dos faces do dado marcados no tabuleiro. A pesquisa presentemente relatada, modela o problema através de Grafos, e propõe duas classes de algoritmos de solução. A primeira classe, pertencente aos algoritmos exatos, é constituída por um algoritmo em backtracking aparelhado com um retorno realizado através de regras lógicas e limite da melhor solução encontrada. A segunda classe de algoritmos é constituída por metaheurísticas do tipo Computação Evolucionária, Busca Local Aleatorizada e GRASP (Greed Randomized Adaptative Search). Para os algoritmos foram criados três operadores específicos da seguinte forma: de reestruturação, de recombinação com duas soluções e construtivo guloso aleatório. O algoritmo exato foi testado em tabuleiros 4x4 a 8x8 esgotando a possibilidade de tratamento computacional dos casos maiores em virtude da explosão em tempo de processamento. Os algoritmos heurísticos foram testados nos tabuleiros 5x5 até 14x14. Segundo a metodologia de avaliação utilizada, os resultados encontrados pelos algoritmos heurísticos sugere um melhor potencial de desempenho para o algoritmo GRASP.
ABSTRACT
The Hiker Dice was a game recently proposed in a software designed by Mara Kuzmich and Leonardo Goldbarg. In the game a dice is responsible for building a trail on an n x m board. As the dice waits upon a cell on the board, it prints the side that touches the surface. The game shows the “Hamiltonian Path Problem Simple Maximum Hiker Dice (Hidi-CHS) in trays Compact Nth”, this problem is then characterized by looking for a Hamiltonian Path that maximize the sum of marked sides on the board. The research now related, models the problem through Graphs, and proposes two classes of solution algorithms. The first class, belonging to the exact algorithms, is formed by a backtracking algorithm planed with a return through logical rules and limiting the best found solution. The second class of algorithms is composed by metaheuristics type Evolutionary Computing, Local Ramdomized search and GRASP (Greed Randomized Adaptative Search). Three specific operators for the algorithms were created as follows: restructuring, recombination with two solutions and random greedy constructive.The exact algorithm was teste on 4x4 to 8x8 boards exhausting the possibility of higher computational treatment of cases due to the explosion in processing time. The heuristics algorithms were tested on 5x5 to 14x14 boards. According to the applied methodology for evaluation, the results acheived by the heuristics algorithms suggests a better performance for the GRASP algorithm.
LISTA DE FIGURAS
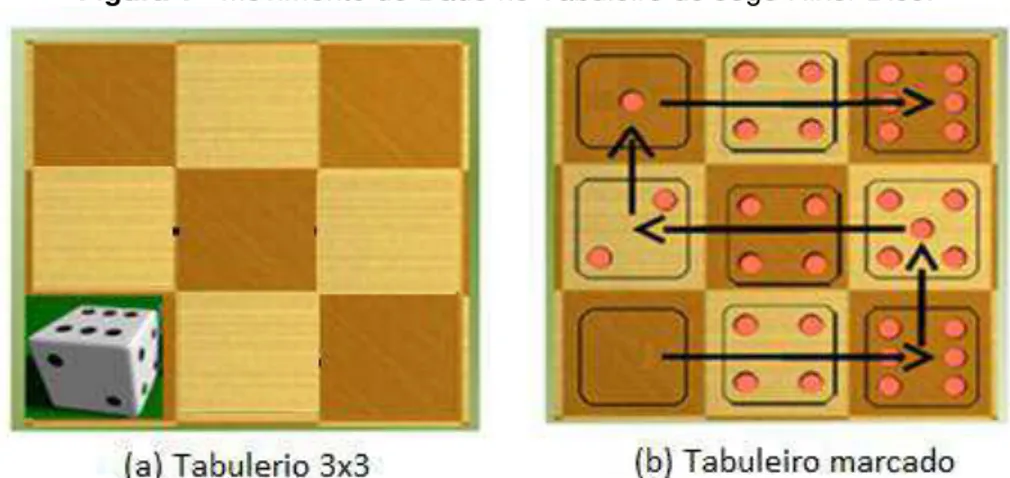
FIGURA 1 - MOVIMENTO DO DADO NO TABULEIRO DO JOGO HIKER DICE. ... 14
FIGURA 2– EXEMPLIFICAÇÃO DO DADO. ... 17
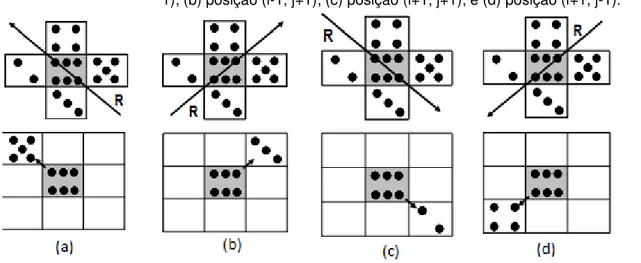
FIGURA 3 - JUMPS À DIREITA ONDE AS FACES PROJETADAS OCUPAM AS SEGUINTES POSIÇÕES: (A) POSIÇÃO (I-1, J-1); (B) POSIÇÃO (I-1, J+1); (C) POSIÇÃO (I+1, J+1); E (D) POSIÇÃO (I+1, J-1). ... 18
FIGURA 4– TRILHAS DO DADO SOBRE UM TABULEIRO. ... 19
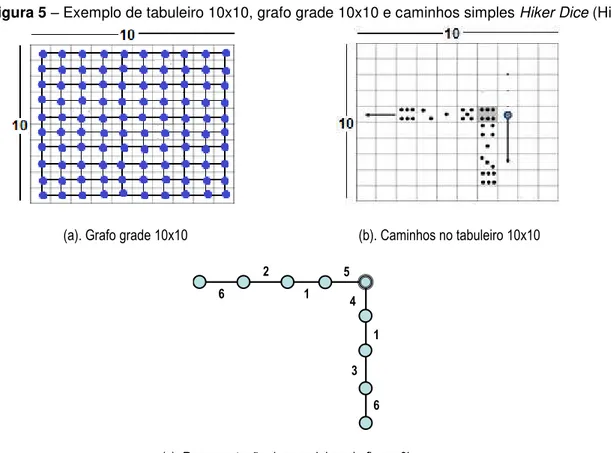
FIGURA 5– EXEMPLO DE TABULEIRO 10X10, GRAFO GRADE 10X10 E CAMINHOS SIMPLES HIKER DICE (HIDI). ... 20
FIGURA 6 - EXEMPLOS DE RESTRIÇÕES. ... 21
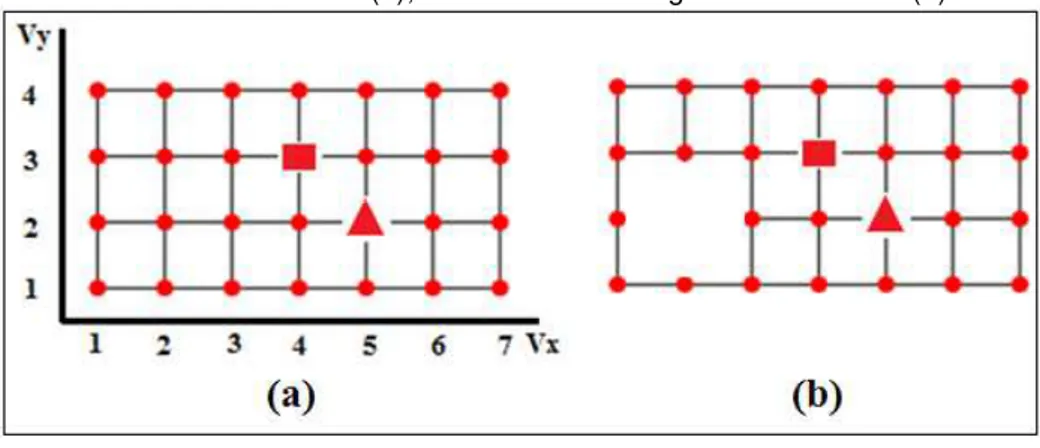
FIGURA 7 - GRAFOS GRADE R7, 4 COM OS VÉRTICES DEFINIDOS POR COORDENADAS: GRAFO GRADE TETRÁGANO SOLIDO (A), GRAFO GRADE TETRÁGONO COM BURACO (B). 23 FIGURA 8 - GRAFO GRADE COM CICLOS DIJUNTOS. ... 24
FIGURA 9 - GRAFO GRADE ORIGINAL (A), E GRAFO GRADE AUXILIAR COM VÉRTICES E ARESTAS FICTÍCIOS (B). ... 26
FIGURA 10 - GRAFO GRADE COM CICLOS DEFINIDOS (A), FUSÃO DOS CICLOS (B). ... 26
FIGURA 11– EXEMPLO DE VÉRTICES TERMINAIS. ... 27
FIGURA 12– EXEMPLO DE PONTO DE ISOLAMENTO. ... 29
FIGURA 13– EXEMPLO DE VÉRTICES ADJACENTES DA POSIÇÃO CORRENTE. ... 29
FIGURA 14– MARCA GRAFO 1. ... 30
FIGURA 15– MARCA GRAFO 2. ... 31
FIGURA 16– ESTRUTURA CRUZ... 32
FIGURA 17– EXEMPLO DE ROLAMENTO DO DADO NA DIREÇÃO VERTICAL E HORIZONTAL. ... 33
FIGURA 18– EXEMPLO DE TABULEIRO E GRAFO GRADE 3X3. ... 34
FIGURA 19– EXEMPLO DE MOVIMENTO DO DADO. ... 35
FIGURA 20 - ELEMENTO DA ESTRUTURA PILHA. ... 37
FIGURA 21– GRAFO GRADE 3 X 3 (A); CONSTRUÇÃO DO CAMINHO (B), (C), (D) E (E); EXEMPLO DE ÁRVORE DE ESTADO (F). ... 39
FIGURA 22 – GRAFO GRADE 4X4 E SOLUÇÃO INICIAL (S*). ... 49
FIGURA 23 – RELAÇÃO DE ADJACÊNCIA DO INTERVALO DE REESTRUTURAÇÃO NO GRAFO GRADE 4X4. ... 50
FIGURA 24 – SOLUÇÃO REESTRUTURADA. ... 50
FIGURA 25– EXEMPLO RECOMBINAÇÃO. ... 55
FIGURA 26 – NOVO CAMINHO NO GRAFO GRADE 4X4. ... 56
FIGURA 27 – EXEMPLO CONSTRUÇÃO PRIMEIRO NÍVEL. ... 60
FIGURA 28 – EXEMPLO CONSTRUÇÃO SEGUNDO NÍVEL. ... 61
FIGURA 29 – EXEMPLO CONSTRUÇÃO TERCEIRO NÍVEL. ... 62
FIGURA 30 - GRAFO (N, M). ... 85
FIGURA 31 - EXEMPLO DE CAMINHO FECHADO EM UM GRAFO G. ... 86
FIGURA 32– EXEMPLO DE UM GRAFO GRADE. ... 87
FIGURA 33 - PRODUTO CARTESIANO ENTRE DOIS GRAFOS CAMINHOS RESULTA EM GRAFO GRADE. ... 87
LISTA DE ALGORITMOS E PROCEDIMENTOS
ALGORITMO 1– ALGORITMO EXATO. ... 41
ALGORITMO 2– BUSCA LOCAL. ... 43
ALGORITMO 3 - GRASP ADAPTADO COM OS OPERADORES: CONSTRUTIVO GULOSO ALEÁTORIO E REESTRUTURAÇÃO. ... 45
ALGORITMO 4– GENÉTICO ADAPTADO COM OS OPERADORES: RECOMBINAÇÃO E REESTRUTURAÇÃO. ... 47
PROCEDIMENTO 1 - REESTRUTURAÇÃO ... 51
PROCEDIMENTO 2– MODIFICAR INTERVALO ... 53
PROCEDIMENTO 3 - RECOMBINAÇÃO ... 58
PROCEDIMENTO 4 – CONSTRUÇÃO GULOSA ALEATÓRIA. ... 64
PROCEDIMENTO 5– CONSTRUÇÃO PRIMEIRO NÍVEL. ... 66
PROCEDIMENTO 6 – CONSTRUÇÃO SEGUNDO NÍVEL. ... 67
PROCEDIMENTO 7– CONSTRUÇÃO TERCEIRO NÍVEL. ... 69
LISTA DE TABELAS
TABELA 1– RESULTADOS EXATOS ENCONTRADOS. ... 73
TABELA 2– CASO DE TESTE: TABULEIRO 3X3. ... 75
TABELA 3 - CONFIGURAÇÕES FILTRADAS PARA O BUSCA LOCAL NO TABULEIRO 8X8. ... 78
TABELA 4 - CONFIGURAÇÕES FILTRADAS PARA O GRASP NO TABULEIRO 8X8. ... 79
TABELA 5 - CONFIGURAÇÕES FILTRADAS PARA O GENÉTICO NO TABULEIRO 8X8. ... 80
TABELA 6– RESULTADOS HEURÍSTICOS. ... 82
TABELA 7 – COLETA DE DADOS DAS CONFIGURAÇÕES APLICADA AO BUSCA LOCAL NO TABULEIRO 8X8. ... 92
TABELA 8 - COLETA DE DADOS DAS CONFIGURAÇÕES APLICADA AO GRASP NO TABULEIRO 8X8. ... 93
SUMÁRIO
1 INTRODUÇÃO ... 13
1.1 JOGO HIKER DICE ... 14
1.1.1 O PROBLEMA DO CAMINHO HAMILTONIANO SIMPLES MÁXIMO HIKER DICE (CHS-HIDI) EM TABULEIROS COMPACTOS DE ORDEM N . 15 1.2 OBJETIVOS ... 16
1.2.1 Geral ... 16
1.2.2 Específicos ... 16
1.3 DIVISÃO DO TRABALHO ... 16
2 CARACTERÍSTICAS DO HIKER DICE ... 17
3 O PROBLEMA DO CAMINHO HAMILTONIANO EM GRAFOS GRADE ... 22
4 ESTRUTURAS E PROCEDIMENTOS PARA HIKER DICE ... 27
4.1 VÉRTICES TERMINAIS ... 27
4.2 PONTO DE ISOLAMENTO ... 27
4.3 VÉRTICES ADJACENTES DA POSIÇÃO CORRENTE DO CAMINHO ... 29
4.4 MARCAÇÃO DO GRAFO ... 30
4.4.1 Marca Grafo 1 ... 30
4.4.2 Marca Grafo 2 ... 30
4.5 REPRESENTAÇÃO COMPUTACIONAL DE UMA SOLUÇÃO HIKER DICE .. 31
4.6 MOVIMENTO DE ROLAMENTO DO DADO SOBRE O TABULEIRO ... 31
4.6.1 Estrutura Para Representação e Movimento do Dado ... 31
4.6.2 Movimento de Rolamento do Dado ... 33
4.7 ATUALIZAR O VETOR DE SOLUÇÕES ... 35
5 ABORDAGEM EXATA ... 37
6 ABORDAGEM HEURÍSTICA ... 42
6.1 ALGORITMOS ADAPTADOS COM OS OPERADORES PROPOSTOS ... 42
6.1.1 Busca Local ... 42
6.1.2 GRASP (Greedy Randomized Adaptive Search Procedure) ... 44
6.1.3 Algoritmo Genético ... 45
6.2 OPERADORES ... 49
6.2.1 Procedimento Reestruturação ... 49
6.2.2 Procedimento Recombinação ... 55
6.2.4 Procedimento de Reparação do Caminho Ramiltoniano ... 70
7 RESULTADOS ... 73
7.1 RESULTADO EXATO ... 73
7.2 REFINAMENTO DOS PARÂMENTROS PARA AS HEURÍSTICAS ... 74
7.2.1 Metodologia para Refinamento dos Parâmetros ... 74
7.2.1.1 Exemplo de Faixa de Valores para os Parâmetros ... 74
7.2.1.2 Exemplo de Filtragem das Configurações ... 74
7.2.1.3 Teste não-paramétrico de Kruskal-Wallis (1952) ... 75
7.2.2 Ajuste dos Parâmetros ... 76
7.2.2.1 Busca Local ... 77
7.2.2.2 GRASP ... 78
7.2.2.3 Genético ... 79
7.3 RESULTADOS HEURÍSTICOS ... 81
7.3.1 Resultados dos Algoritmos ... 81
8 CONCLUSÃO ... 83
8.1 TRABALHOS FUTUROS ... 84
APÊNDICE 1 - CONCEITOS BÁSICOS EM TEORIA DOS GRAFOS ... 85
APÊNDICE 2 - RESULTADOS EXATOS ... 89
APÊNDICE 3 - RESULTADOS DOS REFINAMENTOS DOS PARÂMENTROS ... 92
APÊNDICE 4 - RESULTADOS HEURISTICOS DO BUSCA LOCAL ... 95
APÊNDICE 5 - RESULTADOS HEURISTICOS DO GENÉTICO ... 100
APÊNDICE 6 - RESULTADOS HEURISTICOS DO GRASP... 105
1 INTRODUÇÃO
Na Ciência da Computação existe uma atenção crescente relacionada aos jogos de raciocínio logico que demonstram natureza combinatória. Por causa das aplicações práticas que muitos deles podem demostrar; como também, o desenvolvimento de algoritmos computacionais com capacidade de enfrentar o raciocínio humano com possibilidade de vitória.
O inicio das pesquisas relacionadas ao desenvolvimento de algoritmos computacionais que confrontassem o raciocínio humano com alguma chance de vitória, ocorreu na década de 90. Nessa época, foi marcante a disputa no xadrez entre o computador Deep Blue da IBM e ex-campeão Garry Kasparov. Na primeira disputa, em um total de seis (6) jogos, em 1996, Deep Blue surpreende a todos ao ganhar uma e empatar duas partidas contra Kasparov, entretanto, o computador da IBM perdeu três vezes. Na segunda disputa, no dia 11 de maio de 1997, o desafio foi finalizado com duas vitórias e três empates de Deep Blue, contra uma vitória de Kasparov. Na cidade de New York entre os dias 11 e 18 de Novembro de 2003, aconteceu mais uma disputa de Kasparov contra uma maquina, desta vez foi o computador X3D Fritz, equipado por 4 processadores Intel Pentium Xeon com 2.8GHz. Nesta disputa, houve dois jogos empatados, uma vitória para Kasparov e outra para computador X3D Fritz. Assim sendo, tornana-se evidente a capacidade de certo algoritmo computacional confrontar o raciocínio humano com chance de vitória (GOLDBARG M.; OLIVEIRA; GOLDBARG, E., 2011).
Um novo significado na popularização dos jogos de raciocínio lógico aconteceu na década de 90. Devido a evolução computacional relacionada às interfaces e modernos meios de mídia, muitos desses jogos começaram a ter sua analise de complexidade de soluções estudadas, como o Xadrez (FRAENKEL; LICHTENSTEIN, 1981), Go (LICHTENSTEIN; SIPSER, 1980), Sokoban (DOR; ZWICK, 1999), Soduko (YATO; SETA, 2003) Minesweeper (KAYE, 2000), Tantrix (HOLZER, M.; HOLZER, W., 2004), Lemmings (CORMODE, 2004), Spiral Galaxies (FRIEDMAN, 1992), Tertrix (HOOGEBOOM; KOSTERS, 2004), dentre outros.
Neste trabalho é abordado um jogo de raciocínio lógico associado ao problema dos caminhos hamiltonianos em grafos grade, denominado Hiker Dice.
1.1 JOGO HIKER DICE
O Hiker Dice foi um jogo proposto recentemente em um software projetado por Mara Kuzmich e Leonardo Goldbarg. No jogo um dado é responsável pela construção de uma trilha sobre um tabuleiro n x n. O dado após ser posicionado em uma casa (célula) do tabuleiro com uma configuração inicial conhecida realiza uma sequência de movimentos. Em cada casa visitada o dado imprime (marca) a face inferior, precisamente a que entra em contato com a superfície do tabuleiro. Ganha o jogador que conseguir construir a trilha que apresente o maior somatório das faces do dado (GOLDBARG M.; GOLDBARG E., 2012).
Na Figura 1 (a) é mostrado um dado localizado inicialmente na parte inferior esquerda do tabuleiro, com a seguinte configuração: a face um (1) voltada para baixo; a face seis (6) para cima; a face quatro (4) para a direita; a face dois (2) voltada para frente; a face cinco (5) para trás e a face três (3) para a esquerda. A Figura 1(b) mostra um caminho hamiltoniano definido pelo movimento (rolamento) do dado no tabuleiro cujas casas (células do tabuleiro) foram impressas (marcadas) pela face inferior do dado ao entrar em contato com a superfície do tabuleiro; nesse caminho, as faces impressas no tabuleiro com soma igual a 32.
1.1.1 O PROBLEMA DO CAMINHO HAMILTONIANO SIMPLES MÁXIMO HIKER DICE (CHS-HIDI) EM TABULEIROS COMPACTOS DE ORDEM N
O presente trabalho aborda o “Problema do Caminho Hamiltoniano Simples Máximo Hiker Dice (CHS-HiDi) em Tabuleiros Compactos de ordem N”.
Um caminho Hamiltoniano simples no tabuleiro Hiker Dice é um caminho que cobre todas as células do tabuleiro definido pelo movimento de “rolamento do dado” (o deslocamento do dado segue o giro natural do cubo sobre a superfície do tabuleiro).
Basicamente o CHS-HiDi é um caminho Hamiltoniano desenvolvido em um grafo grade quadrado que maximiza o seu comprimento, sem que seja possível, a priori, conhecer o valor das arestas do caminho Hamiltoniano desenvolvido.
Denomina-se de tabuleiro compacto retangular ao tabuleiro retangular em que todas as células podem ser ocupadas através de rolamentos realizados por um dado posicionado inicialmente em qualquer célula do tabuleiro.
1.2 OBJETIVOS
1.2.1 Geral
Construir classes de algoritmos de soluções para o problema do Caminho Hamiltoniano Simples Máximo (CHS-HiDi) em Tabuleiros Compactos de ordem n.
1.2.2 Específicos
1. Modelar o problema do CHS-HiDi através de grafos. 2. Criar um algoritmo exato para o problema do CHS-HiDi.
3. Criar operadores construtivos para o problema do CHS-HiDi, a fim de, adaptá-los aos algoritmos de Busca Local, GRASP e Genético.
4. Realizar experimentos computacionais com o algoritmo exato e, com os algoritmos heurísticos de Busca Local, GRASP e Genético.
1.3 DIVISÃO DO TRABALHO
2 CARACTERÍSTICAS DO HIKER DICE
Um dado é um cubo que possui uma distribuição de números em suas faces. Tradicionalmente os dados apresentam a distribuição de pontos de 1 a 6, de fato uma enumeração das faces. A configuração tradicional do dado apresenta os valores 1 e 6, 4 e 3 e 5 e 2 localizados em faces opostas do cubo, como mostra a representação planar do cubo na Figura 2 (a). No presente trabalho considera-se o padrão de distribuição de números pelas faces do dado como uma variável de entrada do problema, todavia, quando nada for dito, a configuração tradicional será a considerada.
Figura 2– Exemplificação do dado.
(a). Representação plana das faces do dado (b). Rolando o dado
Define-se um tabuleiro como uma grade de células em formato retangular que pode suportar, via de regra, a realização de vários tipos de jogos lógicos.
Um dado se desloca de uma célula para outra através de um movimento. São possíveis três tipos de movimento: Rolamento, Jump e Sjump.
O rolamento de um dado sobre um tabuleiro sempre se dá sobre uma célula vizinha e na direção do giro natural do cubo sobre a aresta da base voltada para a célula que será ocupada, em um movimento horizontal ou vertical, considerando como as direções horizontal e vertical as laterais ortogonais do tabuleiro. A Figura 2 (b) exemplifica um rolamento.
utilizar uma das duas faces. O jump à direita projeta a face não adjacente situada à direita em relação ao sentido de movimento do dado. O jump à esquerda a face projetada será aquela situada à esquerda. A Figura 3 exemplifica os jumps à direita.
Figura 3 - Jumps à direita onde as faces projetadas ocupam as seguintes posições: (a) posição (i-1, j-1); (b) posição (i-1, j+j-1); (c) posição (i+1, j+j-1); e (d) posição (i+1, j-1).
O Sjump é qualquer outro movimento que não ocupe células vizinhas à posição corrente do dado.
Considerando que o dado ao se movimentar em um tabuleiro imprima nesse tabuleiro a sua face inferior e que permanecerá em contato com a célula do tabuleiro, o tabuleiro exibirá uma sequência de marcação na medida em que um dado se movimentar sobre sua superfície. Uma sequência de movimentos forma uma trilha do dado. A soma das marcações da trilha constitui o comprimento da trilha.
Uma trilha formada exclusivamente por rolamentos do dado é denominada de trilha simples.
Figura 4– Trilhas do dado sobre um tabuleiro.
O valor de uma trilha é o somatório dos pontos impressos nas células da trilha, independentemente de serem remarcados.
Um caminho do dado em um tabuleiro consiste em uma sequência de movimentos do dado de forma que nenhuma posição do tabuleiro seja revisitada. Um caminho formado exclusivamente por rolamentos é dito caminho simples.
Seja um tabuleiro de células quadradas como mostra a Figura 5, pode-se associar a esse tabuleiro o grafo G = (N, M). As células do tabuleiro são representadas pelos vértices e as arestas do grafo representam as relações de vizinhança entre as células do tabuleiro. Nesse grafo, denominado de grafo tabuleiro, a aresta (i-j) representa a possibilidade de movimento do dado da célula i para a célula j do tabuleiro. Considerando-se o dado assentado em uma célula inicial do tabuleiro, define-se o valor do caminho de i ao vértice j como a soma de todos os valores das arestas pertencentes ao caminho i-j. Observe-se que, para o cálculo de comprimento do caminho i-j, não se computa, por convenção, o valor da face inferior do dado na célula inicial, a célula i.
No grafo anteriormente definido os valores das arestas somente poderão ser determinados quando for conhecida a sequência de rolamento do dado.
desenvolvimento de dois caminhos possíveis a partir da posição ocupada pelo dado da Figura 5 (b).
Quando um rolamento realiza a visita sequencial de todas as faces do dado em uma certa direção é dito rolamento completo. Para os dados tradicionais, a soma de cada par de faces opostas é igual a 7, no rolamento completo é impresso sobre o tabuleiro dois pares de faces opostas; desta forma, o comprimento de um rolamento completo será constante e igual a 14.
Figura 5– Exemplo de tabuleiro 10x10, grafo grade 10x10 e caminhos simples Hiker Dice (HiDi).
(a). Grafo grade 10x10 (b). Caminhos no tabuleiro 10x10
(c). Representação dos caminhos da figura 6b
Circunstancialmente o problema pode exibir restrições ao movimento. Uma restrição de movimento é constituída por um conjunto de atributos que devem ser satisfeitos por essas operações na formação de qualquer trilha.
Os atributos de movimento podem se referir a certas células do tabuleiro, sendo então definidos como restrições de tabuleiro. Uma restrição de tabuleiro comum é a impossibilidade de ocupação da célula. Outra restrição é a especificação de um ou mais valores de impressão não aceitável. A Figura 6 (a) exemplifica em negrito as células de visita proibida. A Figura 6 (b) exibe exemplos de valores
4
1
3
6 5
1 2
proibidos para a face de rolamento. A letra O significa que a célula referida não aceita a visita de uma face ímpar. A letra E significa que a visita de uma face par é proibida.
Figura 6 - Exemplos de Restrições.
(a). No grafo grade o dado não pode visitar as células em cor preta.
(b). No grafo grade as células com valores numericos e
as células com letras representam restrições impostas ao dado.
3 O PROBLEMA DO CAMINHO HAMILTONIANO EM GRAFOS GRADE
O problema de encontrar caminhos ou ciclos que passassem por todos os vértices em um grafo qualquer sem admitir vértices repetidos, foi proposto em 1856 por Thomas Penyngton Kirkman. No trabalho (Kirkman, 1856) foram analisadas as condições em tipos de sólidos da existência de caminhos e ciclos que não repetissem vértices ou arestas (LAPORTE, 2006; GROPP, 2006).
Um pouco mais tarde o problema de encontrar os caminhos que passassem por todos os vértices do grafo iniciando e terminando no mesmo vértice foi denominado de Hamiltoniano devido ao jogo “Around the World” criado em 1857 por Willian Rowan Hamilton (GOLDBARG, M.; GOLDBARG, E., 2012). O jogo tinha a forma de um dodecaedro1, no qual cada vértice representava uma cidade importante na época. O objetivo era encontrar um caminho passando por todas as cidades de forma que iniciasse e terminasse na mesma cidade e nunca repetisse uma cidade já visitada, então uma solução desse jogo passou a ser chamada de ciclo Hamiltoniano.
Segundo Goldbarg e Goldbarg (2012, p. 217), “um grafo é dito hamiltoniano, se possui um ciclo hamiltoniano; um grafo é dito semi-hamiltoniano se possui um caminho hamiltoniano”.
O Problema do Caminho Hamiltoniano Simples Máximo HiDi em Tabuleiros Compactos (CHS-HiDi) é desenvolvido em grafos grade pois é esse o tipo de grafo formado pelos rolamentos do dado.
Um dos primeiros estudos relacionados a Caminhos Hamiltonianos em grafo grade foi apresentado em Luccio e Mugnia (1978), cujos autores tentavam resolver o problema do caminho hamiltoniano em algumas classes de grafos, inclusive os grafos grade retangulares.
Denotando por G∞ um grafo infinito no qual os vértices são todos os pontos
do plano com coordenadas inteiras, dois vértices distintos são conectados se e
somente se a distancia Euclidiana entre eles é igual a um (1). O grafo grade R(m, n) é unicamente um subgrafo induzido de G∞, onde o conjunto de vértices V(R(m, n)) =
{v: 1 ≤ Vx ≤ m e 1 ≤ Vy ≤ n} são definidos pelas coordenadas no plano cartesiano. (ITAI et al., 1982).
De acordo com Weisstein (2013), “nesse tipo de grafo a quantidade de vértices pode ser encontrada pela equação mn e a quantidade de arestas pela equação (m-1)n + (n-1)m = 2mn - m - n”.
Na Figura 7 (a) e (b) são exemplificados os grafos grade R7,4 sem buraco e com buraco (com um conjunto de vértices ausentes), nesses grafos os vértices pode ser localizados pelas coordenadas inteiras (Vx, Vy) definidas no plano cartesiano. Como exemplo, o vértice de forma quadrada está localizado na coordenada V(4, 3) e, o vértice triangular está localizado na coordenada V(5, 2). Segundo as definições relatadas no trabalho de Weisstein (2013), o grafo da Figura 7 (a), apresenta pelas equações um total de 28 vértices e precisamente 45 arestas.
Figura 7 - Grafos Grade R7, 4 com os vértices definidos por coordenadas: Grafo Grade Tetrágano
Solido (a), Grafo Grade Tetrágono com Buraco (b).
Fonte: Adaptado de Weisstein (2013).
Zamfirescu e Zamfirescu (1992), disponibilizaram as condições necessárias para um grafo grade sólido ser hamiltoniano. Itai et al. (1982) provaram que o problema do caminho ou ciclo hamiltoniano para a classe de grafo grade sólido é NP-Completo.
em dois conjuntos, onde cada aresta apresenta seus vértices terminais em conjuntos diferentes); o maior grau de um vértice no grafo será 4 (SALMAN, 2005). No Apêndice 1 são mostradas algumas definições básicas.
Alguns autores estabelecem algoritmos para a enumeração dos diferentes caminhos hamiltonianos em grafos grade. Kwong e Rogers (1994) apresentam um método matricial de contagem. Stoyan e Strehl (1996) geram funções para a enumeração dos caminhos hamiltonianos em grafos grades com uma das dimensões menor ou igual a 6.
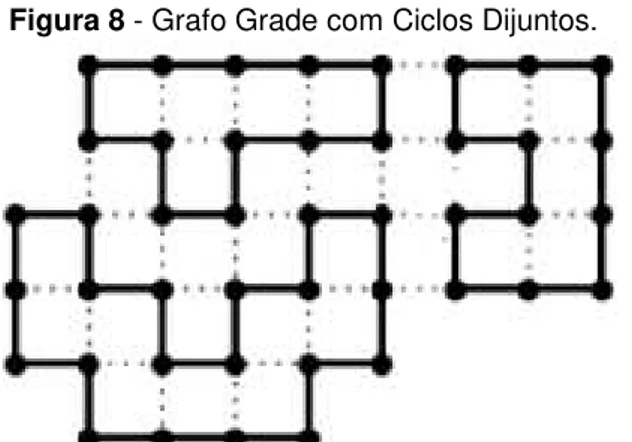
Lenhart e Umans (1997) apresentaram um algoritmo para encontrar ciclos hamiltonianos em grafos grade usando a técnica de fusão de ciclo. Primeiro, o algoritmo proposto encontra um conjunto de ciclos disjuntos que cobrem exatamente os vértices do grafo G, onde cada subgrafo nesse conjunto apresenta os vértices com grau dois. Segundo, o algoritmo faz a fusão dos componentes encontrados com finalidade de formar um ciclo hamiltoniano. Então, repetidamente a transformação identifica um conjunto de ciclos que reduz o número de componentes e em seguida realiza a fusão dos componentes. Esse processo encontra um ciclo hamiltoniano ou simplesmente termina com múltiplos componentes. A Figura 8 exemplifica os ciclos encontrados em grafo grade.
Figura 8 - Grafo Grade com Ciclos Dijuntos.
Fonte: Adaptado de Lenhart & Umans (1997).
Segundo, o algoritmo constrói em cada submalha um caminho ou ciclo hamiltoniano que dependerá unicamente da dimensão que foi atribuída para a submalha. E finalmente, o algoritmo junta todos os caminhos ou ciclos hamiltonianos criados nas submalhas em um único componente. Apresenta ao final um caminho ou ciclo hamiltoniano, ou simplesmente vários componentes não conectados.
Islam et al. (2007) demonstram que o problema do ciclo hamiltonano em grafos grade compactos hexagonais2 (categoria de grafos grades apresentam faces com seis lados) é NP-Completo.
Koromilas (2011) apresentou um trabalho que aplica as técnicas de fusão de ciclos, mas usando a redução de emparelhamento (matching) para melhorar a busca do ciclo hamiltoniano. A definição de emparelhamento é apresentada no Apêndice 1. O algoritmo primeiro constrói um grafo grade auxiliar do grafo grade original usando a seguinte regra: (i) dois vértices fictícios são adicionados em cada aresta do grafo e, (ii) um vértice clone é criado para cada vértice original, o vértice clone é conectado aos vértices fictícios adjacentes ao vértice original. Como mostram as Figura 9 (a) e (b). Um emparelhamento no grafo auxiliar apresenta um conjunto de ciclos hamiltonianos no grafo original, se o emparelhamento não pode ser obtido, então não existe um conjunto de ciclos hamiltonianos válidos para serem fundidos no grafo grade original, e assim, não pode encontrar um ciclo hamiltoniano.
Figura 9 - Grafo grade original (a), e grafo grade auxiliar com vértices e arestas fictícios (b).
Fonte: Adaptado de Koromilas (2011).
O emparelhamento apresentado no grafo auxiliar será usado para o conjunto de ciclos hamiltonianos que começa a construção dos caminhos com base nas arestas tracejadas entre os vértices fictícios. As Figura 10 (a) e (b) mostram o grafo dividido pelo conjunto de ciclos hamiltoniano, e o ciclo hamiltoniano definido pela fusão dos ciclos.
Figura 10 - Grafo Grade com Ciclos Definidos (a), Fusão dos Ciclos (b).
4 ESTRUTURAS E PROCEDIMENTOS PARA HIKER DICE
4.1 VÉRTICES TERMINAIS
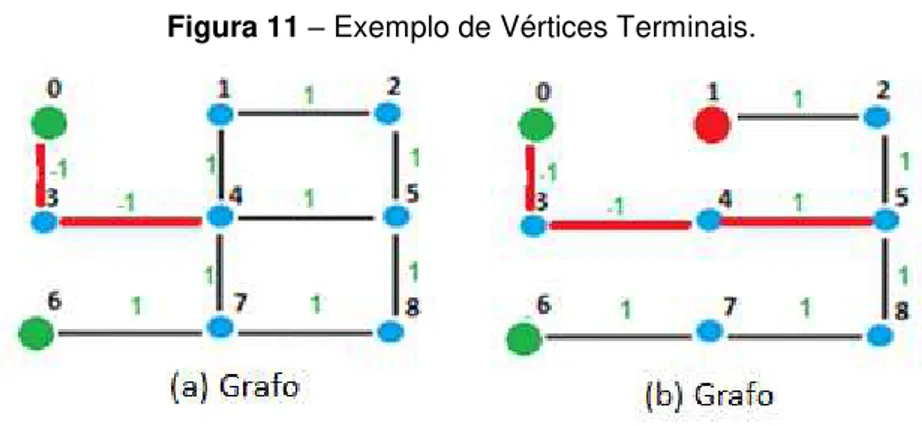
Um Caminho Hamiltoniano em um grafo grade terá no final da construção dois vértices terminais, um vértice inicial e um vértice final, ambos com grau 1 (um). Sendo assim, o “Procedimento Vértices Terminais” tem como função manter um controle sobre a quantidade de vértices no grafo grade com grau igual a um (1).
Na Figura 11 (a), os vértices terminais para o caminho (0-3-4) já existem no grafo G, os vértices 0 e 6.
O procedimento tem como entrada um vértice (v), o grafo G (matriz de adjacência) e como saída, uma condição verdadeira (para o vértice “v” sendo viável) ou falsa (para o vértice “v” sendo não viável).
Para o caminho, na Figura 11 (a), supondo o vértice (5) passado como entrada, o procedimento resultará o caminho (0-3-4-5) no grafo (G); na Figura 11 (b), o caminho construído resultou no grafo G, o vértice um (1) com grau 1.
Logo, o procedimento ao adicionar o vértice 5 retorna uma condição falsa; visto que o grafo G apresenta além dos vértices 0 e 6, o vértice um (1) com grau igual a 1.
Figura 11– Exemplo de Vértices Terminais.
4.2 PONTO DE ISOLAMENTO
sequência não resultará um Caminho Hamiltoniano; dessa forma, o vértice 7 se tornou inviável para construção do Caminho Hamiltoniano.
No exemplo da Figura 12 (a), o “Procedimento Ponto de Isolamento” tem como entrada o vértice (7), um grafo G (matriz de adjacência), uma copia do caminho (0-3-4) e como saída, uma condição verdadeira ou falsa.
Os passos são os seguinte:
1. Adicionar o vértice (7) ao caminho (0-3-4), como mostra a Figura 12(b); 2. Calcular o número de vértices adicionados ao caminho. No caso da Figura
12 (b), apresenta um total de quatro (4) vértices;
3. Aplicar uma Busca em Largura, a partir de algum vértice adjacente ao último vértice adicionado ao caminho (0-3-4-7); a busca não pode explorar os vértices do caminho (0-3-4-7);
4. Observe a Figura 12 (b), se a Busca em Largura começar no vértice 8, a busca explora os vértices (8, 5, 2 e 1), um total de quatro (4) vértices; do contrario, começando no vértice 6, a busca explora apenas o vértice 6, um total de um (1) vértice;
5. Calcular a expressão (n_vertices = total_caminho + total_busca_largura). No exemplo da Figura 12 (b), a busca em largura pode explorar no máximo 4 vértices (total_busca_largura = 4), o caminho apresenta um total de 4 vértices (total_caminho = 4); logo, a expressão resulta (n_vertices = 8);
Figura 12– Exemplo de Ponto de Isolamento.
4.3 VÉRTICES ADJACENTES DA POSIÇÃO CORRENTE DO CAMINHO
O grafo grade usado para representar o tabuleiro define inicialmente as adjacência entre os vértices com o valor 1, como mostra a Figura 13 (a). No decorre da construção do caminho no grafo, as arestas que fazem parte do caminho vão sendo marcadas com -1 e com 0, as arestas que não fazem parte do caminho.
A Figura 13 (b) exemplifica um caminho definido pelos vértices 0-3-4, as arestas nesse caminho são marcadas com valor (-1) e, as arestas 0-1 e 3-6 são removidas, marcadas com valor (0).
O “Procedimento Vértices Adjacentes da Posição Corrente no Caminho” tem como entrada um vértice (v), um grafo G (matriz de adjacência) e como saída, uma lista com os vértices adjacentes ao vértice (v) no grafo G, cujas arestas tenham marcação com valor (1).
No exemplo da Figura 13 (b), supondo o vértice (4) passado como entrada, o procedimento retornará uma lista com os vértices (1, 5 e 7), apenas as adjacências com arestas com marcação igual a 1.
4.4 MARCAÇÃO DO GRAFO
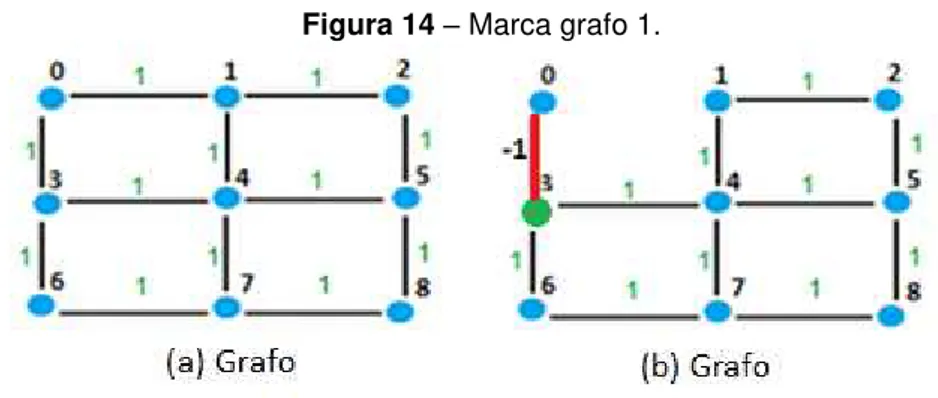
4.4.1 Marca Grafo 1
O “Procedimento Marca Grafo 1” tem como entrada um grafo G (matriz de adjacência), um vetor de inteiros (v_caminho) que representa uma copia do caminho em construção e como saída, o grafo G marcado com as posições do caminho.
O algoritmo realiza os seguintes passos:
1. Definir o vértice (v1) como o penúltimo vértice do vetor (v_caminho); 2. Definir o vértice (v2) como o último vértice do vetor (v_caminho); 3. Marcar a aresta (v1-v2) com valor (-1);
4. Remover as arestas do vértice (v1) que não fazem parte do caminho. No exemplo da Figura 14, faça o vértice (v1 = 0) e vértice (v2 = 3). A aresta (v1-v2) é marcada com valor (-1). E as arestas do vértice (v1) que não fazem parte do caminho são removidas (marcadas com valor 0), nesse caso apenas a aresta (0-1).
Figura 14– Marca grafo 1.
4.4.2 Marca Grafo 2
O “Procedimento Marco Grafo 2” tem como entrada um grafo G (matriz de adjacência), um vetor de inteiros (v_caminho) que representa uma copia do caminho em construção e como saída, o grafo G marcado.
O algoritmo realiza os seguintes passos:
4. Marcar as arestas entre vértice (v1) e seus vértices adjacentes que não fazem parte do caminho com valor 1;
No exemplo da Figura 15 (a), faça o vértice (v1 = 3) e vértice (v2 = 4). A aresta (v1-v2) é marcada com (1). E as arestas entre o vértice (v1) e seus vértices adjacentes que não fazem parte do caminho são marcadas com valor (1).
Figura 15– Marca grafo 2.
4.5 REPRESENTAÇÃO COMPUTACIONAL DE UMA SOLUÇÃO HIKER DICE
Neste trabalho uma “solução Hiker Dice” é representada por um vetor de inteiros para guardar os vértices do Caminho Hamiltoniano; um vetor de inteiros para guardar as faces do dado impressas sobre o Caminho Hamiltoniano e; uma variável numerica para guardar o somatório das faces.
4.6 MOVIMENTO DE ROLAMENTO DO DADO SOBRE O TABULEIRO
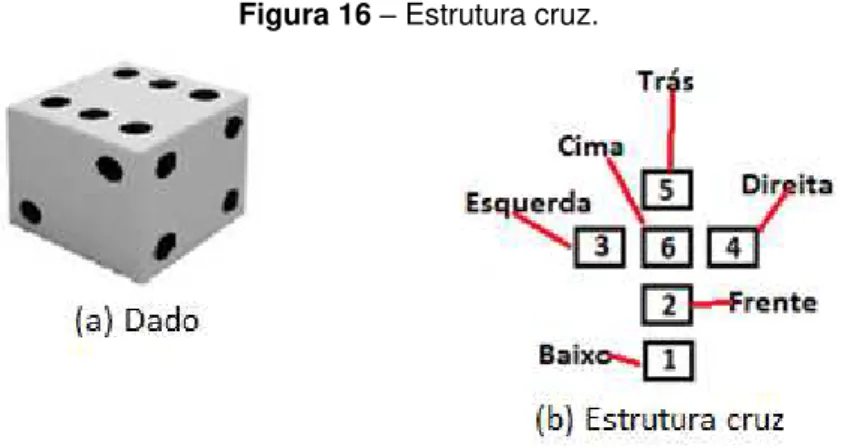
4.6.1 Estrutura Para Representação e Movimento do Dado
Figura 16– Estrutura cruz.
O rolamento do dado no tabuleiro acontece da seguinte forma: imaginemos um dado em certa localização no tabuleiro com uma configuração inicial conhecida, como mostra a Figura 17 (a), a partir deste estado inicial, o dado poderá fazer um rolamento na vertical (indo para cima ou para baixo da posição corrente), ou na horizontal (indo para a esquerda ou direita da posição corrente).
A Figura 17 exemplifica o rolamento sobre um tabuleiro:
Indo para cima da posição corrente, o dado parte da posição com a configuração inicial, como na Figura 17 (b), e faz algumas regras de permutação para chegar a próxima configuração, como na Figura 17 (c). A posição trás de valor 5 recebe o valor 6; a posição cima de valor 6 recebe o valor 2; a posição frente de valor 2 recebe o valor 1 e a posição baixo de valor 1 recebe o valor 5;
Indo para baixo da posição corrente, o dado parte da posição com a configuração inicial, como na Figura 17 (b), e faz algumas regras de permutação para chegar a próxima configuração, como na Figura 17 (d). A posição trás de valor 5 recebe o valor 1; a posição cima de valor 6 recebe o valor 5; a posição frente de valor 2 recebe o valor 6 e a posição baixo de valor 1 recebe o valor 2;
Indo para direita da posição corrente, o dado parte da posição com a configuração inicial, como na Figura 17 (b), e faz algumas regras de permutação para chegar a próxima configuração, como na Figura 17 (f). A posição esquerda de valor 3 recebe o valor 1; a posição direita de valor 4 recebe o valor 6; a posição cima de valor 6 recebe o valor 3 e a posição baixo de valor 1 recebe o valor 4.
Figura 17– Exemplo de rolamento do dado na direção vertical e horizontal.
Em uma linguagem de programação orientada a objetos a estrutura cruz pode facilmente ser representada por uma classe; as faces do dado sendo os atributos e, os movimentos do dado sobre tabuleiro representados pelos métodos da classe (responsáveis em fazer as permutações das faces para cada sentido de movimento na horizontal ou vertical).
4.6.2 Movimento de Rolamento do Dado
Figura 18– Exemplo de tabuleiro e grafo grade 3x3.
O “Procedimento Rolamento do Dado” tem como entrada um grafa grade G, um vetor de inteiros com um copia do caminho sobre o grafo grade G, e como sáida, apresenta um vetor de inteiros com as faces do dado que seriam impressas (marcadas) sobre o caminho no tabuleiro e o somatório das faces impressas.
O tabuleiro Hiker Dice é representado pelo grafo grade que segui um padrão de rotulação nos vértices igual a Figura 18 (b); nesse grafo grade, os vértices são rotulados crescentimente da esquerda para direita com valores inteiros a partir do vértice localizado no canto superior esquerdo do grafo grade G.
Supondo o caminho (0-1-4-6) apresentado na Figura 19 (a), e supondo também o dado localizado sobre o vértice 0 do grafo grade, e com a configuração inicial conhecida, na Figura 19 (b), teremos o seguinte movimento de rolamento do dado sobre o caminho:
No movimento para direita, o dado sempre se movimenta do vértice sobre a posição corrente para um vértice adjacente que é maior em uma unidade; no exemplo, na Figura 19 (a), o dado sobre o vértice 0 se movimenta para o vértice 1; após o movimento, o dado muda para a configura da Figura 19 (c);
No movimento para baixo, o dado sempre se movimenta do vértice sobre a posição corrente para um vértice adjacente que é maior em mais de uma unidade; no exemplo, na Figura 19 (a), o dado sobre o vértice 1 se movimenta para o vértice 4; após o movimento, o dado muda para a configura da Figura 19 (d);
unidade; no exemplo, na Figura 19 (a), o dado sobre o vértice 4 se movimenta para o vértice 3; após o movimento, o dado muda para a configura da Figura 19 (e);
No movimento para cima, o dado sempre se movimenta do vértice sobre a posição corrente para um vértice adjacente que é menor em mais de uma unidade.
Figura 19– Exemplo de movimento do Dado.
4.7 ATUALIZAR O VETOR DE SOLUÇÕES
O “Procedimento Atualizar o Vetor de Soluções” tem como entrada o vetor de soluções (v_solucao) e a nova solução construída (nova_s) e como saída, o vetor de soluções atualizado. O procedimento realiza uma das três regras para atualização:
1. Verificar se o vetor de soluções (v_solucao) está vazio; caso verdade, a nova solução (nova_s) é adicionada ao vetor e o procedimento finalizado; 2. Verificar se o valor objetivo da nova solução (nova_s) é igual aos valores
solução (nova_s) é adicionada ao vetor (v_solucao) e o procedimento finalizado;
5 ABORDAGEM EXATA
O algoritmo exato para o problema Hiker Dice é um Backtracking usando uma estrutura pilha. Cada elemento da pilha apresenta dois compartimentos para guardar informação do caminho em construção. A Figura 20 exemplifica um elemento da pilha. O primeiro, guarda um vértice referente ao caminho em construção no tabuleiro (parte em amarelo); o segundo, guarda uma lista referente às ramificações (vizinhos) do vértice escolhido (parte em azul).
Figura 20 - Elemento da estrutura pilha.
Passos do algoritmo:
1. Adicionar como primeiro elemento na pilha um vértice do grafo que represente o início do caminho na parte amarela e suas ramificações (vizinhos), na parte em azul. Depois, serão realizados os passos seguintes até a pilha ficar vazia;
2. Verificar se a pilha não está vazia para continuar o procedimento no passo 3. Se estiver, finalizar procedimento no passo 9;
3. Verificar se a lista do topo da pilha é maior que zero. Se for o caso, deve-se fazer o passo 4; caso contrário, o dedeve-sempilhamento (passo 8);
4. Selecionar um vértice presente na lista do topo da pilha; depois, marcá-lo como vizitado;
6. Se verdadeiro, o passo 5, adicionar como próximo elemento da pilha o vértice selecionado no passo 4 na parte amarela, e seus vizinho(s) na parte azul;
7. Verificar se a parte amarela da pilha já apresenta um caminho hamiltoniano no grafo. Em caso verdadeiro, construir uma solução com o rolamento do dado no caminho construído;
8. Desempilhar um elemento na pilha; depois, continua no passo 2; 9. Finalizar execução.
Supondo que o caminho comece na posição 0 (zero) do grafo da Figura 21 (a), tem-se, a parti desse vértice, as opções de ir para a posição 1 e 3. Então, adicionamos o primeiro elemento na pilha, o vértice 0 (zero) na parte amarela e os vértices 1 e 3 na parte em azul, como mostra a Figura 21 (b).
Em seguida, o algoritmo adiciona o segundo elemento. O algoritmo verifica se a lista do topo da pilha, como mostra a Figura 21 (b), não está vazia; se verdadeiro, o primeiro elemento da lista é selecionado, o vértice 1, e obedecendo à condição de viabilidade (ver seção 4) é adicionado na parte amarela da pilha e seus vizinhos, os vértices 2 e 4, serão adicionados na parte em azul, como mostra a Figura 21 (c).
O empilhamento na estrutura será realizado até o algoritmo não conseguir adicionar mais elementos na pilha, como mostra a Figura 21 (d), nesse momento a parte amarela da pilha define um Caminho Hamiltoniano. Como a lista do topo da pilha está vazia o algoritmo começa a fazer alguns desempilhamentos até encontrar o primeiro elemento na pilha cuja lista não seja vazia.
Na Figura 21 (e), os elementos da pilha selecionados em vermelhos são todos removidos no desempilhamento por terem listas vazias; depois, o empilhamento começa novamente ao encontrar um elemento na pilha cuja lista não seja vazia.
Figura 21– Grafo Grade 3 x 3 (a); Construção do caminho (b), (c), (d) e (e); Exemplo de Árvore de Estado (f).
O Algoritmo 1 tem como entrada um Grafo Grade G que representa o tabuleiro e como saída, apresenta uma ou mais de uma solução3. A linha 1 declara uma estrutura tipo pilha. A linha 2 define o primeiro vértice do grafo que será adicionado ao caminho, nesse caso o vértice 0 (zero). A linha 3 executa um procedimento para retornar a lista de vértices adjacentes ao vértice (v) (procedimento disponível na seção 4.3). A linha 4 adiciona na pilha o vértice (v) no primeiro compartimento e a lista com vértices adjacentes (lista_v), no segundo compartimento.
3 Uma solução é representada por dois vetores de inteiros, um para o caminho, outro para
As linhas de números 5 a 25 farão a busca de todas as soluções para o grafo que está sendo analisado. A linha 5 dará continuidade a busca das soluções se a pilha não estiver vazia. A linha 6, verificará a condição de empilhamento e desempilhamento. O empilhamento será feito entre as linhas 7 e 13; e o desempilhamento, entre as linhas 20 e 23.
Caso a condição de empilhamento seja verdadeira, a linha 7 executa a seleção do primeiro vértice na lista do topo da pilha. A linha 8 remove da lista do topo da pilha o vértice selecionado, impede a seleção de vértices repetidos em iterações futuras. A linha 9 verifica as condições de viabilidade do vértice selecionado (disponível na seção 4). A linha 10 retorna os vizinhos do vértice (v) e a linha 11, adiciona o próximo elemento na pilha. Na linha 12, o grafo é marcado com o procedimento (descrito na seção 4.4.1). Nas linhas 9, 12, 16 e 21, o procedimento (retorna_caminho( )) retorna um vetor de inteiros correspondente ao caminho definido pela parte amarela da pilha.
As linhas de números 14 a 18 farão a construção de uma solução. A linha 14 verifica se o tamanho da pilha é igual a quantidade vértices do grafo; caso verdade, a linha16 executa o procedimento (rolamento_dado(), disponível na seção 4.6) para construir uma solução com base no caminho. A linha 16 executa o procedimento (atualiza_solucoes(), disponível na seção 4.7) para atualizar o vetor de soluções.
Algoritmo 1– Algoritmo Exato. Exato_HikerDice ( )
Entrada: G(V, A)
Saída: v_solucao (vetor de soluções) 0 // Inicio
1 Pilha pilha 2 v ← 0
3 lista_v ← vertices_adjacentes (v, G) 4 pilha.add(0, lista_v)
5 Equanto(pilha ≠ ∅) faça
6 Se (pilha.topo.lista > 0) então 7 v ← pilha.topo.lista.ponto_frente 8 pilha.topo.ponto_frente_remove
9 Se (ponto_isolamento (v, retorna_caminho(pilha), G) == T e vertices_terminais(v, retorna_caminho(pilha), G) == T) 10 lista_v ← vertices_adjacentes (v, G);
11 pilha.add(v, lista_v)
12 marca_grafo1(G, retorna_caminho(pilha)) 13 Fim_se
14 Se (pilha.tamanho == |V(G)|) faça 15 Solucao nova_s
16 nova_s ← rolamento_dado(retorna_caminho(pilha)) 17 v_solucao ← atualizar_solucoes(v_solucao, nova_s) 18 Fim_se
19 Contrario
20 Se (pilha ≠ ∅)) faça
21 marca_grafo2(G, retorna_caminho(pilha)) 22 pilha.desempilhar_elemento
6 ABORDAGEM HEURÍSTICA
Na seção 6.1, serão apresentados os Algoritmos Heurísticos e na seção 6.2, os operadores propostos para o problema Hiker Dice.
6.1 ALGORITMOS ADAPTADOS COM OS OPERADORES PROPOSTOS
6.1.1 Busca Local
Um algoritmo de Busca Local define para cada solução uma vizinhança de soluções que apresentam características muito próximas da solução corrente. O algoritmo analisa na vizinhança a solução com melhor valor objetivo (para um problema de maximização ou minimização). Se tal solução vizinha for encontrada, torna-se a nova solução corrente.
Um algoritmo de Busca Local inicia com uma solução arbitrária e termina em um mínimo local, onde não é mais possível qualquer tipo de melhoria. Pode-se utilizar a Busca Local de melhor movimento, que substitui a solução corrente por uma solução que melhora o custo após a busca em toda a vizinhança; e a outra possibilidade é a busca local de primeira melhora, o qual aceita a primeira melhor solução (RUSSELLE; NORVIG, 2003).
O Algoritmo 2 (Buca_Local) tem como entrada uma solução inicial (S*), os parâmetros (N e T) para o operador de reestruturação e, como saída, a melhor solução (S) encontrada no decorrer das iterações.
A linha 2 declara uma variável boleana (melhoria_it) para definir a busca local com melhoria iterativa, enquanto tiver melhoria na vizinhança o algoritmo é executado.
As linhas de números 3 a 19 executam as iterações para encontrar melhoria na vizinhança.
linha 8 gera um vizinho usando o operador. A linha 9 adiciona o vizinho encontrado no vetor de vizinhos (V).
Algoritmo 2– Busca Local. Busca_Local()
Entrada:
S* (solução inicial);
N (número de vizinhos a serem gerados);
T (valor para definir o tamanho do intervalo de reestruturação). Saida: S (melhor solução encontrada).
1 //inicio
2 melhoria_it ← verdade
3 Enquanto (melhoria_it == verdade) faça 4 melhoria_it ← falso
5
6 V (vetor para soluções vizinhas) 7 Para (i ← 0 até N) faça
8 s_vizinha ← Operador.reestruturacao(S*,T ,G)
9 V.add (s_vizinha)
10 Fim_para
11
12 Para (i ← 0 até V.tamanho) faça
13 Se (S*.valor_objetivo < V[i].valor_objetivo) faça 14 S*← V[i]
15 melhoria_it ← verdade
16 Fim_se
17 Fim_para 18
19 Fim_enquanto
6.1.2 GRASP (Greedy Randomized Adaptive Search Procedure)
O GRASP consiste na execução de duas fases: primeiro cria uma solução inicial e depois efetua uma Busca Local para melhorar a qualidade da solução inicial. O diferencial deste algoritmo para outros está na geração da solução inicial, baseada nas três primeiras iniciais de sua sigla em inglês: gulosa (Greedy), aleatória (Randomized) e adaptativa (Adaptive).
A primeira fase do GRASP garante em cada iteração uma solução gerada de forma gulosa adaptativa e aleatória. Os passos da construção da solução inicial (RESEND; RIBEIRO, 2003):
1. Definir a lista de candidatos (LC) com todos os componentes para a formação da solução;
2. Definir a lista de candidatos restrita (LCR), com base nos melhores componentes da lista de candidatos (LC);
3. Selecionar na lista de candidatos restrita (LCR) algum componente que ainda não tenha sido atribuído à solução;
4. Se a solução não foi finalizada execute o passo 1; do contrário, execute o passo 5;
5. Fim de execução.
A segunda fase consiste em uma Busca Local (com finalidade de encontrar alguma melhoria), aplicada na solução inicial.
O Algoritmo 3 (GRASP) tem como entrada o número de iterações (It), os parâmetros (Alfa e Taxa_g) para o operador construtivo guloso aleatório, e como saída, a melhor solução (S) encontrada no decorrer das iterações.
As linhas de números 2 a 12 executam nas iterações as duas fases do GRASP para encontrar uma boa solução (S). A linha 3 define em cada iteração a solução (S*) construída pelo operador construtivo (Operador Construtivo Aleatório, disponível na seção 6.2.3).
Algoritmo 3 - GRASP adaptado com os operadores: Construtivo Guloso Aleátorio e Reestruturação. GRASP( )
Entrada:
It (número de iterações);
Alfa (define o tamanho da lista de candidatos restrita no operador construtivo guloso aleatório);
Taxa_g (tamanho do caminho constuido de forma gulosa no operador construtivo guloso aleatório).
Saida: S (melhor solução encontrada) 0 //inicio
1 iteração ← 1
2 Enquanto (iteração <= it) faça
3 S* ← Operador.contrucao_gulosa_aleatoria(alfa, taxa_g)
4
5 s_vizinha ← Busca_Local(S*, 5, 0.5) 6
7 Se (S.valor_objetivo < s_vizinha. valor_objetivo) faça
8 S ← s_vizinha
9 Fim_se
10
11 iteração ← iteração + 1 12 Fim_enquanto
6.1.3 Algoritmo Genético
Algoritmos Genéticos (AGs) são técnicas de otimização para encontrar soluções aproximativas, que usam princípios da biologia evolutiva, como: seleção natural, recombinação e, mutação (GOLDBERG, 1989).
Linden (2008, p. 57), resume o algoritmo genético através dos seguintes passos:
1. Inicializar a população de indivíduos; 2. Avaliar cada indivíduo na população;
4. Aplicar os operadores de recombinação e mutação aos pais selecionados com objetivo de gerar os indivíduos da nova geração;
5. Avalizar os novo indivíduos e inseri-los na população;
6. Se condição de parada é satisfeita, finalizar no passo 7. Contrario, volte para o passo 2.
7. Finalizar algoritmo.
O Algoritmo 4 (Genetico) tem como entrada uma população, um valor de probabilidade (P_r) para recombinação e, um valor probabilidade (P_m) para mutação e, como saída, a melhor solução (S) encontrada no decorrer das gerações.
A linha 1 executa o procedimento (melhor_individo()) para encontrar o melhor indivíduo da população. A linha 2 define uma variável (melhoria_it) para definir o genético com melhoria iterativa, se o algoritmo genético não tiver melhoria numa janela de 100 gerações, o algoritmo para a executado. As linhas de números 4 a 36 serão executadas enquanto a condição de melhoria for válida. As linhas 5 e 6 executam o procedimento (selecao_roleta()) para selecionar dois pais.
A linha 8 sorteia uma probabilidade para recombinação. Caso verdade, a condição na linha 9, o algoritmo executará os procedimentos para reprodução. As linhas 10 e 11 executam o procedimento (recombinacao(), disponível na seção 6.2.2) com objetivo de construir os filhos, a ordem dos pais passados como entrada no procedimento influencia a primeira parte do material genético na solução filha.
A linha 13 sorteia a probabilidade de mutação. Caso verdade, a linha 14, os procedimentos para mutação são aplicados em cada filho. As linhas 15 e 16 executam o procedimento (reestruturacao(), disponível na seção 6.2.1) equivalente a uma mutação.
Algoritmo 4– Genético adaptado com os operadores: Recombinação e Reestruturação. Genetico ()
Entrada:
Populacao (população criada a partir de alguma regra); P_r (probabilidade de recombinação);
P_m (probalidade de mutação).
Saida: S (melhor solução encontrada). 0 //inicio
1 S ← melhor_individo (populacao) 2 melhoria_it ← verdade
3 contador ← 1
4 Enquanto (melhoria_it == verdade) faça 5 pai_1 ← selecao_roleta (populacao) 6 pai_2 ← selecao_roleta (populacao)
7
8 sorteio_r ← [0, 1]
9 Se (sorteio_r < P_r) faça
10 filho_1 ← Operador.recombinacao(pai_1, pai_2, G) 11 filho_2 ← Operador.recombinacao(pai_2, pai_1, G)
12
13 sorteio_m ← [0, 1]
14 Se (sorteio_m < P_m) faça
15 filho_1 ← Operador.reestruturacao (filho_1, 0.5, G) 16 filho_2 ← Operador.reestruturacao (filho_2, 0.5, G) 17 Fim_se
Continuação
21 Se (filho_1. valor_objetivo > S.valor_objetivo) faça 22 S ← filho_1
23 contador ← 0 24 Fim_se
25
26 Se (filho_2. valor_objetivo > S.valor_objetivo) faça 27 S ← filho_2
28 contador ← 0
29 Fim_se
30
31 atualizar_populacao (populacao, filho_1, filho_2, pai_1, pai_2)
32
33 contador ← contador +1 34 Se (contador == 100) faça 35 melhoria_it ← falso
36 Fim_se
37 Fim_enquanto
A linha 31 executa o procedimento (atualizar_populacao()) para atualizar a população através de um torneio entre os indivíduos filhos e pais passados como entrada. Na primeira regra, se os filhos gerados forem melhores que seus pais, a população substitui os pais por seus filhos. Na segunda regra, caso um filho seja melhor que algum pai, a população substitui esse pai por esse filho. Na terceira regra, caso nenhum filho não seja melhor do que nenhum pai, a população substitui o pior pai pelo melhor filho com objetivo de garantir alguma diversidade.
6.2 OPERADORES
6.2.1 Procedimento Reestruturação
O operador de reestruturação funciona trabalhando com uma solução. Gera uma nova solução a partir do intervalo de reestruturação definido por dois pontos extremos no caminho da solução inicial. Como exemplo de reestruturação é considerado, na Figura 22, uma solução construída a partir da posição inicial 0 (zero) do grafo grade 4x4.
Figura 22 – Grafo grade 4x4 e solução inicial (S*).
Primeiro, o tamanho do intervalor de restruturação e o vértice extremo inicial são definidos para selecionar o intervalo de reestruturação no caminho da solução inicial (S*). No exemplo, na Figura 22 (b), supondo o tamanho do intervalo de reestruturação com 60% dos vértices do caminho e o extremo inicial (vértice 0); logo, temos o seguinte intervalo de reestruturação (0-1-2-6-10-9-5-4-8).
Figura 23 – Relação de adjacência do intervalo de reestruturação no grafo grade 4x4.
Terceiro, uma Busca em Profundidade é realizada a partir do extremo inicial 0 (zero) do grafo grade 4x4, na Figura 23 (b), com finalidade de construir um novo intervalo que terá os mesmos vértices extremos (inicial e final) e o mesmo tamanho do intervalo de reestruturação. No exemplo, o intervalo de reestruturação (0-1-2-6-10-9-5-4-8) pode ser modificado para o novo intervalo (0-4-5-1-2-6-10-9-8).
Por último, o novo intervalo (0-4-5-1-2-6-10-9-8) substitui o intervalo de reestruturação (0-1-2-6-10-9-5-4-8) no caminho da solução inicial (S*); desta forma, a solução, Figura 24, é construída.
Figura 24 – Solução reestruturada.
O Procedimento 1 (reestruturacao ()) tem como entrada uma solução inicial (S*), um grafo grade G (matriz de adjacência), uma variável numérica (T) que define um valor porcentual para o tamanho do intervalo de reestruturação (assume valor máximo de 0,5); como saída, uma nova solução (Sr).
(indice_inicial_maximo) guarda um valor correspondente ao índice máximo para o extremo inicial no caminho da solução (S*).
Na linha 3, a variável numérica (in_extremo_inicial) armazena o índice com o extremo inicial para o intervalo de reestruturação. Na linha 4, a variável numérica (in_extremo_final) armazena o índice com o extremo final para o intervalo de reestruturação.
Na linha 6, o procedimento (modificar_intervalo()) faz a reestruturação de um novo intervalo. A linha 8 verifica o novo intervalo (novo_intervalo) diferente de vazio; caso verdadeiro, o novo intervalo (novo_intervalo) é substituído pelo intervalo de reestruturação no caminho da solução (S*).
Na linha 9, o procedimento (novo_caminho()) substitui no caminho da solução (S*) o novo intervalo (novo_intervalo). A linha 10 executa o procedimento (rolamento_dado(), disponível na seção 4.6) para fazer o rolamento do dado sobre o caminho (n_caminho). E, na linha 13, a nova solução (Sr) é retornada.
Procedimento 1 - Reestruturação reestruturacao ()
Entrada: S* (Solução inicial), T (define o tamanho do intervalo de reestruturação), G (grafo grade)
Saída: Sr (Solução reestruturada) // Inicio
1 tamanho_intervalo ← S*.caminho_tamanho * T
2 indice_inicial_maximo ← S*.caminho_tamanho – tamanho_intervalo
3 in_extremo_inicial ← [0, indice_inicial_maximo]
4 in_extremo_final ← in_extremo_inicial + tamanho_intervalo 5
6 novo_intervalo ← modificar_intervalo (in_extremo_inicial, in_extremo_final, S*, G)
7
8 Se(novo_intervalo ≠ ∅)faça
9 n_caminho ← novo_caminho(novo_intervalo, S*.caminho, in_extremo_inicial,
in_extremo_final)
10 rolamento_dado(n_caminho, Sr) 11 Fim_se
12
O Procedimento 2 (modificar_intervalo ()) tem como entrada as variáveis numéricas (in_inicial e in_final) para definir o intervalo de reestruturação no caminho da solução inicial (S*), um grafo grade G (matriz de adjacência) e como saída, um vetor de inteiros (intervalo_r) com o novo intervalo reestruturado.
Na linha 1, o procedimento (marca_caminho_no_grafo ()) marca o caminho da solução (S*) no grafo grade G, as arestas entre os vértices do caminho da solução inicial (S*) terão marcação igual a -1 (menos um) e as demais arestas terão marcação igual a 0 (zero).
Na linha 3, o vetor de inteiros (intervalo_r) é declarado para definir o intervalo a ser reestruturado. Nas linhas de números 4 a 6, o vetor (intervalo_r) armazena os vértices entre os índices (in_inicial e in_final) no caminho da solução inicial (S*).
Na linha 8, o procedimento (marca_intervalo_no_grafo ()) marca o vetor de inteiros (intervalo_r) no grafo grade G; nessa marcação, as arestas entre os vértices do intervalo (intervalo_r) terão marcação igual a (1).
A linha 10 define a estrutura (Pilha) definida na seção 6. Na linha 11, a variável numérica (v) armazena o primeiro vértice do vetor de inteiros (intervalo_r). Na linha 12, a lista (lista_v) é declarada para armazenar os vértices adjacentes do vértice (v), com procedimento disponível na seção 4.3. Na linha 13, o primeiro elemento da pilha é adicionada com o vértice (v) e seus vértices adjacentes (lista_v). Na linha 15, a variável numérica (K) é declarada para guardar um valor igual à quantidade de vértices do grafo grade G, esse valor controla o limite máximo de execução do laço na linha 17.
Nas linhas de números 18 a 26, o empilhamento é executado até a lista do topo da pilha ficar vazia. Na linha 19, a variável numérica (v) guarda o vértice da lista do topo da pilha que apresenta o maior grau no grafo grade G. Na linha 20, o vértice de maior grau selecionado será removido da lista do topo da pilha para evitar ser selecionado em iterações futuras.
e; na linha 24, o procedimento (marca_grafo1(), disponível na seção 4.4.1) marca o vértice (v) no grafo grade G.
Procedimento 2– Modificar Intervalo modificar_intervalo ()
Entrada: in_inicial (índice do extremo inicial), in_final (índice do extremo final), S* (solução inicial), G (Grafo)
Saída: novo_intervalo (vetor de inteiros) // Inicio
1 marca_caminho_no_grafo(S*.caminho, G) 2
3 intervalo_r
4 Para(i ← in_inicial; i <= in_final; i++) faça
5 intervalo_r.add(S*.caminho[i]) 6 Fim_para
8 marca_intervalo_no_grafo(intervalo_r, G) 9
10 Pilha pilha
11 v ← intervalo_r.primeiro
12 lista_v ← pega_vizinhos(v, G)
13 pilha.add(v, lista_v)
15 K ← |G(V)|
16
17 Para (j ← 0 até K ) faça
18 Enquanto( pilha.topo.lista ≠ Ø ) faça 19 v ← vertice_maior_grau(pilha.topo.lista)
20 pilha.topo.lista.remove(v)
21 Se (ponto_isolamento(v, retorna_caminho(pilha)) == T) faça 22 lista_v ← pega_vizinhos(v, G)
23 pilha.add(v, lista_v)
24 marca_grafo1(G, retorna_caminho(pilha))
25 Fim_se
26 Fim_enquanto 27
28 Se(pilha.tamanho == intervalo_r.tamanho) faça 29 Se(teste_intervalo(pilha) == verdadeiro) faça 30 novo_intervalo ← retorna_caminho(pilha)
31 j ← K
32 Fim_se
33 Contrario Se (pilha == Ø) faça
34 j ← K
35 Fim_se 36
38 marca_grafo2(G, retorna_caminho(pilha)) 39 pilha.desempilha
40 Fim_enquanto 41 Fim_para
42 Retornar novo_intervalo
As linhas de números 28 a 35 verificam as condições de saída do laço mais externo. A linha 28 verifica o tamanho da pilha igual à quantidade de vértices do vetor (intervalo_r); caso verdadeiro, o procedimento (teste_intervalo()) verifica o caminho definido pela pilha diferente do caminho (intervalo_r) e, os vértices extremos do caminho na pilha iguais aos vértices extremos do caminho no vetor (intervalo_r); se verdadeiro, o vetor (novo_intervalo) armazenar o intervalo reestruturado definido pela pilha, e na linha 31, a variável numérica (j) é atualizada com valor máximo para sair do laço.
A linha 33 verifica a pilha vazia; se verdadeiro, a variável (j) armazena um valor máximo para sair do laço.
6.2.2 Procedimento Recombinação
O operador de recombinação funciona trabalhando com duas soluções. A “nova solução” é gerada através de um ponto de recombinação entre os caminhos das duas soluções envolventes.
Para um exemplo de recombinação são consideradas três soluções Hiker Dice construídas sobre o tabuleiro 4x4, como mostram as Figura 25 (a), (b) e (c). Os caminhos das soluções Hiker Dice, na Figura 25 (a) e (b), são usadas para gerar o caminho da “nova solução” na Figura 25 (c).
Figura 25– Exemplo Recombinação.
Inicialmente, define-se a “solução dominante”, essa solução apresenta o primeiro material genético para o caminho da “nova solução”. No exemplo, supondo a solução, ver Figura 25 (a), como dominante; logo, o caminho ( 0-1-2-3-7-6-5-4-8-9-10-11-15-14-13-12) disponibilizará a primeira parte genética.
na “solução dominante”; logo, o caminho da “nova solução” terá os vértices 0-1-2-3-7-6-5-4.
Terceiro, seleciona-se o último vértice no caminho da “nova solução” ( 0-1-2-3-7-6-5-4). No exemplo, o vértice (4) é selecionado para ponto de recombinação entre os caminhos das soluções envolventes.
Quarto, verifica-se a viabilidade do ponto de recombinação selecionado (vértice 4) com duas condições: na primeira condição, por exemplo, o sucessor do ponto de recombinação no caminho da “solução não-dominante” (vértice 8) não pode estar presente no caminho da “nova solução” (0-1-2-3-7-6-5-4), logo, a primeira condição é verdadeira; na segunda condição, o sucessor do ponto de recombinação no caminho da “solução não-dominante” (vértice 8) não pode ser “ponto de isolamento”, quando unido ao caminho da “nova solução” (0-1-2-3-7-6-5-4), como mostra a Figura 26, o grafo grade após ser marcado pelo caminho ainda permite a construção do caminho hamiltoniano, sendo assim, a segunda condição também é verdadeira.
Figura 26 – Novo caminho no grafo grade 4x4.