Controle preditivo bilinear aplicado a um motor de indução

Universidade Federal do Rio Grande do Norte

Centro de Tecnologia

Programa de Pós-Graduação em Engenharia Elétrica

Controle Preditivo Bilinear Aplicado a Um

Motor de Indução.

Adjair Ferreira Barros Filho

Prof. Dr. Andrés Ortiz Salazar

Orientador

Prof. Dr. André Laurindo Maitelli

Co-Orientador

Natal-RN

Adjair Ferreira Barros Filho

Controle Preditivo Bilinear Aplicado a um

Motor de Indução.

D i s s e r t a ç ã o a p r e s e n t a d a c o m o r e q u i s i t o p a r c i a l o b t e n ç ã o d o g r a u d e M e s t r e e m C i ê n c i a s d e E n g e n h a r i a E l é t r i c a .

C u r s o d e P ó s - G r a d u a ç ã o e m E n g e n h a r i a E l é t r i c a , C e n t r o d e T e c n o l o g i a , U n i v e r s i d a d e F e d e r a l d o R i o G r a n d e d o N o r t e .

O r i e n t a d o r : P r o f . D r . A n d r é s O r t i z S a l a z a r C o - O r i e n t a d o r : P r o f . D r . A n d r é L a u r i n d o M a i t e l l i

Natal-RN

Divisão de Serviços Técnicos

Catalogação da Publicação na Fonte. UFRN / Biblioteca Central Zila Mamede

Barros Filho, Adjair Ferreira.

Controle preditivo bilinear aplicado a um motor de indução / Adjair Ferreira Barros Filho. – Natal, RN, 2003.

114 p.

Orientador : Andrés Ortiz Salazar. Co-orientadora : André Laurindo Maitelli.

Dissertação(Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Tecnologia. Programa de Pós-Graduação em Engenharia Elétrica.

1. Motor de indução - Tese. 2. Controle preditivo bilinear - Tese. 3. Modelos matemáticos - Tese. I. Salazar, Andrés Ortiz. II. Maitelli, André Laurindo. III. Título.

Controle Preditivo Bilinear Aplicado a um Motor

de Indução Trifásico

Adjair Ferreira Barros Filho

Dissertação apresentada à coordenação do Curso de Pós-Graduação

em Engenharia Elétrica da Universidade Federal do Rio Grande do

Norte como requisito parcial à obtenção do grau de Mestre em

Ciências de Engenharia Elétrica.

Aprovada por:

Prof. Dr. Andrés Ortiz Salazar- UFRN

Prof. Dr. André Laurindo Maitelli – UFRN

Prof. Dr. Pablo Javier Alrima – UFRN

Prof. Dr. Adhemar de Barros Fontes – UFBA

À minha esposa, Solange

Aos meus filhos, Hallysson, Jessyka e Vitor

Aos meus pais

Agradecimentos

Aos professores Andrés Ortiz, André Maitelli e Adhemar de Barros pela

dedicação, amizade e orientação neste trabalho.

Aos meus familiares e amigos pelo incentivo.

À UFRN, CNPQ e CEFET-RN pelo apoio financeiro.

Aos colegas professores da Gerência de Indústria do CEFET-RN.

E aos professores, alunos e funcionários do departamento de Pós- Graduação

em Engenharia Elétrica da UFRN pelo apoio e amizade, especialmente a Fábio

Soares, Felipe, João Maria, Fabiano, Ewerton e Paulo Sérgio pelo apoio técnico.

SUMÁRIO

Agradecimentos v

Sumário vi

Lista de símbolos e abreviaturas ix

Lista de figuras xi

Resumo xiii

Abstract xiv

CAPÍTULO I – INTRODUÇÃO

CAPÍTULO II – CONTROLADORES PREDITIVOS

2.1 Introdução ao controle preditivo 06

2.2 Conceito 07

2.3 Modelos monovariáveis de entrada e saída 10

2.3.1 Modelos paramétricos: 11

2.3.1.1 Modelo ARX 12

2.3.1.2 Modelo ARIX 12

2.3.1.3 Modelo ARMAX 12

2.3.1.4 Modelo ARIMAX 13

2.4 Preditores: caso monovariável 13

2.4.1 Introdução 13

2.4.2 Preditores i-passos à frente para o modelo ARX 14

2.4.4 Preditor i-passos à frente para o modelo geral 18

2.4.5 Preditores i-passos à frente de sistemas com retardo 20

2.5 Funções objetivo e seu reflexo na propriedade do controlador 22

2.5.1Função objetivo de passo único 22

2.5.2 Função objetivo multi-passo 29

2.6 Controlador Preditivo Generalizado 30

2.6.1Introdução 30

2.6.2 Formulação do Controlador Preditivo Generalizado 31

2.7 Conclusões 39

3.1 Introdução 40

3.2 Modelo Bilinear 42

3.3 Uma Retrospectiva dos Controladores Preditivos Bilineares 43

3.4 Controlador Preditivo Bilinear Generalizado 46

3.4.1 Aproximação quasilinear por degrau de tempo 46

3.4.2 Controlador Preditivo Bilinear Generalizado 48

3.5 Modelo Monovariável quasilinear por degrau de tempo compensado 51

3.5.1Propriedade do termo de compensação 55

3.5.2 Estrutura do termo de compensação 56

3.6 Controlador Preditivo Bilinear Generalizado Compensado 56

3.7 Conclusões 62

CAPÍTULO IV– MODELAGEM DO MOTOR DE INDUÇÃO E

IDENTIFICAÇÃO DOS MODELOS MATEMÁTICOS PARA OS

CONTROLADORES PREDITIVOS E O (PI) 63

4.1 Introdução 63

4.2 Modelagem do Motor de Indução Trifásico 63

4.3 Modelo Vetorial com Orientação dada pelo campo do Rotor 64

4.4 Controle Vetorial Orientado pelo Campo do Rotor 65

_{4.5 Identificação dos Modelos Matemáticos 66}

_{4.5.1 Modelo linear Clássico (PI) 67}

4.5.2 Modelos Preditivos 70

_{4.6 Conclusões 71}

CAPÍTULO V–

DESCRIÇÃO DA BANCADA DE TESTES

5.1 _{Introdução 72}

5.2 Circuito de Comando e Força 72

5.3 Configuração do Inversor de freqüência 73

5.4 Software Utilizado 75

5.4.1 Descrição do software 75

5.4.2 Instrumentos Virtuais 76

5.4.3 Interface homem-máquina 76

5.5 Instrumentação para o controle e supervisão do motor 78

5.5.1 Processamento 78

5.5.2 Diagrama Funcional da Bancada 78

CAPÍTULO VI – RESULTADOS PRÁTICOS

6.1 Introdução 80

6.2 Resultados 80

6.3 Conclusões 86

CAPÍTULO VII – CONCLUSÕES GERAIS DO TRABALHO

7.1 Introdução 87

7.2 Sugestões para a continuidade dessa linha de pesquisa 89

APÊNDICE

A

APÊNDICE

B

APÊNDICE

C

Símbolos e Abreviaturas

Controle Preditivo

ARX: Auto-regressivo com sinal exógeno;

ARIX: Auto-regressivo Integral com sinal exógeno;

ARMAX: Auto-regressivo, Média Móvel, com sinal Exógeno;

ARMAX: Auto-regressivo, Média Móvel, com sinal Exógeno;

ARIMAX: Auto-regressivo, Integral, Média Móvel, com sinal Exógeno;

CPBG: Controlador Preditivo Bilinear Generalizado;

QLDT_{: Quase Linear Por Degrau de Tempo;}

d: retardo do sistema;

DMC: Dynamic matrix control;

FIR: Finite Impulse Response;

FSR: Finite Step Response;

GMV: Generalised Minima Variance;

GPC: Generalised Predictive Control;

GRG: Gradiente reduzido generalizado;

LGR: Lugar Geométrico das Raízes;

LQ: Linear quadrático;

LQC: Linear quadratic control;

MPC: Model Predictive Control;

MAC: Model Algorithm Control;

Max(a,b): Máximo entre n_a e n_b;

MPHC: Controle Preditivo Baseado em Modelo Heurístico;

NARMAX: Não linear, Auto-regressivo, Média Móvel, com sinal Exógeno;

NARIMAX:Não linear, Auto-regressivo, Integral, Média Móvel, com sinal Exógeno;

NU: Horizonte de controle;

NY: Horizonte de predição;

N1 : Horizonte mínimo de predição;

Kp: Constante de erro de posição;

PQS: Programação quadrática sucessiva;

SBPR: Sinal Binário Pseudo Randômico;

SISO: Single input single output;

λ: Fator de ponderação do controle;

+

ˆ( )

y k i : Predição i-passos à frente da saída baseada em informações disponíveis

até o instante k;

Motor de Indução

Is1, is2, is3 Correntes instantâneas nos enrolamentos do estator;

Ir1, ir2, ir3 Correntes Instantâneas nos enrolamentos do rotor;

Rs, Rr Resistências dos enrolamentos de estator e rotor, respectivamente;

Ls, Le Indutâncias próprias dos enrolamentos de estator e rotor,

respectivamente;

ωs Velocidade angular síncrona;

ω Velocidade do motor;

ψx, ψr Vetores fluxo do estator e fluxo do rotor, respectivamente;

FIGURAS

Figura n.º 2.1- Conceito de Horizonte preditivo...07

Figura n.º 2.2- Estrutura básica do MPC...09

Figura n.º 2.3-Analogia do MPC...10

Figura n.º 2.4-Diagrama de Blocos do Modelo do Processo......11

Figura n.º 2.5-Diagrama de Blocos do Sistema em Malha Fechada...23

Figura n.º 2.6-Diagrama de Blocos do Sistema em Malha Fechada...27

Figura n.º 2.7-Diagrama de blocos do modelo do processo...32

Figura n.º 2.8-Diagrama de blocos do sistema em malha fachada...38

Figura n.º 3.1- Diagrama representando o Termo de Compensação...53

Figura n.º 4.1- Modelo inverso da Máquina de Indução utilizada para Controle Vetorial...64

Figura n.º 4.2- Controle Vetorial Indireto da Máquina de Indução...65

Figura n.º 4.3- Comparação entre três diferentes sintonias para o controlador PI...67

Figura n.º 4.4- Comparação entre a média ponto a ponto e um único teste...68

Figura n.º 5.1- Circuito de Comando e Força...72

Figura n.º 5.3- Diagrama de Blocos da Bancada...74

Figura n.º 5.4- Tela de apresentação da interface homem-máquina, em labview, da bancada de testes...76

Figura n.º 5.5- Diagrama funcional da bancada de testes...77

Figura n.º 6.1- Resposta para uma Variação de +5% no valor do set-pointe...80

Figura n.º 6.2- Sinal de controle para uma variação de +5% do set-point...81

Figura n.º 6.3- Resposta para uma variação de +10% da carga...82

Figura n.º 6.4- Sinal de controle para uma variação de +10% da carga...83

Figura n.º 6.5- Resposta para uma variação de –10% da carga...84

Resumo

Controladores Preditivos Bilineares aplicado a um Motor de

Indução.

O presente trabalho baseia-se na aplicação da técnica de controle preditivo

bilinear em um motor de indução. O controle preditivo bilinear, caso particular do

controle preditivo não linear, têm despertado grande interesse, uma vez que

apresenta a vantagem de ser mais simples que o não linear em geral e mais

representativo que o linear. Um dos métodos, aqui adotado, utiliza o modelo

“quase linear por degrau de tempo” baseado no Controlador Preditivo

Generalizado. A modelagem do motor de indução é feita através do controle

Vetorial com orientação dada pelo campo do rotor indireto. O sistema é formado

por um motor de indução de 3 HP com rotor em gaiola de esquilo, acionado por

uma bancada de testes desenvolvida para esse trabalho. Foram obtidos

resultados para uma variação de +5% no valor do set-point e resultados para uma

variação de +10% e –10% no valor da carga nominal aplicada ao motor. Os

resultados comprovam uma boa eficiência dos controladores preditivos bilineares,

Abstract

Bilinear Predictive Controllers applied in an induction

motor drive

Capítulo I

Introdução

1.1 Motivação

Os motores de Indução vêm gradativamente ocupando o espaço que era

destinado aos motores de corrente contínua (CC) na aplicação em acionamentos

de alto desempenho [ Leonhard, 1996].

Entre as vantagens em relação à máquina CC, destacam-se a robustez,

baixo custo, menor freqüência de manutenção e, no caso de um motor com rotor

em gaiola de esquilo, a ausência de contatos deslizantes. Por não possuir

escovas, o que diminui a possibilidade de faiscamento, os motores de indução,

mais especificamente os de rotor tipo gaiola de esquilo, podem ser usados em

ambientes com um certo grau de risco a incêndios e explosões. No entanto, na

máquina CC o controle de velocidade se dá de uma forma bastante simples, uma

vez que o torque e o fluxo podem ser impostos à máquina de uma forma

desacoplada , ou seja, estabelecido o fluxo, o conjugado pode ser controlado

através da corrente de armadura. Desta forma os motores de CC eram os mais

preferidos em acionamentos de alto desempenho.

Na década de 70, porém, Blashcke propôs a técnica de controle vetorial,

baseada na orientação dada pelo campo do rotor, aplicada a motores de indução

[Blashcke, 1972]. A grande novidade foi à escolha do fluxo do rotor como

referência do eixo d, o que tornou possível projetar um sistema de controle

desacoplado semelhante ao da máquina de CC, quando o motor é alimentado por

Com o avanço da eletrônica de potência, mais precisamente na década de

80, e do surgimento de microprocessadores cada vez mais rápidos e de menor

custo, foi possível a implementação do controle vetorial orientado pelo campo. Na

realidade, a alimentação do motor por fontes de correntes só pode ser feita com a

utilização de um inversor de fonte de tensão (VSI) modulado por largura de pulso

(PWM) e controlado por corrente. Esse fato tornou o acionamento de alto

desempenho dos motores de indução cada vez mais competitivo com o da

máquina de CC. De fato, com o controle vetorial o motor de indução, por ter uma

menor inércia de rotor, alcança a velocidade desejada mais rapidamente obtendo

assim, um melhor desempenho transitório.

Dentre as técnicas de controle de velocidade do motor de indução, foi

escolhida para o presente trabalho, uma abordagem de controle preditivo baseado

em modelos bilineares, que é um caso particular da técnica de controle preditivo

baseado em modelos não-lineares. Devido à estrutura não-linear dos motores de

indução, a modelagem se torna mais complexa, de forma que sua simplificação

para um modelo linear requer algumas aproximações e restrições. Desta forma,

um modelo linear para representação de processos não-lineares tem uma

deficiência destacada, tendo em vista que modelos simples são freqüentemente

inadequados, e uma aproximação mais realista é necessária, [Doyle III, et al.

(1995)]. O controlador preditivo não linear, que utiliza um modelo não linear, mais

realista é freqüentemente mais complexo, sacrifica a simplicidade associada as

técnicas lineares de forma a alcançar um melhor desempenho. No entanto,

embora não exista argumentação, no conceito básico do MPC, contra a utilização

de um modelo não-linear, o seu desenvolvimento não é simples e existem

algumas questões em aberto, [Camacho & Bordons (1999)], tais como:

.a complexidade computacional para resolver o algoritmo de controle

preditivo baseado em modelos não lineares- CPNL;

.a falta de resultados teóricos no que se refere a robustez, para o sistemas

não lineares.

Como caso particular da técnica de controle preditivo baseado em sistemas

não lineares, aqueles baseados em modelos bilineares, técnica de controle

abordada no presente trabalho, tem despertado grande interesse uma vez que:

.embora pertençam a uma classe de sistemas bilineares, estes apresentam

a vantagem de ser mais simples que o não linear em geral e mais representativos

que o linear;

.a bilinearidade está presente em vários sistemas físicos e químicos,

inclusive no motor de indução;

.o modelo bilinear, utilizado pelo controlador, é linear nos parâmetros, fato

que permite a utilização do algoritmo dos mínimos quadrados recursivo na

estimação destes, ou ainda, pode-se utilizar quase a totalidade das técnicas de

identificação desenvolvidas para sistemas lineares;

Esta técnica foi desenvolvida e implementada em colunas de destilação de

tolueno por [Fontes A. B., Duarte. A. A] e teve grande êxito na implementação do

controle preditivo bilinear Compensado. Ainda, a técnica referenciada será

implementada no motor de indução trifásico, tendo em vista o comportamento não

linear, sendo, em especial, o modelo bilinear uma forma natural de representação

deste, segundo [Figalli (1984)].

Para a implementação do controle, foi montada uma bancada de testes que

é composta por um inversor (WEG), um motor de indução de 3 HP, um gerador

1.2 Objetivos do trabalho

O presente trabalho tem como objetivos principais:

- _{Aplicar controladores preditivos bilineares a um motor de indução trifásico;}

- _{Implementar o controlador preditivo GPC bilinear compensado, analisando}

seu desempenho em ralação aos modelos linear clássico (PI), preditivo

linear e o GPC bilinear aplicados a um motor de indução trifásico.

- _{Implementar uma bancada de testes, capaz de se adequar a aplicação de}

diversos controladores que venham a ser desenvolvidos em outros

trabalhos de dissertação ou de final de curso.

1.3 Apresentação da Dissertação

A dissertação foi organizada segundo a ordem descrita logo a seguir:

. no capítulo 2 é mostrado um histórico referente ao controle preditivo de

uma forma geral, são abordado de forma sucinta os modelos e preditores

referentes ao controle preditivo e por fim o controlador preditivo generalizado

(GPC).

. no capítulo 3 será introduzido um estudo sobre o controlador preditivo

bilinear. Onde serão abordados os principais algoritmos existentes e a estratégia

de controle.

. no capítulo 4 será feita a modelagem matemática do motor de indução,

que utiliza as variáveis referidas ao estator ou rotor da máquina. Em seguida, será

mostrado o modelo matemático do motor de indução que usa uma abordagem

vetorial utilizando o fluxo no rotor como referência para as variáveis do modelo.

Será apresentado também o controle vetorial que consegue simplificar o modelo

do motor de indução. E por último, serão apresentados os modelos matemáticos

dos controladores PI, preditivo linear, GPC bilinear com aproximação quase linear

por degrau de tempo e GPC bilinear compensado aproximação quase linear por

. No capítulo 5 será feita uma descrição da bancada de testes, onde serão

abordados o acionamento, funcionamento, interfaces, software e problemas

ocorridos durante a implementação da bancada.

. No capítulo 6 será feita uma análise dos resultados obtidos na prática,

fazendo uma comparação entre os controladores em termos de Tempo de

Resposta e o Esforço do Controle, quando submetidos a variações no valor do

set-point e na carga acoplada ao eixo do motor.

. No capítulo 7 são apresentadas as conclusões do trabalho e as

CAPÍTULO II

CONTROLADORES PREDITIVOS

2.1 Introdução ao Controle Preditivo

Controle preditivo, nome dado à maneira pela qual a lei de controle é

calculada, refere-se a uma classe de algoritmos que calcula uma seqüência de

ajustes no sinal de controle de forma a otimizar o comportamento futuro da saída

de uma planta. Originalmente desenvolvida para atender a necessidade de

controle especializado de refinarias de petróleo, esta técnica de controle recebeu

bastante destaque na última década. Obteve grande aceitabilidade no ambiente

industrial, com uma grande variedade de aplicação em várias áreas, incluindo

indústria química, processamento de alimentos, automotiva, aeroespacial,

metalúrgica e de papel. Isto porque, os controladores preditivos têm-se mostrado

bastantes eficazes no controle de plantas monovariáveis e multivariáveis, com

retardo, de fase não mínima e instáveis, fato que caracteriza a maioria dos

processos industriais, os quais têm seus próprios critérios de desempenho e

exigência de confiabilidade. Diferentemente das técnicas de controle usuais, os

controladores preditivos baseiam-se na predição do comportamento futuro da

saída(s) do processo a ser controlado. Esta predição, por sua vez, é obtida

através de um modelo do processo, o qual supõe-se disponível. Utilizam-se então,

os valores futuros preditos da(s) saída(s) para calcular a ação de controle. Além

do mais, em contraste com outros métodos, os controladores preditivos têm-se

2.2 Conceito

O controle preditivo é uma técnica de controle, discreta no tempo, que faz

uso de um modelo explícito do processo, para calcular uma seqüência de controle

futura, tal que leve a saída predita a seguir uma dada trajetória de referência. Esse

conceito pode ser ilustrado para o caso SISO, através da Figura 2.1.

Figura 2.1 – Conceito de Horizonte Preditivo

As variáveis u(k), y(k) e r(k) representam os valores no instante atual k da

variável manipulada ou sinal de controle, da variável controlada ou saída do

processo e do sinal de referência, respectivamente. Os valores futuros dessas

variáveis são definidos pelos seguintes vetores:

[

]

[

[

]

= +

= + +

= + +

L

L

L

( ) ( 1)

ˆ ˆ( 1) ˆ( )

( 1) ( )

T

T

T

u u k u k NU

y y k y k NY

r r k r k NY

]

−

)

(2.1)

Em que:

representa o valor estimado de y(k) i-passos à frente;

+

ˆ( y k i

NY = Horizonte de predição;

NU = Horizonte de controle.

O comportamento futuro do processo é calculado dentro do horizonte de

predição NY, usando um modelo previamente determinado e validado do processo

e levando em consideração as NU ações de controle a serem fornecidas ao

As ações de controle são calculadas de forma que a saída predita obtenha

determinadas características desejadas em relação ao sinal de referência

utilizado, características estas, mensuradas através de um determinado índice de

desempenho. O sinal de referência, também conhecido como “trajetória de

referência”, pode ser considerado tanto um valor constante, como uma trajetória

filtrada por um modelo de referência, normalmente de primeira ou de segunda

ordem. O primeiro elemento da seqüência de controle obtida é aplicada ao

processo, sendo desconsiderados os demais. No instante de amostragem

seguinte, todo o procedimento é repetido, utilizando as informações medidas mais

recentes. Esta metodologia é conhecida como “Princípio do Horizonte Móvel”,

(Receding Horizont) e foi proposta por Propoi em 1963.

Com a finalidade de se quantificar a qualidade de rastreamento da saída

predita do processo em relação à trajetória de referência, utiliza-se uma “Função

Objetivo”. Esta função, normalmente, relaciona as variáveis y, u e r. Um exemplo

simples de função objetivo é:

[

]

= =

=

∑

1 1

ˆ( ) ( ) . (

NY NU

j N i

J y k j r k j

∑

Em que:

N1 = Horizonte mínimo de predição;

NU e NY são como já definidos em 2.1.

A minimização dessa função em relação a u gera a seqüência de ações de

controle num determinado horizonte de predição. Nesse sentido, a seqüência

encontrada é ótima com relação a função objetivo que é minimizada num

determinado instante. Dessa forma, os valores futuros da diferença entre y e r são

minimizados e, portanto, quando o modelo do processo disponível o representa

fielmente, e quando o sistema não está sujeito a distúrbios, nem restrições, a

saída do processo acompanhará a “trajetória de referência”, nos instantes de

amostragem, exatamente conforme previsto. Caso contrário, haverá um erro,

A estrutura básica capaz de implementar a estratégia de Controle Preditivo,

conforme descrito, é mostrada na figura 2.2 a seguir. Nesta, o modelo é utilizado

para predizer os valores futuros das saídas da planta, baseado em valores

presentes e passados e ainda nas futuras ações de controle ótimas propostas.

Estas ações são calculadas por um otimizador, tendo em vista uma função

objetivo, que considera o erro de rastreamento futuro, como também as

restrições.

Figura 2.2 – Estrutura básica do MPC

Se o processo em questão tiver tempo morto associado, o procedimento a

ser utilizado deve ser o mesmo, exceto que o limite inferior do somatório da função

objetivo deve ser mudado. Se este for um múltiplo do período de amostragem,

então os limites passarão a ser de i = td / T até NY.

Um outro aspecto a ser observado é que o cálculo da seqüência de ações de

controle é um problema de otimização ou, mais especificamente, um problema de

minimização. Usualmente, a solução deste requer um procedimento iterativo, que,

no entanto, será evitado quando o critério é quadrático, o modelo é linear e não

existem restrições. Neste caso, existe uma solução analítica. Deve-se observar,

no entanto, que a função objetivo ideal necessitaria ser baseada em

especificações de projeto, tais como: “tempo de estabilização”; “overshoot“; “tempo de subida”; “margem de ganho”; etc. Neste contexto, o problema de

otimização resultante seria de difícil solução. Esta é, portanto, a razão pela qual

função quadrática. Com isso as especificações de projeto devem ser transladadas

para os parâmetros da função objetivo quadrática, de forma que quando esta é

minimizada, as especificações acima mencionadas, sejam atendidas.

Pode-se observar ainda que a “Estratégia de Controle Preditivo” é muito

similar à utilizada no processo de dirigir um carro, conforme ilustração

apresentada em (Camacho & Bordons, 1999), mostrada na figura a seguir. Neste,

o motorista conhece a trajetória de referência desejada para um horizonte de

controle finito e considerando as características do carro, o que corresponde a um

modelo mental, decide que ações de controle executar, tais como: acelerar,

atrasar e mudar a direção, de forma a seguir uma trajetória desejada. Somente a

primeira ação de controle é executada em cada instante e o procedimento é

novamente repetido para a decisão da nova ação de controle nos mesmos moldes

do horizonte móvel.

Figura 2.3 – Analogia do MPC (Segundo Camacho & Bordons)

2.3 Modelos monovariáveis de entrada e saída

Existem diversas famílias de modelos matemáticos que podem ser utilizadas

para representar matematicamente o comportamento dinâmico de um processo,

dentre eles encontram-se modelos de entrada-saída paramétricos e

não-paramétricos mono e multivariáveis, os modelos via espaço de estados, etc.

(Goodwin e Sin, 1984). No caso em estudo, será enfocado, neste capítulo, os

modelos monovariáveis de entrada e saída. No capítulo IV, será apresentado o

caso multivariável, que é uma extensão dos modelos monovariáveis a seguir

2.3.1 Modelos paramétricos:

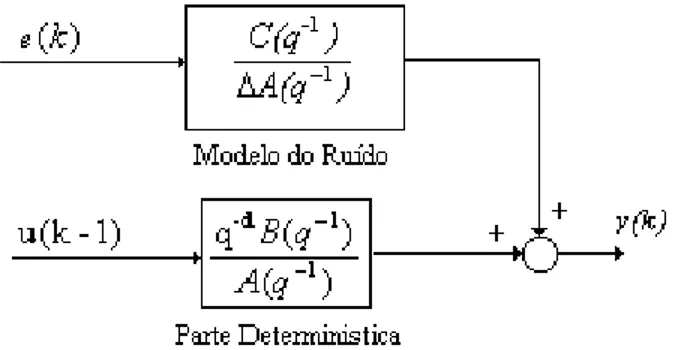
Os modelos lineares paramétricos, de uma forma geral, podem ser

representados através da expressão:

− − −

− −

= (₁ 1) − + ₁( 1)

( ) ( 1) ( )

( ) ( ) ( )

d

q B q C q

y k u k e k

A q D q A q−1

−

−

b nc

(2.3)

[-parte determinística-] [-modelo do ruído-]

Em que: - q-1 representa o operador atraso unitário;

- y(k) é a saída do processo;

- d é o retardo, em múltiplos do período de amostragem (d ≥ 0);

- u(k) é a saída do controlador;

- e(k) é um ruído “branco” e gaussiano, com média zero e variância σ2.

Os polinômios A(q-1), B(q-1), C(q-1) e D(q-1), são dados por:

−

− −

− −

− − −

= + + + +

= + + + +

= + + + +

= + + + +

1 1 2 1 2

1 1 2

0 1 2

1 1 1

1 2

1 1 1

1 2

) 1

1

) 1

- - -na

na

- n

nb

-

-nc nd nd

A(q a q a q . . . a q B(q ) b b q b q . . . b q C(q ) c q c q . . . c q D(q d q d q . . . d q

(2.4)

Em que: na, nb, nc e ndsão os graus dos polinômios A(q-1), B(q-1), C(q-1) e

D(q-1), respectivamente.

Em termos de diagrama de blocos, tem-se que:

2.3.1.1 Modelo auto-regressivo com sinal exógeno (ARX).

Neste caso, tem-se que: na=n ; nb≤n , nc = nd =0. Com isso, o modelo resultante é:

− −

−

= ₁ 1 − +1 1

d

-q B(-q )

y(k) u(k ) e(k) A(q ) A(q )1

+

=1

(2.5)

ou ainda,

−1 ₌ − −1 ₋

1

d

A(q ) y(k) q B(q ) u(k ) e(k) (2.6)

2.3.1.2 Modelo Auto regressivo Integral com sinal exógeno (ARIX)

Neste caso tem-se: . Isto resulta no seguinte

modelo:

= =0

na n, nb < n, nc e nd

− −

− −

= ₁ 1 − + ₁

1

1 1

1

d

q B(q )

y(k) u(k ) e(k)

A(q ) ( + d q ) A(q )−1 (2.7)

Fazendo d1= -1, o polinômio D(q -1) corresponde à introdução da ação

integral no controlador, o qual elimina o erro de regime ao degrau. Neste caso,

D(q-1) é normalmente representado por ∆. Com isso tem-se que:

− −

−

= − +

∆

1

1 1

1 1

d

-q B(-q )

y(k) u(k ) e(k)

A(q ) A(q ) (2.8)

ou ainda,

−1 _{∆ =} − −1 _{∆ +}

1

d

A(q ) y(k) q B(q ) u(k - ) e(k) (2.9)

2.3.1.3 Modelo Auto-regressivo, Média Móvel, com sinal Exógeno (ARMAX ou

CARMA).

− −

− −

= ₁ 1 1 + 1₁

d

-q B(-q ) C(q ) y(k) u(k - ) e(k)

A(q ) A(q ) (2.10)

ou ainda,

−1 -d −1 _{1 +}

A(q )y(k) = q B(q )u(k - ) C(q )e(k−1 ) (2.11)

2.3.1.4 Modelo Auto-regressivo, Integral, Média Móvel com sinal Exógeno

(ARIMAX ou CARIMA).

Neste caso, tem-se que: na=n ; nb≤n, nc >0e nd = 1

∆

, que corresponde a

. Com isso, tem-se que: −1 ₌ 1₌

1

-D(q ) - q

− −

−

= − +

∆

1 1

1 1 1

d

-q B(-q ) C(q ) y(k) u(k ) e(k)

A(q ) A(q ) (2.12)

ou ainda,

−1 _∆ −1 _{∆ − +}

1

-d

-A(q ) y(k) = q B(q ) u(k ) C(q )e(k1 ) (2.13)

2.4 Preditores: caso monovariável

2.4.1 Introdução:

Em controle preditivo, para o cálculo das ações futuras de controle, é

necessário que se faça uma predição da saída, isto é, da variável controlada. Para

tanto, utiliza-se um modelo pré-definido do processo a ser controlado. Este modelo

permite predizer a saída em t=k+i, usando as informações passadas, conhecidas,

das ações de controle e/ou saídas do processo, e as saídas futuras do controlador

a serem calculadas. Os algoritmos que efetuam esse cálculo são denominados

A predição, baseada num modelo dinâmico refere-se a previsão da saída

com um determinado instante de tempo maior que o instante de tempo atual, a

partir de informação disponíveis até o instante k.

2.4.2 Preditores i-passos à frente para o modelo ARX –Diophantine

Considere o modelo ARX, descrito anteriormente, isto é:

−1 ₌ −1 _{− +}

1

A(q )y(k) B(q )u(k ) e(k) (2.14) A saída y(k) i-passos à frente, obtida a partir desta equação é dada por:

−

− −

+ = B(q )1₁ + − +1 1 ₁ +

y(k i) u(k i ) e(k i)

A(q ) A(q ) (2.15)

Observa-se nesta equação que y(k +i) depende de valores passados e/ou futuros das variáveis envolvidas, isto é: y, u e e. Por outro lado, sabe-se que a

melhor estimativa de y(k+i), isto é y(kˆ +i), satisfaz a condição a seguir:

ε

+ = + − 2

ˆ min [

r

y (k i) { y (k i) r] } (2.16) cuja solução é

{

}

ε

+ = +

ˆ( ) (

y k i y k i) (2.17)

Este estimador é conhecido como estimador de Bayer ou “estimador de risco

quadrático mínimo”. Assim, quando e(k) é um ruído “branco”, gaussiano, de média

zero, a melhor estimativa de y(k+i), é o seu valor determinístico. Então, com o

objetivo de separar a dependência de y(k+i), das informações passadas e futuras,

introduz-se as seguintes identidades polinomiais, conhecidas como equação

diofantina:

− − −

− = +

1 1

1

1 i i

i

G (q ) F (q ) q

A(q ) A(q )−1 , (2.18)

−

− −

−

= +

= + +L +

1 1

1 1

1 1

0 1 1

1

. - -(i - ) i

- -(n- )

i n

F (q ) f q + . . . + f q G (q ) g g q g q

1 1 i

(2.19)

Deve-se observar que:

1) o grau de Fi(q-1) é i-1 e o de Gi(q-1) é n-1;

2) a solução desta equação é apresentada no Apêndice A, e pode ser

obtida usando uma divisão polinomial ou através de relações recursivas

entre soluções sucessivas

Assim, utilizando a equação 2.18, tem-se que:

− − − −   + = _ + +   1 1 1 1 1

- i i i

B(q ) G (q )

y(k i) u (k + i - ) + F (q ) q e k i

A(q ) A(q )−1  ( ) (2.20)

Que pode ser rescrita na forma:

−

− −

+ = 1 1 + 1

1 1 1

-- i

i

B(q ) G (q )

y(k i) u(k + i - ) + F (q )e(k + i) e(k)

A(q ) A(q ) (2.21)

Da equação (2.14), tem-se que:

−

= 1 − -1_{) 1}

e(k) A(q )y(k) B(q u(k− ) (2.22)

Então substituindo em (2.20), resulta em:

(

)

− −

− −

− −

+ = 1 + − + 1 + + 1 1 − −

1 1 1 1

i i

B(q ) G (q )

y(k i) u(k i ) F(q )e(k i) A(q )y(k) B(q )u(k )

A(q ) A(q )

−1

(2.23)

Que pode ser reescrita da forma:

− − − − − −   + = _ − _ + − +   1 1 1 1 1 1 1 i -i i G(q )

y(k i) B(q ) q u(k i ) F (q )e(k + i) + G (q )y(k) A(q ) A(q )

1 _(2.24)

Tendo em vista a que:

− − − − = 1 1 1 1 1 )

-i i -i

G (q )

q F

A(q ) A(q ) (q (2.25)

− −

+ = 1 1 + − +₁ -1 + + 1 ₎

i i i

y(k i) B(q )F (q )u(k i ) F (q )e(k i) G (q )y(k- (2.26) Por outro lado como:

−1 _{= +} −1₊ −2_{+ +} 0 1 2

-nb nb

B(q ) b b q b q . . . b q e −1 = +1 ₁ −1+ + ₋₁ - i−

i i

F (q ) f q . . . f q( 1)

−1) nb i 1 + − 1 nb i + − 1 nb i

− −1)

− −1)

−1

)

1 então,

α α α

− − − − +

+ −

= + + +

1 1 1

0 1 1

(nb i i

B(q )F (q ) q . . . q , · (2.27)

ou seja, é um polinômio de grau (nb+i-1), o qual pode ser rescrito na

forma:

−1 −

i

B(q )F (q )

α α α α α α

− − − − − − − − − −

− + +

= + + + + + +L +

1 1 1 1) 1

0 1 1 1 1

(i i i i nb

i i i i

B(q )F (q ) q . . . q q q q

Ou ainda:

α α α α α α

− − − − − − − −

− + +

= + + + + + +L +

1 1 1 1) 1

0 1 1 ( 1 1 )

(i i nb

i i i i

B(q )F (q ) q . . . q q q q

Definindo agora

α − α α − α

−

= + + +

1 1

0 1 1 (i i

(q ) q . . . q (2.28)

β − α α − α

+ + −

= + + +

1 1

1 1

(nb i i nb i

(q ) q . . . q (2.29) tem-se que:

α β

−1 −1 ₌ −1 ₊ −i i

B(q )F (q ) (q ) q (q ) (2.30) Substituindo esta equação na equação 2.26 do preditor, resulta em:

α − −β − −

+ = 1 + 1 + − + 1 + + 1

[ i ( ] 1 _{i i}

-y(k i) (q ) q q ) u(k i ) F (q )e(k i) G (q )y(k) (2.31) Que pode ser rescrita na forma:

β − α −

+ = 1 −₁ -1_{) ( )}+ 1 + ₁ + -1 +

i i

y(k i) (q )u(k ) + G (q y k (q )u(k i - ) F (q )e(k i (2.32) Tendo em vista os graus dos polinômios β(q-1), Gi(q-1), α(q-1) e Fi(q-1), tem-se

então que:

β − α α α

+ +

− = − + − + + +

1

1 1

1 _i 1 _i 2 _{n b i}

-(q )u (k ) u (k ) u(k ) . . . u (k - nb )

( )

que

)

n

α ₁ ( )

1

) −

−

− +L + − +

1

0 1 ( 1) 1 ( 1 i

G (q )y(k) = g y(k) + g y k g y k n , que corresponde a valores de y até o instante k, portanto valores também disponíveis;

α − α α

−

+ − = + − + + − + L +

1

0 1

1 1) 2 _i

(q )u (k i ) u (k i u (k i ) u k que contém valores de u, do instante k até o instante (k+i-1), portanto, não

disponíveis. Estes valores correspondem a valores futuros de u(k);

−

−

+ = + + + − +L + +

1

1

) ( 1 1

i i

F (q )e(k i e k i) f e(k i ) f e(k ), que contém somente valores futuros de e(k).

Desta análise, pode-se escrever a equação do preditor, separando futuro e

passado, na forma:

β − − α −

+ = 1 − + 1 + 1 + + 1 +

1 _i 1 _i

-y(k i) (q )u(k ) G (q )y(k) (q )u(k i - ) F (q )e(k i (2.33) [...passado...] [...futuro...]

Observando-se a equação anterior, verifica-se que e(k) aparece somente

com valores futuros. Tendo em vista, o que já foi mencionado anteriormente, o

estimador de risco quadrático mínimo, isto é, o valor estimado de y(k+i) é

{

}

ε

+ = +

ˆ( ) (

y k i y k i) . Sendo assim, o preditor i-passos à frente de mínima

variância é dado por:

{

}

ε β − α − −

+ = 1 − + 1 + 1 + − + 1 +

ˆ - 1 1

i i

y(k i) (q )u(k ) G (q )y(k) (q )u(k i ) F (q )e(k i) (2.34) ou ainda,

{

}

ε β − α − ε −

+ = 1 − + 1 + 1 + − + 1 +

ˆ - 1 1 {

i i

y(k i) (q )u(k ) G (q )y(k) (q )u(k i ) F (q )e(k i)} (2.35)

Como,

{

}

{

}

{

}

{

}

ε − ε ε ε

−

+ = + + + − +L + +

1

1 1 1

i i

F (q )e(k i) e(k i) f e(k i ) f e(k 1 (2.36) )

e ainda, tenho em vista que e(k) é por hipótese um ruído “branco”, gaussiano, de

média zero, isto é:

}

{

então,

β − − α −

+ = 1 − + 1 + 1 + −

ˆ( ) ( ) ( 1) _i( ) ( ) ( ) (

y k i q u k G q y k q u k i 1) (2.38)

2.4.3 Preditor i-passos à frente para o modelo geral.

Considerando agora o modelo geral:

− −

− −

= ( 1₁) − + ₁( 1)

( ) ( 1) ( )

( ) ( ) ( )

B q C q

y k u k e k

A q D q A q−1 (2.39)

A saída y k( ) i-passos à frente é dada por:

− −

− − −

+ = ( 1₁) + − + ₁( 1) ₁ +

( ) ( 1) (

( ) ( ) ( )

B q C q

y k i u k i e k i

A q D q A q ) (2.40)

Utilizando a identidade polinomial:

− −

− −

− − = + − −

1 1

1

1 1 1

( ) ( )

( )

( ) ( ) ( ) ( )

i i i

C q G q

F q q

D q A q D q A q 1 (2.41)

sendo grau_{{ (} −1_)}= i-1 e grau

i

F q _{{ (} −1_)}=_max( − _, + −₁₎

i c a

G q n i n n_d . Substituindo na equação anterior, tem-se que:

− − − − − −  + = + − +_ + +   1 1 1 1 1 ( ) ( )

( ) ( 1) ( ) (

( ) ( ) ( )

i i i

B q G q

y k i u k i F q q e k i

A q D q A q−

 

1 ) (2.42)

Ou ainda,

− −

−

− − −

+ = 1 + − + 1 + 1 +

1 1 1

( ) ( )

( ) ( 1) ( ) ( ) (

( ) ( ) ( )

i

i

B q G q

y k i u k i e k F q e k i

A q D q A q )

)

(2.43)

Da equação (2.39) tem-se que:

A q( −1) (D q−1) ( )y k =B q( −1) (D q−1) (u k− +1) C q( −1) (e k (2.44) tal que:

− − − −

− −

= ( 1) (₁ 1) − ( 1) (₁ 1)

( ) ( ) ( 1)

( ) ( )

A q D q B q D q

e k y k u k

Substituindo na equação (2.43), resulta em: − − − − − − − − − − − −   + = + − + _ − − _   + +

1 1 1 1 1

1 1 1 1 1

1

( ) ( ) ( ) ( ) ( ) ( )

( ) ( 1) ( ) ( 1)

( ) ( ) ( ) ( ) ( )

( ) ( )

i

i

B q G q A q D q B q D q

y k i u k i y k u k

A q D q A q C q C q

F q e k i

1 (2.46) Ou ainda, − − − − − − − − + = + − − − + + + +

1 1 1

1 1 1

1

( ) ( ) ( ) ( )

( ) ( 1) ( 1) ( )

( ) ( ) ( ) ( )

( ) ( )

i i

i

B q G q B q G q

y k i u k i u k y k

A q A q C q C q

F q e k i

−1 1

(2.47)

Esta equação pode ser reescrita na forma:

− − − − − − − − − − − − −   + = _ − _ + − +  + + +

1 1 1 1

1 1 1 1 1

1

1 1

( ) ( ) ( ) ( )

( ) ( 1)

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) i i i i

B q D q C q G q

y k i q u k i

C q D q A q A q D q G q

y k F q e k i C q

 _(2.48)

Tendo em vista a equação (2.41), tem-se que:

− − − −

−

− −

+ = 1 1 1 + − + 1 + 1 +

1 1

( ) ( ) ( ) ( )

( ) ( 1) ( ) ( ) (

( ) ( )

i i

i

B q D q F q G q

y k i u k i y k F q e k i

C q C q ) (2.49)

Utilizando-se agora a seguinte identidade polinomial:

− − − −

− −

− = +

1 1 1

1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) i i i

B q D q F q I q H q q

C q C q−

1 1 i

) ) 1

(2.50)

em que e são polinômios de graus i-1 e max ( , ,

respectivamente, e substituindo-se em (2.49), tem-se que: −1

(

i

H q I q_i( −1 n_b+n n_{d c})−

− −

− −

− −

+ = 1 − + 1 + 1 + − + +

1 1

( ) ( )

( ) ( 1) ( ) ( ) ( 1) ( ) (

( ) ( )

i i

i i

I q G q

y k i u k y k H q u k i F q e k i

C q C q

1

) (2.51)

− −

−

− −

+ = 1 − + 1 + 1 + −

1 1

( ) ( )

ˆ( ) ( 1) ( ) ( ) (

( ) ( )

i i

i

I q G q

y k i u k y k H q u k i

C q C q 1)

)

(2.52)

2.4.4 Preditores i-passos à frente de sistemas com retardo

Em um sistema com um retardo de dinstantes de amostragem, uma entrada

u(k), gerado em t tem efeito na saída y somente a partir do instante . Então, na estratégia de controle preditivo, a seqüência de controle

deve ser calculada de forma que a saída predita do

processo alcance a trajetória desejada definida por

. Desta forma, utilizando preditores i-passos à frente, na

presença de retardo, será efetuada a predição

=k −1) d L ( 1 + ( NY

= + +1

t k d L

( ), , (

u k u k

+ + L

( 1

r k d

+NY −

+ +

ˆ y k d

), ,r k

+

ˆ

) y k( NY

)

+

ˆ( )

y k i como função de

, com i d , sendo o “horizonte de predição”. Isto

significa que na existência de retardo o horizonte de predição deve satisfazer:

. Considere, então, o sistema descrito por:

+ − u k i d

≥ +1

NY d

−

( 1) = +1,L ,NY NY

−1 ₌ − −1 ₋

( ) ( ) d ( ) ( 1) (

A q y k q B q u k +e k) (2.53) Então:

− −

− −

+ = d B(q )1₁ + − +1 1 ₁

y(k i) q u(k i ) e(k + i

A(q ) A(q ) ) (2.54)

Ou ainda,

−

−

+ = B(q )1₁ + − − +1 1

y(k i) u(k i d ) e(k + i

A(q ) A(q )−1 ) (2.55)

com i ≥ +d 1

Utilizando a identidade polinomial

− − − − = + 1 1 1 1 ( ) ( ) ( ) i i i G q F q q

A q A q−1 ( )

em queF q₍ −1 e G q são polinômios de graus (i-1) e (n-1), respectivamente.

i ) )

−1 ( i Tem-se que: − − − − −   + = + − − +_ + +   1 1 1 1 ( ) ( )

( ) ( 1) ( ) (

( ) ( )

i i i

B q G q

y k i u k i d F q q e k i

A q A q−1  ) (2.57)

Ou ainda,

− −

−

− −

+ = 1 + − − + 1 + 1 +

1 1

( ) ( )

( ) ( 1) ( ) ( ) (

( ) ( )

i

i

B q G q

y k i u k i d e k F q e k i

A q A q )

− )

(2.58)

Como

− − −

= 1 − 1

( ) ( ) ( ) d ( ) ( 1

e k A q y k q B q u k (2.59) então: − − − − − − − + = + − − − − − + + + +

1 1 1

1

1 1

1

( ) ( ) ( )

( ) ( 1) ( 1) ( ) ( )

( ) ( )

( ) ( )

i

i

i

B q B q G q

y k i u k i d u k d G q y k

A q A q

F q e k i

(2.60) ou ainda, − − − − − − −   + = _ − _ + − − + +   + + 1 1 1 1 1 1

1 ( )

( ) ( ) ( 1) ( ) ( )

( ) ( ) ( ) ( ) i i i i G q

y k i B q q u k i d G q y k

A q A q F q e k i

(2.61)

Tendo em vista a identidade polinomial (2.56), tem-se que:

− − − −

+ = 1 1 + − − + 1 + 1 +

( ) ( ) (_i ) ( 1) _i( ) ( ) _i( ) (

y k i B q F q u k i d G q y k F q e k i)

)

(2.62)

ou ainda,

− − − − −

+ = 1 1 − + 1 + 1 +

( ) i d ( ) (_i ) ( 1) _i( ) ( ) _i( ) (

y k i q B q F q u k G q y k F q e k i (2.63) Lembrando que ( −1) ( −1)=α₀ +α₁ −1+L +α _{+ −1} −(nb i

i

B q F q q q + −1)

nb i

)

β −1

)

, então

refere-se somente a valores passados de u(k). Portanto,

quando i d y(k+i) dependerá também de valores futuros de u . Fazendo: −1 −1 ₋

( ) (_i ) ( 1

B q F q u k ≥ +1,

α

−1 −1 ₌ −1 ₊ − −( )

( ) (_i ) ( ) i d (

tem-se que:

α

β

 

+ =_ 1 + ( ) 1 _ + − − + 1 + 1 +

( ) ( ) i d ( ) ( 1) _i( ) ( ) _i( ) (

y k i q q q u k i d G q y k F q e k i)

)

1)

)

1 1)

(2.65)

ou ainda,

β − − α − −

+ = 1 − + 1 + 1 + − − + 1 +

( ) ( ) ( 1) _i( ) ( ) ( ) ( 1) _i( ) (

y k i q u k G q y k q u k i d F q e k i (2.66)

E o preditor i-passos à frente, de mínima variância é:

β − − α −

+ = 1 − + 1 + 1 + − −

ˆ ( ) ( ) ( 1) _i( ) ( ) ( ) (

y k i q u k G q y k q u k i d (2.67)

Neste caso, a análise do erro de predição é dado por:

−

∈₍ + =_{) (} + −_{) ˆ(} + =_{) (} 1_{) (} +

i

k i y k i y k i F q e k i (2.68) Ou ainda,

−

∈(k + =i) e k( + +i) f e k₁ ( + − +i 1) L +f e k_i ( + (2.69)

Se e(k) é um ruído “branco”, com

ε

{

}

e variância unitária, então a variância do erro de predição é dada por:

Var{ (∈ k+i) }2 = +1 f₁2+f₂2+L +f_i−2₁ (2.71) Esta equação mostra que a variância do erro de predição aumenta à medida

que o horizonte de predição cresce.

2.5 Funções Objetivo e seu reflexo na propriedade do controlador

Em controle preditivo, a minimização de uma “Função Objetivo” produz uma

lei de controle preditiva, a qual é caracterizada pela escolha dessa função.

2.5.1 Função Objetivo de Passo Único:

2.5.1-a – Função objetivo baseada no erro de rastreamento

Neste caso, trata-se de uma função objetivo simples que considera somente

[

]

= + − + 2

ˆ( 1) ( 1)

J y k r k (2.72) Nesta função, somente uma previsão é usada, que é y(kˆ +1). Por isto, esta é

denominada de “Função Objetivo de Passo Único”. Para mostrar que tipo de

controlador é obtido quando a função objetivo, acima definida, é utilizada,

considere o modelo ARX, cujo preditor 1-passo à frente é dado por:

β − α −

+ = 1 − + 1 +

1

ˆ( 1) ( ) ( 1) ( ) ( ) ( ) (

y k q u k q u k G q−1 y k)

1 ₎

−1

1)

(2.73)

Ou ainda,

− −

+ = 1 +

1

ˆ( 1) ( ) ( ) ( ) (

y k a q u k G q y k (2.74) com:

(2.75)

α β

−1 ₌ −1 ₊ −1

( ) ( ) ( )

a q q q q

Das condições de otimalidade, ou seja derivando (2.72) com respeito a u,

após substituição de (2.74) e igualando a zero, conclui-se que a função objetivo é

minimizada quando y(kˆ + =1) r k( + . Isto produz a seguinte lei de controle:

−

−

+ −

= 1 1

1

( 1) ( ) ( ( )

( ) r k G q y k u k

a q

)

(2.76)

Deve-se observar que é necessário o conhecimento antecipado da trajetória

de referência a ser seguida. Desta lei de controle pode-se chegar ao seguinte

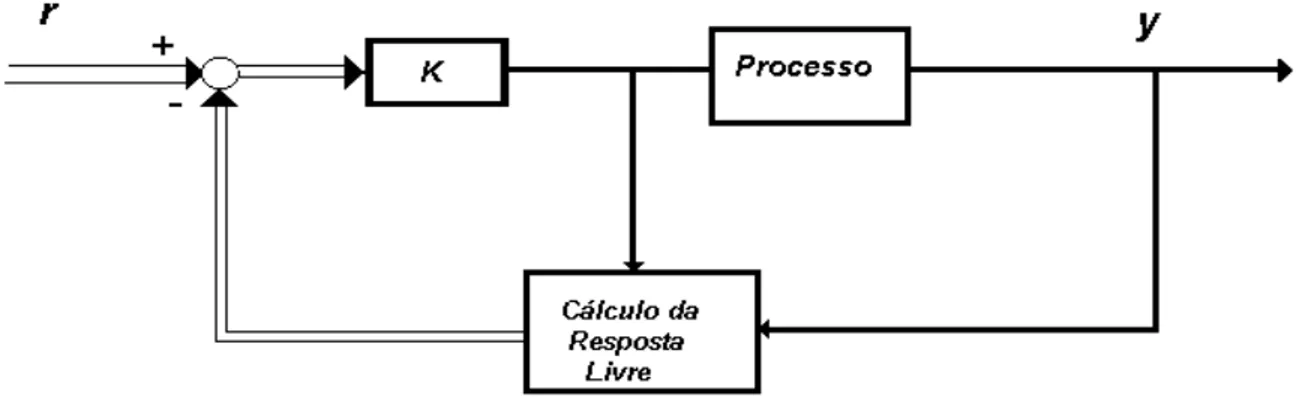
sistema em malha fechada:

A análise da malha fechada mostra que: − − − − − − − − − − − − − − − = + + + + 1 1

1 1 1

1 1 1 1 1 1

1 1

1 1 1 1

( ) 1

( ) ( ) ( )

( ) ( 1) ( )

( ) ( ) ( ) ( )

1 1

( ) ( ) ( ) ( )

q B q

a q A q A q

y k r k e k

q B q G q q B q G q

a q A q a q A q

(2.77) Ou ainda, − − − − − − − − − − − − − = + + + + 1 1

1 1 1 1 1 1 1

1 1 1 1 1 1

( )

( ) ( 1)

( ) ( ) ( ) ( )

( )

( )

( ) ( ) ( ) ( )

q B q

y k r k

a q A q q B q G q a q

e k a q A q q B q G q

+

(2.78)

Da equação do modelo, tem-se que:

−

− −

+ = ( 1₁) + 1 ₁ +

( 1) ( ) ( 1

( ) ( )

B q

y k u k e k

A q A q ) (2.79)

Tendo em vista a identidade polinomial 2.56, tem-se que:

− −

− −

+ = 1 + 1 + + 1 1

1 1

( ) ( )

( 1) ( ) ( ) ( 1) (

( ) ( )

B q G q

y k u k F q e k e k

A q A q−1 ) (2.80)

Tendo em vista agora que _{e k( )}= _{A q(} −1_{) ( )y k} −_{B q(} −1_{) (u k} −_{1), então:}

−

− − − −

−  

+ = 1 _ − 1 1 _ + 1 + 1 +

1 1 1

1

( )

( 1) 1 ( ) ( ) ( ) ( ) ( ) ( 1 ( )

B q

y k q G q u k G q y k F q e k

A q ) (2.81)

Com isso tem-se que:

−

− − −

−  

+ = 1 _ − 1 1 _ + 1

1 1

1

( )

ˆ( 1) 1 ( ) ( ) ( ) (

( ) B q

y k q G q u k G q y k

A q ) (2.82)

e ainda:

−

− −

− 

= 1 _ −

1 1

1 1

( )

( ) 1 ( )

( ) B q

a q q G q

A q

−



1 _(2.83)

−

− − − − − − −

−  −  +

1

1 1 1 1 1 1

1 1

1

( )

1 ( ) ( ) ( ) ( ) (

( ) B q

q G q A q q B q G q B q

A q =

1

) (2.84)

Substituindo esse resultado na equação da saída do sistema em malha

fechada, tem-se que:

− − −

−

− −

−

= 1 + + 1 1 1 1

1 1

( ) [1 ( )]

( ) ( 1) ( )

( ) ( )

B q q G q

y k q r k e k

A q B q (2.85)

Ou ainda, − − − − −   = + +_ − _   1 1 1 1 1 1

1 ( )

( ) ( 1) ( )

( ) ( ) q G q

y k q r k e k

A q A q (2.86)

Que também pode ser escrita na forma,

−

= 1 + +

1

( ) ( 1) ( ) ( )

y k q r k F q−1e k

)

(2.87)

Deste resultado pode-se concluir que:

1. a lei de controle obtida da minimização da função objetivo de passo único,

impõe a colocação dos pólos em malha fechada exatamente nos zeros da

função de transferência do processo, isto é: raízes de . Com isto,

pode-se concluir que para processos de fase não mínima ou com zeros

próximos ao circulo unitário, esta lei de controle é inviável; −1

(

B q

2. na ausência de ruído, a equação (2.87) mostra que a saída do processo

rastreia a referência desejada em um tempo mínimo, que neste caso é o

período de amostragem. Neste sentido, o controlador é idêntico ao

controlador dead-beat e, portanto, a saída deste, isto é u(k), geralmente apresenta valores elevados.

2.5.1-b Função objetivo baseada no erro de rastreamento e na ponderação

do sinal de controle.

Neste caso, a função objetivo é da forma:

[

]

= + − + 2+ ₂

ˆ( 1) ( 1) ( )

E assim, uma condição necessária de otimalidade que pode ser usada na

obtenção da lei de controle é:

[

]

∂ ∂ _ρ

∂ ∂  +  =_ + − + + =   ˆ( 1) ˆ

2 ( 1) ( 1) 2 ( ) 0

( )

J y k

y r k u k

u u k  (2.89)

o que implica em:

∂

ρ ∂

+ = −1 ˆ + − + ˆ

( ) [ ( 1) ( 1)]

( )

y k u k y k r k

u k ( 1) ) (2.90) Como: − −

+ = 1 + 1

1

ˆ( 1) ( ) ( ) ( ) (

y k a q u k G q y k (2.91) então, ∂ ∂ + ₌ 0 ˆ( 1) ( ) y k b

u k (2.92)

uma vez que ∂

∂ =

( ) 0 ( )

y k

u k e que , conforme as equações (2.28)

e (2.81).

−1 −1 ₌ 1

B(q )F (q ) a(q )−1

Isto resulta em:

ρ

= − + − + 0

1 ˆ

( ) [ ( 1) ( 1)]

u k y k r k b (2.93)

Ou ainda,

ρ − −

= − _ 1 + 1 − +

1

1

( ) ( ) ( ) ( ) ( ) ( 1)

u k a q u k G q y k r k b₀ (2.94)

Reescrevendo esta equação, tem-se que :

ρ − ρ

  _{+ =  + −}      1 0 1 1

1 b a q( ) u k( ) r k( 1) G q₁( −1) ( )y k b₀ (2.95)

ρ ρ − − = + − + + 1

0 0 1

1

0 0

( )

( ) ( 1) ( )

( ) ( )

b b G q

u k r k y k

b a q b a q−1 (2.96)

Chega-se assim ao seguinte diagrama de blocos:

Figura 2.6 – Diagrama de Blocos do Sistema em Malha fechada

Do diagrama de blocos e substituindo a expressão de a −1

q

( ) obtém-se:

ρ ρ ρ − − − − − + = + + + + 1 1 1 1 1 1 ( )

( ) ( 1) ( )

( ) ( )

1 1

( ) ( )

q boB q

y k r k e k

A q A q

boB q boB q

−1 (2.97)

ou ainda,

ρ ρ ρ − − − − − − − + = + + + +

1 1 1

1 1 1 1

( ) ( )

( ) ( 1) ( )

( ) ( ) ( ) ( )

boB q q boB q

y k r k e k

boB q A q boB q A q (2.98)

Da equação anterior pode-se concluir que:

1. os pólos de malha fechada dependem da ponderação ρ sobre a ação de

controle. Quando ρ>0 e pequeno, tem-se que os pólos de malha fechada

estarão próximos aos zeros do processo e assim para sistemas de fase não

mínima a lei de controle é inviável;

2. quando ρ>0 , a variância da saída do processo é maior do que a variância do