Transient drawdown solution for a constant pumping test in finite two-zone confined aquifers

(1)

HESSD

8, 9299–9321, 2011

Transient drawdown solution for a constant pumping

test

C.-T. Wang et al.

Title Page

Abstract Introduction

Conclusions References

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Printer-friendly Version Interactive Discussion

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

Hydrol. Earth Syst. Sci. Discuss., 8, 9299–9321, 2011 www.hydrol-earth-syst-sci-discuss.net/8/9299/2011/ doi:10.5194/hessd-8-9299-2011

Hydrology and Earth System Sciences Discussions

This discussion paper is/has been under review for the journal Hydrology and Earth System Sciences (HESS). Please refer to the corresponding final paper in HESS if available.

Transient drawdown solution for a

constant pumping test in finite

two-zone confined aquifers

C.-T. Wang1,2, H.-D. Yeh2, and C.-S. Tsai2

1

Taiwan Branch, MWH Americas Inc., Taipei, Taiwan

2

Institute of Environmental Engineering, National Chiao Tung University, Hsinchu, Taiwan

Received: 25 August 2011 – Accepted: 20 September 2011 – Published: 18 October 2011

Correspondence to: H.-D. Yeh (hdyeh@mail.nctu.edu.tw)

(2)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

Abstract

The drawdown solution has been widely used to analyze pumping test data for the determination of aquifer parameters when coupled with an optimization scheme. The solution can also be used to predict the drawdown due to pumping and design the dewatering system. The drawdown solution for flow toward a finite-radius well with a

5

skin zone in a confined aquifer of infinite extent in radial direction had been developed before. To our best knowledge, the drawdown solution in confined aquifers of finite extent so far has never before been presented in the groundwater literature. This ar-ticle presents a mathematical model for describing the drawdown distribution due to a constant-flux pumping from a finite-radius well with a skin zone in confined aquifers of

10

finite extent. The analytical solution of the model is developed by applying the meth-ods of Laplace transforms and Bromwich contour integral. This solution can be used to investigate the eff_{ects of finite boundary and conductivity ratio on the drawdown}

distribution. In addition, the inverse relationship between Laplace- and time-domain variables is used to develop the large time solution which can reduce to the Thiem

15

solution if there is no skin zone.

1 Introduction

The famous Theis solution (1935) was first introduced in the groundwater literature to describe the transient drawdown distribution induced by a constant pumping at a well of infinitesimal well radius in a homogeneous and isotropic confined aquifer of infinite

20

extent. The radius of a well is in fact not zero in the real-world problems. It is well recognized that the solution developed based on the assumption of zero well radius can not give accurate drawdown predictions near the wellbore. Van Everdingen and Hurst (1949) developed the transient pressure solutions for the constant flow in finite and infinite confined reservoirs with considering the eff_{ect of well radius but neglecting}

25

the skin eff_{ect. Note that the term skin e}ff_{ect is used to reflect the increase or}

(3)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

With the introduction of functions commonly occurring in groundwater flow problems, Hantush (1964) gave an analytical solution and two approximate solutions for a con-stant pumping in confined aquifers with a finite well radius. Chen (1984) gave a short review on the use of the remote finite boundary condition in the groundwater litera-ture. He proposed a modified Theis equation for describing the drawdown distribution

5

in a confined aquifer of finite extent and gave a time criterion for the use of the Theis equation to predict drawdown in a finite aquifer. Wang and Yeh (2008) gave an exten-sive review on the relationship between the transient solution and steady-state solution for constant-flux and constant-head tests in aquifers of finite extent and infinite extent. They mentioned that the drawdown solution of the finite aquifer, rather than the infinite

10

aquifer, can reduce to the Thiem solution when the time becomes large enough. A positive skin is referred to a zone near the well having lower permeability than the original formation due to well construction. On the other hand, a negative skin is a zone has higher permeability than other part of aquifer formation. With considering a finite-thickness skin or patchy zone, Butler (1988) and Barker and Herbert (1988)

15

developed Laplace-domain solutions for the transient drawdown induced by a constant pumping without considering the eff_{ect of the well radius in confined aquifers.}

No-vakowski (1989) mentioned in a study that the thickness of the skin zone may range from a few millimeters to several meters. He presented a Laplace domain drawdown solution for a confined aquifer under a constant pumping with considering the eff_ects

20

of skin zone and wellbore storage. Butler and Liu (1993) presented a Laplace-domain solution for drawdown due to a point-source pumping in a uniform aquifer with an ar-bitrarily located disk of anomalous properties. In addition, they also gave a large-time solution based on the inverse relationship between the Laplace variable and time vari-able. Yeh et al. (2003) presented an analytical drawdown solution for the pumping

25

test in an infinite confined aquifer by taking into account the eff_{ects of the well storage}

and the finite-thickness skin. They mentioned that the eff_{ect of skin zone is}

(4)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

unconfined aquifer of infinite extent with a partially penetration well, finite-thickness skin. Yet, they adopted an approach such as a finite diff_{erence method to discretize the}

well screen for handling non-uniform wellbore flux problems.

The existing drawdown solutions for radial two-zone confined aquifers of infinite ex-tent under constant-flux pumping were all developed in Laplace domain except the

5

one given by Yeh et al. (2003) which was a time domain solution. Yeh et al.’s solu-tion (2003) is in terms of an improper integral integrating from zero to infinity and its integrand comprises a singularity at the origin. In addition, the integrand is an oscilla-tory function with many product terms of the Bessel functions of the first and second kinds of zero and first orders. The numerical calculation of their solution is therefore

10

time-consuming and very diffi_{cult to achieve accurate results. To avoid such}

numeri-cal diffi_{culties, we therefore propose an alternative analytical solution developed from}

a mathematical model similar to that of Yeh et al. (2003), except that the aquifer is of horizontally finite extent. The solution of the model is also developed by applying the methods of Laplace transforms and Bromwich contour integral. The integration of the

15

contour integral in Yeh et al. (2003) results in a single branch point with no singularity at zero of the complex variable. Thus, a branch cut along the negative real axis of the contour should be chosen and thus a closed contour is produced. Such a procedure finally results in a complicated solution presented in Yeh et al. (2003). On the other hand, the integration of the contour integral arisen from the Laplace domain solution in

20

our model has a simple pole at the origin and finite number of poles at other locations. The residue theorem is therefore adapted to obtain the time domain solutions for the skin zone or formation zone. These two solutions are in terms of a logarithmic function plus a summation term, rather than an integral, with the Bessel functions of the first and second kinds of orders zero and first. The solutions are much easier to calculate

25

than those of Yeh et al. (2003) indeed involving a singularity in the integral. In addition, large-time solutions in simpler forms are also developed by employing the relationship of small Laplace-domain variable p versus large time-domain variable t, hereinafter referred to SPLT (Yeh and Wang, 2007), to the Laplace-domain solution.

(5)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

2 Mathematical model

2.1 Mathematical statement

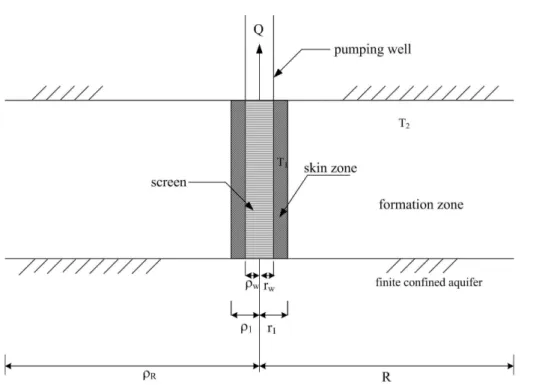
The assumptions involved in the development of the mathematical model are: (1) the confined aquifer is homogeneous, isotropic, and of finite extent in radial direction; (2) the well fully penetrates the aquifer and has a finite well radius; (3) a skin zone

5

is present around the pumping well as shown in Fig. 1; (4) the well discharge rate is maintained constant through out the entire pumping test.

The governing equations describing the drawdown distributions(r,t) in the skin zone and formation zone are, respectively,

∂2s1

∂r2 +

1

r ∂s1

∂r = S1

T1

∂s1

∂t rw≤r < r1 (1)

10

∂2s2

∂r2 +

1

r ∂s2

∂r = S2

T2

∂s2

∂t r1≤r < R (2)

where subscripts 1 and 2 express the skin zone and the formation zone, respectively,

r is the radial distance from the central line of the pumping well,r_wis the well radius,

r1is the outer radius of the skin zone,R is the distance from the central line of the well

to the outer boundary,t is the pumping time,S is the storage coeffi_{cient, and}_T _{is the}

15

transmissivity.

Prior to pumping, there is no drawdown over the area that will be influenced by the test. Thus, the initial conditions for skin zone and formation can be written as

s1(r,0)=s2(r,0)=0 (3)

In addition, the drawdown atR is also considered to be zero. The flux along the

well-20

bore is maintained at a constant rateQ. Thus, the outer and inner boundary conditions can be expressed, respectively, as

(6)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

d s1

dr

_r=_r_w

= −Q

2πrwT1

(5)

The continuity requirements for the drawdown and flux at the interface between the skin zone and formation zone are, respectively,

s1(r1,t)=s2(r1,t) (6)

T1

∂s1(r1,t)

∂r =T2

∂s2(r1,t)

∂r (7)

5

2.2 Laplace-domain solution

The solutions of Eqs. (1) and (2) subject to Eqs. (3)–(7) can be easily found using the method of Laplace transforms. The results are

¯

s1= −Q

4πT2

1

p

2T2

rwT1q1

Φ₁_I₀₍_q₁_r₎₋Φ₂_K₀₍_q₁_r₎ Φ₁_I₁₍_q₁_r_w₎+ Φ₂_K₁₍_q₁_r_w₎

(8)

¯

s2= −Q

4πT2

1

p

2T2

rwT1q1

Φ₁_I₀₍_q₁_r₁₎₋Φ₂_K₀₍_q₁_r₁₎

[Φ₁_I₁₍_q₁_r_w₎+ Φ₂_K₁₍_q₁_r_w_)]

1

ϕ

(9)

10

with

Φ₁=_φ

s

S2T2

S1T1

K0(q1r1)K0(q2r1)−K1(q1r1)K0(q2r1) (10)

Φ₂=_φ

s

S2T2

S1T1

I0(q1r1)K0(q2r1)+I1(q1r1)K0(q2r1) (11)

φ=I0(q2R)K1(q2r1)+I1(q2r1)K0(q2R)

I0(q2R)K0(q2r1)−I0(q2r1)K0(q2R)

(12)

(7)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

ϕ= I0(q2R)K0(q2r)−I0(q2r)K0(q2R)

I0(q2R)K0(q2r1)−I0(q2r1)K0(q2R)

(13)

Note that pis the Laplace variable, q1=

q

pS1

T1,q2=

q

pS2

T2,I0 and K0 are the

modified Bessel functions of the first and second kinds of order zero, respectively, and

I1andK1are the modified Bessel functions of the first and second kinds of order first,

respectively.

5

The values ofγ andωcan reduce toK1(q2r1)

K0(q2r1) andK0(q2r)

K0(q2r1),

re-spectively, whenR approaches infinity. Equations (8) and (9) are then equivalent to the solutions presented in Yeh et al. (2003, p. 750) as

¯

s1=

Q

4πT₂

1

p

2T2

r_wT₁q₁

ψ2K0(q1r)+ψ1I0(q1r)

ψ2K1(q1rw)−ψ1I1(q1rw)

(14)

¯

s2=

Q

4πT2

1

p

2T2

rwT1q1

(ψ2K0(q1r1)+ψ1I0(q1r1))

(ψ2K1(q1rw)−ψ1I1(q1rw))

K0(q2r)

K0(q2r1)

(15)

10

with

ψ1=K1(q1r1)K0(q2r1)−

s

S2T2

S₁T₁K0(q1r1)K1(q2r1) (16)

ψ2=I1(q1r1)K0(q2r1)+

s

S2T2

S1T1

I0(q1r1)K1(q2r1) (17)

2.3 Time-domain solution

The transient drawdown solution in time domain can be obtained by applying the

15

(8)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

solution. Detailed development is shown in Appendix A and the result for the drawdown distribution in skin and formation zones is, respectively,

s1=

Q

2πT1

lnr1

r + T1

T2

lnR

r₁− π r_w

∞

X

n=₁

exp

−T1

S1

α_n2t

·

αn(J1(αnrw)Y0(αnr)−Y1(αnrw)J0(αnr))

ς_n2hB_n2+ _ζ₍_B_n_C_n+_A_n_D_n₎+_{ζ A}_n_B_n_/α_n

/r1+ζ2A2n i

−α_n2



 

 

(18)

and

5

s2=₂_πTQ

2

n

lnR_r−_rπ

w ∞

P

n=1

exp−T1

S₁α

2

nt

αn(J1(αnrw)Y0(αnr1)−Y1(αnr1)J0(αnrw))·(Y0(ξαnR)J0(ξαnr)−Y0(ξαnr)J0(ξαnR))

[ς2

nBn[Bn2+ζ(BnCn+AnDn)/r1+ζ AnBn/αn+ζ2A2n]−α2n]

(19)

with

ςn=

−α_nJ1(αnrw) −ζ AnJ0(αnr)−BnJ1(αnr)

(20)

A_n=

J₁(ξα_nr₁)Y₀(ξα_nR)−J₀(ξα_nR)Y₁(ξα_nr₁)

(21)

Bn=J0(ξαnR)Y0(ξαnr1)−J0(ξαnr1)Y0(ξαnR) (22)

10

Cn=−ξR[J1(ξαnr1)Y1(ξαnR)−J1(ξαnR)Y1(ξαnr1)]−ξr1Bn−

A_n αn

(23)

D_n=_ξR_[_J₁₍_ξα_n_R₎_Y₀₍_ξα_n_r₁₎₋_J₀₍_ξα_n_r₁₎_Y₁₍_ξα_n_R_)]₋_ξr₁_A_n ₍₂₄₎

(9)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

whereJ0 and Y0are the Bessel functions of the first and second kinds of order zero,

respectively,J1and Y1 are the Bessel functions of the first and second kinds of order

first, respectively,ξ=

q

T1S2/T2S1,ζ=

q

S2T2/S1T1, and±αn are the roots of

αJ1(ξαr1)Y0(ξαR)−αJ0(ξαR)Y1(ξαr1)

·ζ

Y1(αrw)J0(αr1)−Y0(αr1)J1(αrw)

₊

J0(ξαr1)Y0(ξαR)−J0(ξαR)Y0(ξαr1)

·[αY1(αr1)J1(αrw)−αJ1(αr1)Y1(αrw)]=0

(25)

When ignoring the presence of skin zone, Eq. (19) can reduces to

5

s= Q 2πT

n

lnR_r−_rπ

w ∞

P

n=1

exp−T_Sα2_nt·(J1(αnrw)Y0(αnr)−Y1(αnrw)J0(αnr))

αn[J₁2(αnrw)−J02(αnR)]/J 2 0(αnR)

(26)

whereαn are the roots of J1(αrw)Y0(αR)−Y1(αrw)J0(αR)=0. Note that Eq. (26) is

exactly the same as the equation presented in Wang and Yeh (2008, Eq. 11). Addi-tionally, the steady-state solution can be obtained from Eqs. (18) and (19) in the limit of time approaching infinity.

10

2.4 Large-time solution

The drawdown solution for two-zone confined aquifers of finite-extent at large times can be obtained by applying the SPLT technique and L’Hospital rule to Eqs. (8) and (9). Some limits of the Bessel functions with small arguments are given as I0(x)∼1,

I1(x)∼x

2, K0(x)∼ −ln(x), and K1(x)∼1/x when x approaches zero (Abramowitz

15

and Stegun, 1979, p. 375). The Laplace-domain drawdown distribution in skin zone and formation zone for smallpcan then be obtained, respectively, as

s1(r,p)=

Q

2πT1p

lnr1

r + T1

T2

lnR

r1

(27)

s2(r,p)=

Q

2πT2p

lnR

(10)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

Accordingly, the large-time drawdown solutions can then be obtained by taking the inverse Laplace transform to Eqs. (27) and (28) as

s1(r,t)=

Q

2πT1

lnr1

r + T1

T2

lnR

r1

(29)

s2(r,t)=

Q

2πT2

lnR

r (30)

The time invariant Eqs. (29) and (30) can also be obtained by applying the method

5

of Tauberian theory (Sneddon, 1972) to Eqs. (8) and (9). This result indicates that the drawdown solution can reach its steady-state solution in confined aquifers of finite extent as declared in Wang and Yeh (2008). In addition, both Eqs. (29) and (30) can reduce to the Thiem solution if there is no skin zone, i.e.r1equalsrwandT1equalsT2.

2.5 Dimensionless solution 10

Dimensionless variables are introduced as follows: κ =_T₂

T1, γ =S2

S1, τ=

T2t

.

S2r 2 w, ρ=r

rw, ρ1=r1

rw, ρR=R

rw, and sD=s(4πT2)

Q whereκ represents conductivity ratio, γ represents the ratio of storage coeffi_cient, _ρ _represents

dimen-sionless distance,ρ1 represents dimensionless skin thickness, ρR represents

dimen-sionless distance of the outer boundary, andsDrepresents the transient distribution of

15

dimensionless drawdown. The drawdown solutions in Eqs. (18) and (19) then becomes

s1=2κ

lnρ1

ρ +

1

κln ρR

ρ1 −π

∞

X

n=1

exp−γ

κβ

2

nτ

·

ωn(J1(βn)Y0(βnρ)−Y1(βn)J0(βnρ))

ς_Dn2 hb2_n+ _ζ₍_b_n_c_n+_a_n_d_n₎+_{ζ a}_n_b_n_/β_n

/ρ1+ζ2a2n i

−β_n2



 

 

(31)

(11)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

s2=2κ

n

lnρR

ρ −π

∞

P

n=₁

exp−γ_κβ_n2τ

βn(J1(βn)Y0(βnρ1)−Y1(βnρ1)J0(βn))·(Y0(ξβnρR)J0(ξβnρ)−Y0(ξβnρ)J0(ξβnρR))

[ς2

Dn[b2n+(ζ(bncn+andn)+ζ anbn/βn)/ρ1+ζ2a2n]−βn2]

(32)

whereβn=rwαn are the roots of

βJ1(ξβρ1)Y0(ξβρR)−βJ0(ξβρR)Y1(ξβρ1)

·ζ

Y1(β)J0(βρ1)−Y0(βρ1)J1(β)

₊

J0(ξβρ1)Y0(ξβρR)−J0(ξβρR)Y0(ξβρ1)

·[βY1(βρ1)J1(β)−βJ1(βρ1)Y1(β)]=0

(33)

and

ς_Dn= −βnJ1(βn)

−ζ a_nJ0(βnρ1)−bnJ1(βnρ1)

(34)

5

an=J1(ξβnρ1)Y0(ξβnρR)−J0(ξβnρR)Y1(ξβnρ1) (35)

b_n=_J₀₍_ξβ_n_ρ_R₎_Y₀₍_ξβ_n_ρ₁₎₋_J₀₍_ξβ_n_ρ₁₎_Y₀₍_ξβ_n_ρ_R₎ ₍₃₆₎

10

c_n=₋_ξρ_R_[_J₁₍_ξβ_n_ρ₁₎_Y₁₍_ξβ_n_ρ_R₎₋_J₁₍_ξβ_n_ρ_R₎_Y₁₍_ξβ_n_ρ₁_)]₋_ξρ₁_b_n₋an

βn

(37)

d_n=_ξρ_R_[_J₁₍_ξβ_n_ρ_R₎_Y₀₍_ξβ_n_ρ₁₎₋_J₀₍_ξβ_n_ρ₁₎_Y₁₍_ξβ_n_ρ_R_)]₋_ξρ₁_a_n ₍₃₈₎

The numerical calculations for Eqs. (31) and (32) are achieved by finding the roots of Eq. (33) first using Newton’s method and then adding the summation term fornup

15

(12)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

3 Advantages and applications of the present solution

3.1 Advantages over the existing solutions

The analytical solution developed herein has the following two advantages over Yeh et al.’s solution (2003). First, the present solutions can give the same predicted draw-downs as Yeh et al.’ solution (2003) if the outer boundary distance in the present

so-5

lution is very large. In other words, the solutions presented in Yeh et al. (2003) can be considered as a special case of the present solution. Second, the transient draw-down solution in Yeh et al. (2003) is given in terms of an improper integral integrating from zero to infinity and its integrand has a singularity at the origin. Due to the pres-ence of singular point, the solution is very diffi_{cult to accurately calculate. In contrast,}

10

the present solution is composed of infinite series and can be easily calculated with accuracy to fifth decimal.

3.2 Potential applications

Due to the presence of skin zone, an aquifer system is characterized by five parame-ters, i.e. the outer radius of the skin zone and the transmissivity and storage coeffi_cient

15

for each of the skin and aquifer zones. Once the parameters are known, the pre-sented solution can be used to predict the spatial or temporal drawdown distributions in both the skin and formation zones and explore the physical insight of the constant-flux test in two-zone aquifer systems. On the other hand, those five parameters can be determined via the data analyses if the parameter values are not available. The

deter-20

mination of unknown parameters is in fact a subject of inverse problems. Type-curve approach is common for the parameter estimation. However, it is almost impossible to develop type-curves for the parameter estimation because the unknown parameters of two-zone aquifers are too many. Alternative ways in determining those five unknown parameters are to use the presented solution in conjunction with the algorithm of

ex-25

tended Kalman filter (e.g. Leng and Yeh, 2003; Yeh and Huang, 2005) or a heuristic

(13)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

optimization approach such as simulated annealing (e.g. Lin and Yeh, 2005; Yeh et al., 2007).

The present solution can also be used to verify recently developed numerical codes for predicting the drawdown distribution in two-zone aquifer systems. Generally, the sensitivity analysis (Liou and Yeh, 1997) can be performed to assess the impacts of

5

parameter uncertainty on the predicted drawdown. If the predicted drawdown is very sensitive to a specific parameter, a small change in that parameter will result in a large change in the predicted drawdown. On the contrary, the change in a less sensitive pa-rameter has little influence on the predicted result, reflecting a fact that a less sensitive parameter is diffi_{cult to be accurately estimated. With the present solution, one can}

10

easily perform the sensitivity analysis for two-zone confined aquifer systems to assess the overall responsiveness and sensitivity to targeted parameters (e.g. Huang and Yeh, 2007).

4 Results and discussion

Since the Yeh et al. (2003) have investigated the eff_{ects of the parameters, such as}

15

the skin type, skin thickness and well radius, on the drawdown distribution for two-zone aquifer systems, this study therefore concentrates on the eff_{ects of finite boundary and}

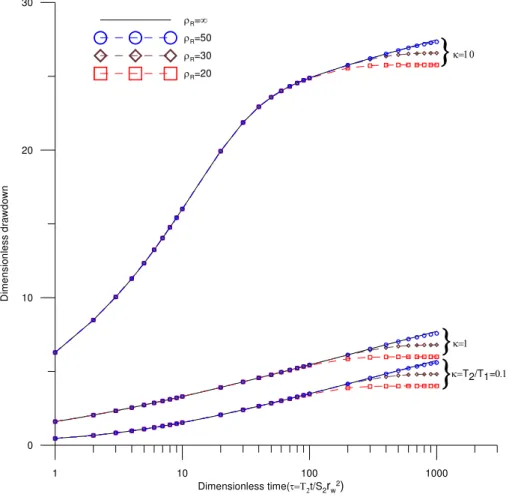
conductivity ratio on the drawdown distribution. Figures 2 and 3 depict the dimension-less predicted drawdowns at ρ=_{1 (at wellbore) and 10 (i.e. in the formation zone),}

respectively, whenρ1=3 for κ=0.1, 1, and 10. Note that κ less than 1 denotes for

20

the case of a negative skin and greater than 1 for the case of a positive skin. Figure 2 shows the comparison of the wellbore drawdown in the aquifer of finite-extent to that in the one of infinite extent. Both drawdown curves match very well beforeτ <100. How-ever, the curves gradually deviate from one another afterτ >100, indicating that the solution of finite aquifers can no longer be used to approximate the solution of infinite

25

aquifer at large times because of the importance of boundary eff_{ect on the drawdown}

(14)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

the time becomes very large. On the other hand, the wellbore drawdown in infinite aquifers continuously increases with dimensionless time. Figure 2 also demonstrates the eff_{ect of skin property on the wellbore drawdown distribution. The aquifer with a}

positive skin has larger wellbore drawdowns than the one with a negative skin at the same pumping rate. Figure 3 presents the drawdown distributions atρ=_{10 for}_ρ₁=₃

5

andκ=₀_._{1, 1, and 10. It reveals that the drawdown in an aquifer with a negative skin is}

larger than that in the one with a positive skin. In other words, the eff_{ect of skin property}

on the drawdown distribution in the formation zone is opposed to that at the wellbore. The diff_{erence in drawdown distribution between aquifers with} _κ=_{1 and 10 at} _ρ=₁

shown in Fig. 2 is significantly larger than those withκ=₀_._{1 and 1 at}_ρ=_{1 (Fig. 2) and}

10

those withκ=_{1 and 10 at}_ρ=_{10 shown in Fig. 3, indicating that the two-zone aquifer}

system is rather sensitive to the pumping in positive skin cases.

5 Conclusions

A mathematical model has been developed to describe the drawdown distribution for a pumping test performed in a two-zone confined aquifer of finite extent. The

Laplace-15

domain solution of the model for skin zone and formation zone is obtained by applying the method of Laplace transforms. The analytical solution (in time domain) is then developed by the Bromwich contour integral method. The drawdown distribution pre-dicted from the analytical solution shows that the dimensionless drawdown distribution in a finite aquifer is significantly diff_{erent from that in an infinite one at large pumping}

20

times. In other word, the drawdown solution of finite aquifer is applicable to predict that of an infinite aquifer only under the condition that the time is not large enough. In addition, the two-zone aquifer system is rather sensitive to the pumping in positive skin cases.

A large-time drawdown solution is also developed in this article based on the inverse

25

relationship of Laplace- and time-domain variables. Surprisingly, this large-time so-lution is exactly the same as the steady-state soso-lution, indicating that the soso-lution of

(15)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

finite two-zone aquifers can reach its steady-state solution at large times. In addition, the large-time solution has been shown to reduce to the Thiem solution if neglecting the presence of skin zone.

Appendix A 5

Derivation of Eqs. (18) and (19)

The drawdown solution in time domain, denoted as s(t) obtained by applying the Bromwich integral method (Carslaw and Jaeger, 1959) to the Laplace domain solu-tion ¯s(p) is expressed as

s(t)=_L−1

s(p) = 1

2πi

Zr+i∞ r−i∞

epts(p)d p (A1)

10

wherei is an imaginary unit andr_e is a real constant which is so large that all of the real parts of the poles are smaller than it. The graph of the Bromwich integral contains a close contour with a semicircle and a straight line parallel to the imaginary axis. According to Jordan’s Lemma, the integration for the semicircle tends to be zero when it radius approaches infinity. Based on the residue theorem, Eq. (A1) can be written as

15

s(t)=

∞

X

n=1

Res

epts(p);gn (A2)

wherep_nare the poles in the complex plane. There are infinite singularities ins(p) and obviously one pole atp=_0.

Introducing the following two variables

∆ =_q₁_[Φ₁_I₁₍_q₁_r_w₎+ Φ₂_K₁₍_q₁_r_w_)] _(A3)

20

Ψ =_Φ

1I0(q1r)−Φ2K0(q1r)

(16)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

Equation (8) can then be expressed as

¯

s₁= −Q

4πT2

2T2

rwT1

1

p

Ψ₍_p₎ ∆₍_p₎

(A5)

Let∆ =_{0, the roots}_α_n _in_p=_p_n=₍₋_T₁_α2_n₎_/S₁ _{can be then determined form Eq. (A3).}

Substitutingp=_p_n=₍₋_T₁_α_n2₎_/S₁ _{into Eq. (A3) yields Eq. (25). From the following}

for-mula (Kreyszig, 1999), the residue of the pole atp=_{0 is}

5

Res{epts(p);0}=_lim

p→0s(p)e

pt₍_p₋₀₎ _(A6)

Substituting Eq. (A5) into Eq. (A6) and applying L’Hopital’s rule results in

Res{epts(p);0}= Q

2πT1

lnr1

r + T₁ T2

lnR

r1

(A7)

The other residues at the simple polep=_p_n=₋_T₁_α_n2_/S₁_{are expressed as}

Res{epts(p);p_n}= _lim

p→pn

s(p)ept(p−p_n) (A8)

10

Applying L’Hopital’s rule to Eq. (A8), the denominator term inside the brackets of Eq. (A5) becomes

pd∆ d p

p=₋T₁α2

n/S1

=

1 2q

d∆

d q

q₁=i α_n,q₂=i κα_n

=

1 2q1

n

q1

h

Φ′

1I1(q1rw)+ Φ ′

2K1(q1rw)

i

+_r_w_q₁_Φ

1I0(q1rw)−Φ2K0(q1rw)

o

(A9)

where the variablesΦ₁_andΦ₂_{are defined in Eqs. (10) and (11), respectively, and}Φ′ 1

15

andΦ′

2are the first differentiations ofΦ1andΦ2, respectively.

(17)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

To simplify Eq. (A8), a variableς_nis assumed based on Eq. (A3) and∆ =_0:

ςn=

q1I1(q1rw)K0(ξq1r1) −Φ₂

(I0(ξq1R)K0(ξq1r1)−I0(ξq1r1)K0(ξq1R)

= q1K1(q1rw)K0(ξq1r1) Φ₁

(I0(ξq1R)K0(ξq1r1)−I0(ξq1r1)K0(ξq1R)

(A10)

Two recurrence formulas (Carslaw and Jaeger, 1959, p. 490) are adopted to eliminate the imaginary unit in Eq. (8) as follows:

5

K_vze±12πi

=_±1

2πi e

∓1 2vπi[−J

v(z)±i Yv(z)] (A11)

and

Iv

ze±12πi

=_e±12vπiJ_v(z) (A12)

Substituting Eqs. (A11) and (A12) into Eq. (A10) yields

−αnJ1(αnrw) −ζ AnJ0(αnr1)−BnJ1(αnr1)

= αnY1(αnrw)

ζ AnY0(αnr1)+BnY1(αnr1)

=_ς_n _(A13)

10

The result of substituting Eq. (A13) into Eq. (A9) is

h

pd∆

d p i

p=₋T₁α2

n/S1

=h1 2q

d∆

d q i

q₁=i α_n,q₂=i κα_n

= 1

2ς_n n

ς2n h

B2n+ ζ(BnCn+AnDn)+ζ AnBn/αn

/r1+ζ 2

A2n i

−α2n

o (A14)

where the constants appeared on the right-hand side of Eq. (A14) are defined in Eqs. (20)–(24). Similarly, the numerator of Eq. (A5) can also be obtained as

Ψ =παn

2ς_n

J1(αnrw)Y0(αnr)−Y1(αnrw)J0(αnr)

(A15)

(18)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

The residues at the polesp=_p_n=₋_T₁_α_n2_/S₁_are

Res{epts(p);pn}= −Q

2πrwT1

∞

X

n=1

exp −α

2

ntT1

S1

!

α_n(J1(αnrw)Y0(αnr)−Y1(αnrw)J0(αnr))

ξ2

n h

(ζ A_n)2₊_B2

n+ζ (BnCn+AnDn)+AnBn/αn

/r₁i−α_n



 

 

(A16)

Therefore, Eq. (A2) can be expressed as

h(t)= _Res

epts(p);0 +_Res

epts(p);pn (A17)

5

Finally, the solution for the drawdown distribution in the skin zone can then be ob-tained as Eq. (18). The solution for the drawdown distribution in the formation zone can also be obtained in a similar way as Eq. (19).

Acknowledgements. This research is partially supported by the Taiwan National Science Coun-cil under the contract numbers NSC 99-NU-E-009-001, NSC 99-2221-E-009-062-MY3, and

10

NSC 100-2221-E-009-106.

References

Abramowitz, M. and Stegun, I. A.: Handbook of Mathematical Functions, Dover publications, New York, 1970.

Baker, J. A. and Herbert, R.: Pumping test in patchy aquifer, Ground Water, 20, 150–155,

15

1988.

Barry D. A., Parlange, J. Y., and Li, L.: Approximation for the exponential integral (Theis well function), J. Hydrol., 227, 287–291, 2000.

Batu, V.: Aquifer Hydraulics, John Wiley & Sons, New York, 1998.

Butler Jr., J. J.: Pumping tests in nonuniform aquifers-The radially symmetric case, J. Hydrol.,

20

101, 15–30, 1988.

(19)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

Butler Jr., J. J. and Liu, W. Z.: Pumping tests in nonuniform aquifers: The radially asymmetric case, Water Resour. Res., 29, 259–269, 1993.

Carslaw, H. S. and Jaeger, J. C.: Conduction of Heat in Solids, 2nd edn., Oxford University Press, London, 1959.

Chen, C. S.: A reinvestigation of the analytical solution for drawdown distributions in a finite

con-5

fined aquifer, Water Resour. Res., 20, 1466–1468, doi:10.1029/WR020i010p01466, 1984. Hantush, M. S.: Hydraulics of wells, in: Advances in Hydroscience, Academic Press, New York,

1964.

Huang, Y. C. and Yeh, H. D.: The use of sensitivity analysis in on-line aquifer parameter esti-mation, J. Hydrol., 335, 406–418, 2007.

10

Ingersoll, L. R., Adler, F. T. W., Plass, H. J., and Ingersoll, A. G.: Theory of earth heat exchang-ers for the heat pump, HPAC Engineering, 113–122, 1950.

Ingersoll, L. R., Zobel, O. J., and Ingersoll, A. C.: Heat conduction with engineering, geological, and other applications, 2nd edn., Madison, University Wisconsin Press, 1954.

Kreyszig, E.: Advanced engineering mathematics, John Wiley & Sons Inc., New York, 1999.

15

Leng, C. H. and Yeh, H. D.: Aquifer parameter identification using the extended Kalman filter, Water Resour. Res., 39, 1062, doi:10.1029/2001WR000840, 2003.

Lin, Y. C. and Yeh, H. D.: Trihalomethane species forecast using optimization method: genetic algorithm and simulated annealing, J. Comput. Civil Eng., 19, 248–257, 2005.

Liou, T. S. and Yeh, H. D.: Conditional expectation for evaluation of risk groundwater flow and

20

solute transport: one-dimensional analysis, J. Hydrol., 199, 378–402, 1997.

Novakowski, K. S.: A Composite Analytical Model for Analysis of Pumping Tests Affected by Well Bore Storage and Finite Thickness Skin, Water Resour. Res., 25, 1937–1946, 1989. Perina, T. and Lee, T. C.: General well function for pumping from a confined, leaky, or

uncon-fined aquifer, J. Hydrol., 317, 239–260, 2006.

25

Prodanoff, J. H. A., Mansur, W. J., and Mascarenhas, F. C. B.: Numerical evaluation of Theis and Hantush-Jacob well functions, J. Hydrol., 318, 173–183, 2006.

Sneddon, I. N.: The Use of Integral Transforms, New York, McGraw-Hill, 1972.

Streltsova, T. D.: Well Testing in Heterogeneous Formations, John Wiley and Sons, Inc., New York, 45–49, 1988.

30

(20)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

Tseng, P. H. and Lee, T. C.: Numerical evaluation of exponential integral: Theis well function approximation, J. Hydrol., 281, 129–146, 1998.

Van Everdingen, A. F. and Hurst, W.: The application of the Laplace transformation to flow problems in reservoirs, Pet. Trans. AIME, 186, 305–324, 1949.

Wang, C. T. and Yeh, H. D.: Obtaining the steady-state drawdown solutions of constant-head

5

and constant-flux tests, Hydrol. Process., 22, 3456–3461, 2008.

Yeh, H. D. and Huang, Y. C.: Parameter estimation for leaky aquifers using the extended Kalman filter and considering model and data measurement uncertainties, J. Hydrol., 302, 28–45, 2005.

Yeh, H. D. and Wang, C. T.: Large-time solutions for groundwater flow problems

us-10

ing the relationship of small p versus large t, Water Resour. Res., 43, W06502, doi:10.1029/2006WR005472, 2007.

Yeh, H. D., Chang, T. H., and Lin, Y. C.: Groundwater contaminant source identification by a hybrid heuristic approach, Water Resour. Res., 43, W09420, doi:10.1029/2005WR004731, 2007.

15

Yeh, H. D., Yang, S. Y., and Peng, H. Y.: A new closed-form solution for a radial two-layer drawdown equation for groundwater under constant-flux pumping in a finite-radius well, Adv. Water Resour., 26, 747–757, 2003.

(21)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

(22)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

1 10 100 1000

Dimensionless time(τ=Τ2t/S2rw2)

0 10 20

30 _{New Legend}

ρR=∞

ρR=50

ρR=30 ρR=20

D

imensi

o

n

less d

raw

d

ow

n

κ=10

κ=1

κ=T2/T1=0.1

ρ = (

ρ1 = 3 κ .1, 1 10.

Fig. 2. The drawdown curves predicted at ρ=1 (wellbore) for infinite aquifers denoted by

the solid line and for finite aquifers having the outer boundary distances of 20, 30, and 50 represented by the dashed lines with the symbols of circle, diamond, and square, respectively, forρ₁=_{3 and}_κ=₀_._{1, 1 and 10.}

(23)

HESSD

8, 9299–9321, 2011

test

C.-T. Wang et al.

Title Page

Tables Figures

◭ ◮

Back Close

Full Screen / Esc

Discussion

P

a

per

|

Dis

cussion

P

a

per

|

Discussion

P

a

per

|

Discussio

n

P

a

per

|

1 10 100 1000

Dimensionless time(τ=Τt/Sr2₎

2 2 w 0

1 2 3

D

im

e

ns

io

nl

e

s

d

ra

w

dow

n

New Legend

ρR=¶ ρR=50 ρR=30 ρR=20

κ=0.1

κ=1 κ=10

ρR=20

ρR=30

ρR=50

ρR=¶

ρ = (

ρ1 = 3 κ .1, 1 10.

Fig. 3.The drawdown curves predicted atρ=10 (in formation zone) for infinite aquifers denoted