Universaidade em sistemas da mecâniaestatística de não equilíbrio com estados absorventes e percolação geográfica

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE FÍSICA TE ÓRICA E EXPERIMENTAL PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

Universalidade em Sistemas da Mecˆ

anica

Estat´ıstica de N˜

ao Equil´ıbrio com Estados

Absorventes e Percolac

¸˜

ao Geogr´

afica

Sharon Dantas da Cunha

Orientador: Prof. Dr. Luciano Rodrigues da Silva

Tese de doutorado apresentada ao Departamento de F´ısica Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial à obten¸cão do grau de DOUTOR em FÍSICA.

(2)

Para Pessoas Especiais:

(3)

Agradecimentos

Agrade¸co a Deus por ter me iluminado durante este trabalho.

Ao Professor Luciano Rodrigues da Silva pela orienta¸c˜ao segura e competente.

Agrade¸co também aos Professores, Ronald Dickman (UFMG), Fernando Dantas Nobre (CBPF), Umberto Laino Fulco (UFRN), José Soares de Andrade Júnior (UFC), Hans Hermann (UFC), pelas contribui¸cões e publica¸cões desta tese.

Aos professores do Departamento de F´ısica que deram contribui¸cões à minha forma¸cão e carreira cient´ıfica.

Aos colegas do Departamento de F´ısica da UFRN e da Petrobras.

Aos colegas do bacharelado em F´ısica, Darlan, F´abio Fereira, Samyr J´acome e Thiago Ribeiro.

Aos Funcion´arios do DFTE, em especial Celina e Jacira, pelos servi¸cos prestados.

(4)

Resumo

Sistemas Complexos têm despertado bastante interesse na comunidade cient´ıfica nestas duas últimas décadas. Exemplos desta área são os Autômatos Celulares, dentre os quais citamos o de Domany-Kinzel (ACDK) e o Processo de Contato (PC) que estudaremos no primeiro cap´ıtulo desta tese. Determinamos a criticalidade destes sistemas usando o Método de Busca Automática e o Regime de Tempo Curto (RTC). Os nossos resultados confirmaram que o ACDK e o PC pertencem a classe de universalidade da Percola¸cão Direcionada.

No segundo cap´ıtulo, estudamos a difusão de part´ıculas em dois modelos de Pilhas de Areia Estocásticas. Caracterizamos a difusão através da constante de difusãoD, definida através da rela¸cão h(∆x)2_i _{= 2Dt. Os resultados das nossas simula¸cões computacionais}

(colapsos de dados e RTC) mostraram que esta constante pode usada para estudar as propriedades cr´ıticas. Ambos os modelos pertencem a classe de universalidade da per-cola¸cão direcionada conservativa. Também estudamos o comportamento do deslocamento quadrático da posi¸cão no tempo que é dependente da configura¸cão inicial e do valor dep. No terceiro, criamos um modelo numérico, denominado de ”Percola¸cão Geográfica”, para estudar as linhas divisórias, fractais cujas aplica¸cões estão nas mais distintas áreas. Neste modelo, preenchemos a rede com valores entre 0 e 1 a partir de uma distribui¸cão de probabilidade, ordenamos estes valores, sempre guardando a sua localiza¸cão, e procuramos o s´ıtio pk que faz a rede percolar. Quando encontramos este s´ıtio, o retiramos da rede,

(5)

Abstract

Complex systems have stimulated much interest in the scientific community in the last twenty years. Examples this area are the Domany-Kinzel cellular automaton and Contact Process that are studied in the first chapter this tesis. We determine the critical behavior of these systems using the spontaneous-search method and short-time dynamics (STD). Ours results confirm that the DKCA e CP belong to universality class of Directed Percolation.

In the second chapter, we study the particle difusion in two models of stochastic sandpiles. We characterize the difusion through diffusion constant D, definite through in the relation h(∆x)2_i _{= 2Dt. The results of our simulations, using finite size scalling}

and STD, show that the diffusion constant can be used to study critical properties. Both models belong to universality class of Conserved Directed Percolation. We also study that the mean-square particle displacement in time, and characterize its dependence on the initial configuration and particle density.

In the third chapter, we introduce a computacional model, called ”Geographic Perco-lation”, to study watersheds, fractals with aplications in various areas of science. In this model, sites of a network are assigned values between 0 and 1 following a given probability distribution, we order this values, keeping always its localization, and searchpk site that

(6)

Sum´

ario

Agradecimentos ii

Resumo iii

Abstract iv

Introdu¸c˜ao 1

1 Autˆomato Celular de Domany-Kinzel, e Processo de Contato 7

1.1 Introdu¸c˜ao . . . 7

1.2 M´etodo de Busca Autom´atica. . . 10

1.3 Regime de Tempo Curto . . . 12

1.4 Autˆomato Celular de Domany-Kinzel . . . 14

1.5 Processo de Contato. . . 29

1.6 Conclus˜oes . . . 37

2 Pilhas de Areia 38 2.1 Introdu¸c˜ao . . . 38

2.2 Modelos . . . 39

2.3 Simula¸c˜oes Monte Carlo . . . 41

2.4 Conclus˜oes . . . 56

3 Percola¸cão Geográfica 57 3.1 Introdu¸cão . . . 57

3.2 Modelo . . . 60

(7)

3.4 Resultados . . . 69 3.5 Conclus˜oes . . . 74

4 Conclus˜oes e Perspectivas 75

4.1 Conclus˜oes . . . 75 4.2 Perspectivas . . . 76

(8)

Lista de Figuras

1 Modelo da pilha de areia no qual surgem avalanches de vários tamanhos devido a ausência de escala. . . 2 1.1 Interpreta¸cão dos comprimentos de correla¸cão ν⊥ e νk nas regiões subcr´ıtica

(esquerda) e supercr´ıtica (direita). Nas figuras A e B mostramos como o

aglo-merado cresce a partir de um s´ıtio ativo. Na figura C e D, mostramos como o

aglomerado cresce quando a rede est´a totalmente ocupada. As escalas indicadas

para ξ_k eξ⊥devem ser interpretadas como média de várias realiza¸cões [1]. . . . 9 1.2 Evolu¸cão temporal do Método de Busca Automático. a) Na região cr´ıtica o

sistema fica oscilando em torno de um valor m´edio. b)Amplia¸c˜ao (zoom) da

parte tracejada. . . 11 1.3 Diagrama de Fases para o ACDK, mostrando os resultados obtidos por

apro-xima¸c˜ao por s´ıtio e por par, e os dados obtidos por simula¸c˜ao computacional

[2]. . . 15 1.4 Diagrama de fases para o ACDK. Neste diagrama podemos ver as duas fases, a

congelada e a ativa. Neste diagrama destacamos alguns pontos conhecidos na

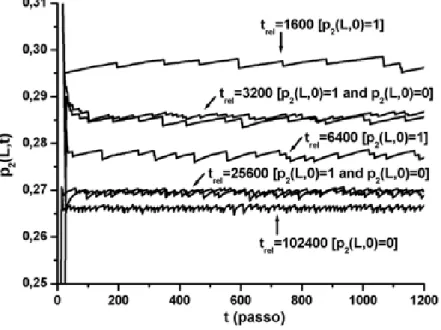
literatura. . . 16 1.5 Comportamento do MBA para diferentes de tempos de relaxa¸c˜ao trel.. . . 17

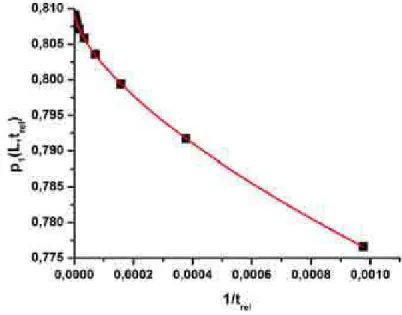
1.6 Extrapola¸cão no tempo de relaxa¸cão trel. O resultado que obtemos é o valor de

p1 para trel → ∞para um tamanho fixo. . . 18

1.7 Extrapola¸c˜ao para tamanho infinito (L → ∞) para p2 = 0,0 (figura maior), e

p2= 0,5 (figura menor). . . 19

(9)

1.9 Diagrama de Fases da ACDK. Neste diagrama evidˆenciamos as duas regras usa-das na TPG [3]. . . 22 1.10 Extrapola¸c˜ao para tamanho infinito (L→ ∞). . . 25 1.11 Comportamento no RTC com amostra saturada (fronteira congelada-ativa), e

com 50% dos s´ıtios modificados (fronteira caótica-não-caótica). . . 26 1.12 Comportamento no RTC quando iniciamos o sistema com apenas um s´ıtio ativo

(fronteira congelada-ativa), e com o dano unitário (fronteira caótica-não-caótica). 27 1.13 Taxas de transi¸cão para o caso unidimensional do PC [4]. . . 29 1.14 Extrapola¸cão para tamanho infinito (L→ ∞). . . 32 1.15 Extrapola¸cão para tamanho infinito (L → ∞) para tim = 2 (gráfico maior), e

tim= 5 (gr´afico menor). . . 33

1.16 Comportamento de pC versus tim. . . 34

1.17 Comportamento no RTC de ρdo PC tradicional (tim= 0 (quadrado)) e

tempo-rizado (tim= 5 (c´ırculo)), quando iniciamos o sistema saturado. . . 35

1.18 Comportamento no RTC de ρdo PC tradicional (tim= 0 (quadrado)) e

tempo-rizado (tim= 3 (c´ırculo)), quando iniciamos a amostra com um s´ıtio ativo. . . . 35

2.1 Exemplo de uma configura¸c˜ao t´ıpica que acontece no modelo II. As part´ıculas em azul ou branco pertencem ao s´ıtio, e em vermelho indica uma configura¸c˜ao

não permitida devido a restri¸cão do modelo, logo o excesso é devolvido ao s´ıtio

de origem. a) e b) Difusão total. c) a e) Difusão parcial. f) Não ocorre difusão. . 43 2.2 Comportamento do deslocamento quadrático médio versus tempo no modelo I,

para (da esquerda para direita) p = 1,94894; 0,95568; e 0,94898. Temos dois

comportamentos distintos, no in´ıcio, subdifusivo (linha tracejada), e no regime

estacion´ario, linear (linha cont´ınua). . . 45 2.3 < (∆xj)2 > versus t no modelo II para (da esquerda para direita) p =

0,95568; 0,94898; e 1,94898. Novamente, temos dois comportamentos

distin-tos, subdifusivo (linha tracejada), e linear (linha cont´ınua). . . 45 2.4 Comportamento de De ρ versus t. O regime estacion´ario compreende a regi˜ao

(10)

2.5 Constante de difus˜ao D no regime estacion´ario versus ∆ = p−pc no modelo I

para os tamanho indicados. . . 47 2.6 D no regime estacionário versus ∆ no modelo II. . . 47 2.7 Fra¸cão de s´ıtios ativos ρ no regime estacionário versus ∆ no modelo I para os

tamanhos indicados. . . 48 2.8 ρ no regime estacion´ario versus ∆ no modelo II. . . 48 2.9 ρ (s´ımbolos abertos) e D (s´ımbolos cheios) versus ∆ nos modelos I (quadrados)

e II (circulos), para L= 50 000. . . 49 2.10 Constante de difus˜ao modificada D∗=Lβ/ν⊥_D_{versus distˆancia do ponto cr´ıtico}

modificada ∆∗ ₌_L1/ν⊥_{∆ para o modelo I para os tamanhos indicados.} . . . 50 2.11 D∗ versus ∆∗ para o modelo II. . . 50 2.12 Fra¸c˜ao de s´ıtios ativos modificadoρ∗ =Lβ/ν⊥_ρ _{versus distˆancia do ponto cr´ıtico}

modificada ∆∗ =L1/ν⊥_{∆ no modelo I para os tamanhos indicados.} . . . 51 2.13 ρ∗ versus ∆∗ _{para o modelo II.} _{. . . 51}

2.14 Deslocamento quadrático médio h[∆x]2i versus t para diferentes configura¸cões iniciais. Distribuindo as part´ıculas aleatoriamente (linha cont´ınua), obtemos um

comportamento subdifusivo, e com um s´ıtio ativo (linha tracejada), um

compor-tamento superdifusivo. . . 53 2.15 Decaimento inicial da Fra¸c˜ao de s´ıtios ativos (quadrado) e da constante de difus˜ao

(c´ırculo) no ponto cr´ıtico para o modelo II quando distribu´ımos as part´ıculas

aleatoriamente para L= 50 000. . . 54 2.16 Crescimento inicial da fra¸c˜ao de s´ıtios ativos (quadrados) e da constante de

difus˜ao (c´ırculos) no ponto cr´ıtico para o modelo II quando iniciamos com um

s´ıtio ativo para L= 50 000. . . 55 3.1 Parte da Bacia do Rio S˜ao Francisco na regi˜ao Nordeste do Brasil. Este rio separa

parte do estado de Pernambuco (PE) e Bahia (BA), e os estados de Sergipe (SE)

(11)

3.3 Relevo artificial criado no software Surfer a partir dos dados percola¸cão Ge-ográfica em 3-D. As cores representam diferentes alturas em rela¸cão a uma altura

de referˆencia. . . 60 3.4 Redes bidimensionais com diferentes valores de probabilidade de preenchimento.

No limite de L → ∞, a percola¸c˜ao sempre existir´a com probabilidade 1 para p > pc. . . 61

3.5 Evolu¸cão da Percola¸cão Geográfica, onde a cor vermelha corresponde aos s´ıtios percolantes. . . 63 3.6 Estrutura final formada na Percola¸cão Geográfica. . . 63 3.7 Exemplo de uma cordlheira artificial formada a da partir Percola¸cão Geográfica. 64 3.8 Estrutura final da Percola¸cão Geográfica Isotrópica por s´ıtios. Neste caso o

sistema pode percolar nas duas dire¸c˜oes, e no final divide a regi˜ao em quatro

partes. . . 64 3.9 Fotografia de um relevo real. . . 65 3.10 Forma¸cão dos aglomerados usando o algoritmo de Hoshen-Kopelman. . . 67 3.11 Ilustra¸cão da adi¸cão do s´ıtio ”?” na rede que fará a liga¸cão de vários rótulos

diferentes. Neste caso, o novo s´ıtio e a vizinhan¸ca ficar˜ao com o r´otulo de menor

valor. . . 68 3.12 A massa M das linhas divis´orias. A massa se comporta de acordo com a rela¸c˜ao

3.1. O gráfico menor mostra o resultado quando usamos o método das caixas. . 70 3.13 Comportamento da rugosidade w versus L na escala logar´ıtmica. A inclina¸cão

nos fornece o expoente de rugosidade que neste caso ´e igual a 1,0 com erro na

segunda casa decimal. . . 71 3.14 Massa da superf´ıcieM versus L na escala logar´ıtmica. A massa se comporta de

acordo com a rela¸cão 3.1.. . . 72 3.15 Cálculo da dimensão fractal usando o método das caixas para as linhas divisórias

(12)

Lista de Tabelas

1.1 Tabela de probabilidades de transi¸c˜ao para o ACDK. . . 14

1.2 Tabela dos valores de p1C obtidos com o MBA. . . 20

1.3 Tabela dos valores de p2C obtidos com o MBA. . . 25

1.4 Tabela com os expoentes cr´ıticos obtidos com o RTC. . . 28

1.5 Tabela com os expoentes cr´ıticos, para ambas as fronteiras, obtidos com o RTC e o MBA. . . 28

1.6 Tabela com os valores de pC para diferentes tempos de imuniza¸c˜ao (tim). . . 33

(13)

Introdu¸

c˜

ao

(14)

no comportamento dos terremotos que comentamos anteriomente. A ausência de escala também é observada em sistemas que permanecem em equil´ıbrio metaestável, por exem-plo, já vimos em filmes, desenhos, etc em que os alpinistas não podem gritar para que as avalanches não ocorram, ou seja, a perturba¸cão (grito, um pequeno floco de neve) faz com que o sistema alcance a estabilidade através destas avalanches que não sabemos o seu tamanho. Outro exemplo é o relógio de areia no qual o fluxo de areia é constante, e devido ao empilhamento também surgem avalanches de vários tamanhos. Este empilhamento é a idéia do modelo da pilha de areia como podemos ver na figura 1. A medida que acontece as avalanches, a inclina¸cão da pilha varia de um valor m´ınimo (estado subcr´ıtico) onde acontecem os de pequena intensidade, a um valor máximo (supercr´ıtico), os de grandes intensidade. Já o estado cr´ıtico (intermediário) é caracterizado por avalanches de todos os tamanhos.

Figura 1: Modelo da pilha de areia no qual surgem avalanches de v´arios tamanhos devido a ausˆencia de escala.

(15)

mo-ratória, calote, etc de uma ou várias empresas. Observamos isso no último semestre do ano de 2008, com a crise nos Estados Unidos no qual muitas empresas no mundo perde-ram seu valor de mercado. Também temos instabilidades no corpo humano, por exemplo, um pequeno est´ımulo pode causar um infarto, como também um choque, ou reanima¸cão card´ıaca, pode ocasionar uma arritmia card´ıaca em uma pessoa sã, ou devolver os bati-mentos em sua normalidade.

Alguns dos sistemas que citamos anteriormente vão para o estado cr´ıtico através de um agente que provoca mudan¸cas, ou seja, uma dinâmica. No caso dos terremotos, a dinâmica é o movimento das placas tectônicas, nas montanhas, as avalanches ocorrem devido a deposi¸cão natural da neve, no relógio de areia, o empilhamento dos grãos de areia, na bolsa de valores, a especula¸cão financeira. Os sistemas se dirigem para a região de criticalidade, que é uma bacia atratora, devido a modifica¸cão de algum parâmetro. Esta propriedade que os sistemas possuem é chamada de Criticalidade Auto-Organizada (Self-Organizated Criticality) que foi descoberta e proposta por Bak,Thang e Wiesenfeld [7, 8]. Um dos objetivos desta teoria é estudar alguns problemas da natureza fora do equil´ıbrio (sistemas não conservativos que dissipam energia como forma de buscar a criticalidade), que estão sempre relaxando e apresentam alguma irregularidade no decorrer do tempo. A invariância de escala em sistemas naturais não é explicada simplesmente mostrando o comportamento dos elementos do sistema, e a Criticalidade Auto-Organizada (CAC) fornece argumentos para esta invariância de escala.

(16)

onde H(s) é o Hamiltoniano microscópico [1, 9]. Em princ´ıpio, este ensemble fornece o cálculo do valor esperado de um observável independente do tempo dado pela soma sobre todos os estados poss´ıveis do sistema, que em muitos casos é muito dif´ıcil representá-lo. De fato, embora numerosas solu¸cões exatas sejam encontradas [1, 10], a grande maioria dos sistemas estocásticos ainda não podem ser resolvidos exatamente. Para investigar tais sistemas, são usadas técnicas aproximativas tais como expansão em séries [11] e grupo de renormaliza¸cão [12]. Na ME de equil´ıbrio temos ferramentas teóricas bem desenvolvidas. Do ponto de vista f´ısico é interessante investigar sistemas estocásticos em que os graus de liberdade microscópicos se comportem coletivamente em grandes escalas [13, 14], que é observado quando o sistema sofre uma transi¸cão de fase, por exemplo, quando o modelo de Ising bidimensional sofre uma transi¸cão de fase, observa-se o tamanho médio dos dom´ınios que diverge quando a temperatura cr´ıtica é alcan¸cada [15].

Outra caracter´ıstica importante nos SC é que na maioria dos casos a evolu¸cão tem-poral inicia de um estado inicial que é muito longe do equil´ıbrio. Desta forma, o tempo de relaxa¸cão até o estado estacionário depende das propriedades dinâmicas espec´ıficas de cada sistema. Quando observamos a evolu¸cão temporal a partir da segunda lei da Termodinâmica, que governa o comportamento de todos os sistemas, implicitamente diz que esta evolu¸cão parte de uma configura¸cão para outra de máxima entropia. Quando inclu´ımos a vizinhan¸ca, alguns sistemas apresentam um comportamento espontâneo to-talmente oposto, ao custo do aumento da entropia da vizinhan¸ca. A partir de uma configura¸cão inicial, o sistema atinge uma configura¸cão bastante complexa [16].

Como foi comentado anteriormente, podemos trocar a descri¸cão determin´ıstica por uma estocástica, ou seja, o grau de liberdade segue uma probabilidade Pt(s) que é

(17)

de coexistˆencia de oito fluidos distintos (Ne, Ar, Kr, Xe,N2, O2, CO e CH4) se ajustam

a uma só curva se o expoente β associado ao parâmetro de ordem dos fluidos for 1/3. A partir deste momento, o conceito de classe de universalidade é bastante usado quando se estuda fenômenos cr´ıticos de sistemas f´ısicos, que são totalmente descorrelacionados, e se comportam da mesma forma perto da transi¸cão de fase caracterizado pelos mesmos expoentes cr´ıticos. O número de classes de universalidade parece ser limitado e deve ser uma importante tarefa classificá-las, similar aos elementos da tabela periódica.

Uma das classes de universalidade mais famosa na ME é a percola¸cão direcionada (PD) que engloba vários sistemas que têm em comum uma transi¸cão de fase cont´ınua de uma fase ativa para um único estado absorvente, seguindo uma dinâmica local bem definida com intera¸cão de curto alcance [1, 4, 18, 19]. Neste ano surgiu a primeira evidência experimental do PD [20, 21] em cristais l´ıquidos [22, 23]. Neste trabalho, os autores discutem detalhadamente os experimentos e as análises feitas que mostram claramente os expoentes cr´ıticos da PD, como também as suas rela¸cões de escala. No cap´ıtulo 1 desta tese estudaremos dois sistemas distintos, cujos expoentes criticos pertencem, em sua maioria, a classe de unviversalidade da PD, o autômato celular de Domany-Kinzel (ACDK) e o Processo de Contato (PC). Para caracterizar a criticalidade destes sistemas (ponto e expoente cr´ıticos) usamos o método de busca automática (MBA), e o regime de tempo curto (RTC). O MBA é inspirado na CAC no qual uma equa¸cão de recorrência leva o sistema para a região do ponto cr´ıtico e foi aplicado inicialmente em pol´ımeros ramificados [24]. Já o RTC, usa a evolu¸cão temporal do parâmetro de ordem no ponto cr´ıtico, bem antes do equil´ıbrio estacionário, para obter rela¸cões de expoentes cr´ıticos, com a vantagem de usar pouco tempo computacional, e apresentar pequenos valores de comprimento de correla¸cão espacial e temporal, levando a uma substancial redu¸cão de efeitos de tamanho finito.

(18)

cr´ıticos através de colapso de dados em dois modelos diferentes de pilhas de areia. Além da criticalidade, estudamos o RTC, usando D e ρ, e o deslocamento quadrático médio (< ∆x2 _{>). Neste ´}_{ultimo, conseguimos mostrar que antes de} _ρ _{entrar no regime}

esta-cionário, a difusão das part´ıculas é anômala e fortemente dependente da configura¸cão inicial, e no regime estacionário, o deslocamento quadrático é proporcional ao tempo.

(19)

Cap´ıtulo 1

Autˆ

omato Celular de

Domany-Kinzel, e Processo de

Contato

1.1 Introdu¸

c˜

ao

(20)

fator fundamental e representa uma importante fun¸cão, sendo considerado uma dimensão adicional, como comentamos no cap´ıtulo anterior. Assim, o tempo e o espa¸co apresentam caracter´ısticas e propriedades distintas, de tal forma que se associa os ´ındices k e ⊥, respectivamente. A transi¸cão de fase é caracterizada por dois comprimentos de correla¸cão independentes, chamados de comprimento de correla¸cão temporal ξk, e comprimento de

correla¸c˜ao espacial ξ⊥. Estes comprimentos divergem na criticalidade, com diferentes

expoentes, νk e ν⊥, como indicamos nas equa¸c˜oes 1.1 e 1.2.

ξk ∼ |p−pc|−νk (1.1)

ξ⊥ ∼ |p−pc|−ν⊥ (1.2)

Geralmente os expoentesν⊥ e νk s˜ao diferentes, e no regime de escala os dois

compri-mentos s˜ao relacionados como:

ξk ∼ξ⊥z, (1.3)

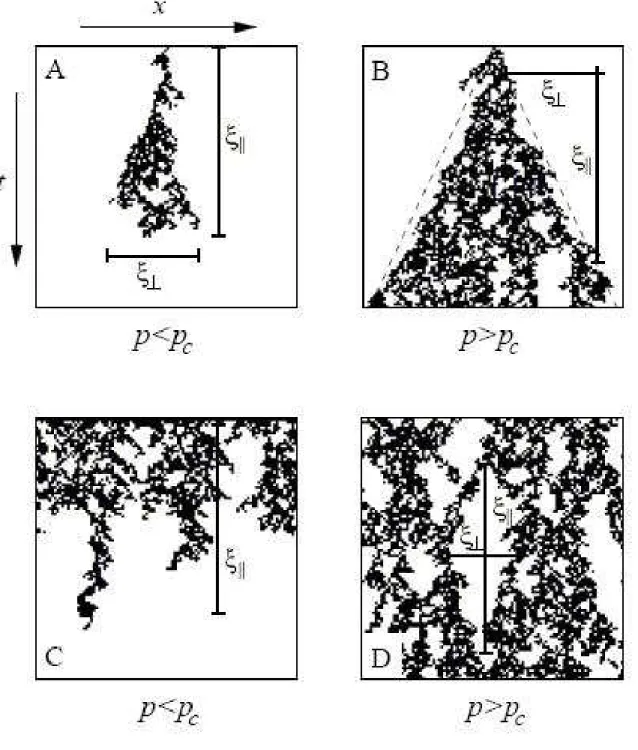
onde z é o expoente dinâmico, cujo valor éz=νk/ν⊥. Na figura 1.1 ilustramos o significado

f´ısico dos comprimentos de correla¸c˜ao ξk e ξ⊥, no qual apresentamos o comportamento

no regime subcr´ıtico e supercr´ıtico. Quando iniciamos o sistema com apenas um s´ıtio ativo, na fase inativa, os aglomerados formados tem a forma de uma gota (figura A), e os tamanhos m´edios do tamanho lateral e do tempo de vida s˜ao proporcionais a ξ⊥ e

ξk, respectivamente. Ap´os a criticalidade os aglomerados crescem em forma de um cone

(figura B), e o ângulo de abertura é determinado pela razãoξ⊥/ξk. Se iniciarmos o sistema

totalmente com a rede totalmente ocupada, na fase inativa o comprimento de correla¸c˜ao ξk representa o tempo de decaimento (figura C), enquanto no estado estacion´ario, os

(21)

Figura 1.1: Interpreta¸cão dos comprimentos de correla¸cão ν⊥ e νk nas regiões subcr´ıtica

(es-querda) e supercr´ıtica (direita). Nas figuras A e B mostramos como o aglomerado cresce a partir

de um s´ıtio ativo. Na figura C e D, mostramos como o aglomerado cresce quando a rede est´a

totalmente ocupada. As escalas indicadas paraξk e ξ⊥devem ser interpretadas como m´edia de

(22)

Os modelos básicos da ME de não-equil´ıbrio são o Autômato Celular de Domany-Kinzel (ACDK), considerado uma extensão da percola¸cão direcionada [32, 33], e o Pro-cesso de Contato (PC) [34]. Estudaremos ambos os modelos neste cap´ıtulo. Estes modelos possuem regras locais, que envolvem os seus primeiros vizinhos, contém elementos básicos de irreversibilidade, e exibem transi¸cão de fase em 1-D (neste caso consideraremos so-mente a dimensão espacial)[1, 4, 35]. Nas duas próximas se¸cões comentaremos sobre os dois métodos que usaremos para caracterizar a transi¸cão de fase, o Método de Busca Au-tomática (MBA), e o regime de tempos curtos (RTC). E nas se¸cões seguintes aplicaremos estes métodos no ACDK, no PC com a inclusão do tempo de imuniza¸cão, conforme foi mostrado por da Silva Jr [36].

1.2 M´

etodo de Busca Autom´

atica

Comentamos no cap´ıtulo anterior que o trabalho de Per Bak et al [7, 8] trouxe um novo conceito para a ME que foi a CAC, no qual os sistemas dinâmicos se dirigem espontaneamente para a região cr´ıtica (bacia atratora). Um conceito para este fenômeno foi proposto por Sornette et al [37] baseado na idéia de que uma fun¸cão de controle leva o sistema para a vizinhan¸ca do ponto cr´ıtico. Inspirado neste conceito, surge o MBA que usa uma equa¸cão de recorrência com o propósito de levar o sistema para a criticalidade, ou seja, esta equa¸cão é uma fun¸cão de controle. Pensando na pilha de areia, é como adicionar grãos até ocorrer as avalanches, sempre observando a quantidade de grãos que a levou à região cr´ıtica. Escolhendo o parâmetro de ordem apropriado, a recorrência faz com que o sistema encontre a criticalidade. A equa¸cão de recorrência do MBA, equa¸cão 1.4, envolve duas variáveis (X(t), Y(t)) associadas aos parâmetros f´ısicos do sistema.

X(t+ 1) =X(t)−α(Y(t)−Y∗) (1.4) Estas variáveis mudam a cada passote convergirá para um valor estacionárioX∗ _após

um certo n´umero de passos, compat´ıvel com o valor estacion´arioY∗_{, valor muito pequeno,}

(23)

Figura 1.2: Evolu¸cão temporal do Método de Busca Automático. a) Na região cr´ıtica o sistema fica oscilando em torno de um valor médio. b)Amplia¸cão (zoom) da parte tracejada.

O valor estacion´ario de X∗ _{depende da escolha do valor de}_Y∗_{, e tamb´em da escolha}

de X(0), que irá fornecer Y(0), compat´ıvel com o intervalo definido no sistema. Assim os parâmetros a ser investigados [(X(t), Y(t)) variam de (X(0), Y(0)) até o valores esta-cionários (X∗_{, Y}∗_{). A razão de convergência é controlada pela varável} _{α, ou seja, esta}

variável controla a forma como o sistema alcan¸ca a criticalidade. Se α for grande, o sistema convergirá rapidamente para a região cr´ıtica, porém fornecerá um valor de X∗

com um desvio muito grande. Se α for pequeno, convergirá lentamente, ou seja, demo-rará mais passos computacionais para chegar na criticalidade, porém com a vantagem de obter X∗ _{com desvio muito pequeno. Com estes requisitos é interessante que o valor de}

(24)

para a determina¸c˜ao da temperatura cr´ıtica, ondeX ≡K =J/(kBT) (proporcional ao

in-verso da temperatura) eY ≡m(magnetiza¸c˜ao por spinm=N−1P

ihSii). No PC [44], a

probabilidade cr´ıtica de recupera¸cão, no qualX ≡λ (taxa de infeçcão) eY ≡N (número de infectados naquele passo) e no ACDK [45, 46] na determina¸cão da fonteira cr´ıtica nas duas fronteiras, como iremos comentar adiante. Nas próximas se¸cões aplicaremos o MBA no ACDK e no PC tradicional e temporizado.

1.3 Regime de Tempo Curto

As técnicas tradicionais para a obten¸cão dos expoentes cr´ıticos necessitam de um tempo de relaxa¸cão muito grande, principalmente próximo do ponto cr´ıtico. Isto era necessário, pois se pensava que o comportamento universal só era alcan¸cado no regime estacionário, pois as correla¸cões próximas da região de ponto cr´ıtico são muito intensas, ficando dif´ıcil obter configura¸cões não correlacionadas [47]. Tentando contornar este problema Huse [48] e Janssen et al [49] descobriram que o comportamento universal acontece muito antes de atingir o equil´ıbrio. Neste caso, o tempo funciona como comprimento, se observarmos do ponto de vista da teoria de escala para sistemas finitos. Assim surgiu o RTC, uma importante ferramenta na investiga¸cão de fenômenos cr´ıticos [50], com a vantagem do pouco tempo computacional envolvido quando conhecemos o ponto cr´ıtico, e pequenos valores de comprimento de correla¸cão espacial e temporal, levando a uma substancial redu¸cão de efeitos de tamanho finito. O RTC trata do comportamento dos k-ésimos momentos antes do equil´ıbrio, dependente das condi¸cões iniciais. Estas rela¸cões foram verficados numericamente na literatura por [50, 51, 52, 53, 54]. Por exemplo, para o modelo de Ising, descrito em termos de variáveis binárias,Si(t) = ±1, ok-ésimo momento

da magnetiza¸c˜ao no tempo ´e:

M(k)(t) = 1 Nkh

N

X

i=1

Si(t)

!k

i (1.5)

(25)

Se a magnetiza¸cão inicial é pequena, M(0) ≪ 1, a magnetiza¸cão, ou seja, o primeiro momento (M(1)_(t)_≡_M_{(t) se comporta:}

M(t)∼M(0)tθ (1.6)

O expoente θ relaciona o crescimento da magnetiza¸cão com o tempo na temperatura cr´ıtica. Para calcularθ da equa¸cão 1.6, devemos considerar diferentes e pequenos valores (embora finitos) valores de M(0), e então extrapolamos o valor de M(0)→ 0. Agora, se iniciarmos o sistema com a configura¸cão completamente ordenada [M(0) = 1], a magne-tiza¸cão segue a lei de potência,

M(t)∼t−β/(νz) _(1.7)

onde β, ν (que corresponde ν⊥ nos sistemas da ME n˜ao-equil´ıbrio), e z ´e o expoente

(26)

1.4 Autˆ

omato Celular de Domany-Kinzel

Comentamos anteriormente que o ACDK é um dos modelos básicos da ME de Não-Equil´ıbrio [35]. Neste modelo, em uma rede de tamanho L, seus s´ıtios podem assumir dois estados, ηi = 0 (falso, vazio) ou ηi = 1 (verdadeiro, cheio), onde i=1, 2, 3,..., L. As

probabilidades de transi¸cão deste sistema possuem regras locais, ou seja, depende dos seus primeiros vizinhos. Temos dois esquemas de atualiza¸cão, o simétrico cuja probabilidade de transi¸cão depende do estado dos seus primeiros vizinhos, P(ηi−1(t), ηi+1(t)|ηi(t+ 1)),

e o não-simétrico, cuja probabilidade depende do estado do s´ıtio em questão e de um dos seus vizinhos, P(ηi−1(t), ηi(t)|ηi(t+ 1)) ou P(ηi(t), ηi+1(t)|ηi(t+ 1)). Neste trabalho

usaremos, por razões computacionais, o esquema não simétrico [55, 56, 57]. Outro fato interessante é que a probabilidade é simétrica, como indicamos na equa¸cão 1.8:

P(0,1|1) =P(1,0|1) =p1 (1.8)

Quando temos dois s´ıtios diferentes, a probabilidade de transi¸c˜ao usada ´e p1, e dois

s´ıtios com estados η= 1, a probabilidade usada ´ep2. O ACDK possui uma configura¸c˜ao

absorvente, ou seja, se na atualiza¸cão de um s´ıtio temos dois s´ıtios com estadosη= 0 na regra de transi¸cão, o s´ıtio fica com estado nulo. Na tabela 1.1 apresentamos as regras de transi¸cão pra o ACDK.

ηi,t|(ηi,t−1ηi+1,t−1) (1,1) (0,1) ou (1,0) (0,0)

1 p2 p1 0

0 1−p2 1−p1 1

Tabela 1.1: Tabela de probabilidades de transi¸c˜ao para o ACDK.

Para encontrar a transi¸c˜ao de fases do ACDK, temos que encontrar quais probabili-dades cr´ıticas (valores de p1 e p2) que faz o sistema mudar de fase. Na literatura temos

(27)

Figura 1.3: Diagrama de Fases para o ACDK, mostrando os resultados obtidos por aproxima¸c˜ao por s´ıtio e por par, e os dados obtidos por simula¸c˜ao computacional [2].

Quando simulamos o ACDK, escolhemos uma configura¸cão inicial, por exemplo, 50% de chances para cada estado, e a partir desta configura¸cão, o sistema evolui de acordo com uma dinâmica s´ıncrona e tempo discreto, ou seja, todos os s´ıtios são visitados a cada ∆t = 1. Usando as regras de transi¸cão da tabela 1.1 e o parâmetro de ordem,ρ, chamada de densidade de s´ıtios ativos, magnetiza¸cão ou atividade, expressa através da equa¸cão 1.9, caracterizamos as duas fases no ACDK que é fun¸cão dos valores de p1,p2 e do tempo de

relaxa¸c˜ao, conforme previsto no trabalho de Domany e Kinzel [32, 58].

ρ= 1 L

L

X

i=1

ηi, (1.9)

(28)

Figura 1.4: Diagrama de fases para o ACDK. Neste diagrama podemos ver as duas fases, a congelada e a ativa. Neste diagrama destacamos alguns pontos conhecidos na literatura.

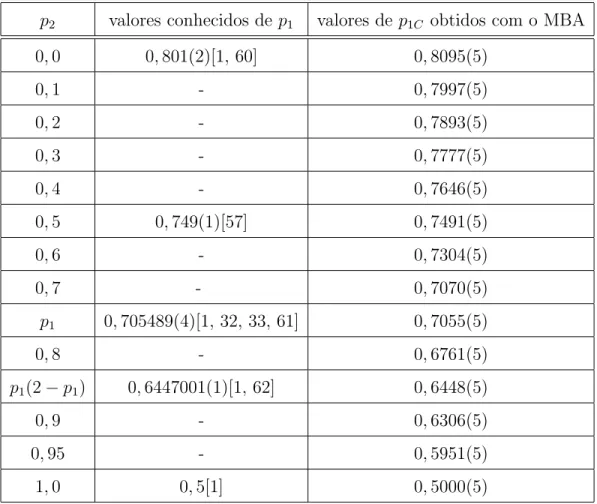
No diagrama 1.4, destacamos cinco pontos cr´ıticos que s˜ao conhecidos na literatura ao longo de sua linha cr´ıtica. O primeiro,p2 = 0 ep1 = 0,801(2), corresponde a concentra¸c˜ao

inicial no autˆomato celular da regra 18 de Wolfram [1, 60], o segundo p2 = 0,5 e p1 =

0,749(1) [57], o terceiro, p1 = p2 = 0,705489(4), a percola¸c˜ao direcionada por s´ıtio

[1, 32, 33, 61], o quarto, p1 = 0,6447001(1) e p2 = p1(2−p1), a percola¸c˜ao direcionada

por liga¸c˜ao [1, 62], e o quinto,p1 = 0,5 ep2 = 1,0, a percola¸c˜ao direcionada compacta [1].

Usaremos estes pontos para comparar com os pontos cr´ıticos que iremos obter usando o MBA.

Na segunda se¸cão deste cap´ıtulo, comentamos como o MBA funciona e para determi-nar a fronteira cr´ıtica congelada-ativa do ACDK, usaremos uma equa¸cão de recorrência, idêntica a 1.4, usando o parâmetro de ordemρ e escolhendo p2 fixo para procurar p1, ou

(29)

podemos ver na equa¸c˜ao 1.10.

p1(L, t+ 1) =p1(L, t)−b[ρ(t)−(1/L)] (1.10)

onde a constantebé um pequeno valor positivo que controla a razão de convergência para a fronteira cr´ıtica. Quando a fronteira cr´ıtica é alcan¸cada, flutua¸cões da ordem O(1/L) ocorrem em torno do ponto cr´ıtico procurado. Para cada passo t, temos um valor dife-rente dep1, e também uma configura¸cão inicial diferente correspondente à 50% de chances

para cada estado. Deixamos o sistema relaxar at´e um certo tempo de relaxa¸c˜ao trel, e

medimos o valor do parâmetro de ordem, e usamos a equa¸cão de recorrência 1.10, para obter o novo valor de p1. Depois de aplicar a equa¸cão de recorrência, dependendo do

valor de b da equa¸cão 1.10, podemos obter uma convergência depois de t = 100 passos, ou seja, este método fornece valores estacionários exigindo um tempo computacional re-lativamente pequeno. Outro fato interessante é que o MBA se dirige para o ponto cr´ıtico independentemente do valor inicial, como podemos ver na figura 1.5. Para isso, basta que o o valor inicial esteja dentro do dom´ınio da variável, que no caso da fonteira cr´ıtica 0 ≤ p1 ≤ 1. Os nossos dados confirmam que os valores estacionários obtidos com MBA

s˜ao fortemente dependentes do trel, fato que tamb´em podemos ver nas figuras 1.5 e 1.6.

(30)

Para obter os resultados no limite Termodinâmico, precisamos fazer inicialmente extra-pola¸cões para um tempo infinito de relaxa¸cão, ou seja,trel→ ∞. Para essa extrapola¸cão

usamos um ajuste n˜ao-linear usando a equa¸c˜ao 1.11 para umL fixo.

p1(L, trel)−p¯1(L, trel → ∞)∼t−relα (1.11)

ondeαé o expoente de ajuste, p1(L, trel) é o valor médio dos valores obtidos com o MBA

na região estacionária, ¯p1(L, trel → ∞) é o valor extrapolado quando trel → ∞. Daqui

por diante usaremos a nota¸c˜ao ¯p1(L, trel→ ∞)≡p¯1(L). Para obter ¯p1(L), usamos v´arios

tempos de relaxa¸cão, num total de 11 pontos, na extrapola¸cão, e para cada um destes pontos temos 3 amostras que foram combinadas de 177147 maneiras diferentes. Para esses ajustes, usamos no programa o pacote cminpak, dispon´ıvel na internet. A vantagem de usar este pacote é a rapidez com que obtemos as variáveis de ajustes, e assim a média e o desvio padrão delas. Na figura 1.6 mostramos um desses gráficos que foram extrapolados.

Figura 1.6: Extrapola¸cão no tempo de relaxa¸cãotrel. O resultado que obtemos é o valor dep1

(31)

Os tempos de relaxa¸c˜ao usados variaram de trel = 1024 `a trel = 1048576, e no regime

estacionário do MBA (a partir de 150 passos) usamos os 2150 passos seguintes para o menor tempo de relaxa¸cão, e 150 passos, para o maior tempo de relaxa¸cão. Depois que obtemos os valores de ¯p1(L) para cada L, fazemos outra extrapola¸cão para obter o limite

termodinâmico para L → ∞, usando novamente uma extrapola¸cão não-linear, equa¸cão 1.12 para obter p1C que é o ponto cr´ıtico que procuramos.

¯

p1(L)−p1C ∼L−1/ν⊥ (1.12)

Simulamos tamanhos que variam de L = 128 à L = 16384, sendo que para o ajuste, usamos L = 2048, L = 4096, L = 8192 e L = 16384. Na figura 1.7 mostramos a extrapola¸cão usando para L→ ∞parap2 = 0,0 ep2 = 0,5. O expoente da extrapola¸cão

para ambos ´e 1/ν⊥ = 0,91(5), compat´ıvel com o valor da literatura.

Figura 1.7: Extrapola¸c˜ao para tamanho infinito (L → ∞) para p2 = 0,0 (figura maior), e

p2 = 0,5 (figura menor).

(32)

absorvente. Mesmo utilizando tempos de relaxa¸cão menores e menos pontos(6 pontos) na extrapola¸cão no tempo de relaxa¸cão, também obtemos resultados bem próximos, o que mostra uma boa eficácia do MBA.

p2 valores conhecidos de p1 valores de p1C obtidos com o MBA

0,0 0,801(2)[1, 60] 0,8095(5)

0,1 - 0,7997(5)

0,2 - 0,7893(5)

0,3 - 0,7777(5)

0,4 - 0,7646(5)

0,5 0,749(1)[57] 0,7491(5)

0,6 - 0,7304(5)

0,7 - 0,7070(5)

p1 0,705489(4)[1, 32, 33, 61] 0,7055(5)

0,8 - 0,6761(5)

p1(2−p1) 0,6447001(1)[1, 62] 0,6448(5)

0,9 - 0,6306(5)

0,95 - 0,5951(5)

1,0 0,5[1] 0,5000(5)

(33)

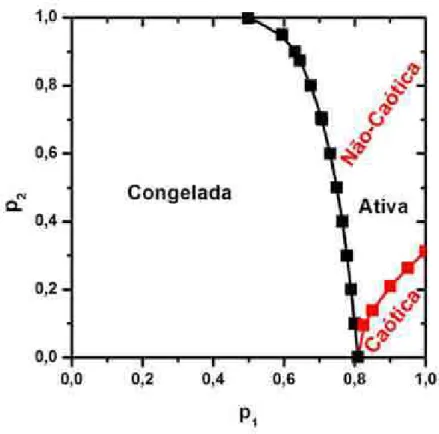
Usando o parâmetro de ordem ρ obtemos duas fases, uma ativa e outra não ativa (congelada). Usando a técnica de propaga¸cão de danos (TPG), conseguimos obter duas novas fases dentro da fase ativa, uma com propaga¸cão de dano e outra sem, como podemos ver na figura 1.8, e conforme previsto inicialmente por Martins et al [55].

Figura 1.8: Diagrama de Fases para o ACDK. Nela podemos ver as trˆes fases, uma congelada, e as ativas com e sem propaga¸c˜ao de dano.

A TPG foi desenvolvida por Kauffman [63] no contexto dos autômatos celulares, sendo posteriormente aplicada em sistemas constitu´ıdos de sub-unidades interagentes [64, 65]. Esta técnica é bastante aplicada na ME com o objetivo de investigar as propriedades dinâmicas de um sistema. Ferramenta usada para estabelecer conexões entre aspectos dinâmicos e propriedades estáticas termodinâmicas, que consiste em observar duas amos-tras que diferem apenas por alguns s´ıtios, ou seja, em um sistema cooperativoAdescrito por variáveis discretasηi(t), ondei= 1,2,3, ..., L, o dano corresponde a inversão de alguns

(34)

ηB_i (t) = 1−η_iA(t), (1.13) onde o sistema B é a cópia modificada. Uma das regras de evolu¸cão dinâmica, usa a mesma regra de transi¸cão e sequência de número aleatórios para o sistema A e sistema B (regra 1). Outras regras foram desenvolvidas, sorteando um número aleatório para o sistema A e outro para diferente para o B (regra 2) [66, 3]. Comparando as duas regras notamos que existe uma diferen¸ca nos pontos cr´ıticos, como podemos ver na figura 1.9. Estas diferen¸cas foram descobertas por Bagnoli [67], que estudou a propaga¸cão de danos no ACDK usando a teoria de campo médio. Nesta tese usaremos a regra ”1”, ou seja, a que usa a mesma sequencia de numeros aleatórios para os dois sistemas A e B.

Figura 1.9: Diagrama de Fases da ACDK. Neste diagrama evidˆenciamos as duas regras usadas na TPG [3].

A poss´ıvel diferen¸ca existente depois de um certo tempo de relaxa¸cão, é denominado de dano que é medido através de uma variável denominada distância de Hamming [68], que é a fra¸cão total de s´ıtios que diferem entre os dois sistemas. Matematicamente a distância de Hamming é definida como:

Ψ(t) = 1 L

N

X

i=1

|η_iA−η_iB|, (1.14)

(35)

Enumerando os passos da TPG, temos:

1. Escolhe-se a configura¸cão inicial, e deixa o sistema relaxar até atingir o regime estacionário:

2. Depois copia a configura¸c˜ao para um novo sistema (sistema B), escolhendo alguns s´ıtios fixos ou aleat´orios para provocar a mudan¸ca (dano inicial):

3. Deixa os dois sistemas evolu´ırem, com a mesma dinâmica e no caso da regra 1, mesma sequencia de números aleatórios, e regra 2, números aleatórios diferentes: 4. Após um tempo de relaxa¸cão, mede-se quão diferente estão as duas cópias através

da distˆancia de Hamming.

Se a distância de Hamming for nula, após os passos acima, o dano desapareceu. Caso contrário, o dano se propagou ao longo de todo o sistema. Para obter o diagrama de fases com a fase ativa dividida em duas partes (fase caótica e não-caótica), como foi mostrado na figura 1.8, vamos usar o MBA e adaptar a equa¸cão de recorrência 1.10 que usamos anteriormente. As principais mudan¸cas são:

1. Vamos deixar p1 fixo, e procurar p2:

2. Vamos substituirρ, que caracteriza a fase ativa, por Ψ que caracteriza a fase ca´otica:

Fazendo as substiui¸cões, a equa¸cão de recorrência para a fase caótica fica:

p2(L, t+ 1) =p2(L, t) +b′[Ψ(t)−(1/L)] (1.15)

onde as constantes b′ _{é um pequeno valor positivo que controla a razão de convergência}

para a fronteira cr´ıtica. Quando a fronteira cr´ıtica é alcan¸cada, flutua¸cões da ordem O(1/L) ocorrem em torno do ponto cr´ıtico procurado. Análogo com o que fizemos ante-riormente, para cada passo t, temos um valor diferente de p2, e uma configura¸cão inicial

diferente (50% η = 1; 50% η = 0). Antes de provocar o dano no sistema, deixamos o sistema relaxar para que ele entre no estado estacion´ario. O tempo de relaxa¸c˜ao que usamos foi t′_rel = 1000 para p1 = 0,825 e t

′

rel = 200 para os demais pontos (p1 ≥ 0,85).

(36)

tempo para atingir o regime estacionário. Após atingir o regime estacionário, provocamos o dano no sistema (Ψ(0) = 0,5). Deixamos os sistemas A e B relaxarem até um certo tempo de relaxa¸cão trel, usando a mesma sequência de números aleatórios, medimos o

valor do dano através da equa¸cão 1.14, e usamos seu valor na equa¸cão de recorrência 1.15 para obter o novo valor dep2. Depois de aplicar a equa¸cão de recorrência algumas vezes,

dependendo do valor de b′ _{desta equa¸c˜ao, podemos obter uma convergˆencia depois de}

t= 100 passos. Obtemos a criticalidade independente do valor inicial dep2, basta que ele

esteja no dentro do dom´ınio da vari´avel, (0≤p2 ≤1). Os nossos dados novamente

confir-mam que os valores estacion´arios obtidos com MBA s˜ao fortemente dependentes do trel,

com comportamento an´alogo aos da fronteira congelada-ativa, como mostrado nas figuras 1.5 e 1.6. Para obter p2C, ou seja, o ponto cr´ıtico no limite termodinˆamico, precisamos

fazer inicialmente extrapola¸c˜oes para um tempo infinito de relaxa¸c˜ao (trel → ∞), usando

um ajuste não-linear da equa¸cão 1.16 para umLfixo. Os passos a seguir são análogos ao que fizemos anteriormente, no qual usaremos os mesmos tempos de relaxa¸cão e número de amostras.

p2(L, trel)−p¯2(L, trel → ∞)∼t−α

′

rel (1.16)

E com os valores de ¯p2(L, trel → ∞)≡p¯2(L), faremos outra extrapola¸c˜ao para obter o

comportamento paraL→ ∞, usando a rela¸c˜ao 1.17 para obter p2C que ´e o ponto cr´ıtico

que procuramos.

¯

p2(L)−p2C ∼L−1/ν

′

(37)

Na figura 1.10 mostramos a extrapola¸c˜ao para L→ ∞ parap1 = 1,0. O expoente da

extrapola¸c˜ao ´e 1/ν′

⊥ = 0,915.

Figura 1.10: Extrapola¸c˜ao para tamanho infinito (L→ ∞).

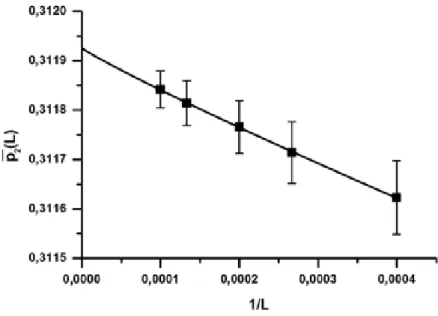
O diagrama que mostramos anteriormente, figura 1.8, foi obtido usando o MBA, e na tabela 1.3, mostramos os valores dos pontos cr´ıticos que obtemos, e comparamos com os da literatura. Também obtemos uma precisão muito boa, considerando que o erro está na terceira casa decimal.

p1 valores conhecidos dep2 valores dep2C obtidos com o MBA

0,825 - 0,0946±0,0003

0,850 0,1400±0,0002 [69] 0,1390±0,0003

0,900 - 0,2092±0,0001

0,950 - 0,2641±0,0003

1,000 0,31215±0,00004 [69] 0,3119±0,0002

(38)

Além dos pontos cr´ıticos, comentamos anteriormente que a transi¸cão de fase fica bem caracterizada com o tripleto de expoentes cr´ıticos (β, ν⊥, νk), e na terceira se¸cão mostramos

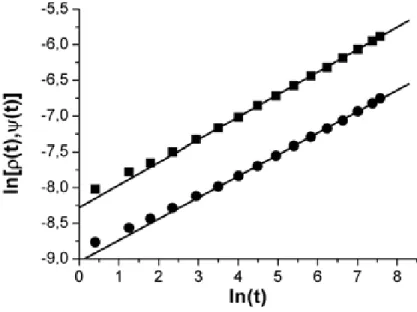
que podemos obter alguns expoentes cr´ıticos através do comportamento dos parâmetros de ordem no tempo (regime de tempo curto). Nesta técnica analisamos a propaga¸cão de atividade, e do dano, no tempo com o ponto cr´ıtico que obtemos com o MBA (ta-belas 1.2 e 1.3). Em ambas as fronteiras, temos duas formas de fazer essa análise, a primeira, iniciamos o sistema com o máximo valor do parâmetro de ordem, ou seja,ρ= 1 (sistema saturado) na fronteira congelada-ativa, e na caótica não-caótica, Ψ = 0,5. Na segunda fronteira, só podemos provocar o dano após atingir o regime estacionário. O tempo máximo que usamos foi t= 2000, e o comportamento dos parâmetros de ordem é proporcional aβ/νk, na fronteira congelada-ativa, eβ′/νk′. Na figura 1.11 mostramos este

comportamento na escala logar´ıtmica para 10000 amostras.

Figura 1.11: Comportamento no RTC com amostra saturada (fronteira congelada-ativa), e com 50% dos s´ıtios modificados (fronteira caótica-não-caótica).

Na fronteira congelada-ativa, em todos os pontos cr´ıticos, com exce¸c˜ao dos extremos, todos tiveram o mesmo valor. No extremo correspondente a p2 = 0, n˜ao tivemos

(39)

J´a no extremo correspondente `a p2 = 1,0, o sistema sempre fica saturado. A segunda

análise, corresponde a iniciarmos o sistema no ponto cr´ıtico com apenas um s´ıtio ativo na fronteira congelada-ativa, e um dano unitário na fronteira caótica não-caótica. Na primeira fronteira, escolhe-se um s´ıtio aleatoriamente na rede para ficar ativo ηi = 1,

enquanto que os demais ficam sem atividade ηj = 0 ∀j 6= i. J´a na segunda fronteira,

deixamos o sistema entrar no regime estacionário, e modificamos somente um s´ıtio, ou seja, os sistemas A e B só são diferentes devido a um s´ıtio, ou seja, ηB

i = 1 − ηiA e

ηB

j =ηjA∀j 6=i. Em ambos os casos, o parˆametro de ordem cresce proporcional ao tempo,

e o expoente neste caso ´e denominado deθ, para a primeira fronteira, eθ′_{, para a segunda.}

Os expoentes de propaga¸c˜ao β/νk, θ, e z, denominado de expoente dinˆamico, satisfazem

a rela¸c˜ao de hiperescala

2β νk

+θ = 1

z (1.18)

Usando novamente um tempo m´aximo de rela¸c˜ao t = 2000, e 10000 amostras inde-pendentes, obtemos o comportamento mostrado na figura 1.12 na escala logar´ıtmica.

(40)

Na tabela 1.4, mostramos os expoentes que obtemos com o RTC nas duas fronteiras.

β/νk 0,155±0,005

θ 0,308±0,005 β′_/ν′

k 0,154±0,006

θ′ _0,₃₁₆_±_0,₀₀₄

Tabela 1.4: Tabela com os expoentes cr´ıticos obtidos com o RTC.

Em resumo, com as rela¸c˜oes do regime de tempo curto presentes na tabela 1.4, e com o expoente obtido com o MBA, obtemos os seguintes expoentes, que comparamos com os da literatura.

Expoentes Fronteira Fronteira PD

Cr´ıticos Congelada-Ativa Não-Caótica Caótica Ref. [62] ν⊥, ν⊥′ 1,099±0,015 1,094±0,014 1,096854(4)

θ, θ′ _0,₃₀₈_±_0,₀₀₅ _0,₃₁₆_±_0,₀₀₄ _0,_313686(8)

z, z′ _1,₆₁₈_±_0,₀₃₉ _1,₆₀₂_±_0,₀₄₁ _1,_580745(10)

νk, νk′ 1,778±0,052 1,752±0,037 1,733847(6)

β, β′ _0,₂₇₆_±_0,₀₀₉ _0,₂₇₀_±_0,₀₁₁ _0,_276486(8)

Tabela 1.5: Tabela com os expoentes cr´ıticos, para ambas as fronteiras, obtidos com o RTC e o MBA.

Com estes resultados, com exce¸cão do extremo superior, todos os pontos da fron-teira congelada-ativa pertencem à classe de universalidade da PD, ou seja, apresentam os mesmos expoentes cr´ıticos, e o extremo superior, p2 = 1,0 e p1 = 0,5, pertence à

(41)

1.5 Processo de Contato

Comentamos anteriormente 1ue um dos modelos básicos da ME de não-equil´ıbrio é o processo de contato. Este modelo foi proposto inicialmente por Harris [34] em 1974, e vastamente explorado na literatura [72, 73, 74, 75, 76]. Modelo criado para explicar a propaga¸cão de uma epidemia simples, no qual é governado por uma equa¸cão mestra, apresenta uma transi¸cão de fase no modelo unidimensional [1, 35]. Neste modelo, uma rede d-dimensional L, possui Ld _{s´ıtios que podem assumir dois estados,} _η _{= 0 ou} _η _{= 1,}

indiv´ıduo são ou infectado (doente). Um indiv´ıduo pode ficar infectado se pelo menos um de seus vizinhos estiver infectado. A taxa de infeçcãoλe o número de vizinhos infectados, n, define as probabilidades de transi¸cões de um estado para outro como podemos ver na equa¸cões 1.19, para cria¸cão, e 1.20, para aniquila¸cão.

p(0→1) = nλ

2d(1 +λ) (1.19)

p(1→0) = 1−p(0→1) (1.20)

Na figura 1.13 mostramos as taxas de transi¸c˜ao no modelo unidimensional, onde o c´ırculo (figura cheia) representa o estado ηi = 1 e a circunferˆencia (figura vazia), ηi = 0.

Figura 1.13: Taxas de transi¸c˜ao para o caso unidimensional do PC [4].

(42)

os Ld _{da rede d-dimensional. A cada unidade de tempo,} _Ld _{s´ıtios s˜ao visitados, ou seja,}

para cada s´ıtio sorteado o tempo sofre um incremento ∆t= 1/Ld _{mesmo que n˜ao ocorra}

cria¸cão ou aniquila¸cão. A desvantagem deste método é a baixa eficiência quando temos situa¸cões de baixa densidade de s´ıtios ocupados já que o sorteio na grande maioria vai para s´ıtios vazios. Uma maneira equivalente e mais eficiente, principalmente em situa¸cões com poucos s´ıtios ativos, é fazer uma lista com os NA s´ıtios ocupados, onde o sorteio

agora é feito aleatoriamente a partir desta lista. O incremento temporal não é fixo e varia de acordo com a atividade do sistema, ou seja, ∆t = 1/NA. O processo de cria¸cão ocorre

com probabilidade p = λ/(1 +λ) e uma aniquila¸cão ocorre com probabilidade 1−p. No caso unidimensional, na cria¸cão, um dos primeiros vizinhos do s´ıtio é escolhido com probabilidade 1/2 para que a nova part´ıcula seja criada caso ele seja vazio. Observando a expressão 1.19, isto corresponde ao cason = 2, onde por hipótese o outro vizinho do s´ıtio escolhido é vazio. Vamos considerar um s´ıtio vazio que tenha dois vizinhos preenchidos, uma part´ıcula pode ser criada pela part´ıcula da esquerda comp = (1/2)λ/(1 +λ), onde (1/2) se remete a escolha do s´ıtio da esquerda pelo s´ıtio vazio em questão. A mesma coisa acontece com o da direita por simetria. O que resulta em p = (1/2)λ/(1 +λ) + (1/2)λ/(1 +λ) = λ/(1 +λ), equivalente a equa¸cão 1.19 para n= 2 e d= 1, o que mostra que a segunda maneira de implementar o CP é equivalente à primeira (convencional). As formula¸cões que comentamos se diferem no regime de tempos curtos, mas possuem a mesma propriedade estacionária em tempos longos [4].

No PC existe a infeçcão e a cura espontânea. A cura não garante a imunidade do indiv´ıduo. Se todos os s´ıtios ficam com valores nulos, ou seja, todos os indiv´ıduos do sistema ficam curados, a doen¸ca desaparece. Neste caso, o sistema fica estável em um estado absorvente caracterizado pela ausência de atividade, ou seja, nenhum indiv´ıduo fica infectado nesta região. O sistema também pode evoluir para um estado ativo estável, que neste caso não é necessário que todos os indiv´ıduos fiquem infectados, basta que uma certa quantidade de s´ıtios permane¸cam ativos. A fronteira entre a região ativa e a região congelada é caracterizada pela taxa cr´ıticaλC e até o momento não existe resultado exato

para ele. Existem resultados para simula¸cões Monte Carlo [4, 77] e análises de série [4] no qual fornecem λC ≃3,2978 [4, 59]. Um resultado mais satisfatório é λC = 3,29785(5)

(43)

na segunda se¸cão deste cap´ıtulo. A equa¸cão de recorrência do MBA para o PC será fun¸cão da taxa de infeçcão e do parâmetro de ordem. O parâmetro de ordem é a ”magnetiza¸cão”, ou densidade de atividade, idêntica ao do ACDK na caracteriza¸cão da fronteira congelada-ativa. Trabalharemos com a variável p em vez deλ, que se relacionam através da equa¸cão 1.19. Assim a equa¸cão de recorrência fica:

p(L, t+ 1) =p(L, t)−b[ρ(t)−(1/L)] (1.21) onde a constantebé um pequeno valor positivo que controla a razão de convergência para a fronteira cr´ıtica, e ρ(t) é dada pela equa¸cão 1.9. A equa¸cão 1.21 é bem parecida com a 1.10, com uma diferen¸ca que no ACDK t´ınhamos duas probabilidades, e no PC só temos uma. O comportamento destas equa¸cões são idênticos, ou seja, acontecem flutua¸cões da ordem O(1/L) quando a criticalidade é alcan¸cada, e isso independe do valor inicial (0 ≤ p ≤ 1). Os nossos resultados confirmam que os valores estacionários obtidos com MBA para o PC são fortemente dependentes dotrel, idêntico ao ACDK. Para um Lfixo,

faremos extrapola¸c˜oes com a equa¸c˜ao 1.22.

p(L, trel)−p(L, t¯ rel → ∞)∼t−relα (1.22)

onde α é o expoente de ajuste, p(L, trel) é o valor médio dos valores obtidos com o

MBA na região estacionária, e ¯p(L, trel → ∞) é o valor extrapolado quando trel → ∞.

Usando a nota¸cão ¯p1(L, trel → ∞) ≡ p¯1(L), para obter esta variável, usamos vários

tempos de relaxa¸cão, num total de 11 pontos, na extrapola¸cão, e para cada um destes pontos temos 3 amostras que foram permutadas para obtermos 177147 gráficos a serem ajustados. Os tempos de relaxa¸cão usados variaram detrel = 1024 à trel= 1048576, e no

regime estacionário do MBA (a partir de 150 passos) usamos os 2150 passos seguintes para o menor tempo de relaxa¸cão, e 150 passos, para o maior tempo de relaxa¸cão. Depois que obtemos os valores de ¯p(L) para cada L, fazemos outra extrapola¸cão para obter o limite termodinâmico para L → ∞, usando novamente uma extrapola¸cão não-linear, equa¸cão 1.12 para obter pC que é o ponto cr´ıtico que procuramos.

¯

(44)

Simulamos tamanhos que variam de L = 128 `a L = 16384, sendo que para o ajuste, usamosL= 2048, L= 4096,L= 8192 e L= 16384, como podemos ver na figura 1.14.

Figura 1.14: Extrapola¸c˜ao para tamanho infinito (L→ ∞).

O valor de p = 0,76733(1)(λ = 3,2979(1)) que obtemos ´e compat´ıvel com a melhor estimativa da literatura.

Como vimos, no PC existe a infeçcão e a cura espontânea que não garante a imunidade do indiv´ıduo. Para garantir a imunidade parcial, vamos incluir um tempo de imuniza¸cão (tim) para o PC, isto é, vamos garantir um per´ıodo de imunidade ao indiv´ıduo no sistema,

e chamaremos dePC temporizado. Quando o tempo de imuniza¸c˜ao for nulo (tim= 0),

obtemos oPC tradicionalque mostramos anteriormente. Quando o indiv´ıduo sofre uma infeçcão, e é curado, ele passa um certo tempo imunizado, ou seja, durante este per´ıodo, mesmo que ele tenha contato com indiv´ıduos infectados, ele não ficará doente. Passado o tempo de imuniza¸cão, ele poderá ser infectado novamente, e este tempo é presente em sistemas reais, ou seja, quando tomamos uma vacina, passamos um certo tempo imune até surgir uma nova varia¸cão desta doen¸ca, e o exemplo mais comum é o v´ırus da gripe que sofrem várias muta¸cões durante os últimos anos. Vamos usar o MBA para obter o ponto cr´ıtico para este caso usando cinco tempos de imuniza¸cão (tim = 1,0;tim = 2,0;tim =

(45)

para obter o ponto cr´ıtico para o PC temporizado. Fazendo a extrapola¸cão temporal, obtemos ¯p(L), e fazendo a extrapola¸cão em L, obtemos o limite termodinâmico, ou seja, pC. Na figura mostramos duas extrapola¸cões temporais para dois tempos de imuniza¸cão.

Figura 1.15: Extrapola¸c˜ao para tamanho infinito (L → ∞) para tim = 2 (gr´afico maior), e

tim= 5 (gr´afico menor).

Na tabela 1.6 mostramos os valores que obtemos para todos os tempos de imuniza¸c˜ao estudados.

tim = 0,0 0,76733(5)

tim = 1,0 0,80967(5)

tim = 2,0 0,83651(5)

tim = 3,0 0,85545(5)

tim = 4,0 0,86975(5)

tim = 5,0 0,88106(5)

(46)

Na figura 1.16 mostramos o comportamento de pC versus tim.

Figura 1.16: Comportamento de pC versustim.

Conhecendo os pontos cr´ıticos, vamos determinar, a partir do RTC, rela¸c˜oes que contˆem o tripleto de expoentes cr´ıticos (β, ν⊥, νk). Da mesma forma que fizemos para

o ACDK na fronteira congelada-ativa, faremos para o PC. Quando iniciamos o sistema totalmente saturado, ou seja, todos os s´ıtios com estado ηi = 1, obtemos a rela¸c˜ao β/νk

(decaimento do parˆametro de ordem), e quando iniciamos o sistema com apenas um s´ıtio ativo, obtemos o expoente θ (crescimento do parˆametro de ordem). Usando L = 10000, mostramos na figura 1.17 o comportamento para tim = 0 e tim = 5 do decaimento de ρ

usando 1000 amostras, e na figura 1.18 para 20000 amostras para tim = 0 e tim = 3, o

(47)

Figura 1.17: Comportamento no RTC deρ do PC tradicional (tim= 0 (quadrado)) e

tempori-zado (tim= 5 (c´ırculo)), quando iniciamos o sistema saturado.

Figura 1.18: Comportamento no RTC deρ do PC tradicional (tim= 0 (quadrado)) e

(48)

Na tabela 1.7 resumimos os expoentes obtidos com o RTC para os seis tempos de imuniza¸c˜ao estudado (0≤tim≤5,0).

tim β/νk θ

0,0 0,161(2) 0,307(4) 1,0 0,164(5) 0,334(9) 2,0 0,165(4) 0,339(5) 3,0 0,165(3) 0,336(5) 4,0 0,164(5) 0,336(5) 5,0 0,166(4) 0,332(7)

Tabela 1.7: Tabela com as rela¸c˜oes obtidas com o RTC para o PC tradicional e temporizado.

Usando o valor de ν⊥ obtidos, e os valores dos expoentes do regime de tempo curto,

obtemos os tripleto de expoente cr´ıticos, que ´e apresentado na tabela 1.8.

tim β νk ν⊥

0,0 0,282± 0,009 1,749 ± 0,038 1,10 ± 0,01 1,0 0,273± 0,021 1,657 ± 0,077 1,10 ± 0,02 2,0 0,271± 0,017 1,644 ± 0,063 1,10 ± 0,02 3,0 0,273± 0,015 1,652 ± 0,058 1,10 ± 0,02 4,0 0,272± 0,020 1,657 ± 0,069 1,10 ± 0,02 5,0 0,275± 0,019 1,657 ± 0,074 1,10 ± 0,02

Tabela 1.8: Tabela com as estimativas de expoentes cr´ıticos do PC tradicional e temporizado.

Atrav´es das tabelas 1.7 e 1.8 observamos que o tempo de imuniza¸c˜ao nulo (tim = 0)

pertence a classe de universalidade da PD, resultado já conhecido na literatura. Para tem-pos de imuniza¸cão diferente de zero (processo de contato temporizado), sabemos que ele é uma versão do modelo SIRS (suscept´ıvel, infectado,recuperado, suscept´ıvel) e pertence a classe de universalidade da PD [80, 81]. As estimativas do expoenteνk possui um erro na

(49)

1.6 Conclus˜

oes

(50)

Cap´ıtulo 2

Pilhas de Areia

2.1 Introdu¸

c˜

ao

No cap´ıtulo 1, comentamos sobre a criticalidade auto-organizada (CAC), e vimos que o modelo padrão para explicar este conceito é a pilha de areia [7, 8]. Neste modelo, a medida que adicionamos grãos ao sistema, ele tende para uma situa¸cão cr´ıtica onde surgem avalanches de vários tamanhos, ou seja, estas avalanches seguem uma lei de potência. A CAC presente neste modelo, e a adi¸cão de part´ıculas, que é o mecanismo de controle ou dinâmica do sistema, levam o sistema para sua região cr´ıtica [82, 83]. Neste caso, o sistema apresenta uma transi¸cão de fase entre uma fase absorvente e outra ativa nos modelos das pilhas de areia conservativas, que possuem uma dinâmica local e um número fixo de part´ıculas [82, 84, 85, 86, 87, 88, 89]. Estas pilhas de areia são caracterizadas pela não conserva¸cão do parâmetro de ordem (fra¸cão de s´ıtios ativos), que é ligado ao campo conservativo, e não envolve a região sem atividade [90]. As pilhas de areia conservativas pertencem à classe de universalidade da percola¸cão direcionada conservativa (PDC), é diferente da percola¸cão direcionada padrão [25], que comentamos no cap´ıtulo anterior com o ACDK e o PC.

(51)

fases, e obtém as principais simetrias e leis de conserva¸cão do sistema. Importantes passos nesta dire¸cão são os recentes estudos da equa¸cão de Langevin [25, 91] para PDC. Os valo-res dos expoentes cr´ıticos mostrados na referência [25] estão em boa concordância com os obtidos nas simula¸cões de gás de rede conservativo [92, 93], que exibem a mesma simetria e leis de conserva¸cão das pilhas de areia estocáticas. Os expoentes obtidos da equa¸cão de Langevin também são consistentes com as melhores estimativas das pilhas de areia bidimensionais [25]. Agora temos uma boa evidência que a pilha de areia unidimensional pertence à classe de universalidade da PDC [94, 95].

Neste cap´ıtulo mostraremos um aspecto das pilhas de areia que tem recebido pouca aten¸cão na literatura, a difusão de part´ıculas nos modelos Não-restrito e Restrito das pilhas de areia conservativas. A dinâmica nestes modelos envolve a transferência de part´ıculas entre os s´ıtios vizinhos, e os resultados das nossas simula¸cões Monte Carlo mostram que a contante de difusão D, definida através da rela¸cão h(∆x)2_i _{= 2Dt, onde}

∆x é o deslocamento de cada grão, possui um comportamento de escala similar ao do parâmetro de ordem ρ, conforme mostraremos nas próximas se¸cões. Na próxima se¸cão detalharemos os dois modelos estudados, e logo após mostraremos os resultados das nossas simula¸cões computacionais.

2.2 Modelos

Nesta tese estudaremos duas versões do modelo unidimensional das pilhas de areia conservativas, relacionada ao modelo de Manna [96, 97]. Nestes sistemas a configura¸cão é definida pelo conjunto de variáveis ocupadasz1, ..., zL, ondezi é o número de part´ıculas de

cada s´ıtio de uma rede unidimensionalL com condi¸cões periódicas de contorno. Um s´ıtio é considerado ativo quando possui duas ou mais part´ıculas (zi ≥2). Designamos por NA

o número de s´ıtios ativos na rede. Os dois modelos que estudaremos são versões de um processo de Markov no tempo cont´ınuo. Neste caso o incremento temporal é ∆t = 1/NA,

e a dinâmica em cada intervalo de tempo envolve a transferência de part´ıculas de um dos s´ıtios ativos para os seus primeiros vizinhos. A cada intervalo o número de s´ıtios ativo (NA) pode mudar, e a dinâmica cessará quando não existir s´ıtios ativos. Em ambos os

(52)

diferenciam da seguinte forma:

Modelo N˜ao-Restrito (I) [98]: Quando o s´ıtio idecai, duas part´ıculas s˜ao transferidas deste s´ıtio para os primeiros vizinhos (i−1 e/ou i+ 1) de maneira independente com probabilidades iguais.

Modelo Restrito (II) [99, 94]: A dinâmica é a mesma do modelo I, exceto que o s´ıtio não pode ter mais de duas part´ıculas. Se na transferência, o s´ıtio que recebeu a part´ıcula possui mais de dois grãos, o excesso é devolvido ao s´ıtio que provocou o decaimento.

Devido ao modelo II ter um conjunto pequeno de estados, isto faz com que ele seja mais conveniente para análises por aproxima¸cão de cluster [100]. Existe uma clara evidência numérica que o modelo II pertence à classe de universalidade da PDC [94]; O modelo I compartilha a mesma simetria e quantidade conservada do modelo II, desta forma também pertence a classe da PDC.

Nas pilhas de areia conservativas, a densidade de part´ıculaspfunciona como parâmetro de controle. Na região subcr´ıtica (p > pc), o sistema após um certo de tempo entra no

estado absorvente (NA = 0), enquanto que para p > pc, a atividade continua

indefi-nidamente, no limite de tamanho infinito. Para sistemas finitos, a atividade continua indefinidademente para p > 1 (1 ≤ p≤ 2, para o caso restrito). O parâmetro de ordem associado a esta transi¸cão de fase é a densidade de atividadeρ, dado pela fra¸cão de s´ıtios ativos. Simula¸cões mostram que existe uma transi¸cão de fase cont´ınua, cujas melhores es-timativas parapc são 0,9488 e 0,92978, para os modelos I e II, respectivamente. Observe

que quandop > 1, os s´ıtios ativos sempre existem, e note que pc ´e menor que 1.

Na próxima se¸cão mostraremos os resultados das simula¸cões Monte Carlo para o des-locamento quadrático médioh[∆x]2_i_{, a constante de difusão}_{D, e o parâmetro de ordem}_ρ.

(53)

2.3 Simula¸

c˜

oes Monte Carlo

Nesta se¸cão abordaremos a difusão das part´ıculas nos dois modelos de pilhas de areia conservativas que comentamos na se¸cão anterior. Comentamos que nestes modelos quando um s´ıtio é ativo, ele está apto a transferir part´ıculas para os seus primeiros vizinhos. Para iniciar o estudo da difusão das part´ıculas, usaremos a equa¸cão de difusão usual que não leva em conta se no sistema existe fonte ou sorvedouro de part´ıculas, conforme está expressa na equa¸cão 2.1:

∂̺ ∂t =D

∂2_̺

∂t2 (2.1)

A solu¸cão da equa¸cão 2.1 é:

̺(t, x)∝e−(x−x0) 2

4Dt (2.2)

O denominador da equa¸cão 2.2 é igual ao dobro do desvio quadrático médio que é proporcional a constante de difusão D e comporta-se linearmente com o tempo, como podemos ver na equa¸cão seguinte:

h[∆x]2i= 2Dt (2.3)

onde ∆x=x(t)−x(0). A partir deste resultado, nos modelos que definimos anteriormente, para cada part´ıcula j da rede temos um ∆xj, que iremos definir de maneira equivalente

em termos do n´umero de pulos dado pelas part´ıculas no tempo t para esquerda (h+_j(t)), e para a direita (h−j (t)). Fica claro que h+j (0) = h−j (0) = 0. Desta forma, a varia¸c˜ao de

posi¸c˜ao para a part´ıcula fica:

∆xj(t) = h+j(t)−h−j (t) (2.4)

A rela¸cão 2.4 conta toda a história da part´ıcula j desde a sua posi¸cão inicial xj(0)

at´e a posi¸c˜ao xj(t), ou seja, a cada tempo t a part´ıcula j se difunde, e ∆xj muda por

±1, tal que h[∆xj(t)]2i =hhj+(t) +h−j (t)i ≡ hhj(t)i, isto é, o número médio de pulos no

(54)

h[∆xj(t)]2i= 2Dt (2.5)

Nas nossas simula¸cões, a configura¸cão inicial consiste em distribuir aleatoriamente as N part´ıculas numa rede unidimensional de tamanho L, com a restri¸cão de no máximo duas part´ıculas por s´ıtio no modelo II. Quando estudamos somente o parâmetro de ordem ρ nos preocupamos somente com a quantidade de part´ıculas em cada s´ıtio. Já quando estudamos a difusão, temos que saber quais part´ıculas estão naquele s´ıtio, e isto faz com que nossas simula¸cões agora sejam um pouco mais lentas em rela¸cão ao primeiro estudo, pois temos que guardar a posi¸cão e o deslocamento de todas as part´ıculas (∆xj),

para poder determinar D a partir da equa¸cão 2.5. A identifica¸cão das part´ıculas se dá no momento da configura¸cão inicial, e não muda durante a simula¸cão. A dinâmica dos modelos I e II consiste em sortear um dos NA s´ıtios ativos, e distribuir duas part´ıculas

para os seus primeiros vizinhos. As part´ıculas possuem a mesma probabilidade de ir para esquerda, ou para direita. No modelo I, um s´ıtio ativo temzj part´ıculas, e a probabilidade

de uma part´ıcula ser escolhida ´e 2/zj. Neste caso obrigatoriamente, as duas part´ıculas

escolhidas se difundem para o local sorteado. Já no modelo II, isso não acontece, pois temos restri¸cão de altura, ou seja, no máximo duas part´ıculas por s´ıtio. Dependendo da ocupa¸cão da vizinhan¸ca, a difusão pode acontecer totalmente (as duas part´ıculas foram para o(s) s´ıtio(s) escolhido(s), parcialmente (uma das part´ıculas permaneceu no s´ıtio de origem), ou não acontecer (as duas part´ıculas permanecem no s´ıtio de origem). Na figura 2.1 mostramos uma configura¸cão t´ıpica do modelo II. As part´ıculas em azul ou branco pertencem ao s´ıtio, e a cor vermelha indica que a part´ıcula não pode permancer naquele local e tem que voltar ao s´ıtio de origem. Quando as part´ıculas ficam na cor azul, o s´ıtio é ativo. A ocupa¸cao de s´ıtios próximos são correlacionados, e o tempo de espera entre deslocamentos suscessivos de uma da part´ıcula não são independentes. Por estas razões, a rela¸cão entre a quantidade de pulos e a fra¸cão de s´ıtios ativos envolve efeitos sutis, diferente nos dois modelos estudados. Apesar disso é razoável esperar que para p→ pc,

(55)

Figura 2.1: Exemplo de uma configura¸cão t´ıpica que acontece no modelo II. As part´ıculas em azul ou branco pertencem ao s´ıtio, e em vermelho indica uma configura¸cão não permitida devido

a restri¸cão do modelo, logo o excesso é devolvido ao s´ıtio de origem. a) e b) Difusão total. c) a

(56)

Com as regras estabelecidas para a difusão de part´ıculas na rede, simulamos os modelos I e II com condi¸cões periódicas para redes de quatro tamanhosL= 6 250, 12 500, 25 000, e 50 000, usando oito amostras independentes para o menor tamanho, seis paraL= 12 500, e quatro para os demais tamanhos. Usamos 11 valores diferentes dep, entre o pc ep= 2.

As simula¸cões foram até um tempo máximo de 106 _{à 6}_×₁₀9 _{para pontos próximos do}

ponto cr´ıtico. Tamb´em usamos caixas logar´ıtmicas na an´alise de dados.

Inicialmente, analisamos a evolu¸cão temporal do deslocamento quadrático médio das part´ıculas, equa¸cão 2.6.

h[∆xj(t)]2i ∝tγ (2.6)

Este comportamento nos permite caracterizar o tipo de difusão [101, 102]. A difusão usual é quando o deslocamento quadrático é proporcional ao tempo (γ = 1), e não-linear (difusão anômala) quando γ < 1, ou γ > 1. Neste caso temos o processo de difusão anômala subdifusivo, ou superdifusivo, respectivamente. Para os dois modelos que estu-damos, analisamos a evolu¸cão temporal do deslocamento quadrático usando três valores diferentes de p (fizemos a média sobre 4 amostras) para L = 50 000. O primeiro corres-ponde ao comportamento subdifusivo das part´ıculas no regime inicial (linha tracejada das figuras 2.2 e 2.3) que segue um comportamento com γ = 0,86(1). Neste caso ocorre um crescimento lento do desvio quadrático médio, que se acentua quando p → pc, ou seja,

quanto mais próximo do ponto cr´ıtico, maior o intervalo que ocorre a difusão anômala. O segundo corresponde a região estacionária, que comentaremos adiante, confirmando que

h[∆xj(t)]2icresce linearmente com t (linha cont´ınua das figuras 2.2 e 2.3), o que confirma

a rela¸c˜ao 2.5. O tempo de simula¸c˜ao para obter o comportamento linear de h[∆xj(t)]2i