Fraturas e caminhos ótimos na rede de Barabasi-Albert

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE FÍSICA TE ÓRICA E EXPERIMENTAL PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

Fraturas de Caminhos ´

Otimos na Rede de

Barab´

asi-Albert

THIAGO CRIS ´OSTOMO CARLOS NUNES

(2)

Fraturas de Caminhos ´

Otimos na Rede de

Barab´

asi-Albert

Disserta¸cão de mestrado apresentada ao Programa de Pós-Gradua¸cão em F´ısica do Departamento de F´ısica Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial para obten¸cão do grau de mestre em F´ısica.

Orientador: Prof. Dr. Luciano Rodrigues da Silva Co-Orientador: Dr. Gabriel Alves Mendes

(3)

Agradecimentos

Agrade¸co a minha verdadeira fam´ılia, meus pais, meu irm˜ao e minha querida e amada av´o, por me acolherem nas horas de cansa¸co e stresse me fazendo acreditar que tudo daria certo mesmo quando tudo parecia perdido.

Ao professor e orientador Dr. Luciano Rodrigues da Silva por todo seu apoio para a realiza¸c˜ao deste trabalho e principalmente pela ajuda no amadurecimento dos meus conhe-cimentos.

Ao meu co-orientador Dr. Gabriel Mendes pela orienta¸cão e discussões nesse trabalho. Aos amigos do grupo de pesquisa, MSc. Antonio Marques, MSc. Tiago Medeiros, MSc. Thiago Rafael e o MSc. Maur´ıcio Lopes, e a mestranda Samurai Gomes de Aguiar pelas discussões e ajudas durante o desenvolvimento desta disserta¸cão.

`

A Mariana Barbosa da Silva, uma grande amiga que me cativou por completo e que nunca mediu esfor¸cos para me acalmar nas horas de turbulˆencia.

`

(4)

Seguindo a linha do trabalho de Andrade e colaboradores (2009) em redes regulares, nós investigamos o problema da fratura através do caminho ótimo (optimal path cracks -OPC) em Redes Complexas. Neste problema nós associamos para cada s´ıtio uma determinada energia. O caminho ótimo é definido como aquele, dentre todos os poss´ıveis, que atravessa o sistema e tem o menor custo, ou seja, a menor soma das energias ao longo do caminho. Uma vez que o caminho ótimo é determinado, em cada passo, nós bloqueamos o s´ıtio com maior energia e a partir de então um novo caminho ótimo é calculado. Este procedimento é repetido até que exista um conjunto de s´ıtios bloqueados que forma uma fratura macroscópica a qual conecta lados opostos do sistema. O método é aplicado numa rede de lado L e a densidade de s´ıtios removidos é computada. Como observado no trabalho de Andrade e colaboradores, o sistema fraturado que nós estudamos também apresenta diferentes comportamentos dependendo do n´ıvel da desordem, que pode ser fraca, moderada ou forte. No regime de desordem fraca e moderada, a densidade de s´ıtios removidos no sistema não depende do tamanho L no caso de redes regulares, enquanto no regime de desordem forte a densidade se torna substancialmente dependente de L. Nós fizemos o mesmo tipo de estudo para Redes Complexas. Neste caso, cada novo s´ıtio é conectado a m s´ıtios que já estão presentes na rede. Como no trabalho anterior, nós observamos que a densidade de s´ıtios removidos apresenta um comportamento similar. Além disso, um novo resultado é obtido, isto é, nós analisamos a dependência da desordem com o parâmetro de liga¸cão m.

(5)

Abstract

Following the study of Andrade et al. (2009) on regular square lattices, here we investigate the problem of optimal path cracks (OPC) in Complex Networks. In this problem we associate to each site a determined energy. The optimum path is defined as the one among all possible paths that crosses the system which has the minimum cost, namely the sum of the energies along the path. Once the optimum path is determined, at each step, one blocks its site with highest energy, and then a new optimal path is calculated. This procedure is repeated until there is a set of blocked sites forming a macroscopic fracture which connects the opposite sides of the system. The method is applied to a lattice of size L and the density of removed sites is computed. As observed in the work by Andrade et al. (2009), the fractured system studied here also presents different behaviors depending on the level of disorder, namely weak, moderated and strong disorder intensities. In the regime of weak and moderated disorder, while the density of removed sites in the system does not depend of the size L in the case of regular lattices, in the regime of high disorder the density becomes substantially dependent on L. We did the same type of study for Complex Networks. In this case, each new site is connected with m previous ones. As in the previous work, we observe that the density of removed sites presents a similar behavior. Moreover, a new result is obtained, i.e., we analyze the dependency of the disorder with the attachment parameter m.

(6)

Introdu¸c˜ao 2

1 Percola¸c˜ao 4

1.1 Introdu¸c˜ao . . . 4

1.2 Percola¸c˜ao por s´ıtios . . . 4

1.3 Percola¸c˜ao por liga¸c˜oes . . . 6

1.4 Leis de escala . . . 7

1.5 Fractais e percola¸c˜ao . . . 9

1.5.1 Dimens˜ao fractal do aglomerado percolante . . . 10

2 Conceitos b´asicos e caracter´ısticas de redes 12 2.1 Introdu¸c˜ao . . . 12

2.2 Conceitos b´asicos de redes . . . 15

2.2.1 Distribui¸c˜ao de conectividade . . . 15

2.2.2 Coeficiente de agrega¸c˜ao . . . 16

2.2.3 6 graus de separa¸c˜ao . . . 17

2.2.4 Mundo pequeno . . . 18

2.3 Modelos de redes . . . 19

2.3.1 Modelo de Erd¨os e R´enyi . . . 19

2.3.2 Propriedades de grafos aleat´orios . . . 21

2.3.3 Modelo de Wattz e Strogatz . . . 25

2.3.4 Modelo de Barab´asi e Albert . . . 26

2.3.5 Propriedades do modelo de Barab´asi e Albert . . . 29

3 O problema do caminho m´ınimo 32 3.1 Introdu¸c˜ao . . . 32

3.2 Algoritmo de Dijkstra . . . 34

3.3 Heap bin´aria . . . 37

(7)

3.3.1 Inserindo um elemento na heap . . . 39 3.3.2 Extraindo um elemento da heap . . . 40

4 Redes de fraturas 42

4.1 Introdu¸cão . . . 42 4.2 Fraturas de caminhos ótimos . . . 43 4.2.1 Modelo de fraturas de caminhos ótimos . . . 44 5 Fraturas de caminhos ótimos na rede de Barabási-Albert 51 5.1 Introdu¸cão . . . 51 5.2 Aplica¸cão do Modelo de Optimal Path Crack na rede de Barabási-Albert . . 52 5.3 Regime de desordem baixa . . . 53 5.4 Regime de desordem moderada . . . 56 5.5 Regime de desordem alta . . . 58

6 Conclus˜oes 64

Bibliografia 66

(8)

1.1 Percola¸cão por s´ıtios em rede quadrada. Redes com lado L = 16 e com dife-rentes probabilidades de ocupa¸cão. Em p_≈0.59 surge o aglomerado percolante. 5 1.2 Percola¸cão por s´ıtios em rede quadrada. Em vermelho o aglomerado percolante

que conecta a margem esquerda à margem direita da rede. . . 5 1.3 Percola¸cão por liga¸cão em rede quadrada. As liga¸cões conectadas entre si

formam os aglomerados. Em vermelho, o aglomerado percolante . . . 6 1.4 Curvas P∞×p para diferentes tamanhos L de rede em percola¸c˜ao por s´ıtios.

P∞ cresce com pseguindo uma lei de potˆencia(eq. 1.2). . . 8

1.5 Comportamento do comprimento de correla¸cão ξ(p) em fun¸cão de p. Vemos que ξ(p) diverge na região cr´ıtica dep. . . 9 2.1 a) Representa¸cão das pontes de Königsberg. b) Grafo de Euler para o problema

das pontes de Königsberg. As pontes são representadas pelas liga¸cões e as por¸cões de terra pelos nós. . . 13 2.2 Representa¸cão esquemática de uma rede. O nó destacado em vermelho tem

conectividade 5 (k = 5). . . 13 2.3 a) Representa¸c˜ao da rede de Bethe. Esse ´e um exemplo de uma rede tipo

árvore. b) Exemplo de uma rede com presen¸ca de circuito de ordem n = 3, representado pelos nós em vermelho e pelas liga¸cões em azul. Essa rede possui número de nós N = 8 e número de liga¸cões L = 8. Com esses dados, usando a rela¸cãoI =L+ 1₋N, podemos determinar o número de circuitos presentes na rede. Nesse caso, temos I = 1. . . 14 2.4 Figura de um nó ν e seus primeiros vizinhos, vemos que kν = 6 resultando

cν = 1/3. . . 17

2.5 Mapa dos Estados Unidos destacando os estados de Nebraska e Kansas ao cen-tro e massachusetts ao canto, ambos representando respectivamente os pontos de saida e chegada das cartas. . . 18

(9)

2.6 Figura (a) referente a N = 10 nós isolados, onde depois é conectado cada par de nós com probabilidadep. Figura (b) mostra o grafo em um estágio ava¸cado de conexões. . . 20 2.7 Processo de evolu¸cão de um grafo para o modelo de Erdös-Rényi. (A) Come¸camos

com N = 10 nós isolados, depois conectamos cada par de nós com probabili-dade p. (B) e (C) mostram diferentes estágios no desenvolvimento do grafo, correspondentes a probabilidades p = 0.1 e p = 0.15 respectivamente. Po-demos notar o surgimento de árvores (uma de ordem 3, linhas tracejadas) e ciclos (um ciclo de ordem 3, linhas tracejadas) num grafo, e um aglomerado que conecta metade dos nós em p= 0.15 = 1.5/N. . . 20 2.8 A figura exibe os processos de conexões dos nós para o modelo de

Wattz-Strogatz, o qual interpola entre um c´ırculo regular e uma rede aleatória sem alterar o número de nós ou arestas. Em tal figura come¸ca-se comN = 10 nós, cada nó conectado aos seus quatro primeiros vizinhos. Para p= 0 o c´ırculo se mantém inalterado; com o aumento de p a rede aumenta desordenadamente até p= 1 onde todas as arestas são re-conectadas aleatoriamente. . . 25 2.9 Tamanho do caminho L(p) e coeficiente de agrega¸cão C(p) para o modelo de

Wattz-Strogatz. Os dados estão normalizados para os valores de L(0) e C(0) para um rede regular. Há uma rápida queda no caminho médio L(p), o que corresponde ao efeito de mundo pequeno, e durante esta queda nota-se que C(p) permanece quase constante, indicando que a transi¸cão para o mundo pequeno é quase indetectável à n´ıvel local. . . 26 2.10 Figuras referentes a redes livres de escala para o modelo de Barabási-Albert.

(a) Figura paraN = 8 nós que se conectam segundo uma distribi¸cão de conec-tividade em lei de potência P(k) = k−γ_{. (b) Figura para uma rede de escala}

livre após a adi¸cão de vários nós. . . 27 2.11 Caracter´ıstica do caminho médiolpelo tamanhoN da rede de Barabási-Albert

com _hk_i= 4, comparada com um grafo aleatório de mesmo tamanho e mesma conectividade média. . . 30 2.12 Coeficiente de agrega¸cão pelo tamanho da rede de (BA) com _hk_i= 4,

compa-rada com o coeficiente de agrega¸c˜ao de um grafo aleat´orio com Crand ≈ hki/N. 31

3.1 Grafo das rotas entre as cidades A e B. Os vértices são as cidades, as arestas são os trechos entre as cidades com seus respectivos pesos dados em Km. As arestas tracejadas em vermelho formam um dos menores caminhos. . . 33

(10)

As arestas que estão sombreadas indicam que π(v) = u, e os vértices em preto pertencem ao conjunto S. Os vértices brancos pertencem ao conjuntoQ, e os vértices sombreados são aqueles que têm menor valor em tal conjunto. . . 37 3.3 Na figura acima temos uma Heap, que é uma árvore binária completa e de

prioridade, pois o valor de cada nó é menor ou igual que os de seus filhos. Para termos uma árvore binária de prioridade completa é preciso que seus n´ıveis estejam cheios, com poss´ıvel exce¸cão do último, ao qual está preenchido da esquerda para a direita até um certo ponto. . . 38 3.4 Uma simples e interessante representa¸cão de uma heap usando vetores. Temos

que a raiz ocupará o primeiro elemento do vetor A[1] = 2 e seus filhos ocupam as posi¸cões A[2] = 4 pois tal posi¸cão é 2_×(´ındice do pai) e A[3] = 9 pois é 2_×(´ındice do pai) + 1. Assim os filhos de A[2] ocuparão as posi¸cões A[4] = 6 e A[5] = 5 e os filhos de A[3] ocuparam as posi¸cões A[6] e A[7], que para o nosso caso só será A[6] = 98 e A[7] = 10. . . 39 3.5 a) Inserimos o elemento de prioridade 3 na última posi¸cão da heap, ou seja,

a esquerda do elemento de prioridade 5. b) Comparamos o valor do elemento inserido com o valor do seu pai (nó com valor 5) com o intuito de tornar a árvore novamente de prioridade, caso o elemento inserido seja menor que seu pai eles trocam de posi¸cão na heap. . . 40 3.6 Para o nosso exemplo a raiz ficará com o valor 81, logo em seguida

compara-se o nó raiz com compara-seus filhos e trocam-compara-se os valores sucessivamente caso os filhos tenham um valor menor que o do pai até que se encontre a posi¸cão que satisfa¸ca a prioridade da heap, ou seja, uma posi¸cão em que o pai é menor do que qualquer um dos filhos ou até não ter mais elementos . . . 41 4.1 Falha de San Andreas na California. Considerando apenas uma fratura

sim-ples, o encontrado para tal falha é que sua dimensão fractal é em torno de Df rac≈1.15 (5). . . 43

(11)

4.2 As figuras (a) e (b) mostram o regime de desordem fraca para realiza¸cões equivalentes: em (a) as energias dos s´ıtios são distribu´ıdas seguindo a lei de potência P(ǫi) ∝ _ǫ1_i com βD = 0.002, enquanto que em (b) as energias são

uniformemente distribu´ıdas. As figuras (c) e (d) mostram fraturas para βD =

6 e βD = 100, sendo que a figura (c) corresponde ao regime de desordem

intermediário e a figura (d) o regime de desordem forte. O backbone da fratura é mostrado em vermelho, os s´ıtios pertencentes ao maior cluster da fratura, com ausência do backbone, estão em azul, e os s´ıtios bloqueados que não fazem parte da fratura e do backbone estão em verde. . . 46 4.3 Dependência logar´ıtmica da massa de todos os s´ıtios bloqueadosMt formando

o OPC, o cluster de todos os s´ıtios na fratura Mf, e a massa do backbone da

fratura, pelo tamanho L do sistema para β = 0.002 . . . 48 4.4 Dependˆencia logar´ıtmica da massa de todos os s´ıtios bloqueadosMt formando

o OPC, o cluster de todos os s´ıtios na fratura Mf, e a massa do backbone da

fratura que parte o sistema, pelo tamanho L do sistema para βD = 6. Para

este valor intermedi´ario de βD podemos indentificar o crossover no regime de

desordem forte para o regime de desordem fraca que depende do tamanho do sistema . . . 49 4.5 Transi¸c˜ao da desordem forte para a desordem fraca no modelo de OPC. As

curvas exibem o comportamento da densidade de todos os s´ıtios bloqueadosρt

pelo parâmetro de desordem do sistema. Estas curvas apresentam três regimes. Para a desordem fraca (βD <1), onde vemos uma satura¸cão na densidade de

s´ıtios bloqueados em torno de ρt= 0.22. Para desordem intermedi´aria vemos

que a densidade diminui com o parâmetro de desordem e que não há uma dependência em rela¸cão ao tamanho do sistema. Para regimes de desordem forte vemos que o valor da densidade depende do tamanho L do sistema. . . 50 5.1 Número total Mt de s´ıtios bloqueados como fun¸cão do tamanhoN do sistema

para o regime de desordem baixa. Nas curvas referentes `a m = 2, m = 4 e m = 8 foram usadas redes de tamanho 1000, 2000, 4000, 8000, 16000, 32000 e 64000, sendo que para cada rede foram simuladas cerca de 12000 amostras. . 54 5.2 Rede de Barab´asi-Albert para m = 4(A) e m = 8(B) e N = 100 no regime

de desordem baixa. Os s´ıtios em verde são os que permanecem na rede, os em vermelho são os s´ıtios bloqueados (Fratura) e os s´ıtios em azul são os que compreendem o caminho ótimo. . . 55

(12)

5.3 N´umero total Mt de s´ıtios bloqueados como fun¸c˜ao do tamanhoN do sistema

para o regime de desordem moderada. Nas curvas referentes `a m = 2, m= 4 e m= 8 foram usadas redes de tamanho 1000, 2000, 4000, 8000, 16000, 32000 e 64000, sendo que para cada rede foram simuladas cerca de 12000 amostras. 56 5.4 Rede de Barab´asi-Albert param = 4(A) e m= 8(B) e N = 100 no regime de

desordem moderada. Os s´ıtios em verde são os que permanecem na rede, os em vermelho são os s´ıtios bloqueados (Fratura) e os s´ıtios em azul são os que compreendem o caminho ótimo. . . 57 5.5 Número total Mt de s´ıtios bloqueados como fun¸cão do tamanhoN do sistema

para o regime de desordem alta. Nas curvas referentes `a m = 2, m = 4 e m = 8 foram usadas redes de tamanho 1000, 2000, 4000, 8000, 16000, 32000 e 64000, sendo que para cada rede foram simuladas cerca de 12000 amostras. . 58 5.6 Rede de Barab´asi-Albert para m = 4(A) e m = 8(B) e N = 100 no regime

de desordem alta. Os s´ıtios em verde são os que permanecem na rede, os em vermelho são os s´ıtios bloqueados (Fratura) e os s´ıtios em azul são os que compreendem o caminho ótimo. . . 59 5.7 Parâmetro de desordem βD como fun¸cão da fra¸cão de s´ıtios bloqueados no

sistema para m = 2. Foram usadas redes de tamanho 1000, 2000 e 4000. Nas curvas acima vemos três diferentes regimes, o de desordem baixa, o de desordem moderada e de desordem alta. . . 60 5.8 Parâmetro de desordem βD como fun¸cão da fra¸cão de s´ıtios bloqueados no

(13)

Introdu¸

c˜

ao

Como podemos observar na natureza, estamos rodeados de materiais dos quais suas es-truturas apresentam algum tipo de desordem, que microscopicamente podem ter rela¸cão com espa¸cos vazios, descolamentos e até mesmo composi¸cão estrutural, o que os torna suscet´ıveis a fraturas que dependem significamente do grau de desordem em que o dado material se encontra. Existem basicamente dois regimes de desordem, um regime de baixa desordem, onde os elementos pertencentes a um determinado sistema têm uma propriedade que em si não diferencia muito uma da outras, e existe o regime de alta desordem, definido justamente de forma contraria à anterior, cujos elementos de um sistema podem ter uma propriedade que se diferencia significamente uma da outras.

Encontramos também na natureza sistemas que são ditos Sistemas Complexos, pois é formado por um grande número de unidades simples, mas cuja intera¸cão entre eles influen-cia o comportamento de todo o sistema, sendo sua complexidade dada pela quantidade de informa¸cão necessária para descrevê-la. Dentre os Sistemas Complexos, estão as Redes Com-plexas, que descrevem vários sistemas reais, tais como a sociedade, uma rede de indiv´ıduos ligados por várias rela¸cões sociais, a Internet, uma rede de roteadores conectados por várias conexões, ou até mesmo uma célula, uma rede de substratos conectados por rea¸cões qu´ımicas. Resultados da topologia de tais redes encontraram que, independente da natureza do sistema e da identidade de seus constituintes, suas distribui¸cões de conectividade P(k) decai como uma lei de potênciaP(k) = k−γ_{. Esses resultados são as primeiras evidências de que algumas}

grandes redes podem se auto organizarem como uma rede em escala livre.

A origem do comportamento de escala livre tem sido explicada por dois mecanismos básicos que estão presentes em muitos sistemas reais. Primeiro, a rede se desenvolve com a adi¸cão de novos s´ıtios. Segundo, é mais provável que a um s´ıtio ser adicionado à rede o mesmo se conecte a outros nós com altos valores de conectividade (liga¸cão preferencial).

Assim o alto interesse de entender a topologia das Redes Complexas tem resultado em um desenvolvimento de um n´umero consider´avel de modelos redes, assim como modelos que

(14)

(15)

Cap´ıtulo 1

Percola¸

c˜

ao

1.1 Introdu¸

c˜

ao

Percola¸cão é um modelo matemático desenvolvido com o propósito de resolver proble-mas em meios aleatórios agregados a conceitos geométricos e probabil´ısticos. Introduzido formalmente em 1957 por Broadbent e Hammersley o modelo de percola¸cão é um processo do qual um fluido se dispersa através de um meio aleatório [1]. Para exemplificar melhor essa situa¸cão, imagine uma rocha colocada dentro de um recipiente com água, fa¸camos agora o seguinte questionamento: qual a probabilidade do centro da rocha está molhada? A for-mula¸cão de um modelo para representar tal situa¸cão fez surgir o modelo de percola¸cão [2]. O termo percola¸cão vem da semelhan¸ca que tal processo tem quando comparado ao processo de fluxo do café no coador (percolator em inglês). Desde então qualquer sistema cuja estrutura espacial seja aleatória, a teoria de percola¸cão pode ser aplicada, por tal motivo a teoria de percola¸cão tem encontrado aplica¸cões em diversas áreas, como na propaga¸cão de epidemias, modelagem em propaga¸cão em fogo nas florestas, redes elétricas desordenadas, etc.

Vamos abaixo fazer uma breve introdu¸c˜ao a alguns conceitos da teoria de percola¸c˜ao.

1.2 Percola¸

c˜

ao por s´ıtios

Podemos descrever o modelo de percola¸cão por s´ıtios tomando inicialmente uma rede quadrada comN_×N s´ıtios [3]. Considera-se que cada s´ıtio ou célula da rede seja ocupado de forma aleatória com uma probabilidadep, ou permane¸ca vazio com uma probabilidade 1₋p. Na Figura 1.1 podemos ver redes de mesmo tamanho mas com diferentes probabilidades de

(16)

ocupa¸cão dos s´ıtios. Observe que há forma¸cão de aglomerados, que são conjuntos de s´ıtios que têm um lado em comum, os quais chamamos de primeiros vizinhos. Notamos que à medida que a probabilidade de ocupa¸cãopaumenta, os aglomerados ficam cada vez maiores, assim a percola¸cão ocorre quando existe um aglomerado que conecta as bordas da rede (Figura 1.2). Existe então um valor cr´ıtico bem definido,p=pc, a partir do qual se forma um aglomerado

que liga uma extremidade a outra da rede, fazendo o sistema percolar. Tal valor corresponde ao limiar de percola¸cão e é a probabilidade m´ınima necessária para que exista pelo menos um caminho percolante.

Figura 1.1: Percola¸c˜ao por s´ıtios em rede quadrada. Redes com lado L = 16 e com diferentes probabilidades de ocupa¸c˜ao. Emp_≈0.59 surge o aglomerado percolante [4].

Figura 1.2: Percola¸c˜ao por s´ıtios em rede quadrada. Em vermelho o aglomerado percolante que conecta a margem esquerda `a margem direita da rede [35].

(17)

6

de percola¸cão, que é o menor valor de p para o qual o sistema percola. Esse valor separa duas fases distintas: para p < pc, o sistema não percola e não existe nenhum caminho que

conecte as margens opostas da rede, para p > pc, o sistema percola pois existe pelo menos

um caminho que conecte as margens rede, por onde pode fluir por exemplo uma corrente elétrica, um fluido, etc. Dizemos então que ocorreu uma transi¸cão de fase, pois o sistema exibe diferentes propriedades acima e abaixo depc. Como a transi¸cão de fase é regulada por

um parâmetro que reflete as caracter´ısticas geométricas do sistema, dizemos que se trata de uma transi¸cão de fase geométrica.

1.3 Percola¸

c˜

ao por liga¸

c˜

oes

Neste tipo de percola¸cão consideramos uma rede composta por N _×N s´ıtios, os quais podem estar ligados por segmentos de reta, ver Figura 1.3. Assim como na percola¸cão por s´ıtios, as liga¸cões são preenchidas aleatoriamente com probabilidade p. Em uma rede quadrada, uma liga¸cão tem mais vizinhos do que um s´ıtio, ou seja, enquanto que um s´ıtio tem quatro s´ıtios como primeiros vizinhos, uma liga¸cão tem seis liga¸cões como primeiros vizinhos, o que facilita a forma¸cão de aglomerados na percola¸cão por liga¸cões. Deste modo é necessário um percentual menor de liga¸cões para formar o aglomerado percolante e assim o limiar de percola¸cão por liga¸cões (pc) é menor que o limiar de percola¸cão por s´ıtios.

(18)

1.4 Leis de escala

Como visto na se¸cão anterior, o modelo de percola¸cão é um exemplo de fenômeno cr´ıtico, pois em um determinada probabilidade (pc) ocorre uma transi¸cão de fase. Esta transi¸cão de

fase é puramente geométrica, pois apenas o valor do parâmetro que reflete as caracter´ısticas geométricas do sistema,pc, separa uma fase na qual existem aglomerados finitos de liga¸cões,

de uma fase onde est´a presente o aglomerado infinito.

Associadas aos fenômenos cr´ıticos estão as leis de escala e a estas os expoentes cr´ıticos. O estudo dos expoentes cr´ıticos tem revelado que eles são independentes da maior parte dos parâmetros do sistema, como por exemplo, a topologia da rede. Este fato é chamado invariância e os sistemas que possuem os mesmo valores de expoentes cr´ıticos são ditos pertencentes a uma mesma classe de universalidade [5].

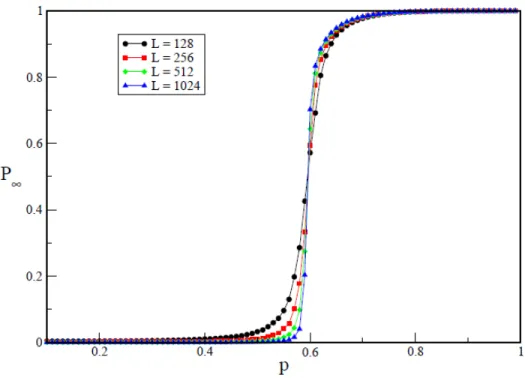
Uma grandeza comumente tratada em trabalhos cient´ıficos ´e a probabilidade P∞ de um

s´ıtio ocupado ou uma liga¸c˜ao ocupada pertencer ao aglomerado infinito [4]. Essa probabili-dade ´e definida como

P∞ =

n´umero de s´ıtios do aglomerado infinito

número total de s´ıtios ocupados (1.1) Vemos que tal valor também representa a fra¸cão de s´ıtios que fazem parte do aglomerado percolante quando este se expande pela rede infinita emp=pc.

Em p= pc existe uma transi¸cão entre duas fases macroscópicas: uma com “ausência do

aglomerado percolante” e a outra com “presen¸ca do aglomerado percolante”. Para p < pc

n˜ao existe aglomerado infinito eP∞→0, ver Figura 1.4. Para p≥pc, aparece o aglomerado

infinito e P∞ pr´oximo do ponto cr´ıtico comporta-se como:

P∞(p)≈

(

0 se p < pc

(p₋pc)β se p > pc

(1.2)

Como P∞ descreve a ordem nos sistemas de percola¸c˜ao, o mesmo pode ser identificado

como o parˆametro de ordem destes sistemas, sendo β o expoente cr´ıtico relacionado a este parˆametro.

Outra grandeza é o comprimento de correla¸cão ξ que se refere ao comprimento dos aglo-merados finitos, abaixo e acima de pc, sendo definida como a distância média entre dois

(19)

aglome-8

Figura 1.4: CurvasP∞×ppara diferentes tamanhosLde rede em percola¸c˜ao por s´ıtios. P∞cresce

comp seguindo uma lei de potˆencia (eq. 1.2).

rado percolante tem o tamanho do comprimento da rede, L, logo se L tende ao infinito o comprimento de correla¸c˜ao diverge nesse ponto, ver Figura 1.5.

ξ(p)_≈(p₋pc)−ν (1.3)

O expoenteν exibe o mesmo valor abaixo e acima do limiar de percola¸c˜ao pc.

Outra grandeza frequentemente estudada em percola¸cão é o número médio de s´ıtios, ou a massa, S, de um aglomerado finito, que também diverge nas proximidades de pc. Tal

grandeza se comporta como:

S(p)_{≈ |}p₋pc|−γ (1.4)

O expoenteγ tamb´em ´e o mesmo acima e abaixo de pc.

(20)

Figura 1.5: Comportamento do comprimento de correla¸cão ξ(p) em fun¸cão de p [4]. Vemos que ξ(p) diverge na região cr´ıtica de p.

também não dependem do tipo de percola¸cão (por s´ıtios, por liga¸cão, etc), mas dependem apenas da dimensionalidade do sistema.

1.5 Fractais e percola¸

c˜

ao

Quando dizemos que um plano é bidimensional e que o espa¸co é tridimensional estamos nos referindo ao conceito de dimensão Euclidiana. Em tal conceito a dimensão Euclidiana pode ser entendida como a dimensão na qual os objetos são relacionados ao espa¸co no qual estão inseridos, e, portanto pontos têm dimensão zero, retas assim como curvas têm di-mensão 1, planos têm didi-mensão 2, e sólidos têm didi-mensão 3. Tal conceito pode ser ampliado sucessivamente atén dimensões, sendo n um número inteiro.

(21)

10

A geometria fractal [6], em especial a dimensão fractal, tem sido objeto de estudo de di-versas áreas, pois uma grande variedade de estruturas complexas tem sido quantitativamente descritas utilizando-se de tal teoria como ferramenta, e com aplicabilidades como caracte-riza¸cão de objetos, analise e reconhecimento de padrões em imagens, etc.

Os fractais são objetos com uma estrutura muito irregular, ou quebrada, e que possuem algumas caracter´ısticas peculiares que os diferenciam das outras formas geométricas, em tais caracter´ısticas está presente à auto-similaridade em diferentes n´ıveis de escala e dimensões que são fracionárias.

O termo fractal foi criado em 1975 pelo matemático chamado Benoit Mandelbrot [6], sendo o motivo de tal termo o adjetivo latino fractus, que significa quebrar, devido à estrutura irregular dos fractais. Em seu livro intitulado The Fractal Geometry of Nature, Mandelbrot cita a defini¸cão formal de fractal:

“Um fractal é, por defini¸cão, um conjunto para o qual a dimensão de Hausdorff - Besi-covitch excede, estritamente, a dimensão topológica.”

A dimens˜ao D de Hausdorff - Besicovitch ´e definida quando δ _→0 como:

Md=

X

h(d) = Xγ(d)δd=γ(d)N(δ)δd_−→ (

0 se d > D

∞ se d < D (1.5) Para o conjunto de pontosSa qual a d-medidaMdde tal conjunto muda de zero a infinito,

sendoN(d) o número de fun¸cões testesh(d) necessárias para cobrir o conjunto S de pontos, γ(d) o fator geométrico,d é a dimensão da medida e δ é o comprimento. A dimensão D de Hausdorff - Besicovitch é chamada de dimensão fractal.

1.5.1 Dimens˜

ao fractal do aglomerado percolante

Próximo ao limiar de percola¸cão, o aglomerado percolante apresenta a propriedade de auto-similaridade e comporta-se como um fractal, possibilitando a descri¸cão da estrutura dos aglomerados percolantes através de conceitos fractais. Como vimos, se a probabilidade de ocupa¸cão é maio ou menor quepc, o comprimento de correla¸cãoξ descreve o tamanho médio

dos aglomerados finitos do sistema, e em pc, ξ diverge e existem buracos no aglomerado

percolante. O aglomerado percolante pode ser auto-similar apenas nas escalas de tamanho menores que ξ, pois ξ ´e finito para valores maiores que pc, logo acima de pc, em escalas de

(22)

M(L, ξ)_≈  



Ldf se L≪ξ ξdf

L ξ

d

se L_≫ξ (1.6)

A probabilidade de que um s´ıtio arbitrário no interior de um disco de raio r, menor do queξ, perten¸ca ao aglomerado percolante é a razão entre o número de s´ıtios no aglomerado percolante e o número total de s´ıtios,

P∞ ≈

M(r)

M ≈

rdf

rd , r < ξ. (1.7)

Tal equa¸cão também é válida se considerarmos r = aξ, onde a é uma constante arbitraria menor que 1, ou seja, 0< a <1. Assim substituindor =aξ em (1.7) obtemos,

P∞≈

ξdf

ξd (1.8)

Logo podemos relacionar os expoentes cr´ıticos β e ν com a dimens˜ao fractal df dos

aglomerado percolantes, pois das equa¸c˜oes (1.2), (1.3) e (1.8) vemos que

(p₋pc)β ≈(p−pc)ν(d−df)

Ou seja,

df =d−

β

ν (1.9)

Esta rela¸cão mostra que a dimensão fractaldf do aglomerado percolante empcé um expoente

que depende de β e ν, como tais expoentes são universais então df é também um expoente

(23)

Cap´ıtulo 2

Conceitos b´

asicos e caracter´ısticas de

redes

2.1 Introdu¸

c˜

ao

Redes complexas são abundantes na natureza, descrevendo diversos sistemas reais, tais como a sociedade, uma rede de indiv´ıduos ligados por várias rela¸cões sociais, a Internet, uma rede de roteadores conectados por varias conexões, a World Wide Web, uma enorme rede virtual de páginas na Web conectadas por links, ou até mesmo uma célula, uma rede de substratos conectados por rea¸cões qu´ımicas [23]. Mas o que exatamente significa uma rede? Como e quais mecanismos determinam a topologia de tais redes? Questionamentos como esses têm induzido a comunidade cient´ıfica a tentar compreender muitos fenômenos da natureza relativos a essas áreas de estudo, usando uma important´ıssima teoria matemática como ferramenta, a teoria de grafos.

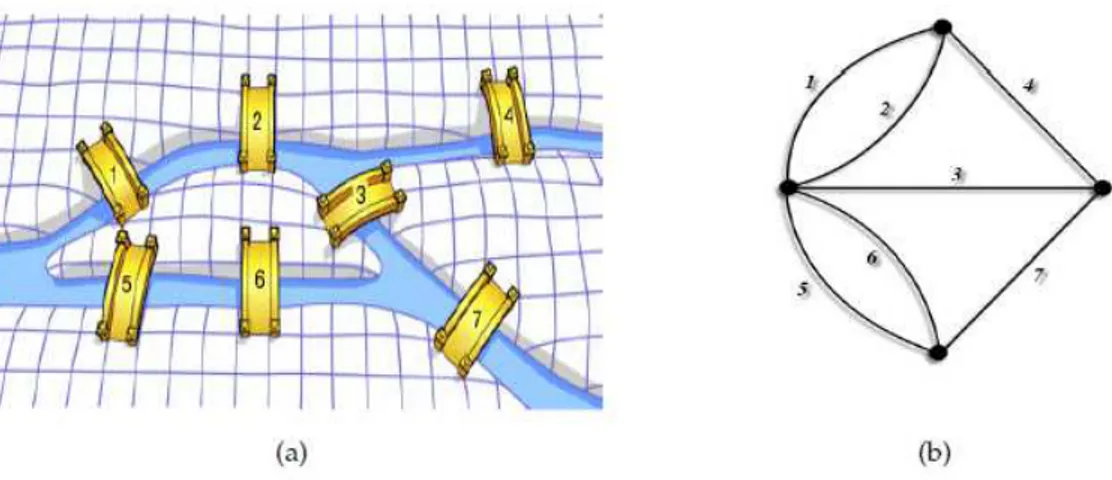
O estudo das redes teve sua origem na teoria dos grafos, quando o matemático Leonard Euler, por volta de 1735, resolveu o problema das pontes de Königsberg [24]. Tal problema consiste em saber se é poss´ıvel atravessar as sete pontes do rio Pregel, rio que corta a cidade de Königsberg, passando sobre cada uma das pontes uma única vez e assim regressar ao ponto de partida, ver Figura 2.1. Para solucionar o problema Euler usou um artif´ıcio matemático em que ele transformou as pontes em segmentos e as por¸cões de terra em pontos, e chegou à conclusão que o problema era insolúvel [13]. Essa prova é considerada o ponto de partida do ramo da Matemática conhecido como Teoria de Grafos.

Temos ent˜ao na Teoria de Grafos, uma teoria que nos possibilita um tratamento

(24)

Figura 2.1: a) Representa¸cão das pontes de Königsberg. b) Grafo de Euler para o problema das pontes de Königsberg. As pontes são representadas pelas liga¸cões e as por¸cões de terra pelos nós.

temático para redes, uma vez que as redes podem ser representadas por grafos [25]. Assim uma rede (ou grafo) é um objeto matemático do qual é constitu´ıdo de um conjunto de vértices (nós), conectados via linhas (liga¸cões, arestas ou arcos), ver Figura 2.2.

Figura 2.2: Representa¸cão esquemática de uma rede. O nó destacado em vermelho tem conectivi-dade 5 (k= 5).

Uma das caracter´ısticas locais mais simples de um nó é a sua conectividade k, que é o número de liga¸cões que ele apresenta, representando também o número total de seus vizi-nhos mais próximos, ver Figura 2.2. Em uma rede onde suas arestas têm dire¸cão (directed networks), a conectividade dos nós tem duas importantes componentes: o número de liga¸cões de sa´ıdakout

(25)

14

chegam ao n´oi), sendo a conectividade total de tal n´o dada por ki =kiin+kouti .

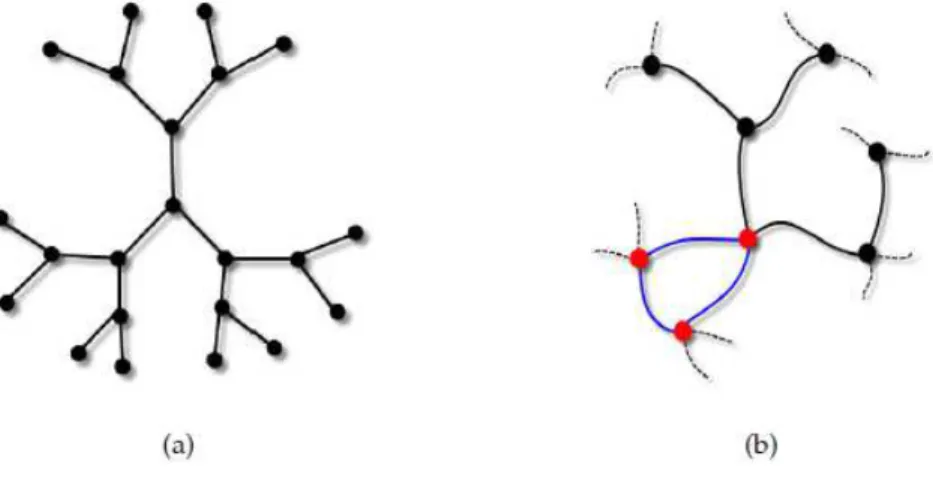
Um tipo importante de grafo são as árvores, que são grafos que não contem circuitos, desta forma existe somente um caminho ligando cada par de nós (Figura 2.3(a)), em particular uma árvore conectada comN nós apresenta um número deL=N₋1 liga¸cões. Se esse grafo não possuir partes separadas, ela é dita uma árvore conectada. Um circuito de ordemn, é definido como um caminho fechado comk liga¸cões tais que cada duas liga¸cões consecutivas, e somente elas, têm um nó comum [26], ver Figura 2.3(b). Em geral o númeroI de circuitos num grafo conectado, cujas liga¸cões não são direcionadas, relaciona-se com o número de liga¸cões e nós pela expressão I =L+ 1₋N.

Figura 2.3: a) Representa¸cão da rede de Bethe. Esse é um exemplo de uma rede tipo árvore. b) Exemplo de uma rede com presen¸ca de circuito de ordemn= 3, representado pelos nós em vermelho e pelas liga¸cões em azul. Essa rede possui número de nósN = 8 e número de liga¸cõesL= 8. Com esses dados, usando a rela¸cão I =L+ 1₋N, podemos determinar o número de circuitos presentes na rede. Nesse caso, temosI = 1.

Outro caso interessante de grafos, é o grafo aleatório, que é um grafo que pode ser definido como um arranjo desordenado de liga¸cões. A no¸cão de aleatoriedade não é aplicável a um ´

unico grafo, assim a descri¸cão estat´ıstica completa de redes aleatórias sugere uma descri¸cão de ensembles estat´ısticos correspondentes. Esse ensemble é definido como o conjunto de seus membros, onde cada membro tem sua própria probabilidade de realiza¸cão, ou seja, uma dada rede aleatória é um grafo com uma probabilidade, e assim por diante.

(26)

serão conectados. Já as redes dinâmicas são aquelas onde, em cada tempo, um novo vértice é adicionado, e ligado à algum s´ıtio pré-existente.

2.2 Conceitos b´

asicos de redes

2.2.1 Distribui¸

c˜

ao de conectividade

Como a conectividade dos vértices em uma rede é distribu´ıda estatisticamente, logo podemos definir uma fun¸cão que represente tais distribui¸cões, a distribui¸cão de conectividade. Introduziremos uma distribui¸cão de conectividade para a rede tal que p(k, s, N) nos dê a probabilidade de que um dado nó s escolhido aleatoriamente tenha k liga¸cões em uma rede de tamanhoN, ou equivalentemente a fra¸cão de nós na rede que têm conectividadek. Assim a distribui¸cão de conectividade total é definida como

P(k, N) =

N

X

s=1

p(k, s, N). (2.1)

Para o caso de grafos que suas arestas têm dire¸cão, precisamos considerar duas distri-bui¸cões, a distribui¸cão de entrada pi_(k

i, s, N) e a distribui¸c˜ao de sa´ıda po(ko, s, N), onde

podemos definir a distribui¸c˜ao total de entrada comopi_(k

i, N) e a distribui¸c˜ao total de sa´ıda

po_(k

o, N). Podemos obter a informa¸c˜ao de como a conectividade se distribui entre os n´os de

uma rede calculando os momentos da distribui¸cão. O n-ésimo momento de P(k) é definido como:

k2

=X

k

knP(k). (2.2)

O primeiro momento então é dado como _hk_i, que é a conectividade média da rede [27]. Demonstrarei a seguir exemplos das distribui¸cões de conectividade mais encontradas no estudo de redes complexas.

(1) Distribui¸cão de Poisson: desde que todos os nós em um grafo aleatório são estatistica-mente equivalentes, o grafo segue uma distribui¸cão de conectividade tal que a probabilidade de que um nó escolhido aleatoriamente tenha uma conectividade k tem a mesma forma de P(ki =k). Para N grande e fixado hki a distribui¸cão de conectividade se aproxima de uma

(27)

16

P(k) = e−hkihki

k

k! . (2.3)

(2) Distribui¸cão exponencial: a distribui¸cão exponencial é obtida para sistemas que não estão em equil´ıbrio, ou seja, em grafos crescidos aleatoriamente através de adi¸cões simultâneas de vértices e arestas. Tal distribui¸cão é dada por:

P(k)_∝e−k/hki. (2.4)

(3) Distribui¸cão em lei de potência: resultados emp´ıricos para muitas redes reais mostram uma distribui¸cão que contrasta com a distribui¸cão de Poisson. Esta distribui¸cão de conec-tividade é dada por: P(k) = k−γ _para _γ ₆_{= 0. Tais redes são chamadas de redes livres de}

escala.

2.2.2 Coeficiente de agrega¸

c˜

ao

O coeficiente de agrega¸cãoC é um dos mais importantes parâmetros usados para carac-terizar a topologia de redes complexas. Tal coeficiente nos dá a probabilidade de que os dois vizinhos mais próximos de um dado nó também sejam vizinhos entre si. Para um dado nói da rede, tendo ele ki arestas as quais o conecta com ki outros nós, o valor do coeficiente de

agrega¸cão deié dado pela rela¸cão entre o número de arestas Ei existentes entre esses ki nós

e o n´umero total de ki(ki−1)/2 de arestas poss´ıveis onde

Ci =

2Ei

ki(ki−1)

(2.5)

A média deCi sobre os vértices de conectividadek nos forneceC(k) como uma agrega¸cão

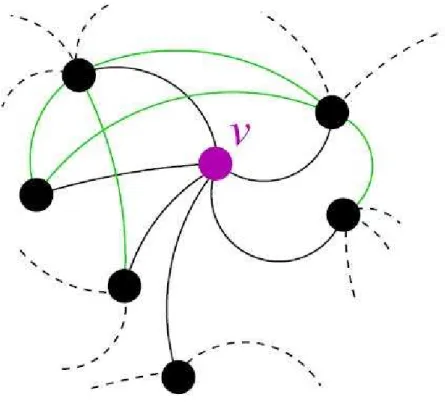
local dependente da conectividade, o qual mostra a probabilidade de que dois vizinhos próximos de um nó de conectividade k estejam ligados entre si, ver Figura 2.4. A conec-tividade média é definida como

hC_i=_hCii=

X

k

P(k)C(k). (2.6)

(28)

hC_{i ≡} hEii

hki(ki−1)/2i

= P

kP(k)hE(k)i

(_hk2_{i − h}_k_i_)/2 (2.7) onde_hC_ié a probabilidade que exista uma aresta entre dois vizinhos de um vértice escolhido aleatoriamente. Podemos dizer que a agrega¸cão _hC_i demonstra a densidade de pequenos loops de tamanho 3 em uma rede.

Figura 2.4: Figura de um n´o ν e seus primeiros vizinhos, vemos que kν = 6 resultandocν = 1/3.

2.2.3 6 graus de separa¸

c˜

ao

Em 1967 o sociólogo norte-americano Stanley Milgram [29] realizou um experimento com o propósito de estimar o número real de passos em uma rede de conhecidos, em tal experimento Milgram selecionou aleatoriamente pessoas em Nebraska e as pediu para enviar cartas às pessoas em Massachusetts (Figura 2.5), identificadas por alguns dados pessoais como nome e ocupa¸cão. Tal experimento consistia em:

(29)

18

(2) Se vocˆe conhece a pessoa alvo mande essa carta diretamente para ela, se n˜ao repasse a carta para algum conhecido que provavelmente a conhe¸ca.

(3) Quando a carta chegar à pessoa alvo, esta deverá enviar a mesma de volta para o pesquisador em questão.

Milgram chegou ao resultado surpreendente que dentro de uma rede de 200 milhões de nós (habitantes), o número de conexões necessárias para alcan¸car a pessoa alvo tinha um valor médio de 6.

Figura 2.5: Mapa dos Estados Unidos destacando os estados de Nebraska e Kansas ao centro e massachusetts ao canto, ambos representando respectivamente os pontos de saida e chegada das cartas.

2.2.4 Mundo pequeno

(30)

média comparada ao do modelo de rede aleatória de Erdös-Rényi (ER) para tamanho e conectividade média.

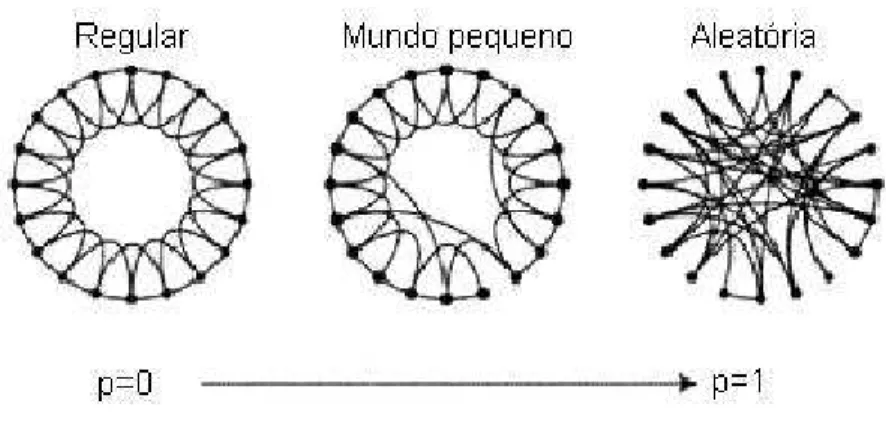
Um dos primeiros modelos de redes com alto coeficiente de agrega¸cão e menor caminho médio foi introduzido por Watts e Strogatz [28], os quais definiram tais redes como sendo de mundo pequeno, redes que tem altos coeficientes de agrega¸cão e diâmetros que crescem logaritmicamente com o número de nós. O modelo proposto por Watts e Strogatz tem como ideia central come¸car com uma rede bem estruturada, como um c´ırculo ou uma grade (Figura 2.8), os quais têm um alto coeficiente de agrega¸cão, mas também uma grande distância entre seus nós, e aleatoriamente re-conectar as arestas da rede com o propósito de reduzir seu diâmetro (confira pág. 25). De uma forma detalhada come¸camos a rede com um c´ırculo com N nós, no qual cada nó é simetricamente conectado aos seus 2m vizinhos mais próximos nos dando um total de K =mN arestas. Depois, cada aresta é re-conectada aleatoriamente a um nó escolhido com probabilidade p. Note que para p = 0 temos uma rede regular, enquanto que para p = 1 temos um grafo aleatório com a restri¸cão de que cada nó tenha uma conectividade m´ınima dada porkmin =m, ver Figura 2.8.

2.3 Modelos de redes

A principal fun¸cão dos modelos de redes é explicar o aparecimento e o comportamento de algumas das mais importantes caracter´ısticas de redes. Como tais modelos são ferramentas que desempenham um papel crucial na nossa compreensão das redes complexas, precisamos prestar aten¸cão a alguns dos mais importantes modelos.

2.3.1 Modelo de Erd¨

os e R´

enyi

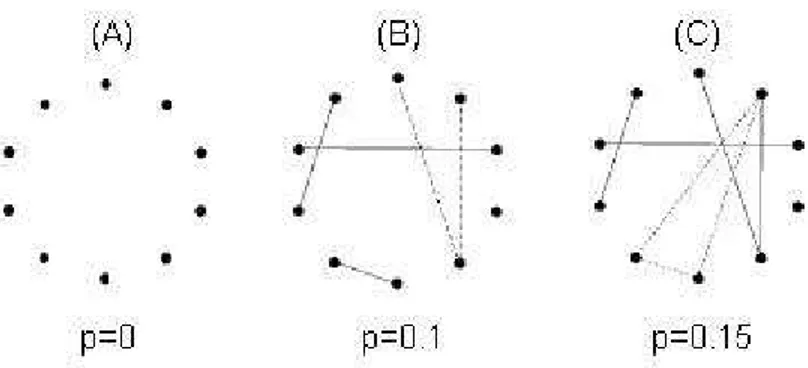
Segundo o modelo de grafos aleatórios de Erdös - Rényi (ER) [31], come¸camos com N nós e conectamos cada par de nós com poss´ıveis N[N₂−1] arestas com uma mesma probabi-lidade p (Figura 2.7), criando um grafo de aproximadamente pN[N₂−1] liga¸cões distribu´ıdas aleatoriamente , ver Figura 2.6. No total é uma combina¸cão deCn

N[N−1]/2 grafos com N nós en arestas. Conseqüentemente o número total de arestas é uma variável aleatória com valor esperadoE(n) =pN[N ₋1]/2.

(31)

20

Figura 2.6: Figura (a) referente a N = 10 nós isolados, onde depois é conectado cada par de nós com probabilidadep. Figura (b) mostra o grafo em um estágio ava¸cado de conexões. Figura retirada da ref. [30]

Figura 2.7: Processo de evolu¸cão de um grafo para o modelo de Erdös-Rényi. (A) Come¸camos com N = 10 nós isolados, depois conectamos cada par de nós com probabilidade p. (B) e (C) mostram diferentes estágios no desenvolvimento do grafo, correspondentes a probabilidadesp= 0.1 ep= 0.15 respectivamente. Podemos notar o surgimento de árvores (uma de ordem 3, linhas tracejadas) e ciclos (um ciclo de ordem 3, linhas tracejadas) num grafo, e um aglomerado que conecta metade dos nós emp= 0.15 = 1.5/N. Figura retirada da ref [26].

aleatórios é estudar as propriedades do espa¸co de probabilidades associada a grafos com N nós quando N _{→ ∞}, com um principal objetivo de determinar para qual probabilidade de conexãop, uma particular propriedade do grafo irão surgir.

(32)

2.3.2 Propriedades de grafos aleat´

orios

A. Subgrafos

Seja G1 = (E1, V1) um grafo de E1 arestas e V1 nós, inteiramente contido em um grafo G = (E, V) de tal forma que todos os V1 nós e todas as E1 arestas de G1 são também nós deV e arestas de E, logo dizemos que G1 é um subgrafo de G. A apari¸cão de subgrafos foi a primeira propriedade de grafos aleatórios estudada por Erdös e Rényi (1959) [31], como exemplo de subgrafos temos um circuito (Figura 2.7), seja tal circuito de ordemk, para que o mesmo tenha um circuito de k arestas, a cada par de arestas consecutivas tem que haver somente um nó em comum, ou seja, graficamente um triângulo é um circuito de ordem 3, e um retângulo é um circuito de ordem 4 e assim por diante. Vemos então que a conectividade média de um circuito e igual a dois, já que cada nó tem duas arestas. Como exemplos de subgrafos temos também as árvores, um grafo de ordem k com k nós e k₋1 arestas, e nenhum dos seus sub grafos são circuitos, logo árvores não formam circuitos. A conectividade média de uma árvore de ordem k é dada por _hk_i= 2₋2/k sub-grafos completos de ordem k altamente conectados, com k nós e todos as poss´ıveis k(k₋1) arestas.

Um interessante problema na teoria dos grafos é determinar segundo a sua evolu¸cão a probabilidade cr´ıtica Pc(N) em que quase todo grafo contem uma determinada árvore de

certa ordem, e determinar se existe uma probabilidade cr´ıtica que marca o aparecimento de subgrafos com k nós e l arestas. Como exemplo, vamos considerar o processo de evolu¸cão descrito na Figura 2.7 para um grafoG=GN,p. Come¸ca-se comN nós isolados e em seguida

conectamos cada par de nós com probabilidadep. Para pequenas probabilidades de conexão as arestas estão desconectadas, e como o número de arestas aumenta, dois nós podem se conectar e formar uma árvore de ordem 3.

Nosso primeiro objetivo para responder sobre probabilidade cr´ıtica de aparecimento de sub grafos é determinar quantos subgrafos existem em um grafo aleatório, tal prova foi feita por Bollobás em 1985. Para isso considere um grafo aleatório G = GN,p e um pequeno

subgrafoF com k nós el arestas. Os k nós podem ser escolhidos do número totalN de nós em CN

k formas e as l arestas s˜ao formadas com probabilidade pl. Podemos ent˜ao permutar

osk nós e obter k!/anovos grafos, onde aé o número de grafos que são isomórficos. O valor esperado de subgrafosF contidos em G é dado por

E(X) =C_Nk k! ap

l_∼

= N

k_pl

(33)

22

Tal equa¸c˜ao nos mostra que sep(N)Nk/l _→_{0 com}_N _→_{0, o n´}_{umero esperado de subgrafos}

E(X)_→0, ou seja, nenhum dos grafos aleat´orios contem um sub grafoF. SeP(N) = cN−k/l_,

o número médio de grafos é um número finito dado por λ=cl_{/a, indicando que esta fun¸cão}

pode ser a probabilidade cr´ıtica. Pode-se testar se tal fun¸cão é válida calculando a distribui¸cão dos números de sub grafos,Pp(X =r), obtendo

lim

N→∞Pp(X =r) =e −λλr

r!. (2.9)

e a probabilidade que Gcontenha pelo menos um subgrafo ´e

Pp(G⊃F) =

∞

X

r=1

Pp(X =r) = 1−e−λ, (2.10)

o qual converge para 1 com o aumento dec, ocorrendo o mesmo para valores depsatisfazendo pNk/l _{→ ∞}_.

A probabilidade cr´ıtica de que quase todo o grafo contenha um subgrafo com k n´os e l arestas ´ePc(N) =cN−k/l. Alguns casos importantes podem ser explicitados, como veremos

a seguir na equa¸c˜ao (2.10).

(a) A probabilidade cr´ıtica de ter uma ´arvore de ordemk ´ePc(N) =cN−k/(k−1);

(b) A probabilidade cr´ıtica de ter um circuito de ordemk ´ePc(N) =cN−1;

(c) A probabilidade cr´ıtica de ter um subgrafo completo de ordem k ´ePc(N) = cN−2/(k−1).

B. Distribui¸c˜ao de conectividade

Em um grafo aleatório com probabilidade p de conexão, a conectividade ki de um nó i

segue uma distribui¸c˜ao binomial com parˆametrosN ₋1 e p:

P(ki =k) = pk(1−p)n−1−kCkN−1. (2.11)

Esta probabilidade representa o número de formas ao qual k arestas podem ser ligadas de um dado nó, onde pk _{é a probabilidade de ter} _k _{arestas, (1}₋_p)N−1−k _{é a probabilidade de}

que as outras probabilidade estejam ausentes e CN−1

k é o número de diferentes combina¸cões

em que as liga¸c˜oes podem estar distribu´ıdas.

Vamos primeiro estudar o n´umeros de n´os com conectividade k, ou seja Xk, com o

(34)

De acordo com a equa¸cão (2.11), o valor esperado do número de nós com conectividade k, é

E(Xk) =N P(ki =k) =λk, (2.12)

onde

λk =N pk(1₋p)n−1−kC_Nk₋₁. (2.13) A distribui¸c˜ao dos valores deXk ondeP(Xk =r) aproxima-se de uma distribui¸c˜ao de Poisson

dada por

Pp(Xk =r) = e−λk

λr k

r!. (2.14)

Assim o número de nós com conectividadek segue uma distribui¸cão de Poisson com valor médio λk. Vemos que o valor esperado da distribui¸cão (2.14) é fun¸cão de λk que é dada

pela equa¸cão (2.13). A distribui¸cão de Poisson decai rapidamente para grandes valores de r, o desvio padrão da distribui¸cão é dado por σk = √λk. Com uma boa aproxima¸cão a

distribui¸cão de conectividade de um grafo aleatório é uma distribui¸cão binomial,

P(k) =pk(1₋p)n−1−kC_Nk₋₁. (2.15) Ao qual para grandes valores N pode ser reescrita como uma distribui¸c˜ao de Poisson,

P(k)∼=e−pN(pN)

k

k! =e

−hkihki

k

k! . (2.16)

Nas analises de conectividade máxima e m´ınima, os resultados indicam que para altos valores de p ambas as conectividades máximas e m´ınimas são determinadas e finitas. Por exemplo, se p(N) ∼= N−1−1/k_{, quase não se tem grafos com nós cuja conectividade seja}

(35)

24

C. Diˆametro da rede

O diâmetro de um grafo é definido como a distância máxima entre qualquer par de nós. Sendo mais preciso, o diâmetro de um grafo que contêm aglomerados isolados (desconectado) é infinito. Grafos aleatórios tendem a ter pequenos diâmetros, a razão para isto é que grafos aleatórios tendem a propagar-se, com alta probabilidade o número de nós a uma distâncial de um dado nó não é muito menor que_hk_il. Igualando_hk_ilcomN encontra-se que o diâmetro é proporcional a ln(N)/ln(_hk_i), logo depende logaritmicamente do número de nós.

Quando considera-se todos os grafos comN nós e probabilidade de conexãop, o intervalo de valores em que os diâmetros desses grafos podem variar é muito pequena, conclusão esta que para muitos valores dep, quase todos os grafos com N epequivalentes tem precisamente o mesmo diâmetro, que é geralmente em torno de

d= ln(N) ln(pN) =

ln(N)

ln(_hk_i). (2.17)

Seguem abaixo alguns resultados importantes:

(a) Se_hk_i=pN <1, teremos que um grafo t´ıpico é composto de árvores isoladas e seu diâmetro é igual ao diâmetro de uma árvore.

(b) Se_hk_i>1, um aglomerado gigante aparece. O diâmetro do grafo é igual ao diâmetro do aglomerado se _hk_i>3.5.

(c) Se_hk_{i ≥} ln(N), quase todo o grafo ´e conectado.

Pode-se através do cálculo da menor distância média (tamanho do menor caminho médio) entre quaisquer dois nós encontrar outra maneira de caracterizar o espalhamento do grafo aleatório. Espera-se que o tamanho do menor caminho médio varie com o número de nós de forma igual ao diâmetro,

lRand∼=

ln(N)

ln(_hk_i). (2.18)

D. Coeficiente de agrega¸c˜ao

(36)

que considerar que um nó esteja conectado a um dos seus primeiros vizinhos, conseq¨ uente-mente o coeficiente de agrega¸cão de um grafo aleatório é

CRand=p= h

k_i

N . (2.19)

2.3.3 Modelo de Wattz e Strogatz

Watts e Strogatz [28] propuseram um modelo que interpola uma rede de dimensão finita e um grafo aleatório. O algoritmo de tal modelo é explicitado abaixo, ver Figura 2.8 [26]: (a) - Come¸ca-se com um c´ırculo regular comN nós do qual cada nó está conectado aos seus k primeiros vizinhos, com o propósito de ter uma rede conectada em todos os momentos, considere N _≫K _≫ln(N)_≫1.

(b) - Com uma probabilidadep reescreve-se aleatoriamente cada aresta da rede de tal forma que auto conexões e conexões duplas são exclu´ıdas. Este processo incluipN k/2 liga¸cões de longo alcance as quais conecta nós de diferentes vizinhan¸cas. Podemos através da varia¸cão dep monitorar a transi¸cão da rede entrep= 0 (rede regular) e p= 1 (rede aleatória).

Figura 2.8: A figura exibe os processos de conexões dos nós para o modelo de Wattz-Strogatz, o qual interpola entre um c´ırculo regular e uma rede aleatória sem alterar o número de nós ou arestas. Em tal figura come¸ca-se com N = 10 nós, cada nó conectado aos seus quatro primeiros vizinhos. Parap= 0 o c´ırculo se mantém inalterado; com o aumento depa conectividade dos s´ıtios aumentam desordenadamente até p = 1 onde todas as arestas são re-conectadas aleatoriamente. Figura retirada da ref [26].

(37)

26

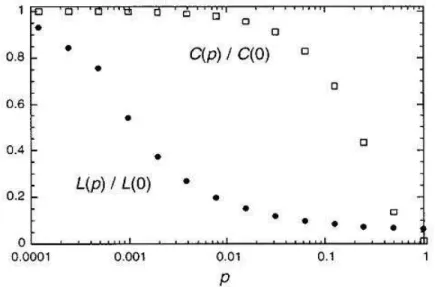
e C(0) _≈ 3/4. Vemos que l varia linearmente com o tamanho do sistema, e o coeficiente de agrega¸cão é elevado. Por outro lado, o sistema converge para um grafo aleatório onde l(1) _≈ ln(N)/ln(k) e C(1) _≈ k/N se p _→ 1, assim l varia logaritmicamente com N, e o coeficiente de agrega¸cão decresce com N. Os casos limites indicam que altos valores de C estão sempre associados com altos valores del, e pequenos valores deC com pequenos valores del. Mas ao contrario, Watts e Strogatz encontraram que há um amplo intervalo dep para o qual l(p) estar próximo de l(1) ainda que C(p) _≫ C(1), ver Figura 2.9. Este regime se origina em uma rápida queda de l(p) para pequenos valores de p, enquanto C(p) fica quase inalterado. A coexistência de pequenos l e grandes C concorda com as caracter´ısticas de redes reais.

Figura 2.9: Tamanho do caminho L(p) e coeficiente de agrega¸cão C(p) para o modelo de Wattz-Strogatz. Os dados estão normalizados para os valores deL(0) eC(0) para um rede regular. Há uma rápida queda no caminho médio L(p), o que corresponde ao efeito de mundo pequeno, e durante esta queda nota-se queC(p) permanece quase constante, indicando que a transi¸cão para o mundo pequeno é quase indetectável à n´ıvel local. Figura retirada da ref [26].

2.3.4 Modelo de Barab´

asi e Albert

O alto desenvolvimento no entendimento de redes complexas permitiu a descoberta de que muitas redes reais têm sua distribui¸cão de conectividade que segue uma lei de potência, P(k) _≈k−γ_{. Essas redes são chamadas de redes livres de escala, como uma lei de potência}

n˜ao suporta uma escala caracter´ıstica.

(38)

que são aleatoriamente conectados, sem modificarN. Em contraste, redes reais são melhor descritas como sistemas abertos que crescem continuamente com a adi¸cão de novos nós. Come¸cando com um número pequeno de nós, à um número de nós que aumentam com o tempo da rede.

Em tais modelos, a probabilidade de que dois nós sejam conectados é independente da conectividade dos nós. Mas em muitas redes reais, a probabilidade de se conectar a um nó depende da conectividade dos nós, ou seja, é altamente provável ligar um nó com um alto número de conexões, uma propriedade chamada de liga¸cão preferencial.

Figura 2.10: Figuras referentes a redes livres de escala para o modelo de Barabási-Albert. (a) Figura para N = 8 nós que se conectam segundo uma distribi¸cão de conectividade em lei de potênciaP(k) =k−γ. (b) Figura para uma rede de escala livre após a adi¸cão de vários nós. Figura retirada da ref [30].

O modelo introduzido por Barabási e Albert (BA) (Figura 2.10) reune essas carac-ter´ısticas. E foi o primeiro modelo de redes a exibir uma distribui¸cão de conectividade em lei de potência. O algoritmo do modelo de (BA) está explicitado abaixo.

(a) Crescimento da rede: come¸ca-se com um número pequeno de nós (m0), e a cada passo no tempo, adiciona-se um novo nó comm(_≤m0) arestas que conecta o novo nó am diferentes nós presentes no sistema.

(b) Liga¸cão preferencial: quando se escolhe quais nós um novo nó vai se conectar, assumi-se que a probabilidadeQ

(39)

28

Y

(ki) = ki/

X

j

kj. (2.20)

Depois de t passos no tempo tal procedimento resulta em uma rede com N =t+m0 n´os e mtarestas.

Para estudarmos a evolu¸cão da conectividade dos s´ıtios e a distribui¸cão da conectividade da rede, veremos uma aproxima¸cão anal´ıtica com o propósito de calcular as propriedades dinâmicas do modelo de livre escala, que foi proposta por Barabási e Albert (1999), o trata-mento cont´ınuo.

Tratamento cont´ınuo [32]: o tratamento cont´ınuo calcula a dependˆencia temporal da conectividadeki de um dado n´o i. Tal conectividade aumenta assim que um novo s´ıtio entra

na rede e se conecta ao n´o i, e a taxa com queki varia ´e proporcional aQ(ki). Seja ki uma

vari´avel real e continua,ki satisfaz a seguinte equa¸c˜ao

∂ki

∂t =m Y

(ki) = m

ki

PN−1

j=1 kj

. (2.21)

onde a soma é sobre todos os nós já existentes no sistema, deste modo P

jkj = 2mt−m,

logo a equa¸c˜ao (2.21) pode ser escrita como, ∂ki

∂t = ki

2t. (2.22)

A solu¸cão para tal equa¸cão, levando em conta a condi¸cão de que cada novo nó i adicionado a rede temki(ti) =m, é

ki(t) = m

t ti

β

(2.23)

com β = 1

2. Vemos que na equa¸cão (2.23) a conectividade de todos os nós evolui da mesma forma, seguindo uma lei de potência. Pode-se a partir da equa¸cão (2.23) escrever a probabi-lidade de que um nó tenha uma conectividade ki(t) menor que k,P[ki(t)< k],

P[ki(t)< k] =P

ti >

m1/β_t

k1/β

. (2.24)

(40)

a uma densidade de probabilidade constante P(ti) =

1

m0+t. (2.25)

Substituindo na equa¸c˜ao (2.24) obtemos

P

ti >

m1/β_t

k1/β

= 1₋ m

1/β_t

k1/β_(t₊_m0₎. (2.26)

A distribui¸c˜ao de conectividadeP(k) pode ser obtida usando

P(k) = ∂P[ki(t)< k]

∂k =

2m1/β_t

t+m0 1

k1/β+1, (2.27)

que no limite de t_{→ ∞} nos d´a,

P(k) = 2m1/βk−γ (2.28)

com γ = 1

β + 1 = 3. Sendo independente de m, o que esta de acordo com os resultados

num´ericos.

2.3.5 Propriedades do modelo de Barab´

asi e Albert

A. Tamanho do caminho m´edio

Comparando o tamanho do caminho médio da rede de Barabási-Albert com o tamanho do caminho médio de uma rede aleatória de mesmo tamanho e mesma conectividade média, vemos que na rede de Barabási-Albert o tamanho do caminho médio é menor para qualquer valor deN. Tal diferen¸ca é exibida na Figura 2.11 que mostra o tamanho do caminho médio da rede de Barabási-Albert com uma conectividade média_hk_i= 4 como uma fun¸cão de uma rede de tamanhoN, indicando que a heterogeneidades da topologia de redes livres de escala é mais eficiente em aproximar nós que a topologia homogênea de redes aleatórias. O tamanho do caminho médio da rede de Barabási-Albert cresce aproximadamente de forma logar´ıtmica com N,

(41)

30

mostrando o efeito de mundo pequeno presente na rede de Barab´asi-Albert.

Figura 2.11: Caracter´ıstica do caminho m´ediol pelo tamanhoN da rede de Barab´asi-Albert com

hk_i = 4, comparada com um grafo aleat´orio de mesmo tamanho e mesma conectividade m´edia. Figura retirada da ref. [26].

B. Coeficiente de agrega¸c˜ao

O coeficiente de agrega¸cão da rede de Barabási-Albert com conectividade média _hk_i= 4 comparada com o coeficiente de agrega¸cãoCrand =hki/N para redes aleatórias, é mostrada

(42)

(43)

Cap´ıtulo 3

O problema do caminho m´ınimo

3.1 Introdu¸

c˜

ao

Em teoria dos grafos, o problema do caminho m´ınimo ou problema do caminho mais curto consiste em minimizar o custo da travessia entre dois vértices quaisquer de um grafo [7]. Em tal problema temos um grafo G= (V, E), onde V é o conjunto de vértices e E é o conjunto de arestas (u;v), sendo cada aresta (u;v) orientada do vértice u para o vértice v. A cada aresta (u;v) é atribu´ıda uma fun¸cão peso w(u;v) :E _{→ ℜ}, onde o peso do caminho p=< v0, v1, ..., vk−1, vk> será a soma dos pesos de todas as arestas pertencentes ao grafoG,

w(u;v) =w(v0, v1, ..., vk−1, vk) = k

X

i=1

w(vi−1, vi) (3.1)

Definimos o peso do caminho mais curtoδ de u para v como sendo:

δ(u, v) = (

minnw(p):u _→p vo se h´a um caminho de u para v

∞ de outro modo (3.2)

Assim, o caminho mais curto do vértice u para o vértice v será definido como qualquer caminho pcom peso w(p) =δ(u;v).

Um exemplo prático do problema do caminho m´ınimo é que se imaginarmos duas cidades, A e B, onde as mesmas são ligadas por rotas, sendo que cada rota é composta por vários trechos, calculamos o caminho de menor distância entre as duas cidades, conhecendo-se os trechos adjacentes de todas as rotas. Assim podemos resolver tal problema de uma maneira bem simples, tentando todos os caminhos poss´ıveis até descobrirmos o mais curto entre as

(44)

duas cidades. Mas, quando o número de rotas é muito grande, esta forma de solu¸cão se tornará inviável. Afim de facilitar o problema, podemos excluir rotas com ciclos ou mesmo rotas que se afastam demais das cidades. São idéias como essas que vários algoritmos de busca de menores caminhos utilizam para resolver o problema de maneira mais eficiente.

Na Figura 3.1, mostramos duas cidades citadas no exemplo anterior, consideramos os vértices como as interseçcões entre os trechos, as arestas como os trechos e os pesos como os comprimentos de cada trecho. Poder´ıamos também exemplificar o problema do menor caminho de tal forma que os pesos fossem dados por uma outra fun¸cão, como por exemplo, o tempo gasto para percorrer cada trecho.

Figura 3.1: Grafo das rotas entre as cidades A e B. Os vértices são as cidades, as arestas são os trechos entre as cidades com seus respectivos pesos dados em Km. As arestas tracejadas em vermelho formam um dos menores caminhos.

H´a algumas variantes do problema do caminho mais curto. As principais s˜ao as seguintes:

• Encontrar o caminho mais curto entre um v´ertice fonte s _∈ V para todos os outros v´ertices v _∈ V,

• Encontrar o caminho mais curto até um determinado vértice de destino t _∈ V a partir de cada vértice v _∈ V,

(45)

34

• Encontrar o caminho mais curto desde u atév para todos os pares de vérticesu e v. O caminho mais curto de um vérticeupara um vérticev sempre será bem definido quando estamos lidando com pesos que são positivos, já para pesos que são negativos, o caminho mais curto só é bem definido caso o grafo G(V, E) não contenha nenhum ciclo de pesos negativos alcan¸cáveis a partir do vértice origemu. Alguns algoritmos, como o algoritmo de Dijkstra [7], consideram que todos os pesos em um grafo são sempre positivos, outros, como o algoritmo de Bellman-Ford [7], trabalham com a possibilidade de haver pesos negativos. Lembremos que no problema do caminho mais curto os pesos podem ser positivos e/ou negativos.

Além de calcularmos o peso do caminho mais curto também é necessário calcular os vértices que compõe o caminho mais curto, para isso, dado um grafo G(V;E), mantemos para cada vértice v _∈ V um predecessorπ[v] que será nulo ou igual ao vértice anterior à v. Assim, na execu¸cão do algoritmo de caminhos mais curtos não é necessário que os valores de π indiquem os caminhos mais curtos, pois nesse caso estamos interessados no subgrafo predecessorGπ = (Vπ;Eπ) induzido pelos valores deπ. Logo, o conjunto de vérticesVπ é um

conjunto de v´ertices de Gcom predecessores n˜ao nulos, incluindo a origem s:

Vπ ={v ∈V :π[v]6=nulo} ∪ {s} (3.3)

SendoEπ o conjunto de arestas induzidas pelos valoresπ correspondentes aos v´ertices Vπ:

Eπ ={(π[v], v)∈E :v ∈Vπ− {s}} (3.4)

Uma ´arvore de caminhos mais curtos enraizada no v´ertice s pode ser interpretada como um sub-grafo de antecessoresG′

= (V′

, E′

) onde V′

⊆ V e E′

⊆ E, tal que 1. V′

´e o conjunto de v´ertices acess´ıveis a partir de s em G. 2. G′

forma uma ´arvore enraizada com raiz no v´ertice s, e 3. Para todo v pertencente V′

, o único caminho desde o vértice s até o vértice v em G′

´e o caminho mais curto desde s at´e v em G.

3.2 Algoritmo de Dijkstra

(46)

de Dijkstra é ainda um dos mais usados para resolver o problema do caminho mais curto entre vértices de um grafo dirigido cujo peso das arestas sejam positivos, logo iremos supor que w(u, v) _≥ 0 para cada aresta (u, v) _∈ E. Sua técnica principal é a relaxa¸cão, processo baseado em um teste que consiste em diminuir repetidamente um limite superior no próprio peso do caminho mais curto de cada vértice, ou seja, para cada vértice v pertencente a V, mantemos um atributo d[v], que é o limite superior sobre o peso de um caminho mais curto desde a origem s até v, e o diminu´ımos repetidamente até que esse limite superior se torne igual aos pesos dos caminhos mais curtos existentes. A seguir explicaremos detalhadamente o funcionamento do algoritmo de Dijkstra.

Dado um vértice fonte s, definiremos alguns conjuntos para uma melhor explica¸cão do funcionamento do algoritmo de Dijkstra. Definiremos primeiro o conjunto S de todos os vértices v que já têm o caminho mais curto final bem determinado, onde o algoritmo de Dijkstra adiciona u à S depois de selecionar repetidamente o vértice u _≥ V ₋S com uma estimativa m´ınima de caminhos mais curtos. O conjuntoQdado por Q=V ₋S e os vetores já ditos anteriormente d[v], que é o custo do caminho entre os vértices s e v e o vetor π[v] que é o vértice antecessor ao vértice v.

INICIALIZE-FONTE-UNICA (G;s) 1 Para cada v´ertice v _∈V[G] 2 Fa¸ca

3 d[v]_{← ∞}

4 π[v]_←N U LO 5 d[s]_←0

No pseudocódigo mostrado acima fazemos d[s] = 0, pois como partiremos do vértice s o custo até ele mesmo é nulo. Como não temos nenhuma informa¸cão sobre algum caminho para outro vértice v, Faremos também d[v] = _∞ (_∀v ₆= s), pois a pior hipótese é que tal caminho não exista, sendo assim o custo torna-se infinito. Por último definiremos todos os antecessores de um vértice v como nulos, π[v] = 0 (_∀v _∈V).

(47)

36

sobre a aresta (u, v)):

RELAXE (u;v;w)

1 Se d[v]> d[u] +w(u;v) 2 Ent˜ao

3 d[v]_←d[u] +w(u;v)

4 π[v]_←u

Vemos no pseudocódigo acima que nas linhas 3 e 4 a etapa de relaxamento pode diminuir o valor da estimativa de caminho mais curto d[v] e atualizar o vetor dos antecessores de v, π[v]. Abaixo veremos o pseudocódigo completo, combinando as partes de inicializa¸cão e de relaxa¸cão do algoritmo de Dijkstra.

DIJKSTRA (G;w;s)

1 INICIALIZE-FONTE-UNICA (G;s) 2 S _←0

3 Q_←V[G]

4 Enquanto Q₆= 0

5 Fa¸cau_←EXT RAIR₋M IN IM O(Q) 6 S _←S_{∪ {}u_}

7 Para cada v´ertice v _∈Adj[u] 8 Fa¸ca RELAXE (u;v;w)

onde, Adj[u] representam todos os v´ertices adjacentes a u.

(48)

Figura 3.2: A execu¸cão passo a passo do algoritmo de Dijkstra. Dentro dos vértices é mostrado as estimativas de caminhos mais curtos a partir do vértice fontes. As arestas que estão sombreadas indicam que π[v] = u, e os vértices em preto pertencem ao conjunto S. Os vértices brancos pertencem ao conjuntoQ, e os vértices sombreados são aqueles que têm menor valor em tal conjunto [7].

atualizando assim a estimativa d[v] e o antecessor π[v], verificando se o caminho mais curto at´ev pode ser melhorado passando pelo v´ertice u.

3.3 Heap bin´

aria

O ordenamento de dados que usamos é a estrutura de dados chamada de Heap (binário), pois é um arranjo que pode ser visto como uma árvore binária praticamente completa, ver Figura 3.3. Cada nó da árvore corresponde a um elemento no arranjo que armazena um determinado valor, que em o nosso caso são os m´ınimos do conjunto Q no algoritmo de Dijkstra.