Análises estatísticas em redes complexas homofílicas

(1)

DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL PROGRAMA DE PÓS

-

GRADUAÇÃO EM FÍSICA

A

NÁLISES

E

STATÍSTICAS EM

R

EDES

C

OMPLEXAS

H

OMOFÍLICAS

A

NTONIO

M

ARQUES DOS

S

ANTOS

NATAL

-

RN

(2)

ANÁLISES

E

STATÍSTICAS EM

REDES

COMPLEXAS

HOMOFÍLICAS

Tese de Doutorado_{apresentada ao Programa de Pós-Graduação} em Física do Departamento de Física Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito par-cial para a obtenção do grau dedoutor_{em Física.}

Orientador: Prof. Dr. Luciano Rodrigues da Silva Co-orientador: Dr. Gabriel Alves Mendes

NATAL

-

RN

(3)

ÀDeus, à minha família. Em especial à minha mãe Maria da Conceição, ao meu paiBartolomeu Ferreira, aos meus irmãos, à minha namorada Marília Gabriela.

(4)

Agradecimento é sempre um ato de reconhecimento grandioso, para a vida e para a alma humana, é fonte inesgotável de gratidão para com aqueles que fazem da nossa vida, um constante compartilhar de momentos únicos e insubstituíveis.

Primeiramente quero agradecer a DEUS o que seria de mim sem a fé que eu tenho nele.

Ao meu orientador, professor Dr. Luciano Rodrigues da Silva, por todo o apoio

e conhecimento que me deu durante o tempo que passei no Programa de Pós-Graduação e, especialmente pela conﬁança em mim depositada ao assumir a orientação.

Ao meu co-orientador Dr. Gabriel Alves Mendespela colaboração, paciência e

por seus conhecimentos repassados durante todo o desenvolvimento do trabalho.

Ao Dr. Mauricio Lopes de Almeida pelos momentos de descontração,

compa-nheirismo, e pelos inúmeros auxílios durante a realização deste trabalho.

Aos secretários da Pós-Graduação Celina Pinheiro e Francisco Silvestre.

A Universidade Federal do Rio Grande do Norte, por ter me dado a oportunidade de concluir meu mestrado e doutorado em um programa de excelência e ter-me proporci-onado a obtenção dos conhecimentos necessários para a realização e concretização deste trabalho.

A todos os professores, em especial os que contribuiram para minha formação e também aqueles funcionários que poucos são citados mais que muito colaboram man-tendo o ambiente limpo e mas agradável. Dentre eles posso citar Adeída, que Deus aben-çoe.

Aos amigos do DFTE, em especial os do grupo de pesquisa, MSc. Gerdivane,

Mestranda Larissa Ribeiro, Renann Gleyson, MSc. Samuraí Gomes Aguiar, Thamires Germano, MSc. Tiago Medeiros, MSc.Tiago Crisostomose MSc. Thiago Rafael.

A Dona Euzélia, Veruska, seu Ivo, Taynná, Rubens e Wanessa, por toda preocu-pação, atenção, dedicação e carinho durante esses seis anos que passei no programa, isso fez deles pessoas especiais e hoje são mais que amigos, considero parte da minha família, agradeço a Deus por ter colocado voces na minha vida.

(5)

sempre mostrando que tudo vai dá certo no ﬁnal. Obrigado amigos e a tantos outros que não citei aqui por que são muitos, mas que com certeza não irei esquecer todo o auxílio que me deram.

Agradeço a Dona Arlete, seu "Didi", Max, Renato, Evilânia, que foram as pessoas que me acolheram assim que cheguei em Natal. Obrigado por todo o apoio e todo auxílio, voces foram fundamentais no início da jornada. Realmente sem palavras para agradecer, que Deus os abençoe sempre.

A minha namorada Marília Gabriela ofereço um agradecimento mais do que es-pecial por ter vivenciado comigo passo a passo todos os detalhes do trabalho. Por ter me ajudado, por ter me dado todo o apoio que necessitava nos momentos mais difíceis, todo carinho, respeito, e por tornar minha vida mais feliz.

A meus amigos da igreja, Aline Torres, Luana Pereira, Edvanilson Alves, Elida Rodrigues e Ravenia, pela acolhida no ínicio da caminhada no grupo, por sempre acredi-tarem em meu potencial, por sempre acrediacredi-tarem em mim, por todas as orações.

A meus irmãos, Walbermark, Walbetise, Bartolomeu, Walberto, Walbelice, Walbe-nice e Walbenise pelo companheirismo, pela força e motivação. Agradeço também ao(s) meu(s) cunhado(as) Edwilson, Fabiana e Kristiane por todas as orações, palavras de apoio, a todos meus primos(as), tios(as), por toda a torcida, por toda a conﬁança.

Um super agradecimento a meus pais, Maria da Conceiçao e Bartolomeu Ferreira dos Santos que souberam me amar, me educar, me transmitindo os mais valorosos saberes, compartilhando comigo cada vitória, cada derrota, cada lágrima e alegrias. O meu eterno agradecimento, AMO VOCÊS.

À CAPES pelo apoio ﬁnanceiro.

(6)

que as vitórias vêem, elas vêem quando aprendemos a valo-rizar Deus, os amigos e a família só assim temos bagagem suficiente para vencer o confronto final.”

(Vitor Belfort)

(7)

Propomos um simples processo de crescimento de rede complexa, onde a ligação preferencial contém dois parâmetros essenciais: a homofilia, tendência que sítios locais têm de ligar-se com outros similares, bem como o número de vizinhos ligados. Assim obtivemos uma rede que contempla o modelo de Barabási-Albert (BA) e o modelo Ho-mofílico de livre escala onde o parâmetro de controle ajusta o grau de importância da homofilia no processo da ligação preferencial. Os resultados embasam uma discussão de-talhada sobre os diferentes tipos de correlações, em especial a correlação da qualidade, que foi introduzida nesta tese, e comparações entre o modelo BA, modelo homofílico de livre escala, e nosso modelo atual, considerando suas propriedades topológicas: grau de distribuição, tempo de dependência da conectividade e o coeficiente de agregação.

Palavras-Chave: Redes complexas; Leis de Potência; Ligação Preferencial; Corre-lações.

(8)

We propose a simple complex network growth process, where the preferential binding contains two essential parameters: homophily, a trend that local sites have to connect with other like, as well as the number of connected neighbors. Thus we obtained a network covering the model of Barabási-Albert (BA) and the scale-free model homophi-lic where the control parameter sets the degree of importance of homophily in the process of preferential binding. The results support a detailed discussion of the different types of correlations, especially the correlation of quality, which was introduced in this thesis, and comparisons between the BA model, homophilic model of free range, and our cur-rent model, considering its topological properties: degree distribution, connectivity time dependence and the coefﬁcient of aggregation.

Keywords: Complex networks; Power-laws; Preferential attachment, correlations.

(9)

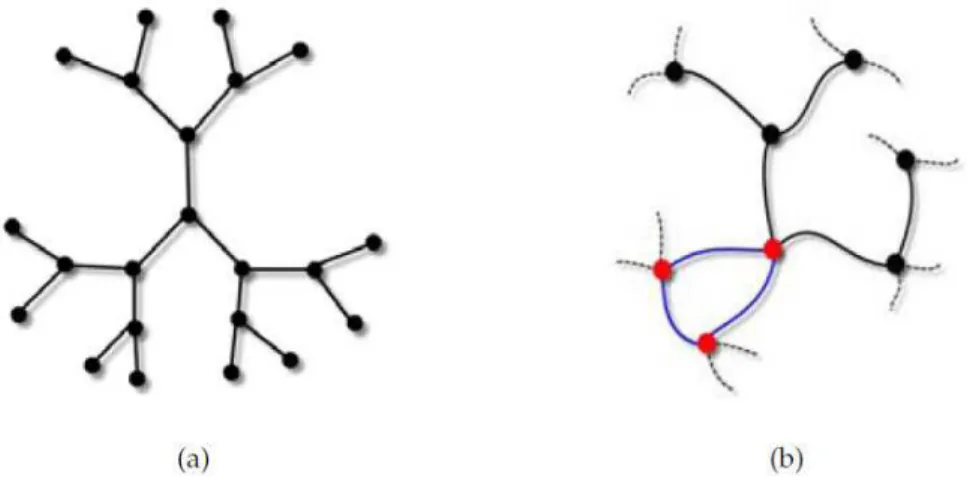
2.1 Representação esquemática de uma rede. Figura proveniente da ref [16]. . . 5 2.2 a) Representação da rede de Bethe. Este é um exemplo de uma rede tipo árvore.

b) Exemplo de uma rede com presença de circuito de ordemn = 3, representado

pelos nós em vermelho e pelas ligações em azul. Essa rede possui número de nós

N = 8e número de ligações L = 8. Assim podemos determinar o número de

circuitos, neste caso temosI = 1. Figura proveniente da ref [16]. . . 6

2.3 O conceito do coeﬁciente de agregração do sítio ié obtido quando conhecemos seus primeiros vizinhos e sabemos como estes estão ligados entre si. Para esta ﬁgura temoszi = 6eyi= 5logoCi(zi) = 1₃. Figura proveniente da Ref [16]. . . 10

2.4 Ataque aleatório. A figura 2.4 (a) mostra a estrutura da rede, a figura (b) mostra os sítios que vão ser atacados, (sítios amarelos), e a figura (c) mostra a estrutura da rede após o ataque, mostrando que a maior parte da rede ainda continua conec-tada. Isso significa que a rede é robusta a esse tipo de ataque. . . 12 2.5 Ataque dirigido. A figura 2.5 (a) mostra a estrutura da rede, a figura (b) mostra os

sítios que vão ser atacados, (sítios amarelos), e a ﬁgura (c) mostra a estrutura da rede após o ataque, mostrando que a rede se desfragmentou de forma rápida. Isso signiﬁca que a rede não é robusta a esse tipo de ataque. . . 12

(10)

(a)⟨knn(k)⟩cresce com a conectividade dos sítios, indicando a presença de

corre-lações de grau positivas na rede (assortatividade). Em (b) mostra uma tendência decrescente de⟨knn(k)⟩o que signiﬁca que a rede é negativamente correlacionada

(disassortatividade). Finalmente, em (c), com⟨knn(k)⟩constante, a rede é

descor-relacionada. Figura proveniente da Ref [20]. . . 15 2.7 Mapa dos Estados Unidos. Os estados em amarelo (Nebraska e Kansas)

represen-tam a origem das correspondências e o estado em verde (Massachusetts) repre-senta o destino ﬁnal. Figura proveniente da Ref [20]. . . 17 2.8 Esquema do experimento de Stanley Milgram. Figura proveniente da Ref [20]. . . 17 2.9 Comportamento da distribuição de conectividade da Rede WWW. Figura

proveni-ente da Ref [18]. . . 18 2.10 Distribuição de links saindo (a) e entrado (b) em uma Web page. Em (c), menor

caminho médio como uma função do tamanho da rede. Figura proveniente da Ref [17]. . . 20 2.11 Rede de colaborações de atores de cinema com 212250⟨k⟩ = 28,78eγator = 2,3.

Figura proveniente da Ref. [23]. . . 21

3.1 A ﬁgura mostra a evolução temporal da conectividade para o modelo BA. Figura proveniente da Ref. [26]. . . 24 3.2 Distribuição de conectividade do modelo de Barabási-Albert. Figura proveniente

da Ref. [26]. . . 25 3.3 Gráﬁco do menor caminho médiolpelo tamanho da redeN, no modelo de

Barabási-Albert com⟨k⟩= 4, comparado com um grafo aleatório de igual tamanho e mesma

conectividade média. Figura proveniente da Ref. [13].. . . 27 3.4 Coeﬁciente de agregação versus o tamanho da rede do modelo de Barabási-Albert

com⟨k⟩ = 4, comparado com o coeﬁciente de agregação de um grafo aleatório,

Crand ≃ ⟨k⟩/N. Figura proveniente da Ref. [13]. . . 28

(11)

0.6, 0.9. Note que em cada caso kη(t) segue uma lei de potência e o expoente

dinâmicoβ(η), dado pela inclinação dek(t), aumenta comη. Figura proveniente

da Ref. [27]. . . 34 3.6 Comportamento assintótico deCcomt→ ∞, note que há acordo com a previsão

analítica, linha tracejada, (Equação3.25). Figura proveniente da Ref. [27]. . . 35 3.7 Distribuição de conectividade no modelo de qualidade, obtida para uma rede com

m= 1eN = 105. Figura proveniente da Ref. [26]. . . 36

3.8 Dependência do expoente dinâmicoβ(η)com o parâmetro da qualidadeηpara o

caso de uma distribuição uniforme,ρ(η) = constante.Os círculos foram obtidos

por simulação numérica, enquanto a linha corresponde a predição analíticaβ(η) =

η/1,255. Figura proveniente da Ref. [27]. . . 37 4.1 A distribuição de conectividades para o modelo homofílico (m = 1 eN = 105_),

onde ambos os eixos estão em escala logarítmica. Ela segue uma lei de potência

P(k)∼k−λ, comγ = 2.84±0.01, mostrando que a rede é livre de escala. . . 41

4.2 (a) Dependência temporal da conectividade,⟨ki(t, t0)⟩, para sítios com caracterís-ticasη=0.1,0.5e0.8. Note que⟨ki(t, t0)⟩segue uma lei de potência em cada caso e a inclinação cresce linearmente comηaté o sítio apresentar característica igual a

0.5. Após esse valor, a inclinação decresce e é, aproximadamente, igual as de sítios com características abaixo de0.5. (b) O expoente dinâmicoβcomo uma função de

η. Ele é obtido da inclinação de⟨ki(t, t0)⟩versusη(βé uniformemente distribuído,

m = 1eN = 105). O valor máximo deβ ocorre paraη =0.5e é igual a0.55, seu

valor mínimo é0.37 emη=0.0(ouη =1.0), indicando que sítios comη ≈ 0.5

ad-quirem, em média, mais conexões. Isso permite que sítios com características em torno de0.5entrem na rede em um tempo posterior e, ainda assim, consigam um maior número de ligações do que outros que já estão nela há muito mais tempo.. . 42

(12)

sítio faz apenas uma nova ligação,m = 1, com um sítio pré-existente. Os valores

para a característica intrínseca de cada sítio são:η1 = 0,5,η2 = 0,1,η3 = 0,6,η4 =

0,2,η5 = 0,4. Ao decidir onde estabelecer uma nova ligação (linha pontilhada), o novo sítio prefere conectar-se com outro de características similares e com maior número de conexões, conjuntamente. Figura proveniente da Ref. [20] . . . 47 5.2 Distribuição de conectividades cumulativaP(K)para modelo homofílico

genera-lizado LE (valores típicosσ,m0=m= 1,N = 105,η, é distribuído uniformemente, média tomada sobre12000realizações independentes) representada em escala

lo-garítmica. Segue a lei de potência.P(k)∝k−γ, com valores variando entre2.84(2)

e2.92(1). Este comportamento revela a ausência de valores típicos para a

conecti-vidade dos sítios. . . 48 5.3 Dependência do expoenteγ comσ (m0 = m = 1, N = 105,η, é uniformemente

distribuído, e com média acima de12000em realizações). Para σ = 0o modelo

BA é recuperado; por outro lado, a rede homofílica de livre escala é alcançada por

σ= 1. Um resultado interessante é observado quandoσ= 2, o expoenteγé mínimo. 49

5.4 Dependência temporal da conectividade média⟨ki(t, t0)⟩, para sítios com η=0.1,

0.3, 0.5, 0.7 e 0.9 ( m0 = m = 1, N = 105, η é uniformemente distribuído e a média é feita com12000 realizações independentes). Comparações entre ﬁguras (a) e (b) mostram que⟨ki(t, t0)⟩segue a lei de potência em cada caso e o expoente dinâmicoβ(η)é dependente deσ. Para altos valores deσouσ= 0, todos os sítios

aumentam sua conectividade no tempo como⟨ki(t, t0)⟩ ∝ (t/t0)β onde β = 1/2 e t0 é o tempo em que o sítio i foi adicionado ao sistema, independente de sua característica intrínseca.. . . 50 5.5 Dependência do expoente dinâmicoβcomη(m0 =m= 1,N = 105,ηé

uniforme-mente distribuído e com média realizada sobre12000realizações independentes) paraσ = 0(modelo BA),2e10. O valor máximo deβé0.55emη= 0.5e emσ = 2,

indicando que sítios comη em torno de 0.5adquirem, em média, mais ligações.

Isso possibilita que sítios, com característica intrínseca em torno de0.5, entrem na

rede um tempo depois e superem sítios que estão na rede por um tempo maior. Paraσ = 0ou10, o expoenteβé o mesmo, consequentemente, todos os sítios são igualmente bem sucedidos em adquirir ligações e independentes do tempo. . . 51

(13)

independentes): dependência do coeﬁciente de agregaçãoC(k)com o número de

vizinhoskdos sítios para diferentes valores deα em (número de ligações

adici-onadas a cada passo de tempo). O gráﬁco retrata que o coeﬁciente de agregação apresenta dois comportamentos: (i) para valores menores quek∼ 100, alto

coefi-ciente de agregação e uma lei de potência é observada; (ii) enquanto para valores maiores que k ∼ 100, o coeficiente de agregação está estabilizado. Assim, isso acontece independente do parâmetroα, mas é influenciado pelo parâmetrom. . . 53

5.7 O grau médio dos vizinhos de um sítio,< knn >, como uma função do graukdo

sítio. Ele mostra que a correlação do grau exibe mistura disassortativa. Os símbo-los são resultados de simulação numérica do modelo homofílico generalizado LE (o tamanho da rede foi ﬁxado em105 _sítios,_m

0 = m,σ = 1e média sobre12000 amostras). . . 54 5.8 O grau médio< knn >dos vizinhos de um sítio como uma função da característica

intrínseca do sítioη. Os símbolos são resultados da simulação numérica do modelo

homofílico generalizado LE (o tamanho da rede foi ﬁxado em105 sítios,m0 = m,

σ = 1e com média obtida de12000realizações independentes). Em cada gráﬁco

foram usados valores diferentes paraα: (a)α= 0, isto é, a característica intrínseca é distribuída uniformemente, (b) α = 1; (c) α = 2; (d) α = 10. Para α = 0 o comportamento é simétrico e para valores maiores queα = 0 há uma quebra da

simetria em< knn>. . . 55

5.9 A característica intrínseca média< ηnn >dos vizinhos de um sítio como uma

fun-ção da característica intrínseca do sítioη. As curvas são resultados da simulação

numérica do modelo homofílico generalizado LE (o tamanho da rede foi ﬁxado em

105_sítios,_m

0=m,σ= 1e com média sobre12000realizações independentes). Em cada gráﬁco, valores diferentes deα foram usados: (a) α = 0, ou seja, a

caracte-rística intrínseca é uniformemente distribuída; (b) α = 1; (c) α = 2; (d)α = 10.

Na proporção em queαaumenta, um salto aparece na característica intrínseca

mé-dia< ηnn >devido à distribuição não homogênea da característica intrínseca (Ver

equação 3). Note que o parâmetromé independente em cada ﬁgura.. . . 56

(14)

1 Introdução 1

2 Conceitos Fundamentais 4

2.1 O que são Redes? . . . 4

2.2 Distribuição de Conectividade . . . 7

2.3 Menor Caminho Médio . . . 8

2.4 Coeﬁciente de Agregação . . . 9

2.5 Robustez . . . 11

2.6 Correlações da Conectividade . . . 13

2.7 Redes Reais . . . 15

2.7.1 6 graus de separação . . . 15

2.7.2 Internet . . . 17

2.7.3 World Wide Web . . . 19

2.7.4 Rede de colaborações de atores de cinema . . . 20

2.7.5 Rede celular . . . 21

3 Modelos de Redes Complexas 22 3.1 Modelo de Barabási - (BA) . . . 22

(15)

3.2.2 Coeﬁciente de Agregação . . . 27

3.3 Modelo de Bianconi - (BB) . . . 28

3.3.1 Modelo Livre de Escala . . . 32

3.3.2 Distribuição de qualidade uniforme . . . 32

4 Rede Complexa Homofílica 38 4.1 Introdução . . . 38

4.2 Modelo Homofílico . . . 39

4.3 Resultados e Discussões . . . 40

5 Generalização da Rede Complexa Homofílica 44 5.1 Introdução . . . 44

5.2 Modelo Generalizado . . . 45

5.3 Resultados . . . 47

5.3.1 Resultados Topológicos . . . 47

5.3.2 Resultados em Correlações . . . 52

6 Conclusões 57

Referências Bibliográficas 59

(16)

INTRODUÇÃO

Nas últimas décadas uma verdadeira revolução tem surgido na ciência, interdis-ciplinarizando vária áreas aparentemente desconexas como Física, Biologia, Economia, Informática, entre outros. Fenômenos com um alo grau de complexidade como os ob-servados em avalanches, terremotos, batidas do coração, o funcionamento do cérebro, a organização das estruturas linguísticas, o comportamento caótico das bolsas de valores, o dobramento das proteínas, as informações codiﬁcadas do DNA, os processos de catá-lise,entre outros, começam a ser entendidos, de uma forma uniﬁcada e lógica dentro de um campo de pesquisa conhecido, atualmente, como Sistemas Complexos [1], com suas várias áreas, como podemos citar caos, autômatos celulares, difusão anômala, percolação, redes complexas. Nesta tese focaremos o estudo sobre as Redes Complexas.

Tradicionalmente o estudo em Redes Complexas tem sua origem na teoria dos grafos. Os grafos são usados para descrever diferentes sistemas em uma forma compacta e simples, facilitando o entendimento dos conceitos e propriedades inerentes do sistema e do próprio modelo representação (grafo ou rede). A teoria dos grafos tem suas raízes no século XVIII com o famoso problema das pontes de Konigsberg [2], solucionado por Euler. Euler escreveu um curto artigo sobre um divertido problema que teve como palco Konigs-berg, uma cidade não muito distante de sua casa. Devido a existência do rio Pregel e da vocação da cidade para os negócios, uma vez que possuía uma frota muito requisitada de navios, os mercadores locais e seus familiares podiam desfrutar de uma vida

(17)

vel. As boas condições econômicas da cidade eram tais que os responsáveis pela mesma construíram nada menos do que sete pontes em vários pontos da cidade. A maioria das pontes, 5 de um total de 7, conectavam a elegante Ilha Kneiphof, cercada pelo rio Pregel, com o restante da cidade. As outras duas pontes ligavam os outros pontos da cidade. A população de Konigsberg, aproveitando o clima de harmonia e a paz da cidade, no tempo livre se divertia com o seguinte quebra-cabeças: "É possível encontrar um caminho atra-vessando as sete pontes sem nunca atravessar uma mesma ponte duas vezes?"Contudo, ninguém foi capaz de encontrar um caminho que satisﬁzesse o quebra-cabeças até que uma nova ponte fosse construída em 1875. Entretanto, quase 150 anos antes da constru-ção da nova ponte, em 1736, Euler ofereceu uma rigorosa prova matemática dizendo que não existia um caminho que passasse por todas as sete pontes uma única vez. Além de resolver o problema das pontes de Konigsberg, Euler, de forma não intencional, iniciou uma nova área da matemática conhecida como teoria dos grafos. Essa teoria é hoje a base de todo nosso conhecimento sobre redes, conjunto de nós conectados por arestas. A partir de Euler, outros estudiosos se dedicaram a compreender os vários tipos de grafos e como se dava sua estrutura, ou seja, como seus nós se organizavam.

Desde os anos 50, grandes redes aparentemente sem princípios organizacionais tem sido descritas através da Teoria dos grafos. Por volta de 1960, os matemáticos Paul Erdos e Alfred Renyi ﬁzeram as primeiras análises em Redes Complexas Aleatórias. No modelo de Erdos-Renyi, começamos comN nós e todo par é conectado com probabilidade p, criando uma rede com aproximadamentepN(N −1)/2ligações distribuídas aleatoria-mente [3]. Baseado no modelo de Erdos-Renyi podemos indagar sobre uma questão: redes reais se comportam de maneira aleatória? mais adiante discutiremos sobre essa questão e sobre outros modelos utilizados para gerar redes complexas.

(18)

valor, em geral, entre 2 e 3 [6]. Além dessa medida, pode-se caracterizar as redes reais através de várias outras medidas, duas outras frequentemente usadas é o menor caminho e o coeﬁciente de agregação (mede o número de triângulos presentes na rede), que estão combinadas, deﬁnem a propriedade de mundo pequeno, amplamente discutido na tese. É importante ressaltar que apesar de exibir várias medidas em redes, a distribuição de conectividade em lei de potência é a mais discutida. De certa forma, P (k) ∼ k−γ_{, é um}

dos motivos da diminuição do famoso modelo de Erdos-Renyi, modelo padrão durante quase 30 anos.

(19)

CONCEITOS FUNDAMENTAIS

As Redes Complexas estão presentes em nosso dia a dia: Como por exemplo, a rede mundial de computadores (a Internet), as redes sociais, redes de transmissão de doenças, redes terroristas, entre outras. Mas o que é exatamente uma rede? Quais os tipos de redes que existem? Quais são suas propriedades? O estudo da maioria das Redes Complexas foi motivado pelo desejo de entender vários sistemas reais. Neste capítulo revisaremos os conceitos fundamentais necessários para a compreensão desses sistemas e mostraremos algumas características gerais de algumas redes reais.

2.1 O que são Redes?

De uma maneira bem simples, uma rede é um conjunto de vértices (sítios ou nós) conectados entre si via linhas (ver Figura2.1) (arestas ou arcos) [12], através de analogia,

podemos representar um sistema formado por pessoas, proteínas, a internet, aeroportos, entre outros. Um sítio muito conectado é chamado de pólo ou "hub". Algumas caracte-rísticas podem ser associadas aos sítios e as ligações da rede, como por exemplo, peso, sentido, etc. No caso que as ligações sentido o sistema estudado é dito direcionado. Caso contrário é dita não direcionada. Também podemos gerar redes através de um algoritmo de crescimento assim existirá uma regra para estabelecer ligações entre os sítios.

(20)

O número total de conexões de um sítio é chamado de conectividadek. Na rede

com ligações dirigidas, o número de ligações que entram no sítio é chamado de conectivi-dade de entradaki, e o número de arestas que saem do vértice é chamado de conectividade

de saídak0. Dessa formak =ki+k0.

Figura 2.1: Representação esquemática de uma rede. Figura proveniente da ref [16].

Um caso particularmente interessante sobre os grafos, diz respeito às árvores (ver Figura2.2). As árvores são um tipo de grafo em que existe, exatamente, um único caminho

ligando cada par de nós [13]. Podemos ainda dizer que uma árvore é uma rede sem circuitos. Se uma árvore não tem partes separadas, é chamada árvore conectada. Uma árvore conectada que contamN sítios possuiL=N−1ligações. Em geral o númeroIde circuitos num grafo conectado com ligações sem direção é relacionado ao número da suas ligações e sítios por:

I =L+ 1−N (2.1)

Outro tipo interessante de rede são as redes aleatórias. Em termos gerais, redes aleatórias podem ser deﬁnidas como sendo um arranjo desordenado de ligações [9, 11]. A inerente aleatoriedade do sistema, associada a este processo, faz com que as ligações entre os sítios nem sempre dêem origem ao mesmo arranjo, então dessa forma o conceito não é tão simples assim. Para a Física Estatística, uma rede aleatória não é única, e sim uma rede particular de um ensemble estatístico de todas as realizações possíveis, onde cada realização tem seu peso estatístico.

Para os físicos as redes aleatórias podem ser: estáticas ou dinâmicas. Vamos in-troduzir essas idéias mostrando alguns exemplos simples.

(21)

Figura 2.2: a) Representação da rede de Bethe. Este é um exemplo de uma rede tipo árvore. b) Exemplo de uma rede com presença de circuito de ordemn= 3, representado pelos nós em verme-lho e pelas ligações em azul. Essa rede possui número de nósN = 8e número de ligaçõesL = 8.

Assim podemos determinar o número de circuitos, neste caso temosI = 1. Figura proveniente da

ref [16].

• O número total de vértices é ﬁxado.

• Escolhe-se aleatoriamente o par de vértices que serão conectados.

Um dos primeiros exemplos desse tipo de rede ou grafo, foi proposto por Erdos e Renyi em 1959 e é conhecido como grafo aleatório. Neste modelo, os nós são estatistica-mente independentes e equivalentes.

Um exemplo de rede aleatória evoluindo no tempo é um grafo aleatório simples crescendo através de adições simultâneas de vértices e arestas. O algoritmo deste grafo é:

• Em cada tempo, um novo vértice é adicionado ao grafo.

• Simultaneamente, um par de vértices escolhidos aleatoriamente são conectados por uma aresta.

(22)

Isso é possível porque o número de ligações não desaparecem e, assim, a não homoge-neidade da rede diminuirá. Um estado de equilíbrio pode ser aproximado somente se as ligações mais antigas desaparecerem de tempo em tempo.

2.2 Distribuição de Conectividade

A distribuição de conectividade é a característica mais simples de uma rede po-rém muito importante na classiﬁcação dos diferentes tipos de redes quanto a sua topolo-gia. Portanto, a análise da distribuição é fundamental ao criar um modelo de rede, pois esta determina a classe do grafo. Além do mais, em muitas situações o conhecimento da distribuição de conectividade é suﬁciente para o entendimento da rede e o que está acontecendo nela.

Em algumas Redes Complexas nem todos os nós vão apresentar a mesma cone-ctividade. Observaremos que existem nós mais conectados que outros. Informações de como a conectividade está distribuída entre os nós numa rede não direcionada é dada pelo gráﬁcoP(k), ou pelo cálculo dos momentos de distribuição. O momento de ordem né dado como:

⟨kn⟩=∑

k

knP (k) (2.2)

O primeiro momento é a conectividade média da rede [9, 11]. O segundo mo-mento mede as ﬂutuações da distribuição de conectividade.

(1)Distribuição de Poisson:

A distribuição de conectividade tipo Poisson é expressa pela Equação2.3.

P(k) = e

−⟨k⟩_⟨_k_⟩k

k! (2.3)

onde⟨k⟩é a conectividade média [14]. Um grafo aleatório tem sua conectividade seguindo

(23)

(2)Distribuição tipo Lei de Potência:

A distribuição de conectividade tipo lei de potência é expressa pela Equação2.4.

P(k)∝k−γ _(2.4)

com k ̸= 0 e γ sendo o expoente da distribuição [14]. Ao contrário da distribuição de

Poisson, redes que possuem distribuição de conexões comportando-se como lei de potên-cia não apresentam uma escala característica para sua conectividade. Essa “liberdade de conexão” faz com que tais redes sejam chamadas delivre de escala.

(3)Distribuição Discreta:

Esse espectro de conectividade é típico de redes que crescem deterministicamente [15]. As simulações desta tese tem distribuição discreta.

2.3 Menor Caminho Médio

Num grafo, conexões que ligam os vértices formam um caminho. Dados dois vér-tices pode haver caminho entre eles, mesmo que estes não estejam diretamente conecta-dos. O comprimento do menor caminho, ou caminho geodésico, é o caminho mais curto entre dois vértices quaisquer. No caso de um grafo desconectado composto por mais de um componente, o diâmetro é inﬁnito uma vez que não pode ser possível estabelecer um caminho entre os diversos componentes. Contudo, sempre é possível redeﬁnir o diâmetro do grafo como sendo o diâmetro máximo de seus agrupamentos.

A distância geodésica média entre pares de vértices de uma rede não direcionada é dada pela Equação2.5,

l = 2

N(N −1)

∑

i>j

di,j (2.5)

ondedi,jé a distância geodésica entre os vérticesiej. A média dedi,j tomada sobre todos

osN(N −1)/2pares de vértices resulta no menor caminho médiol.

Alternativamente, pode-se estimar o valor delnuma rede aleatória do tipo árvore.

(24)

um sítio qualquer pode visitar, em média, outroszsítios afastados a uma distância de um

passo. Generalizando, pode-se falar que após l passos este sítio visitará outros zl _sítios.

A estimativa dadistância característica da rede, isto é, o menor caminho médio, é obtida através da relaçãoN ∼zl. Dessa relação, chega-se a Equação2.6.

l≈ lnN

lnz (2.6)

Na expressão acima, o fato delrelacionar-se comlnN torna-se explícito o porquê

da pequena distância entre os pares de sítios na rede. Esta particularidade está presente no comportamento de algumas redes reais e é, comumente, conhecida como “efeito de mundo pequeno”.

2.4 Coeficiente de Agregação

O coeﬁciente de agregação de um vértice descreve a presença de conexões entre os primeiros vizinhos dele [13].

Podemos deﬁnir o coeﬁciente de agregação da seguinte forma: Consideramos uma rede com arestas sem direções e tomamos um vértice i que apresenta _z_i vizinhos mais próximos. Observemos dentre o número total de vizinhos do vérticeiquantos estão ligados entre si. A agregação máxima do vértice i é obtida quando todas as _z₍_z ₋₁₎_/₂ arestas possíveis estão presentes conectando todos os seus primeiros vizinhos.

O coeﬁciente de agregação de um vértice i qualquer da rede é deﬁnido como sendo a razão entre a quantidade total de arestas que conectam seus primeiros vizinhos

yi e o número máximo possível de arestas entre todos estes vizinhos mais próximos zi,

conforme a Equação2.7.

Ci =

2yi

zi(zi−1)

(2.7) ondeCi, assume valores no intervalo0≤Ci ≤1. QuandoCi = 0sabe-se que os vizinhos

do vérticei“não se conhecem” e, portanto, não estabelecem conexões entre si. No entanto, quandoCi = 1 existem todas as conexões possíveis entre todos os primeiros vizinhos do

(25)

A Figura 2.3, ilustra um exemplo simples. Nesse exemplo, temos um nói(símbolo

vermelho) conectado a seis primeiros vizinhos (símbolos pretos). Queremos determinar o seu coeﬁciente de agregação. Para isso devemos veriﬁcar inicialmente, qual a vizinhança deie quantos dos seus primeiros vizinhos estão conectados entre si. Neste caso, podemos

ver que cinco dos seus seis vizinhos estão conectados (linhas verdes), ou seja,yi = 5e o

número de conexões do sítio i é zi = 6. Assim é possível mostrar que o coeﬁciente de

agregação do nóiéCi(zi) = 1₃.

Figura 2.3: O conceito do coeﬁciente de agregração do sítioié obtido quando conhecemos seus primeiros vizinhos e sabemos como estes estão ligados entre si. Para esta ﬁgura temoszi = 6e yi= 5logoCi(zi) = 1₃. Figura proveniente da Ref [16].

O coeﬁciente de agregação de toda a rede, ou seja, o coeﬁciente de agregação médio, é obtido fazendo a média dosCi′_s pelo número total de vértices, de acordo com a

Equação2.8,

C = 1

N

∑

i

Ci =

1

N

∑

i

2yi

zi(zi−1)

(2.8)

(26)

2.5 Robustez

Falhas aleatórias e ataques maliciosos em redes de larga escala e em crescimento, como a Internet, podem causar danos em escala proporcionalmente grande - um ataque a um único hub pode degradar o desempenho de milhões de conexões, podendo afetar a rede como um todo.

Danos às redes podem ser causados por diversos fatores, entre eles, falhas e ata-ques. Falhas ocorrem aleatoriamente, afetando um vértice independente de qualquer ca-racterística especíﬁca. Por outro lado, ataques maliciosos têm alvos especíﬁcos, escolhi-dos, possivelmente, devido a suas características (conectividade, pontos de articulação, etc.) e podem obedecer a seqüências estratégicas.

Uma propriedade estática importante das redes é sua robustez. A robustez (ou resiliência) de uma rede é medida pela sua capacidade em manter-se conectada frente à remoção de alguns dos seus vértices. Existem diversas estratégias de remoção de vértices. Essas estratégias são classiﬁcadas como estratégias locais ou globais. A estratégia local mais simples, é a remoção aleatória. Nesta estratégia, todos os vértices são consultados e removidos com uma probabilidadepuniforme e independente do estado (ativo/inativo)

dos seus vizinhos ou de seu grau de conectividade. De maneira geral, a remoção aleatória pode ser associada a falhas esporádicas nos vértices que compõem uma rede.

Por outro lado, existe uma estratégia global que consiste em retirar os vértices mais conectados, maximizando o número de conexões desativadas. Esta estratégia re-quer que todos os vértices sejam classiﬁcados de acordo com seu grau de conectividade e então, removidos da rede seguindo a ordem decrescente de graus de conectividade. Tal estratégia é conhecida como ataque dirigido [16].

(27)

Figura 2.4: Ataque aleatório. A figura 2.4 (a) mostra a estrutura da rede, a figura (b) mostra os sítios que vão ser atacados, (sítios amarelos), e a figura (c) mostra a estrutura da rede após o ataque, mostrando que a maior parte da rede ainda continua conectada. Isso significa que a rede é robusta a esse tipo de ataque.

(28)

2.6 Correlações da Conectividade

Sabemos que a distribuição de conectividade de uma rede fornece um panorama geral a respeito das interconexões entre os sítios. Mas além da distribuição de conecti-vidade, é possível caracterizar as redes pela presença de correlações [17]. Embora pa-reça plausível que um sítio possa se conectar a outro independente das características do segundo, isto não ocorre na maioria dos casos reais. É comum encontrarmos, em tais sistemas, exemplos de padrões de conexões que se estabelecem pela preferência de nós se conectarem com outros nós de características similares ou até mesmo opostas. Depen-dendo das características dos nós, isso dá origem a vários tipos de correlações. Entretanto, quando consideramos apenas a topologia da rede, o principal tipo de correlação é a cor-relação grau-grau [17].

É importante ressaltar que todos os modelos de crescimento de redes estão corre-lacionados, pois em processos de crescimento a presença de ligações entre os nós depende da idade e do grau desses nós, e existe uma assimetria entre os nós mais jovens e os nós mais velhos. Portanto as correlações sempre existem, entretanto depende do modelo do sistema estudado.

Em termos de medidas, correlações grau-grau podem ser, teoricamente, expressas por meio da probabilidade condicionalP(

k′

/k)

. Esta representa a chance de uma ligação, escolhida ao acaso, conectar sítios de grau k′

e k ou, em outras palavras, representa a

probabilidade de que uma ligação aponte para um sítio de grauk′

, condicionada ao fato que ela tem origem em um sítio de grauk. Do ponto de vista numérico, é mais

conve-niente caracterizar as correlações grau-grau pelo conceito de grau médio dos primeiros vizinhos de um nó com conectividadek (brevemente chamado grau médio dos primeiros

vizinhos). Embora menos rigorosa, esta abordagem alternativa, para estudar correlações, tem sido bastante usada na literatura e permite encontrar como nós de diferentes graus estão interconectados. Para isso, toma-se como base o grau médio dos primeiros vizinhos como uma função do grauk dos sítios⟨knn,i(k)⟩

A ﬁm de obter esta função, consideraremos um sítioicom grauki, e calculamos o

(29)

knn,i =

1

ki

∑

j∈V(i)

kj (2.9)

onde a soma se dá sobre todos os vizinhos do sítioi. Desta quantidade podemos obter a

função, ⟨knn,i(k)⟩para analisar o comportamento das correlações de grau, que é

formal-mente deﬁnida como [18]:

⟨knn(k)⟩=

1

Nk

∑

i/ki=k

knn,i (2.10)

em queNké o número de sítios com grauke o somatório é feito sobre aqueles sítios com

conectividadeki =k.

A curva resultante desta função pode ser facilmente interpretada e é a base para uma primeira classiﬁcação das redes complexas [19] via correlações de grau. Se⟨knn(k)⟩

for uma função crescente do grauk, a rede apresenta mistura assortativa por grau; isto

é, sítios altamente conectados estão, em média, ligados a vizinhos que também possuem muitas conexões. Na situação oposta, quando⟨knn(k)⟩é uma função decrescente, a rede

analisada exibe mistura disassortativa, indicando que sítios com poucas conexões, em mé-dia, têm vizinhança com sítios altamente conectados e vice-versa. Na ausência de correla-ções,⟨knn(k)⟩é uma função constante, sugerindo que o grau dos vizinhos é independente

da conectividade do sítio em questão.

Podemos também inspecionar as correlações grau-grau, de uma rede, por meio de uma outra quantidade, menos rigorosa que knn,i, mas que, historicamente, tem sido

amplamente usada pelos sociólogos. Ela é conhecida como coeﬁciente de correlação de Pearson e tem a seguinte deﬁnição [11].

r =

⟨

kk′⟩

l− ⟨k⟩l

⟨

k′⟩

l

⟨k2_⟩

l− ⟨k⟩

2

l

(2.11)

Aqui k ek′

são os graus dos nós das extremidades de uma ligação, e⟨⟩_l indica a média sobre todas as ligações da rede. O coeﬁciente de Pearson é uma função de correla-ção de par padrão, adequadamente normalizada de tal maneira quer varia no intervalo

(30)

interco-nexões da rede. Caso a rede tenha, em média, nós pouco conectados ligados a vizinhos bastante conectados e vice-versa (mistura disassortativa), entãor < 0, e uma correlação

negativa se faz presente.

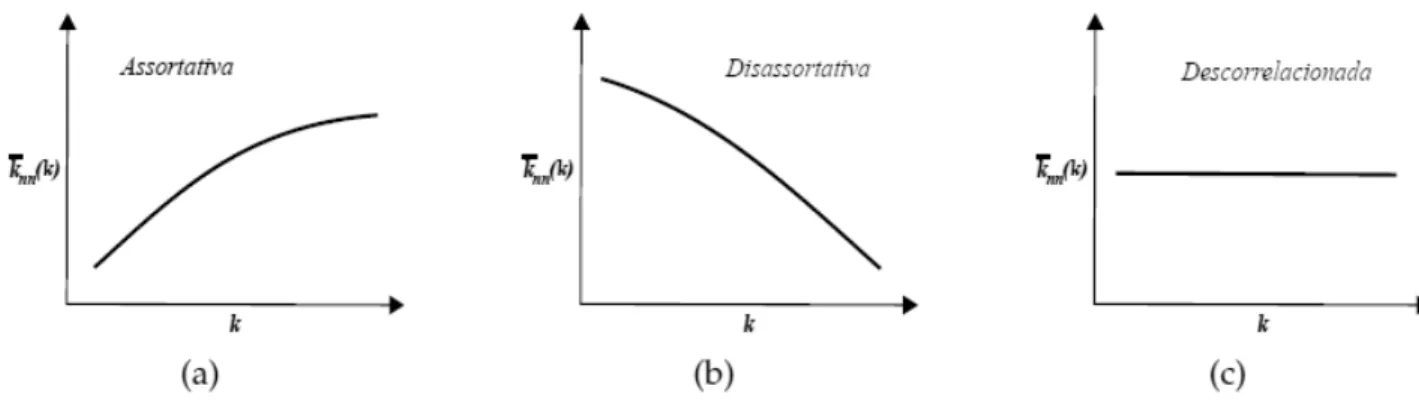
Figura 2.6:Grau médio dos vizinhos mais próximos. Esta quantidade mede quão correlacionados está o grau médio dos primeiros vizinhos de sítios com conectividadek. Em (a) ⟨knn(k)⟩ cresce

com a conectividade dos sítios, indicando a presença de correlações de grau positivas na rede (assortatividade). Em (b) mostra uma tendência decrescente de⟨knn(k)⟩o que signiﬁca que a rede

é negativamente correlacionada (disassortatividade). Finalmente, em (c), com⟨knn(k)⟩constante,

a rede é descorrelacionada. Figura proveniente da Ref [20].

2.7 Redes Reais

Para que se possa modelar um problema real em uma Rede Complexa, necessita-se, antes de mais nada, identiﬁcar os elementos que a compõe e, sobretudo, saber como tais elementos interagem. Nos anos recentes, isso vem sendo feito com vários sistemas reais, objetivando-se assim, identiﬁcar e compreender suas características e/ou proprie-dades topológicas. Procurando seguir essa lógica, veremos daqui por diante, exemplos de sistemas reais que foram modelados sob a forma de redes e falaremos sobre algumas características topológicas apresentadas pelas mesmas.

2.7.1 6 graus de separação

(31)

em mais um de seus experimentos sociais. O objetivo de Milgram agora era encontrar a distância entre duas pessoas quaisquer nos EUA. Para dar início a esse experimento duas pessoas foram escolhidas como alvo. A primeira foi a esposa de um estudante de teologia em Sharon, Massachusetts; e a segunda foi um corretor em Boston. O próximo passo foi escolher as cidades de Wichita, no Kansas, e Omaha, no Nebraska, como ponto de partida para o estudo.

O experimento de Milgram exigiu o envio de cartas para moradores, aleatoria-mente escolhidos, de Wichita e Omaha pedindo a eles que participassem de um estudo de contato social na sociedade americana. A carta continha informações sobre duas pessoas escolhidas como alvos, junto com as seguintes instruções:

COMO PARTICIPAR DO ESTUDO

(1) Cada pessoa que receber o caderno deve adicionar seu nome nele. Isto serve para rastrear de quem partiu o envelope, evitando que este volte para uma mesma pessoa.

(2) Se você não conhece a pessoa alvo, não tente contactá-la diretamente. Ao invés disso, repasse este caderno para alguém que você conhece e acredite que, este, tenha maior chance de conhecer a pessoa alvo.

(3) Se você conhece a pessoa alvo, envie este documento diretamente para ele(a).

(4) Ao enviar o caderno, cada pessoa deve retirar uma página dele, preenchê-la e remetê-preenchê-la ao cientista. Esta, sem dúvida, é uma fase muito importante do estudo, pois ela permite, a Milgram, acompanhar o progresso da experiência ao longo do trajeto do caderno até chegar a pessoa alvo. Nas mãos da pes-soa alvo o caderno deve, agora, ser enviado ao Psicológo para a conclusão do experimento.

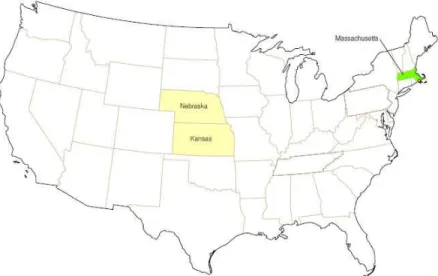
A Figura2.7mostra o Mapa dos Estados Unidos e a Figura2.8mostra o resultado ﬁnal da experiência.

(32)

Figura 2.7: Mapa dos Estados Unidos. Os estados em amarelo (Nebraska e Kansas) representam a origem das correspondências e o estado em verde (Massachusetts) representa o destino ﬁnal. Figura proveniente da Ref [20].

Figura 2.8: Esquema do experimento de Stanley Milgram. Figura proveniente da Ref [20].

2.7.2 Internet

(33)

re-presentam um único nó, onde a ligação se estabelece entre dois domínios se existir, pelo menos, um roteador que os conecte.

Um aspecto de especial interesse, demonstrado pela Internet, está relacionado a grande quantidade de nós que ela apresenta, quando comparada com outros sistemas re-ais. Tal aspecto é importante do ponto de vista das análises estatistícas feitas na rede, e estas revelaram que a Internet, tanto a nível de roteadores quanto de domínios, apre-senta propriedades topológicas não triviais; entre elas, a distribuição de conectividade comportando-se como lei de potência. Esse fato confere a Internet, a inclusão numa classe de redes denominadas livres de escala.

Figura 2.9:Comportamento da distribuição de conectividade da Rede WWW. Figura proveniente da Ref [18].

Outras características da Internet, como menor caminho médio e coeﬁciente de agregação, ratiﬁcam a inclusão dela nessa classe de redes. Pastor-Satorras et al [18], estu-dando a Internet a nível de domínios, entre 1997 e 1999, obtiveram valores para o menor caminho médio situados abaixo de 4. Estes são diferentes daqueles exibidos por grafos aleatórios clássicos, quando têm-se o mesmo número total de vértices e conexões. Em particular, para a Internet no ano de 1998, a relação entre o menor caminho¯_l/¯

lrand era de

0.6.

(34)

alcançar a maioria dos vértices e isso faz a Internet exibir o caráter de mundo pequeno. A nível de roteadores, o menor caminho médio é¯_l_≈₁₀_{, valor ligeiramente menor do que o} de seu correspondente grafo aleatório clássico.

2.7.3 World Wide Web

A WWW é uma coleção de webpages armazenadas em muitos servidores ao redor do mundo. Estas páginas são acessadas usando um protoloco de comunicação conhecido como HTTP (Hyper Text Transfer Protocol). Este processo dita os detalhes de pedido en-viado pelo cliente para uma certa página. A WWW é uma das maiores redes para o qual as informações topológicas estão atualmente disponíveis. Os nós da rede são representa-dos pelos documentos (webpages) e as ligações são representadas por hyperlinks (URLs) que apontam de um documento para outro. Devido à importância que a WWW tem no cotidiano das pessoas (informação, marketing, pesquisa...), tem crescido muito o interesse por pesquisa desse sistema.

As ligações na WWW são direcionadas, portanto a rede é caracterizada por dois tipos de distribuição: a distribuição de conectividade de saída e entrada do nó, Pout(k),

Pin(k)respectivamente. Estudos tem mostrado que ambas as distribuições tem uma cauda

em lei de potência. Para um subconjunto da rede WWW comN = 32579o expoente carac-terístico da distribuição encontrado em 1999 [6] foiγin = 2.1eγout = 2.45. Posteriormente

Broder et al, em 2000 [22], calcularam o expoenteγin eγout da distribuição e veriﬁcaram

que, para uma amostra de 200 milhões de documentos,γin = 2.1eγout = 2.72mostrando

uma constância noγin um aumento no γout. Apesar do grande número de nós, a WWW

(35)

Figura 2.10: Distribuição de links saindo (a) e entrado (b) em uma Web page. Em (c), menor caminho médio como uma função do tamanho da rede. Figura proveniente da Ref [17].

2.7.4 Rede de colaborações de atores de cinema

(36)

ﬁlme é uma lei de potência parakgrande, que segueP(k)∼k−γator, onde_γ

ator = 2,3±0.1.

Ver ﬁgura2.11.

Figura 2.11: Rede de colaborações de atores de cinema com 212250 ⟨k⟩ = 28,78 eγator = 2,3.

Figura proveniente da Ref. [23].

2.7.5 Rede celular

Jeong et al. (2000) [24], estudaram o metabolismo de 43 organismos, representa-dos em três domínios da vida, e organizaram numa rede em que os nós são os substratos (como ATP, ADP, H2O) e a conexão representa a direção predominante da reação química em que esses substratos podem participar. A distribuição de saída e de entrada é em lei de potência para todos organismos, com o expoente variando entre2,0e2,4. O coeﬁciente de

agregação não foi calculado e quanto ao menor caminho médio foi3,3aproximadamente para todos organismos.

(37)

MODELOS DE REDES COMPLEXAS

3.1 Modelo de Barabási - (BA)

Os modelos discutidos até agora possuem um número ﬁxoN de vértices que são

aleatoriamente conectados ou reordenados. Já no modelo de Barabási e Albert, a rede cresce com a adição contínua de novos sítios [6]. Começam com um pequeno número de sítios e com o passar do tempo, o número de sítios aumenta durante a idade da rede por adições sucessivas de sítios novos.

Baseado nos dois princípios fundamentais: crescimento contínuo e conexão pre-fencial, Barabási e Albert propuseram o modelo decorrente das seguintes regras:

(1)Inicia-se a rede comm0sítios.

(2)A cada passo de tempo é adicionado um novo sítio. Esse sítio é conectado

com outrosm(≤m0) sítios do aglomerado da rede pré-existente.

(3) A probabilidade de uma conexão ser feita com um determinado sítio i é

proporcional akie é dada por l

(38)

Π(ki) = ki ∑ j kj (3.1)

(4)Repete-se as operações (2) e (3) até o tamanho desejado e após tpassos de

tempo, a rede teráN =m0+tsítios emtligações.

Tratamento contínuo: Foi introduzido por Barabási, Albert e Jeong [6] com o

in-tuito de calcular a dependência temporal da conectividade ki, de um dado sítio i. Essa

conectividade ki cresce à medida que novos sítios entram na rede e ligam-se ao sítio

i, sendo a probabilidade desse processoΠ(ki). Admitindo que ki é uma variável real e

contínua, a taxa de variação temporal com queki muda, deve ser proporcional a Π(ki).

Consequentementekisatisfaz a Equação dinâmica m.

∂ki

∂t =mΠ(ki) =m ki N−1

∑

j=1

kj

(3.2)

Observando que a soma no denominador não considera os sítios que estão sendo introduzidos na rede e que cada ligação é simétrica e por isso contada duas vezes, notemos que no limitet→ ∞, a soma é dada pela Equação n.

N−1

∑

j=1

kj = 2(mt−m)⇒2mt (3.3)

A simples substituição da Equação n em 3.2, leva a Equação o.

∂ki

∂t = ki

2t (3.4)

Sabendo que o sítio i é adicionado na rede no tempoti com o número inicial de

conexõeski = m, a solução da Equação o com a condição inicialki(ti) = m é dada pela

Equação p.

ki(t) =m

(

t ti

)β

com β = 1

(39)

A Equação p mostra que a conectividade de todos os sítios evolui da mesma forma e segue uma lei de potência, com expoente bem deﬁnido. Como mostra a Figura3.1.

Figura 3.1: A ﬁgura mostra a evolução temporal da conectividade para o modelo BA. Figura proveniente da Ref. [26].

Usando a Equação p, podemos escrever a probabilidade de um nó ter uma cone-ctividadeki(t)menor quek,P[ki(t)< k], dada pela Equação q.

P

[

mt

β

tβ_i < k

]

=P

[

tβ_i > mt

β

k

]

=P

[

ti >

mβ1t

kβ1

]

(3.6)

A incorporação de novos sítios na rede se dá em intervalos de tempos iguais. Logo, os valores ti obedecem a uma densidade de probabilidade constante, dada pela

Equação r,

P(ti) =

1

m0 + 1

(3.7) substituindo esta na Equação q obtém-se a Equação s.

P

[

ti >

m1βt

kβ1

]

= 1− m 1

βt

kβ1(m

0+t)

(40)

A distribuição de conectividadeP(k)pode ser obtida usando a Equação t.

P(k) = ∂P[ki(t)< k]

∂k =

2mβ1t

m0+t

1

kβ1+1

. (3.9)

No limite,t → ∞, temos a Equação u,

P(k)∼2mβ1k−γ, (3.10)

onde o expoente da lei de potência é dado por:

γ = 1

β + 1 = 3, com β =

1

2. (3.11)

Esse valor concorda muito bem com os resultados numéricos ver Figura3.2.

Figura 3.2: Distribuição de conectividade do modelo de Barabási-Albert. Figura proveniente da Ref. [26].

(41)

Equa-ção t prevê que assintoticamente a distribuiEqua-ção de conectividade, do modelo de Barabási-Albert, independe do tempo (e do tamanho da redeN = m0 +t), indicando que, apesar

do crescimento contínuo, a rede atinge um estado estacionário livre de escala.

3.2 Propriedades do Modelo de Barabási-Albert

Embora o modelo de Barabási-Albert apresente distribuição de conectividade com cauda em lei de potência, ele tem outras propriedades que podem concordar ou não com os resultados empíricos das redes reais. Como discutido no capítulo anterior, uma caracte-rística marcante de algumas redes reais é a coexistência da alta agregação com o pequeno comprimento do caminho médio (efeito de mundo pequeno). Dessa forma, precisamos investigar se a rede gerada pelo modelo de Barabási-Albert possui o caráter de mundo pequeno.

3.2.1 Comprimento do Menor Caminho Médio

A Figura3.3mostra a comparação entre o comprimento do menor caminho médio da rede de Barabási-Albert e de uma rede aleatória. Para efeitos de comparação, a cone-ctividade média,⟨k⟩ = 4e o tamanho da redeN. O gráﬁco ilustra que o comprimento do

menor caminho médio no modelo de Barabási-Albert é menor que o de uma rede aleató-ria, para qualquer valor deN. Ou seja neste modelo a rede é mais coesa e o comprimento

do menor caminho médio da rede de Barabási-Albert cresce logaritmicamente comN de

acordo com a Equação tt.

l =A ln(N −B) +C (3.12)

(42)

Figura 3.3:Gráﬁco do menor caminho médiolpelo tamanho da redeN, no modelo de

Barabási-Albert com⟨k⟩= 4, comparado com um grafo aleatório de igual tamanho e mesma conectividade

média. Figura proveniente da Ref. [13].

3.2.2 Coeficiente de Agregação

A Figura3.4mostra o coeﬁciente de agregação da rede de Barabási-Albert e para um grafo aleatório,Crand ≃ ⟨k⟩/N, ambos com a mesma conectividade⟨k⟩= 4e tamanhos

diferentes. O coeﬁciente de agregação da rede livre de escala é cerca de cinco vezes maior que o de um grafo aleatório, e diminui lentamente com o crescimento da rede. Além do mais o coeﬁciente de agregação da rede livre de escala segue uma lei de potência C ∼

(43)

Figura 3.4: Coeﬁciente de agregação versus o tamanho da rede do modelo de Barabási-Albert com⟨k⟩ = 4, comparado com o coeﬁciente de agregação de um grafo aleatório,Crand ≃ ⟨k⟩/N.

Figura proveniente da Ref. [13].

3.3 Modelo de Bianconi - (BB)

No sentido de fornecer um modelo simples que nos permita investigar, em termos quantitativos, o aspecto competitivo das redes reais, Bianconi e Barabási adicionaram na ligação preferencial um fator de qualidade ηi, para cada sítio da rede. Levando-se em

consideração que a existência de uma qualidade modiﬁca a ligação preferencial dos sí-tios, ao competir por ligações, encontraremos que sítios com diferentes qualidades terão ritmos distintos para sua evolução de conectividade. Em outras palavras, a dependência temporal da conectividade dos sítios continuará, como no modelo de Barabási-Albert, se-guindo uma lei de potência (ki(t) ∼ tβi). Entretanto, o expoente dinâmicoβi dependerá

da qualidade do nó.

(44)

(1) Inicia-se a rede com m0 sítios, onde cada um deles possui um parâmetro de

qualidade η. A qualidade é escolhida aleatoriamente respeitando uma distribuição de

qualidadeρ(η)(que se mantém constante ao longo do tempo).

(2)A cada passo de tempo é adicionado um novo sítio que já possui um parâmetro

de qualidadeη, escolhido a partir da distribuição de qualidade (passo1). Esse novo sítio é, então, conectado com outrosm(≤m0) sítios do aglomerado da rede pré-existente.

(3)A probabilidade do novo sítio se conectar com um sítioi, que já está presente

na rede, é proporcional a conectividade ki e a qualidade ηi desse sítio i, e é dada pela

Equação xx.

Πi =

ηiki

∑

j

ηjkj

. (3.13)

(4)Repete-se as operações (2) e (3) até o tamanho desejado. Para tempos bastante

longos,t → ∞, a rede teráN =m0+tsítios emtligações.

Essa generalização da ligação preferencial, incorpora a combinação mais simples possível que a qualidade e conectividade presentes determinem a taxa com que novas ligações são adicionadas a um dado sítio, isto é, possibilita ao sítio relativamente mais jovem que possui algumas ligações obter uma alta taxa de conexões. Para isso basta ter um grande parâmetro. Sendo assim o mesmo pode ter a chance de vir a ser um pólo.

Com o desejo de discutir as propriedades de escala do modelo acima, em primeiro lugar, utilizaremos a teoria contínua que permite-nos prever a distribuição de conectivi-dade. Os detalhes sobre a teoria contínua foram tratados na seção3.1. Um sítioi

aumen-tará sua conectividade ki, numa taxa que é proporcional a probabilidade do novo sítio

ligar-se a ele, de acordo com a Equação hh

∂ki

∂t =m ηiki

∑

j

ηjkj

. (3.14)

O fatormretrata o fato de que cada novo sítio, adicionado na rede, incrementam

ligações ao sistema. Um caso particular éρ(η) = δ(η−1), onde todas as qualidades são

iguais. Substituindo essa distribuição na Equação hh encontra-se o modelo de Barabási-Albert que prediz ki(t) ∼ t1/2. Naturalmente, para resolver a Equação 3.14 Bianconi e

(45)

da conectividade dos nóskisegue uma lei de potência. Entretanto, haverá multiescala no

sistema, pois o expoente dinâmico dependerá da qualidadeηi do sítio em questão, logo

kηi(t, t0) = m

(

t t0

)β(ηi)

, (3.15)

onde t0 é o tempo em que o nó i foi incorporado ao sistema. Um outro aspecto, a ser

observado, é que o expoente dinâmico, β(η), é limitado no intervalo 0 < β(η) < 1, pois um sítio sempre aumenta o número de ligações no tempo (β(η)>0) e sua conectividade, ki(t), não pode aumentar mais rapidamente quet(β(η)<1). Agora, calcularemos a média

da soma∑

jηjkj. Considerando que cada sítio seja "criado"num tempo diferente de t0, a

soma sobrej pode ser escrita como uma integral emt0.

=

∫

dη ρ(η)η mtβ(η)

∫ t

1

dt0

tβ₀(η)

=

∫

dη ηρ(η)m(t−t

β(η)₎

1−β(η) . (3.16)

Já que β(η) < 1, no limite em que t → ∞, tβ(η) _{pode ser desprezado quando}

comparado comt, dessa forma, obtemos

⟨ ∑

j

ηjkj

⟩

=Cmt(1 +O(t−ϵ)), (3.17)

onde

ϵ = (1−maxβ(η))>0, C =

∫

dη ρ(η) η

1−β(η). (3.18)

Usando a Equação qual05, e a notaçãokη =kηi(t, t0), a Equação dinâmica hh pode ser escrita como,

∂kη

∂t = ηkη

(46)

a qual tem uma solução da forma (qual03), onde

β(η) = η

C, (3.20)

conﬁrmando, assim, a natureza auto-consistente da suposição da Equação (qual03). Note-mos queβ(η)depende deC e, logicamente, dependerá deρ(η). Desse modo, precisamos

determinar o valor deC. Na Equação (qual06), substituimos β(η)porη/C, o que resulta em

1 =

∫ ηmax

0

dηρ(η)_C 1

η −1

, (3.21)

ondeηmaxé a máxima qualidade possível no sistema. Aparentemente a Equação (qual09)

é uma integral com uma singularidade. Porém, comoβ(η) =η/C <1para qualquer valor deη, temosC > ηmax, dessa forma, o limite de integração nunca atinge essa singularidade.

Note que, se ∑

jηjkj ≤ ηmax

∑

jkj = 2mtηmax, temos, usando a Equação (qual05), que

C≤2ηmax.

Finalmente, podemos calcular a distribuição de conectividadeP(k), que fornece

a probabilidade de um sítio ter k ligações. Se existisse um único expoente dinâmico β,

a distribuição de conectividade seguiria a lei de potênciaP(k) ∼ k−γ_{, onde o expoente}

da conectividade é dado porγ = 1/β+ 1. Entretanto, no modelo de Bianconi-Barabási,

temos um espectro de valores para o expoente dinâmicoβ(η) e, dessa forma, P(k) será obtida pela média de diferentes leis de potência. Para encontrarP(k)precisamos calcular a probabilidade acumulada para um certo sítio,kη > k, logo

P[kη(t)> k] = P

[

t0 < t

(

m k

)_Cη]

= t

(

m k

)C_η

(3.22)

(47)

P(k) =

∫ ηmax

0

dη ∂P[kη(t)> k] ∂t

∝

∫ ηmax

0

dη ρ(η)C

η

(

m k

)C_η+1

(3.23)

a qual depende da escolha da distribuição de qualidadeρ(η).

Dada a distribuição de qualidadeρ(η), a teoria contínua permite-nos prever a di-nâmica da rede, descrita através do expoente dinâmicoβ(η)(Equações qual08 e qual09), e a topologia, caracterizada pela distribuição de conectividade P(k) (qual11). Para de-monstrar a validade destas previsões, a seguir calcularemos essas quantidades para dois casos: No primeiro utilizaremos uma distribuição de qualidade que recupera o modelo livre de escala (modelo de Barabási-Albert); e no segundo usaremos uma distribuição de qualidade uniforme.

3.3.1 Modelo Livre de Escala

O Modelo de Barabási-Albert é um dos mais simples (ligação preferencial de-pende apenas da conectividade dos sítios) e apresenta todos os sítios com a mesma qua-lidade (note que seηi = constante, da Equação obtêm-se a Equação dinâmica do modelo

de Barabási-Albert). Dessa forma, podemos representar a distribuição de qualidade desse modelo da seguinte maneira, ρ(η) = δ(η −1)que inserindo na Equação 3.21,

encontra-mosC = 2, que indicará o maior valor possível paraC. Usando a Equação3.20, obtemos

β = 1/2e da Equação3.23chegamos a P(k) ∼ k−3_{; a bem conhecida relação do modelo}

livre de escala que foi tratada na seção 3.1. Podemos notar que o modelo de

Barabási-Albert representa um caso limite do modelo de qualidade considerado na seção anterior, com o expoente da conectividade possuindo o maior valor possível.

3.3.2 Distribuição de qualidade uniforme

(48)

existem sítios com diferentes qualidades competindo por ligações (modelo de Bianconi-Barabási). Para conseguir essa dinâmica insere-se na Equação 3.23uma distribuição de qualidade uniforme. Esta é obtida quando as qualidades são escolhidas uniformemente do intervalo [0,1], ou seja, ρ(η) = constante. Com isso, é possível observar diferentes

valores para o expoente dinâmicoβ (múltiplas escalas). A constanteC pode ser

determi-nada da Equação3.21. Fazendo uma mudança de variável apropriada, ondey = C−ηe dy=−dη, teremos

1 =

∫ C

C−1

dy(C−1)

y . (3.24)

Essa integral fornece a seguinte expressão

exp(−2/C) = 1−1/C, (3.25)

a partir da qual encontra-seC∗ _{= 1}_,_{255. De acordo com a Equação}₃_._{20, cada sítio terá um} expoente dinâmico diferente dado porβ(η)∼ _Cη∗. Utilizando a Equação3.23, teremos

P(k)∝

∫ 1 0 dη C ∗ η 1

k1+C∗_/η ∼

k−(1+C∗₎

log(k) , (3.26)

isto é, a distribuição de conectividade segue uma lei de potência generalizada, com um logaritmo inverso. A validade da teoria contínua para o modelo de Bianconi-Barabási foi veriﬁcada através de simulações númericas. Para a veriﬁcação, utilizou-se uma distribui-ção de qualidade uniforme, onde as qualidades foram escolhidas com igual probabilidade do intervalo [0,1]. O maior interesse era testar a validade da Equação3.15, já que ela

pre-via o comportamento da evolução temporal da conectividade dos sítios com diferentes parâmetros de qualidadesη.

Na ﬁgura 3.5 têm-se a constatação de que ki(t) segue uma lei de potência para

todosη. Já na Figura3.8, vemos que o expoente de escalaβ(η)depende deη, sendo maior

para nós com maior qualidade. A Equação3.17prevê que a soma⟨∑

iηiki⟩/mt → C∗ no

limite t → ∞, onde C∗ _{é dado pela Equação}₃_.₂₅ _sendo _C∗ _{= 1}_._{255, como indicado na} Figura3.6. Por ﬁm, na Figura3.7vemos a concordância entre a predição da Equação3.26 e os resultados numéricos para a distribuição de conectividadeP(k).

(49)

neste a existência de alguns sítios que possuem uma alta conectividade ("hubs ou pólos") e aparecem como uma longa linha horizontal num gráﬁco log-log, sendo encontrados em vários sistemas reais, incluindo a rede WWW e a rede metabólica das células. Isso indica que "super pólos"é uma característica de sistemas competitivos.

Figura 3.5: Simulação numérica para uma rede comm = 1e comN = 105, mostrando a

depen-dência temporal da conectividadekη(t), para sítios com qualidadeη = 0.3,0.6,0.9. Note que em

(50)

(51)

Figura 3.7: Distribuição de conectividade no modelo de qualidade, obtida para uma rede com

(52)

Figura 3.8: Dependência do expoente dinâmico β(η) com o parâmetro da qualidadeη para o caso de uma distribuição uniforme,ρ(η) = constante.Os círculos foram obtidos por simulação

numérica, enquanto a linha corresponde a predição analíticaβ(η) = η/1,255. Figura proveniente

(53)

REDE COMPLEXA HOMOFÍLICA

4.1 Introdução

É de conhecimento geral que o processo de formação de conexões, entre os sítios de uma rede, é inﬂuenciado por diferentes aspectos. Por exemplo, no modelo proposto por Barabási-Albert (BA), a idade dos sítios dá origem ao efeito de vantagem cumulativa, fazendo que os sítios mais velhos tenham uma alta conectividade e recebam mais cone-xões à medida que a rede cresce. Esta dinâmica é garantida pela chamada regra de ligação preferencial do modelo, a qual inevitavelmente produzirá correlações e uma assimetria entre a conectividade dos sítios mais jovens e os sítios mais velhos. Estes, invariavelmente, serão os sítios mais conectados da rede e, de certo modo, são os responsáveis diretos pela cauda em lei de potência para a distribuição de conectividades.

Já no modelo elaborado por Bianconi-Barabási (BB), além da conectividade dos sítios, outro aspecto, presente na ligação preferencial, que desempenha um papel impor-tante na formação de ligações é conhecido como qualidade. Ele simboliza a qualidade intríseca dos sítios e pode representar, por exemplo, o contéudo de uma web page na WWW ou o talento de um ator na rede de atores de ﬁlmes. Dependendo do parâmetro da qualidade um sítio jovem pode adquirir, em um intervalo de tempo relativamente curto, uma quantidade signiﬁcativa de ligações, ultrapassar sítios mais velhos e eventualmente torna-se um pólo da rede.

(54)

É sabido que, em muitas redes reais, os sítios possuem suas próprias característi-cas que, dependendo do contexto, podem ganhar diferentes interpretações. Por exemplo, em redes sociais, a cada indivíduo pode ser atribuído idade, gênero, etnia, nível de esco-laridade ou outros parâmetros que representam suas demais preferências; na rede de in-teração de proteínas, cada proteína é caracterizada por suas funções biológicas; na WWW as web pages são classiﬁcadas com base em seu conteúdo. Para estas, e para muitas outras redes, as evidências empíricas indicam que um fator que desempenha papel fundamental para a adição de novas ligações entre sítios é a similaridade entre as características dos mesmos.

Semelhanças nas características de pessoas, por exemplo, elevam a probabilidade para que se estabeleçam vínculos entre elas. Tanto é assim que observamos facilmente como pessoas tendem a se relacionar por compartilharem a mesma fé, mesmo time de futebol, por gostarem do mesmo cantor e etc.

Em todas as situações mencionadas anteriormente, as chances de formação de co-nexões aumentam mediante o partilhamento de algo comum entre os entes. Esta tendên-cia para se estabelecer ligações entre aqueles de características semelhantes é conhecida como homoﬁlia.

4.2 Modelo Homofílico

Os exemplos discutidos anteriormente enfatizam que as diferentes características dos sítios são, digamos, as suas habilidades para competir por ligações. No entanto, estas são mais acentuadamente favorecidas entre constituintes similares. Para levar em conta esta tendência, foi introduzido um termo chamado similitude ver Ref. [38],Aij =|ηi−ηj|,

ondeηi eηjrepresentam, respectivamente, as características intrísecas dos sítosiej.

Ob-serve que o termo de similitude favaorece o contato entre os sítios de características simi-lares com um taxa muito maior do que entre aqueles de características dissimisimi-lares.

O algoritmo do modelo é descrito abaixo

Primeiro passo: Começamos com a rede contendom0sítios, onde as características

de cada um deles estão reunidas no parâmetroηi, o qual tem valor inalterado no tempo e é