Poderia Arquimedes ter calculado
π
com areia e um bast˜
ao?
(Could Archimedes have calculatedπwith sand and a stick?)Fernanda J. Dellajustina
1, Luciano C. Martins
Departamento de F´ısica, Universidade do Estado de Santa Catarina, Joinville, SC, Brasil
Recebido em 17/2/14; Aceito em 23/3/14; Publicado em 31/7/2014
Neste artigo propomos trˆes m´etodos para determinar numericamente o valor de uma das constantes mais famosas e importantes da matem´atica, a constanteπ. Apresentamos um m´etodo num´erico inspirado no m´etodo original de Arquimedes, um m´etodo mecˆanico experimental que utiliza areia e um bast˜ao, e finalmente, a partir de um modelo baseado na ideia de probabilidade, o m´etodo de Monte Carlo que ´e usado para a determina¸c˜ao deπ. O aparato experimental usado ´e bastante simples e de baixo custo, facilitando a utiliza¸c˜ao do m´etodo experimental e sua aplica¸c˜ao no ensino de f´ısica e matem´atica em escolas de Ensino M´edio.
Palavras-chave: valor num´erico deπ, m´etodo experimental para obterπ, m´etodo de Monte Carlo para calcu-larπ.
We propose three methods to numerically determine the value of one of the most famous and important mathematical constants, the constantπ. We present a numerical method inspired by the original method of Archimedes, an experimental mechanical method that uses sand and a stick, and finally, from a model based on the idea of probability, the Monte Carlo method is used for the evaluation ofπ. The experimental apparatus is very simple and of low cost, which makes easy the use of the experimental method and its application in physics and mathematics courses at high-school level.
Keywords: numerical value ofπ, experimental method to determineπ, Monte Carlo method to determineπ.
1. Introdu¸
c˜
ao
Arquimedes de Siracusa (287-212 a.C.), um dos mais importantes cientistas da antiguidade [1], entre outras fa¸canhas calculou quantos gr˜aos de areia haveria no uni-verso. Para isso utilizou o modelo heliocˆentrico de Aris-tarco de Samos, e quase todo o conhecimento de sua ´epoca, tendo sido um dos pioneiros na constru¸c˜ao de um sistema num´erico para operar e representar n´umeros gi-gantes. Ele muitas vezes fazia seus c´alculos escrevendo na areia, com um bast˜ao, pois nessa ´epoca o papel era raro e precioso demais para rascunhos e desenhos.
Dentre muitos feitos inovadores para a ciˆencia, Ar-quimedes utilizou um engenhoso m´etodo geom´etrico para estimar um intervalo de valores num´ericos que de-limitou o valor de uma das constantes mais famosas e importantes da matem´atica, a constante π. Poderia Arquimedes ter determinado experimentalmente o va-lor dessa constante utilizando apenas areia, o seu bast˜ao como alavanca e considera¸c˜oes de simetria e aleatorie-dade? A resposta a essa pergunta ´e sim, como
demons-traremos nesse trabalho.
O n´umero π ´e conhecido desde a Babilˆonia de onde se tem os primeiros registros de aproxima¸c˜oes num´ericas do valor da constante [2]. Acredita-se tamb´em que os eg´ıpcios tinham conhecimento do valor deπ, o qual foi utilizado para a constru¸c˜ao da grande pirˆamide de Giz´e que possui um per´ımetro de 1.760 cˆovados2 e uma altura de 280 cˆovados, de forma que a rela¸c˜ao 1.760/280≈6,29 que ´e aproximadamente iguai 2π≈6,28 [3].
Abordagens instrucionais contemporˆaneas esperam os alunos se tornem produtores ativos de conhecimento. Isso leva `a necessidade de cria¸c˜ao de ferramentas de en-sino e tarefas que podem oferecer aos alunos oportuni-dades de aprendizagem ativa [4]. Neste estudo utiliza-mos a experiˆencia computacional como uma integra¸c˜ao da ciˆencia computacional com o m´etodo de aprendi-zagem por descoberta. O experimento computacional suporta ambos os tipos de pesquisa, a explora¸c˜ao ex-perimental, bem como a pesquisa criativa, ajudando os alunos a desenvolver modelos n˜ao s´o de explora¸c˜ao, mas
1
E-mail: fernandadellajustina@gmail.com.
2
Unidade de medida de comprimento que foi usada por diversas civiliza¸c˜oes antigas, entre eles os babilˆonios, eg´ıpcios e hebreus. Era baseada no comprimento do antebra¸co, da ponta do dedo m´edio at´e o cotovelo. O cˆovado real dos antigos eg´ıpcios media 50 cm, o dos romanos media 45 cm.
tamb´em de modelos consistentes. A extensa literatura cient´ıfica ´e uma evidˆencia robusta de que as simula¸c˜oes de computador podem melhorar a instru¸c˜ao tradicional, especialmente na medida em que as atividades labora-toriais s˜ao consideradas [5, 6].
Propomos um experimento pr´atico e simples que ilustra o conceito emp´ırico de probabilidade e como se pode chegar intuitivamente na ideia central do m´etodo de Monte Carlo [7], muito utilizado em simula¸c˜oes num´ericas feitas em computadores. No experimento proposto, apenas uma medida linear simples feita com r´egua ser´a usada para a determina¸c˜ao da constanteπ, com o uso de areia e um bast˜ao apoiado, para equilibrar e comparar massas como uma balan¸ca primitiva.
Para revis˜ao e motiva¸c˜ao, apresentamos na Se¸c˜ao 2. a relevˆancia e a utilidade pr´atica da constante π, pra que se possa entender melhor o porque de tanto inte-resse e esfor¸co hist´orico de tantos povos e civiliza¸c˜oes na sua determina¸c˜ao.
Discutimos brevemente na Se¸c˜ao 3. o m´etodo ori-ginal de Arquimedes para a determina¸c˜ao geom´etrica de π, que a seguir ser´a comparado com outros trˆes m´etodos, um m´etodo num´erico, um m´etodo experimen-tal e outro por simula¸c˜ao computacional, o m´etodo de Monte Carlo [7, 8], respectivamente nas Se¸c˜oes. 4. a 7.. Ao final, na Se¸c˜ao 8., comparamos os m´etodos apre-sentados e resumimos as principais conclus˜oes finais deste trabalho.
2.
Qual a utilidade da constante
π
?
O n´umeroπ, ´e definido como a raz˜ao do per´ımetroS de uma circunferˆencia pelo seu diˆametroD, ou seja,
π≡ S
D , (1)
e a partir desta defini¸c˜ao, o per´ımetro da circunferˆencia pode ser escrito comoS = 2πR, j´a que o seu diˆametro ´eD= 2R.
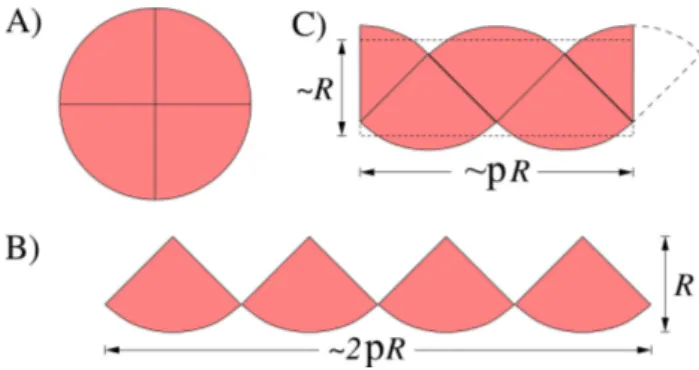
A ´area do c´ırculo pode ser obtida a partir do seu per´ımetro usando-se o seguinte argumento geom´etrico. Considere um c´ırculo partido em N setores idˆenticos, sendo N um n´umero par. Por exemplo, paraN = 4, veja a Fig. 1A. Reorganizando-se os setores do c´ırculo conforme mostra a Fig. 1B, dividindo-se esse padr˜ao ao meio e dispondo-os como mostra a Fig. 1C, obte-mos uma primeira aproxima¸c˜ao para a ´area do c´ırculo, considerando o retˆangulo de baseπRe alturaR, sendo
A≈πR2, (2)
j´a que existe uma pequena diferen¸ca entre as ´areas do retˆangulo e dos setores originais do c´ırculo. Ao se divi-dir o c´ırculo em um grande n´umero de partes (N ≫4), obteremos uma melhor aproxima¸c˜ao com a ´area do retˆangulo da Fig. 1C, e pode-se mostrar que no limite N → ∞, a f´ormula aproximada dada pela Eq. (2) se torna exata, ou seja, uma igualdade.
Figura 1 - C´ırculo de raioRpartido em 4 setores idˆenticos, B) os setores alinhados e C) reorganizados na forma aproximada de um retˆangulo.
Um racioc´ınio an´alogo pode ser usado para a ob-ten¸c˜ao do volume de uma esfera, seccionando-a em N setores esf´ericos idˆenticos e reorganizando-os na forma aproximada de um paralelep´ıpedo, que no limiteN → ∞ter´a o volume exato da esferaV = 4πR3/3.
Em resumo, o per´ımetro de uma circunferˆencia, ´a ´area de um c´ırculo e o volume de uma esfera, s˜ao quan-tidades geom´etricas diretamente proporcionais ao valor da constanteπ, da´ı a importˆancia do seu c´alculo exato. Todas essas rela¸c˜oes envolvendo a constanteπforam de-monstradas rigorosamente por Arquimedes atrav´es do m´etodo da exaust˜ao de Eudoxo, e apresentadas nos seus livros A Medida do C´ırculoeSobre a Esfera e o Cilin-dro.
3.
O m´
etodo geom´
etrico de Arquimedes
No ano de 250 a.C. Arquimedes estimou o valor de π, atrav´es de um engenhoso m´etodo geom´etrico, uti-lizando pol´ıgonos regulares inscritos e circunscritos a uma circunferˆencia de diˆametro unit´ario, e portanto de per´ımetro π, conforme prevˆe a Eq. (1). Como o per´ımetro do pol´ıgono inscrito Si ´e menor que
o per´ımetro da circunferˆencia, e este, menor que o per´ımetro do pol´ıgono circunscrito Sc, Arquimedes
de-limitou um intervalo para o valor da constante procu-rada, ou seja,
Si< π < Sc. (3)
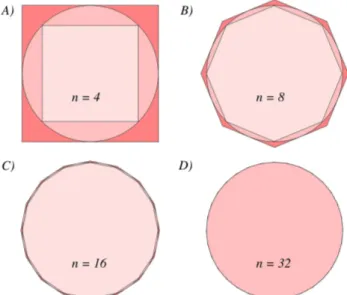
A medida que o n´umero de lados dos pol´ıgonos for sendo aumentado, o valor deπpoder´a ser calculado com uma precis˜ao cada vez maior, pois o per´ımetro dos pol´ıgonos tendem ao da circunferˆencia.
Figura 2 - M´etodo de Arquimedes para estimar o valor deπpor pol´ıgonos regulares inscritos e circunscritos numa circunferˆencia, para pol´ıgonos de 4, 8, 16 e 32 lados.
A ideia ´e simples, mas os c´alculos necess´arios s˜ao trabalhosos, se considerarmos que n˜ao existia ainda a trigonometria e muito menos as ferramentas modernas do c´alculo na ´epoca de Arquimedes, mas apenas a ge-ometria euclidiana, aritm´etica e ´algebra elementares. Cerca de um s´eculo antes de Arquimedes, o fil´osofo grego Arist´oteles havia demostrado a incomensurabili-dade [9] da diagonal de um quadrado com rela¸c˜ao ao seu lado, pois aquela medida n˜ao podia ser expressa como uma fra¸c˜ao desta, o que chamamos hoje de n´umero irra-cional, sendo que a matem´atica grega n˜ao considerava v´alida a existˆencia de tais n´umeros que n˜ao podiam ser medidos ou calculados exatamente.
Repetindo o processo, com pol´ıgonos inscritos e cir-cunscritos de at´e 96 lados, Arquimedes demonstrou que o n´umero procurado deve satisfazer a desigualdade
3 +10
71 < π <3 + 1
7 , (4)
ou seja 3,140< π <3,143. Tomando-se o valor m´edio do intervalo acima, obtemos o melhor valor de Arqui-medes para a constante como sendo
π= 3 +141
994 ≈3,1418 (5)
uma aproxima¸c˜ao correta at´e a terceira casa decimal, com o ultimo algarismo sendo o duvidoso.
4.
O m´
etodo num´
erico
Adaptando a ideia original de Arquimedes, calcu-laremos com um m´etodo num´erico as aproxima¸c˜oes num´ericas de π. Para a ´area de um c´ırculo com raio unit´ario, vale uma desigualdade similar `aquela da Eq. (3), dada por
Ai< π < Ac. (6)
ondeAi e Ac s˜ao as ´areas de pol´ıgonos inscritos e
cir-cunscritos ao c´ırculo.
Assim, para o c´alculo deπ, ao inv´es do per´ımetro, vamos considerar a ´area de pol´ıgonos com n´umero de la-dosn= 4,8,16,32, . . . ,2m, ou seja, potˆencias de 2, para
m = 2,3,4, . . .. Partindo da Eq. (6), vamos escrever uma express˜ao para as sucessivas ´areas dos pol´ıgonos inscritos no c´ırculo que sejam fun¸c˜ao do n´umero de lados dos pol´ıgonos, e para isso, come¸caremos dese-nhando um quadrado inscrito no c´ırculo, conforme a Fig. 2A. Tra¸cando as diagonais do quadrado obtemos 4 triˆangulos, cujas ´areas s˜ao f´aceis de determinar, pois a ´area de um triˆangulo ´e a metade da ´area de um retˆangulo com a base e a altura do pr´oprio triˆangulo.
Figura 3 - Um triˆanguloABCde um pol´ıgono A) inscrito e B) circunscrito num c´ırculo s˜ao aproxima¸c˜oes para a ´area do setor circular.
O triˆangulo inscrito mostrado na Fig. 3A possui ´area Ai,n=R2 sin(θn/2) cos(θn/2) =R2 sin(θn), sendo que
para um pol´ıgono regular denlados,θn = 360◦/n.
As-sim, como a ´area do c´ırculo foi dividida em nsetores, podemos aproximar a ´area do c´ırculo com raio unit´ario, e portanto,
Ai=n Ai,n= (n/2) sin(360◦/n) (7)
j´a que sin(2α) = 2 sinαcosα´e uma identidade v´alida para qualquer ˆanguloα. De modo similar, o triˆangulo circunscrito da Fig. 3B possui ´areaAc,n=R2 tan(θ/2),
e para pol´ıgonos regulares denlados, circunscritos no c´ırculo de raio unit´ario, temos
Ac =n Ac,n=ntan(180◦/n). (8)
A partir dessas ´areas podemos calcularπcom uma precis˜ao muito grande. A Tabela 4. mostra os resulta-dos obtiresulta-dos para as primeiras aproxima¸c˜oes deπ.
Tabela 1 - Aproxima¸c˜oes deπobtidas com o m´etodo num´erico, para alguns valores den.
m n Ai< π π < Ac
Verificamos nesta tabela que conseguimos estimar o valor deπ com 15 casas decimais para m= 28, sendo portanto suficiente um pol´ıgono com 228= 268,435,456 lados, para se obter o valor deπcom a precis˜ao dupla padr˜ao. O m´etodo num´erico apresentado aqui ´e um m´etodo exato, pois ap´os um n´umero finito de passos podemos determinar o valor num´erico deπcom a uma precis˜ao finita qualquer. Os dados da Tabela 4. fo-ram obtidos com o c´odigo em linguagem C, listado no Apˆendice 9.1..
5.
O modelo
Com base na Fig. 2A podemos escrever uma rela¸c˜ao en-tre o lado do quadrado circunscrito e o raio da c´ırculo, dada por 2R=L, e definindo-se a raz˜aopentre a ´area do c´ırculo e a ´area do quadrado temos
p= Ac Aq
=πR 2 L2 =
π
4 (9)
que ´e a fra¸c˜ao da ´area do quadrado ocupada pelo c´ırculo.
Isolando πna equa¸c˜ao anterior temos
π= 4p (10)
sendo esta a rela¸c˜ao fundamental a partir da qual po-demos determinar o valor π, sendo necess´ario apenas calcular a fra¸c˜aop.
6.
O m´
etodo experimental
Para a determina¸c˜ao da fra¸c˜aopda Eq. (10) podemos usar gr˜aos de areia para determinar experimentalmente o valor deπ, usando um aparato experimental bastante simples e f´acil de montar. Tal aparato consiste numa caixa quadrada de lado internoLe alturahe um tronco de cilindro com raio externo igual aL/2 e mesma altura da caixa, que dever´a ser encaixado dentro desta caixa, veja na Fig. 4.
Figura 4 - Esquema de montagem do experimento para calcular
πusando areia.
Os valores para o tamanho da caixa devem ser es-colhidos com o crit´erio de uma boa medida, baseada no volume e peso da areia que ser´a colocada dentro da caixa, para que n˜ao seja muito grande, e muito pesada,
e nem muito pouca, dif´ıcil de pesar. No arranjo expe-rimental que montamos para fazer as medidas usamos L= 33,10 cm e h= 7,50 cm.
A caixa pode ser feita de qualquer material que su-porte o peso sem se deformar, sem perder ou misturar os gr˜aos de areia durante a coleta para a realiza¸c˜ao das medidas. Veja na Fig. 5 o aparato experimental que montamos.
Figura 5 - Montagem experimental para a determina¸c˜ao doπcom a caixa de areia vazia (acima) e cheia de areia (abaixo), com a borda do cilindro pintada de azul.
Para medir o n´umero π vamos precisar ainda de areia bem seca, para que ela n˜ao fique grudada na pa-rede da caixa ou no tronco de cilindro, ou forme cavida-des sem preenchimento uniforme, interferindo assim nos resultados num´ericos. Com a areia preenchemos a caixa e o cilindro, raspando a parte superior para remover o excesso de areia e nivelar a superf´ıcie de forma mais plana poss´ıvel. Na sequˆencia vamos separar em um saco a areia externa ao tronco de cilindro, que chama-mos demr, e em outro saco a areia interna ao cilindro
mc, nesta ordem. Na ´ultima etapa do experimento
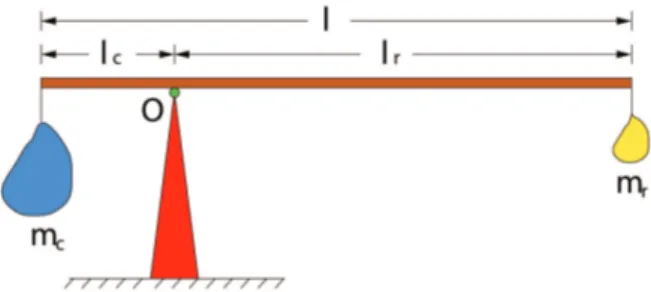
Figura 6 - Balan¸ca esquem´atica usada na compara¸c˜ao de massas das massasmremcde areia.
Para montagem da balan¸ca usamos um cabo de vas-soura, com um gancho em cada ponta, e um pequeno peda¸co de madeira na forma de um prisma triangular para fazer o apoio. Se apoiado no seu centro de gra-vidade, o sistema pode ficar em repouso, como uma gangorra em equil´ıbrio. Esse m´etodo foi desenvolvido por Arquimedes para determinar o centro de gravidade de um corpo ou de uma figura geom´etrica, baseado no seu princ´ıpio de alavanca e no conceito de torque. Para que o sistema fique em equil´ıbrio, os torques devem ser compensados, ou seja, sua soma deve ser nula. Ma-tematicamente, o momento das massas em rela¸c˜ao ao ponto de apoio deve ser nulo, pois esse ponto ´e o centro de massa do sistema, ent˜ao
lcmc =lrmr, (11)
e isolando a massa contida no cilindro temos
mc=mr
lr
lc
. (12)
A partir da Eq. (10), e como as massas s˜ao pro-porcionais as volumes, e portanto `as ´areas superficiais, temos
π= 4 mc mc+mr
. (13)
Pela Eq. (12), eliminando-se as massas mc e mr da
express˜ao acima temos
π= 4 lr lc+lr
= 4lr
l, (14)
ondel=lc+lr´e a distˆancia entre as massas
equilibra-das no bast˜ao.
Dessa forma podemos determinar π simplesmente a partir da raz˜ao entre o comprimento do bast˜ao e a distˆancia lr do ponto onde mr esta pendurada at´e o
ponto de apoioO.
No modelo simplificado descrito acima a massa do bast˜ao n˜ao foi considerada no c´alculo, o que acarreta um pequeno erro na medida experimental de π. Para corrigir esse erro, ap´os marcado o pontoOde equil´ıbrio das massas, voltamos a reequilibrar apenas o bast˜ao e um pequeno contra-peso colocado na mesma posi¸c˜ao que a massa mc estava. Com esse procedimento,
ga-rantimos que o centro de massa do bast˜ao, com o con-trapeso, coincida com o ponto O anterior. Ap´os esse
ajuste, recolocamos as mesmas massasmcemrem seus
lugares anteriores e reequilibramos o sistema inteiro, juntamente com o bast˜ao e o contrapeso. Devido a pre-sen¸ca do contrapeso, o novo ponto de equil´ıbrio ser´a encontrado `a direita de O, a uma pequena distˆancia ϵ. Ent˜ao, para esse bast˜ao compensado pelo contra-peso, a nova distˆancia da massamr at´e o novo ponto
de equil´ıbrio ser´a tamb´em aumentado na mesma quan-tidadeϵ. Com esse ajuste, podemos calcular o valor de πpela f´ormula corrigida
π= 4lr+ϵ
l . (15)
Escrevendo-se as equa¸c˜oes exatas para o sistema completo, com o contrapeso que reequilibra o bast˜ao na posi¸c˜ao originalO, obtemos uma equa¸c˜ao exata para o c´alculo deπ, por´em bastante complicada, dada por
π= 4
(
l2
−2llr+ 2lr2 )
ϵ+l2l
r−3llr2+ 2lr3
l(
lϵ+l2−3ll
r+ 2lr2
) . (16)
Essa f´ormula exata pode ser expandida em s´erie de Taylor, em torno do valorϵ= 0, donde obtemos a s´erie
π= 4lr+ϵ
l +
4ϵ2 l2−3l l
r+ 2l2r
+O(
ϵ3)
, (17)
donde conclu´ımos que a f´ormula corrigida dada pela Eq. (15) ´e a corre¸c˜ao de primeira ordem da f´ormula exata acima. No modelo exato acima, ainda assim n˜ao consideramos a massa dos dois pequenos ganchos usa-dos para a sustenta¸c˜ao usa-dos sacos contendo as massas mc emr, e tamb´em desprezamos as massas dos sacos
pl´asticos utilizados. Como se vˆe, o modelo acima ainda n˜ao ´e um modelo exato, mas apenas um modelo me-lhorado. Em f´ısica, os modelos exatos s˜ao um limite inating´ıvel, e por mais que melhoremos o nosso mo-delo, sempre ser´a apenas um modelo para descrever um fenˆomeno ou experimento f´ısico [10].
Para a medi¸c˜ao experimental deπutilizamos o apa-rato mostrado na Figs. 5A e 5B para a determina¸c˜ao das massas mc e mr, atrav´es do equil´ıbrio das massas
penduradas no bast˜ao conforme mostra a Fig. 6. Uti-lizamos inicialmente areia e depois gr˜aos de arroz para preencher a caixa, e com o uso das f´ormulas apresenta-das acima, obtivemos as aproxima¸c˜oes num´ericas para a constanteπ, atrav´es das medidas delr eϵ, sendo que
a distˆancia entre os ganchos que sustentam as massas foi mantida sempre fixa eml= 99,8 cm. Os resultados podem ser vistos na Tabela 6..
Tabela 2 - Resultados experimentais de π para um bast˜ao de comprimentol= 99,8 cm.
Material / Medida lr(cm) π πcorr πexato
Areia
1 77,6 3,11 3,12 3,12 2 78,0 3,13 3,14 3,14 Arroz
De forma alternativa, podemos obter experimental-mente o valor deπatrav´es das medidas das massasmc
emrem uma balan¸ca, ou atrav´es das medidas dos seus
respectivos volumes, Vc eVr, o que tamb´em medimos.
Veja-se os resultados mostrados nas Tabelas 6. e 6..
Tabela 3 - Resultados experimentais deπobtidos com medidas dos volumesVceVr.
Material / Medida Vc(mL) Vr (mL) π
AReia 6450 1750 3,146 Arroz 6615 1760 3,159
O valor m´edio de πobtido a partir de todos as me-didas parciais mostradas nas Tabelas 6., 6. e 6. ´e, com a margem normal de erro, ¯π= 3,136±0,006.
Tabela 4 - Resultados experimentais deπobtidos com medidas das massasmcemr.
Material / Medida mc(kg) mr(kg) π
Areia 10,110 2,726 3,150 Arroz 5,630 1,524 3,148
Este m´etodo experimental usando gr˜aos de areia para preencher um volume pode ser comparado com o m´etodo de Monte Carlo que veremos na se¸c˜ao 7.. No m´etodo de Monte Carlo a raz˜ao entre o n´umero de pon-tos pertencentes ao c´ırculo e o total de ponpon-tos ´e propor-cional aπ, sendo que quanto maior o n´umero de pontos melhor ´e a aproxima¸c˜ao do valor num´erico deπ.
No nosso experimento, de forma semelhante ao m´etodo de Monte Carlo, o valor deπ´e obtido, indire-tamente, pela propor¸c˜ao dos gr˜aos de areia pertencente ao tronco cil´ındrico e o resto sobrante que pertenciam a caixa originalmente. Mas e qual seria o total de gr˜aos de areia na caixa? Seria compar´avel ao total de pontos que usamos na simula¸c˜ao de Monte Carlo? Para responder estas perguntas vamos estimas a quantidade de gr˜ao de areia contida na caixa. Para isto vamos considerar que um gr˜ao de areia seja aproximadamente esf´erico. Segundo a escala de Krumbein-Wentwort [11, 12] um gr˜ao de areia de tamanho m´edio, como foi o caso usado no nosso experimento, tem aproximadamente 0,25 mm de diˆametro m´edio, e portanto o volume de apenas um gr˜ao seria da ordem de 8,2 ×10−3 mm3. Ent˜ao, num
volume de 1,0 cm3 de areia existem aproximadamente 1,2 ×105 gr˜aos de areia. A caixa usada no nosso ex-perimento tinha um volume de Vcaixa =L2h = (33,1
cm)2
×7,5 cm = 8,2 ×103 cm3 = 8,2 L, e continha aproximadamente 1,0×109gr˜aos de areia.
7.
M´
etodo de Monte Carlo
Na natureza observamos muitos fenˆomenos que n˜ao po-dem ser descritos de forma exata ou determin´ıstica, mas podem ser entendidos atrav´es do uso da estat´ıstica. Por exemplo, durante uma chuva regular em um local aberto, as gotas caem no ch˜ao em posi¸c˜oes que n˜ao po-dem ser previstas, e se observarmos o fenˆomeno sobre
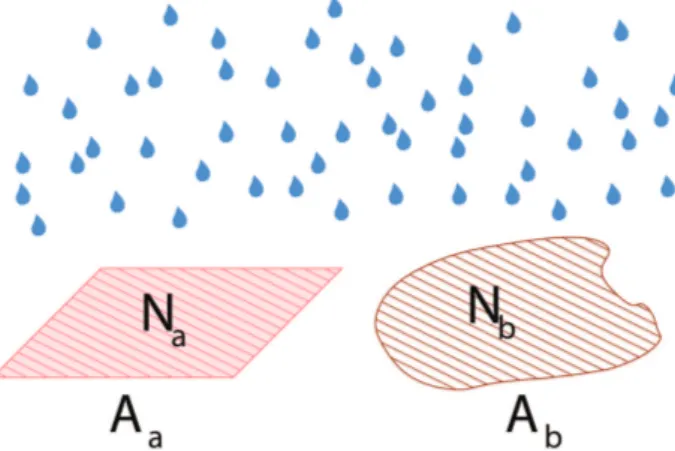
uma dada superf´ıcie durante um tempo razoavelmente longo, depois que muitas gotas caem, somos levados a uma hip´otese estat´ıstica fundamental: se n˜ao sabemos onde e quando uma gota cair´a sobre a superf´ıcie, ent˜ao uma gota pode cair em qualquer lugar, num dado ins-tante, de forma que a chance ou probabilidade deve ser uniforme sobre a superf´ıcie, j´a que n˜ao existe raz˜ao para que uma certa regi˜ao seja privilegiada em rela¸c˜ao `a ou-tra, ou que as gotas apresentem um padr˜ao espacial ou temporal nesse fenˆomeno. Consideramos ent˜ao que a queda de cada gota de chuva representa um evento in-dependente, e a observa¸c˜ao de um grande n´umero des-ses eventos pode ser tratada estatisticamente, embora os eventos individuais sejam imprevis´ıveis (aleat´orios). Por simetria, ou pura ignorˆancia dos eventos individu-ais, podemos supor que a quantidade de gotas que caem numa determinada ´area seja proporcional ao tamanho da ´area, ao intervalo de tempo em que se observa o fenˆomeno e da taxa m´edia com que as gotas caem, veja a Fig. 7.
Figura 7 - O n´umero de gotas de chuva que caem sobre uma placa horizontal, em um determinado intervalo de tempo, ´e proporcio-nal ao tamanho da ´area.
Se compararmos duas ´areas diferentes, expostas `a mesma chuva e durante um mesmo intervalo de tempo suficientemente longo, podemos pensar empiricamente que a raz˜ao das quantidades de gotas que caem nas ´areas seja a mesma raz˜ao das ´areas consideradas, res-pectivamente, isto ´e,
Na
Nb ≈
Aa
Ab
. (18)
Os meteorologistas costumam usar essa mesma ideia para medir a quantidade de chuva que cai numa regi˜ao, pois medem em mil´ımetros (mm) a altura total (di´aria, mensal ou anual) da coluna de ´agua que se forma dentro de um tubo (pluviˆometro).
Determina-se numericamente a integral da fun¸c˜aof so-bre um volume conhecido V, atrav´es da defini¸c˜ao do valor m´edio,
f ≡V1
∫
V
f(x, y, z, . . .)dV . (19)
Aplicando-se esse m´etodo para o c´alculo da ´area de um c´ırculo, geramos pontos aleat´orios (x, y) com dis-tribui¸c˜ao uniforme dentro de um quadrado circunscrito a um c´ırculo, e verificamos quantos pontos pertencem ao c´ırculo, para a determina¸c˜ao num´erica da fra¸c˜ao p da ´area do quadrado que pertence ao c´ırculo, e assim, determinamos πatrav´es da Eq. (10).
Quando falamos em escolher um ponto dentro do quadrado, n˜ao se trata de uma escolha definida ou pre-vis´ıvel, mas sim de uma escolha aleat´oria, ou seja, que n˜ao tem uma regra definida para a escolha dos pon-tos de forma que a escolha de um ponto n˜ao tem ne-nhuma rela¸c˜ao com a escolha do ponto seguinte ou do ponto anterior. Esta ideia intuitiva de aleatoriedade ´e fundamental para a aplica¸c˜ao deste m´etodo, pois se, por exemplo, definirmos que todos os pontos devem cair dentro do c´ırculo ent˜ao sabemos que todos os pon-tos ir˜ao pertencer ao c´ırculo, caracterizando assim uma probabilidade viciada.
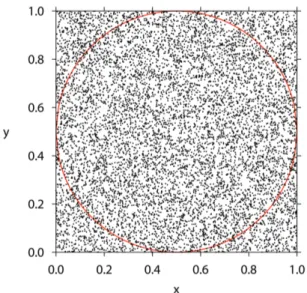
Para isso sortearemosN pontos dentro da regi˜ao de-limitada pelo quadrado, isto ´e, no intervalo 0 ≤x≤1 e 0≤y ≤1, conforme a Fig. 8. Deste total de pontos uma certa quantidadeNc cair˜ao dentro da c´ırculo.
O objetivo deste procedimento seria o de preencher toda a ´area do quadrado com os pontos, resultando na ´area total do quadrado, sendo que no limite em queN tender a infinito teremos a ´area exata do quadrado e do c´ırculo, cuja raz˜ao dar´a p, com o qual calculamosπ.
Como n˜ao se pode gerar infinitos pontos dentro de um quadrado, podemos obter sucessivas aproxima¸c˜oes paraπaumentando cada vez mais o n´umero de pontos N, permitindo assim que me¸camos o valor deπcom a precis˜ao que desejarmos. Para efeito de ilustra¸c˜ao mon-tamos a Tabela 7. com os respectivos valores deπpara cada valor deN utilizado.
Tabela 5 - Aproxima¸c˜oes de π obtidas pelo m´etodo de Monte Carlo.
Amostra N Nc π
1 10 7 2,80000000
2 100 82 3,28000000
3 1.000 775 3,10000000
4 10.000 7.791 3,11640000 5 100.000 78.355 3,13420000 6 1.000.000 785.500 3,14200000 7 10.000.000 7.854.138 3,14165520 8 100.000.000 78.540.838 3,14163352 9 1.000.000.000 785.396.509 3,14158604 10 10.000.000.000 7.853.983.189 3,14159328 11 100.000.000.000 78.539.489.819 3,14157959 12 1.000.000.000.000 785.397.975.760 3,14159190
A probabilidadepdefinida na Eq. (9) pode ser ava-liada numericamente pela fra¸c˜ao do n´umero de ponto que caem dentro do c´ırculoNc, em rela¸c˜ao ao n´umero
total de pontosN, ou seja,
p= Nc
N , (20)
que substitu´ıda na equa¸c˜ao (10) resultar´a,
π= 4Nc
N , (21)
considerando-se um grande n´umeroN de pontos. Usando o gerador randˆomico [13] sorteamos pontos (x, y) dentro do quadrado unit´ario, e a distˆancia r de cada ponto ao centro do c´ırculo ´e dada pela m´etrica euclidianar2= (x
−x0)2+ (y
−y0)2, onde (x
0, y0) ´e o centro do c´ırculo. O exemplo mostrado na Fig. 8 utiliza um c´ırculo de diˆametro unit´ario, ou seja,x0=y0= 1/2. Usando a medidar determinamos se o ponto sorteado pertence ou n˜ao ao c´ırculo, no caso em que r ≤ R, e assim determinamos o n´umero de pontos Nc que
pertencem ao c´ırculo. Por exemplo, a Fig. 8 mos-traN = 10.000 pontos colocados na regi˜ao delimitada pelo quadrado gerados com o programa de computa-dor listado no Apˆendice 9.2.. Neste exemplo, contamos Nc= 7.863 pontos dentro c´ırculo, e portanto a
probabi-lidade experimental de um dosNpontos ser encontrado dentro do c´ırculo ´ep≈7.863/10.000 = 0,7863, ou seja, para essa simula¸c˜ao simples podemos estimar o valor deπ= 4p≈3,145. A convergˆencia do valor estimado pelo m´etodo de Monte Carlo para π´e lenta, como em todo m´etodo estat´ıstico, a m´edia converge para o valor esperado (exato) com erro inversamente proporcional `a√N, de modo que para ganharmos cada novo d´ıgito decimal, temos que aumentarN em um fator 100. Por exemplo, observe na Tabela 7., que para N = 1012 o erro na estimativa do valorπ est´a na sexta casa deci-mal, pois 1/√1012= 10−6.
Em linguagens de programa¸c˜ao usuais, como o F ORT RAN e C, existem geradores de n´umeros aleat´orios [14] nativos da pr´opria linguagem. Em linguagem C o gerador ´e chamado usando a fun¸c˜ao rand(), que retorna um inteiro aleat´orio uniformemente distribu´ıdo no intervalo (0;RAN D M AX), sendo ne-cess´aria a convers˜ao deste n´umero inteiro para os re-ais, dividindo-o pelo seu valor m´aximoRAN D M AX, cujo resultado ser´a um n´umero aleat´orio uniforme-mente distribu´ıdo no intervalo [0,1]. Em FORTRAN, existe j´a um gerador de n´umeros aleat´orios reais, j´a normalizados no intervalo unit´ario, chamadoRAN D() ou DRAN D(0), dependendo da vers˜ao da linguagem. Veja no apˆendice 9.2. uma implementa¸c˜ao computaci-onal em linguagem F ORT RAN do m´etodo de Monte Carlo3. A partir deste programa geramos os dados vis-tos na Tabela 7. que s˜ao as sucessivas aproxima¸c˜oes de π, paraN = 10m, comm= 1,2,3, . . . ,12.
8.
Conclus˜
ao
Revimos o m´etodo geom´etrico original de Arquimedes para o c´alculo deπe apresentamos um m´etodo experi-mental mecˆanico simples, que permite calcular π com areia e um bast˜ao, apenas com uma medida simples de comprimento.
Apresentamos um modelo corrigido e um argumento f´ısico para sua implementa¸c˜ao, caso particular de um modelo mais geral e exato, e mostramos que o modelo corrigido nada mais ´e que a corre¸c˜ao de primeira ordem do modelo exato apresentado.
Introduzimos de forma intuitiva e aplicamos a ideia fundamental que levou ao m´etodo de Monte Carlo apli-cado para a determina¸c˜ao num´erica da constanteπ.
Recalculamos o valor de πusando diferentes n´ıveis de investiga¸c˜ao, desde a ideia original de Arquimedes at´e o m´etodo de Monte Carlo, mas abstrato, mas que utiliza ideias simples que poderiam ter sido exploradas pelo pr´oprio Arquimedes, em seu tempo, pois chegou a resolver problemas muito mais complexos do que esse, mesmo para a sua ´epoca.
9.
Apˆ
endices
9.1. C´odigo C: m´etodo num´erico
// −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
// C´al c u l o de π por p o l´ıgonos i n s c r i t o s // e c i r c u n s c r i t o s a um c´ır c u l o u n i t´ar i o // −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
#include<s t d i o . h>
#include<s t d l i b . h>
#include<math . h>
i n t main ( ){
i n t m;
double n , THETA, Ai , Ac , A360 ;
A360 = 2 . 0 e0∗a c o s (−1.0 e0 ) ; // 360 g r a u s
f o r(m = 2 ; m< 3 2 ; m++){ n = pow ( 2 . 0 e0 , m) ; THETA = A360/n ;
Ai = ( n / 2 . 0 e0 ) ∗ s i n (THETA) ; Ac = n ∗ tan (THETA/ 2 . 0 e0 ) ;
p r i n t f ( ”%d %f %f %f\n” , m, n , Ai , Ac ) ; }
return( 0 ) ; }
9.2. C´odigo FORTRAN: m´etodo de Monte Carlo
C ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗
PROGRAMPI METODO MONTE CARLO
IMPLICIT NONE
INTEGER I ,M,NC,BLOCO,N
DOUBLE PRECISIONX, Y, S2 , R2 , PI ,RAND C ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗
M=1 NC=0 BLOCO=10 N=1000000000 R2=1.0D0 C
C INICIALIZA O GERADOR DRAND
CALLSRAND( 1 2 3 4 5 6 7 ) C
DO I =1 ,N
C PONTO (X,Y) ALEAT´ORIO X = 1 . 0 D0∗RAND( ) Y = 1 . 0 D0∗RAND( ) C
C DIST ˆANCIA DE (X,Y) AO CENTRO ( 0 , 0 ) S2 = X∗X + Y∗Y
C
C PONTO EST´A DENTRO DO C´IRCULO?
IF( S2 .LE. R2) NC = NC + 1 C
C APROXIMA O VALOR DE π
PI = 4 . 0 D0 ∗ DFLOAT(NC) / I C
C IMPRIME A CADA POTˆENCIA DE 10
IF(MOD( I ,BLOCO) .EQ. 0 ) THEN WRITE(∗, 1 ) M, I , NC, 4 . 0 D0∗PI BLOCO = BLOCO ∗ 10
M = M + 1
ENDIF ENDDO
1 FORMAT( I2 , 2 I16 , F18 . 1 5 )
END
Referˆ
encias
[1] T.G. Chondros. Mechanism and Machine Theory 45, 1766 (2010).
[2] B.T. and D. Garber. Historia Mathematica 25, 75 (1998).
[3] L. Cooper.Historia Mathematica38(4), 455 (2011).
3
[4] S. Psycharis.Computers & Education56, 547 (2011).
[5] N. Rutten, W.R. van Joolingen and J.T. van der Veen.
Computers & Education58, 136 (2012).
[6] K.E. Chang, Y.L. Chen, H.Y. Lin and Y.T. Sung. Com-puters & Education51, 1486 (2008).
[7] N. Metropolis.Los Alamos Science15, (1987).
[8] T. Pang. An Introduction to Computational Physics
(Cambridge University Press, Cambridge, 2010), 2a
ed.
[9] K. von Fritz.Annals of Mathematics46, 242 (1945).
[10] J.M. Ferrater Dicion´ario de Filosofia (Dom Quixote, Lisboa, 1978). Preparado por E.G.A. Belsunce e E. Olaso, traduzido do espanhol por A.J. Massano e M. Palmeirim.
[11] C.K. Wentwort.Journal of Geology30, 377 (1922).
[12] W.C. Krumbein.J. of Sed. Pretrol4, 65 (1934).
[13] D.E. Knuth.Commun. ACM17, 667 (1974).