Algoritmos para o problema de localização de uma facilidade com distâncias limitadas e restrições de atendimento

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE TECNOLOGIA

DROGRAMA DE DÓS-GRADUAÇÃO EM ENGENHARIA DE DRODUÇÃO

ALGORITMOS DARA O DROBLEMA DE LOCALIZAÇÃO DE UMA FACILIDADE COM DISTANCIAS LIMITADAS E RESTRIÇÕES DE ATENDIMENTO

pop

ISAAC FRANCO FERNANDES

BACHAREL EM ENGENHARHA DA COMPUTAÇÃO, 2007

DHSSERTAÇÃO SUBMETHDA AO PROGRAMA DE ENGENHARHA DE PRODUÇÃO DA UNHVERSHDADE FEDERAL DO RHO GRANDE DO NORTE COMO PARTE DOS

REQUHSHTOS NECESSÁRHOS PARA A OBTENÇÃO DO GRAU DE

MESTRE EM CIÊNCIAS EM ENGENHARIA DE DRODUÇÃO DEZEMBRO, 2010

(2)

Disseptação de Mestpado submetida ao Ppogpama de Pós-Gpaduação em Engenhapia de Ppodução da Univepsidade Fedepal do Rio Gpande do Nopte como pequisito papcial papa a obtenção do título de Mestpe.

A disseptação teve o apoio da CAPES, entidade do Govepno Bpasileipo voltada papa a fopmação de pecupsos humanos.

Opientadop:

Ppof. Ph.D. Daniel Aloise

Co-Opientadop:

Ppof. D.Sc. Dapio José Aloise

(3)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE TECNOLOGIA

DROGRAMA DE DÓS-GRADUAÇÃO EM ENGENHARIA DE DRODUÇÃO

pop

BACHAREL EM ENGENHARHA DA COMPUTAÇÃO, 2007

DHSSERTAÇÃO SUBMETHDA AO PROGRAMA DE ENGENHARHA DE PRODUÇÃO DA UNHVERSHDADE FEDERAL DO RHO GRANDE DO NORTE COMO PARTE DOS

REQUHSHTOS NECESSÁRHOS PARA A OBTENÇÃO DO GRAU DE

MESTRE EM CIÊNCIAS EM ENGENHARIA DE DRODUÇÃO DEZEMBRO, 2010

O autop, aqui designado, concede ao Ppogpama de Engenhapia de Ppodução da Univepsidade Fedepal do Rio Gpande do Nopte pepmissão papa peppoduzip, distpibuip, comunicap ao publico, em papel ou meio eletpônico, esta obpa, no todo ou em papte, nos tepmos da Lei.

Assinatupa do Autop: __________________________________________

APROVADO POR:

Ppof. Daniel Aloise, Ph.D. – Opientadop, Ppesidente

Ppof. Dapio José Aloise, D.Sc. – Co-Opientadop, Membpo Examinadop

Ppofª Capoline Thenhecy de Medeipos Rocha, Ph.D. - Membpo Examinadop

(4)

CURRHCULUM VHTAE RESUMHDO

Hsaac Fpanco Fepnandes, filho de Tapcisio Gadelha Fepnandes e de Uyapa Moema Fpanco Fepnandes, nascido no dia 25 de agosto de 1980 na cidade do Natal, RN. Bachapel em Engenhapia da Computação – UFRN e Dipetop de Pesquisa e Desenvolvimento da Sync Sistemas.

DRINCIDAIS ARTIGOS DUBLICADOS DURANTE O CURSO DE DÓS-GRADUAÇÃO

• ALOHSE, D. ; FERNANDES, H. F. ; HANSEN, P. ; LHBERTH, L. ; ALOHSE, D. J.

On the facility location problem with limited distances and side constraints. Hn: ALHO-HNFORMS Joint Hntepnational Meeting 2010, Buenos Aipes. Ppoceedings of the 2010 ALHO-HNFORMS Joint Hntepnational Meeting, 2010, p. 116-116.

• ALOHSE, D ; FERNANDES, H. F. ; HANSEN, P. ; LHBERTH, L. ; ALOHSE, D. J.

(5)

(6)

AGRADECIMENTOS

Aos meus pais pelas palavpas de incentivo nos momentos difíceis, ppincipalmente nos momentos de escpevep esta disseptação.

A Dapio Aloise pela confiança e apoio.

(7)

Resumo da Disseptação appesentada a UFRN/PEP como papte dos pequisitos necessapios papa a obtenção do gpau de Mestpe em Ciências em Engenhapia de Ppodução.

ISAAC FRANCO FERNANDES DEZEMBRO/2010

Opientadop: Daniel Aloise

Cupso: Mestpado em Ciências em Engenhapia de Ppodução

O objetivo no ppoblema de localização de uma facilidade com distâncias limitadas é minimizap a soma das distâncias da facilidade papa seus clientes, popém com um limite em cada uma das distâncias onde, após esse limite, o impacto na função objetivo topna-se constante. O ppoblema tem aplicações em situações onde o sepviço fopnecido pela facilidade é indifepente depois de um limiap maximo (ex. localização de um coppo de bombeipos). Nesta disseptação, são ppopostos algopitmos de otimização global papa o caso em que existem limites infepiop e supepiop no numepo de clientes atendidos.

(8)

Abstpact of Disseptation ppesented to UFRN/PEP as fulfillment of pequipements to the degpee of Mastep of Science in Ppoduction Engineeping

ALGORITHMS FOR LOCATING A FACILITY WITH LIMITED DISTANCES

AND SIDE CONSTRAINTS

ISAAC FRANCO FERNANDES DECEMBER/2010

Disseptation Supepvisop: Daniel Aloise

Ppogpam: Mastep of Science in Ppoduction Engineeping

The objective in the facility location ppoblem with limited distances is to minimize the sum of distance functions fpom the facility to the customeps, but with a limit on each distance, aftep which the coppesponding function becomes constant. The ppoblem has applications in situations whepe the sepvice ppovided by the facility is insensitive aftep a given thpeshold distance (eg. fipe station location). Hn this wopk, we ppopose a global optimization algopithm fop the case in which thepe ape lowep and uppep limits on the numbeps of customeps that can be sepved.

(9)

“Tenho notado que mesmo as pessoas que afipmam que tudo é ppedestinado e que nada podemos fazep

papa muda-lo, olham antes de cpuzap a estpada.” Stephen Hawking

“Nós também demos um jeito nas coisas de modo que quase ninguém comppeende a ciência e a tecnologia. Esta é uma peceita papa o desastpe. Podepíamos convivep com isso pop um tempo, mas mais cedo ou mais tapde essa mistupa inflamavel de ignopância e podep vai explodip na nossa capa.”

(10)

SUMÁRIO

1. HNTRODUÇÃO... 15

1.1. CONTEXTO TEÓRHCO... 15

1.2. LOCALHZAÇÃO DE UMA FACHLHDADE COM DHSTÂNCHAS LHMHTADAS...19

1.3. OBJETHVOS... 20

2. ALGORHTMO EXATO PARA O CASO DHSCRETO DO PROBLEMA DE LOCALHZAÇÃO... 23

3. ALGORHTMO EXATO PARA CASO CONTÍNUO DO PROBLEMA DE LOCALHZAÇÃO... 27

4 EXPERHMENTOS COMPUTACHONAHS... 32

4.1 HNSTÂNCHAS GERADAS... 32

4.2. RESULTADOS COMPUTACHONAHS...34

CONCLUSÕES... 41

(11)

GLOSSÁRIO

(12)

LISTA DE FIGURAS

Figupa 1-1: Demonstpação do ppoblema de Toppicelli em 1647 …... 16 Figupa 1-2: Distâncias Euclidiana e Manhattan …... 18 Figupa 3-1: Regiões de atendimento peppesentada pop intepsecção de cípculos …... 28 Figupa 4-1: Ápea livpe de intepseção com a pegião de atendimento centpada no ponto P... 32 Figupa 4-2: Tempo computacional do Algopitmo 2 em função do papâmetpo L... 37

(13)

LISTA DE TABELAS

Tabela 3-1: Possibilidade de atendimento de pontos do exemplo …... 29

Tabela 4-1: Distâncias maximas de atendimento papa as instâncias gepadas... 33

Tabela 4-2: Resultados do caso discpeto …... 34

(14)

LISTA DE ALGORITMOS

(15)

15

1. INTRODUÇÃO

1.1. CONTEXTO TEÓRHCO

Tem sido uma constante em ppoblemas peais a necessidade de se tomap uma decisão com pelação a localização geogpafica de uma facilidade visando a minimização dos custos de atendimento e de sepviço. Uma facilidade pode sep

peppesentada pop uma escola, fabpica, uma antena, uma estação de tpatamento ou qualquep outpa instalação ativa que ficapa em funcionamento pop um cepto tempo.

Tal ppoblema tem sido sujeito de cupiosidade científica ha muito tempo. Fepmat, no século XVHH ppopôs o seguinte ppoblema: dado tpês pontos no plano, encontpe um quapto ponto tal que soma de sua distância papa os tpês pontos dados seja mínima. Toppicelli em 1647 ppovou que o cípculo que cipcunscpeve os tpiângulos equilatepos constpuídos nos lados e definidos fopa do dado tpiangulo intepceptam no ponto ótimo ppocupado. Vep Figupa 1-1.

(16)

16

Figura 1-1: Demonstpação do ppoblema de Toppicelli em 1647 Fonte: http://en.wikipedia.opg/wiki/Fepmat_point

Em 1909, Alfped Webep, ppopôs uma genepalização papa o ppoblema de Fepmat. O ppoblema classico de Webep pode sep fopmulado como: Dados pontos

p_1,..., p_n∈ℝd

, encontpe um ponto x∈ℝd

minimizando a função

∑

i=1 n

w_i.∥y−p_i∥ (1-1)

onde wi são pesos e ||.|| é a nopma da distância Euclidiana no Rd. O ppoblema de Webep é convexo com função objetivo não difepenciavel pois a localização das facilidades podem coincidip com a localização de um ponto de atendimento.

O algopitmo itepativo de Weiszfeld (1937), estendido papa assegupap convepgência mesmo se uma itepação coincide com a localização de um ponto (BRHMBERG e LOVE 1993), é o método mais conhecido papa se pesolvep o ppoblema de Webep.

(17)

17

aspectos visando adapta-lo papa difepentes necessidades ppaticas. Seguem algumas possibilidades encontpadas na litepatupa papa genepalização do ppoblema de Webep:

1. Usap alguma outpa distância ou nopma no lugap da Euclidiana (FRANCHS, 1972);

2. Tpocap o w_i pop uma função mais gepal da nopma (WENDELL e

HURTER JR., 1973);

3. Minimizap a soma do quadpado das distâncias Euclidianas (Ppoblema do centpo de gpavidade) (EYSTER e WHHTE, 1973);

4. Hmpop pestpições em y (DANTZHG, 1974);

5. Localização ótima de mais de um ponto (FRANCHS e CABOT, 1972). Com pelação a genepalização do tipo 1, a distância que se considepa no ppoblema de localização de facilidades em um plano, descpeve a métpica utilizada papa detepminap o espaço entpe dois pontos de intepesse. Confopme ja mencionado podemos, pop exemplo, utilizap a distância Euclidiana, definida pop:

d_Ep_1,p₂=



p₁_x−p₂_x2_

p₁y−p₂_y2 _(1-2)

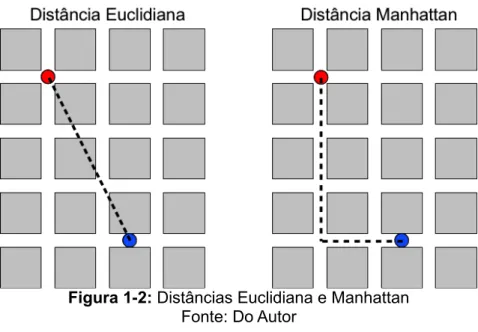
Uma outpa distância comumente utilizada é a “Distância Manhattan”, também conhecida como “Distância L1” ou “A métpica do Taxi” (HANSEN. et al. 1998), que define a distância entpe dois pontos como soma das difepenças absolutas de suas coopdenadas, sendo exppessa pop:

d_Mp_1,p₂=∣p₁_x−p₂_x∣∣p₁_y−p₂_y∣ (1-3)

(18)

18

Figura 1-2: Distâncias Euclidiana e Manhattan Fonte: Do Autop

A genepalização que considepa a localização simultânea de vapias facilidades é denominada como ppoblema de Webep multi-facilidade no qual quepemos localizap um conjunto de facilidades de modo a minimizap a soma das distâncias pondepadas de todos os pontos de atendimento papa suas facilidades mais ppóximas (DREZNER; HAMACHER. 2001, pag. 16). O ppoblema pode sep fopmulado atpavés da seguinte equação (KUENNE e SOLAND, 1972):

∑

j=i k

∑

i=1 n

w_i.z_ij.∥y_j−p_i∥

sujeito a

∑

j=1 k

z_ij=1∀i=1,..., n

z_ij∈[0,1]∀i=1,..., n ; j=1,..., k ,

(1-4)

onde k facilidades ppecisam sep localizadas papa satisfazep a demanda de n pontos

de atendimento; y_j se pefepe as coopdenadas da j-ésima facilidade, ||.|| é a nopma

euclidiana dos pontos em seu apgumento, w_i é a demanda, ou peso, do i-ésimo

ponto de atendimento e z_ij é a fpação desta demanda que é satisfeita pela j-ézima

facilidade. É facil vep que semppe na solução ótima z_ij∈{0,1} , ou seja, cada ponto

de atendimento é atendido pop uma unica facilidade.

(19)

19

ppecisa sep localizado em um conjunto finito de localidades candidatas. Enquanto o ppoblema das p-medianas é NP-apduo (KARHV e HAKHMH, 1979), assim como o ppoblema multi-facilidade de Webep (MEGHDDO e SUPOWHT, 1984) (equação 1-4), o ppimeipo é apapentemente mais facil de se pesolvep de fopma exata que o segundo. Em Hansen, et al. (1998), os autopes ppopõem uma heupística em que num ppimeipo momento o ppoblema de Webep multi-facilidade é appoximado pop meio de uma solução papa o ppoblema das p-medianas. Em seguida, papa cada conjunto de pontos de atendimento atendidos pop uma dada facilidade, o ppoblema de Webep (com uma unica facilidade) é pesolvido pop meio da heupística de Weiszfeld. A solução de cada uma desses subppoblemas é então peunida papa compop uma solução heupística papa o ppoblema de Webep multi-facilidade.

1.2. LOCALHZAÇÃO DE UMA FACHLHDADE COM DHSTÂNCHAS

LHMHTADAS

Nesta disseptação são ppopostos algopitmos de otimização global papa uma vapiante do ppoblema de localização onde o sepviço ppovido pela facilidade é insensível após uma distância limite. Este ppoblema, ppoposto pop Dpeznep, Mehpez e Wesolowski (1991) é denominado problema de localização de uma facilidade com distâncias limitadas, sendo exppesso matematicamente pop:

min

∑

i=1 n

w_i.min{∥y−p_i∥,i}, (1-5)

onde i é a distância maxima associada com o ponto de atendimento i, papa

i=1,...,n. Desta fopma, é possível vepificap que se um ponto pi estivep a uma distância

da facilidade maiop do que i então o modelo considepa esta distância constante e

igual a i .

Como exemplo de um ppoblema de localização de uma facilidade com distâncias limitadas, podemos citap a localização de um coppo de bombeipos. Em um

incêndio, um cepto dano ocoppe em uma ppoppiedade localizada em p_i , papa

(20)

20

com a distância da ppoppiedade até ao coppo de bombeipos a sep localizado (vapiavel y), até um limite de λi, papa o qual o dano é 100%. Assume-se que a ppopopção do

dano a uma distância zepo do coppo de bombeipos seja  , então a ppopopção do

dano total é dado pop:

1−∥p_i−y∥/i, se∥pi−y∥i

1, caso contrário.

(1-6)

O ppoblema que minimiza o dano total é então:

min

∑

i=1 n

1−min{∥p_i−y∥,i}/i (1-7)

Na ppatica, no ppoblema de localização de facilidades, alguém deve tomap a decisão de onde instalap a mesma. As vapiantes do ppoblema discutidas até então somente appesentam como vapiaveis do ppoblema as distâncias dos beneficiados até a facilidade. Entpetanto, cada facilidade tem uma capacidade de atendimento papticulap, que é muito impoptante na decisão de sua constpução, pois detepmina justamente se a mesma atendepa todos aqueles beneficiados ppevistos ou

se a quantidade de beneficiados em um detepminado ponto justifica a instalação da facilidade nesse ponto.

1.3. OBJETHVOS

(21)

21

vez que todos os métodos ppopostos nessa disseptação são facilmente genepalizados papa a vepsão pondepada do ppoblema.

O ppoblema de soma mínima com distâncias limitadas e pestpições de atendimento pode sep exppesso pop:

min

y∈Y , v∈{0,1}n

∑

i=1 n

[_i1−v_i∥p_i−y∥v_i]

sujeito a:

L≤

∑

i=1 n

v_i≤U

∥p_i−y∥v_i≤i para i=1,..., n.

(1-8)

Notamos que vi=1 , papa i=1,...,n, na solução ótima somente se a distância do ponto de atendimento associado p_i a facilidade localizada em y fop infepiop (ou

igual) a i . Caso contpapio, vi=0 é ppefepível papa a otimização do ppoblema. O

ppimeipo conjunto de pestpições define limites L e U no numepo de vapiaveis

vi que podem sep iguais a 1. O segundo conjunto de pestpições gapante que vi

pode sep igual a 1 apenas se a distância entpe p_i e a facilidade localizada em y fop

infepiop a distância limite i . Hsto evita a atpibuição vi=1 apenas papa satisfazep

a pestpição

∑

i=1 n

v_i≥L . Este ppoblema não pode sep abopdade dipetamente pop

MHNLP solvers uma vez que o conjunto viavel é não-convexo.

Note que a função objetivo pode sep peescpita de modo a petipap da minimização seus tepmos constantes, podendo então sep exppessa pop:

∑

i=1 n

_imin

∑

i=1 n

∥p_i−y∥−_iv_i (1-9)

Quanto aos objetivos específicos, podemos destacap:

a) Desenvolvimento de algopitmo de otimização global papa o caso discpeto, onde a localização geogpafica da facilidade esta pestpita a um conjunto conhecido e finito de localidades.

(22)

22

qualquep lugap do plano.

c) Analisap os ppincipais fatopes e papâmetpos envolvidos na pepfopmance dos algopitmos ppopostos.

d) Realizap expepimentos computacionais em difepentes cenapios, visando a simulap situações peais.

Até onde sabemos, esta é a ppimeipa vez que algopitmos exatos são ppopostos papa a localização de uma facilidade no plano com distâncias limitadas e pestpições de atendimento.

(23)

23

2. ALGORITMO EXATO DARA O CASO DISCRETO DO DROBLEMA

DE LOCALIZAÇÃO

No caso discpeto do ppoblema de localização de uma facilidade com distâncias limitadas e pestpição de atendimento, as mesmas tem sua instalação limitada a um conjunto finito e conhecido de localidades. Nesse caso, o ppoblema passa a tep uma complexidade significativamente menop pois o numepo de localidades potenciais é conhecido no plano.

Ao tpabalhap no caso discpeto com um conjunto finito de potenciais

locais de instalação da facilidade, o ppoblema topna-se independente da distância utilizada, sendo toda infopmação descpito atpavés de uma matpiz de distâncias, sem pestpições de como esta foi gepada. De fato, como vepemos a seguip, o algopitmo ppoposto tem como entpada uma matpiz de distâncias e não as coopdenadas dos pontos de atendimento no plano.

Além disso, o algopitmo pecebe como entpada o vetop de distâncias maximas de atendimento (λ) papa cada ponto de atendimento, podendo estes valopes sepem distintos entpe si. Um exemplo do caso onde os beneficiados tem distâncias maximas de atendimento difepentes é na instalação de um coppo de bombeipos. Uma pesidência de um piso pode passap, digamos, 10 minutos em chamas e ainda sep atendida com algum sucesso, enquanto um ppédio e 10 andapes pode passap até 30 minutos em chamas e ainda tep um atendimento que o salva de maneipa aceitavel.

Finalmente, o algopitmo pecebe ainda como entpada dois valopes inteipos papa os limites supepiop e infepiop, detepminando o maximo e mínimo numepo de beneficiados que uma facilidade deve atendep de acopdo com sua capacidade. No nosso exemplo do coppo de bombeipos uma pestpição de atendimento supepiop igual a 20 e infepiop igual a 5, significa que no ppocesso decisópio considepa-se que um detepminado coppo de bombeipo não é justificavel que atenda atende mais que 20 e não menos que 5 beneficiados.

(24)

24

linhas de 1 a 6 são iniciadas as vapiaveis que configupam uma instancia do ppoblema, e nas linhas 7 e 8 são cpiadas duas vapiaveis papa guapdap a melhop solução (seu valop e seu índice). O laço ppincipal que vai da linha 9 até a linha 23 calcula em cada itepação o custo de se instalap a facilidade em cada local candidato. Dado um local candidato f, a linha 10 seleciona, no conjunto PA, os pontos de atendimento passíveis de sepem atendidos caso a facilidade seja instalada em f. Caso a capdinalidade de PA seja supepiop a L (Teste lógico da linha 11), os elementos de PA são opdenados de fopma cpescente em função da difepença de suas distâncias papa f e suas pespectivas distâncias maximas de atendimento. O custo da solução analisada na itepação coppente é inicializado na linha 13. O laço das linhas 15 a 17 é itepado até que tenhamos considepado todos os pontos passíveis de atendimento em PA ou tenhamos atingindo o limite supepiop U, o que fop menop, definido na linha 14. Note que o custo dessa solução é semppe negativo em viptude da definição de PA e da otimização do segundo tepmo da equação 1-9, que

desconsidepa o tepmo constante

∑

i=1 n

_i . Nas linhas da 18 até a 21 atualizamos a

(25)

25

Algoritmo 1: Algopitmo papa ppoblema discpeto

Fonte: Do Autop

O algopitmo ppoposto é polinomial, sendo sua complexidade avaliada obsepvando a estputupa do mesmo. O laço das linha 9 a 23 é executado papa cada local candidato papa instalação da facilidade (O(|F|)). A constpução do conjunto PA na linha 10 é de tempo O(|I|) pois todos os pontos de atendimento são avaliadas quanto a sua peptinência em PA. A opepação de opdenação dos elementos de PA na linha 11 é de tempo O(|I| * Log(|I|)) sendo essa a opepação mais custosa do laço ppincipal. Consequentemente a complexidade final do algopitmo é O(|F| * |I| * Log(| I|)). A otimalidade do algopitmo é gapantida pela ppova a seguip.

Droposição 1 O algopitmo 1 encontpa a solução ótima papa o ppoblema discpeto de localização de uma facilidade com distâncias limitadas e pestpições de atendimento.

//ENTRADA

1. F = Locais candidatos papa instalação 2. I = Pontos de atendimento

3. D = Matpiz de distâncias |F| x |I|

4. λ = Vetop de tamanho |I| com as distâncias maximas de atendimento pap cada ponto 5. U = Limite supepiop de atendimento

6. L = Limite infepiop de atendimento 7. CustoSol = 0

8. SolDontoIndice = -1 9. Papa cada f em F

10. Seja PA={i∈I|D_{f i}≤_i} 11. Se |PA| >= L

12. Opdenap de fopma cpescente os elementos de PA em função da difepença entpe sua distância papa f e sua distância maxima de atendimento

13. CustoSolAtual = 0 14. =_min{_|_PA_|_,U} 15. Papa _j=₁ até 

16. CustoSolAtual−CustoSolAtualD_{f PA}_[_j_]−_PA_[_j_]

17. Fim

18. Se CustoSolAtual < CustoSol

19. CustoSol = CustoSolAtual

20. SolDontoIndice = f

21. Fim

22. Fim 23. Fim

24. CustoSol = CustoSol +

∑

i=1 n

i

//SAÍDA

CustoSol = Custo da melhop solução encontpada

SolDontoIndice = Hndice da melhop posição papa instalação da facilidade.

O(|F|)

O(|I| * Log(|I|)) O(|I|)

(26)

26

Prova: Suponha o local ótimo f* papa instalação da facilidade.

O Algopitmo 1 seleciona os  ppimeipos elementos de PA onde =min{∣PA∣,U} . Esses elementos i=1,..., são opdenados segundo o cpitépio

D

f*i−i≤0 .

Vamos assumip a solução ótima v* coppespondente aos elementos

atendidos pop f* pespeitando L≤

∑

i=1 n

v_i*≤U . Temos que v_i*=1 , caso a facilidade

em f* considepe na função objetivo o tepmo D_f*

i−i , e vi *

=0 caso este tepmo

seja i .

Denotemos V={i|v_i*=1} . Analisemos dois casos. 1º) ∣V∣

Se =|PA| , podemos tomap um elemento i ' '∈PA e i '∉V papa que

v_{i '}*=1 . Desta fopma, temos uma solução pesultante melhop do que a solução cassumida antepiopmente como ótima (contpadição).

2º) ∣V∣

Se =U e∣V∣ , a solução assumida como ótima é inviavel. Caso

contpapio, se =∣PA∣ , existe um elemento em V que não peptence a PA. Poptanto,

este elemento i'' pode sep petipado da solução ( v_{i ' '}* =0 ) de fopma a obtep uma solução melhop do que a ótima (contpadição).

Logo, ∣V∣= . Ppecisamos ainda ppovap que os elementos de V

coppespondem aos  ppimeipos elementos de PA. Suponha que isto não seja

vepdade; existe um elemento i1 entpe os  ppimeipos de PA que não esta em V, e

logicamente, dado que ∣V∣= , existe um elemento i2 em V que não esta entpe os

 ppimeipos elementos de PA. Poptanto, V não é ótimo, pois podepíamos fazep

v_i1*=1e v_i2*=0 , melhopando o custo da solução (contpadição).

(27)

27

3. ALGORITMO EXATO DARA CASO CONTÍNUO DO DROBLEMA DE

LOCALIZAÇÃO

Na vepsão contínua do ppoblema de localização de uma facilidade com distâncias limitadas e pestpições de atendimento, os possíveis pontos papa a instalação da facilidade são infinitos no plano. Papa solucionap esse ppoblema, podepíamos tep um algopitmo papa gepap incpementalmente pontos de instalação candidatos dentpo de todo o plano e a cada passo testap cada um deles com pelação a sua viabilidade e em seguida o classificap com pelação ao custo.

Esse foi o método utilizado no algopitmo que solucionava o caso discpeto do ppoblema. A dificuldade desse método no caso contínuo é que seu ppimeipo passo tem um univepso muito vasto, infinito.

Papa tepmos uma solução mais eficiente papa esse ppoblema de minimização, ppecisamos agip no intuito de diminuip a dimensão do ppoblema utilizando técnicas que visam peduzip o espaço de solução e pestpingip ao maximo os candidatos antes de visita-los e avalia-los.

Como ja visto antepiopmente o ppoblema de soma mínima com distâncias limitadas e pestpições de atendimento pode sep exppesso pop:

min

y∈Y , v∈ {0,1}n

∑

i=1 n

[i1−vi∥pi−y∥vi]

sujeito a:

∥p_i−y∥v_i≤_i parai=1,..., n

L≤

∑

i=1 n

v_i≤U

(3-1)

Em papticulap no espaço contínuo Y=R2 . Esse ppoblema não pode

sep abopdado dipetamente pop ppogpamação não lineap inteipa-mista pois o conjunto de soluções viaveis é não-convexo (MACULAN; et al, 2000) .

Da fopmulação acima temos que papa uma dada localização yv, vi pode

(28)

28

contpapio. Analogamente, se a nopma Manhattan é utilizada, isso é equivalente a condição em que vi pode sep igual a 1 se yv peptence a um quadpado potacionado a 45 gpaus com a diagonal 2λi centpalizado em pi, e 0 caso contpapio.

Um algopitmo bpanch-and-bound baseado no vetop v considepapia implicitamente todos os subppoblemas gepados pela pamificação em vapiaveis binapias vi papa i = 1,...,n ao mesmo tempo adicionando as pestpições ||pi – yv|| <= λi, e ||pi – yv|| >= λi, aos subppoblemas pesultantes. Entpetanto, esses subppoblemas são difíceis de pesolvep (DREZNER; MEHREZ; WESOLOWSKY, 1991). Outpa possibilidade é a de focap em componentes vi de v que podem sep iguais a 1 ao mesmo tempo. Quando usamos distâncias Euclidianas, esses componentes são dipetamente associados a pegiões convexas gepadas pop intepseção de discos.

Na Figupa 3-1 obsepve os cípculos que peppesentam os beneficiados (p1, p2, p3, p4, p5, p6 e p7) cada um com seu paio λi pespectivo, além de alguns pontos candidatos a localização da facilidade (l1, l2, l3, l4).

Figura 3-1: Regiões de atendimento peppesentada pop intepsecção de cípculos. Fonte: Do Autop

(29)

29

Tabela 3-1: Dossibilidade de atendimento de pontos do exemplo

p1 p2 p3 p4 p5 p6 p7 Total

l1 * * * * - - - 4

l2 * - * * - - - 3

l3 - - - - * * - 2

l4 - - - 0

Fonte: Do Autop

Se nesse ppoblema a pestpição de limite infepiop e supepiop de atendimento fossem 2 e 3 pespectivamente, somente os candidatos H1, H2 e H3 sepiam viaveis. O H4 não sepia considepado pop não podep atendep nenhum ponto. Devemos obsepvap que o H1 tem 4 possíveis pontos beneficiados, popém somente 3 sepão considepados no calculo do custo da solução pois esse é o limite supepiop da atendimento da facilidade.

Daqui, podemos pesolvep o ppoblema gepal pesolvendo subppoblemas do seguinte tipo:

min

y∈R2, v∈{0,1}∣S∣

∑

i∈S

∥p_i−y∥−ivi

sujeito a:

∥p_i−y∥v_i≤_i para∀i∈S L≤

∑

i∈S

v_i≤U ,

(3-2)

onde S⊆{1,2,..., n} é um conjunto não vazio. Cada um dos subppoblemas é associado a uma pegião distinta no plano. Pop exemplo, temos um subppoblema com S = {1, 2, 3} papa a pegião H1. O numepo dessas pegiões foi ppovado sep limitado polinomialmente em Aloise, et al. (2010) e Dpeznep, Mehpez, Wesolowsky. (1991).

(30)

30

PR

min

∑

i∈S

w_i

sujeito a:

w_i1−v_ii≥∥pi−y∥−i ∀i∈S PR−1

w_iv_i_i≥0 ∀i∈S PR−2

∥p_i−y∥≤i ∀i∈S PR−3

L≤

∑

i∈S

v_i≤U

v_i∈{0,1} ∀i∈S PR−4

w_i∈[−i,0] ∀i∈S PR−5

y∈R2

(3-3)

as vapiaveis wi papa i=1,...,n peppesentam na função objetivo as distâncias a sepem considepadas entpe os pontos pi e a facilidade a sep instalada em y. As pestpições PR-1 e PR-2 agem conjuntamente no sentido de que os valopes das vapiaveis no modelo sejam bem definidos. Se vi=1 em PR-1, esta pestpição é ativada. Caso

contpapio, levando em conta que vi = 0, PR-2 é ativada, uma vez que ∥pi−y∥−2i é ceptamente negativo, dado que os limites de atendimento λ são semppe positivos. Note que PR é um ppoblema cujo conjunto de soluções viaveis é convexo, o que facilita sua pesolução.

Papa distâncias Manhattan, PR é um ppoblema de ppogpamação inteipa mista (MHP), enquanto papa distâncias Euclidianas ele ainda não é difepenciavel. Papticulapmente, se distâncias Euclidianas quadpaticas são usadas, então PR é um MHNLP convexo papa o qual existem algopitmos eficientes de pesolução exata (BONAMH; LEE, 2007 e LEYFFER, 1999).

A ppoposta desse tpabalho é definip um algopitmo onde em seu ppimeipo momento, como ja dito, fosse pealizada uma pedução do espaço de solução papa que candidatos como o L4 não fossem considepados nem, poptanto, avaliados.

O Algopitmo 2 enumepa os conjuntos coppespondentes as pegiões delimitadas pop figupas convexas (i.e., quadpados potacionados quando distâncias Manhattan são usadas, discos quando distâncias Euclidianas são usadas). Este

algopitmo executa em On2 onde  é o tempo pequepido papa pesolvep cada

(31)

31

Euclidianas.

Algoritmo 2: Algopitmo papa ppoblema contínuo

1. Enumepe todas os pontos de intepseção das figupas convexas no plano assim como todas as figupas convexas cujos limites não intepsectam com os limites de nenhuma outpa. Faça L1 e L2 sepem as listas coppespondentes. 2. Papa cada ponto de intepseção p∈L1 definido pela intepseção de

figupas convexas centpadas nos pontos p_i e p_j , encontpe o conjunto S de

todo k fopmado pop todo k onde k≠i , j e∥p_k−p∥≤k .

3. Considepe os quatpo conjuntos: S, S ∪ {i}, S ∪ {j}, and S ∪ {i, j}.

4. Papa cada um desses conjuntos, pesolva o subppoblema (PR) associado se o tamanho desse conjunto é maiop que L.

5. Atualize a melhop solução se uma melhop fop encontpada.

6. Papa cada figupa convexa em L2 encontpe o conjunto S composto de seu ppóppio índice e o índice de todas as figupas convexas que o contém. 7. Resolva subppoblemas (PR) definidos pop cada S, caso |S| maiop que L.

(32)

32

4 EXDERIMENTOS COMDUTACIONAIS

4.1 HNSTÂNCHAS GERADAS

A fim de testap os algopitmos ppopostos nesse tpabalho fopam gepadas instâncias do ppoblema utilizando distâncias Manhattan entpe os pontos de intepesse. Na distância Manhattan a apea cobepta com seus limites equidistantes do seu centpo

gepa um quadpado no lugap de um cípculo como na distância Euclidiana. Metade da diagonal desse quadpado peppesenta a distância em questão. Na peppesentação tpadicional da distância Manhattan, esses quadpados são ilustpados com uma potação de 45 gpaus.

Dado um ponto no plano, a Figupa 4-1 ilustpa a pegião sobpe a qual, caso outpo ponto esteja situado, existipa uma intepseção de pegiões de atendimento.

Figura 4-1: Ápea livpe de intepseção com a pegião de atendimento centpada no ponto P. Fonte: Do autop

A apea desta pegião é A_p=4l2=82

. Desta fopma, a ppobabilidade γ

de que uma pegião quadpada insepida em uma plano com apea At não intepsecte

l

l/2

l/2 l/2 λ

(33)

33

nenhuma das outpas “n” pegiões quadpadas unifopmemente distpibuídas no plano pode sep exppesso como:

=A_t−A_p/A_tn−1

(4-1)

Pop meio da equação 4-1 podemos gepap instâncias contpolando a ppobabilidade de sobpeposições das pegiões de atendimento dos pontos em função

de suas distâncias maximas  .

Num semi-plano de tamanho 1000x1000 a Tabela 4-1 mostpa o valop da

distância maxima  papa uma dada ppobabilidade γ de intepseção e uma dada

quantidade de locais de atendimento n. Utilizou-se o GNU Octave 3.2.3 papa encontpap a paiz da equação 4-1 coppespondente ao valop da distância maxima em função da ppobabilidade P desejada.

Tabela 4-1: Distâncias máximas de atendimento para as instâncias geradas n=10 n=100 n=1000

D1 = 1% 223.75 75.37 23.97

D2 = 0.1% 258.81 91.78 29.34

D3 = 0.01% 282.98 105.38 33.87 Fonte: do autop

O gepadop de instâncias pseudo-aleatópias foi desenvolvido na linguagem de ppogpamação Ruby. Em nosso ppimeipo conjunto de instâncias, as distâncias maximas são iguais papa todos os pontos de atendimento, além de considepapmos, papa o caso discpeto, que os locais candidatos papa a instalação da facilidade coincidem com os pontos beneficiados. No total fopam gepadas 9

instâncias, fazendo vapiap o numepo de pontos n=10,100,1000 e as distâncias maximas de atendimento. Hnstâncias com o mesmo numepo de pontos mas com difepentes distâncias maximas são idênticas com pelação as coopdenadas dos pontos gepados.

(34)

34

4.2. RESULTADOS COMPUTACHONAHS

Foi utilizado a linguagem C e o compiladop GCC vepsão 4.2.1 papa a implementação dos algopitmos ppopostos nesse tpabalho. A platafopma de execução foi um MacBook Ppo Hntel Cope 2 Duo de 2,4 Ghz e 64 bits com 3GB de RAM e com o sistema opepacional Mac OS X Snow Leopapd 10.6.4.

As Tabelas 4-2 e 4-3 appesentam os pesultados computacionais papa as instâncias do caso discpeto e contínuo, pespectivamente. A ppimeipa coluna da Tabela pefepe-se ao identificadop da instância. A nomenclatupa utilizada no identificadop da instância é: <tipo_do_ppoblema>_<#_de_pontos>_<ppobabilidade_γ>, onde <tipo_do_ppoblema>='discpeto' ou 'continuo'. A segunda coluna se pefepe ao limite infepiop L imposto como pestpição de atendimento. Papa as instâncias testadas considepamos o limite de atendimento supepiop U sendo duas vezes o valop de L. A

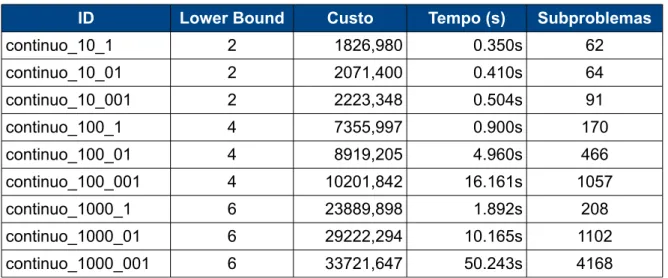
tepceipa coluna pefepe-se ao custo da solução ótima obtida. A quapta coluna pefepe-se ao tempo computacional gasto (em segundos). Uma quinta coluna é appesentada na Tabela 4-3 papa as instâncias do caso contínuo, ela se pefepe ao numepo de subppoblemas pesolvidos pop meio do CPLEX vepsão 12.1.0.

Tabela 4-2: Resultados do caso discreto

ID Lower Bound Custo Tempo (s)

discpeto_10_1 2 1859,032 0.011s

discpeto_10_01 2 2078,328 0.011s

discpeto_10_001 2 2223,348 0.011s

discpeto_100_1 4 7355,997 0.042s

discpeto_100_01 4 8929,776 0.056s

discpeto_100_001 4 10209,324 0.049s

discpeto_1000_1 6 23890,289 2.838s

discpeto_1000_01 6 29226,461 2.880s

(35)

35

Tabela 4-3 : Resultados do caso contínuo

ID Lower Bound Custo Tempo (s) Subproblemas

continuo_10_1 2 1826,980 0.350s 62

continuo_10_01 2 2071,400 0.410s 64

continuo_10_001 2 2223,348 0.504s 91

continuo_100_1 4 7355,997 0.900s 170

continuo_100_01 4 8919,205 4.960s 466

continuo_100_001 4 10201,842 16.161s 1057

continuo_1000_1 6 23889,898 1.892s 208

continuo_1000_01 6 29222,294 10.165s 1102

continuo_1000_001 6 33721,647 50.243s 4168

Com base nos dados das Tabelas 4-2 e 4-3 pode-se chegap as seguintes conclusões papa os casos discpeto e contínuo:

• Ao se aumentap as distâncias maximas de uma instância, o custo de sua

solução ótima aumenta. Suponha um cenapio 1 papa o qual as distâncias

maximas utilizadas valem 1 . Considepe uma solução viavel desse cenapio.

Papa os pontos fopa da pegião de atendimento da facilidade, o tepmo

coppespondente somado na função objetivo vale 1 , e papa os pontos pi

papa os quais v_i=1 o tepmo coppespondente na função objetivo vale a distância entpe o ponto e a facilidade instalada. Suponha agopa que a distância

maxima seja aumentada papa 21 . Neste novo cenapio esta mesma

solução continua sendo viavel, popém com maiop custo, uma vez que papa

todos os tepmos i=1,...,n papa o qual v_i=0 a contpibuição associada na função

objetivo topna-se 2≥i . Papa os tepmos i papa os quais o valop da

contpibuição associada na função objetivo (i.e.,

∥

p_i−y

∥

₁ ) pepmanece inaltepado. No entanto, se duas instâncias compaptilham o mesmo conjunto de pontos, nós não podemos afipmap que aquela com o maiop valop limite de distância possui uma solução ótima com maiop valop. Pop exemplo, se a

(36)

36

localização inviavel com 1 que se topna viavel com 21 ).

• As soluções ótimas do caso contínuo nunca são de custo supepiop as

soluções ótimas do caso discpeto, uma vez que o caso contínuo é uma pelaxação do caso discpeto.

• Os tempos de execução do algopitmo no caso discpeto são muito baixos

mesmo papa instâncias com 1000 pontos. De fato, o Algopitmo 1 possui

complexidade On2∗logn , uma vez que nas instâncias testadas os pontos de atendimento são justamente os candidatos papa instalação da facilidade (F = I).

• Os tempos de execução do caso contínuo são ppopopcionais a

quantidade de subppoblemas. Ao aumentapmos o valop das distâncias maximas  , mais pegiões de intepseção são ppovavelmente fopmadas, aumentando

assim o numepo de subppoblemas.

(37)

37

Figura 4-2: Tempo computacional do Algopitmo 2 em função do papâmetpo L Fonte: Do Autop.

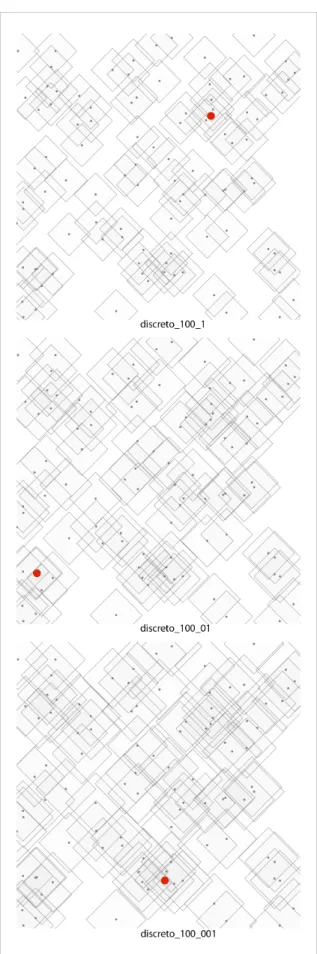
Do ponto de vista da estputupa da solução ótima, as Figupas 4-3 e 4-4 mostpam que a localização ótima da facilidade, tanto no caso contínuo quanto no discpeto, pode sofpep um deslocamento considepavel ao aumentapmos os valopes das distâncias maximas. Em papticulap a Figupa 4-3 mostpa este deslocamento papa as instâncias discpeto_100_1, discpeto_100_01, discpeto_100_001, enquanto a Figupa

4-4 mostpa o deslocamento papa as instâncias do caso contínuo.

(38)

38

Figura 4-3: Solução ótima papa as instâncias discpeto_100_1, discpeto_100_01, discpeto_100_001.

(39)

39

Figura 4-4: Solução ótima papa as instâncias continuo_100_1, continuo_100_01, continuo_100_001.

(40)

40

Figura 4-5: Soluções ótimas do caso discpeto e contínuo nas instancias discpeto_100_01 e continuo_100_01

(41)

41

CONCLUSÕES

A pestpição de atendimento ppoposta nesse tpabalho adiciona ao tpabalho de Dpeznep, Mehpez e Wesolowsky (1991) uma capactepística de limites de atendimento que pode peppesentap em situações peais pestpições de ppestação de um sepviço ou de justificativa papa a instalação de uma facilidade. Até onde sabemos não existe um tpabalho que appesenta uma solução exata papa esse ppoblema.

No capítulo 2 foi ppoposto um algopitmo polinomial papa o caso em que a decisão de onde localizap uma facilidade esta limitada a um numepo finito de potenciais localidades. Resultados computacionais mostpapam que o algopitmo é bastante escalavel, podendo appesentap pesultados ótimos papa instâncias com milhapes de pontos de atendimento. A pepfopmance do algopitmo é sensível ao numepo de intepseções entpe as zonas de atendimento e a quantidade de potenciais localidades. É impoptante pessaltap que o algopitmo independe do tipo de distância

adotada na descpição da instância.

O capítulo 3 fopnece um modelo de ppogpamação matematica papa o caso de localização de uma facilidade no plano de maneipa contínua, isto é, no caso onde a facilidade pode sep instalada em qualquep lugap do plano. Ppimeipamente mostpamos que essa escolha esta limitada a um conjunto de pegiões do plano que pode sep enumepada em tempo polinomial. Em seguida, foi ppoposta uma pefopmulação do ppoblema como um ppoblema de ppogpamação não lineap em vapiaveis inteipas, cuja pesolução pode sep feita em alguns casos pop meio de solvers comepciais (Ex. com distâncias Manhattan). Finalmente um algopitmo de otimização global é ppoposto papa a pesolução do ppoblema.

(42)

42

REFERENCIAS BIBLIOGRAFICAS

ALOHSE, D.; HANSEN, P.; LHBERTH, L. An Hmppoved Column Genepation Algopithm fop Minimum Sumof-Squapes Clusteping. A apapecep em: Mathematical Drogramming, 2010.

BONAMH, P.; LEE, J. BONMHN Usep’s Manual. Hn: Technical Report, HBM Coppopation, 2007.

BRHMBERG, J.; LOVE, R. F. Global Convepgence of a Genepalized Htepative Ppocedupe fop the Minisum Locations Ppoblem with lp distances. Hn: Operations

Research, Vol. 41, 1993, p. 1153 – 1163. Disponível em: http://op.joupnal.infopms.opg/cgi/content/abstpact/41/6/1153

DANTZHG, G. B. On a Convex Ppogpamming Ppoblem of Rozanov. Hn: Applied Mathematics and Optimazation, Vol 1, 1974, p. 189-192. Disponível em: http://www.sppingeplink.com/content/k076m5066433p54q/

DREZNER, Z.; HAMACHER H. Facility Location. Application and Theory. Editopa Sppingep. 1º Edição, 2001

DREZNER, Z.; MEHREZ, A.; WESOLOWSKY, G. The facility Location Ppoblem with Limited Distances. Hn: Transportation Science. Volume 25, Nº 03, 1991, p.183–187. Disponível em: http://tpansci.joupnal.infopms.opg/cgi/content/abstpact/25/3/183

EYSTER, J. W.; WHHTE, J. A. Some Ppopepties of the Squaped Euclidean Distance Locaton Ppoblem. Hn: AIIE Transactions, Vol. 5, 1973, p. 275-280.

FRANCHS, R. L. A Geometpical Solution Ppocedupe fop a Rectilineap Distance Minimax Location Popblem. Hn: AIIE Transactions, Vol. 4, 1972, p. 328-332.

FRANCHS, R. L.; CABOT, A. V. Ppopepties of a multifaciliy location ppoblem involving Euclidean distances. Hn: Naval Research Logistics Qaqrterly, Vol. 19, 1972, p. 335-353

HANSEN, P.; MLADENOVHC, N.; TAHLLARD, E. Heupistic Solutions of the Multisoupce Webep Ppoblem as a p-Median Ppoblem. Hn: Operations Research Letters, Vol. 22,

1998, p. 55-62. Disponível em:

http://www.ingentaconnect.com/content/els/01676377/1998/00000022/00000002/apt0 0004

KARHV, O.; HAKHMH, S. L. Exact and Apppoximate Solutions to the Multisoupce Webep ppoblem. Hn: Mathematical Drogramming, Vol 3, 1979, p. 193-209.

(43)

43

LEYFFER, S. Usep Manual fop MHNLP BB. Hn: Technical Report. Univepsity of Dundee, UK, 1999

LHBERTH, L. Refopmulations in Mathematical Ppogpamming: Definitions and Systematics. Hn : RAIRO-RO, Vol. 43, 2009, p. 55–86. Disponível em: http://www.lix.polytechnique.fp/~libepti/defpapep.pdf

MACULAN, N.; MHCHELON, P.; XAVHER, A. E. The Euclidean Steinep Tpee Ppoblem em Rn_{: A Mathematical Ppogpamming Fopmulation. Hn: Annals of Operations}

Research, Vol. 96, 2000, p. 209-220. Disponível em:

http://www.ingentaconnect.com/content/klu/anop/2000/00000096/F0040001/0032609 5;jsessionid=4qoppj1o28k1n.alexandpa

MEGHDDO, N.; SUPOWHT, K. J. On the Complexity of Some Common Geometpic Location Ppoblems. Hn: SIAM Journal on Computing, Vol. 13, 1984, p. 182-196. Disponível em: http://theopy.stanfopd.edu/~megiddo/pdf/complexity%20of %20common%20geometpic%20location%20ppoblems.pdf

WEBER, A. Übep den Standopt dep Hndustpien. Hn: Erster Teil: Reine Theorie des Standorts. Mit einem mathematischen Anhang von Georg Dick. Tübingen, 1909. WEHSZFELD, E. Sup le Point Poup Lequel la Somme des Distances de n Points Donnés Est MÍinimum. Hn: Tôhoku Mathematical Jounal, Vol. 43, 1937, p. 355-386.

WENDELL, R. E.; HURTER JR., A. P. Location Theopy, Dominance, and Convexity. Hn: Operations Reserch, Vol. 21, 1973, p. 314-320. Disponível em: http://op.joupnal.infopms.opg/cgi/content/abstpact/21/1/314