Uma investigação de algoritmos exatos e metaheurísticos aplicados ao nonograma

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXATAS E DA TERRA

DEPARTAMENTO DE INFORMÁTICA E MATEMÁTICA APLICADA PROGRAMA DE PÓS-GRADUAÇÃO EM SISTEMAS E COMPUTAÇÃO

MESTRADO ACADÊMICO EM SISTEMAS E COMPUTAÇÃO

Uma Investigação de Algoritmos Exatos e

Metaheurísticos Aplicados ao Nonograma

Camila Nascimento de Oliveira Taumaturgo

(2)

Camila Nascimento de Oliveira Taumaturgo

Uma Investigação de Algoritmos Exatos e Metaheurísticos

Aplicados ao Nonograma

Dissertação de Mestrado apresentado ao Programa de Pós-Graduação em Sistemas e Computação do Departamento de Informática e Matemática Aplicada da Universidade Federal do Rio Grande do Norte como requisito parcial para a obtenção do grau de Mestre em Sistemas e Computação.

Linha de pesquisa:

Algoritmos Experimentais

Orientadora

Prof.ª Dra. Elizabeth Ferreira Gouvêa Goldbarg

PPgSC – Programa de Pós-Graduação em Sistemas e Computação DIMAp – Departamento de Informática e Matemática Aplicada

CCET – Centro de Ciências Exatas e da Terra UFRN – Universidade Federal do Rio Grande do Norte

(3)

(4)

Dissertação de Mestrado sob o título Uma Investigação de Algoritmos Exatos e

Metaheurísticos Aplicados ao Nonograma apresentado por Camila Nascimento de

Oliveira Taumaturgo e aceita pelo Programa de Pós-Graduação em Sistemas e Computação do Departamento de Informática e Matemática Aplicada da Universidade Federal do Rio Grande do Norte, sendo aprovada por todos os membros da banca examinadora abaixo especificada:

__________________________________________ Prof.ª Dra. Elizabeth Ferreira Gouvêa Goldbarg

Presidente

DIMAp – Departamento de Informática e Matemática Aplicada UFRN – Universidade Federal do Rio Grande do Norte

__________________________________________ Prof. Dr. Marco César Goldbarg

Examinador interno à Instituição

DIMAp – Departamento de Informática e Matemática Aplicada UFRN – Universidade Federal do Rio Grande do Norte

__________________________________________ Prof.ª Dra. Iloneide Carlos de Oliveira Ramos

Examinadora externa ao Programa DEST – Departamento de Estatística

UFRN – Universidade Federal do Rio Grande do Norte

__________________________________________ Prof. Dr. Antônio Carlos Gay Thomé

Examinador externo à Instituição Departamento de Ciência da Computação UFRJ – Universidade Federal do Rio de Janeiro

(5)

(6)

Agradecimentos

Quero agradecer primeiramente a Deus, por me ter me concedido tantas graças, por ter me dado forças, amor e ter colocado na minha vida pessoas muito especiais que tornaram meus dias mais fáceis e prazerosos.

Em especial, quero agradecer e dedicar este trabalho ao meu amado esposo Renato, por sempre estar ao meu lado e disposto a me ajudar, por compreender minhas preocupações e angústias durante todo o trabalho. Obrigada por ter abdicado de suas férias para estar ao me lado no fim desta fase tão importante na minha vida.

Não posso deixar de agradecer aos meus familiares mais próximos. Aos meus irmãos pela confiança e admiração ao meu trabalho. Ao meu pai que, sendo professor e mestre, me inspirou nesta jornada. Em especial, à minha mãe, pelo carinho, paciência e pela torcida; sei que ela é minha maior fã, e sua dedicação me inspira a me tornar uma profissional e mãe amorosa e dedicada. E aos meus sobrinhos, principalmente Ana Lu, que entendeu todas as vezes que eu disse que ela não poderia dormir na minha casa porque eu estava terminando meu Mestrado.

Quero agradecer aos meus sogros e às minhas duas cunhadas pela amizade e pelo carinho. Eles realmente são minha família, e agradeço a Deus por ter posto eles na minha vida.

Quero agradecer aos meus amigos da UFRN. A Juliana Araújo, por sempre estar feliz ao meu lado, me dando apoio e me incentivando. A Everton Cavalcante, pelos seus conselhos e sua amizade, e eu sei que ele sempre está disposto a me ajudar em qualquer situação; muito obrigada! A Alba Sandyra, minha amiga da UFRN mais antiga, que sempre tem conselhos sábios, é sincera e fiel; obrigada, Albinha, pela sua amizade.

Aos colegas do LAE quero agradecer pelos momentos de descontração e pelas novas amizades que fiz durante o Mestrado, e espero que essas amizades sejam eternas. Em especial, agradeço a Silvia, que iniciou o trabalho com os Nonogramas, me concedeu tudo que havia pesquisado e sempre esteve disposta a me ajudar e a tirar minhas dúvidas. Com certeza, sem a ajuda de Silvia, meu Mestrado teria sido mais complicado.

(7)

Ainda que eu caminhe por um vale tenebroso, nenhum mal temerei, pois estás junto a mim.

(8)

Uma Investigação de Algoritmos Exatos e Metaheurísticos

Aplicados ao Nonograma

Autora: B.Sc. Camila Nascimento de Oliveira Taumaturgo Orientadora: Prof.ª Dra. Elizabeth Ferreira Gouvêa Goldbarg

R

ESUMO

O Nonograma é um jogo lógico cujo problema de decisão associado é NP-completo. Ele possui aplicação em problemas de identificação de padrões e de compactação de dados, dentre outros. O jogo consiste em determinar uma alocação de cores em pixels distribuídos em uma matriz N  M atendendo restrições em linhas e colunas. Um Nonograma é codificado através de vetores cujos elementos especificam o número de

pixels existentes em cada coluna e linha de uma figura, sem especificar suas

coordenadas. Este trabalho apresenta abordagens exatas e heurísticas para solucionar o Nonograma. A Busca em Profundidade foi uma das abordagens exatas escolhida, por ser um exemplo típico de algoritmo de força bruta de fácil implementação. Outra abordagem exata implementada foi baseada no algoritmo Las Vegas, através do qual se pretende investigar se a aleatoriedade introduzida pelo algoritmo Las Vegas traria algum benefício em relação à Busca em Profundidade. O Nonograma também é transformado em um Problema de Satisfação de Restrições. Três abordagens heurísticas são propostas: uma Busca Tabu e dois algoritmos Memético. Uma nova abordagem para o cálculo da função objetivo é proposta neste trabalho. As abordagens são testadas em 234 casos de teste de tamanho entre 5 x 5 e 100 x 100, incluindo Nonogramas lógicos e aleatórios.

Palavras-chave: Nonograma. Busca em Profundidade. Las Vegas. Problema de

(9)

Exact and Metaheuristic Algorithms Research Applied to

Nonogram

Author: Camila Nascimento de Oliveira Taumaturgo, B.Sc. Supervisor: Prof. Elizabeth Ferreira Gouvêa Goldbarg, Ph.D.

A

BSTRACT

Nonogram is a logical puzzle whose associated decision problem is NP-complete. It has applications in pattern recognition problems and data compression, among others. The puzzle consists in determining an assignment of colors to pixels distributed in a N  M matrix that satisfies line and column constraints. A Nonogram is encoded by a vector whose elements specify the number of pixels in each row and column of a figure without specifying their coordinates. This work presents exact and heuristic approaches to solve Nonograms. The depth first search was one of the chosen exact approaches because it is a typical example of brute search algorithm that is easy to implement. Another implemented exact approach was based on the Las Vegas algorithm, so that we intend to investigate whether the randomness introduce by the Las Vegas-based algorithm would be an advantage over the depth first search. The Nonogram is also transformed into a Constraint Satisfaction Problem. Three heuristics approaches are proposed: a Tabu Search and two memetic algorithms. A new function to calculate the objective function is proposed. The approaches are applied on 234 instances, the size of the instances ranging from 5 x 5 to 100 x 100 size, and including logical and random Nonograms.

Keywords: Nonogram. Depth First Search. Las Vegas. Constraint Satisfaction Problem.

(10)

Lista de Figuras

Figura 1 – Imagem binária com suas projeções horizontal e vertical (Fonte: Batenburg, 2005) 19 Figura 2 – Esquerda: Descrição de um Nonograma. Direita: Solução correspondente do

Nonograma (Fonte: Pic-a-Pix) ... 20

Figura 3 – Exemplo de um Nonograma preto-e-branco e sua solução ... 24

Figura 4 – Nonograma Colorido ... 24

Figura 5 – (a) Dado um puzzle. (b) Três alocações possíveis de blocos para a linha 1. (c) Duas alocações possíveis de blocos para a linha 2. (d) Duas alocações possíveis de blocos para a linha 3. (e) Uma alocação de bloco para a linha 4. ... 35

Figura 6 – Transformando o Nonograma em cláusulas lógicas para as linhas... 47

Figura 7 – Possibilidades da linha 1 ... 49

Figura 10 – Possibilidade da linha 4 ... 50

Figura 12 – Um exemplo de DFS. (a) Dado um puzzle. (b) Três possíveis soluções para a linha 1. (c) Duas soluções possíveis para a linha 2. (d) Duas soluções possíveis para a linha 3. (e) Uma solução possível para a linha 4. (f) Árvore de busca de (a). ... 51

Figura 13 – Passo 1 da busca em profundidade com Backtracking ... 51

(11)

Figura 22 – Sorteia-se uma possibilidade para a segunda linha. Nota-se uma violação. A seguencia 3 torna-se proibida. ... 55 Figura 23 – Sorteia-se uma possibilidade para a primeira linha e para a segunda linha. Percebe-se uma violação e a Percebe-seguência 4-1 torna-Percebe-se proibida. ... 55 Figura 24 – A sequencia 4 torna-se proibida. Sorteia-se uma possibilidade para a primeira linha. ... 55 Figura 25 – Sorteia-se uma possibilidade para a segunda linha, percebe-se uma violação. A

sequência 1 torna-se proibida. ... 55 Figura 26 – Sorteia-se uma possibilidade para a primeira e segunda linha. ... 56 Figura 27 – Sorteia-se uma possibilidade para a terceira linha, percebe-se uma violação. A

sequência 2-1-1 torna-se proibida. Sorteia-se outra possibilidade para a terceira linha, e a sequência 2-1-2 torna-se proibida. ... 56 Figura 28 – Sorteia-se uma possibilidade para a terceira e quarta linha. ... 56 Figura 29 – Sorteia-se uma possibilidade para a terceira linha. A solução do puzzle é

encontrada. ... 57 Figura 30 – Solução não viável de um Nonograma ... 59 Figura 31 – Exemplo de alocação inicial dos blocos ... 60 Figura 32 –CruzCorte: (a) pai1; (b) pai2; (c) Filho resultante do cruzamento do pai1 com o pai2 ... 66 Figura 33 – (a) Número médio de pixels não resolvidos para puzzles 30 x 30 gerados

aleatoriamente, para uma6 porcentagem variável de pixels pretos, ao usar o Solver1; barras de erro indicam desvio padrão. (b) Como em (a) para FullSettle (topo do gráfico), Solver0 (meio do gráfico) e Solver1, sem o

(12)

Lista de Gráficos

Gráfico 1 – Quantidade de combinações possíveis para os casos de teste do Benchmark Puzzle

(2012). ... 36 Gráfico 2 – Tempo em segundos para gerar todas as alocações possíveis de blocos para cada

linha e coluna dos casos de teste do Benchmark Puzzles (2012) ... 36 Gráfico 3 – Quantidade de combinações possíveis para os casos de teste do Nonogram Solver

(2012). ... 37

Gráfico 4 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e coluna dos casos de teste do Nonogram Solver (2012). ... 37 Gráfico 5 – Quantidade de combinações para os casos de teste 10 x 10 do RanPuz ... 38 Gráfico 6 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e

coluna dos casos de teste do RanPuz com tamanho 10 x 10 ... 38 Gráfico 7 – Quantidade de combinações para os casos de teste 20 x 20 do RanPuz ... 39 Gráfico 8 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e

coluna dos casos de teste do RanPuz com tamanho 20 x 20 ... 39 Gráfico 9 – Quantidade de combinações para os casos de teste 30 x 30 do RanPuz ... 40 Gráfico 10 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e

(13)

Lista de Tabelas

Tabela 1 – Resumo das onze regras lógicas de Jing et al. (2009) e Yu et al. (2009) ... 41

Tabela 2 – Resultados da aplicação das regras lógicas para os casos de teste do Benchmark Puzzles (2012) ... 43

Tabela 3 – Resultados da aplicação das regras lógicas para os casos de teste do siteNonogram Solver (2012)... 43

Tabela 4 – Resultados da aplicação das regras lógicas para os casos de teste aleatórios ... 44

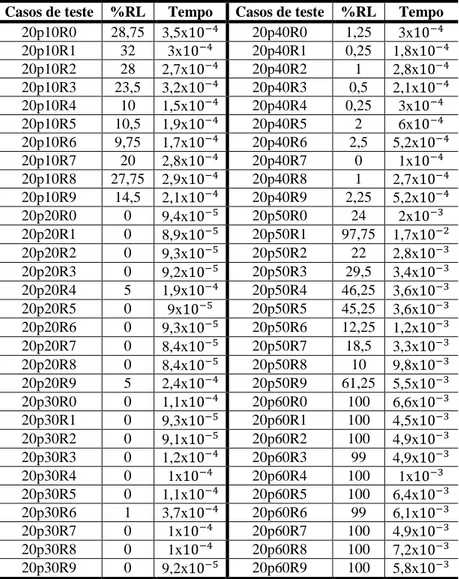
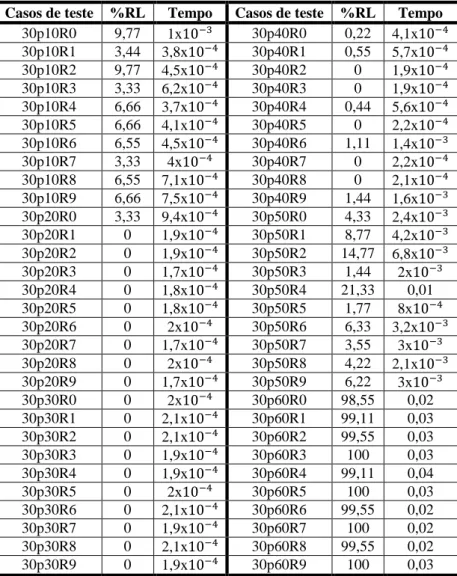
Tabela 5 – Resultados da aplicação das regras lógicas para os casos de teste aleatórios do RanPuz ... 45

Tabela 6 – Resultados da aplicação das regras lógicas para os casos de teste aleatórios do RanPuz ... 46

Tabela 7 – Resultados do MiniSat par os casos de teste retirados de jogos para dispositivos móveis ... 48

Tabela 8 – Resultado do DFS e Las Vegas para os casos de teste do Benchmark Puzzles (2012). ... 57

Tabela 9 – p-valores em relação à função objetivo para a decisão da construção da solução inicial ... 70

Tabela 10 –p-valores em relação à função objetivo para o parâmetro iter ... 71

Tabela 11 –p-valores em relação ao tempo para o parâmetro iter ... 71

Tabela 12 –p-valores em relação à função objetivo para o parâmetro iterG (400 x 600) ... 72

Tabela 13 –p-valores em relação ao tempo para o parâmetro iterG (400 x 600) ... 72

Tabela 14 –p-valores em relação à função objetivo para o parâmetro iterG (200 x 400) ... 73

Tabela 15 –p-valores em relação à função objetivo para o parâmetro cont (200 x 500) ... 73

Tabela 16 –p-valores em relação ao tempo para o parâmetro cont (300 x 500) ... 74

Tabela 17 –p-valores em relação à função objetivo para o parâmetro cont (100 x 300) ... 74

(14)

Tabela 20 –p-valores em relação ao tempo para a decisão do tamanho da população ... 76

Tabela 21 –p-valores em relação à função objetivo para a decisão do número de gerações ... 77 Tabela 22 –p-valores em relação à função objetivo para a forma de seleção dos pais ... 78 Tabela 23 –p-valores em relação ao tempo para a decisão da forma de seleção dos pais ... 78 Tabela 24 –p-valores em relação à função objetivo para o método de cruzamento ... 79

Tabela 25 –p-valores em relação à função objetivo para a decisão da taxa de cruzamento .... 80

Tabela 26 –p-valores em relação ao tempo para a decisão da taxa de cruzamento ... 81 Tabela 27 –p-valores em relação à função objetivo para a decisão da taxa de mutação ... 81 Tabela 28 –p-valores em relação à função objetivo para a decisão do número de iterações da

busca local ... 82 Tabela 29 – p-valores em relação à função objetivo para a decisão de nPixel ... 83 Tabela 30 – p-valores em relação à função objetivo para a decisão de pAltRC ... 84 Tabela 31 – Resultados do TabuGrama para os casos de teste do Benchmark Puzzles (2012) .. 85 Tabela 32 – Resultados do TabuGrama para os casos de teste do Nonogram Solver (2012) ... 85

(15)

Tabela 41 – Resultados do Memetico2 para os casos de teste do Benchmark puzzles (2012) .. 92

Tabela 42 – Resultados do Memetico2 para os casos de teste do Nonogram Solver (2012) ... 92 Tabela 43 – Resultados do Memetico2 para os casos de teste do RanPuz com tamanho 10 x 10 ... 93 Tabela 44 – Resultados do Memetico2 para os casos de teste do RanPuz com tamanho 20 x 20 ... 93 Tabela 45 – Resultados do Memetico2 para os casos de teste do RanPuz com tamanho 30 x 30 ... 94 Tabela 46 – p-valores em relação ao tempo para as comparações das heurísticas propostas

para os casos de teste do Benchmark puzzles (2012) ... 95

Tabela 47 – p-valores em relação à função objetivo para as comparações das heurísticas propostas para os casos de teste do Nonogram Solver (2012) ... 96 Tabela 48 – p-valores em relação ao tempo para as comparações das heurísticas propostas

para os casos de teste do RanPuz com o tamanho 10x10 ... 96

Tabela 49 – p-valores em relação à função objetivo para as comparações das heurísticas propostas para os casos de teste do RanPuz com o tamanho 20x20 ... 97 Tabela 50 – p-valores em relação à função objetivo para as comparações das heurísticas

(16)

Lista de Quadros

Quadro 1 – Procedimento de busca local ... 61

Quadro 2 – Pseudo-código do algoritmo Tabugrama ... 62

Quadro 3 – Procedimento Busca Local do TabuGrama ... 63

Quadro 4 – Pseudo-código do algoritmo Memetico1 ... 65

(17)

Lista de abreviaturas e siglas

B&W – Blach and White (Preto e branco) CCD – Charge-coupled device

CSP – Constraint Satisfaction Problem CTO – Chief technology officer

DFS – Depth First Search (Busca em Profundidade) DT – Discrete Tomography (Tomografia Discreta) FNC – Forma Normal Conjuntiva

LTS – Long Term Support PS – Soluções possíveis

RAM _– Random Access Memory

RGB _– Red-green-blue / vermelho-verde-azul SAT _– Satisfabilidades

SBPO _– Simpósio Brasileiro de Pesquisa Operacional

(18)

Sumário

1 Introdução ... 19

1.1 Objetivos e Contribuições ... 21

1.2 Organização do trabalho ... 22

1.3 Contribuições ... 23

2 O Nonograma ... 24

2.1 História do Nonograma ... 25

2.2 Casos de Teste ... 26

3 Trabalhos Relacionados ... 28

4 Pré-processamento ... 34

5 Abordagem Exata ... 41

5.1 Regras lógicas ... 41

5.2 Nonograma como um problema de Satisfação de Restrições ... 46

5.3 Busca em Profundidade ... 48

5.4 Las Vegas Sistemático ... 54

6 Abordagem Heurística ... 58

6.1 Função objetivo ... 58

6.2 Construção da Solução inicial ... 60

6.3 Busca Local... 61

6.4 Busca Tabu ... 61

6.5 Memético ... 64

7 Experimentos Computacionais ... 69

7.1 Estudo dos parâmetros ... 69

7.1.1 TabuGrama ... 69

7.1.2 Memetico1 ... 75

7.1.3 Memetico2 ... 82

7.2 Resultados ... 84

7.2.1 TabuGrama ... 84

7.2.2 Memetico1 ... 88

(19)

7.3 Comparações ... 95

8 Conclusão ... 99

8.2 Trabalhos Futuros ... 100

(20)

1 Introdução

Os jogos de raciocínio lógico que possuem natureza combinatória têm recebido uma crescente atenção na Ciência da Computação em virtude do avanço do estado da arte dos algoritmos para solucionar esses tipos de jogos e o fato de que diversos deles possuem importantes aplicações práticas. Com o auxílio da ferramenta computacional e dos recentes meios de mídia novos jogos combinatórios se popularizaram ao longo da década de 90. Dentre eles encontra-se o Nonograma que consiste em determinar uma

alocação de cores em pixels distribuídos em uma matriz N  M atendendo restrições em linhas e colunas, o qual foi demonstrado ser NP-completo por Ueda e Nagao (1996). O Nonograma possui aplicações na transmissão de imagens (Sohn et al., 2007) e na reconstrução de uma imagem discreta a partir de suas projeções, sendo uma generalização do problema da Tomografia Discreta (Batenburg, 2005).

Segundo Batenburg (2005), o problema da Tomografia Discreta (Discrete

Tomography - DT) consiste na reconstrução de uma imagem discreta a partir de suas

projeções. Um dos problemas principais é a reconstrução de uma imagem binária (preta e branca) a partir de apenas duas projeções, horizontal e vertical (ver Figura 1). Ryser (1957) forneceu um algoritmo de tempo polinomial para encontrar uma solução para a DT. No entanto, no geral um grande número de soluções pode existir. Entre as aplicações da DT estão a reconstrução da estrutura do cristal a partir de projeções obtidas por microscopia eletrônica (Kisielowski, et al., 1995); (Schwander, et al., 1993) e a reconstrução de imagens angiográficas em imagens médicas (Onnasch & Prause, 1999); (Gerbrands & Slump, 1982).

Figura 1 – Imagem binária com suas projeções horizontal e vertical (Fonte: Batenburg, 2005)

(21)

organização horizontal e vertical dos pixels pretos ao longo de cada linha e coluna (Batenburg, 2005). A partir da descrição do Nonograma, transformando o puzzle em uma DT, solucionando esse último, uma de suas soluções será a solução do Nonograma.

Figura 2 – Esquerda: Descrição de um Nonograma. Direita: Solução correspondente do Nonograma (Fonte: Pic-a-Pix)

Segundo Batenburg e Kosters (2009) o Nonograma também pode ser relacionado a vários problemas job scheduling, onde cada linha corresponde a um único processador e os trabalhos para os processadores são indicados pelas descrições das linhas. Em muitos problemas de scheduling, o tipo de restrição que ocorre nos Nonogramas só é aplicável às linhas ou às colunas, mas geralmente não em ambas.

Com o avanço das imagens em alta definição, torna-se cada dia mais necessário desenvolver métodos que transmitam imagens de forma otimizada. O fato de o Nonograma ser um problema NP-Completo indica que nem todos os quebra-cabeças podem ser resolvidos em um tempo aceitável usando apenas regras lógicas simples ou abordagens exatas, podendo levar dias ou até anos para se encontrar a solução.

Podem ser considerados diferentes níveis de dificuldade dos Nonogramas. Os que aparecem em revistas e jornais podem ser resolvidos aplicando uma série de regras lógicas simples, cada uma das quais considerando apenas uma única linha ou coluna. Esses quebra-cabeças sempre terão uma única solução. Por outro lado, Nonogramas grandes e aleatórios podem ser muito difíceis de resolver e podem ter várias soluções ou nenhuma.

(22)

(Herik, Van Den, & Iida, 2000); (Khoo & Zubek, 2002). Por outro lado, o interesse na aplicação de abordagens heurísticas para resolver quebra-cabeças e jogos tem sido crescente por diversos motivos, por exemplo, tentar solucionar jogos facilita no aprendizado de heurísticas atraindo a atenção dos alunos (Vaccaro & Guest, 2005); (Jefferson, et al., 2006); (Smith, 2007); (Lucas & Kendall, 2006).

Os Nonogramas podem ser lógicos, aqueles que podem ser resolvidos utilizando apenas regras lógicas, ou aleatórios, aqueles gerados aleatoriamente. No geral, Nonogramas lógicos são considerados fáceis porque podem ser resolvidos através de deduções sobre suas restrições. Já os Nonogramas aleatórios podem ser fáceis ou difíceis dependendo da porcentagem de pixels pretos que os mesmos possuem e seus tamanhos. De forma geral, o desafio em solucionar Nonogramas está ligado às restrições do problema. Tais restrições dificultam a elaboração de busca locais eficientes para o problema.

Em relação a algoritmos para solucionar Nonogramas, existem dois principais tipos de abordagens que são aplicadas: algoritmos exatos e abordagens metaheurísticas. As técnicas exatas incluem Programação Linear (Bosh, 2000 e Mingote, 2009), busca em profundidade (Wiggers, 2004), combinações de regas lógicas (Jing, et al., 2009 e Yen, et al., 2010), entre outras (Salcedo-Sanz, et al., 2007; Batenburg e Kosters, 2009). As abordagens heurísticas propostas para o Nonograma incluem Algoritmo Memético (Batenburg e Kosters, 2004), Genético (Wiggers, 2004), Algoritmos Culturais (Ochoa et

al., 2009), dentre outros. A maioria dos métodos anteriores resolvem Nonogramas

pequenos ou lógicos e não apresentam comparação entre os métodos.

O presente trabalho visa fazer um estudo de algoritmos exatos e heurísticos para aplicar a Nonogramas lógicos e aleatórios de tamanhos variados. No geral, na literatura, Nonogramas lógicos são considerados com mais frequência em detrimento aos Nonogramas aleatórios. Sendo assim, o objetivo deste trabalho é estudar melhor a eficácia das heurísticas para os casos de testes aleatórios.

1.1 Objetivos e Contribuições

Este trabalho tem os seguintes objetivos:

(23)

Profundidade (DFS – Depth First Search) é um exemplo típico de força bruta de fácil implementação. Tal abordagem é semelhante à abordagem de Jing et al. (2009). Neste trabalho, para tentar reduzir o tempo de execução do DFS foi implementado o

Backtracking, Jing et al. (2009) implementaram o Branch Bound. Com o propósito de

testar um algoritmo probabilístico foi implementada uma abordagem Las Vegas. Devido às restrições de linhas e colunas do Nonograma, foi desenvolvido um modelo de satisfação de restrições para solucionar o mesmo. Tal resolução é feita através de um

solver, o MiniSat (Eén, 2003).

- Apresentar duas novas abordagens metaheurísticas para o Nonograma baseadas nas metaheurísticas Busca Tabu e Algoritmo Memético e comparar seus resultados com outros já apresentados na literatura.

- Fazer um experimento computacional levando em consideração problemas lógicos e aleatórios com tamanhos que variam de 5 x 5 até 100 x 100, considerados de grande porte em comparação com os demais apresentados na literatura.

Neste trabalho é analisada uma proposta para o cálculo da função objetivo apresentada por Maia (2010). Tal função objetivo considera as restrições do problema de uma forma mais completa que as propostas em trabalhos anteriores. Na literatura, no geral, o cálculo da função objetivo compara o número de 1’s e 0’s em cada linha e

coluna de uma solução do jogo com o número desejado de 1’s e 0’s. Tal abordagem não mensura corretamente a distância que uma solução atual do jogo está da solução correta.

1.2 Organização do trabalho

(24)

avaliação das soluções. Posteriormente, no Capítulo 7 são realizados os experimentos computacionais, expondo o estudo dos parâmetros, os resultados e as comparações entre as abordagens propostas. Finalmente, no Capítulo 8 conclui-se o trabalho.

1.3 Contribuições

Em 2011 foi publicado no Simpósio Brasileiro de Pesquisa Operacional (SBPO) uma abordagem da Busca Tabu para solucionar o Nonograma. A abordagem utiliza os 16 casos de teste classificados como muito difícil retiradas do Benchmark

Puzzles (2011). A busca local realiza o deslizamento de um bloco em uma linha ou

(25)

2 O Nonograma

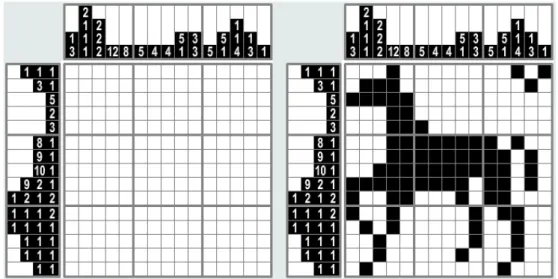
O Nonograma é um jogo interessante, que assume a forma de uma grade N x M com números situados à esquerda das linhas e no topo das colunas. Existem dois tipos de Nonograma o preto-e-branco (Black and White - B&W) e o colorido. No Nonograma preto-e-branco os números ao lado das linhas e acima das colunas dão informações sobre quantas células têm de ser preenchidas na mesma linha ou na mesma coluna, respectivamente, na ordem em que os números aparecem. Com dois ou mais números os blocos de células na grade devem ser separados por pelo menos um pixel em branco. A Figura 3 mostra um exemplo de um Nonograma B&W. Quando todos os requisitos das linhas e colunas são satisfeitos o Nonograma foi resolvido.

Figura 3 – Exemplo de um Nonograma preto-e-branco e sua solução

Figura 4 – Nonograma Colorido

(26)

por pelo menos um pixel branco já que os dois primeiros blocos possuem cores diferentes. Já os dois últimos blocos precisam ser separados por pelo menos um pixel em branco. Para aprender como resolver Nonogramas lógicos B&W consulte Dorant (2005).

2.1 História do Nonograma

Nonogramas são também conhecidos por diversos outros nomes, incluindo

Paint by Numbers, Griddlers, Pic-a-Pix, Picross, PrismaPixels, Pixel Puzzles,

Crucipixel, Edel, FigurePic, Grafilogika, Hanjie, Illust-Logic, Japanese Crosswords,

Japanese Puzzles, Kare Karala!, Logic Art, Logic Square, Logicolor, Logik-Puzzles,

Logimage, Obrazki logiczne, Zakódované obrázky, Maľované krížovky, Oekaki Logic,

Oekaki-Mate, Paint Logic, Shchor Uftor, Gobelini, Picture Logic e Tsunamii. Eles

também são chamados de Paint by Sudoku e Binary Coloring Books, apesar de esses nomes serem totalmente imprecisos (Wikipedia, 2012).

Em 1987, Non Ishida, um editor gráfico japonês, ganhou uma competição em Tóquio pelo design de grades de imagens usando luzes de arranha-céus que são ligadas ou desligadas. Ao mesmo tempo, e sem conexão, um profissional japonês de quebra-cabeças chamado Tetsuya Nishio inventou o mesmo puzzle. Em 1988, Noh Ishida publicou três puzzles no Japão sob o nome de “Window Art Puzzles” e Tetsuya Nishio nomeou seu puzzle de Oekaki Logic, que significa “desenho lógico”. Em 1990, James Dalgety, no Reino Unido, inventou o nome Nonograma depois que Non Ishida, e The

Sunday Telegraph começou a publicá-lo semanalmente (Conceptis Puzzles, 2012).

Em 1993, Non Ishida publicou o primeiro livro de Nonogramas no Japão e, mais tarde, o Sunday Telegraph publicou um outro livro no Reino Unido, intitulado The

book of Nonograms. O quebra-cabeça japonês rapidamente se espalhou pelo mundo, e

começou a ser publicado nos Estados Unidos, Suécia, África do Sul, Israel e outros países. Nos últimos anos, a popularidade desses puzzles tem aumentado bastante. Existem várias empresas que publicam revistas e páginas da web dedicadas apenas para os quebra-cabeças japoneses.

Em 1994, Dave Green, que viria a ser fundador e presidente da Conceptis

Puzzles, visita Tóquio, onde conhece esses enigmas de lógica pela primeira vez. Junto

(27)

computador foi desenvolvido os primeiros puzzles B&W são produzidos e o nome Pic-a-Pix é inventado.

Em 1998 The Sunday Telegraph publicou uma competição para escolher o seu próprio nome para o puzzle. Griddler foi o nome vencedor escolhido pelos leitores do jornal. No outono de 1999, The Sunday Telegraph publicou o primeiro livro de

Griddler, e tem publicado um por ano desde então.

Os Nonogramas encontrados nas revistas são sempre resolvidos utilizando lógicas simples. Isto significa que a solução pode ser encontrada com o raciocínio elementar e sem deduções complexas. Em implementações posteriores serão utilizados casos de teste que não são resolvidos apenas com raciocínio lógico elementar. O Nonograma foi demonstrado ser NP-completo por Ueda e Nagao (1996). O fato de solucionar Nonogramas ser NP-completo indica que nem todos os puzzles podem ser resolvidos usando simples regras lógicas.

2.2 Casos de Teste

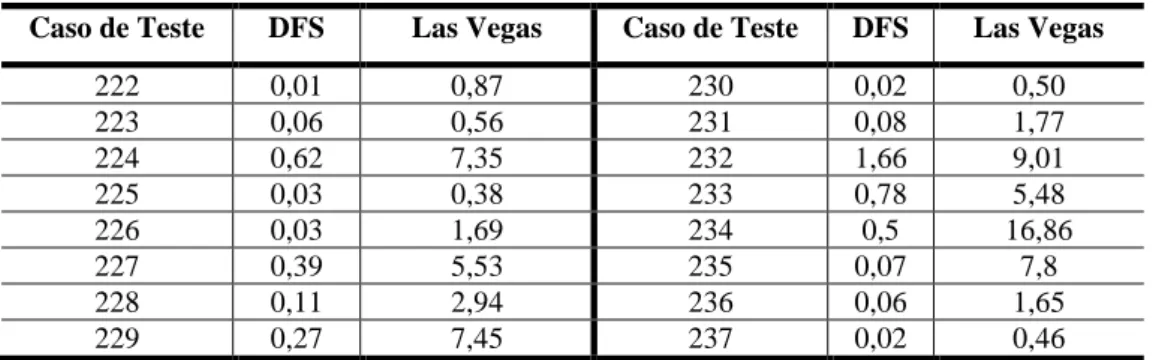
Foram utilizados 16 casos de teste classificados como muito difíceis retirados do Benchmark Puzzles (2012). Nesse site há cerca de 200 quebra-cabeças classificados com estrelas de 1 a 9, as com 9 estrelas indicam os jogos mais difíceis. Neste trabalho é utilizado apenas os Nonogramas com 8 e 9 estrelas. Todos os casos de teste desse site possuem tamanho 10 x 10. Cada caso de teste retirado do Benchmark Puzzles (2012) possui apenas uma solução. Esses casos de teste foram utilizados por Ortiz García et al. (2008) e por Goldbarg et al. (2011).

(28)

de pixels pretos do mesmo e < > o número do caso de teste. Como por exemplo: 10p10R0.

Também são utilizados outros oito casos de teste retirados de jogos para dispositivos móveis com o intuito de testar o MiniSat (Eén, 2003). Esses 8 casos de teste são lógicos, resolvidos utilizando apenas regras lógicas e possuem os seguintes tamanhos: 5 x 5, 6 x 5, 6 x 6, 7 x 5, 8 x 4 e 9 x 6.

(29)

3 Trabalhos Relacionados

O problema da formação de imagens, a partir de informações sobre seus pixels, está recebendo intensa atenção, especialmente em anos recentes. Além de constituir em um desafio lógico, pode implicar na redução da informação necessária à transmissão dos dados de uma figura. Um dos primeiros trabalhos publicados para a solução desse problema deve-se a Bosch (2000) que apresentou uma abordagem por Programação Linear.

Wiggers (2004) propôs um algoritmo genético e compara seu desempenho ao de um algoritmo de busca em profundidade (depth first search – DFS). O algoritmo genético proposto emprega uma população de 100 cromossomos, operando com uma taxa de mutação igual a 5% e uma taxa de crossover igual a 60% e utiliza o método da roleta para realizar a seleção para a reprodução. O operador de mutação do algoritmo é simples e apenas altera o valor de um gene (um posição aleatória) em um cromossomo. A função objetivo é calculada da mesma forma que é feito para um problema de satisfabilidade (SAT) conforme apresentado por Jong e Spears (1989). No trabalho, o desempenho dos algoritmos é definido a partir do número de avaliações necessárias para resolver o problema. Os algoritmos são comparados usando cinco tamanhos sucessivos do jogo: grades 5 x 5 a 10 x 10. Para tamanhos pequenos do jogo (5 x 5 e 6 x 6) o algoritmo DFS encontra o resultado em um menor número de avaliações. Para tamanhos maiores o algoritmo genético encontra o resultado com menos avaliações do que o DFS.

Batenburg e Kosters (2004) desenvolveram um algoritmo memético que executa, após cada operação de recombinação ou mutação, uma busca hill-climbing até que a solução atinja um ótimo local. A função de avalição de uma imagem pode ser obtida pela soma dos desvios de todas as linhas e colunas. O tamanho da população foi definido igual a 1000 indivíduos, o número de filhos que são criados a cada geração é fixo e igual a 500. Os autores relatam que o algoritmo resolve um jogo 25 x 25 em 80 minutos e um 30 x 30 em 12 horas em um Pentium IV com 2.4 GHz. Um outro jogo 25 x 25 não foi resolvido, pois o algoritmo converge a um ótimo local.

(30)

formas? No trabalho os autores fornecem um método para responder ambas as perguntas.

Sohn et al. (2007) propuseram um método de reconhecimento do alfabeto impresso utilizando o Nonograma. Um documento é copiado por uma câmera CCD (charge-coupled device) e convertido em uma imagem preta e branca. Os caracteres são extraídos da imagem através do método histograma e são normalizados com um tamanho fixo. Aplica-se o puzzle ao caractere normalizado e assim a imagem é traduzida em uma informação numérica. Feito isso, o caractere é reconhecido aplicando-se a informação numérica desse ao modelo padrão. Por fim, o caractere reconhecido é exportado para um processador de texto editável.

Salcedo-Sanz et al. (2007a) aplicaram na solução do jogo algoritmos evolucionários com aprendizado. O trabalho emprega uma função objetivo para avaliar a configuração corrente do jogo que compara o número de 1’s e 0’s em cada linha e coluna de uma solução do jogo com o número desejado de 1’s e 0’s. Os autores descrevem três diferentes abordagens de solução com a taxa de crossover e a taxa de mutação em todas as abordagens. Na primeira, um algoritmo genético canônico é apresentado, e esse não é capaz de resolver o problema. Na segunda abordagem, operadores especiais de recombinação são sugeridos. A solução inicial é criada a partir da localização dos blocos dentro dos limites possíveis dos mesmos – mais à esquerda e mais à direita possível, respeitando apenas a viabilidade das colunas. Feito isso, o operador de recombinação troca alelos (que são colunas do tabuleiro de jogo) entre os pais. Segundo o relato do experimento, essa abordagem consegue viabilizar quase todas as alocações de blocos, todavia não consegue fazê-lo para todo o tabuleiro. A última abordagem é a segunda abordagem acrescida de uma busca local (Hill

Climbing), de modo que essa melhoria no algoritmo consegue fazer com que a solução

do jogo seja encontrada. Os autores definem que o número máximo de avaliações executadas pelos algoritmos evolucionários fosse fixado em 50.000 – a população em 100 indivíduos e a execução terminada após 500 gerações.

Salcedo-Sanz et al. (2007b) implementaram duas abordagem heurísticas

ad-hoc para o Nonograma, uma combinatória e outra lógica. A primeira, Combinatorial

Ad-hoc heuristic, baseia-se em tentar possíveis combinações de soluções em cada linha

(31)

jogo e pode ser estendida para solucionar puzzles coloridos, sendo composta por cinco sub-procedimentos lógicos que visam completar o jogo. Ambas as heurísticas iniciam o algoritmo com um procedimento de pré-processamento que implementa três sub-procedimentos lógicos que visam preencher alguns quadrados. Os autores utilizam como casos testes os exemplos dos Nonogramas B&W e colorido do site Conceptis

Puzzle. São solucionados 20 quebra-cabeças (dos quais 12 são B&W), sendo o menor

15 × 15 e o maior 60 × 145. Eles compararam as duas heurísticas propostas com o algoritmo apresentado por Salcedo-Sanz et al. (2007a) e com o algoritmo de solução do

site Conceptis Puzzle, chegando à conclusão de que a abordagem Logic ad-hoc heuristic

mostra-se superior às demais.

Ortiz-García et al. (2007) propuseram um gerador automático de Nonogramas lógicos, que podem ser resolvidos por pessoas, B&W e coloridos a partir de qualquer imagem digital de cores RGB (red – green – blue / vermelho – verde – azul). Apresentaram também uma interface de visualização que fornece várias ferramentas úteis para a finalização do processo de geração do quebra-cabeça, como a possibilidade de mudar as cores e exibir o processo de solução do puzzle.

Ortiz-García et al. (2008) implementaram um algoritmo híbrido evolucionário-lógico para resolver qualquer tipo de Nonograma japonês preto-e-branco, incluindo aqueles classificados como muito difíceis. Eles propuseram o cálculo de uma probabilidade a priori para um pixel ser colorido (pintado com a cor preta) ou não. Essas probabilidades são utilizadas para inicialização da população de cromossomos e em um operador de mutação especial. A seleção dos indivíduos é feita através do método da roleta. O operador de recombinação adotado é o de dois pontos. Há um operador de mutação swap que desliza os blocos pintados e um segundo operador de mutação denominado diversity guided mutation. O algoritmo é aparelhado também com uma busca local que aplica as regras lógicas definidas em Salcedo-Sanz et al. (2007a), buscando viabilizar a alocação dos blocos no tabuleiro. Aplicou-se o algoritmo a todos os puzzles com 8 e 9 estrelas retirados do Benchmark Puzzles (2012), no qual todos possuem o tamanho 10 x 10. O algoritmo resolveu o quebra-cabeça em 100% das 50 execuções para doze casos de teste, e outros quatro com uma porcentagem acima de 94% e comparou seus resultados com Salcedo-Sanz et al. (2007a).

(32)

trabalho (Ortiz-García et al. 2008) e aplicaram essa heurística na solução tanto do Nonograma quanto do Light-up puzzle. Os autores aplicam sua abordagem a 16 casos teste, tabuleiros 10 x 10, classificados como difíceis. A comparação foi feita com o algoritmo de Salcedo-Sanz (2007b) e eles mostraram que a abordagem proposta é mais eficiente do que a de comparação.

Mingote (2009) apresenta uma abordagem de Programação Linear Inteira para Nonogramas B&W e coloridos. O autor generaliza a aproximação de Bosh (2000) desenvolvida apenas para Nonogramas B&W. Foi desenvolvido um gerador de Nonogramas que permite definir a resolução do puzzle, o seu número de cores e densidade (número de células pintadas versus resolução).

Batenburg e Kosters (2009) inicialmente consideraram duas relaxações para o Nonograma que podem ser solucionadas em tempo polinomial. Tais relaxações podem preencher o puzzle parcialmente. O puzzle resultado das relaxações é combinado a um problema 2-Satisfabilidade (2-SAT), no qual se pode deduzir as cores de alguns pixels. Esse processo (relaxações e 2-SAT) é repetido iterativamente possibilitando resolver completamente ou parcialmente o quebra-cabeça. Nos casos em que os puzzles são resolvidos parcialmente significa que o mesmo possui diferentes soluções. Os autores testaram o algoritmo proposto em três bancos de casos de teste; imagens randômicas, imagens hv-convex e puzzles pequenos (5x5).

Jing et al. (2009) propuseram um método para a resolução do jogo em duas fases. Na primeira fase onze regras lógicas são deduzidas e utilizadas para fixar alguns quadrados como pretos ou brancos. Na segunda fase o algoritmo DFS é aplicado para resolver os quadrados desconhecidos remanescentes, implementado conjuntamente com uma estratégia branch and bound para melhorar o tempo de processamento.

Ochoa et al. (2009) implementaram uma abordagem multiobjetivo através de um algoritmo cultural para resolver o Nonograma. O algoritmo cultural implementado emprega uma busca local hill-climbing. Os autores apresentaram uma solução para um caso teste 20×20 que levou 80 minutos para ser obtida em um Pentium IV com 2.4GHz.

(33)

algumas células, posteriormente foi utilizado um algoritmo backtracking cronológico para determinar a cor das células remanescentes. Segundo os autores tal abordagem mostrou-se superior às duas abordagens de Wiggers (2004).

Yen et al. (2010) apresentaram uma abordagem com duas fases para solucionar Nonogramas lógicos. Na primeira fase é construído um banco de dados com possíveis combinações para cada linha, na segunda é feita uma interseção dessas combinações do banco. A abordagem mostrou-se superior às propostas de Jing et al. (2009) e Yu et al. (2009).

Tsai e Chou (2011) propuseram um algoritmo genético para solucionar os Nonogramas. Uma codificação condensada foi utilizada para representar uma solução do puzzle, onde exibe os pixels brancos reais e os pixels pretos condensados em uma linha, mantendo a viabilidade nas linhas. A população inicial é gerada utilizando a codificação condensada. O cruzamento troca linhas entre os pais, e a mutação desloca um pixel preto em uma linha. O algoritmo genético proposto foi testado em dois puzzles 15 x 15, e solucionou os mesmos.

Tsai et al. (2012) utilizaram os Nonogramas para ensinar algoritmos evolucionários. Um algoritmo genético inteligente (IGA) é proposto e comparado a um algoritmo genético canônico (CGA), demostrando que o IGA pode encontrar a solução correta do puzzle eficientemente, enquanto o CGA não pode. O objetivo da proposta é fazer os estudantes perceberem que estão trabalhando com um método baseado em algoritmos genéticos e um problema de otimização combinatória. A abordagem IGA utiliza uma codificação condensada eficaz para representar uma solução do puzzle. No artigo foi feita uma comparação entre as duas abordagem utilizando um puzzle 15 x 15

(“Bear”).

Tsai (2012) propôs um algoritmo genético baseado no método taguchi (TBGA) para solucionar o Nonograma. O autor comparou o TBGA a um algoritmo genético canônico, mostrando que a primeira abordagem é superior a segunda. As abordagens propostas utilizam uma codificação condensada eficaz para representar uma solução do

puzzle. O tamanho da população foi definida igual a 100 indivíduos, os pais são

(34)

(35)

4 Pré

-

processamento

Todos os experimentos foram realizados em uma máquina com processador Intel Core i7-2600K 3,40 GHz e 4Gb de RAM. A codificação foi feita utilizando a linguagem C++ e sistema operacional Ubuntu 12.04.01 LTS.

Mensurar a dificuldade de um Nonograma não é um problema trivial, porém alguns fatores podem indicar a dificuldade dos mesmos, como por exemplo: tamanho do

puzzle; quantidade de pixels pretos; porcentagem de pixels decididos no puzzle após a

aplicação de regras lógicas e quantidade de possibilidades de alocação dos blocos para cada linha (ou coluna) do quebra-cabeça.

São denominados de blocos os números situados à esquerda das linhas e no topo das colunas de um puzzle, ver Figura 5 (a). Considerando uma linha, é possível calcular os limites mais a esquerda e mais a direita de alocação desse bloco (Salcedo-Sanz et al., 2007a).

Os limites ( ) para cada bloco , onde define a posição mais a esquerda e a posição mais a direita do bloco preto j de uma linha qualquer. Isto

significa que o bloco j apenas pode ser alocado entre o intercalo . Esses limites para os blocos das linhas são inicialmente obtidos da seguinte forma:

(1) ∑ (2) ∑ ( ) (3) (4)

Onde, é o tamanho do bloco , a quantidade de blocos pretos para uma determinada coluna e a quantidade de colunas. O mesmo raciocínio é utilizado para calcular os limites dos blocos das colunas.

O limite mais a esquerda do primeiro bloco (j = 1) de uma linha é dado pela equação 1, para os demais blocos é dado pela equação 2. O limite mais a direita do último bloco (j = d) de uma linha é dado pela equação 4, para os demais é dado pela equação 3.

(36)

possíveis desses blocos para cada linha (ou coluna), que são mostradas na Figura 5 (b, c, d, e). Gerar todas as alocações possíveis dos blocos para as linhas e colunas pode ser útil para as abordagens exatas e heurísticas. O número total destas alocações para cada linha (ou coluna), no geral é bem alto. Nos gráficos 1 a 10 são exibidas as quantidades de alocações possíveis de blocos para as linhas e colunas e os tempos computacional utilizados para gerá-las, para os casos de teste do Benckmarck Puzzles (2012).

Figura 5 – (a) Dado um puzzle. (b) Três alocações possíveis de blocos para a linha 1. (c) Duas alocações possíveis de blocos para a linha 2. (d) Duas alocações possíveis de blocos para a linha 3. (e) Uma alocação de

bloco para a linha 4.

No exemplo da Figura 5 observa-se que para um puzzle de tamanho 4 x 6 existem 12 (3 x 2 x 2 x 1) combinações de alocações possíveis dos blocos considerando as linhas. Antes de gerar as alocações possíveis dos blocos são aplicadas as regras lógicas de Jing et al. (2009) visando reduzir os limites de alocação. Vale salientar que o tempo gasto para aplicar as mesmas foram desprezíveis (ver Seção 5.1).

(37)

Gráfico 1– Quantidade de combinações possíveis para os casos de teste do Benchmark Puzzle (2012).

Gráfico 2 – Tempo em segundos para gerar todas as alocações possíveis de blocos para cada linha e coluna dos casos de teste do Benchmark Puzzles (2012)

Como os casos de teste do Benchmark Puzzles (2012) são pequenos (10 x 10) gerar todas as alocações possíveis de blocos para cada linha e coluna não consome muito tempo. Verifica-se que o maior tempo foi na ordem de 10-4 segundos.

Dos trinta casos de teste retiradas do site Nonogram Solver (2012), quinze foram totalmente resolvidos apenas utilizando-se as regras lógicas. Os resultados das quantidades de combinações possíveis para cada linha e coluna dos outros quinze são mostrados no Gráfico 3, o tempo gasto em segundos para gerar essas soluções possíveis é mostrado no Gráfico 4. Os Gráficos 3 e 4 utilizam a escala logarítmica

0,00E+00 2,00E+18 4,00E+18 6,00E+18 8,00E+18 1,00E+19 1,20E+19 1,40E+19 1,60E+19 In st_ 222 In st_ 223 In st_ 224 In st_ 225 In st_ 226 In st_ 22 7 In st_ 228 In st_ 229 In st_ 230 In st_ 231 In st_ 232 In st_ 233 In st_ 23 4 In st_ 235 In st_ 236 In st_ 237 N ú m e ro d e Possi b il id ad e s

Casos de teste

Possibilidades linhas Possibilidades Colunas 0 0,00005 0,0001 0,00015 0,0002 0,00025 0,0003 0,00035 0,0004 0,00045 0,0005 Tem p o e m se g u n d o s

(38)

Gráfico 3 – Quantidade de combinações possíveis para os casos de teste do Nonogram Solver (2012).

Gráfico 4 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e coluna dos casos de teste do Nonogram Solver (2012).

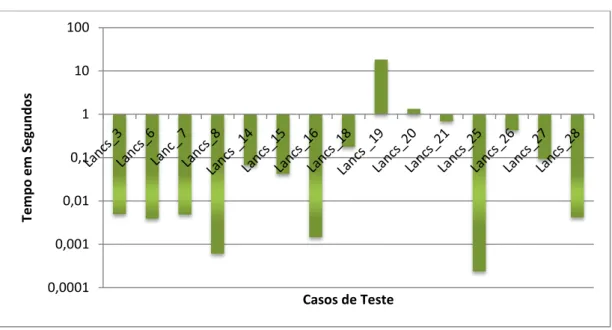
Nos casos de teste do Nonogram Solver (2012), como possui puzzles maiores, percebe-se que o tempo para gerar as alocações possíveis de blocos para cada linha e coluna pode ser elevado. Por exemplo, o caso de teste Lancs_19 (33 x 33) gastou aproximadamente 18 segundos para gerar todas as alocações possíveis de blocos para cada linha e coluna.

Os gráficos 5, 7 e 9 exibem as quantidades de combinações possíveis para os casos de teste aleatórios do RanPuz com tamanhos iguais a 10 x 10, 20 x 20 e 30 x 30 respectivamente, e os gráficos 6, 8 e 10 mostram o tempo gasto para gerar essas alocações possíveis de blocos. Para os casos de teste com sessenta por cento de pixels

1,00E+00 1,00E+12 1,00E+24 1,00E+36 1,00E+48 1,00E+60 1,00E+72 1,00E+84 1,00E+96 1,00E+108 1,00E+120 1,00E+132

Possibilidades Linhas Possibilidades Colunas

0,0001 0,001 0,01 0,1 1 10 100

Tem

p

o

e

m

Segu

n

d

o

s

(39)

pretos, a aplicação das regras lógicas resolve mais de noventa e nove por cento dos

pixels desses puzzles.

Os casos de teste do RanPuz com tamanho 10 x 10 e sessenta por cento de

pixels pretos foram todos resolvidos através das regras lógicas. De acordo com o

Gráfico 5 as quantidades de combinações para os casos de teste com tamanho 10 x 10 são inferiores a combinações, um valor considerado baixo. Já de acordo com o Gráfico 6 observa-se que os tempos para gerar as alocações possíveis de blocos para as linhas e colunas são inferiores a segundos.

Gráfico 5 – Quantidade de combinações para os casos de teste 10 x 10 do RanPuz

Gráfico 6 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e coluna dos casos de teste do RanPuz com tamanho 10 x 10

A partir do Gráfico 7 analisam-se que os casos de testes com tamanho 20 x 20

1 100 10000 1000000 100000000 1E+10 1E+12 1E+14 1E+16 10 p 1 0R0 10 p 1 0R3 10 p 1 0R6 10 p 1 0R9 10 p 2 0R2 10 p 2 0R5 10 p 2 0R8 10 p 3 0R1 10 p 3 0R4 10 p 3 0R7 10 p 4 0R0 10 p 4 0R3 10 p 4 0R 6 10 p 4 0R9 10 p 5 0R2 10 p 5 0R5 10 p 5 0R8 10 p 6 0R1 10 p 6 0R4 10 p 6 0R7 N ú m e ro d e Possi b il id ad e s

Casos de teste

Possibilidades Linhas Possibilidades Colunas 0 0,0002 0,0004 0,0006 0,0008 0,001 0,0012 Tem p o e m se g u n d o s

(40)

e entre 20 a 40 por cento de pixels pretos possuem mais combinações, tornando-os mais difíceis. Os tempos para gerar as alocações possíveis de blocos para esses casos de teste são inferiores a 0,5 segundos.

Gráfico 8 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e coluna dos casos de teste do RanPuz com tamanho 20 x 20

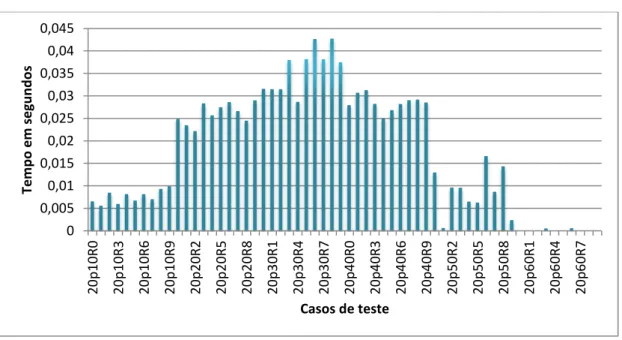
Verifica-se que para os casos de teste com tamanho 30 x 30 o tempo gasto para gerar as alocações possíveis de blocos é alto (Gráfico 10), devido à quantidade de combinações elevada (Gráfico 9). É importante ressaltar que gerar todas as alocações possíveis de blocos torna-se indesejável com o aumente do tamanho do puzzle.

1,00E+00 1,00E+06 1,00E+12 1,00E+18 1,00E+24 1,00E+30 1,00E+36 1,00E+42 1,00E+48 1,00E+54 1,00E+60 20 p 1 0R0 20 p 1 0R3 20 p 1 0R6 20 p 1 0R9 20 p 2 0R2 20 p 2 0R5 20 p 2 0R8 20 p 3 0R1 20 p 3 0R4 20 p 3 0R7 20 p 4 0R0 20 p 4 0R3 20 p 4 0R6 20 p 4 0R9 20 p 5 0R2 20 p 5 0R5 20 p 5 0R8 20 p 6 0R1 20 p 6 0R4 20 p 6 0R7 N ú m e rp d e Po ssi b il id ad e s

Casos de teste

Possibilidades Linhas Possibilidades Colunas 0 0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0,045 20 p 1 0R0 20 p 1 0R3 20 p 1 0R6 20 p 1 0R9 20 p 2 0R2 20 p 2 0R5 20 p 2 0R 8 20 p 3 0R1 20 p 3 0R4 20 p 3 0R7 20 p 4 0R0 20 p 4 0R 3 20 p 4 0R6 20 p 4 0R9 20 p 5 0R2 20 p 5 0R5 20 p 5 0R8 20 p 6 0R1 20 p 6 0R4 20 p 6 0R7 Tem p o e m se g u n d o s

(41)

Gráfico 10 – Tempo em segundos para gerar as alocações possíveis de blocos para cada linha e coluna dos casos de teste do RanPuz com tamanho 30 x 30.

De acordo com os gráficos observa-se que com o aumento do tamanho do

puzzle, aumenta-se a quantidade de combinações para as linhas ou colunas. Também é

possível inferir que os casos de teste com porcentagens de pixels pretos entre 20 e 40 por cento possuem mais combinações. Sabe-se que quanto maior o número de combinações maior é a dificuldade de solucionar o puzzle.

1,00E+00 1,00E+13 1,00E+26 1,00E+39 1,00E+52 1,00E+65 1,00E+78 1,00E+91 1,00E+104 1,00E+117 1,00E+130 1,00E+143 30 p 1 0R0 30 p 1 0R3 30 p 1 0R6 30 p 1 0R9 30 p 2 0R2 30 p 2 0R5 30 p 2 0R8 30 p 3 0R1 30 p 3 0R4 30 p 3 0R7 30 p 4 0R0 30 p 4 0R 3 30 p 4 0R6 30 p 4 0R9 30 p 5 0R2 30 p 5 0R5 30 p 5 0R8 30 p 6 0R1 30 p 6 0R4 30 p 6 0R7 N ú m e ro d e Possi b il id ad e s

Casos de Teste

Possibilidades Linhas Possibilidades Colunas 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 Tem p o e m se g u n d o s

(42)

5 Abordagem Exata

Algumas abordagens exatas, como visto no Capítulo 3, foram propostas para solucionar o Nonograma. Porém, por ser um problema NP-Completo (Ueda e Nagao, 1996) haverá grades cuja solução via métodos exatos poderá levar horas ou até anos. Por isso, a abordagem heurística é justificada. Jing et al. (2009) e Yu et al. (2009) propuseram uma abordagem exata para resolver Nonogramas B&W lógicos, abordagem essa que consiste na implementação de onze regras lógicas e posteriormente é realizada uma busca em profundidade com cortes na abordagem de Jing et al. (2009) e um

backtracking cronológico na abordagem de Yu et al. (2009). Neste trabalho, essas onze

regras lógicas foram implementadas e testadas em todos dos casos de teste. Tais regras lógicas poderão resolver parcialmente o puzzle e reduzir o espaço de busca da heurística.

5.1 Regras lógicas

As onze regras lógicas de Jing et al. (2009) e Yu et al. (2009) são baseadas nos limites, mais a direita e mais a esquerda, dos blocos. Essas regras podem ser divididas em três partes. A primeira determina quais pixels devem ser coloridos ou deixados em branco, a segunda parte refina os limites dos blocos e a terceira além de refinar os limites dos blocos também define quais pixels devem ser deixados em branco ou coloridos. Cada regras é aplicada a cada linha e coluna, todas as regras são aplicadas sequencialmente e iterativamente. No início todas os pixels são considerados desconhecidos. A Tabela 1 mostra resumidamente as regras lógicas de Jing et al. (2009) e Yu et al. (2009).

As regras lógicas implementadas utilizam as ideias de limites ( ) para cada bloco , demostrado no Capítulo 4.

Tabela 1 – Resumo das onze regras lógicas de Jing et al. (2009) e Yu et al. (2009)

Regras da Primeira Parte

Todas as regras desta parte são usadas para pintar ou deixar em branco um determinado pixel.

Regra 1.1 Para cada intervalo de um bloco, alguns pixels devem ser pintados (preto) se todas as possíveis soluções desse bloco tem interseções.

Regra 1.2 Quando um pixel não pertence ao intervalo de qualquer bloco, o mesmo deve ser deixado vazio(branco).

(43)

esse pixel é 1, o pixel anterior

deve ser deixado em branco. Da mesma forma, quando o último pixel do limite de um bloco é pintado, iremos verificar se esse pixel é coberto por outros blocos. Se o tamanho de todos os blocos que cobrem esse pixel é 1, o pixel posterior deve ser branco.

Regra 1.4 Pode haver alguns segmentos pretos em uma linha (ou coluna). Se dois segmentos pretos consecutivos com um pixel desconhecido entre eles, são combinados formando um novo segmento com tamanho maior do que o tamanho do maior bloco que cobre esse novo segmento, então esse pixel deverá ser branco.

Regra 1.5 Alguns pixels brancos podem obstruir a expansão de alguns segmentos pretos. Podemos usar esta propriedade para colorir mais pixels. Por outro lado, para um segmento preto coberto por limites de blocos nos quais tem o mesmo tamanho, se o tamanho do segmento for igual ao comprimento dos blocos que o cobrem, os dois pixels das extremidades desse segmento deve ser deixado em branco.

Regras da Segunda Parte As regras desta parte são designadas a refinar os limites dos blocos

Regra 2.1 Para dois blocos consecutivos e , o ponto inicial (final) do bloco deve estar na frente do ponto inicial (final) do bloco .

Regra 2.2 Deve haver ao menos um pixel branco entre dois blocos, então podemos atualizar os limites do bloco se o pixel

ou é preto.

Regra 2.3 Nos limites de um bloco pode haver um ou mais segmentos pretos. Alguns segmentos pretos podem ter tamanhos maiores do que o tamanho do bloco , e outros não. Para cada segmento com o tamanho maior do que o bloco , se pudermos determinar que esse segmento pertence a um bloco anterior ou posterior ao bloco , podemos atualizar os limites do bloco .

Regras da Terceira Parte

O propósito das regras desta parte não é apenas determinas quais pixels devem ser coloridos ou deixados em branco, mas também refinar os limites de alguns blocos.

Regra 3.1 Quando diversos pixels pretos que pertencem ao mesmo limite de um bloco estão espalhados, todos os pixels desconhecidos entre eles devem ser preenchidos para forma um novo segmento, e os limites desse bloco pode ser atualizado.

Regra 3.2 Alguns pixels brancos podem estar espalhados dentro dos limites de um bloco , então haverá alguns segmentos limitados por esses pixels em branco. O tamanho desses segmentos pode ser menos do que o tamanho do bloco , esses segmentos podem ser pulados, e os limites do bloco pode ser atualizado.

Regra 3.3 Esta regra foi desenvolvida para resolver situações onde o intervalo do bloco não sobrepõe o intervalo do bloco e .

As regras abaixas serão explicadas para a situação em que o intervalo do bloco não sobrepõe o intervalo do bloco .

Regra 3.3-1 Caso 1: O pixel é preto.

Como o intervalo do bloco não sobrepõe o intervalo do bloco , quando primeiro pixel do limite do bloco é preto, podemos terminar de preencher o bloco.

Regra 3.3-2 Caso 2: Um pixel branco aparece depois de um pixel preto .

Então os pixels antes de não pertence ao limite do bloco , e os limites desse bloco devem ser atualizados.

Regra 3.3-3 Caso 3: Há mais de um segmento preto dentro dos limites do bloco . Dentro dos limites encontre o primeiro e o segundo segmento preto. Se o tamanho do novo segmento, após junta-los, for maior do que o bloco , então esses dois segmentos não podem pertencer ao mesmo limite. Se o intervalo do bloco não sobrepõe o intervalo do bloco , podemos tratar esta situação de forma similar (Regras 3.3-1 a 3.3-3).

(44)

Benchmark Puzzles (2012). Sabe-se que todos esses casos de teste possuem o tamanho

10 x 10, e o tempo de execução das regras lógicas para os mesmos foi menor que _segundos.

Tabela 2 – Resultados da aplicação das regras lógicas para os casos de teste do Benchmark Puzzles (2012)

Casos de teste %RL Casos de teste %RL Casos de teste %RL Casos de teste %RL

222 6 226 7 230 11 234 6

223 1 227 11 231 6 235 3

224 15 228 2 232 2 236 3

225 0 229 14 233 5 237 0

A partir da Tabela 2 percebe-se que poucos pixels são decididos aplicando as regras lógicas, devido à aleatoriedade dos puzzles em questão.

Na Tabela 3 são mostrados os resultados para os casos de teste retirados do site

Nonogram Solver (2012). A segunda coluna contém o tamanho do puzzle , a terceira mostra a porcentagem do puzzle (%RL) que foi resolvido utilizando-se as regras lógicas, a quarta mostra o tempo gasto para executar as regras lógicas em segundos.

Para os casos de teste da Tabela 3 percebe-se que em alguns casos mais pixels são resolvidos utilizando as regras lógicas. Dos 30 casos de teste 15 são totalmente resolvidos apenas utilizando as regras lógicas, devido ao caráter lógico de tais puzzles. Outros três são resolvidos mais de 90% do puzzle, o que significa que tais quebra-cabeças possuem mais de uma solução.

Tabela 3 – Resultados da aplicação das regras lógicas para os casos de teste do site Nonogram Solver (2012)

Caso de teste Tamanho %RL Tempo (s) Caso de teste Tamanho %RL Tempo (s)

Lancs_1 100 x 75 100 0,07 Lancs_16 30 x 30 99 0,02

Lancs_2 15 x 15 100 0,001 Lancs_17 30 x 30 100 0,02

Lancs_3 15 x 15 20,9 0,0003 Lancs_18 35 x 50 91 0,02

Lancs_4 15 x 13 100 0,0006 Lancs_19 33 x 33 16 0,009

Lancs_5 20 x 20 100 0,004 Lancs_20 30 x 22 5 0,0004

Lancs_6 15 x 15 17 0,0001 Lancs_21 35 x 50 86,6 0,03

Lancs_7 15 x 15 7 0,0001 Lancs_22 40 x 50 100 0,09

Lancs_8 15 x 20 95 0,0002 Lancs_23 30 x 35 100 0,1

Lancs_9 20 x 20 100 0,002 Lancs_24 75 x 100 100 0,1

Lancs_10 25 x 25 100 0,001 Lancs_25 8 x 8 87 0,0003

Lancs_11 20 x 20 100 0,0005 Lancs_26 35 x 25 52 0,002

Lancs_12 25 x 35 100 0,005 Lancs_27 20 x 25 11 0,0007

Lancs_13 35 x 25 100 0,004 Lancs_28 15 x 15 17 0,0002

Lancs_14 25 x 25 12 0,0006 Lancs_29 35 x 45 100 0,06

Lancs_15 18 x 21 27 0,0006 Lancs_30 100 x 100 100 0,2

(45)

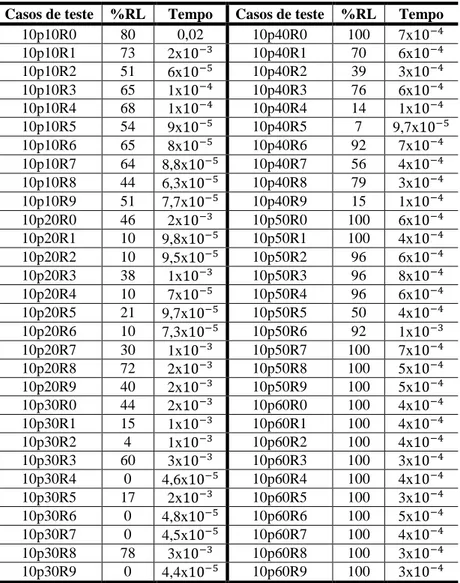
porcentagem de pixels (%RL) decididos após a aplicação das regras lógica e a terceira o tempo gasto para executar as regras em segundos. Novamente, o tempo gasto para executar as regras lógicas é insignificante. Na Tabela 4 todos os casos de testes possuem o tamanho 10 x 10 e as porcentagens de pixels pretos varia de 10 a 60 por cento. De acordo com os dados da Tabela 4 percebe-se que casos de teste com porcentagens de

pixels pretos iguais ou acima de 50 por cento são resolvidos através das regras lógicas,

tornando esses puzzles mais fáceis. Convém observar que os casos de teste mais difíceis são os com 30 por cento de pixels pretos.

Tabela 4 – Resultados da aplicação das regras lógicas para os casos de teste aleatórios

Casos de teste %RL Tempo Casos de teste %RL Tempo

10p10R0 80 0,02 10p40R0 100 7x

10p10R1 73 2x 10p40R1 70 6x

10p10R2 51 6x 10p40R2 39 3x

10p10R3 65 1x 10p40R3 76 6x

10p10R4 68 1x 10p40R4 14 1x

10p10R5 54 9x 10p40R5 7 9,7x

10p10R6 65 8x 10p40R6 92 7x

10p10R7 64 8,8x 10p40R7 56 4x