Programa de P´os-Gradua¸c˜ao em Engenharia El´etrica
Compress˜
ao Seletiva de Imagens Coloridas com
Detec¸c˜
ao Autom´
atica de Regi˜
oes de Interesse
Diego de Miranda Gomes
Orientador: Prof. Dr. Adri˜ao Duarte D´oria Neto
Programa de P´os-Gradua¸c˜ao em Engenharia El´etrica
Compress˜
ao Seletiva de Imagens Coloridas com
Detec¸c˜
ao Autom´
atica de Regi˜
oes de Interesse
Diego de Miranda Gomes
Disserta¸c˜ao submetida ao Programa de P´os-Gradua¸c˜ao em Engenharia El´etrica da Uni-versidade Federal do Rio Grande do Norte como parte dos requisitos necess´arios para a obten¸c˜ao do grau de Mestre em Ciˆencias.
Orientador: Prof. Dr. Adri˜ao Duarte D´oria Neto
Ao meu orientador, prof. Adri˜ao, pela orienta¸c˜ao, por ajudar na minha forma¸c˜ao e pela amizade.
Ao prof. Jorge Dantas de Melo por sempre estar disposto a ajudar, pelas colabora¸c˜oes e sugest˜oes.
Ao amigo Allan de Medeiros Martins, pela ajuda, dicas, id´eias, e-mails respondidos, incentivos, etc...
Aos professores Francisco das Chagas Mota e Pablo Javier Alsina, pela aten¸c˜ao dis-pensada, enquanto coordenadores do PPGEE.
Aos professores e amigos do LECA-DCA.
Um agradecimento especial a Luciana, minha noiva, pelo companheirismo e carinho e por (quase) sempre ser compreensiva enquanto eu estava ocupado com o trabalho. Te amo!
Finalmente a todos que contribu´ıram, direta ou indiretamente, para a conclus˜ao deste trabalho.
A compress˜ao seletiva de imagens tende a ser cada vez mais utilizada, visto que diver-sas aplica¸c˜oes fazem uso de imagens digitais que em alguns casos n˜ao permitem perdas de informa¸c˜oes em certas regi˜oes. Por´em, existem aplica¸c˜oes nas quais essas imagens s˜ao cap-turadas e armazenadas automaticamente, impossibilitando a um usu´ario indicar as regi˜oes da imagem que devem ser comprimidas sem perdas. Uma solu¸c˜ao para esse problema seria a detec¸c˜ao autom´atica das regi˜oes de interesse, um problema muito dif´ıcil de ser resolvido em casos gerais. Em certos casos, no entanto, pode-se utilizar t´ecnicas inteligentes para detectar essas regi˜oes. Esta disserta¸c˜ao apresenta um compressor seletivo de imagens col-oridas onde as regi˜oes de interesse, previamente fornecidas, s˜ao comprimidas totalmente sem perdas. Este m´etodo faz uso da transformada wavelet para descorrelacionar os pixels da imagem, de uma rede neural competitiva para realizar uma quantiza¸c˜ao vetorial, da morfologia matem´atica e do c´odigo adaptativo de Huffman. Al´em da op¸c˜ao da sele¸c˜ao manual das regi˜oes de interesse, existem duas op¸c˜oes de detec¸c˜ao autom´atica: um m´etodo de segmenta¸c˜ao de texturas, onde a textura com maior freq¨uˆencia ´e selecionada para ser a regi˜ao de interesse, e um novo m´etodo de detec¸c˜ao de faces onde a regi˜ao da face ´e com-primida sem perdas. Os resultados mostram que ambos os m´etodos podem ser utilizados com o algoritmo de compress˜ao, fornecendo a este o mapa de regi˜ao de interesse.
There has been an increasing tendency on the use of selective image compression, since several applications make use of digital images and the loss of information in certain regions is not allowed in some cases. However, there are applications in which these images are captured and stored automatically making it impossible to the user to select the regions of interest to be compressed in a lossless manner. A possible solution for this matter would be the automatic selection of these regions, a very difficult problem to solve in general cases. Nevertheless, it is possible to use intelligent techniques to detect these regions in specific cases. This work proposes a selective color image compression method in which regions of interest, previously chosen, are compressed in a lossless manner. This method uses the wavelet transform to decorrelate the pixels of the image, competitive neural network to make a vectorial quantization, mathematical morphology, and Huffman adaptive coding. There are two options for automatic detection in addition to the manual one: a method of texture segmentation, in which the highest frequency texture is selected to be the region of interest, and a new face detection method where the region of the face will be lossless compressed. The results show that both can be successfully used with the compression method, giving the map of the region of interest as an input.
Resumo ii
Abstract iii
Lista de Figuras vi
Lista de Tabelas ix
Lista de Algoritmos x
1 Introdu¸c˜ao 1
1.1 Motiva¸c˜oes . . . 1
1.2 Objetivos . . . 2
1.3 Organiza¸c˜ao da Disserta¸c˜ao . . . 3
2 Imagens Digitais 5 2.1 Introdu¸c˜ao . . . 5
2.2 Modelo de Cores . . . 6
2.2.1 Modelo de Cor RGB . . . 6
2.2.2 Modelo de Cor YUV . . . 7
2.3 M´etodos de Processamento de Imagens Utilizados . . . 8
2.3.1 Histograma . . . 8
2.3.2 Equaliza¸c˜ao de Histograma . . . 9
2.3.3 Auto-Contraste . . . 10
2.3.4 Transformada de Hotelling (KLT) . . . 11
3.2 Compress˜ao de Imagens . . . 17
3.2.1 Redundˆancia de Codifica¸c˜ao . . . 17
3.2.2 Redundˆancia Interpixel . . . 17
3.2.3 Redundˆancia Psicovisual . . . 17
3.3 Crit´erios de Fidelidade . . . 18
3.4 Compress˜ao sem Perdas . . . 19
3.4.1 Codifica¸c˜ao Adaptativa de Huffman . . . 20
3.4.2 Codifica¸c˜ao de Comprimento de Varredura . . . 21
3.5 Compress˜ao com Perdas . . . 21
4 A Transformada Wavelet 23 4.1 Introdu¸c˜ao . . . 23
4.2 Vis˜ao Geral . . . 23
4.3 An´alise de Multiresolu¸c˜ao . . . 24
4.4 Transformada Wavelet Discreta . . . 27
4.5 Bancos de Filtros e Wavelets . . . 28
4.5.1 Transformada Wavelet Discreta Utilizando Bancos de Filtros . . . . 28
4.6 Transformada Wavelet Aplicada `as Imagens Digitais . . . 30
4.7 Lifting Scheme . . . 32
5 Redes Neurais 34 5.1 Introdu¸c˜ao . . . 34
5.2 Conceitos B´asicos . . . 34
5.3 Redes Neurais Competitivas . . . 37
5.4 Algoritmo de Treinamento para Espa¸cos Discretos . . . 40
5.5 Quantiza¸c˜ao Vetorial . . . 41
5.6 Reconhecimento de Padr˜oes . . . 42
6 Morfologia Matem´atica 44 6.1 Introdu¸c˜ao . . . 44
6.3 Aplica¸c˜ao dos Operadores Morfol´ogicos . . . 47
7 M´etodo de Compress˜ao Seletiva 50 7.1 Introdu¸c˜ao . . . 50
7.2 Vis˜ao Geral . . . 50
7.3 Compressor com Perdas . . . 53
7.4 Compressor com Perdas Para os Canais U e V . . . 57
7.5 Compressor sem Perdas . . . 57
7.6 Resultados . . . 58
8 Sele¸c˜ao Autom´atica de Regi˜oes de Interesse 62 8.1 Introdu¸c˜ao . . . 62
8.2 Segmenta¸c˜ao de Texturas . . . 62
8.2.1 Resultados da Segmenta¸c˜ao . . . 64
8.3 Detec¸c˜ao de Face . . . 64
8.3.1 Resultados da Detec¸c˜ao de Face . . . 71
9 Resultados e conclus˜oes 74 9.1 Conclus˜oes . . . 76
9.2 Propostas para trabalhos futuros . . . 77
Referˆencias Bibliogr´aficas 78
2.1 Exemplo de imagem digital com a conven¸c˜ao dos eixos utilizada na sua
representa¸c˜ao. . . 6
2.2 Cubo de cores RGB. . . 7
2.3 Uma imagem e o seu histograma. . . 9
2.4 Resultado da equaliza¸c˜ao de histograma. . . 10
2.5 Resultado da aplica¸c˜ao do auto-contraste. . . 11
2.6 Estrutura de vizinhan¸ca utilizada no algoritmo. . . 14
2.7 Exemplo das condi¸c˜oes (a) e (b) do passo 1 do algoritmo. Nesse caso N(p1) = 4 eS(p1) = 3. . . 14
2.8 Uma regi˜ao e o seu respectivo esqueleto. . . 15
3.1 Arvore de´ Huffman juntamente com as probabilidades dos s´ımbolos e os c´odigos dos mesmos. . . 20
3.2 Modelo de um compressor com perdas. . . 22
4.1 Uma mesma imagem em quatro resolu¸c˜oes diferentes. Da esquerda, para a direita e de cima para baixo: a) Vi, b) Vi−1, c) Vi−2 e d)Vi−3. . . 26
4.2 C´alculo dos coeficientes wavelets de expans˜ao. . . 29
4.3 Transformada wavelet discreta utilizando uma estrutura em ´arvore. . . 29
4.4 C´alculo de um n´ıvel da IDWT. . . 30
4.5 Transformada IDWT utilizando uma estrutura em ´arvore. . . 30
4.6 Transformada wavelet de dois n´ıveis aplicada a uma imagem. . . 31
4.7 Resultado de uma transformada wavelet discreta aplicada a uma imagem. . 32
4.8 Diagrama de blocos do lifting scheme. . . 32
5.4 Arquitetura b´asica de uma rede neural competitiva onde cada neurˆonio est´a totalmente conectado aos n´os de entrada (setas preenchidas) e conectados entre si atrav´es de arcos inibidores (setas abertas). . . 38 5.5 Dados a serem classificados. . . 39 5.6 Dados ap´os classifica¸c˜ao com o algoritmo competitivo. Os neurˆonios, no
fim do treinamento, est˜ao marcados com cruzes pretas. . . 40 6.1 Elemento estruturante. . . 46 6.2 Figura Utilizada nos testes. . . 46 6.3 Resultado da dilata¸c˜ao da Figura 6.2 pelo elemento estruturante da Figura
6.1. . . 46 6.4 Resultado da eros˜ao da Figura 6.2 pelo elemento estruturante da Figura 6.1. 47 6.5 Imagem representando um mapa de coeficientes significativos. . . 48 6.6 Operadores utilizados: a) primeira dilata¸c˜ao, b) segunda dilata¸c˜ao e c)
imagem final ap´os eros˜ao. . . 49 7.1 Diagrama de blocos do m´etodo de compress˜ao seletiva de imagens coloridas. 51 7.2 Diagrama de blocos do descompressor. . . 52 7.3 Diagrama de blocos para o compressor com perdas do canal Y. . . 53 7.4 Exemplo do canal Y fornecido como entrada do compressor com perdas. . . 54 7.5 Mapa obtido da etapa de limiariza¸c˜ao. Os pixels brancos representam
coeficientes significantes. . . 55 7.6 Resultado da aplica¸c˜ao dos operadores morfol´ogicos. . . 55 7.7 Resultado da quantiza¸c˜ao vetorial do mapa de coeficientes significantes. . . 56 7.8 Diagrama de blocos do compressor sem perdas. . . 58 7.9 Resultados da compress˜ao com perdas para algumas imagens. . . 59 7.10 Peppers original e comprimida com taxa de compress˜ao 10,52 e PSNR 21,69. 59 7.11 Airplane F-16 original e comprimida com taxa de compress˜ao 10,43 e PSNR
31,35. . . 60
7.13 Orf virus lesions com as les˜oes comprimidas sem perdas e taxa de
com-press˜ao de 10,76. . . 61
8.1 Diagrama de blocos do m´etodo de segmenta¸c˜ao de texturas. . . 63
8.2 Imagem sint´etica de textura o mapa resultante da segmenta¸c˜ao autom´atica. 64 8.3 Imagem montada com texturas reais e o mapa resultante. . . 65
8.4 Outra imagem montada com texturas reais e o mapa resultante. . . 65
8.5 Ultima imagem montada com texturas reais e mapa resultante. . . 65´
8.6 Imagem de c´elulas obtida de um microsc´opio eletrˆonico e mapa resultante. 66 8.7 Valores U e V para os pixels de uma imagem. Os pontos azuis s˜ao os pixels de pele. . . 67
8.8 Uma imagem para ser realizada a detec¸c˜ao de face. . . 67
8.9 Mapa de pele obtido ap´os a segmenta¸c˜ao. . . 68
8.10 Mapa de pele obtido ap´os a aplica¸c˜ao dos operadores morfol´ogicos. . . 69
8.11 Mapa de pele ap´os a esqueletiza¸c˜ao e a rota¸c˜ao da regi˜ao da face. . . 70
8.12 Resultado final da rota¸c˜ao de face. . . 70
8.13 Resultados da detec¸c˜ao de face. . . 72
8.14 Resultado da detec¸c˜ao de face em imagens de m´ultiplas faces. . . 73
9.1 Imagem sint´etica de textura com regi˜ao de interesse comprimida sem perdas. 74 9.2 Imagem de c´elulas com as regi˜oes de interesse comprimidas sem perdas. . . 75
9.3 Resultado da compress˜ao da Figura 8.13. . . 75
9.4 Resultado da compress˜ao da Figura 8.14. . . 76
3.1 Escala de notas da “Television Allocations Study Organization”[21] . . . . 18 7.1 Coeficientes do Filtro Wavelet biortogonal SWE(13,7) [28] . . . 54
5.1 Treinamento competitivo . . . 39 8.1 M´etodo de detec¸c˜ao de faces . . . 68
Introdu¸c˜
ao
1.1
Motiva¸c˜
oes
As imagens digitais s˜ao muito difundidas e o seu uso ´e abrangente, sendo utilizadas na medicina, seguran¸ca, educa¸c˜ao, lazer e diversas outras aplica¸c˜oes. Para a transmiss˜ao ou armazenamento das mesmas ´e desej´avel que, devido aos tamanhos dos arquivos, sejam comprimidas. Para isso, existem diversos m´etodos de compress˜ao de imagens que tˆem como objetivo reduzir a quantidade de dados necess´arios para representar uma imagem digital. Essa redu¸c˜ao de dados ´e poss´ıvel atrav´es da identifica¸c˜ao e redu¸c˜ao (ou remo¸c˜ao) das redundˆancias contidas na imagem. A compress˜ao da imagem pode se dar com perda ou sem perda de informa¸c˜ao.
Na compress˜ao com perdas ´e poss´ıvel atingir altas taxas de compress˜ao por´em, existe alguma perda de informa¸c˜ao na imagem. A compress˜ao sem perdas atinge, geralmente, baixas taxas de compress˜ao, mas n˜ao existe perda de informa¸c˜ao, ou seja, na etapa de descompress˜ao a imagem ´e reconstru´ıda perfeitamente.
que sejam poss´ıveis altas taxas de compress˜ao e mesmo assim permitir que a imagem seja utilizada para os fins a que se destina, ´e o uso de t´ecnicas de compress˜ao mistas, onde regi˜oes de interesse s˜ao selecionadas e comprimidas sem perdas e o restante da imagem ´e comprimido com perdas.
O padr˜ao JPEG 2000 [2] permite que sejam escolhidas regi˜oes de interesse. Por´em, este m´etodo n˜ao garante uma reconstru¸c˜ao perfeita das regi˜oes. Ele garante apenas que a regi˜ao de interesse ser´a comprimida com “a m´axima qualidade poss´ıvel” com rela¸c˜ao ao resto da imagem.
Normalmente as regi˜oes de interesse s˜ao definidas manualmente. Em casos em que n˜ao ´e poss´ıvel a existˆencia de um usu´ario, ´e interessante que essas regi˜oes sejam, de alguma forma, determinadas automaticamente. Para um prop´osito geral, essa tarefa ´e muito dif´ıcil. Por´em, podem-se utilizar algumas t´ecnicas em que, para casos espec´ıficos, as regi˜oes de interesse s˜ao determinadas automaticamente. Em [3, 4] mostram-se m´etodos em que as regi˜oes de interesse s˜ao codificadas com diferentes n´ıveis de qualidade. Em [5] mostra-se uma aplica¸c˜ao em que a regi˜ao de interesse ´e automaticamente detectada para um caso espec´ıfico e em [6] um m´etodo em que regi˜oes de interesse s˜ao definidas baseadas nas texturas. Outros trabalhos tratam apenas da codifica¸c˜ao de regi˜oes de interesse como em [7, 8].
1.2
Objetivos
Este trabalho prop˜oe um m´etodo de compress˜ao seletiva de imagens coloridas com a possibilidade de se utilizar em m´ultiplas regi˜oes de interesse. A compress˜ao ´e totalmente sem perdas, possibilitando o uso do m´etodo em aplica¸c˜oes em que n˜ao seja permitido (ou n˜ao recomend´avel) a perda de informa¸c˜oes nessas regi˜oes.
tecidos orgˆanicos, como amostras de folhas ou c´elulas.
Outra op¸c˜ao proposta nesta disserta¸c˜ao ´e a detec¸c˜ao autom´atica de faces. Aqui, as imagens coloridas podem ser em ambientes diferentes, a pessoa pode estar com a face rotacionada em rela¸c˜ao ao plano e pode existir mais de uma pessoa na imagem. Uma exigˆencia ´e que a face seja frontal. Essa aplica¸c˜ao pode ser utilizada em sistemas de seguran¸ca, onde ´e recomend´avel que a regi˜ao da face n˜ao sofra perdas, para que n˜ao possa haver d´uvidas na identifica¸c˜ao da pessoa. O m´etodo que ser´a apresentado ´e baseado no template matching onde ´e feito um pr´e-processamento para tornar o processo mais r´apido. Existem diversas t´ecnicas de detec¸c˜ao de face em imagens coloridas como em [9, 10, 11]. O m´etodo aqui apresentado possui algoritmo de simples implementa¸c˜ao e r´apido processamento.
Por fim, um aplicativo foi desenvolvido para facilitar a utiliza¸c˜ao dos m´etodos anal-isados neste trabalho. Ele permite que as regi˜oes de interesse sejam selecionadas man-ualmente ou utilizando uma das t´ecnicas de sele¸c˜ao autom´atica descritas acima. Deve-se levar em conta contudo que, os m´etodos de sele¸c˜ao autom´atica n˜ao tˆem a necessidade de interven¸c˜ao do usu´ario e s´o est˜ao no aplicativo para fins de testes.
1.3
Organiza¸c˜
ao da Disserta¸c˜
ao
Imagens Digitais
2.1
Introdu¸c˜
ao
Uma imagem em escala de cinza pode ser considerada como uma fun¸c˜ao de intensi-dade luminosa bidimensional, denotada pela fun¸c˜ao f(x, y). O valor da amplitude f nas coordenadas espaciais (x, y) d´a a intensidade (brilho) da imagem naquele ponto. Como a luz ´e uma forma de energia, a fun¸c˜ao f(x, y) ´e definida positiva.
Uma imagem digital ´e uma imagemf(x, y) discretizada tanto em coordenadas espaci-ais quanto em brilho [12]. A digitaliza¸c˜ao das coordenadas espaciespaci-ais (x, y) ´e denominada amostragem da imagem e a digitaliza¸c˜ao da amplitude ´e chamada quantiza¸c˜ao em n´ıveis de cinza. Uma forma de representar a imagem digital ´e na forma de matriz como mostrado na equa¸c˜ao (2.1) onde cada elemento desta matriz armazena um valor correspondente a um n´ıvel de cinza. Cada elemento desta matriz ´e denominado de pixel.
f(x, y) =
f(0,0) f(0,1) · · · f(0, M−1) f(1,0) f(1,1) · · · f(1, M−1)
... ... . .. ...
f(N −1,0) f(N −1,1) · · · f(N −1, M−1)
(2.1)
Figura 2.1: Exemplo de imagem digital com a conven¸c˜ao dos eixos utilizada na sua representa¸c˜ao.
2.2
Modelo de Cores
Os modelos de cores s˜ao sistemas de coordenadas tridimensionais onde uma cor ´e representada por um ´unico ponto [12]. A maioria dos modelos de cores existentes s˜ao para o uso em hardware (como monitores coloridos e impressoras) ou para aplica¸c˜oes envolvendo manipula¸c˜ao de cores. Os modelos mais comuns s˜ao o RGB para monitores e uma ampla classe de cˆameras coloridas; o CMY para impressoras coloridas e o YUV, utilizado na transmiss˜ao de TV e que ser´a mostrado na subse¸c˜ao 2.2.2. Outros modelos de cores s˜ao o HSV e o HSI, utilizados em manipula¸c˜ao de imagens coloridas.
2.2.1
Modelo de Cor RGB
Figura 2.2: Cubo de cores RGB.
a partir da origem. No caso do cubo da Figura 2.2 as cores est˜ao normalizadas entre [0,1]. Imagens no modelo de cores RGB consistem em trˆes planos de imagem independentes, um para cada cor prim´aria. Na compress˜ao de imagens coloridas esse modelo de cor n˜ao ´e interessante de ser utilizado, pois suas camadas s˜ao muito correlacionadas e, para obter vantagens na compress˜ao, deve-se converter a imagem para um espa¸co de cor mais descorrelacionado.
2.2.2
Modelo de Cor YUV
seja necess´aria uma menor banda para a transmiss˜ao em YUV em compara¸c˜ao com RGB (no caso de transmiss˜ao digital, menos bits). A compatibilidade com a TV preto e branco tamb´em ´e garantida pois a componente Y ´e a vers˜ao equivalente em escala de cinza da imagem RGB. A convers˜ao de RGB para YUV [13] ´e definida como:
Y U V =
0.299 0.587 0.114
−0.147 −0.289 0.436 0.615 −0.515 −0.100
· R G B
. (2.2)
Para fazer a transforma¸c˜ao de YUV para RGB ´e necess´ario apenas utilizar a matriz inversa. Esse espa¸co de cor foi utilizado neste trabalho, pois, dessa forma, as componentes U e V, que s˜ao de menor importˆancia, podem utilizar o mapa de coeficientes significantes obtidos da camada Y. Mais detalhes sobre como ´e isso ´e feito ser˜ao apresentados no Cap´ıtulo 7, que trata sobre o m´etodo de compress˜ao seletiva.
2.3
M´
etodos de Processamento de Imagens
Utiliza-dos
Nesse trabalho s˜ao utilizadas algumas t´ecnicas de processamento digital de imagens para que os m´etodos de detec¸c˜ao de face e de segmenta¸c˜ao possam ser utilizados. Al-gumas t´ecnicas s˜ao abordadas nesta se¸c˜ao, a saber: transformada de Hotteling (tamb´em conhecida como transformada Karhunen-L`oeve-KLT), o auto-contraste e a equaliza¸c˜ao de histograma e o algoritmo para encontrar o esqueleto de uma figura bin´aria [12]
2.3.1
Histograma
Seja uma imagem digital em n´ıveis de cinza quantizados em 8 bits. Para essa imagem, ser˜ao poss´ıveis 256 n´ıveis de cinza. Um histograma ´e uma fun¸c˜ao discreta p[rk] = nk/n,
onde rk ´e o k-´esimo n´ıvel de cinza,nk ´e o n´umero de pixels na imagem com esse n´ıvel de
cinza, n ´e o n´umero de pixels da imagem e k = 0,1,2, . . .255.
Ou seja,p[rk] fornece a estimativa de probabilidade da ocorrˆencia do n´ıvel de cinzark
Uma opera¸c˜ao desse tipo ´e chamada de transforma¸c˜ao de histograma, que ´e dada por
s=T(r) (2.3)
onde r ´e um valor de intensidade do pixel de uma imagem e s ser´a o novo valor de intensidade para esse pixel. O que define a transforma¸c˜ao ´e a opera¸c˜ao que se deseja aplicar na imagem.
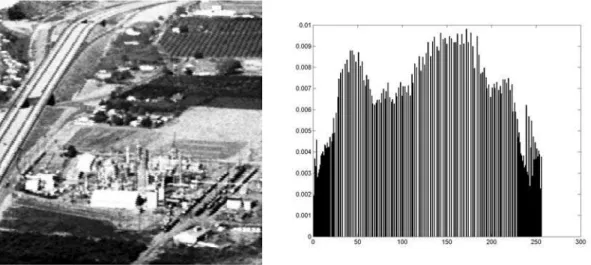
Em imagens coloridas geralmente s˜ao utilizados trˆes histogramas, um para cada ca-mada de cor. N˜ao necessariamente s˜ao utilizados o espa¸co de cor RGB. Dependendo da aplica¸c˜ao da imagem, pode-se utilizar outro espa¸co de cor, como o YUV. A Figura 2.3 [14] mostra uma imagem e o seu respectivo histograma, onde ´e poss´ıvel notar que existe uma certa concentra¸c˜ao de n´ıveis de cinza.
Figura 2.3: Uma imagem e o seu histograma.
2.3.2
Equaliza¸c˜
ao de Histograma
A equaliza¸c˜ao de histograma ´e uma t´ecnica utilizada para obter um histograma uni-forme com a inten¸c˜ao de aumentar o contraste da imagem. A transforma¸c˜ao de histograma que realiza essa fun¸c˜ao ´e definida como [12]
sk =T(rk) = k
X
j=0
nj
n =
k
X
j=0
pr(rj) 0≤rk ≤255 e k= 0,1, ...,255. (2.4)
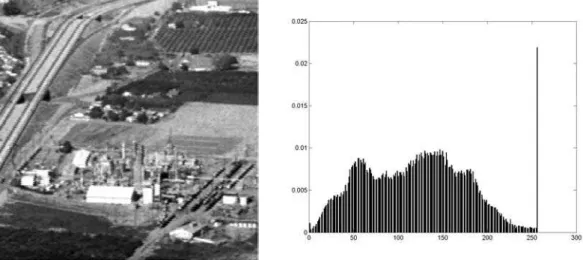
juntamente com o seu histograma, foi obtida a partir de programas implementados para esse trabalho. ´E poss´ıvel notar a ocorrˆencia do “espalhamento” do histograma e um aumento de contraste na imagem.
Figura 2.4: Resultado da equaliza¸c˜ao de histograma.
2.3.3
Auto-Contraste
O auto-contraste, assim como a equaliza¸c˜ao, tem o objetivo de aumentar o contraste da imagem de maneira que se tenha uma certa ocorrˆencia de todos os n´ıveis de cinza. Diferentemente da equaliza¸c˜ao, o auto-contraste n˜ao modifica a forma do histograma por´em ´e necess´ario informar dois parˆametros para a fun¸c˜ao de transforma¸c˜ao que ´e definida como [15]:
T(rk) =
n1 se rk ≤n1
TL(rk) se n1 < rk< n2
n2 se rk ≥n2
(2.5)
n1 e n2 s˜ao os chamados n´ıveis truncados eTL(rk) ´e uma transforma¸c˜ao linear, dado por:
TL(rk) =
255 n2−n1
(rk−n1). (2.6)
Um exemplo da aplica¸c˜ao do auto-contraste ´e mostrado na Figura 2.5 com n1 = 20 e
Figura 2.5: Resultado da aplica¸c˜ao do auto-contraste.
2.3.4
Transformada de Hotelling (KLT)
A transformada de Hotelling baseia-se em propriedades estat´ısticas de representa¸c˜ao de vetores. Ela tem v´arias propriedades ´uteis que a tornam uma importante ferramenta para o processamento de imagens [12]. Seja um conjunto X de vetores do tipo
x= x1 x2 ... xn (2.7)
Ovetor m´edio, do conjunto de vetores, ´e dado por
mX=E{X} (2.8)
em queE{·}´e a fun¸c˜ao valor esperado. O valor esperado de um vetor ou matriz ´e obtido ao se tomar o valor esperado de cada um de seus elementos.
A matriz de covariˆancia do conjunto de vetores ´e definida como
Cx=E{(x−mX)(x−mX)T} (2.9)
ondeT indica transposi¸c˜ao de matriz. Se vetorxtem dimens˜aon,Cxe (x−mx)(x−mx)T
s˜ao matrizes de ordem n×n. O elementocii deCx´e a variˆancia de xi, o i-´esimo
compo-nente dos vetoresxno conjunto, e o elementocij deCx´e a covariˆancia entre os elementos
xi e xj desses vetores. A matriz Cx ´e real e sim´etrica e se os elementos xi e xj s˜ao
O vetor m´edio e a matriz de covariˆancia podem ser aproximados por
mx =
1 M
M
X
k=1
xk (2.10)
e
Cx =
1 M
M
X
k=1
xkxTk −mxmxT, (2.11)
onde M ´e o n´umero de amostras.
Como a matriz Cx ´e real e sim´etrica, ´e sempre poss´ıvel encontrar um conjunto de
n autovetores ortonormais [16]. Sejam ei e λi, i = 1,2, . . . , n, os autovetores e
au-tovalores correspondentes de Cx, em ordem decrescente de modo que λj ≥ λj+1 para
j = 1,2, . . . , n−1. Seja Auma matriz cujas linhas s˜ao formadas a partir dos autovetores de Cx, ordenados de maneira que a primeira linha corresponda ao maior autovalor e a
´
ultima, ao menor autovalor.
A transformada de Hotteling se d´a mapeando os vetores x em vetores y de acordo com
y=A(x−mx) (2.12)
a m´edia dos vetores y resultantes dessa transforma¸c˜ao ´e zero, my = 0, e a matriz de
covariˆancia pode ser obtida em termos de A e Cx atrav´es de
Cy=ACxAT. (2.13)
A matriz Cy ´e uma matriz diagonal, onde os elementos ao longo da diagonal principal
s˜ao os autovalores de Cx:
Cy=
λ1 0
λ2
. ..
0 λn
(2.14)
Como os elementos fora da diagonal principal s˜ao zero, os elementos do vetor y s˜ao descorrelacionados. Al´em disso as matrizes Cy e Cx possuem os mesmos autovalores e
mesmos autovetores.
No primeiro caso ela ´e utilizada para descorrelacionar as camadas de cores R, G e B. Nesse caso, o conjunto de vetores de entrada ser˜ao os pixels de cada uma camada de cor e a sa´ıda ser´a uma nova imagem com as camadas de cores descorrelacionadas. Para o segundo caso, ela ´e utilizada para detectar se uma face est´a rotacionada e o seu ˆangulo de rota¸c˜ao. Para isso os vetores de entrada ser˜ao dois, um para as coordenadas do eixo x e outro para as coordenadas do eixo y dos locais dos pixels em que s˜ao identificados como pele. A partir dos autovetores da matriz de correla¸c˜ao Cx, ´e poss´ıvel encontrar o ˆangulo
e a rela¸c˜ao entre a largura e a altura da regi˜ao de pele para identificar regi˜oes que n˜ao s˜ao faces, como, por exemplo, um bra¸co.
2.3.5
Algoritmo de Esqueletiza¸c˜
ao
A esqueletiza¸c˜ao ´e aplicada em imagens bin´arias para encontrar o esqueleto de uma regi˜ao. A esqueletiza¸c˜ao consiste em reduzir uma regi˜ao planar a um grafo. Essa opera¸c˜ao ´e utilizada em diversos problemas de processamento de imagem como inspe¸c˜ao autom´atica de circuitos el´etricos e em aplica¸c˜oes m´edicas [12, 17].
O algoritmo utilizado nesse trabalho foi a transforma¸c˜ao do eixo m´edio (Medial Axis Transform - MAT) [18]. A MAT de uma regi˜ao R com borda B ´e definida da seguinte forma: para cada ponto pem R, encontramos seu vizinho mais pr´oximo emB. Septiver mais de um vizinho desse tipo, ent˜ao diz-se que ele pertence ao eixo m´edio (ou esqueleto) de R. O conceito de “mais pr´oximo” depende da m´etrica utilizada. Nesse trabalho foi utilizada a distˆancia Euclidiana. O algoritmo utilizado para encontrar a MAT apaga iterativamente os pontos de borda de uma regi˜ao respeitando algumas restri¸c˜oes nas quais a elimina¸c˜ao desses pontos n˜ao deve ocorrer: (1) remo¸c˜ao de pontos extremos; (2) quebra de conectividade; (3) causar a eros˜ao excessiva da regi˜ao.
Assume-se que as regi˜oes bin´arias s˜ao compostas por pixels de valor 1 e o fundo de pixels de valor 0. O m´etodo consiste na aplica¸c˜ao sucessiva de dois passos aos pontos de contorno da regi˜ao. Um ponto de contorno ´e um pixel de valor 1 que possua ao menos um vizinho de 8 com valor 0. Seja um pixel p1; a Figura 2.6 mostra os seus vizinhos de
condi¸c˜oes forem satisfeitas:
(a) 2≤N(p1)≤6;
(b) S(p1) = 1;
(c) p2·p4 ·p6 = 0;
(d) p4·p6·p8 = 0
(2.15)
em que N(p1) ´e o n´umero de vizinhos n˜ao nulos de p1, e S(p1) ´e o n´umero de transi¸c˜oes
0-1 na seq¨uˆencia ordenada, p2, p3, . . . , p8, p9, p2. Por exemplo, N(p1) = 4 e S(p1) = 3 na
Figura 2.7.
p9 p2 p3
p8 p1 p4
p7 p6 p5
Figura 2.6: Estrutura de vizinhan¸ca utilizada no algoritmo.
0 0 1
1 p1 0
1 0 1
Figura 2.7: Exemplo das condi¸c˜oes (a) e (b) do passo 1 do algoritmo. Nesse casoN(p1) = 4
e S(p1) = 3.
No segundo passo, as condi¸c˜oes (a) e (b) continuam as mesmas, mas as condi¸c˜oes (c) e (d) s˜ao modificadas para
(c´) p2·p4·p8 = 0;
(d´) p2·p6·p8 = 0.
(2.16)
Compress˜
ao
3.1
Introdu¸c˜
ao
Hoje em dia as informa¸c˜oes digitais j´a fazem parte das nossas vidas e as usamos em nosso trabalho, para o nosso entretenimento, para obter informa¸c˜oes, etc. Sinais digitais possuem algumas vantagens em rela¸c˜ao aos anal´ogicos: s˜ao f´aceis de serem armazenados e transmitidos a longas distˆancias sem acumular distor¸c˜oes e o armazenamento apresenta maior resistˆencia a degrada¸c˜oes [19].
Por´em, dados digitais em sua forma natural, ou seja, sem nenhuma forma de com-press˜ao ou processamento, tendem a necessitar de muitos bits para serem representados. Por exemplo, uma imagem colorida digital com a resolu¸c˜ao de 1024×768 pixels e 24 bits/pixel necessita de mais de 2 Mbytes para ser representada.
Compress˜ao de dados permite a representa¸c˜ao digital eficiente de um sinal, ou seja, ´e a representa¸c˜ao de um sinal, de forma digital, utilizando a menor quantidade de bits poss´ıvel, mantendo-se ainda uma qualidade aceit´avel. O sinal pode representar dados, imagens est´aticas, voz, ´audio, v´ıdeo ou qualquer informa¸c˜ao que necessita ser transmitida ou armazenada. A compress˜ao de dados pode ser de duas formas: sem perdas, onde o sinal ´e reconstru´ıdo de forma perfeita ou com perdas onde a reconstru¸c˜ao n˜ao ´e perfeita
3.2
Compress˜
ao de Imagens
A maioria dos sinais digitais possui redundˆancias quando est˜ao em seu estado natural e as imagens digitais n˜ao fogem `a regra. Existem, basicamente, trˆes redundˆancias que podem ser identificadas e exploradas [12]: redundˆancia de codifica¸c˜ao, redundˆancia inter-pixels e redundˆanciapsicovisual. O objetivo de um compressor ´e eliminar ou reduzir uma ou mais dessas redundˆancias. A seguir, cada uma delas ser´a explicada.
3.2.1
Redundˆ
ancia de Codifica¸c˜
ao
Em uma codifica¸c˜ao bin´aria natural (por exemplo, codifica¸c˜ao em n´ıveis de cinza) ´e atribu´ıdo o mesmo n´umero de bits tanto para os valores de cinza menos prov´aveis quanto para os mais prov´aveis. Quando isto ocorre diz-se que existe a redundˆancia de codifica¸c˜ao. Uma maneira de reduzir ou eliminar esta redundˆancia ´e atribuir c´odigos bin´arios adequados de acordo com a probabilidade de ocorrˆencia de determinado n´ıvel de cinza: c´odigos bin´arios menores para valores que ocorrem com mais freq¨uˆencia e c´odigos bin´arios maiores para os que ocorrem com menos freq¨uˆencia.
3.2.2
Redundˆ
ancia Interpixel
Esta redundˆancia ´e mais diretamente ligada a imagem em si e n˜ao a forma como cada pixel ´e representado. Ela ocorre quando o valor de algum pixel (ou um valor aproximado) pode ser previsto, por exemplo, pelo valor de seus vizinhos. Diz-se ent˜ao que estes pixels s˜ao correlacionados. Portanto, a informa¸c˜ao trazida por este pixel ´e muito pouca ou nenhuma. Para eliminar esta redundˆancia utiliza-se, na pr´atica, uma transformada nos pixels da imagem. A imagem resultante geralmente perde o aspecto original, por´em ela pode ser reconstru´ıda aplicando-se a transformada inversa. No dom´ınio da transformada, ´e poss´ıvel identificar os pixels que trazem poucas informa¸c˜oes e elimin´a-los sem que haja perdas significativas na imagem.
3.2.3
Redundˆ
ancia Psicovisual
regi˜oes como as bordas de uma imagem s˜ao de interesse especial para o sistema de vis˜ao. Esta redundˆancia pode ser reduzida fazendo a quantiza¸c˜ao de n´ıveis de cinza dos pixels. Isto causa perda de dados da imagem, por´em a perda de informa¸c˜ao pode ser pouca. Por exemplo, o m´etodo de quantiza¸c˜ao em n´ıveis de cinza melhorada (IGS - ”Improved Gray-Scale quantization”) [20] reduz uma imagem com 256 n´ıveis de cinza em uma equivalente de 16 n´ıveis sem que haja uma perda visivelmente significativa.
3.3
Crit´
erios de Fidelidade
Existem duas categorias de crit´erios de avalia¸c˜ao da qualidade de uma imagem com-primida: os objetivos e os subjetivos. Os subjetivos s˜ao feitos apresentando-se a imagem resultante para um determinado n´umero de pessoas e interrogando-as quanto `a qualidade da mesma em rela¸c˜ao `a original, por exemplo, fornecendo notas como mostradas na tabela 3.1.
Tabela 3.1: Escala de notas da “Television Allocations Study Organization”[21]
Valor Nota Descri¸c˜ao
1 Excelente Imagem de qualidade extremamente alta, t˜ao boa quanto se
possa desejar.
2 Boa Imagem de alta qualidade, permitindo visualiza¸c˜ao
agrad´avel. A interferˆencia n˜ao prejudica.
3 Regular Imagem de qualidade aceit´avel. A interferˆencia n˜ao
preju-dica.
4 Limite Imagem de qualidade ruim; vocˆe gostaria de poder melhor´
a-la. A interferˆencia ´e um tanto prejudicial.
5 Inferior Imagem muito ruim, mas vocˆe pode apreci´a-la. Interferˆencia
prejudicial faz-se definitivamente presente.
6 In´util Imagem t˜ao ruim que vocˆe n˜ao pode apreci´a-la.
´e necess´ario um n´umero significativo de pessoas, o que dificulta o uso do mesmo.
Neste trabalho foi utilizado o PSNR (Peak Signal to Noise Ratio - Rela¸c˜ao Pico de Sinal/Ru´ıdo), que ´e um crit´erio objetivo, para aferi¸c˜ao da qualidade das imagens.O PSNR ´e definido como [12]:
P SN R(I,I) = 10ˆ ·log10 255
2
e2
ms(I,I)ˆ
, (3.1)
ondeI´e a imagem original e ˆI´e a imagem resultante da compress˜ao, 255 ´e o valor m´aximo poss´ıvel para a intensidade de um pixel e o e2ms ´e o erro m´edio quadr´atico definido, para
imagens em escala de cinza, como
e2ms = 1 M N M X i=1 N X j=1 h
I(i, j)−I(i, j)ˆ i2, (3.2)
e para imagens em RGB
e2ms = 1 3·M N
M X i=1 N X j=1 X RGB h
I(i, j)−I(i, j)ˆ i2, (3.3)
onde M e N s˜ao as dimens˜oes da imagem e o 3 refere-se as trˆes camadas de cores da imagem.
3.4
Compress˜
ao sem Perdas
As t´ecnicas de compress˜ao sem perdas garantem a reconstru¸c˜ao perfeita do sinal orig-inal [19]. Por exemplo, os arquivos de um computador, quando s˜ao comprimidos para liberar espa¸co do disco r´ıgido, devem ser comprimidos sem perdas. Em imagens, algumas aplica¸c˜oes tamb´em n˜ao permitem perda de dados. Imagens m´edicas para diagn´ostico n˜ao podem ser comprimidas com perdas, seja por motivos legais (de acordo com o sistema legal de alguns pa´ıses) ou por medo do m´edico de fazer um diagn´ostico errado [1].
3.4.1
Codifica¸c˜
ao Adaptativa de
Huffman
Uma das t´ecnicas mais populares de compress˜ao sem perdas ´e a codifica¸c˜ao adaptativa de Huffman [22]. O que este algoritmo faz ´e fornecer para s´ımbolos que ocorrem com mais freq¨uˆencia c´odigos bin´arios de comprimento menor e para s´ımbolos menos freq¨uentes c´odigos bin´arios maiores. O algoritmo de Huffman cria o c´odigo ´otimo para o conjunto de s´ımbolos e probabilidades sob a restri¸c˜ao de que os s´ımbolos sejam codificados um por vez.
Uma vez que o c´odigo tenha sido criado, a codifica¸c˜ao/decodifica¸c˜ao ´e feita a partir de uma tabela gerada de uma ´arvore denominada m´ınima ou de Huffman. Um exemplo desta ´arvore ´e mostrado na Figura 3.1 onde tamb´em s˜ao mostradas as probabilidades de ocorrˆencia de cada s´ımbolo. O c´odigo gerado ´e um c´odigo prefixado, onde nenhum c´odigo ´e prefixo de outro. Dessa forma, qualquer cadeia de s´ımbolos codificados utilizando-se o algoritmo Huffman pode ser decodificada atrav´es do exame de s´ımbolos individuais da esquerda para a direita.
Figura 3.1: ´Arvore de Huffman juntamente com as probabilidades dos s´ımbolos e os c´odigos dos mesmos.
Por exemplo, seja o c´odigo bin´ario da Figura 3.1 e uma cadeia 010100111100 codificada por ele. A primeira palavra codificada seria a 01010, que ´e o c´odigo da palavra s´ımbolo a3. O pr´oximo c´odigo v´alido ´e 011, que corresponde aa1. Se o processo for continuado o
3.4.2
Codifica¸c˜
ao de Comprimento de Varredura
A codifica¸c˜ao de comprimento de varredura [12] consiste em trocar uma seq¨uˆencia de s´ımbolos pelo n´umero de vezes que o s´ımbolo se repete seguido do pr´oprio s´ımbolo. Por exemplo, seja o conjunto de caracteres abaixo:
AAF F F CDDDAAADDDDDCCCF F F F BBBB a vers˜ao codificada da cadeia acima poderia ser:
2A3F1C3D3A5D3C4F4B
Este m´etodo simples torna-se eficiente quando o c´odigo a ser comprimido possui muitas repeti¸c˜oes, e este ´e justamente o caso em que este m´etodo ´e utilizado no trabalho. Como ser´a visto no Cap´ıtulo 7, a codifica¸c˜ao de comprimento de varredura ´e utilizada para comprimir o mapa de regi˜oes de interesse que ´e uma imagem bin´aria composta por muitos bits zeros e algumas regi˜oes contendo bits uns.
3.5
Compress˜
ao com Perdas
Os m´etodos de compress˜ao com perdas [12], ao contr´ario dos m´etodos de compress˜ao sem perdas, podem atingir altas taxas de compress˜ao em detrimento da perda de in-forma¸c˜ao da imagem que, em alguns casos, pode ser at´e impercept´ıvel ao ser humano. Estes m´etodos s˜ao divididos em dois tipos principais: a codifica¸c˜ao previsora com per-das e a codifica¸c˜ao por transformada. S´o ser´a discutida neste trabalho a compress˜ao por transformada.
a imagem ´e novamente obtida. Em imagens naturais, ap´os a transformada, o n´umero de coeficientes de baixa magnitude ´e grande e os mesmos podem ser quantizados de maneira grosseira ou at´e mesmo descartados, obtendo-se assim altas taxas de compress˜ao, com perda aceit´avel de qualidade.
Figura 3.2: Modelo de um compressor com perdas.
A Transformada Wavelet
4.1
Introdu¸c˜
ao
A transformada wavelet que ´e uma ferramenta matem´atica vers´atil com um conte´udo muito rico e com um grande potencial de aplica¸c˜oes [23]. Entre outras aplica¸c˜oes, ela ´e usada em processamento de sinais, compress˜ao de imagens, processos estoc´asticos, es-tat´ıstica, economia e geologia [24]. Al´em de abordar um pouco da teoria sobre wavelets, neste Cap´ıtulo ser˜ao discutidos a an´alise em multiresolu¸c˜ao, bancos de filtros e transfor-mada wavelet e aplica¸c˜oes desta transfortransfor-mada em compress˜ao de imagens.
4.2
Vis˜
ao Geral
A transformada de um sinal consiste em mapear o mesmo de seu dom´ınio original para o dom´ınio da transformada. Dessa forma ´e poss´ıvel observar propriedades do sinal que seriam mais dif´ıceis ou imposs´ıveis de serem observadas no dom´ınio original. A trans-formada wavelet possui a caracter´ıstica de decompor o sinal em diferentes componentes de freq¨uˆencia, permitindo o estudo de cada componente separadamente. Dessa forma, diferentemente da transformada de Fourier, que perde completamente a dependˆencia en-tre tempo e espa¸co, a transformada wavelet ´e capaz de obter informa¸c˜oes tanto sobre a freq¨uˆencia quanto sobre o tempo.
A transformada wavelet [25] decomp˜oe um sinal em dilata¸c˜oes e transla¸c˜oes de wavelets. Uma wavelet ´e uma fun¸c˜aoψ ∈L2(
R), ondeL2(
integr´avel cuja energia ´e limitada e de m´edia zero:
Z +∞
−∞
ψ(t)dt = 0. (4.1)
Ela ´e normalizada kψk = 1, com o seu centro em t = 0. A fun¸c˜ao ψ ´e tamb´em chamada wavelet-m˜ae e uma fam´ılia de wavelets s˜ao geradas a partir dela escalando em s e transladando, no tempo, por u:
ψu,s(t) =
1
√
sψ
t−u s
. (4.2)
Essas wavelets geradas continuam normalizadas,kψu,sk= 1. A transformada wavelet
de f ∈L2(
R) no tempo u em escala s ´e definida como: W f(u, s) =hf, ψu,si=
Z +∞
−∞
f(t)√1
sψ
∗
t−u s
dt. (4.3)
onde hf, ψu,si representa o produto interno de f e ψu,s e ψ∗ representa o complexo
conjugado de ψ.
4.3
An´
alise de Multiresolu¸c˜
ao
Uma importante caracter´ıstica da transformada wavelet ´e a multiresolu¸c˜ao [26]. Uti-lizando a resolu¸c˜ao adequada de um sinal, permite-se que sejam processados somente os detalhes relevantes para uma determinada tarefa. Nesta se¸c˜ao ser˜ao discutidos alguns aspectos da multiresolu¸c˜ao.
O conceito de multiresolu¸c˜ao ´e baseado em cinco princ´ıpios b´asicos [27]:
1. Existe uma seq¨uˆencia de subespa¸cos aninhados contidos em L2(R) cada qual
repre-sentando uma resolu¸c˜ao,
V−∞· · · ⊂V−1 ⊂V0 ⊂V1 ⊂. . . V∞=L2(R). (4.4)
Cada subespa¸coVipossui diferentes vetores de bases, os quais determinam diferentes
n´ıveis de resolu¸c˜ao no tempo/espa¸co. Quanto maior o ´ındice, a resolu¸c˜ao torna-se mais refinada;
2. Existe uma fun¸c˜aoϕ(t), chamada fun¸c˜ao de escala, que, com os seus deslocamentos no tempo, formam a base ortonormal do subespa¸co V0,
3. A mudan¸ca de subespa¸cos de escalas adjacentes ´e feita de acordo com a seguinte propriedade:
f(t)∈Vi ⇐⇒f(2t)∈Vi+1; (4.6)
4. Deslocamentos no tempo de um sinalf(t)∈Vi est˜ao restritos ao mesmo subespa¸co
Vi. Esta propriedade ´e chamada invariˆancia do deslocamento frente `as escalas,
f(t)∈Vi =⇒f(t−n)∈Vi,∀n∈Z; (4.7)
5. O espa¸co L2(R) cont´em todos os subespa¸cos e portanto ´e o espa¸co de maior
reso-lu¸c˜ao. E a ´unica fun¸c˜ao que pode ser representada em qualquer escala ´e a fun¸c˜ao nula,
[
i∈Z
Vi =L2(R) e
\
i∈Z
Vi ={0}. (4.8)
A partir das propriedades descritas acima ´e poss´ıvel provar que a base ortonormal para cada subespa¸co Vi pode ser constru´ıda, a partir do prot´otipoϕ(t), base deV0, como
mostrado abaixo
ϕi,k = 2i/2ϕ(2it−k), i, k∈Z (4.9)
onde o fator 2i/2 ´e usado para garantir a norma unit´aria.
A partir de ϕ(t) ∈ V0, V0 ⊂ V1 e 21/2ϕ(2t−k) ser base ortonormal de V1, pode-se
escrever ϕ(t) como combina¸c˜ao linear de ϕ(2t−k), k ∈Z, de acordo com
ϕ(t) = X
k
h0[k]·21/2ϕ(2t−k), k∈Z (4.10)
onde h0[k] s˜ao os coeficientes de escala.
A partir das bases anteriores, um sinal f(t)∈Vi pode ser representado como:
f(t) = X
m
αi(m)·ϕi,m(t). (4.11)
Com os coeficientes de expans˜ao
αi(m) = hf(t), ϕi,m(t)i. (4.12)
espa¸co. As imagens resultantes foram obtidas utilizando algoritmos implementados para este trabalho.
Uma fun¸c˜aoϕ(2i+1t) ´e comprimida por um fator 2 no eixo do tempo em compara¸c˜ao
com a fun¸c˜ao ϕ(2it). Ent˜ao um sinal em um espa¸co V
i+1 tem o dobro da resolu¸c˜ao de um
sinal em um espa¸co Vi.
Figura 4.1: Uma mesma imagem em quatro resolu¸c˜oes diferentes. Da esquerda, para a direita e de cima para baixo: a) Vi, b) Vi−1, c) Vi−2 e d)Vi−3.
A partir da Figura 4.1 ´e clara a perda de qualidade (informa¸c˜ao) entre as imagens de resolu¸c˜oes mais baixas. Estas informa¸c˜oes perdidas s˜ao, ent˜ao, representadas em um subespa¸co complementar: para todo subespa¸co Vi ⊂Vi+1, existe um subespa¸co ortogonal
Wi de tal forma que Vi+1 pode ser representado como uma soma direta, indicada pelo
s´ımbolo ⊕, o que significa que qualquer elemento em Vi+1 pode ser expresso como uma
soma de dois elementos ortogonais, um de Vi e outro de Wi:
Vi+1 =Vi⊕Wi, i∈Z. (4.13)
Oespa¸co complementar Wi ´e gerado por uma base ortonormal
onde ψ(t) ´e a wavelet-m˜ae. Portanto, uma fun¸c˜ao f(t)∈Wi pode ser escrita como
f(t) = X
m
βi(m)·ψi,m(t), (4.15)
onde
βi(m) =hf(t), ψi,m(t)i. (4.16)
ComoWi ⊂Vi+1, a fun¸c˜ao f(t) pode tamb´em ser expandida em termos de fun¸c˜oes de
escalaϕi+1,k(t) do espa¸coVi+1. A wavelet-m˜ae, comi=k= 0, pode tamb´em ser expressa
utilizando a base do espa¸co V1:
ψ(t) =Xh1(n)ϕ(2t−n). (4.17)
O espa¸coVi em (4.13) pode tamb´em ser decomposto em uma soma diretaVi =Vi−1⊕
Wi−1, assim como o espa¸co Vi−1 e assim por diante. A decomposi¸c˜ao do espa¸co L2(R) de
acordo com (4.4) pode tamb´em ser reescrita como:
L2(R) =Vj⊕Wj⊕Wj+1⊕ · · · ⊕W−1⊕W0⊕W1⊕ · · · (4.18)
O ´ındice j ´e arbitr´ario e denota a profundidade da decomposi¸c˜ao.
A proje¸c˜ao de uma fun¸c˜ao f(t) ∈ L2(R) em subespa¸cos de acordo com (4.18)
cor-responde a transformada wavelet. Essencialmente, esta proje¸c˜ao consiste em calcular os coeficientes de expans˜ao. A expans˜ao de uma fun¸c˜aof(t) em termos de fun¸c˜oes escalares e wavelets, a partir de (4.18), (4.11) e (4.15), ´e
f(t) = X
m
αj(m)ϕj,m(t) +
∞ X
i=j
X
m
βi(m)ψi,m(t). (4.19)
4.4
Transformada Wavelet Discreta
Na pr´atica, os sinais s˜ao projetados em um n´umero finito de subespa¸cos. Neste caso, eles precisam ser elementos de um certo subespa¸co de L2(R). Seja um sinal f(t) tal que:
f(t)∈V0 ⊂L2(R). (4.20)
A decomposi¸c˜ao em (4.18) ´e ent˜ao an´aloga
Se os coeficientes de expans˜ao α0(m) de um sinalf(t)∈V0 s˜ao conhecidos, ent˜ao para
calcular a s´erie de expans˜ao wavelet da fun¸c˜ao ´e necess´ario somente obter αj(m) e βj(m)
a partir de α0(m). Esta ´e uma computa¸c˜ao discreta e tamb´em ´e conhecida como
trans-formada wavelet discreta (Discrete Wavelet Transform - DWT). A seguir, ser´a mostrado como obter a transformada wavelet discreta e a sua inversa a partir de bancos de filtros.
4.5
Bancos de Filtros e Wavelets
A utiliza¸c˜ao conjunta de wavelets e bancos de filtros de reconstru¸c˜ao perfeita leva a uma implementa¸c˜ao computacional eficiente da DWT e estabelece um significado pr´atico para esta transformada [27].
4.5.1
Transformada Wavelet Discreta Utilizando Bancos de
Fil-tros
Ser´a mostrado aqui como ´e feita a computa¸c˜ao dos coeficientes de expans˜ao da proje¸c˜ao de um sinal em um espa¸co Vi+1 nos subespa¸cosVi eWi atrav´es de um banco de filtros de
dois canais.
Inicialmente, tem-se o sinal f(t) =X
n
αi+1(n)·ϕi+1,n(t)∈Vi+1, (4.22)
cujos coeficientes αi+1(n) devem ser conhecidos. Como Vi+1 = Vi⊕Wi, este sinal pode
ser expandido como combina¸c˜oes das bases de Vi e Wi:
f(t) = X
n
αi(m)·ϕi,m+
X
m
β(m)·ψi,m(t). (4.23)
Na pr´atica, deve-se calcular os coeficientes desconhecidos αi(m) e βi(m) a partir dos
coeficientes conhecidos αi+1(m) Esse c´alculo pode ser feito fazendo a convolu¸c˜ao dos
coeficientes αi+1(m) com as s´eries h0(−n) e h1(−n), respectivamente, e, em seguida,
fazendo uma subamostragem por um fator 2:
αi(m) = h0(−n)∗αi+1(n)|n=2m; (4.24)
onde ∗ indica a opera¸c˜ao de convolu¸c˜ao.
A Figura 4.2 esquematiza este processo. Portanto, o c´alculo dos coeficientes da decom-posi¸c˜ao de um sinal ´e feito por um banco de filtros de an´alise com respostas ao impulso h0(−n) eh1(−n). O sinalf(t)∈Vi+1 possui o dobro da resolu¸c˜ao comparado com as suas
proje¸c˜oes. Por´em, os coeficientes de expans˜ao αi(m) e βi(m) necessitam da metade das
amostras dos coeficientes αi+1(m).
Figura 4.2: C´alculo dos coeficientes wavelets de expans˜ao.
A proje¸c˜ao de Vi+1 em Vi corresponde a uma filtragem passa-baixa e a proje¸c˜ao em
Wi a uma filtragem passa-alta. Ent˜ao h0(−n) ´e um filtro passa-baixa digital e h1(−n) ´e
um filtro passa-alta digital complementar associado.
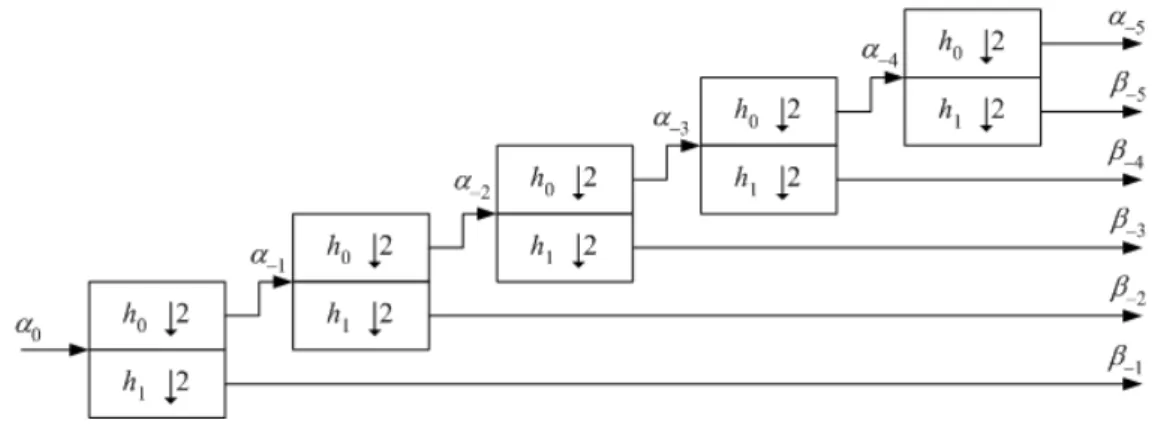
Se forem conectados, repetidamente, bancos de filtros de an´alise de dois canais nas sa´ıdas passa-baixa do banco mostrado na Figura 4.2, ent˜ao a decomposi¸c˜ao se dar´a de acordo a Figura 4.3 em um esquema estruturado em ´arvore.
Figura 4.3: Transformada wavelet discreta utilizando uma estrutura em ´arvore. Os coeficientesβ−1 at´eβ−5, das wavelets, podem ser pensados como sinais discretos de
alta freq¨uˆencia enquanto o coeficiente α−5, da fun¸c˜ao de escala, pode ser pensado como
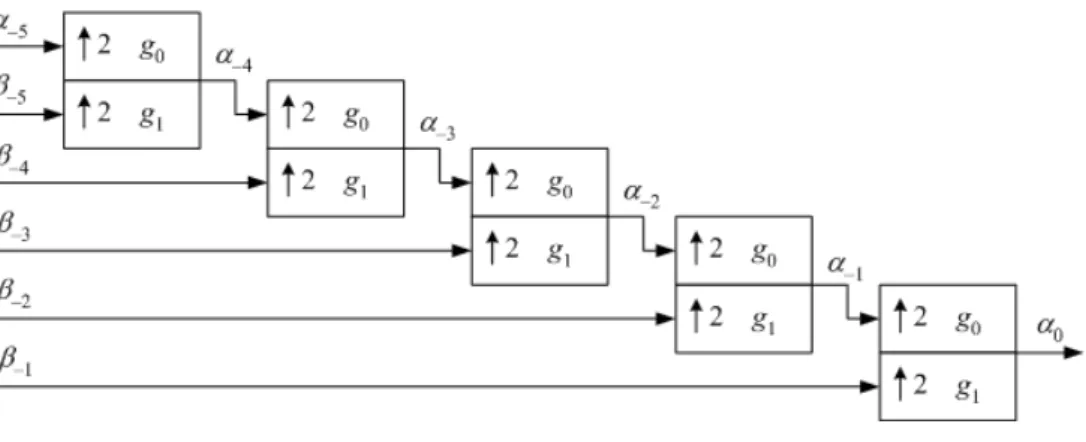
Atransformada wavelet discreta inversa(Inverse Discrete Wavelet Transform- IDWT) ´e feita utilizando bancos de filtros de s´ıntese. Ela ´e feita unindo dois sinais dos subespa¸cos Vi e Wi em um sinal do subespa¸co Vi+1. Isso faz com que o novo sinal possua o dobro da
resolu¸c˜ao dos sinais anteriores.
A Figura 4.4 mostra como ´e feita esta uni˜ao. Assim como na Figura 4.3, a transformada wavelet discreta inversa tamb´em faz uso de um esquema estruturado em ´arvore, como mostrado na Figura 4.5.
Figura 4.4: C´alculo de um n´ıvel da IDWT.
Figura 4.5: Transformada IDWT utilizando uma estrutura em ´arvore.
4.6
Transformada Wavelet Aplicada `
as Imagens
Dig-itais
cada n´ıvel de decomposi¸c˜ao obtido pela transformada wavelet unidimensional, alternamos a dire¸c˜ao processada.
Por exemplo, suponha primeiramente as linhas de uma imagem contidas no espa¸coV0
ap´os aplicada a transformada nas linhas, elas passar˜ao para os subespa¸cos V−1 e W−1.
Fazendo o mesmo processo agora para as colunas passaremos elas do espa¸co V0 para os
subespa¸cos V−1 e W−1. Ap´os isso estar´a terminado um n´ıvel da transformada wavelet
aplicada `a imagem. A imagem original no espa¸co V0×V0 passar´a a ser quatro subimagens
nos subespa¸cos V−1×V−1, V−1×W−1,W−1×V−1 e W−1×W−1. Para um segundo n´ıvel
da transformada wavelet o mesmo procedimento deve ser feito agora para a subimagem contida no espa¸co V−1 ×V−1. Feito isso, a subimagem ser´a substitu´ıda por mais quatro
novamente, que por sua vez estar˜ao nos subespa¸cos V−2×V−2, V−2×W−2, W−2×V−2 e
W−2×W−2. A Figura 4.6 mostra o esquema da transformada wavelet de 2 n´ıveis em uma
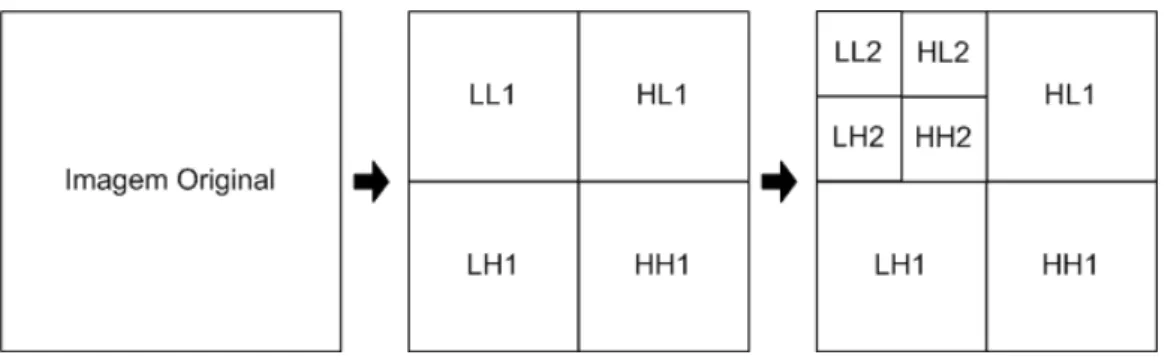
imagem, L significa baixas freq¨uˆencias e o H altas freq¨uˆencias, ent˜ao LL1 ´e o subespa¸co V−1×V−1, LH1 ´e o V−1×W−1 e assim por diante. J´a a Figura 4.7 mostra a transformada
wavelet de 3 n´ıveis aplicada `a imagem de Lena [14], onde a imagem resultante foi obtida a partir de software implementado para este trabalho.
Figura 4.6: Transformada wavelet de dois n´ıveis aplicada a uma imagem.
Depois de aplicada a transformada wavelet, o resultado ser´a uma subimagem composta por coeficientes do subespa¸coV−j×V−j, ondej´e o n´ıvel da transformada wavelet, e v´arios
Figura 4.7: Resultado de uma transformada wavelet discreta aplicada a uma imagem.
wavelet ´e uma ´otima ferramenta para a compress˜ao de imagens digitais.
4.7
Lifting Scheme
A transformada wavelet utilizando olifting scheme ´e tamb´em chamada de wavelet de segunda gera¸c˜ao por possuir vantagens (como velocidade, por exemplo) sobre a transfor-mada tradicional mostrada anteriormente [28]. O diagrama de blocos dessa transfortransfor-mada ´e mostrado na Figura 4.8. Esse processo envolve basicamente trˆes passos: separa¸c˜ao, predi¸c˜ao e atualiza¸c˜ao.
Figura 4.8: Diagrama de blocos do lifting scheme.
pares e a outra as ´ımpares. Ou seja:
αi(n) = αi+1(2n)
βi(n) = αi+1(2n+ 1)
(4.26)
Na predi¸c˜ao, a informa¸c˜ao contida na seq¨uˆencia ´ımpar βi(n) ´e subtra´ıda por uma
predi¸c˜ao baseada em αi(n):
βi(n) =βi(n)−
X
m
e
sni(m)αi(m) (4.27)
onde sen
i(m) s˜ao coeficientes pr´e-definidos conforme o tipo de transformada wavelet
uti-lizada (e.g. Haar, Daubechie, biortogonais, etc).
Dessa forma, a correla¸c˜ao entre αi(n) e βi(n) ´e retirada, deixando um conjunto βi(n)
que pode sofrer um limiar com menor perda de qualidade do que o caso do conjuntoβi(n)
original. Esse passo estabelece os coeficientes da transformada wavelet no n´ıvel i como sendo o conjunto βi(n).
A etapa de atualiza¸c˜ao ´e feita para assegurar que propriedades globais do sinal de entrada, como o valor m´edio, sejam herdados por αi(n). A atualiza¸c˜ao ´e feita utilizando
os coeficientes wavelet obtidos do passo anterior:
αi(n) =αi(n)−
X
m
sni(m)βi(m) (4.28)
onde sn
i(m) s˜ao coeficientes pr´e-definidos conforme o tipo de transformada wavelet
uti-lizada.
Para cada tipo de wavelet uma seq¨uˆencia de predi¸c˜oes e atualiza¸c˜oes, com seus respec-tivos coeficientes, ´e necess´aria. Ap´os essa etapa, os coeficientes s˜ao normalizados:
αi(n) = nlαi(n)
βi(n) =nhβi(n)
(4.29)
onde nLnH = 1. Exemplos do uso do lifting scheme para alguns tipos de transformada
Redes Neurais
5.1
Introdu¸c˜
ao
Este Cap´ıtulo ir´a abordar as redes neurais artificiais, que s˜ao tamb´em chamadas sim-plesmente de “redes neurais”. Ser˜ao discutidos detalhes da rede neural competitiva que ´e uma rede neural auto-organiz´avel. Ser´a mostrado o uso dessa rede como um quantizador vetorial e como um classificador de padr˜oes e os algoritmos de treinamento utilizados.
5.2
Conceitos B´
asicos
Uma rede ´e uma m´aquina que deve aprender a realizar uma tarefa particular ou uma fun¸c˜ao de interesse. Para isso as redes neurais empregam uma interliga¸c˜ao maci¸ca de c´elulas computacionais simples denominadas “neurˆonios” ou “unidades de processa-mento”. Haykin [30] define uma rede neural da seguinte forma:
Uma rede neural ´e um processador maci¸camente paralelo distribu´ıdo, constitu´ıdo de
unidades de processamento simples que tˆem a propens˜ao natural para armazenar
conhe-cimento experimental e torn´a-lo dispon´ıvel para o uso. Ele se assemelha ao c´erebro em
dois aspectos:
1. O conhecimento ´e adquirido pela rede a partir de seu ambiente atrav´es de um pro-cesso de aprendizagem.
Outra caracter´ıstica da rede neural artificial que a assemelha ao c´erebro humano ´e que se algum dos seus neurˆonios “morre” a rede pode continuar funcionando bem. Al´em disso, tamb´em podem ser feitas modifica¸c˜oes na arquitetura da rede inserindo-se ou removendo-se neurˆonios. O modelo do neurˆonio artificial ´e mostrado na Figura 5.1, onde xi ´e cada
elemento do vetor xde entrada, wki ´e o peso sin´aptico do neurˆonio k ligado a entrada xi
eϕ(.) ´e uma fun¸c˜ao de ativa¸c˜ao que pode ser uma fun¸c˜ao sigm´oide, tangente sigm´oide ou mesmo uma fun¸c˜ao puramente linear [30].
Figura 5.1: Modelo de um neurˆonio artificial.
O processo de aprendizagem ´e um algoritmo que vai definir como ser˜ao modificados os pesos sin´apticos da rede. Esses algoritmos s˜ao divididos em duas classes principais, ou paradigmas de aprendizagem, que s˜ao a aprendizagem supervisionada e a aprendizagem n˜ao supervisionada. De uma forma geral o processo de aprendizagem ´e da seguinte forma:
1. A rede neural ´e estimulada por um ambiente;
2. A rede neural sofre modifica¸c˜oes nos seus pesos sin´apticos como resultado desta estimula¸c˜ao;
3. A rede neural responde de uma maneira nova ao ambiente, devido `as modifica¸c˜oes ocorridas na sua estrutura interna.
processo de aprendizagem a rede neural deve ter a capacidade de emular o professor e a partir da´ı poder lidar com o ambiente por si mesma. Aplica¸c˜oes de redes neurais desse tipo s˜ao a classifica¸c˜ao de padr˜oes e a aproxima¸c˜ao de fun¸c˜oes. A rede neural mais conhecida para ser utilizada na aprendizagem supervisionada ´e a Perceptron de M´ultiplas Camadas onde o algoritmo de treinamento mais utilizado ´e o algoritmo de retropropaga¸c˜ao (back propagation) [31].
Figura 5.2: Diagrama de blocos da aprendizagem supervisionada.
Apesar de atingir bons resultados, essas redes neurais necessitam sempre da figura do professor que deve conhecer o ambiente e fornecer as respostas ´otimas para determinado est´ımulo do ambiente. Por´em nem sempre ´e poss´ıvel conhecer a resposta ´otima e, para isso, foram desenvolvidos os m´etodos de aprendizagem n˜ao supervisionada.
A aprendizagem n˜ao supervisionada ainda pode ser classificada como aprendizagem por refor¸co e aprendizagem auto-organizada. Na aprendizagem por refor¸co [32] ao inv´es de um professor existe a figura do cr´ıtico que, depois do sistema de aprendizagem sofrer um est´ımulo do ambiente, ´e respons´avel em classificar a¸c˜ao como boa ou ruim aplicando uma penaliza¸c˜ao ou uma recompensa.
Naaprendizagem auto-organizada n˜ao existe nem a figura do professor nem do cr´ıtico, como ´e mostrado na Figura 5.3. A rede tem a habilidade de formar representa¸c˜oes internas para codificar as caracter´ısticas da entrada e, desse modo, de criar automaticamente novas classes [33].
Uma rede neural auto-organiz´avel bastante importante ´e o mapa auto-organiz´avel de Kohonen [34]. Seu principal objetivo ´e transformar um padr˜ao de sinal incidente de di-mens˜ao arbitr´aria em um mapa discreto uni ou bidimensional e realizar esta transforma¸c˜ao adaptativamente de uma maneira topologicamente ordenada. Neste trabalho foi utilizada a rede neural competitiva por oferecer um algoritmo mais simples e r´apido para realizar a quantiza¸c˜ao vetorial.
5.3
Redes Neurais Competitivas
Como o nome sugere, nesta rede neural os neurˆonios “competem” entre si para que somente um neurˆonio esteja ativo quando um determinado est´ımulo do ambiente seja apli-cado `a sua entrada, ao contr´ario da aprendizagem hebbiana [35], onde v´arios neurˆonios da sa´ıda podem estar ativos simultaneamente. Segundo Rumelhart e Zipser [36], exis-tem trˆes elementos b´asicos para que uma regra de aprendizagem possa ser considerada competitiva:
• Um conjunto de neurˆonios que s˜ao todos iguais entre si, exceto pelos pesos sin´apticos distribu´ıdos aleatoriamente, e que por isso respondem diferentemente a um dado conjunto de padr˜oes de entrada;
• Um limite imposto sobre a “for¸ca” de cada neurˆonio;
• Um mecanismo que permita a competi¸c˜ao entre os neurˆonios onde somente um deles estar´a ativo em determinado instante. Este neurˆonio ´e chamado de neurˆonio vencedor leva tudo.
Os neurˆonios da rede aprendem a se especializar em agrupamentos de padr˜oes similares se tornando detectores de caracter´ısticas para classes diferentes de padr˜oes de entrada. A arquitetura mais simples de uma rede neural competitiva ´e mostrada na Figura 5.4 onde todos os neurˆonios est˜ao totalmente conectados aos n´os de entrada e tamb´em conectados uns com os outros atrav´es de arcos inibidores.
Quando um neurˆoniok´e considerado vencedor significa que seu campo local induzido, vk, para um padr˜ao de entradax, ´e o maior dentre todos os neurˆonios da rede. O sinal de
Figura 5.4: Arquitetura b´asica de uma rede neural competitiva onde cada neurˆonio est´a totalmente conectado aos n´os de entrada (setas preenchidas) e conectados entre si atrav´es de arcos inibidores (setas abertas).
´e colocado em 0, ou seja:
yk =
1 se vk> vj para todosj,j 6=k
0 caso contr´ario (5.1)
onde vk indica o qu˜ao pr´oximo o neurˆonio k ´e do padr˜ao de entrada x, que pode ser
definido como o produto interno,
vk = m
X
i=1
wki·xi, (5.2)
ou pela distˆancia euclidiana,
vk =
v u u t m X i=1
[wki−xi]2. (5.3)
Para o caso da distancia euclidiana a regra da equa¸c˜ao (5.1) deve ser modificada para o neurˆonio com menor vk. Nas equa¸c˜oes (5.2) e (5.3) wki representa o peso sin´aptico
conectando o n´o de entrada i ao neurˆonio k.
Segundo aregra de aprendizagem competitiva padr˜aoos neurˆonios considerados perde-dores n˜ao sofrer˜ao nenhuma atualiza¸c˜ao nos pesos sin´apticos. Os pesos sin´apticos do neurˆonio vencedor devem ser atualizados de acordo com a seguinte equa¸c˜ao:
∆wki =η(xj−wki). (5.4)
Algoritmo 5.1 Treinamento competitivo
Entrada: n´umero de neurˆonios, condi¸c˜ao de parada
Enquanton˜ao atingir a condi¸c˜ao de parada Fa¸ca
Sortear um padr˜ao de entrada x
kc ⇐minx=1...kkx−wik {Encontrar o neurˆonio vencedor}
wc(t+ 1) ⇐wc(t) +η(t)·[x(t)−wc(t)]{Atualizar pesos do neurˆonio vencedor}
t =t+ 1
Fim Enquanto
do vetor padr˜ao de entrada x. No Algoritmo 5.1 ´e mostrado um pseudo-algoritmo do treinamento competitivo.
Para exemplificar o funcionamento de uma rede neural competitiva e a sua capacidade de identificar padr˜oes, foi apresentado `a rede o conjunto de dados bidimensionais da Figura 5.5. Neste caso foram utilizados cinco neurˆonios que primeiramente estavam em posi¸c˜oes aleat´orias no espa¸co bidimensional. Na medida que o algoritmo de treinamento ´e executado os neurˆonios “caminham” para regi˜oes centrais dos agrupamentos de dados. O fim do treinamento ´e mostrado na Figura 5.6. ´E poss´ıvel perceber que cada um dos neurˆonios se deslocou para um centro diferente. As figuras foram obtidas a partir de algoritmos implementados para uso neste trabalho.
Figura 5.6: Dados ap´os classifica¸c˜ao com o algoritmo competitivo. Os neurˆonios, no fim do treinamento, est˜ao marcados com cruzes pretas.
As redes neurais competitivas s˜ao muito utilizadas para agrupamento de padr˜oes. Para esse exemplo ´e f´acil para o ser humano identificar que existem cinco regi˜oes bem distintas. Se fosse em um caso de trˆes dimens˜oes j´a seria mais dif´ıcil identificar esses aglomerados e para o caso de quatro ou mais se torna imposs´ıvel identificar os agrupamentos. Entretanto as redes neurais s˜ao capazes de generalizar esse processo para qualquer dimens˜ao.
5.4
Algoritmo de Treinamento para Espa¸cos
Discre-tos
O algoritmo tradicional funciona muito bem em espa¸cos m-dimensionais cont´ınuos, por´em em espa¸cos m-dimensionais discretos e bin´arios o tempo de treinamento torna-se elevado. Como ser´a visto no Cap´ıtulo 7, a rede neural ser´a utilizada em um espa¸co bin´ario e para agilizar o treinamento o algoritmo utilizado n˜ao foi o tradicional.
O algoritmo utilizado foi desenvolvido por Almeida Filho et al. [37] e se comporta muito bem para espa¸cos discretos ou bin´arios. Al´em disso, ele possui todas as carac-ter´ısticas necess´arias, que foram mostradas anteriormente, para ser considerado um algo-ritmo de treinamento competitivo.
um. Assumindo que cada valor de entrada est´a no intervalo {min, . . . , max}(i.e., min≤ xi ≤ max, i = 1,2, . . . , n), o limite imposto a cada neurˆonio ´e n·max. A defini¸c˜ao do
neurˆonio vencedor ´e a mesma do algoritmo tradicional, por´em a atualiza¸c˜ao do mesmo ´e feita de acordo com
∆wki =η·sgn[xk−wki], (5.5)
onde sgn(.) ´e a fun¸c˜ao sinal que assume o valor +1 se o valor do parˆametro for positivo 0 se for zero e −1 se for negativo. O fator de aprendizagem η ´e dado por
η= max−min
m , (5.6)
onde m ´e o n´umero de passos (escolhido arbitrariamente) necess´arios para modificar um peso sin´aptico do seu menor valor para o seu maior valor.
Se o valor demfor escolhido de forma queηseja um n´umero inteiro todas as opera¸c˜oes matem´aticas ser˜ao realizadas com aritm´etica inteira, fazendo que a sua execu¸c˜ao seja mais r´apida.
5.5
Quantiza¸c˜
ao Vetorial
A quantiza¸c˜ao vetorial ´e uma t´ecnica que explora a estrutura subjacente dos vetores de entrada para o prop´osito de compress˜ao de dados [38]. Especificamente, um espa¸co de entrada ´e dividido em um n´umero de regi˜oes distintas e para cada regi˜ao ´e definido um vetor de reconstru¸c˜ao. Quando um novo vetor de entrada ´e apresentado ao quantizador ´e determinada, inicialmente, a regi˜ao na qual o vetor se encontra e ela ´e ent˜ao representada pelo vetor de reconstru¸c˜ao para aquela regi˜ao. Com isso, utilizando uma vers˜ao codificada deste vetor de reconstru¸c˜ao para armazenamento ou transmiss˜ao no lugar do vetor de entrada original, pode-se obter uma consider´avel economia em armazenagem ou largura de banda de transmiss˜ao, `as custas de alguma distor¸c˜ao. A cole¸c˜ao de poss´ıveis vetores de reprodu¸c˜ao ´e chamada de livro de c´odigo (codebook) do quantizador e seus membros s˜ao denominados palavras de c´odigo (codewords).
regra do vizinho mais pr´oximo baseada na m´etrica euclidiana [38]. A Figura 5.6 mostra o espa¸co de entrada, ap´os o treinamento, dividido em cinco c´elulas com os seus vetores associados (os neurˆonios ap´os o treinamento). Cada c´elula cont´em aqueles pontos do espa¸co de entrada que s˜ao os mais pr´oximos do vetor dentre a totalidade destes pontos.
Neste trabalho, a quantiza¸c˜ao vetorial ´e utilizada para comprimir um mapa bin´ario de coeficientes significantes, como ser´a mostrado na se¸c˜ao 7.3, e a regra de aprendizagem utilizada na rede neural competitiva foi a mostrada na se¸c˜ao 5.4.
5.6
Reconhecimento de Padr˜
oes
Para os seres humanos, reconhecer padr˜oes ´e uma tarefa muito simples. Recebemos dados do mundo `a nossa volta atrav´es dos nossos sentidos e somos capazes de reconhecer a fonte dos dados. Somos capazes de reconhecer o rosto de algu´em mesmo envelhecido alguns anos, reconhecer a voz por uma linha telefˆonica mesmo com algum ru´ıdo e diferenciar entre um alimento bom ou estragado pelo olfato. Os humanos realizam o reconhecimento de padr˜oes atrav´es de um processo de aprendizagem; o mesmo acontece com as redes neurais [30].
O reconhecimento de padr˜oes ´e formalmente definido como o processo pelo qual um padr˜ao/sinal recebido ´e atribu´ıdo a uma classe dentre um n´umero predeterminado de
classes (categorias). Uma rede neural realiza o reconhecimento de padr˜oes passando inicialmente por uma se¸c˜ao de treinamento, durante a qual se apresenta repetidamente `a rede um conjunto de padr˜oes de entrada junto com a categoria `a qual cada padr˜ao particular pertence. Mais tarde, apresenta-se `a rede um novo padr˜ao que n˜ao foi visto antes, mas que pertence `a mesma popula¸c˜ao de padr˜oes utilizada para treinar a rede. A rede ´e capaz de identificar a classe daquele padr˜ao particular por causa da informa¸c˜ao que ela extraiu dos dados de treinamento. O reconhecimento de padr˜oes realizado por uma rede neural ´e de natureza estat´ıstica, com os padr˜oes sendo representados por pontos em um espa¸co de decis˜ao multidimensional. O espa¸co de decis˜ao ´e dividido em regi˜oes, cada uma das quais associada a uma classe e as fronteiras de decis˜ao s˜ao determinadas pelo processo de treinamento.
Morfologia Matem´
atica
6.1
Introdu¸c˜
ao
A palavra “morfologia” significa “estudo de formas”. Este termo ´e utilizado em in´umeras ´areas cient´ıficas incluindo a biologia e a geografia [39]. Em processamento de imagens, morfologia matem´atica ´e uma ferramenta para extra¸c˜ao de componentes de uma imagem que s˜ao ´uteis para a sua representa¸c˜ao e descri¸c˜ao. A t´ecnica foi inicialmente desenvolvida por Matheron [40] e Serra [41] na Ecole des Mines em Paris (na Ecole des Mines eles estavam interessados na an´alise de dados geol´ogicos e na estrutura de mate-riais). Morfologia matem´atica fornece fronteiras, esqueletos e fecho convexo. Tamb´em ´e utilizada para pr´e e p´os-processamento, como filtragem morfol´ogica, afinamento e poda (pruning) [12].