UNIVERSIDADE FEDERAL DE ALAGOAS
Mestrado Profissional em Matemática em Rede Nacional
PROFMAT
DISSERTAÇÃO DE MESTRADO
Ensaios Fractais à Luz do Ensino Médio
Genilton José Cavalcante de Oliveira
UNIVERSIDADE FEDERAL DE ALAGOAS
INSTITUTO DE MATEMÁTICA
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL
- PROFMAT
GENILTON JOSÉ CAVALCANTE DE OLIVEIRA
Ensaios Fractais à Luz do Ensino Médio
GENILTON JOSÉ CAVALCANTE DE OLIVEIRA
Ensaios Fractais à Luz do Ensino Médio
Dissertação de Mestrado apresentada ao MES-TRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL - PROFMAT do Insti-tuto de Matemática da Universidade Federal de Alagoas como requisito parcial para obtenção do grau de Mestre em Matemática.
Orientador: Gregório Manoel da Silva Neto
Catalogação na fonte
Universidade Federal de Alagoas
Biblioteca Central
Divisão de Tratamento Técnico
Bibliotecária Responsável: Helena Cristina Pimentel do Vale
O48e Oliveira, Genilton José Cavalcante de.
Ensaios fractais à luz do ensino médio / Genilton José Cavalcante de Oliveira. – 2016.
150 f. il.
Orientador: Gregório Manoel da Silva Neto
Dissertação (Mestrado em Matemática) – Universidade Federal de Alagoas. Programa de Pós-Graduação em Matemática. Maceió, 2016.
Inclui bibliografia e apêndices.
1. Geometria – Ensino auxiliado por computador. 2. Logo (Linguagem de
programação de computador). 3. Fractais. I. Título.
A
GRADECIMENTOS
A Deus pela sustentação diária e por me ajudar a superar todas as tribulações,
À Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), pelo aporte financeiro no decorrer do curso de Mestrado.
Aos meus colegas da turma do PROFMAT pelo convívio e pelos diversos momentos de descontração.
Ao professor Gregório pela orientação, paciência, e acolhimento do tema. À minha esposa Lidiana pelo constante afeto e incentivo nesse curso. Ao meu casal de filhos Gabrielle e Asafe pelo amor incondicional. À minha mãe por alicerçar meus primeiros passos.
Ao professor, Dayveson Noberto pela criteriosa revisão ortográfica do trabalho, Ao professor, Francisco Djnnathan pelas sugestões em algumas seções do trabalho,
R
ESUMO
A presente dissertação foi concebida para apresentar noções elementares da geometria fractal, incluindo exemplos, o histórico, aplicações e oportunidades de sua abordagem em contextos de sala de aula. Vale ressaltar que a motivação inicial do trabalho foi fazer um experimento da abordagem dos fractais em conjunto com os conteúdos afim de auxiliar o ensino/aprendizagem dos meus alunos, através do aspecto estético das formas fractais. Registramos que em muitas passagens, abrimos mão do rigor na linguagem matemática para adequar teor do trabalho aos conteúdos dos estudantes de nível médio. O atrativo aspecto visual e a possibilidade de constru-ção dos objetos fractais geométricos são devidamente explorados para manifestar a curiosidade dos estudantes em praticar e pesquisar mais sobre o tema. Este trabalho também contém ati-vidades desenvolvidas e sugeridas com seus devidos roteiros de desenvolvimento, incluindo atividades com construção de fractais no computador por meio da linguagem de programação LOGO. Nos capítulos finais há um tutorial e uma breve descrição de softwares que fazem a interpretação/execução, dos comandos LOGO e programas que visualizam o conjunto de Man-delbrot. Ao final, alguns estudantes manifestaram interesse em aprender geometria para testar os seus conhecimentos na prática usando a LOGO. As atividades realizadas foram executadas nas dependências doInstituto Federal de Educação, Ciência e Tecnologia do Rio Grande do Norte - IFRN - Campus Macau, com o devido registro dos resultados.
A
BSTRACT
This research was designed to present basic notions of fractal geometry, including examples, the history, applications and opportunities to their approach in the classroom contexts. It is noteworthy that the initial motivation of this study was to conduct an experiment of the fractal approach in conjunction with the content in order to assist the teaching / learning of my stu-dents, through the aesthetic appearance of fractal shapes. We note that in many places, we give the rigorous mathematical language to suit the work content to high school students of the con-tents. The attractive visual appearance and the possibility of construction of geometrical fractal objects are properly exploited to express curiosity of students in practice and more research on the subject. This work also has developed activities and suggested to their proper deve-lopment roadmaps, including activities with fractal construction on the computer through the LOGO programming language. In the final chapters there is a tutorial and a brief description of software that make the interpretation / implementation of LOGO commands and programs that visualize the Mandelbrot set. At the end, some students expressed interest in learning ge-ometry to test their knowledge in practice using the LOGO. The activities were carried out in dependencies of it Federal Institute of Education, Science and Technology of Rio Grande do Norte - IFRN - Campus Macau, with proper registration of the results.
L
ISTA DE
F
IGURAS
1.1 Sequência 1
2n na reta real . . . 22
2.1 Construção do Fractal de Apolônio . . . 31
2.2 Níveis do fractal de Apolônio . . . 31
2.3 Níveis do fractal pentagonal de Durer . . . 31
2.4 Conjunto de Cantor . . . 32
2.5 Ilha de Koch . . . 32
2.6 Tipos de autossemelhança . . . 34
2.7 Partes de um brócolis . . . 34
2.8 Outros exemplos de fractais naturais . . . 35
2.9 Dimensões na Geometria Euclidiana. . . 36
2.10 Níveis da Curva de Koch e a da Curva de Koch Quádrica. . . 37
2.11 Segmento de reta dividido em 4 partes . . . 38
2.12 Quadrado com lado dividido em 4 partes . . . 38
2.13 Cubo com aresta dividida em 4 partes . . . 39
2.14 Metodo de contagem de caixas . . . 40
2.15 Fotos microscópicas de células epteliais . . . 42
2.16 Imagem com quadros semelhantes destacados . . . 43
2.17 Multidão de personagens com características fractais . . . 44
2.18 Geração da superfície montanhosa . . . 45
2.19 Exemplos de quadros semelhantes na imagem . . . 46
2.20 Exemplos de quadros semelhantes na imagem . . . 47
2.21 Mosaico da Catedral de S. Maria . . . 47
2.22 Templo Vishnu, Varanasi-Índia. . . 48
2.23 Imagens da Square Federation . . . 48
3.1 Georg Cantor - 1867. . . 50
3.2 Primeiros 5 níveis do Conjunto de Cantor(K). . . 51
3.3 Helge von Koch. . . 53
3.4 Níveis da curva de Koch (zoom destacando parte autosemelhante). . . 54
3.5 Curva de Koch - Nível 4 . . . 57
3.6 Concepções artísticas de um floco de neve . . . 57
3.7 Níveis do Floco de Neve de Koch. . . 58
3.8 Auto retrato de Dürer - 1500 . . . 60
3.9 Fractal hexagonal de Dürer . . . 60
3.10 a) Ilha de Koch (centro), b) Curvas de Koch (lados) . . . 62
10 LISTA DE FIGURAS
3.11 Giuseppe Peano . . . 62
3.12 Primeiros cinco níveis da curva de peano . . . 63
3.13 Monumento em Cuneo-Itália - Curva de Peano-Hilbert cunhada na pedra . . . 64
3.14 Waclaw Sierpinski . . . 65
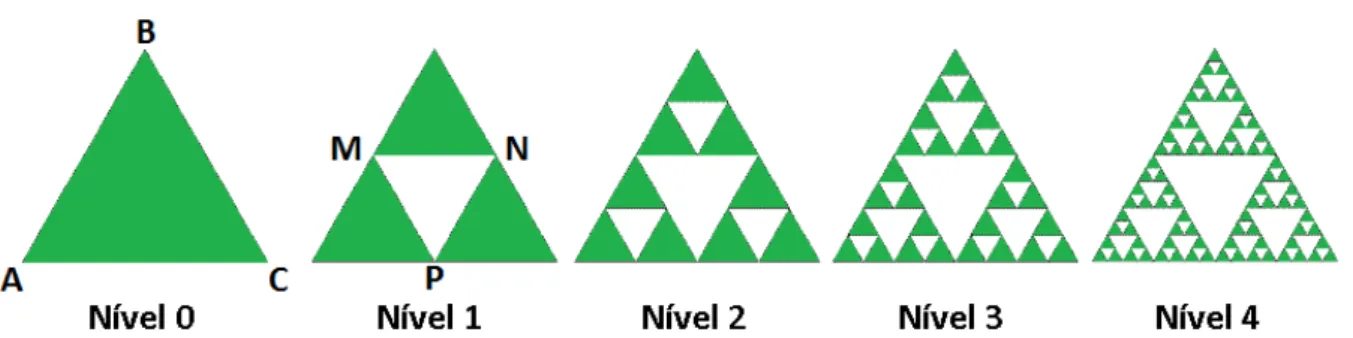
3.15 Primeiros níveis do triângulo de Sierpinski. . . 66
3.16 Logomarca do PROFMAT . . . 66
3.17 Objeto gerador da Curva de Sierpinski . . . 68
3.18 Criação do triângulo de Sierpinski com o objeto gerador. . . 69
3.19 Etapas do tapete de Sierpinski . . . 69
3.20 Conjunto de Cantor na diagonal do tapete de Sierpinski . . . 71
3.21 Karl Menger - 1937 . . . 72
3.22 Níveis da Esponja de Menger . . . 72
3.23 Esponja de Menger por junção . . . 73
3.24 Esponja de Menger com “entradas” . . . 73
3.25 Secções da Esponja de Menger . . . 75
3.26 Fractal da secção deE. . . 76
3.27 Benoît Mandelbrot . . . 77
3.28 Conjunto de Mandelbrot (Representação com asteriscos) . . . 77
3.29 Conjunto de mandelbrot . . . 78
3.30 Conjunto de Mandelbrot colorido . . . 78
3.31 Ampliações no conjuntoM . . . 79
3.32 Triângulo gerador do Fractal Pinwheel . . . 80
3.33 divisão do triângulo na razão√55 . . . 81
3.34 Níveis do Fractal Pinwheel . . . 81
3.35 Fractal Pinwheel por ampliação . . . 83
3.36 Diagrama de fatores naturais de 1 a 49 . . . 84
3.37 Organização das três duplas de pontos. . . 85
3.38 Organização dos 5 grupos de 6 pontos. . . 85
3.39 Diagramas den=25 com pontos unidos pelas linhas . . . 86
3.40 Diagrama de fatores do número 15 . . . 86
3.41 Diagramas de 81 (Triângulo de Sierpinski), 125 (fractal de Dürer pentagonal) e 121 . . . 86
4.1 triângulo pequeno . . . 89
4.2 Construção gradual do STS . . . 89
4.3 Desenhos de triângulos na folha . . . 89
4.4 Triângulos da base mais claros . . . 90
4.5 Triângulos produzidos pelos alunos . . . 93
4.6 Cálculos dos exercícios da atividade 1. . . 94
4.7 Imagens das tarefas concluídas . . . 95
4.8 Níveis do triângulo de Sierpinski com latas . . . 95
4.9 Cálculos dos exercícios da atividade 1. . . 98
4.10 Níveis 4 e 5 do triângulo de Sierpinski Metálico . . . 98
4.11 Moldes do cubo gerador . . . 100
LISTA DE FIGURAS 11
4.13 Esponja nível 1 . . . 101
4.14 Esponja de Menger no nível 2 . . . 101
4.15 Ornamentação com as esponjas de menger de nível 1 . . . 103
4.16 Parte frontal da MEM - 8 esponjas de nível 2. . . 103
4.17 Imagens naturais . . . 105
4.18 Fractal 1 . . . 106
4.19 Variação da curva de Peano com triângulos . . . 106
4.20 Curva de Koch quádrica . . . 106
4.21 Variação do Conjunto de Cantor . . . 107
4.22 Passos do cartão fractal - nível 1 . . . 107
4.23 Passos nível 1 . . . 108
4.24 Passos. . . 108
4.25 Continuando os passos nas novas dobras - Níveis 2 e 3 . . . 108
4.26 Exemplo de fractal criado . . . 109
4.27 Fractal com círculos . . . 110
4.28 FractalF . . . 110
5.1 Ambientes que interpretam a linguagem logo . . . 113
5.2 Segmento de reta gerado pelos comandos PD 45 PF 100. . . 114
5.3 Quadrado desenhado com a sequência de comandos . . . 114
5.4 Resultados dos comandos com aninhamentos do REPITA . . . 115
5.5 Janela com a edição do comando QUAD . . . 115
5.6 Resultados dos comandos . . . 116
5.7 Estrutura da curva de Koch . . . 117
5.8 Execução: rotina KOCH (Nível 4) . . . 118
5.9 Tela do Turtle Draw em um smartphone Android . . . 119
5.10 Resultados dos comandos 1 e 2 . . . 119
5.11 Quadrado pintado. . . 122
5.12 Espiral de Teodoro . . . 122
5.13 Tela inicial do Ultra Fractal . . . 124
5.14 Aplicando zoom . . . 124
5.15 Abas da mini-janela Fractal Properties . . . 125
5.16 Criando/Escolhendo um novo fractal . . . 125
5.17 Escolhendo um novo fractal e configurações . . . 126
5.18 Conjunto de Mandelbrot para os expoentes 3, 4 e 5 . . . 126
5.19 Porção com 250 e 1000 iterações . . . 126
5.20 Tela inicial do Fractoid . . . 127
5.21 Diferentes quantidades de iterações . . . 128
5.22 Conjunto de Mandelbrot com as funçõesf eg . . . 128
5.23 Variações de algoritmo de cores . . . 129
5.24 Itens da opção mais do fractoid . . . 129
A.1 Idioma na instalação do FMSLogo . . . 134
12 LISTA DE FIGURAS
A.3 Partes da tela do FMSLogo . . . 134
A.4 Tabela das 16 cores básicas do FMSLogo . . . 138
A.5 REPITA com CONTEVEZES . . . 139
A.6 Resultados dos exemplos 2 e 5 . . . 140
A.7 Definindo e executando o comando QUADRADO . . . 140
A.8 Janela com resultado dos comandos . . . 141
A.9 Rotina POLIGONO desenhando um heptágono . . . 142
A.10 Executando a rotina fatorial . . . 143
A.11 Chamando a rotina TRI_RECURSIVO . . . 144
B.1 Resultado ARVORESIMPLES . . . 145
B.2 Resultado comando CANTOR . . . 146
B.3 Rotina koch (Nível 4) . . . 146
B.4 Rotina koch (Nível 4) . . . 147
B.5 Rotina koch (Nível 4) . . . 147
B.6 Rotina koch (Nível 4) . . . 148
B.7 Rotina koch (Nível 4) . . . 148
B.8 Rotina PEANO2 (Nível 3) . . . 149
B.9 Rotina KOCH2 (Nível 3) . . . 149
B.10 Rotina CANTOR2 (Nível 2) . . . 150
B.11 Rotina MINKOWSKI (Nível 2) . . . 151
B.12 Execução Quadrado3 . . . 151
S
UMÁRIO
INTRODUÇÃO 17
1 Começando com generalidades 21
1.1 Sequências de números reais . . . 21
1.1.1 O limite de uma sequência . . . 21
1.1.2 Progressão Geométrica . . . 23
1.1.2.1 Termo Geral da P.G . . . 23
1.1.2.2 Exemplos . . . 24
1.1.2.3 A Soma dos n primeiros termos de uma P.G . . . 24
1.1.2.4 Soma dos termos de uma P.G infinita . . . 25
1.2 Logaritmos . . . 26
1.2.1 Propriedades operatórias dos Logaritmos . . . 27
1.3 Iterações . . . 27
1.4 Algoritmos . . . 28
1.4.0.1 Algoritmo: Trocar pneu do carro . . . 28
2 Conceitos e histórico dos fractais 30 2.1 Pre-história dos Fractais . . . 30
2.1.1 Características dos fractais . . . 33
2.2 Dimensão Fractal . . . 35
2.2.1 Dimensão por Autossimilaridade . . . 38
2.2.1.1 Segmento de reta . . . 38
2.2.1.2 Quadrado . . . 38
2.2.1.3 Cubo . . . 38
2.2.2 Dimensão por contagem de caixas (box-counting) . . . 40
2.3 A presença dos fractais em outras áreas . . . 41
2.3.1 Fractais na medicina . . . 41
2.3.2 Fractais na informática . . . 42
2.3.2.1 Compressão de imagens/vídeos . . . 42
2.3.2.2 Multidão fractal . . . 43
2.3.2.3 Geração de superfícies montanhosas . . . 43
2.3.3 Fractais nas Artes . . . 44
2.3.4 Fractais na arquitetura . . . 46
3 Estudo de alguns fractais 49
14 SUMÁRIO
3.1 Fractais pioneiros . . . 49
3.1.1 O Conjunto de Cantor . . . 49
3.1.1.1 Construção do conjunto de Cantor . . . 50
3.1.1.2 A Dimensão deK . . . 53
3.1.2 As Curvas Koch . . . 53
3.1.2.1 Construção da Curva de Kock . . . 53
3.1.2.2 Análise da Curva de Kock . . . 54
3.1.2.3 A Dimensão da curva de Koch . . . 56
3.1.3 O Floco de Neve de Koch . . . 57
3.1.3.1 Construção do Floco de Neve de Koch . . . 58
3.1.3.2 Estudo do Floco de Neve de Koch . . . 58
3.1.3.3 A Dimensão do Floco de Neve de Koch . . . 59
3.1.4 O Fractal de Dürer . . . 59
3.1.4.1 O processo de construção . . . 59
3.1.4.2 Estudo do fractal Hexagonal de Dürer . . . 60
3.1.4.3 Dimensão do fractal de Dürer . . . 61
3.1.4.4 Curiosidades do fractal de Dürer . . . 61
3.1.5 A Curva de Peano . . . 62
3.1.5.1 Construção da Curva de Peano . . . 63
3.1.5.2 Estudo da Curva de Peano . . . 63
3.1.5.3 Dimensão da Curva de Peano . . . 64
3.1.6 O Triângulo de Sierpinski . . . 65
3.1.6.1 Construção do Triângulo de Sierpinski . . . 65
3.1.6.2 Estudo do triângulo de Sierpinski . . . 66
3.1.6.3 Medida do lado e quantidade de triângulos: . . . 66
3.1.6.4 Perímetro e área: . . . 67
3.1.6.5 Dimensão do triângulo de Sierpinski . . . 67
3.1.7 Outros processos de construção . . . 68
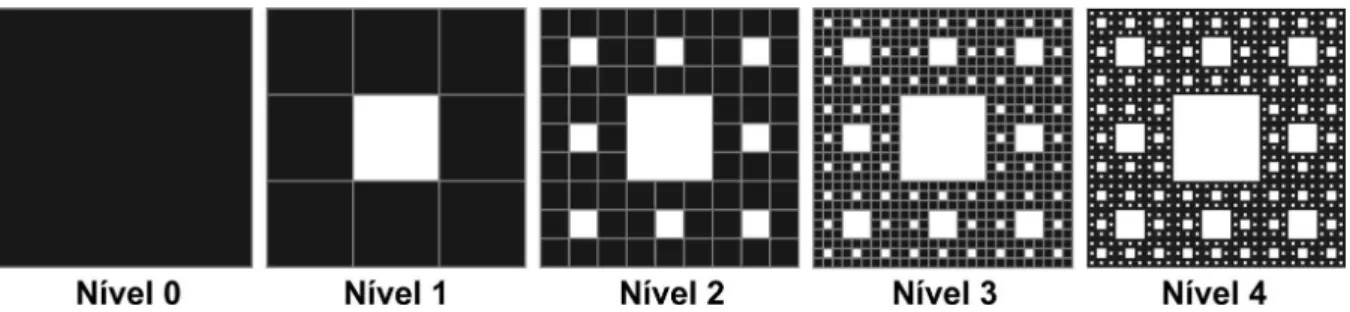
3.1.8 O Tapete de Sierpinski . . . 68
3.1.8.1 Construção do tapete de Sierpinski . . . 68
3.1.8.2 Estudo do Tapete de Sierpinski . . . 69
3.1.9 A Esponja de Menger . . . 71
3.1.9.1 Construção da esponja Menger . . . 71
3.1.9.2 Outra forma de construção . . . 73
3.1.9.3 Estudo da Esponja de Menger . . . 73
3.1.9.4 Propriedades da Esponja de Menger . . . 75
3.1.9.5 Dimensão da Esponja de Menger . . . 76
3.1.10 O Conjunto de Mandelbrot . . . 76
3.2 Outros Fractais . . . 80
3.2.1 O Fractal Pinwheel . . . 80
3.2.1.1 Construção do Fractal Pinwheel . . . 80
3.2.1.2 Estudo do Fractal Pinwheel . . . 81
3.2.1.3 Dimensão do fractal . . . 83
SUMÁRIO 15
3.2.2.1 Construção do diagrama . . . 84
4 Fractais em contextos de sala de aula 88 4.1 Atividades desenvolvidas . . . 88
4.1.1 Atividade 1 - Super Triângulo de Sierpinski . . . 88
4.1.1.1 As características do STS . . . 88
4.1.1.2 Objetivo Geral . . . 90
4.1.1.3 Objetivos da atividade . . . 90
4.1.1.4 Pré-requisitos da atividade . . . 90
4.1.1.5 Público alvo . . . 91
4.1.1.6 Tempo necessário . . . 91
4.1.1.7 Desenvolvimento da atividade . . . 91
4.1.1.8 Solução da atividade . . . 91
4.1.1.9 Material Usado . . . 92
4.1.1.10 Considerações sobre a atividade . . . 92
4.1.1.11 Resultados . . . 93
4.1.2 Atividade 2 - Triângulo de Sierpinski Metálico . . . 94
4.1.2.1 Objetivo geral . . . 94
4.1.2.2 Objetivos da atividade . . . 95
4.1.2.3 Pré-requisitos da atividade . . . 96
4.1.2.4 Público alvo . . . 96
4.1.2.5 Tempo necessário . . . 96
4.1.2.6 Material utilizado . . . 96
4.1.2.7 Desenvolvimento da atividade . . . 97
4.1.2.8 Considerações sobre a atividade . . . 97
4.1.2.9 Resultados . . . 97
4.1.3 Atividade 3 - Mega Esponja de Menger . . . 98
4.1.3.1 Características da Mega Esponja de Menger . . . 98
4.1.3.2 Objetivo geral . . . 99
4.1.3.3 Objetivos da atividade . . . 99
4.1.3.4 Público alvo . . . 99
4.1.3.5 Tempo necessário . . . 99
4.1.3.6 Material Usado . . . 99
4.1.3.7 Desenvolvimento da Atividade . . . 100
4.1.3.8 Solução do problema . . . 101
4.1.3.9 Considerações sobre a atividade . . . 102
4.1.3.10 Resultados . . . 102
4.2 Atividades propostas . . . 103
4.2.1 Atividade 1 - Investigando fractais na natureza . . . 103
4.2.1.1 Objetivos da atividade . . . 104
4.2.1.2 Roteiro da atividade . . . 104
4.2.1.3 Público alvo . . . 104
4.2.1.4 Tempo necessário . . . 104
16 SUMÁRIO
4.2.2 Atividade 2 - Calculando a dimensão fractal . . . 105
4.2.2.1 Objetivos . . . 105
4.2.2.2 Pré-requisitos . . . 105
4.2.2.3 Público alvo . . . 105
4.2.2.4 Materiais . . . 106
4.2.2.5 Tempo necessário . . . 106
4.2.2.6 Roteiro da atividade . . . 106
4.2.3 Atividade 3 - Cartões Fractais . . . 107
4.2.3.1 Objetivo . . . 107
4.2.3.2 Roteiro da atividade . . . 107
4.2.4 Atividade 4 - Criando o próprio fractal . . . 109
4.3 Lista de questões envolvendo fractais . . . 109
4.3.1 Progressão geométrica . . . 109
4.3.2 Equações exponenciais . . . 111
4.3.3 Análise combinatória . . . 111
5 Atividades com softwares e fractais 112 5.1 A Linguagem LOGO . . . 112
5.1.1 Os ambientes que interpretam a linguagem LOGO . . . 112
5.1.2 Um primeiro contato com o FMSLogo . . . 113
5.1.2.1 O comando APRENDA . . . 114
5.1.2.2 Alguns fractais feitos no LOGO . . . 116
5.1.3 O aplicativo Turtle Draw . . . 118
5.2 Atividades com a linguagem LOGO . . . 120
5.2.1 Atividade 1 . . . 120
5.2.1.1 Pré-requisitos . . . 120
5.2.1.2 Objetivos . . . 120
5.2.1.3 Público alvo . . . 120
5.2.1.4 Tempo necessário . . . 120
5.2.1.5 Roteiro da atividade . . . 120
5.2.1.6 Escreva os comandos em LOGO para desenhar as figuras abaixo . . . 121
5.2.1.7 1. Nível simples . . . 121
5.2.1.8 2. Nível intermediário . . . 121
5.2.2 Atividade 2 . . . 121
5.2.2.1 Pré-requisitos . . . 121
5.2.2.2 Objetivos . . . 121
5.2.2.3 Roteiro da atividade . . . 121
5.2.2.4 Considerações sobre as Atividades . . . 123
5.3 Programas para visualizar o Conjunto de Mandelbrot . . . 123
5.3.1 O software Ultra Fractal . . . 123
5.3.1.1 Instalação . . . 123
5.3.1.2 Aplicando Zoom . . . 124
5.3.1.3 Algumas configurações do Ultra Fractal . . . 125
5.3.2 O aplicativo Fractoid . . . 127
5.3.3 Configurações . . . 127
5.3.3.1 Opção reset . . . 127
5.3.3.2 Opção Change Max Iterations . . . 127
5.3.3.3 Opção Change Colors . . . 127
5.3.3.4 Opção Change Equation . . . 128
5.3.3.5 Opção Change Algorithm . . . 128
5.3.3.6 Opção Mais . . . 128
6 Considerações finais 130 A Tutorial FMSLogo 133 A.0.1 Breve histórico . . . 133
A.0.2 Instalação do FMSLogo . . . 133
A.0.2.1 Instalando... . . 133
A.0.3 O primeiro contato . . . 134
A.0.4 Comandos básicos . . . 135
A.0.5 Comentários em LOGO . . . 137
A.0.6 Os comandos ROTULE, ESCREVA e MOSTRE . . . 137
A.0.7 Usando cores no FMSlogo . . . 137
A.0.8 O Comando REPITA . . . 138
A.0.8.1 Exemplos . . . 139
A.0.9 O comando APRENDA . . . 139
A.0.10 Variáveis no LOGO . . . 141
A.0.11 Comando SE . . . 142
A.0.12 Rotinas recursivas no LOGO . . . 143
A.0.13 Algumas considerações . . . 144
B Comandos das imagens e atividades LOGO 145 B.0.1 Árvore . . . 145
B.0.2 Conjunto de Cantor . . . 146
B.0.3 Curva de Peano . . . 146
B.0.4 Curva de Koch . . . 146
B.0.5 Floco de neve de Koch . . . 147
B.0.6 Triângulo de Sierpinski - Solução 1 . . . 147
B.0.7 Triângulo de Sierpinski - Solução 2 . . . 148
B.0.8 Variação da Curva de Peano . . . 149
B.0.9 Curva de Koch Quádrica . . . 149
B.0.10 Variação do Conjunto de Cantor . . . 149
B.0.11 Solução das atividades propostas . . . 150
B.0.12 Ilha de Minkowski . . . 151
B.0.13 Quadrado pintado . . . 151
I
NTRODUÇÃO
Orientado pela dificuldade de aprendizado dos meus alunos e pela minha própria curiosidade em conhecer mais dos objetos fractais, tomei a decisão de adaptar minhas aulas de modo a buscar a atenção das minhas turmas pelo atraente aspecto estético das imagens fractais. A geometria fractal, além de seu interessante design, característico das imagens autossimilares, possui uma estreita relação com a natureza, com as artes e diversas competências da matemática do ensino médio. Neste trabalho, esta geometria foi explorada em contextos de sala de aula, paralelamente aos conteúdos de sequências, funções exponenciais, áreas e perímetros, como uma forma de diversificar a abordagem desses assuntos. Além disso, as atividades em grupo e realizadas no computador, manifestaram a curiosidade e uma maior interação entre alunos para o estudo dos assuntos estudados. As imagens utilizadas no trabalho, em sua maioria, foram de autoria própria, sendo construídas através dos softwares CorelDraw, Microsoft Paint e FMSLogo, sendo este último abordado no capítulo 5.
A abordagem da geometria fractal, de forma concomitante com os assuntos do nível médio, pode despertar o interesse, e ampliar a percepção geométrica do aluno levando-o a uma reflexão sobre o que está “por trás” da estética daquelas formas. Neste sentido, a Secretaria de Estado da Educação do Paraná, teve a feliz iniciativa de incluir expressamente a geometria fractal nas suas Diretrizes Curriculares da Educação Básica - DCE, o documento preceitua o seguinte:
Na geometria dos fractais, pode-se explorar: o floco de neve e a curva de Koch; tri-ângulo e tapete de Sierpinski, conduzindo o aluno a refletir e observar o senso es-tético presente nessas entidades geométricas,estendendo para as suas propriedades... As abordagens das Geometrias: fractal, hiperbólica e elíptica não se encerram, uni-camente, nos conteúdos aqui elencados. Desde que explore conceitos básicos, o pro-fessor tem a liberdade de investigar e realizar outras abordagens. Os conceitos destes conteúdos são fundamentais para que o aluno do Ensino Médio amplie seu conheci-mento e pensaconheci-mento geométrico. [PAR08]
No que tange ao uso de recursos tecnológicos, o computador torna-se um aliado para o ensino da matemática. Os PCNs fazem menção ao estímulo do pensamento, autonomia e uma nova relação professor-aluno:
As experiências escolares com o computador também têm mostrado que seu uso efe-tivo pode levar ao estabelecimento de uma nova relação professor-aluno, marcada por uma maior proximidade, interação e colaboração. ... como meio para desensolver au-tonomia pelo uso dosoftwareque possibilite pensar, refletir e criar soluções; [Nac99]
19
No capítulo 2 temos um breve histórico dos fractais, apresentando seus conceitos, caracte-rísticas e enfatizando a presença dessas formas na natureza e em outras áreas do conhecimento. Ainda no capítulo, existe uma breve fundamentação de duas expressões que permitem calcular a dimensão fractal.
No capítulo 3 apresentamos um estudo mais detalhado dos fractais considerados pioneiros: O Conjunto de Cantor, as Curvas de Koch, o Fractal de Durer, a Curva de Peano, o Triângulo e o Tapete de Sierpinski, a Esponja de Menger e o Conjunto de Mandelbrot. Nesse capítulo também foram abordados dois fractais criados após os anos 90: o Fractal Pinwheel e o Diagrama de Fatores.
No capítulo 4 temos o roteiro de atividades desenvolvidas e outras sugeridas, todas elas vin-culadas diretamente aos fractais. Algumas atividades envolvem mais de uma turma, permitindo uma divertida interação com muitos alunos. Ainda neste capítulo, temos as considerações e o registro fotográfico dos trabalhos dos alunos.
No capítulo 5 resumimos as funcionalidades de 4 softwares. Os dois primeiros permitem a construção de fractais através da Linguagem de programação LOGO, e os demais servem para vizualizar o conjunto de Mandelbrot. Destaco que os softwaresTurtle DraweFractintexecuta em dispositivos móveis. O capítulo ainda disponibiliza atividades voltadas à construção de figuras planas e fractais no ambiente FMSLogo.
No capítulo 6 temos as conclusões do trabalho, descrevendo alguns resultados quanto a par-ticipação dos alunos, bem como considerações sobre os desdobramentos das atividades cons-tantes nos capítulos 4 e 5. Este capítulo também inclui sugestões para trabalhos futuros a respeito de outros fractais que não explorados aqui.
L
ISTA DE
T
ABELAS
2.1 Número de objetos similares nas dimensões Euclidianas: fatores de redução 2 e 4) . . . 39
2.2 Resumo do comportamento denkeloglognkk . . . 41
3.1 Resumo do conjuntoKn . . . 51 3.2 Evolução deNkeCk . . . 55 3.3 Resumo do estudo da curva de Koch . . . 56 3.4 Resumo do comportamento do Fractal Hexagonal de Dürer . . . 61 3.5 Evolução deCkeNKna Curva de Peano . . . 64 3.6 Quantidade de triângulos e medida do lado - nívelk. . . 67 3.7 Lado e quantidade de triângulos do nívelk . . . 70 3.8 Tamanho da aresta e número de cubos. . . 72
3.9 Valores deNk,AkePkao longo dos níveis do Fractal de Pinwheel. . . 82 4.1 Quadro com quantitativos do T.S.M . . . 96 4.2 Informações sobre o cartão fractal . . . 109
1. C
OMEÇANDO COM GENERALIDADES
“Não lhes explico tudo, para não privá-los do prazer de aprenderem sozinhos.”
René Descartes.
Este capítulo apresenta alguns conceitos preliminares, necessários à compreensão do tema deste trabalho, incluindo assuntos relacionados à área de informática.
1.1.
Sequências de números reais
Definição 1.1.1. Uma sequência, ou sucessão, é uma lista ordenada de números reais. Os ele-mentos da sequência são indexados por números naturais. Mais precisamente, uma sequência de números reais é uma funçãoa:N→Rque associa cada número naturalna um número real a(n). O valora(n), para todon∈N, é representado poran, ou seja, on-ésimo termo da
sequên-cia. Escreveremos (a1,a2,a3...,an, ...), ou simplesmente(an), para designar uma sequência a
qualquer.
Definição 1.1.2. Uma sequência(an)é dita sequência recorrente (ou simplesmente recorrência)
se cada termo an seguinte é determinado em função de termos anteriores. Dado um inteiro
positivok, a sequência recorrente de ordemké tal que:
an+k= f(an+k−1,an+k−2, ...,an+1,an),∀k,n∈N.
Exemplos de recorrência:
a) (xn) = (1,1,2,3,5,8,13,21, ...),(Sequência de Fibonacci1)
onde,x1=x2=1 exn+2=xn+1+xn,paran>0.
b) (yn) = (1,1,1,2,2,3,4,5,7,9,12,16,21,28...),(Sequência de Padovam2)
onde,y1=y2=y3=1 eyn+3=yn+1+yn,paran>0.
c) (zn) = (1,1,2,3,5,11,26, ...)
onde,z1=z2=1 ezn+3=zn·zn+1+zn+2,paran>0.
1.1.1. O limite de uma sequência
Consideremos a sequência(an) =
1
2, 1 4,
1 8,···,
1 2n,···
. Representando seus 4 primei-ros termos (em preto) na reta real (fig. 1.1), temos:
1Leonardo Fibonacci (1170-1250), também conhecido como Leonardo de Pisa, foi um matemático italiano
autor da sequência bastante conhecida que leva seu nome.
2Richard Padovan nasceu em 1935, é arquiteto e estudou na Architectural Association, Londres (1952-57). É
autor do livro - “Proportion: Science, Philosophy, Architecture”
Figura 1.1 Sequência 1
2nna reta real
Fonte: [IDD+01], (adaptado)
Notemos que os termos da sequência se aproximam de zero, isto é, quando n é bastante “grande” o n-ésimo termo da sequência (an) estará tão próximo de zero quanto desejarmos.
Assim, se quisermos que a distância entre(an)e zero seja menor que 10001 , deveremos ter:
1 2n−0
< 1 1000 então: 1 2n <
1
1000⇒2n>1000⇒n>9
Isto significa que a partir do 10o termo, os termos da sequencia estarão próximos de 0, com aproximação menor que 1
1000
Em geral, dada uma aproximaçãoε>0, é possível encontrar um númeron0tal que∀n>n0,
teremos 1 2n−0
<
ε.
Nessas condições, dizemos que o limite de 1
2n, quandontende a infinito é zero, ou converge
para zero. Esse limite é representado por:
lim
n→∞ 1 2n =0
Definição 1.1.3. Uma sequência (an) = (a1,a2,a3, ...,an, ...) tem limite L, se dado ε >0 é
possível obter um número naturaln0tal que∀n>n0teremos|an−L|<ε. Neste caso,
indica-se
lim
n→∞
an=L
.
Também dizemos que se a sequência(an)tem limiteL, então(an)é limitada, ou converge
para L. Destacamos, que se−1<q<1, então toda sequência(an) = (1,q,q2,q3, ...,qn, ...),
converge para zero quandontende ao infinito, ou seja, Se|q|<1, então
lim
n→∞
1. (an) =
1,2
3, 4 9,
8 27, ...,
2
3
n
, ...
2. (bn) = (1,0.5,0.25,0.125, ...,(0.5)n, ...)
3. (cn) =
1,−1
3, 1 9,−
1 27, ...,
−13
n
, ...
1.1.2. Progressão Geométrica
Definição 1.1.4. Dados a,q∈R, chama-se Progressão Geométrica (P.G.) a recorrência (an)
dada por:
a1=a
an=an−1.q,∀n∈N,n≥2
Em outras palavras, a P.G. é uma sequência cujo próximo termo é igual ao produto do termo anterior com uma constante realqchamadarazão da P.G.
Exemplos:
(bn) = (3,6,12,24,48, ...) q=2.
(cn) =
9,3,1,1
3, 1 9, ...
q= 1
3.
(dn) = 2,2√3,6,6√3, ... q=√3.
1.1.2.1. Termo Geral da P.G
Usando a definição 1.1.4, vejamos uma expressão que nos permite determinar qualquer termoana partir do termoa1e da razãoq, considerandoa1eqnão nulos. Temos que,
a2 = a1·q a3 = a2·q a4 = a3·q
... ... an−1 = an−2·q
an = an−1·q
Multiplicando-se membro a membro todas asn−1 equações, obtemos:
✚a✚2·✚a✚3·✚a✚4·...·✘✘an−✘1·an = a1·✚a✚2·✚a✚3·...·✘✘an−✘2·✘✘an−✘1·qn−1
an = a1·qn−1
1.1.2.2. Exemplos
1. Determinar o 11otermo da sequência(b n) =
3,3√2,6,6√2, ...
Solução:
Conforme a definição 1.1.4,a2=a1·q⇒q= a2 a1 =
3√2
3 =
√ 2
Então, usando a fórmula do termos geral temos, a11=a1·q10=3·(√2)10=3·√1024=96
2. A sequência (cn) =
−4,2,−1,−1
2, ...,− 1 512
tem 13 termos. Obtenha o valor do termo central.
Solução:
Segue-se da definição 3 que,q=a2
a1 ⇒q= 2
−4 =− 1 2
O termo central é exatamentea7, logo,
a7=a1·q6⇒a7=−4·
−12
6
⇒a7=− 4
64 =− 1 16
3. Prove que se(a1,a2,a3, ...), é uma P.G., então(a21,a22,a23, ...)também é. Demonstração:
Sejaan=a1·qn−1ebn=a2n, logobn= (a1·qn−1)2=a21·(q2)n−1. Tomando a2
1=c1 e q2=r, teremos bn=c1·rn−1 que é o termo geral de uma P.G. de razãore primeiro termo igual ac1.
1.1.2.3. A Soma dos n primeiros termos de uma P.G
Seja a P.G(an) = (a1,a2, ...,an−1,an, ...). Queremos obter uma expressão que determine o
valor da somaSndosnprimeiros termos de(an).
Seja,
Sn=a1+a2+...+an−1+an (1.1)
Multiplicando (1.1) porq, obtemos
usando a definição 1.1.4 em cada termo obtemos,
q·Sn=a2+a3+...+an+an·q (1.2)
Tomando a diferença (1.2)−(1.1), obtemos:
q·Sn−Sn = (✚a✚2+✚a✚3+...+✘✘an−✘1+✚a✚n+an·q)−(a1+✚a✚2+...+✘✘an−✘1+✚a✚n)
⇒Sn(q−1) = an·q−a1, masan=a1·qn−1 ⇒Sn(q−1) = a1·qn−1·q−a1=a1·qn−a1, ⇒Sn(q−1) = a1(qn−1)
Portanto, supondoq6=1 temos:
Sn=a1q
n−1
q−1. (1.3)
Paraq=1 temos quean=a1·qn−1⇒an=a1·1n−1=a1, para todon. Logo, Sn=a1+a2+···+an=a1+a1+···+a1=n·a1
1.1.2.4. Soma dos termos de uma P.G infinita
Seja a sequência(an) =
2,1,1
2, 1 4,···
.Temos quea1=2 eq= 1
2, logo, os primeiros termos de(an)são:
a1 = 2
a2 = 2·
1
2
1
=2
2 =1 a3 = 2·
1
2
2
=2
4 =0,5 a4 = 2·
1 2
3
=2
8 =0,25 a5 = 2·
1
2
4
= 2
16 =0,125
... ...
a10 = 2·
1
2
9
= 2
512 =0,00390625
... ...
Percebemos que, quandonaumenta, o valor deandiminui e se aproxima cada vez mais de
zero. Matematicamente falando, dizemos que o limite de an vai para zero, ou converge para
lim
n→∞an= 0.
Mais adiante usaremos o fato de que para todo k ∈R, tal que−1<k <1, a sequência
(an) = (1,k,k2,k3,···), converge para zero, ou seja,
lim
n→∞
kn=0.
Vamos determinar a somaSndos termos de uma P.G infinita, de razãoq, onde|q|<1. Em
outras palavras queremos saber o valor deSnquandontende ao infinito.
De fato,
lim
n→∞
Sn=nlim
→∞
a1 ✒
0
qn−1 q−1 =
−a1 q−1 =
a1 1−q. Portanto, para todoq∈R, tal que|q|<1,
Sn= 1a1
−q. Exemplo 1.1.1. Determine o valor da soma1+ 1
10+ 1 100+ 1 1000+ 1
10000+... Solução:Trata-se da soma infinita dos termos de uma P.G, tal quea1=1 eq= 1
10<1, logo,
Sn= a1
1−q = 1 10 1− 1
10 = 1 10 9 10 = 1 9.
1.2.
Logaritmos
Definição 1.2.1. Sejama,b∈R∗+, com0<a6=1. O expoentex, tal queax=b, é chamado de
logaritmo debna basea, o qual denotamos por:
logab=x⇔ax=b.
Exemplos:
a) log28=3⇔23=8
b) log√
327=6⇔ √
36=27 c) log1
5125=−3⇔
1
5
−3
1.2.1. Propriedades operatórias dos Logaritmos
Sejama,b,c∈Rtais que, 0<a6=1,b>0 ec>0, então:
a) loga(b·c) =logab+logac; b) loga(b
c) =logab−logac; c) logabn=n·logab; d) alogab=b;
e) logab= logcb
logca,com 0<c6=1 (mudança de base).
1.3.
Iterações
O processo de iteração de uma função consiste na aplicação de f nela própriakvezes (k composições), comk∈N. Para simplificar a notação, faremos:
f1(x) = f(x)
f2(x) = f(f(x))
f3(x) = f(f(f(x)))
fk(x) = f(f(···f(x)···))
| {z }
kvezes
Em particular, definimos f0(x) =x. As funções iteradas são estudadas largamente no campo dos fractais.
Definição 1.3.1. Seja f :A→Bex∈A. A sequência de iteradas f0(x),f1(x),f2(x),f3(x),···
é chamada órbita de x.
Exemplo 1.3.1. Seja f :C→C, definida por f(x) =x2. A órbita dex=2por f é: f0(2),f1(2),f2(2),f3(2),···
f0(2) = 2
f1(2) = 22=4
f2(2) = f(f(2)) =42=16 f3(2) = f(f(f(2))) =162=256
... ...
1.4.
Algoritmos
Definição 1.4.1. Um algoritmo pode ser definido como uma sequência lógica e finita de passos (instruções) usada para resolver um determinado problema ou executar uma tarefa.
Segundo [FC08], ao estabelecer um algoritmo, estamos determinando um padrão de com-portamento que deverá ser seguido (uma norma de execução de ações) para alcançar o resultado de um problema. Ainda de acordo com [FC08], para o desenvolvimento de um algoritmo efici-ente, é necessário obedecermos algumas premissas básicas no momento de sua elaboração:
• Definir ações simples e sem ambiguidade;
• Organizar as ações de forma ordenada;
• Estabelecer as ações dentro de uma sequência finita de passos.
Dentre as inúmeras ações que os algoritmos são capazes de realizar, podemos destacar:
1. Ler e escrever dados;
2. Avaliar expressões algébricas, relacionais e lógicas;
3. Tomar decisões com base nos resultados das expressões avaliadas;
4. Repetir um conjunto de ações de acordo com uma condição;
5. Construir objetos geométricos.
A sequência abaixo é um exemplo simples de um algoritmo (sem condições ou repetições) para a troca de um pneu. Assim, notamos que a utilidade dos algoritmos independem da área de conhecimento ou domínio de aplicação.
1.4.0.1. Algoritmo: Trocar pneu do carro
1. Desligar o carro;
2. Abrir o porta-mals e pegar as ferramentas (chave e macaco); 3. Pegar o estepe;
4. Suspender o carro com o macaco; 5. Remover os 4 parafusos do pneu furado; 6. Colocar o estepe;
7. Colocar os 4 parafusos; 8. Baixar o carro com o macaco;
2. C
ONCEITOS E HISTÓRICO DOS FRACTAIS
A Geometria Fractal mudará profundamente a sua forma de ver as coisas. Con-tinuar lendo pode ser perigoso. Existe o risco de perda definitiva da visão ino-fensiva que tens das nuvens, florestas, galáxias, folhas, penas, pedras, montanhas, tapeçaria e muitas outras coisas. Nunca mais irá recuperar as suas interpretações de todos esses objetos que até agora eram familiares.
Michael Fielding Barnsley [Bar14]
No presente capítulo mostraremos uma pequena introdução dos fractais geométricos apre-sentando resumidamente suas características e conceitos, afim de trazer uma compreensão mí-nima desse tema para aplicá-lo em paralelo aos conteúdos do ensino nível médio. Neste tra-balho adotaremos o conceito de que os fractais são formas geométricas, com grande riqueza de detalhes, cujas partes contém cópias autossemelhantes de si mesmas. Veremos um pouco da pre-história, a presença na natureza e a idéia de dimensão fractal. Em virtude das aplica-ções da geometria fractal em diversos ramos da ciência, ela ganhou um lugar de destaque na matemática, em especial, no estudo dos fenômenos caóticos1;
2.1.
Pre-história dos Fractais
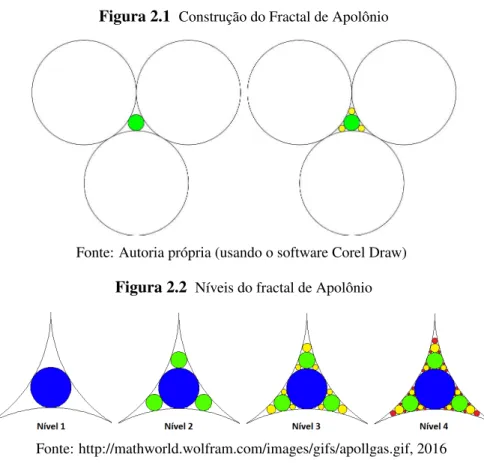
Provavelmente, considerando a época em que viveu Apolônio2, as formas mais antigas, com características autossimilares, são os fractais de Apolônio cuja origem depreende-se do problema dos círculos de Apolônio. Um caso particular desses fractais, inicia com um processo que envolve três círculos congruentes e tangentes entre si. No primeiro passo, constrói-se um círculo menor tangente aos 3 círculos iniciais. O fractal de Apolônio é produzido através da construção sucessiva de círculos tangentes nos espaços vazios entre os círculos criados em passos anteriores. Veja esta construção nas figs. 2.1 e 2.2.
Passados mais de 16 séculos, Albrecht Dürer (1471-1528) produziu uma figura com pa-drões fractais com base em um pentágono regular, opentágono de Dürer, fig. 2.3. Um fractal hexagonal com estas características será estudado no capítulo 3.
Apesar da existência milenar de algumas formas com padrões fractais, a idéia que temos hoje, passou por um longo período de amadurecimento através dos estudos de alguns mate-máticos do século XIX e XX, motivados a investigar curvas e superfícies com características diferentes daquelas da Geometria Euclidiana, ou seja, formas que não se encaixavam em retas e planos, cones e esperas, curvas e superfícies as quais são sempre “lisas” e regulares.
Segundo Ian Stewart em [LG10], a regularidade desses elementos não apresenta nenhuma estrutura detalhadas em menor escala, superfícies são sempre superfícies e curvas continuam sendo curvas por mais que sejam ampliadas, uma característica fundamental para que as téc-nicas seculares da análise e do cálculo funcionassem. As téctéc-nicas consistem em aproximar
1A teoria do Caos ocupa-se do estudo de fenômenos que são altamente sensíveis às condições iniciais em que
são submetidos. Isso significa que alterações mínimas de um estado inicial podem implicar em grandes variações futuras e pouca previsibilidade.
2Apolônio de Perga (262 a.C. - 190 a.C.) era um matemático e astrônomo grego da escola alexandrina, chamado
de “o Grande Geômetra”, viveu em Alexandria, Éfeso e Perga.
Figura 2.1 Construção do Fractal de Apolônio
Fonte: Autoria própria (usando o software Corel Draw)
Figura 2.2 Níveis do fractal de Apolônio
Fonte: http://mathworld.wolfram.com/images/gifs/apollgas.gif, 2016
Figura 2.3 Níveis do fractal pentagonal de Durer
Fonte: Autoria própria (utilizando o software Corel Draw)
curvas por retas tangentes e superfícies por planos tangentes, porém, esses princípios simples-mente não funcionam em superfícies/curvas muito irregulares.
Os matemáticos da época, com seus perfis curiosos e “caçadores de contra-exemplos", ima-ginaram curvas altamente irregulares que, no início, eram vistas como parte de uma galeria de “monstros matemático”. O objetivo, conforme [LG10], era mostrar as limitações da análise clássica, pois durante os séculos XVII e XIX, acreditava-se que qualquer curva contínua, ex-ceto aquelas que tinham dobras e interrupções, possuía retas tangentes (derivadas) em quase todos os seus pontos.
Entretanto, para a surpresa dos matemáticos presentes, Karl Theodor Wilhelm Weierstrass, em uma palestra na academia de Berlim, em 18 de julho de 1872, provou que esta afirmação era falsa. Ele apresentou uma de, uma classe de curvas, que são contínas, porém, sem derivada em nenhum de seus pontos. Veja diversas outras curvas desta natureza em [Thi03].
conter todos os pontos da superfície de um quadrado unitário. Esse fato trouxe questionamentos quanto a idéia clássica de dimensão, pois uma curva unidimensional, era capaz de preencher completamente uma superfície plana. O estudo pioneiro de Peano deu origem a uma nova categoria de curvas: As curvas que preenchem o plano.
No final do século XIX, conforme [CEJ12], matemáticos estavam estabelecendo as bases para a moderna teoria dos conjuntos e nessa época surgiram conjuntos com propriedades “es-tranhas”. Em 1883, Georg Cantor, idealizou o mais simples destes: O conjunto de Cantor. O conjunto, inicia a partir do intervalo K0 = [0,1]. Em um primeiro estágio, remove-se o terço
médio aberto(13,23)deK0, gerando o conjuntoK1composto por dois segmentos disjuntos. Essa regra é aplicada continuamente a cada segmento que permanece e assim obtemos o conjunto de Cantor (fig. 2.4).
Figura 2.4 Conjunto de Cantor
Fonte: Autoria própria
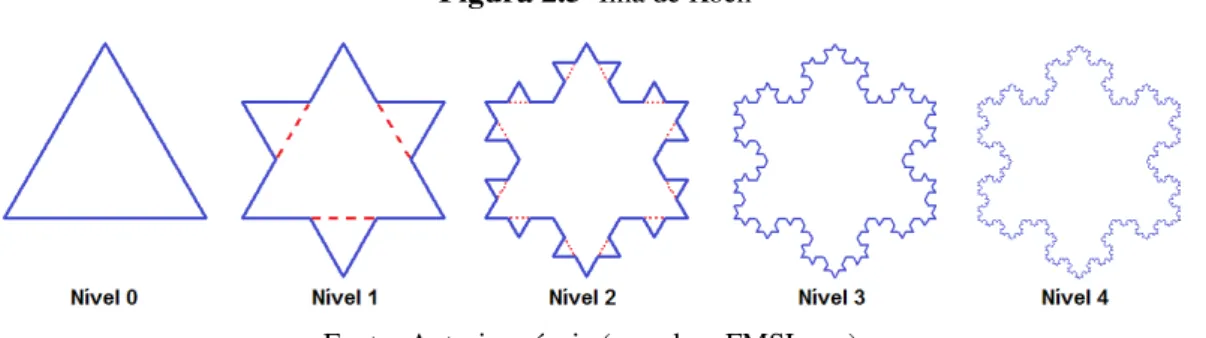
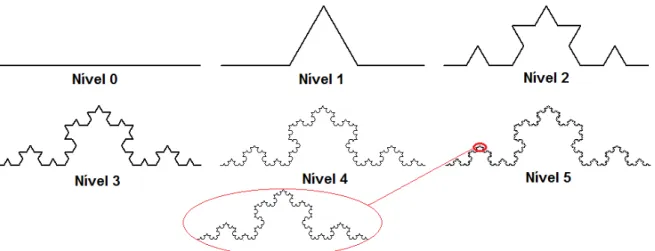
Em 1904, Helge von Koch, introduziu a sua Curva de Koch (fig. 2.10), um objeto criado a partir de um segmento de reta, que em um primeiro passo, tem seu terço médio substituído por um triângulo equilátero sem a base. Aplicando essa regra infinitas vezes em cada segmento restante, obtemos a Curva de Koch. Mais tarde, em 1906, Koch apresentou outra curva análoga que recebeu o nome deFloco de Neve de Koch (ou ilha de Koch), fig. 2.5. Essa curva equivale a três Curvas de Koch ao longo dos lados de um triângulo equilátero. No capítulo 3 veremos que a Ilha de Koch, é um “monstro matemático” cuja área finita é delimitada por uma fronteira infinita.
Figura 2.5 Ilha de Koch
Fonte: Autoria própria (usando o FMSLogo)
A descoberta desses “monstros” dividiu o pensamento matemático da época, para alguns, esses objetos eram apenas “extravagantes” e meramente artificiais, jamais seriam aplicáveis ao estudo de fenômenos naturais, para outros, como David Hilbert3referiam-se a tais descobertas como um “paraíso”, uma nova visão para os limites do cálculo e da análise, fonte de inspiração
para o estudo de novas classes de curvas. Anos mais tarde, Mandelbrot com sua visão siste-mática, enxergou justamente o contrário, para ele, a geometria dos fractais é capaz de incluir montanhas e nuvens:
...muitas formas da natureza - por exemplo, as formas das montanhas, nuvens, pedras trincadas e árvores - são demasiadamente complicadas para a Geometria Euclidiana. Montanhas não são cones. Nuvens não são esferas. Zonas costeiras de uma ilha não são círculos. Os rios não fluem em linha reta. Portanto, temos de ir além de Euclides se queremos estender a ciência relativa aos aspectos de natureza. [LG10]
2.1.1. Características dos fractais
Os fractais, independente de onde são encontrados ou da sua regra de formação, possuem características marcantes que os diferenciam dos demais objetos geométricos. A autosseme-lhança, a dimensão não-inteira e a infinidade de detalhes são inerentes a todos os fractais. A autossemelhança diz respeito ao grau de similaridade que os fractais apresentam a medida que são ampliados, ou seja, o quanto as partes são parecidas ao todos, por menores que sejam. Conforme [Jan08], os tipos de autossemelhança são:
a) Autossemelhança exata ou estrita: É o tipo mais restrito de similaridade, quaisquer partes do fractal contém cópias reduzidas do todo. Em outras palavras, o fractal com este tipo de similaridade, é composto por miniaturas perfeitas de si mesmo. Apenas os fractais estabelecidos por bases matemáticas são estritamente autossemelhantes, eles também são conhecidos comofractais puros.
b) autossemelhança aproximada ou estatística:É o caso menos evidente de auto-semelhança, exige-se que o fractal tenha medidas numéricas ou estatísticas as quais se preservem com a mudança de escala. Boa parte dos elementos da natureza obedecem a autossemelhança estatística, neles, suas partes não são idênticas, mas parecidas com o todo. [Jan08] diz que:
O que existe nas figuras da natureza é uma auto-semelhança aproximada em diferentes escalas. Essa auto-semelhança aproximada é chamada de auto-semelhança estatística, porque, em diferentes escalas, essa auto-semelhança existe em média. Nos fractais matemáticos, as partes são cópias exatas do todo, mas nos fractais naturais as partes são apenas reminiscências do todo. [Jan08]
A fig. 2.6 ilustra a autossemelhança exata de uma árvore, criada em um software, e a autossemelhança aproximada de uma árvore real.
Alguns dos fractais com a característica de serem exatamente autossemelhantes são: a Curva de Koch, o triângulo de Sierpinski, o Conjunto de Cantor, a Esponja de Menger e ou-tros fractais que veremos em detalhes no capítulo 3. As árvores, o couve-flor, brônquios e bronquíolos, conchas, nuvens e rios são exemplos de fractais com autossemelhança estatística,
Figura 2.6 Tipos de autossemelhança
Fonte: [Tay02](adaptado)
pois eles contém partes, que mantém a estrutura do tudo, mas não são idênticas. Uma muda de uma árvore, é uma pequena árvore; um pedaço de brócolis, tem o “tronco” verde-claro e suas extremidades em verde-escuro, ou seja, as propriedades do brócolis são mantidas.
Figura 2.7 Partes de um brócolis
Figura 2.8 Outros exemplos de fractais naturais
(a) Couve-flor da espécie Romanesco (b) Tentáculo de polvo
(c) Brôquios e bronquíolos (d) Babosa (e) Árvore Sangue do Dragão
2.2.
Dimensão Fractal
“Não há ramo da Matemática, por mais abstrato que seja, que não possa um dia vir a ser aplicado aos fenômenos do mundo real.”
(Nicolay Lobachevsky)
No ensino básico, temos o primeiro contato com as formas mais simples da Geometria Euclidiana: ponto, segmentos de reta, polígonos, círculos, paralelepípedos, cones, pirâmides, esferas. Nesse período somos ensinados a calcular medidas de comprimentos, perímetros, áreas e volumes. Em face desse aprendizado, temos uma noção bem intuitiva de dimensão. Segundo [LG10], o conceito de dimensão, nos moldes da Geometria Euclidiana, nos diz que:
1. Um segmento de reta tem dimensão 1, pois entende-se que qualquer ponto do segmento pode ser especificado usando apenas uma coordenada, um número. Um pontoA está a uma distância dexunidades de uma extremidade do segmento.
3. Um cubo tem dimensão 3, pois entende-se que qualquer pontoAdo cubo pode ser espe-cificado usando apenas três coordenadas (x,y,z). Onde x, y ezrepresentam respectiva-mente, as distâncias deAaté a face esquerda, a face inferior e a face traseira.
Nesse sentido, um ponto, isoladamente, não tem direções, portanto tem dimensão 0. Uma linha tem um sentido de direção, no quadrado encontram-se em duas direções (o plano), e no cubo temos três. Princípios semelhantes a estes se aplicam em superfícies e linhas curvas. Uma linha curva tem dimensão 1, a superfície de um objeto liso, como uma esfera ou um toro, possuem dimensão 2. Um objeto sólido, como uma esfera sólida ou um toro sólido, tem dimensão 3. Neste aspecto, a dimensão sempre representa um número inteiro. Um ponto, uma reta, uma superfície e um sólido possuem dimensões 0, 1, 2 e 3, respectivamente. Veja fig. 2.9.
Figura 2.9 Dimensões na Geometria Euclidiana.
Fonte: [LG10]
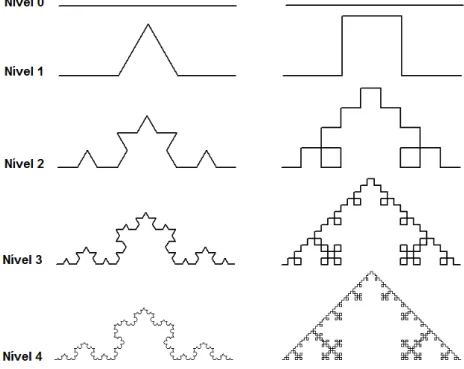
Para estabelecer alguns princípios da dimensão fractal, vamos tomar como referência duas curvas: a Curva de Koch, cujo processo de construção foi descrito brevemente na seção, 2.1, e uma variação dela constituída por substituições do terço médio por quadrados sem base, a Curva de Koch Quádrica, ambas inciadas com um segmento de tamanho 1.
A medida que os níveis avançam, o perímetro da curva de Koch, aumenta 43, então, em seu no k-ésimo nível, o perímetro Pk = 43k (Veja tabela 3.3). Analogamente, a curva de koch
quádrica aumenta 53, de forma que no nível k seu perímetro vale P′
k = 53
k
. Em ambas as curvas, o perímetro é infinito pois:
lim
k→∞
4
3
k
= lim
k→∞
5
3
k
=∞.
A respeito da complexidade destas curvas, [dAMdBM+08] menciona o seguinte:
Uma curva deste tipo, devido à sua complexidade infinita, contém um número de in-finitas “dobras” que, se ampliadas, continuam aparecendo indefinidamente. Devido a este infinito detalhamento, esta curva “ocupa” mais “espaço” que uma linha convenci-onal, possuindo assim uma dimensão fractal maior que 1.0, sem chegar, no entanto, a ocupar o espaço de uma faixa que a contém (dimensão 2.0). Desta maneira, conceito de dimensão fractal,D, está intimamente relacionado com a estrutura de ocupação do espaço da figura.
Figura 2.10 Níveis da Curva de Koch e a da Curva de Koch Quádrica.
Fonte: Autoria própria, usando o FMSLogo
mais de espaço. Portanto, é razoável imaginar que 1<D1<D2<2, logo, ambas as dimensões
não são números inteiros.
Intuitivamente, as dimensões dos objetos da geometria euclidiana com suas construções ba-seadas substancialmente em ponto, reta, plano e espaço, são mais simples de assimilar. Entre-tanto, no caso da geometria dos fractais, não temos uma percepção dimensional tão imediada, pois não há uma forma única de construção elementar para os fractais, cada um possui a sua regra individual de formação.
O matemático Felix Hausdorff4, estabeleceu uma medida dimensional, aperfeiçoada por Besicovitch5, bastante complexa e abrangente que permite calcular a dimensão de diversos conjuntos, sejam eles fractais, ou não. Posteriormente, Mandelbrot utilizou os estudos de Hausdorff-Besingovich para medir e comparar os fractais, isto é, esse trabalho serviu de base para determinar o quanto um objeto fractal é mais “rugoso” ou “espaçoso” que outro.
Veremos duas formas de medir a dimensão fractal de figuras a partir de idéias elementares oriundas da própria Geometria euclidiana: A dimensão por autossimilaridade e a Dimensão por contagem de caixas.
4Felix Hausdorff (Breslávia, 8 de novembro de 1868 - Bonn 26 de janeiro de 1942), matemático alemão,
considerado um dos fundadores da topologia.
5Abram Samoilovitch Besicovitch (Berdyansk, 23 de janeiro de 1891 - Cambridge 2 de novembro de 1970),
2.2.1. Dimensão por Autossimilaridade
Esta dimensão é adequada apenas para os fractais que apresentam autossimilaridade exata. Utilizando exemplos da própria própria Geometria Euclidiana, iremos determinar uma fórmula que expressa a dimensão fractal de um objeto, a qual resulta fundamentalmente, em valores não-inteiros.
Tomemos inicialmente, um segmento de reta, um quadrado e um cubo. Iremos dividir os lados de cada um desses objetos emrpartes congruentes e em seguida verificar a relação entre r, a quantidadende partes obtidas e a dimensãoDdo objeto.
2.2.1.1. Segmento de reta
Vamos dividir um segmento de reta, emr=4 partes congruentes:
Figura 2.11 Segmento de reta dividido em 4 partes
Fonte: Autor
Obtemos então,n=41segmentos congruentes de tamanho 14.
2.2.1.2. Quadrado
Analogamente, dividindo o lado de um quadrado emr=4 partes iguais, obtemosn=42 quadrados congruentes.
Figura 2.12 Quadrado com lado dividido em 4 partes
Fonte: Autor
2.2.1.3. Cubo
No caso de um cubo, ao dividir sua aresta igualmente emr=4 partes, obtemosn=43
cubos congruentes.
SejaD, a dimensão de cada um desses objetos. Podemos relacionar os valores der,neD, estão relacionados da seguinte forma:
n=rD (2.1)
Figura 2.13 Cubo com aresta dividida em 4 partes
Fonte: Autor
logn=logrD⇒logn=Dlogr.
portanto:
D=logn
logr. (2.2)
Vejamos uma tabela com o resumo dos resultados referentes a expressão 2.1 na reta, no quadrado e no cubo.
Dimensão 1 Dimensão 2 Dimensão 3
r
=
2
cópias 21=2 22=4 23=8
r
=
4
cópias 41=4 42=16 43=64
Fonte: Autor
Tabela 2.1 Número de objetos similares nas dimensões Euclidianas: fatores de redução 2 e 4)
Por construção, na curva de Koch Quádrica, os segmentos são divididos emr=3 partes, de forma que cada uma geran=5 novos segmentos, portanto, pela equação 2.2, a dimensão desta
curva vale:
D= logn
logr = 5
3 ∼=1,4649
2.2.2. Dimensão por contagem de caixas (box-counting)
Existem inúmeras fórmulas que são utilizadas para determinar da dimensão fractal de um objeto. O método da dimensão por contagem de caixas (box-counting) é um dos mais utilizados por sua simples implementação computacional. O algoritmo para o cálculo dessa dimensão considera uma figura qualquer coberta por um conjunto de retângulos. Inicialmente desenhamos um único retângulo de forma a conter uma figura planaF qualquer. Em seguida divide-se cada lado do retângulo emkpartes iguais, obtendo assimk2retângulos semelhantes. Definição 2.2.1. Seja nk, o número de retângulos que interceptam pelo menos um ponto de uma figura F contida em uma malha. A dimensão fractalDda figura é dada por:
D= lim
k→∞ lognk
logk
Vamos acompanhar uma aplicação desse método na figura abaixo. Os quadrados em azul são aqueles que contém algum ponto da imagem. Por simplicidade, dividimos o retângulo em uma quantidade de partes iguais a potências crescentes de 2.
Figura 2.14 Metodo de contagem de caixas
Fonte: Autoria própria.
Vejamos uma tabela resumo com a evoluçãonkedkpara cada valor dek:
k nk logk lognk loglognkk
2 4 0,30103 0,60206 2
4 12 0,60206 1,07918 1,79248 8 36 0,90309 1,55630 1,72330 16 148 1,20412 2,17026 1,80236 32 1056 1,50515 3,02366 2,00887
Fonte: Autoria própria.
Tabela 2.2 Resumo do comportamento denkeloglognkk
counting, notamos que ele pode ser usado para uma grande variedade de objetos geométricos, sejam eles autossimilares ou não.
2.3.
A presença dos fractais em outras áreas
Nesta seção, iremos descrever uma amostra das inúmeras aplicações dos fractais em diversos ramos científicos. Graças a visão sistemática de Mandelbrot, o estudo dos fractais passou a ter uma relação mais estreita com a modelagem de fenômenos físicos, biológicos, geológicos, econômicos e até métodos computacionais. Atualmente, a comunidade científica está em uma constante publicação de trabalhos com foco nas aplicações da geometria fractal.
2.3.1. Fractais na medicina
Uma das utilidades da dimensão fractal, especialmente no estudo do câncer, é caracteri-zação do estágio em que se encontra os tumores malignos no sistema nervoso central. Imagens adquiridas através de ressonância magnética, foram comparadas à imagens de cistos (tumores benignos), imagens de gliomas (tumores malignos) e imagens de lesões massivas. Concluiu-se que, com a técnica da dimensão fractal, é possível obter uma melhor distinção entre os tumores benignos dos malignos pelo fato destes últimos possuírem uma característica marcante relativa a maior irregularidade do seu contorno. Assim, extraindo-se a dimensão fractal desses contor-nos, pode-se distinguir os tumores e, posteriormente, analisar o estágio em que se encontram. Entre os trabalhos que utilizam a técnica da dimensão fractal na medicina podemos destacar:
• Análise fractal do contorno ósseo e o contorno dental através de imagens radiográficas; • Cálculo da dimensão fractal de células cancerígenas para identificação de risco de câncer
de mama;
• Outras investigações com fractais através de imagens oriundas de ressonância magnética, doppler, ultrasom e tomografia computadorizada.
nesse caso a dimensão fractal delas será substancialmente maior que a dimensão das células normais, figs. 2.15(a) e 2.15(d).
Figura 2.15 Fotos microscópicas de células epteliais
Fonte: [DGWS15](adaptada)
2.3.2. Fractais na informática
A indústria cinematográfica, os processos de compressão e visualização de imagens e vídeos e a simulação de ambientes e paisagens naturais utilizam técnicas baseadas nos padrões da geometria fractal. A geração de imagens montanhosas, cenas com diversos personagens fazem uso de padrões autossimilares.
2.3.2.1. Compressão de imagens/vídeos
Muitas pessoas desconhecem o padrão de imagem Fractal Image File - FIF. Esta tecno-logia foi descontinuada há algum tempo, todavia, sua metodotecno-logia de compressão e descom-pressão ainda é objeto de estudo e ao longo dos anos vem obtendo melhorias significativas. Os arquivos FIF, apesar da sua ótima taxa de compressão, perderam espaço para os arquivos tipo JPEG6, pois apesar de ocuparem mais memória, os JPEG consomem menos tempo para comprimir uma imagem.
Na época das imagens FIF, o matemático Michael Barnsley7e sua equipe registraram várias patentes relacionadas a fundamentos matemáticos e computacionais para o tratamento de ima-gens, visando minimizar o consumo de memória e a velocidade de compressão/descompressão. Uma dessas patentes foi voltada para a compactação fractal de imagens. Em linhas gerais, um desses métodos consiste em particionar uma imagem em quadros e identificar quais destes são
6Joint Photographic Experts Group JPEG. Grupo de trabalho especializado na criação de padrões de
codifica-ção de imagens. Mais detalhes emhttps://jpeg.org/about.html
7Michael Fielding Barnsley, nasceu em 1946, Matemático Britânico além de pesquisador e empresário com
semelhantes. Assim partes similares da imagem seriam gravadas uma única vez, evitando assim a redundância no armazenamento dos dados. Veja fig. 2.16
Figura 2.16 Imagem com quadros semelhantes destacados
(a) Imagem original (b) Semelhantes nos quadros
Fonte: http://www.rasip.fer.hr/research/compress/algorithms/adv/fraccomp/index.html, 2015
Uma das aplicações desse método é utilizado para otimizar o armazenamento de vídeos criados com a tecnologia 4K. Para se ter uma idéia, esses vídeos, cuja resolução (quantidade de pixels8) é 4 vezes maior que o atual padrão full HD (1920 x 1080 pixels), utilizam uma grande quantidade de memória para serem armazenados. Dessa forma, imagens e vídeos 4K, consomem muito espaço em memória e necessitam de eficientes algoritmos de compactação para viabilizar a sua transmissão e reprodução.
2.3.2.2. Multidão fractal
Atualmente, os efeitos especiais são bastante utilizados para representar multidões nas ce-nas que necessitam de muitos personagens. Constata-se por observação, que a autossemelhança é usada na reunião de objetos e/ou pessoas, pois aplicando um fator de redução e o uso aleatório de fisionomias em um grupo de personagens, os softwares cinematográficos criam verdadeiras multidões fractais. No filme de animação “Os minions” (2015), as técnicas que usam partes autossimilares estão presentes na distribuição de um grande volume de personagens ao longo de uma superfície na neve. Veja fig. 2.17
2.3.2.3. Geração de superfícies montanhosas
Com o vertiginoso avanço da computação gráfica, é pouco provável que a paisagem montanhosa que apreciamos em um filme seja 100% real. Adiante, iremos ilustrar um algoritmo simples que permite, mediante um programa de computador ou manualmente, a criação de uma superfície montanhosa utilizando subdivisões randômicas de um triângulo qualquer. A superfície final gerada tem um aspecto fractal.
Figura 2.17 Multidão de personagens com características fractais
(a) Cena da animação - Os Minions
(b) Áreas semelhantes destacadas em escalas menores Fonte: Autoria própria.
Partindo de um triângulo no espaço, é possível gerar superfície montanhosa conforme o seguinte processo:
1. Determinam-se os pontos médios dos lados do triângulo;
2. Unir esses pontos médios com segmentos de reta, gerando assim, quatro novos triângu-los;
3. Deslocar, aleatoriamente, os pontos médios para cima ou para baixo dentro de uma vari-ação de altura ou profundidade.
4. Repetir recursivamente, nos triângulos obtidos, os passos anterioreskvezes considerando que, a cada novo passo, a variação de altura/profundidade deverá ser igual metade da variação anterior;
Vale destacar que alguns softwares controlam o nível de aspereza de montanhas e rele-vos através da dimensão fractal, quanto maior a dimensão mais áspera será superfície. Caso contrário, se a dimensão se aproxima de dois, a superfície ficará cada vez mais "lisa".
2.3.3. Fractais nas Artes
Figura 2.18 Geração da superfície montanhosa
(a) Triangulo inicial (b) Montanha nível 1
(c) Montanha nível 2 (d) Montanha nível 3
(e) Montanha nível 4
Fonte: https://pt.wikipedia.org/wiki/Fractal, 2015 (adaptado)
ciências exatas, sinto muitas vezes que tenho mais em comum com os matemáticos do que com os meus colegas artistas.” (Maurits Cornelius Escher)
O atraente visual dos fractais trouxe mais ênfase ao casamento das artes com a matemá-tica. As fórmulas matemáticas, e as iterações, produzem, através de softwares fractais, bonitas imagens com diferentes estilos (3D, coloridas, em tons de cinza). Muito tempo antes, alguns artistas já produziam suas obras utilizando o formas autossimilares. O modelo da geometria fractal se encaixa perfeitamente na intuição artística dos pintores. Maurits Cornelius Escher e Salvador Dali são dois desses gigantes artistas cujos quadros eram recheados de imagens que diminuiam de tamanho recursivamente, até o limite da menor gravura possível que suas mãos fossem capazes de desenhar. Em especial, Escher demonstra um gosto especial pelas estruturas autossemelhantes.
Até aqueles que não apreciam a matemática, percebem com facilidade, a constante miniatu-rização das imagens em seus quadros famosos. Escher é quase uma unanimidade nas citações contidas nas literaturas alusivas à matemática com a arte; seu estilo é bastante apreciado tanto pela beleza quanto pelo capricho característico de seus quadros que sempre apelam para a in-tuição de infinito.
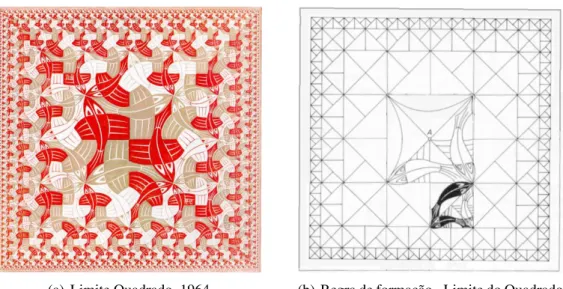
A regra de formação (acompanhe na fig. 2.20) da obra limite do quadrado (fig. 2.19(b)) consiste no seguinte:
Figura 2.19 Exemplos de quadros semelhantes na imagem
(a) Limite circular I, 1958 (b) Limite Quadrado, 1964
Fonte:http://www.bb.com.br/docs/pub/inst/img/EscherCatalogo.pdf, 2015
2. Identifique o centro da folha e desenhe um quadrado central de ladoℓ1= ℓ0
2 (quadrado de 1ª geração).
3. Em seguida, ao redor do quadrado de 1ª geração, desenhe quadrados de ladoℓ2= ℓ1
2 =
ℓ0
4, ou seja, os quadrados de 2ª geração.
4. Desenhe, até preencher a folha de papel, os quadrados ao redor daqueles da geração anterior. Por fim, divida os quadrados traçados em triângulos retângulos de acordo com a figura 2.20.
2.3.4. Fractais na arquitetura
Obras arquitetônicas atuais e de longas datas, eram construídas com características au-tosemelhantes. Veremos algumas imagens, de construções seculares, cuja composição exibe o apelo aos padrões fractais. Os detalhes autossimilares enalteciam essas construções.
A Catedral de S. Maria, Anagni-Itália, construída no séc. XIII, ainda contém mosaicos que apresentam um padrão fractal, mais precisamente, a disposição dos ladrilhos, são análogas ao triângulo de Sierpinski, o qual veremos no Capítulo 3.
Na fig. 2.22(a) podemos ver a forma fractal do templo hindu Vishnu, compostos por picos autossimilares. A regra de formação do templo, fig. 2.22(b), mostra um esboço das etapas de construção do templo Vishnu com uma vista lateral e outra vista superior parcial.
Figura 2.20 Exemplos de quadros semelhantes na imagem
(a) Limite Quadrado, 1964 (b) Regra de formação - Limite do Quadrado Fonte: http://amadora.cienciaviva.pt.../Escher_PAV.pdf, 2015 (adaptado)
Figura 2.21 Mosaico da Catedral de S. Maria
Figura 2.22 Templo Vishnu, Varanasi-Índia.
(a) Templo Vishnu (b) Autossimilaridade do templo Fonte: http://fractalenlightenment.com/...the-fractal-structure-of-hindu-temples, 2016
Figura 2.23 Imagens da Square Federation