Curso de matematica para economistas: capitulo V: otimização dinamica

t i

----.-

-..,--ISSN 0104-8910

CURSO DE MATEMÁTICA PARA ECONOMISTAS-CAPÍTULO V: OTIMIZAÇÃO DINÂMICA

Rubens Penha Cysne

Humberto de Athayde Moreira

Curso de Matemática para Economistas Capítulos V

Otimização Dinâmica

Rubens Penha Cysne Humberto de Athayde Moreira

Setembro de 1996

Endereço para Contato:

Escola de Pós Graduação em Economia da Fundação Getulio Vargas

Praia de Botafogo 190, 110. andar, Sala 1124 Rio de Janeiro -RJ -Brasil

Telefone: 55-21-552-5099 Fax: 55-21-536-9409

e-mail:

PREFÁCIO

Os autores objetivam, com este trabalho, bem como com aqueles que lhe precederam (capítulos l, 2, 3 e 4). registrar as suas experiências ao longo dos últimos anos ministrando cadeiras de matemática nos cursos de pós-graduação em economia da Fundação Getulio Vargas, da UFF (Universidade Federal Fluminense) e da PUC-RJ.

Reveste-se de constante repetição em tais cursos a discussão sobre que pontos abordar, bem como com qual grau de profundidade. e em que ordem. É neste sentido que os autores esperam. com a sequência didática aqui apresentada, trazer alguma contribuição para o assunto.

Este capítulo em particular baseia-se fundamentalmente no trabalho desenvolvido no capítulo VI do livro Dinâmica Macroecônomia, de autoria de Mário Henrique Simonsen. Com a aquiescência do autor, que a princípio seria um dos participantes do trabalho, não o tendo feito por motivos de saúde, uma das seções deste texto é transcrita de trechos selecionados do livro, e outras apresentadas sob uma abordagem alternativa. Em adição, resolve-se grande parte dos exercícios propostos do referido capítulo do Dinâmica. bem como alguns novos exercícios.

CAPÍTULOS

OTIMIZAÇÃO DINÂMICA

1. Cálculo de Variações -Caso Discreto

Trataremos nesta seção de encontrar seqüências x = (X I .X2 ••••• X, ••• ) que

-maximizem séries do tipo

I.

_,=1

g, (x .. X,_I)' onde g, representa uma função côncava diferenciável e definida para x, e X,_I pertencentes a um intervalo aberto da reta.

Supõe-se dado o ponto de partida xO•

Como exemplo desta situação, pode-se tomar o caso de uma empresa que, na ausência de custos de ajustamento, tem o seu lucro no mês t dado por a· b' . y, - ｹｾＬ＠ onde y representa o número de homens empregados por mês na produção e a e b são constantes reais positivas. Incluindo-se o custo de mudança de um nível de emprego para outro, dado por c( y, - y H ) 2 , esta empresa tratará de maximizar o valor atual de seu lucro

b' 2 ( ) ? ..

a y, - y, - c y, - Y'-I -, C = constante positIva

à taxa de desconto v num horizonte de planejamento infinito. Matematicamente, o problema expressa-se por

-ma.?'

F(y) =

I.

v' . (ab' y, - y,2 - c(y, _ Y,_I ) 2) ,

Iy,',..

,=1

onde Y = (y I ,Y 2 •••• ,Y , , ... ) é uma seqüência de níveis de emprego. Supõe-se dado

o nível inicial Yo.

Antes de passarmos à caracterização da solução do problema, utilizando para tal as equações de Euler - Lagrange, precisamos de uma digressão envolvendo alguns conceitos prévios. Dentre estes, destacam-se as definições e propriedades de funcionais côncavos, pontos internos e do diferencial de Gateaux.

Funcionais Côncavos

Ao longo de toda esta seção denotaremos por L um espaço vetorial real e por C um conjunto convexo neste espaço (C

c

L).

Definição: F: C ｾ＠ 9t é dito ser um funcional côncavo (resp. estritamente côncavo) se F«(l-a)x + ay) ｾ＠ (resp.> )(1-a)F(x) +aF(y) para todo x, y E C, x ;t y, e

°

< a < I: F: C ｾ＠ 9t é dito ser um funcional convexo se -F for um funcional côncavo.

Definição: Dado C um subconjunto convexo do espaço vetorial L e x E C, definimos

S(X)={hEL;3a>0 tal que X+ahEC} e l(x)=S(x)Il(-S(x)).

Exemplo: Dado L = Z-(9t) =

{(x,)

;

X I E 9t, 'v'

r

E N e

ｳｵｾｸ＠

,I

é finito } considere o

lEI! lEI!

conjunto convexo C= 1:(9t) = {(X'),EI! EZ-(9t);X,

ｾｯＬ＠

'VtEN}. Temos que

x =

(1/t)

_lEI! E 1:, mas h = (-1,-1,-1, ... ,-1, ... )

e

S(x), pois para que isto ocorresse

seria necessário que x + Â.h E I: para algum Â. > 0, i.e, l/r + Â(-1) ｾ＠ 0, 'Vr E N, o que evidentemente não ocorre.

LemaJ.J. Sejam F: C ｾＹｴ＠ um funcional côncavo, x EC e h E S (X). Definamos

F(x

+

Â.h) - F(x) _

g(.,x,h):(O,a] ｾ＠ 9t tal que g(Â.,x,h) = . Entao:

Â. .

i) g(.,x,h) é função não crescente de Â.;

ii) g(Â,x,h) + g(Â,x,-h) S 0, para h E I (x) e a suficientemente pequeno;

iii) F(x+ah)-F (x) S ag (Â., x, h) SF(x)-F(x-ah), para h E I(x) e a suficientemente pequeno;

. ) F' h) l' F(x+Â.h)-F(x). h l() F'( h)' fi .

IV (x, = Im eXiste, e se E x, x, e Imto;

￀ｾｏＧ＠ Â.

v) F(x + ah) -F(x) S a F'(x,h) S F(x) - F(x-ah), para h E l(x) e a suficientemente

pequeno;

Demonstracão:

i) Seja O<Â.'<Â.Sa. x+J1 Â. h = (1-Jl)x+Jl (x+Â.h)

e F é funcional côncavo, temos:

Então

F(x+ J1 Â. h) ｾ＠ (1-Jl)F(x) + Jl F(x+ Â. h) ｾ＠ F(x + J.L Â h) - F(x) ｾ＠ J.L (F(x + Â h) - F(x»)

Â.'= J1 Â., com

°

< Jl < 1.

ｾ＠ J1 Â. g(Jl Â, x, h) ｾ＠ Jl Â. g(Â, x, ｨＩｾ＠ g(Â.', x, h) ｾ＠ g(Â, x, h) Portanto g(.,x,h) é não-crescente.

ii) Como F é funcional côncavo temos que:

ｾ＠

F(x+ Â h)+

ｾ＠

F(x-Â h) S

ｆＨｾ＠

(x+Â h)+

ｾ＠

(x-Â h») = F(x) ｾ＠ F(x+Â. h)+ F(x-Â. h) S 2 F(x)

Como

· F(x+Àh)+F(x-Àh)-2F(x)

Asslm,g(À,x,h)+g(À,x,-h)= À $O,\iÀE(O,a].

iii) Pelo item (i), g(À,x,h) ｾ＠ g(a,x,h) e g(À,x,-h) ｾ＠ g(a,x,-h), \iÀ E (O,a]. Pelo ítem

(ii) g(À,x,h) $ -g(À,x,-h) e portanto g{À,x,h) $ - g{a,x,-h}, \i À E (O, a] . Assim,

F(x+ah)- F(x)

=

ag{a,x,h} $ ag(À,x,h} $ -ag(a,x,-h}

=

F(x)- F(x-ah).

iv) A função g(.,x, h): ＨｏＬ｡｝ｾ＠ 9t é não crescente (ítem

(i».

Portanto existe o limite F(x,h)=SUD g(À,x,h)(podendo ser +00). Se h E I(x), pelo item (iii) g(.,x,h) é

ÀE(b.al

limitada superiormente, logo F'{x, h) deve ser finito.

v) É consequência imediata dos ítens (iii) e (iv) .•

ExempLo: Seja ｆＺＹｴｾ＠ 9t tal que F(x) =

Ixl.

É fácil verificar que

F'(O,I) = 1 = F'(O,-l). Neste exemplo F'(O, 1) representa a derivada à direita de F em

°

e -F'(O,-I) a derivada à esquerda de F em O.

Definição: Dado um conjunto convexo Cc L, definiremos

C

= {x E C;S(x) = L }. o

O conjunto C é chamado de conjunto de pontos internos de C.

o

No exemplo anterior, x

=

(1,1, ... ,1, ... ) E (I : ). De fato, seja h E 1- então Ih,1 $ n , \it E

ｾＬ＠

para algum n>O constante. Tomemos 0< Ã. $

Yn.

Neste caso x + Ã.h E I:, pois 1 + Ã.h I ｾ＠ 1-Ã.n ｾ＠ 0, \il E ｾＮ＠ Observe, porém, que

L:.

=

{(X')'EIC

Er;X, >O} é diferente de

cl:)'

uma vez que

(I/t)'EIC

E

L:.

mas não

o

pertence a I : .

o Teorema J.J.(Teorema do Máximo): Seja F: ｃｾＹｴ＠ um funcional côncavo e Xo E C.

Então, para que F(x) passe por um máximo (absoluto) no ponto Xo é necessário e suficiente que F(xo,h) $ 0, 'Vh E L.

Demonstração:

Suponhamos inicialmente que Xo E C seja um ponto de máximo. Seja hE L. Como

o

.lO E C, existe a>

°

tal que Xo + Â.h E C, 'VÃ. E (O,a]. Então F(xo _{+Â.h)- F(xo) $ 0, 'VÃ. E (O,a]. Fazendo}

ￃＮｾｏﾷ＠

_{tem-se que F(xo,h) $ 0, 'Vh}

_e

_L.

Ã.

Reciprocamente, seja x E C, então h = x - Xo E L. Logo pelo lema 1.1. v,

Como F'(x,h)SO para todo h E L, devemos terF(x)-F(xo)SF'(xo,x-xo)S

°

para

todo x E

c..

Teorema 1.2. (Teorema do limite): Seja, para cada n e N, Fn:C -+ ｾ＠ um funcional

o

côncavo. Suponhamos que lim Fn (x) = 0, "i/ x E C. Se Xo E C então

n-+-o

Demonstracão: Como Xo E C, existe a >

°

tal que Xo + a h, Xo - a h E C. Pela hipótese dado E > 0, existe 1lo e N tal que "i/n > no '

/Fn _(xo)/ < Ea I 2

/Fn (x_o +ah)/ < Ea/2

/Fn (x_{o -} ah)/ < Eal 2

Pelo lema l.l.v.,

- E a < Fn (x o + ah) - Fn (x o ) S a Fn' _(xo ' h) S Fn _(xo ) - Fn _(xo - ah) S Ea .

Assim, dado E > 0, existe 1lo e N tal que "i/n > _{no tem-se /F: (xo' h)/} < E .•

Teorema 1.3. (Teorema da série convergente): Seja {Fn:C -+ ｾｽｄｅｉｃ＠ uma seqüência de funcionais côncavos. Suponhamos que a série

n=1

seja convergente para todo x E C. Então S: C -+ ｾ＠ é um funcional côncavo e dado

o

-X_o E C, tem-se S' (xo ,h) =

L

Fn'(x_O ,h), "i/ h e L.

n=1

n _

Demonstracão: Defina _{Sn(x) =}

LF.(x)

_{e Rn(x) = LF.(x) para cada}

1=1 l=n+1

n e N, "i/ x e C. Temos que Sn e Rn são funcionais côncavos definidos em C (Prove !), tais que S = Sn + Rn ,"i/n E N. Seja h e L. Então

n

ｓＧＨｸｯＬｨＩ］ｌｆＮＧＨｸｯＬｨＩＫｒｾＨｸｯＬｨＩＬ＠

_{'v'neN. Como limRn(xo) = 0, pelo teorema}

1=1

n.

-anterior temos lim R; _(xo ,h) _{= O. Logo S'(xo' h) =}

L

_{F.'(xo, h) .•}

11-'- 1=1

Definição: Seja L um espaço vetorial real, C

c

L convexo e G: C -+ ｾ＠ um funcional.

o

G(x + aJl) - G(X) .

eXiste para todo h E L. Neste caso, ÔG( x. h) é notação para

ex

diferencial de Gateaux de G no ponto x na direção h.

Observação: Quando L = 9tn diferenciabilidade à Gateaux significa existência de derivada direcional em toda direção.

Teorema 1.4. Sejam F,F,: C ｾ＠ 9t funcionais côncavos, t =1,2 ... Então:

°

a) F é diferenciável no sentido de Gateaux em x E C se, e somente se

F'(x,h) + F'(x,-h) = 0, V'h E L.

o

b) Suponha que F é diferenciável no sentido de Gateaux em X_o E C. Então X

o

é um ponto de máximo para F se, e somente se ÔF( xo' h) = 0, V'h E L.

c) Suponhamos que

F,

é diferenciável no sentido de Gateaux em

-Xo E C, V'I E N, e que a série S(x) = I F; (x) seja convergente para todo x E C. Então

1=1

S(x) é um funcional côncavo e diferenciável no sentido de Gateaux em

-Xo e ÔS(xo,h) = IOF;(xo,h), V'h E L.

1=1

Demonstracão:

a) É consequencla imediata da definição e do fato que Iim F(x + cxh) - F(x) = F'(x, h) e lim F(x +cxh) - F(x) = -F'(x,-h), V'h E L.

｡ｾｏＧ＠ ex ｡ｾｏＭ ex

b) Se F passa por um máximo em _xo' pelo teorema do máximo temos que F'(xo,h) SOe F'(xo,-h) S 0, V'h E L.Como F é diferenciável no sentido de Gateaux

no ponto _xo' pelo ítem (a) segue-se que

F'(xo,h) = -F'(xo,-h). Assim ÔF(xo,h) = F'(xo,h) = O. Por outro lado, se ôF(xo,h) = 0, V'h E L ,então F'(xo,h) = ôF(xo,h) = 0, V'h E L. Pelo teorema do

máximo F passa por um máximo em X_o'

c) Pelo teorema da série convergente:

-

-S'(xo,h)

=

I F;'(xo,h) e S'(xo,-h)

=

I F;'(xo,-h).

1=1 1=1

Como F, é diferencial no sentido de Gateaux em X_o temos pelo ítem (a) que

novamente pelo ítem (a) S será diferenciável no sentido de Gateaux e

-ÔS(xo,h) = LôF; (xo,h) .•

1=1

Consideremos agora, para cada 1 e K, g,:9t2 _{-79t um funcional côncavo}

diferenciável à Gateaux tal que sua derivada direcional dependa linearmente da direção (observe que esta hipótese é atendida em particular se g, for diferenciável no sentido usual do cálculo-Frechét e Stolz- definido no capítulo 3, para cada te K ).0 problema típico abordado no início desta seção pode ser fonnulada da seguinte fonna: encontrar uma seqüência (xo,xl' .... xl' ... ) de números reais que

-maximize

L

gl (XI' XI_I) com X_o dado inicialmente.

1=1

Mais precisamente, iremos dividir este problema em dois casos:

Caso a) O espaço de seqüências sob o qual iremos trabalhar será

L =

r

(9t) = {

x

= (x, );:1; x, e 9t, \:;/1 e K e

ｳｵｾｸＬＱ＠

é finito}. Neste espaço

'EI!

-consideraremos o conjunto _{C={X eL; Lgl(x"xl_1}) converge e é finito} e

1=1

suporemos que C seja convexo em L.

-Seja então F(X)= Lgl(X"xl_1 ), X=(XI)IEI! EC.

1=1

o

Observe que se C::t:. 0 temos que F(X) não assume valor mais infinito para o

X e L. De fato, seja X o e C e X e L arbitrário, então existe a e (0,1) tal que Xo + ah = aX + (1-_{a)Xo e C, onde} h _{= X - Xo. Pela concavidade}

de F tem-se que: aF(X) + (1-_{a)F(Xo) S F(} aX _{+ (1- a)Xo) o que implica que}

ｆＨｘＩｓｾＨｆＨｘｯＫ｡ｨＩＭＨＱＭ｡ＩｆＨｘｯﾻ＠

_a e este último valor é finito pela definição de

c.

Por hipótese cada funcional g, é diferenciável a Gateaux e sua derivada direcional depende linearmente da direção. Assim,

ôg,(X,h) = gah, + gtyh'_I' onde X = (x ... ,x1 ••• ) e h = (h, ... ,h" ... ) com ho = O.

-Assim pelo teorema da série convergente temos: ÔF(X,h) = L(gah, + gtyhl-l)

1=1

o

Teorema _{1.5. Para que o máximo de F(X) em C ocorra em Xo e C é necessário e} suficiente que se verifiquem:

onde as derivadas parciais são calculadas no ponto X o'

n

Demonstracão: Pelo que vimos acima: DF(Xo,h) = _{lim I<g,xh, + gryh ,_I)} (I).

n ... - ₁₌₁

Definindo e, = (0,0, ... ,0, . 1. . O, ... ) temos: ÔF(Xo,e, ) = glX + g(I+I)V' 'Vt ｾ＠ 1

1 -bima posrçio .

Suponhamos inicialmente que F passe por um máximo em Xo' Pelo teorema 1.4 (b) 6F(Xo,h) = 0, 'Vh E L. Em particular: ôF(Xo,e, ) = ga +g(I+I)Y= 0, 'Vt ｾ＠ 1 (11).

Substituindo

(m

em (I) obtemos: ôF(Xo.h) = _{limgDJ(h n. Como ÔF(Xo.h)} =

°

para

n ...

-toda seqüência limitada h, fazendo h, = 1, 'VI ｾ＠ 1, devemos ter limgDJ( = O.

n ...

-o

Reciprocamente, vemos que se Xo E C é tal que satisfaz a equação de Euler

então (por um raciocínio semelhante ao acima): ôF(Xo,h) = _{JimgDJ(h n, 'Vh} E L e se

n ...

-satisfaz a condição de transversalidade então ÔF(Xo,h) = 0, 'Vh E L. De fato, se hEL , (h n )nEII é uma seqüência limitada. Novamente usando o teorema 1.4(b), temos que Xo é um ponto de máximo para F..

Observação: Tendo em vista a equação de Euler, a condição de transversalidade também pode ser escrita sob a forma lim gny

=

O.

n ...

-Caso b) O espaço considerado agora será o das sequenclas. Neste caso queremos estabelecer quando uma seqüência limitada Xo que satisfaz a equação de Euler e a condição de transversaJidade é tal que _F(Xo) ｾ＠ F(X) para toda seqüência X

(possívelmente ilimitada). Este problema será chamado problema da dominância.

n

Defina: Fn(X) = Ig,(xl'x,_1) para cada n E ｾ＠ e para toda seqüência real

1=1

Teorema _{1.6. Sejam Xo uma seqüência limitada que satisfaz a equação de Euler,}

(a)

uma seqüência de reais positivos que tende a

°

e que atende a seguinte 11 IIEII

propriedade: se lim

a"x"

;t

°

então JimFn(X) = -00. Então para que Xo maximize

ｉｉｾ｟＠ ｮｾ＠

F(X) no conjunto das seqüências, é suficiente que a seqüência (glU' I a..)IIEII seja limitada, onde as derivadas parciais glU' são calculadas no ponto X_o·

n

Fn(X)-Fn(Xo)SL(g,xhl+gryhl_I) com as derivadas parciais calculadas em Xo. 1=1

Como X o atende a equação de Euler

F,,( X) - F,,(X_o) $ g",h" = (g", / a" )(a"h,,)

Como Xo é uma seqüência limitada ,

(a x)

tende a zero se. e somente se

" " "eM

(a.h) tende a zero, visto que a" _ｾ＠ O. Portanto por hipótese ou

.. " iteM

F,,(X) ｾ＠ -00 OU F,,(X) $ F,,(Xo)' Em todo caso F(X):5 F(Xo)' o que prova o

resultado .•

Observação: Note que, como a" ｾ＠ O, a condição de que g", / a" seja limitada implica a condição de transversalidade.

Voltemos agora ao exemplo do início da seção. Vamos resolvê-lo de uma forma mais genérica: suponhamos que se queira determinar a seqüência

-X=(XI'X2, ... ,x" ... ) que maximiza F(X)=L ｶｬＨＲ｡ｇＧｸＬＭ｢ｸｾＭ､ＨｸＬＭ 1_1)2) =1

dado X_o, onde a,b,d,G, v são reais positivas com G ｾ＠ 1 e O <vG 2 < 1.

De acordo com a análise teórica precedente, tentaremos resolver este problema inicialmente no espaço das sequências limitadas, para depois passarmos ao estudo das condições de dominância. Para que a equação de Euler e a condição de transversal idade não levem a uma seqüência ilimitada, faremos inicialmente a mudança de variáveis I x, = G'yt' t = },2,... Com isto o problema se toma

-max

F(Y) =

L

(vG2)'(2ay,-bl-d(y, -G-1

Yt-I)2), Y=(YI'Y2"")'

,=1

Em primeiro lugar se Y = (y 1"'" Y I"") é uma seqüência limitada de números reais, então existe M>O tal que

I

2ay, - bl- d (y, - G-I )"_1)2

1<

M, 'Vt e N. Como 0< vG 2 < 1 tem-se que F(Y) é absolutamente convergente, logo convergente, para cada seqüência limitada Y. Além disso, gu = (vG2)'(2a-2by, -2d(y, -G-IYI_I»' g(t+I)Y =2(vG2

)'+'dG-' (YI+,- G-'y,). Observe que o subíndice x em gu faz menção à primeira variável (y I) e o subíndice y se refere à segunda variável (y '-I)'

Portanto a equação de Euler será:

- ｾＭＭＭＭ

-e a condição d-e transv-ersalidad-e s-erá: lim( vG2

)' (Y ,+1 - G -I y,) = O.

,

...

-Vamos analisar o polinômio característico associado à equação de Euler:

p(r) = vdGr2 - (b + d(l + v»r + dG-1 •

Temos que â=(b+d(l+v»2-4d 2v>d 2(l+v)2-4d2v=d 2(l_v/ >0 o que implica que existem duas raízes reais distintas ri e r₂ para p( r). Pelos sinais dos coeficientes de p(r) tem-se que ri> O e r₂ > O. Como p(G-I) = -bG-1 < O e p(vG)-. < O devemos ter:

0< 'i < G-I:s; I < (vG)-1 < r₂• (I)

Obtemos como solução da equação de Euler: ｹｾ＠ _{= k +CI}

ri

_{+c2 r; com c. e} C 2

constantes a determinar e k = a I . b+d(l-vG)(l-G- )

Entre as soluções acima, só são limitadas aquelas em que C

2 =0, i.e., Y? = k +c. r.l, ou ainda,

ｙｾ＠

= k + (yg - k)'i'. É faci) ver que a condição de transversal idade é satisfeita para esta seqüência.

Vamos agora analisar a solução geral do problema no espaço das seqüências. Trata-se de discutir o problema da dominância: observe que

(vG2)1 (2ay, - _｢ｹｾ＠ -d(y, - G-·YI-I)2):s; (vG 2)1 (2ay I - _{｢ｹｾＩＮ＠}

Tome an =(vG2)n, V'neN. Temos que lima_{n ... _ n} =0, a_n >0, V'neN e, no ponto yO,

se que (glU / a,,) é limitada. Resta agora observar que dada uma seqüência (y,,) tal que a"Y" não tende para zero quando n tende a infinito, então F" (Y) tende a menos infinito. Dada uma seqüência real qualquer Y = (y I )IEIC tal que lim aDy D :;r!:

°

e F(Y)

D ... •

existe, defina y' = (Y:)'EIC e N por y: = y, se cp(Y,):S; O e Y: = _ｾ＠ se CP(YI) > O, onde cp(x)= 2ax - bx2. Como

Ya

é ponto de máximo de cp devemos ter F(Y):s; F(Y')

-

-onde F(Y) = L(vG2)'cp(y,), Como Um aS_n :;r!: 0, existe E>O e uma subseqüência

1=.

(nt)tEIC

tais que aDt Iy Dt ｉｾ＠ t, V'k e N, i.e., Defina

ｎＮ］ｻｮ･ｎ［ｹｾ］ｾｽ＠ e N₂ =N-N_{I •} Temos que

F(Y') =

L

(vG2)D

｣ｰＨｹｾＩ＠

+

L

(vG2_)D

｣ｰＨｹｾﾻ＠

DEIC, DEIC2

+

portanto

L

(vG2)D

｣ｰＨｹｾＩ＠

= -00. Verificamos assim o critério da dominância.

DEIC2

Finalmente a solução será dada por XI = kG '

+

(x_{o -} k)r' onde r = ri G e por (I)

Finalizaremos esta seção enunciando o Teorema de Kuhn e Tucker no caso geral. Sua demonstração pode ser encontrada em Simonsen (1983).

Forma Geral do Teorema de Kuhn e Tucker

Seja L um espaço vetorial real.Um subconjunto K

c

L não vazio é dito ser um cone quando

x E K _ｾ＠ Â.x E K, 'VI.. _ｾ＠

o.

Dizemos que um cone convexo P

c

L é positivo quando:

i) P:I;L

ii) L é o subespaço gerado por P.

o

iii)P:I; 0.

Exemplos:

1) Se L =

9t"

então

9t:

é um cone positivo em L.

2) Se L = C([a,b]) = {i; i:[a,b]-+

9t

contínua} C· ([a,b)) =

{f

E L; i(x)

ｾ＠

O, \tx E [a,bJ} é um cone positivo em L.

então

Dado P cL um cone positivo, g um funcionaI linear g:L -+

9t

diz-se positivo se g(x) ｾ＠ O, \tx E P. Diremos também que x ｾ＠ y, x,y E L, quando x - y E P e x > y

o quando x - y E P.

Sejam L, M espaços vetoriais reais, P um cone positivo em L e C

c

N convexo. Uma função G:C ｾｌ＠ diz-se côncava quando:

G«(l- a)x + ay) ｾ＠ (1-a)G(x) +aG(y), 'Vx, y E C e \ta E [0,1].

Teorema 1.7. (Fonna geral do teorema de Kuhn e Tucker): Sejam L, M espaços vetoriais reais, P

c

L cone positivo e C

c

M um conjunto convexo não vazio; F:C -+

9t

funcional côncavo e G:C ｾｌ＠ uma função côncava. Suponhamos que exista i E C tal que G(i) > O (condição de Slater) e seja

E

=

{x E C;G(x) ｾ＠ O}.

Então, para que o máximo de F em

E

ocorra em _xo' é necessário e suficiente que exista um funcional linear positivo g:L ｾ＠

9t

tal que \tx E C se tenha:

ｆＨｸｯＩ］ｆＨｸｯＩＫｧＨｇＨｸｯﾻｾｆＨｸＩＫｧ＠ (G(x». Se _G(xo) >0, g será identicamente

r

-Exercícios resolvidos:

I) Numa economia, as variáveis da taxa de inflação correlacionam-se com a taxa de desemprego de acordo com a equação: V - V,

=

b (Te, - Te, -I) onde 7t, indica a taxa de inflação no período t, V, a taxa de desemprego nesse período, V a taxa de desemprego quando a inflação não se altera. No período inicial, a taxa de desemprego é igual a V e a taxa de inflação 7t_o' Tanto o desemprego quanto a inflação causam

desconforto à sociedade, a qual deseja minimizar o valor descontado do sacrifício

-L

v' (Q7t; + SV,2), onde v, Q e S são constantes positivas, sendo v E (O, l).Detennine

,=1

as trajetórias ótimas das taxas de inflação e de desemprego.

-Solução: Trata-se de max -

L

v' (QTe,2 + SV,2)

{Jf,+ •. u,., ｽｾＮｮ＠ ,=1

s.a. V

-v,

=b(Te, -Te,_I)

7t_o' V_o dados

-ou seja, ｭ｡ｾ＠ -

L

v' [QTe,2 + S(V + b(Te'_1 - Te,

»

2]

{Ir,.) },.o 1=1

7t_odado

-2

. ｾＧ｛Ｇ＠ - , ,] vSV

ouamda, ｭ｡ｾ＠ - ｾｶ＠ QTe,- +2SVb(Te,_1 -Te,)+Sb-(Te'_1 -Te,)-

-{Ir,ol },.n ,=1 I - v

A equação de Euler nos dá:

2QTe, - 2S V b - 2Sb 2 (Te'_1 -Te,) +V [ 2S Vb

+

2Sb 2 (Te, -Te,+I)] = O, ':/t ｾ＠ I

e isto implica que:

vSb 2Te'+I_(Q +Sb 2 +vSb 2)Te, +Sb2_{Te,_1 +(l-v )SVb =0, ':/t ｾ＠ 1}

Vamos resolver esta equação de diferenças primeiro detenninando a solução da homogênea e depois a solução particular correspondente.Seja então a equação característica da homogênea:

vSb2_r2 _-(Q+Sb2 _{+vSb 2)r+Sb 2 = O}

Temos que .1

=

(Q+(l+v)Sb2

)2 -4vS2b4

=

Q2 +2Q(l+v)Sb 2 +(l-V)2 S2b4 o que

implica que .1 > O. Portanto: Q+(1 + v)Sb2_-.JK

r =

...;:...---:..._....;..."....--I 2vSb2

Q+(1 + v)Sb2 _+.JK

e r =

...;:...---:..._....;..."....--2 2vSb2

são as raízes (positivas) do polinômio característico. Observe que O < r, < _{1 e r2} > 1. De fato, r, < 1 (::) Q + (1- v)Sb2 <

JX (::)

Q2 + 2(1- v)QSb2 _{+ (1-V)2 S2b}4

< Q2 + 2(1 + v)QSb2 _{+ (1- V)2 S2b}4

(::) 2v > O

e _r2

>

1 (::) Q + (1-v)Sb2

+.,fK

>

O .Portanto a solução homogênea da equação de

diferenças é: Ｗｴｾ＠ = cl (ri )1 + c2 (r2)1 , cl ' c2 constantes arbitrárias.

Vamos tentar como solução particular a solução constante

(vSb2-Q-Sb2-vSb2_+Sb2_{)K+(I_v)SUb=O => K= (I-v)SUb}

Q Portanto a solução geral é dada por 1t, = Ｑｴｾ＠ + ＱｴｾＬ＠ I. e.,

, ,(1-v)SUb

1t, =cl(rl) +c₂(r2) + Q .

A condição de transversalidade exige que c2 = O, visto que r2 > I. Assim a solução

, (1-v)SUb (v -l)SUb

será 7t, = c l (ri) + logo devemos ter _{cl = 7to +} e

Q

Q

v,

= V + b(7t'_1 -7t,).

O leitor poderá verificar que a seqüência (a,,) = (v") atende as condições do teorema da dominância.

2) Seja g,(x,y,z) uma seqüência de funções côncavas e diferenciáveis definidas no

ｾＳＮ＠ Discuta o problema de maximizar

..

L

g,(X"Xf-l,X,_2)

,=2

dadas as condições iniciais Xo e XI.

Solução:

..

Consideremos L = {x; x: K

ｾ＠ ｾ＠

com Xo e XI fixados} e F:C

ｾ＠

ｾ＠

tal que

F(x)= Lg,(X"X'_I,X'_2) onde C={x € L; F(x) existe e é finito}. Vamos supor que C

seja convexo. Dado x· E C. seja a tal que x· + Â.e k E C, 'V À E [-a, a]. A função

fk :[-a,a]

ｾ＠ ｾ＠

tal que

f

k (À) = F(x· + Â.e_{k )} é um funcional côncavo diferenciável e

O é _{um ponto de máximo de fk e portanto O deve ser um ponto crítico.} Assim:

f; (O) = gkx + gCk+l)y + gCk+2)z = O 'Vk _ｾ＠ 2 (I)

(onde as derivadas parciais acima estão calculadas em x·). Portanto a equação de Euler (I) é uma condição necessária para x· ser um ótimo de F. Agora dado

h = (O, O, h 2 h3 ,···) E L podemos calcular a diferencial de Gateaux de F no ponto x·

na direção h e obter (pelo teorema do máximo)

n

aF(x· ,h) = lim _{ｄｾ｟ｾ＠}

ｾ＠

_{(glXhl + gtyh'_1 + grzh,_2) =}

o.

Substituindo a equação de Euler:

1=2

gCl+2)z = -glX - gCI+I)y tem-se que:

n ..

LglX h , +gtyhf-l +grzht-2 =g211h 2 +g311 h3 +g3yh 2 + LglXh, +gtyh'-I-[gC'-2/1I +gc'-l)y]h'_2

'=2 '=4

. n_

,=4 ,,- ,=4

］ｧＲｸｾ＠

+g3xh3 +

ｧｨｾ＠

+ lim[igr.rh, - gC'-2)Xh'-2]+ lim[igl).h,_1 - gCt-I)yh,_2]

= lim(g(,,_I).l'h"_1 + gllA'h" + g"yh,,_I) = O ( *)

ＬＬｾＭ

Tomando h

=

(0,0,0, I ,0, I ,0, ... ) e substituindo teremos que o limite acima será o limite da sequência (g 3. ' g 3. + g 4, ' g 5r ' g 5. + g 6, ... ) .Por outro lado se tomarmos h

=

(0,0,0,0,1,0,1,0,1, ... ) então o limite acima será o limite da seqüência (g 4.1 ' g 4.1 + g Sr ' g 6.1 ' g 6.1 + g 7., ••• ). Concluímos assim que as seqüências dos índices pares e dos índices ímpares das seqüências (gnx

+

g(n+I)Y )nell e (gnx )nell convergem a zero visto que são subsequências das seqüências acima obtidas, as quais convergem a zero. Portanto, _limgnx

+

g(n+I),

=

°

e lim g"-r = O. Logo lim,g-,,-,

=

°

e

n - + - ·

n-+-lim gnv =

°

(11). n-+oo .

Chamaremos estas condições (limites) de condições de transversalidade .

.

Vemos assim que para x· E C ser um ponto de máximo de F é necessário que (I) e (ll) sejam satisfeitos. Pode-se verificar a partir do teorema do limite e de ( *) que (I) e

(ll) também são condições suficientes para x· ser um ponto de máximo de F.

Observação: A primeira parte da demonstração deste exercício mostra que a equação o

de Euler é uma condição necessária sem necessáriamente x· E C e F ser diferenciável

a Gauteaux em x·, bastando que as derivadas direcionais de F estejam definidas nas direções e_{k ,} k = 2, ... , o que evidentemente ocorre já que g, é diferenciável para

o todo t ;;:: 2. Por outro lado as condições de tranversalidade necessitam que x· E C.

3) Resolva o problema de "comer o bolo ao longo do tempo"

-ｭｾｸｉｶｬｆＬ＠

{l,},., 1=1

-s.a.

Ix, =c

,=1

e x, ｾ＠

o,

t = 1,2, ... onde c é uma constante positiva e v E (0,1).

Solução: Em primeiro lugar, observe que resolver este problema é equivalente a resolver

-max

I

v'

F,

(I)

{.I,

r:.,

,=1

-s.a.

Ix,

Se

,=1

x, ｾ＠

o,

t = 1,2, ...

pela monotonicidade (estrita) da função raiz quadrada. Seja C={(x .. x₂ , ••• ) E r(9t); x,

ｾ＠

O, V't E N}=Ç(9t). Então C c r(9t) é convexo.

-Definindo F(X)=.I v'

F"

onde X =(x, ,x2 , ••• ) E C , temos que F:C ｾ＠ 9t está bem , .. I

problema (1). Para isto precisamos garantir que a condição de Slater é satisfeita para a restrição em (1). De fato, basta tomar

i

=(xl )/EIC tal que XI

］ＭＭｾＭｉ＠

.. -I c, t

=

1,2, ....

Temos que

f

XI

=.::.

< c. Assim pelo teorema de Kuhn e Tucker, para que X· e

ç

,=1 2

resolva o problema acima é necessário e suficiente que exista Â, ｾ＠ O tal que X· seja o ótimo para

-max

L(X)=

L

(v\G,-

-

Âx,)+

Àc (11)

,=1

x

= {x, };:I e L.:" (90

tal que A(

c

-

t.

x:

)

= O • Observe que como

.f.:

'R.

-->

'R

é crescente, devemos ter

-c=

LX;

.

Além disso, x; > O, "dt e N. De fato, se existe 10 e N tal que ,=1

{

X;

se 1 :;; 10 e 1 :;; 10

+

I x; =0 e x; +1> O então defina

x

e

ｬＺＨｾＩ＠ por

x,

= I . .

o o -₂ x _'0+1 se 1 = t _o ou 1 = 1 _o

+

I

Pela concavidade estrita de _ｾ＠ temos que

ｾｾｉｾｉｾｾ＠

v"2 Xlo+1 + v v"2 Xlo+1 >"2 V Xlo+1 +"2 v V Xlo+1 ｾ＠ V V Xlo+1

lo

ｾ＠

10+1

ｾ＠

10+1

ｾ＠

ｾ＠ V V"2 Xlo +1 + V v"2Xln+1 > V VXln+1

-

-Logo

F(

X)

>

F(

X • ) e

L

x,

=

LX;

= c o que é absurdo. Da mesma forma,

conclui-,=1 '=1

se que não pode existir to e N tal que x;o > O e X:,,+I = O donde segue-se o afirmado. Se

x·

é ótimo para (ll) e

x;

> O, "d t e N, devemos ter, para cada

te

N, g, (s) =

L(x·

+ se,), definido em uma vizinhança aberta em O, com derivada O

em O _{(onde el é a seqüência cujos termos são todos nulos exceto o t-ésimo que é igual}

. '() 1 , 1 ,

,2. 2,

aI), I.e.,g, O =2 v r--/I,=O, "dleN ｾＴＯＱＬ＠ x, =v , "dleN. Somando,

"'x,

v2

ｾ＠

Â,2 = ₄ c{ _l-v

2)'

Portanto

obtemos

o

x· =c{I-v2_)v2

(,-I),

t=I.2, ....

Como limx;=O, tem-seque x· EC. Logo não

, ｉｾ＠

podemos usar os teoremas 1.1 e 1.2 para concluir que de fato x· é ótimo para (TI).

Para cada r E N, defina L, (x) = v'

Fx

-

Àx, x ｾ＠ O. temos para À. dado como acima

L;(x;

)=0.

Além disso

L,

é côncava e diferenciável em 9\ .... ,

'tfr

E

N.

Logo

para

x=(x,

)'EN

E

1.:"

(9\),

L, (x,)

-

L, (x;)

$

L,'(x; )(x,

-

x;

)=0.

Portanto,

-

-L

L, (x,

)

+..te

$

L

L, (x:)

+..te

provando assim que

x·

é ótimo para (11).

,=1 ,=1

4) Uma economia com coeficiente de desconto v das utilidades futuras, ü<v<l, maximiza

-Lv'(-Th,2 -Rn}), T>O, R>O

(1)

,=1

onde h é o desvio do produto (In y /

y)

e 1t a taxa de inflação. As expectativas

inflacionárias

(1r,')

modelam-se sob a forma

1r,'

= 1r,_I' A curva de Phillips é dada

por h, = 1r, -1(,. Os valores iniciais da inflação e do desvio do produto são iguais,

respectivamente, a 1ro e O (zero). Nestas condições,

a) Defina a variável hiato acumulado R, =

ho

ＫｾＫ＠ ... +h, e obtenha as expressões para

h, e 1r, em função de R,.

b) Substitua

h,

e

Te,

em (I) pelas suas expressões em função de

R,

e resolva o problema de maximização apresentado. Em particular, obtenha as expressões de

Te,

e

h,

em função da(s) raiz (raízes) do polinômio característico e de 1ro'

c) Observe, em sua solução que a(s) raíz (raízes) do polinômio característico são funções de v, R, T, parâmetros do problema. Através de um exercício de estática camparativa, determine como varia a opção por um tratamento de choque ou gradualismo no combate à inflação em função desses três parâmetros.

d) Para que valores convergem, respectivamente, 1r, e h, ?

e) Observe que, no problema apresentado, a sociedade não distingue entre recessão ou desvio de produto positivo, colocando em peso negativo para ambas as possibilidades. Este fato é intuitivamente compatível com a sua resposta do item anterior?

Solução:

a)

Te,

=

R,

+

Teo

'

h,

=

R,

-

R,_,

b)

maxfv'(-T{R, _R,_1)2 -R{R, +Teor)

,=1

onde

gt,x =vt(-2T(Ht -Ht_I)-2R(Rt

+1r

o))

g t

+ I, y =

vt

+ 1 (

Ｒｾ＠

H t

+

1 -

H t

))

Condição de Transversalidade: lim \,r ... 1

(2T(Hr

+

1 -

Hr))

== O

r--Polinômio Característico: f(x) = vTx= - (TU + v) + R)x + T = O Discriminante: ｾ＠ = T2_{(1-V)2 + R}2 _{+ 2R(T(J +}

_v))

_{> O}

f(I)=-R<O

Análise Adicional do Polinômio Característico:

f

(-

1)

=

2 T( 1 + v) + R > O

ri r₂ =

Ijv

Conclusões: O < r) < 1 <

Ijv

< r₂

A solução limitada para

Hr

deve ser da fonna H, = SP+c) r)'

onde, por substituição, conclui-se que a solução particular SP = - 1fo. A solução acima atende à condição de transversal idade.

limv'+) 2T(c) (ri -I)rl')=O

,

...

pois r) < 1.

As soluções do problema são então:

H, = 1fo (- 1

+

r/ )

h,

=

1fo(rl - 1) r/-I

r

_ｾ＠ 1

-

-

,

li" - 1fo ri

c) Estática Comparativa: Como

f/(r))

< O (visto tratar-se

r)

da menor das raízes de um trinômio do segundo grau com coeficiente líder positivo), obtém-se, a partir do polinômio característico e por aplicação do teorema da função implícita,

ar

l - Tr) (r) -1)

-=

<O

iJv

f'

(ri)

ar

-

(1-r )(1-vr )

_) = I 1>0

(J]'

f

'(ri)

ar)

r)

:) - , <O

dR

f

(r)

Conclusões: Como r) mede o gradualismo no combate à inflação (observe a expressão

do 1f, em função de r) para obter esta conclusão) conclui-se, como era de se esperar intuitivamente, que o ataque à inflação será tão mais rápido: i) quanto maior v, ou seja, quanto mais a sociedade valorizar o futuro relativamente ao presente; ii) quanto maior a aversão à inflação (medida pelo coeficiente R) e; iii) quanto menor a aversão ao desvio do produto (medida pelo coeficiente T).

d) Ambos convergem para zero.

zero. Maximizando-se uma expansão função dependente apenas de ｨＬｾ＠ e

li, ,

entretanto, é razoável esperar-se, no limite h = 1r = O.

5) Uma sociedade maximiza a utilidade descontada de seu consumo ao longo do tempo.

,=0

sujeita às restrições (l _{+ 7t'+1 )ml+1 = ml + hl + 1- cl - Sl} c, = F(m, ,s,)

Obtenha a condição de primeira ordem

(1)

(2)

e

(3)

I+Fm(ml·sl) =(l+p)(1+7t) O'(C,_I) X, ,onde X

t =[Fs(mt,st)]-I[l+Fs(mt,st)] Fs(m .. s,) , O'(c,) Xl_I

Solução:

De (2) e (3) obtém-se, dados 1C,+1 e h,

f(ml'm,+l'c l) = c, - F(ml'-(1 + 7t'+1 )ml+1 + ml + hl + I-cl) = O (4) o que nos permite obter, pelo teorema da função implícita, c, =G(m, ,mal) (5)

-Substituindo-se (5) em (I), devemos maximizar

L(1

+p)-l U(G(ml' mt+I». Fazendo-,=0

se gl =(l+pflU(G(ml'm l+l

»

temos, objetivando escrever a equação de Euler,

gl.l =(l+p)-'O'(c,).G1(m"mt+l) (6)

(7)

onde os sub-índices I e 2 em g e G denotam as derivadas parciais, respectivamente, em relação à primeira e segunda variável da função.

Utilizando-se derivação implícita em (4) obtém-se G ( ) =

df/drn

l = FS(mI'Sl) + Fm(ml'sl)

I ml,mt+1

df/dc

l I+Fs(ml's,)

G (m m _{)= -df/dm t +1 =_ (l+7t t + I)Fs(m t ,st)}

2 t ' t + I

dfldc

I + F (m s)

G2 (m'_1 ,m,) =

(9)

t S t' t

-(l+1C_{t )Fs (mt _ l ,st_l)}

I

+

F _S (m _t-l' St _- 1 )

(8)

e daí,

Substituindo-se (8) e (9), respectivamente em (6) e (7), obtém-se a equação de Euler.

, F, em, ,s, ) + F", em, ,s, ) (1 + p)U' (C,_I ). (1 + 1C, ). F, (m'_1 ,S,_I )

U (c,). _I

_{+ .•}

F

=

1 F )

(m, ,s, )

+

,(m'_I' S'_I

Dividindo-se ambos os membros por F',{m"s,), obtém-se

1+ Fm{ml's.> = (l+p)(l+7t,). U'{C,_I)

ＮｾＬ＠

onde X, é definido como no enunciado F,{m, ,s,) V'{c,) X'_I

-6) Uma economia maximiza

L(I

+p)-I U(c_{l )}

sujeita às restrições:

d, =G(z, ,v,)

d, SlXZ,

c, = F(x, ,d, )s,

1=0

(1 + 1Z',+1 )(X'+I +Z'+I) =x,

+

Z, + h, + l-c, -s, -v,

(1)

(2)

(3) (4) (5)

A título de ilustração econômica, a segunda equação pode ser entendida como tecnologia bancária que utiliza reservas (z,) e tempo (v,) para produzir depósitos à vista (d,). A terceira equação estabelece as reservas compulsórias mínimas como percentual de depósitos à vista como sendo igual a uma constante a. A equação (4) traduz o fato de que os consumidores utilizam moeda (x,), depósitos à vista (d,) e tempo de compras (s,) para obter seu fluxo de consumo c,. Por último, (5) impõe a restriç.ão de caixa do consumidor, sendo h, uma transferência exógena do governo.

Neste problema, os consumidores determinam otimamente, de forma exógena, as variáveis x, vez. Mostre que as condições de primeira ordem do estado estacionário implicam em

F. (x,d)s = rF(x,d) G_z (z, v) + Àa = rGv(z, v)

(1 + À)F(x,d) = Fd (x,d)sGv (z, v)

onde r = (1

+

p)(1

+

tr) é a taxa nominal de juros e À ｾ＠ O é o multiplicador de Lagrange associado ao problema pelo teorema de Kuhn e Tucker.

Solução: Substituindo-se (5) e (2) em (4),

c, - F(x, ,G(z, , v, »(-(1 + 1Z"+1 )(X'+I

+

Z'+I )

+

x,

+

z,

+

h, + 1-c, - v, ) = O (6)

Substituindo-se (2) em (3),

(7)

Seja Ｈ｣ｾＬ｣［＠ ,c;, ... ) é uma seqüência de consumo que maximiza (1) com as restrições do problema. Consideremos agora o problema pelo maximizar a função de uma variável (Cio)'

-L[(1 + p)-' U(c; )]+ (1 + p)-'O U(c,o) + (1 + p) -('0-1) U(C'o_l)

É claro que a solução para este problema deve ser c,

=

<

pois se houvese

P I'

ê, _{o ｾ＠} c,' (1 satisfazendo à com U(ê, {l ) > V(c; {l ), então a seqüência _{Ｈ｣ｾＬ｣［＠} .... ) não seria ótima para o problema original.

Este raciocínio, aliado à utilização do teorema de Kuhn e Tucker, nos permite concluir, uma vez que tomemos uma derivada direcional no espaço de seqüências na direção e,o = (0,0, ... .1,0,0, ... ), (com o 1 na to-ésima posição), que o ponto de ótimo deve satisfazer a Lx = Ly = Lz = 0,

I() I() I()

onde L é o Lagrangeano

L({3,o ,{3'o-1 ) = (1 + p) -'o V (c'o ({3,o ,{3'o-1

»

+ (1 + p) -(lo-I) V (C'o-I ({3,o ,{3'o-1 ) + I(az,o - G(z,o ,v'o

»

(

onde as derivadas parciais de U destas variáveis são obtidas utilizando-se o teorema da função implícita e a equação (6), e ｾＧｯ＠ representa o vetor de variáveis (x,,,, v'o ,z'o)' Tomando inicialmente a derivada de Lagrangeano com relação à variável x'o:

F.(to)·s, +F(x, ,G(z, ,v,» 1 F(x,_ .. G(z,_ .. v,_I))(-(1+.

(1+p)-'OV'(c) o o o o +(1+p)-UO-IV'(C) o o o

'o 1 + F(x,o ,G(z,o ' v'o

»

'0-1 1 + F(x'o_1 ,G(Z'o_1 ,V'o-I»

Utilizando-se uma notação mais adequada, temos daí que

U' )W

Fx(to)s +1=(l+p)(l+7t) (C'o-I 'o =I+r,o' F(t) _o

'o

,

U'(c ) W _{'o ,o-I}

I+F(to) F(to-I) ,

onde W, = _{. Segue dai que Fx(to)s, = r, F(to)'}

o _{F(to) I+F(to-l)} o o

No "steady state" podemos escrever F. (x ,d)s = rF(x ,d), obtendo a primeira igualdade.

Derivemos agora (8) com relação a v, . Temos _o

(l

+

p)-'O V'(c,o )[Fd(to).G,.(to)· s'o - F(to)] _ 1

+

F(to) = ÀG,.(to)

(observe que C'o-I não depende de v'o ) .

ÂO +

p)'O

O +

F{to»Gv (to)

Segue daí que Fd(to)'s,o . Gy{to) = V'(c) +F{to)·

'o

ｾＨｉ＠ + p) 'o (1 + F)G y F

No "steady state", temos FdsGy + .

U'(c)

Fazendo, o que o teorema de Kuhn e Tucker nos permite para

ｾＨｬ＠ +p)IO (1 + F(t »G . _

G > O Â = o y , temos a terceIra relaçao, F G s = (1 + Â)F .

v ' U'(c(to»F(to) ti y

Finalmente, derivemos agora o Lagrangeano (8) com relação a Zl_o' lembrando que tanto CID quanto CIO-I são funções de z'o:

(1 +

r"

U' (c ) [Fd _{(to)G z (tll)s,o + F(to)] + (1 +}

pr(to-I)

_U' (c _ ) _{[-F(tn -1)(1 + 1t, )] +} I(a _ _{G (t}

»

= o

r - - -

--Segue que daí,

Fd(tO)·Gz(tO)·S'n ] U(Clu - 1)(1 )(1 ) W_I X(1+p)III(1+F(t o))

---..:.;..+

=

+p +1t - - - (a-G (t »

F(to) U(c_{l )} I Wt-I _U(c,)F(to) Z o

D d fi . -a e InJçao antenor e . d 1 11. = ---'---...;.. À,(1+p)'°(1+F(to»G,

U' (Cio ). F{to)

Fd (to)·G. (to)'s, Â

_ _ _ • _ _ _ｾｯ＠ +]

=

I+r- (a-G.(to»'

F(to) G,. (to)

-Trabalhando no "steady state" e lembrando

Fd = F(1

+

Â) (l

+

Â)FG!s = r

ＭｾＨ｡＠

_ G.).

G,.s FG, .. s G,

-Segue daí, finalmente, a segunda relação apresentada, G_z (z, v)

+

À,a = rG v (z, v).

Exercícios propostos:

I) Verifique que a função g: SR:! ｾ＠ SR tal que

{ X).2

2 -4 ,se x

*

O

g(x,y) = Ox

+

y

,se x = O

é diferenciável a Gateaux em (0,0) embora não seja nem contínua neste ponto.

2) Analise o problema da dominância no exercício resolvido número 1.

3) Generalize o exercício resolvido (2) para g; s côncavas e diferenciáveis definidas no SR".

4) Seja F:C ｾ＠ SR um funcional côncavo e Xo E C. Mostre que para que F(x) passe por um máximo no ponto Xo é necessário e suficiente que F (xo,h) $ O, Vh E Sexo)'

5) Nas mesmas condições do teorema do limite, mostre que se

Xo E C então lim F;(xo,h)=O, Vh E I(xo). Faça o mesmo para o teorema da

n-+-série convergente.

6) Apresente a condição de primeira ordem do problema de maxlmlzação de

-LO

+p)-I U(cl'ml)Sujeito a restrição (1 +7t1+1 )ml+_l = _ml -C_{I +} j, j > O

1=0

Obs: Esse problema pode ser interpretado como a maximização de utilidade de consumidor sujeito a uma restrição de caixa. Tal utilidade supõe-se função do consumido e dos encaixes reais. (Ver Sidrauski (1967) e Lucas (1993».

7) Resolva o seguinte exercício:

-max

L

/3'

(F(h,) - G(TC,»

,=1

s.a. h, - a h,_, = b(TC, -TCt-/)

{

a E [0,1); F(x) = x - x2; G(x) = x2 onde

S.2.Cálculo de variações -Caso Contínuo

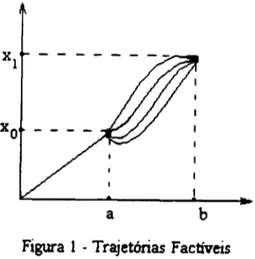
Existe uma classe de problemas em matemática que pretende descobrir uma trajetória ótima ao longo do tempo que maximize a integral de uma função que depende da posição, da velocidade e do tempo para cada instante. Esta técnica, que apresenta diversas aplicações em economia, imita o cálculo clássico no sentido que se uma trajetória soluciona um problema deste tipo, ela é uma trajetória "crítica" entre todas as trajetórias "próximas". A equação que estabelece esta condição é a Equação de Euler-Lagrange. Além disso a condição dada por esta equação será suficiente para caracterização do ponto de máximo se a função em questão for côncava fixada a coordenada correspondente ao tempo, para todo instante do tempo. Vamos à descrição matemática deste modelo.

Sejam C

c 9t

2

aberto, [a, b]

c 9t

um intervalo fechado limitado e

f:C ｸ｛｡Ｌ｢｝ｾ＠

9t

uma função continuamente diferenciável.

o

problema principal em cálculo de variações é encontrar uma função x: [a, b] ｾ＠

9t

continuamente diferenciável tal que:

i) x(a)

=

Xo e x(b)

=

x" onde xo'x, são números reais dados,

ii) (x(t),x(t»eCparatodote[a,b] e

s:

f(x(t),x(t),t)dt =

max

s:

f(y(t),y(t),t)dt

s.a. y:[a,b] ｾ＠

9t

de classe C'

satisfazendo (i) e (ii)

dx

onde x(t) = dt (1) .

X

o

-a b

Figura 1 - Trajetórias Factíveis

Antes, de passarmos à solução deste problema, precisamos de alguns resultados preliminares:

Lema 2.1. Seja

ｧＺ｛｡Ｌ｢｝ｾｾ＠

contínua tal que

J:

(g(t»2dt=0. Então g(t) = O para todo t e [a, b].

Demonstracão: Suponhamos que exista to e [a, b] tal que g (to) ｾ＠

o.

Por continuidade, é possível encontrar um intervalo [tl't₂]c[a,b] tal que

( _g(t) )2 ｾ＠ (g(tO»2 2 _,'tIte [ _{1 .. 12 ,comt}]

J !!:to !!:/₂ e IJ *t2.

J

h

2

J"

(

)2

g(/o

)2

Portanto, (g(t» dt _ｾ＠ - g(t) dt _ｾ＠ 2 (12 - tJ) > O o que é absurdo._

a

'I

Lema 2.2. Seja g:[a,b]-+ 9t contínua tal que para todo h: [a,b]-+ 9t continuamente

J

b •

diferenciável com h(a)

=

h(b) = O se tenha a g(t)h(t)dt =

o.

Então g(t) = c para todo

te [a,b], onde c é uma constante.

Demonstracão: Seja c a constante tal que c(b-a) = 1:g(t)dl. Definamos

ｨＺ｛｡Ｌ｢｝ｾｾ＠

tal que h(t)=

ｉｾＨｧＨｳＩＭ｣ｽＮｩｳＮ＠

É fácil ver que h é continuamente diferenciável, h(a) = h(b) = O e pelo teorema fundamental do cálculo ｾＨｴＩ］ｧＨｴＩＭ｣Ｎ＠

Segue-se, pela hipótese do lema, que:

0=

1:

g(t)h(t)dt

=

1:

g(t)h(t)dt - c(h(b) - h(a»

=

s:

(g(t) - c)h(t)dt =

s:

(g(t) - C)2 dt

c.-Lema 2.3. Sejam ｧｬＬｧＲＺ｛｡Ｌ｢｝ｾ＠ ｾ＠ contínuas tais que para toda Iz: ｛｡Ｎ｢｝Ｔｾ＠

continuamente diferenciável com h(a)

=

h(b)

=

O se tenha

f(gl(t)h(t)+g2(t)h(t»)dt=O. Então g2(t) é continuamente diferenciável e

g2(r)=gl(t).

Demonstracão: Seja G(t)=

f

g I (s)ds, 'Vt E [a,b]. Integrando-se por partes e usando

o fato que h(a) = h(b) = O tem-se que:

f

g I (t )h(t )dt =

-f

G(t )h(t )dt

para todo h nas condições acima.

Logo a hipótese do lema equivale a supor que, para todo h nas condições do enunciado acima:

s:

(g2(t) - G(t»)h(t)dt = O. Segue-se do lema 2.2 que

g2(t)=G(t)+c, onde c é uma constante. Portanto g2(t) é continuamente diferenciável e g2(t) = G(t) =

gl(t).-Teorema 2.4. Se x:[a, b] ｾ＠ 9t satisfaz (i), (ii) apresentadas ao início desta seção então satisfará a equação de Euler:

d

dt fi: (x(t), x(t),t) = fx (x(t), x(t),t), 'Vt E [a,b]

,ou de forma mais abreviada,

ao longo de x(t), onde fx e fi: são as derivadas parciais defem relação a primeira e segunda variáveis, respectivamente.

Demonstracão:Nosso primeiro passo deve ser demonstrar a existência de

a

> O tal

que se possa definir F: [a,b] x [-a ,a ] ｾ＠ 9t dada por

F(t,a)

=

!

(x(t)

+

ah(t),x(t)

+

ah(t),t)

e J: [-a ,a] ｾ＠ 9t dada por

h b

l(a)=] F(t,a)dt=] !(x+ah(t),x+xh(t),t)dt

" "

Seja ｨＺ｛｡Ｌ｢｝ｾｾ＠ continuamente diferenciável tal que h(a)=h(b)=O. Para

cada

lE[a,b]

considere r,>O tal que:

B( (x(t), x(r) ),2 r, ) c C (onde B(p,r) = Iv E 91' ;IIv - plk rJ),o que pode ser obtido,

uma vez que C é abeno. Defina B,

=

B(x(t),i(t»,

r,)

e p

=

maxll(h(s),h(s»1I SE[".hj

(observe que p < +00 visto que o conjunto [a,b] é compacto e lI(h(s),h(s»1I é função contínua em s). Como a família {Br LE[a.bj é uma cobenura abena de T={(x{t),i{t»;te[a,b]} que é compacto tem-se que existem tl' ... ,tke[a,b] tais

*

que

TeU

B / . Seja r = min ri e tomemos então O < a <

y;,.

Fica fácil ver que pela

;=1 • ISISk

construção acima podemos então definir ｆＺ｛｡Ｌ｢｝ｸ｛Ｍ｡Ｌ｡｝ｾｾ＠ por

F{t,a) =f(x(t)+a h(t),i(t)+ah(t),t) visto que

(x(t)+ah{t),i{t)+ah(t»eC, 't(t,a)e[a,b]x[-a,a]. De fato, para cada tE [a,b], existe ie {l, ... ,k) tal que (x(t), i(t» e B,. e para cada a e [-a,a)

I/(x(t; ),i(t;» - (x(t)

+

aJz (t),i(t) +aJÍ(t»

II

s

Il<x(t; ),i{t;» - (x(t),i(t»11

+lla(h(t),h(t»11

S ri

+

lalp S ri

+

ap S ri

+

r S _2ri.

Assim (x(t) + aJz(t),i(t) + aJÍ(t» e B«x(t; ),i(t; »,2r;)

c

C.

Como f é continuamente diferenciável, o mesmo ocorrerá com F. Defina agora J:[-a,ã]

ｾ＠ ｾ＠

tal que l(a) = fF(t,a)dt. Pela regra Leibniz

u

dl

Jh

aF

-(a) = -(t,a)dt.

da u aa

Assim

&

Jb

.

-(O) = [f .. (x(t),i(t),t)h(t) + fi (x{t),i(t),t)h(t)]dt .

da a

Por hipótese J (O) ｾ＠ J (a), 'ta e [ -a, a] . Segue-se que O é um ponto de máximo de l, e portanto é um ponto crítico, isto é, J'(O) = O. Pelo lema 2.3 e pela arbitrariedade da escolha da função nas condições acima temos o resultado que queríamos demonstrar (tome gl(t)=fr(x{t),i(t),t) e

Teorema 2.5. ( condição necessária de Legendre ): Supondo f de classe ｃｾＮ＠ se

ｸＺ｛｡Ｌ｢｝ｾｾ＠ satisfaz (i) e (ii) então fu. (x(t),x(r),t):SO, ｾ＠ t E [a.b] (onde f,. é a

derivada de segunda ordem de f).

Demonstração: Fica à cargo do leitor.

A recíproca do teorema 2.4 nem sempre é verdadeira mas valerá no caso em que C além de aberto for convexo e para cada tE[a,b], f(x,y,t) for uma função côncava em (x,y). Está é a essência do seguinte:

Teorema 2.6. Seja ｸＺ｛｡Ｌ｢｝ｾ＠ 9t satisfazendo (i), a primeira parte de (ii) (ou seja, não

maximiza necessariamente) e a equação de Euler. Suponha, além disso, que C é convexo e f(x,y,t) é uma função côncava em (x,y) para cada tE [a,b]. Então x(t) de fato maximiza em (ii).

Demonstração: Seja ｹＺ｛｡Ｌ｢｝ｾ＠ 9t satisfazendo (i) e a primeira parte de (ii), condições apresentadas no início desta seção. Para cada tE [a,b] aplicamos a desigualdade do subgradiente para funções côncavas e obtemos:

f(y(t),y(t),t) - f(x(t),x(t),t):S f" (x(t),x(t),t) h(t) + fj: (x(t),x(t),t)h(t) onde

h{t) = y{t) - x{t). Integrando em [a,b] o segundo membro da desigualdade acima,

aplicando a equação de Euler e omitindo a dependência dos parâmetros teremos:

J

h .

Jh(d

·t

u(f"h+ fj:h)dt = u dtfj:h+ f,h ft = h(b)fj: (x(b),x(b),b)-h(a)fj:(x(a),i(a),a) = O

já que h{a)

=

h{b)

=

O. Portanto, pela desigualdade acima

I:f(y(t), y(t),t)dt:S I:f(X(t),i(t),t)dt. Como y é arbitrário, segue-se o afirmado .•

Transversalidade

Nosso objetivo nesta seção é melhorar num ceno sentido a situação já estudada, isto é, dá maior liberdade de escolha para as trajetórias, não fixando as extremidades destas. Observe, porém, que esta análise qualitativa não se emprega em todas as situações uma vez que o problema estudado poderá impor naturalmente condições nas extremidades.

Suponhamos que só a extremidade inicial x(a) = Xo da função procurada seja dada, a extremidade final x(b) podendo assumir qualquer valor dentro do campo de definição da função f(x(t),x(t),t). Escrevamos:

i') x(a) = Xo

Temos os seguintes teoremas:

Teorema 2.7. Se x:[a,b]---+

9t

satisfaz (i'), (ii), então satisfará a equação de Euler e a condição de transversal idade fx (x(b), x(b),b) = O.

Demonstrafrão: A equação de Euler será atendida via uma demonstração semelhante ao teorema 2.4. Seja h:[a, b] ---+

9t

continuamente diferenciável com h(a)

=

O. Por raciocínio análogo ao apresentado no teorema 2.4 chegaríamos a:

r

(I:.

(x(t), x(t), t)h(t)

+

fx (x(t), x(t), t)Ji(t») dt = O Aplicando a equação de Euler e integrando por panes temos:

h(b)fx (x(b),x(b),b) = O.

Como h é arbitrário, escolhendo-se h tal que ｨＨ｢Ｉｾ＠ O e tem-se que

fi (x(b),x(b),b) = O .•

Teorema 2.8. Seja x:[a, b] ---+

9t

satisfazendo (i'), a primeira pane de (ii), a equação de Euler e a condição de tranversalidade. Suponha, além disso, que C é convexo e f(x,y, t) é uma função côncava em (x,y) para cada te [a,b]. Então x(t) de fato maximiza em (ii).

Demonstracão: A demonstração transcorerá de forma idêntica a do teorema 2.5 exceto que h(b) pode ser não nulo, mas o que precisamos de fato é que

Exemplos:

]) O problema da taxa ótima de crescimento:

Suponhamos que o produto x(t) de uma sociedade seja proporcional ao seu estoque de capital K(t):

x(t)

=

aK(t).

O produto desdobra-se no consumo c(t) mais investimento líquido

X(t): x(t) = c(t) + X(t). O problema da taxa ótima de crescimento é planejar as trajetórias do produto, do consumo e do investimento, que satisfaçam as relações acima e maximize o valor descontado da utilidade do consumo ao longo do período de programação.

Para fixarmos idéias, suponhamos a

=

1, a função utilidade ｕＺｾＫ＠ ｾ＠ ｾＫ＠ dada por U(x)

=

ｾ＠

(crescente e esritamente côncava), a taxa de juros i

=

ｾＬ＠

o estoque de capital inicial da sociedade K(O)

=

1, o estoque final é K (])

=

2, e que tenhamos T =

I.

Queremos então maximizar

T

J

e -il U (c(t) )dt

o

ou seja, maximizar

Usando as relações acima temos c(t) = K(t) - X(t). Assim o problema fica

s.a. K(O) = 1 e K(l) = 2 Considere f: C x [0,1] ｾ＠ ｾ＠

(x,y,t) H e-X' (x- y)X, ｯｮ､･ｃ］ｻＨｸＬｙＩｅｾＡＫ［＠ x> y}'

Temos que C é convexo aberto e para cada t e[O,I), f(x,y,t) é função côncava em (x,y).

suficiente para o ótimo deste problema. No caso.

-151 -15 ₁

e ｾ＠ - -e :

-f.

= -

(x - y) y, e fy = - -(x - y) 15 •

2 2

-15' -15'

. e - - . - e .

Assim, fx (K(t), K(t),t)

=

-2-(c(t» 15 e fi (K(t), K(t), t)

=

2 (c(t»"y,

-Y,' -Y,' -L(I

e - _ e' _ en _

A equação de Euler fica então, -2-c y, =

4

c >5 é

+

4

c y, o que implica que 2 c = é

+

c ｾ＠ é = c ｾ＠ c(t) = Co e' onde Co é o consumo inicial. Portanto,

K(t) - /(t) = coe' cuja solução geral será: K(t) = (Ko - cot) el

• Sabemos que K(O)

=

1 e K( 1)

=

2, logo Ko = 1 e então (1

+

co)e

=

2 ｾ＠ Co

= -

Ye

+

1. Determinando assim as trajetórias ótimas de consumo e capital, e conseqüentemente a trajetória ótima do produto.

2) Vejamos uma aplicação à macroeconomia do cálculo de variações em horizonte finito. Para isto, iniciemos supondo que uma economia tem uma função de perda dada por

a>O

onde h

=

In ji - In y, y sendo o índice do produto e ji o índice de produto de pleno emprego e 7t a taxa de inflação. Admite-se que a economia tem ojeriza à inflação e a

operar fora do pleno emprego, seja para mais ou para menos. Ao mesmo tempo, quanto maior a, maior a ojeriza à inflação relativamente ao hiato de produto h.

Num horizonte de planejamento do período t

=

O ao período t

=

T, suponhamos que o objetivo seja reduzir-se à zero a inflação minimizando o valor atual da perda, descontada à taxa v de preferência intertemporal, ou seja, resolver

Supõe-se adicionalmente que no instante t

=

O a economia esteja operando à

pleno emprego h

=

O com uma taxa de inflação

no

igual à taxa esperada de inflação ＨｮｾＩＮ＠ Valem também as relações:

(Equação de Cagan de fonnação de expectativas)

o ponto sobre a variável denotando a sua variação em relação ao tempo. No tempo T a economia deve ter inflação zero (igual à inflação esperada) e estar operando com pleno emprego.

Solução:

Destas três equações obtém-se:

-VI I [

i

a?

i

a a

2]

a. a

e U(rr,h)

=

e-v ＨｲｦＳＩｾ＠ +a(fj+rr)

=

J(rr ,rr )

Sendo J(rra, ia) uma função convexa, a equação de Euler nos dará a condição suficiente para mínimo. Temos

aJ

ia a -VI

--=2a(-+rr )e

arr·

f3

aJ

2[( I

+

ar

2

J ..

a

a]_VI

- - = rr +-·rr

e

ai.

r

2f32

f3

d (

aJ

J

aJ

b ' d·ti·aI

Fazendo-se - - - = :lo-a O tem-se a equação 1 erencl dI

a

ia UI'

•• a •• a ｡ＨｶＫｾＩＧｙＲｾ＠

rr - V rr - crr = O onde c = 2 .

l+ay

o

polinômio característico é dado por P( r) = r2

- vr - c com ll. > O, rI r

2 =-c

e 'i +'2 = v. Segue que uma das raízes é maior que zero ('i ' por escolha) e a outra ('2)