Uma Fundamentação Intervalar Aplicada à Morfologia Matemática

Departamento de Computação e Automação

Uma Fundamentação Intervalar Aplicada à

Morfologia Matemática

Doutorando: Marcia Maria de Castro Cruz

Uma Fundamentação Intervalar Aplicada à

Morfologia Matemática

Orientadores:

Prof. Dr. Adrião Duarte Dória Neto

Prof. Dr. Regivan Hugo Nunes Santiago

Tese submetida ao programa de Pós-Graduação em Engenharia Elétrica e de Computação da Universidade Federal do Rio Grande do Norte como parte dos requisitos para obtenção do grau de DOUTOR em CIÊNCIAS.

Catalogação da publicação na fonte. UFRN / Biblioteca Central “Zila Mamede” Seção de Processos Técnicos

Cruz, Marcia

Uma Fundamentação Intervalar Aplicada à Morfologia Matemática / Marcia Maria de Castro Cruz. Natal: 2008.

xviii. 109p.

Orientador: Prof. Dr. Adrião Duarte Dória Neto Orientador: Prof. Dr. Regivan Hugo Nunes Santiago

Tese (Doutorado) - Universidade Federal do Rio Grande do Norte. Centro de Tecnologia. Programa de Pós-Graduação em Engenharia Elétrica.

1. Processamento de Imagens Intervalares 2. Morfologia Matemática 3. Matemática Intervalar 4. Incerteza 5. Reticulados Completo 6. Imagens Indefinidas 7. Dilatação 8. Erosão

Marcia Maria de Castro Cruz

Tese apresentada à Coordenação do Curso de Pós-Graduação em Engenharia Elétrica e de Computação da Universidade Federal do Rio Grande do Norte como requisito parcial à obtenção do grau de Doutor em Ciências. Aprovada, em 05 de Setembro de 2008, pela Comissão Examinadora formada com os seguintes membros:

Composição da Banca Examinadora:

Adrião Duarte Dória Neto: UFRN, (Doutor), Orientador

Graçaliz Pereira Dimuro: UCPEL, (Doutor), Examinador

Benjamín René Callejas Bedregal: UFRN, (Doutor), Examinador

Aarão Lyra, (Doutor), Examinador: UnP

Ronei Marcos de Moraes: UFPB, (Doutor), Examinador

Agradecimentos

Após esta difícil jornada, quero agradecer a todos aqueles que, de diferentes formas, contribuíram para a realização desse trabalho.

Na impossibilidade de citar todos os nomes, destaco alguns, na certeza de que sou grato a todos que direta ou indiretamente contribuíram para o sucesso deste trabalho.

A Deus, o ser SUPREMO do universo, presente em todos os momentos.

Aos meus amados esposo e filhos (em ordem hereditária), Rubens Leão de Andrade, Janaina de Castro Leão e Izan de Castro leão pelo estímulo, carinho, amor e apoio na concretização deste trabalho.

Em especial, um profundo agradecimento ao meu filho Izan que, por muitas vezes me ajudou em vários aspectos desta tese, tais como obtenção de algumas imagens.

A minha mãe, que mesmo de longe sempre torceu pelo meu sucesso em tudo que faço, em especial para esse trabalho.

Ao meus irmão Jadilson Rubens, que foi um dos maiores incentivadores da minha vida acadêmica. Também as minhas irmãs, Rita de Cássia e Regina Celi pela amizade.

Um especial agradecimento a minha querida avó Francisca Amélia (codinome Yayá), que já não está mais entre nós, mas que foi uma das pessoas mais importantes da minha vida. Se não fosse por ela, certamente não chegaria onde eu cheguei, pois foi ela uma das maiores incentivadoras da minha vida estudantil e acadêmica.

curso de mestrado e aceitou mais uma vez o desafio de me orientar em um curso de maior responsabilidade que é o doutorado. Graças as suas sugestões e críticas, algumas vezes duras, ele conseguiu me mostrar o caminho de aprimoramento dos meus limitados conhecimentos científicos, na área de matemática aplicada. Ao Professor adrião, também devo externar meu profundo reconhecimento pela credibilidade em mim depositada. Também agradeço de coração ao professor Benjamím que aceitou me ajudar em momentos difíceis durante o desenvolvimento desse trabalho e foi de extrema importância para a finalização deste trabalho. A todos vocês, os meus mais sinceros agradecimentos.

Aos Professores do DCA, LECA e DIMAp, pelas significativas contribuições que enriqueceram este estudo. Em especial ao professor José Alfredo Costa, que além dos seus ensinamentos como professor, participou de outras atividades tal como a colaboração conjunta de um trabalho em um importante congresso nacional de matemática aplicada, o CNMAC.

Ao Prof. Dr. Junior Barrera, da USP de São Paulo, pelas importantes sugestões e pela grande atenção que me teve quando necessitei da ajuda de seus conhecimentos.

Lista de figuras vii

Resumo xii

Abstract xiii

1 Introdução 1

2 Uma Abordagem da Morfologia Matemática Clássica 7

2.1 Morfologia matemática para imagens binária . . . 8

2.1.1 Conceitos básicos da teoria dos conjuntos . . . 9

2.1.2 As operações de Minkowski . . . 9

2.1.3 Os operadores elementares da morfologia matemática . . . 10

2.1.4 Outros operadores morfológicos . . . 12

2.1.5 Algumas importantes aplicações das operações morfológicas binárias . . . 16

2.2 Abordagem algébrica dos operadores morfológicos como reticulado completo . . . 17

2.2.1 Análise binária e reticulados . . . 17

2.2.2 Álgebra de Boole das funções binárias . . . 18

2.2.3 Relação de ordem e reticulados . . . 19

2.2.4 A estrutura dos operadores elementares da morfologia matemática sobre{0,1}E . . . 21

2.3 Morfologia matemática para imagens em níveis de cinza . . . 24

imagens em tons de cinza . . . 25

2.3.2 Outros operadores morfológicos . . . 27

3 Uma Abordagem da Matemática Intervalar 28 3.1 Introdução . . . 28

3.2 Análise intervalar . . . 29

3.3 Definições básicas . . . 29

3.3.1 Aritmética intervalar . . . 31

3.3.2 Propriedades da aritmética intervalar . . . 33

3.3.3 Relações de ordem . . . 35

4 Processamento de Imagens Digitais Intervalares 36 4.1 Introdução . . . 36

4.2 Definições . . . 37

4.3 Operações lógicas-aritméticas entre pixels intervalares . . . 38

5 Morfologia para imagens binárias intervalares 43 5.1 Construção do espaço algébricoΩ . . . 45

5.2 Imagens binárias contendo incertezas . . . 49

5.2.1 Operações básicas . . . 49

5.3 Operações derivadas . . . 53

5.4 Morfologia sobre imagens binárias intervalares . . . 54

5.4.1 Operadores sobre imagens binárias intervalares . . . 55

5.4.2 Translação, reflexão e invariança por translação . . . 58

5.4.3 Operações de Minkowiski . . . 60

5.4.4 Conclusão do capítulo . . . 64

6 Um Modelo Intervalar para Imagens em Níveis de Cinza 66 6.1 Construção do espaço algébrico para imagens intervalares em escala de cinzas . . . 69

6.2 O reticulado completo das imagens sobreΩN . . . 73

6.3 Operações morfológicas para imagens intervalars em níveis de cinza . . . 77

6.3.1 Operações básicas . . . 79

6.3.2 Dilatação e erosão para imagens intervalares em níveis de cinzas . 79 6.3.3 Outros operadores morfológicos . . . 94

6.3.4 Potenciais aplicações . . . 96

6.3.5 Consclusão sobre o capítulo . . . 97

7 Considerações Finais 98 7.1 Principais contribuições . . . 99

7.1.1 Na matemática intervalar . . . 99

7.1.2 Na morfologia matemática . . . 99

7.2 Perspectivas . . . 100

7.3 Conclusão final . . . 100

2.1 Operações de translação e reflexão . . . 9

2.2 Operações de soma e subtração de Minkowski . . . 10

2.3 Exemplo de elementos estruturante em uma imagem binária . . . 11

2.4 Efeitos da dilatação e da erosão em uma imagem binária . . . 12

2.5 Efeitos da operação de abertura em uma imagem binária . . . 13

2.6 Efeitos da operação de fechamento em uma imagem binária . . . 14

2.7 Exemplo de uma operação de gradiente morfológico em imagem binária . 14 2.8 Exemplo de filtragem morfológica em uma imagem binária . . . 15

2.9 Exemplo de uma operação hit-or-miss . . . . 15

2.10 Exemplo de uma operação de extração de contorno em uma imagem binária 16 2.11 Exemplo de esqueletos binários . . . 17

2.12 Uma imagem binária . . . 18

2.13 Gráfico de uma função binária . . . 18

2.14 Representação de uma imagem binária . . . 19

2.15 Imagem da Lena e os efeitos causados pelos operadores de dilatação e erosão . . . 27

3.1 N⊆Z⊆Q⊆R⊆IR . . . . 30

3.2 Par ordenado intervalar . . . 31

3.3 Representação geométrica da interseção emR . . . 34

3.4 Representação geométrica da união emR . . . 35

4.1 Imagem média da Lena disjunta com uma imagem constante. . . 41

4.2 Imagem média da Lena conjunta com uma imagem constante. . . 41

4.3 Imagem da Lena original e negativa. . . 42

5.1 Imagem Binarizada . . . 44

5.2 Operações básicas e algumas operações derivadas sobre imagens binárias intervalares . . . 55

5.3 Operações Morfológicas para imagens binárias intervalares intervalares . 64 6.1 Imagens apresentando um processo de segmentação em uma mama com suspeito de nódulo canceroso. (a) Imagem original, (b) imagem binarizada e (c) imagem segmentada com o nódulo destacado. . . 67

6.2 Estrutura do reticuladoΩN . . . 70

6.3 Uma função intervalar com uma translação horizontal. . . 80

6.4 Uma função intervalar com uma translação vertical. . . 80

6.5 Uma função intervalar com uma translação morfológica. . . 81

6.6 Imagem representada por uma função F e por uma função estrurante G . . 89

6.7 Dilatação intervalar de F pela função estrurante G . . . . 91

N Conjunto dos números naturais

∀ Para todo

∃ Existe

N Conjunto dos números naturais

N+ Conjunto dos números naturais positivos

Z Conjunto dos números inteiros

Q Conjunto dos números racionais

R Conjunto dos números reais

R+ Conjunto dos números reais positivos

Rn Conjunto dos números reais no espaço n

IR Conjunto dos intervalos reais

IN Conjunto dos intervalos naturais

xi Elemento x da posição i de uma sequência

ai j Elemento de uma matriz na posição i relativo a linha e j relativo a coluna

A= [a1,a2] Intervalo de extremos a1e a2

A= (a1,a2) Par ordenado A de abscissa a1e ordenada a2 max{X} Maior elemento do conjunto X

min{X} Menor elemento do conjunto X

∨(F) Supremo de uma função

⊇ Subconjunto, contém ou igual

⊑ Relação de ordem do domínio contínuo real

∈ Pertence

6∈ Não pertence

S

União

T

Interseção ASB União convexa

≤ Menor ou igual

≥ Maior ou igual

≤KM Menor ou igual na ordem de Kulisch-Miranker

≪ menor ou igual na ordem parcial emC

Menor ou igual na ordem da aproximação dist Distância entre intervalos

|A| Módulo do intervalo A diam Diâmetro de um intervalo med Ponto médio de um intervalo

ℜ Relação binária entre intervalos

f :R→R Função f cujo domínio e contra-domínio é conjunto dos números reais

∨ Disjunção

∧ Conjunção

Ω Conjunto de valores

ΩN Conjunto finito de valores intervalares

ΩE _{Conjunto das funções que representam imagens binárias intervalares}

ΩE

N Conjunto das funções que representam imagens intervalares em níveis de cinza

⊕ Operador de dilatação

⊖ Operador de erosão ˙

+ Soma limitada ˙

− Diferença limitada

⊤ Maior elemento

Resumo

Introdução

A área de processamento de imagens digitais está evoluindo continuamente, e a cada dia surgem novas técnicas cada vez mais sofisticadas para a análise de imagens digitais. Estudos mais avançados desta área inicialmente foram direcionados para o processamento de imagens espaciais, porém as pesquisas foram se estendendo e hoje atinge as mais diversas áreas do mundo científico. Durante os últimos anos tem havido um aumento crescente no nível de interesse desta área, voltada para morfologia matemática, redes neurais, lógica fuzzy entre outras. Alguns trabalhos de processamento de imagens, entre livros e artigos que serviram de fontes de pesquisa nesse trabalho, podem ser encontrados em [20, 35, 45, 57]

Uma das questões ao longo dos anos, que tem sido aprimorada no processamento de imagens digitais, são a ocorrência de erros decorrentes de alguma(s) etapas do processo de análise de imagens. Várias metodologias vem sendo usadas para o controle desses erros, uma delas é através da teoria fuzzy que de um modo geral lida com esse tipo de problema. Existe uma ampla literatura que aborda a teoria fuzzy e o processamento de imagens, incluindo morfologia matemática. Algumas dessas abordagens podem ser encontradas em([16, 22]). Outras são através de wavelets ([23]) e também de modelos de distribuição probabilístico tal como, processo estocástico [39, 70]. Podemos citar por exemplo, um estudo relativo à avaliação de imagens para diagnósticos específicos, como no caso de uma imagem médica ou simplesmente uma região em um mapa onde existe a necessidade de exatidão, uma vez que certeza é um fator fundamental nestes casos. Os diversos trabalhos nesta área têm como objetivo a melhoria da informação visual para a interpretação do

automática através de máquinas.

O processamento de imagens digitais envolve operações computacionais que capturam uma imagem real e a discretiza espacialmente em uma matriz de pixel. Os erros numéricos ocorrem com facilidade, uma vez que, diversos fatores influenciam na aquisição da imagem como a iluminação, reflectância dos objetos e capacidade limitada ao aparelho de captura. As imagens intervalares possibilitam um controle maior da informação. Alguns trabalhos destacam-se na área de processamento de imagens digitais, dentre eles citam-se [32, 34, 52, 69], nos quais constatou-citam-se que foram realizadas importantes abordagens e algumas aplicações para a processamento de imagens digitais usando a lógica fuzzy, redes neurais e morfologia fuzzy. Pode-se citar por exemplo, o desenvolvimento de filtros fuzzy e a extensão de algumas redes neurais para a utilização da lógica fuzzy em aplicações em clusterização de imagens [52]. Algumas aplicações da lógica fuzzy utilizadas no processamento de imagens digitais incluindo morfologia matemática podem ser vistas em [53] e [1]. Outras referências sobre a teoria fuzzy podem ser encontradas em [10, 42, 49, 69].

A morfologia matemática é uma das áreas de destaque do processamento de imagens com inúmeras práticas de análise de imagens, tais como: filtragens de ruídos, reconhecimento e classificação de padrões, segmentação, reconstrução, extração de objetos de interesse, etc. Introduzida na década de 60 por Jean Serra e George Matheron na Ècole Nationale Superiéure des Mines de Paris [46? ], através da morfologia matemática é possível se fazer transformações entre reticulados completos, os quais são chamados de operadores morfológicos. Inicialmente foi construída para imagens binárias com base na teoria dos conjuntos onde foram introduzidos os operadores elementares dilatação e erosão. Alguns anos depois, na década de 80, Serra e Matheron, pecebendo uma série de características interessantes destes operadores, formalizaram a teoria para o dominio dos reticulados completos. Essa formalização levou a ampliação e generalização da área para imagens em escala de cinzas e depois também para imagens a cores. Importantes trabalhos sobre morfologia matemática que apresentam abordagens teóricas, modelos e importantes aplicações, podem ser vistos em [24, 25, 41, 63].

de tratar questões de exatidão e eficiência que surgem na prática da computação científica e na resolução de problemas numéricos. Moore apresentou uma arimetica para intervalos, com base na aritmética dos reais. A matemática intervalar se apresenta como uma ferramenta poderosa para a análise e controle de erros em computação científica. Pela sua natureza de tratar os números não mais como entes pontuais, mas como intervalos que encapsulam estes números, é possível, de uma forma segura, armazenar os dados físicos através de uma medida provável e um possível porcentual de erro associado. Isto faz com que, ao final do processo matemático-computacional, se tenha uma estimativa da influência destes erros de entrada no resultado final obtido. Existem um número significativo de trabalhos desenvolvidos nesta área, dentre eles pode-se citar: [12, 13, 17, 51, 56]

Atualmente, a matemática intervalar ultrapassou as fronteiras das aplicações numéricas, sendo muito utilizada para aplicações no tratamento e modelagem da incerteza em computação, no processamento de informações fuzzy, na teoria de controle, na inteligência artificial, representação do conhecimento, redes, computação gráfica, processamento de imagens e diversas outras aplicações em ciência e tecnologia que lidam com dados incertos. [38, 59]. Pode-se dizer que a computação intervalar tem sido bem sucedida em aplicações em áreas como engenharia elétrica, física, engenharia química, localização de depósitos de minerais e petróleo, estimação de erros em sistemas de laser, engenharia da computação, no controle da mobilidade de robôs, cálculo da relação profundidade-pressão em reservatórios, modelagem geométrica e Sistema multiresolucional. Pode-se citar, por exemplo, trabalhos recentes tais como, o desenvolvido por Grigoletti e Dimuro em [55] que apresentou um software para a análise de circuitos elétricos baseado na filosofia de software livre e na Matemática Intervalar. Este é capaz de automaticamente avaliar a influência das tolerâncias dos valores nominais dos resistores sobre as tensões nodais do circuito elétrico.

o modelo clássico binário, com a inclusão da informação de incerteza. A estrutura reticular dessas imagens permitiu definir os operadores morfológicos, onde as incertezas são tratadas localmente. O segundo modelo, estende o modelo clássico de imagens em níveis de cinza, onde as funções que representam essas imagens são mapeadas em um conjunto finito de valores intervalares. A estrutura algébrica desse conjunto pertence a classe dos reticulados [37], o que também permitiu definir os operadores elementares da morfologia matemática, dilatação e erosão. A teoria, será baseada na matemática intervalar, ou seja, apresenta-se uma generalização da teoria da morfologia clássica para a teoria intervalar, onde ao invés de lidar com imagens de valores pontuais (pixels), lida-se com valores (pixels) intervalares. Dessa forma, será mostrado que, os modelos intervalares apresentados, satisfazem as propriedades fundamentais para a introdução dos operadores morfológicas nessa ótica.

O principal objetivo do uso de intervalos será lidar com questões de incertezas em pixels de imagens. Esses problemas em geral ocorrem principalmente por causa dos erros durante a aquisição ou processo de discretização da imagem original (contínua) para a imagem digital (discreta). Tais erros, na maioria das vezes, conduzem a incertezas com relação à intensidade do brilho de pixels da imagem levando a importantes perdas de informações.

Como trabalhos mais recentes, algumas pesquisas foram feitas envolvendo matemática intervalar e processamento de imagens. Kearfott e Kreinovch em [33] apresentam uma abordagem sobre o uso de métodos intervalares em sistemas de multi-resolução. Naquele trabalho é mostrado que a estimativa do erro quando são tomadas aproximações de imagens de baixa resolução podem ser controladas por métodos intervalares. Uma outra importante contribuição nessa linha pode ser encontrada em [4] onde Lyra, desenvolve "Uma Fundamentação Matemática para o Processamento de Imagens Digitais Intervalares".

de um método de segmentação de imagens em mamas densas, usando imagens digitais intervalares. Para lidar com problemas de incerteza pesquisadores da área de morfologia matemática tem feito uso de métodos através da teoria fuzzy. Existem diversas abordagens sobre essa teoria em operações morfológicas [10, 29]. Esse trabalho tem similaridade com a teoria fuzzy, pois também lida com indecisões ou imprecisões em determinadas regiões de uma imagem. Tanto a teoria fuzzy, quanto a teoria intervalar, são ferramentas usadas para tratar as incertezas e otimização de erros computacionais. Entretanto, esta é a primeira abordagem que relaciona as duas áreas: morfolologia matemática e matemática intervalar e, obviamente o objetivo é introduzir um modelo intervalar que permita estimar erros com a melhor precisão possível.

As imagens intervalares possibilitam um controle maior da informação, subsidiando melhor ao especialista nas tomadas de decisões, por exemplo, buscar em uma imagem intervalar de um mamograma regiões fundamentais, como uma área suspeita de existência de nódulo canceroso. Neste caso, o especialista vai poder obter informações (intervalares), visualizar e decidir, de forma que garanta um diagnóstico mais preciso sobre o grau gravidade do caso.

A contribuição científica desse trabalho é oferecer uma abordagem teórica ao mundo científico em que são integradas duas importantes áreas: Morfologia Matemática e Matemática Intervalar, que permita tratar com problemas das incertezas que frequentemente aparecem no tratamento de imagens. Será oferecido então, mais uma ferramenta de controle de erros computacionais, abrindo caminho para o estudo prático dos novos modelos, bem como, a obtenção de um maior controle nas variações decorrentes de fatores que levam as incertezas. Será dado ênfase aos conceitos oriundos da matemática intervalar, herdando a característica desta abordagem, que é o controle do erro computacional, que poderá advir de ruídos, do processo de aquisição, digitalização, bem como, processos de filtragens, processos de segmentação, ou de algum outro que são utilizados no processamento de imagens morflogicamente.

Esta discertação está dividida em sete capítulos descritos a seguir:

Capítulo 1. Introdução.

imagens binárias quanto para imagens em tons de cinza, apresentando inclusive algumas técnicas e aplicações usando os operadores morfológicos.

Capítulo 3. Uma abordagem da matemática intervalar: Para esse capítulo, serão

apresentados os principais conceitos da matemática intervalar que nortearão o desenvolvimento desta tese, tais como a arimética de Moore e algumas propriedades algébricas desta teoria que serão de fundamental importância no desenvolvimento do modelo aqui proposto.

Capítulo 4. O processamento de imagens digitais intervalares: Aqui, apresenta-se

uma noção da abordagem feita por Lyra (e colaboradores), onde ele introduz uma abordagem matemática de conceitos fundamentais do processamento de imagens que foram redefinidos sob uma nova visão: a visão intervalar.

Capítulo 5. Um modelo intervalar para lidar com incertezas entre dois pixels de

imagens: Neste capítulo, será introduzido o primeiro resultado modelo intervalar

para um conjuto de três elementos, com o objetivo de lidar localmente com as questões de incertezas em imagens.

Capítulo 6. Um modelo intervalar para imagens em escala de cinzas: Neste capítulo,

apresenta-se uma abordagem mais geral, que estende o modelo apresentado no Capítulo 5. Em outras palavras, introduz-se uma teoria intervalar para lidar com questões de incertezas, em um sentido mais amplo no caso de tons de cinza, ou seja, considera-se um conjunto que engloba valores de tons de cinza para conjuntos finitos.

Uma Abordagem da Morfologia

Matemática Clássica

Uma forma elegante de resolver problemas de processamento de imagens é através da utilização de uma base teórica consistente. Uma destas teorias é a morfologia matemática. Esta teoria diz que é possível fazer transformações entre reticulados completos, os quais são chamados de operadores morfológicos. Na morfologia matemática existem quatro classes básicas de operadores: dilatação, erosão, anti-dilatação e anti-erosão, chamadas de operadores elementares. Banon e Barrera em [36] provaram que todos os operadores morfológicos, no caso binário, invariantes por translação podem ser obtidos a partir de combinações de operadores elementares juntamente com as operações de união e intersecção. Usando estes operadores elementares é possível construir uma linguagem formal, a linguagem morfológica, e sua implementação é chamada máquina morfológica. Um exemplo de uma máquina morfológica é a MMach ([25]). Neste capítulo apresentaremos alguns conceitos básicos da morfologia matemática clássica.

Morfologia Matemática pode ser descrita como uma ferramenta para extração de componentes de uma imagem digital que sejam úteis na representação e descrição da forma de uma região, como por exemplo, detecção de bordas. Outro aspecto do uso das técnicas morfológicas está no pré e pós processamento de imagens, como filtragem. As operações morfológicas elementares, a dilatação e a erosão, foram introduzidos a partir das noções de soma e subtração de Minkowski. Inicialmente as transformações foram produzidas para imagens binárias (i.e. cujos pixels podem tomar apenas os valores 0

elementos estruturantes, que as sondam localmente. Na dilatação, verifica-se quando o elemento estruturante toca o objeto (i.e., os pixels da imagem binária que têm o valor 1) e na erosão, quando ele está contido. De acordo com a definição desses operadores, obtem-se como resultado, uma imagem transformada. As bases teóricas da morfologia matemática para subconjuntos foram formalizadas pelos próprios Serra e Matheron, que estudando as dilatações e erosões, descobriram uma coleção de propriedades e chegaram a um resultado bastante interessante: "qualquer operador invariante por translação e isotônico ou crescente (i.e., que preserva a relação de inclusão) pode ser decomposto como um supremo de erosões ou ínfimo de dilatações. Em outros palavras, as dilatações e erosões são os elementos fundamentais para construir uma ampla classe de operadores". A morfologia matemática tem se mostrado útil na extração de componentes da imagem na representação e descrição da forma da região, tais como: extração do contorno, esqueletos morfológicos, fecho convexo, filtragem morfológica, afinamento, espessamento, etc.

Conjuntos em morfologia matemática representam objetos em uma imagem. O elemento do conjunto é a coordenada (x,y) do pixel que pertence ao objeto do espaço

discreto Z2. A Morfologia matemática consiste em extrair informações relativas à geometria e à topologia de um conjunto desconhecido de uma imagem, a partir de transformações de formas, realizadas através dos operadores dilatação e erosão. A dilatação faz com que os objetos dilatem ou aumentem de tamanho. A erosão faz com que eles encolham. A quantidade e maneira como eles aumentam ou encolhem depende da escolha do "elemento estruturante". No caso das imagens binárias, a morfologia matemática pode ser definida como sendo um conjunto básico de operações que são utilizadas para transformar a estrutura geométrica de uma imagem.

2.1

Morfologia matemática para imagens binária

2.1.1

Conceitos básicos da teoria dos conjuntos

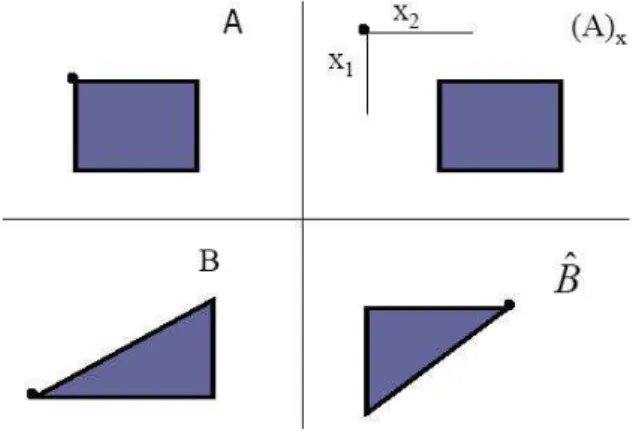
Sejam A e B dois conjuntos, cujos componentes são pares ordenados dados por a= (a1,a2)e b= (b1,b2), respectivamente.

A somaé dada por: A+B= (a1+b1,a2+b2) A diferença é dada por A−B= (a1−b1,a2−b2).

A translação de A por x= (x1,x2), é definida como:(A)x={c|c=a+x,∀a∈A}

A reflexão é definida porBb={x|x=−b,∀a∈B}

O complemento do conjunto A é definida por: Ac={x|x6∈A}

A Figura 2.1 mostra duas importantes operações básicas sobre conjuntos que serão utilizada nesse trabalho.

Figura 2.1: Operações de translação e reflexão

2.1.2

As operações de Minkowski

A adição de Minkowski baseada na teoria dos conjuntos foi proposta por Minkowski (1903) para caracterizar medidas integrais de certos conjuntos esparsos. A adição de Minkowski pode ser definida como a seguir [25].

Seja E o conjunto de pares ordenados tal que E = Z×Z e Sejam A e B dois subconjuntos de E.

A soma de Minkowski é definida por:

A⊕B= [

b∈B

(A+{b}) (2.1.2)

E a subtração de Minkowski é definida por:

A−B={x∈E|∀b∈B,∃a∈A : x=a−b} (2.1.3) Ou equivalentemente

A⊖B= \

b∈B

(A− {b}) (2.1.4)

A Figura 2.2 (extraída de [25]) mostra exemplos da soma e subtração de Minkowski respectivamente.

Figura 2.2: Operações de soma e subtração de Minkowski

2.1.3

Os operadores elementares da morfologia matemática

As transformações sobre imagens binárias, fazendo uso das dilatações e erosões dependem de padrões predefinidos (forma e tamanho), denominados elementos estruturantes, que são comparados ao conjunto desconhecido da imagem. O resultado desta transformação permite avaliar tal conjunto. O elemento estruturante é um

sobre a estrutura geométrica da imagem. O tipo e a natureza da informação extraída depende necessariamente do tipo do elemento estruturante e do tipo da imagem estudada. Por exemplo, a natureza bordas quadradas e desejamos obter bordas arredondadas. Nesse caso, escolhe-se um elemento estruturante na forma circular.

Figura 2.3: Exemplo de elementos estruturante em uma imagem binária

Seja E =Z×Z, uma grade definida no espaço Euclidiano bidimensional e A e B subconjuntos de E, a operação de dilatação é definida por

A⊕B={x|Bbx∩A6=φ} (2.1.5) Ou

A⊕B={x|[Bbx∩A]⊆A} (2.1.6) A erosão é definida por

A⊖B={x|(B)x⊆A} (2.1.7) Em termos da soma e subtração de Minkowski, as operações de dilatação e erosão são definidas respectivamente por

A⊕B={x∈E|x=a+b,a∈A,b∈B} (2.1.8)

A⊖B={x∈E|x+b∈A∀b∈B} (2.1.9) Ou equivalentemente por

A⊕B= [

b∈B

(A+{b}) (2.1.10)

A⊖B= \

b∈B

(A− {b}) (2.1.11)

Figura 2.4: Efeitos da dilatação e da erosão em uma imagem binária

2.1.4

Outros operadores morfológicos

Os operadores dilatação e erosão, aplicados isoladamente, são transformações que nem sempre evidenciam características das imagens, mas permitem construir algumas funções muito interessantes, como por exemplo, o fechamento, a abertura, o gradiente morfológico entre outros.

Abertura

É uma operação que consiste em aplicar-se uma erosão seguida de dilatação. A abertura de um conjunto, denotada A◦B, é definida como:

A◦B= (A⊖B)⊕B (2.1.12)

A operação de abertura tem como principais efeitos:

• Separar objetos muito próximos em uma imagem, ou seja, criar espaços (aberturas) entre objetos na imagem;

• Eliminar ruídos (pixels negros aleatoriamente espalhados em toda a imagem);

• Regularizar os contornos e eliminar pequenas "ilhas"e "cabos"estreitos de uma imagem binária;

Figura 2.5: Efeitos da operação de abertura em uma imagem binária

Fechamento

É uma operação que consiste em aplicar-se uma dilatação seguida por erosão. O fechamento, é definido como:

A•B= (A⊕B)⊖B (2.1.13)

A operação de fechamento tem como principais efeitos:

• Eliminar espaços entre objetos em uma imagem;

• Eliminar falhas dentro dos objetos da imagem (pixels brancos em um objeto negro, por exemplo);

• Suavizar as bordas de um objeto na imagem.

• Suprimir pequenos "lagos"e "canais"estreitos em uma imagem

Utilizando-se a mesma imagem e o mesmo elemento estruturante do exemplo anterior, a Figura 2.6 mostra uma operação de fechamento, no caso, o objetivo é a eliminação de uma fenda. A figura é descrita do seguinte modo: (a) imagem original; (b) Aplicação da dilatação; (c) Imagem resultante da dilatação; (d) Aplicação da erosão sob a imagem (c); (e) Imagem resultante obtida por fechamento.

Gradiente Morfológico

Figura 2.6: Efeitos da operação de fechamento em uma imagem binária

contorno de objetos em figuras binárias e realçar o contorno de objetos em imagens em tons de cinza. Essa operação é composta de três operações: erosão, dilatação e subtração e é definido como sendo a diferença entre a dilatação e a erosão.

Grad(A) = (A⊕B)−(A⊖B) (2.1.14) A Figura 2.7 mostra um exemplo

Figura 2.7: Exemplo de uma operação de gradiente morfológico em imagem binária

Filtros Morfológicos

Exploram propriedades geométricas dos sinais. As máscaras são os elementos estruturantes que apresentam valores 0 ou 1 na matriz que correspondem ao pixel considerado. Os filtros morfológicos básicos são: filtro da mediana, erosão e dilatação. O processo de filtragem são sequências de operações de abertura e fechamento. A Figura 2.8 apresenta um exemplo de filtragem morfológica para imagem binária usando operadores de abertura e fechamento.

Figura 2.8: Exemplo de filtragem morfológica em uma imagem binária

É possível combinar erosão e dilatação para produzir um operador que tem uma ação como esta: acerto e erro (folga). O operador leva dois elementos, o primeiro é o acerto e o outro é o erro. O operador é definido por

A⊗B= (A⊖B1)∩(Ac⊕B2) (2.1.15) onde A é a imagem original e B1 e B2 são os elementos estrurantes. A Figura 2.9 mostra uma aplicação do operador hit-or-miss.

Figura 2.9: Exemplo de uma operação hit-or-miss

Extração de Fronteiras A fronteira de um conjunto A, denotadoβ(A)pode ser obtida como segue

β(A) =A−(A⊖B) (2.1.16)

Figura 2.10: Exemplo de uma operação de extração de contorno em uma imagem binária

2.1.5

Algumas importantes aplicações das operações morfológicas

binárias

A principal aplicação de morfologia, no caso de imagens binárias, é a extração de componentes da imagem que sejam úteis na representação e na descrição de formas. Algoritmos que fazem o afinamento, o espessamento, a extração de fronteiras e o esqueleto de uma região, entre outros, são bastante úteis nesse expediente. O afinamento visa remover os pixels de um grupo de componentes conectados, até restar apenas um estreito conjunto. Pode ser definido em função da transformada Hit-or-miss.

Outra importante aplicação para a representação estrutural da forma de um objeto consiste na obtenção do seu esqueleto através do algoritmo de afinamento. Em vez de bordas pode-se extrair seu eixo medial, que são linhas finas que condensam a informação original enquanto se tenta preservar a homotopia dos objetos. Esse processo é bastante utilizado em problemas de inspeção automática de circuitos impressos, e também bastante útil na segmentação morfológica.

Existem duas formas de esqueletização. Lantuejoul ([19]) definiu um tipo particular de esqueleto, usando transformações da morfologia matemática, para aplicações na compressão de dados, com a intenção de que o objeto original pudesse ser reconstruído a partir do seu esqueleto. Este tipo de esqueleto também tem aplicações úteis para a representação e o reconhecimento de objetos. O esqueleto pode ser definido como uma sucessão de operações de erosão dados por

S(A) =

n

[

k=0

Onde Sk(A)é dado por

Sk(A) = (A⊖kB)−(A⊖kB)◦B (2.1.18) onde k=1,2, ...n. A Figura 2.11, mostra um exemplo de esqueleto binário.

Figura 2.11: Exemplo de esqueletos binários

2.2

Abordagem algébrica dos operadores morfológicos

como reticulado completo

Nesta seção será feita uma abordagem algébrica dos operadores morfológicos como reticulado completo, que foi desenvolvida por Banon e Barrera em [25]. A estrutura algébrica desses operadores morfológicos como reticulados, foi introduzida no início da década de 80 pelos criadores Matheron e Serra que, a partir daí mudaram os rumos da teoria.

Antes de apresentar a estrutura dos reticulados e dos operadores morfológicos nesse domínio, será feita uma breve introdução de análise das imagens binárias.

2.2.1

Análise binária e reticulados

Seja E um conjunto não vazio. As imagens binárias podem ser representadas por subconjuntos, ou equivalentemente, por funções binárias. Seja X um subconjunto de E e

Figura 2.12: Uma imagem binária

Definição 2.2.1 Uma função binária é definida e denotada por f : E → {0,1}, isto é,

para cada valor de E a função toma valor 0 ou 1. Sendo{0,1}E o conjunto de todas as funções binárias, então f ∈ {0,1}E.

A Figura 2.13 mostra o gráfico de uma função binária. Observe que o gráfico é formado pelo conjunto de pontos da forma(x,f(x)).

Figura 2.13: Gráfico de uma função binária

Observe tambem na Figura 2.13 que a representação por uma função binária a imagem, é assimilada à função binária que toma o valor 0, nos elementos x de E que representam a posição dos pixels pretos e o valor 1, nos elementos x de E que representam a posição dos pixels brancos. A função binária f é chamada de imagem e para todo x em E, o par(x,f(x))é chamado de pixel da imagem f , x é a posição do pixel e f(x)é seu valor. A Figura 2.14, mostra a representação de uma imagem binária.

2.2.2

Álgebra de Boole das funções binárias

Figura 2.14: Representação de uma imagem binária

estrutura de Álgebra de Boole.

Seja{0,1}E o conjunto das funções binárias.h{0,1}E,∨,∧,∼i, onde∨,∧e∼são as operações de união, interseção e complemento respectivamente, dadas por:

(f1∨f2)(x) = f1(x)∨f2(x) (2.2.1)

(f1∧f2)(x) = f1(x)∧f2(x) (2.2.2)

(∼ f)(x) =∼ f(x) (2.2.3) forma uma álgebra de Boole,

Extensão das operações de união e interseção das funções Binárias

A união e a interseção de uma família dos elementos fié o elemento de{0,1}E definido respectivamente por

∨(fi)i∈I(x) =   

1 , se∃i∈I,fi(x) =1 0 , caso contrário

(2.2.4)

∧(fi)i∈I(x) =   

1 , se∀i∈I,fi(x) =1 0 , caso contrário

(2.2.5)

Se I for vazio entãoWfi(x)→0 eVfi(x)→1,∀x∈E

2.2.3

Relação de ordem e reticulados

O conjunto {0,1}E das funções binárias definidas em E provido da relação de ordem "menor que"forma um conjunto parcialmente ordenado, denotado({0,1}E,≤), ou seja≤

satisfaz os três axiomas: (prova em [25], pp 22)

• f(x)≤ f(x)(reflexividade)

• f(x)≤g(x)e g(x)≤ f(x)⇒ f(x) =g(x)(anti-simetria)

• f(x)≤g(x)e g(x)≤h(x)⇒ f(x)≤h(x)(transitividade)

Reticulados

Muitos conjuntos parcialmente ordenados gozam da propriedade de conterem o ínfimo e o supremo de um par qualquer de elementos do sistema. Os reticulados por exemplo é um deles. Essa característica dos reticulados nos permite usá-las em teorias tanto algébrica como lógicas.

Definição 2.2.2 Seja(

L

L

L.

L

L

supremo em L denotados por x∧y e x∨y, respectivamente. Se além disso,

L

x∨(y∧z) = (x∨y)∧(x∨z)e x∧(y∨z) = (x∧y)∨(x∧z)

é dito distributivo.

Exemplo 2.2.6

O conjunto de todas as funções reais de variável real definidos num intervalo a≤

x≤b, parcialmente ordenados pela relação f ≤g, se e somente se f(x)≤g(x)para todo x∈[a,b] é um reticulado. O supremo é a função definida por (f ∨g)(x) =

max{f(x),g(x)}e o ínfimo é a função definida por(f∧g)(x) =min{f(x),g(x)} •

• Seja℘a coleção dos subconjuntos de X , ( ou o conjunto das partes de X ). Então

(℘(X),∩,∪)é um reticulado distributivo, onde∧ ≡ ∩e∨ ≡ ∪.

Definição 2.2.3 (Reticulado Completo) Seja (L,∧,∨) um reticulado. L diz-se um reticulado completo se todo subconjunto X ⊆L tem supremo e tem ínfimo, denotados por WX eVX (ou supX e in f X ), respectivamente. Podemos dizer que um reticulado completo é uma estrutura do tipo(L,∧,∨,V,W), onde∧,∨,VeWsão definidos acima. L

diz-se distributivo se(∧X)WY =Wx∧y|x∈X,Y ∈Y e(WX)∧Y =∧x∧y|x∈X,y∈Y e (∧X)WY = ∧x∧y|x∈X,y∈Y . Em particular L deve satisfazer as equações de

distributividade com relação as operações∧e∨.

Exemplo 2.2.7 A estrutura(℘(X),T,S)é um reticulado completo distributivo,

Reticulado das funções binárias

O conjunto parcialmente ordenado ({0,1}E,≤) das funções binárias definidas em E,

provido das operações de união e interseção, forma um reticulado completo. Em outros termos, para todo conjunto de indices I, estas operações verificam os dois axiomas abaixo. Para toda família(fi)i∈I em({0,1}E temos que

(∨fi)i∈I =supFi (2.2.8)

(∧fi)i∈I =in f Fi (2.2.9) onde

Fi={f ∈ {0,1}E|∃i∈I,fi= f} (2.2.10)

2.2.4

A estrutura dos operadores elementares da morfologia

matemática sobre

{

0

,

1

}

classe pertencente ao conjunto das funções {0,1}E. Todos esses conceitos tiveram com base o trabalho desenvolvido por Banon e Barrera em [25]. Por questão de simplificação notacional, daqui para a frente o símbolo

T

{0,1}E.

Definição 2.2.4 (extensividade e anti-extensividade): Um operador ψ sobre

T

extensivo se, e somente se, para todo f ∈

T

Definição 2.2.5 (idempotência): Um operador unárioψsobre

T

T

T

Definição 2.2.6 (Operador isotônico): Um operdor ψ sobre

T

T

Definição 2.2.7 (Operador antitônico): Um operdor ψ sobre

T

decrescente) se e somente se, f,g∈

T

A proposição a seguir mostra definições equivalentes de um operador isotônico.

Proposição 2.2.8 Seja ψ∈[

T

T

• (1)ψé isotônico;

• (2) Para toda família de imagens{fi} ⊆

T

• (3) Para toda família de imagens{fi} ⊆

T

A prova dessa proposição pode ser encontrada em [25], pp 33.

A proposição a seguir apresenta definições equivalentes de um operador antitônico.

• (1)ψé antitônico;

• (2) Para toda família de imagens{fi} ⊆

T

• (3) Para toda família de imagens{fi} ⊆

T

A prova é análoga a da proposição anterior ([25], pp 33).

No que segue apresentaremos as definições das quatro classes fundamentais dos operadores elementares da morfologia matemática que são: dilatações, erosões,

anti-dilatações e anti-erosões

Definição 2.2.10 (dilatação) Um operador ψ sobre

T

T

ψ(sup{fi}) =supψ({fi})

Uma erosão se e somente se, para toda família de imagens{fi} ⊆

T

ψ(in f{fi}) =in fψ({fi})

é uma anti-dilatação se e somente se, para toda família de imagens{fi} ⊆

T

ψ(sup{fi}) =in fψ({fi})

Uma anti-erosãose e somente se, para toda família de imagens ternárias{fi} ⊆

T

ψ(in f{fi}) =supψ({fi})

Proposição 2.2.11 (isotonia das dilatações e erosões) as dilatações e erosões são

isotônicas.

A prova dessa proposição pode ser encontrada em [25].

Definição 2.2.12 (relação de ordem dos operadores) Dado dois operadoresψ,ϕ∈[

T

T

T

T

ψ(f(x))≤ϕ(f(x))

i.e,h[

T

T

um conjunto parcialmente ordenado. Este conjunto munido das operações de supremo e de ínfimo estendidas às famílias de operadores forma também um reticulado completo (por herança do reticulado do conjunto das funções binárias). Em outras palavras, para todo conjunto de índices I, estas operações verificam que, para toda família (Ψi)i∈I de operadores sobre

T

W

i∈IΨi(f) =supΨi(f)

V

i∈IΨi(f) =in fΨi(f)

OndeΨI é a imagem de I através da família(Ψi)i∈I, i.e.,

ΨI ={Ψ∈

T

I

A condição para um subconjunto de um reticulado completo ser um reticulado completo, é que ele seja superiormente ou inferiormente fechado sobre o reticulado. Segundo Banon e Barrera em [25], o conjunto das dilatações das erosões é superiormente (inferiormente) fechado de[

T

T

2.3

Morfologia matemática para imagens em níveis de

cinza

2.3.1

Os operadores elementares da morfologia matemática para

imagens em tons de cinza

Da mesma forma que imagens binária, os operadores elementares da morfologia matemática para o caso de imagens em níveis de cinza, a dilatação e erosão são definidos dualmente. No caso binário, apresentou-se a estrutura algébrica dos operadores morfológicos como reticulados completos, definidos de acordo com a álgebra das operações de Minkowiski e representados em uma grade do espaço Euclidiano bidimensional. Para o caso de tons de cinza, estes operadores possuem uma estrutura algébrica similar, estendido para o espaço euclidiano n-dimensional, satisfazendo também as características de um reticulado completo. Além disso satisfazem a várias propriedades correspondentes ao caso binário, tais como comutatividade, associatividade e distributividade.

Nesta seção, apresentam-se as definições básicas dos operadores dilatação e erosão e alguns dos principais operadores morfológicos tais como, abertura, fechamento, gradiente morfológico, filtros sequenciais e transformada top-hat.

Antes de definir estes operadores, necessita-se apresentar algumas definições básicas. Vale salientar que os resultados e definições apresentados nesta seção são baseados nas definições clássicas para o caso de imagens pontuais. ([27])

Na morfologia clássica, os modelos para imagens em tons de cinza são representados matematicamente pelo mapeamento f : E→

L

L

L

L

[0,1]ou o conjunto finito{0,1, ...N}, para algum∈N

Definição 2.3.1 Dados duas funções f,g∈

L. As operações de supremo e de ínfimo entre

f e g, são definidas respectivamente por:

(f∨g)(x) = f(x)∨g(x) (2.3.1)

de f por u, fu: E →

L

L

(fu+v)(x) = f(x−u) +v (2.3.3)

Definição 2.3.3 Dado uma imagem g e x∈E, A reflexão de g é definida por_bg(x) =g(−x) Definição 2.3.4 (Operações de Minkowiski) Dada dois sinais f,g ∈

L. A soma e a

f⊖g= ^

u∈E

{fu−gb(u)} (2.3.4)

f⊕g= _

u∈E

{fu+g(u)} (2.3.5)

Definição 2.3.5 Dada duas imagens em níveis de cinzas f e g, então

εg(f)(x) =

^

u∈E

[f(x−u)−gb(u)] (2.3.6)

∆g(f)(x) =

_

u∈E

[f(x−u) +g(u)] (2.3.7)

εg(f) = (f ⊖g)(x) e ∆g(f) = (f ⊕g)(x) são uma erosão e uma dilatação, respectivamente. g é chamada de função aditiva estruturante

Efeitos gerais causados pelos operadores dilatação e erosão

No caso da dilatação, se todos os valores da função estruturante são positivos, a imagem de saída aumenta a luminosidade, em consequência, detalhes escuros ou são reduzidos ou são eliminados, dependendo de como os seus valores e formas estão relacionados om o elemento estruturante usado para a dilatação

No caso da erosão, se todos os elementos da função estruturante são positivos, a imagem de saída fica mais escura, consequentemente os detalhes claros na imagem de entrada ficam menores do que o elemento estruturante é reduzido. O grau de redução é determinado pelos níveis de cinza dos vizinhos e pela forma e amplitude do elemento estruturante.

Figura 2.15: Imagem da Lena e os efeitos causados pelos operadores de dilatação e erosão

2.3.2

Outros operadores morfológicos

Tal como o caso binário, podemos definir outras operações morfológicas para imagens em tons de cinza onde as mais básicas são a abertura e o fechamento. Estas operações são consideradas os filtros básicos da morfologia matemática e são definidas respectivamente por:

f◦g= (f ⊖g)⊕g (2.3.8)

f•g= (f ⊕g)⊖g (2.3.9)

Para extrair contornos da imagem em geral é utilizado a operação de gradiente

morfológico. Esta operação envolve três operações: dilatação, erosão e subtração e é

definida por:

Grad(f,g)(x) = (f⊕g)(x)−(f⊖G)(x) (2.3.10) Uma outra importante operação em imagens em tons de cinza é a transformada top hat ou chapéu mexicano. O objetivo principal dessa operação é extrair componentes com

baixo contraste em relaçao ao fundo. É importante por exemplo, para realçar detalhes da imagem na presença de sombra. Esses filtros podem ser definidos de dois modos: claro e escuro e são dados respectivamente pelas equações:

Uma Abordagem da Matemática

Intervalar

3.1

Introdução

A matemática intervalar busca dar suporte para resolver problemas em dois aspectos fundamentais da computação científica: Um deles é na criação de um modelo computacional que reflita com exatidão o controle e análise dos erros que ocorrem no processo computacional; o outro é na escolha de técnicas de programação adequadas para desenvolvimento de softwares científicos buscando no final do processo matemático-computacional, uma boa estimativa da evidência dos erros de entrada. Na literatura existem diferentes abordagens para a computabilidade nos números reais, mas, uma importante diferença entre estas abordagens está na maneira como é representado o número real [64].

A aritmética intervalar permite o cálculo de extremos seguros para as soluções de um problema . Operações aritméticas com máxima precisão são necessárias para se ter uma aritmética de alta exatidão. Elas são definidas de forma que só um arredondamento é aplicado nas operações aritméticas básicas, resultando que o valor calculado e o valor exato diferem por apenas um arredondamento. Uma aplicação da aritmética intervalar poderá levar a extremos confiáveis [55]. O uso desta aritmética, aliada a um controle rígido dos algoritmos, é objeto do atual estado da arte nesta área. Nesta

seção serão apresentados alguns conceitos da aritmética intervalar, fundamentais para o desenvolvimento dos principais resultados dessa tese.

3.2

Análise intervalar

A qualidade do resultado em computação científica depende do conhecimento e controle dos erros na computação. Algoritmos convencionais, chamados algoritmos pontuais, computam uma resposta e, algumas vezes, uma estimativa do erro. No entanto, o usuário não pode conseguir uma resposta exata sem o auxílio de uma análise rigorosa dos erros, o qual é extensa, dispendiosa e nem sempre viável [7]. Desta forma, a obtenção de uma solução numérica para um problema real, aplicando os métodos numéricos tradicionais, geralmente conduz a aproximação dos resultados. Por outro lado, técnicas intervalares podem ser programadas em computadores de tal modo que a computação possua uma rigorosa e completa análise do erro no resultado. Muitas vezes, para melhor compreender como se comporta globalmente o erro durante a evolução dos cálculos numéricos, torna-se necessário identificar qual a sua origem ou fonte.

3.3

Definições básicas

Nesta seção apresentam-se algumas definições básicas da aritmética intervalar que foi introduzida por Moore e Sunaga paralelamente [60, 66]. Essas definições serão importantes para esse trabalho, porque nos Capítulos 5 e 6 serão apresentados dois modelos intervalares em imagens aplicada a morfologia matemática. A estrutura algébrica desses modelos, requerem algumas vezes operações intervalares entre elementos de conjuntos.

Definição 3.3.1 Intervalo de Números Reais

Seja R o conjunto dos números reais, e sejam x1,x2 ∈ R tais que x1 ≤ x2 Então, o conjunto {x∈R|x1≤x≤x2} é um intervalo de números reais ou simplesmente um intervalo, e será denotado por[x1,x2].

IR={[x1,x2]|x1,x2∈Re x1≤x2}

Os pontos do conjunto dos intervalos de números reais serão denotados usualmente por letras latinas maiúsculas.

Neste trabalho, os intervalos são usados com a finalidade de aproximar valores imprecisos. Neste sentido, não será utilizado a forma tradicional de representação geométrica, visto que, neste caso, associando-se a cada extremo do intervalo um eixo cartesiano, constrói-se uma representação cartesiana, enquanto que aqui, o intervalo está associado a um ponto real impreciso no mesmo eixo.

Todo número real x∈R pode ser visto como um intervalo de IR. Para tanto, basta identificar os pontos x∈R com os intervalos pontuais X = [x,x], onde X ∈IR. Estes

intervalos também são chamados de intervalos degenerados ou intervalos pontuais. Assim vale a seguinte cadeia de inclusões:

Figura 3.1: N ⊆Z⊆Q⊆R⊆IR

Vendo cada intervalo da reta como um conjunto, a noção de igualdade entre dois intervalos é dada pela noção de igualdade entre conjuntos, ou seja,

A=B⇔ ∀x∈A⇒x∈B e∀x∈B⇒x∈A

Definição 3.3.3 Igualdade entre Intervalos

a1=b1e a2=b2

Definição 3.3.4 Região Intervalar

Uma região intervalar é uma porção contida em Rncujos limites são bem definidos e variáveis.

Definição 3.3.5 Par Ordenado Intervalar

Sejam os intervalos A= [a1,a2]e B= [b1,b2]. Definimos Par ordenado(A; B)à região intervalar([a1,a2];[b1,b2])em que os intervalos A e B são denominados respectivamente abscissa intervalar e ordenada intervalar.

Geometricamente, um par ordenado intervalar é visto como uma região intervalar no plano, conforme podemos ver na figura 3.2.

Figura 3.2: Par ordenado intervalar

3.3.1

Aritmética intervalar

Consideremos os intervalos X = [x1,x2]e Y = [y1,y2], então:

1. X+Y = [x1,x2] + [y1,y2] = [x1+y1,x2+y2]

2. X−Y = [x1,x2]−[y1,y2] = [x1−y2,x2−y1]

3. X×Y = [x1,x2]×[y1,y2] = [min{x1y1,x1y2,x2y1,x2y2},max{x1y1,x1y2,x2y1,x2y2}]

4. _X1 =h_x21,_x11

i

se x1>0 ou x2<0

5. X÷Y =X×_Y1 = [x1,x2]× h

1 y2,

1 y1

i

, se 06∈Y Operações de reais com intervalos:

Sejam a∈R e X = [a1,a2]. Valem:

1. a+X = [a,a] + [a1,a2] = [a+a1,a+a2]

2. a−X = [a,a]−[a1,a2] = [a−a2,a−a1]

3. a×X =a×[a1,a2] = [a×a1,a×a2]

4. X_a = [a1_a,a2]= [a1_a,a2_a], para a6=0

Nota-se que a imagem de cada uma das operações intervalares básicas é uma extensão exata da operação real correspondente.

Teorema 3.3.6 Sejam os intervalos X= [x1,x2]e Y = [y1,y2], então:

1. X+Y ={r+s|r∈X e s∈Y}

2. X−Y ={r−s|r∈X e s∈Y}

3. X×Y = [x1,x2]×[y1,y2] ={r×s|r∈X e s∈Y}

5. X÷Y ={r÷s|r∈X e s∈Y}, se 06∈Y

Prova

Se a expressão intervalar for composta, não haverá necessariamente uma correspondência exata de tais operações. Por exemplo, se f(x) =x2−x, for estendida com elementos intervalares, temos F(X) =X2−X ou F(X) =X(X−1).

Neste caso, têm resultados diferentes, porém inclusos, ou seja, para X = [0,1], temos:

F(X) =X2−X = [0,1]2−[0,1] = [0,1] + [−1,0] = [−1,1]

F(X) =X(X−1) = [0,1]×([0,1]−[1,1]) = [0,1]×[−1,0] = [−1,0]

Portanto,[−1,1]6= [−1,0], mas[−1,0]⊆[−1,1].

3.3.2

Propriedades da aritmética intervalar

Teorema 3.3.7 A aritmética intervalar é subdistributiva no sentido que, se X,Y e Z são

intervalos, então X(Y+Z)⊆XY+X Z [61].

Assim, embora adição e multiplicação de intervalos sejam comutativas e associativas, não mantém a lei da distributividade. Além disso, embora os intervalos pontuais [0,0]

e [1,1] sejam identidades aditiva e multiplicativa, respectivamente, não existe inversos

aditivos e multiplicativos, isto é:

• [1,2]−[1,2] = [1,2] + [−2,−1] = [−1,1]

• [1,2]÷[1,2] = [1,2]×1₂,1=1₂,2

(α×β)×A = (α×β)×[a1,a2]

= [(α×β)×a2,(α×β)×a1]paraα×β<0

= [α×β×a2,α×β×a1]

=α×[β×a1,β×a2]paraβ≥0 (inverteremos a posição deαpor

β, caso contrário)

=α×(β×[a1,a2])

=α×(β×A).

Definição 3.3.8 Interseção entre dois Intervalos

Sejam A= [a1,a2]e B= [b1,b2]dois intervalos. se max{a1,b1} ≤min{a2,b2}, define-se a interdefine-seção dos intervalos A e B como define-sendo o intervalo

Exemplo 3.3.1 1. [2,5]T[3,8] = [max{2,3},min{5,8}] = [3,5]

2. [3,8]T[−1,10] = [max{3,−1},min{8,10}] = [3,8]

3. [−3,2]T[2,5] = [max{−3,2},min{2,5}] = [2,2]

A Figura 3.3 dá a interpretação geométrica da operação de interseção de intervalos na reta real:

Figura 3.3: Representação geométrica da interseção emR

Teorema 3.3.9 Propriedade da interseção

Sejam A,B,C,D∈IR. Se A⊆C, B⊆D e, se ATB está definido, então CTD está

definido e:

A\B⊆C\D

A prova deste teorema pode ser vista em [54]

Exemplo 3.3.2 Sejam A= [3,5],B= [−1,4],C= [2,8] e D= [−1,6]. Assim, A⊆C e

B⊆D, então, ATB= [3,4], CTD= [2,6]e[3,4]⊆[2,6].

Definição 3.3.10 União entre dois Intervalos

Sejam A= [a1,a2]e B= [b1,b2]dois intervalos tais que ATB está definido. Define-se a união dos intervalos A e B como sendo o intervalo:

Exemplo 3.3.3 1. [2,5]S[3,8] = [min{2,3},max{5,8}] = [2,8];

2. [3,8]S[−1,10] = [min{3,−1},max{8,10}] = [−1,10]; 3. [−3,2]S[2,5] = [min{−3,2},max{2,5}] = [−3,5]; 4. [−3,2]S[3,8] =não está definido.

A figura 3.4 dá a interpretação geométrica da operação de união de intervalos na reta real:

Figura 3.4: Representação geométrica da união emR

3.3.3

Relações de ordem

É possível definir muitas relações de ordem paciais, sobre IR. Dentre elas podemos destacar:

Definição 3.3.11 Ordem de Inclusão

Sejam X = [r,s]e Y = [t,u]. Então, X é menor ou igual a Y , representado por X≤Y ,

se t≤r e s≤u.

Kulisch e Miranker [68], definiram a seguinte ordem:

Definição 3.3.12 Ordem de Kulisch-Miranker

Seja X = [r,s]e Y = [t,u]. Então X é menor ou igual a Y , representado por X ≤KMY , se r≤t e s≤u.

Processamento de Imagens Digitais

Intervalares

4.1

Introdução

Nesta seção serão apresentados alguns conceitos de imagens digitais intervalares que foram introduzidas por Lyra em [4]. Considera-se que os conceitos apresentados neste capítulo, são importantes porque no capítulo 6 será introduzido um modelo intervalar para imagens em níveis de cinza e que foi desenvolvido sobre esse tipo de imagens.

Uma imagem intervalar refere-se a uma função luminosa bidimensional, denotada por F(x,y), em que um intervalo assume a amplitude de F nas coordenadas espaciais

(x,y)dando a intensidade (brilho) da imagem naquele ponto em relação a um coeficiente

de tolerância que determina a diferença entre o limite superior e inferior do intervalo. Da mesma forma que as imagens digitais, para ser adequada para o processamento computacional, a imagem precisa ser digitalizada tanto espacialmente quanto em amplitude. A digitalização das coordenadas espaciais (x,y) é denominada amostragem

da imagem e a quantização em níveis de cinza ocorre de forma contínua, em um intervalo diminuindo a perda neste processo de discretização. O objetivo do modelo intervalar para imagens digitais desenvolvido por Lyra, foi definir uma imagem intervalar em que, através de software/hardware, seja convertido o valor de cada pixel digitalizado em um intervalo. A diferença entre o limite superior e o inferior, dependerá da relação com que o pixel