JAYME DO CARMO MACEDO LEME ASPECTOS PROCESSUAIS E ESTRUTURAIS DA

JAYME DO CARMO MACEDO LEME

ASPECTOS PROCESSUAIS E ESTRUTURAIS DA

NOÇÃO DE DERIVADA

MESTRADO EM EDUCAÇÃO MATEMÁTICA

PUC / SP

SÃO PAULO

JAYME DO CARMO MACEDO LEME

ASPECTOS PROCESSUAIS E ESTRUTURAIS DA

NOÇÃO DE DERIVADA

Dissertação apresentada à Banca

Examinadora da Pontifícia Universidade

Católica de São Paulo, como exigência parcial

para obtenção do título de

MESTRE EM

EDUCAÇÃO MATEMÁTICA

, sob orientação

da

Profª. Drª. Sonia Barbosa Camargo Igliori.

PUC / SP

SÃO PAULO

Banca Examinadora

______________________________

______________________________

À minha mãe,

Marilia

Macedo

, por ter doado a

vida aos seus filhos. Sozinha, ela nos carregou

num trono ao longo de uma vida sofrida,

absorvendo às dificuldades para si própria com

intuito de nos proporcionar uma vida melhor.

Minha retribuição a seus esforços é colher o

que plantou, oferecendo-lhe esse fruto com

amor, carinho e fraternidade.

Ao meu pai,

Jayme Leme.

“

Comece fazendo o que é necessário, depois

o que é possível e de repente você

estará fazendo o impossível

”.

AGRADECIMENTOS

A Deus que me deu forças para percorrer este árduo caminho.

À minha amiga e orientadora,

professora

doutora Sonia Barbosa Camargo Igliori

, a luz

que iluminou meu caminho pela longa estrada

do conhecimento. Esses anos de trabalho em

conjunto, promoveram-me uma visão mais

ampla das noções matemáticas e uma

responsabilidade perante a vida e o saber. Um

grande abraço carinhoso, com direito à Reserva

VIP no meu Coração.

À

professora doutora Maria Cristina Souza de

Albuquerque Maranhão

, as excelentes

sugestões apresentadas na qualificação. Sua

perspicácia me proporcionou uma compreensão

mais profunda sobre o referencial teórico

adotado, oferecendo-me condições de uma

análise mais consistente.

À

professora doutora

Claudia Coelho de

Segadas Vianna

, pela participação da Banca

Examinadora e às sugestões que me foram

muito proveitosas.

À minha mãe,

Marilia Macedo

, pela força,

compreensão e amparo. Nesse período, passou

por momentos difíceis, mas com seu grande

coração de mãe, compreendeu minha ausência,

que tanto lhe fez falta.

Ao meu filho,

Jayme Luiz Leme

, pela

compreensão da minha ausência nesses últimos

anos. Espero que esse sacrifício involuntário,

propicie-lhe melhores condições de vida e que,

futuramente, ajude-o a se tornar um vencedor.

Aos meus irmãos,

César Augusto do Carmo

Macedo Leme

e

Mariana Macedo Leme

Caríssio

, ao apoio prestado nesse período.

A todos os professores

do

Programa de

Pós-Graduação em Educação Matemática

, a

competência, o preparo e a exigência.

Ao meu amigo e ex-professor

Eugênio Cezar

Silveira

, a presteza e apoio oferecidos.

À

CAPES

, pela ajuda financeira dispensada a

pesquisa.

Aos meus colegas, pelo convívio, alegrias e

tristezas compartilhadas nessa jornada.

Aos meus amigos Sandro, Conceição,

Armando, Lylian e Wagner, pelas contribuições

na fase de pesquisa.

Ao professor Galdino, pelos esclarecimentos

matemáticos.

À professora

Lulu Healy

, a presteza e ajuda

oferecida.

À professora Luiza, a leitura dos originais.

RESUMO

Esta pesquisa pretendeu buscar possíveis causas de dificuldades para a compreensão conceitual da noção de derivada. Utilizamos o pressuposto teórico de Sfard (1991), segundo o qual, noções abstratas podem ser concebidas de duas maneiras fundamentalmente diferentes: estruturalmente – como objetos, e

operacionalmente – como processos. A transição de uma concepção “processo” para uma concepção “objeto” decorre da conquista dos estágios de interiorização,

condensação e reificação. A pesquisa foi desenvolvida por meio de análise de um livro didático, selecionado a partir de critérios, relacionados à abordagem do Cálculo, e a conteúdos específicos de derivada. As análises possibilitaram apresentar como conclusão, as seguintes causas: a dificuldades inerentes ao desenvolvimento do pensamento científico; o privilégio da representação simbólica da derivada, encontrado nos livros didáticos; a falta de atividades, discussões ou exercícios que propicie os estudantes atingirem o estágio de reificação.

ABSTRACT

This research aims to investigate possible causes for the difficulties associated with conceptual understandings of the notion of the derivative. We use the theoretical perspective of Sfard (1991), in which she proposes that abstract notions can be conceived in two fundamentally different ways: structurally – as objects, and operationally – as processes. The transition from a "process" conception to an "object" conception involves negotiating the stages of interiorization, condensation and reification. The research was developed through an analysis of textbooks, chosen according to criteria related to the approach to Calculus as well as the specific content addressing the derivative. The analyses enabled the identification of the following causes: the inherent difficulties the development of scientific thinking; the privileging of symbolic representations of the derivative found in textbooks; and the lack of activities, discussions or exercises that enable the students to reach the reification stage.

SUMÁRIO

INTRODUÇÃO... 14

CAPÍTULO

1

PROBLEMÁTICA E QUADRO TEÓRICO

1.1. Introdução ... 17

1.2. Fundamentação teórica... 20

CAPÍTULO

2

A NOÇÃO DE DERIVADA

2.1. Introdução ... 30

2.2. Estudo sobre aspectos processuais e estruturais

da noção de derivada ... 30 2.2.1. Desenvolvimento da noção de número ... 32

2.2.2. Estágios cognitivos na aprendizagem da

noção de derivada ... 34 2.3. Arquitetura conceitual da derivada ... 37

CAPÍTULO

3

PROCEDIMENTOS METODOLÓGICOS

3.1. Introdução ... 41

3.2. Levantamento de livros didáticos... 43

3.3. Escolha do livro didático para análise... 49

3.4. Análise do livro Cálculo, um novo horizonte... 58

3.4.1. Objetos familiares ... 58

3.4.2. A noção de derivada ... 67

CAPÍTULO

4

Conclusão ... 79

BIBLIOGRAFIA ... 82

INTRODUÇÃO

O ensino e aprendizagem das noções do Cálculo Diferencial, como noções de função e limite, têm sido objeto de estudo de várias pesquisas em Educação Matemática. Algumas delas focalizam concepção de estudantes (Tall e Vinner, 1983; Cornu, 1981; Sierpinska, 1981), outras apresentam um enfoque epistemológico (Cornu, 1983) e há ainda outras que resultam na elaboração de engenharias didáticas (Robinet, 1983). Nossa pesquisa tem como proposta investigar algumas causas de dificuldades para a compreensão conceitual da noção de derivada, direcionando a investigação sob uma perspectiva de ordem cognitiva, delimitada ao processo de conceitualização de noções abstratas.

Para tal, foi assumido o pressuposto teórico de Sfard (1991), segundo o qual noções abstratas, como é o caso da derivada, podem ser concebidas de duas maneiras fundamentalmente diferentes: estruturalmente – como objetos, e

operacionalmente – como processos. Segundo esse referencial, processos de aprendizagem e de resolução de problema, consistem em uma intricada articulação entre concepções operacionais e estruturais da mesma noção.

determinar as possíveis articulações entre as representações da noção de derivada.

Minha prática docente, como professor de Cálculo, permite-me atribuir uma forte ênfase, na utilização de técnicas, durante o processo de ensino/aprendizagem da noção de derivada. Porém, nós professores de Cálculo, reconhecemos as dificuldades dos alunos para a compreensão conceitual dos conteúdos envolvidos.

A escolha da direção deste trabalho fundamenta-se no fato de que nos parece primordial buscar as causas das dificuldades se queremos enfrentá-las.

A busca das razões das dificuldades de aprendizagem em matemática tem sido alvo de interesse de profissionais da área, gerando pesquisas em Educação Matemática. Estas têm indicado que as causas das dificuldades podem estar relacionadas a fatores diversos, uma vez que a aprendizagem das noções científicas, como as da matemática, envolve questões complexas. Há algumas pesquisas, como Sfard (1991), que se propõem a apresentar algumas respostas a questionamentos, como o exposto por Poincaré:

Como pode acontecer que existam pessoas que não entendam matemática? Se a ciência invoca apenas as regras de lógica aceitas por todas as mentes bem formadas... como pode ocorrer que existam algumas pessoas que são totalmente insensíveis (impenetráveis) a ela?

(Sfard, 1991 apud Poincaré, 1952; Originalmente publicado em 1908).

Questionamentos como estes, analisados segundo vários referenciais teóricos, podem ser objetos de estudo da Educação Matemática.

Nosso objetivo com a presente pesquisa é analisar a conceitualização da derivada num livro de Cálculo à luz dos estágios de conceitualização de uma noção matemática, apresentados por Sfard (1991). Com isso, esperamos provocar reflexões sobre modos de “ver” os objetos abstratos e identificar algumas causas de dificuldades de compreensão conceitual da noção de derivada.

Apresentamos, no primeiro capítulo, nossa problematização da questão de pesquisa e uma exposição dos referenciais teóricos.

Realizamos, no segundo capítulo, um estudo sobre a noção de derivada quanto a suas características processuais e estruturais, no mesmo molde que Sfard desenvolveu com a noção de número. Ainda nesse capítulo, apresentamos os fundamentos de uma ferramenta de análise denominada de

Arquitetura Conceitual da Derivada, elaborada por Kendal (2001), além de levantarmos questionamentos sobre o desenvolvimento do pensamento científico.

Relatamos, no terceiro capítulo, os procedimentos metodológicos, detalhando o modo como escolhemos um livro para ser analisado à luz de nosso referencial teórico, e realizamos algumas análises sobre os conteúdos que abordam a noção de derivada.

CAPÍTULO I

Problemática e Quadro Teórico

1.1. INTRODUÇÃO

Nossa prática docente tem mostrado que os alunos obtêm maior sucesso em tarefas que envolvem cálculos operatórios do que naquelas de caráter conceitual. Esse fato é muito observado quando se trata de exercícios relacionados à noção de derivada. Muitas vezes isso se dá em razão da abordagem de ensino, mas não parece ser essa a única razão. Mesmo que o professor trabalhe com uma abordagem de ensino que priorize tarefas de caráter conceitual, isto não significa que os alunos deixarão de priorizar os aspectos processuais.

Algumas pesquisas em torno do assunto em questão, e que apresentaremos neste capítulo, também apontam nessa direção e ressaltam a possibilidade de dificuldades intrínsecas ao aprendizado de noções abstratas.

Essas pesquisas indicam a existência de especificidades inerentes às noções abstratas de níveis mais altos, ligadas às dificuldades que ocorrem no processo de ensino-aprendizagem.

Conforme Sfard (1991):

É necessário indagar a respeito das mais básicas questões epistemológicas relativas à natureza do conhecimento matemático, pois deve haver algo realmente especial e único no tipo de pensamento envolvido na construção do universo matemático.

A existência de tais especificidades nos faz admitir que existem certas características intrínsecas à aprendizagem da noção de derivada, relacionadas ao desenvolvimento do pensamento científico de noções abstratas.

O processo de conceitualização de uma noção científica ocorre num embate entre dificuldades a serem vencidas, na relação entre conhecimentos prévios e novos, configurando-se em estágios de estruturalização.

Tufle (1988) apresenta uma pesquisa envolvendo questões de Cálculo, em que a porcentagem de sucesso da aplicação de técnicas varia entre 73% a 92%, e a porcentagem de sucesso do uso de conceitos varia entre 7% a 22%.

Vinner et al. (1990) atestam que muitos alunos que estudaram Cálculo possuem um conhecimento superficial sobre conceitos desta disciplina. Indicam, também, que isso é fruto do sistema atual de educação, pois tanto professores como alunos enfatizam, no ensino e na aprendizagem da matemática, a perspectiva processual, evitando a estrutural. Apontam causas psicológicas, educacionais, sociais e até políticas para esse fenômeno.

Depoimentos como estes parecem revelar que esses alunos estão num estágio de conhecimento em que as técnicas operatórias já são conhecidas. No entanto, tais técnicas não são suficientes para propiciar a compreensão conceitual dessa noção.

As dificuldades apresentadas pelos alunos, relativamente à resolução de problemas que enfoquem mais conceitos do que técnicas operatórias são, em geral, interpretadas como resultantes de abordagens de ensino que priorizam a utilização de regras e cálculos. Encontramos, porém, na teoria de Sfard, indicação de que as causas das dificuldades podem estar além das abordagens de ensino, estando relacionadas ao processo de estruturação do pensamento científico.

Sfard (1991) ressalta que:

Diferentemente de objetos materiais, as elaborações de matemática avançada são totalmente inacessíveis para nossos sentidos – elas só podem ser vistas pelos olhos de nossa mente. Além disso, mesmo quando desenhamos uma função ou escrevemos um número, temos o cuidado em enfatizar que tal signo no papel é uma entre as várias representações possíveis da mesma entidade abstrata, que não pode ser vista nem tocada... “Ver”, de alguma forma, estes invisíveis objetos parece ser um componente essencial da habilidade matemática, e a falta de tal capacidade pode ser uma das maiores razões dos porquês da matemática parecer impermeáveis à várias “mentes bem formadas”. Esse tipo de concepção será chamada de estrutural .

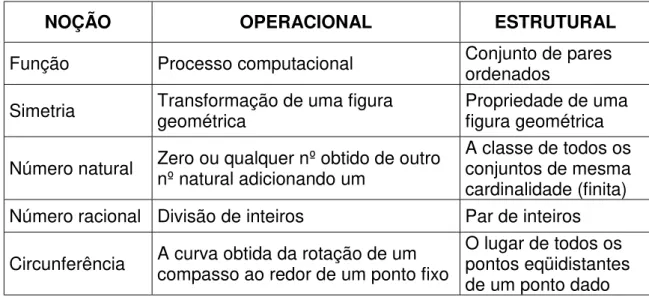
A tabela 1 sintetiza a dualidade de algumas noções matemáticas apresentadas por Sfard (1991):

NOÇÃO OPERACIONAL ESTRUTURAL

Função Processo computacional Conjunto de pares_ordenados

Simetria Transformação de uma figura_geométrica Propriedade de uma_{figura geométrica}

Número natural Zero ou qualquer nº obtido de outro_{nº natural adicionando um} A classe de todos osconjuntos de mesma cardinalidade (finita) Número racional Divisão de inteiros Par de inteiros

Circunferência A curva obtida da rotação de um_{compasso ao redor de um ponto fixo} O lugar de todos ospontos eqüidistantes de um ponto dado

Tabela 1

1.2. FUNDAMENTAÇÃO TEÓRICA

Segundo Sfard (1991), uma noção matemática abstrata pode ser concebida de duas maneiras fundamentalmente diferentes: operacionalmente

Hadamard afirma que:

Eu preciso de uma imagem para que tenha a simultânea visão de todos os elementos ... que agarrar todos juntos para fazer deles algo inteiro...; para realizar sínteses..., e dar ao conceito sua fisionomia.

(Sfard, 1991 apud Hadamard, 1949)

Do mesmo modo, Sfard atesta que interpretar uma noção como objeto,

significa poder referir-se a ela como se fosse algo real, uma estrutura estática, existindo em algum lugar no espaço e no tempo, podendo-se reconhecer a idéia à “primeira vista” e manipulá-la por inteiro, sem entrar em detalhes. Agora, interpretar uma noção como processo implica olhá-la como algo dinâmico em que o processo se evidencia como uma seqüência de ações, não se configurando como uma entidade estática.

Apesar de as concepções operacionais e estruturais de uma mesma noção matemática tomarem rumos divergentes, elas se completam, tornando-se partes integrantes da mesma noção, na qual uma complementa a outra. Tentar denotar o grau de importância entre essas duas concepções é como determinar se o pé esquerdo é mais importante que o direito numa caminhada.

Tendo por base a perspectiva de concepção de uma noção matemática como processo ou como objeto, e as relações entre os dois, Sfard (1991) distingue três etapas na conceitualização de uma noção: interiorização, condensação e reificação.

• Interiorização

1 2 3 4 5 6 7 8 9 10 1

2 3 4 5 6 7 8 9

necessita ser, na verdade, executado. Esses processos enfocam os esforços cognitivos sobre a manipulação dos objetos matemáticos familiares.

Pelos estudos feitos, elaboramos os seguintes exemplos:

a) Use o gráfico da função

)

(

x

f

y

=

apresentado ao lado, para estimar a inclinação da reta tangente em

x

=

6

.

Nesse primeiro estágio, o sujeito está adquirindo familiaridade com o processo de determinação da inclinação da reta tangente. Para resolução desta tarefa, seus esforços cognitivos se concentrarão na busca dos processos para resolução do problema.

b) Determine a derivada da função

f

(

x

)

=

x

2 em

x

=

3

.

Aqui, os esforços cognitivos serão utilizados na manipulação de operações algébricas para a solução da tarefa. É o processo que produz o resultado e é ele que está sendo enfatizado nesse momento, seja pelo cálculo de limite, seja pelas regras de derivação.

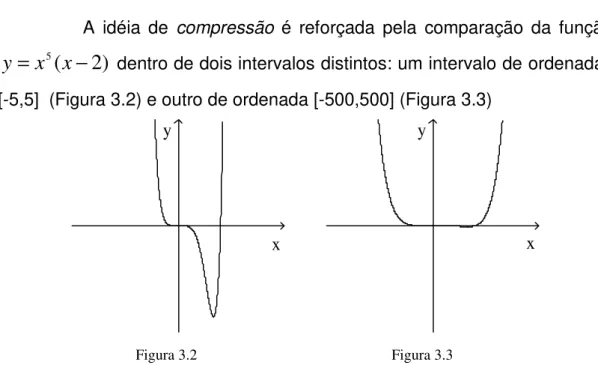
No entanto, a interiorização dos processos utilizados na resolução dos exemplos a) e b), não dá suporte para que o sujeito determine o crescimento e decrescimento de funções, por exemplo, a função

f

(

x

)

₌

x

3

₋

2

x

2

₋

2

x

_.

• Condensação

É uma etapa de síntese, na qual seqüências extensas de operações tornam-se em unidades mais compactas. Nesse estágio, o estudante é capaz de pensar sobre um dado processo, sem a necessidade de entrar em seus detalhes. Nesta etapa, processos poderão ser combinados com outros processos, tornando-se mais fáceis às comparações e generalizações.

Retomemos os exemplos da fase anterior. Para estudar o crescimento e decrescimento da função

f

(

x

)

=

x

3

−

2

x

2

−

2

x

_{, o processo de “estimar a}

inclinação da reta” (exemplo a.) não é detalhado para “visualizar” os intervalos em que a derivada seja positiva (Figura 1), sendo tratado quase como um objeto.

Também os esforços cognitivos não estão sendo utilizados para calcular

f

'

(exemplo b.), mas, sim, utilizados para determinar os extremos dos intervalos de crescimento e decrescimento da função dada.

-3 -2 -1 1 2 3 4

-5 -4 -3 -2 -1 1

Figura 1

• Reificação

Ocorre quando o estudante torna-se capaz de conceber a noção como um objeto. Esta é a etapa mais difícil de ser alcançada no processo de conceitualização de uma noção matemática.

quantitativas, a reificação é instantânea e qualitativa, onde um processo se solidifica como um objeto, uma estrutura estática. Várias representações de um conceito tornam-se semanticamente unificadas por esta construção abstrata e puramente imaginativa. A nova entidade é logo desligada do processo que a produziu e começam a emergir novos significados, pois esta se torna membro de uma outra categoria. Em certo momento, esta categoria torna-se a base definitiva para a existência de novos objetos. O sujeito pode agora investigar propriedades gerais de tal categoria e as relações entre suas diversas representações.

Sfard relata sobre uma dificuldade inerente ao estágio de reificação, levantando questões do tipo: “Por quê a reificação é obviamente tão difícil?”, “Por quê os próprios matemáticos precisaram de vários séculos para chegar nas versões estruturais completas dos conceitos mais básicos como número e função?”.

De acordo com Sfard, essas três fases devem ser entendidas como uma hierarquia no desenvolvimento do pensamento matemático, significando que um estágio não pode ser alcançado sem passar pelos anteriores. A transgressão dessa hierarquia pode desenvolver uma abordagem pseudo-estrutural, isto é, uma tendência para que o sujeito identifique a noção como uma de suas representações.

Sfard enfatiza que na reificação ocorre a unificação semântica de várias representações. Kendal (2001) faz um levantamento das representações que envolvem o conceito de derivada, fornecendo-nos subsídios mais específicos sobre a noção pesquisada.

Apesar de Kendal não referenciar Sfard em sua pesquisa, seu trabalho apresenta grande instrumental teórico de análise e é compatível com a teoria de Sfard.

Dado de entrada

Processo cognitivo

Saída

Exemplo:

Seja a função

_f

(

_x

)

₌

_x

2

₋

5

_x

₊

6

_{. Determine a inclinação da reta tangente à} curva no ponto (0,6).

Fragmentando a questão temos:

Seja a função

f

(

x

)

=

x

2

−

5

x

+

6

! Dado de entrada

Determine a inclinação da reta tangente

...

! Saída

! Processo cognitivo

Com foco na estrutura das questões, Kendal (2001) formulou três características para analisar as representações da derivada:

I. Representação de entrada

A representação de entrada é dependente do dado de entrada e é classificada como:

" Numérica (N), se o dado é numérico (pares ordenados ou tabelas contendo valores de

x

e

f

(

x

)

), permitindo o cálculo de uma taxa de variação ou uma taxa de variação instantânea.

" Gráfica (G), se o dado é gráfico (reta tangente à curva), possibilitando interpretar a derivada num ponto como a inclinação da reta tangente à curva nesse ponto.

" Simbólica (S), se o dado é um símbolo













_,

_f

_'

dx

dy

, possibilitando

encontrar o resultado por certas regras de diferenciação.

II. Representação de saída

A representação de saída é dependente da solicitação da questão, sendo classificada como:

" Numérica (n), se a questão solicita encontrar (ou explicar sobre) uma taxa de variação.

" Gráfica (g), se a questão solicita encontrar (ou explicar sobre) a inclinação da reta tangente num ponto.

" Simbólica (s), se a questão solicita encontrar (ou explicar sobre) a derivada como uma expressão simbólica.

III. Processo cognitivo relacionando às representações de entrada e saída

Um processo cognitivo é necessário para obtenção do resultado da questão, expresso na representação de saída, sendo definido como:

" Formulação (F) é a habilidade de reconhecer a representação de

" Interpretação (I) é a habilidade de raciocinar sobre uma entrada, isto é, explicar em linguagem natural ou dar o significado equivalente de uma derivada nas representações numérica, gráfica ou simbólica.

Kendal (2001) apresenta duas questões para exemplificar a forma de integração entre a entrada, processo cognitivo e saída:

Questão A.

Uma curva tem a equação

g

(

x

)

=

5

x

3

−

6

x

2

+

3

x

−

6

. Encontre a inclinação da reta tangente ao gráfico de

g

no ponto de abscissa -1.

O dado de entrada é uma função expressada simbolicamente, logo a representação é simbólica (S). Se uma diferenciação simbólica é efetuada, utilizando-se regras simbólicas na função dada, o processo é a formulação de uma derivação simbólica (F). A frase “Encontre a inclinação....” indica que uma saída gráfica (g) é requerida. A habilidade1 _{é codificada como: [representação de}

entrada, processo, representação de saída], logo [S F g].

Questão B.

A função derivada de

f

é dada por

f

'

(

x

)

=

x

3

−

5

x

+

3

. Qual é a inclinação da reta tangente ao gráfico da curva

y

=

f

(

x

)

, quando

x

=

1

?

O dado de entrada apresenta a derivada por símbolos, logo a representação é simbólica (S). Este dado precisa ser reinterpretado como inclinação, logo o processo é de interpretação (I) da derivada na representação

1 _{Achamos conveniente traduzir “competency” como “habilidade”, por se tratar de um “saber fazer”, ou seja,}

simbólica com uma inclinação da reta tangente. A frase “Encontre a inclinação....” indica que uma saída gráfica (g) é requerida. A habilidade codificada é [S I g].

As três características apresentadas podem ser combinadas, formando dezoito habilidades, sintetizadas na tabela 2:

Tabela 2

A importância das representações de uma noção matemática é ressaltada por Tall (1997):

O modo como as representações numéricas e simbólicas se ampliam, envolve uma interessante forma de desenvolvimento cognitivo. Há recorrentes ciclos de atividades em que um processo, como o de contagem, torna-se um conceito, como número. Como outros exemplos podemos citar o processo de adição, que se torna o conceito de soma, o processo de divisões em partes iguais que se torna o conceito de fração, o processo de razão, que se torna o conceito de taxa e o processo de cálculo de limite que se torna o conceito de limite.

Com o intuito de aproximar a teoria de Sfard (1991) com a pesquisa de Kendal (2001), ressaltamos que “a dupla natureza de construções matemáticas pode ser notificada por meio de vários tipos de representações. Algumas representações parecem mais suscetíveis de interpretação estrutural do que outras” (Sfard, 1991), como se pode observar na tabela 3:

ENTRADA

Numérica (N) Gráfica (G) Simbólica (S)

Numérica (n)

N F n N I n

G F n G I n

S F n S I n

Gráfica (g)

N F g N I g

G F g G I g

S F g S I g

SAÍDA

Simbólica (s)

N F s N I s

G F s G I s

(Função x²)

Representação OPERACIONAL ESTRUTURAL

NUMÉRICA

Entrada Processo Saída 5 (5)² 25 -7 (-7)² 49 x (x)² x²

SIMBÓLICA

f

(

x

)

=

x

2

GRÁFICA É a curva formada pelos_pontos

₍

_x

_,

_f

₍

_x

₎

₎

_,

_x

_∈

_R

Uma parábola.

CAPÍTULO II

A Noção de Derivada

2.1. INTRODUÇÃO

Com vistas ao entendimento do processo de conceitualização da noção de derivada, elaboramos alguns estudos. No primeiro procuramos, como fez Sfard (1991) a respeito das noções de números naturais, números complexos e funções, analisar os aspectos denominados operacional e estrutural da derivada. Num segundo, levantamos questões relacionadas com as representações numéricas, gráficas e simbólicas dessa noção. Num terceiro estudo, levantamos questões sobre o desenvolvimento do pensamento científico.

2.2. ESTUDO SOBRE ASPECTOS PROCESSUAIS E ESTRUTURAIS DA NOÇÃO DE DERIVADA

Nós partimos da forma habitual de se apresentar a noção de derivada nos cursos de Cálculo.

“Definimos derivada de uma função

f

como a função denotada por

'

f

, tal que seu valor em qualquer número

x

do domínio de

f

seja dado por

x

x

f

x

x

f

x

f

x

∆

∆

∆

)

(

)

(

lim

)

´(

0

−

+

=

→ , se esse limite existir” (Leithold, 1994). Podemos

Observa-se nesse tipo de definição que um objeto abstrato (derivada) é introduzido a partir de outros abstratos (função, limite).

Nessa abordagem, a noção de derivada é apresentada aparentemente como uma entidade existente, real, como um objeto estático que pode ser manipulado. Essa noção, assim apresentada, assume de início uma característica estrutural.

Historicamente, percebemos que a gênese da noção de derivada teve outra característica, conforme mostramos no breve histórico a seguir:

A noção de derivada é produto de uma grande evolução na qual Newton e Leibniz desempenharam papéis decisivos. Essa evolução emergiu da necessidade de resolver dois grandes problemas em aberto. Primeiro, o problema das tangentes (determinar a reta tangente a uma curva). Segundo, o problema das quadraturas (calcular a área determinada sob uma curva dada).

O problema das tangentes, cujo enfoque é gráfico, formulou-se do interesse de pesquisadores em encontrar máximos e mínimos de funções. Para caracterizar estes pontos, parecia natural utilizar retas tangentes à curva. A generalização de encontrar as retas tangentes em qualquer ponto da curva levou ao procedimento em que para se determinar a inclinação da reta tangente no ponto

(

x

0

,

f

(

x

0

)

)

, dava-se um incremento h a

x

0 e traçava-se uma reta secante

à

(

x

₀

,

f

(

x

₀

)

)

e

(

x

₀

+

h

,

f

(

x

₀

+

h

)

)

. A posição limite das secantes quando h

→

0 determinava uma reta que se denominou reta tangente.

Os pesquisadores também buscavam um modo de calcular a velocidade de um objeto em um determinado momento. Quando a ciência se referencia a um intervalo de tempo, a velocidade média desse intervalo é definida pela razão entre as medidas do espaço percorrido durante o intervalo e do próprio intervalo de tempo

(

∆s/∆t

)

. Já uma “velocidade instantânea” é dada pela velocidade média, quando

∆

t

→

0. O procedimento encontrado para se calcular

a velocidade instantânea foi por meio do cálculo do limite













→

t

s

t

∆

∆

∆ 0

A História revela que a gênese da noção de derivada constituiu-se na busca de processos para resolução de problemas, caracterizando-se um modo predominantemente operacional.

A derivada é abordada, por alguns livros de Cálculo, pela sua característica estrutural, diferentemente da forma de como se apresenta na evolução histórica. Essas abordagens antagônicas instigaram-nos a fazer um estudo da noção de derivada à luz do desenvolvimento do pensamento científico. Esse estudo levou-nos ao trabalho de Sfard relativo à evolução de número. Apresentamos, a seguir, alguns pontos desse trabalho.

2.2.1. Desenvolvimento da Noção de Número

Estágio de Interiorização

Estágio de Condensação

Neste estágio, o número se desvincula do processo de contagem e é tratado em sua totalidade. Operações como adição, subtração, multiplicação e divisão podem ser aplicadas sem a utilização do processo de contagem, como no estágio anterior. Os números recebem o status de "quantificador", tendo a função de indicar uma quantidade de objetos.

O acesso à condensação decorre da proficiência do sujeito em combinar o processo compactado com outros processos computacionais, como manipulações aritméticas, manipulações com conjuntos, e outras.

Estágio de Reificação

O estágio de reificação é o mais difícil de ser alcançado, pois exige “ver” os processos compactados, que até o momento podiam ser combinados e comparados com outros processos, como objeto. Essa “transformação” do

processo em objeto possibilita a criação de novos processos com base nesse novo objeto.

No caso estudado, o processo de contagem compactado deve ser “visto” como número natural. Esse novo objeto (número natural) possibilitará o desenvolvimento de novos processos, como o de subtração cujo resultado seja um número inteiro negativo.

causou muitas surpresas e perplexidades. Muito tempo transcorreu antes que os matemáticos fossem capazes de separar a noção de número do processo de medida. Após esse período, o conjunto de números foi ampliado novamente, incluindo os irracionais aos inteiros e frações.

2.2.2. Estágios Cognitivos na Aprendizagem da Noção de Derivada

As noções de derivada e de número são frutos da produção humana. Num estudo histórico, observam-se certos degraus que foram conquistados após longos períodos, possibilitando-nos estudar a noção de derivada, de forma semelhante ao estudo feito por Sfard sobre números. Esse estudo nos permitiu enfocar a noção de derivada nos estágios de interiorização, condensação e

reificação.

Interiorização

Essa fase caracteriza-se pela ação dos processos sobre objetos familiares. Nesta pesquisa, os objetos considerados familiares à noção de derivada são: limite, função, taxa de variação, coeficiente angular de uma reta, equação de uma reta e reta tangente (de forma intuitiva).

No que segue, expomos alguns exemplos de processos atuando sobre os objetos familiares indicados:

• Cálculo (processo) de limite (objeto).

Para se obter a derivada de uma função

y

=

f

(

x

)

em

x

=

x

₀, é necessário efetuar uma operação (processo) sobre um objeto familiar (limite), ou

seja,

0 0

)

(

)

(

lim

0

x

x

x

f

x

f

x

x

−

−

→ .

Para se obter a função

f

'

é necessário realizar procedimentos algébricos, como aplicação de regras ou cálculos de limites.

• Obtenção da derivada de uma função

y

=

f

(

x

)

em

x

=

x

₀,

Nesta tarefa, o processo é caracterizado pelas manipulações algébricas para obter

f

'

e determinar seu valor funcional em

x

₀. Neste caso, o

objeto familiar é função (valor funcional).

• Obtenção do coeficiente angular da reta tangente (processo) a uma

curva (objeto) num ponto dado, a partir de estimativas.

O processo é caracterizado pela obtenção do coeficiente angular da reta tangente. Essa reta tem que ser dada ou concebida de forma intuitiva.

• Interpretar (processo) a derivada em

x

₀, como inclinação da reta

tangente (objeto) em

(

x

₀

,

f

(

x

₀

)

)

.

• Interpretar (processo) a derivada em

x

₀, como a taxa de variação instantânea

em

x

₀ (objeto).

Condensação

Nesse estágio, Sfard diz que há uma compactação de processos

Destacamos alguns processos que consideramos compactados:

• Capacidade de “visualizar” os pontos do gráfico de uma função em que a derivada é positiva, negativa ou nula.

• Capacidade de interpretar a derivada nas representações numérica, gráfica e simbólica.

• Capacidade de utilização da noção de derivada para o estudo de extremos relativos, teorema do valor médio e construção de funções.

• Capacidade de interpretar a derivada, nas áreas das ciências e economia, como lucro marginal, rendimento marginal, custo marginal, velocidade instantânea, aceleração instantânea entre outros.

• Capacidade de conceber a reta tangente no ponto

(

x

₀

,

f

(

x

₀

))

como a reta cujo coeficiente angular é

f

'

(

x

0

)

.

Esses processos compactados envolvem articulações entre as representações da derivada, tanto de característica operacional como de característica estrutural, conforme ilustração da tabela 4.

DERIVADA

Representação OPERACIONAL ESTRUTURAL

Numérica

(

)

,

∆

→

0

∆

∆

_x

x

x

f

_{É a taxa de variação}

instantânea.

Simbólica Regras algébricas._{Regras de diferenciação.}

h

x

f

h

x

f

h

)

(

)

(

lim

0

−

+

→

Gráfica É a posição limite da_{secante PQ, P}

!Q.

É o coeficiente angular da reta tangente num ponto P.

Tabela 4

Reificação

Essa nova “visão” de derivada funde os processos compactados

envolvidos nas representações numérica, gráfica e simbólica. Nesse estágio, o sujeito não “vê” mais a derivada apenas como um limite de uma função de razão incremental, nem apenas como uma inclinação de uma reta tangente num ponto e nem apenas como uma taxa de variação instantânea.

As representações da noção de derivada, nos três contextos citados, foram objetos de estudo do trabalho de Kendal (2001). O assunto de seu trabalho que nos interessa será discutido a seguir.

2.3. ARQUITETURA CONCEITUAL DA DERIVADA

A tese de doutorado de Kendal (2001) objetiva explorar o impacto do ensino, na compreensão dos estudantes do conceito de derivada. A compreensão da noção de derivada foi medida usando-se a inovadora Arquitetura Conceitual da Derivada, que foi desenvolvida para descrever a compreensão da noção de derivada.

Essa Arquitetura consiste em dezoito habilidades de formulação e interpretação das representações da noção em questão.

Fizemos um recorte do trabalho de Kendal, a fim de enfocar a articulação entre as representações numérica, gráfica e simbólica. A pesquisadora conclui que o desenvolvimento da noção de derivada está intimamente ligado às habilidades de articulação entre suas representações.

Mapa Conceitual de Representações de Diferenciação

Figura 2.1.

Na figura 2.1. as representações numérica, simbólica e gráfica são representadas por um círculo e as setas indicam as articulações entre elas. Informações do “mundo real” foram agregadas à representação numérica como dados numéricos de entrada (N). A representação simbólica incorpora o processo de limite quando regras padrões de diferenciação são empregadas e o resultado é uma função simbólica ou um valor específico em um ponto.

NUMÉRICA

x

f

(

x

)

∆

f

(

x

)

/

∆

x

Taxa de Variação Instantânea

SIMBÓLICA

)

(

'

),

(

'

,

f

x

f

a

dx

dy

Regras de derivação

h

x

f

h

x

f

h

)

(

)

(

lim

0

−

+

→

GRÁFICA

Aproximação local de uma curva como uma

linha reta

Inclinação da curva

Inclinação da tangente num ponto

2.4. DESENVOLVIMENTO DO PENSAMENTO CIENTÍFICO

Nosso terceiro estudo refere-se ao desenvolvimento do pensamento científico.

A Educação Matemática tem como um de seus objetos, investigar o modo do desenvolvimento do pensamento matemático. Nesta pesquisa, esse desenvolvimento é compreendido como indissociável da aprendizagem de noções científicas. Essa compreensão respalda-se em considerar o pensamento como Rubinstein e Vinagrova:

O processo do pensamento é compreendido como uma atividade do sujeito interagindo com o mundo externo. O pensamento é um processo de contínua interação do homem com o objeto...

(Rubinstein, 1958 apud PME – 23 Conference)

... é necessário ensinar os alunos a aplicar, a usar suas habilidades mentais, sendo o desenvolvimento dessas habilidades um problema importante do ensino.

(Vinagrova, 1958 apud PME – 23 Conference)

Tall, em seu artigo Funções e Cálculo, relata as possibilidades de abordagens do ensino de Cálculo:

Há, portanto, um espectro de abordagens possíveis para o ensino do Cálculo, abrangendo desde o Cálculo imerso no mundo real em que a intuição pode ser construída ordenadamente usando a representação visuo-espacial, passando pelas representações numéricas, simbólicas e gráficas do Cálculo teórico até a representação formal, constituída por definição-teorema-prova, que é uma abordagem da Análise.

A tabela 5 sintetiza as abordagens do Cálculo, apresentadas por Tall:

REPRESENTAÇÕES

Visuo-espacial Numérica Simbólica Gráfica Formal

Ordenativa Observação

Quantitativa Aproximação

Manipulativa Manipulação

Qualitativa Visualização

Dedutiva Definição

Cálculo

Mundo real Cálculo Teórico Análise

Tabela 5

Vergnaud expõe, ainda, uma completa definição do conceito de derivada, incluindo o conhecimento processual de diferenciação e a ligação entre suas representações.

... o conceito de derivada envolve conhecimentos de representações numéricas, gráficas e simbólicas, e um processo cognitivo relacionando-as. Cada representação de diferenciação é associada a um específico conhecimento processual.

(Vergnaud, 1998 apud Kendal, 2001)

CAPÍTULO III

Procedimentos Metodológicos

3.1. INTRODUÇÃO

Neste capítulo, apresentamos um panorama da elaboração da pesquisa e os procedimentos metodológicos utilizados.

Iniciamos com uma pesquisa bibliográfica para levantamento das investigações existentes sobre o assunto. Em seguida, buscamos um quadro teórico que possibilitasse diagnosticar algo que evidencie, pelo menos em alguns aspectos, motivos das dificuldades relatadas nas pesquisas que encontramos. O quadro teórico que possibilitou essa investigação foi encontrado em Sfard (1991). Utilizamos como ferramenta de análise a Arquitetura Conceitual da Derivada, apresentada no trabalho de Kendal (2001).

Levantamos, como ponto de partida, algumas possibilidades de investigação para diagnosticar, segundo nosso referencial teórico, algumas razões que justificam as dificuldades encontradas na conceitualização da noção de derivada.

(figura 3.1)

Figura 3.1

Conceitualização de uma Noção Matemática

Teoria Sfard

Arquitetura Conceitual da Derivada

Alunos Professores Livros Derivada

Operacional

Estrutural

• A primeira possibilidade, referente ao processo investigativo do saber matemático, aponta para um estudo dos processos cognitivos relacionados ao desenvolvimento do pensamento científico.

• A segunda, visa a investigar, em grupos de alunos, possíveis causas de dificuldades para a compreensão conceitual da derivada, utilizando a

Arquitetura Conceitual da Derivada. Tal investigação tem como foco o teste elaborado por Kendal (ANEXO I), possibilitando verificar a disponibilidade de articulação das representações de derivada. Ele é composto por 18 questões, sendo que cada uma envolve uma das 18 habilidades de articulação entre as representações numéricas, gráficas, simbólicas e dois processos cognitivos. A análise dos resultados pode indicar que tipo de mudanças de representações os alunos apresentam facilidades ou dificuldades.

• A terceira possibilidade esta direcionada à investigação com professores da disciplina de Cálculo, por meio de um questionário (ANEXO II), a fim de coletar dados sobre os tipos de questões que os professores costumam trabalhar com os alunos. A análise desse levantamento pode propiciar subsídios para detectar se a prática docente contribui como geradora de dificuldades da conceitualização da derivada.

• A última possibilidade se refere à análise de livros didáticos à luz de referenciais teóricos.

Dentre as quatro possibilidades apresentadas, escolhemos a de análise de livros didáticos, adequando-a aos referenciais adotados em nossa fundamentação teórica.

3.2. LEVANTAMENTO DE LIVROS DIDÁTICOS

Inicialmente, efetuamos um levantamento de amostra significativa de livros didáticos de Cálculo nos acervos das bibliotecas das Instituições Oswaldo Cruz, PUC-SP e USP.

A amostra se constituiu em 34 livros abrangendo o período de 1963 a 2002. Essa diversidade nos levou à elaboração de critérios para selecionar o livro a ser analisado nesta pesquisa.

Após o levantamento, efetivamos uma classificação dos livros utilizando o referencial de Tall (1997), o qual apresenta três abordagens para o ensino do Cálculo:

I. O Cálculo imerso no mundo real;

II. O Cálculo teórico que envolve representações numéricas, gráficas e simbólicas;

III. O Cálculo formal que utiliza definições-teoremas-provas.

Autores de livros didáticos também apresentam divergências de pontos de vista na elaboração de seus livros:

Parece não haver acordo sobre o que deva constituir um primeiro curso de Cálculo e Geometria Analítica. Insistem alguns que a única via para compreender realmente o Cálculo principia com um estudo completo do sistema dos números reais, desenvolvendo passo a passo de uma maneira lógica e rigorosa. Argumentam outros que o Cálculo é fundamentalmente um instrumento para engenheiros e físicos; conseqüentemente acreditam que o curso deve conduzir às aplicações do Cálculo, fazendo apelo à intuição para, depois, pela prática de resolução de problemas, desenvolver a destreza manipulatória. Há muito de correto em ambos os pontos de vista. O Cálculo é uma ciência dedutiva e um ramo da Matemática Pura. Ao mesmo tempo é muito importante lembrar que o Cálculo tem raízes profundas em problemas físicos e que muito de sua potência e beleza deriva da variedade de suas aplicações.

Essas possíveis abordagens nos permitiram elaborar três critérios para categorizar os livros de Cálculo:

• Primeiro critério (C1) – Livros que abordam os conteúdos do Cálculo com ênfase nos problemas práticos e reais.

• Segundo critério (C2) – Livros que abordam os conteúdos do Cálculo de forma mais teórica, enfatizando suas representações.

• Terceiro critério (C3) – Livros que abordam os conteúdos do Cálculo da maneira formal, apresentando o conteúdo por meio de definições, teoremas e provas.

Para a categorização dos livros por meio dos critérios citados, consideramos a organização dos conteúdos específicos e sua forma de apresentação, o que nos levou à seguinte classificação:

" Classificamos pelo critério C3, os livros que apresentavam os conteúdos de maneira formal (definição – teorema – prova), por exemplo:

Toda reta é um gráfico de uma equação linear em x e y. Assim temos:

Teorema 1. Toda reta é o gráfico de uma equação linear em x e y. (Prova).

Teorema 2. o gráfico da equação y = mx + k é a reta não vertical com inclinação m e intersecção y igual a k.

(Prova).

Teorema 3. Duas retas são paralelas se e somente se tem a mesma inclinação. (Prova).

Teorema 4. Se duas retas não verticais são perpendiculares, então a inclinação de uma é negativo do inverso da inclinação da outra.

(Prova). Teorema 5. . . . . : (Prova). :

Os livros selecionados por esse critério foram:

1. Edwin Moise. Cálculo, um curso universitário. USP, 1970. 2. George Thomas. Cálculo. USP, 1970.

3. Michael Spivak. Cálculo infinitesimal. Reverte, 1970.

4. Miquel & Merino. Curso de Cálculo Diferencial. Mestre Jou, 1966. 5. Nilson Machado. Cálculo. Atual, 1977.

6. N. Piskunov. Cálculo Diferencial e Integral. Lopes da Silva, 1979. 7. Richard Courant. Cálculo Diferencial e Integral. Globo, 1963. 8. Roberto Romano. Cálculo Diferencial e Integral. Atlas, 1983. 9. Wilfred Kaplan. Cálculo e Álgebra Linear. LTC, 1972.

" Classificamos pelo critério C2, os livros que apresentavam seus conteúdos de maneira teórica (definição – exemplo – exercícios), por exemplo:

y = mx + b

O número b, que é a ordenada do ponto onde a reta intercepta o eixo y, é chamado de intercepto y da reta. Conseqüentemente, a equação acima é a chamada forma inclinação-intercepto. Essa forma é extremamente útil, pois nos dá imediatamente a inclinação da reta...

Exemplo: Ache a inclinação da reta cuja equação é 6x + 5y – 7 = 0... Exercícios: Ache a equação da reta, cuja inclinação é 4 e passa por (2,3)...

(Louis Leithold, 1994 – O Cálculo com Geometria Analítica)

Os livros selecionados por esse critério foram:

1. Al Shenk. Cálculo e Geometria Analítica. Campus, 1984. 2. Diva Flemming. Cálculo A. Makron, 1992.

4. Edwards & Penney. Cálculo com Geometria Analítica. PHB, 1997. 5. Frank Ayres. Cálculo Diferencial e Integral. McGraw-Hill, 1994.

6. George Simmons. Cálculo com Geometria Analítica. McGraw-Hill, 1987.

7. Geraldo Ávila. Cálculo I. LTC, 1978.

8. Hamilton Guidorizzi. Cálculo Diferencial e integral. USP, 1987. 9. Howard Anton. Cálculo, um novo horizonte. Bookman, 2000. 10. James Stewart. Cálculo. Pioneira-Thomson Learning, 2002.

11. Laurence Hoffmann. Cálculo, um curso moderno e suas aplicações. LTC, 2002.

12. Larry Goldstein. Cálculo e suas aplicações. Hemus, 1981.

13. Larson-Hostler-Edwards. Cálculo com Geometria Analítica. LTC, 1998.

14. Louis Leithold. O Cálculo com Geometria Analítica. Harbra, 1994. 15. Luiz Rocha. Curso dirigido de Cálculo Diferencial e integral. Nobel,

1973.

16. Munem & Foulis. Cálculo. LTC, 1982.

17. Mustafa Munem. Cálculo. Guanabara dois, 1982.

18. Paulo Boulos. Cálculo Diferencial e Integral. Makron, 1999. 19. Pedro Morettin. Cálculo, funções de uma variável. Atual, 1981. 20. Robert Seeley. Cálculo de uma variável. LTC, 1975.

21. Serge Lang. Cálculo. Livros Técnicos, 1971. 22. Tom Apostol. Cálculo. Reverte, 1983.

23. Ubiratan D’Ambrosio. Cálculo e introdução à Análise. Nacional, 1975.

24. Willian Granville. Elementos do Cálculo Diferencial e Integral. Científica, 1966.

Não encontramos livros que pudessem ser categorizados pelo critério C1, ou seja, que apresentassem ênfase significativa nos problemas de Cálculo imerso no mundo real. Alguns livros apresentavam mais problemas práticos do que outros, no entanto, a abordagem não deixa de ser a teórica.

Tall (1997) ressalta que “a definição formal e teoremas da Análise requerem diferentes qualidades cognitivas que são inapropriadas num primeiro curso de Cálculo. Isso sugere uma penalidade aos cursos que tentam construir definições formais e teoremas com iniciantes”. Essa afirmação de Tall nos levou a descartar os livros selecionados por C3 para escolha do livro a ser analisado.

Por conseqüência, fomos à busca de novos critérios para selecionar qual livro, dos classificados em C2, escolheríamos para análise.

Encontramos, nas leituras dos prefácios de alguns desses livros, indicações sobre a intenção dos autores em enfatizar o caráter conceitual das noções do Cálculo, objeto de nossa pesquisa. Com isso, determinamos como novo critério de seleção, livros que enfocassem a compreensão conceitual das noções do Cálculo.

Em geral, observamos uma forte tendência dos autores em formular livros com uma linguagem mais acessível para os alunos, detalhando minuciosamente os passos para propiciar a compreensão dos conteúdos:

O livro foi escrito tendo em vista dois objetivos principais: primeiro, o de expor todas as explicações com a clareza e acessibilidade apropriadas, de modo que os alunos não tivessem qualquer dificuldade na leitura e no aprendizado do livro; segundo, o de possibilitar que os estudantes aplicassem os princípios apreendidos à resolução de problemas práticos, graças à facilidade adquirida mediante o estudo do livro.

As explanações passo a passo, os inúmeros exemplos descritivos e a ampla variedade de exercícios continuam ser os aspectos relevantes do livro nesta edição. Uma vez que um livro texto deve ser escrito para o estudante, empenhei-me em manter uma apresentação de acordo com a experiência e maturidade de um principiante, sem deixar que qualquer passagem fosse omitida ou ficasse sem explicação.

(Louis Leithold, 1994 – O Cálculo com Geometria Analítica)

No entanto, percebemos que livros mais atuais apresentam outros ingredientes, como a intenção de enfocar a compreensão conceitual das noções do Cálculo e às representações numérica, gráfica e simbólica. Essa tendência foi encontrada no prefácio de dois livros:

Quando comecei a escrever a primeira edição de Cálculo, quase 25 anos atrás, o conteúdo e a organização de um curso de Cálculo eram praticamente universais... Contudo, os tempos mudam, e a era de um curso de Cálculo universal e padrão parece destinada aos baús do porão, junto com a régua de cálculo e selos de 1 centavo... Esta é uma grande revisão. Alinhando-se com as tendências atuais do Cálculo, a meta desta edição é focalizar mais na

compreensão conceitual e na aplicabilidade... A “regra dos quatros” refere-se à aprerefere-sentação do material do ponto de vista verbal, algébrico, visual e numérico. (grifo nosso)

(Howard Anton, 2000 – Cálculo, um Novo Horizonte)

A ênfase está na compreensão dos conceitos. Penso que todos concordam que essa deve ser a meta principal do ensino do Cálculo. De fato, o ímpeto para o atual movimento de reforma do Cálculo vem da Conferência de Tulane, de 1986, que formulou como recomendação fundamental: Focalizar na compreensão conceitual. Tentei implementar essa meta através da Regra de Três: “Tópicos devem ser apresentados geométrica, numérica e algebricamente”. Visualização, experimentação numérica e gráfica e outras abordagens mudaram radicalmente a forma de ensinar o raciocínio conceitual. Mais recentemente, a Regra de Três foi expandida, tornando-se Regra de Quatro, com acréscimo do ponto de vista verbal ou descritivo. (grifo nosso)

Nesses dois livros os autores declaram a intenção de focalizar a conceitualização do Cálculo, objeto de nossa investigação, razão pela qual os selecionamos dentre os demais.

Para escolher o livro a ser analisado, fizemos um levantamento do conteúdo de derivada de cada desses livros, a fim de averiguar qual deles apresentava mais possibilidades de análise, segundo nosso referencial teórico.

3.3. ESCOLHA DO LIVRO DIDÁTICO PARA ANÁLISE

Como os livros de Howard Anton e James Stewart enfocavam as representações das noções do Cálculo, nossa análise, à luz da Arquitetura Conceitual da Derivada, procurou levantar as “habilidades” de articulação entre as representações de derivada, detectadas nos exercícios.

Apresentamos os resultados obtidos, no formato [ENTRADA, processo cognitivo, saída] a fim de destacar as “habilidades” e a porcentagem que cada uma apresenta em relação ao total de exercícios.

Análise dos exercícios do livro Cálculo (James Stewart, 2002)

Analisamos 264 exercícios relacionados à derivada e suas representações. Dentre as dezoito “habilidades” mencionadas na Arquitetura Conceitual da Derivada, foram encontradas apenas cinco, sendo que algumas apresentam um valor desprezível se comparadas com a totalidade.

• Simbólica– Formulação – simbólica – [S F s] (70,1%)

(entrada) (processo cognitivo) (saída) (codificação)

(Exercício 3, p. 189)

Diferencie a função

f

(

x

)

=

x

2

+

3

x

+

4

.

(Exercício 1, p. 195)

Encontre a derivada de

_y

₌

(

_x

2

₊

1

)(

_x

3

₊

1

)

_{de duas maneiras:} usando a Regra do Produto e fazendo primeiro a multiplicação. As respostas são iguais?

(Exercício 2, p. 195)

Encontre a derivada da função

x

x

x

x

x

F

(

)

3

.

• Simbólica – Formulação – gráfica – [S F g] (15,9%)

(Exercício 23, p. 195)

Encontre uma equação da reta tangente à curva em um dado ponto.

1

2

+

=

x

x

y

, (1,1)

(Exercício 28, p. 195) (a) A curva ₂

1

x

x

y

+

=

é chamada de serpentina. Encontre uma

equação da reta tangente a essa curva no ponto (3, 0.3).

(Exercício 13, p. 154)

(a) Encontre a inclinação da reta tangente à parábola

y

=

1

+

x

+

x

2 no ponto onde

x

=

a

.

(b) Encontre a inclinação das retas tangentes nos pontos cujas coordenadas

x

são (i) -1, (ii)

2 1

− , (iii) 1.

(c) Faça o gráfico da curva e das três retas tangentes em uma tela em comum.

• Simbólica – Formulação – numérica – [S F n] (12,5%)

(Exercício 7, p. 205)

A função posição de uma partícula é dada por

0

7

5

,

4

)

(

_t

=

_t

3

−

_t

2

−

_t

_t

≥

s

Quando a partícula atinge a velocidade de

5

m

s

?

(Exercício 14, p. 206)

(a) O volume de uma célula esférica em crescimento é 3

3 4

r

V = π , onde

o raio r é medido em micrômetros

(

₁

_µ

m

₌

₁₀

−6

m

)

_{. Encontre a taxa de variação}

média de V em relação à r quando r varia de

(i) 5 a 8

µ

m

(i) 5 a 6

µ

m

(i) 5 a 5,1

µ

m

(b) Encontre a taxa de variação instantânea de V em relação a r

• Gráfica – Formulação – simbólica – [G F s] (1,1%)

(Exercício 2, p. 171)

Use o gráfico dado para estimar o valor de cada derivada.

(a)

f

'

(

1

)

(b)

f

'

(

2

)

(c)

f

'

(

3

)

(d)

f

'

(

4

)

(Exercício 3, p. 171)

Use o gráfico dado para estimar o valor de cada derivada. (a)

f

'

(

−

2

)

(b)

f

'

(

−

1

)

(c)

f

'

(

0

)

(d)

f

'

(

1

)

(e)

f

'

(

2

)

x y

1 1

• Gráfica – Formulação – gráfica – [G F g] (0,4%)

(Exercício 4, p. 171)

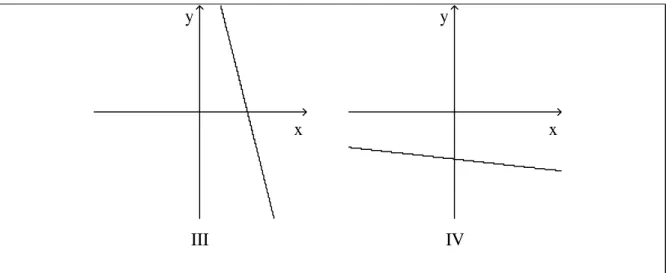
Associe o gráfico de cada função em (a)-(d) com o gráfico de sua derivada em I-IV. Dê razões para sua escolha

(a) (b) (c)

x y

x y

...

(I) (II) (III)

x y

x y

A tabela a seguir sintetiza os dados coletados.

Cálculo, um Novo Horizonte (Howard Anton, 2000)

Foram analisados 95 exercícios, propiciando o desenvolvimento de oito “habilidades”.

Iremos expor amostras de exercícios do livro para cada habilidade apresentada:

• Simbólica– Formulação – simbólica – [S F s] (65,3%)

(entrada) (processo cognitivo) (saída) (codificação)

(Exercício 21, p. 187)

Ache

f

'

(

t

)

se

f

₍

t

₎

=

₄

t

2

+

t

(Exercício 15, p. 187)

Use a fórmula

h

x

f

h

x

f

dx

dy

h

)

(

)

(

lim

0

−

+

=

→ para encontrar

_dx

dy

.

x

y

=

1

Codificação Quantidade Percentual

S F s

185 70,1%

S F g

42 15,9%

S F n

33 12,5%

G F s

3 1,1%

G F g

1 0,4%

• Simbólica – Formulação – gráfica – [S F g] (12,6%)

(Exercício 9, p. 187)

Encontre a equação da reta tangente a

y

=

f

(

x

)

no ponto

x

=

a

2

3

)

(

x

x

f

=

;

a

=

3

(Exercício 26, p. 202)

Ache a equação da reta tangente ao gráfico de sen x nos pontos (a) x=0 (b) x=π (c) x=π/4

• Simbólica – Formulação – numérica – [S F n] (9,5%)

(Exercício 1-2, p. 175)

São dados a função

y

=

f

(

x

)

e os valores x0 e x1.

(a) Ache a taxa de variação média de y em relação a x no intervalo [x0 e x1.]

(b) Ache a taxa de variação instantânea de y em relação a x em um ponto genérico x0.

1.

2

2

x

y

=

; x0=3, x1=4

2.

_y

=

_x

3 _{; x}

• Simbólica – Interpretação – simbólica – [S I s] (1,1%)

(Exercício 24, p. 187)

Ache uma função

f

tal que

f

'

(

x

)

=

1

para todo

x

e dê um argumento informal para justificar a sua resposta.

• Simbólica – Interpretação – gráfica – [S I g] (3,2%)

(Exercício 7, p. 187)

Dado que

f

(

3

)

=

−

1

e

f

'

(

3

)

=

5

. Ache uma equação para reta tangente ao gráfico de

y

=

f

(

x

)

no ponto onde

x

=

3

.

• Gráfica – Formulação – gráfica – [G F g] (3,2%)

(Exercício 25, p. 187)

Esboce o gráfico da derivada das funções cujos gráficos são dados:

(a) (c)

x y

x

y

• Gráfica – Formulação – numérica – [G F n] (3,2%)

(Exercício 9, p. 176)

A figura abaixo mostra a curva de posição versus tempo para um elevador que se move para cima até 60 m e, então, descarrega seus passageiros.

(a) Estime a velocidade instantânea do elevador quando t = 10s.

5 10 15 20 10

20 30 40 50 60 70

• Gráfica – Interpretação – simbólica – [G I s] (2,1%)

(Exercício 3, p. 186)

Se for dada uma equação da reta tangente no ponto

(

a

,

f

(

a

)

)

, sobre a curva

y

=

f

(

x

)

, como você faria para calcular

f

'

(

a

)

?

A tabela 7 sintetiza os dados coletados. Codificação Quantidade Percentual

S F s 62 65,3%

S F g 12 12,6%

S F n 9 9,5%

S I s 1 1,1%

S I g 3 3,2%

G F g 3 3,2%

G F n 3 3,2%

G I s 2 2,1%