E. Formenti (Ed.): AUTOMATA and JAC 2012 conferences EPTCS 90, 2012, pp. 151–165, doi:10.4204/EPTCS.90.13
c
H. Umeo, K. Nishide & K. Kubo This work is licensed under the Creative Commons Attribution License.
Multi-Dimensional Cellular Automata
HIROSHIUMEO
University of Osaka Electro-Communication
umeo@cyt.osakac.ac.jp
KINUONISHIDE
University of Osaka Electro-Communication
nishide@cyt.osakac.ac.jp
KEISUKEKUBO
University of Osaka Electro-Communication
kubo@cyt.osakac.ac.jp
The firing squad synchronization problem (FSSP) on cellular automata has been studied extensively for more than forty years, and a rich variety of synchronization algorithms have been proposed for not only one-dimensional arrays but two-dimensional arrays. In the present paper, we propose a simple recursive-halving based optimum-time synchronization algorithm that can synchronize any
rectangle arrays of sizem×n with a general at one corner in m+n+max(m,n)−3 steps. The
algorithm is a natural expansion of the well-known FSSP algorithms proposed by Balzer [1967], Gerken [1987], and Waksman [1966] and it can be easily expanded to three-dimensional arrays, even to multi-dimensional arrays with a general at any position of the array. The algorithm proposed is isotropic concerning the side-lengths of multi-dimensional arrays and its algorithmic correctness is transparent and easily verified.
1
Introduction
We study a synchronization problem that gives a finite-state protocol for synchronizing large-scale cellu-lar automata. The synchronization in cellucellu-lar automata has been known as a firing squad synchronization problem (FSSP) since its development, in which it was originally proposed by J. Myhill in Moore [1964] to synchronize all parts of self-reproducing cellular automata. The problem has been studied extensively for more than forty years [1-23], and a rich variety of synchronization algorithms have been proposed for not only one-dimensional (1D) arrays but two-dimensional (2D) arrays. The 1D FSSP is described as follows: given a one-dimensional array ofnidentical cellular automata, including ageneralat one end that is activated at timet=0, we want to design the automata such that,at some future time, all the cells willsimultaneouslyand,for the first time, enter a specialfiringstate.
Some questions may arise:
– How can we synchronize multi-dimensional arrays?
– Can we expand those 2D FSSP algorithms proposed so far to 3D arrays, or more generally to multi-dimensional arrays?
– Can we generalize those 2D FSSP algorithms to generalized ones, in which an initial general is located at any position of the array?
– What is a lower bound of time steps needed for synchronizing multi-dimensional arrays with a general at one corner?
In the present paper, we attempt to answer these questions by proposing a new, simple recursive-halving based synchronization algorithm for 2D rectangle cellular automata. The algorithm can synchro-nize any 2D rectangle array of sizem×nwith a general at one corner inm+n+max(m,n)−3 steps. An implementation in terms of local transition rules is also given on a 2D cellular automaton, not only for the array with a general at one corner but a generalized case.
The algorithms proposed in this paper are interesting in the following view points.
– The 2D algorithm proposed is isotropic with respect to shape of a given rectangle array, i.e. no need to control the FSSP algorithm for longer-than-wide and wider-than-long input rectangles.
– The algorithm proposed can be easily expanded to 3D arrays, even to multi-dimensional arrays.
– The algorithm is a natural generalization of the well-known 1D FSSP algorithms developed by Waksman [1966], Balzer [1967] and Gerken [1987]. It gives us a new view point of those classical 1D FSSP algorithms based on recursive-halving.
– The algorithm can be expanded to a generalized FSSP solution, where an initial general is at an arbitrary position of a given array.
– The algorithm can be generalized to an optimum-time generalized FSSP solution.
In Section 2 we give a description of the 2D FSSP and review some basic results on 2D FSSP algo-rithms. Section 3 defines the recursive-halving marking on 1D arrays and gives some preliminary lemmas for the construction of 2D FSSP algorithms. In Sections 4, 5, and 6 we present a new 2D FSSP algorithm based on the recursive-halving marking and several multi-dimensional expansions. Two implementations in terms of 2D cellular automata are also presented for the optimum-time FSSP algorithms. Most of the descriptions of the multi-dimensional FSSP algorithms are based on the 2D FSSP algorithms. Some expanded and generalized theorems for multi-dimensional arrays are given without proofs.
2
Firing Squad Synchronization Problem on Two-Dimensional Arrays
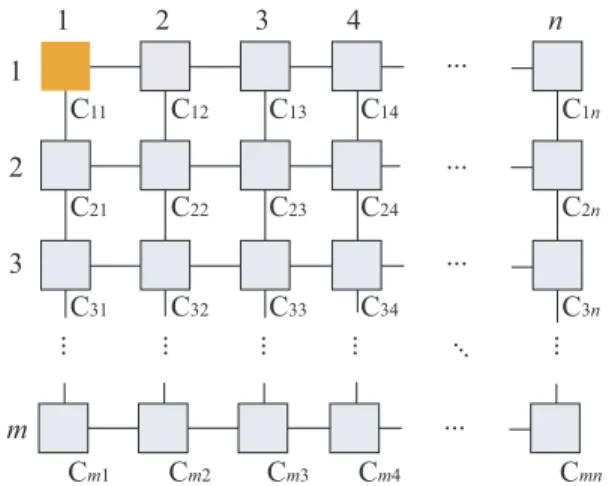
Figure 1 shows a finite two-dimensional (2D) cellular automaton consisting ofm×n cells. Each cell is an identical (except the border cells) finite-state automaton. The array operates in lock-step mode in such a way that the next state of each cell (except border cells) is determined by both its own present state and the present states of its north, south, east and west neighbors. All cells (soldiers), except the north-west corner cell (general), are initially in the quiescent state at timet=0 with the property that the next state of a quiescent cell with quiescent neighbors is the quiescent state again. At timet=0, the north-west corner cell C11is in thefire-when-readystate, which is the initiation signal for the array. The
firing squad synchronization problem is to determine a description (state set and next-state function) for cells that ensures all cells enter thefirestate at exactly the same time and for the first time. The tricky part of the problem is that the same kind of soldier having a fixed number of states must be synchronized, regardless of the sizem×nof the array. The set of states and next state function must be independent of mandn.
1 2 3 n
1
2
3
...
...
...
C11 C12 C13 C1n
C21 C22 C23
C31 C32
C2n
C33 C3n
4
C14
C24
C34
m ...
Cm1 Cm2 Cm3 Cm4 Cmn
... ... ... ... ... ...
Figure 1: A two-dimensional (2D) cellular automaton.
a six-state synchronization algorithm which, at present, is the algorithm having the fewest states for 1D arrays.
On the other hand, several synchronization algorithms on 2D arrays have been proposed by Beyer [1969], Grasselli [1975], Shinahr [1974], Szwerinski [1982], Schmid [2003], Schmid and Worsch [2004], Umeo, Maeda, Hisaoka and Teraoka [2006], and Umeo and Uchino [2008]. It has been shown indepen-dently by Beyer [1969] and Shinahr [1974] that there exists no 2D cellular automaton that can synchro-nize any 2D array of sizem×nin less thanm+n+max(m,n)−3 steps. In addition they first proposed an optimum-time synchronization algorithm that can synchronize any 2D array of size m×n in opti-mumm+n+max(m,n)−3 steps. Shinahr [1974] gave a 28-state implementation. Umeo, Hisaoka and Akiguchi [2005] presented a new 12-state synchronization algorithm operating in optimum-step, realizing a smallest solution to the rectangle synchronization problem at present.
As for the time optimality of the 2D FSSP algorithms, the following theorems have been shown.
Theorem 1Beyer[1969],Shinahr[1974]There exists no cellular automaton that can synchronize any 2D array
of sizem×nin less thanm+n+max(m,n)−3 steps, where the general is located at one corner of the array.
Theorem 2Shinahr[1974],Umeo,Hisaoka,and Akiguchi[2005] There exists a cellular automaton that can
synchro-nize any 2D array of sizem×nat exactlym+n+max(m,n)−3 steps, where the general is located at one corner of the array.
3
Recursive-Halving Marking
In this section, we develop a marking schema for 1D arrays referred to asrecursive-halving marking. The marking schema prints a special mark on cells in a cellular space defined by the recursive-halving marking. The marking itself is based on a 1D FSSP synchronization algorithm. It will be effectively used for constructing multi-dimensional FSSP algorithms operating in optimum-time.
x=
(
(i+j)/2 |S|: odd
(i+j−1)/2,(i+j+1)/2 |S|: even. (1)
The recursive-halving marking for a given cellular spaceS= [1...n] is defined as follows:
Recursive-Halving Marking: RHM
Algorithm RHM(S) begin
if|S| ≥2then
if|S|is oddthen
marka center cell CxinS;
SL:= [1...x];SR:= [x...n];
RHML(SL);RHMR(SR);
else
markcenter cells Cxand Cx+1inS;
SL:= [1...x];SR:= [x+1...n];
RHML(SL);RHMR(SR);
end
Left-Side Recursive-Halving Marking: RHML
Algorithm RHML(S)
begin
while|S|>2do
if|S|is oddthen
marka center cell CxinS;
SL:= [1...x];RHML(SL);
else
markcenter cells Cxand Cx+1inS;
SL:= [1...x];RHML(SL);
end
Right-Side Recursive-Halving Marking: RHMR
Algorithm RHMR(S) begin
while|S|>2do
if|S|is oddthen
marka center cell CxinS;
SR:= [x...n];RHMR(SR);
else
markcenter cells Cxand Cx+1inS;
SR:= [x+1...n];RHMR(SR);
end
For example, we consider a cellular spaceS= [1...15] consisting of 15 cells. The first center cell is C8, then the second one is C4, C5and C11, C12, and the last one is C2, C3, C13, C14, respectively. In case
S= [1...17], we get C9, C5, C13, C3, C15, and C2, C16after four iterations.
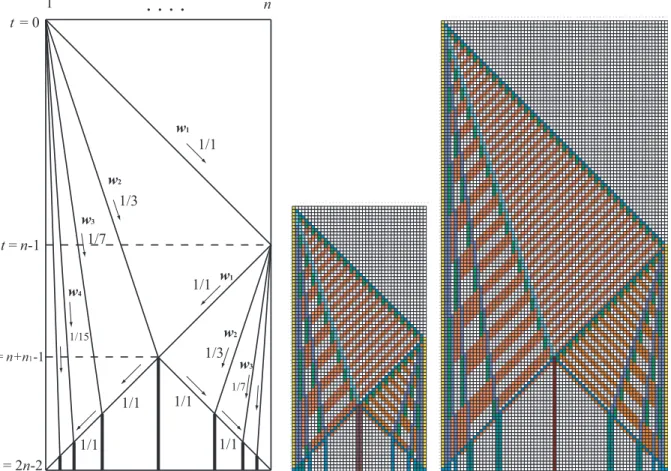
Figure 2 (left) shows a space-time diagram for the marking. At timet=0, the leftmost cell C1
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666769687071 0GQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 1GBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 2GOBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 3GOKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 4GOKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 5GOOCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 6GEOQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 7GEOQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 8GEOOCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 9GEKOQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 10GEKOQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 11GEKOOCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 12GEKCOQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 13GEECOQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 14GEECOOCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 15GEECKOQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 16GEEQKOQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 17GEEQKOOCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 18GEEQKCOQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 19GEEQCCOQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 20GEEECCOOCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 21GEKECCKOQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 22GEKECQKOQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 23GEKEQQKOOCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 24GEKEQQKCOQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 25GEKEQQCCOQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 26GEKEQCCCOOCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 27GEKEECCCKOQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 28GEKCECCQKOQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 29GEECECQQKOOCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 30GEECEQQQKCOQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 31GEECEQQQCCOQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 32GEECEQQCCCOOCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 33GEECEQCCCCKOQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 34GEECEECCCQKOQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 35GEECKECCQQKOOCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 36GEEQKECQQQKCOQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 37GEEQKEQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 38GEEQKEQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 39GEEQKEQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 40GEEQKEQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 41GEEQKEECCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 42GEEQKCECCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 43GEEQCCECQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQ 44GEEECCEQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQ 45GEKECCEQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQ 46GEKECCEQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQ 47GEKECCEQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQ 48GEKECCEECCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQ 49GEKECCKECCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQ 50GEKECQKECQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQ 51GEKEQQKEQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQ 52GEKEQQKEQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQ 53GEKEQQKEQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQ 54GEKEQQKEQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQ 55GEKEQQKEECCCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQ 56GEKEQQKCECCQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQ 57GEKEQQCCECQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQ 58GEKEQCCCEQQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQ 59GEKEECCCEQQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQ 60GEKCECCCEQQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQ 61GEECECCCEQCCCCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQ 62GEECECCCEECCCQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQQ 63GEECECCCKECCQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQQQ 64GEECECCQKECQQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQQQ 65GEECECQQKEQQQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQQQ 66GEECEQQQKEQQQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQQQ 67GEECEQQQKEQQCCCCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQQQ 68GEECEQQQKEQCCCCQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCBQQ 69GEECEQQQKEECCCQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCKBQ 70GEECEQQQKCECCQQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQKCG 71GEECEQQQCCECQQQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBG 72GEECEQQCCCEQQQQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBDG 73GEECEQCCCCEQQQCCCCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBKEG 74GEECEECCCCEQQCCCCQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBDKEG 75GEECKECCCCEQCCCCQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBKDEEG 76GEEQKECCCCEECCCQQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBDKQEEG 77GEEQKECCCCKECCQQQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBKDDQEEG 78GEEQKECCCQKECQQQQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBDKQDEEEG 79GEEQKECCQQKEQQQQCCCCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBKDDQQEKEG 80GEEQKECQQQKEQQQCCCCQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBDKQDDQEKEG 81GEEQKEQQQQKEQQCCCCQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBKDDQQDEEKEG 82GEEQKEQQQQKEQCCCCQQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQQCCQQCBDKQDDQQEDKEG 83GEEQKEQQQQKEECCCQQQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCQQCBKDDQQDDQEDEEG 84GEEQKEQQQQKCECCQQQQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQQCBDKQDDQQDEEDEEG 85GEEQKEQQQQCCECQQQQCCCCQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQQCBKDDQQDDQQEKDEEG 86GEEQKEQQQCCCEQQQQCCCCQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQQCBDKQDDQQDDQEKQEEG 87GEEQKEQQCCCCEQQQCCCCQQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCBKDDQQDDQQDEEKQEEG 88GEEQKEQCCCCCEQQCCCCQQQQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCBDKQDDQQDDQQEDKQEEG 89GEEQKEECCCCCEQCCCCQQQQCCCCQQKOOCQQCCQQCCQQCCQQCCQQCBKDDQQDDQQDDQEDDQEEG 90GEEQKCECCCCCEECCCQQQQCCCCQQQKCOQQCCQQCCQQCCQQCCQQCBDKQDDQQDDQQDEEDDEEEG 91GEEQCCECCCCCKECCQQQQCCCCQQQQCCOQCCQQCCQQCCQQCCQQCBKDDQQDDQQDDQQEKDDEKEG 92GEEECCECCCCQKECQQQQCCCCQQQQCCCOOCQQCCQQCCQQCCQQCBDKQDDQQDDQQDDQEKQDEKEG 93GEKECCECCCQQKEQQQQCCCCQQQQCCCCKOQQCCQQCCQQCCQQCBKDDQQDDQQDDQQDEEKQQEKEG 94GEKECCECCQQQKEQQQCCCCQQQQCCCCQKOQCCQQCCQQCCQQCBDKQDDQQDDQQDDQQEDKQQEKEG 95GEKECCECQQQQKEQQCCCCQQQQCCCCQQKOOCQQCCQQCCQQCBKDDQQDDQQDDQQDDQEDDQQEKEG 96GEKECCEQQQQQKEQCCCCQQQQCCCCQQQKCOQQCCQQCCQQCBDKQDDQQDDQQDDQQDEEDDDQEKEG 97GEKECCEQQQQQKEECCCQQQQCCCCQQQQCCOQCCQQCCQQCBKDDQQDDQQDDQQDDQQEKDDDEEKEG 98GEKECCEQQQQQKCECCQQQQCCCCQQQQCCCOOCQQCCQQCBDKQDDQQDDQQDDQQDDQEKQDDEDKEG 99GEKECCEQQQQQCCECQQQQCCCCQQQQCCCCKOQQCCQQCBKDDQQDDQQDDQQDDQQDEEKQQDEDEEG 100GEKECCEQQQQCCCEQQQQCCCCQQQQCCCCQKOQCCQQCBDKQDDQQDDQQDDQQDDQQEDKQQQEDEEG 101GEKECCEQQQCCCCEQQQCCCCQQQQCCCCQQKOOCQQCBKDDQQDDQQDDQQDDQQDDQEDDQQQEDEEG 102GEKECCEQQCCCCCEQQCCCCQQQQCCCCQQQKCOQQCBDKQDDQQDDQQDDQQDDQQDEEDDDQQEDEEG 103GEKECCEQCCCCCCEQCCCCQQQQCCCCQQQQCCOQCBKDDQQDDQQDDQQDDQQDDQQEKDDDDQEDEEG 104GEKECCEECCCCCCEECCCQQQQCCCCQQQQCCCOOBDKQDDQQDDQQDDQQDDQQDDQEKQDDDEEDEEG 105GEKECCKECCCCCCKECCQQQQCCCCQQQQCCCCKMKDDQQDDQQDDQQDDQQDDQQDEEKQQDDEKDEEG 106GEKECQKECCCCCQKECQQQQCCCCQQQQCCCCQAMAQDDQQDDQQDDQQDDQQDDQQEDKQQQDEKQEEG 107GEKEQQKECCCCQQKEQQQQCCCCQQQQCCCCQACMDAQDDQQDDQQDDQQDDQQDDQEDDQQQQEKQEEG 108GEKEQQKECCCQQQKEQQQCCCCQQQQCCCCQACQMQDAQDDQQDDQQDDQQDDQQDEEDDDQQQEKQEEG 109GEKEQQKECCQQQQKEQQCCCCQQQQCCCCQACQQMQQDAQDDQQDDQQDDQQDDQQEKDDDDQQEKQEEG 110GEKEQQKECQQQQQKEQCCCCQQQQCCCCQACQQQMQQQDAQDDQQDDQQDDQQDDQEKQDDDDQEKQEEG 111GEKEQQKEQQQQQQKEECCCQQQQCCCCQACQQQQMQQQQDAQDDQQDDQQDDQQDEEKQQDDDEEKQEEG 112GEKEQQKEQQQQQQKCECCQQQQCCCCQACQQQQQMQQQQQDAQDDQQDDQQDDQQEDKQQQDDEDKQEEG 113GEKEQQKEQQQQQQCCECQQQQCCCCQACQQQQQQMQQQQQQDAQDDQQDDQQDDQEDDQQQQDEDDQEEG 114GEKEQQKEQQQQQCCCEQQQQCCCCQACQQQQQQQMQQQQQQQDAQDDQQDDQQDEEDDDQQQQEDDEEEG 115GEKEQQKEQQQQCCCCEQQQCCCCQACQQQQQQQQMQQQQQQQQDAQDDQQDDQQEKDDDDQQQEDDEKEG 116GEKEQQKEQQQCCCCCEQQCCCCQACQQQQQQQQQMQQQQQQQQQDAQDDQQDDQEKQDDDDQQEDDEKEG 117GEKEQQKEQQCCCCCCEQCCCCQACQQQQQQQQQQMQQQQQQQQQQDAQDDQQDEEKQQDDDDQEDDEKEG 118GEKEQQKEQCCCCCCCEECCCQACQQQQQQQQQQQMQQQQQQQQQQQDAQDDQQEDKQQQDDDEEDDEKEG 119GEKEQQKEECCCCCCCKECCQACQQQQQQQQQQQQMQQQQQQQQQQQQDAQDDQEDDQQQQDDEKDDEKEG 120GEKEQQKCECCCCCCQKECQACQQQQQQQQQQQQQMQQQQQQQQQQQQQDAQDEEDDDQQQQDEKQDEKEG 121GEKEQQCCECCCCCQQKEQACQQQQQQQQQQQQQQMQQQQQQQQQQQQQQDAQEKDDDDQQQQEKQQEKEG 122GEKEQCCCECCCCQQQKEACQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQDAEKQDDDDQQQEKQQEKEG 123GEKEECCCECCCQQQQKUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUKQQDDDDQQEKQQEKEG 124GEKCECCCECCQQQQQAUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUAQQQDDDDQEKQQEKEG 125GEECECCCECQQQQQACUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUDAQQQDDDEEKQQEKEG 126GEECECCCEQQQQQACQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQDAQQQDDEDKQQEKEG 127GEECECCCEQQQQACQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQDAQQQDEDDQQEKEG 128GEECECCCEQQQACQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQDAQQQEDDDQEKEG 129GEECECCCEQQACQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQDAQQEDDDEEKEG 130GEECECCCEQACQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQDAQEDDDEDKEG 131GEECECCCEACQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQDAEDDDEDEEG 132GEECECCCUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUDDDEDEEG 133GEECECCBUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUBDDEDEEG 134GEECECBCUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUDBDEDEEG 135GEECEBCQUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUQDBEDEEG 136GEECIQQQUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUQQQIDEEG 137GEEBIQQQUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUQQQIBEEG 138GEIQIQQQUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUQQQIQIEG 139GIIQIQQQUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUQQQIQIIG 140IIIQIQQQUUQQQQQQQUUQQQQQQQQQQQQQQQQMQQQQQQQQQQQQQQQQUUQQQQQQQUUQQQIQIII 123456789101112131415161718192021222324252627282930313233343536373839404142
0GQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 1GBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 2GOBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 3GOKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 4GOKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 5GOOCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 6GEOQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 7GEOQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 8GEOOCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 9GEKOQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 10GEKOQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 11GEKOOCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 12GEKCOQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 13GEECOQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQQQ 14GEECOOCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQQQ 15GEECKOQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQQQ 16GEEQKOQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQQQ 17GEEQKOOCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQQQ 18GEEQKCOQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQQQ 19GEEQCCOQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQQQ 20GEEECCOOCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQQQ 21GEKECCKOQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQQQ 22GEKECQKOQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQQQ 23GEKEQQKOOCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQQQ 24GEKEQQKCOQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQQQ 25GEKEQQCCOQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQQQ 26GEKEQCCCOOCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQQQ 27GEKEECCCKOQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQQQ 28GEKCECCQKOQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQQQ 29GEECECQQKOOCQQCCQQCCQQCCQQCCKBQQQQQQQQQQQQ 30GEECEQQQKCOQQCCQQCCQQCCQQCCQKCBQQQQQQQQQQQ 31GEECEQQQCCOQCCQQCCQQCCQQCCQQCCKBQQQQQQQQQQ 32GEECEQQCCCOOCQQCCQQCCQQCCQQCCQKCBQQQQQQQQQ 33GEECEQCCCCKOQQCCQQCCQQCCQQCCQQCCKBQQQQQQQQ 34GEECEECCCQKOQCCQQCCQQCCQQCCQQCCQKCBQQQQQQQ 35GEECKECCQQKOOCQQCCQQCCQQCCQQCCQQCCKBQQQQQQ 36GEEQKECQQQKCOQQCCQQCCQQCCQQCCQQCCQKCBQQQQQ 37GEEQKEQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCKBQQQQ 38GEEQKEQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQKCBQQQ 39GEEQKEQQCCCCKOQQCCQQCCQQCCQQCCQQCCQQCCKBQQ 40GEEQKEQCCCCQKOQCCQQCCQQCCQQCCQQCCQQCCQKCBQ 41GEEQKEECCCQQKOOCQQCCQQCCQQCCQQCCQQCCQQCCKG 42GEEQKCECCQQQKCOQQCCQQCCQQCCQQCCQQCCQQCCQAG 43GEEQCCECQQQQCCOQCCQQCCQQCCQQCCQQCCQQCCQADG 44GEEECCEQQQQCCCOOCQQCCQQCCQQCCQQCCQQCCQAKEG 45GEKECCEQQQCCCCKOQQCCQQCCQQCCQQCCQQCCQADKEG 46GEKECCEQQCCCCQKOQCCQQCCQQCCQQCCQQCCQAKDEEG 47GEKECCEQCCCCQQKOOCQQCCQQCCQQCCQQCCQADKQEEG 48GEKECCEECCCQQQKCOQQCCQQCCQQCCQQCCQAKDDQEEG 49GEKECCKECCQQQQCCOQCCQQCCQQCCQQCCQADKQDEEEG 50GEKECQKECQQQQCCCOOCQQCCQQCCQQCCQAKDDQQEKEG 51GEKEQQKEQQQQCCCCKOQQCCQQCCQQCCQADKQDDQEKEG 52GEKEQQKEQQQCCCCQKOQCCQQCCQQCCQAKDDQQDEEKEG 53GEKEQQKEQQCCCCQQKOOCQQCCQQCCQADKQDDQQEDKEG 54GEKEQQKEQCCCCQQQKCOQQCCQQCCQAKDDQQDDQEDEEG 55GEKEQQKEECCCQQQQCCOQCCQQCCQADKQDDQQDEEDEEG 56GEKEQQKCECCQQQQCCCOOCQQCCQAKDDQQDDQQEKDEEG 57GEKEQQCCECQQQQCCCCKOQQCCQADKQDDQQDDQEKQEEG 58GEKEQCCCEQQQQCCCCQKOQCCQAKDDQQDDQQDEEKQEEG 59GEKEECCCEQQQCCCCQQKOOCQADKQDDQQDDQQEDKQEEG 60GEKCECCCEQQCCCCQQQKCOQAKDDQQDDQQDDQEDDQEEG 61GEECECCCEQCCCCQQQQCCOADKQDDQQDDQQDEEDDEEEG 62GEECECCCEECCCQQQQCCCWWDDQQDDQQDDQQEKDDEKEG 63GEECECCCKECCQQQQCCCBWWBDDQQDDQQDDQEKQDEKEG 64GEECECCQKECQQQQCCCBCWWDBDDQQDDQQDEEKQQEKEG 65GEECECQQKEQQQQCCCBCQWWQDBDDQQDDQQEDKQQEKEG 66GEECEQQQKEQQQCCCBCQQWWQQDBDDQQDDQEDDQQEKEG 67GEECEQQQKEQQCCCBCQQQWWQQQDBDDQQDEEDDDQEKEG 68GEECEQQQKEQCCCBCQQQQWWQQQQDBDDQQEKDDDEEKEG 69GEECEQQQKEECCBCQQQQQWWQQQQQDBDDQEKQDDEDKEG 70GEECEQQQKCECBCQQQQQQWWQQQQQQDBDEEKQQDEDEEG 71GEECEQQQCCEBCQQQQQQQWWQQQQQQQDBEDKQQQEDEEG 72GEECEQQCCCIQQQQQQQQQWWQQQQQQQQQIDDQQQEDEEG 73GEECEQCCCBIQQQQQQQQQWWQQQQQQQQQIBDDQQEDEEG 74GEECEECCBCIQQQQQQQQQWWQQQQQQQQQIDBDDQEDEEG 75GEECKECBCQIQQQQQQQQQWWQQQQQQQQQIQDBDEEDEEG 76GEEQKEBCQQIQQQQQQQQQWWQQQQQQQQQIQQDBEKDEEG 77GEEQKIQQQQIQQQQQQQQQWWQQQQQQQQQIQQQQIKQEEG 78GEEQAIQQQQIQQQQQQQQQWWQQQQQQQQQIQQQQIAQEEG 79GEEACIQQQQIQQQQQQQQQWWQQQQQQQQQIQQQQIDAEEG 80GEUUQIQQQQIQQQQQQQQQWWQQQQQQQQQIQQQQIQUUEG 81GIUUQIQQQQIQQQQQQQQQWWQQQQQQQQQIQQQQIQUUIG 82IIUUQIQQQQIQQQQQQQQQWWQQQQQQQQQIQQQQIQUUII
1 . . . . n
1/1 1/3
1/7
t = 0
t = 2n-2
1/1 1/1 w1 w3 w2 w1 w2 w3 1/7 1/15 w4 1/3 1/1 1/1 1/1
t = n-1
t = n+n1-1
Figure 2: Space-time diagram for recursive-halving marking on 1D array of lengthn(left) and some snapshots for the marking on 42 (middle) and 71 (right) cells, respectively.
wherek=1,2,3, ...,. The 1/1-speed signalw1arrives at Cnat timet=n−1. Then, the rightmost cell
Cnalso emits an infinite set of signalsw1,w2, ...,wk, .., each propagating in the left direction at 1/(2k−1)
speed, wherek=1,2,3, ..., . The readers can find that each crossing of two signals, shown in Fig. 2 (left), enables the marking at middle points defined by the recursive-halving. A finite state realization for generating the infinite set of signals above is a well-known technique employed in Balzer [1967], Gerken [1987], and Waksman [1966] for the implementations of the optimum-time synchronization algorithms on 1D arrays.
We have developed a simple implementation of the recursive-halving marking on a 13-state, 314-rule cellular automaton. In Fig. 2 (middle and right) we present several snapshots for the marking on 42 and 71 cells, respectively. Thus we have:
Lemma 3There exists a 1D 13-state, 314-rule cellular automaton that can print the recursive-halving
marking in any cellular space of lengthnin 2n−2 steps.
An optimum-time complexity 2n−2 needed for synchronizing cellular space of lengthnin the classi-cal WBG-type (Waksman [1966], Balzer [1967], and Gerken [1987]) FSSP algorithms can be interpreted as follows: LetSbe a cellular space of length n=2n1+1, wheren1≥1. The first center mark inSis
yielding a final synchronization at timet1D−opt=3n1+n1=4n1=2n−2. In the casen=2n1, where
n1≥1, the first center mark is printed simultaneously on cells Cn1 and Cn1+1at timet1D−center=3n1−1.
Additionaln1−1 steps are required for the marking and synchronization thereafter, yielding the final
synchronization at timet1D−opt=3n1−1+n1−1=4n1−2=2n−2.
t1D−center=
(
3n1 |S|=2n1+1,
3n1−1 |S|=2n1.
(2)
Thus, additional t1D−sync steps are required for the synchronization for a cellular space with the
recursive-halving marks:
t1D−sync=
(
n1 |S|=2n1+1,
n1−1 |S|=2n1.
(3)
1 n
1/1
1/1
t = 0
1/1 1/1
1/1 1/1
1/1 1/1
1/1 1/1 G
1/1
1/1
1/1 1/1
1/1 1/1 1/1
1/1 1/1 1/1
t = tsync
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 0 G I I Q I Q Q QM2 Q Q Q I Q I I G 1 G I I Q I Q Q Q2 M2 C2Q Q I Q I I G 2 G I I Q I Q Q2 Q2 M2 C2 C2Q I Q I I G 3 G I I Q I Q2 L2 Q2 M2 C2 R2 C2 I Q I I G 4 G I I QM2 A2L2 Q2 M2 C2 R2 B2 M2 Q I I G 5 G I I Q2 M2 B2 Q2 Q2 M2 C2 C2 A2 M2 C2 I I G 6 G I M2 Q2 M2 C2 M2 Q2 M2 C2 M2 Q2 M2 C2 M2 I G 7 G M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 G 8 F F F F F F F F F F F F F F F F F
123456789101112131415161718192021222324252627282930313
0GUUUUQQUUQQQQQQM2 M2QQQQQQUUQQUUUUG
1GUUUUQQUUQQQQQQ2 M2 M2 C2QQQQQUUQQUUUUG
2GUUUUQQUUQQQQQ2 Q2 M2 M2 C2 C2QQQQUUQQUUUUG
3GUUUUQQUUQQQQ2 L2 Q2 M2 M2 C2 R2 C2QQQUUQQUUUUG
4GUUUUQQUUQQQ2 A2L2 Q2 M2 M2 C2 R2 B2 C2QQUUQQUUUUG
5GUUUUQQUUQQ2 L2A2 Q2 Q2 M2 M2 C2 C2 B2 R2 C2QUUQQUUUUG
6GUUUUQQUUQ2 A2L2L2 Q2 Q2 M2 M2 C2 C2 R2 R2 B2 C2UUQQUUUUG
7GUUUUQQUMM L2A2 A2L2 Q2 Q2 M2 M2 C2 C2 R2 B2 B2 R2 MMUQQUUUUG
8GUUUUQQM2 M2 L2L2A2 Q2 Q2 Q2 M2 M2 C2 C2 C2 B2 R2 R2 M2 M2QQUUUUG
9GUUUUQQ2 M2 M2 C2 L2L2 Q2 L2 Q2 M2 M2 C2 R2 C2 R2 R2 Q2 M2 M2 C2QUUUUG
10GUUUUQ2 Q2 M2 M2 C2 C2 L2 Q2 L2 Q2 M2 M2 C2 R2 C2 R2 Q2 Q2 M2 M2 C2 C2UUUUG
11GUUUMM L2 Q2 M2 M2 C2 R2 C2 Q2 L2 Q2 M2 M2 C2 R2 C2 Q2 L2 Q2 M2 M2 C2 R2 MMUUUG
12GUUM2 M2 L2 Q2 M2 M2 C2 R2 M2 M2 L2 Q2 M2 M2 C2 R2 M2 M2 L2 Q2 M2 M2 C2 R2 M2 M2UUG
13GUMM M2 M2 C2 Q2 M2 M2 C2 Q2 M2 M2 C2 Q2 M2 M2 C2 Q2 M2 M2 C2 Q2 M2 M2 C2 Q2 M2 M2 MMUG
14GM2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2 M2G
15FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
Figure 3: Space-time diagram for synchronizing a cellular space with recursive-halving marking (left) and some snapshots for the synchronization on 17 (middle) and 32 (right) cells, respectively.
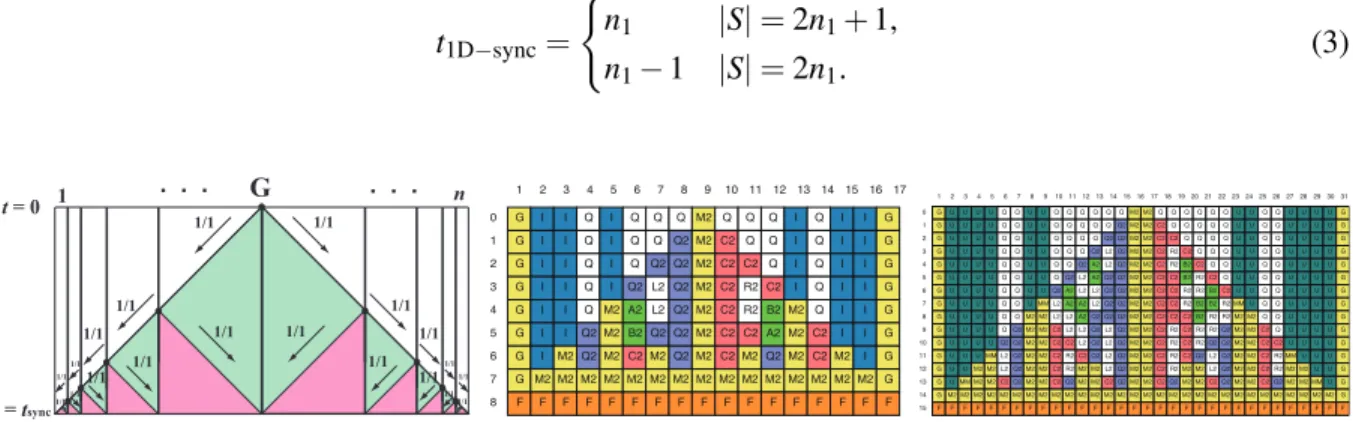
In this way, it can be easily seen that any cellular space of lengthnwith the recursive-halving marking initially with a general on a center cell or two generals on adjacent center cells can be synchronized in
⌈n/2⌉ −1 optimum-steps. In Fig. 3, we illustrate a space-time diagram for synchronizing a cellular space with recursive-halving marking (left) and some snapshots for the synchronization on 17 (middle) and 32 (right) cells, respectively. Thus we have:
Lemma 4Any 1D cellular spaceSof lengthnwith the recursive-halving marking initially with a
gen-eral(s) on a center cell(s) inScan be synchronized in⌈n/2⌉ −1 optimum-steps.
As was seen, the first marking of center cell(s) plays an important role. We print a special mark for the first center cell(s) of a given cellular space. On the other hand, for the center cells generated thereafter are marked with a different symbol from the first one.
G
Step 1 Step 2 Step 3
Step 0
4
An Optimum-Time 2D FSSP Algorithm
A
14.1 Overview of the AlgorithmA1
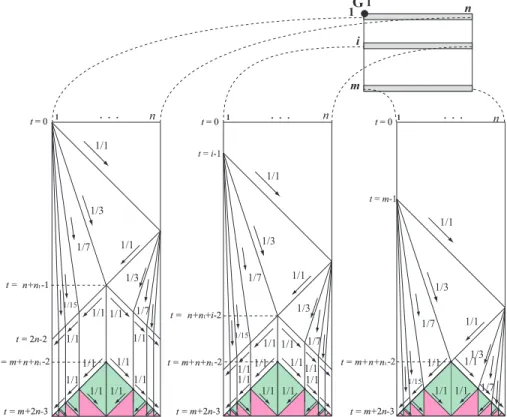
We assume that an initial general G is on the north-west corner cell C11 of a given array of sizem×
n. The algorithm consists of three phases: a marking phase, a pre-synchronization phase and a final synchronization phase. An overview of the 2D synchronization algorithmA1is as follows:
Step 1. Startthe recursive-halving marking for cells on each row and column,find acenter cell(s) of
the given array, andgeneratea new general(s) on the center cell(s). Note that a crossing(s) of the center column(s) with the center row(s) is a center cell(s) of the array.
Step 2. Pre-synchronizethe center column(s) using Lemma 4, which is initiated by the general in Step
1. Every cell on the center column(s) acts as a general at the following Step 3.
Step 3. Synchronizeeach row using Lemma 4, initiated by the general generated in Step 2. This yields
the final synchronization of the array.
t = 0 = 01
t = 0 = 0 1
i
n
1 1
m
t =
t = 2n-n-2
t = 0 = 0 1
G
1/1 1/1
1/1 1/1
1/15
1/1
1/3
1/7 1/1
1/3
1/7 1/1
1/1 1/1
1/1
1/1
1/1 1/1 1/1
1/1 1/1
1/1 1/1
1/1 1/1
1/1 1/1
t =
t = n+nn+n1-1-1
t =
t = +i-2-2
n n
n
t =
t = m+m+ -2-2
t =
t = 2m+m+ -2-2
t =
t = 2m+n-m+n-3 t =
t = 2m+n-m+n-3 t =
t = 2m+n-m+n-3
n+n
n+n1
n+n
n+n1
n1 t = t = 2m+m+n1-2-2 t = t = 2m+m+n1-2-2
1/15
1/1
1/3
1/7 1/1
1/3
1/7 1/1
1/1 1/1
1/1
1/15
1/1
1/3
1/7 1/1
1/3
1/7 1/1
1/1 1/1
1/1
t = = i-i-1
t = = m-m-1
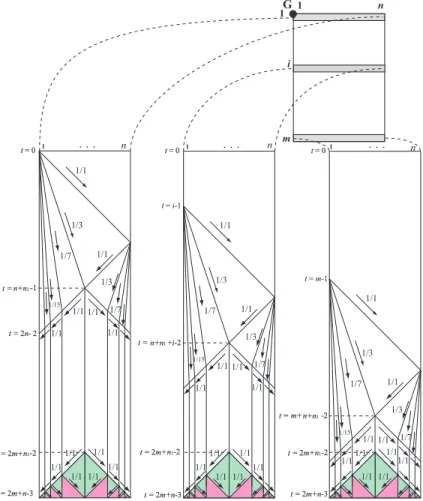
Figure 5: Space-time diagrams for the synchronization algorithm on the 1st,ith, andmth rows of a longer-than-wide rectangle array of sizem×n, respectively.
2m1+1,n=2n1+1, wherem1,n1≥1. The algorithm operates as follows:
1. At timet=0 an initial general on the north-west corner emits a 1/1-speed signal along the first row and column to print recursive-halving marks. Once a center mark is printed, it is copied to the adjacent row and column. At timet=3m1+n1, a center mark of the center column of the array is
marked, and the center mark of the center row is marked at timet=3n1+m1. The center of the
array is marked at timet=t2D−center=max(3m1+n1,3n1+m1).
2. Using Lemma 4, the center column will be synchronized with a tentative pre-firing state at time t=t2D−center+m1.
3. Once the center column could be synchronized with the pre-firing state, then the cell Ci,n1+1
ini-tiates the synchronization for the ith row for each isuch that 1≤i≤m. Using Lemma 4, for anyi,1≤i≤m, theith row will be synchronized at timet=t2D−center+m1+n1=max(3m1+
n1,3n1+m1) +m1+n1=max(2m1+1,2n1+1) +2m1+2n1−1=m+n+max(m,n)−3. Thus,
the array can be synchronized at timet=m+n+max(m,n)−3 in optimum-steps.
t = 0 = 01
t = 0 = 0 1
i
n
1 1
m
t =
t = 2n-n-2
t = 0 = 0 1
G
1/1 1/1
1/1 1/1
1/15
1/1
1/3
1/7 1/1
1/3
1/7 1/1
1/1 1/1
1/1
1/1
1/1 1/1 1/1
1/1 1/1
1/1 1/1
1/1 1/1
1/1 1/1
t =
t = n+nn+n1-1-1
t =
t = +i-2-2
n n
n
t =
t = m+m+2n-n-3
t =
t = m+m+ -2-2
t =
t = m+m+2n-n-3
t =
t = m+m+2n-n-3
n+n
n+n1
n+n
n+n1
t =
t = m+m+n+nn+n1-2-2 t = t = m+m+n+nn+n1-2-2 1/15
1/1
1/3
1/7 1/1
1/3
1/7 1/1
1/1 1/1
1/1
1/15
1/1
1/3
1/7 1/1
1/3
1/7
t = = i-1-1
t = = m-1-1
Figure 6: Space-diagrams of the synchronization algorithm on the 1st,ith, and mth rows of a wider-than-long rectangle array of sizem×n, respectively.
t = 0
123456789101112
1 1G2G QQQQQQQQQQQ 2QQQQQQQQQQQQ
3QQQQQQQQQQQQ
4QQQQQQQQQQQQ
5QQQQQQQQQQQQ 6QQQQQQQQQQQQ
7QQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 1
123456789101112
1 1G2G 1BQQQQQQQQQQ 22BQQQQQQQQQQQ
3QQQQQQQQQQQQ
4QQQQQQQQQQQQ
5QQQQQQQQQQQQ 6QQQQQQQQQQQQ
7QQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 2
123456789101112
1 1G2G 1O 1BQQQQQQQQQ 22OQQQQQQQQQQQ
32BQQQQQQQQQQQ
4QQQQQQQQQQQQ
5QQQQQQQQQQQQ 6QQQQQQQQQQQQ
7QQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 3
123456789101112
1 1G2G 1O 1K 1BQQQQQQQQ 22OQQQQQQQQQQQ
32KQQQQQQQQQQQ
42BQQQQQQQQQQQ
5QQQQQQQQQQQQ 6QQQQQQQQQQQQ
7QQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 4
123456789101112
1 1G2G 1O 1K 1C 1BQQQQQQQ 22OQQQQQQQQQQQ
32KQQQQQQQQQQQ
42CQQQQQQQQQQQ
52BQQQQQQQQQQQ 6QQQQQQQQQQQQ
7QQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 5
123456789101112
1 1G2G 1O 1O 1C 1K 1BQQQQQQ 22OQQQQQQQQQQQ
32OQQQQQQQQQQQ
42CQQQQQQQQQQQ
52KQQQQQQQQQQQ 62BQQQQQQQQQQQ
7QQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 6
123456789101112
1 1G2G 1E 1O Q1K1C1BQQQQQ 22EQQQQQQQQQQQ
32OQQQQQQQQQQQ
4QQQQQQQQQQQQ
52KQQQQQQQQQQQ 62CQQQQQQQQQQQ
72BQQQQQQQQQQQ
8QQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 7
123456789101112
1 1G2G 1E 1O Q 1C 1C 1K 1BQQQQ 22EQQQQQQQQQQQ
32OQQQQQQQQQQQ
4QQQQQQQQQQQQ
52CQQQQQQQQQQQ 62CQQQQQQQQQQQ
72KQQQQQQQQQQQ
82BQQQQQQQQQQQ
9QQQQQQQQQQQQ
t = 8
123456789101112
1 1G2G 1E 1O 1O 1C Q1K1C1BQQQ 22EQQQQQQQQQQQ
32OQQQQQQQQQQQ
42OQQQQQQQQQQQ
52CQQQQQQQQQQQ 6QQQQQQQQQQQQ
72KQQQQQQQQQQQ
82CQQQQQQQQQQQ
9 1G2G QQQQQQQQQQQ
t = 9
123456789101112
1 1G2G 1E 1K 1O QQ1C1C1K1BQQ 22EQQQQQQQQQQQ
32KQQQQQQQQQQQ
42OQQQQQQQQQQQ
5QQQQQQQQQQQQ 6QQQQQQQQQQQQ
72CQQQQQQQQQQQ
82BQQQQQQQQQQQ
9 1G2G1x2G QQQQQQQQQQ
t = 10
123456789101112
1 1G2G 1E 1K 1O Q 1C 1C Q1K1C1BQ 22EQQQQQQQQQQQ
32KQQQQQQQQQQQ
42OQQQQQQQQQQQ
5QQQQQQQQQQQQ 62CQQQQQQQQQQQ
72BQQQQQQQQQQQ
82DQQQQQQQQQQQ
9 1G2G1x2G1x2G QQQQQQQQQ
t = 11
123456789101112
1 1G2G 1E 1K 1O 1O 1C QQ1C1C1K 1G2G 22EQQQQQQQQQQQ
32KQQQQQQQQQQQ
42OQQQQQQQQQQQ
52OQQQQQQQQQQQ 62BQQQQQQQQQQQ
72KQQQQQQQQQQQ
82EQQQQQQQQQQQ
9 1G2G1x2G1x2G1x2G QQQQQQQQ
t = 12
123456789101112
1 1G2G 1E 1K 1C 1O QQ1C1CQ1A 1G2G 22EQQQQQQQQQQ 1G2x
32KQQQQQQQQQQQ
42CQQQQQQQQQQQ
52MQQQQQQQQQQQ 62DQQQQQQQQQQQ
72KQQQQQQQQQQQ
82EQQQQQQQQQQQ
9 1G2G1x2G1x2G1x2G1x2G QQQQQQQ
t = 13
123456789101112
1 1G2G 1E 1E 1C 1O Q 1C 1C Q 1A 1D 1G2G 22EQQQQQQQQQQ 1G2x
32EQQQQQQQQQQ 1G2x
42BQQQQQQQQQQQ
52x2MQQQQQQQQQQ 62BQQQQQQQQQQQ
72EQQQQQQQQQQQ
82EQQQQQQQQQQQ
9 1G2G1x2G1x2G1x2G1x2G1x2G QQQQQQ
t = 14
123456789101112 1 1G2G 1E 1E 1C 1O 1O 1C Q 1A 1K 1E 1G2G
22EQQQQQQQQQQ 1G2x
32IQQQQQQQQQQ 1G2x 42xQQQQQQQQQQ 1G2x
52x2M 2MQQQQQQQQQ
62xQQQQQQQQQQQ
72IQQQQQQQQQQQ 82EQQQQQQQQQQQ
9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G QQQQQ
t = 15
123456789101112
1 1G2G 1E 1E 1C 1K 1O Q 1A 1D 1K 1E 1G2G 22IQQQQQQQQQQ 1G2x
32x2IQQQQQQQQQ 1G2x
42xQQQQQQQQQQ 1G2x 52x2M 2M 2MQQQQQQQ 1G2x
62xQQQQQQQQQQQ
72x2IQQQQQQQQQQ
82IQQQQQQQQQQQ 9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G QQQQ
t = 16
123456789101112
1 1G2G 1E 1EQ1K1O1A1K1D1E1E 1G2G 22x2IQQQQQQQQQ 1G2x
32x2I2IQQQQQQQQ 1G2x
42xQQQQQQQQQQ 1G2x 52x2M 2M 2M 2MQQQQQQ 1G2x
62xQQQQQQQQQQ 1G2x
72x2I2IQQQQQQQQQ
82x2IQQQQQQQQQQ 9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G QQQ
t = 17
123456789101112
1 1G2G 1E 1EQ1K1W 1M1KQ1E1E 1G2G 22x2I2IQQQQQQQQ 1G2x
32x2I2I2IQQQQQQQ 1G2x
42xQQQQQQQQQQ 1G2x 52x2M 2M 2M 2M 2MQQQQQ 1G2x
62xQQQQQQQQQQ 1G2x
72x2I2I2IQQQQQQQ 1G2x
82x2I2IQQQQQQQQQ 9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G QQ
t = 18
123456789101112
1 1G2G 1E 1EQ1A1x1x1AQ1E1E 1G2G 22x2I2I2IQ1W 1MQQQQ 1G2x
32x2I2I2I2IQQQQQQ 1G2x
42xQQQQQQQQQQ 1G2x 52x2M 2M 2M 2M 2M 2MQQQQ 1G2x
62xQQQQQQQQQQ 1G2x
72x2I2I2I2IQQQQQQ 1G2x
82x2I2I2IQQQQQQQ 1G2x 9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G Q
t = 19
123456789101112
1 1G2G 1E 1E 1A 1x 1x 1x 1x 1A 1E 1E 1G2G 22x2I2I2I2I1W 1MQQQQ 1G2x
32x2I2I2I2I 1W2I 1MQQQQ 1G2x
42xQQQQQQQQQQ 1G2x 52x2M 2M 2M 2M 2M 2M 2MQQQ 1G2x
62xQQQQQQQQQQ 1G2x
72x2I2I2I2I2IQQQQQ 1G2x
82x2I2I2I2IQQQQQQ 1G2x 9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 20
123456789101112
1 1G2G 1E1I1U1x1x1x1x1U1I1E 1G2G
22x2I2I2I2I 1W2I 1MQQQQ 1G2x 32x2I2I2I2I 1W2I1M2I QQQQ 1G2x
42xQQQQ1W 1MQQQQ 1G2x
52x2M 2M 2M 2M 2M 2M 2M 2MQQ 1G2x
62xQQQQQQQQQQ 1G2x 72x2I2I2I2I2I2IQQQQ 1G2x
82x2I2I2I2I2IQQQQQ 1G2x
9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 21
123456789101112
1 1G2G 1I1x1x1x1x1x1x1x1x1I 1G2G
22x2I1I2I 1U2I 2I 1W2I1M2I Q1U1IQ 1G2x
32x2I2I2I2I 1W2I1M2I 2IQQQ 1G2x 42xQQQQ1W 1MQQQQ 1G2x
52x2M 2M 2M 2M M^ M^ 2M 2M 2MQ 1G2x
62xQQQQQQQQQQ 1G2x
72x2I2I2I2I2I2I2IQQQ 1G2x 82x2I2I2I2I2I2IQQQQ 1G2x
9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 22
123456789101112
1 1G2G 1x 1x 1x 1x 1x 1x 1x 1x 1x 1x 1G2G
22x 1I2I 1I2I 1U2I 2I 1W2I1M2I 2I1U1I1I 1G2x
32x2I1I2I 1U2I 2I 1W2I1M2I 2I 1U2I 1IQ 1G2x 42xQQQQC-C-QQQQ 1G2x
52x2M 2M 2M 2MM-M-2M 2M 2M 2M 1G2x
62xQQQQQ-Q-QQQQ 1G2x
72x2I2I2I2I2I2I2I2IQQ 1G2x 82x2I2I2I2I2I2I2IQQQ 1G2x
9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 23
123456789101112
1 1G2G 1x 1x 1x 1x 1x 1x 1x 1x 1x 1x 1G2G
22x 1I2I 1I2I 1U2I 2I 1W2I1M2I 2I 1U2I 1I1I 1G2x
32x 1I2I 1I2I 1U2I 2IM-M-2I 1U2I 1I2I1I 1G2x 42xQ1I1UQC-C-Q1U1IQ 1G2x
52x2M 2M 2M 2MM-M-2M 2M 2M 2M 1G2x
62xQQQQQ-Q-QQQQ 1G2x
72x2I2I2I2IM-M-2I2I2IQ 1G2x 82x2I2I2I2I2I2I2I2IQQ 1G2x
9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 24
123456789101112
1 1G2G 1x 1x 1x 1x 1x 1x 1x 1x 1x 1x 1G2G
22x 1I2I 1I2I 1U2I 2IM-M-2I 1U2I 1I2I1I 1G2x
32x 1I2I 1I2I 1U2I 2IM-M-2I 1U2I 1I2I 1I2I 1G2x 42x1I1I1UQM-M-Q1U1I1I 1G2x
52x2M 1I2M1U2M 2MM-M-2M 1U2M1I2M 2M 1G2x
62xQQQQM-M-QQQQ 1G2x
72x2I2I2I2IM-M-2I2I2I2I 1G2x 82x2I2I2I2IM-M-2I2I2IQ 1G2x
9 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 25
123456789101112
1 1G2G 1x 1x 1x 1x M+ M+ 1x 1x 1x 1x 1G2G
22x 1I2I 1I2I 1U2I 2IM+ M+2I 1U2I 1I2I 1I2I 1G2x
32x 1I2I 1I2I 1U2I 2IM+ M+2I 1U2I 1I2I 1I2I 1G2x 42x1I1I1UQM+ M+Q1U1I1I 1G2x
52x 1I2M1I2M1U2M 2M M+ M+ 2M 1U2M1I2M1I2M1G2x
62xQ1I1UQM+ M+Q1U1IQ 1G2x
72x2I2I2I2IM+ M+2I2I2I2I 1G2x 82x2I2I2I2IM+ M+2I2I2I2I 1G2x
9 1G2G1x2G1x2G1x2G1x2G M+ M+ 1x2G1x2G1x2G1x2G1G2G
t = 26
123456789101112
1 1G2G 1x 1x 1x Q+ M+ M+ C+ 1x 1x 1x 1G2G
22x 1I2I 1I2I 1U2I Q+ M+ M+ C+ 1U2I 1I2I 1I2I 1G2x
32x 1I2I 1I2I 1U2I Q+ M+ M+ C+ 1U2I 1I2I 1I2I 1G2x 42x1I1I1U Q+ M+ M+ C+1U1I1I 1G2x
52x 1I2M1I2M1U2M Q+ M+ M+ C+ 1U2M1I2M1I2M1G2x
62x1I1I1U Q+ M+ M+ C+1U1I1I 1G2x
72x2I1I2I 1U2I Q+ M+ M+ C+ 1U2I 1I2I2I 1G2x 82x2I2I2IQ+ M+ M+ C+2I2I2I 1G2x
9 1G2G1x2G1x2G1x2G Q+ M+ M+ C+ 1x2G1x2G1x2G1G2G
t = 27
123456789101112
1 1G2G 1x 1x MM+ Q+ M+ M+ C+ MM+ 1x 1x 1G2G
22x 1I2I 1I2I MM+ Q+ M+ M+ C+ MM+ 1I2I 1I2I 1G2x
32x 1I2I 1I2I MM+ Q+ M+ M+ C+ MM+ 1I2I 1I2I 1G2x 42x1I1I MM+ Q+ M+ M+ C+ MM+ 1I1I 1G2x
52x 1I2M1I2MMM+ Q+ M+ M+ C+ MM+1I2M1I2M1G2x
62x1I1I MM+ Q+ M+ M+ C+ MM+ 1I1I 1G2x
72x 1I2I 1I2I MM+ Q+ M+ M+ C+ MM+ 1I2I 1I2I 1G2x 82x2I1I2I MM+ Q+ M+ M+ C+ MM+ 1I2I2I 1G2x
9 1G2G1x2G1x2G Q+ Q+ M+ M+ C+ C+ 1x2G1x2G1G2G
t = 28
123456789101112
1 1G2G 1x M+ M+ Q+ M+ M+ C+ M+ M+ 1x 1G2G 22x 1I2I M+ M+ Q+ M+ M+ C+ M+ M+ 1I2I 1G2x
32x 1I2I M+ M+ Q+ M+ M+ C+ M+ M+ 1I2I 1G2x
42x1IM+ M+ Q+ M+ M+ C+ M+ M+1I 1G2x 52x 1I2M M+ M+ Q+ M+ M+ C+ M+ M+ 1I2M1G2x
62x1IM+ M+ Q+ M+ M+ C+ M+ M+1I 1G2x
72x 1I2I M+ M+ Q+ M+ M+ C+ M+ M+ 1I2I 1G2x
82x 1I2I M+ M+ Q+ M+ M+ C+ M+ M+ 1I2I 1G2x 9 1G2G1x2G M+ M+ Q+ M+ M+ C+ M+ M+ 1x2G1G2G
t = 29
123456789101112
1 1G2G M+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2G 22xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x
32xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x
42xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x 52xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x
62xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x
72xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x
82xM+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2x 9 1G2G M+ M+ M+ M+ M+ M+ M+ M+ M+ M+ 1G2G
t = 30
123456789101112
1FFFFFFFFFFFF 2FFFFFFFFFFFF
3FFFFFFFFFFFF
4FFFFFFFFFFFF
5FFFFFFFFFFFF 6FFFFFFFFFFFF
7FFFFFFFFFFFF
8FFFFFFFFFFFF
9FFFFFFFFFFFF
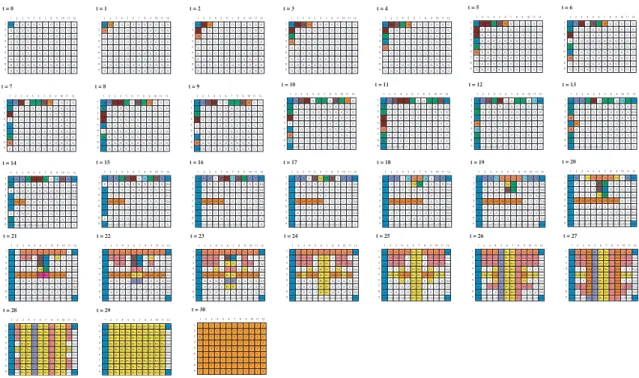
Figure 7: Snapshots for synchronization on a 9×12 array.
each marking operation has been finished before the arrival of the first wake-up signal for the synchro-nization. The algorithm operates in optimum-steps in a similar way for the rectangles such as case 1: m=2m1+1,n=2n1, case 2: m=2m1,n=2n1+1, and case 3:m=2m1,n=2n1.
Thus, we can establish the following theorem.
Theorem 5The synchronization algorithmA1can synchronize anym×nrectangular array in optimum
m+n+max(m,n)−3 steps.
We have implemented the algorithmA1on a 2D cellular automaton having 60 states and 13633 local
rules. In Figures 7 and 8 we present some snapshots of the synchronization processes of the algorithm on 9×12 and 12×9 arrays, respectively.
5
Expansion to Multi-Dimensional Arrays
5.1 Three-Dimensional Arrays
In this section, we show that there exists no algorithm that can synchronize any 3D array of sizem×n×ℓ with a general at an arbitrary corner in less thanm+n+ℓ+max(m,n, ℓ)−4 steps.
Theorem 6The minimum time in which the firing squad synchronization could occur is no earlier than
m+n+ℓ+max(m,n, ℓ)−4 for any 3D array of sizem×n×ℓwith a general at an arbitrary corner cell. Proof. The proof is made by contradiction. Without loss of generality, we assume thatℓ≤m≤n. It is assumed that there is a cellular automatonM that can synchronize an array of sizem0×n0×ℓ0
t = 0
123456789 1 1G2G QQQQQQQQ 2QQQQQQQQQ 3QQQQQQQQQ 4QQQQQQQQQ 5QQQQQQQQQ 6QQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 1
123456789 1 1G2G 1BQQQQQQQ 22BQQQQQQQQ 3QQQQQQQQQ 4QQQQQQQQQ 5QQQQQQQQQ 6QQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 2
123456789 1 1G2G 1O 1BQQQQQQ 22OQQQQQQQQ 32BQQQQQQQQ 4QQQQQQQQQ 5QQQQQQQQQ 6QQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 3
123456789 1 1G2G 1O 1K 1BQQQQQ 22OQQQQQQQQ 32KQQQQQQQQ 42BQQQQQQQQ 5QQQQQQQQQ 6QQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 4
123456789 1 1G2G 1O 1K 1C 1BQQQQ 22OQQQQQQQQ 32KQQQQQQQQ 42CQQQQQQQQ 52BQQQQQQQQ 6QQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 5
123456789 1 1G2G 1O 1O 1C 1K 1BQQQ 22OQQQQQQQQ 32OQQQQQQQQ 42CQQQQQQQQ 52KQQQQQQQQ 62BQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 6
123456789 1 1G2G 1E 1O Q1K1C1BQQ 22EQQQQQQQQ 32OQQQQQQQQ 4QQQQQQQQQ 52KQQQQQQQQ 62CQQQQQQQQ 72BQQQQQQQQ 8QQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 7
123456789 1 1G2G 1E 1O Q 1C 1C 1K 1BQ 22EQQQQQQQQ 32OQQQQQQQQ 4QQQQQQQQQ 52CQQQQQQQQ 62CQQQQQQQQ 72KQQQQQQQQ 82BQQQQQQQQ 9QQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 8
123456789 1 1G2G 1E 1O 1O 1C Q1K1C 1G2G 22EQQQQQQQQ 32OQQQQQQQQ 42OQQQQQQQQ 52CQQQQQQQQ 6QQQQQQQQQ 72KQQQQQQQQ 82CQQQQQQQQ 92BQQQQQQQQ 10QQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 9
123456789 1 1G2G 1E 1K 1O QQ1C1B 1G2G 22EQQQQQQQ 1G2x 32KQQQQQQQQ 42OQQQQQQQQ 5QQQQQQQQQ 6QQQQQQQQQ 72CQQQQQQQQ 82CQQQQQQQQ 92KQQQQQQQQ 102BQQQQQQQQ 11QQQQQQQQQ 12QQQQQQQQQ
t = 10
123456789 1 1G2G 1E 1K 1O Q 1C 1B 1D 1G2G 22EQQQQQQQ 1G2x 32KQQQQQQQ 1G2x 42OQQQQQQQQ 5QQQQQQQQQ 62CQQQQQQQQ 72CQQQQQQQQ 8QQQQQQQQQ 92KQQQQQQQQ 102CQQQQQQQQ 112BQQQQQQQQ 12QQQQQQQQQ
t = 11
123456789 1 1G2G 1E 1K 1O 1O 1B 1K 1E 1G2G 22EQQQQQQQ 1G2x 32KQQQQQQQ 1G2x 42OQQQQQQQ 1G2x 52OQQQQQQQQ 62CQQQQQQQQ 7QQQQQQQQQ 8QQQQQQQQQ 92CQQQQQQQQ 102CQQQQQQQQ 112KQQQQQQQQ 12 1G2G QQQQQQQQ
t = 12
123456789 1 1G2G 1E 1K 1C 1M 1D 1K 1E 1G2G 22EQQQQQQQ 1G2x 32KQQQQQQQ 1G2x 42CQQQQQQQ 1G2x 52OQQQQQQQ 1G2x 6QQQQQQQQQ 7QQQQQQQQQ 82CQQQQQQQQ 92CQQQQQQQQ 10QQQQQQQQQ 11
2AQQQQQQQQ 12 1G2G1x2G QQQQQQQ
t = 13
123456789 1 1G2G 1E 1E 1B 1x 1B 1E 1E 1G2G 22EQQQ1MQQQ 1G2x 32EQQQQQQQ 1G2x 42CQQQQQQQ 1G2x 52OQQQQQQQ 1G2x 6QQQQQQQQ 1G2x 72CQQQQQQQQ 82CQQQQQQQQ 9QQQQQQQQQ 102AQQQQQQQQ 11
2DQQQQQQQQ 12 1G2G1x2G1x2G QQQQQQ
t = 14
123456789 1 1G2G 1E1I1x1x1x1I1E 1G2G 22EQQQ1MQQQ 1G2x 32EQQQ1MQQQ 1G2x 42CQQQQQQQ 1G2x 52OQQQQQQQ 1G2x 62OQQQQQQQ 1G2x 72CQQQQQQQ 1G2x 8QQQQQQQQQ 92AQQQQQQQQ 102KQQQQQQQQ 11
2EQQQQQQQQ 12 1G2G1x2G1x2G1x2G QQQQQ
t = 15
123456789 1 1G2G 1I1x1x1x1x1x1I 1G2G 22EQ1IQ1MQ1IQ 1G2x 32EQQQ1MQQQ 1G2x 42CQQQ1MQQQ 1G2x 52KQQQQQQQ 1G2x 62OQQQQQQQ 1G2x 7QQQQQQQQ 1G2x 82AQQQQQQQ 1G2x 92DQQQQQQQQ 102KQQQQQQQQ 11
2EQQQQQQQQ 12 1G2G1x2G1x2G1x2G1x2G QQQQ
t = 16
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22E1I1IQ1MQ1I1I 1G2x 32EQ1IQ1MQ1IQ 1G2x 4QQQQ1MQQQ 1G2x 52KQQQ1MQQQ 1G2x 62OQQQQQQQ 1G2x 72AQQQQQQQ 1G2x 82KQQQQQQQ 1G2x 92DQQQQQQQ 1G2x 102EQQQQQQQQ 112EQQQQQQQQ 12 1G2G1x2G1x2G1x2G1x2G1x2G QQQ
t = 17
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22E1I1IQ1MQ1I1I 1G2x 32E1I1IQ1MQ1I1I 1G2x 4QQ1IQ1MQ1IQ 1G2x 52KQQQ1MQQQ 1G2x 62WQQQ1MQQQ 1G2x 72MQQQQQQQ 1G2x 82KQQQQQQQ 1G2x 9QQQQQQQQ 1G2x 102EQQQQQQQ 1G2x 112EQQQQQQQQ 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G QQ
t = 18
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22E1I1IQ1MQ1I1I 1G2x 3
2E1I1IQ1MQ1I1I 1G2x 4Q1I1IQ1MQ1I1I 1G2x 52AQ1IQ1MQ1IQ 1G2x 62x2WQQ1MQQQ 1G2x 72x2MQQ1MQQQ 1G2x 82AQQQQQQQ 1G2x 9QQQQQQQQ 1G2x 102EQQQQQQQ 1G2x 112EQQQQQQQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G Q
t = 19
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22E1I1IQ1MQ1I1I 1G2x 3
2E1I1IQ1MQ1I1I 1G2x 42A1I1IQ1MQ1I1I 1G2x 52x1I1IQ1MQ1I1I 1G2x 62x2W 1I2W Q1MQ1IQ 1G2x 72x2M 2MQ1MQQQ 1G2x 82xQQQ1MQQQ 1G2x 92AQQQQQQQ 1G2x 102EQQQQQQQ 1G2x 112EQQQQQQQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 20
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22E1I1IQ1MQ1I1I 1G2x 3
2I1I1IQ1MQ1I1I 1G2x 42U1I1IQ1MQ1I1I 1G2x 52x1I1IQ1MQ1I1I 1G2x 62x 1I2W1I2W 2W 1MQ1I1I 1G2x 72x2M 1I2M 2M 1MQ1IQ 1G2x 82xQQQ1MQQQ 1G2x 92UQQQ1MQQQ 1G2x 102IQQQQQQQ 1G2x 112EQQQQQQQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 21
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22I1I1IQ1MQ1I1I 1G2x 3
2x 1I2I1IQ1MQ1I1I 1G2x 42x 1I2U 1IQ1MQ1I1I 1G2x 52x1I1IQ1MQ1I1I 1G2x 62x 1I2W1I2W 2W M^Q1I1I 1G2x 72x 1I2M1I2M 2M M^Q1I1I 1G2x 82xQ1IQ1MQ1IQ 1G2x 92x2UQQ1MQQQ 1G2x 102x2IQQ1MQQQ 1G2x 112IQQQQQQQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 22
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22x 1I2I1IQ1MQ1I1I 1G2x 3
2x 1I2I 1I2IQ1MQ1I1I 1G2x 42x 1I2U 1I2U Q1MQ1I1I 1G2x 52x1I1IQC-Q1I1I 1G2x 62x 1I2W1I2W 2W M-Q1I1I 1G2x 72x 1I2M1I2M 2MM-Q1I1I 1G2x 82x1I1IQQ-Q1I1I 1G2x 92x2U 1I2U Q1MQ1IQ 1G2x 102x2I2IQ1MQQQ 1G2x 112x2IQQ1MQQQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 23
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22x 1I2I 1I2IQ1MQ1I1I 1G2x 3
2x 1I2I 1I2I2I1MQ1I1I 1G2x 42x 1I2U 1I2U 2UC-Q1I1I 1G2x 52x1I1IQC-Q1I1I 1G2x 62x 1I2W1I2W 2W M-Q1I1I 1G2x 72x 1I2M1I2M 2MM-Q1I1I 1G2x 82x1I1IQQ-Q1I1I 1G2x 92x 1I2U 1I2U 2UQ-Q1I1I 1G2x 102x2I1I2I2I1MQ1IQ 1G2x 112x2I2IQ1MQQQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 24
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22x 1I2I 1I2I2I1MQ1I1I 1G2x 32x 1I2I 1I2I2IM-Q1I1I 1G2x 42x 1I2U 1I2U 2UM-Q1I1I 1G2x 52x1I1IQC-Q1I1I 1G2x 62x 1I2W1I2W 2W M-Q1I1I 1G2x 72x 1I2M1I2M 2MM-Q1I1I 1G2x 82x1I1IQQ-Q1I1I 1G2x 92x 1I2U 1I2U 2UM-Q1I1I 1G2x 102x 1I2I 1I2I2IM-Q1I1I 1G2x 112x2I1I2I2I1MQ1IQ 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 25
123456789 1 1G2G 1x 1x 1x 1x 1x 1x 1x 1G2G 22x 1I2I 1I2I2IM-Q1I1I 1G2x 32x 1I2I 1I2I2IM-Q1I1I 1G2x 42x 1I2U 1I2U 2UM-Q1I1I 1G2x 52x1I1IQM-Q1I1I 1G2x 62x 1I2W1I2W 2W M-Q1I1I 1G2x 72x 1I2M1I2M 2MM-Q1I1I 1G2x 82x1I1IQM-Q1I1I 1G2x 92x 1I2U 1I2U 2UM-Q1I1I 1G2x 102x 1I2I 1I2I2IM-Q1I1I 1G2x 112x 1I2I 1I2I2IM-Q1I1I 1G2x 12 1G2G1x2G1x2G1x2G1x2G1x2G1x2G1x2G1G2G
t = 26
123456789 1 1G2G 1x 1x 1x M+ 1x 1x 1x 1G2G 22x 1I2I 1I2I2IM+Q1I1I 1G2x 32x 1I2I 1I2I2IM+Q1I1I 1G2x 42x 1I2U 1I2U 2U M+Q1I1I 1G2x 52x1I1IQM+Q1I1I 1G2x 62x 1I2W1I2W 2W M+Q1I1I 1G2x 72x 1I2M1I2M 2M M+Q1I1I 1G2x 82x1I1IQM+Q1I1I 1G2x 92x 1I2U 1I2U 2U M+Q1I1I 1G2x 102x 1I2I 1I2I2IM+Q1I1I 1G2x 112x 1I2I 1I2I2IM+Q1I1I 1G2x 12 1G2G1x2G1x2G1x2G M+ 1x2G1x2G1x2G1G2G
t = 27
123456789 1 1G2G 1x 1x Q+ M+ C+ 1x 1x 1G2G 22x 1I2I 1I2I Q+ M+ C+1I1I 1G2x 32x 1I2I 1I2I Q+ M+ C+1I1I 1G2x 42x 1I2U 1I2U Q+ M+ C+1I1I 1G2x 52x1I1IQ+ M+ C+1I1I 1G2x 62x 1I2W1I2W Q+ M+ C+1I1I 1G2x 72x 1I2M1I2M Q+ M+ C+1I1I 1G2x 82x1I1IQ+ M+ C+1I1I 1G2x 92x 1I2U 1I2U Q+ M+ C+1I1I 1G2x 102x 1I2I 1I2I Q+ M+ C+1I1I 1G2x 112x 1I2I 1I2I Q+ M+ C+1I1I 1G2x 12 1G2G1x2G1x2G Q+ M+ C+ 1x2G1x2G1G2G
t = 28
123456789 1 1G2G 1x M+ Q+ M+ C+ M+ 1x 1G2G 22x 1I2I M+ Q+ M+ C+ M+1I 1G2x 32x 1I2I M+ Q+ M+ C+ M+1I 1G2x 42x 1I2U M+ Q+ M+ C+ M+1I 1G2x 52x1IM+ Q+ M+ C+ M+1I 1G2x 62x 1I2W M+ Q+ M+ C+ M+1I 1G2x 72x 1I2M M+ Q+ M+ C+ M+1I 1G2x 82x1IM+ Q+ M+ C+ M+1I 1G2x 92x 1I2U M+ Q+ M+ C+ M+1I 1G2x 102x 1I2I M+ Q+ M+ C+ M+1I 1G2x 112x 1I2I M+ Q+ M+ C+ M+1I 1G2x 12 1G2G1x2G M+ Q+ M+ C+ M+ 1x2G1G2G
t = 29
123456789 1 1G2G M+ M+ M+ M+ M+ M+ M+ 1G2G 22xM+ M+ M+ M+ M+ M+ M+ 1G2x 32xM+ M+ M+ M+ M+ M+ M+ 1G2x 42xM+ M+ M+ M+ M+ M+ M+ 1G2x 52xM+ M+ M+ M+ M+ M+ M+ 1G2x 62xM+ M+ M+ M+ M+ M+ M+ 1G2x 72xM+ M+ M+ M+ M+ M+ M+ 1G2x 82xM+ M+ M+ M+ M+ M+ M+ 1G2x 92xM+ M+ M+ M+ M+ M+ M+ 1G2x 102xM+ M+ M+ M+ M+ M+ M+ 1G2x 112xM+ M+ M+ M+ M+ M+ M+ 1G2x 12 1G2G M+ M+ M+ M+ M+ M+ M+ 1G2G
t = 30
123456789 1FF FFFFFFF 2FF FFFFFFF 3FF FFFFFFF 4FF FFFFFFF 5FF FFFFFFF 6FF FFFFFFF 7FF FFFFFFF 8FF FFFFFFF 9FF FFFFFFF 10FF FFFFFFF 11FF FFFFFFF 12FF FFFFFFF
Figure 8: Snapshots for synchronization on a 12×9 array.
t0<m0+2n0+ℓ0−4 (4)
Now consider the state of cell Cm0 1ℓ0 at timet=t0. Letiandkbe any integer such that 1≤i≤m0
and 1≤k≤ℓ0. Consider the signal propagation from the cell C1 1 1 to Cm0 1ℓ0 via any cell Ci n0 k. It
takes:
(i−1) + (n0−1) + (k−1) + (m0−i) + (n0−1) + (ℓ0−k)
=m0+2n0+ℓ0−4 (5)
steps for the signal to travel from C1 1 1 to Cm01ℓ0 via any cell Ci n0 k. The state of the cell Cm01ℓ0 at
stept=t0entered the final firing state unaffected by any cells on the plane{Ci n0k|1≤i≤m0,1≤k≤ℓ0
}. Therefore, if another three-dimensional array of sizem0×n0×ℓ0 was added to the right side of the
original array (that is, the new array is of sizem0×2n0×ℓ0), the cell Cm01ℓ0 would still enter the final
firing state at stept=t0. This is because the cell structureM is fixed, cell operation is deterministic
and nothing has changed as far as the cell Cm0 1ℓ0 is concerned. Sincet0<m0+2n0+ℓ0−4, the cell
Cm0 1ℓ0 will still be in a quiescent state at timet=t0. Therefore the cell structure does not represent
a solution and this is a contradiction. In a similar way, the argument carries over in the cases such as ℓ≤n≤m,n≤ℓ≤m, ..., and so forth.
The synchronization algorithmA1for 2D arrays can be easily expanded to 3D arrays. See Figure 9
which illustrates the synchronization schema for 3D cellular automaton. Thus, we have:
Theorem 7There exists an optimum-time synchronization algorithmA2that can synchronize any
three-dimensional array of sizen1×n2×n3with a general at C1,1,1in optimumn1+n2+n3+max(n1,n2,n3)−
4 steps.
G G G
Step 1
Step 0 Step 2 Step 3 Step 4
Figure 9: Synchronization scheme for a three-dimensional cellular automaton.
5.2 Multi-Dimensional Arrays
AkD FSSP algorithmA3is sketched as follows:
Step 1. Startthe recursive-halving marking on cells along each dimension,findacenter cell(s) of the
given array,generatea general(s) on the center cell(s), andpre-synchronizethe center point(s): zero-dimensional sub-array of the array.
Step 2. Pre-synchronizea 1D sub-array along the 1st dimension containing the pre-synchronized center
cell.
Step 3. - Stepk. For j=2 to k−1, by increasing the number of dimensions, pre-synchronizea jD
sub-array containing the pre-synchronized(j−1)D sub-array.
Stepk+1. SynchronizethekD array. This yields the final synchronization of the given array.
Theorems 6 and 7 can be expanded to thekD arrays.
Theorem 9There exists no cellular automaton that can synchronize anykD array of sizen1×n2×...×nk
with a general at C1,1,...,1in less than∑ki=1ni+max(n1,n2, ...,nk)−k−1 steps
Theorem 10There exists an optimum-time synchronization algorithmA3that can synchronize anykD
array of sizen1×n2×...×nk with a general at C1,1,...,1in optimum∑ki=1ni+max(n1,n2, ...,nk)−k−1
steps.
6
Generalization as to General’s Position
6.1 Generalized FSSP on 1D Arrays
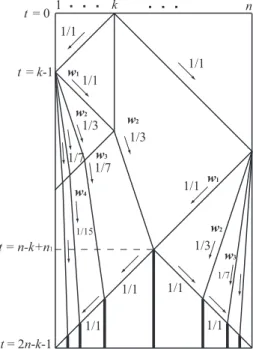
The recursive-halving marking scheme on 1D array can be easily expanded to the generalized case where the initial general is located at any position of the array. Figure 10 illustrates a space-time diagram for the recursive-halving marking on 1D array of lengthnwith a general on Ck,1≤k≤n. The marking is
1 n
1/1 1/3
1/7 t = 0
1/1
1/1
w1
w3 w2 w2
w3
1/7
1/15
w4
1/3
1/1
1/1
1/1
w1
1/1
1/3
w2
1/7 1/1
t = n-k+n1
k
t = k-1
t = 2n-k-1
Figure 10: Space-time diagram for recursive-halving marking on 1D array of lengthnwith a general at any position.
Theorem 11 Moore and Langdon[1968] The minimum time in which the generalized firing squad
synchro-nization could occur isn−2+max(k,n−k+1)steps, where the general is located on thekth cell from left end.
Theorem 12Moore and Langdon[1968] There exists a 17-state cellular automaton that can synchronize any
one-dimensional array of lengthnin optimumn−2+max(k,n−k+1)steps, where the general is located on thekth cell from left end.
An optimum-time complexityn−2+max(k,n−k+1)needed for synchronizing cellular space of length n in the classical ML-type (Moore and Langdon [1968]) generalized FSSP algorithm can be interpreted as follows: LetS be a cellular space of lengthn=2n1+1, wheren1≥1. The first center
mark inSis printed on cell Cn1+1 at timet1Dg−center=3n1−min(k−1,n−k). Additionaln1 steps are
required for the markings thereafter, yielding a final synchronization at timet1Dg−opt=3n1−min(k−
1,n−k) +n1=4n1−min(k−1,n−k) =2n−2−min(k−1,n−k) =n−2+max(k,n−k+1).
In the casen=2n1, where n1≥1, the first center mark is printed simultaneously on cells Cn1 and
Cn1+1 at timet1Dg−center =3n1−1−min(k−1,n−k). Note that two cells Cn1 and Cn1+1 are
pre-synchronized at timet1Dg−center=3n1−1−min(k−1,n−k). Additionaln1−1 steps are required for
the marking thereafter, yielding the final synchronization at timet1Dg−opt=3n1−1−min(k−1,n−k) +
n1−1=4n1−2−min(k−1,n−k) =2n−2−min(k−1,n−k) =n−2+max(k,n−k+1).
t1Dg−center=
(
3n1−min(k−1,n−k) |S|=2n1+1,
3n1−1−min(k−1,n−k) |S|=2n1.
(6)
recursive-halving marks:
t1Dg−sync=
(
n1 |S|=2n1+1,
n1−1 |S|=2n1.
(7)
6.2 Generalized FSSP on 2D Arrays
By a similar method employed in Section 4, we can develop the following theorem for the generalized case.
Theorem 13There exists no 2D cellular automaton that can synchronize any 2D array of sizem×nwith
an initial general on Cr,sin less thanm+n+max(m,n)−min(r,m−r+1)−min(s,n−s+1)−1 steps,
where 1≤r≤m,1≤s≤n.
Now we are going to present a generalized optimum-time FSSP Algorithm A4 for 2D arrays. We
assume that an initial general G is on the cell Cr,sof a given array of sizem×n, where 1≤r≤m,1≤
s≤n. The algorithm consists of three phases: a marking phase, a pre-synchronization phase and a final synchronization phase. An overview of the 2-D synchronization algorithmA4is as follows:
Step 1. Startthe recursive-halving marking for cells on each row and column,find acenter cell(s) of
the given array, andgeneratea new general(s) on the center cell(s). Note that a crossing(s) of the center column(s) with the center row(s) is a center cell(s) of the array.
Step 2. Pre-synchronizethe center column(s) using Lemma 4, which is initiated by the general in step
1. Every cell on the center column(s) acts as a general at the next Step 3.
Step 3. Synchronizeeach row using Lemma 4, initiated by the general generated in Step 2. This yields
the final synchronization of the array.
The array can be synchronized at timet=m+n+max(m,n)−min(r,m−r+1)−min(s,n−s+1)−1 in optimum-steps.
Theorem 14There exists an optimum-time synchronization algorithmA4that can synchronize anym×n
rectangular array with a general at Cr,sin optimumm+n+max(m,n)−min(r,m−r+1)−min(s,n−
s+1)−1 steps, where 1≤r≤m,1≤s≤n.
We have implemented the algorithmA4 on a 2D cellular automaton having 269 states and 163662
local rules. We have checked the rule set for any array of size m×n, with 2≤m,n≤100, and any general’s position in the array. In Figure 11 we present some snapshots of the synchronization processes of the algorithm on an 8×13 array with a general on C3,5.
6.3 Generalized FSSP on Multi-Dimensional Arrays
Theorems 13 and 14 can be expanded to three or more dimensional arrays.
Theorem 15The minimum time in which the firing squad synchronization could occur is no earlier than
n1+n2+n3+max(n1,n2,n3)−min(r1,n1−r1+1)−min(r2,n2−r2+1)−min(r3,n3−r3+1)−1 for
any 3D array of sizen1×n2×n3with a general at Cr1,r2,r3.
Theorem 16 There exists an optimum-time synchronization algorithm A5 that can synchronize any
3D array of size n1×n2×n3 with a general at Cr1,r2,r3 in optimum n1+n2+n3+max(n1,n2,n3)−
t = 0
12345678910111213 1QQQQQQQQQQQQQ 2QQQQQQQQQQQQQ 3QQQQGGGGQQQQQQQQ 4QQQQQQQQQQQQQ 5QQQQQQQQQQQQQ 6QQQQQQQQQQQQQ 7QQQQQQQQQQQQQ 8QQQQQQQQQQQQQ
t = 1
12345678910111213 1QQQQQQQQQQQQQ 2QQQQ2BQQQQQQQQ 3QQQ1B1K2K1BQQQQQQQ 4QQQQ2BQQQQQQQQ 5QQQQQQQQQQQQQ 6QQQQQQQQQQQQQ 7QQQQQQQQQQQQQ 8QQQQQQQQQQQQQ
t = 2
12345678910111213 1QQQQ2GQQQQQQQQ 2QQQQ2DQQQQQQQQ 3QQ1B1D1K2K1C1BQQQQQQ 4QQQQ2CQQQQQQQQ 5QQQQ2BQQQQQQQQ 6QQQQQQQQQQQQQ 7QQQQQQQQQQQQQ 8QQQQQQQQQQQQQ
t = 3
12345678910111213 1QQQ2G2G2GQQQQQQQ 2QQQQ2BQQQQQQQQ 3Q1B1K1D1Q2Q1C1K1BQQQQQ 4QQQQ2CQQQQQQQQ 5QQQQ2KQQQQQQQQ 6QQQQ2BQQQQQQQQ 7QQQQQQQQQQQQQ 8QQQQQQQQQQQQQ
t = 4
12345678910111213 1QQ2G2G2G2G2GQQQQQQ 2QQQQ2OQQQQQQQQ 31G1D1K1Q1Q2O1Q1K1C1BQQQQ 4QQQQ2QQQQQQQQQ 5QQQQ2KQQQQQQQQ 6QQQQ2CQQQQQQQQ 7QQQQ2BQQQQQQQQ 8QQQQQQQQQQQQQ
t = 5
12345678910111213 1Q2G2G2G2G2G2G2GQQQQQ 21GQQQ2EQQQQQQQQ 31G1B1D1Q1Q2O1Q1C1C1K1BQQQ 41GQQQ2QQQQQQQQQ 5QQQQ2CQQQQQQQQ 6QQQQ2CQQQQQQQQ 7QQQQ2KQQQQQQQQ 8QQQQ2GQQQQQQQQ
t = 6
12345678910111213 11G2G2G2G2G2G2G2G2G2GQQQQ 21GQQQ2EQQQQQQQQ 31G1C1B1D1Q2O1C1C1Q1K1C1BQQ 41GQQQ2OQQQQQQQQ 51GQQQ2CQQQQQQQQ 6QQQQ2QQQQQQQQQ 7QQQQ2AQQQQQQQQ 8QQQ2G2G2GQQQQQQQ
t = 7
12345678910111213 11G2G2G2G2G2G2G2G2G2G2GQQQ 21GQQQ2EQQQQQQQQ 31G1E1K1B1Q2K1C1Q1Q1C1C1K1BQ 41GQQQ2OQQQQQQQQ 51GQQQ2QQQQQQQQQ 61GQQQ2AQQQQQQQQ 7QQQQ2DQQQQQQQQ 8QQ2G2G2G2G2GQQQQQQ
t = 8
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2GQQ 21GQQQ2EQQQQQQQQ 31G1E1K1C1O2K1Q1Q1C1C1Q1K1C1G 41GQQQ2OQQQQQQQQ 51GQQQ2AQQQQQQQQ 61GQQQ2KQQQQQQQQ 71GQQQ2EQQQQQQQQ 8Q2G2G2G2G2G2G2GQQQQQ
t = 9
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2GQ 21GQQQ2EQQQQQQQ1G 31G1E1E1C1O2K1Q1C1C1Q1Q1C1B1G 41GQQQ2WQQQQQQQ1G 51GQQQ2MQQQQQQQQ 61GQQQ2KQQQQQQQQ 71GQQQ2EQQQQQQQQ 81G2G2G2G2G2G2G2G2G2GQQQQ
t = 10
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2G1G2G 21GQQQ2EQQQQQQQ1G 31G1E1E1C1O2A1O1C1Q1Q1C1B1D1G 41GQQ2W2W2WQQQQQQ1G 51GQQ2M2M2MQQQQQQ1G 61GQQQ2AQQQQQQQQ 71GQQQ2EQQQQQQQQ 81G2G2G2G2G2G2G2G2G2G2GQQQ
t = 11
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2G1G2G 21GQQQ2IQQQQQQQ1G 31G1E1E1C1K2U1O1Q1Q1C1B1K1E1G 41GQ2W2W2W2W2WQQQQQ1G 51GQ2M2M2M2M2MQQQQQ1G 61GQQQ2UQQQQQQQ1G 71GQQQ2IQQQQQQQQ 81G2G2G2G2G2G2G2G2G2G2G2GQQ
t = 12
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2G1G2G 21GQQ2I2I2IQQQQQQ1G 31G1E1E1Q2U1K2U1O2U1Q1C1B1D1K1E1G 41G2W2W2W2W2W2W2WQQQQ1G 51G2M2M2M2M2M2M2MQQQQ1G 61GQQ2U2U2UQQQQQQ1G 71GQQ2I2I2IQQQQQQ1G 81G2G2G2G2G2G2G2G2G2G2G2G2GQ
t = 13
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2G1G2G 21GQ2I2I2I2I2IQQQQQ1G 31G1E1E2U1Q2U1K2U1O2U1O2U1B1K1D1E1E1G 41G2W2W2W2W2W2W2W2W2WQQQ1G 51G2M2M2M2M2M2M2M2M2MQQQ1G 61GQ2U2U2U2U2UQQQQQ1G 71GQ2I2I2I2I2IQQQQQ1G 81G2G2G2G2G2G2G2G2G2G2G2G2G1G2G
t = 14
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2G1G2G 21G2I2I2I2I2I2I2IQQQQ1G 31G1E2U1E2U1Q2U1K2U1C2U1N2U1D2U1K1Q1E1E1G 41G2W2W2W2W2W2W2W2W2W2WQQ1G 51G2M2M2M2M2M2M2M2M2M2MQQ1G 61G2U2U2U2U2U2U2UQQQQ1G 71G2I2I2I2I2I2I2IQQQQ1G 81G2G2G2G2G2G2G2G2G2G2G2G2G1G2G
t = 15
12345678910111213 11G2G2G2G2G2G2G2G2G2G2G2G2G1G2G 21G2I2I2I2I2I2I1N2I2I2IQQQ1G 31G2U1E2U1E2U1Q2U1C2U1B2U1N2U1B2U1D2U1Q1E1E1G 41G2W2W2W2W2W2W1N2W2W2W2W2WQ1G 51G2M2M2M2M2M2M2M2M2M2M2MQ1G 61G2U2U2U2U2U2U2U2U2UQQQ1G 71G2I2I2I2I2I2I2I2I2IQQQ1G 81G2G2G2G2G2G2G2G2G2G2G2G2G1G2G
t = 16
12345678910111213 11G2G2G2G2G2G2G1N2G2G2G2G2G2G1G2G 21G2I2I2I2I2I2I1N2I2I2I2IQQ1G 31G2U1E2U1E2U1E2U1B2U1C2U1N2U1D2U1B2U1E2U1E1E1G 41G2W2W2W2W2W2WM-2W2W2W2W2W1G 51G2M2M2M2M2M2MM-2M2M2M2M2M1G 61G2U2U2U2U2U2U2U2U2U2UQQ1G 71G2I2I2I2I2I2I2I2I2I2IQQ1G 81G2G2G2G2G2G2G2G2G2G2G2G2G1G2G
t = 17
12345678910111213 11G2G2G2G2G2G2G1N2G2G2G2G2G2G1G2G 21G2I2I2I2I2I2I1N2I2I2I2I2IQ1G 31G2U1E2U1K2U1I2U1C2U2UMM-2U1D2U1I2U1K2U1E1G 41G2W2W2W2W2W2WM-2W2W2W2W2W1G2W 51G2M2M2M2M2M2MM-2M2M2M2M2M1G2M 61G2U2U2U2U2U2UMM-2U2U2U2UQ1G 71G2I2I2I2I2I2I2I2I2I2I2IQ1G 81G2G2G2G2G2G2G2G2G2G2G2G2G1G2G
t = 18
12345678910111213 11G2G2G2G2G2G2G1N2G2G2G2G2G2G1G2G 21G2I2I2I1I2I2I2IM-2I2I1I2I2I2I1G 31G2U1E2U1A2U1I2U2U2UM-2U2U1I2U1A2U1E2U1G 41G2W2W2W1I2W2W2WM-2W2W1I2W2W2W1G2W 51G2M2M2M2M2M2MM-2M2M2M2M2M1G2M 61G2U2U2U2U2U2UM-2U2U2U2U2U1G 71G2I2I2I2I2I2IM-2I2I2I2I2I1G 81G2G2G2G2G2G2G2G2G2G2G2G2G1G2G
t = 19
12345678910111213 11G2G2G2G1I2G2G2GM+2G2G1I2G2G2G1G2G 21G2I2I2I1I2I2I2IM+2I2I1I2I2I2I1G2I 31G2U1I2U1U2U1I2U2U2UM+2U2U1I2U1U2U1I2U1G2U 41G2W2W2W1I2W2W2WM+2W2W1I2W2W2W1G2W 51G2M2M2M1I2M2M2MM+2M2M1I2M2M2M1G2M 61G2U2U2U2U2U2UM+2U2U2U2U2U1G2U 71G2I2I2I2I2I2IM+2I2I2I2I2I1G2I 81G2G2G2G2G2G2GM+2G2G2G2G2G1G2G
t = 20
12345678910111213 11G2G2G2G1I2G2GQ+M+C+2G1I2G2G2G1G2G 21G2I1I2I1U2I1I2I2IQ+M+C+2I1I2I1U2I1I2I1G2I 31G2U1I2U1U2U1I2U2UQ+M+C+2U1I2U1U2U1I2U1G2U 41G2W 1I2W 1U2W 1I2W2WQ+M+C+2W1I2W 1U2W 1I2W 1G2W 51G2M2M2M1I2M2MQ+M+C+2M1I2M2M2M1G2M 61G2U2U2U1I2U2UQ+M+C+2U1I2U2U2U1G2U 71G2I2I2I2I2IQ+M+C+2I2I2I2I1G2I 81G2G2G2G2G2GQ+M+C+2G2G2G2G1G2G
t = 21
12345678910111213 11G2G1I2G1U2G1I2GQ+Q+M+C+C+1I2G1U2G1I2G1G2G 21G2I1I2I1U2I1I2IQ+Q+M+C+C+1I2I1U2I1I2I1G2I 31G2U1I2U1U2U1I2UQ+Q+M+C+C+1I2U1U2U1I2U1G2U 41G2W 1I2W 1U2W 1I2WQ+Q+M+C+C+1I2W 1U2W 1I2W 1G2W 51G2M1I2M1U2M1I2MQ+Q+M+C+C+1I2M1U2M1I2M1G2M 61G2U2U2U1I2UQ+Q+M+C+C+1I2U2U2U1G2U 71G2I2I2I1I2IQ+Q+M+C+C+1I2I2I2I1G2I 81G2G2G2G2GQ+Q+M+C+C+2G2G2G1G2G
t = 22
12345678910111213 11G2G1I2G1U2GM+L-Q+M+C+R-M+1U2G1I2G1G2G 21G2I1I2I1U2IM+L-Q+M+C+R-M+1U2I1I2I1G2I 31G2U1I2U1U2UM+L-Q+M+C+R-M+1U2U1I2U1G2U 41G2W 1I2W 1U2WM+L-Q+M+C+R-M+1U2W 1I2W 1G2W 51G2M1I2M1U2MM+L-Q+M+C+R-M+1U2M1I2M1G2M 61G2U1I2U1U2UM+L-Q+M+C+R-M+1U2U1I2U1G2U 71G2I2I2IM+L-Q+M+C+R-M+2I2I1G2I 81G2G2G2GM+L-Q+M+C+R-M+2G2G1G2G
t = 23
12345678910111213 11G2G1I2GMM+M+C+Q+M+C+Q+M+MM+1I2G1G2G 21G2I1I2IMM+M+C+Q+M+C+Q+M+MM+1I2I1G2I 31G2U1I2UMM+M+C+Q+M+C+Q+M+MM+1I2U1G2U 41G2W 1I2WMM+M+C+Q+M+C+Q+M+MM+1I2W 1G2W 51G2M1I2MMM+M+C+Q+M+C+Q+M+MM+1I2M1G2M 61G2U1I2UMM+M+C+Q+M+C+Q+M+MM+1I2U1G2U 71G2I1I2IMM+M+C+Q+M+C+Q+M+MM+1I2I1G2I 81G2G2GQ+M+C+Q+M+C+Q+M+C+2G1G2G
t = 24
12345678910111213 11G2GM+M+M+M+M+M+M+M+M+M+M+1G2G 21G2IM+M+M+M+M+M+M+M+M+M+M+1G2I 31G2UM+M+M+M+M+M+M+M+M+M+M+1G2U 41G2WM+M+M+M+M+M+M+M+M+M+M+1G2W 51G2MM+M+M+M+M+M+M+M+M+M+M+1G2M 61G2UM+M+M+M+M+M+M+M+M+M+M+1G2U 71G2IM+M+M+M+M+M+M+M+M+M+M+1G2I 81G2GM+M+M+M+M+M+M+M+M+M+M+1G2G
t = 25
12345678910111213 1FFFFFFFFFFFFF 2FFFFFFFFFFFFF 3FFFFFFFFFFFFF 4FFFFFFFFFFFFF 5FFFFFFFFFFFFF 6FFFFFFFFFFFFF 7FFFFFFFFFFFFF 8FFFFFFFFFFFFF
Figure 11: Snapshots of the generalized synchronization algorithmA4on an 8×13 array with a general
on C3,5.
Theorem 17There exists no cellular automaton that can synchronize anykD array of sizen1×n2×...×
nkwith a general at Cr1,r2,...,rkin less than∑
k
i=1ni+max(n1,n2, ...,nk)−∑ki=1min(ri,ni−ri+1)−1 steps.
Theorem 18There exists an optimum-time synchronization algorithmA6that can synchronize anykD
array of size n1×n2×...×nk with a general at Cr1,r2,...,rk in optimum ∑
k
i=1ni+max(n1,n2, ...,nk)−
∑ki=1min(ri,ni−ri+1)−1 steps.
7
Conclusions
We have proposed a new class of optimum-time multi-dimensional FSSP algorithms based on recursive-halving marking. The class includes the well-known optimum-time FSSP algorithms developed by Waksman [1964], Balzer [1966] and Gerken [1987] with a general at one end and Moore and Lang-don [1968] with a general at any position.
AcknowledgmentsThe authors would like to thank reviewers for helpful comments.
Bibliography
[1] R. Balzer: An 8-state minimal time solution to the firing squad synchronization problem.Information and
Control, vol. 10 (1967), pp. 22-42, doi:10.1016/S0019-9958(67)90032-0.
[2] W. T. Beyer: Recognition of topological invariants by iterative arrays. Ph.D. Thesis, MIT, (1969), pp. 144.
[3] H. D. Gerken. (1987): ¨Uber Synchronisationsprobleme bei Zellularautomaten.Diplomarbeit, Institut f¨ur
The-oretische Informatik, Technische Universit¨at Braunschweig, pp. 50.
[4] E. Goto: A minimal time solution of the firing squad problem. Dittoed course notes for Applied Mathematics 298, Harvard University, (1962), pp. 52-59.
[5] A. Grasselli: Synchronization of cellular arrays: The firing squad problem in two dimensions.Information