Pablo Abreu de Morais
Correlações e interações de longo alcance em meios
desordenados: linhas costeiras e transição de
Anderson
Pablo Abreu de Morais
Correlações e interações de longo alcance em meios
desordenados: linhas costeiras e transição de
Anderson
Tese apresentada ao Curso de Pós-Graduação em Física da Universidade Federal do Ceará como parte dos requisitos para a obtenção do título de Doutor em Física.
Prof. José Soares de Andrade Júnior.
DOUTORADO EM FÍSICA DEPARTAMENTO DE FÍSICA
CENTRO DECIÊNCIAS
UNIVERSIDADEFEDERAL DOCEARÁ
Dedicatória
Agradecimentos
Quero agradecer a todos que contribuíram de forma direta ou indireta para a realização desta tese. Em especial:
– Ao Prof. José Soares de Andrade Júnior pela oportunidade e orientação;
– Ao Prof. Hans Jürgen Herrmann pelos ensinamentos e pelo convite para visitar o seu grupo de pesquisa no ETH;
– Ao Prof. Marcelo Lyra pelo convite para conhecer o departamento de Física da UFAL;
– Ao meu avô João Costa por ser o meu referencial de honestidade, humildade e bom caráter;
– Aos meus pais por sempre acreditarem em mim;
– Aos meus irmãos, Max e Argus, pelo companheirismo e incentivo nos momentos mais adversos;
– À Pamela pelo carinho e apoio incondicionais;
– Aos meus amigos por todos os bons momentos proporcionados durante o doutorado;
– Ao Vladimir e todos os funcionários da livraria Arte e Ciência pela amizade e atenção a mim dispensadas;
– Ao Batista e sua família pela amizade;
– Ao Departamento de Física da UFC e seus funcionários;
Resumo
Muitos fenômenos físicos têm forte dependência da desordem do meio no qual ocorrem. A teoria de localização de Anderson, por exemplo, estabelece que a introdução de desordem em
sistemas eletrônicos pode promover a transição metal-isolante, também conhecida como tran-sição de Anderson. Contudo, para sistemas de baixa dimensionalidade, segundo essa mesma
teoria, qualquer grau finito de desordem não correlacionada pode promover a localização ex-ponencial de todas as funções eletrônicas. A teoria geral de localização deAndersoné violada
quando correlações e interações de longo alcance são utilizadas. Nesse cenário, a transição metal-isolante ocorre também para sistemas de baixa dimensionalidade. Nos problemas relaci-onados com redes, as ligações de longo alcance são responsáveis pela pequena distância média entre indivíduos pertencentes à mesma rede social. Esse fenômeno é popularmente conhecido como os seis graus de separação. Além disso, Kleinberg [13] mostrou que a introdução de
uma distribuição em lei de potência de ligações de longo alcance em uma “rede substrato” gera um mínimo no tempo de envio de uma informação de um sítio fonte a um sítio alvo da rede. Nesta tese, investigamos como a desordem de longo alcance altera a classe de universalidade de dois modelos matemáticos que representam os seguintes problemas físicos: o processo de ero-são na costa de paisagens correlacionadas e a transição deslocalização-localização dos modos normais de vibração de uma cadeia harmônica com ligações de longo alcance restritas por uma função custo. No primeiro modelo, mostramos que correlações espaciais de longo alcance nas propriedades geológicas da costa, no regime crítico do nosso modelo, gera um espectro de li-nhas costeiras fractais cujas dimensões fractais variam entreD=1.33 e 1.00 quando variamos o
expoente deHurstno intervalo 0<H<1. Além disso, quando utilizamos superfícies não corre-lacionadas, as linha costeiras, para erosões marítimas muito intensas, são auto-afins e pertencem à mesma classe de universalidade das interfaces descritas pela equação deKardar-Parisi-Zhang
(KPZ). No segundo modelo, mostramos que ligações de longo alcance inseridas em uma cadeia
harmônica com uma probabilidade decaindo com o tamanho da ligação, p∼r−α, restritas por
Abstract
Many physical phenomena have strong dependence on the disorder of the medium in which they occur. TheAndersontheory localization, for example, states that the introduction of
disor-der in electronic systems can promote the metal-insulator transition, also known as Anderson
transition. However, for low dimensional systems, according to the same theory, any finite de-gree of uncorrelated disorder is able to promote the exponential localization of all electronic functions. The general Andersontheory localization is violated when long-range correlations
and long-range interactions are used. In this scenario, the metal-insulator transition also occurs for low dimensional systems. In network problems, the long-range connections are responsible for the short average distance between individuals belonging to the same social network. This phenomenon is popularly known as six degrees of separation. Furthermore,Kleinbergshowed
that the introduction of a power-law distribution of long-range links in a network produces a minimum in the transmission time information from a source site to a target site network . In this thesis, we investigate how the long-range disorder changes the universality class of two mathematical models that represent the following physical problems: the erosion process in correlated landscapes and the delocalization-localization transition of the normal modes of a harmonic chain with long range connections restricted by a cost function. In the first model, we show that long-range spatial correlations in the geological properties of the coast, in the criti-cal regime of our model, generates a spectrum of fractals shorelines whose fractal dimensions vary between D = 1.33 and 1.00 when we vary the Hurst exponent in the range 0<H <1.
Furthermore, when we use uncorrelated surfaces, the shoreline, for very intense sea erosion, are self-affine and belong to the same universality class of the interfaces described by the equation ofKardar-Parisi-Zhang(KPZ). In the second model, we show that long-range links in a chain
harmonic inserted with a probability with decreasing size of the bond, p∼r−α, restricted by a
Sumário
Lista de Figuras
Lista de Tabelas
1 Introdução p. 20
2 Conceitos de fractais e teoria da percolação p. 22
2.1 Introdução aos fractais . . . p. 22
2.2 Definição e propriedades dos fractais . . . p. 22
2.2.1 Auto-similaridade . . . p. 23
2.2.2 Dimensão Fractal . . . p. 24
2.2.3 Método Box-counting . . . p. 27
2.2.4 Método Yardstick . . . p. 28
2.2.5 Auto-afinidade . . . p. 29
2.3 Fractalidade em séries temporais . . . p. 33
2.3.1 Rescaled range analysis . . . p. 34
2.4 Leis de escala em processos dinâmicos . . . p. 35
2.4.1 Equação de Kardar-Parisi-Zhang . . . p. 37
2.5 Introdução à percolação . . . p. 37
2.5.1 Percolação de sítios . . . p. 38
2.5.2 Percolação por ligação . . . p. 39
2.5.3 Expoentes críticos e leis de escala . . . p. 42
2.5.5 Percolação invasiva . . . p. 48
2.5.6 Modelo . . . p. 49
3 Conceitos e propriedades de redes p. 51
3.1 Introdução . . . p. 51
3.1.1 As pontes de Königsberg . . . p. 52
3.2 Formalismo matemático . . . p. 53
3.3 Propriedades das redes . . . p. 54
3.3.1 Distribuição de conectividade . . . p. 55
3.3.2 Diâmetro e Caminho mínimo ou geodésico . . . p. 55
3.3.3 Coeficiente de aglomeração . . . p. 56
3.3.4 Correlação grau-grau . . . p. 58
3.3.5 Matriz adjacência . . . p. 58
3.3.6 Matriz Laplaciana . . . p. 60
3.4 O modelo de Erdös-Rényi . . . p. 62
3.5 Rede de mundo-pequeno . . . p. 64
3.5.1 Modelo de Watts e Strogatz . . . p. 65
3.6 Redes livres de escala . . . p. 67
3.6.1 Modelo de Barabàsi-Albert . . . p. 68
4 Fractalidade de linhas costeiras de paisagens correlacionadas p. 70
4.1 Introdução . . . p. 70
4.2 O modelo . . . p. 71
4.3 Litologia não correlacionada . . . p. 72
4.3.1 Dimensão fractal . . . p. 74
4.3.2 Equação Kardar-Parisi-Zhang . . . p. 75
4.5 Conclusões . . . p. 79
5 Transições geométrica e de Anderson em cadeias harmônicas com restrição
no acoplamento de longo alcance p. 81
5.1 Introdução . . . p. 81
5.2 Modelo e Formalismo . . . p. 84
5.3 Transição de Fase Geométrica . . . p. 87
5.4 Transição de Anderson . . . p. 89
5.5 Conclusões . . . p. 93
6 Conclusões e perspectivas p. 95
Lista de Figuras
2.1 Construção do conjunto de Cantor. (a) Começamos com uma reta represen-tando intervalo [0,1]. (b) Dividimos o segmento de rede mostrado em (a) em três partes iguais e descartamos a parte central. (c) Dividimos cada um dos dois segmentos de reta mostrados em (b) em três partes iguais e novamente descartamos as partes intermediárias. (d) Repetimos o mesmo processo apli-cado em (a) e (b). Para cada iteração associamos um número nchamado de
geração. No limiten→∞obtemos o conjunto deCantor. . . p. 24
2.2 Imagem de satélite disponibilizada pela NASA do litoral de Angra dos Reis. Podemos observar que a linha costeira apresenta irregularidades em suas for-mas, mostrando uma complexidade geométrica característica de estruturas
fractais. . . p. 25
2.3 Construção da triângulo deSierpinski. (a) Geramos um triângulo.
Normal-mente utiliza-se um triângulo equilátero. (b) Reduzimos os lados do triângulo pela metade. Após isso, geramos três cópias desse triângulo reduzido e as po-sicionamos de modo que cada uma delas toque as outras duas em um vértice. (c) e (d) Repetimos o procedimento descrito em (b) em cada nova iteraçãon.
No limite de muitas iterações obtemos o triângulo deSierpinski. . . p. 27
2.4 Ilustração do métodobox-countingaplicado à folha de samambaia.
Coloca-mos a folha de samambaia em uma grade formada por quadrados de ladoδ. Em seguida, devemos contar quantos quadrados N(δ)são necessários para cobrir toda a folha. Esse procedimento deve ser feito para grades regulares cada vez mais refinadas até o limite numéricoδ→0. O módulo da inclinação do gráfico N(�)contra 1/� na escala log-log fornece a dimensão fractalDf
2.5 Ilustração do método yardstickaplicado à linha costeira de Angra dos Reis.
Cobrimos o perímetro da linha costeira utilizando segmentos de reta de ta-manho�. Após isso, devemos contar o número de segmentos de retaN(�) ne-cessários para cobrir o perímetro da linha costeira. Esse procedimento deve ser feito utilizando segmentos de reta cada vez menores até o limite numérico
�→0. O módulo da inclinação do gráficoN(�)contra 1/�na escalalog-log
fornece a dimensão fractalDf da linha costeira de Angra dos Reis. . . p. 29
2.6 O efeito de transformações isotrópicaTie anisotrópicaTa em um círculo. A transformação isotrópica Ti reescala o diâmetro do círculo por um fator 2, enquanto a transformação anisotrópicaTareescala os “diâmetros” horizontal e vertical do círculo por um fator 4 e 2, respectivamente. Figura extraída da
Ref. [1]. . . p. 30
2.7 Construção de um fractal auto-afim determinístico. (a) a diagonal de um re-tângulo é dividida em quatro partes cujas componentes horizontais são iguais; (b) a reta mostrada em (a) é trocada pela estrutura mostrada em (b); (c) repe-timos o procedimento adotado em (b) para os quatro segmentos de reta. Se nós reescalonarmos isotropicamente a parte mostrada na caixa pontilhada em
(c), obteremos o objeto mostrado na caixa à direita que é diferente de (b). . . p. 31
2.8 Ilustração esquemática do reservatório ideal deHurst. Figura extraída da Ref.
[1]. . . p. 35
2.9 Ilustração da vizinhança de Von Neumann: (a) os sítios pintados de cinza
representam os primeiros vizinhos, enquanto em (b), os sítios pintados de cinza representam o conjunto formado pelos primeiros e segundos vizinhos
deVon Neumanndo sítio pintado central da rede pintado de vermelho. . . p. 38
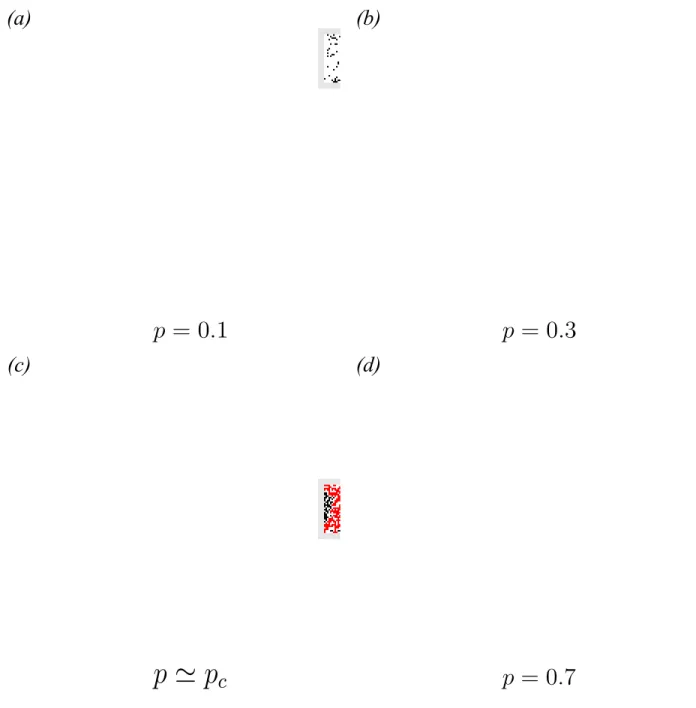
2.10 Configurações típicas do modelo de percolação por sítio para uma rede qua-drada de lado L= 128 e diferentes valores de probabilidade de ocupação
p. Para p< pc, o sistema apresenta pequenos agregados isolados, enquanto que para p=0.5927� pc, é formado um agregado percolante conectando as
bordas do sistema. Para p> pc, esse agregado ocupa quase toda a rede. O
2.11 Configurações típicas do modelo de percolação por ligação para uma rede quadrada de ladoL=128 e diferentes valores de probabilidade de ocupação
p. Para p< pc, o sistema apresenta pequenos agregados isolados, enquanto que para p= pc =0.5, é formado um agregado percolante conectando as bordas do sistema. Para p> pc, esse agregado ocupa quase toda a rede. O
agregado percolante está em vermelho e os agregados isolados estão em preto. p. 41
2.12 Gráfico da fração de elementos pertencentes ao agregado percolante P em
função da probabilidade de ocupação p para (a) percolação por sítio e (b)
percolação por ligação. As curvas são médias obtidas sobre 1000 amostras para redes quadradas de lado L=128 e L=1024. As linhas tracejadas in-dicam os limiares de percolação pc�0.5927 e pc=0.5 para percolação por
sítio e ligação, respectivamente. . . p. 43
2.13 Gráfico da massaMdo agregado percolante no ponto crítico pccomo função do tamanho L do sistema. Cada ponto da curva foi obtido a partir de uma
média sobre 1000 realizações independentes. O valor obtido da dimensão fractal do agreado percolante foiD=1.89. Este resultado é compatível com
os resultados da literatura [2, 3] . . . p. 45
2.14 Gráfico da distribuição acumulada Ns como função do tamanho sdos agre-gados no ponto crítico. Utilizamos uma rede quadrada de ladoL=8192. Os resultados são médias obtidas sobre 100 amostras. A partir da inclinação da curva, obtivemos 1−τ=−1.05. Logo, o expoente deFisheréτ=2.05. Este
resultado é compatível com o resultado da literatura [3]. . . p. 46
2.15 Modelo de percolação de sítios para uma rede quadrada de ladoL=1024 na probabilidade crítica pc de ocupação. O agregado percolante, mostrado em vermelho, apresenta uma estrutura fractal e conecta as bordas do sistema. Os demais agregados, cuja distribuição de tamanho é controlada pelo expoente
deFisher, são mostrados em outras cores. . . p. 47
3.1 A Representação do problema das pontes deKönigsberge o seu grafo
3.2 Ilustração de dois grafos: (a) grafo simples comN=5 sítios en=4 ligações. O conjunto de vérticesV={1, 2, 3, 4, 5} e o conjunto de ligaçõesL={(1,3),
(1,5), (2,5) e (3,5)} definem a topologia da rede; (b) grafo contendo tanto
auto-ligação como multi-ligação. Os conjuntos de vértices e ligações são dados por V={ 1, 2, 3, 4, 5} e L={(1,2), (2,2), (2,3), (2,4), (4,5), (4,5) e
(4,5)}, respectivamente. . . p. 54
3.3 Representação do caminho mínimo entre dois vértices. O caminho mínimo
entre os vérticesv1ev7está marcado de vermelho. . . p. 56
3.4 Ilustração do conceito de triângulo em redes. Se a linha pontilhada se tornar uma ligação, o caminho fechado formado pelos vérticesv1,v2ev3é chamado de triângulo. Caso a ligação(v2,v3)não exista, chamamos essa estrutura de
trio conectado. . . p. 56
3.5 Exemplo do coeficiente de aglomeração de um sítio. O coeficiente de aglo-meração local do sítio azul é dado pela razão entre número de ligações efe-tivas e o número de ligações possíveis entre os seus vizinhos. As ligações efetivas são representadas pelas linhas sólidas pretas, enquanto as ligações possíveis, mas não existentes, são representadas pelas linhas vermelhas pon-tilhadas. Mostramos três configurações: (a) todos os vizinhos do sítio azul são conectados entre si, caracterizando c=1; (b) Apenas um dos vizinhos do sítio azul tem vizinho em comum, formando um triângulo dentre os três possíveis, configurando c=1/3; (c) O grafo não apresenta a formação de
nenhum triângulo e, consequentemente, tem coeficiente de aglomeraçãoc=0. p. 57
3.6 Resultado obtido porStanley Milgramno seu famoso experimento sobre
con-tatos sociais [4]. Foram necessárias, em média, 5.5 pessoas intermediárias
para que a carta alcançasse o alvo. Gráfico extraído da Ref. [5]. . . p. 64
3.7 (a) Rede regular ordenada em forma de uma estrutura k-ringcom k=2. (b)
Redemundo-pequenoconstruída a partir do substrato mostrado em (a)
utili-zando uma probabilidade p=0.1 de redirecionar suas ligações. Esse
proce-dimento é o considerado no modelo original deWatts e Strogatz. . . p. 65
3.8 (a) Rede de mundo-pequeno construída inserindo ligações aleatórias com
probabilidade p=0.1 à uma rede regular quadrada. (b) A estrutura dos k=3
3.9 Estrutura regular k-ring com k=2 se transformando em uma rede aleatória
através do incremento da probabilidade pde redirecionar ligações. Entre os
comportamentos extremos, regular (p=0) e aleatório (p=1), a rede passa por um estágio intermediário, chamado de mundo-pequeno, cujas principais características são: o alto coeficiente de aglomeração e a pequena distância
mínima média. . . p. 67
4.1 Configurações típicas obtidas com o modelo de erosão para litologias não correlacionadas em uma rede regular quadrada com 5122 sítios. Os sítios azuis (sítios mar) representam o mar, enquanto os demais sítios representam os sítios da costa (sítios terra). Três regimes diferentes são obtidos: (a) sub-crítico: acontece para processos erosivos fracos (f < fc) e a linha costeira é
rugosa, mas não fractal; (b) crítico: Acontece para f = fce a linha costeira é fractal auto-similar; (c) supercrítico: Acontece para erosões fortes f > fce a
linha costeira não é mais auto-similar, mas auto-afim. . . p. 71
4.2 Dependência da probabilidadePs com o fator de erosão do mar, f, para pai-sagens geradas com uma distribuição uniforme do parâmetro de litologia,l.
Uma transição é observada de um regime subcrítico, f < fc, para uma
inva-são perpétua, regime supercrítico, f > fc. A transição ocorre para fc= 0.523 ±0.001, estimada a partir do cruzamento das curvas. Cada curva corresponde
a diferentes tamanhos de sistema,L2, comL={128, 256, 512 e 1024},
calcu-ladas sobre {800, 400, 200 e 100} amostras, respectivamente. . . p. 73
4.3 Dependência da massa da linha costeira (número de sítios) com o tamanho do sistema no regime crítico, f = fc. A dimensão fractalD=1.34±0.01 foi
obtida a partir do melhor ajuste do conjunto de dados. Foram consideradas redes quadradas de dimensãoL2, comL={32, 64, 128, 256, 512, 1024},
uti-lizando uma distribuição uniforme do parâmetro de litologia. Os resultados são médias sobre {3200, 1600, 800, 400, 200, 100} realizações
independen-tes. O gráfico menor mostra o número de bastões necessários para cobrir a linha costeira como função do inverso do tamanho dos bastões. Os resultados foram obtidos para uma rede de dimensãoL=1024 e 102amostras. A
dimen-são fractalD=1.33±0.01 foi obtida a partir do melhor ajuste do conjunto
de dados. Os resultados obtidos pelos dois métodos são equivalentes dentro
4.4 Escalonamento de tamanho finito da dependência temporal da rugosidade da linha costeira no regime supercrítico (f =0.9). Redes quadradas de dimen-sõesLx ×Ly, com Lx=L eLy=128L, foram utilizadas. O tempot foi re-escalonado em unidades deLz, ondezé o expoente dinâmico. A rugosidade
foi reescalonada em unidades deLα, ondeα é o expoente de rugosidade. O melhor colapso das curvas foi obtido para os expoentes α =0.48±0.04 e
z=1.55±0.11, que são valores consistentes com a classe de universalidade Kardar-Parisi-Zhang (KPZ)[6]. O expoente de crescimento,β, é dado pela inclinação da linha reta, como mostrado na figura. O gráfico menor mostra a dependência temporal da rugosidade da linha costeira, onde podemos ob-servar um tempo de transição,t=tx. Os resultados são médias obtidas para
L={32, 64, 128, 256} sobre {3200, 1600, 800, 400} realizações
independen-tes, respectivamente. . . p. 75
4.5 Dependência do expoente de crescimento, β, com o tamanho do sistema. Esses resultados indicam que, no limite termodinâmico, β converge para o valor 1/3 como na classe de universalidadeKardar-Parisi-Zhang (KPZ). Os
resultados obtidos são médias para tamanhos de sistemaL={32, 64, 128, 256,
512} sobre {3200, 1600, 800, 400} realizações independentes, respectivamente. p. 76
4.6 Configurações da distribuição inicial do parâmetro de litologia (a, b e c) e as respectivas configurações após a dinâmica de erosão (d, e e f) para o fator de erosão crítico, (f = fc), para três diferentes paisagens geradas com correla-ções espaciais de longo alcance, e valores diferentes do expoente de Hurst:
(a) e (d) H=0.0; (b) e (e) H=0.2; (c) e (f) H=0.8. O esquema de cores dos sítios da costa representa o valor do parâmetro de litologia,l, e aos sítios mar
foram atribuídos o valor l =0. As configurações foram obtidas para redes
quadradas com 5122sítios. . . p. 78
4.7 Dimensão fractalD da linha costeira como função do expoente deHurst H.
A dimensão fractal decresce de D=1.34, para H =0, até D=1.04, para
H =1.0. A linha pontilhada indica a dimensão fractal da linha costeira para o caso da litologia não correlacionada (D=1.33). Cada ponto foi obtido a partir do gráfico do número de sítios ou massa da linha costeira como função do tamanho do sistemaL. Os resultados obtidos são médias para os tamanhos
L={32, 64, 128, 256, 512, 1024} sobre {3200, 1600, 800, 400, 200, 100}
5.1 (a) Conexões de um sítio i na rede deKleinberg. Cada sítio ida rede é
co-nectado com os seus quatro primeiros vizinhos, pintados de vermelho, além de possuir uma ligação de longo alcance com outro sítio, pintado de preto, escolhido aleatoriamente com probabilidader−α, onderé a distância de
Ma-nhatanentre os dois sítios. (b) Gráfico do tempotemédio de entrega de uma informação entre um sítio alvoaescolhido aleatoriamente e um sítio fonteb
como função do expoente α da distribuição de probabilidade das conexões
de longo alcance. Esse gráfico foi extraído da referência [7]. . . p. 82
5.2 Caminho mínimo médio ��� como função do expoenteα da distribuição de probabilidade das conexões de longo alcance. Foi considerada a restrição do comprimento total de ligações de longo alcance∑ri j=N, ondeNé o número total de sítios da rede regular quadrada utilizada. Podemos observar um cami-nho mínimo médio ótimo paraα =3. As curvas são valores médios obtidos para os tamanhos de rede N={5122,10242,20482} sobre {10000,3500,25}
realizações, respectivamente. Esse gráfico foi extraído da referência [8]. . . . p. 84
5.3 Número de molas conectando sítios que não são primeiros vizinhos versus o expoente α da distribuição em lei de potência das ligações adicionais, para diferentes tamanhos de rede e parâmetro de custo λ =1. Pode-se verificar uma transição de uma fase caracterizada por um número finito de molas, para baixos valores de α, para uma fase apresentando diversas ligações adicio-nais conectando sítios que não são primeiros vizinhos entre si, para valores
elevados deα. . . p. 87
5.4 Representação das funções auxiliares g(N,N�,α) versus α obtidas a partir dos dados mostrados na Figura 5.3. A cadeia de tamanho N� =8192 foi utilizada para gerar todas as curvas. O cruzamento das curvas em um único ponto, localizado na transição topológicaα∗=3/2, separa a fase geométrica caracterizada por um número finito de molas adicionais do regime onde o
5.5 O espectro do número de participação dentro do limite da frequência de banda para uma cadeia com N=8192, parâmetro de custoλ =5, e valores distintos do expoente α da distribuição de lei de potência das ligações de longo al-cance. Podemos observar que o número inicial da participação decresce com o aumento do expoente α, mas voltar a crescer com α no regime de valo-res elevados deα. No topo da banda, os modos vibracionais são fortemente
localizados em torno dos defeitos. . . p. 90
5.6 Número de participação média dos modos vibracionais contra o expoente da lei de potência α para o parâmetro de custo λ =5 e diferentes tamanhos de cadeia. Os dados sugerem uma transição de Anderson dos modos deslo-calizados para valores pequenos de α para modos localizados para valores grandes deα. O crescimento dePpara valores muito grandes deα sinaliza
o último decrescimento do grau de desordem no limite deα→∞. . . p. 92
5.7 O conjunto de funções auxiliaresh(N,N�,α)obtidas a partir dos dados repor-tados na Fig. 5.6 contra o expoente da lei de potênciaα. Em todas as curvas N’=8192. O ponto comum de cruzamento entre as curvas localiza a transição de Anderson em αc�1.25 e o expoente de escalonamento da função par-ticipação φ �0.7. O mínimo de h indica a situação de máxima desordem
Lista de Tabelas
2.1 Tabela mostrando o limiar de percolação pcpara diferentes redes regulares [3]. p. 42
2.2 Tabela mostrando as dimensões fractais associadas às estruturas associadas
20
1
Introdução
Muitos fenômenos físicos têm forte dependência da desordem dos meios nos quais ocor-rem. Processos difusivos de gases em meios reais, por exemplo, podem ser simulados a partir de modelos de percolação que incorporam a desordem do meio utilizando uma distribuição aleató-ria da concentração de poros [10]. Já naFísica do Estado Sólido, as propriedades de transporte
eletrônico dos sólidos variam de acordo com as suas propriedades estruturais e composicionais. A teoria de localização deAndersonestabelece que uma quantidade finita de desordem é capaz
de promover uma transição metal-isolante, fazendo com que um sólido passe de um regime de transporte efetivo de partículas até um regime no qual as funções de ondas eletrônicas são localizadas, confinando os elétrons em regiões espaciais limitadas [11]. Contudo, a teoria de
Andersonafirma que para sistemas de baixa dimensionalidade, dimensão topológicad = 1 e 2,
qualquer quantidade finita de desordem no meio localiza as funções de onda eletrônica, impos-sibilitando a transição metal-isolante. No entanto, foi mostrado que essa transição pode ocorrer se correlações [12, 13, 14, 15, 16] e acoplamentos de longo-alcance [17, 18, 19, 20, 21] forem consideradas. A presença de desordem em sólidos também está relacionada com o limiar de tensão que esses objetos resistem sem sofrer fraturas.
Em redes sociais, as ligações de longo alcance reduzem substancialmente a “distância” média entre as pessoas e causam o efeito de mundo pequeno, conhecido popularmente como
os seis graus de separação. Em um trabalho anterior, Kleinberg [7] mostrou que ligações de
longo alcance distribuídas de acordo com uma probabilidade decaindo em lei de potência com o tamanho da ligação,p∼r−α, otimizam o processo de transporte em redes complexas quando
utiliza-se apenas o conhecimento local da topologia da rede. O transporte otimizado ocorre para o expoente α =d, onde d é a dimensão topológica da rede. Li et al. [8] tornaram o modelo
de Kleinbergmais realista e associaram um custo à distribuição de ligações de longo alcance
e mostraram que, com essa restrição, o transporte ótimo ocorre paraα =d+1 para ambos os tipos de conhecimento da topologia da rede: local e global.
1 Introdução 21
as transições topológica e deAndersonem cadeias harmônicas com ligações de longo alcance.
Esta tese está organizada da forma descrita a seguir.
No capítulo 2, definimos o conceito de fractalidade e apresentamos algumas das proprieda-des mais importantes dos objetos fractais. Dentre essas propriedaproprieda-des, exploramos os conceitos de auto-similaridade, dimensão fractal e auto-afinidade. Também apresentamos ferramentas
matemáticas para identificar e analisar essas características. Dentre essas ferramentas matemá-ticas, destacamos os métodosyardstickebox-countingutilizados para calcular dimensão fractal.
Também introduzimos o conceito de percolação e apresentamos os modelos de percolação por sítio, por ligação e invasiva. Abordamos o fenômeno de criticalidade e apresentamos as leis de escala que são comuns à todos os sistemas percolantes.
No capítulo 3, fazemos uma breve contextualização histórica do surgimento daTeoria dos
grafos, apresentamos algumas das principais propriedades dos grafos ou redes e introduzimos
os modelos de construção de rede deErdös-Rényi, Barabási-AlberteWatts-Strogatz.
No capítulo 4, propomos um modelo de erosão baseado em uma variante do algoritmo de percolação que utiliza regras locais de enfraquecimento. Aplicamos o nosso modelo em paisa-gens artificiais e estudamos como as correlações espaciais de longo alcance afetam o processo de erosão dessas paisagens.
No capítulo 5, estudamos os modos normais de vibração de uma cadeia harmônica com ligações de longo alcance distribuídas com probabilidade decaindo com o tamanho da ligação,
p∼r−α, considerando uma função custo associada à essa distribuição. Além disso, analisamos
as transições topológica e deAndersonque ocorrem nesse sistema.
22
2
Conceitos de fractais e teoria da
percolação
2.1
Introdução aos fractais
Até o início do século XIXacreditava-se que todas as formas da natureza eram redutíveis
às formas geométricas regulares, chamadas de “perfeitas”. Hoje sabemos que ageometria
Eu-clidiana não é capaz de descrever muitas das estruturas comumente encontradas na natureza.
Objetos de formas irregulares como nuvens, árvores, linhas costeiras e deltas de rios não podem ser descritos, sem perdas significativas de informação, como figuras planas ou espaciais regu-lares. Esses objetos de geometria irregular são chamados de fractais e são descritos por uma geometria “especial” chamada degeometria fractal.
O termo fractal foi cunhado porBenoit B. Mandelbrot, considerado o pai dageometria
frac-tal, no ano de 1975. No entanto, é importante ressaltar que antes desse período diversos fractais
já haviam sido descritos. O conjunto deCantor, a curva deKoche a curva dePeanosão alguns
dos exemplos [22]. Contudo,Mandelbrotfoi o primeiro a mostrar que esses fractais
matemáti-cos apresentavam comportamentos comuns à diversas estruturas encontradas na natureza [23]. Esses resultados foram apresentados no livroThe Fractal Geometry of the Nature, publicado no
ano de 1982 [23].
2.2
Definição e propriedades dos fractais
De maneira simplificada, podemos definir os fractais como sendo objetos de complexidade infinita que não podem ser descritos pela geometria Euclidiana. A natureza não se limita às
formas “perfeitas¨, pois muitas de suas estruturas são complexas e irregulares. Mandelbrot
2.2 Definição e propriedades dos fractais 23
“Nuvens não são esferas, montanhas não são cones, linhas costeiras não são cír-culos, cascas não são lisas, nem relâmpagos viajam em linha reta”.
A ausência de escala típica ou auto-similaridade e uma dimensão fractal associada às suas estruturas, são algumas das principais propriedades dos objetos fractais. Em casos especiais, alguns fractais apresentam a propriedade de auto-afinidade.
2.2.1
Auto-similaridade
Um objeto é dito auto-similar se o mesmo é invariante com respeito à mudança de escala. Em outras palavras, isso significa que uma pequena parte do objeto é uma réplica em escala me-nor do objeto todo. O conjunto deCantor, cujo processo de construção iterativa para sucessivas
gerações é mostrado na Fig. 2.1, é um dos mais simples e conhecidos objetos auto-similares [24]. Para gerar o conjunto deCantor, começamos com um segmento de reta representando o
intervalo [0,1] na iteração ou geraçãon=0. Dividimos esse segmento de reta em três partes
iguais e descartamos o pedaço do meio. Os dois segmentos remanescentes são divididos em três partes iguais e as partes centrais de cada divisão são descartadas. Após isso, cada um dos quatro segmentos restantes são divididos em três partes iguais e novamente os segmentos cen-trais de cada divisão são descartados. Esse processo continua “ad infinitum”. Notemos que a
estrutura da geraçãon=2aparece em diferentes escalas na Fig. 2.1. No caso limite, após
infi-nitas iterações (n=∞), essa estrutura se repetirá infinitas vezes em escalas distintas, ilustrando duas das principais características dos fractais clássicos: a auto-similaridade, caracterizada pela presença de cópias do sistema em diferentes escalas, e a complexidade infinita decorrente do número infinito de iterações.
Utilizando o formalismo matemático, a auto-similaridade é definida como uma propriedade de simetria do sistema. Um objeto auto-similar é invariante sob uma transformação isotrópica, ou seja, uma dilatação simples. Considerando um objetoS formado por um conjunto de
pon-tos R= (x1, x2, x3, ..., xn) e aplicando uma transformação de similaridade (ou dilatação) com um fator de escalonamentob, obtemos o conjunto de pontos bR= (bx1, bx2, bx3, ..., bxn). O
conjuntoSformado por partículas de coordenadasRé auto-similar se ele é invariante sob essa
transformação [24]. Essa invariância de escala é o que define os fractais determinísticos. O conjunto de Cantor, o tapete de Sierpinski, o triângulo de Sierpinski e a curva de Koch são
2.2 Definição e propriedades dos fractais 24
�����
�����
�����
�����
���
���
���
���
Figura 2.1: Construção do conjunto de Cantor. (a) Começamos com uma reta representando intervalo [0,1]. (b) Dividimos o segmento de rede mostrado em (a) em três partes iguais e descartamos a parte central. (c) Dividimos cada um dos dois segmentos de reta mostrados em (b) em três partes iguais e novamente descartamos as partes intermediárias. (d) Repetimos o mesmo processo aplicado em (a) e (b). Para cada iteração associamos um númeron chamado
de geração. No limiten→∞obtemos o conjunto deCantor.
auto-similares no rigor matemático, apresentam similaridades geométricas em suas estruturas de diferentes escalas e apresentam propriedades estatísticas invariantes sob transformações de similaridade.
2.2.2
Dimensão Fractal
SegundoMandelbrot, um fractal é um conjunto cuja dimensãoHausdorff-Besicovitch, Df, excede a sua dimensão topológica. Portanto, para caracterizar a fractalidade de um objeto, devemos calcular a sua dimensão deHausdorff-Besicovitchou fractalDf ∗.
A dimensão de encaixe,dE, é definida como sendo a menor dimensão Euclidianana qual um dado objeto pode ser inserido. Cobrindo-se um objeto regular arbitrário comN(l)elementos
idênticos de tamanho linear �, podemos calcular o volume V(�) do mesmo de acordo com a
equação abaixo:
V(�) =N(�)�dE. (2.1)
ComoV(�)não depende da unidade de medida de�, utilizando a Eq. 2.1, encontramos que
N(�)∼�−dE. (2.2)
∗Por ser utilizada para caracterizar a fractalidade de objetos, a dimensão deHausdorff-Besicovitché comumente
2.2 Definição e propriedades dos fractais 25
2.2 Definição e propriedades dos fractais 26
De modo geral, a ocupação espacial dos fractais se dá de modo que
N(�)∼�−Df. (2.3)
Objetos comDf <dE são chamados de fractais†. Da Eq. 2.3, temos
Df =lim �→0
ln N(�)
ln(1/�). (2.4)
Para o conjunto de Cantor, mostrado na Fig. 2.1, utilizamos como unidade de medida do conjunto na geração no tamanho do menor intervalo,�k= (1/3)n. Para uma dada geraçãon, o número de segmentos de tamanho�néN(�n) =2n. Utilizando a Eq. 2.4, encontramos que a dimensão fractal do conjunto de Cantor é
Df =
ln(2)
ln(3) �0.639. (2.5)
Pode-se questionar se o método utilizado acima permite calcular a dimensão fractal de quaisquer fractais determinísticos. Para mostrar que sim, calcularemos a dimensão fractalDf de um triângulo deSierpinski- generalização em duas dimensões do conjunto deCantor. Um
dos modos de construir o triângulo de Sierpinski é utilizando o seguinte algoritmo:(1)geramos um triângulo (Fig. 2.3 (a)). Normalmente utiliza-se um triângulo equilátero.(2) Diminuímos pela metade os lados do triângulo e posicionamos três cópias desse triângulo reduzido de modo que cada uma delas toque as outras duas em um vértice (Fig. 2.3 (b)). (3) Repetimos inde-finidamente o passo (2) para cada configuração gerada. Na Fig. 2.3, mostramos o processo
de construção do triângulo de Sierpinski até a geração n=3. Na geração n, precisamos de
N(�) =3ntriângulos de tamanho linear�= (1/2)npara cobrir o triângulo deSierpinski. Utili-zando a Eq. 2.4, encontramos a dimensão fractal
Df =
ln(3)
ln(2) =1.585. (2.6)
Também podemos utilizar a Eq. 2.4 para calcular a dimensão fractal de fractais aleató-rios. Aplicando a mesma metodologia descrita anteriormente, podemos calcular, por exem-plo, o comprimento da linha costeira de Angra dos Reis, apresentada na Fig. 2.2, dado por
�N(�) =l1−Df. O comprimento da linha costeira é melhor calculado quando diminuimos a
unidade de medida �. O gráfico log-log de N(�) como função de 1/� é uma linha reta, cuja inclinação fornece o valor da dimensão fractal (ver sec. 2.2.4). Existem diversos métodos
†Rigorosamente falando, um objeto é dito fractal seD
f >d, ondedé a dimensão topológica do objeto;d=0
2.2 Definição e propriedades dos fractais 27
numéricos para calcular a dimensão fractal Df dos fractais aleatórios. Apresentaremos dois dos mais importantes: métodosBox counting e yardstick [2]. Outros métodos numéricos são
apresentados em detalhes nas referências [22, 24, 2].
�����
�����
�����
�����
���
���
���
���
Figura 2.3: Construção da triângulo de Sierpinski. (a) Geramos um triângulo. Normalmente
utiliza-se um triângulo equilátero. (b) Reduzimos os lados do triângulo pela metade. Após isso, geramos três cópias desse triângulo reduzido e as posicionamos de modo que cada uma delas toque as outras duas em um vértice. (c) e (d) Repetimos o procedimento descrito em (b) em cada nova iteraçãon. No limite de muitas iterações obtemos o triângulo deSierpinski.
2.2.3
Método Box-counting
Devido a sua simplicidade e grande aplicabilidade, obox-countingé um dos métodos
numé-ricos mais utilizados para calcular dimensão fractal. Para aplicar esse método, basta colocar um dado objeto em uma grade regular formada por quadrados de ladoδ e contar quantos quadrados
N(δ)são necessários para cobrir todo o objeto. No limiteδ →0, sabemos que oN(δ)∼δ−Df
2.2 Definição e propriedades dos fractais 28
2.2.4
Método Yardstick
Este método é semelhante aobox-counting. No entanto, ao invés de contarmos o número
de caixas necessárias para cobrir um objeto, devemos contar o número de segmentos N(�)de tamanho� necessários para cobrir todo o perímetro de um dado objeto. Neste caso, a
inclina-ção do gráfico do logaritmo de N(�)como função do logaritmo de 1/�dá a dimensão fractal.
Esse método é o mais apropriado para se calcular a dimensão fractal de interfaces como linhas costeiras. Na Fig. 2.5, mostramos o método yardstick aplicado ao litoral de Angra dos Reis.
Podemos observar que quanto menor a dimensão do segmento�utilizado, melhor estipulamos a
dimensão do perímetro da linha costeira e, consequentemente, melhor será a precisão do cálculo da dimensão fractal.
Figura 2.4: Ilustração do método box-countingaplicado à folha de samambaia. Colocamos a
2.2 Definição e propriedades dos fractais 29
Figura 2.5: Ilustração do método yardstickaplicado à linha costeira de Angra dos Reis.
Co-brimos o perímetro da linha costeira utilizando segmentos de reta de tamanho �. Após isso,
devemos contar o número de segmentos de reta N(�) necessários para cobrir o perímetro da linha costeira. Esse procedimento deve ser feito utilizando segmentos de reta cada vez menores até o limite numérico � →0. O módulo da inclinação do gráfico N(�) contra 1/� na escala log-logfornece a dimensão fractalDf da linha costeira de Angra dos Reis.
2.2.5
Auto-afinidade
2.2 Definição e propriedades dos fractais 30
são chamados de auto-similares. No entanto, existem casos de interesse onde a invariância sob transformações isotrópicas não é respeitada. Nesta tese, estamos particularmente interessados em uma subclasse desses fractais que é invariante sob transformação anisotrópica‡e é descrita pelas chamadas funções auto-afins [24]. Essas funções são utilizadas na descrição de superfícies desordenadas [22, 24, 2, 25]. Os fractais que são invariantes sob transformações anisotrópicas são chamados de auto-afins. A diferença entre as transformações isotrópica e anisotrópica é ilustrada na Fig. 2.6.
�
�
��
�
�
�
�
�
�
Figura 2.6: O efeito de transformações isotrópicaTie anisotrópicaTa em um círculo. A trans-formação isotrópicaTireescala o diâmetro do círculo por um fator 2, enquanto a transformação anisotrópica Ta reescala os “diâmetros” horizontal e vertical do círculo por um fator 4 e 2, respectivamente. Figura extraída da Ref. [1].
A construção de um fractal determinístico auto-afim descrito por uma função auto-afim é mostrada na Fig. 2.7: (a) a diagonal de um retângulo é dividida em quatro partes cujas componentes horizontais são iguais; (b) a reta mostrada em (a) é trocada pela estrutura mostrada em (b); (c) repetimos o procedimento adotado em (b) para os quatro segmentos de reta. Se nós reescalonarmos isotropicamente a parte mostrada na caixa pontilhada da Fig. 2.7(c), não obteremos um objeto idêntico ao mostrado na Fig. 2.7 (b). Contudo, podemos aplicar uma transformação anisotrópica de modo que isso ocorra. Esse modelo introduz uma função auto-afim,h(x), ondexé definido no intervalo [0,1].
‡Um reescalonamento anisotrópico tem diferentes fatores de escalonamento para as diferentes dimensões
2.2 Definição e propriedades dos fractais 31
Uma relação de escalonamento análoga à mostrada para fractais auto-similares, Eq. 2.3, pode ser formulada para fractais auto-afins como
h(x)∼b−αh(bx), (2.7)
ondeα é chamado de expoente deHölderou de auto-afinidade e fornece uma medida da
“ru-gosidade” da funçãoh(x).
���
���
���
Figura 2.7: Construção de um fractal auto-afim determinístico. (a) a diagonal de um retângulo é dividida em quatro partes cujas componentes horizontais são iguais; (b) a reta mostrada em (a) é trocada pela estrutura mostrada em (b); (c) repetimos o procedimento adotado em (b) para os quatro segmentos de reta. Se nós reescalonarmos isotropicamente a parte mostrada na caixa pontilhada em (c), obteremos o objeto mostrado na caixa à direita que é diferente de (b).
A Eq. 2.7 mostra que uma função auto-afim deve ser reescalonada de modo diferente nas direções vertical e horizontal: se nós expandirmos a função por um fator b na direção
horizontal (x→bx), devemos necessariamente expandir a função por um fator bα na direção
2.2 Definição e propriedades dos fractais 32
espaciais, dada pela Eq. 2.7, faça com que o objeto reescalonado seja uma cópia do objeto obtido na geração anterior. Para o caso particular α =1, a transformação é isotrópica e o sistema é auto-similar. Podemos utilizar a Eq. 2.7 para encontrar o expoenteα de um modelo determinístico. No nosso modelo, por exemplo, devemos usar os fatores de escala horizontal
b=4 e verticalbα =2 para sobrepor o objeto destacado na Fig. 2.7(c) com o mostrado na Fig. 2.7(b). Da expressão 2.7, temos
α =ln b2
ln b1 =
ln2 ln4=
1
2. (2.8)
Uma consequência importante da equação de auto-afinidade é a relação de escala da di-ferença de altura ∆≡|h(x1)−h(x2)| entre dois pontos com a distância �≡|x1−x2| que os separa. Os fractais auto-afins que obedecem a relação (2.7) tem a seguinte lei de potência como solução dessa equação [24],
∆∼�α. (2.9)
Além do expoente de rugosidadeα, pode-se associar uma dimensão fractalDf a uma fun-ção auto-afim. Consideremos uma funfun-ção auto-afim definida no intervalo [0,1] que desejamos cobrir com caixas de lado�. Inicialmente, nós dividimos o domínio horizontal da função emNs segmentos, onde cada segmento tem uma largura�=1/Ns. No intervalo horizontal de tamanho
�, a altura é modificada de acordo com a relação (2.9), de modo que precisamos∆/�∼�α−1 cai-xas para cobrir a variação de um segmento. ParaNs segmentos, o número de caixas necessárias é
N(�)∼Ns�α−1∼�α−2. (2.10)
A partir da expressão 2.3, obtemos que a dimensão fractal é dada por
Df =2−α. (2.11)
É importante notar que os argumentos utilizados para derivar a Eq. 2.10 são válidos apenas se ∆��. Para um intervalo horizontal� suficientemente grande, ∆> �, o número de caixas
necessárias para cobrir a função escala de acordo com N(�)∼1/�, e não mais seguindo a relação (2.10). Desse modo, teremosDf =2−α para pequenas escalas de tamanho, eDf =1 para grandes escalas de tamanho.
Acaminhada aleatóriaem uma dimensão é o exemplo mais simples de um fractal auto-afim
2.3 Fractalidade em séries temporais 33
de tempo a partícula pode sofrer um deslocamento∆x=|x(t+1)−x(t)|=1 para a esquerda ou direita com igual probabilidade p=1/2. Como os deslocamentos em cada passo de tempo são independentes, podemos calcular a probabilidadeP(x,t)de encontrarmos a partícula na posição
x após transcorrido um intervalo de tempo ∆t. No limite ∆t →0 o movimento é contínuo e
obtemos a distribuiçãoGaussiana[24, 2],
P(x,t) =√1 2πtexp
�
−x 2
2t �
. (2.12)
Essa função apresenta valor médio�x�=0 e desvio padrão dado por
�[x(t2)−x(t1)]2]�1/2∼ |t2−t1|1/2, (2.13)
onde o desvio padrão escala com o tempo do mesmo modo que a variação de altura∆=|h(x1)−
h(x2)| escala com α na Eq. 2.9. Das expressões (2.9), (2.11) e (2.13), encontramos que a dimensão fractal associada àcaminhada aleatóriaem uma dimensão é
Df =2−α =2−0.5=1.5. (2.14)
É possível generalizar a Eq. 2.13 para diferentes expoentes de rugosidade α utilizando o conceito de movimentobrownianofracionário [26], cujo desvio padrão é dado por
�[x(t2)−x(t1)]2]�1/2∼ |t2−t1|α. (2.15)
O movimento browniano fracionário é utilizado para gerar superfícies correlacionadas com
diferentes expoentes de rugosidadeα [22, 24, 2, 25].
2.3
Fractalidade em séries temporais
Em 1963,Mandelbrot, ao estudar a variação do preço de ativos do mercado financeiro em
situações especulativas, analisou graficamente séries temporais diárias e mensais do preço do algodão no período de 1816 à 1950. Mandelbrot observou que essas séries, mesmo quando
2.3 Fractalidade em séries temporais 34
2.3.1
Rescaled range analysis
Harold E. Hurstera hidrólogo e passou boa parte da sua vida estudando o rio Nilo e
pro-blemas relacionados com o armazenamento de água. Nesse contexto, ele desenvolveu o método estatísticoR/S analysis. Para ilustrar esse método, utilizaremos o exemplo do reservatório de
água ideal discutido por Hurstno seu livro Long-Term Storage: An experimental Study [27].
Suponha que você deseja construir um reservatório de água em um lago e precisa descobrir, baseado apenas nos registros históricos da vazão do lago, qual volume de água esse reservatório deve comportar para que ele nunca fique vazio ou transborde. Para que isso ocorra, conside-rando que o reservatório recebe em cada anotum volume de águaξ(t)e deixa escoar de forma controlada um volume de água�ξ�τ(ver Fig. 2.8), o volume médio escoado por ano no período τ deve ser dado por,
�ξ�τ = 1
τ
τ
∑
t=1
ξ(t) (2.16)
Dessa forma, o volume de água armazenadoX(t,τ)no reservatório no tempot é dado por
X(t,τ) = t
∑
u=1
[ξ(u)− �ξ�τ]. (2.17)
A diferença entre os volumes mínimo e máximo armazenados no reservatório para um dado períodoτ, define orange R(τ),
R(τ) = max
1≤t≤τ X(t,τ)−1min≤t≤τX(t,τ). (2.18)
Após investigar diversos fenômenos naturais [27], Hurst observou que a razão adimensional
R/S, ondeSé o desvio padrão,
S=
�
1 τ
τ
∑
t=1
[ξ(t)− �ξ�τ]2 �12
, (2.19)
poderia ser utilizado para comparar as séries temporais de diferentes fenômenos. Ele observou a seguinte lei de escala empírica,
R/S= (τ/2)H. (2.20)
O expoente H é chamado de expoente de Hurst e é utilizado para verificar se uma série
2.4 Leis de escala em processos dinâmicos 35
�
�
�
�
���
�
�
���
�
���
�
�
�
�
�
Figura 2.8: Ilustração esquemática do reservatório ideal deHurst. Figura extraída da Ref. [1].
comH >1/2 apresentam comportamento persistente ou correlacionado, enquanto séries com
H <1/2 são anti-persistentes ou anti-correlacionadas [27]. A maior parte dos fenômenos
na-turais observados apresentamH >1/2. Séries com H =1/2 se comportam de acordo com o
movimentobrowniano. O expoente deHurstse relaciona com o expoente de rugosidadeα do movimentobrownianode acordo com a relação,
α =2H, (2.21)
e a relação entreHe a dimensão fractalDf é expressa por,
Df =2−H. (2.22)
2.4
Leis de escala em processos dinâmicos
2.4 Leis de escala em processos dinâmicos 36
das costas litorâneas [29]. No ramo tecnológico, o processo de deposição de átomos - utilizado na manufatura de chips de computadores e outros dispositivos semicondutores - gera estruturas cuja organização espacial dos átomos tem estreita relação com a funcionalidade do dispositivo gerado.
De modo geral, processos aleatórios de crescimento de interface geram estruturas rugosas [24]. A largura da interfaceW(L,t)de um sistema de dimensão linearLnum dado instante de
tempot, definida como,
w(L,t)≡
�
1
L
L
∑
i=1
[h(i,t)−h¯(t)], (2.23)
é utilizada para caracterizar a sua rugosidade; h(i,t) é a altura da coluna i no instante t, e
o valor médio ¯h é calculado sobre todas as colunas da interface. Muitas ferramentas foram
desenvolvidas para analisar o crescimento de superfícies desordenadas. Uma das mais utilizadas e eficientes é o método do escalonamento, que consiste em relacionar grandezas e expoentes através de leis e relações de escalas. Para muitos sistemas, por exemplo, nós encontramos que a largura da interfaceW(L,t)escala como uma lei de potência do tempo,
W(t)∼tβ. (2.24)
Após um tempo suficientemente longo, a interface para de crescer e satura em um valorW(L) que cresce como uma lei de potência do tamanho do sistema,
W(L)∼Lα, (2.25)
onde α e β são chamados de expoentes de crescimento e de rugosidade, respectivamente. O tempo de saturação,tx, para o qual a interface deixa de ser descrita pela Eq. 2.24 e passa a se
comportar de acordo com a Eq. 2.25, também tem uma dependência com o tamanho do sistema e escala como a lei de potência,
tx∼Lz, (2.26)
onde z é chamado de expoente dinâmico. Os expoentesα, β ez não são independentes e se
relacionam através da relação de escalonamento deFamily-Vicsek[30],
W(L,t)∼Lαf� t Lz
�
. (2.27)
2.5 Introdução à percolação 37
de sistemas com diferentes tamanhos [24]. Os expoentes α, β ez também se relacionam de
acordo com,
z= α
β. (2.28)
Modelos discretos como o de deposição balística, deposição aleatória e deposição aleatória com relaxação da superfície foram propostos com o objetivo de reproduzir e explicar alguns dos comportamentos encontrados em dinâmicas em meios desordenados [24]. Quando se deseja modelar problemas mais complicados, muitas vezes se faz necessário associar uma equação contínua ao modelo discreto de crescimento de interface. Nesta tese, estamos particularmente interessados na equação deKardar-Parisi-Zhang, descrita brevemente na seção seguinte.
2.4.1
Equação de Kardar-Parisi-Zhang
A equação deKardar-Parisi-Zhang(KPZ), dada por,
∂h(x,t) ∂t =ν∇
2h+λ 2(∇h)
2+η(x,t), (2.29)
é uma equação diferencial parcial não linear estocástica que descreve a evolução temporal da alturah(x,t)da interface. O primeiro termo,ν∇2h, descreve a relaxação da interface causada
pela tensão superficial ν. O termo não linear, λ
2(∇h)2, descreve o processo de crescimento lateral da interface. A intensidade com que esse crescimento ocorre é ajustada pelo parâmetroλ. Por último, o termoη(x,t)é um ruído considerado para incorporar a característica estocástica do processo de crescimento da interface. A Eq. 2.29 pode ser resolvida considerando a equação de Fokker-Plank e o teorema flutuação-dissipação [24]. Os expoentes obtidos são α =1/2,
β =1/3 e z=3/2. No capítulo 4, mostramos que a interface principal do modelo de erosão
proposto por nós, para valores altos da força erosiva do mar, se comporta de acordo com a equaçãoKPZ.
2.5
Introdução à percolação
Em 1957, ao estudar processos difusivos de gases em meios desordenados, Broadbent e
Hammersely notaram que a difusão de um gás em um filtro poroso é fortemente influenciada
Broad-2.5 Introdução à percolação 38
bent e Hammerselydesenvolveram a teoria da percolação [10]. A partir desse trabalho pioneiro,
conceitos de percolação passaram a ser utilizados para descrever diversos fenômenos físicos e químicos como o processo de congelamento, o transporte em materiais amorfos, o “salto” de condução em supercondutores dopados, o efeito Hall quântico, dentre muitas outras aplicações [31]. Stanley[32] foi o primeiro a observar que redes percolantes apresentam estruturas fractais
e são fundamentais para descrever características geométricas de sistemas aleatórios.
2.5.1
Percolação de sítios
Como mencionado anteriormente, a teoria da percolação pode ser aplicada em diferentes ramos da ciência. Devido a essa generalidade, existem diversos modelos de percolação aplicada: fogo na floresta, espalhamento de epidemia e rede de resistores são alguns exemplos [22, 3, 33]. No entanto, todos esses modelos apresentam em comum as suas principais características: expoentes críticos e leis de escala [22, 24, 3, 33]. Pela sua simplicidade, o modelo de percolação ordinária de sítios em rede quadrada será apresentado nessa seção para ilustrar o comportamento crítico de sistemas percolantes.
(a) Ilustração dos primeiros vizinhos de
Von Neumann do sítio central de uma
rede quadrada.
(b) Ilustração dos primeiros e segundos vizinhos deVon Neumanndo sítio central
de uma rede quadrada.
Figura 2.9: Ilustração da vizinhança deVon Neumann: (a) os sítios pintados de cinza
represen-tam os primeiros vizinhos, enquanto em (b), os sítios pintados de cinza represenrepresen-tam o conjunto formado pelos primeiros e segundos vizinhos deVon Neumanndo sítio pintado central da rede
pintado de vermelho.
Suponha uma rede quadrada de dimensãoL x L, onde cada sítio é ocupado com uma
proba-bilidade de ocupação pe vazio ou desocupado com uma probabilidade(1−p). Para pequenos valores de p, a concentração de sítios ocupados é muito baixa e a rede é caracterizada pela
2.5 Introdução à percolação 39
vizinhos ocupados (Fig. 2.10 (a)). Os conjuntos de sítios vizinhos ocupados são chamados de agregados. Nesse modelo, adotamos a vizinhança deVon Neumann, que considera que os
pri-meiros vizinhos de um sítio são aqueles localizados imediatamente acima, abaixo, à esquerda e à direita do mesmo (ver Fig. 2.9). O aumento da probabilidade de ocupação pfaz com que a
concentração de sítios ocupados se torne cada vez maior, acarretando na formação de agrega-dos também maiores (Fig. 2.10 (b)). Para um dado valor crítico de probabilidade de ocupação,
p=pc, um agregado percolante, mostrado em vermelho na Fig. 2.10 (c), é formado. Quando o sistema apresenta um agregado percolante ou incipiente, diz-se que o sistema percolou, pois existe um agregado conectando as bordas do sistema, fazendo com que o transporte através da rede seja possível. Para p> pc, o agregado percolante toma praticamente todo o sistema Fig.
2.10 (d). Desse modo, temos dois regimes bem definidos: para p< pc, o sistema apresenta apenas alguns poucos agregados isolados, enquanto que para p>pc, um agregado percolante emerge conectando a rede.
2.5.2
Percolação por ligação
De modo semelhante à percolação por sítio, podemos definir a percolação por ligação. Para isso, consideraremos novamente uma rede quadrada LxL com vizinhança de Von Neumann,
porém, ao invés de considerarmos que um sítio é ocupado com probabilidade p, consideramos
que uma ligação entre dois sítios é ocupada de forma aleatória com probabilidade pe vazia ou
desocupada com probabilidade (1−p). Configurações desse modelo para diferentes valores de psão mostradas na Fig. 2.11. Podemos, por exemplo, aplicar o modelo de percolação por
ligação a uma rede onde as ligações representam resistores. Nesse caso, se aplicássemos uma diferença de potencial (ddp) à rede, as fases isolante e condutora do sistema seriam facilmente
2.5 Introdução à percolação 40
���
���
���
���
Figura 2.10: Configurações típicas do modelo de percolação por sítio para uma rede quadrada de lado L=128 e diferentes valores de probabilidade de ocupação p. Para p<pc, o sistema
apresenta pequenos agregados isolados, enquanto que para p=0.5927� pc, é formado um
2.5 Introdução à percolação 41
���
���
���
���
Figura 2.11: Configurações típicas do modelo de percolação por ligação para uma rede qua-drada de lado L=128 e diferentes valores de probabilidade de ocupação p. Para p< pc, o sistema apresenta pequenos agregados isolados, enquanto que parap=pc=0.5, é formado um agregado percolante conectando as bordas do sistema. Para p>pc, esse agregado ocupa quase
2.5 Introdução à percolação 42
Também podemos aplicar o modelo de percolação por sítio e por ligação para outras geo-metrias como as redes triangular, hexagonal e cúbica. Na tabela 2.1, mostramos os valores do limiar de percolação pc para diferentes redes regulares [3].
Geometria da rede Percolação de sítios Percolação de ligações
Quadrada 0.5927 1/2∗
Triangular 1/2∗ �0.652∗
Hexagonal 0.6962 �0.3473∗
Cúbica 0.3116 0.2488
Tabela 2.1: Tabela mostrando o limiar de percolaçãopc para diferentes redes regulares [3].
2.5.3
Expoentes críticos e leis de escala
Todo sistema na iminência de sofrer uma transição de fase, de segunda ordem, apresenta comportamentos não triviais expressos por leis de escala e expoentes críticos. Sistemas que apresentam expoentes críticos em comum pertencem à mesma classe de universalidade [22, 24, 32, 3, 33, 34]. Para analisar a transição geométrica de percolação, consideramos uma rede quadrada onde adotamos como parâmetro de ordem a fração de sítios pertencentes ao maior agregado,P(L,p), dada por,
P(L,p) =M(L,p)
L2 , (2.30)
ondeL2é o número total de sítios da rede eMé a massa ou número de sítios do maior agregado.
As propriedades do sistema percolante só serão bem definidas no limite termodinâmico [34],
L→∞, onde a expressão (2.30) se torna,
P(∞,p) = lim L→∞
M(L,p)
L2 . (2.31)
Sabemos que para p> pc, o agregado percolante ocupa quase toda a rede (Figs. 2.10(d) e 2.11(c)). Portanto, para que a relação (2.31) esteja de acordo com esse resultado, a massa do agregado percolante M(L,p) deve escalar com o número de sítios L2 da rede para p> pc.
Matematicamente, temos,
M(∞,p>pc)∼L2. (2.32)
A Fig. 2.12 mostra o comportamento do parâmetro de ordemP(L,p)em função da
2.5 Introdução à percolação 43
bilidade de ocupação ppara os modelos de percolação por sítio e ligação em redes quadradas.
Vemos que a curvaP(L,p)varia continuamente com o aumento sistemático dep, à medida que
aumentamos o tamanho do sistema, se aproximando do comportamento crítico,
P(∞,p) =0 se p<pc;
P(∞,p)>0 se p>pc.
(2.33)
No entanto, a curva P(L,p) sofre de fato uma transição de segunda ordem apenas no limite termodinâmico (L→∞) [34]. As Figs. 2.12a e 2.12b indicam que a percolação por ligação apresenta uma probabilidade de ocupação crítica menor do que a encontrada para a percolação por sítio. Para o primeiro caso, pc=0.5, enquanto que para o segundo pc�0.5927 [3]. Apesar dessa diferença no limiar de percolação, os problemas de percolação por sítio e ligação em redes regulares pertencem à mesma classe de universalidade e apresentam as mesmas leis de escala e expoentes críticos mostrados a seguir.
���� ���� ���� ���� ���� ���� ����
�
���� ���� ���� ���� ���� ���� ���� ����
�
������� ��������
(a) Percolação por sítio.
���� ���� ���� ���� ���� ���� ���� ���� ����
�
���� ���� ���� ���� ���� ����
�
������� ��������
(b) Percolação por ligação.
Figura 2.12: Gráfico da fração de elementos pertencentes ao agregado percolantePem função
da probabilidade de ocupação p para (a) percolação por sítio e (b) percolação por ligação.
As curvas são médias obtidas sobre 1000 amostras para redes quadradas de lado L=128 e
L=1024. As linhas tracejadas indicam os limiares de percolação pc�0.5927 e pc=0.5 para percolação por sítio e ligação, respectivamente.
No entorno da região crítica, p≈pc, temos um comportamento em lei de potência da fração de
sítios pertencentes ao agregado percolante, expresso por,
P(∞,p)∼(p−pc)β, (2.34)
ondeβé um expoente crítico. Para a percolação em duas dimensões, temosβ =5/36≈0.1389,
enquanto, em três dimensões, temosβ ≈0.4 [2]. A transição de percolação em duas dimensões
2.5 Introdução à percolação 44
T <Tc, o ferromagneto apresenta magnetização espontânea. Nesse caso, a magnetização m,
assumida como parâmetro de ordem, sofre uma transição de segunda ordem como função da temperatura, de modo que,
m(T) =0 seT >Tc ;
m(T)>0 seT <Tc .
(2.35)
Comparando as relações (2.33) e (2.35) vemos que elas são análogas. No entorno da região crítica,T ≈Tc, temos,
m∼(Tc−T)β, (2.36)
que é equivalente à Eq. 2.34.
Outra grandeza importante no estudo de percolação é a massa ou quantidade de sítios do maior agregado M(L,p). No limite termodinâmico, L→∞, para p< pc, a massa do maior agregado cresce logaritmicamente com o tamanho da redeL, enquanto que para p> pc, temos
M(L,p)∼L2, expressando matematicamente que o maior aglomerado ocupa uma fração de
toda a rede. Na região crítica, p≈ pc, a massa do maior agregado escala como uma lei de
potência do tamanho do sistema L, tendo a dimensão fractal do maior aglomerado D como
expoente. Na Fig. 2.13, estimamos a dimensão fractal do aglomerado percolante D≈1.89
em duas dimensões calculando a inclinação da curva da sua massa como função do tamanho do sistema. Este resultado é compatível com os resultados da literatura [2, 3]. Esse método é chamado de escalonamento da massa e é similar ao método box-countingmostrado na seção
2.2.3. Em três dimensões, temosD≈2.5 [3]. Agrupando esses resultados, obtemos,
M(L,p)∼
lnL se p<pc;
LD se p≈pc;
L2 se p>pc.
(2.37)
No entorno da região crítica, p≈ pc, o sistema apresenta uma distribuição de agregados sem tamanho característico, como mostrado na Fig. 2.15. Esse comportamento é descrito pela distribuição em lei de potência,
ns∼sτ, (2.38)
2.5 Introdução à percolação 45
acumuladaN(s)[35], dada por,
Ns= s
∑
s�=1
ns�∼s−(τ−1). (2.39)
��� ��� ��� ��� ���
�
������ ��� ��� ��� ��� ���
�
����
Figura 2.13: Gráfico da massa M do agregado percolante no ponto crítico pc como função do tamanho L do sistema. Cada ponto da curva foi obtido a partir de uma média sobre 1000
realizações independentes. O valor obtido da dimensão fractal do agreado percolante foiD= 1.89. Este resultado é compatível com os resultados da literatura [2, 3]
O gráficoNs como função desem escala logarítmica é mostrado na Fig. 2.14, cuja incli-nação somada de uma unidade fornece o expoente deFisherτ =2.05 [3]. Outra grandeza que
diverge como lei de potência na criticalidade é o comprimento de correlaçãoξ, definido como a distância média entre dois sítios pertencentes ao mesmo agregado. Para p≈pc, temos,
ξ =|p−pc|−ν, (2.40)
comν = 4/3 para duas dimensões eν ≈0.88 em três dimensões [31, 3]. A probabilidade de um sítio pertencer ao maior agregado escala como,
P(∞,p)∼(p−pc)β ∼ξD−E. (2.41)
A partir da expressão (2.41), relacionamos os expoentes críticosβ eν de acordo com,
2.5 Introdução à percolação 46
��� ��� ��� ��� ���
�
������ ��� ��� ��� ���
�
�
����
Figura 2.14: Gráfico da distribuição acumulada Ns como função do tamanhos dos agregados no ponto crítico. Utilizamos uma rede quadrada de lado L=8192. Os resultados são médias obtidas sobre 100 amostras. A partir da inclinação da curva, obtivemos 1−τ=−1.05. Logo, o
expoente deFisheréτ =2.05. Este resultado é compatível com o resultado da literatura [3].
onded é a dimensão topológica do sistema. Outra propriedade importante em sistemas
perco-lantes é a distância mínima ou química�entre dois sítios separados por uma distância
Euclidi-ana r, que escala segundo
�∼rDmin, (2.43)
ondeDmin é a dimensão fractal associada à distância mínima.
2.5.4
Estruturas fractais
O agregado percolante possui algumas estruturas internas que também possuem geometria fractal. Dentre essas estruturas, podemos destacar:
• A espinha dorsal, definida como o caminho que de fato a corrente elétrica percorre ao atravessar a rede;
2.5 Introdução à percolação 47
Figura 2.15: Modelo de percolação de sítios para uma rede quadrada de lado L =1024 na probabilidade crítica pcde ocupação. O agregado percolante, mostrado em vermelho, apresenta uma estrutura fractal e conecta as bordas do sistema. Os demais agregados, cuja distribuição de tamanho é controlada pelo expoente deFisher, são mostrados em outras cores.
• As ligações vermelhas que são os sítios por onde toda a corrente elétrica passa, ou seja, se imaginarmos uma rede de resistores submetida a uma diferença de potencial (ddp), os
sítios por onde toda a corrente passa seriam os pontos vermelhos;
• O perímetro externo, formado pelos sítios do agregado principal que tem vizinhos não ocupados;
• O esqueleto, composto pela união de todos os caminhos mais curtos de um sítio a todos os outros sítios para uma dada distância química�;
![Figura 2.1: Construção do conjunto de Cantor. (a) Começamos com uma reta representando intervalo [0,1]](https://thumb-eu.123doks.com/thumbv2/123dok_br/15343147.560095/24.918.210.754.106.278/figura-construção-conjunto-cantor-começamos-reta-representando-intervalo.webp)