Uma Sequência Didática para o Ensino da Matemática com o Software Geogebra

(1)

59 estudos , Goiânia, v . 41, n. 1, p . 59-75, jan./mar . 2014.

DUELCI APARECIDO DE FREITAS VAZ, PAULO CESAR CRUVINEL DE JESUS*

Resumo: neste artigo, apresentamos os resultados obtidos no

desenvol-vimento de uma proposta de trabalho para verificar a eficácia de uma se-quência didática denominada por Vaz (2012) de Investigação Matemática com o Geogebra que pode ser resumidamente enunciada em quatro etapas, a saber: experimentar, conjecturar, formalizar e generalizar o conhecimento matemático.

Palavras-chave: Ensino tecnológico. Matemática. Geogebra.

Construti-vismo.

UMA SEQUÊNCIA DIDÁTICA

PARA O ENSINO DA MATEMÁTICA

COM O SOFTWARE GEOGEBRA*

E

ste trabalho relata nossas experiências desenvolvidas em um projeto de pesquisa que buscava investigar as potencialidades pedagógicas do software Geogebra. A fundamentação teórica utilizada prevê um trabalho articulando as linhas: Investigação Matemática em Sala de Aula, In-formática na Educação Matemática e Teoria Histórico Cultural.Tal articula-ção foi denominada por VAZ (2012) como Investigaarticula-ção Matemática com o Geogebra.

Nos parágrafos seguintes esclarecemos detalhadamente nossa pesquisa com a esperança de que as reflexões aqui abordadas contribuam de forma positiva para os professores que necessitam trilhar novos caminhos metodo-lógicos na Educação Matemática.

CONSTRUTIVISMO, TECNOLOGIA E INVESTIGAÇÃO MATEMÁTICA A parte prática do projeto foi realizada no laboratório de informática para os alunos do curso de licenciatura em matemática, com atividades que

(2)

contemplassem a quadra, sugerida por VAZ (2012): conjecturar, experimentar, forma-lizar e generaforma-lizar. As atividades eram preparadas previamente em encontros semanais. Ministramos aula de vários conteúdos, como: funções, matriz, sistemas de equações, geometria analítica, entre outros. Embora o foco do trabalho fosse funções, aprovei-tamos para abordar temas diversos para melhor capacitar os envolvidos. Noaprovei-tamos que trabalhar com essa proposta e com esses alunos foi importante, pois percebemos a possibilidade de retirardo processo educacional a ênfase na memória sem significado, fazendo com que o aluno se aproprie do saber e não apenas o interiorize. Percebe-mos em muitas situações que o conhecimento emerge do processo de estabelecer as relações significativas com outro conhecimento já elaborado pelo sujeito, ampliando e transformando sua estrutura conceitual. O que permite que se estabeleçam novas relações à medida que novas experiências são construídas. De acordo com Moretto (2001, p. 42):“[...] O simples decorar uma “definição” é o que chamamos de interiori-zação da informação. Quando damos a ela um significado dentro do contexto de nossas experiências pessoais e do contexto social em que vivemos, diremos que houve uma “apropriação do conhecimento”. Essa é uma característica importante do construtivis-mo que propõe que o aluno participe ativamente do próprio aprendizado, mediante a experimentação, a pesquisa em grupo e o desenvolvimento do raciocínio, entre outros procedimentos. Nesta direção, o professor tem papel fundamental no processo e deve agir como mediador, trabalhando com o aluno e não para o aluno, como é costume na nossa educação. Isso permite que o aluno, a partir de sua ação, vá estabelecendo as propriedades dos objetos e construindo as características do mundo. Mais do que uma linha pedagógica, o construtivismo é uma teoria psicológica que busca explicar como se modificam as estratégias de conhecimento do individuo no decorrer de sua vida. O professor utilizando o método dialético proporciona novas sínteses do conhecimento, mostrando, quando necessário, as contradições do pensamento do educando relaciona-do ao conhecimento matemático, aproveitanrelaciona-do, inclusive, experiências anteriores relaciona-dos alunos.

EPISTEMOLOGIA DO PROFESSOR DE MATEMÁTICA

Trabalhar com a proposta de VAZ (2012) mostrou-nos a importância de introdu-zir as novas tecnologias no ensino da matemática. A iniciativa de adotar determinada metodologia em aula é uma questão que está intimamente relacionada com a formação do professor.

Abordaremos aqui duas destas epistemologias presentes na formação do profes-sor de Matemática que são: a tradicional e a construtivista. A tentativa é apenas fazer um paralelo a fim de mostrar que nossa proposta rompe com o ensino usual e dá pos-sibilidades de ação através de um trabalho coletivo em sala de aula.

O ensino tradicional tem suas origens fundadas no empirismo, no positivismo e na psicologia comportamentalista. Moretto (2001, p. 42) nos diz que para os segui-dores dessas correntes “[...]as verdades correspondentes ao conhecimento são aquelas que correspondem à descrição dos objetos como eles são em si mesmos”. Os conhe-cimentos, para o professor com visão tradicional, são descrições referentes ao mundo,

(3)

por isso em aula ele descreve os objetos, independentemente do contexto do observa-dor. Portanto o aluno aprende e descreve o que aprendeu, reproduzindo diretamente o que o professor fez. Neste caso, dizemos que o professor é apenas um transmissor e o aluno um receptor de conhecimento. Isso essencialmente é o que caracteriza o ensino tradicional.

Por outro lado, no construtivista dizemos que o ensino é realizado fazendo expe-riências, utilizando objetos visíveis, palpáveis ou sensitivos. Estas experiências fazem com que o aluno interaja com o objeto de conhecimento e construa seu pensamento num processo contínuo. Dizemos então que o professortrabalha com o aluno fazendo que ele deixe de ser um receptor e passe a ser um elaborador, um sujeito do conheci-mento. O professor age sempre como mediador, ou seja, facilitador do processo de aprendizagem. Sua presença e atitude nesta linha é indispensável.

Na nossa proposta, procuramos nos basear no princípio de que o aluno está em constante desenvolvimento, cuja atividade espontânea e natural é condição para seu crescimento físico e intelectual. Portanto é fundamental que exista a participação ativa do aluno no espaço em que o professor reserva para as descobertas do educando. TECNOLOGIA NA EDUCAÇÃO MATEMÁTICA

Diante dos avanços e das novas propostas de formação de professores de Mate-mática, os professores têm à sua disposição várias metodologias diferenciadas que po-dem ser aplicadas em sala de aula. Esses novos recursos permitem planejar atividades estimulantes. O professor, enquanto mediador, cria situações aumentando a autoestima dos alunos, além de permitir novos valores, verifica a dificuldade de aprendizagem de determinados conteúdos, oportunizando situações propícias à aprendizagem. O pro-fessor mediador tem papel significativo, é dele a missão de buscar alternativas viáveis para estimular o interesse dos alunos, tornando-os participativos nas aulas, se transfor-mando em sujeitos colaborativos no processo de ensino e aprendizagem.

Pensando nisto, realizamos várias experiências de estudos fundamentadas na metodologia construtivista, buscando integrar a tecnologia, o construtivismo e o co-nhecimento matemático. Nosso objetivo estava em avaliar o potencial pedagógico de novas metodologias, uma forma de mostrar que a aprendizagem do aluno pode ser potencializada quando planejamos atividades integradoras de conhecimentos.

Constatamos que para o professor, independente da disciplina, é essencial seu preparo em relação a especificidade de seu conhecimento, conhecer bem o conteúdo de sua disciplina, para ministrar uma aula a contento. O educador deve dominar bem o software para assim, realizar um ensino do conteúdo com qualidade. Por fim, só podemos ter uma atitude de professor construtivista se realmente nos apropriarmos desse conhecimento. Mas não basta ter o conhecimento matemático, o conhecimento tecnológico e o construtivismo, é necessário fazer a integração desses três elementos para que a proposta funcione.

Assim, fizemos um longo trabalho de preparação dos conteúdos, da teoria histó-rico cultural e do software. Escolhemos para trabalhar e estudar o software Geogebra por vários motivos. É um software livre, permitindo que os alunos descubram

(4)

con-62 estudos , Goiânia, v . 41, n. 1, p . 59-75, jan./mar . 2014.

jecturas e tambémfaçam releituras importantes de conteúdos matemáticos anteriores. Outro fator é a possibilidade de trabalhar a questão da construção do saber, isto é, com esse software podemos inverter o processo de ensino aprendizagem, passando de um modelo baseado na informação para um modelo que permite ao aluno jogar o jogo, isto é, construir o saber, através da possibilidade de experimentar, conjecturar, formalizar e generalizar a matemática, permitindo que o professor trabalhe com o aluno, uma tendência moderna da Educação Matemática.

UMA BREVE HISTÓRIA DO GEOGEBRA

O software Geogebra foi criado na universidade of Salzburg, na Áustria, no ano de 2001, pelo austríaco Markus Hohenwarter. Hoje, continua desenvolvendo seu tra-balho na universidade Atlantic localizada na Florida. Markus Hohenwarter criou o Geogebra com o objetivo de melhorar o desempenho dos alunos em todos os níveis da educação matemática.

O software integra conceitos de álgebra e geometria, o austríaco então decidiu colocar o nome de Geogebra, união de geometria com álgebra, está escrito em lingua-gem Java e está disponível em múltiplas plataformas.

O Geogebra é um software que permite trabalhar quase todos os conteúdos abor-dados no ensino fundamental, médio e superior. Suas principais características: livre acesso, possui imensas possibilidades pedagógicas, permitindo uma boa interatividade entre professor, aluno e conhecimento matemático, possibilitando trabalhar teoremas, construção de conceitos, testar hipóteses, fazer releituras importantes de conteúdos matemáticos, além de fácil manuseio. Pela facilidade de adaptação, podemos com seu uso, trabalhar o processo de ensino aprendizagem, passando de um modelo baseado na informação para um modelo fundamentado na construção do saber. O software possui uma visualização extraordinária dos gráficos, faz com que o aluno teste conjecturas relacionados com a opção de movimentar os objetos. Possibilita como está relatado em muitos trabalhos, visualizar caminhos para formalizar os resultados. Abaixo, ilus-tramos a página inicial do Geogebra (Figura 1).

(5)

A partir da sua invenção o software vem ganhando vários prêmios internacio-nais, até hoje já são oito listados a seguir: EASA 2002 – European Academic Software Award (Ronneby, Suécia), Learnie Award 2003 – Austrian Educational Software Award (Viena, Áustria), Digita 2004- German Educational Software Award (Colônia, Alema-nha), Comenius 2004 – German Educational Media Award (Berlim, AlemaAlema-nha), Lear-nieAward 2005 – Austrian Educational Software Award for “Spezielle Relativitätsthe-oriemit GeoGebra” (Viena, Áustria), Trophées du Libre 2005 - Prêmio Internacional de Software Livre, categoria Educação (Soissons, França), Twinning Award 2006 - 1º Prêmio no “Desafio dos Círculos” com GeoGebra (Linz, Áustria), Learnie Award 2006 - Prêmio Austríaco de Software Educacional (Viena, Áustria).

INVESTIGAÇÃO MATEMÁTICA NA SALA DE AULA

O objetivo específico do projeto de pesquisa era aplicar uma proposta metodo-lógica para ensinar matemática, através da Investigação Matemática com o Geogebra. Esclareceremos um pouco essa temática. Investigar é procurar, examinar, procurar o que ainda não se conhece, questionar e procurar responder, para isso é preciso querer saber e estar curioso. Para PONTE (2003) a Investigação Matemática pode ser asso-ciada simplesmente a procurar conhecer, compreender um problema matemático, daí ser possível associar as atividades de investigar e lecionar. Do ponto de vista de um matemático investigar é procurar resolver problemas de todas as categorias, dentro de sua área específica. Essencialmente, investigar é a principal tarefa do matemático. Ela pode ser realizada em diversos níveis. Um matemático pode se deter na tentativa de resolver um problema aberto, aquele que ainda é uma conjectura e isso é uma trabalho muito importante. Mas o conhecimento já construído historicamente pode ser trabalha-do de forma investigativa com o aluno. O que sei enquanto matemático, pode ser um mistério para meus alunos.

Dentro deste processo de investigação, existem duas vertentes que são propos-tas aos alunos, a saber: tarefa e atividade. Tarefa é a proposta de trabalho feita pelo professor e a atividade é o envolvimento dos alunos para realizarem a tarefa proposta. Na investigação, existe a possibilidade de que os alunos não sejam simplesmente re-solvedores, mas também que reflitam, discutam entre si suas ideias e métodos de reso-lução, procurando solucionar suas próprias dúvidas e questionamentos. Neste caso, o professor assume um papel de muita importância na atividade investigativa, pois é ele quem desafia e instiga os alunos, ou seja, fazendo com que os alunos reflitam sobre o trabalho e busquem informações necessárias tendo um acompanhamento do seu desen-volvimento neste processo e auxiliando com informações que possam contribuir com os alunos. O professor também precisa encarar o erro do aluno como algo natural para não ocorrer o desestimulo.

Na disciplina de Matemática, ou em qualquer outra disciplina, o envolvimen-to do aluno é uma condição fundamental para a aprendizagem, daí a importância do professor, pois tudo depende da proposta apresentada, dos objetivos, das ações, das suas concepções, das oportunidades aproveitadas em sala de aula e das ativi-dades dos alunos.

(6)

INVESTIGAÇÃO MATEMÁTICA COM O GEOGEBRA

As atividades matemáticas planejadas tendo como fundamento a Investigação Ma-temática com o Geogebra no artigo sugerido por Vaz (2012) consistem essencialmente de quatro etapas: experimentar, conjecturar formalizar e generalizar. Estas sugestões foram obtidas pelas diversas experiências que foram realizadas durante a pesquisa e também em experiências anteriores. Abaixo esclarecemos melhor o significado desses termos.

Experimentar aqui significa que podemos usar o software, juntamente com o aluno para que ele mesmo faça suas experiências, movimente os objetos matemáticos, perceba as relações entre eles, comapare álgebra e geometria, enfim, interaja com o objeto do saber.

Conjecturar significa que depois de perceber as relações oriundas da experimen-tação é possível vislumbrar propriedades, relações, resultados gerais importantes para o bom desenvolvimento do ensino da Matemática. Uma vez feita à conjectura, o aluno pode enunciá-la como um resultado que pode ser verdadeiro ou falso.

Formalizar seria então a demonstração propriamente dita, ou evidenciar uma contra-proposição da conjectura levantada com um argumento pedagógico compatível à série que se está trabalhando.

Generalizar é o importante nível, pois após realizar os três níveis de construção de conhecimento é a hora de generalizar o resultado, ou seja, investigar outras situações e podendo até achar algumas situações particulares e por fim explorar o resultado obtido.

Muitas atividades propostas levaram em consideração essa quadra. No nosso projeto, primeiramente estas atividades eram planejadas e testadas antes de serem le-vadas para sala de aula ou laboratório.

RELATOS DE PESQUISA: DESCRIÇÃO DE LUGARES E PESSOAS.

Após três meses de projeto de iniciação cientifica, demos inicio a elaboração das atividades para por fim serem aplicadas. Estas elaborações aconteceram no transcorrer de um ano, que também foi utilizado para estudar teorias e aprender a trabalhar com o software.

Muitas atividades eram oriundas de outras experiências e foram aproveitadas devido a suas potencialidades. No período deagosto à dezembro de 2011elaboramos diversas atividades para serem aplicadas.Após as atividades serem catalogadas, damos início a aplicação das mesmas. Foram três grupos de alunos envolvidos. Os que cursa-vam a disciplinade Metodologia do Ensino da Matemáticado curso deLicenciatura em Matemática do IFG em 2012/1. Alunos que cursavam a segunda série do ensino médio do Colégio Evolução em 2012/2. Alunos que cursavam a chamada Prática Profissional do curso de Licenciatura em Matemática do IFG, em 2012/2.

RELATOS DE EXPERIÊNCIAS

Relatamos aqui algumas atividades criadas e aplicadas usando o software Geo-gebra. Também apresentando a nossa sugestão metodológica para o ensino da

(7)

mate-65 estudos , Goiânia, v . 41, n. 1, p . 59-75, jan./mar . 2014.

mática. Todas estas atividades foram aplicadas no desenvolvimento do projeto de pes-quisa. As aulas eram aplicadas no laboratório de informática do IFG com capacidade para 25 pessoas.

O primeiro relato refere-se a experiência com os alunos que cursavam a segunda série do ensino médio no Colégio Evolução. Decidimos levar os alunos do Colégio Evolução para o IFG, pois representava uma excelente oportunidade de aplicar nossa proposta para um grupo que até então desconhecia este tipo de trabalho. Essa ativida-de foi planejada, para assim, colocar em prática o nosso projeto. Decidimos trabalhar com os alunos da segunda série do ensino médio, aplicando uma atividade planejada e trabalhada em outras situações anteriores e que permitia o aluno perceber o caráter dedutivo e generalizante da Matemática, sobre matrizes e determinantes, descrita em Vaz (2012).

Após a autorização da escola e dos pais para levar os alunos para esta aula diferenciada, marcamos a atividade para o dia 18 de Outubro de 2012, das 08h00min às 11h00min da manhã. Convidamos vinte alunos, dos quais quatorze compareceram.

Iniciamos a aula fazendo a apresentação do software, ou seja, nome, como obter, aonde foi inventado e as principais ferramentas. Após esta introdução, damos inicio a nossa aula.

UMA INTRIGANTE PROPRIEDADE DE MATRIZES

De acordo com Vaz (2012, p. 44), o professor ao trabalhar com o aluno, com ati-vidades bem planejadas, possibilita ao aluno conjecturar, perceber propriedades, mas no nosso caso, como o saber matemático tem o caráter da abstração e da generalização, o professor deve propor argumentos pedagógicos complementares e adequados à sé-rie que estaremos trabalhando, formalizando os resultados teóricos suscitados a partir dessa empiria, consolidando nossos objetivos.

Esta atividade foi sugerida justamente porque cumpre com todas as etapas da proposta sugerida por Vaz (2012). Mesmo que o conteúdo de determinantes não use apelo gráfico, no lado esquerdo da tela do software, existe uma janela, chamada de

janela de álgebra, onde o aluno acompanha todo o procedimento e escrita algébrica do tal conteúdo.

Esta atividade é uma releitura do conteúdo relacionado à matriz e determinante e refere-se a uma intrigante propriedade das matrizes quadradas que possuem números consecutivos nas linhas.

O aluno seguindo alguns passos consegue visualizar que o determinante de toda matriz de números consecutivos de ordem 2x2 terá como resultado sempre -2. Ainda mais, todo determinante de matriz com números consecutivos nas linhas de ordem 3x3 em diante é nulo.

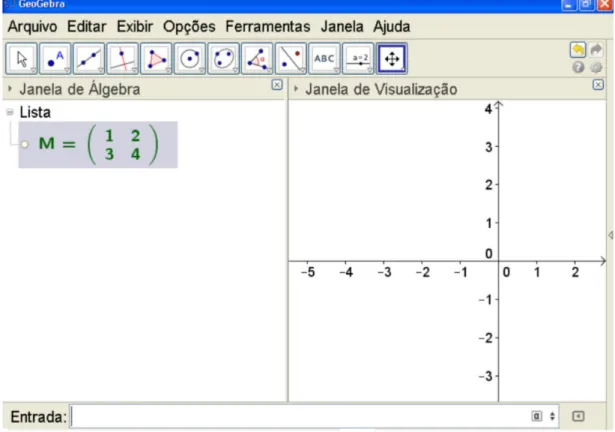
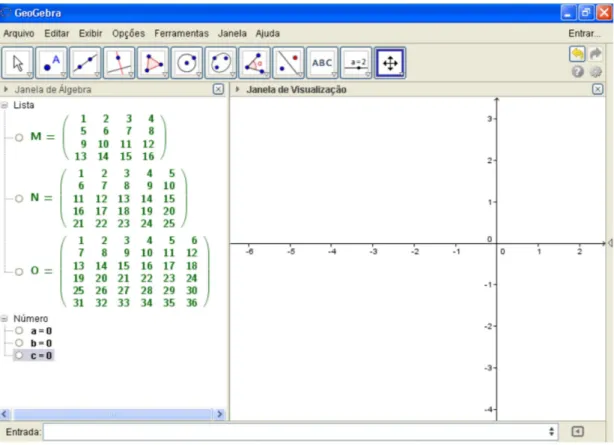
Iniciamos a atividade solicitando que os alunos digitem na caixa de entrada M = {{1, 2}, {3, 4} e dê “enter”. Isto significa que esta digitando a matriz de ordem 2x2 e também uma matriz de números consecutivos: .

(8)

Figura 2: Matriz de ordem 2x2 e de números consecutivos

Em seguida, na mesma caixa de entrada digite Determinante [M], logo, visua-lizará na janela de álgebra a matriz e logo a baixo o determinante calculado.

(9)

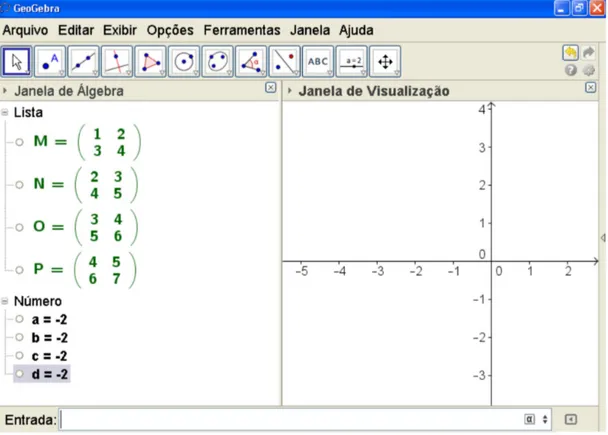
Depois de experimentar diversas matrizes escritas e calculado os respectivos determinantes é natural o aluno conjecturar que toda matriz assim constituída tem determinante nulo. Para verificar se isso é verdade, fizemos, como planejado, mais alguns experimentos com os alunos.

Figura 4: Determinante de Matrizes 2x2

Nesta parte da aula, realizamos a etapa da conjectura e experimentação. A eta-pa seguinte é a busca pela formalização da propriedade. O trabalho deve ser realizado com a participação do aluno. Nesta parte foi solicitado ao aluno que formalizasse esta conjectura no quadro. A propriedade foi formalizada calculando o determinante da matriz quadrada 2x2, M = {{n, n+1},{n+2, n+3}}, onde n é um real qualquer. Sendo assim temos: M = e DetM = n(n + 3) – (n + 1)(n + 2) = (n² + 3n) – (n² + 2n + n + 2) = n² + 3n – n² – 2n – n – 2 = 3n – 2n – n – 2 = 3n – 3n – 2 = - 2, não importando o valor de n. Isso determina o fim da terceira etapa, a formalização.

Na sequência incentivamos os alunos a pensarem em outros casos. Não demo-rou muito para alguém perguntar se a mesma propriedade valeria para outras matrizes de outras ordens. Neste momento,caminhamos para colocar em prática a generalização da atividade.

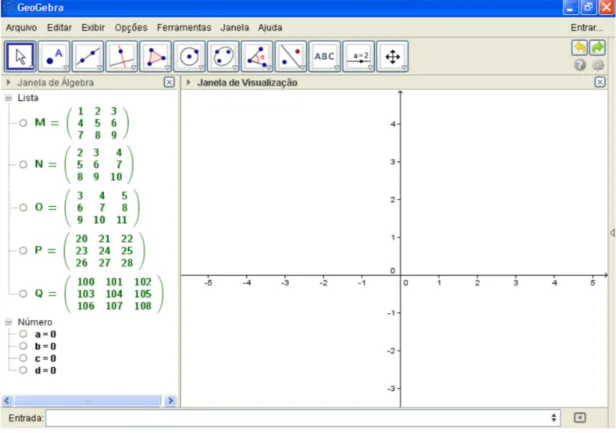
Repetimos o mesmo procedimento feito anteriormente para uma matriz de or-dem 3x3. Lembrando que a matriz de oror-dem 3x3 é escrita da seguinte maneira: M = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}. A figura 5 a seguir mostra várias matrizes de ordem 3x3 e seus respectivos determinantes.

(10)

Figura 5: Matrizes de ordem 3x3 e seus respectivos determinantes

Ao trabalhar com as matrizes de ordem 3x3, os alunos de depararam com uma surpresa, os determinantes das matrizes resultam em zero. E depois de vários exemplos todos estavam convencidos de que realmente o determinante é sempre nulo. Aqui mais uma vez contemplamos a experimentação e a conjectura. A prova da pro-priedade ou a formalização foi então solicitada e realizada como segue, neste caso um aluno conseguiu fazer os cálculos utilizando regras de determinantes usuais, como segue. M = {{n, n + 1, n + 2}, {n + 3, n + 4, n + 5}, {n + 6, n + 7, n + 8}} detM = = [(n).(n + 4).(n + 8) + (n + 1).(n + 5).(n + 6) + (n + 2).(n + 3).(n + 7)] – [ (n + 1).(n + 3).(n + 8) + (n).(n + 5).(n + 7) + (n + 2).(n + 4).(n + 6)] = [(n² + 4n).(n + 8) + (n² + 5n + n + 5).(n + 6) + (n² + 3n + 2n + 6).(n + 7)] – [(n² + 3n + n + 3).(n + 8) + (n² + 5n).(n + 7) + (n² + 4n + 2n + 8).(n + 6)]= [(n² + 4n). (n + 8) + (n² + 6n + 5).(n + 6) + (n² + 5n + 6).(n + 7)] – [(n² + 4n + 3).(n + 8) + (n² + 5n).(n + 7) + (n² + 6n + 8).(n + 6)]= [(n³ + 8n² + 4n² + 32n) + (n³ + 6n² + 6n² + 36n + 5n + 30) + (n³ + 7n² + 5n² + 35n + 6n + 42)] - [(n³ + 8n² + 4n² + 32n + 3n + 24) + (n³ + 7n² + 5n² + 35n) + (n³ + 6n² + 6n²+ 36n + 8n + 48)]= (n³ + 12n² + 32n) + (n³ + 12n² + 41n + 30) + (n³ + 12n² + 41n + 42) – [(n³ + 12n² + 35n + 24) + (n³ + 12n² + 35n) + (n³ + 12n² + 44n + 48)]= (3n³ + 36n² + 114n + 72) – (3n³ + 36n² + 114n + 72)=3n³ – 3n³ + 36n² – 36n² + 114n –114n + 72 – 72= 0.

Após essa formalização, continuamos a instigar o aluno com perguntas na ten-tativa de levá-los a pensar os outros casos, trabalhando a generalização da propriedade,

(11)

criando novas conjecturas. Neste caso, orientamos que eles fizessem investigações nos casos 4x4 e 5x5, no próprio software. Para por fim generalizarmos para todo caso nxn.

Figura 6: Casos 4x4 e 5x5, no próprio software

Devido ao tempo não conseguimos trabalhar toda experiência, embora em Vaz (2012) toda experiência é relatada e enunciado o resultado geral, a saber: toda matriz quadrada de ordem maior ou igual a três em que os números são consecutivos possui determinante nulo. Nas mesmas condições, quando a matriz é 2x2 o determinante é sempre -2.

Esta atividade aplicada, além de ser ilustrativa da proposta, mostra a agilidade do software e sua importância na realização desta tarefa, pois supondo que o professor te-nha que resolver no mínimo três tipos de determinantes de cada ordem, além de perder muito tempo calculando estes determinantes na sala de aula, principalmente de ordem 3x3 em diante, pode acontecer que os alunos fiquem desinteressados da aula por causa dos grandes cálculos envolvidos.

O segundo e terceiro grupo que trabalhamos foram alunos que cursavam a disci-plina de Metodologia do Ensino da Matemática e alunos da Prática profissional2012/1, também do curso de Licenciatura em Matemática do IFG.

De início realizamos algumas reuniões de planejamento nas quais foram previs-tas o que iríamos ministrar nessas disciplinas. Sendo assim, usamos a mesma meto-dologia para ambas.

As aulas eram aplicadas no laboratório do IFG, no turno vespertino, com uma duração de 90 minutos. Dividíamos estas aulas em três partes: era iniciada pelo profes-sor Duelci (30 minutos), dizendo o que seria aplicada na aula com algumas orientações

(12)

sobre as barras de ferramentas do software, depois o aluno de iniciação científica dava continuidade (30 minutos), aplicando atividades relativas à função. No restante da aula eram discutidas eventuais dúvidas.

No final do curso, pedimos aos alunos que criassem algumas atividades usando as sugestões metodológicas estudadas com o Geogebra.

Apresentamos agora uma atividade que foi desenvolvida com este grupo. Esta atividade tinha o objetivo de ensinar ao aluno que o software possibilitava ampliar o alcance de nosso olhar e criar conjecturas importantes para o desenvolvimento mate-mático. A ideia era inicialmente solicitar ao aluno que descrevesse o que aconteceria com a família de parábolas dada por f(x)=ax2_{+x+1, quando variamos o parâmetro a,}

. A pergunta seguinte seria se ele seria capaz de visualizar o que aconteceria com o extremo ou vértice das funções quando o parâmetro a percorre determinando intervalo. As etapas estão arroladas abaixo.

Para mostrar esse caráter de estender o nosso olhar, basta seguir a sequência. Também podemos destacar todas as etapas da sequência didática anunciada.

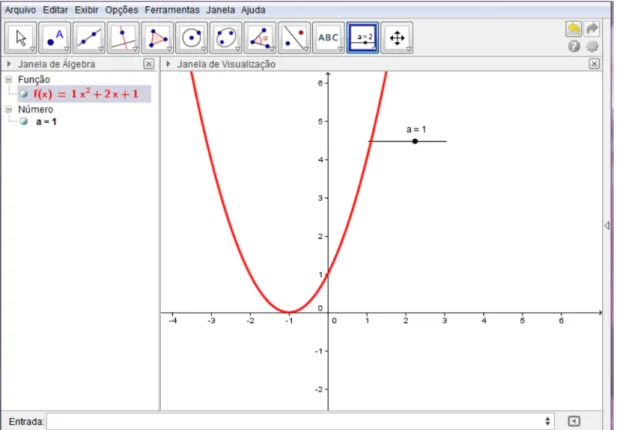
Construa um seletor ou controle deslizante, onde o coeficiente a varia no inter-valo de -5 a 5.

Figura 7: Seletor ou controle deslizante

(13)

71 estudos , Goiânia, v . 41, n. 1, p . 59-75, jan./mar . 2014. Figura 8: Função f(x) = a x² + 2x + 1

Clique com o botão direito do mouse no seletor e selecione animar, para ver o que acontece com o gráfico.

Clique com o botão direito do mouse na parábola e selecione a função habilitar rastro, em seguida, movimente o seletor.

Figura 9: Função habilitar rastro

Observando o gráfico, vimos que a parábola se move até se transformar em uma reta e em seguida volta a ser a parábola.

(14)

es-72 estudos , Goiânia, v . 41, n. 1, p . 59-75, jan./mar . 2014.

querdo de sua tela. Fique atento que ao mover a tela do software, automaticamente a habilitação do rastro desaparece.

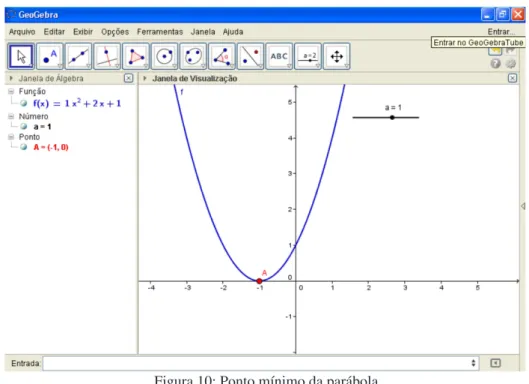
Novamente na entrada algébrica, digite a palavra Extremo, logo sairá à opção polinômio, clique no mesmo e em seguida digite o nome da função, neste caso, f e novamente, dê “enter”.

Observado o gráfico, podemos ver que surge um ponto no vértice da parábola, este ponto está se referindo ao ponto mínimo da parábola.

Figura 10: Ponto mínimo da parábola

Após essa análise, vá ao ponto de mínimo ou extremo e ative o habilitar rastro. Note que para qualquer que seja o valor do coeficiente a, o rastro formado pelo o extremo, mostra que o gráfico tende a ser uma reta.

(15)

Ao realizar esta atividade, conjecturamos e experimentamos a ideia proposta. Agora deveríamos formalizar esta ideia, ou seja, mostrar matematicamente se a con-jectura é verdadeira ou não. A parte formal da proposta.

Sendo assim, vamos verificar se o gráfico formado pelo o extremo, é uma reta, fazendo os seguintes cálculos. y = ax² + 2x + 1, onde o a Є R 0. Calculando o x do vértice e o y do vértice temos. x = - e y = - . Assim, y = - x+1, uma reta. Mas note que x nunca será zero, assim somos obrigado a perceber que o ponto (0, 1) não faz parte da solução. Essa tarefa é realizada sempre proporcionando a participação do aluno, com perguntas apropriadas na condução do processo para que aluno perceba todas as passagens.

Após mostrar esta pequena observação ao aluno, concluímos que não é uma reta, mas uma reta menos o ponto (0,1): R = . Observe que ao fim desta parte, concluímos a formalização.

Após a realização dessa atividade com os alunos, muitas questões foram susci-tadas relacionadas aos outros coeficientes, no caso b e c. Neste caso, agimos com o espírito investigador propondo realizar uma nova investigação.

A dinâmica da atividade consistia em orientações constantes, baseamo-nos na pesquisa-ação, interferindo no processo com a finalidade de alcançarmos nossos ob-jetivos.

Quando os alunos terminaram de realizar a parte final da atividade, eles então exploraram todas as etapas da proposta, generalizando para todos os coeficientes de uma função quadrática.

Esta atividade aplicada, além de explorar a proposta, mostra outras potencia-lidades do software, por exemplo, caso o professor tivesse que fazer a investigação utilizando o processo usual gastaria muito tempo na elaboração e finalização com-pleta da investigação. Além de perder muito tempo fazendo os gráficos dentro de sala aula, pode acontecer que o aluno não consiga perceber o que acontece com cada extremo.

CONCLUSÃO

Concluímos nosso relato de pesquisa reafirmando nossas expectativas que já ti-nham sido descritas em VAZ (2012). Destacamos a imensa capacidade de movimentar os objetos matemáticos que o software permite e assim realizar a experimentação, fato es-quecido na educação matemática que hoje se caracteriza pela descrição das experiências de outros e se baseia na transmissão dos fatos científicos desenvolvidos ao longo da his-tória. Salientamos a imensa capacidade de trabalhar com famílias de funções, perceber propriedades que o nosso olhar limitado não enxerga. Em muitas atividades planejadas para determinado fim o aluno detectou e nos surpreendeu apontando outras propriedades colocando-nos numa situação de aceitar os desafios de iniciar uma nova investigação.

Quanto a proposta, percebemos sua importância num cenário de formação de professores. É muito comum professores já formados não aderirem as novas

(16)

possi-74 estudos , Goiânia, v . 41, n. 1, p . 59-75, jan./mar . 2014.

bilidades de ensino devido exclusivamente ao fato de terem uma formação limitada. Uma proposta dessa natureza deve ser levada para outras instâncias que trabalham a formação continuada e em serviço de professores, pois percebemos que os professores, em sua grande maioria, não estão preparados para integrar em sua prática uma meto-dologia desse porte.

Cumpre observar que neste trabalho, estabelecemos um critério importante de aprender e ensinar Matemática simultaneamente que leva em consideração a participa-ção efetiva do aluno no processo, fato considerado relevante na prática de um ensino de qualidade e na formação de uma educação significativa.

Finalizando nossa conclusão salientamos a incrível capacidade que este software possibilita de desenvolver a sensibilidade do educando em descobrir resultados impor-tantes como foram os aqui apresentados.

A SEQUENCE DIDACTIC FOR TEACHING MATH WITH THE SOFTWARE GEOGEBRA

Abstract: this paper, we present the results obtained in the development of a proposal for

work was to check the effectiveness of an integrated constructivist teaching sequence with Geogebra software proposed by VAZ (2012), called Mathematical Research with Geogebra which can be briefly enunciated in four stages, namely: experience, conjecture, formalize and generalize the mathematical knowledge.

Keywords: Technology education. Mathematical. Geogebra. Vygotsky. Referências

BICUDO, M.A.V. (Org.). Pesquisa em Educação Matemática: concepções & perspec-tivas. São Paulo: Edunesp, 1999.

BORBA, M.C.; PENTEADO, M.G. Informática e Educação Matemática. Belo Hori-zonte: Autêntica, 2001.

BRITO, G. S.; PURIFICAÇÂO, I. Educação e novas tecnologias: um repensar. Cu-ritiba: Ibpex, 2006.

CURY, Helena Noronha. Análise de erros: o que podemos aprender com as respostas dos alunos.Belo Horizonte: Autêntica, 2007.

FIORENTINI, D. (Org.). Formação de professores de matemática. Campinas: Mer-cado de Letras, 2003.

FIORENTINI, D.; LORENZATO, S. Investigação em educação matemática: percur-sos teóricos e metodológicos. Campinas: Autores Associados, 2006.

LORENZATO, S. (Org.). O laboratório de ensino de matemática na formação de

professores. Campinas: Autores Associados, 2006.

MORETTO, V. P. Prova um momento privilegiado de estudo, não um acerto de contas. Rio de Janeiro: Lamparina, 2008.

(17)

PONTE, J. P.; BROCARDO, J. OLIVERIA, H. Investigações matemáticas na sala de

aula. Belo Horizonte: Autêntica, 2006.

VAZ, D.A.F. Experimentando, conjecturando, formalizando e generalizando: articu-lando investigação matemática com o Geogebra. Revista Educatica. Goiânia, v. 15, n. 1, p. 39-51, jan./jun. 2012.

* Recebido em: 11.01.2014. Aprovado em: 28.01.2014. DUELCI APARECIDO DE FREITAS VAZ

Doutor em Educação Matemática (UNESP-RC-SP). Professor na PUC Goiás e no IFG. E-mail: duelci. vaz@ig.com.br.

PAULO CESAR CRUVINEL DE JESUS