Secretaria de Educação a Distância- SEDIS Coordenadora da Produção dos Materiais

André Gustavo Campos Pereira

Joaquim Elias de Freitas

Roosewelt Fonseca Soares

Cálculo I

D I S C I P L I N A

Mais primitivas e

as somas de Riemann

Autores

aula

Divisão de Serviços Técnicos

Catalogação da publicação na Fonte. UFRN/Biblioteca Central “Zila Mamede” Governo Federal

Presidente da República

Luiz Inácio Lula da Silva

Ministro da Educação

Fernando Haddad

Secretário de Educação a Distância – SEED

Carlos Eduardo Bielschowsky

Universidade Federal do Rio Grande do Norte

Reitor

José Ivonildo do Rêgo

Vice-Reitora

Ângela Maria Paiva Cruz

Secretária de Educação a Distância

Vera Lúcia do Amaral

Secretaria de Educação a Distância- SEDIS

Coordenadora da Produção dos Materiais

Marta Maria Castanho Almeida Pernambuco

Coordenador de Edição

Ary Sergio Braga Olinisky

Projeto Gráfico

Ivana Lima

Revisores de Estrutura e Linguagem

Eugenio Tavares Borges Jânio Gustavo Barbosa Thalyta Mabel Nobre Barbosa

Revisora das Normas da ABNT

Verônica Pinheiro da Silva

Revisoras de Língua Portuguesa

Janaina Tomaz Capistrano Sandra Cristinne Xavier da Câmara

Revisores Técnicos

Leonardo Chagas da Silva Thaísa Maria Simplício Lemos

Revisora Tipográfica

Nouraide Queiroz

Ilustradora

Carolina Costa

Editoração de Imagens

Adauto Harley Carolina Costa

Diagramadores

Bruno de Souza Melo Dimetrius de Carvalho Ferreira Ivana Lima Johann Jean Evangelista de Melo

Adaptação para Módulo Matemático

André Quintiliano Bezerra da Silva Kalinne Rayana Cavalcanti Pereira Thaísa Maria Simplício Lemos

Colaboradora

Viviane Simioli Medeiros Campos

Imagens Utilizadas

Apresentação

N

a aula 8 (A primitiva), estudamos a primitiva de uma função e calculamos muitas primitivas. Nesta aula, continuaremos o estudo das primitivas e começaremos a trilhar o caminho no sentido de explicar por que as estudamos. Além disso, introduziremos a idéia de como calcular a área sob a curva de uma função.

Objetivos

Mais primitivas

Na aula 8, vimos que utilizando as regras da derivada da soma, da diferença e de uma constante vezes uma função provamos que

฀

฀f฀x)dx=฀ ฀

f฀x)dx

฀

฀f฀x) +g฀x))฀x= ฀

f฀x)฀x+ ฀

g฀x)฀x e

฀

฀f฀x)฀g฀x))฀x= ฀

f฀x)฀x฀ ฀

g฀x)฀x.

E também que ฀

฀f฀฀x)g฀x) +f฀x)g฀฀x))dx=f฀x)g฀x) +฀

e

 ฀

f฀x) g฀x)

_฀

dx=

 ฀

f฀฀x)g฀x)฀f฀x)g฀฀x) g฀x)฀



dx= f฀x) g฀x) +฀.

Nesta aula, calcularemos a primitiva de uma função que envolva a regra da cadeia, ou seja, que envolva compostas.

Consideremos g฀I ฀J,f ฀J ฀Re฀ ฀J ฀R a primitiva de f. Vimos na aula 5

(Derivadas de funções compostas) que

฀฀฀g฀x)))฀ _=฀฀_{฀g฀x))฀g}฀_฀x).

Por F ser a primitiva de f, temos que ฀฀฀y) =f฀y) para todo y฀฀, e podemos

reescrever a equação anterior como ฀฀฀g฀x)))฀ =f฀g฀x))_฀g฀฀x).

Por outro lado, se essa igualdade é verdade para todo x_฀฀, então, por definição, ฀฀g฀x)) é a primitiva de฀฀g฀x))฀g฀฀x) e podemos então escrever

฀

f฀g฀x))g฀฀x)dx=฀฀g฀x)) +K.

Na aula 4 (A derivada), fizemos alguns cálculos determinando u=฀฀x), o que implica ฀u

฀x =g฀฀x) ou, em forma de diferencial, temos ฀u=g฀฀x)฀x. Substituindo essa notação na equação (1), temos

฀

f฀u)du=฀฀u) +K. (Equação 2)

O processo de transformação da equação (1) na equação (2) pela substituição de u=g฀x)e฀u=g฀฀x)฀x é chamado de método da substituição u.

Observação Algumas condições sobre as funções g฀฀ ฀J,f ฀J ฀R são necessárias para que possamos realizar tal substituição, entretanto, para um primeiro curso de cálculo, as funções que utilizaremos estarão satisfazendo tais condições.

Exemplo 1

Calcule ฀ ฀x2+ 1)5฀2x฀x.

Pelo que foi explicado anteriormente, devemos identificar as funções envolvidas, ou seja, a g฀฀฀฀e af ฀฀฀฀. Neste exemplo, se olharmos bem, veremos uma

composta ฀฀2_{+ 1)}5฀ _{envolvendo as funções ฀฀x) =x}5฀ _{e ฀฀x) =x}฀_{+ 1. Note que se}

considerarmos tais funções temos que ฀ ฀x2_{+ 1)}5฀_2x฀x= ฀

f฀g฀x))g฀฀x)฀x, cujo

resultado é ฀฀g฀x)) +K, onde F é a primitiva da f. Calculemos então F:

฀฀x) = ฀

f฀x)dx= ฀

x5฀dx= x 51

51.

Portanto, ฀

฀x2+1)5฀2xdx= ฀

f฀g฀x))g฀฀x)dx=฀฀g฀x))+K= g฀x)

51

51 +K=

฀x2+ 1)51

51 +K

E a substituição u?

Outra maneira é fazendo a substituição u. Se tomarmos ฀=x฀฀ 1, então, ฀u

฀x = ฀x฀฀u= ฀x฀x. Assim, podemos reescrever a integral anterior como ฀

฀x2+ 1)5฀2xdx= ฀

u5฀du= u

51

51 +฀ =

฀x2+ 1)51

51 +฀.

Observação - É importante dar-se conta de que no método da substituição u você controla a escolha de u, mas, uma vez feita a escolha, você não tem controle sobre a expressão resultante

para du. Desse modo, no exemplo anterior, escolhemos ฀=x฀฀ 1, mas ฀u= ฀x฀x foi calculado. Afortunadamente, a nossa escolha de u, combinada com du calculado, funcionou

perfeitamente para produzir uma integral envolvendo u fácil de calcular. Porém, em geral,

o método da substituição u falhará, se o u escolhido e o du calculado produzirem um

integrando, no qual persistem expressões envolvendo x, ou se não for possível calcular a

integral resultante. Dessa forma, por exemplo, a substituição ฀=x฀฀ 1, ฀u= ฀x฀x não irá funcionar para a integral

฀

pois a substituição transformará a integral anterior em ฀

u5฀฀os฀x)du,

que ainda contém uma expressão envolvendo x.

De uma forma geral, não há um método seguro e rápido para escolher u e, em alguns

casos, nenhuma escolha de u funcionará. Em tais casos, outros métodos serão necessários,

alguns dos quais serão estudados nas próximas aulas. Fazer a escolha apropriada de u virá

com a experiência, mas será útil seguir o roteiro seguinte combinado com um domínio das integrais básicas. (ANTON, 2000, p. 392).

Roteiro

1. Faça a escolha para

u, digamos uu==฀฀฀฀xx)).

2. Calcule

฀u฀u

฀x

฀x ==gg฀฀฀฀xx)).

3. Faça a substituição u

u==฀฀฀฀xx)), ฀u฀u==gg฀฀฀฀xx))฀x฀x.

Neste ponto, toda a integral deve estar em termos de u; nenhum x deve

continuar. Se isso não acontecer, deve-se tentar uma nova escolha para u.

4. Calcule a integral resultante, se possível.

5. Substitua

u por g(x); assim, a resposta fi nal estará em termos de x.

(ANTON, 2000, p. 392).

Exemplo 2

Calcule ฀

sen฀x+ 9)฀x.

Solução

De imediato, vemos uma composta s฀n฀x+ 9) das funções f฀x) =s฀n฀x) e

฀฀x) =x+ 9. Note que ฀฀฀x) = 1, o que nos garante que a integral anterior pode ser

escrita como ฀

sen฀x+ 9)฀x=฀ f฀g฀x))g฀฀x)฀x. Encontrando a primitiva da f, temos

฀

฀

sen฀x+ 9)dx=฀ f฀g฀x))g฀฀x)dx=฀฀g฀x)) +K

=฀cos฀g฀x)) +K=฀cos฀x+ 9) +K.

Outra forma é chamar u=x฀ 9฀ ฀u

฀x = 1฀฀u=฀x; substituindo u, ud na integral, temos

฀

sen฀u)du=฀cos฀u) +฀=฀cos฀x+ 9) +฀.

Exemplo 3

Calcule ฀ ฀os฀5x)dx.

Solução

De imediato, vemos uma composta ฀os฀5x) das funções f฀x) =฀os฀x) e ฀฀x) = 5x . Temos, então, que ฀฀฀x) = 5. Agora não temos mais que a integral está escrita na forma

฀

f฀g฀x))g฀฀x)฀x, pois para que isso ocorresse deveríamos ter a seguinte integral ฀

฀os฀5x)5dx= 5 ฀

฀os฀5x)dx.

Ora, mas podemos fazer manipulações com ฀

฀os฀5x)dx para obtermos essa integral. Basta verificar que



cos฀5x)dx= 5 5



cos฀5x)dx= 1 5

฀

cos฀5x)5dx



= 1 5

฀

f฀g฀x))g฀_฀x)dx₌ ฀฀g฀x))

5 +K.

Calculando a primitiva de f, temos

฀

฀os฀x)dx=sen฀x) e, portanto,

฀

cos฀5x)dx= sen฀g฀x))

5 +฀=

sen฀5x)

5 +฀.

Outra forma é chamar u= ฀x฀ ฀u_฀x = ฀฀ ฀u_฀ =฀x; substituindo u, ud na integral,

temos ฀

cos฀u)du 5 =

1 5

฀

cos฀u)du= 1

5sen฀u) +฀ =

sen฀5x)

Atividade 1

Exemplo 4

Calcule฀ sen฀x)฀_{฀os฀x)dx.}

Calcule as seguintes integrais indefi nidas (tente encontrar a substituição u. Caso não consiga, poderá enconrar algumas sugestões ao fi nal desta aula)

a)

฀฀ 22xx฀฀xx฀฀+ 1)+ 1)฀3฀3฀x฀x

b)

฀฀ _55x x฀฀ x

x55_{฀ 1฀ 1}฀x฀x

c)

฀฀ _{1 ฀1 ฀}ee฀฀_ee฀฀฀x฀x

d)

฀฀

ee฀฀฀฀฀x฀x

e)

฀฀ ee฀฀฀฀1 ฀1 ฀ee฀฀฀฀_฀t฀t

f)

฀฀

cos

cos฀4฀4฀฀))11฀฀sensen฀4฀4฀฀))d฀d฀

g)

฀฀ xx√√xx_฀฀฀฀฀x฀x

h)

฀฀

x฀osx

x฀osx฀3฀3xx฀฀))dxdx

i)

฀฀ ees฀ns฀n฀฀xx))฀os฀os฀฀xx))dxdx

Solução

Podemos observar uma composta das funções f฀x) =x฀_{eg฀x) =s฀n฀x).}

Note que g฀฀x) =฀os฀x), o que nos garante que a integral anterior pode ser escrita como

฀

sen฀x)฀_{฀os฀x)dx=}

฀

f฀g฀x))g฀_{฀x)dx. Encontrando a primitiva da f, temos} ฀ _x฀_฀x= x3

฀

e, portanto, ฀

sen฀x)฀_cos฀x)dx=฀ _f฀g฀x))g฀_{฀x)dx=฀฀g฀x))+K=} g฀x)3

3 +K=

sen฀x)3

3 +K

฀

sen฀x)฀_cos฀x)dx=฀ _f฀g฀x))g฀_{฀x)dx=฀฀g฀x))+K =} g฀x)3

3 +K =

sen฀x)3

3 +K.

Outra forma é chamar u=sen฀x)_฀ du

dx =฀os฀x)฀du=฀os฀x)dx; substituindo

u, du na integral, temos

฀

u฀du= u

3

3 +฀ =

sen฀x)3

y

x

b a

y = f(x)

A área sob uma curva e

as integrais definidas

V

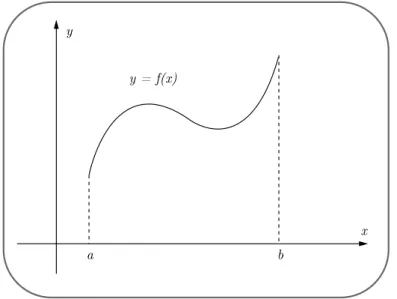
ocê já parou para se perguntar alguma vez na vida qual o significado da área da região limitada superiormente pelo gráfico de uma função y=฀฀x), que consideraremos por um instante não-negativa em seu intervalo de definição ฀฀x฀b; inferiormente pelo eixo x; e lateralmente pelas retas verticais x = a e x = b, como mostrado na Figura 1?

Figura 1 - Área A limitada superiormente pelo gráfico da função y=฀฀x); inferiormente pelo eixo x; e

lateralmente pelas retas verticais x฀฀ e x฀฀.

Vamos pensar juntos: se a curva representa a velocidade instantânea de um automóvel no tempo, então, a área representará a distância percorrida por esse automóvel do instante a ao instante b.

Se o gráfico representa a vazão instantânea de um líquido que está fluindo por um dado duto, então, a área representará a quantidade de líquido que fluiu do instante a ao instante b.

De maneira geral, sempre que um gráfico é construído para representar algum fenômeno, a área sob o gráfico tem algum significado relativo ao problema modelado.

Começaremos tratando do problema de encontrar a área da região limitada superiormente pelo gráfico de uma função y=฀฀x), que consideramos inicialmente não-negativa em seu intervalo de definição ฀_฀x_฀b; inferiormente pelo eixo x; e lateralmente pelas retas

verticais x฀฀ e x฀฀, como mostrado na Figura 1.

Suponhamos que a função y =฀฀x) é contínua no intervalo ฀a฀ b]. Ou seja, relembrando, isso significa que lim

x฀฀f฀x) =f฀฀) ou, ainda, que o gráfico de f não tem saltos nem furos

Além disso, suponhamos também que f seja limitada superiormente e inferiormente,

o que significa dizer que existe um número real positivo K, tal que _|f฀x)_{| ฀}฀ para todo x

em ฀a฀ b], e que existem os valores máximo e mínimo de f em ฀a฀ b].

Somas de Riemann

Para calcular a área pretendida, executaremos os seguintes procedimentos:

1. Subdividir o intervalo fechado

฀a฀ b] em n subintervalos usando um conjunto

P ฀{x฀฀ x1฀฀ ฀ ฀฀ x_฀฀1฀ x฀฀฀ ฀ ฀ ฀ xn฀1฀ xn} com n + 1 pontos, onde

a฀x฀ ฀ x1฀฀ ฀ ฀฀ x฀฀1฀ x฀฀฀ ฀ ฀฀ xn฀1 ฀ xn฀b, definindo n subintervalos ฀x฀, x1],฀x1, x2], ฀ ฀ ฀ ,฀x฀฀1, x฀], ฀ ฀ ฀ ,฀xn฀1, xn]. A um tal conjunto P denominamos de

partição de ฀a฀ b];

2. Em cada subintervalo fechado ฀x

฀฀฀฀ x฀], com k= ฀,2, ฀ ฀ ฀ , n, escolher ฀฀ um ponto, tal que ฀฀฀฀ ฀฀฀฀฀฀. Denotamos por ฀฀ a área do retângulo de base =f(x฀)฀x฀ ฀฀฀ e altura ฀฀x฀), ou seja, ฀฀=f(x฀)฀x฀;

3.

Denominar por A_n a soma das áreas dos n sub-retângulos definidos anteriormente, isto é,

฀n= n

฀

฀=฀

S฀= n

฀

฀=฀

f(x฀)฀฀x฀;

4.

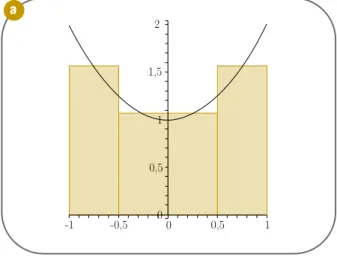
Façamos a quantidade de pontos da partição crescer indefinidamente, ou seja, tender para infinito.

Só para termos a noção de que esse limite de fato é a área: faremos o gráfico de ฀฀x) =x฀_{+ 1 no intervalo [฀฀฀฀]; faremos a aproximação por 4, 10 e 30 divisões do domínio}

2

1,5

1

0,5

0,5 1 -0,5

-1 00

a

2

1,5

1

0,5

0,5 1 -0,5

-1 00

x

c

2

1,5

1

0,5

0,5 1 -0,5

-1 00

x

b

Figura 2 - a) Aproximação da área sob a curva quando tomando partições de 4 e tomando ฀฀ como

sendo o ponto médio do subintervalo correspondente; b) aproximação da área sob a curva quando tomando partições de 10 e tomando ฀฀ como sendo o ponto médio do subintervalo correspondente;

c) aproximação da área sob a curva quando tomando partições de 30 e tomando ฀฀ como sendo o ponto

y

f(-0,6)

3

2

1

-1

-1 1 2 3 4

x f(0,6)

f(1,3)

f(2,5)

f (3,2)

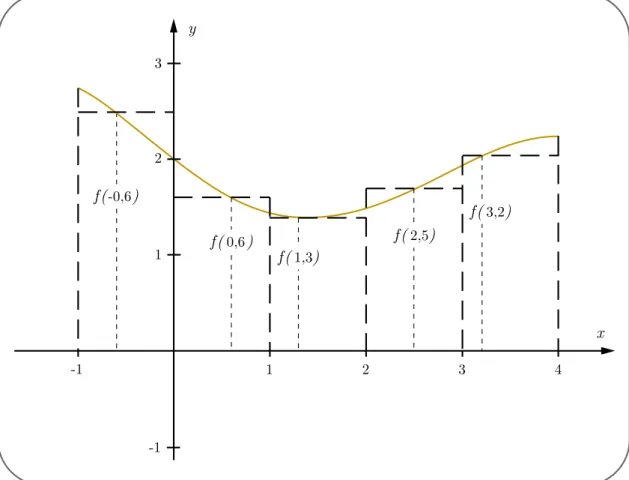
Figura 3 - Uma soma de Riemann da função ฀฀x) =฀฀x฀7)sin฀x))

9 + 2 para a partição P={฀1฀฀฀1฀2฀3฀4} e com a escolha dos x฀฀฀

x฀=฀฀฀6฀ x2= ฀฀6฀ x3= 1฀3฀ x4= 2฀5ex5= 3฀2.

Cálculo da área utilizando essa partição

฀฀ =

5

฀

k=฀

f(xk)฀xk ,

A฀ =f฀฀0฀6)·1 +f฀0฀6)·1 +f฀1฀3)·1 +f฀2฀5)·1 +f฀3฀2)·1

A฀ = 2฀5฀1 ฀ 1฀6฀1 ฀ 1฀4฀1 ฀ 1฀7฀1 ฀ 2฀5฀1

x y

f(x)

a b

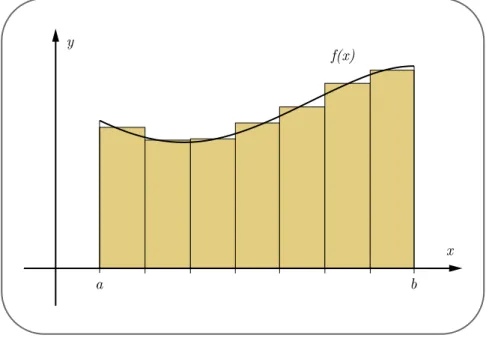
Figura 4- Aproximação da área sob a curva usando sete retângulos

Denominamos por norma de P, denotada por ฀฀฀, ao comprimento do maior subintervalo [x฀฀฀, x฀], k= ฀,2, ฀ ฀ ฀ , n.

Observação 1 - No item 1) se representarmos por ฀฀฀ o comprimento do k-ésimo subintervalo [x฀฀฀, x฀], k= ฀,2,3, ฀ ฀ ฀ , n, teremos, portanto, ฀฀฀=฀฀฀฀฀฀฀ e

n

฀

฀=฀

฀x฀ =b฀฀, pois

n

฀

฀=1

฀฀฀ = ฀฀1+ ฀฀2+ ฀฀3+฀ ฀ ฀+ ฀฀฀+ ฀฀฀฀1+฀ ฀ ฀+ ฀฀n฀1+ ฀฀n,

e como ฀฀_฀=฀฀฀฀฀฀฀=฀฀฀฀฀+฀฀, temos

n

฀

฀=1

฀฀฀ =฀฀฀+฀1฀฀1+฀2฀฀2+· · ·

฀฀_฀฀1+฀_฀฀1฀฀฀+฀฀+· · · ฀฀n฀1+฀n฀1+฀n.

Note que nessa soma todas as parcelas intermediárias se cancelam, restando apenas os extremos –x₀ e x_n. Portanto,

n

฀

฀=1

Defi nição 1

Se ฀ [฀ [a฀ ba฀ b]]฀฀RR for positiva e contínua em ฀฀a฀ ba฀ b]], então, a área sob a curva

y

y==฀฀฀฀xx)) no intervalo ฀฀a฀ ba฀ b]] é defi nida por ฀฀= lim= lim

n

n฀∞฀∞฀฀nn= lim= limnn฀∞฀∞

n n ฀

฀

฀ ฀=฀=฀

f

f((xx฀฀))฀฀฀฀xx.

A observação seguinte é muito importante e, mesmo não sendo oportuno prová-la neste momento do curso, convém deixá-la registrada.

Observação 3 - Esta defi nição é satisfatória para nossos propósitos nesta disciplina. Conforme já destacamos, queremos ressaltar que apenas a usaremos quando: f ฀ [a฀ b]฀R for

contínua, porque nesse caso podemos mostrar que o limite anterior não depende da escolha dos pontos x฀, x฀฀฀ ฀x฀฀x฀, k= ฀,2, ฀ ฀ ฀ , n escolhidos.

Antes de apresentarmos os exemplos, discutiremos um pouco sobre o procedimento 4 (das somas de Riemann), a saber, fazer a quantidade de pontos da partição crescer indefi nidamente, ou seja, tender para infi nito.

Vamos lá! Quando tomamos a partição no procedimento 1), iniciamos então com n + 1

pontos, certo? Se queremos que essa quantidade cresça, quem deve crescer: o n ou o 1?

Ora, o 1 não tem como crescer, pois ele é fi xo, a única quantidade passível de crescimento é o n. Assim, fazer a quantidade de pontos da partição crescer é fazer com que esse n seja cada vez maior, e fazer uma quantidade fi car cada vez maior é fazê-la crescer

indefi nidamente, e fazê-la crescer indefi nidamente é fazê-la se aproximar do infi nito ou, em outras palavras, fazê-la tender ao infi nito. Então, teremos que o n tomará valores cada

vez maiores, por exemplo, n = 10, 100, 1000, 10000, .... .

Se isso acontece com n, o que acontece com o valor de ฀

฀? Quando trabalhamos com frações, quando o numerador (>0) está fi xo e o denominador cresce, o que acontece com a fração? Ela decresce! Ilustrando isso com os valores anteriores, temos

1

n = ฀฀1,฀฀฀1,฀฀฀฀1,฀฀฀฀฀1, ฀ ฀ ฀ Então, se o denominador tender para infi nito (ou seja,

assumir valores cada vez maiores), temos que a fração assumirá valores positivos cada vez menores. Mas se a fração está assumindo valores positivos cada vez menores, teremos que cada vez mais ela estará se aproximando de zero (0), ou seja, a fração tenderá para 0 quando o denominador tender para infi nito. Em linguagem de limites, podemos escrever isso como Observação 2 - No item 2), se considerarmos a norma ฀฀฀ como uma constante, todos os subintervalos ฀x฀฀฀฀ x฀] terão o mesmo comprimento. Assim, ฀฀฀ = ฀฀, onde

฀x= b฀฀

n , e podemos escrever An da seguinte forma

฀n= n

฀

฀=฀

S฀ = n

฀

฀=฀

0 1 2 3 4

0 1 2

x

3 4

Figura 5 - Gráfico de f: [฀฀ b]฀R, a função definida por ฀฀x) =x.

Solução

Na Figura 5, vemos que a região limitada superiormente pelo gráfico, inferiormente pelo eixo x e lateralmente pela reta vertical x = b é um triângulo com base b e altura b. Logo, sua

área A é dada por ฀= b

฀

฀.

No entanto, estamos interessados em verificar que o processo de aproximação pela soma das áreas de pequenos retângulos dá o mesmo resultado.

Seja P ฀_฀x฀, x1, x2, ฀ ฀ ฀ , x฀฀1, x฀} uma partição do intervalo [฀฀ b], tal que

฀ =x฀ ฀ x1 ฀ x2 ฀฀ ฀ ฀฀ x฀฀1 ฀ x฀=b.

Do mesmo modo, temos, quando n tende a infinito, n฀, n3, ฀ ฀ ฀ , ou seja, todos tenderão para infinito, o que implicará pela explicação anterior:

lim

฀฀∞

1

n฀ = lim_฀฀∞

1

n3 = lim_฀฀∞

1

n4 =฀ ฀ ฀= ฀.

Com essa idéia em mente, partamos para os exemplos.

Exemplo 5

Seja f : [฀฀ b]_฀R a função definida por ฀฀x) =x, a função identidade. Apresentamos

Note que essa função é contínua, então, podemos tomar valores para os pontos da partição de modo que o comprimento da norma da partição seja constante. Tomemos os seguintes pontos como os da partição

x฀ = 0, x1=

b n, x2=

2b n, x3 =

3b

n, ฀ ฀ ฀ , x฀฀1 =

฀n_฀1)b n , x฀=

nb n =b.

Desse modo, as bases dos retângulos são todas de comprimentos iguais a ฀x= ฀ n , ou seja, ฀x= ฀฀0

n , que é o comprimento do intervalo [฀฀ b] dividido pelo número de pontos da partição, menos um. Vamos considerar as alturas dos retângulos como sendo ฀฀x฀), onde k= ฀,2,3, ฀ ฀ ฀ , n.

Então, f฀x฀) =x฀ = ฀

n, f฀x฀) =x฀=

2฀

n, ..., f฀x฀) =x฀= n฀

n =฀. Logo,

se chamarmos de S

n a soma de todos os n retângulos de base ฀฀฀ e altura ฀฀x฀), obteremos

S฀= ฀ b n  ฀ b n  + ฀_2b n  ฀ b n  +฀ ฀ ฀+ ฀_฀n ฀1)b n  ฀ b n  + ฀ nb n  ฀ b n 

= b฀

n฀[1 + 2 +฀ ฀ ฀+ ฀n฀1) +n].

Usando a fórmula 1 + 2 +฀ ฀ ฀+ ฀n_฀1) +n= n฀n+ 1)

2 , temos

฀฀=

b฀

n฀ ฀

n฀n+ 1)

2 =

b฀

2 ฀ n+ 1

n =

b฀

2 ฀

฀

1 + 1 n



.

Portanto, concluímos que a área da região é igual ao limite

lim

฀฀∞฀฀= lim฀฀∞

b฀

2 ฀

฀

1 ฀ 1

n



= b฀

2 ,

conforme esperávamos.

Exemplo 6

Vamos considerar agora a função f : [฀฀ b]฀R definida por y=฀฀x) =x฀, a função quadrática. Desejamos encontrar a área A da região limitada superiormente por esse gráfico,

inferiormente pelo eixo x e lateralmente pela reta vertical x฀฀.

Estamos interessados em usar o processo de aproximação pela soma das áreas de pequenos retângulos para obter a área desejada A.

Atividade 2

Tomemos novamente os mesmos valores utilizados no exemplo 5 para os pontos da partição:

x฀= 0, x1 =

b n, x2 =

2b n, x3=

3b

n, ฀ ฀ ฀ , x฀฀1=

฀n฀1)b n , x฀=

nb n =b. Desse modo, as bases dos retângulos são todas de comprimentos iguais a ฀x= ฀

n. Vamos considerar as alturas dos retângulos como sendo ฀฀x฀฀฀), onde k= ฀,2,3, ฀ ฀ ฀ , n.

Então, f฀x฀) =f฀0) = 0, f฀x1) = ฀_b

n 2

, f฀x2) = ฀_2b

n 2

, ฀ ฀ ฀ , f฀x฀฀1) = ฀_฀n

฀1)b n

2

.

Logo, se chamarmos de

s

_n a soma de todos os n retângulos de base ฀฀ e altura ฀฀x_฀฀฀),

obteremos

S฀= 0· ฀ b n  + ฀ b n

฀฀_b

n  + ฀₂ b n

฀฀_b

n



+฀ ฀ ฀+

฀_฀

n_฀1)b n

฀฀_b

n



= b3

n3[1 + 2฀+฀ ฀ ฀+ ฀n฀1)฀].

Usando a fórmula 1 + 2฀_{+฀ ฀ ฀+ ฀n฀1)}฀ ₌ ฀n฀1)·n·฀2n฀1)

6 , fi camos com

฀฀=

b฀ n฀ ·

฀n฀1)·n·฀2n฀1)

6 =

b฀

6 ·

n฀1 n ·

n n·

2n฀1 n , ฀฀= b฀ 6 · ฀ ฀฀ ฀ n  · ฀

2฀ ฀ n



.

Portanto, concluímos que a área da região é igual ao limite

lim

฀฀∞฀฀= lim฀฀∞

b฀ 6 · ฀ ฀฀ ฀ n  · ฀

2฀ ฀ n



= b฀ 6 ·2 =

b฀ 3 .

Resumindo, lim ฀฀∞฀฀=

b฀

฀ .

Calcule as seguintes somas de Riemann utilizando as partições dadas a seguir.

a)

Usando a escolha dos pontos ฀฀฀฀฀฀==฀฀฀฀฀฀฀฀ , mostre que a área A sob o

gráfi co da função yy฀฀฀฀฀฀ no intervalo [฀[฀฀ b฀ b]] é ฀฀== bb

฀ ฀

฀฀ .

b)

Usando a escolha dos pontos ฀฀฀฀฀฀==฀฀฀฀, ache a área sob o gráfi co da função

identidade y = x no intervalo [฀[฀฀ b฀ b]].

c)

Usando a escolha dos pontos ฀฀฀฀฀฀==฀฀฀฀, ache a área sob o gráfi co da função

Resumo

Nesta aula, a continuação do estudo das primitivas nos permitiu: encontrar primitivas utilizando a técnica da substituição u; e mostrar como se aproxima uma área abaixo de uma curva por retângulos, introduzindo as somas de Riemann, bem como usá-las para calcular áreas de regiões limitadas por gráficos de funções contínuas positivas.

Auto-avaliação

Descreva com suas palavras o procedimento de aproximação da área sob um gráfico utilizando retângulos.

Se no procedimento 2) das somas de Riemann você escolhesse como ฀฀฀฀ ฀฀฀฀฀฀:

a) tal que ฀

฀x฀) é o menor valor que a f assume no intervalo ฀x฀฀฀฀ x฀];

b) tal que ฀฀x

฀) é o maior valor que a f assume no intervalo ฀x฀฀฀฀ x฀].

O que poderíamos dizer sobre a soma obtida em a) com relação à soma obtida em b)?

Referências

ANTON, Howard. Cálculo: um novo horizonte. 6. ed. Porto Alegre: Bookman, 2000. v 1.

SIMMONS, George F. Cálculo: com geometria analítica. São Paulo: McGraw-Hill, 1987. v 1. THOMAS, George B. Cálculo. São Paulo: Addison Wesley, 2002.

1