André Gustavo Campos Pereira
Joaquim Elias de Freitas
Roosewelt Fonseca Soares
Cálculo I
D I S C I P L I N A
Propriedades da integral
definida e técnicas de integração
Autores
aula
Divisão de Serviços Técnicos
Catalogação da publicação na Fonte. UFRN/Biblioteca Central “Zila Mamede” Governo Federal
Presidente da República Luiz Inácio Lula da Silva Ministro da Educação Fernando Haddad
Secretário de Educação a Distância – SEED Carlos Eduardo Bielschowsky
Universidade Federal do Rio Grande do Norte
Reitor
José Ivonildo do Rêgo
Vice-Reitora
Ângela Maria Paiva Cruz
Secretária de Educação a Distância Vera Lúcia do Amaral
Secretaria de Educação a Distância- SEDIS
Coordenadora da Produção dos Materiais Marta Maria Castanho Almeida Pernambuco
Coordenador de Edição Ary Sergio Braga Olinisky
Projeto Gráfico Ivana Lima
Revisores de Estrutura e Linguagem Eugenio Tavares Borges
Jânio Gustavo Barbosa Thalyta Mabel Nobre Barbosa
Revisora das Normas da ABNT Verônica Pinheiro da Silva
Revisoras de Língua Portuguesa Janaina Tomaz Capistrano Sandra Cristinne Xavier da Câmara
Revisores Técnicos Leonardo Chagas da Silva Thaísa Maria Simplício Lemos
Revisora Tipográfica Nouraide Queiroz
Ilustradora Carolina Costa
Editoração de Imagens Adauto Harley Carolina Costa
Diagramadores Bruno de Souza Melo Dimetrius de Carvalho Ferreira Ivana Lima Johann Jean Evangelista de Melo
Adaptação para Módulo Matemático André Quintiliano Bezerra da Silva Kalinne Rayana Cavalcanti Pereira Thaísa Maria Simplício Lemos
Colaboradora Viviane Simioli Medeiros Campos
Apresentação
N
a aula 10 (A integral definida), apresentamos a definição de integral definida e utilizamos o teorema fundamental do cálculo para calcular tais integrais quando a função que estamos integrando é contínua. Nesta aula, estudaremos as propriedades da integral definida e algumas técnicas (técnicas de integração) que nos permitem calcular a integral mesmo que a função não tenha uma primitiva aparente.Objetivos
+ +
-
-y
f(x)
b x
a
Propriedades
Assim como mostramos na aula 8 (A primitiva), podemos usar outras variáveis de integração (para expressar a variável independente) para expressar uma integral definida,
tais como b
ft)t, 2
gx)xe x
ft)t.
Não sei se você notou, mas na definição das somas de Riemann, e posteriormente no
cálculo da integral definida b
fx)x, não falamos se a função f era positiva, negativa
ou podia mudar de sinal no intervalo que a estamos estudando, no caso a b]. Entretanto, é bom perceber que quando estamos analisando num subintervalo onde a função f é
negativa o termo (¯x)x será negativo, e, como estamos somando todos eles, teremos que lim
n
k=1
(¯xk)xk conterá parcelas positivas e negativas, sendo que as parcelas negativas representarão a “área” do retângulo de “altura” (x) (as aspas foram colocadas
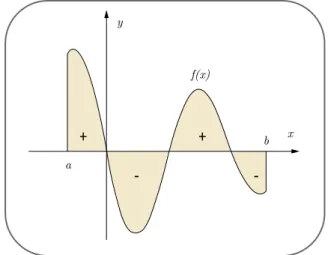
porque(x) é negativo e não existe altura em área negativas) e base . A soma da área desses retângulos nos dará a área entre a curva e o eixo. Assim, em termos de áreas podemos dizer que a soma de Riemann calcula a soma das áreas entre o eixo e o gráfico da função, observando que se a função é positiva o valor dessa “área” é positiva, se negativa a “área” será negativa. Tal resultado negativo apenas indicará que a função no intervalo de integração produz área maior abaixo do eixo do que acima. A Figura 1 ilustra essa discussão de forma mais simplificada.
Figura 1 - Sinal que a área terá no cálculo da integral
1
0,5
0
-0,5
-1
0 1 2 3 4 5 6
x
Figura 2 - Gráfico do seno no intervalo [,2]
Como ela é contínua e possui primitiva, temos que 2
senx)dx=cosx)2 =cos2)cos0)) =11) =1 + 1 = 0.
Ou seja, se observarmos apenas como área, teremos que a área seria zero. Ora, vemos claramente que a área não é zero. Então, tal integral não quer dizer área, e sim que a soma das áreas onde a área acima do gráfico recebe valor positivo e abaixo negativo é igual a zero. Isso ficou claro?
E se quisermos calcular a área dessas regiões? É o que veremos na próxima seção. Como a aplicação de integral não se resume ao cálculo de áreas, não mais nos referiremos à integral como a área abaixo do gráfico da f, senão teríamos que ficar colocando
aspas todas as vezes que aparecesse um número negativo.
Como encontrar a área total
Para determinar analiticamente a área entre o gráfico da função y=x) e o eixo x no
intervalo a b] proceda do seguinte modo.
1)
Particione o intervalo a b] com as raízes da função f;2)
Integre a função f em cada subintervalo;3)
Some os valores absolutos das integrais.Exemplo 1
Determine a área total da região entre a curva y= e o eixo x no intervalo fechado 3≤≤.
Solução
As raízes da função x) =x2x são x=2 e x=0. Construindo a partição P do intervalo [3, 2] com as raízes da função, obtemos P={3,2,0,2}.
Integral sobre [3, 2]:
3
x2x)x=
x 3
3 x
3 =
2)3
3
3)3
3 + 2)3)
=43;
integral sobre [3, 0]:
2
x22x)x=
x
3
3 x2
2
=
02)
3
3 + 02)2
=83+ 4 = 43;
integral sobre [0, 2]: 2
x22x)x=
x
3
3 x2 2
= 23
3 0 + 220
=83 4 =203 ;
área incluída:
2
3
x22x)x + 2
x22x)x+ 2
x22x)x = 43
+43 +
203
= 43 +43 +203 .
A área total entre o eixo x e a curva x) =x2x é 8
Exemplo 2
Determine a área total da região entre a curva y= e o eixo x, no intervalo fechado ≤≤.
Solução
As raízes da função x) =x4x são x=2 x= ex= 2. Construindo a
partição P do intervalo [2, 2] com as raízes da função, obtemos P ={22}.
Integral sobre [2, 0]:
2
x34x)x=
x4
4 2x2
2
=
02)
4
4 0 + 22)2
=164 + 8 = 4;
integral sobre [0, 2]: 2
x34x)x=
x4
4 2x2 2
= 24
4 0 + 22)2+ 0
= 16
4 8 = 48 =4;
área incluída:
2
x34x)x+
2
x34x)x
= 4 +| 4|= 4 + 4 = 8.
Procedendo da mesma maneira, calcularemos a área entre o gráfi co e o eixo x.
Na defi nição de integral defi nida, supusemos que o limite inferior a é menor que o limite superior b, ou seja, a b. Devido às propriedades da integral defi nida, é conveniente que estendamos esta defi nição aos demais casos abea b.
Defi nição 1
Seja f uma função integrável no intervalo fechado [a, b] e c um ponto qualquer em [a, b], então, defi nimos:
I)
bb f
fxx))xx==
bb
f
fxx))xx;
II)
ffxx))xx= 0= 0.
a c c x y f(x) f(x)dx c a
∫ ∫baf(x)dx
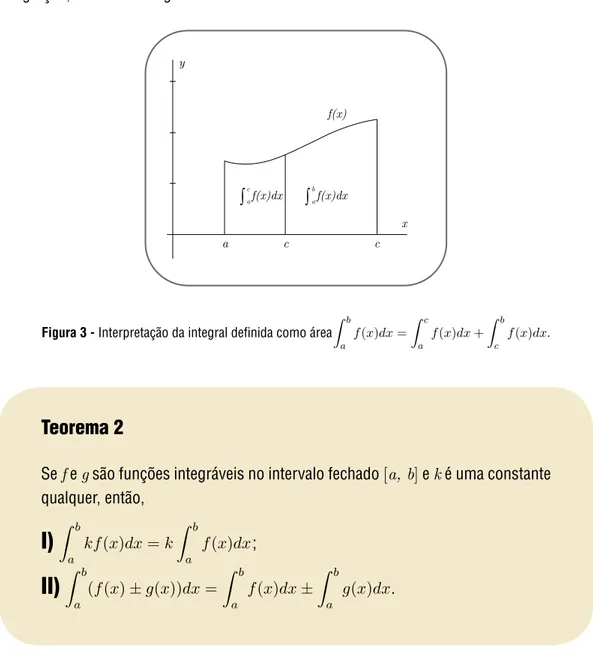
Teorema 1
Se f é uma função integrável no intervalo fechado [a, b] e se c é um ponto
qualquer em [a, b], então,
bb
f
fxx))xx==
cc
f
fxx))xx++
bb
c c f
fxx))xx..
Esse teorema é facilmente entendido interpretando-se a integral defi nida como o cálculo da área entre o eixo dos x e o gráfi co do integrando do limite inferior ao limite superior de
integração, conforme a Figura 3.
Figura 3 - Interpretação da integral defi nida como área b
fx)x=
c
fx)x+
b
c
fx)x.
Teorema 2
Se f e g são funções integráveis no intervalo fechado [a, b] e k é uma constante
qualquer, então,
I)
bb kf
kfxx))xx==kk bb
f fxx))xx;;;
II)
bb
ffxx))ggxx))))xx== bb
f
fxx))xx bb
g gxx))xx.
A integral defi nida tem os limites de integração b
fx)x e o resultado é um número,
enquanto a integral indefi nida fx)x não tem limites de integração e tem como resultado
uma função ou uma família de funções (a primitiva).
Exemplo 3
Seja f uma função constante defi nida pela equação fx) =, onde K é um número
constante. Então, b
fx)dx= b
dx= b
dx=xb =ba).
Geometricamente, isso signifi ca que um retângulo com largura b – a e altura tem
uma área igual a ||ba) unidades quadradas.
Em particular,
b
dx=
b
dx=b
e
b
0dx= 0·b) = 0.
Teorema 3
(Teorema do valor médio para integrais)Suponhamos que f seja uma função contínua no intervalo [a, b]. Então, existe
um número c em [a, b] tal que
cc))··bb) =) =
bb
f
fxx))dxdx.
Defi nição 2
(Valor médio de uma função em um intervalo)Seja f uma função integrável no intervalo [a, b]. Então, o valor médio de f em [a, b] é dado por
1 1 b b
bb
f fxx))dxdx..
Exemplo 4
Calcule o valor médio da função f definida por x) =x no intervalo [1, 4] e calcule um valor de c, nesse intervalo, tal que f (c) dê seu valor médio.
Solução
O valor médio desejado é dado por
1 41
4
x2x= 1 3
1
34313)
= 7.
Necessitamos encontrar o valor de c, com 4, tal que f) == 7. Então,
=.
Exemplo 5
(Determinando áreas com primitivas)Determine a área da região entre o eixo x e o gráfico da função x) =x3x2x no intervalo fechado ≤≤2.
Solução
Primeiro, determine as raízes da função f. Como
x) =x3x2x=x·x+ 1)x2),,
as raízes são x= x=1ex= 2. As raízes [–1, 2] são particionadas em dois subintervalos [–1, 0], em que x)0, e [0, 2], em que x)0. Integramos f ao longo de cada subintervalo e somamos os valores absolutos dos valores calculados.
Integral sobre [–1, 0]:
[10] :
1
x3x22x)dx=
x4
4
x3
3 x2
1
= 0
1
4 +
1 3 1
= 5
12;
integral sobre [0, 2]:
[02] :
2
x3x22x)dx=
x4
4
x3
3 x2 2
=
483 4
=83;;
área incluída: área total incluída é a soma dos valores absolutos das integrais no intervalo total particionado
1
x3x22x)x+ 2
x3x22x)x
= 125 + 83
Atividade 1
1
2
3
4
5
sua resposta
Calcule o valor médio da função f definida por x) =x no intervalo [1, 4] e calcule um valor de c, nesse intervalo, tal que f(c) dê seu valor médio.
Determine a área total da região entre o eixo x e o gráfico da função x) =x no intervalo fechado ≤≤.
Determine a área total da região entre o eixo x e o gráfico da função x) =x1 no intervalo fechado ≤≤.
Determine a área da região entre o eixo x e o gráfico da função x) =x+ 1, no intervalo fechado ≤≤.
Técnicas de integração
Integral por partes
Quando não podemos encontrar uma primitiva para o integrando de modo que se possa aplicar os teoremas vistos nas aulas anteriores, devemos buscar outros métodos para calcular a integral. Um deles é a da integração por partes.
Sejam u e v funções deriváveis de x, aplicando a regra de derivação do produto temos
xuv) =u v x+v
u x,
uv
x =
xuv)v u x.
Integrando ambos os membros em relação a x, obtemos a menos de constantes
uv
xx=
xuv)x
vu xx,
uv
xx=uv
vu xx.
Esta é a fórmula de integral por partes que pode ser reescrita na forma diferencial
a seguir
uvuv
vu.
Esta fórmula transforma uma integral em outra. Em alguns casos não conseguimos calcular a primeira integral, mas conseguimos a calcular a segunda, como veremos em alguns exemplos a seguir.
Esta técnica é muito usada nos casos quando se tem o produto de dois dos três tipos de funções: monômios em x, exponenciais e senos ou cossenos.
Exemplo 6
Calcule a integral
xsenxx pelo método da integração por partes.
Solução
Como não conseguimos visualizar uma primitiva imediata para xsnx), devemos tentar outra forma de calcular essa integral. Vamos tentar utilizar integração por partes, ou
seja, tentaremos usar a fórmula
uvuv
vu. Para tanto, devemos identificar
Uma tentativa natural seria ux dvsenxdx, pois com isso
xsenxx
uv
e assim já estaríamos com o primeiro membro da fórmula da mudança de variáveis. Calculemos os termos do segundo membro. Para isso, precisamos saber quem é v e du.
Sabemos que é dv, logo, para encontrar v precisamos apenas integrar dv, já
que
dv =v. No momento, não nos preocuparemos com as constantes,
para que fixemos nossa atenção no procedimento que deveremos executar. Assim,
v=
dv =
senx)dx=osx).
Como u=x, derivando u em relação a x teremos que u
x = x) = 1u=x e
assim o segundo membro pode ser escrito como
uv
vdu=xosx))
osx))dx; escrevendo a equação toda, temos
xsenxdx=x·osx)
osx)dx,
xsenxdx=xosx+
osxdx,
xsenxdx=xosx+senx.
Note que quando estamos trabalhando com integrais impróprias (sem os limites de integração) encontramos uma primitiva para o integrando, logo temos que a primitiva de xsenx)é xcosx) +senx) +.
Exemplo 7
Calcule a integral xosxdx.
Solução
Devemos identificar quem fará o papel de u e de v. Uma tentativa natural seria
u=x dv =cosx)dx. Assim,
xosxdx
udv, e usando integração por partes
temos
uvuv
vu.
Calculando v e du, temos dudx v
Substituindo u, due v no 2º membro da fórmula de integral por partes, obtemos
xosxdx=x·senx
senxdx,
xosdx=xsenxosx),
xosxdx=xsenx+osx.
A partir disso, podemos dizer que a primitiva de xcosx)éxsenx) +cosx) +.
Às vezes, precisamos utilizar a integração por partes mais de uma vez para chegarmos ao resultado, como ilustramos no exemplo a seguir
Exemplo 8
Calcule a integral
xsenxx.
Solução
Devemos identificar quem fará o papel de u e de v. Uma tentativa natural seria
u=x dv=senx)dx. Assim,
xsenx)x=
uv, e usando integração por
partes temos
uvuv
vu.
Calculando v e du, temos
du dx = x
) = 2x⇒du= 2xdxev=
senx)dx=osx).
Substituindo u, due v no 2º membro da fórmula de integral por partes, obtemos
xsenxdx=x·osx)
osx)2xdx,
xsenxdx=xosx+ 2
xosxdx
Note que a integral xosxdx foi calculada no exemplo 5, utilizando o resultado
obtido, chegamos a
xsenxdx=xosx+ 2xsenx+osx),
xsenxdx=xosx+ 2xsenx+ 2osx.
A partir daí, podemos dizer que a primitiva de xsnx) é
Exemplo 9
Calcule a integral indefinida xex.
Solução
Devemos identificar quem fará o papel de u e de v. Uma tentativa natural seria
ux dv edx. Assim, xex uv, e usando integração por partes temos
uvuv
vu.
Calculando v e du, temos u
x = x)= 1u=x e v
exe. Substituindo u, due v no 2º membro da fórmula de integral por partes,
xexx·e
ex,
xexxee
Daí podemos dizer que a primitiva de xeéxee.
Você poderá perguntar: e se quisermos utilizar a integração por partes para calcular a integral definida ao invés da integral indefinida?
A idéia é exatamente a mesma, vamos repetir o procedimento anterior para ilustrar a única mudança,
Sejam u e v funções deriváveis de x. Aplicando-se a regra de derivação do produto temos
xuv) =u v x +v
u x,
uv
x =
xuv)v u x.
Calculando a integral definida no mesmo intervalo de integração em ambos os membros em relação a x, obtemos (a mudança foi exatamente aqui)
b
uv
xx=
b
xuv)x
b
vu xx,
b
uv
x =uv
b
b
Esta é a fórmula de integral por partes (definida) que pode ser reescrita na forma
diferencial a seguir
v
uvuvb
b
vu.
Neste ponto quero deixar claro que as mudanças são feitas como anteriormente, ou seja, tanto o u quanto o v são funções de x e fizemos apenas as substituições
necessárias para continuarmos com a igualdade. Refaçamos os exemplos anteriores, agora para integral definida.
Exemplo 10
Calcule a integral
xosxdx.
Solução
Usando as mesmas escolhas do exemplo 7, teremos que
2
xcosxdx=x·senx
2 2 senxdx 2
xcosxdx=
2sen
2
0sen0)cosx)
2 , 2
xcosxdx=
2
cos
2
cos0))=
2 1
Exemplo 11
Calcule a integral
x2senxx.
Solução
Usando as mesmas escolhas do exemplo 6, teremos que
2
x2senxdx=x2·cosx)
2 2
cosx)2xdx,
2
x2senxdx=
22cos
2
02cos0))
+ 2
2
cosx)xdx= 2
Atividade 2
1
2
3
4
5
sua resposta
Calcule a integral
x
xosxdxosxdx pelo método da integração por partes.
Calcule a integral
x
xeexx pelo método da integração por partes.
Utilize o método da substituição e a integração por partes para calcular a integral
da da x
xeexx .
Utilize o método da substituição e a integração por partes para calcular a integral
da da
da substituição da substituição
x
x22ososxx22))dxdx .
Utilize o método da substituição e a integração por partes para calcular a integral
da da
da substituição da substituição da substituição da substituição
x
Resumo
1
2
3
Vimos nesta aula que a idéia de utilizar a integral apenas como área sob o gráfico de uma função pode causar certa confusão e que para calcular a área total devemos somar as áreas acima do eixo e tomar o valor positivo da integral que supostamente calcularia a área entre o gráfico e o eixo dos x. Vimos também que nem sempre a primitiva de uma função pode ser obtida de forma direta para que possamos usar o teorema fundamental do cálculo para resolver a integral. Quando isso acontece, podemos utilizar técnicas de integração para resolver a integral. Nesta aula, vimos ainda a técnica de integração por partes.
Auto-avaliação
Qual a diferença entre o resultado de uma integral definida e de uma indefinida?
Escreva com suas palavras o que ficou claro na discussão sobre utilizar a integral definida para cálculo de área compreendida entre o gráfico da função e o eixo x.
Você poderia fazer uma analogia com derivadas e escrever quais propriedades se repetem? Por exemplo, a derivada de uma função vezes uma constante é igual a constante vezes a derivada da função e a integral de uma constante vezes uma função é igual a constante vezes a integral da função.
Referências
ANTON, Howard. Cálculo:um novo horizonte. 6. ed. Porto Alegre: Bookman, 2000. v 1.
GUIDORIZZI, Hamilton Luiz. Um curso de cálculo. 5. ed. Rio de Janeiro: LTC, 2001. v 1.
SIMMONS, George F. Cálculo: com geometria analítica. São Paulo: McGraw-Hill, 1987. v 1.
![Figura 2 - Gráfico do seno no intervalo [,2]](https://thumb-eu.123doks.com/thumbv2/123dok_br/16340053.720840/5.892.230.536.224.484/figura-gráfico-do-seno-no-intervalo.webp)