Análise teórica do escoamento bifásico em evaporadores cilíndricos via transformada integral

Programa de Pós-Graduação em Engenharia Mecânica Mestrado – Doutorado

ANÁLISE TEÓRICA DO ESCOAMENTO BIFÁSICO EM

EVAPORADORES CILÍNDRICOS VIA TRANSFORMADA

INTEGRAL

por

Ediman Dias Novo

Dissertação de Mestrado apresentada à Universidade Federal da Paraíba para obtenção do grau de Mestre.

ANÁLISE TEÓRICA DO ESCOAMENTO BIFÁSICO EM

EVAPORADORES CILÍNDRICOS VIA TRANSFORMADA

INTEGRAL

Dissertação apresentada ao Programa de Pós-Graduação em Engenharia Mecânica da Universidade Federal da Paraíba, como parte dos requisitos para obtenção do título de Mestre em Engenharia Mecânica.

Orientador: Professor Dr. Carlos Antônio Cabral dos Santos.

N945a Novo, Ediman Dias.

Análise teórica do escoamento bifásico em evaporadores cilíndricos via transformada integral / Ediman Dias Novo.-- João Pessoa, 2003.

65f. : il.

Orientador: Carlos Antônio Cabral dos Santos Dissertação (Mestrado) – UFPB/CT

1. Engenharia mecânica. 2. GITT. 3. Escoamento bifásico. 4. Evaporador.

.

DEDICATÓRIA

AGRADECIMENTOS

Agradeço primeiramente a Deus, que nos concede a fé e a força necessária para a superação dos obstáculos e por ter me guiado em todos os momentos da minha vida.

Ao professor Orientador, Carlos Antônio Cabral dos Santos, pela paciência, companheirismo e pela sua imprescindível contribuição a esse trabalho.

Aos amigos do LES-UFPB: Jean Pierre, Jacques César, Vanderlan e tantos outros, com os quais convivi.

Agradeço a todos os professores, com os quais tive a oportunidade de caminhar junto.

ANÁLISE TEÓRICA DO ESCOAMENTO BIFÁSICO EM

EVAPORADORES CILÍNDRICOS VIA TRANSFORMADA INTEGRAL

RESUMO

Neste trabalho analisamos um trocador de calor do tipo evaporador cilíndrico, largamente utilizado em refrigeradores domésticos. O escoamento interno ocorre com um fluido em mudança de fase. As equações representativas do problema em estudo são as equações da conservação da massa, da quantidade de movimento e da energia. A ferramenta utilizada para solucionar estas equações diferenciais é a Técnica da Transformada Integral Generalizada (GITT), que produz soluções híbridas tanto para o campo hidrodinâmico como para o campo térmico.

O modelo considera que este evaporador é um tubo reto, com escoamento estratificado, onde ambas as fases, líquida e gasosa, podem escoar com velocidades diferentes. Para evitar a complexidade de se modelar cada fase separadamente é introduzido o conceito de fração de vazio. Os campos de velocidade e térmico são estudados na forma adimensional e formam um problema acoplado. O campo térmico é representado em função da entalpia.

THEORICAL ANALYSIS OF TWO PHASE FLOW IN CYLINDRICAL

EVAPORATORS BY INTEGRAL TRANSFORM

ABSTRACT

In this work we analyze a heat exchanger type cylindrical evaporator usually employed on the domestic refrigerators. The internal flow occurs with a fluid in phase change process. Equations representing the problem under study are the equations of conservation of mass momentum and energy. The tool used to solve these differential equations is the generalized integral transform technique (GITT) produces hybrid solutions for both the hydrodynamic field as for the thermal field.

The used model for the evaporator considers it as straight duct and with stratified flow where both phase liquid and vapor can flow with different too. To avoid mathematical complexity of modeling each phase separately is introduced the void fraction concept. The thermal and hydrodynamic fields are studied on the dimensional form and combine as a coupled problem. The thermal field is plotted against enthalpy.

SUMÁRIO

CAPÍTULO 1...………...01

1.1 MOTIVAÇÃO E OBJETIVOS...01

1.2 MÉTODOS DE ANÁLISE...02

1.2.1 Modelo Homogêneo...02

1.2.2 Modelo Separado...03

1.2.3 Método dos Modelos de Escoamento...03

1.3 MODELOS DE ESCOAMENTO...03

1.3.1 Modelos de Escoamentos Concorrentes Horizontais...04

1.3.2 Mapeamento de Transições dos Modelos de Escoamento...05

1.4 OCORRÊNCIAS DE ESCOAMENTO BIFÁSICO...07

1.4.1 Indústria...07

1.4.2 Aplicações...07

1.5 – REVISÃO BIBLIOGRÁFICA...08

CAPÍTULO 2...10

2.1 GENERALIDADES...10

2.2 LEIS DE CONSERVAÇÃO...12

2.2.1 Conservação da Massa...12

2.2.2 - Conservação da Quantidade de Movimento...15

2.2.3 – Conservação da energia para a região bifásica...16

CAPÍTULO 3...18

CAPÍTULO 5...32

5.1 ANÁLISE DOS RESULTADOS PARA O CAMPO DE VELOCIDADES...32

5.2 – ANÁLISE DOS RESULTADOS PARA O CAMPO DE ENTALPIA...38

5.3 CONCLUSÕES E SUGESTÕES...40

REFERÊNCIAS BIBLIOGRÁFICAS...41

APÊNDICE ...44

A - EQUAÇÃO DA QUANTIDADE DE MOVIMENTO ADIMENSIONAL...44

B - EQUAÇÃO DA ENERGIA ADIMENSIONAL...46

LISTA DE FIGURAS

Figura. 1.1 - Modelos de escoamento em dutos horizontais...04

Figura 1.2 - Mapa de transição para escoamento horizontal...06

Figura 2.1 - Escoamento estratificado...11

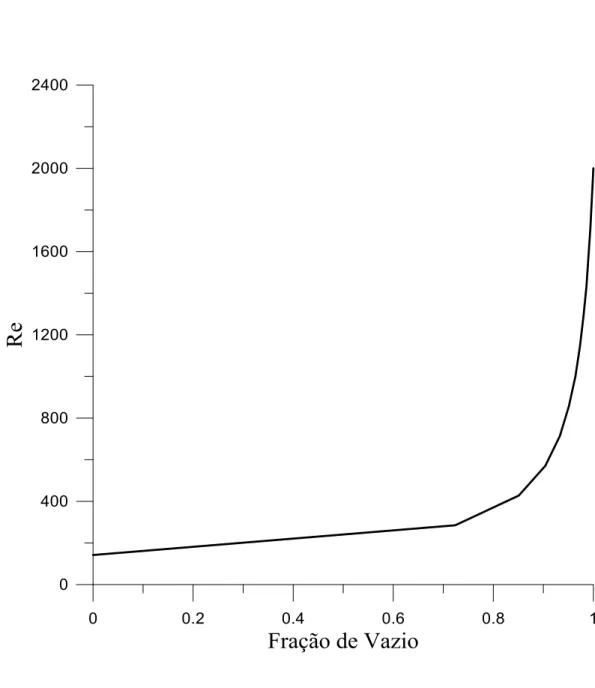
Figura 5.1 – Variação da fração de vazio com o número de Reynolds...35

Figura 5.2 – Variação do número de Reynolds com o título...36

LISTA DE TABELAS

LISTA DE SÍMBOLOS E ABREVIATURAS

A - Área

Bi - Número de Biot Cp - Calor específico.

CV - Coeficiente do campo de velocidades. CT - Coeficiente do campo térmico.

f - Coeficiente definido pela expressão (3.22) g - Gravidade

G - Velocidade de fluxo h - Entalpia

H - Entalpia adimensional

J0 - Função de Bessel de primeira espécie e ordem zero. J1 - Função de Bessel de primeira espécie e ordem um. k - Condutividade térmica

K - Condutividade térmica adimensional m - Fluxo de massa.

Nu - Número de Nusselt. p - Pressão

P - Pressão adimensional Pe - Número de Peclet Pr - Número de Prandtl Ec - Numero de Eckert q - Fluxo de calor r - Raio

VISCADI - Viscosidade adimensional

Vz(r,z) - Componente axial do campo de velocidade. X - Título

z - Comprimento

Z - Comprimento adimensional.

Letras Gregas



~ - Coeficiente definido pela expressão (2.12)  - Massa específica

 - Fração de vazio.  - Viscosidade dinâmica

 - Autofunção normalizada do campo de velocidade.  - Autovalor relacionado à função .

 - Autovalor relacionado à função 

 - Dissipação viscosa

 - Autofunção normalizada do campo térmico.

Subscritos

a - Adimensional. bi - Bifásico e - Entrada g - Gás

CAPÍTULO I

INTRODUÇÃO

1.1- MOTIVAÇÃO E OBJETIVOS

O fenômeno da evaporação e da condensação em dutos, independentemente da seção, bem como da posição em que estes se encontrem (vertical, horizontal ou inclinado) é um assunto extremamente importante e de reconhecido interesse na ciência dos termofluidos. O projeto de caldeiras aquatubulares, equipamentos de refrigeração, reatores nucleares resfriados a água, condensadores, evaporadores, além de outros itens existentes em instalações industriais térmicas e químicas, dependem de um sólido conhecimento dos processos de transferência de calor e dinâmica dos fluidos que ocorrem durante a evaporação e condensação convectiva.

Entende-se por evaporação convectiva “a adição de calor a um fluido escoando na fase líquida de forma tal que ocorra geração de vapor” (Collier, 1980). Esta definição exclui os processos “flash” onde a geração de vapor ocorre tão somente como resultado de uma redução na pressão do sistema. Na maioria das aplicações, entretanto, os dois processos ocorrem simultaneamente e, dessa forma, não podem ser claramente separados. Inversamente, a condensação convectiva é definida como “a remoção de calor de um fluido escoando na fase gasosa de forma tal que o vapor seja convertido em líquido” (Collier, 1980).

equipamento tal como mudanças no regime de escoamento ou no processo de transferência de calor. Na condensação, assim como na evaporação, estes processos estão fortemente acoplados e este acoplamento é muito maior do que o existente nos escoamentos monofásicos. A remoção ou adição de calor de um escoamento bifásico causará variações tanto na quantidade como na distribuição de cada fase bem como no modelo ou topologia do escoamento que, por sua vez, induzirão variações nos processos de transferência de calor local. Em função das contínuas mudanças nas propriedades termo-hidráulicas do escoamento, a situação em um dado ponto ao longo do eixo do duto poderá nunca ser totalmente hidráulica ou termicamente desenvolvida. Além do mais, por não estar em situação de equilíbrio, é necessário conhecer a variação das propriedades do escoamento à jusante do ponto considerado. Estas informações são necessárias para definir tanto a magnitude quanto a direção de afastamento do equilíbrio. A estas dificuldades adiciona-se o fato de que certas situações envolvem propriedades que variam com o tempo e outras, ausência do equilíbrio termodinâmico, percebe-se assim a grande complexidade do problema que está sendo analisado.

A proposta primaria deste trabalho é analisar os processos de evaporação em dutos de seção circular no qual escoam fluidos utilizados em equipamentos de refrigeração comercial (os conhecidos CFCs e HFCs).

1.2 – MÉTODOS DE ANÁLISE

1.2.1 - Modelo Homogêneo

Nesta abordagem, a mais simples aproximação do problema, o escoamento bifásico é assumido como se fosse um escoamento monofásico cujas pseudopropriedades são valores médios de cada fase separadamente. É também conhecido como o modelo do “fator de atrito” ou “fluxo de neblina” (Collier, 1980).

1.2.2 - Modelo Separado

Neste modelo as duas fases do escoamento são consideradas como artificialmente segregadas. Dois conjuntos de equações básicas podem ser escritos para cada fase e, alternativamente, as equações podem ser combinadas. Estas, por sua vez, devem trazer informações a respeito da área ocupada por cada fase (ou alternativamente, sobre a velocidade delas) e interações por atrito com as paredes do duto bem como entre elas próprias (Collier, 1980).

1.2.3 - Método dos “Modelos de Escoamento”

Nesta aproximação mais sofisticada, o escoamento bifásico é considerado um arranjo em uma das três ou quatro geometrias previamente definidas. Estas geometrias são baseadas nas várias configurações ou modelos de escoamento encontrados quando um gás e um líquido escoam juntos em canal. As equações básicas são solucionadas dentro da estrutura de cada uma destas representações idealizadas. Para se aplicar este modelo é necessário saber quando cada fase deve ser usada e ter habilidade para predizer a transição de um modelo para o outro (Collier, 1980).

1.3 – MODELOS DE ESCOAMENTO

estudo do escoamento gás-líquido. Entretanto, talvez a maior importância no estudo do escoamento bifásico seja a topologia ou geometria deste.

Quando um fluido escoando em um duto começa a mudar de fase, a mistura líquido-vapor gerada assume uma variedade de configurações conhecidas como modelos de escoamento. Um modelo particular dependerá das condições de pressão, escoamento, fluxo de calor e geometria do canal. Cada um dos modelos tem um nome descritivo e, no projeto de trocadores de calor, é desejável prever que modelo ou seqüência de modelos ocorrerá de forma que uma teoria hidráulica ou de transferência de calor apropriada àquele modelo possa ser corretamente escolhida (Collier, 1980). A seguir são mostrados alguns dos modelos mais

usados.

1.3.1 - Modelos de Escoamentos Concorrentes Horizontais

Os modelos observados neste tipo de escoamento, em dutos circulares horizontais ou inclinados, são bastante complicados pela assimetria das fases resultantes da influência da gravidade. Alguns dos modelos geralmente aceitos são mostrados a seguir (Figura 1.1).

Figura. 1.1 Modelos de escoamento em dutos horizontais.

a) Borbulhante b) Pistonado

c) Estratificado d) Ondas

- Escoamento Borbulhante. Neste modelo a fase gasosa é distribuída discretamente em forma de bolhas no meio da fase líquida. Em uma extremidade podem ser pequenas e esféricas enquanto na outra, grandes e ovaladas sem, contudo, tomarem o diâmetro do tubo. As bolhas de vapor tendem a viajar na parte superior do duto.

- Pistonado. Neste modelo as bolhas têm a forma alongada e ocupam aproximadamente o diâmetro do tubo e tendem a viajar na metade superior do tubo.

- Estratificado. Este modelo só ocorre para as fases líquida e gasosa viajando em velocidades muito baixas. As duas fases escoam separadamente com uma interface relativamente lisa.

- Ondas. A crescente velocidade da fase gasosa provoca uma perturbação na interface resultando no aparecimento de ondas viajando na direção do escoamento.

- Slug. Um aumento na velocidade do vapor gera o aparecimento de ondas na interface líquido-vapor que se propaga ao longo do canal em alta velocidade. A superfície superior do tubo por trás da onda é umedecida por um filme residual que escoa para a massa de líquido.

- Anular. Com o vapor escoando em alta velocidade resultará na formação de um centro ocupado totalmente pelo gás com uma película líquida sobre toda a periferia do duto. Este filme pode ou não ser contínuo ao longo de toda circunferência do duto, mas será evidentemente, mais espesso na base do duto.

1.3.2 - Mapeamento de Transições dos Modelos de Escoamento

Um método de representação das várias transições é o mapeamento, onde cada modelo é representado como áreas em um gráfico, cujos eixos coordenados são as velocidades reais de cada fase ou parâmetros generalizados contendo estas velocidades. Os modelos de escoamento também são influenciados por um número grande de variáveis secundárias, mas é impossível representá-las em um gráfico bi-dimensional. O uso das velocidades superficiais reais como eixos do mapa restringe sua aplicação a uma situação particular, mas embora a escolha de um parâmetro mais generalizado possa ser mais adequado para representar uma situação particular de transição, é improvável que este mesmo parâmetro seja apropriado para uma transição diferente governada por um diferente balanço de forças.

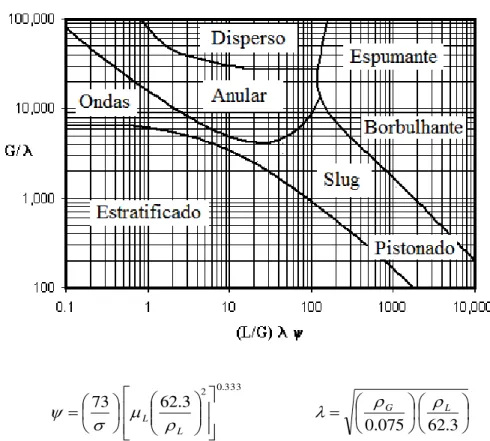
Um método alternativo e mais flexível que supera esta dificuldade é examinar cada transição individualmente e derivar um critério válido para aquela transição particular. Um exemplo de mapa de transição utilizado para escoamento horizontal pode ser visto a seguir (Figura 1.2).

         

   

   

  

            

3 . 62 075 . 0 3

. 62

73 2 0.333 _{G L}

L L

 

 

  

1.4 – OCORRÊNCIAS DE ESCOAMENTO BIFÁSICO

A seguir são mostrados ramos industriais que envolvem escoamento bifásico e alguns exemplos de aplicação:

1.4.1 Indústria

- Automotiva (climatização, transmissão, ar/combustível) - Eletrônica (resfriamento bifásico, condensação)

- Aeroespacial (controle térmico, propulsão, ar/combustível)

- Geração de energia (Instalações de potência com ciclo de Rankine) - Petroquímica e farmacêutica (transporte de gás, injeção de vapor)

1.4.2 Aplicações

- Simulação e dimensionamento de caldeiras, evaporadores e condensadores.

- Análise dos ciclos de Rankine e de compressão de vapor, incluindo respostas dinâmicas. - Processos de estrangulamento, incluindo refrigeração de Joule-Thomson com saída bifásica. - Projeto e simulação de bombeamento em tubos capilar e tubulações de vapor.

- Simulação de termosifão bifásico.

- Sistemas de distribuição e armazenamento de gás incluindo os efeitos de condensação. - Sistemas ar/combustão.

- Golpes de líquido e outros efeitos transientes rápidos incluindo “flash”, colunas de separação e outras oscilações em linhas bifásicas.

- Trocadores de calor condensados a ar e psicrometria do ar úmido, incluindo condensação sobre eletrônicos.

1.5 – REVISÃO BIBLIOGRÁFICA

A Técnica da Transformada Integral Clássica é um método puramente analítico de solução de problemas difusivos, que consiste na transformação de equações diferenciais parciais num sistema de equações diferenciais ordinárias desacoplado. A grande limitação desta técnica se deve à impossibilidade de resolver sistemas acoplados, implicando na resolução de sistemas lineares transformáveis, ou seja, problemas que podem ser transformados em sistemas desacoplados, ou que apresentam o problema auxiliar de fácil resolução. Existe uma vasta gama de trabalhos compilados por MIKHAILOV e ÖZISIK (1984). Como a maioria dos problemas existentes na natureza são regidos por equações não lineares, sentiu-se a necessidade de modificar e aperfeiçoar a técnica para permitir a resolução destes, então, surgiu a Técnica da Transformada Integral Generalizada com o trabalho de ÖZISIK e MURRAY (1974) sobre a solução de problemas difusivos com coeficientes nas condições de contorno variáveis.

A Técnica da transformada integral generalizada, mais conhecida pelas iniciais GITT - oriundas do inglês – possibilitou a resolução de equações tanto lineares como não lineares, através de uma solução híbrida analítico-numérica. Um trabalho bem completo e sistemático a respeito da GITT foi realizado por COTTA (1993), o qual dividiu os problemas nas seguintes categorias:

- Problemas com coeficientes variáveis na equação. Estes problemas tratam da análise transiente de aletas com dissipação dependente do tempo, desenvolvimento simultâneo de velocidade e temperatura no interior de dutos.

- Problemas com coeficientes variáveis nas condições de contorno. Aqui, incluem-se os problemas com coeficientes dependentes do tempo (condução com número de Biot variável) e problemas com coeficientes dependentes da variável espacial (convecção forçada em dutos aletados).

irregular e consistem de materiais/fases diferentes, com propriedades de transporte e termofísicas distintas.

- Problemas que envolvem problemas auxiliares complicados. Tais problemas são muito

aplicados na convecção forçada interna, periódica e transiente, na análise de trocadores de calor bitubulares e na secagem de meios porosos capilares.

- Problemas não lineares. Nesta categoria se encontra a maioria dos problemas práticos na engenharia, particularmente na mecânica dos fluidos e transferência de calor, onde pode-se citar: condução de calor com condutividade térmica variável, solução das equações de camada limite e solução das equações de Navier-Stokes.

CAPÍTULO II

FORMULAÇÃO DO PROBLEMA

2.1 GENERALIDADES

Como visto no capítulo anterior, são várias as ocorrências do escoamento bifásico de interesse prático na engenharia e, em virtude disto, um trabalho que cobrisse todos os campos se tornaria muito extenso. Dentre estes vários campos está a indústria da refrigeração e do condicionamento de ar, que oferece uma gama de variedades de pesquisas neste tipo de escoamento, haja vista a necessidade de troca dos fluidos refrigerantes convencionais pelos alternativos, que não atacam a camada de ozônio.

O trocador de calor em estudo consiste de um tubo em forma de serpentina. O modelo baseia-se na solução das equações unidimensionais da conservação da massa, da quantidade de movimento e da energia.

Para a modelagem do problema serão levadas em consideração as seguintes hipóteses: - O evaporador é considerado como um tubo reto, haja vista que as curvas têm raio muito grande em relação ao diâmetro deste;

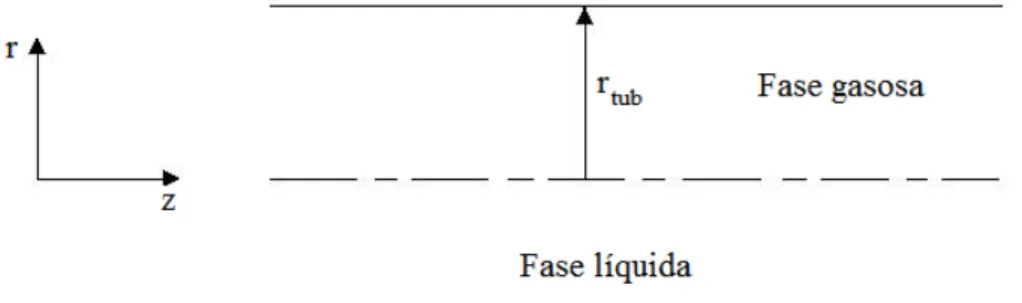
- O escoamento é estratificado (Figura 2.1); - Regime permanente;

- Coordenadas cilíndricas;

- VV_z(r,z).

- Não existe condução de calor na direção axial; - O tubo está na posição horizontal.

Figura 2.1 Escoamento estratificado

2.2 LEIS DE CONSERVAÇÃO

2.2.1 Conservação da Massa

A equação da continuidade na forma vetorial, para o escoamento monofásico, é escrita como segue:

0   

 V

Dt

D _ 

(2.1)

Aplicando-se as hipóteses simplificadoras na equação (2.1) esta assume a seguinte forma:

0 ) , ( )

,

( 

    

z r v z z z r

vz  z



(2.2)

Reorganizando a equação (2.2), temos:



( , )



0 



z r v

z  z (2.3)

Sabe-se que

A m z r vz



 ) , (

 (2.4)

Na região bifásica a equação (2.4) pode ser escrita para ambas as fases simultaneamente. Assim,

A m m

A

m g  l

Ou A A z r v A A z r v A m l l l g g

g ( , )  ( , )

    (2.6) ) 1 ( ; :

Onde   

A A A

A_{g l}

(2.7,8)

Substituindo-se as equações (2.7 e 2.8) em (2.6) obtém-se

] 1 )[ , ( ) , (      

 v r z v r z

A m l l g g  (2.9)

Manipulando-se a equação (2.9) esta assume a seguinte forma

      _   desl l g g R z r v A

m _{( , )  } [1 ] _(2.10)

) , ( ) , ( : Onde z r v z r v R l g

desl  (2.11)

Fazendo-se       _   desl l g R ] 1 [ ~ _{ }  

 (2.12)

Pode-se escrever a equação (2.10) da seguinte forma

~

Infelizmente a equação acima se aplica somente ao modelo homogêneo, ou seja, para ambas as fases viajando à mesma velocidade. Tal conclusão se deve ao fato de que nos extremos da região de saturação a razão de deslizamento ou é nula ou tende a infinito, já que uma das fases deixará de existir. Nesse caso,

) , ( ) , ( ) ,

(r z v r z v r z

vg  l  (2.14)

e a razão de deslizamento seria unitária, ou seja,

1 ) , (

) , (

 

z r v

z r v R

l g

desl (2.15)

Como nosso trabalho visa estabelecer um modelo que permita a análise tanto do modelo homogêneo quanto do modelo separado, faremos uso da seguinte expressão:

G z r v A m

g 

 ( , )~



(2.16)

onde “G” é a velocidade de massa do fluido refrigerante.

Dessa forma, a equação da continuidade para qualquer que seja a região será representada como segue:

 

0 



G

z (2.17)

2.2.2 - Conservação da Quantidade de Movimento

A forma vetorial da equação da quantidade de movimento para escoamento monofásico é: g V p Dt V

D  _  _

   2  _(2.18)

Fazendo-se uso das hipóteses simplificadoras, e fazendo-se uma análise de escala sobre os efeitos viscosos, a equação (2.18) assume a seguinte forma:

                 r z r v r r r z p z z r v z r

v z z

z ) , ( 1 ) , ( ) , ( 

 (2.19)

Escrevendo-se a equação (2.19) para a região bifásica temos:

               r z r v r r r dz dp z z r v

G z,bi( , ) bi _bi1 z,bi( , ) _(2.20)

onde: _bi _gx_l(1x) (2.21)

As condições de contorno são:

e bi

z r v

v_, ( ,0) (2.22)

0 ) , 0 ( , _   r z

vzbi _(2.23)

0 ) , (

, r z 

2.2.3 – Conservação da energia para a região bifásica

Seguindo-se a linha de raciocínio anterior escrevemos a forma monofásica da equação da conservação da energia:

           

 V V

Dt Dp p V q Dt

Dh     _ 2 



 

g r

Dt D v

Dt D

g  

  _             2 2 (2.25)

Aplicando-se as hipóteses simplificadoras na equação acima, fazendo-se uma análise de escala sobre os efeitos difusivos e convectivos e desprezando-se os efeitos viscosos na direção axial, temos:

 

_{ }

2

2 1 1 z z z z r z v z v z v r r r v r rq r z h v                  _ 

 (2.26)

Escrevendo-se a condução de calor radial em função da entalpia na equação (2.26) e aplicando-se a regra da cadeia na última parcela do lado direito temos:

 

z z z z p z v z v z v r r r v r h r r r C k z h v                      

 1 _ 1 _ 2

 (2.27)

Reorganizando-se a equação acima obtemos:

                             z v v z v r r r v r h r r r C k z h v z z z z p

z  

 1 1 (2.28)

A equação (2.28) pode ainda ser reescrita da seguinte forma:

z p v r h r r r C k z h v _z p z _              1

Escrevendo-se a equação (2.29) para a região bifásica, temos então:

z p v r h r r r C

k z h

G bi

bi z bi

bi p

bi bi

      

  

 

 

, ,

1

(2.30)

A equação (2.30) é a equação da energia para a região bifásica do escoamento do fluido refrigerante para uma pequena seção do tubo. As condições de contorno são:

 

e

bi r h

h ,0  (2.31)

 

0 , 0

  

r z

hbi _(2.32)

 

,

_

_{ }

_,

_

₀

  

 



h z r h k h r

z r h

t bi bi conv t

CAPÍTULO III

CAMPO DE VELOCIDADES

3.1 SOLUÇÃO DO CAMPO HIDRODINÂMICO VIA GITT

Este capítulo tem por objetivo mostrar a metodologia de uso da técnica da transformada integral generalizada (GITT), como ferramenta na obtenção da solução do problema de velocidade para o escoamento bifásico em tubo circular.

Seguindo o formalismo da GITT, o problema principal a ser solucionado, ou seja, a equação (2.20) será representado na forma adimensional. Para tanto serão utilizados os seguintes grupos adimensionais:

t

r r

R ;

t

r z

Z  ;





 

e bi

v z r v Z R

V* ,  ,

2 *

e e

bi

v p P



 ;

e bi

a _



  ;

e bi

a _

  

Dessa forma, a adimensionalização (ver apêndice) da equação unidimensional simplificada da quantidade de movimento resulta na seguinte expressão:













_

  

 

  

 

  



R Z R V R R R dZ

dP Z

Z R V Z R

V _a

e a

, 1

Re 2 1

, ,

* *

* _

As condições de contorno e inicial do problema, na forma adimensional são:

1 ) 0 , (

* _

R

V (3.2)

0 ) , 0 (

*

  

R Z

V _(3.3)

0 ) , 1 (

* _

Z

V (3.4)

O campo de velocidade é formado por duas parcelas, conforme mostra a equação abaixo:



R Z

 

V R Z



V

 

R

V* ,  ,  _ (3.5)

onde:

 

₂



₁ 2



R R

V_   (3.6)

Na equação (3.5), a primeira parcela refere-se ao desenvolvimento hidrodinâmico e a outra, representa a contribuição relativa ao escoamento completamente desenvolvido, definida pela equação (3.6).

Introduzindo-se as equações (3.5-6) na equação da quantidade de movimento, equação (3.1), obtemos:





 



 







a e a

e

a

R Z R V R R R

dZ dP Z

Z R V R V Z R V

 



Re 16 ,

1 Re

2

1 ,

,

   

   

 

   

 _

As condições de contorno e de entrada para o campo de velocidade tornam-se então:

 

R V

 

R

V ,0 1 _ (3.8)

0 ) , 0

( _

 

R Z V

(3.9)

0 ) , 1 ( Z 

V (3.10)

O problema auxiliar escolhido, que nos ajudará na solução do problema principal é:

0 ) ( )

( _ 2 _

  



R R dR

R d R dR

d

i i

i  



(3.11)

Com as seguintes condições de contorno:

0 ) 0 ( _

dR d_i

(3.12)

0 ) 1 ( 

i

 (3.13)

O sistema acima, conhecido como problema de Sturm-Liouville, tem a seguinte solução:

) ( ) ,

( R J_{0 i}R

i  

  (3.14)

Os autovalores são obtidos pela auto-condição dada abaixo:

0 ) (

0 i 

J  (3.15)

e o par transformada-inversa (ver apêndice) é

 



_

  



1

0

,Z dR R V R R Z

V_i _i Transformada (3.16)





_



   

  1 , i i i RV Z

Z R

V  Inversa (3.17)

os quais são, respectivamente, o potencial transformado e a fórmula de inversão.

Aplicando-se o operador



1R _i RdR

0  ( ) no problema principal, equação (3.7), e o

operador V R Z dR e

a



1

0 ( , )

Re

2  no problema auxiliar, equação (3.11), somando-se as expressões

resultantes e aplicando-se o teorema de Green, após fazer algumas manipulações matemáticas e fazendo uso das condições de contorno obtém-se a seguinte expressão

  





 







 

 



,

  

0

Re 2 Re 16 1 , , 1 0 2 1 0 1 0 1 0           









 RdR R Z R V dR R R dR R R dZ dP dR Z Z R V R V Z R V R R i i e a i e a i a i     (3.18)

O gradiente de pressão que aparece na equação (3.18) é obtido quando se aplica o

operador



1RdR

0 no problema principal, equação (3.7). Logo

Ou, substituindo-se a transformada e a inversa na equação (3.19):

   

 

 

 

 

e a i i i e a i i i a i i i a dR d Z V dR dZ Z V d R RV dZ Z V d Z V dZ dP Re 16 1 Re 4 2 2 1 1 0 1 1           









       (3.20)

Substituindo-se a equação (3.19) na equação (3.18) e fazendo-se algumas manipulações matemáticas obtém-se:

  

 



    



 



 



 

  



   

  

,



0

Re 2 , 1 Re 4 , 2 , , 2 , , , 1 0 2 1 0 1 0 1 0 1 0 1 0 1 0 1 0              

















  dR Z R V R R dR R Z V R R dR dZ Z R dV R RV dR R R dR dZ Z R dV Z R RV dR R R dR dZ Z R dV R V R R dR dZ Z R dV Z R V R R i i e a i e a i i i i    (3.21)

Substituindo-se o par transformada-inversa na equação (3.21) e reorganizando-se a expressão resultante, obtemos:





 

 

 

1

_{ }

₀

onde:

     



   

1

0

1 R R R R dR

CV _{ijk i j k} (3.23)

 





1

0

2 R R dR

CV i i (3.24)

     



   

1

0

3 R R RV R dR

CV _{ik i k} (3.25)

   



 

1

0

4 R RV R dR

CV k k (3.26)

A equação (3.22) expressa matematicamente o potencial de velocidades em estudo. Este é um problema de valor inicial, cuja condição inicial de entrada transformada é obtida

aplicando-se o operador



1R _i RdR

0  ( ) na condição de contorno, equação (3.8), ou seja,

   

_

   

_

 



 _ 1

0 1

0 1

0Ri RV R,0dR Ri RV R dR Ri R dR (3.27)

Portanto,

 



_

 



_

1

 

0 3 1

0

2

0 R R dR R RdR

A velocidade média do escoamento pode ser determinada analiticamente pela integração do perfil de velocidades, ou seja,





 









     













 1 0 1 0 3 1 0 1 0 1 0 1 0 2 2 , , RdR dR R RdR dR Z R RV RdR dR R V Z R V R Vmédia

   

 

 

1 2 2 2 1 1 0 2 1 1 0 4 1 0 2 1 0 _                           



 

    i i i i i i Z V f R R R dR Z V R R (3.29) Portanto, 1 ) ( 2 1        



  i i i média fV Z

V (3.30)

onde:

 



 1

0R RdR

CAPÍTULO IV

CAMPO TÉRMICO

4.1 SOLUÇÃO DO CAMPO TÉRMICO VIA GITT

Conforme feito para o campo de velocidades, este capítulo mostra a metodologia da técnica da transformada integral generalizada como ferramenta para a solução do problema de temperatura.

A partir da equação unidimensional simplificada da energia para a região bifásica, obtém-se o problema principal adimensionalizado, desenvolve-se o par transformada-integral e soluciona-se o problema de autovalor associado resultante.

Além dos grupos adimensionais utilizados no capítulo anterior, serão usados:

e bi a

e bi a

g e

g bi

Cp Cp Cp

k k K

h h

h h Z R H

 

  

) , (





t e e e e p e e t e e e e e e g e e a a e Gr C k Gr Pe dZ dP R V Z R V h h v R Z R H R R R Cp K Pe Z Z R H        _                  Re 2 Pr 1 2 : Onde ) ( ) , ( ) , ( 1 2 ) , ( 2 (4.1)

As condições de contorno, equações (2.31), (2.32) e (2.33), adimensionalizadas são:

 

R,0 1

H (4.2)

 

0, _0   R Z H (4.3)

 

1, _

_{ }

_{1, 0}   Z BiH R Z H (4.4)

O problema de autovalor associado escolhido é:

 

_ 2_

_{ }

_0        R R dR R d R dR d i i

i  _(4.5)

 

0 _0 

dR

d i _(4.6)

 

1 *

_{ }

₁ i i

Bi dR

d _{ }

(4.7)

A solução analítica do problema (4.5, 6 e 7) é:

) ( ) ,

( R J R

Os autovalores são obtidos através da auto-condição dada abaixo:

i i i J J

Bi* ₀( ) ₁( ) (4.9)

O par transformada-inversa é

dR R R N N R R Z H R Z R H dR Z R H R R Z H i i i i i i i i i i







           1 0 2 1 1 0 ) , ( , ) , ( ) ( : Onde ) ( ) ( ) , ( ) , ( ) ( ) (   (4.10-11)

Operando-se na equação (4.1) com



1R_i RdR

0 ( ) , obtemos:

 

 

Operando-se na equação (4.5) com _{H R Z dR} Cp K Pe a a e



1

0 ( , )

2

, obtemos:





 

  

,



0 2 , 2 1 0 2 1 0          





dR Z R H R R Cp K Pe dR dR R d R dR d Z R H Cp K Pe i i a a e i a a e  (4.13)

Somando-se as equações (4.12) e (4.13), obtemos:

 

 





  



 

( , )



,



 

2 , 2 ) ( ) , ( ) , ( 1 0 1 0 2 1 0 1 0                                        









 dR dR R d R dR d Z R H R Z R H R R R Cp K Pe dR Z R H R R Cp K Pe dR R V Z R V R R dZ dP Ec dR Z Z R H R R i i a a e i i a a e i i

 _(4.14)

Aplicando-se o Teorema de Green na integral do lado direito da igualdade da equação (4.14), esta assume a seguinte forma:

 

 





  







   

1 1 2 , 2 ) ( ) , ( ) , ( 1 0 2 1 0 1 0 ,Z H Γ Bi Bi Cp K Pe dR Z R H R R Cp K Pe dR R V Z R V R R dZ dP Ec dR Z Z R H R R i * a a e i i a a e i i          









Reorganizando-se a equação (4.15), obtemos:

 

  



   

  







   

0 1 1 2 , 2 , ) , ( 1 0 2 1 0 1 0 1 0









             ,Z H Γ Bi Bi Cp K Pe dR Z R H R R Cp K Pe dR R V R R dZ dP Ec dR Z R V R R dZ dP Ec dR Z Z R H R R i * a a e i i a a e i i i  (4.16)

Substituindo-se a expressão de V_ na equação (4.16), obtemos:

Reorganizando-se a equaçãoão (4.17), obtemos:

 

  



 

 

  







   

0 1 1 2 , 2 2 2 , ) , ( 1 0 2 1 0 3 1 0 1 0 1 0











              ,Z H Γ Bi Bi Cp K Pe dR Z R H R R Cp K Pe dR R R dZ dP Ec dR R R dZ dP Ec dR Z R V R R dZ dP Ec dR Z Z R H R R i * a a e i i a a e i i i i  (4.18)

Introduzindo a transformada e a inversa na equação (4.18), obtemos:

   

 

   

 

 

 

 

2





 

1

   

1 0 2 2 2 1 * 2 1 0 3 1 0 1 1 0 1 1 0               











      j j j i j i i i j j j i j j j i Z H Bi Bi Cp K Pe Z H Cp K Pe dR R R dZ dP Ec dR R R dZ dP Ec Z V dR R R R dZ dP Ec dZ Z H d dR R R R  (4.19)

Reorganizando-se a equação (4.19), obtemos então:

 

_{ }



            1 1 2 ₂ 2 1 j j ij i a a e ij j

ij CT H Z

Cp K Pe dZ Z H d

CT  

 

4 5 0

3   _

dZ dP CT dZ dP CT dZ dP Z V

CT _{ij j i}_{ij i}_ij (4.20)

onde:

   



  

1

0

1 R R R dR

CT _{ij i j} (4.21)





   

1 1 2

2 *

j i a

a

e

ij Bi Bi

Cp K Pe

CT     (4.22)

   



 

 1

0

3 Ec R R R dR

CT _{ij i j} (4.23)

 





 1

0 2

4 Ec R R dR

CT i i (4.24)

 



 

1

0 3 2

5 Ec R R dR

CT _{i i} (4.25)

CAPÍTULO V

ANÁLISE DOS RESULTADOS

5.1 – ANÁLISE DOS RESULTADOS PARA O CAMPO DE VELOCIDADES

O Código Computacional foi elaborado em linguagem FORTRAN e implementado em um microcomputador Pentium com processador de 800 MHz, executado em ambiente WINDOWS.

Todos os coeficientes analíticos foram avaliados através do software MATHEMATICA 4.0.

A solução numérica do problema de valor inicial é encontrada com a utilização da sub-rotina DIVIPAG, disponível na biblioteca IMSL, que tem seu algoritmo baseado no método de GEAR, para resolver sistemas de equações diferenciais ordinárias de primeira ordem com alto grau de rigidez.

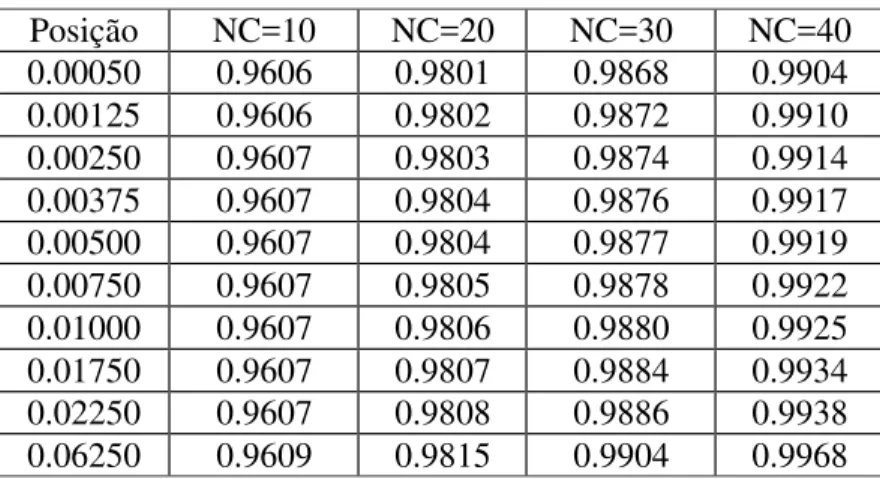
A tabela 5.1 a seguir mostra a convergência da velocidade longitudinal média em diversas posições ao longo do duto, no caso em que o escoamento é bifásico, ou seja, a viscosidade que aparece na equação (3.22) varia com a posição ao longo do tubo.

Tabela 5.1 – Convergência da velocidade longitudinal média para dutos circulares.

Posição NC=10 NC=20 NC=30 NC=40 0.00050 0.9606 0.9801 0.9868 0.9904 0.00125 0.9606 0.9802 0.9872 0.9910 0.00250 0.9607 0.9803 0.9874 0.9914 0.00375 0.9607 0.9804 0.9876 0.9917 0.00500 0.9607 0.9804 0.9877 0.9919 0.00750 0.9607 0.9805 0.9878 0.9922 0.01000 0.9607 0.9806 0.9880 0.9925 0.01750 0.9607 0.9807 0.9884 0.9934 0.02250 0.9607 0.9808 0.9886 0.9938 0.06250 0.9609 0.9815 0.9904 0.9968

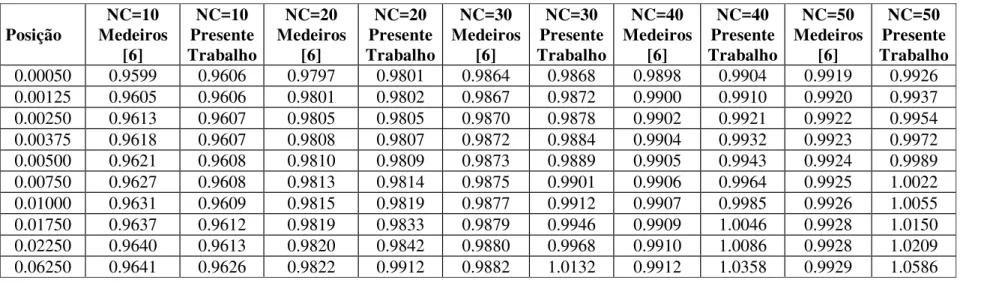
Tabela 5.2 – Convergência da velocidade longitudinal média para dutos circulares e comparação com os resultados obtidos por MEDEIROS (1988).

Posição

NC=10 Medeiros

[6]

NC=10 Presente Trabalho

NC=20 Medeiros

[6]

NC=20 Presente Trabalho

NC=30 Medeiros

[6]

NC=30 Presente Trabalho

NC=40 Medeiros

[6]

NC=40 Presente Trabalho

NC=50 Medeiros

[6]

A figura 5.1 a seguir apresenta a variação da fração de vazio com o número de Reynolds.

A figura 5.2 a seguir mostra a variação do número de Reynolds com o título.

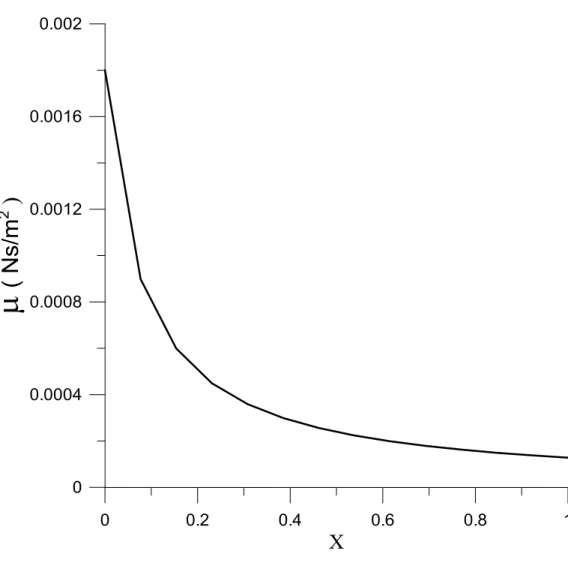
A figura 5.3 a seguir mostra a variação da viscosidade com o título.

5.2 – ANÁLISE DOS RESULTADOS PARA O CAMPO DE ENTALPIA

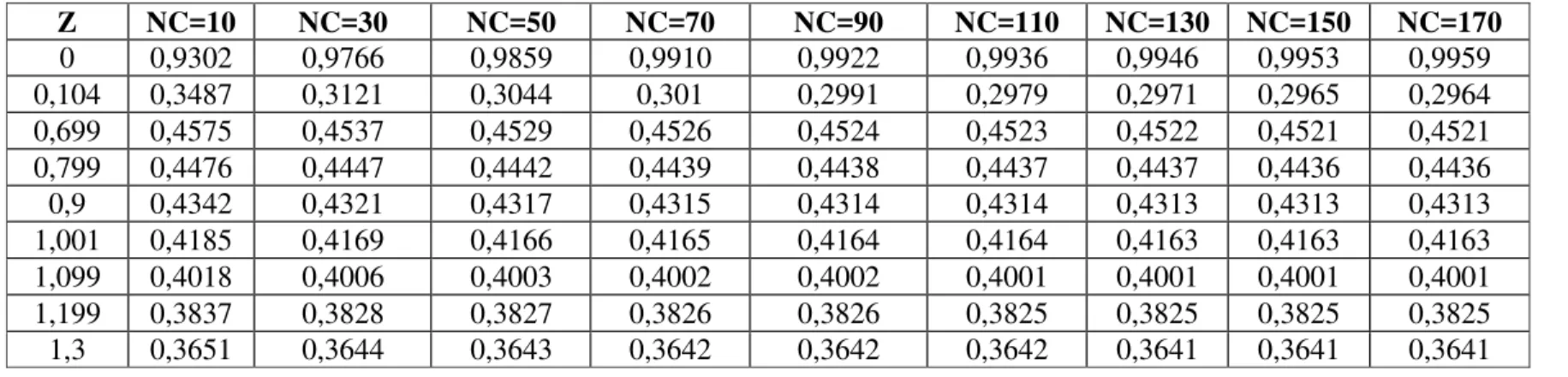
Tabela 5.3 – Análise de convergência para o campo de entalpia

Z NC=10 NC=30 NC=50 NC=70 NC=90 NC=110 NC=130 NC=150 NC=170

5.3 CONCLUSÕES E SUGESTÕES

É apresentada uma simulação do comportamento de um fluido refrigerante escoando em um tubo liso horizontal em processo de evaporação convectiva. Os perfis hidrodinâmico e entálpico para a região bifásica do escoamento são apresentados e o comportamento do fluido, à medida que o título varia, é observado ao longo do trocador. A GITT é usada na transformação integral das equações diferenciais parciais representativas do problema.

O uso da GITT como ferramenta na solução do problema tem como grande trunfo o fato de fornecer uma solução híbrida, isto é, analítico-numérica e um controle de erro pré-estabelecido.

O fenômeno da evaporação é representado no modelo fornecendo-se ao programa valores pré-estabelecidos para o título. Por este motivo é que a equação do campo térmico está representada pela entalpia. Esta expressão, na forma adimensional, resulta exatamente na expressão do título.

Como sugestões para trabalhos futuros cita-se: - Estudo para o regime transiente.

- Simulação para o regime turbulento.

- Fazer o mapeamento da variação dos modelos do escoamento durante a mudança de fase.

- Simulação com fluidos refrigerantes alternativos e comparação com os convencionais. - Estudar a influência das aletas neste modelo.

REFERÊNCIAS BIBLIOGRÁFICAS

COLLIER, J. G., “Convective Boiling and Condensation”, McGraw-Hill, 1980.

WITZEL, O. W. e FONTAINE, W. E., “What are the Heat Transfer Characteristics of wire and Tube Condensers?”, 43rd _{Semiannual Meeting of ASRE, pp. 33-38, November,} 26-28, 1956.

CYPHERS, J. A., CESS, R. D. e SOMERS, E. V., “Heat Transfer Character of Wire -and-Tube Heat Exchangers”, 45rd _{Semiannual Meeting of ASRE, pp. 86-90, December, 1-3,} 1958.

WITZEL, O. W., FONTAINE, W. E. e PAPANEK, W. J., “Convective Films Evaluated for Wire and Tube Heat Exchangers”, ASHRAE Journal, pp.35-37, June, 1959.

COLLICOTT, H. E., FONTAINE, W. E. e WITZELL, O. W., “Radiation and Free Convection Heat Transfer from Wire and Tube Heat Exchangers”, ASHRAE Journal, pp. 79-83, December, 1963.

HOKE, J. L., CLAUSING, A. M. e SWOFFORD, T. D., “An Experimental Investigation of Convective Heat Transfer from Wire-on-Tube Heat Exchangers”, Transactions of the ASME, Vol. 119, pp. 348-356, 1997.

TANDA, G. e TAGLIAFICO, L., “Free Convection Heat Transfer from Wire-and-Tube Heat Exchangers”, Transactions of the ASME, Vol. 119, pp. 370-372, 1997.

WANG, C., CHIANG, C., “Two-Phase Heat Transfer Characteristics for R-22/R-407C in a 6.5 mm smooth Tube”, International Journal of Heat and Fluid Flow, Vol. 18, pp. 550-558, 1997.

JIA, X., TSO, C. P., JOLLY, P. e WONG, Y. W., “Distributed Steady and Dynamic Modelling of Dry-Expansion Evaporators”, International Journal of Refrigeration, Vol. 12, pp. 126-136, 1999.

HERMES, C. J. L, MELO, C. e NEGRÃO, C. O. R., “Modelamento em Regime Transiente de um Condensador do Tipo Arame sobre Tubo com Movimentação Natural de Ar”, XV Congresso Brasileiro de Engenharia Mecânica, Novembro, 22-26, 1999.

WONGWISES, S. SONGNETICHAOVALIT, T., LOKATHADA, N., KRITSADATHIKAM, P., SUCHATAWAT, M. e PIROMPAK, W., “A Comparison of the Flow Characteristics of Refrigerants flowing Through Adiabatic Capillary Tubes”, International Journal of Heat Mass Transfer, Vol. 27, No. 5, pp. 611-621, 2000.

LIN, S., KEW, P. A e CORNWELL, K., “Two-Phase Heat Transfer to a Refrigerant in a 1 mm Diameter Tube”, International Journal of Refrigeration, Vol. 24, pp. 51-56, 2001. CAVALLINI, A., CENSI, G., DEL COL, D. DORETTI, L., LONGO, G. A. E ROSSETTO, L., “Experimental Investigation on Condensation Heat Transfer and Pressure Drop of New HFC Refrigerants (R134a, R125, R32, R410A, R236ea) in a Horizontal Smooth Tube”, International Journal of Refrigeration, Vol. 24, pp. 73-87, 2001.

BEJAN, A., “Convective Heat Transfer”; John Wiley, Colorado, 1984.

COTTA, R. M., ”Integral Transform in Computational Heat and Fluid Flow”, CRC Press, Boca Raton, Florida 1993.

MIKHAILOV, M. D. e ÖZISIK, M. N., “Unified Analysis and solutions of Heat and Mass Diffusion”; John Wiley, New York, 1984.

MEDEIROS, M. J., “Análise Teórica da Convecção Forçada Laminar Transiente em

desenvolvimento Simultâneo em Dutos”, Dissertação de Mestrado, UFPB, 1998. SCHLICHTING, H., “Boundary-Layer Theory”, McGraw-Hill, NY, 1968.

SOUMERAI, H., “Practical Thermodynamic Tools for Heat Exchanger Design Engineers”, John Wiley, 1987.

IMSL Library – MATH/LIB. Houston, Texas, 1989.

PROCESS ASSOCIATES OF AMERICA, “Two-Phase Horizontal Flow Regime Map”,

City, USA, http://www.processassociates.com/index.htm.

C&R TECHNOLOGIES, “Two-Phase Flow Capabilities”, 9 Red Fox Lane, Littleton, Colorado, USA, http://www.crtech.com/index.html.

APÊNDICE

A - EQUAÇÃO DA QUANTIDADE DE MOVIMENTO ADIMENSIONAL Considere a equação unidimensional simplificada da quantidade de movimento

               r z r v r r r dz dp z z r v

G z,bi( , ) bi _bi1 z,bi( , ) _(A.1)

Os grupos adimensionais utilizados são:

Substituindo os grupos adimensionais acima na equação (A.1) resulta                    ) ( ] 2 2 ) , ( [ ) ( 1 ) ( ] [ ) ( ] 2 2 ) , ( [ 2 2 t e e e t t t e a t e t e e e Rr R v v Z R V v R r R r R r Zr d P Gv d Zr R v v Z R V v G   (A.2)

Reorganizando a equação (A.2) tem-se

            _          R R Z R V R R R r v dZ dP r Gv Z Z R V r Gv t e e a t t t e 4 ) , ( 1 ) , ( 2   (A.3)

Reorganizando a equação anterior, temos:

 

dR R d R r v R Z R V R R R r v dZ dP r Gv Z Z R V r Gv t e e a t e e a t e t e 2 2 2 4 1 ) , ( 1 ) , (                    (A.4)

Reorganizando a equação anterior obtemos então:

Dividindo tudo por t e r Gv , obtemos: t e a t a e Gr R Z R V R R R Gr dZ dP Z Z R V   

 1 ( , ) 8

) , (                 (A.6) Ou e a e a R Z R V R R R dZ dP Z Z R V Re 16 ) , ( 1 Re 2 ) , (   _                (A.7) Onde: a e a t e e e t a e r v

Gr   

   Re 2  

Semelhante raciocínio é utilizado para obter as condições de contorno adimensionais.

B - EQUAÇÃO DA ENERGIA ADIMENSIONAL

A equação da energia é escrita como:

z p v r h r r r C k z h G bi bi z bi bi bi               ,

Além dos grupos adimensionais utilizados na adimensionalização da equação da quantidade de movimento, utilizamos aqui também os seguintes grupos adimensionais:

e bi a

e bi a

g e

g bi

Cp Cp Cp

k k K

h h

h h Z R H

 

  

) , (

Substituindo-se os grupos adimensionais na equação (B.1), obtemos:

  

















 

g g e t

h h h Z R H Zr

G ,

 

_ 

  















_

 



g g e t

t t t e e

a a

h h h Z R H Rr Rr Rr Rr Cp

K Cp

K

, 1

  







e g



g



t

h h h Z R H Zr

G  



 _{, (B.2)}

Reorganizando a equação anterior, temos:









_    Z Z R H r h h G t g e ,









_          R Z R H R R Rr h h Cp K Cp K t g e e e a a , 2





 





dZ dP R V Z R V r Gv t e   , 2 (B.3)

A equação anterior é então escrita como:









_            R Z R H R R R Cp K Cp K Gr Z Z R H e e a a t , 1 1 ,





 





dZ dP R V Z R V h h v g e e    , 2 (B.4)

Finalmente, escrevemos a equação anterior como:

C – DESENVOLVIMENTO DO PAR TRANSFORMADA-INVERSA

Considere a representação do potencial V(R,Z) em termos das autofunções(_i,R)

do problema auxiliar na região V como







 

1

, )

, ( ) ( )

, (

i

j

i Z R R V

A Z

R

V   (C.1)

A equação acima nos mostra que o potencial pode ser representado como uma expansão de(i,R) onde, os coeficientes Ai’s são determinados usando-se apropriedade

da ortogonalidade. Assim, operando em (C.1) com



1R _I RdR

0 ( , ) tem-se













1

1

0 1

0 ( , ) ( , ) ( ) ( , ) ( , ) ,

j

j i

i Z R R RdR

A dR Z R V R

R      (C.2)

Para i  j e, fazendo uso da propriedade de ortogonalidade, o lado direito de (C.2) fica

ij j j

j Z R RdR A Z N

A ( ) 1 ( , ) ( )

0

2 _



  (C.3)

e então

dR Z R V R R

N Z

A_j( ) _ij 1 ( _j, ) ( , )

0



   (C.4)

Reorganizando a equação anterior obtém-se

dR Z R V R R

N Z

A _j

ij

j ( , ) ( , )

1 )

( 1

0



   (C.5)