UNIVERSIDADE FEDERAL FLUMINENSE POLO UNIVERSITÁRIO DE VOLTA REDONDA ESCOLA DE ENGENHARIA INDUSTRIAL E METALÚRGICA DE VOLTA REDONDA DEPARTAMENTO DE CIÊNCIAS EXATAS

(1)

POLO UNIVERSITÁRIO DE VOLTA REDONDA

ESCOLA DE ENGENHARIA INDUSTRIAL E METALÚRGICA DE VOLTA REDONDA DEPARTAMENTO DE CIÊNCIAS EXATAS

(2)

POLO UNIVERSITÁRIO DE VOLTA REDONDA

ESCOLA DE ENGENHARIA INDUSTRIAL E METALÚRGICA DE VOLTA REDONDA DEPARTAMENTO DE CIÊNCIAS EXATAS

APOSTILA AUXILIAR DE FÍSICA EXPERIMENTAL

DANIELLA LOPES PINTO – MONITORA DE FÍSICA EXPERIMENTAL I (2014) SÉRGIO FELIPE F. SILVA – MONITOR DE FÍSICA EXP. II (2014) E I (2015)

Apostila auxiliar para os alunos de Física Experimental I, II e III da EEIMVR, cujo objetivo é ajudar no entendimento dos conceitos básicos, sendo estes fundamentais para o cumprimento das atividades das disciplinas.

Capa elaborada pelos autores.

1º Orientador: Prof. D.Sc. Wellington Gomes Dantas 2º Orientador: Prof. D.Sc. Rogério Menezes de Almeida

(3)

Sumário

1 TEORIA DE ERROS ... 1

1.1 Introdução ... 1

1.2 Conceitos básicos ... 1

1.2.1 Média e desvio padrão ... 1

1.2.2 Incertezas ... 2

1.3 Precisão x Acurácia ... 6

1.4 Forma Padrão... 7

1.5 Arredondamento de números ... 8

2 GRÁFICOS ... 13

2.2 Histograma ... 16

2.3 Gráficos logarítmicos ... 17

2.4 Principais erros em gráficos ... 19

3 TABELAS ... 21

3.2 Principais erros em tabelas ... 22

4 LEIS DE POTÊNCIA ... 24

4.2 Métodos de linearização ... 25

4.2.1 Linearização com logaritmo ... 25

4.2.2 Linearização com gráfico em escala logarítmica ... 29

4.2.3 Linearização quando o expoente da lei de escala é conhecido ... 30

5 PROPAGAÇÃO DE ERROS ... 34

6 MÍNIMOS QUADRADOS... 37

6.1 Introdução ... 37

6.2 Considerações e conceitos preliminares ... 37

6.3 Ajuste de uma função linear ... 38

BIBLIOGRAFIA ... 47

(4)

1 TEORIA DE ERROS

1.1 Introdução

Medidas experimentais, diferentemente do que acontece em cálculos teóricos, não fornecem resultados exatos. Toda e qualquer mensuração é afetada por erros que provêm tanto de fontes aleatórias, como condições ambientais e equívocos no ato de medir, como de limitações do próprio instrumento de medida.

Um exemplo em que essas dificuldades ficam evidentes é dado no problema mostrado na Figura 1.1.1, onde se tenta medir o comprimento de uma peça. Observe que as reentrâncias da peça não permitem estabelecer um ponto único de referência para o início e o final da mesma.

Figura 1.1.1: Peça sendo medida com o auxílio de uma régua.

Fonte: Elaborada pelo 1º orientador.

Além disso, é visto que o aparelho de medida também leva a uma incerteza, pois o final da peça pode estar entre duas divisões da régua, o que torna impossível determinar exatamente o valor deste comprimento.

Devido a estas incertezas, é necessário elaborar um método de apresentar resultados de medidas experimentais que contemplem os diferentes gêneros de erros. Nas próximas seções desta apostila, esses métodos serão discutidos, levando a uma forma apropriada para a apresentação dos resultados de medidas experimentais.

1.2 Conceitos básicos

1.2.1 Média e desvio padrão

(5)

medições. Para um maior aprofundamento na análise probabilística da Teoria de Erros, como também de toda a presente apostila, consulte o livro Fundamentos da

Teoria de Erros, de José Henrique Vuolo (Editora Edgard Blücher Ltda.).

O melhor valor aproximado que representa uma grandeza, que se está medindo vezes, é a média, que pode ser calculada pela Eq. (1.1).

= + + + ⋯ + + =∑ (1.1)

Como a melhor aproximação é a média, então a incerteza relacionada a esta medida está ligada à dispersão dos valores ao redor dela. A partir disso, pode-se calcular o desvio padrão, Eq. (1.2), pois este mostra o quanto de variação ou dispersão existe em relação à média.

= ∑ _{− 1}− (1.2)

1.2.2 Incertezas

Uma mesma medição pode estar suscetível a vários tipos de incertezas (erros). Vejamos algumas delas.

Os erros estatísticos, também chamados erros aleatórios, são erros acidentais ou casuais, que podem ser causados por mudanças na temperatura, pressão, umidade, etc. Não necessariamente ocorrem em todas as medições. Esta medida é o desvio padrão do valor médio, que pode ser calculado pela Eq. (1.3).

= Δ í = _√ (1.3)

Onde é o número de medições realizadas.

Exemplo 1.2.1: Dados os seguintes valores, pede-se que o erro estatístico seja calculado.

= 3,6; = 3,9; = 4,1

Resolução:

(6)

̅ =3,6 + 3,9 + 4,1₃ = 3,866

→ Elaboração de tabela auxiliar:

() − (* () − (* + 3,866 ₋ 3,6 0,070756 3,866 ₋3,9 0,001156 3,866 ₋4,1 0,054756

→ Cálculo do desvio padrão:

, ̅ − = 0,126668

= 0,126668_{3 − 1 = 0,251662}

→ Cálculo do erro estatístico:

Δ estat= 0,251662_√3 = 0,145297

Os erros sistemáticos, também chamados de erros instrumentais, são provenientes de características intrínsecas ao instrumento, como o material usado em seus componentes, que influi em uma incerteza na calibração e, consequentemente, na incerteza dos valores obtidos na coleta de dados. Como o próprio nome diz, ocorre sistematicamente em todas as medições (é o mesmo para qualquer medida obtida por tal instrumento).

Há duas formas básicas de erro sistemático de acordo com a natureza do instrumento. Se este for analógico, a incerteza é dada pela metade da menor medida de sua escala, isto é, _/2. Veja o exemplo da Figura 1.2.1.

(7)

Figura 1.2.1: Objeto sendo medido por uma régua milimetrada. Neste caso, sendo a régua um instrumento analógico, seu erro sistemático é sua menor medida dividida por 2, ou seja, 0,5 mm.

Fonte: Elaborada pelos autores.

Se o aparelho for digital, a incerteza é dada como uma unidade da menor medida (algarismo mais à direita no visor do instrumento). Veja a Figura 1.2.2.

Figura 1.2.2: Balança digital com erro de 0,1g. Como neste caso o instrumento é digital, a incerteza é diretamente uma unidade da menor medida fornecida pelo mesmo.

Fonte: BALANÇA digital. Lendo Mais. Disponível em: <http://www.lendomais.com.br/>. Acesso Jan. 2015. Adaptada.

(8)

Os erros adicionais são provenientes de variáveis externas ao experimento, e que influem diretamente na obtenção da medida, como erros humanos (observacional) ou variáveis do ambiente (ambiental). Estas incertezas são estimadas levando em conta os aspectos da medida.

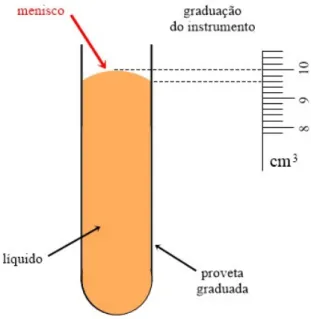
Exemplo 1.2.2: Em uma situação na qual seja necessário realizar uma única medida de volume de um determinado líquido com o auxílio de uma proveta graduada, vide Figura 1.2.3, pode haver a formação de menisco (curvatura superficial do líquido), o que dificulta na obtenção da medida correta no volume. Neste caso, não se pode determinar a incerteza da medida do volume pura e simplesmente considerando somente o erro sistemático (já que o erro estatístico seria nulo por ser medida uma única vez), é necessário também considerar um erro adicional. Veja o motivo.

Note pela figura que o menisco está maior que a incerteza da graduação da proveta (0,1 cm³), a mesmo está, pelo menos, entre 9,6 e 10,0 cm³. Ou seja, o tamanho deste intervalo (0,4 cm³) é maior que o erro sistemático.

Figura 1.2.3: Proveta graduada contendo um líquido cujo volume é medido. Veja no detalhe que existe um menisco que impede a obtenção mais exata da medida.

(9)

pois o menisco impede que o valor mais exato do mesmo seja obtido e tem uma dimensão maior que a incerteza da proveta. Daí vem a necessidade de um erro adicional para compensar essa diferença.

Neste caso, sabe-se pela figura que o líquido não extrapola os limites de 10,0 cm³ e 9,6 cm³. Levando em conta esse intervalo, pode-se estimar um erro adicional como a metade do intervalo (0,2 cm³). Lembre-se de que uma incerteza é representada com o sinal_±, sendo assim, o intervalo da incerteza_± 0,2 cm³ abrange

exatamente o intervalo de 0,4 cm³ entre 10,0 e 9,6 cm³, pois ₊0,2 ₋ (₋0,2) ₌ 0,4 (limite superior menos o limite inferior).

Englobando todos as incertezas anteriores, tem-se o erro total, que é a incerteza resultante (as que existirem), obtida da relação expressa na Eq. (1.4).

Δ 7= ±8 Δ + ∆ + Δ : ; 7 (1.4)

Exemplo 1.2.3: Para o exemplo da proveta graduada acima, tem-se:

Δ< 7= ±8 Δ< + ∆< + Δ<= ;

= ±80 + 0,1 + 0,2 = ±0,3 cm

Note que, tomando a média dos limites do menisco como medida final do volume, o intervalo da incerteza irá conter as medidas dos dois limites do menisco.

<final= 9,8 ± 0,3 cm

limite superior de intervalo → 9,8 + 0,3 = 10,1 cm limite inferior do intervalo = 9,8 − 0,3 = 9,5 cm

1.3 Precisão x Acurácia

(10)

conforme a Eq. (1.5). Pode ser expressa em termos de porcentagem e, quanto menor o seu valor, mais precisa é a medida.

Precisão = MΔ_{̅ M} (1.5)

Acurácia (ou exatidão) é um termo utilizado para descrever valores próximos do valor esperado, ou seja, são valores com erro total pequeno. Pode ser obtida pela Eq. (1.6). Também pode ser expresso em termos de porcentagem e, quanto menor o valor, mais exata a medida.

Acurácia = P esperado− experim

experim P (1.6)

Valores precisos não indicam que os mesmos serão exatos. Deve-se lembrar de que a medida ainda pode possuir um erro sistemático relativamente grande comparado à medida esperada.

1.4 Forma Padrão

Existe uma forma padrão para escrever a média de um conjunto de medidas de mesma natureza e sua respectiva incerteza. Esta é dada no formato da Eq. (1.7).

= ± ∆ 7 (1.7)

Para escrever um valor na forma padrão, deve-se primeiro ajustar sua incerteza obedecendo a seguinte regra.

a) Quando o primeiro algarismo do erro total for 1 ou 2, este deve ser escrito com 2 algarismos significativos.

Exemplo 1.4.1: _{0,1346 → 0,13} _{0,0002316 → 2,3 ∙ 10} S

1,2322 → 1,2 100023,89 → 1,0 ∙ 10T

b) Quando o primeiro algarismo do erro total for 3 ou maior, este pode ser escrito tanto com 1 como com 2 algarismos significativos.

Exemplo 1.4.2: _{3,3446 → 3 ou 3,3} _{0,00716 → 7 ∙ 10 ou 7,2 ∙ 10}

(11)

Observe que zero à esquerda não é algarismo significativo, mas à direita sim. Exemplo 1.4.3: _{Δ = 0,05} possui apenas um algarismo significativo

Δ = 0,050 possui dois algarismos significativos.

Para escrever a medida na forma padrão, após ajustar o número de algarismos significativos da incerteza, deve-se escrever a média acompanhando o número de casas decimais estabelecido para a incerteza.

Exemplo 1.4.4: Escreva na forma padrão, sabendo que

= 5,3421 cm V = 0,2134 cm

Resolução:

→ Respeitando as regras acima, o valor na forma padrão fica:

= 5,34 ± 0,21 cm

1.5 Arredondamento de números

De X000... a X499... faz-se truncamento, ou seja, os algarismos excedentes são eliminados e o valor X é mantido.

Exemplo 1.5.1: 1,34→ 1,3 5,6532→ 5,65 23,542→ 23,54 3,29165→ 3,29

De X500... a X999... faz-se arredondamento, ou seja, os algarismos excedentes são eliminados e o valor X é acrescido em uma unidade.

Exemplo 1.5.2: 7,89_→ 7,9 1,3468_→ 1,35 3,457_→ 3,46 9,341893_→ 9,342

Em X5000... o arredondamento deve transformar o valor X em par. Caso X seja ímpar, este é acrescido em uma unidade, caso já seja par, seu valor é mantido.

(12)

A seguir, tem-se um exemplo prático que engloba conceitos vistos anteriormente.

Exemplo 1.5.4: Um aluno foi encarregado de medir o diâmetro de um disco. Ele tinha à disposição uma régua milimetrada e um paquímetro de erro instrumental igual a 0,05 mm. O aluno realizou, para cada instrumento, 4 medidas do diâmetro, estando estas mostradas na tabela a seguir.

W_R cm W_P cm

6,15 6,095

6,10 6,090

6,05 6,100

6,10 6,000

Pede-se:

a) Qual dos instrumentos é mais preciso? Justifique.

b) A medida final, na forma padrão, do diâmetro para cada um dos instrumentos.

c) Sabendo que a medida do diâmetro especificada no disco, ou seja, a esperada, é de 6 cm, qual das medidas encontradas no item ‘b’ é mais exata? Justifique.

Resolução:

(a) O instrumento mais preciso é o paquímetro, pois as medidas realizadas com este possuem valores todos muito próximos entre si, possuindo pequena dispersão em relação à média. Além disso, é possível comparar as precisões da régua e do paquímetro utilizando a Eq. (1.5):

→ Cálculo da precisão da régua:

Inicialmente, é necessário calcular a média dos valores medidos pela régua:

Y)R =6,15 + 6,10 + 6,05 + 6,10₄ = 6,10 cm

Precisão = M0,05_{6,10M = 0,0081967 = 0,82%}

→ Cálculo da precisão do paquímetro:

(13)

Y)P = 6,095 + 6,090 + 6,100 + 6,000₄ = 6,07125 cm

Precisão = M_{6,07125M = 0,0008236 = 0,082%}0,005

Como o valor da precisão calculado para o paquímetro é menor, este é mais preciso.

(b) Medida do diâmetro na forma padrão:

→ Medidas realizadas com a régua: Primeiro calcula-se a média:

Y)R =6,15 + 6,10 + 6,05 + 6,10₄ = 6,10 cm

Tendo calculado a média, calcula-se o desvio padrão da medida, cujo valor será posteriormente utilizado para o cálculo do erro estatístico.

W)R− WR* [W)R− WR*\+

− 0,05 0,0025

0 0

0,05 0,0025

0 0

∑ 0,005

= 0,005_{3 = 0,040825 cm}

Após calcular o desvio padrão, calcula-se o valor do erro estatístico:

VY] estat =0,040825

√4 = 0,020412 cm

Como a régua é milimetrada, a menor medida que esta pode realizar é de 1 mm. Já que é um instrumento analógico, seu erro instrumental é a metade da menor medida, ou seja, 0,5 mm, que equivale a 0,05 cm.

(14)

VY] total = 8 0,05 + 0,020412 = 0,054006 cm

Desta forma, é possível escrever o valor medido do diâmetro do disco medido pela régua na forma padrão:

Y] = 6,100 ± 0,054 cm

→ Medidas realizadas com o paquímetro:

Realiza-se o mesmo processo acima, no entanto, utilizando os valores medidos pelo paquímetro:

Y)P = 6,095 + 6,090 + 6,100 + 6,000₄ = 6,07125 cm

O desvio padrão:

W)^− W^* [W)^− W^*\

+

− 0,0237 0,00056

− 0,0187 0,00035

− 0,0287 0,00083

0,0713 0,00508

∑ 0,00682

= 0,047675 cm

O erro estatístico:

ΔYP estat = 0,023838 cm

O erro instrumental, nesse caso, já foi fornecido pelo enunciado:

(15)

O erro total:

ΔYP total= 8 0,005 + 0,023838 = 0,0243567 cm

Na forma padrão:

YP = 6,071 ± 0,024 cm

(c) Os valores das medidas realizadas pelo paquímetro são mais exatos, pois possuem menor erro total, sendo portanto mais próximos do valor esperado. Além disso, pode-se calcular o valor da exatidão das medidas realizadas por ambos os instrumentos utilizando a Eq. (1.6).

Cálculo da exatidão da régua:

Exatidão = M6,0 − 6,1_{6,1 M = 0,01639 = 1,6%}

Cálculo da exatidão do paquímetro:

Exatidão = M6,0 − 6,07125_{6,07125 M = 0,01173 = 1,2%}

(16)

2 GRÁFICOS

2.1 Conceitos básicos

Gráfico é a tentativa de se expressar visualmente dados ou valores numéricos, de maneiras diferentes, assim facilitando a compreensão dos mesmos (WIKIPEDIA, 2015). Quando se trata da organização de resultados obtidos em um experimento, eles têm presença certa.

Para a elaboração correta de um gráfico há algumas regras que serão exemplificadas nos itens e figuras abaixo.

a) Apresentar os eixos coordenados, além de um título com uma breve descrição do que trata o gráfico, especificando qual medida e unidade cada eixo representa, indicando também, se necessário, a potência de 10 pela qual os valores da escala estão sendo multiplicados. Veja a Figura 2.1.1.

Figura 2.1.1: Exemplificação de como proceder para a elaboração de um gráfico, com título e unidades especificadas.

(17)

leitura, o que facilita a análise e a compreensão do gráfico. Veja a Figura 2.1.2.

Figura 2.1.2: Gráfico com intervalos e escalas independentes entre si.

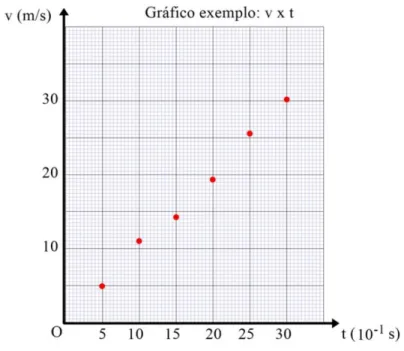
c) Ao marcar os pontos em um gráfico, não se deve fazer uma ligação entre os mesmos ou adicionar os valores respectivos dos pontos projetados nos eixos (ver Figura 2.4.1), os únicos valores presentes nestes devem ser somente os correspondentes aos intervalos já estipulados. A reta será traçada apenas quando for conveniente fazer o ajuste dos pontos (que será abordado mais adiante na apostila). Veja a Figura 2.1.3.

(18)

Figura 2.1.3: Gráfico exemplo com a marcação de pontos aleatórios.

Figura 2.1.4: Exemplo da representação da barra de erro em um gráfico. As barras horizontais indicam o intervalo das medidas na abscissa, e as barras verticais, o intervalo das medidas na

ordenada.

(19)

Figura 2.1.5: Exemplo da representação da barra de erro. Em destaque, o primeiro ponto do gráfico da Figura 2.1.4.

2.2 Histograma

Quando uma série de medidas é realizada, estas se distribuem em torno de um valor central, a média. Esses valores podem ser apresentados em um histograma. Um histograma apresenta os intervalos no eixo e a frequência no eixo _`. Nele há retângulos justapostos em que a base de cada um deles corresponde ao intervalo de classe e a sua altura à respectiva frequência. Veja a Figura 2.2.1.

Figura 2.2.1: Histograma do número de eventos em um determinado tempo.

(20)

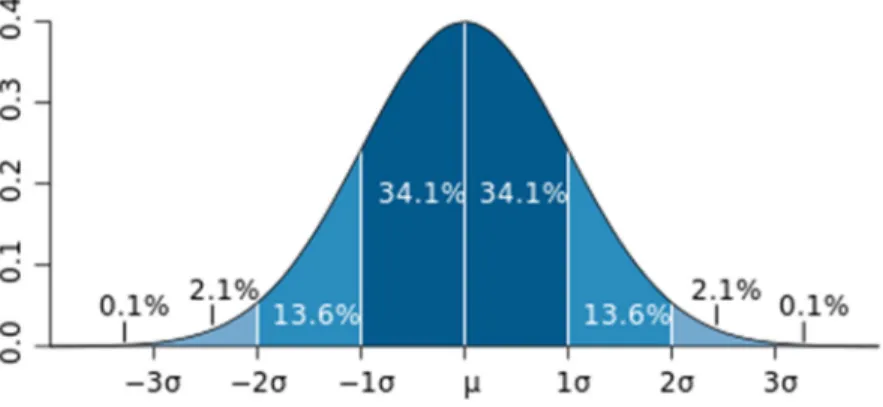
Quando o número de amostras é grande, o formato do histograma assemelha-se a uma curva normal, como mostra a Figura 2.2.2. No centro encontra-assemelha-se a média, e próximo a esta, se encontra uma grande quantidade de valores, tanto para mais quanto para menos.

A partir do valor do desvio padrão da amostra, é possível calcular os intervalos de confiança dos resultados, que se distribuem da seguinte maneira:

→ A área central, próxima à a (média), está a ± (desvio padrão) da média. Em uma distribuição normal, isto representa cerca de 68% do conjunto, enquanto _±2 desde a média representam cerca de 95%, e _±3 cobrem cerca de 99,7%. Veja a Figura 2.2.2.

Figura 2.2.2: Curva normal representada com os intervalos de confiança.

Fonte: CURVA normal. Wikipédia. Disponível em:

<http://pt.wikipedia.org/wiki/Desvio_padr%C3%A3o>. Acesso em Jan. 2015.

2.3 Gráficos logarítmicos

(21)

Exemplo 2.3.1: Com os dados da tabela a seguir, plote um gráfico.

x (u. m.) y (u. m.)

1 1

10 10

100 200

1000 1600

2500 3000

5000 10000

10000 35000

Resolução:

→ Note que os pontos contidos na tabela apresentam-se muito distantes numericamente entre si. O menor valor é da ordem de 100_{, enquanto o maior é da}

ordem de 104_{. Logo, a melhor alternativa seria representa-los em escala logarítmica.}

Veja a seguir.

Outra alternativa seria aplicar logaritmo nos valores da tabela e plotar num gráfico linear. Portanto, lembre-se que existem essas duas alternativas: (i) plotar os valores em gráfico log-log ou (ii) plotar o logaritmo dos valores em gráfico linear.

1 10 100 1000 10000 100000

1 10 100 1000 10000

y

(u

. m

.)

x (u. m.)

(22)

Veja pelo gráfico a seguir que, se os dados fossem representados em escala cartesiana (linear), os três primeiros pontos ficariam muito próximos entre si, impossibilitando sua visualização.

2.4 Principais erros em gráficos

Veja na Figura 2.4.1 alguns dos principais erros e equívocos ao se traçar gráficos. 0

5000 10000 15000 20000 25000 30000 35000 40000

0 2000 4000 6000 8000 10000 12000

y

(u

. m

.)

x (u. m.)

Gráfico y vs. x (escala linear)

(23)

Figura 2.4.1: Erros comuns ao se traçar gráficos.

(24)

3 TABELAS

3.1 Conceitos básicos

Assim como os gráficos, as tabelas são utilizadas para a apresentação e análise de valores obtidos de uma medição. A seguir, são apresentadas algumas informações importantes para a elaboração de uma tabela.

a) As tabelas devem conter o número de linhas e colunas de acordo com a quantidade de valores obtidos. Ela necessita conter o máximo de informações (resumidas), além de uma legenda descritiva sobre o conteúdo da mesma.

b) O cabeçalho da tabela deve apresentar a medida da coluna respectiva, seguida da unidade (quando existir) e, se necessário, a potência de 10 pela qual os valores da coluna estão sendo multiplicados. Os resultados devem ter um número de algarismos significativos adequados, acompanhados por suas respectivas incertezas. Se a incerteza for igual para todo o grupo de medidas, este deve aparecer preferencialmente no cabeçalho; se forem diferentes entre si, devem aparecer ao lado de cada medida. Veja o exemplo na Tabela 3.1.1.

Tabela 3.1.1: Tabela-exemplo com medidas e suas respectivas incertezas.

b ± +, c m/s d ± e, f ec e_s

5,0 5,0

11,0 10,0

14,5 15,0

19,4 20,0

25,5 25,0

30,3 30,0

(25)

Tabela 3.1.2: Tabela-exemplo com ordem de medição, medidas e incertezas respectivas.

* b_*± +, c m/s d*± e, f ec e s

1 5,0 5,0

2 11,0 10,0

3 14,5 15,0

4 19,4 20,0

5 25,5 25,0

6 30,3 30,0

3.2 Principais erros em tabelas

Veja alguns dos erros mais comuns cometidos ao se elaborar uma tabela na Figura 3.2.1 e na Figura 3.2.2.

Figura 3.2.1: Erros comuns ao se elaborar uma tabela (parte 1).

(26)

Figura 3.2.2: Erros comuns ao se elaborar uma tabela (parte 2).

(27)

4 LEIS DE POTÊNCIA

4.1 Conceitos básicos

Nos experimentos de física experimental, é comum se trabalhar com a relação entre duas variáveis físicas. Como exemplo, tem-se a distância (variável dependente) percorrida por um corpo, em queda livre, variando de acordo com o tempo (variável independente), mostrados na Tabela 4.1.1.

Tabela 4.1.1: Tabela exemplificando a relação entre duas variáveis, neste caso, distância percorrida e tempo.

g h d i

4,91 1,00 19,62 2,00 44,15 3,00 78,48 4,00

Quando duas variáveis se relacionam a partir de uma relação onde uma das medidas depende da outra que está elevada a uma certa potência (como por exemplo

` = j_{), diz-se que essas variáveis seguem uma}_{lei de potência}_{(ou lei de escala).} No caso exemplificado acima, considera-se que o movimento saiu do repouso e da origem, logo, a lei de escala do movimento é dada pela Eq. (4.1).

k l =1_{2 ml} (4.1)

Ao traçar os valores da Tabela 4.1.1, obtém-se o gráfico da Figura 4.1.1, onde se nota que os mesmos não seguem uma relação linear, o que de fato constitui uma dificuldade para determinar que tipo de relação as duas variáveis obedecem.

(28)

Figura 4.1.1: Gráfico (em escala linear) dos pontos da Tabela 4.1.1. Veja que os pontos seguem uma tendência parabólica segundo a relação entre deslocamento e tempo expressa na Eq. (4.1).

4.2 Métodos de linearização

4.2.1 Linearização com logaritmo

Convém utilizar este método (que só funciona se a relação entre as variáveis for do tipo lei de potência) quando não é possível determinar que tipo de relação as variáveis medidas obedecem e o expoente da relação não é conhecido. Ao utilizá-lo, a lei de escala é convertida e as variáveis passam a ter uma dependência linear.

Exemplo 4.2.1:

k = nlj

Para linearizar, basta aplicar o logaritmo natural (_{ln ≡ log} ), em ambos os lados da equação:

ln k = ln n ∙ lj

0 10 20 30 40 50 60 70 80 90

0 1 2 3 4 5

D es lo ca m en to ( m ) Tempo (s)

(29)

Utilizando as propriedades de logaritmo:

→ Logaritmo do produto: log m ∙ q = log m + log q

ln k = ln n + ln lj

→ Logaritmo de argumento com expoente: ln mr = q ∙ ln m

ln k = ln n + s ln l

Veja que a equação acima é a equação de uma reta (_{` = m + q} . Relacionando os termos, tem-se:

` = ln k = ln l m = s q = ln n

Note que os termos obedecem a relação de variável dependente (_`) e independente ( ), inclusive o coeficiente de , _m, e a constante _q.

Assim, para construir um novo gráfico, é necessário calcular o logaritmo natural dos valores de _k e de _l. Com isso, os pontos estarão relacionados de forma linear. Veja a Tabela 4.2.1 com os pontos e a Figura 4.2.1 com o gráfico (página seguinte).

Tabela 4.2.1: Dados da Tabela 4.1.1 logaritmizados. Note que os valores não possuem unidade.

tu g tu d

1,59 0,00 2,98 0,69 3,79 1,10 4,36 1,39

(30)

Figura 4.2.1: Gráfico (em escala linear) dos pontos logaritmizados da Tabela 4.2.1. Veja que os dados foram inseridos diretamente em um papel em escala linear. Note também que a origem do gráfico não

está em (0; 0), mas sim em (0; 1,5) para centralizar os pontos no gráfico.

Figura 4.2.2: Melhor reta que aproxima os pontos logaritmizados da Tabela 4.2.1. Neste exemplo em questão, a reta passa por todos, porém isso não é regra, pode existir pontos pelos quais a reta não

passe.

Fonte: Elaborada pelos autores. 1,50 2,00 2,50 3,00 3,50 4,00 4,50 5,00

0,00 0,50 1,00 1,50

ln

(

s)

ln (t)

Gráfico ln(s) vs. ln(t)

1,50 2,00 2,50 3,00 3,50 4,00 4,50 5,00

0,00 0,50 1,00 1,50 2,00

ln

(

s)

ln (t)

Gráfico ln (s) vs. ln (t)

Série de pontos melhor reta

(31)

Após traçar a reta, é possível encontrar o coeficiente angular da equação obtida após a linearização utilizando dois pontos que estão sob a reta. Estes pontos não necessariamente serão pontos da tabela, eles apenas precisam ser pontos pertencentes à reta traçada.

Escolhidos dois pontos pertencentes à reta, _{, `} e _{, `} , o coeficiente angular é encontrado através da Eq. (4.2).

m =` − `₋ = tan v (4.2)

No caso deste exemplo:

m =ln k − ln k_{ln l − ln l}

Nas relações estabelecidas entre a equação linearizada e a equação de uma reta, obteve-se que _{m = s}, logo, ao encontrar o valor do coeficiente angular pelo gráfico, o valor do expoente _s da lei de escala também está sendo encontrado.

Para obter o valor do coeficiente linear (_{ln n}), a única incógnita restante, basta escolher um ponto qualquer que esteja sob a reta e substituí-lo na equação linearizada. Após encontrar o valor do _{ln n}, para calcular o resultado de _n basta utilizar a definição de logaritmo:

log q = , então q = m

Como _{ln n = log n}, então

q = wx

(32)

4.2.2 Linearização com gráfico em escala logarítmica

Para este tipo de gráfico não é necessário linearizar a equação, pois a própria escala do papel se encarrega de fazer essa linearização. Portanto, os pontos a serem inseridos no gráfico são os originais e não os logaritmizados.

Exemplo 4.2.2:

Usando os dados da Tabela 4.1.1, obtém-se o gráfico da Figura 4.2.3 a seguir.

Figura 4.2.3: Gráfico (em escala logarítmica) dos pontos da Tabela 4.1.1. Veja que somente a escala do gráfico está logaritmizada, os pontos inseridos são os originais.

Neste caso, também traça-se a melhor reta, que é a reta que passa próxima a todos os pontos contidos do gráfico, mas não necessariamente passará por cima de todos. Após traçar a reta, escolhe-se arbitrariamente dois pontos que estejam sob a mesma (Dica: escolha pontos próximos de ambas as extremidades da reta). Tais pontos não precisam ser da tabela, mas necessariamente devem ser pontos da reta. Veja a Figura 4.2.4.

Para encontrar o expoente _s, realiza-se um procedimento semelhante ao do caso anterior, no entanto, como a escala deste gráfico não é linear, deve-se medir

1 10 100 1 10 D es lo ca m en to ( m ) Tempo (s)

(33)

com uma régua as distâncias em _` e em entre os pontos escolhidos. Calcula-se, então, o coeficiente angular, Eq. (4.3).

s =Distância em `_{Distância em =}Δ`_{Δ = tan v} _(4.3)

Figura 4.2.4: Gráfico (em escala logarítmica) de deslocamento em função do tempo, no qual _Δ e _Δ` representam as distâncias entre os pontos escolhidos.

Para encontrar o valor de _n, a única incógnita restante, escolhe-se arbitrariamente um ponto que esteja sob a reta e, utilizando suas coordenadas de e

l, substitui-se na lei de escala do movimento e encontra-se o valor de _n.

4.2.3 Linearização quando o expoente da lei de escala é conhecido

Entenda este tipo de linearização através do Exemplo 4.2.3.

Exemplo 4.2.3: Linearize a lei de escala abaixo.

k = nl

1 10 100

1 10

D

es

lo

ca

m

en

to

(

m

)

Tempo (s)

Gráfico s vs. t (em escala logarítmica)

v

Δ`

(34)

No exemplo apresentado faz-se _{l =} , onde é um termo linear qualquer, obtendo assim:

k = n

Desta forma, constrói-se um gráfico em escala linear, de _kvs. l . Para isso,

eleva-se cada um dos valores de tempo _l ao quadrado, de modo que, quando o gráfico for construído, os valores irão se relacionar de forma linear.

Exemplo 4.2.4:

A partir dos dados da Tabela 4.1.1, obtém-se a Tabela 4.2.2 a seguir.

Tabela 4.2.2: Tabela contendo medidas de deslocamento _g e tempo ao quadrado _d+ de um determinado movimento acelerado.

g m d+_i+

4,91 1

19,62 4

44,15 9

78,48 16

A partir dos dados da Tabela 4.2.2, constrói-se o gráfico da Figura 4.2.5. Com a relação criada entre e _l , a lei de escala obtida possui _n como coeficiente angular, portanto, encontra-se seu valor calculando o coeficiente angular da reta obtida na Figura 4.2.5. Como neste caso o expoente já é conhecido, apenas um valor é encontrado, o do coeficiente angular.

(35)

Figura 4.2.5: Gráfico (em escala linear) dos pontos da Tabela 4.2.2. Note que os dados estão tendendo à uma linearidade.

Exemplo 4.2.5: No gráfico da Figura 4.2.6, note que a melhor reta traçada para os pontos não intercepta a origem _{| ≡ 0,0} . Existem duas maneiras para calcular o coeficiente linear, que é o ponto onde a reta intercepta o eixo _`:

Figura 4.2.6: Gráfico do Exemplo 4.2.5, relacionando duas grandezas e _` quaisquer.

0 10 20 30 40 50 60 70 80 90

0 5 10 15 20

D

es

lo

ca

m

en

to

(

m

)

Tempo² (s²)

(36)

a) Tendo feito o gráfico, traça-se a melhor reta e esta é prolongada até que atinja o eixo _`, em _{= 0}. A ordenada deste ponto de interseção é o coeficiente linear desejado.

Atenção! Se a origem do seu eixo não for em zero, isto é, se a abscissa do seu ponto de origem não for igual a zero, a ordenada do ponto de interseção não representará o valor do coeficiente linear.

(37)

5 PROPAGAÇÃO DE ERROS

Há certas situações em que uma medida não é obtida diretamente e, por isso, não é possível determinar de imediato sua incerteza (pela precisão do instrumento ou por erro total, por exemplo). Isso ocorre, geralmente, quando a medida é obtida por uma fórmula.

Devido a uma medida depender de outras que possuam incertezas, surge a necessidade de se propagar as incertezas dessas medidas para a medida alvo.

Seja _` uma função dependente de , , ... , _j, Eq. (5.1), e sendo _Δ , _Δ , ... , _Δ _j seus respectivos erros; o erro propagado de _` é dado pela Eq. (5.2).

` = ` , , … , j (5.1)

_{Δ` = M}~`

~ M ∙ |Δ | + M~ M ∙ |Δ | + ⋯ + M~` ~~`jM ∙ |Δ j|

(5.2)

A ideia aqui é que _` depende de outras medidas ( , , ... , _j) que possuem incertezas (_Δ , _Δ , ... , _Δ _j), então há a necessidade de se propagar essas incertezas, de forma a encontrar uma única outra (_Δ`) que englobe todas as demais. Esta representará a incerteza de _`.

Assim, resolvendo as derivadas parciais e conhecendo _Δ , _Δ , ... , _Δ _j,é possível calcular a incerteza de _`. Vale ressaltar que as incertezas utilizadas na propagação são os erros totais de cada medida.

Caso queira saber como se chegou a essa fórmula de propagação de incertezas, consulte o livro Fundamentos da Teoria de Erros, de José Henrique Vuolo (Editora Edgard Blücher Ltda.). Para saber mais sobre a derivação parcial, consulte o Apêndice A ao final desta apostila.

Exemplo 4.2.1: Calcule a área de uma circunferência de raio _{€ = 1,5 ± 0,3 m} e expresse-a na forma padrão.

Resolução:

(38)

• = ‚ ∙ 1,5 ⇒ • = 7,0686 m

→ Para calcular a incerteza, é necessário propagar o erro do raio para a área. Veja a seguir:

Δ• = M~•_{~€M ∙ |Δ€|}

⇒ Δ• = 8|2‚€| ∙ |Δ€| ⇒ Δ• = 8|2‚ ∙ 1,5| ∙ |0,3| ⇒ Δ• = 2,8274 m

→ Logo, o valor da área na forma padrão é:

• = 7,1 ± 2,8 m

Veja que a incerteza se inicia com o algarismo 2 e deve ser expresso com dois algarismos significativos.

Exemplo 4.2.2: A posição de um certo corpo em movimento retilíneo uniformemente variado (MRUV), cuja aceleração é constante e igual a 1,0 m/s2_{, é}

dada pela seguinte equação:

l = „+ …„l +1_{2 ml}

Calcule o valor da posição na forma padrão para os seguintes valores de posição inicial, velocidade inicial e tempo, com suas respectivas incertezas:

„ = 5,0 ± 1,5 m

…_„ = 3,5 ± 1,0 m/s l = 1,5 ± 0,5 s

Resolução:

→ Para calcular o valor da posição, substitui-se os valores acima na equação dada:

(39)

l = 1,5 = 11,375 m

→ Para encontrar a incerteza da posição, basta propagar com relação a todas as variáveis. Note que não é necessário propagar com relação à aceleração, já que esta é constante e sua incerteza é zero.

Δ = M_~~

„M ∙ |Δ „| + M

~

~…_„M ∙ |Δ…„| + M~~lM ∙ |Δl| ⇒ Δ = 8|1| ∙ |Δ „| + |l| ∙ |Δ…„| + |…„+ ml| ∙ |Δl|

⇒ Δ = 8|1| ∙ |1,5| + |1,5| ∙ |1,0| + |3,5 + 1 ∙ 1,5| ∙ |0,5| ⇒ V = 3,2787 m

Logo, o valor da posição na forma padrão é:

(40)

6 MÍNIMOS QUADRADOS

6.1 Introdução

O Método dos Mínimos Quadrados (MMQ), ou Mínimos Quadrados Ordinários (MQO), é uma técnica de otimização matemática que procura encontrar o melhor ajuste para um conjunto de dados tentando minimizar a soma dos quadrados das diferenças entre o valor estimado e os dados observados (essa diferença é o chamado

χ – “qui-quadrado”, que será abordado mais adiante). Este conjunto de dados pode seguir qualquer tipo relação, como linear, exponencial, quadrática, cúbica, polinomial, etc.

Você pode encontrar uma abordagem mais detalhada dos tópicos abaixo no livro Fundamentos da Teoria de Erros, de José Henrique Vuolo (Editora Edgard Blücher Ltda.).

6.2 Considerações e conceitos preliminares

Suponha que um conjunto de dados _,_` siga uma relação qualquer, como o da Figura 6.2.1, onde cada valor _` tem uma incerteza , podendo estes serem todos iguais ou diferentes entre si (no mínimo um deles diferente dos demais), sendo também que a variável é isenta de erros. Suponha também que estes dados representem um certo fenômeno físico descrito por uma função _{‡ = ‡ , m , m , … , m} onde _{m , m , … , m} são os parâmetros dos modelo.

Define-se o estimador _ˆ , que representa a soma ao quadrado das distâncias verticais entre os pontos experimentais e a função ajustada, por:

ˆ = , ‰[` − ‡ , m , m , … , m \Š (6.1)

(41)

Figura 6.2.1: Representação gráfica de um conjunto de _s dados que obedecem a uma relação qualquer.

6.3 Ajuste de uma função linear

Um certo conjunto de dados segue uma tendência linear. Sua representação gráfica é mostrada no gráfico da Figura 6.3.1.

Figura 6.3.1: Representação gráfica de um conjunto de _s dados que obedecem a uma relação linear.

(42)

Definindo-se

‡ = m + q (6.2)

‹ = 1 (6.3)

A Eq. (6.1) pode ser reescrita como

ˆ = , ‹

j

` − m − q (6.4)

Para minimizar _ˆ e, consequentemente, encontrar a reta que mais se aproxima de todos os pontos, deriva-se parcialmente a Eq. (6.4) em relação aos parâmetros _m e _q e iguala-se a zero:

~ ˆ

~m = 2 , ‹ ` − m − q ∙ − = 0

j

(6.5)

~ ˆ

~q = 2 , ‹ ` − m − q ∙ −1 = 0

j

(6.6)

Deste modo, obtém-se um sistema de duas equações e duas incógnitas:

Œ, ‹ • ∙ m + Œ, ‹ • ∙ q = Œ, ‹ `• (6.7)

_{Œ, ‹ • ∙ m + Œ, ‹• ∙ q = Œ, ‹`•} (6.8)

Ao solucionar o sistema, obtém-se as seguintes equações para _m e _q:

m = ∑ ‹ ∙ ∑ ‹ ` − ∑ ‹` ∙ ∑ ‹_Δ (6.9)

_{q =} ∑ ‹` ∙ ∑ ‹ − ∑ ‹ ` ∙ ∑ ‹

(43)

Onde

Δ = Œ, ‹• ∙ Œ, ‹ • − Œ, ‹ • (6.11)

E cada uma das variâncias (quadrado da incerteza) associados a _m e _q são dados por:

Ž = ∑ ‹_Δ (6.12)

r = ∑ ‹_Δ (6.13)

As Eqs. (6.9) a (6.13) são válidas quando todos os valores são conhecidos, independentemente de serem distintos ou iguais entre si. Somente para o caso em que todas as incertezas de _` são constantes e iguais a , pode-se fazer uso das expressões simplificadas de (6.14) a (6.18).

m = ∑ ` − ∑ ∙ ∑ `_Δ (6.14)

_{q =} ∑ ` ∙ ∑ − ∑ ` ∙ ∑

Δ (6.15)

_{Δ = Œ, • − Œ, •} (6.16)

_Ž _{= Δ} (6.17)

r = ∑_Δ

onde é o número de medições efetuadas.

(6.18)

(44)

=∑j _{− 2}Δ“ (6.19)

onde

Δ“ = ` − m + q (6.20)

Neste caso, é calculado uma incerteza estimada (_Δ“) para cada uma das medidas _` através da Eq. (6.20) (note que esta depende dos valores _m e _q, devendo os mesmos já terem sido calculados de antemão). Faz-se a soma dos quadrados de cada um dos erros estimados e aplica-se a Eq. (6.19), encontrando o valor de que será usado no cálculo das incertezas dos coeficientes _m e _q (Eqs. (6.17) e (6.18)).

Observação: No fim de alguns roteiros e nos formulários de prova das disciplinas de Física Experimental da faculdade:

As Eqs. (6.9) a (6.13) são chamadas de “Mínimos Quadrados (erros

diferentes)”;

As Eqs. (6.14) a (6.20) são chamadas de “Mínimos Quadrados (erros

iguais)”;

Não confunda o dos Mínimos Quadrados com o de desvio padrão, são coisas diferentes.

Exemplo 6.3.1: Em um experimento de movimento retilíneo uniforme foram obtidos os dados da tabela a seguir. Utilize o Método dos Mínimos Quadrados para obter, na forma padrão, os valores da velocidade _… e da posição inicial _k_„.

d s g ± ”g m

0,2 2,3 _± 0,1 0,4 4,7 _± 0,2 0,6 6,9 _± 0,3 0,8 9,1 _± 0,1

Resolução:

i. Encontrar uma equação para o movimento:

(45)

ii. Relacionar os termos da equação aos coeficientes e variáveis de uma reta: _{` = q + m}

Logo, tem-se que:

k = ` k„ = q

… = m l =

Nota: Note que, como _{` = k} e os erros de cada _k são diferentes entre si, deverá ser usado o conjunto de equações com o _‹ (erros diferentes).

iii. Calcular os valores de _‹: Como _{‹ = 1⁄} , tem-se que:

‹ = 100 ‹ = 25 ‹ = 11,1111

‹S = 100

iv. Construir uma tabela auxiliar:

* (* –* —* —*(* —*–* —*(*–* —*(*+

1 0,2 2,3 100 20 230 46 4

2 0,4 4,7 25 10 117,5 47 4

3 0,6 6,9 11,11 6,67 76,67 46 4

4 0,8 9,1 100 80 910 728 64

∑ - - 236,11 116,67 1334,17 867 76

v. Substituir os somatórios nas equações correspondentes para encontrar os valores de _m e _q e suas respectivas incertezas:

m = 11,32051 m/s q = 0,05692 m

(46)

r = 0,13243 m

Como a velocidade _… corresponde ao coeficiente angular _m e a posição inicial

k„ ao coeficiente linear q (conferir item ii da resolução), tem-se os seguintes valores na forma padrão:

… = 11,32 ± 0,23 m/s k_„ = 0,06 ± 0,13 m

Nota: Em alguns casos é necessário linearizar a equação de movimento (passo i da resolução) para sempre trabalhar com a equação de uma reta, ou seja, com dados lineares.

Exemplo 6.3.2: Considere o mesmo exemplo anterior, agora com os dados abaixo. Utilize o Método dos Mínimos Quadrados para obter, na forma padrão, os valores da velocidade _… e da posição inicial _k_„.

d s g ± c, ˜ m

0,2 2,3

0,4 4,7

0,6 6,9

0,8 9,1

Resolução:

i. Equação (linear) para o movimento: _{k = k}_„_{+ …l}

ii. Relação de termos da equação com os coeficientes e variáveis de uma reta:

k = ` k„ = q

… = m l =

(47)

iii. Construção da tabela auxiliar:

* (* –* (*+ –*(*

1 0,2 2,3 0,04 0,46

2 0,4 4,7 0,16 1,88

3 0,6 6,9 0,36 4,14

4 0,8 9,1 0,64 7,28

∑ 2 23 1,2 13,76

iv. Substituição dos somatórios na equações correspondentes para encontrar os valores de _m e _q:

m = 11,3 m/s q = 0,1 m

v. Para calcular as incertezas dos coeficientes, lembre-se que _{= Δ`}. Como _{= Δ` = 0,3}, aplicando as equações correspondentes:

Ž = 0,67082 m/s

r = 0,36742 m

Conforme as relações do item ii da resolução, tem-se os seguintes valores na forma padrão:

… = 11,30 ± 0,67 m/s k„ = 0,10 ± 0,37 m

Exemplo 6.3.3: Considere o mesmo exemplo anterior, agora com os dados abaixo. Utilize o Método dos Mínimos Quadrados para obter, na forma padrão, os valores da velocidade _… e da posição inicial _k_„.

d s g m

0,2 2,3

0,4 4,7

0,6 6,9

(48)

Resolução:

i. Equação (linear) para o movimento: _{k = k}_„_{+ …l}

ii. Relação de termos da equação com os coeficientes e variáveis de uma reta:

k = ` k„ = q

… = m l =

Nota: Note que, como _{` = k} e os erros de cada _k são desconhecidos, deverá ser usado o conjunto de equações com o (erros iguais).

iii. Construção da tabela auxiliar:

* (* –* (*+ –*(*

1 0,2 2,3 0,04 0,46

2 0,4 4,7 0,16 1,88

3 0,6 6,9 0,36 4,14

4 0,8 9,1 0,64 7,28

∑ 2 23 1,2 13,76

iv. Substituição dos somatórios na equações correspondentes para encontrar os valores de _m e _q:

m = 11,3 m/s q = 0,1 m

v. Para calcular as incertezas dos coeficientes, lembre-se que agora é desconhecido, por isso deverá ser estimado através da Eq. (6.19).

* (* –* ™š* ™š* +

1 0,2 2,3 ₋ 0,06 0,0036

2 0,4 4,7 0,08 0,0064

3 0,6 6,9 0,02 0,0004

4 0,8 9,1 ₋ 0,04 0,0016

(49)

= 0,006

Aplicando às equações das incertezas dos coeficientes, encontramos:

Ž = 0,17321 m/s r = 0,094868 m

Conforme as relações do item ii da resolução, tem-se os seguintes valores na forma padrão:

… = 11,30 ± 0,17 m/s k„ = 0,100 ± 0,095 m

(50)

BIBLIOGRAFIA

DE ALMEIDA, R. M.; HÉLIO, O. Física Experimental I. Física VCE, 2011. Disponivel em: <https://sites.google.com/site/fisvce/fisexp1>. Acesso em: Jan. 2015.

DE ARAÚJO, L. E. E. Lei de Potência. [S.l.], p. 4.

MARCONI, J. D. Introdução à Teoria de Erros e Medidas. [S.l.], p. 4.

MARCONI, J. D.; RODRIGUES, V. Experimento 4: Mínimos Quadrados. [S.l.], p. 3.

MARCONI, J. D.; RODRIGUES, V.; DE ARAÚJO, L. E. E. Tabelas e Gráficos. [S.l.].

RODRIGUES, V. Experimento 4: Propagação de Erros. [S.l.].

STEWART, J. Cálculo Volume II. 5ª. ed. São Paulo: Thomson Learning, v. II, 2007.

VUOLO, J. H. Fundamentos da Teoria de Erros. 2ª. ed. São Paulo: Edgard Blücher Ltda., 1996.

WIKIPEDIA. Gráfico. Wikipedia, 2015. Disponivel em:

(51)

APÊNDICE A – Derivação Parcial

A derivada parcial de uma função de várias variáveis consiste em derivar esta função em relação a cada uma de suas variáveis por vez, mantendo as demais como se fossem constantes numéricas. Para uma função _{‡ , , , … ,} _j , a qual depende de _s variáveis, sua derivada parcial é representada por:

~‡ , , , … , j

~ (A.1)

Note a simbologia da derivação parcial. Enquanto a derivada ordinária é representada pela letra ‘_d’, a parcial é representada por uma letra ‘_›’ arredondada, o ‘_∂’. Veja a seguir alguns exemplos de derivação parcial.

Exemplo A.1.1: Seja _{‡ , ` =} _{+ ` − 2`} , calcule as derivadas parciais em relação a e _`.

Resolução:

→ Para realizar o cálculo de uma derivada parcial em relação a , deriva-se somente em relação a este, mantendo a variável _` como uma constante.

~‡ , `

~ = 3 + 2 `

→ Para o cálculo em relação a `, realiza-se o mesmo processo descrito acima, no entanto, mantendo-se como uma constante.

~‡ , `

~` = 3 ` − 4`

Exemplo A.1.2: Calcule a derivada parcial com relação a , _` e _• da função

‡ , `, • = 5 S_{` + ` + 4• + 1}_. Resolução:

(52)

~‡ , `, •