O Fen^omeno de Transi~ao de Fase no
Modelo de Perola~ao de Elos
em d Dimens~oes
Marelo Martins de Oliveira
Departamento deFsia-UFMG
manebosia.ufmg.br
Gast~aoA. Braga
DepartamentodeMatematia -UFMG
gbragamat.ufmg.br
Reebidoem23demaio,2002. Aeito26desetembro,2002.
Estetrabalhotrata,demaneirarigorosa,auto-ontidaeaessvelaumalunodegradua~aoemfsia
e areasans, dof^enomenodetransi~aode fasenum modelode perola~aode elosindependentes
na rede hiperubia d-dimensional. Esses modelos s~ao frequentementeutilizados para desrever
situa~oesdeinteressefsio. Ofen^omenoda\perola~ao"oorrequandoenontramosum
aglome-rado innito em nossa rede. A mudanaque oorre aose passarde um estado em que existem
somenteaglomerados nitosparaoestadoemquehaosurgimentodeumaglomeradoinnitoeo
analogogeometriodeumatransi~aodefaseemme^aniaestatstia. Mostramosqueatransi~ao
defase oorre, pararedeshiperubias emdimens~aod2,emumpontobemdenido,hamado
depontortio,equepodemosassoiarumpar^ametrodeordemaestatransi~aodefase. Dentre
os modelos daFsia que apresentamo fen^omenode transi~ao defase, o modelode perola~aoe
provavelmenteomaissimples.Aomesmotempo,eleexempliaedeixalaraaonex~aoquemuitas
vezesenontramosentreareasdafsia,damatematiaedaprobabilidade.
In this paper we study phase transition phenomenain an independent edge perolation model
on a d-dimensional hyper-ubi lattie. The subjet is treated ina rigorous, self-ontained and
aessible way for undergraduatestudents inphysis and related areas. These models are often
usedtodesribesituationsofphysialinterest. The\perolationphenomena" ourwhenwend
aninnitelusterinthelattie. Thehangefromastatewhere thereare onlynitelusters toa
statewith atleast oneinnityluster isthe geometri analogous ofa phasetransition as known
in statistial mehanis. We show that the phase transition ours, for hyper-ubi latties in
dimensiond2,inawell-denedpoint,knownas theritial point. Weanassoiate anorder
parametertothisphasetransition. Amongallthephysialmodelsthatpresentaphasetransition,
theperolationmodelisprobably oneofthesimplest. Atthe sametime,itis agoodexampleof
theonnetionthatsometimeswendrelatingphysis,mathematisandprobability.
I Introdu~ao
Todosnosjafomosexpostosaofen^omenodetransi~ao
defase. Oexemplomaisomumeatransforma~ao,ao
sevariaratemperatura,daaguanafaselquidaparaa
agua nafasesolida (gelo),ou para aaguana fase
ga-sosa(vapor). Um exemplomenostrivialea mudana
defasenummaterialmagnetio. Umm~a,aoser
aque-ido atemperaturasmuito altas, perdea propriedade
de atrairlimalhas de ferro, isto e, ao sevariar a
tem-peratura, om~a muda da fase magnetia para a fase
paramagnetia.
Onossoobjetivonestetrabalhoeapresentar,de
ma-neira aessvel a umaluno de gradua~ao em Fsia, o
oneito de transi~ao de fase do ponto de vista
ma-tematio. Adotamos o modelo de perola~ao de elos,
a serdenido na proximase~ao, porser
matematia-mentesimplesemsuaformula~aoaomesmotempoque
nosforneeproblemasintrigantementedifeisde
solu-ionar.
Se, por um lado, varios ursos de baharelado
em Fsia ja admitem uma onentra~ao em F
sia-Matematia,poroutrolado,adespeitodosotimos
tex-tosexistentesemportugu^es[1,2℄,emnenhumdelesha
apreoupa~aoemapresentarumavis~aorigorosado
as-sunto. Estetextofoiesritotendoemmenteumaluno
om o perl mais teorio, embora ele tambem possa
ser usado por estudantes om outros interessesou de
outras areasdoonheimento. Otextoeauto-ontido
e pode serusadoomo notas deaulaem um urso de
Fsia-Estatstia,porexemplo.
Estetrabalho estaassim dividido. Nase~ao II
ex-pliamos a ideia por tras do modelo de perola~ao e
forneemos algumas aplia~oes do mesmo. Na se~ao
seguinte introduzimos a nota~ao a ser utilizada e
fa-zemos uma breve revis~ao deprobabilidades. Nase~ao
IVdenimosaprobabilidadedeperola~aoe
argumen-tamos que esta probabilidade deveria funionar omo
umpar^ametroqueindiasseseosistemaestaordenado
ou n~ao. As se~oes V eVI s~ao dediadas ao estudo da
exist^eniaoun~aodeumatransi~aodefaseemumaou
maisdimens~oes.
II O que e perola~ao?
Historiamente, o oneito de perola~ao surge do
es-tudo do fen^omeno de transporte de umuido atraves
deummeioporoso. Porexemplo,opetroleoatravesde
uma roha, ou a agua em um ltrode areia.
Formu-lado no nal da deadade 50 por Broadbent e
Ham-mersley [3℄, o modelo de perola~ao onentra-se em
desreveromeioporoso,queseravistoomoumarede
de anais aleatorios, por onde esoa um uido
deter-minstio. 1
Modelosdeperola~aoenontramaplia~ao
em varias situa~oes fsias de interesse tais omo o
problema da me^ania estatstia de sistemas
ferro-magnetiosdiludos [4℄, no problemadotransporte de
orrenteeletriaatravesdeumaredeompostaporum
grandenumeroderesistores[5℄,emproblemasde
pros-pe~ao de petroleo [6℄e atemesmo na propaga~ao de
epidemiasedein^endiosembosques[7℄.
Modelemosomeioporosoomoumsubstratosolido
em ujo interior existe um ertonumero de pequenos
anais e poros em pontos esolhidos ao aaso. Se o
numerodeanaisforsuientemente grandeent~aoeles
estar~ao interligados e o meio se tornara permeavel a
passagem do uido. Neste asodizemos que houve a
perola~aodouido.
Podemosreformularomodelodesritoaimaam
de que possamostrata-lo analitiamente. Comeemos
supondo queosanais formemum retiulado no
inte-riordo solido,omouma redeubia(veja aFigura1
para um exemplo bidimensional). Cada stio da rede
ent~ao representaria um poro e ada elo representaria
umpequenoanalligandodoisstiosvizinhos.
Figura1. Modelo paraumarohaporosabidimensional
imersaemlquido.
Para simular a passagem do lquido atraves dos
poros, nos diremos que um elo esta aberto om
pro-babilidade p e fehado om probabilidade 1 p, om
0 p 1. Dessa forma, passamos aimaginar
on-gura~oesdeelosabertosefehados. Cadaongura~ao
oorreent~aoomumaertaprobabilidade,dadapor
p jAj
(1 p) jFj
; (1)
ondejAj eonumerodeelos abertos ejFjeonumero
deelos fehadosdaongura~ao (vejaaFigura 2). A
formula aima so tem import^ania se jAj ejFj forem
ambosnitos pois, aso ontrario, a probabilidade de
oorr^eniadeumadadaongura~aoserasemprenula.
Figura2. Tr^es ongura~oes diferentes, porem todas om
exatamente24elosabertose36fehados,emumarede
bi-dimensional 66. A probabilidade de ada uma dessas
ongura~oesep 24
(1 p) 36
:
Na proxima se~ao vamos generalizar este modelo
paraddimens~oes,formulando-onumaredehiperubia
d-dimensional. Esta rede e innita e, por isto, uma
ongura~ao sempre tera peso estatstio nulo.
Sere-mosent~aolevadosadenironjuntosdeongura~oes
ompeso estatstio n~ao nulo. Consideraremosainda
quehaveraelos ligandoapenas doisstiosvizinhos, de
forma que estudaremos a perola~ao de primeiros
vi-zinhos. Mesmo omuma redesimplesobservaremosa
exist^enia de um fen^omeno rtio, araterizado por
uma mudana de fase. A oorr^enia de fen^omenos
rtioseumdosprinipaismotivosdosuessodo
mo-delo de perola~ao de elos. Neste trabalho,
estare-mos interessados nos aspetos matematios da teoria.
Por isto, a nossa exposi~ao se baseia nas refer^enias
[4,8,10℄. Umaexposi~aointrodutoriaemnveldep
os-gradua~aopodeserenontradaem[11℄.
III Nota~ao e algumas deni~oes
iniiais
Desenvolveremos nosso estudo em uma rede
hi-perubia d-dimensional, denotada por L d
= (Z,
E d
). Nesta nota~ao, Z representa o onjunto de
stios(ouverties)e E d
representa oonjunto de elos
(ou liga~oes) da rede. Mais espeiamente, Z d = f(x 1 ;x 2 ;;x
d ) : x
i
2 Z8ig e E d
= f(x;y) 2
Z d
Z d
:kx yk
1
=1g,ondek:k
1
eafun~aodist^ania,
denida omokx yk
1 = P d i=1 jx i y i
j. Emresumo,
ada stio x 2 Z d
e indexado por d numeros inteiros,
ondedeadimens~aoespaialdarede,enquantoqueum
elo e2 E d
e indexadopor umparde stiosx;y 2Z d
daseguinte forma: e=(x;y)=(y;x). Osstiosx ey
s~aohamadosdepontosterminaisdoeloe. Aondi~ao
jjx yjj
1
=1signiaquetrataremosdeummodelode
perola~aodeprimeirosvizinhos(videFig. 3).
Figura3. Osprimeirosvizinhos(rulos)eossegundos
vi-zinhos(tri^angulos)daorigememuma redequadrada
bidi-mensionalsegundoametriadenidapelafun~aodist^ania
kx yk 1 = P d i=1 jx i y i j.
Atribumos a ada elo, aleatoriamente, a
propri-edade aberto ou fehado: ao elo e assoiamos uma
variavel!
e
queassumiraosvalores1(seoeloeaberto)
ou 0 (se o elo e fehado). Deste modo, dizemos que
adaeloedaredeestaraaberto(!
e
=1)om
probabi-lidadepoufehado(!
e
=0)omprobabilidade1 p,
onde0p1. Alemdisso, assumimos queo estado
de um elo n~ao sera afetado por quaisquer outros elos
daredeobtendo,assim,omodelodeperola~aode elos
independentes 2
. Uma ongura~aodeste modelo pode
ser vista omo um vetor om um numero innito de
omponentes,ada omponente estando indexadapor
um elo da rede. Numa linguagem mais formal, uma
ongura~ao! eumponto doonjunto=f0;1g E
d
,
onheidoomoespao de ongura~oes.
Um subonjunto de em que o estado de um
numeronitodeelosedadodeantem~aoehamadode
onjuntoilndrio. Ent~ao,umonjuntoilndrioeda
forma C(f
e1 ;;
en
g) = f! 2 : !
ei =
ei 8i =
1;;ng. Devidoaindepend^eniaentreoselos,
pode-mosfailmenteomputaraprobabilidadedeoorr^enia
do onjunto ilndrio C(f
e
1 ;;
e
n
g). Seja jA
C j o
numerode elosabertosejF
C
jonumerode elos
feha-dosdeC(equivalentemente,jA
C
jeigualaonumerode
's iguaisa1ejF
C
jeigualaonumerode 'siguaisa
0). Ent~ao
P(C(f
e1 ;;
en g))=p
jA C j (1 p) jF C j :
Observe que a formula aima da a probabilidade de
oorr^eniadeumonjuntoenquantoqueaformula(1),
embora similar, da a probabilidade de oorr^enia de
umaongura~ao.
Umonjuntodeelosfe
1 ;e
2 ;;e
n g,e i =(x i ;x i+1 )
serahamadodeaminhoseosvertiesx
1 ;x
2 ;;x
n+1
foremdistintos. Ent~ao,umaminhoeumonjunto
o-nexo de elos, sem auto interse~oes (veja Figura 2-b)
ou seja, os aminhos n~ao admitem voltas (loops). Se
x
1 =x
n+1
ent~aotemos umiruito (veja Figura2-).
Umaminhoeabertosetodososseuseloss~aoabertos.
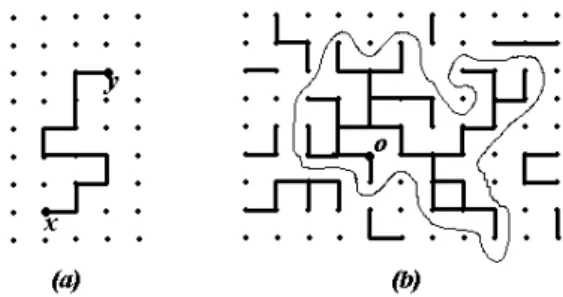
Dois stios da rede, x e y, est~ao onetados (x $ y)
se existir um aminho aberto fe
1 ;e
2 ;:::;e
n
g tal que
x
1
=x ey
n
=y (veja Figura4-a). Observeque todo
aminhoabertodeneumonjuntoilndrio.
Emgeral,umonjunto para oqual sepode denir
um peso estatstio e hamadode evento. Dados dois
eventosA;B2,temosque
P(A[B)=P(A)+P(B) se A\B=;;
P(A)P(B) se AB;
UmsubonjuntoaleatoriodeL d
ontendoum
on-juntodeverties(stios)deZ d
quesejampontos
termi-naisdeelos abertosonexosehamadodeaglomerado
aberto. ChamaremosdeC(x)oaglomeradoaberto
on-tendoovertiexmasrepresentaremosporCo
aglome-rado aberto pela origem (veja Figura4-b). Onumero
devertiesdeC(x)seradenotadoporjC(x)j.
SejaAum onjuntode vertiesdeZ d
. Chamamos
defronteiradeA(edenotamosporA)aoonjuntode
verties de A que s~ao adjaentes ao omplementar de
A.
Figura4. (a)Umaminhodeelosabertosligandoxey.
(b)Oaglomeradoontendoaorigem.
Trabalharemossobreumaredeinnita,que,
diferen-temente da roha em nosso exemplo iniial, n~ao
pos-sui fronteiras. Nesse aso, diremos que oorreu
per-ola~ao quando enontrarmos, om probabilidade n~ao
2
nula,umaglomeradodetamanhoinnitopassandopor
umpontopre-xado. Ofatodearedeserinnita,
jun-tamente om a independ^enia dos elos e a uniidade
do par^ametro p (o mesmo p para todos os elos), nos
garantiraa invari^ania translaionalna rede. Isso
sig-niaqueaorigemnadatemdeespeial, istoe,
pode-mostomarqualquerstiodanossaredeomoaorigem,
onformenossaomodidade.
IV O problema da transi~ao de
fase em perola~ao
Denimosomoprobabilidade de perola~aoa
probabi-lidadedeumdadostiodaredeperteneraum
aglome-radodetamanhoinnito. Esteeventopodetambemser
representado porfx$1gostiox estaonetado
aoinnito. Semperdadegeneralidade,podemostomar
tal stioomosendoaorigem. Dessemodo,denimos
(p)P
p
(jCj=1):
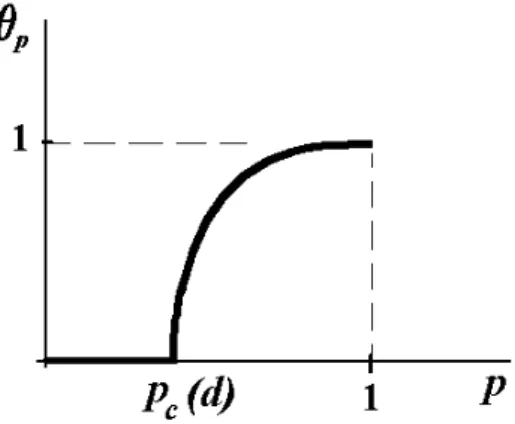
Vamos desreveraseguir,de maneiraheurstia, o
graode omo fun~aode p. Primeiramente,
obser-vamos que (p) e uma fun~ao n~ao deresente de p.
De fato, se aumentarmos o valor de p (grosso modo,
se \abrirmos mais elos" nas ongura~oes que
ontri-buemparaumpesoestatstion~aonulo),ent~aooevento
f0 !1g ontinuaraoorrendo, impliando que e
n~ao deresente. Examinemos, agora, o
omporta-mentodomodeloquandoptomaseusvaloresextremos:
quando p=1,todososelos da redeest~ao abertos, de
modo quetodo stioesta onetado aqualqueroutro.
Em partiular, a origemestaonetada aum numero
innito de outros stios om probabilidade 1, ou seja,
(p)=1;quandop=0,n~aohaelosabertos. Nenhum
stioestaonetadoaqualqueroutro,eempartiular,
aorigemestaonetadaaumnumeronito(nesteaso
zero)deoutrosstios.
Na se~ao VI vamos mostrar que, em qualquer
di-mens~ao espaial d 1, se p 0 ent~ao (p) = 0.
Tambem vamos mostrar que, se a dimens~ao espaial
d epelo menos 2 e se p 1, ent~ao (p) 1. Ent~ao
(p)esimilaraopar^ametrodeordememme^ania
es-tatstiaeseraatravesdesta fun~aoque deniremosa
probabilidade rtia(oupontortio). Essamudana
no estadodarede,de possuirsomente aglomerados
-nitos para o surgimento de um aglomerado innito e
o analogo geometrio de uma transi~ao de fase, omo
quandoaaguapassadelquidoparasolidoauma
deter-minadatemperaturaepress~ao. Conjetura-se[8℄queo
graodeversuspedaformadadanaFigura5para
d2. Naproximase~aovamosmostrar que,emuma
dimens~ao,(p)=0paratodo0p<1,istoe,n~aoha
transi~aodefaseemumadimens~aoespaial.
V Inexist^enia de transi~ao de
fase em dimens~ao d= 1
Iniialmente,onsideremosomodelodeperola~ao
uni-dimensional, e os seguintes eventos: fj C j= 1g,
f0 $ 1g, f0 $ ng e f0 $ ng, onde n 2 N.
Ve-mosque
fjCj=1g=f0$1gf0$ng[f0$ ng:
Da deni~ao de probabilidade de perola~ao
obte-mos
(p)=P(jCj=1)Pf0$ng+Pf0$ ng:
Ja a probabilidade da origem estar onetada ao
stionouaostio nefailmente alulada
Pf0$ng=Pf0$ ng=p n
; (2)
poisqualquerelo entre 0e nouentre 0e ntemque
estarneessariamenteabertoequalqueroutroelopode
estarouabertooufehado. Dessa maneira,
(p)2p n
: (3)
Como n e arbitrario, vemos que a express~ao obtida
aima vai a zero quando n ! 1, para p < 1, o que
noslevaaonluirque
(p)=0;80p<1:
Logo,n~aoobservamosnenhumtipodetransi~aodefase
parad =1, ouseja, n~ao enontramos (om
probabili-dade1)umaglomeradodetamanhoinnitonomodelo
de1dimens~ao. Talresultadotrivial,noentanto,n~aoe
valido paramodelosdeperola~aounidimensionais de
longo alane (lembramos que restringimos nosso
es-tudoao modelosde primeiros vizinhos, queeum
mo-delodeurtoalane).
VI Exist^enia de transi~ao de
fase em dimens~ao d 2
Aoontrariodo quemostramospara d=1, omodelo
deperola~ao emduas ou maisdimens~oes nosreserva
um resultado n~ao trivial 3
. Talvez, usando a sua
in-tui~aofsia,oleitortenhapensadoqueaumentandoa
dimens~aodarede(eportanto,onumerodeliga~oespor
stio),aperola~aopasseaoorrerparapmenorque1,
embora ainda n~ao oorrapara valores pequenos de p.
Eeexatamente issoque oorreemdimens~oesapartir
de2. Naverdadeexisteumvalorrtio,p
,quesepara
essasduasfases. Vamos,ent~ao,provarrigorosamenteo
quedisutimosaima:
Proposi~ao 1 Existem valores p e p, 0 < p p <
1;ambosdependentes dadimens~ao,tais que:
1. (p)=0parad1e para0p<p.
2. (p)>0parad2e parap<p<1.
De aordoomaproposi~aoaima, podemosdenira
probabilidade rtiaomoosupremodetodosos
valo-resdepparaosquais=0
p
supfp:(p)=0g:
Como jadisutimos, p
e fun~ao da dimens~ao, isto e,
p
=p
(d).
E evidente quep
=1emuma dimens~ao.
Seguedaproposi~aoaimaquep
(d)eumnumero
estri-tamentemaiorque0eestritamentemenorque1. Como
orolariodaproposi~ao,temososeguinteteoremaque
resume matematiamente o fen^omeno de transi~ao de
faseemperola~ao.
Teorema 1 Existe, parad2,um valorp
da
proba-bilidade ptal que:
1. 0<p
<1.
2. (p)=0se0p<p
.
3. (p)>0sep
<p1.
Chamaremosde fase subrtiaointervalo0p<p
edefase superrtiaaointervalo1>p>p
. Oponto
p=p
ehamadode pontortioeoomportamento
do sistema na vizinhana deste ponto e bem singular.
A fun~ao funiona omo um par^ametro de ordem:
exeto pelo ponto rtio, se = 0 estaremos na fase
subrtia e se > 0 estaremos na fase superrtia.
Emborasejaonheidoque(p
)=0emd=2,n~aose
sabe seo mesmoeverdade para d> 2(onjetura-se
que(p
)=0parad>2). VejanaFigura5umesboo
dafun~ao (p).
Figura5. Graode(p)pparad2.
Prova da primeira parte da proposi~ao 1:
Con-sideremosuma\aixa"hiperubia,delado\n",dada
por
B(n)=[ n;n℄ d
=fx2Z d
:kx
i
kn;8ig:
Figura6. CaixaB(n),ondexestanafronteiradaaixa.
Ent~ao podemos armar que o onjunto das
on-gura~oesnasquaisaorigemestaonetadaafronteira
da aixaontem oonjunto dasongura~oes em que
aorigemseonetaaoinnito
f!2jCj=1g=f!:o7 !1gf!:o7 !B
n g;8n:
(4)
DenotaremosporjB
n
jaareadafronteiradaaixa
entrada na origem e de lado 2n (isto e, j B
n j
de-notaonumerodestiosqueest~aonasuperfiedeB
n ).
Considerando-seapenas aminhos semvoltas,ou seja,
passeiosaleatoriosautoevitaveis(self-avoiding random
walks),temos de(4)que
(p)P(f!:o7 !B
n
g): (5)
Preisamosagoraontar,ou pelo menosestimar,a
probabilidade dos aminhospossveisque ligam a
ori-gemafronteirada\aixa". Onumerodeaminhossem
loopsdeomprimentoj!jqueligaaorigemafronteira
da aixaeno maximo jB
n
j 2d(2d 1) j!j 1
, pois o
primeiro passo do aminho tem 2d possveis stiosde
destino,adaumdospassosseguintes,ateatingirmosa
fronteira,temnomaximo2d 1op~oespossveisdevido
aaus^enia de loops e,nalmente, podemosalanar a
fronteiradeB
n
emjB
n
jpontosdistintos. Comoada
passo,istoe,adaeloaberto,oorreomprobabilidade
p,temos,de(5),que
P(f!:o7 !B
n g)
X
j!jn jB
n
j2d(2d 1) j!j 1
p j!j
:
(6)
X
j!jn jB
n
j2d(2d 1) j!j 1
p j!j
=
2djB
n j
2d 1 X
k n
(2d 1) k
p k
: (7)
Mas
1
2d 1 X
k n
(2d 1) k
p k
=
[(2d 1)p℄ n
2d 1
1
1 (2d 1)p ;
se (2d 1)p<1: (8)
Ent~ao,substituindo(8)em(7),onseguimosumaotasuperiorparaosegundotermo dadesigualdade (6)
2djB
n j
[(2d 1)p℄ n
2d 1
1
1 (2d 1)p
2dC
d
1 (2d 1)p n
d 1
[(2d 1)p℄ n
:
d
Na desigualdade anterior, usamos que j B
n
j pode
serotadasuperiormentepelaareadeumahiperesfera
entradanaorigem ederaio 2n,i.e., jB
n jC
d n
d 1
.
Assim,adesigualdadeanteriorvaiazeroquandon !
1se(2d 1)p<1. Comooargumentoaimavale8n,
temos que,se0p<1=(2d 1), ent~ao(p)=0.
Paraprovarmosasegunda parteda proposi~ao
te-remosqueusaroseguinteresultado:
Proposi~ao2 (p;d) e uma fun~ao n~ao-deresente
da dimens~ao d.
Prova: Podemosonstruiromodelodeperola~aoem
ddimens~oesemumhiperplano d dimensionaldarede
(d+1) dimensional ontendo a origem. Para tanto,
\desligamos" (delaramos fehados) os elos ligando o
hiperplano ao restodo espao. Chamaremosde C 0
ao
aglomerado daorigemneste modelo(vejaaFigura7).
E fail verqueC 0
C eassim
(p;d)=P
p;d+1 (jC
0
j=1)
P
p;d+1
(jCj=1)=(p;d+1):
Figura7. OaglomeradoC 0
equivaleaoaglomeradoCem
dimens~aod+1.
Prova da segunda parte da proposi~ao 1:
Se-gue da proposi~ao 2 que, para provarmos a segunda
arma~ao da proposi~ao 1, e suente prova-la para
d = 2. Alem disto, omo (p) = 1 P(jCj < 1), e
suiente mostrarque existe umvalor p, estritamente
positivo, tal que P(jCj < 1) < 1para todo pmaior
quepeestritamente menorque1.
Utilizaremos a seguir um argumento semelhante
ao hamado \argumento de Peierls" da me^ania
es-tatstia[8℄. Trabalharemosnarededual deZ 2
,Z 2
=
Z 2
+(1=2;1=2). Da Figura 8efail verquepodemos
assoiar adaelo da redeZ 2
aum elo orrespondente
narededual,emumarela~ao1a1.
Figura8. (a) A rede dual da rede quadradaZ 2
. (b) No
modelo de perola~ao na rede dual, ada elo e delarado
abertooufehadoseoelodaredeoriginalqueointerepta
estaabertooufehado,respetivamente.
Vamosdenirummodelodeperola~aonarededual
Z 2
, baseadono modelo em Z 2
, delarandoos elos e
i
darede dual abertos (om probabilidade p) ou
feha-dos(omprobabilidade1 p)onformeose
i
'sestejam
abertosoufehados. Notemos queaexist^eniade um
iruito de elos fehados na rede dual ao redor da
origem esta relaionada oma exist^enia de um
aglo-meradonitodeelosabertosontendoaorigememZ 2
.
Estefatogeometrio 4
,bemintuitivo,eilustradona
Fi-gura9.
Portanto, temos que P(jCj <1) = P(existe 3
0dual),e omo 1=P(jCj<1)+P(jCj =1),
on-luimosqueP(jCj=1)>0semprequeP(existe 3
Figura9. Umiruitoontendoaorigem.
0 dual)<1,queeoquepassamosaprovar.
Observa-mosque
P(existe30dual)=
= X
P( 30dual) X
n4 X
jj=n
P( 30dual);
ondeaprimeirasomaserefereatodososiruitosde
elosfehadosnarededualeaoredororigem. Asegunda
soma omea de 4porque estee omenortamanho de
iruitopossvel,ao redordaorigem. Aprobabilidade
dentro do ultimo somatorio depende do omprimento
n do iruito, e vale (1 p) n
. Onumerode iruitos
de omprimento n na rede dual ao redor da origem e
no maximo igual a (n43 n 1
) pois, a partir de
um vertie da rede dual (esolhido sobre o eixo dos
y's) temos iniialmente 4 dire~oes para esolher o elo
iniial e, a partir desta esolha, temos no maximo 3
esolhas,sendon onumeromaximode possibilidades.
Alem disso,temos, nomaximonpossveisesolhasdo
vertieiniials^obre oeixodosy's. Dessaforma,
obte-mos
P(existe30dual) 4
3 X
n4
n[3(1 p)℄ n
: (9)
Aexpress~aodoladoesquerdodadesigualdadeaimae
umafun~aoontnuaederesentedepparavaloresde
pmaioresque 2
3
,eanula-sequandop=1. Apliandoo
teoremadovalor intermediario [12℄, podemos onluir
que existep <1tal que asoma aimaeestritamente
menorque1parap>p.
Observa~aoEmespeial,aprovadaproposi~ao1nos
forneeotassuperioreseinferioresparap
,
dependen-tesdadimens~ao 5
, dadaspor:
1
2d 1 p
(d)p:
Agradeimentos
Estetrabalhoepartedeumprojetodeiniia~ao
i-enta[13,14℄desenvolvidopeloprimeiroautorsoba
orientaaodosegundoautor. M.M.de Oliveira
agra-deeaFAPEMIGpelabolsadeiniia~aoienta
du-ranteoperododemaroajulho de2001eao extinto
GrupoPET/CAPES/SESudoDepartamentodeFsia
da UFMG pelo suporte naneiro durante o ano de
2000. OsdoisautoresagradeemaBernardoB.Lima,
Marelo T. Cunha e Remy Sanhis por terem lido e
ritiadovers~oesanterioresdestemanusrito.
Refer^enias
[1℄ H.M.Nussenzveig,CursodeFsiaBasia,E.Bluher,
S~aoPaulo(1981).
[2℄ T. Tome e M.J. de Oliveira, Din^amia Estoastia e
Irreverssibilidade,EdUSP,S~aoPaulo(2001).
[3℄ S. R. Broadbent and J.M. Hammersley, Perolation
Proesses I. Crystals and Mazes, Proeedings of the
CambridgePhylosophialSoiety,53,629-641,(1957).
[4℄ J.ChayesandL.Chayes,PerolationandRandom
Me-dia,inCritialphenomena,randomsystemsandgauge
theories,LesHouhesSessionXLIII1984,K.
Osterwal-derandR.Storaeds.,ElsevierSienePublishersB.V.
(1986).
[5℄ B.I.Shklovskii,A.L.Efros,Perolationtheoryand
on-dutivityofdisorderedsystems,UspekhiFiz.Nauk117,
401(1975).
[6℄ M. Sahini, Appliation of Perolation Theory, Taylor
andFranis,London,(1994).
[7℄ D. Stauer and A. Aharony, Introdution to
Perola-tionTheory,Taylor&Franis,London(1992).
[8℄ G.Grimmett,Perolation,SpringerVerlarg,NewYork
(1989).
[9℄ H. Kesten, Perolation Theory for Mathematiians,
Birkhauser(1982).
[10℄ L.R. Fontes, Perola~ao ,notas doIMPA, Riode
Ja-neiro(1996).
[11℄ L.R.Fontes,Perola~ao,ummodelosimples(e
interes-sante)paraummeioporoso.MatematiaUniversitaria.
Brasil: ,v.28,p.1-17, (2000).
[12℄ G.F. Simmons,Caluloom Geometria Analtia,S~ao
Paulo: MGraw-Hill,(1987).
[13℄ M.M. de Oliveira e G.A. Braga; Um estudo da fase
subrtiaparaomodelodeprimeirosvizinhosemuma
rede hiper- ubia d-dimensional, Livro deresumos da
IXSemanadeIniia~aoCientadaUFMG,Belo
Ho-rizonte,(2000).
[14℄ M.M.deOliveiraeG.A.Braga;AdesigualdadedeVan
denBerg-Kerstenesuasaplia~oesemmodelosde
per-ola~ao,AnaisdaXSemanadeIniia~aoCientada
UFMG,Belo Horizonte,(2001).
5
Kestenmostrouquep(d) 1