Análise multiescala de séries temporais do efeito da cintilação ionosférica nos sinais de satélite GPS a partir de wavelets não decimadas

(1)

ANÁLISE MULTIESCALA DE SÉRIES

TEMPORAIS DO EFEITO DA CINTILAÇÃO

IONOSFÉRICA NOS SINAIS DE SATÉLITE

GPS A PARTIR DE WAVELETS NÃO

DECIMADAS

Gabriela de Oliveira Nascimento Brassarote

Orientador: Profa. Dra. Eniuce Menezes de Souza

Programa: Matemática Aplicada e Computacional

(2)

(3)

UNIVERSIDADE ESTADUAL PAULISTA

Faculdade de Ciências e Tecnologia de Presidente Prudente

Programa de Pós-Graduação em Matemática Aplicada e Computacional

ANÁLISE MULTIESCALA DE SÉRIES

TEMPORAIS DO EFEITO DA CINTILAÇÃO

IONOSFÉRICA NOS SINAIS DE SATÉLITE

GPS A PARTIR DE WAVELETS NÃO

DECIMADAS

Gabriela de Oliveira Nascimento Brassarote

Orientador: Profa. Dra. Eniuce Menezes de Souza

Dissertação apresentada ao Programa de Pós-Graduação em Matemática Aplicada e Computacional da Faculdade de Ciências e Tecnologia da UNESP para obtenção do tí-tulo de Mestre em Matemática Aplicada e Computacional.

(4)

FICHA CATALOGRÁFICA

Brassarote, Gabriela de Oliveira Nascimento.

B832a Análise multiescala de séries temporais do efeito da cintilação ionosférica nos sinais de satélite GPS a partir de wavelets não decimadas / Gabriela de Oliveira Nascimento Brassarote. - Presidente Prudente : [s.n.], 2014

84 f.

Orientador: Eniuce Menezes de Souza

Dissertação (mestrado) - Universidade Estadual Paulista, Faculdade de Ciências e Tecnologia

Inclui bibliografia

(5)

(6)

(7)

Agradecimentos

A Deus, pelo provimento de tudo o que foi necessário para que eu chegasse até aqui, e por ter estado ao meu lado em cada momento da minha vida, principalmente nos de desânimo e diﬁculdade.

À minha orientadora, Profa. Dra. Eniuce Menezes de Souza, pela oportunidade, apoio, conﬁança, e principalmente, pela paciência que sempre teve comigo; e ao Prof. Dr. João Francisco Galera Monico, pelo auxílio e tão preciosas sugestões.

Aos professores do PosMAC e do Departamento de Matemática Estatística e Com-putação, por contribuírem com minha formação acadêmica. Em especial, agradeço aos professores Dr. Aylton Pagamisse e Dr. Messias Meneguette Junior, pelo incentivo e sugestões durante o exame de qualiﬁcação.

Aos funcionários da seção de Pós-Graduação, por serem sempre tão dedicados e pres-tativos.

À Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), pelo apoio ﬁnanceiro.

A todos os colegas da terceira turma do PosMAC, pela convivência e amizade.

Às minhas queridas amigas, Luciene e Mariane, por serem minhas verdadeiras com-panheiras desde a graduação, pela paciência, apoio e orações.

(8)

(9)

Resumo

O estudo da cintilação ionosférica, causada por ﬂutuações na amplitude e na fase de um sinal eletromagnético quando este passa por irregularidades na densidade de elétrons da ionosfera, tem assumido um papel muito importante na pesquisa ionosférica e também no posicionamento por satélite. Isso se deve à crescente inﬂuência do GNSS na navega-ção e no sensoriamento remoto e também pelo fato da cintilanavega-ção degradar severamente o desempenho desses sistemas. Ainda existem muitas lacunas a serem preenchidas para que possa ser proposto algum método efetivo para correção dos efeitos causados nos sinais GNSS ou mesmo previsão da cintilação, principalmente para a região equatorial, em que está situado o Brasil. Portanto, nessa dissertação objetiva-se investigar a cintilação sob uma perspectiva multiescala, abordando para tanto, a análise multirresolução a partir de

wavelets não decimadas. Como consequência, os resultados desta investigação das séries temporais obtidas dos índices S4de cintilação mostram a presença de um padrão que se repete na série em dias consecutivos em que há presença de dados. Tal comportamento periódico, que apresenta formato de "U" mostra estar relacionado com o efeito do mul-ticaminho e pode influenciar na análise do índice S4 de cintilação ionosférica, fazendo-se necessário eliminá-lo. Através da decomposição em multiescala do período com baixos índices de cintilação é possível estimar o efeito do multicaminho, cuja repetibilidade é evidenciada nas escalas mais suaves. Uma vez estimado, esse efeito pode ser removido da série dos índices S4 no período de forte cintilação. Assim, a partir dessa proposta, este efeito deixa de ser expressivo no espectro wavelet e de influenciar posteriores análises da série temporal dos índices de cintilação. Análise de diferentes estações e satélites mos-tram que o efeito da cintilação ionosférica varia conforme a localização da estação e ângulo de elevação e azimute do satélite, por isso, cada caso deve ser tratado individualmente. Portanto, essa dissertação apresenta uma metodologia inovadora para a investigação dos efeitos da cintilação ionosférica sobre os sinais GNSS, mais especificamente sobre os sinais GPS, através da análise do espectro wavelet da série temporal dos índices S4 de cintila-ção, além de dar um primeiro passo em direção a separar o efeito da cintilação de outros efeitos que podem influenciar a análise dos índices S4.

(10)

(11)

Abstract

Multiscale analysis of time series of the eﬀects of ionospheric scintillation from non-decimated wavelet.

The study of the ionospheric scintillation, which is caused by fluctuations in the amplitude and phase of an electromagnetic signal when it passes through irregularities in the density of electrons in the ionosphere, has become very important in ionospheric research and also in satellite positioning. This is due to the increasing influence of GNSS navigation and re-mote sensing, and also because the scintillation severely degrade the performance of these systems. There are still many gaps to be fulfilled before the propositon of some effective method for correcting of the effects of the scintillation on GNSS signals or even its pre-diction, especially for equatorial region, which includes Brazil. This dissertation aims to investigate the ionospheric scintillation under a multiscale aspects using a multiresolution analysis from non-decimated wavelets. The investigation of the time series obtained of the

S4 scintillation index showed the presence of a pattern that is repeated in the series on consecutive days in which there are data. This periodic behavior, which has "U" format and can be related to the effect of the multipath, influences the analysis ofS4ionospheric scintillation index, and should be eliminated. Through multiscale decomposition of the period with low scintillation index it is possible to estimate the multipath effect, which is evident in the smoother scales. Once identified and estimated, this effect can be removed from the S4index series in the strong scintillation period. Thus, from this proposition, it

becomes not significant in the spectrumwavelet, not influencing the analysis of ionosphe-ric scintillation time series. Analysis of the different stations and satellites show the effect of ionospheric scintillation varies with location station and elevation angle and azimuth of the satellite, therefore, each case must be treated individually. Therefore, this work presents an innovative methodology for investigating the effects of ionospheric scintilla-tion on GNSS signals, or GPS signals specifically. by analyzing the spectrum wavelet of the time series of S4scintillation index, and take a first step toward separating the effect of scintillation in relations the other effects that may influence its analysis.

(12)

(13)

Lista de Figuras

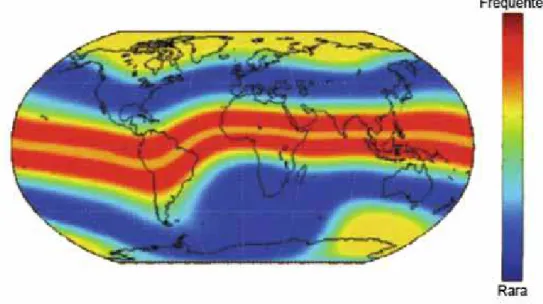
1.1 Intensidade e frequência de ocorrência da cintilação ionosférica. Fonte:

Adaptado de KINTNER JR., et.al. (2009). . . 20

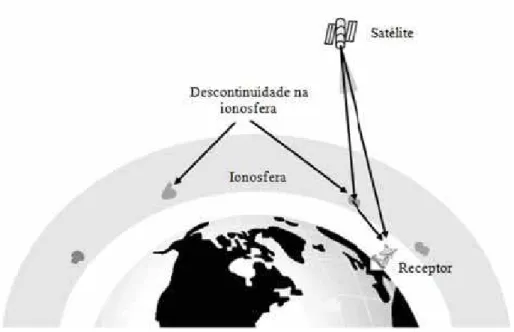
2.1 Cintilação Ionosférica. Fonte: Adaptado de MAINI (2007) . . . 24

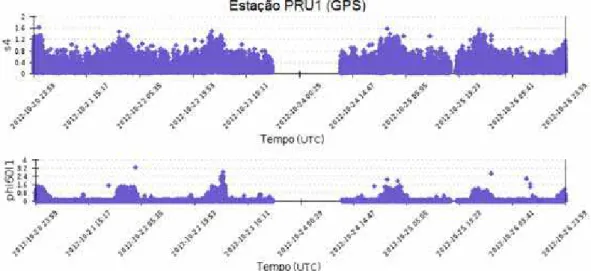
2.2 Comparação dos índices S4 e P hi60 para a estação GPS localizada em Presidente Prudente-SP. . . 25

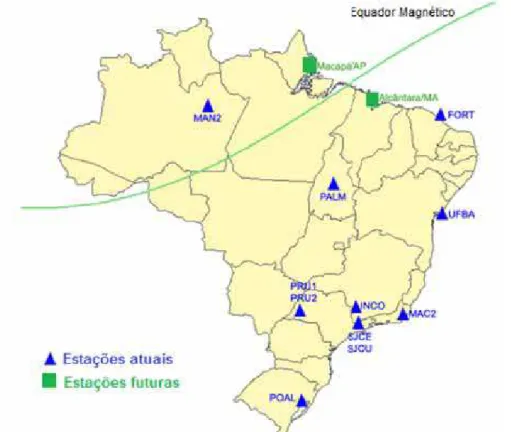
2.3 Distribuição das Estações da Rede CIGALA/CALIBRA. Fonte: Adaptado de CALIBRA (2014) . . . 26

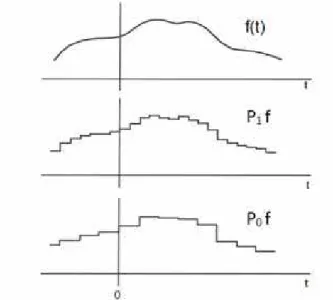
3.1 Sinalf e suas projeções sobreV0eV1. Fonte: Adaptado de DAUBECHIES (1992). . . 33

3.2 Algoritmo Piramidal da TWD. . . 35

3.3 Gráﬁco da função escala de Haar φ(t). . . 36

3.4 Wavelet de Haar ψ(t). . . 37

3.5 Wavelets de Daubechies ψ(t)com p= 2,4,6,10. Fonte: SOUZA (2008) . 37 3.6 Symmlets ψ(t) com p= 2,5,6,10. Fonte: SOUZA (2008) . . . 38

3.7 (À esquerda) Função escala φ; (À direita) Função wavelet ψ Starlet. Fonte: STARK (2010) . . . 39

4.1 TWD de X e TX (vetor X transladado) - coeﬁcientes escalonados em cada escala. . . 41

4.2 TWND de X e TX (vetor X transladado) - coeﬁcientes escalonados em cada escala. . . 42

4.3 Sinal simulado. À direita, as três funções periódicas que compõem o o sinal. 43 4.4 TWD e TWND do sinal simulado - coeﬁcientes escalonados em cada escala. 43 5.1 Decomposição em multiescala através daSymmlet wavelet com 10 momen-tos nulos. . . 56

6.1 Fluxograma da implementação. . . 59

7.1 Índice S4 de cintilação do período de 01/01/2012 a 31/12/2012. . . 61

7.2 Índice S4 de cintilação do período de 12 a 14/03/2012. . . 62

7.3 Índices S4 do período de 12 a 14/03/2012 (topo) e ângulo de elevação do satélite 11 (abaixo). . . 62

7.4 Comparação do índiceS4do satélite 11 com diferentes máscaras de elevação. 63 7.5 Comparação das bases wavelet na análise de índices S4 de cintilação do período de 12 a 14/03/2012. . . 64

7.6 Estimativa do comportamento periódico presente na ST dos índices S4 de cintilação. . . 65

7.7 ÍndicesS4 do período com cintilação forte, após remoção das escalas mais suaves (estimadas no período sem cintilação). . . 66

(14)

LISTA DE FIGURAS 12 7.8 Estimativa do comportamento periódico presente na ST dos índices S4 de

cintilação. . . 67

7.9 Comparação dos índices de cintilação e respectivos periodogramas antes e após remoção do multicaminho. Satélite 11, estação PRU1. . . 68

7.10 Análise wavelet do satélite 1, estação PRU1. . . 70

7.14 Análise wavelet do satélite 11, estação SJCU. . . 75

7.15 Análise wavelet do satélite 11, estação PALM. . . 76

7.16 Análise wavelet do satélite 11, estação POAL. . . 77

7.17 Análise wavelet do satélite 11, estação MAN2. . . 78

(15)

Lista de Tabelas

6.1 Estações da rede CIGALA analisadas. . . 57 6.2 Interpretação da frequência de decomposição em multirresolução. . . 60

7.1 Porcentagem de observações que ultrapassaram o nível de cintilação fraca, antes e após remoção do multicaminho, por estação. . . 80

(16)

(17)

Lista de Siglas

AIE: Anomalia da Ionização Equatorial AMR: Análise Multirresolução

CIGALA: Concept for Ionospheric Scintillation Mitigation for Professional GNSS in Latin America

CALIBRA:Countering GNSS high Accuracy applications Limitations due to Ionosphe-ric disturbances in BRAzil

EWS: EspectroWavelet Evolucionário GNSS: Global Navigation Satellite System

GPS: Global Positioning System

LSW:Locally Stationary Wavelet

ST: Série Temporal

TF: Transformada de Fourier TW: Transformada Wavelet

TWC: Transformada Wavelet Contínua TWD: Transformada Wavelet Discreta

TWND: Transformada Wavelet Não Decimada

(18)

(19)

Sumário

Resumo 7

Abstract 9

Lista de Figuras 10

Lista de Tabelas 12

Lista de Siglas 15

Capítulos

1 Introdução 19

1.1 Objetivos . . . 20

1.2 Conteúdo da dissertação . . . 21

2 O Estudo da Cintilação Ionosférica 23 2.1 A Ionosfera Terrestre . . . 23

2.2 Cintilação ionosférica . . . 24

2.3 Avanços no estudo da Cintilação a partir de wavelets . . . 26

3 Wavelets 29 3.1 O que são wavelets? . . . 29

3.2 TransformadaWavelet . . . 30

3.2.1 Transformada Wavelet Contínua . . . 30

3.2.2 Transformada Wavelet Discreta . . . 31

3.3 Análise Multirresolução . . . 32

3.4 Algoritmo Piramidal da TWD . . . 34

3.5 Escolha de uma basewavelet . . . 35

3.5.1 Características das Wavelets . . . 35

3.5.2 Wavelet de Haar . . . 36

3.5.3 Wavelet de Daubechies . . . 37

3.5.4 Symmlets . . . 37

3.5.5 Starlet . . . 38

3.5.6 Considerações sobre a escolha da base wavelet . . . 39

4 Transformada Wavelet Não Decimada 41 4.1 Os ﬁltroswavelet e escala da TWND . . . 43

4.2 Formulação da TWND . . . 44

4.3 Deﬁnição doj-ésimo nível de coeﬁcientes da TWND . . . 48

(20)

5 Análise Multiescala de Séries Temporais 53

5.1 Séries Temporais Estacionárias . . . 53

5.2 Espectro . . . 54

5.3 Espectro Wavelet Evolucionário (EWS) . . . 54

5.4 Estimação do EWS a partir do Periodograma Wavelet . . . 55

6 Metodologia 57 6.1 Implementação . . . 58

7 Resultados e Análises 61 7.1 Comparação e escolha da Base Wavelet . . . 64

7.2 Estimativa do multicaminho no período de fraca cintilação e remoção no período de cintilação forte . . . 65

7.3 Avaliação dos espectros dos índices S4 de cintilação antes e após remoção do multicaminho, considerando a estimativa de um efeito médio . . . 69

7.3.1 Comparação entre satélites da estação PRU1 . . . 69

7.3.2 Comparação entre diferentes estações . . . 74

8 Conclusões e Trabalhos Futuros 81

(21)

Capítulo

1

Introdução

A tecnologia GNSS (Global Navigation Satellite System) tem se tornado cada vez mais utilizada nas atividades humanas que necessitam de posicionamento, como por exemplo na navegação e no sensoriamento remoto. No entanto, até que o sinal do satélite chegue ao receptor GNSS, efeitos muitas vezes severos, exercem inﬂuência sobre o sinal, ocasionando erros ou até mesmo a perda do sinal do satélite pelo receptor.

A ionosfera é uma das maiores fontes de interferência na propagação dos sinais GNSS. O efeito das irregularidades da densidade dos elétrons presentes na ionosfera, que carac-teriza a cintilação ionosférica, é ainda pior. A cintilação pode enfraquecer ou até mesmo causar a perda total do sinal pelo receptor, causando efeitos signiﬁcativos no posiciona-mento por satélite (CONKER, 2003).

Os efeitos da cintilação são mais severos na região equatorial do planeta, seguida pelas regiões de altas latitudes (principalmente nos pólos) e por ﬁm as de médias latitudes (DAVIES, 1990), como ilustra a Figura (1.1). As ocorrências de cintilação nas regiões de altas latitudes estão relacionadas com períodos de alta atividade solar e outras atividades extremas tais como a ocorrência de tempestades geomagnéticas. Já as ocorrências de cintilação nas regiões equatoriais e de médias latitudes ocorrem devido à anomalia da ionização equatorial (AIE), principalmente no intervalo após o por do sol e antes da meia noite (KELLEY, 1989). Além disso, a magnitude e a ocorrência das cintilações tende a aumentar nos meses de equinócio, período em que o sol está sobre o círculo do equador celeste, e com o aumento da atividade solar (RODRIGUES, 2003). O Brasil, por possuir grande parte de seu território situado no equador geomagnético, sofre intensos efeitos da cintilação ionosférica.

O ideal é que a cintilação seja estudada local e globalmente, devido sua natureza dispersiva e sua variabilidade espacial. Pode ser tratada como séries temporais em que se tem o interesse em entender o processo estocástico gerador da mesma.

Por possuir natureza aleatória e aparentemente não correlacionada, a modelagem da cintilação tem se mostrado complicada e ineﬁciente. No entanto, através de informações quantitativas do índice de cintilação, como o índice S4 que quantiﬁca a cintilação em potência (amplitude), é possível caracterizar e entender as irregularidades ionosféricas que causam a cintilação, bem como estabelecer estratégias de previsão dos efeitos da cintilação que, às vezes, podem tornar o GNSS não efetivo (STRANGEWAYS, 2009).

Pretende-se nessa dissertação investigar os efeitos da cintilação ionosférica nos sinais de satélites GPS (Global Positioning System), que é um dos sistemas GNSS mais co-nhecidos e utilizados atualmente, através da análise da série temporal (ST) proveniente dos índices S4 de cintilação. Devido às irregularidades e espalhamento da camada F da ionosfera, os efeitos da cintilacão nos sinais GPS podem ser não estacionários, exigindo

(22)

1. Introdução 20

Figura 1.1: Intensidade e frequência de ocorrência da cintilação ionosférica. Fonte: Adaptado de KINTNER JR., et.al. (2009).

um método adequado para tal análise. Uma análise tradicional de wavelets, por si só já permite uma análise não paramétrica para séries temporais não estacionárias. Em sua versão decimada, a Transformada Wavelet Discreta (TWD) já tem contribuído bastante para o avanço do posicionamento por satélite (SOUZA, 2004, 2008; KELLER, 2004). Entretanto, devido à usual decimação por 2, em cada escala tem-se metade dos coeﬁcien-tes da escala anterior. Para uma análise completa em multiescala seria necessário que o mesmo número de coeﬁcientes correspondendo a todos os instantes de tempo em que os dados foram coletados fosse mantido para cada escala. Isso é possível com a Transformada

Wavelet Discreta Não Decimada (TWND), a qual é invariante por translação (NASON e SILVERMAN, 1995). Dessa forma, informações e padrões escondidos, que não podem ser detectados no domínio do tempo, podem ser explicitados no domínio espaço-frequência. Essa metodologia aplicada na ST dos índices S4 de cintilação possibilitará identiﬁcar e remover possíveis efeitos cíclicos presentes na série, e que podem inﬂuenciar na análise da cintilação ionosférica.

1.1 Objetivos

O objetivo geral desse trabalho é investigar e caracterizar o efeito da cintilação io-nosférica nos sinais GPS para a região equatorial, em especial a brasileira, a partir da análise multiescala, ou multirresolução, de séries temporais pela TWND. Como objetivos especíﬁcos comparecem:

• investigar a existência de variações cíclicas no efeito da cintilação ionosférica;

• separar o efeito de cintilação ionosférica de outros efeitos que podem inﬂuenciar na análise do índice S4 de cintilação;

• comparar diferentes bases de wavelets e momentos nulos para identiﬁcar umawavelet

(23)

1. Introdução 21

1.2 Conteúdo da dissertação

A organização deste trabalho se dá conforme segue. No capítulo 2 é apresentado brevemente o conceito de cintilação ionosférica, objeto de estudo dessa dissertação. Os capítulos 3 e 4 são dedicados à revisão bibliográﬁca sobre wavelets, sendo que no capítulo 4 é dado uma atenção especial às wavelets não decimadas, destacando o que motivou o seu uso no desenvolvimento deste trabalho. Já o capítulo 5 destina-se à análise de séries temporais por wavelets.

No capítulo 6 é apresentada a metodologia utilizada na investigação dos efeitos da cintilação ionosférica sobre os sinais GPS, deixando para o Capítulo 7 a apresentação e análise dos resultados obtidos através da aplicação da metodologia proposta.

(24)

(25)

Capítulo

2

O Estudo da Cintilação Ionosférica

A ionosfera é uma das maiores fontes de interferência na propagação dos sinais GPS. O efeito das irregularidades da densidade dos elétrons presentes na ionosfera, que caracteriza a cintilação ionosférica, é ainda pior. A cintilação pode enfraquecer ou até mesmo causar a perca total do sinal pelo receptor, causando efeitos signiﬁcativos no posicionamento por satélite. O Brasil, por estar localizado na região equatorial do planeta, sofre intensos efeitos da cintilação ionosférica. Por isso, faz-se necessário estudar os efeitos da cintilação sobre os sinais GPS, para melhor entendê-los e minimizá-los.

2.1 A Ionosfera Terrestre

A ionosfera é uma camada da atmosfera localizada entre 50 a 1000 km de altitude, formada pela interação de radiação solar com diferentes gases que constituem a atmosfera. Dividida em três regiões (ou camadas) D, E e F, por ordem de altitude e densidade crescente de elétrons livres, a ionosfera tem um importante papel na propagação de ondas de rádio, mas também é capaz de afetar severamente um sinal de rádio que passe por ela, inclusive os sinais GPS (CONKER et. al., 2003; MAINI, 2007).

A região D é a camada mais baixa da ionosfera. Abrange uma faixa que se estende do princípio da ionosfera (cerca de 50 km), até aproximadamente 85 km, e encontra-se apenas na região da Terra que está sendo iluminada diretamente pelo sol. Essa camada é de extrema importância nas telecomunicações, pois reﬂete ondas de rádio de banda de frequência entre 3 e 30 KHz (LF e VLF), permitindo que ocorra transmissão de rádio entre locais muito distantes da superfície terrestre (DAVIES, 1990).

Situada entre o ﬁm da região D e cerca de 140 Km, está a camada E, que também é útil na propagação de ondas de rádio e tem sua intensidade variando com o grau de atividade solar e ângulo zenital do sol. Próximo de 90 a 130 km de altitude (dentro da região E), devido a variações na densidade de elétrons, pode-se formar uma nova camada denominada Sporadic-E (DAVIES, 1990) capaz de reﬂetir frequências de até 100 MHz.

A região F, por sua vez, está compreendida basicamente entre 140 e 1000 km de altitude. É nessa região que ocorre a grande maioria das irregularidades que afetam os sinais de rádio, inclusive a cintilação ionosférica. Em períodos de alta atividade a camada F costuma ser dividida em duas regiões: F1 e F2. A região F1 (140 a 200 km), tem sua concentração de elétrons diretamente proporcional à atividade solar e somente é percebida durante o dia. Já a região F2 (200 a 1000 km) é a região mais importante do ponto de vista de comunicação, sendo insensível às variações da radiação solar no decorrer do dia e mantendo sua eﬁciência para propagação de ondas de rádio durante à noite.

(26)

2. O Estudo da Cintilação Ionosférica 24

2.2 Cintilação ionosférica

A cintilação ionosférica é causada por mudanças rápidas na fase e amplitude do sinal de rádio recebido, as quais são causadas por irregularidades na densidade de elétrons ao longo do caminho percorrido pelo sinal na ionosfera (CONKER et al., 2003). Isso, porque devido à grande quantidade de elétrons presentes na região F, formam-se bolsas de concentração local de íons, produzindo descontinuidades na ionosfera. Um sinal de rádio que por ali atravesse, sofre refração que caracteriza a cintilação ionosférica. Como resultado, o sinal chega até seu receptor via dois caminhos, o caminho direto e o refratado, como mostra a Figura (2.1). O sinal resultante é o vetor adição dos sinais direto e refratado (MAINI, 2007).

Figura 2.1: Cintilação Ionosférica. Fonte: Adaptado de MAINI (2007)

Tais mudanças na estrutura do sinal, que caracterizam a cintilação, podem ocorrer tanto em amplitude como em fase (MUSHINI et al., 2012). Embora sejam de pequena escala devido às flutuações rápidas, pode ser intensa o suficiente para causar erros sig-nificativos nas medidas de posicionamento com o sistema GPS e, em muitos casos, a degradação ou até mesmo perda do sinal satélite por um receptor GPS (KINTNER et al. 2007; REZENDE et al, 2010; STRANGEWAYS, 2009).

Uma maneira de caracterizar e entender as irregularidades ionosféricas que causam a cintilação é através dos índices S4 e σφ, que quantiﬁcam a cintilação em potência e

desvio-padrão, respectivamente.

O índice S4, mapeia a intensidade (I) da cintilação ionosférica e é calculado segundo a equação (http://www.inpe.br/scintec/pt/scintil.php):

S4 = I

2₋_I2

I2 ,

em que I = 10logP é a intensidade do sinal, e o operador representa o cálculo da esperança.

Já o índiceσφ, também chamado P hi60, mostra a variação da medida de fase da onda

portadora φ no receptor nos últimos 60 segundos, isto é, quantiﬁca o desvio-padrão da fase do sinal GPS, sendo calculado por

σφ =

(27)

2. O Estudo da Cintilação Ionosférica 25 Nas regiões equatoriais, os índices S4e σφ são fortemente correlacionados, sendo que

em eventos de cintilação ionosférica os valores de ambos os parâmetros chegam a ser numericamente similares, como pode ser observado na Figura (2.2). Por esse motivo, neste trabalho será utilizado apenas o índiceS4para análise do efeito da cintilação sobre o sinal GPS. A convenção mais adotada para classiﬁcação desse indicador relaciona os índices S4 menores que 0,3 como eventos de muito fraca ou nenhuma intensidade, entre 0,3 e 0,5 de intensidade fraca, entre 0,5 e 0,7 de intensidade moderada e maiores que 0,7 de forte intensidade. Ocasionalmente, esse índice pode ultrapassar o valor unitário, chegando a valores próximos a duas unidades (TIWARI, 2011).

Figura 2.2: Comparação dos índices S4 e P hi60 para a estação GPS localizada em Pre-sidente Prudente-SP.

A maior frequência de ocorrências da cintilação ionosferérica está ligada à região equa-torial do planeta, onde a grande maioria dos eventos de cintilação ocorre durante a noite, mais especiﬁcamente na camada F2, entre 200 e 600 km de altura. É raro ocorrer eventos de cintilação durante o dia, porém, quando ocorrem, são decorrentes de efeitos na camada

Sporadic E (DAVIES, 1990).

A importância do estudo da cintilação ionosférica na região equatorial, é tão expressiva que em março de 2010, foi iniciado o projeto CIGALA (Concept for Ionospheric Scintil-lation Mitigation for Professional GNSS in Latin America), com posterior continuação através do projeto CALIBRA (Countering GNSS high Accuracy applications Limitations due to Ionospheric disturbances in BRAzil), cujo objetivo é estudar as causas da cintila-ção ionosférica em baixas latitudes, bem como seus efeitos nas tecnologias em desenvol-vimento. A escolha pela América Latina, em especial o Brasil, se deve a dois motivos: encontra-se em uma das regiões mais críticas do efeito das irregularidades ionosféricas e possui instituições acadêmicas e comerciais de grande relevância para a implementação e desenvolvimento do projeto, tais como UNESP e Petrobras (CALIBRA, 2014).

(28)

2. O Estudo da Cintilação Ionosférica 26

Figura 2.3: Distribuição das Estações da Rede CIGALA/CALIBRA. Fonte: Adaptado de CALIBRA (2014)

2.3 Avanços no estudo da Cintilação a partir de

wave-lets

Trabalhos utilizando a análise wavelet no estudo da cintilação ionosférica têm con-tribuído para um melhor entendimento e caracterização da cintilação nas regiões de alta latitude. Em Materassi et al., (2009) foram analisados escalogramas de wavelets e veriﬁ-cadas estruturas em três escalas nos sinais GPS, uma de grande escala com frequências baixas devido, principalmente, ao movimento do satélite e variâncias suaves da ionosfera; uma escala intermediária, em que estariam os efeitos da cintilação; e uma escala pequena com frequências altas devido aos ruídos. Essa estrutura foi utilizada para melhorar os cálculos dos índices de cintilação para altas latitudes, de maneira que apenas a escala intermediária dos dados foi empregada. Outros trabalhos tem utilizado wavelets para re-mover apenas as baixas frequências e estimar os índices de cintilação para altas latitudes (MUSHINI et al., 2012, TIWARI et al, 2011). Na literatura inglesa, esse procedimento é conhecido como detrending. Resultados muito positivos foram obtidos para dados de alta latitude, de forma que foi sugerido que wavelets fossem utilizadas nos receptores ao invés de ﬁltros Butterworth convencionais.

(29)

2. O Estudo da Cintilação Ionosférica 27 para a região equatorial e de baixas latitudes. Nesse sentido, nesse trabalho tais índices são investigados pela análise multiescalawavelet, inclusive no sentido de avaliar se a partir desse método convencional de detrending, existe a presença de outros efeitos no índiceS4

(30)

(31)

Capítulo

3

Wavelets

A análise wavelet é uma ferramenta matemática que teve seu uso intensiﬁcado nas últimas décadas em uma grande quantidade de aplicações, principalmente nas áreas de análise de sinais e equações diferenciais. Isso se deve à capacidade das wavelets de loca-lização tempo-frequência, apresentando uma visão diferenciada e inovadora na análise de dados não estacionários, como o efeito de cintilação ionosférica.

3.1 O que são

wavelets

_?

Considere o espaçoL2₍_R₎_{de todas as funções mensuráveis de quadrado integrável sobre}

R, também denominado espaço das funções de energia ﬁnita. Ou seja, se ψ(t) _∈ L2(R)

então _−∞+∞_|ψ(t)_|2dt <_∞.

Deﬁnição 1 Uma função ψ(t) _∈ L2₍_R₎ _{é denominada wavelet, se satisfaz as seguintes}

condições:

1. A condição de admissibilidade

Cψ =

+∞

−∞

ψˆ(λ)

2

|λ_| dt <∞ (3.1)

em que _ψ(λ)ˆ _{é a Transformada de Fourier (TF) da função} _ψ _{dada por}

ˆ

ψ(λ) = 1 2π

+∞

−∞

ψ(t)e−iλtdt.

Esta condição (3.1) garante a invertibilidade da Transformada Wavelet (TW). Na maioria dos casos, ela é equivalente a

+∞

−∞

ψ(t)dt = 0,

e estabelece que ψ(t) deve oscilar em torno do eixo x. Por isso, geometricamente, uma wavelet tem o formato de uma onda.

2. A função wavelet deve ter energia unitária, isto é,

_∞

−∞|

ψ(t)_|2dt = 1,

(32)

3.Wavelets 30

garantindo que a função wavelet possua suporte compacto, ou um rápido decaimento de amplitude. Isso indica que ψ(t) será uma onda de curta duração.

Por essas duas condições, a função ψ(t) recebe o nome wavelet (do inglês: onda pe-quena) ou ondaleta (do francês: ondelette), como também é conhecida.

3.2 Transformada

Wavelet

O uso de transformadas serve para observar características de um sinal que estão presentes nele mas não podem ser observadas em um dado domínio. A Transformada de Fourier (TF), por exemplo, muda um sinal do domínio do tempo para o domínio da frequência, representando-o como uma série de senos e cossenos. Porém, a informação tempo é totalmente desorientada no sinal transformado, não sendo sensível a mudanças de freqüência no sinal e mostrando-se apropriada apenas para os chamados sinais esta-cionários: sinais cuja freqüência não muda com o tempo. Mas, como os sinais reais são em geral não estacionários, o ideal é aplicar a TF em parte do sinal, ao invés dele todo. Deste modo, o sinal passa a ser visto em janelas de tamanho ﬁxo e a transformada passa a ser calculada em cada janela, pois dentro dela o sinal tem comportamento estacionário. Este conceito é chamado TF Janelada.

No entanto, é comum a necessidade de aplicação de uma transformada em uma janela de tamanho variável. Essa é a ideia básica da TW, que é uma transformada linear e expande uma função utilizando um conjunto de funções wavelets, funções estas que têm localização espaço-frequência. Deste modo, é possível extrair informações das variações em frequência e tempo de sinais não estacionários.

3.2.1 Transformada

Wavelet

_Contínua

A wavelet mãe ψ _∈ L2₍_R₎ _{dilatada (ou comprimida) por uma fator} _a _{e submetida a}

um deslocamento b dá origem à uma família de funções da forma

ψa,b(t) =

1

|a_|ψ

t₋b a

, a, b_∈R,a=0 (3.2)

em que o fator _√1

|a| é incluído na fórmula para que se conserve a norma unitária de ψ.

Deﬁnição 2 A Transformada Wavelet Contínua (TWC) de uma função f _∈ L2₍_R₎ _é

expressa por

W(a, b) =f, ψa,b=

+∞

−∞

f(t)ψa,b(t)dt=

+∞

−∞

f(t)1

|a_|ψ

t₋b a

dt (3.3)

em que f, ψa,b representa o produto interno de L2 sobre L2([a, b]) deﬁnido por

f, g=

b

a

f(t)g(t)dt, em que f, g_∈L2([a, b]). (3.4)

Os parâmetros a e b se referem à escala e localização da wavelet mãe, e assumem valores contínuos na TWC.

A TWC é inversível, e sua inversa é dada pela seguinte relação

f(t) = 1 Cψ

+∞

−∞

+∞

−∞

W(a, b)ψa,b(t)

dadb

a2 (3.5)

(33)

3.Wavelets 31 Deste modo, um sinal f(t) após transformado pode ser recuperado através da TWC inversa descrita por (3.5).

3.2.2 Transformada

Wavelet

_Discreta

A ﬁm de se obter a Transformada Wavelet Discreta (TWD) utiliza-se parâmetros de dilatação e translação que variam discretamente. Ou seja, para que a transformada seja discretizada, os parâmetrosa, bda equação (3.3) são restritos a umgrid discreto, de modo que

a=a−₀j b =kb0a−0j

em que j, k _∈ _Z e a0 > 1, b0 > 0. A escolha mais popular é a0 = 2 e b0 = 1, por

simplicidade (DAUBECHIES, 1992).

Desta forma, a família de wavelets gerada na equação (3.2) pode ser substituida por

ψj,k(t) =aj/0 2ψ

t₋kb0a−0j

a−0j

=aj/₀ 2ψaj₀t₋kb0

.

Restringindo a0 = 2 e b0 = 1, então existeψ, tal que

ψj,k(t) = 2j/2ψ

2j/2t₋k (3.6)

constitui uma base ortonormal para L2₍_R₎_.

Considere, a partir de agora, dados discretosX = (X0, ..., Xn−1)contidos no conjunto

dos números reais.

Deﬁnição 3 A TWD de X, com relação à wavelet mãe ψ, pode ser deﬁnida como

dj,k = n−1

t=0

Xtψj,k(t), (3.7)

em que n = 2j0 é o número de observações. A equação (3.7) é calculada para j =

0, ..., j0−1e k = 0, ...,2j−1, com j0 ∈Z, representando a escala mais grossa (ou suave)

e percorrendo n coeﬁcientes d (MORETTIN, 2014).

Pode-se também escrever a TWD (3.7) na forma matricial

d=W X,

e tomando condições de fronteira apropriadas, como a TWD é ortogonal, pode-se obter sua inversa dada por

X =W′d,

em que a matriz W′

(34)

3.Wavelets 32

3.3 Análise Multirresolução

Através da Análise Multirresolução (AMR) é possível analisar um sinal em várias escalas de resolução. Seu objetivo é decompor um espaço de funções em subespaços, o que implica decompor um sinalf, em que cada "pedaço" (ou projeção) def está em cada subespaço.

Deﬁnição 4 Uma sequência _{Vj}_j_∈_Z de subespaços fechados de L2(R) é chamada uma

Análise de Multirresolução com função escala φ, se as seguintes propriedades são satis-feitas (BOGGES, 2001; DAUBECHIES, 1992):

1. ..._⊂V₋1 ⊂V0 ⊂V1 ⊂...

2. _jVj =L2(R)

3. _jVj ={0}

4. Invariância em escala: f(t)_∈Vj ⇔f(2−jt)∈V0

5. Invariância em translações: f(t)_∈V0 ⇔f(t−k)∈V0, n ∈Z

6. Existência de uma função escalaφ_∈Vj tal que {φj,k;k∈Z} é uma base ortonormal

em Vj, em que φj,k(t) = 2−j/2φ(2−jt−k).

Considere uma função f _∈ L2₍_R₎_{. O objetivo é obter funções, em vários níveis de}

resolução, que aproximam f. Assim, cada subespaço Vj será constituido por funções

aproximantes, de modo que a projeção ortogonal de f sobre cada Vj, denotada por Pjf,

é a melhor aproximação para f.

A relação Vj ⊂ Vj+1 vista em (P1), indica que ao passar do nível de resolução j

para j+ 1 nenhuma informação é perdida, ao contrário, cada projeção, à medida que j

cresce, contém mais informações (ou detalhes) sobref. Isto indica que quando a resolução aumenta (j _{→ ∞}), Pjf converge para a função original, como mostra (P2) e a Figura

(3.1). Ao contrário, quando f é aproximada a níveis de resolução cada vez menores

(j _{→ −∞}) todas as informações sobre f são perdidas e tem-se Pjf convergindo para a

função nula, o que demonstra a propriedade (P3).

Em (P4) é ressaltado queVj+1 pode ser obtido deVj, isto é, a resolução ﬁca mais ﬁna,

porém, detalhes que aparecem na escala 2j_{, de um nível de resolução} _j_{, também devem}

estar presentes na escala 2j+1_{. Na propriedade (P5) é possível notar que uma função}

f(t₋k), transladada k unidades de f(t), não apresenta mudança de nível de resolução. Tal propriedade, junto à (P6), implica que _{φj,k;j, k ∈Z}é uma base ortonormal em Vj,

para todoj _∈Z, em queφj,k é a função escala (wavelet pai) (MORETTIN, 2014).

Em suma, o princípio básico da AMR é que, desde que uma coleção de subspaços fechados _{Vj;j ∈Z} satisfaz as propriedades (P1) a (P6), existe uma base ortonormal

de wavelets _{ψj,k;j, k ∈Z} de L2(R), com ψj,k(t) = 2−j/2ψ(2−jt−k), tal que para todo

f _∈L2₍

R) (DAUBECHIES, 1992),

Pj+1f = Pjf

aproximação

+

k∈Z

f, ψj,kψj,k

detalhes

.

(35)

3.Wavelets 33

Figura 3.1: Sinal f e suas projeções sobre V0 e V1. Fonte: Adaptado de DAUBECHIES

(1992).

Entretanto ainda falta representar a diferença de informação entre o nível de resolução

j e o mais reﬁnadoj+1, isto é, os detalhes entre um nível e o seguinte. Pode-se, portanto, considerar Wj o espaço das funções da forma

k∈Z

akψ(2jt−k), ak ∈R,

em que somente um número ﬁnito de ak são não-nulos, de modo que Wj seja o

comple-mento ortogonal de Vj em Vj+1 e

Vj+1 =Vj⊕Wj.

Por decomposições sucessivas, segue que

Vj = Wj−1⊕Vj−1

= Wj−1⊕Wj−2⊕Vj−2

...

= Wj−1⊕Wj−2⊕...⊕W0⊕V0,

isto é, cadafj pode ser decomposto unicamente como

f =wj−1+wj−2+...+w0 +f0,

em que cadawl ∈ Wl, 0≤ l ≤j −1 e f0 ∈V0. Quando j tende ao inﬁnito, temos que o

espaçoL2₍_R₎_{pode ser decomposto na seguinte soma direta inﬁnita ortogonal (BOGGESS,}

2001)

L2(R) = V0_⊕W0_⊕W1_⊕...

Deste modo, cada f _∈L2₍_R₎ _{pode ser escrito de modo único como}

f =f0+

∞

j=0

wj,

(36)

3.Wavelets 34

f(t) =

k

cj0,kφj0,k(t) +

j≥j0

k

dj,kψj,k(t), (3.8)

em que

cj0,k =f(t), φj0,k(t)=

∞

−∞f(t)φj0,k(t)dt

dj,k =f(t), ψj,k(t)=

_∞

−∞f(t)ψj,k(t)dt,

(3.9)

e j0 representa o nível de resolução mais baixo (MORETTIN, 2014). Os coeﬁcientes

descritos em (3.9), são denominados coeﬁcientes suave e detalhe.

3.4 Algoritmo Piramidal da TWD

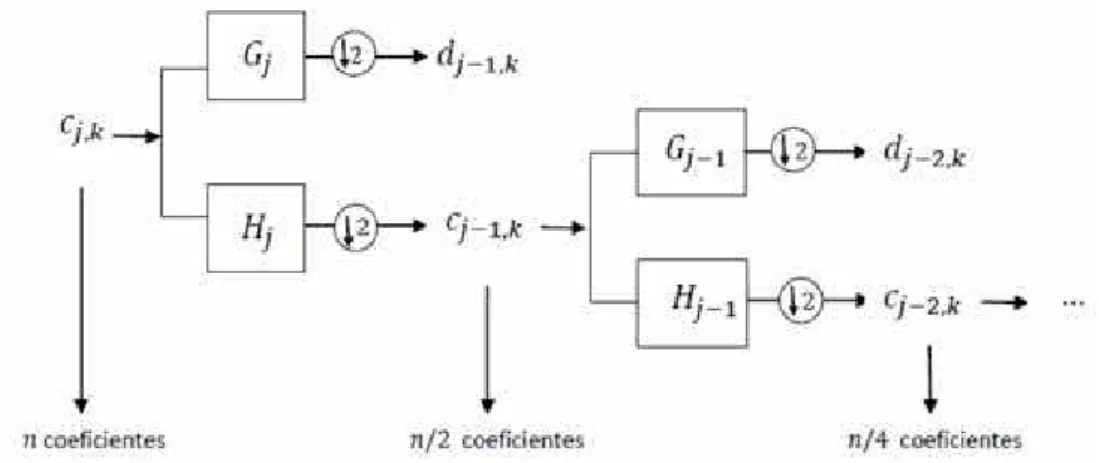
O Algoritmo Piramidal é a forma mais comum para se calcular a TWD e está associado à ideia de AMR, em que os detalhes de alta frequência de um sinal são obtidos pela diferença de informação entre um nível j do algoritmo e um mais refinado j+ 1. Ele está esquematizado pela estrutura de bancos de filtros e utiliza os filtros passa-baixa _{hk} e

passa-alta _{gk}, cujos coeﬁcientes são dados por

hk=

√

2_−∞+∞φ(t)φ(2t₋k)dt gk=

√

2_−∞+∞ψ(t)φ(2t₋k)dt, (3.10)

em que φ é a função escala, conhecida como wavelet pai e ψ é a função wavelet, também chamada de wavelet mãe.

A partir dessa notação, a wavelet pai pode ser expressa como

φ(t) = √2

k

hkφ(2t−k), (3.11)

de modo quehk também é denominado ﬁltro escala.

Por outro lado, da relação entre os ﬁltros hk e gk,

gk= (−1)kh1−k

dita Relação de Quadratura do Filtro, tem-se que a wavelet mãe ψ pode ser escrita como

ψ(t) =√2

k

gkφ(2t−k), (3.12)

em que gk, por sua vez, é também denominado ﬁltro wavelet.

Os coeﬁcientes descritos em (3.9) são resultados da ﬁltragem da função f(t)_∈L2₍_R₎_,

com os respectivos ﬁltros escala e wavelet. Portanto, denotados do seguinte modo

cj,k =f, φj,k=hn−2kcj+1,n

dj,k =f, ψj,k=gn−2kcj+1,n,

(3.13)

com hk e gk dados pela equação (3.10), são também denominados coeﬁcientes escala e

wavelet e constituiem a base do algoritmo piramidal. Nota-se que no j-ésimo passo o algoritmo calcula cj,k e dj,k a partir dos coeﬁcientes suaves do nível j+ 1 (MORETTIN,

2014).

Denotando,

(Hjx) =

n∈Zhn−2kxn

(Gjx) =_n_∈_Zgn−2kxn

(37)

3.Wavelets 35 é possível escrever (3.13) da forma

cj,k =Hjcj+1,k

dj,k =Gjcj+1,k,

em queHj pode ser interpretado como um ﬁltro passa-baixa e Gj um ﬁltro passa-alta.

Desta forma, as equações em (3.13) podem ser vistas como um processo de convolução seguido de uma decimação (downsampling) por dois (notação: _↓2 ), isto é, a cada duas saídas do ﬁltro, uma é desprezada. Assim, no nível j, tem-se metade dos coeﬁcientes do nível j + 1, por isso, o algoritmo é denominado piramidal ou cascata. A Figura (3.2) ilustra o procedimento descrito.

Figura 3.2: Algoritmo Piramidal da TWD.

Para a reconstrução do sinal, que é o mesmo que obter a TWD inversa, o mesmo processo é efetuado inversamente. Os coeficientes obtidos pelo algoritmo piramidal, são aplicados em ordem reversa, de modo que, ao invés de aplicar a decimação, os componen-tes do sinal são interporlados: são inseridos zeros entre os coeficiencomponen-tes da transformada (upsampling) (notação:_↑2) de forma a alongar tais coeficientes.

No algoritmo piramidal de reconstrução, os coeﬁcientescj+1,k são obtidos de cj,k edj,k

da seguinte forma:

cj+1,k =

k

hn−2kcj,k +

gn−2kdj,k.

3.5 Escolha de uma base

wavelet

É possível escolher uma basewavelet apropriada para cada aplicação. Essa escolha está relacionada com o objetivo especíﬁco da análisewavelet, tais como estimativa de um sinal, isolamento de eventos transitórios em uma ST, estimativa de parâmetros em um processo de memória longa, estimativa da variância wavelet, e determinação das características necessárias ao ﬁltro wavelet para que esse objetivo seja alcançado (PERCIVAL, 2000).

3.5.1 Características das

Wavelets

Os fatores que geralmente mais inﬂuenciam na escolha das wavelets são suavidade, simetria, ortogonalidade e suporte compacto.

(38)

3.Wavelets 36

Deﬁnição 5 Uma wavelet ψ _∈L2₍_R₎ _tem _p _{momentos nulos se}

_∞

−∞

tkψ(t)dt= 0, 0_≤k _≤p.

Em geral, quanto maior p, mais suave será ψ. Além disso, se um sinal é bastante suave, possuindo poucas descontinuidades, então os coeﬁcientes wavelet referentes à parte suave do sinal serão muito pequenos ou nulos (NASON, 2008).

Uma wavelet tem suporte compacto se sua energia ﬁca restrita a um intervalo ﬁnito, ou em outras palavras, tem-se:

Deﬁnição 6 Uma função f tem suporte compacto se existe um intervalo fechado e limi-tado fora do qual f(t) = 0.

Nesse caso diz-se que a wavelet tem localização espacial.

Dentre as famílias de wavelets de suporte compacto destacam-se aswavelets de Haar, Daubechies e Symmlets. Todas estas são ortogonais, mas apenas a wavelet de Haar é simétrica.

A simetria e ortogonalidade de uma wavelet são fatores interligados. Em wavelets

ortogonais (exceto o caso de Haar) é impossível obter simetria e reconstrução perfeita se os ﬁltros utilizados para decomposição e reconstrução forem os mesmos.

A seguir serão apresentadas algumas das wavelets já citadas.

3.5.2 Wavelet

_{de Haar}

Deﬁnição 7 A função φ(t) deﬁnida por

φ(t) =

1, se 0_≤t <1 0, caso contrário

cujo gráﬁco aparece na Figura (3.3), é chamada Função escala de Haar.

Figura 3.3: Gráﬁco da função escala de Haar φ(t).

Umawavelet de Haar é gerada por translações e dilatações dessa função escala, sendo representa por

ψ(t) = φ(2t)₋φ(2t₋1)

ou ainda,

ψ(t) =

⎧ ⎨

⎩

1, se0_≤t <1/2

−1, se1/2_≤t_≤1 0, caso contrário.

(39)

3.Wavelets 37

Figura 3.4: Wavelet de Haar ψ(t).

3.5.3 Wavelet

_{de Daubechies}

Ingrid Daubechies (1988), foi a responsável por construir uma família de wavelets

ortogonais em que cada membro da família é representado por um ﬁltro passa-baixa hk

de tamanhoN = 2p, possuindo assim, p momentos nulos e suporte em [₋p+ 1, p]. Quando p = 1, obtem-se a wavelet de Haar. Para p = 2, segue que a DAUB2 tem apenas 4 coeﬁcientes, já que temosN = 4.

As wavelets de Daubechies, diferentemente da wavelet de Haar, não possuem uma forma explícita fechada, sendo calculadas de forma iterativa.

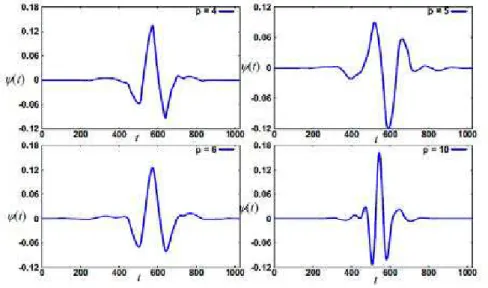
Na Figura (3.5) são apresentadas algumas wavelets de Daubechies calculadas para

p= 2,4,6,10(SOUZA, 2008).

Figura 3.5: Wavelets de Daubechies ψ(t) com p= 2,4,6,10. Fonte: SOUZA (2008)

É possivel notar pela Figura (3.5) que quanto maior o número de coeﬁcientes, maior é o numero de momentos nulos, e portanto, mais suave é awavelet.

3.5.4 Symmlets

Visto que as wavelets de Daubechies eram bastante assimétricas, Daubechies (1992) propôs as Symmlets.

(40)

3.Wavelets 38

Figura 3.6: Symmlets ψ(t)com p= 2,5,6,10. Fonte: SOUZA (2008)

3.5.5 Starlet

A Starlet wavelet, chamada no passado como B3-spline, é muito utilizada na análise de dados astronômicos onde os objetos de estudo são na maioria das vezes isotrópicos (NASON, 1995). Além da fácil implementação, outra razão que motiva o uso daStarlet é que ela não necessita de filtros ortogonais ou biortogonais e ainda oferece uma computação rápida, caso o filtrowavelet satisfaça a condição de separalidade estabelecida porh(k, l) = h(k)h(l), em que k, l são escalas diferentes. Mostra-se, portanto, ideal para lidar com dados de grande escala (tamanho) como é o caso dos dadosS4de cintilação. Uma escolha para os filtros escala e wavelet daStarlet é

hk = [1,4,6,4,1]/16,

gk=δ−hj,k = [−1,−4,10,−4,−1]/16.

(3.15)

Os ﬁltros h, g descritos em (3.15) estão associados às funções escala φ e wavelet ψ, respectivamente. Tais funções são deﬁnidas por

φ(t) = ₁₂1 _|t₋2_|2₋4_|t₋1_|3+ 6_|t_|3₋4_|t+ 1_|3+_|t+ 2_|3, φ(t1, t2) =φ(t1)φ(t2),

1 4ψ(

t1

2,

t2

2) =φ(t1, t2)− 1 4φ(

t1

2,

t2

2)

(3.16)

(41)

3.Wavelets 39

Figura 3.7: (À esquerda) Função escalaφ; (À direita) Funçãowavelet ψ Starlet. Fonte: STARK (2010)

3.5.6 Considerações sobre a escolha da base

wavelet

Diante de tantas possibilidades, há duas considerações importantes para a escolha de uma basewavelet. A primeira, é que ﬁltroswavelet de largura muito pequena (K = 2,4ou

(42)

(43)

Capítulo

4

Transformada

Wavelet

_{Não Decimada}

Como apresentado na seção 3.4, a TWD pode ser vista como um processo de filtragem seguido por uma decimação (diádica) por 2, em que são aproveitados apenas os elementos pares ou ímpares da amostra. A TWD depende da escolha da origem (escolha da deci-mação), que implica dizer que uma translação na entrada dos dados pode resultar em um conjunto de coeficientes wavelet completamente diferente se comparado ao conjunto de dados obtidos com a entrada original, como exemplifica a Figura (4.1).

Figura 4.1: TWD de X e TX (vetor X transladado) - coeﬁcientes escalonados em cada escala.

(44)

4. Transformada WaveletNão Decimada 42 Em algumas aplicações, no entanto, é necessário que o método não seja sensível à origem, ou seja, é preferível que seja invariante à translação, o que é conseguido com a

wavelet não decimada, pois esta leva em consideração todos os elementos: pares e ímpares. Sendo assim, uma translação no sinal de entrada não gera mudanças nos coeﬁcientes

wavelet em relação aos coeﬁcientes wavelet do sinal original, a menos de uma translação, como pode ser visualizado na Figura (4.2).

Figura 4.2: TWND de X e TX (vetor X transladado) - coeﬁcientes escalonados em cada escala.

A wavelet ψj,k para a TWND correspondente à equação (3.6) é dada por

ψj,k(t) = 2j/2ψ

2j(t₋k). (4.1)

A TWND é obtida eliminando-se a decimação na TWD. A cada escala do algoritmo piramidal, os filtros wavelet e escala são modificados pela inserção de zeros entre os ele-mentos do filtro, posteriormente mostrado em (4.12), de modo que ao realizar a convolução entre o sinal e filtro, se obtenhancoeficientes em cada escala do algoritmo. Deste modo, a TWND permite uma análise completa em multiescala, mostrando-se ideal para identificar informações e padrões escondidos, porém presentes nos sinais.

(45)

4. TransformadaWavelet Não Decimada 43

Figura 4.3: Sinal simulado. À direita, as três funções periódicas que compõem o o sinal.

Figura 4.4: TWD e TWND do sinal simulado - coeﬁcientes escalonados em cada escala.

As funcionalidades da TWND aqui descritas, motivam o seu uso na análise de sinais não estacionários, sobretudo, de sinais provenientes dos índices S4 de cintilação ionosfé-rica, em que se pretende uma análise mais detalhada.

4.1 Os ﬁltros

wavelet

_{e escala da TWND}

A TWND do nível j0 para uma série temporal X = [X0, X1, ..., Xn−1] gera

veto-res coluna _W˜₁_,_W˜₂_{, ...,}_W˜_j

0 e V˜j0, todos de dimensão n, tais que o vetor W˜j contêm os

coeﬁcientes wavelets d˜j,k da TWND associados com mudanças em X sobre uma escala

λj = 2j−1, j = 1, ..., j0, e V˜j0 contém os coeﬁcientes escala ˜cj0,k associados com variações

da escala λj0 = 2

j0 (PERCIVAL, 2000). Tais coeﬁcientes wavelet e escala, nada mais

são que o resultado da ﬁltragem da série temporal X com os ﬁltros wavelet e escala da TWND.

Os ﬁltros wavelet _{g˜k} e escala

˜ hk

da TWND são a versão redimensionada dos ﬁltroswavelet _{gk} e escala {hk} deﬁnidos viag˜k =gk/

√

2e˜hk =hk/

√

2. Também estão relacionados pela Relação de Quadratura do Filtro, de modo que

˜

(46)

4. Transformada WaveletNão Decimada 44 As funções de transferência para os ﬁltros _{g˜k} e

˜ hk

da TWND, são dadas pela relação

˜ Gjx

= (Gjx)

√

2

˜ Hjx

= (Hjx)

√

2 ,

(4.3)

em que (Gjx) e (Hjx) são expressos por

G(x) =e−i2πx(K−1)_H(1 2 −x)

H(x)_≡∞_−∞hke−i2πxk =K_k₌₀−1hke−i2πxk

(4.4)

e referem-se às funções de transferência para os ﬁltros wavelet e escala da TWD.

Assim, o resultado da ﬁltragem de uma série temporal _{Xt:t= 0, ..., n−1}, com os

ﬁltros wavelet e escala da TWND é dado, respectivamente por

˜

W1,t =kK=0−1g˜kXt−kmodn

˜

V1,t =Kk=0−1h˜kXt−kmodn, t= 0,1, ..., n−1.

(4.5)

Estas duas sequências constituem a TWND do nível j0 = 1. O termomod da equação

(4.5) permite uma ﬁltragem circular, fazendo com queX seja representado com o mesmo

número de coeﬁcientes em cada escala.

É possível ainda, encontrar uma relação entre os coeﬁcientes escala ewavelet das TWD e TWND, a saber

W1,t ≡21/2W˜1,2t+1 =K_k₌₀−1g˜kX2t+1−kmodn

V1,t≡21/2V˜1,2t+1 =

K−1

k=0 ˜hkX2t+1−kmodn, t = 0, ...,n₂ −1.

(4.6)

4.2 Formulação da TWND

Nesta seção será apresentada a formulação da TWND através de uma abordagem matricial, com base em (PERCIVAL, 2000). No entanto, vale destacar que para ﬁns práticos, a TWND é implementada como um processo de convolução, como descrito na equação (4.5).

A grande motivação para formular a TWND é definir uma transformada que atua semelhantemente à TWD, mas que não sofre sensibilidade na escolha da origem para uma série temporal, ou seja, é invariante à translação. Essa sensibilidade da TWD é devida inteiramente à decimação das saídas dos filtros wavelet e escala de cada estágio (ou nível) do algoritmo piramidal, que a cada duas saídas uma é descartada. As saídas dos filtros que são descartadas no primeiro nível do algoritmo piramidal da TWD, podem ser obtidas aplicando o algoritmo piramidal da TWD no vetor transladado T X ao invés de X. Vale ressaltar que, se o vetor X = [X0, X1, ..., Xn−1]t, então T X = [Xn−1, X0, ..., Xn−2]t será o

vetor X transladado uma unidade, em que Tn é dita uma matriz de translação, dada por

T = ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

0 0 0 0 ... 0 0 1 1 0 0 0 ... 0 0 0 0 1 0 0 ... 0 0 0

... ... ... ... ... ... ... ... 0 0 0 0 ... 1 0 0 0 0 0 0 ... 0 1 0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ . (4.7)

(47)

4. TransformadaWavelet Não Decimada 45 (da TWD) duas vezes, uma vez para X e outra para T X, e depois interceptar os dois conjuntos de coeﬁcientes da TWD (PERCIVAL, 2000).

A primeira aplicação resulta em

% W1 V1 & = % A1 B1 &

X =P1X, (4.8)

em que,

A1 =

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

g1 g0 0 0 0 ... 0 0 0 0 0 g3 g2

g3 g2 g1 g0 0 ... 0 0 0 0 0 0 0

... ... ... ... ... ... ... ... ... ... ... ...

0 0 0 0 0 ... 0 g3 g2 g1 g0 0 0

0 0 0 0 0 ... 0 0 0 g3 g2 g1 g0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ,

B1 =

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

h1 h0 0 0 0 ... 0 0 0 0 0 h3 h2

h3 h2 h1 h0 0 ... 0 0 0 0 0 0 0

... ... ... ... ... ... ... ... ... ... ... ...

0 0 0 0 0 ... 0 h3 h2 h1 h0 0 0

0 0 0 0 0 ... 0 0 0 h3 h2 h1 h0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ e

P1 =

%

A1

B1

&

.

Neste caso, assim como outros, foi exibida uma matriz para o caso K = 4 e n > K, porém o desenvolvimento matemático é geral.

Da equação (4.6), pode-se então denotar os elementos de W1 eV1 por

W1 =

'

21/2_W_˜

1,1,21/2W˜1,3, ...,21/2W˜1,n−1

(t

V1 =

'

21/2_V˜

1,1,21/2V˜1,3, ...,21/2V˜1,n−1

(t

.

Observe que W1 e V1 contém todos os elementos de índice ímpar das sequências de

tamanho n, 21/2_W_˜ 1,t

e 21/2_V_˜ 1,t

, respectivamente, formadas pela convolução circular da série temporal X com os respectivos ﬁltros wavelet _{gk} e escala{hk}.

A segunda aplicação consiste em substituir X por T X e aplicar a TWD ao vetor transladado. Deste modo, obtem-se

%

WT,1

VT,1

&

=P1T X.

Deﬁnindo

PT,1 =P1T =

% A1 B1 & T = %

A1T

B1T

&

=

%

AT,1

BT,1

&

,

pode-se escrever

%

WT,1

VT,1

&

=PT,1X =

%

AT,1

BT,1

&

X, (4.9)

em que

AT,1 =

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣

g0 0 0 0 0 ... 0 0 0 0 g3 g2 g1

g2 g1 g0 0 0 ... 0 0 0 0 0 0 g3

... ... ... ... ... ... ... ... ... ... ... ...

0 0 0 0 0 ... g3 g2 g1 g0 0 0 0

0 0 0 0 0 ... 0 0 g3 g2 g1 g0 0

(48)

4. Transformada WaveletNão Decimada 46 e BT,1 tem a mesma estrutura, substituindo cada gk porhk. ComoA1X é formado pelos

valores de índice ímpar da sequência 21/2_W_˜ 1,t

, então, AT,1X, que é A1X transladado

uma unidade, será formado pelos valores de índice par da sequência 21/2_W˜ 1,t

, ou seja,

WT,1 =

'

21/2W˜1,0,21/2W˜1,2, ...,21/2W˜1,n−2

(t

,

e pelo mesmo argumento, os elementos deVT,1 são dados por

VT,1 =

'

21/2V˜1,0,21/2V˜1,2, ...,21/2V˜1,n−2

(t

.

Com isso, é possível formar os coeﬁcientes wavelet da TWND a partir do reescalo-namento dos elementos de W1 e W1,T intercalados, e de forma semelhante, construir os

coeﬁcientes escala da TWND a partir de V1 e VT,1, isto é,

˜ W1 =

'

˜

W1,0,W˜1,1,W˜1,2, ...,W˜1,n−1

(t

˜ V1 =

'

˜

V1,0,V˜1,1,V˜1,2, ...,V˜1,n−1

(t

.

(4.10)

É notório em (4.10), que os elementos de W˜1 eV˜1 são exatamente as saídas de W˜1,t e

˜

V1,tutilizando os respectivos ﬁltros g˜k e˜hk da TWND, como pode ser observado em (4.5).

Deﬁnindo _A˜₁ _{como uma matriz} _n_×_n _{formada pelos linhas de} _A_T,₁ _e_A₁ _{intercaladas,}

e substituindo cada gk por ˜gk, isto é,

˜ A1 ≡

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ˜

g0 0 0 ... 0 0 0 0 g˜3 ˜g2 g˜1

˜

g1 ˜g0 0 ... 0 0 0 0 0 ˜g3 g˜2

˜

g2 ˜g1 g˜0 ... 0 0 0 0 0 0 g˜3

... ... ... ... ... ... ... ... ... ...

0 0 0 ... 0 ˜g3 g˜2 ˜g1 g˜0 0 0

0 0 0 ... 0 0 g˜3 ˜g2 g˜1 ˜g0 0

0 0 0 ... 0 0 0 ˜g3 g˜2 ˜g1 g˜0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ,

obtem-se W˜1 = ˜A1X. Com uma deﬁnição análoga para B˜1, tem-se V˜1 = ˜B1X. Deste

modo, é possível representar a primeira etapa do algoritmo piramidal da TWND como

% _˜ W1 ˜ V1 & = % _˜ A1 ˜ B1 &

X = ˜P1X,

em que

˜ P1 =

% _˜ A1 ˜ B1 & .

Como Pt

1P1 =In eTtT =In, em que T é a matriz de translação dada em (4.7), segue

que

P_T,t₁PT,1 =TtP1tP1T =In

e então, PT,1 é uma matriz ortonormal. Portanto, obtem-se as seguintes decomposições

para X

X2 =W12+V12

(49)

4. TransformadaWavelet Não Decimada 47 Além disso, desde que

W12+WT,12 = 2

) ) )W˜1

) ) )

2

V12+VT,12 = 2

) ) )V˜1

) ) )

2

.

também é possível obter

X2 =)) )W˜1

) ) )

2

+)) )V˜1

) ) )

2

.

De (4.8) e (4.9) tem-se

X =*At₁, B₁t+

%

W1

V1

&

e

X =*At_T,₁, B_T,t ₁+

%

WT,1

VT,1

&

.

Deste modo, X pode ser escrito como

X = 1 2

*

At₁, B₁t+

% W1 V1 & + 1 2 *

At_T,₁, B_T,t ₁+

%

WT,1

VT,1

&

= 1 2

At₁W1 +B1tV1+AtT,1WT,1+Bt,t1VT,1

= 1 2

At₁W1 +AtT,1WT,1

+ 1 2

B₁tV1+BT,t 1VT,1

= A˜t₁W˜1+ ˜B1tV˜1

= D˜1+ ˜S1

em que_D˜₁ _≡_A˜t

1W˜1 é o coeﬁciente de detalhe do primeiro nível da TWND eS˜1 ≡B˜1tV˜1 é

o correspondente suave.

Ao contrário da TWD, em que é possível obter a relação W12 = D12, isto é, a

energia do coeﬁcientewavelet é a mesma do coeﬁciente de detalhe, na TWND tem-se que

) ) )D˜1

) ) ) 2 = 1 2 ) ) )W˜1

) ) )

2

+W₁tA1AtT,1WT,1

,

ou seja,)) )D˜1

) ) )

2

≤)) )W˜1

) ) )

2

.

O coeﬁciente de detalhe D˜1 da TWND pode ser interpretado como uma operação de

ﬁltragem envolvendoXe um ﬁltrowavelet. Para mais clareza, seja_D˜₁_,t_o_t_{-ésimo elemento}

de_D˜₁_{. Expandindo} _D˜₁ _{= ˜}_At

1W˜1 obtem-se

˜ D1 =

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ˜

g0 g˜1 ˜g2 g˜3 ... 0 0 0 0

0 g˜0 ˜g1 g˜2 ... 0 0 0 0

... ... ... ... ... ... ... ...

0 0 0 0 ... g˜0 ˜g1 g˜2 g˜3

˜

g3 0 0 0 ... 0 ˜g0 g˜1 g˜2

˜

g2 g˜3 0 0 ... 0 0 g˜0 g˜1

˜

g1 g˜2 ˜g3 0 ... 0 0 0 g˜0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ˜ W1,0

˜ W1,1

˜ W1,2

...

˜ W1,n−2

˜ W1,n−1

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ,

donde segue que

˜ D1,t=

K−1

k=0

˜

gkW˜1,t+kmodn =

n−1

k=0

˜

(50)

4. Transformada WaveletNão Decimada 48 em que, _{˜go

k :k = 0, ..., n−1} é o ﬁltro {˜gk :k= 0, ..., K−1} periodizado para tamanho

n.

Foram apresentados, até agora, os coeﬁcientes do primeiro nível da TWND. Na pró-xima seção, tais conceitos serão generalizados de modo a deﬁnir o nívelj da TWND.

4.3 Deﬁnição do

j

-ésimo nível de coeﬁcientes da TWND

Para uma amostra de tamanho n, os coeﬁcientes wavelet e escala da TWND são deﬁnidos, respectivamente, por

˜

Wj,t = Kj−1

k=0 ˜gj,kXt−kmodn

˜

Vj,t =Kk=0j−1h˜j,kXt−kmodn, t= 0,1, ..., n−1,

(4.11)

em que_{˜gj,k :k = 0, ..., Kj−1}e

˜

hj,k :k= 0, ..., Kj −1

são, respectivamente, os ﬁltros

wavelet e escala do nível j da TWND, deﬁnidos via g˜j,k ≡ gj,k/2j/2 e ˜hj,k ≡ hj,k/2j/2 a

partir dos ﬁltros _{gj,k}e {hj,k} de largura Kj ≡(2j −1)(K−1) + 1.

Os filtros da TWND são modificados a cada escala pela inserção de zeros. Ou seja, a cada escala são inseridos 2j−1 _{zeros entre cada um dos} _K _{valores dos filtros} _{_˜_g

j} e

˜ hj da TWND, ˜

g0,0, ...,0

2j−1

,g˜1,0, ...,0

2j−1

, ...,˜gK−2,0, ...,0

2j−1

,g˜K−1

˜

h0,0, ...,0

2j−1

,˜h1,0, ...,0

2j−1

, ...,h˜K−2,0, ...,0

2j−1

,˜hK−1,

(4.12)

que consiste em aplicar um upsample de largura 2j−1_(K₋_{1) + 1}_.

Deste modo, é possível representar a primeira etapa do algoritmo piramidal da TWND

como _% ˜ W1 ˜ V1 & = % _˜ A1 ˜ B1 & X, em que ˜ A1 ≡

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ˜

g0 0 0 ... 0 0 0 0 g˜3 g˜2 g˜1

˜

g1 g˜0 0 ... 0 0 0 0 0 g˜3 g˜2

˜

g2 g˜1 g˜0 ... 0 0 0 0 0 0 g˜3

... ... ... ... ... ... ... ... ... ...

0 0 0 ... 0 ˜g3 g˜2 ˜g1 g˜0 0 0

0 0 0 ... 0 0 g˜3 ˜g2 g˜1 g˜0 0

0 0 0 ... 0 0 0 ˜g3 g˜2 g˜1 g˜0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦

e uma deﬁnição análoga para _B˜₁_.

Na segunda etapa do algoritmo piramidal,

(51)

4. TransformadaWavelet Não Decimada 49 os ﬁltros são modiﬁcados, de modo que a matriz A˜2 é descrita por

˜ A2 ≡

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ˜

g0 0 0 ... 0 ˜g3 0 g˜2 0 g˜1 0

0 ˜g0 0 ... 0 0 g˜3 0 g˜2 0 ˜g1

˜

g1 0 g˜0 ... 0 0 0 g˜3 0 g˜2 0

... ... ... ... ... ... ... ... ... ...

0 0 0 ... g˜2 0 g˜1 0 g˜0 0 0

0 0 0 ... 0 ˜g2 0 g˜1 0 g˜0 0

0 0 0 ... g˜3 0 g˜2 0 g˜1 0 ˜g0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦

e uma deﬁnição análoga para B˜2, substituindo cada g˜k por ˜hk.

É possível também, escrever (4.11) em forma matricial como

Wj = ˜ωjX

˜

Vj = ˜ϑjX,

em que

˜ ωj =

⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ˜ go

j,0 g˜j,no −1 ... g˜oj,2 g˜oj,1

˜ go

j,1 ˜gj,o0 ... g˜oj,3 g˜oj,2

... ... ... ...

˜ go

j,n−2 g˜j,no −3 ... g˜oj,0 g˜oj,n−1

˜ go

j,n−1 g˜j,no −2 ... g˜oj,1 g˜oj,0

⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦

e _ϑ˜_j _{tem a mesma estrutura, substituindo cada} _g_˜o

j,k por˜hoj,k.

Filtrar _{Xt} com ˜gj,k equivale a ﬁltrá-lo com ˜gj,ko . Logo, é possivel reescrever (4.11)

como

˜

Wj,t=nk=0−1˜gj,ko Xt−kmodn

˜

Vj,t =nk=0−1˜hoj,kXt−kmodn, t= 0,1, ..., n−1.

(4.13)

As funções de transferência para os ﬁltroswavelet e escala do j-ésimo nível da TWND são dadas, respectivamente, por

˜

Gj(f)≡G(2˜ j−1f)

,j−2

k=0H(2˜ kf)

˜

Hj(f)≡,j_k−₌₀1H(2˜ kf),

(4.14)

em queG(˜ _·)eH(˜ _·)são as funções transferência para_{˜gk}e

˜ hk

apresentadas na equação (4.3).

Os coeﬁcientes de detalhe e suave do nívelj da TWND são deﬁnidos, respectivamente, por

˜

Dj ≡ω˜tjW˜j

˜

Sj ≡ϑ˜tjV˜j,

em que os elementos de_D˜_j _e _S˜_j _{são expressos por} ˜

Dj,t =nk−=01g˜oj,kW˜j,t+kmodn

˜ Sj,t =

n−1

k=0˜hoj,kV˜j,t+kmodn, t= 0,1, ..., n−1.

Nesses termos, dada uma amostraX de tamanhon, pode-se expressar a decomposição aditiva da TWND por

X =

j0

j=1

˜