Conducão eletrônica e propriedades termodinâmicas da molécula de DNA

(1)

centro de ciˆ

encias exatas e da terra

departamento de f´ısica te´

orica e experimental

programa de p´

os-graduac

¸˜

ao em f´ısica

CONDUC

¸ ˜

AO ELETR ˆ

ONICA E PROPRIEDADES

TERMODIN ˆ

AMICAS DA MOL´

ECULA DE DNA

RICARDO GONDIM SARMENTO

Orientador: Prof. Dr. Umberto Laino Fulco

Co-Orientador: Prof. Dr. Eudenilson Lins de Albuquerque

(2)

CONDUC

¸ ˜

AO ELETR ˆ

ONICA E PROPRIEDADES

TERMODIN ˆ

AMICAS DA MOL´

ECULA DE DNA

Tese de doutorado apresentada ao Departamento de F´ısica Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial à obten¸cão do grau de Doutor em F´ısica.

Orientador: Prof. Dr. Umberto Laino Fulco

Co-Orientador: Prof. Dr. Eudenilson Lins de Albuquerque

(3)

CONDUC

¸ ˜

AO ELETR ˆ

ONICA E PROPRIEDADES

TERMODIN ˆ

AMICAS DA MOL´

ECULA DE DNA

Tese apresentada ao Departamento de F´ısica Te´orica e Experimental da Universidade Fe-deral do Rio Grande do Norte como parte dos requisitos para a obten¸c˜ao do t´ıtulo de Doutor em F´ısica

BANCA EXAMINADORA

Prof. Dr. Umberto Laino Fulco (UFRN)

Prof. Dr. Eudenilson Lins de Albuquerque (UFRN)

Prof. Dr. Rodrigo Andr´e Caetano (UFAL)

Prof. Dr. Ewerton Wagner Santos Caetano (IFCE)

Prof. Dr. Luciano Rodrigues da Silva (UFRN)

(4)

Deus, pela for¸ca concedida para alcan¸car os objetivos.

Aos Meus Pais, Albenes Gomes Sarmento

e Geracina Pinto Gondim Sarmento, que acreditam em mim.

(5)

A maior recompensa do nosso trabalho n˜ao ´e o que nos pagam por ele, mas aquilo em que ele nos transforma.

(John Ruskin).

(6)

Finalizando esta tese de doutorado, n˜ao poderia deixar de registrar o mais profundo agradecimento a todos aqueles que me apoiaram nesta longa jornada e colaboraram para a consolida¸c˜ao deste trabalho.

Ao Prof. Dr. Umberto Laino Fulco, o meu agradecimento por toda a disponibilidade e orienta¸c˜ao prestada.

Ao Prof. Dr. Eudenilson Lins de Albuquerque pela oportunidade, ensinamentos, ori-enta¸cões durante as minhas pós-gradua¸cões e pela confian¸ca depositada. Acima de tudo, um profissional dedicado e apaixonado pela f´ısica, que mantém seu compromisso em formar no-vos cientistas, compartilhando o seu conhecimento e sua experiência, fornecendo os recursos imprescind´ıveis para forma¸cão de um profissional de excelência.

Aos professores participantes da banca examinadora.

Aos meus pais, Albenes Gomes Sarmento e Geracina P. Gondim Sarmento, por terem acreditado e fornecido condi¸cões para que eu conclu´ısse mais uma etapa desta vida, são para vocês, minha gratidão, meu reconhecimento e minhas conquistas.

A Teresa Cristina Ferreira da Silva, pelo companheirismo, dedica¸c˜ao e incentivo ofere-cido antes, durante e, seguramente, por toda a minha trajet´oria de vida e curso profissional.

A Renato Gondim Sarmento e Yasminie pela compreens˜ao e apoio, vocˆes foram muito importante na minha caminhada, meus sinceros agradecimentos.

A minha tia Lurdes Gondim Ferreira e fam´ılia pelo exemplo de vida, crescimento hu-mano, apoio e persistˆencia de colher um futuro melhor atrav´es dos estudos. A tia Lila pelo

(7)

A minha avó, Maria P. Gondim (in memoriam), pelas palavras de carinho que sempre vieram nas horas certas. Um exemplo a ser seguido, pela bondade, justi¸ca e perseveran¸ca em acreditar que dias melhores viriam, com seu ’conhecimento de sabedoria’ - que ensinando-me a coragem de prosseguir, fazendo o ensinando-melhor poss´ıvel a mais profunda dedica¸cão por suas sábias li¸cões de esperan¸ca; sempre repetindo palavras essenciais - como, por exemplo, amor, fé, compreensão, alegria - infundiram-me a confian¸ca necessária para realizar os meus sonhos. Que sua saudosa memória, em seu ”querer bem”, ainda refletem tanta luz e gosto para minha vida, um amor especial.

A todos meus colegas que mesmo longe, ou de perto, incentivaram com a coragem em especial a Willian de Souza Santos, Walmir Belinato e Carla Fabiana Cerqueira Machado.

Aos amigos e colegas da pós-gradua¸cão Nilton Ferreira Frazão, Edvan Moreira, Edi Rozembergh Brasileiro Brandão, Carlos Humberto Oliveira Costa, Gislene Micarla Borges de Lima, Lindon Johnson Freitas Rodrigues, Gabriel Alves Mendes, Antônio de Macedo Filho, Maur´ıcio Lopes de Almeida, Leonardo Mafra Bezerril e Ubiratan Correia Silva pela agradável convivência e contribui¸cões sublimes em pesquisar e ensinar a F´ısica durante a trajetória de 4 anos na UFRN.

A secretária da pós-gradua¸cão Celina Pinheiro pela aten¸cão e prontidão.

A CAPES e o CNPQ pela concess˜ao da bolsa de doutorado.

Por fim agradecemos a todos que, de forma indireta, tamb´em contribu´ıram para a materializa¸c˜ao desta tese.

(8)

Nesta tese, estudamos as propriedades termo-eletrônicas da molécula de DNA. Para tal propósito, fizemos uso de três tipos de modelos com o DNA, todos assumindo uma geome-tria plana (2D), constru´ıdos cada um através das sequências quase-periódicas (Fibonacci e/ou

Rudin-Shapiro) e de uma sequˆencia de DNA natural, parte do cromossomo humano Ch22 .

Os dois primeiros modelos apresentam dois tipos de componentes que são: as bases nitrogena-das (Guanina G, citosina C, Adenina A e Timina T) e um grupamento a¸cúcar-fosfato (SP), enquanto o terceiro modelo apresenta somente as bases nitrogenadas. No primeiro modelo cal-culamos as densidades de estados utilizando o formalismo de Dyson e as transmitâncias pela equa¸cão de Schrödinger independente do tempo. No segundo modelo fizemos uso do processo de renormaliza¸cão para obtemos os perfis das transmitâncias e consequentemente as curvas I (corrente) _× V (voltagem). No terceiro modelo calculamos as densidades de estados pelo for-malismo de Dean e utilizamos os resultados juntamente com a estat´ıstica de Fermi-Dirac para obtemos os potenciais qu´ımicos e os calores espec´ıficos quânticos. Finalmente, comparamos as propriedades f´ısicas encontradas para as sequências quase-periódicas e para aqueles que utilizam um trecho da sequência genômica do DNA (Ch22).

(9)

In this thesis, we study the thermo-electronic properties of the DNA molecule. For this purpose, we used three types of models with the DNA, all assuming a flat geometry (2D), each built by a sequence of quasi-periodic (Fibonacci and / or Rudin-Shapiro) and a sequence of natural DNA, part of the human chromosome Ch22. The first two models have two types

of components that are the nitrogenous bases (guanine G, cytosineC, adenine A and thymine

T) and a cluster sugar-phosphate (SP), while the third has only the nitrogenous bases. In the first model we calculate the density of states using the formalism of Dyson and transmittance for the time independent Schr¨odinger equation . In the second model we used the renormali-zation procedure for the profile of the transmittance and consequently the I (current) versus V (voltage). In the third model we calculate the density of states formalism by Dean and used the results together with the Fermi-Dirac statistics for the chemical potential and the quantum specific heat. Finally, we compare the physical properties found for the quasi-periodic sequences and those that use a portion of the genomic DNA sequence (Ch22).

(10)

Agradecimentos iv

Resumo vi

Abstract vii

Lista de Figuras xii

Lista de Tabelas xiii

1 Introdu¸c˜ao 1

2 A mol´ecula de DNA 4

2.1 Introdu¸c˜ao . . . 4

2.2 Breve hist´orico sobre a descoberta da estrutura do DNA . . . 5

2.3 A estrutura da mol´ecula de DNA . . . 10

2.4 O modelo da dupla h´elice do DNA . . . 11

2.5 O esqueleto de a¸c´ucar-fosfato . . . 14

3 Transporte eletrˆonico em dupla fita do DNA poly(dG)-poly(dC) 16 3.1 Introdu¸c˜ao . . . 16

(11)

3.3 Mecanismos de transporte de cargas . . . 19

3.4 Sequˆencias quase-peri´odicas . . . 20

3.5 Propriedades eletrˆonicas da mol´ecula de DNA . . . 23

3.5.1 Densidade de estado . . . 24

3.5.2 Resultados . . . 27

3.5.3 Transmitˆancia . . . 28

3.6 Conclus˜oes . . . 30

4 Uma abordagem da renormaliza¸cão para descrever o transporte de carga na molécula de DNA 33 4.1 Introdu¸cão . . . 33

4.2 Resultados num´ericos . . . 39

5 Propriedades termodinˆamicas do DNA 44 5.1 Introdu¸c˜ao . . . 44

5.2 Modelo te´orico . . . 45

5.3 Densidade de estado . . . 47

5.4 Calor espec´ıfico quˆantico . . . 49

6 Conclus˜oes e Perspectivas 63 A Apˆendice A 68 A.1 Artigos Publicados e Submetidos . . . 68

(12)

2.1 Rosalind Franklin e o padr˜ao de difra¸c˜ao de raios-X do DNA . . . 7

2.2 Prˆemio Nobel de Medicina: James Watson, Francis Crick e Maurice Wilkins . . 9

2.3 As bases nitrogenadas e o nucleot´ıdeo . . . 10

2.4 Duas sequˆencias complementares de DNA . . . 11

2.5 Representa¸c˜ao da estrutura helicoidal do DNA . . . 12

2.6 Estrutura A-,B- e Z-DNA. . . 14

3.1 Esquema de três poss´ıveis mecanismos para transferência de carga no DNA: (a) Tunelamento coerente, (b) Tunelamento incoerente e (c) thermal hopping. O eixo vertical representa a energia E e o eixo horizontal representa a posi¸cão espacial X. 20 3.2 A sequência quase-periódica deFibonacci para as primeiras gera¸cões, que crescem seguindo a regra de infla¸cão G_→GC e C_→G . . . 21

3.3 A sequência quase-periódica de Rudin-Shapiro para as primeiras gera¸cões, que crescem seguindo a regra de infla¸cão G_→GC,C _→GA, A_→T C e T _→T A. . 22

3.4 Representa¸cão esquemática da fita dupla de DNA, incluindo a contribui¸cão do a¸cúcar-fosfato. . . 23

(13)

poly(dG)-poly(dC), correspondente ao n´umero de pares de nucleot´ıdeos NF B =

610 (linha cheia). Para efeito de compara¸c˜ao estamos mostrando tamb´em o DOS de um segmento do DNA natural, como parte do cromossomo humano Ch22

(linha tracejada). . . 31

3.6 O coeficiente de transmitˆancia TN(E) em fun¸c˜ao da energia E, em unidade de eV. 32

4.1 Esbo¸co ilustrando o processo de renormaliza¸c˜ao de uma etapa do mapeamento do modelo DBL da cadeia de DNA. (a) Modelo DBL-DNA para as sequˆencias de

Fibonacci, Rudin-Shapiro e Ch22; (b) Modelo de renormaliza¸c˜ao da mol´ecula de

DNA-DBL ap´os a primeira etapa da decima¸c˜ao. . . 35

4.2 Coeficiente de transmiss˜ao TN(E) em fun¸c˜ao da energia E (em unidade de eV)

para o modelo DBL-DNA considerando as sequências quase-periódicas de Fibo-nacci e Rudin-Shapiro, cujos números de pares de nucleot´ıdeos são NF B = 34

(linha cheia) eNRS = 32 (linha tracejada), respectivamente. Para efeito de

com-para¸cão, estamos mostrando um segmento de DNA natural, com uma parte do cromossomo humano Ch22, cujo o número de par de nucleot´ıdeo é NCh22 = 32

(linha pontilhada). . . 42

4.3 As caracter´ısticas das correntes-voltagens do DBL-DNA para as sequˆencias de

Fibonacci (linha cheia), Rudin-Shapiro (linha tracejada) e do cromossomo hu-mano Ch22 (linha pontilhada). A inser¸c˜ao mostra a diferencial da condutˆancia

dI / dV versos a voltagem V do dispositivo. . . 43

5.1 Modelo de escada estendida para a fita dupla de DNA . . . 45

5.2 Espectro da densidade de estado para a sequˆencia de Fibonacci com 987 pares de nucleot´ıdeos. . . 54

5.3 Espectro da densidade de estado para a sequˆencia de Rudin-Shapiro com 1024 pares de nucleot´ıdeos. . . 55

5.4 Espectro da densidade de estado para a sequˆencia de Ch22 com 1024 pares de

nucleot´ıdeos. . . 56

5.5 Perfil do potencial qu´ımico para sequˆencia deFibonacci. . . 57

(14)

5.7 Perfil do potencial qu´ımico para sequˆencia deCh22. . . 59

5.8 Perfil do calor espec´ıfico a volume constante (em unidade de Ne) versos a tem-peratura para Fibonacci. . . 60

5.9 Perfil do calor espec´ıfico a volume constante (em unidade de Ne) versos a tem-peratura para Rudin-Shapiro. . . 61

5.10 Perfil do calor espec´ıfico a volume constante (em unidade de Ne) versos a tem-peratura para Ch22. . . 62

(15)

5.1 As energias de ioniza¸c˜ao das bases nitrogenadas e os termos dehopping dos pares de bases complementares (em eV), Ref. [84]. . . 46

5.2 Parˆametros de hopping (em eV) para o modelo de cadeia estendida, ver Fig. 5.1 (Ref. [84]). . . 47

(16)

Cap´ıtulo

1

Introdu¸c˜ao

As células constituem a unidade básica dos seres vivos, elas funcionam cooperativamente como parte de um tecido, órgão ou, independentemente, como um microorganismo unicelular. Nos seres vivos há distintos tipos de células, e cada tipo, desempenha fun¸cão espec´ıfica visando a manuten¸cão da vida no organismo [1].

No organismo as fun¸cões vitais ocorrem precisamente no núcleo das células, nelas en-contramos as informa¸cões genéticas necessárias que são transmitidas de uma gera¸cão a outra. Estas informa¸cões estão armazenadas em pequenos filamentos espiralados denominados de cro-mossomos. Estes são constitu´ıdos de ácido desoxirribonucléico, tendo a fun¸cão de coordenar a atividade celular e transmitir as caracter´ısticas hereditárias. Os ácidos nucléicos estão classifica-dos de dois tipos: Desoxirribo Nucleic Acid (DNA) ou ácido desoxirribonucléico e Ribo Nucleic Acid (RNA) ou ácido ribonucléico, a primeira apresenta na sua composi¸cão qu´ımica o a¸cúcar denominado desoxirribose e o outro a ribose. A diferen¸ca entre ambos os a¸cúcares esta na falta e na presen¸ca do átomo de oxigênio em sua estrutura.

Dentre as maiores descobertas da humanidade, a molécula de DNA tem tanta im-portância que é denominada a molécula da vida, pois através dela conseguimos explicar como as informa¸cões genéticas são copiadas e passadas da célula mãe para célula filha, como também o processo de muta¸cão, entre outros [1].

Todas as informa¸cões genéticas estão armazenadas dentro da célula nos genes. Os genes são denominados as unidades fundamentais da hereditariedade, promovendo as fun¸cões reguladoras ao articularem os aspectos evolutivos, genéticos e de desenvolvimento; organizando

(17)

informa¸cão codificada para s´ıntese de prote´ına. Cada gene é formado por uma sequência es-pec´ıfica mais ou menos longa, de ácidos nucléicos [2].

As tentativas para desvendar os mistérios do mecanismo desses ácidos nucléicos, em particular o DNA, proporcionou avan¸cos cient´ıficos, principalmente relacionados a sua estrutura, permitindo entender o funcionamento da vida e da perpetua¸cão da espécie [3]. A heran¸ca genética tem sua base molecular nos processos precisos de replica¸cão e transmissão do DNA, constituindo desse modo as bases moleculares da heran¸ca genética [4].

Os processos f´ısicos e rea¸cões bioqu´ımicas que ocorrem nos organismos vivos são funda-mentais para seu funcionamento. Estes processos e rea¸cões são regidos por instru¸cões armaze-nadas em seu genoma, que é toda a informa¸cão hereditária de um organismo que está codificada em seu DNA ou RNA [5].

A molécula de DNA é um pol´ımero longo de elevada massa molecular relativa, cons-titu´ıda de quatro monômeros denominados de nucleot´ıdeos (guanina G, citosina C, adenina A e timina T) expostos de forma desordenada na molécula. Por exemplo, o cromossomo hu-mano chamadoCh22 apresenta aproximadamente 6 mm de comprimento e 2×108 nucleot´ıdeos,

permanecendo constante em um volume igual a 500 m3 _{[6]. Essa mol´ecula ´e mensurada em}

nanoescala, por ter diâmetro de cerca de 2 nm e a curvatura da hélice possui cerca de 3,4 a 3,6 nm [7]. A quantidade de informa¸cão armazenada no DNA é significante como objeto de pesquisa cient´ıfico-tecnológico em diversas áreas do conhecimento, pois essa caracter´ıstica da nanoestrutura do DNA permite trabalho na área da Nanociência e Nanotecnologia (N & N).

A ascensão do estudo relacionado ao DNA no final do último século vem sendo marcada por descobertas intrigantes representadas pelos avan¸cos de pesquisas fascinantes a respeito da sua nanoestrutura, resultando em grandes progressos no estudo f´ısico e bioqu´ımico do DNA no campo da nanotecnologia.

(18)

As possibilidades de aplica¸cão do DNA na área da nanotecnologia têm sido sugeridas por ser ideal na fabrica¸cão de dispositivo nanoeletrônico, uma vez que o DNA possui a caracter´ıstica de autoduplica¸cão. Esta particularidade permite a produ¸cão da sua réplica sem a necessidade de utilizar equipamentos, desse modo minimiza investimentos na tecnologia de nanofabrica¸cão [9].

Portanto nesta tese de doutorado, pretendemos estudar algumas propriedades eletrônicas da molécula de DNA propondo, inicialmente, um modelo quase-periódico da sequência de nu-cleot´ıdeos do DNA e comparando este resultado com as propriedades f´ısicas de uma sequência de DNA encontrada na natureza, o cromossomo 22 do genoma humano Ch22.

No Cap´ıtulo 2 abordamos uma breve hist´orico sobre a descoberta da estrutura do DNA, considerando os seus aspectos bioqu´ımicos e f´ısicos, destacando a fun¸c˜ao do esqueleto a¸c´ ucar-fosfato.

No Cap´ıtulo 3 apresentamos uma s´ıntese dos resultados teóricos e experimentais da con-dutividade do DNA, bem como os mecanismos de transporte dessa molécula. Em seguida, ana-lisamos as sequências quase-periódicas de Fibonacci e Rudin-Shapiro que estão sendo aplicadas para efeito de compara¸cão com a molécula em questão. E por fim, obtemos duas propriedades eletrônicas da molécula de DNA que são: a densidade de estado e a transmitância.

No Cap´ıtulo 4 aplicamos o processo de renormaliza¸cão para simplificar o sistema, que também foi modela em termos das sequências já pronunciadas. Obtemos o coeficiente de trans-missividade e o perfil da corrente caracter´ıstica I_×V da cadeia do DNA.

No Cap´ıtulo 5 investigamos as propriedades termo-eletrônicas da molécula de DNA. Inicialmente, calculamos as densidades de estados pelo método de Dean e utilizamos os resul-tados juntamente com a estat´ıstica de Fermi-Dirac para obter o potencial qu´ımico e o calor especifico quântico.

(19)

Cap´ıtulo

2

A mol´ecula de DNA

2.1 Introdu¸c˜

ao

No século XX, as pesquisas sobre os seres vivos demonstraram que no núcleo da célula de um organismo encontram-se estruturas denominadas de cromossomo, este por sinal é constitu´ıdo de prote´ına e DNA. Nas células, as informa¸cões genéticas responsáveis para o desenvolvimento do seres vivos estão localizadas principalmente na molécula de DNA. Atualmente, o estudo sobre essa molécula trouxe benef´ıcios significativos em áreas como: a f´ısica, a biomédica, a genética, agricultura e entre outras; sobretudo, favorecendo o progresso da Nanotecnologia [10]. Nesse contexto, a F´ısica vem desenvolvendo trabalhos cient´ıficos juntamente com outras ciências como; a Biologia e a Qu´ımica, buscando desvendar os mistérios da molécula da vida.

Neste âmbito é relevante o conhecimento da trajetória histórica para relatar as in-forma¸cões dos estudos envolvendo a gênese até os avan¸cos atuais dessa complexa molécula. No século XIX, os estudos da genética tiveram como seu pioneirismo o botânico austr´ıaco Gregor Mendel, em 1865, com os trabalhos dos genes das ervilhas. Posteriormente, foram realizadas investiga¸cões sobre a constitui¸cão qu´ımica, a estrutura e o funcionamento dos genes. Assim, constatou-se o interesse em conhecer a heran¸ca genética, através do estudo envolvendo o controle genético dos caracteres [11].

O estabelecimento da teoria celular, a descoberta do fator hereditário por Mendel e dos genes cromossômicos de Morgan [3] trouxeram o contexto necessário para a compreensão do estudo genético, proporcionando, no século XX, o desvendamento das fun¸cões e estrutura

(20)

da molécula de DNA. Na década de 1950, o biólogo norte-americano James Watson e o f´ısico britânico Francis Crick revelaram a estrutura helicoidal do DNA. O conhecimento da estru-tura ´ıntima do DNA representou um marco na biologia molecular, tendo como consequência, atualmente, algumas aplica¸cões biotecnológicas como os processos de clonagem, os organismos transgênicos e o projeto Genoma Humano [5].

Na atualidade, as controvérsias cient´ıficas relacionadas ao desvendamento e as várias pesquisas do DNA remetem ao estudo tanto bioqu´ımico quanto f´ısico, envolvendo o futuro dessa molécula, levando-nos ao próspero e atraente ramo nanotecnológico. Portanto, neste cap´ıtulo procuramos apresentar um breve histórico descrevendo os conceitos bioqu´ımicos e f´ısicos envolvendo o DNA. Além disso, será destacada a influência do esqueleto a¸cúcar-fosfato nessa molécula.

2.2 Breve hist´

orico sobre a descoberta da estrutura do

DNA

A trajetória dos estudos cient´ıficos envolvendo a descoberta dos genes por Mendel até a divulga¸cão da estrutura do DNA por Watson e Crick foi relevante para compreendermos as etapas do conhecimento da molécula da vida. Assim, pretendemos recapitular os caminhos que levaram ao desvendamento da estrutura do DNA.

Os primeiros conceitos de genética, publicados em 1865, foram desenvolvidos por um monge austr´ıaco, Gregor Mendel, que evidenciou através de cruzamento entre diferentes tipos de ervilhas que certas caracter´ısticas f´ısicas dessas plantas eram transmitidas de gera¸cão para gera¸cão. As distintas caracter´ısticas estariam localizadas e seriam transmitidas em unidades hereditárias. Os estudos dos genes das ervilhas permaneceram por longo tempo ignorado pela comunidade cient´ıfica [3]. Porém, após a concep¸cão da estrutura do DNA, foi necessário cerca de meio século a mais para serem descobertos os processos de decodifica¸cão do DNA, a identifica¸cão e reprodu¸cão de genes isolados e, por fim, o projeto Genoma Humano. A seguir será apresentado um esbo¸co sistemático da trajetória dos estudos envolvendo a molécula de DNA.

(21)

e nitrogênio, essa combina¸cão era uma substância diferente das prote´ınas conhecidas então, ao qual denominou de nucle´ına. Prosseguindo os estudos, em 1889, seu disc´ıpulo Richard Altmann obteve a nucle´ına com alto grau de pureza, comprovando sua natureza ácida e dando-lhe, então, o nome de ácido nucléico [12].

Em 1910, o médico e bioqu´ımico russo-americano Phoebus Aaron Levene foi o pioneiro no estudo dos ácidos nucléicos. Ele descobriu no ácido nucléico a presen¸ca de um a¸cúcar, a ribosa, uma pentose que tinha sido sintetizada por Emil Fischer. Vinte anos depois, Levene constatou que nem todos os ácidos nucléicos continham ribosa, alguns continham um tipo de pentose que não apresentava um átomo de oxigênio e a denominou de desoxirribosa. Assim, averiguou-se que havia, portanto, dois ácidos nucléicos: o ribonucléico (RNA) e o desoxirribo-nucléico (DNA). Albrecht Kossel descobriu que os compostos nitrogenados dos ácidos desoxirribo-nucléicos são formados por dois tipos de bases: as purinas (composto por dois anéis fundidos de cinco e seis átomos) e as pirimidinas (compostos por um anel de seis átomos). A molécula de DNA continha duas purinas (adenina e guanina) e duas pirimidinas (citosina e timina). Na molécula de RNA, a pirimidina (timina) era substitu´ıda por outra, denominada uracila. Durante os anos vinte, a opinião generalizada, era de que o DNA era muito simples, formado de pequenas moléculas. Por esse motivo, Levene defendeu que a molécula de DNA não podia carregar o código genético.

Ainda em 1910, Thomas Hunt Morgan provou que os genes estavam localizados nos cromossomos, o que confirmou a teoria genética da hereditariedade. Outras contribui¸cões foram os estudos sobre a heran¸ca ligada ao sexo e a recombina¸cão dos fatores relacionada à influência dos cromossomos e o trabalho de pesquisa com a mosca da fruta (Drosophila melanogaster), demonstrando como os genes poderiam sofrer muta¸cões. No ano de 1913, Alfred Sturtevant da equipe de Morgan, iniciou o mapeamento dos cromossomos. E em 1915, Morgan, Sturtevant, Muller e Bridges publicaram The Mechanism of Mendelian Heredity (O Mecanismo da Heredi-tariedade Mendeliana), no qual relatam experimentos com drosófilas e mostram que os genes estão linearmente dispostos nos cromossomas. Esses resultados, destacando a genética, rendeu a Morgan o Prêmio Nobel de Medicina, em 1933 [3].

(22)

letras dos aminoácidos das prote´ınas do que o alfabeto de quatro letras de nucleot´ıdeos do DNA. O fato do DNA de ser o material genético básico da célula veio a ser confirmado por cientistas posteriores. O trabalho de Avery inspirou várias pesquisas sobre a estrutura do DNA, agora conhecida como código genético.

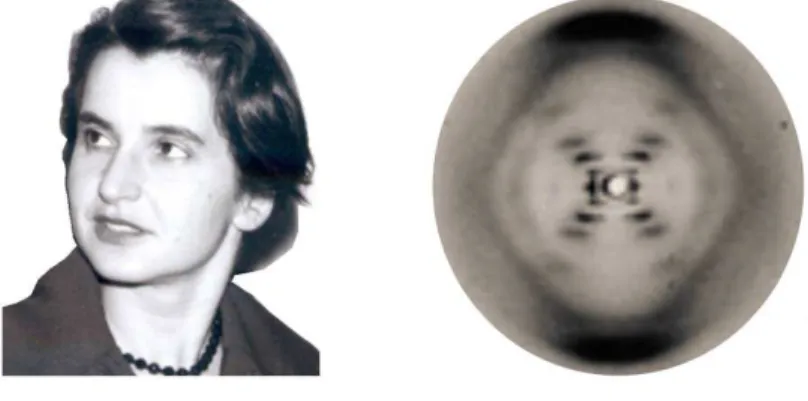
Nos anos 50 aconteceram novas investiga¸cões sobre o DNA a n´ıvel molecular, destacando-se os estudos dos cientistas James Watson e Francis Crick sobre a dupla hélice do DNA [14]. Contudo, a coopera¸cão cient´ıfica entre outros pesquisadores foi relevante nos estudos do DNA. Os trabalhos paralelos, mas concomitante de cientistas como: Pauling no Institute of Technology na Califórnia; Maurice Wilkins, Rosalind Franklin no King’s College em Londres e Watson e Crick na Cambridge University, implicaram no promissor conhecimento do DNA. A contribui¸cão crucial no desvendamento da estrutura do DNA foram às difra¸cões de raios-X e as medi¸cões desta amostra realizada por Rosalind Franklin [15], ver Fig. 2.1.

Figura 2.1: Rosalind Franklin e o padr˜ao de difra¸c˜ao de raios-X do DNA

(23)

em razão dos desentendimentos [3]. Pauling principiou analisar o DNA com base na copia de imagens mais antigas da difra¸cão dos raios-X, esfor¸cando para findar sua pesquisa sobe o DNA, propôs uma estrutura helicoidal de três hélices [16], similar ao primeiro modelo de Watson e Crick.

Peter filho de Linus Pauling foi para Cambridge fazer doutorado com Kendrew. Por interven¸cão dele, Watson e Crick teve conhecimento do artigo publicado por Pauling sobre a estrutura do DNA, no qual estes comentaram que o modelo de Pauling estava incorreto, pois existia um erro básico de qu´ımica, que o autor logo perceberia, sendo necessário reiniciar as pesquisas.

Em uma conversa com Maurice Wilkins no King’s College sobre o artigo de Pauling, Watson recebeu dele uma cópia ilustrada do raio-X de uma forma hidratada do DNA (B-DNA), sem o conhecimento de Franklin, e ficou sabendo de sua conclusão de que os fosfatos deveriam estar do lado de fora da hélice. Esta era muito mais clara e mais n´ıtida que a anterior de Pauling. As imagens e as medi¸cões por ela obtidas foram decisivas na constru¸cão do modelo, pois Watson compreendeu visivelmente que o DNA somente podia ter uma estrutura helicoidal de duas cadeias, com as liga¸cões fosfato-desoxirribosa na parte externa da molécula, o que permitiu que as bases nitrogenadas mais hidrofóbicas se abrigassem no interior da molécula, distante do meio aguoso [3, 14].

No dia 28 de fevereiro de 1953, Watson e Crick na tentativa de modelar a estrutura do DNA fez uso de peda¸cos de cartão simulando as bases (A, C, G e T) para identificar os poss´ıveis modos de intera¸cão. Observou que, os pares de bases A - T e C - G formavam pontes de hidrogênio, de modo que os pares tomassem dimensões quase idênticas, isto permitiria que a estrutura helicoidal do DNA se mantivesse com o mesmo diâmetro, independente do pareamento de bases no interior. Essa acomoda¸cão dos pares de bases atendeu à regra proposta por Chargaff, pela qual A tem quantidades equivalentes a T e C tem quantidades equivalentes a G [17]. Depois de trabalharem sobre esse modelo por mais alguns dias, refinando o mesmo para que fosse coerente com os dados de difra¸cão de raios X, eles chegaram ao modelo final.

No dia 25 de abril de 1953, a estrutura do ácido nucléico descoberto por Watson e Crick foi anunciada na revista inglesa Nature, com o t´ıtulo A Struture for Deoxyribose Nucleic Acid, considerada a contribui¸cão mais importante no campo da biologia depois da teoria da evolu¸cão de Darwin e do estudo genético de Mendel [18].

(24)

revelou a estrutura do DNA, sendo também de fundamental importância e reconhecido os es-tudos de Franklin, que é mencionada pelos cientistas em seus livros [3]. É notório que Watson e Crick trabalharam juntos no inicio de suas carreiras na Universidade de Cambridge, aliando seus recursos interdisciplinares com o franco objetivo de ganhar o Prêmio Nobel, solucionando o mistério do DNA. Eles descobriram a estrutura do DNA, a molécula-chave responsável pelo milagre da diversidade de seres vivos, embora originados pelo mesmo processo genético. Estes pesquisadores ainda afirmavam existir muitas permuta¸cões numa molécula longa e, portanto, parece admiss´ıvel que o sequenciamento preciso das bases constitui o código que contém a informa¸cão genética; destacando também que a estrutura proposta deve ser confirmada pela experimenta¸cão [19].

Figura 2.2: Prˆemio Nobel de Medicina: James Watson, Francis Crick e Maurice Wilkins

O descobrimento da estrutura do DNA sinaliza a nova era dos estudos biotecnológicos, pois foi poss´ıvel desvendar o código genético. Analise da estrutura da prote´ına e os dados de cristalografia de raios-X do B-DNA tornaram-se poss´ıvel o desvendamento da estrutura do DNA e o arranjo covalente do pol´ımero de ácido nucléico.

(25)

2.3 A estrutura da mol´

ecula de DNA

O DNA é uma macromolécula longa formada por seis componentes: uma molécula de a¸cúcar, um grupamento fosfato e quatro blocos estruturais denominados bases nitrogenadas: adenina, timina, citosina e guanina. Deste modo, constituem um alfabeto genético de quatro letras, respectivamente A, T, C e G, codificando a estrutura primária das prote´ınas. A adenina e a guanina possuem uma estrutura de anel duplo, caracter´ıstica de um composto qu´ımico denominado bases púricas (ou pur´ınicas). Enquanto, a timina e a citosina têm uma estrutura em anel único, t´ıpico de um composto qu´ımico chamado bases pirim´ıdicas (ou pirimidinas). As quatro bases do DNA também podem ser colocadas em uma ordem única para cada ser vivo. O esclarecimento deste código foi significativo para o desvendamento do DNA. A constitui¸cão da molécula de DNA por uma sequência de nucleot´ıdeos - composto equipolar de pentose, um grupo fosfato e uma base (púrica ou pirim´ıdica) permite a orienta¸cão das liga¸cões entre as três moléculas constituintes dos nucleot´ıdeos, ver Fig. 2.3.

Figura 2.3: As bases nitrogenadas e o nucleot´ıdeo

(26)

de hidrogênio, onde as bases timina e adenina são sempre emparelhadas por duas pontes de hidrogênio e a guanina com a citosina são sempre emparelhadas por três pontes de hidrogênio, veja Fig. 2.4.

Figura 2.4: Duas sequˆencias complementares de DNA

2.4 O modelo da dupla h´

elice do DNA

(27)

que os pares de bases deveriam ser formados por bases iguais, adenina-adenina, citosina-citosina, guanina-guanina e timina-timina. Estas forma¸cões entre as bases apresentavam pares de bases de tamanhos distintos e a dupla hélice tinha um diâmetro muito variável. Ao ter em mãos os dados da difra¸cão de raio-X do DNA do tipo B, eles puderam observar que o diâmetro externo da dupla hélice é em torno de 2 nm e a distância entre os a¸cúcares é de 1.1 nm. Através desses dados deduziu-se que os pares de bases adenina-timina e citosina-guanina teriam os diâmetros exatos para encaixar perfeitamente dentro da dupla hélice e, além disso, os pares de bases estava de acordo com a regra de Chargaff . Desse modo, pode-se observar que a hélice dá uma volta completa a cada 3,4 nm, que corresponde a cerca de 10 pares de bases e a distância entre dois pares de bases vizinhos é de 0,34 nm, como pode ser visto na Fig 2.5.

Figura 2.5: Representa¸c˜ao da estrutura helicoidal do DNA

(28)

comparada a uma escada espiralada com dois corrimões, sendo que os corrimões correspondem às liga¸cões repetidas de a¸cúcar-fosfato ao longo de todo o comprimento da molécula.

Ainda com base nestes estudos, concluiu-se que na dupla hélice as duas fitas estão em dire¸cões opostas, isto significa que são antiparalelas, ou seja, umas das fitas tem a dire¸cão apropriada da sua s´ıntese 5’ para 3’, enquanto que a outra esta oposta 3’ para 5’[21]. Deste modo, a liga¸cão do a¸cúcar-fosfato ocorre de modo tal que a posi¸cão 3’ da molécula de a¸cúcar liga-se ao agrupamento fosfato que, por sua vez, liga-se a posi¸cão 5’ da molécula de a¸cúcar subsequente, sendo elas antiparalelas [22].

O grupo fosfato conecta-se com pentose através de uma liga¸cão fosfodiéster com a hidro-xila ligada ao carbono 5 da pentose. Para a forma¸cão do DNA, é necessário que ocorra a liga¸cão entre os nucleot´ıdeos, estes formam entre si pontes de fosfato, através de liga¸cões fosfodiéster. Essa circunstância determina a forma¸cão da cadeia de DNA. Isto motiva o crescimento do DNA se fa¸ca na dire¸cão 5’ para 3’, como demonstra a Fig. 2.5. Assim, são feitas as liga¸cões entre os nucleot´ıdeos formando a fita de DNA.

Na literatura existem duas formas de DNA com a hélice girando para a direita, deno-minadas de A-DNA e B-DNA, e a outra forma de DNA gira para a esquerda e é conhecido como Z-DNA, ver Fig 2.6. As distin¸cões das duas formam A-DNA e B-DNA está na distância necessária para fazer uma volta completa da hélice e no ângulo que as bases fazem com o eixo da hélice. A forma B-DNA possui a dupla hélice mais longa e mais fina e cada volta da hélice possui 10 pares de bases. A forma A-DNA tem caracter´ıstica oposta e a cada volta da hélice possui 11 pares de bases. Geralmente, o DNA assume a acomoda¸cão B. Quando há pouca água dispon´ıvel para interagir com a dupla hélice, o DNA assume a acomoda¸cão A-DNA. O Z-DNA difere das duas anteriores, já que esta configura¸cão é mais alongada e mais fina do que o B-DNA. Para completar uma volta na hélice são necessários 12 pares de bases. O DNA em solu¸cão com altas concentra¸cões de cátions assume a conforma¸cão Z-DNA [7].

(29)

Figura 2.6: Estrutura A-,B- e Z-DNA.

entre o empilhamento de base ajudam a estabilizar a dupla fita de DNA. Desse modo, ainda que as pontes de hidrogênio entre os pares de bases sejam liga¸cões fracas, coletivamente elas estabilizam a molécula de DNA [23].

2.5 O esqueleto de a¸c´

ucar-fosfato

O a¸cúcar-fosfato é um componente constante nas moléculas de DNA e RNA é cons-titu´ıdo por uma pentose (ribose RNA e dexorribose DNA) e um agrupamento fosfato formando o corrimão da hélice. A sua fun¸cão é unicamente estrutural, sendo considerado o esqueleto na molécula de DNA e RNA. Para compreender a influência da camada a¸cúcar-fosfato nas pro-priedades de transporte no DNA, é interessante conceber o a¸cúcar-fosfato como um suporte, composto alternadamente de a¸cúcar e fosfato onde ambos são polares. O a¸cúcar-fosfato é com-ponente na arma¸cão da nanoestrutura do DNA, definindo também o sentido da fita. Deste modo, O DNA pode ser dividido estruturalmente em duas por¸cões: o a¸cúcar-fosfato e a base nitrogenada [5].

(30)

de DNA facilita observar a acomoda¸cão ocupada pelo esqueleto a¸cúcar-fosfato externamente na dupla hélice, apresentando as bases nitrogenadas no interior.

Esse delineamento dos aspectos f´ısicos-qu´ımicos decorrentes da composi¸cão do DNA permite apontar as caracter´ısticas hidrof´ılicas do fosfodiéster pela presen¸ca da pentose e o caráter ácido conferido pelo grupo fosfato. A solubilidade externa do DNA relacionada com meio hidrof´ılico, ou seja, o esqueleto fosfodiéster e a neutraliza¸cão das regiões eletricamente saturadas através de pareamentos entre as bases (A-T e C-G) permitiram a existência da região hidrofóbica, sem cargas elétricas livres, localizada no interior do DNA [24].

Desde o descobrimento da estrutura do DNA por Watson e Crick na década de 1950 até os dias de hoje é grande a inquieta¸cão envolvendo o desenvolvimento de pesquisas sobre a molécula da vida. Recentemente, constatou-se fisicamente o transporte de elétrons ao longo da cadeia de DNA, configurando-se em uma temática importante, abrindo novas perspectivas de estudo. A idéia de utilizar o DNA como um fio condutor molecular para o transporte de cargas ao longo da cadeia é um grande avan¸co na nanotecnologia, uma vez que ele tem a capacidade de automontagem. Isto fornece uma vantagem na produ¸cão de dispositivos nanoeletrônicos [8], onde tal possibilidade instiga inúmeros trabalhos de pesquisadores delineando a era da nanoestrutura.

(31)

Cap´ıtulo

3

Transporte eletrˆonico em dupla fita do DNA

poly(dG)-poly(dC)

3.1 Introdu¸c˜

ao

A molécula de DNA desempenha um papel fundamental como portadora de informa¸cões genéticas utilizadas no desenvolvimento e funcionamento dos organismos vivos. Recentemente, os avan¸cos dos estudos a respeito das suas propriedades eletrônicas têm chamado aten¸cão de vários pesquisadores como f´ısicos e qu´ımicos. A principal razão desse interesse é o uso potencial do DNA como dispositivo nanoeletrônico, tanto como modelo quanto elemento na montagem de nanocircuitos. Neste cap´ıtulo faremos uma s´ıntese dos resultados teóricos e experimentais da condutividade do DNA, estudaremos os mecanismos de transporte da molécula de DNA e analisaremos as sequências quase-periódicas que estão sendo aplicadas para efeito de compara¸cão com a molécula em questão e por fim apresentaremos duas propriedades eletrônicas da molécula de DNA que são: a densidade de estado e a transmitância.

3.2 Transporte de cargas no DNA

Os primeiros cientistas a sugerir que o DNA poderia servir como um condutor eletrˆonico foram Daniel Eley e D I Spivey isso ocorreu a mais de 40 anos ap´os a descoberta do DNA por

(32)

Watson e Crick. As idéias desses pesquisadores eram que as intera¸cões π₋π entre os pares de base empilhados no DNA possibilitariam um caminho para as migra¸cões das cargas elétricas [8]. Desde então, varias pesquisas foram realizadas no intuito de investigar sobre a dinâmica de transportes de cargas no interior do DNA, mas para isso consideraram que as extremidades da molécula seriam conectadas a dois elétrodos um doador e outro receptor. No entanto, os trabalhos desenvolvidos sobre as propriedades eletrônicas do DNA permanecem contraditórios, pois os resultados experimentais são inconsistentes em rela¸cão a outros estudos que mostravam poss´ıveis comportamentos da referida molécula como condutor [25, 26], isolante [27, 28] e semi-condutor [29, 30, 31, 32].

As primeiras medidas sobre a condutividade do DNA foram realizados por Fink e Schonenberger em 1999. No experimento, os dois pesquisadores aprisionaram a molécula de DNA de 600 nm entre dois elétrodos, no vácuo. Ao aplicar uma diferen¸ca de potencial foi constatado que a molécula se comportava como um condutor de resistência de 2.5 MΩ. Neste caso, o DNA comporta-se como um condutor, este resultado traz a possibilidade de utiliza¸cão da molécula de DNA em dispositivos nanobioeletrônicos [25, 26].

Em 2000, Pablo e colaboradores mediram a resistência do DNA [27]. A molécula foi depositada em uma superf´ıcie de mica e posto em contato por dois elétrodos de ouro, um deles fixa e o outro móvel. Eles relataram um baixo limite de resistividade de 104 _{Ω.cm em rela¸cão}

ao tamanho do DNA de acordo com o reajuste do elétrodo móvel. Por outro lado, utilizando um método diferente obtiveram um menor limite de resistividade de 106 _{Ω.cm. Estes resultados}

surgerem que o DNA seja um isolante, entrando em contradi¸cão com os resultados do Fink de ser um bom condutor [25]. Pablo e colaboradores suspeitaram que a amostra do experimento de Fink foi contaminada pelos feixes de elétrons de baixa energia no vácuo ocasionando uma diminui¸cão da resistência do DNA. Além disso, a estrutura espacial e o estado eletrônico da molécula de DNA foram grandemente influenciados pelos elétrodos [28].

Em 2001, Watanabe e colaboradores também estudaram sobre a condutividade do DNA e relataram que a molécula se comportava como um semicondutor [29]. Eles depositaram a molécula de DNA em uma superf´ıcie de SiO2/Si (100) e sob um fluxo de gás nitrogênio. As

correntes caracter´ısticas I _×V medidas à temperatura ambiente por uma separa¸cão de 25 nm entre os eletrodos indicaram que a dupla fita de DNA é um semicondutor com voltagem em torno de 2 V. Além disso, a tensão de gate reduz esta voltagem significativamente.

(33)

os substratos SiO2 e os eletrodos de ouro. Eles observaram uma corrente caracter´ıstica I ×V

quase linear quando os eletrodos estavam separados por 30µm. No entanto, quando a distância entre os eletrodos foram reduzidas para 20 nm, a corrente I_×V exibiu caracter´ıstica clara de escadaria, que foi consistente com a previsão teórica baseado no cálculo tight-binding.

Outro trabalho relevante foi realizado pelo grupo de Roy em 2008, que detectou o transporte de cargas do DNA de fita dupla, contendo 80 pares de bases, acoplada entre dois elétrodos SWNT [32]. Eles obtiveram valores das resistências do DNA nos intervalos 25-40 GΩ e 50-65 GΩ respectivamente, em condi¸cão ambiente e a vácuo (10−5 _{torr). Estes resultados}

confirmam que o DNA ´e um semicondutor.

De acordo com os comportamentos sobre a condutividade do DNA, podem se verificar que a molécula é sens´ıvel a qualquer diversifica¸cão das condi¸cões experimentais como: ambiente externo (ar, vácuo e solu¸cão l´ıquida), o contato entre a interface elétrodo-DNA, a dopagem do oxigênio, a sequência de nucleot´ıdeos da cadeia do DNA, e dentre outros. Em nosso estudo, vamos apresentar relatos de alguns fatores que podem interferir na condutividade.

Lee e colaboradores relataram em seu trabalho a influência da umidade e do oxigênio no transporte de cargas no DNA [33]. Estes pesquisadores utilizaram os elétrodos de Au/Ti em seus experimentos, onde as distâncias entre eles variaram de 100-200 nm. Eles analisaram a dopagem do oxigênio no poly(dG)-poly(dC) e no poly(dA)-poly(dT) e poderam verificar que a dopagem no poly(dG)-poly(dC) aumenta a condutância da molécula de DNA efetuando um maior impacto sobre o transporte de cargas. No caso poly(dA)-poly(dT), o efeito da dopagem do oxigênio ocorre ao contrário fazendo diminui a condutividade da molécula de DNA.

Kleine-Ostmann e colaboradores estudaram a influência da molécula da água na con-dutividade em ambas as fitas simples e dupla do DNA [34]. Eles descobriram que a molécula de DNA desidratada apresenta uma baixa condutividade que pode ser comparável ao de um semicondutor de gap largo. No caso, da molécula de DNA hidratada foi verificado que a con-dutividade aumentava exponencialmente com o aumento da umidade. Este fato se atribu´ıa ao acumulo de água na parte externa da estrutura do DNA, precisamente no fosfato.

(34)

3.3 Mecanismos de transporte de cargas

Vários experimentos e estudos teóricos têm demonstrado que as rea¸cões de transferência eletrônica dentro da molécula de DNA podem ser explicadas por uma variedade de processos f´ısicos. Especificamente, escolhemos três principais mecanismos de transporte de carga: tune-lamento coerente, tunetune-lamento incoerente e o thermal hopping.

O processo de tunelamento de elétrons ocorre do doador para o receptor através das varia¸cões das energias dos pares de bases. Este processo ocorre da seguinte forma: o buraco (carga positiva) é entendido como a menor varia¸cão de energia entre os pares de bases e está localizado entre os pares G-C, já os pares A-T funcionam como barreiras de potencial para a passagem de buracos. Desse modo, os buracos podem tunelar entre pares de base G-C ao longo da cadeia. Numa situa¸cão em que a carga positiva pode tunelar através do comprimento total do DNA, a fun¸cão de onda responsável não perde a coerência de fase e o elétron não troca energia com a molécula durante a transferência [35, 36]. Este processo é conhecido como tunelamento coerente ou de único passo Fig 3.1(a).

No entanto, se o processo de tunelamento ocorre sequencialmente entre pares de base G-C mais próximos, a coerência de fase da fun¸cão de onda é perdida durante este processo devido a alguns efeitos de defasagem, tais como espalhamento e vibra¸cões moleculares. O processo mencionado é denominado de tunelamento incoerente ou sequencial Fig 3.1(b). Assim como o tunelamento incoerente, othermal hoppingé um processo de várias etapas, no qual os portadores de carga saltam diversas barreiras de energia em vez de atravessá-las, como mostrado na Fig 3.1(c). Geralmente, esse processo necessita de uma quantidade maior de energia térmica [37].

Berlin e colaboradores fizeram um estudo te´orico sobre o mecanismo de transportes de tunelamento coerente e de thermal hopping usando o modelotight-binding para os nucleot´ıdeos da cadeia unidimensional [38]. A sequˆencia de DNA foi descrita desta maneira (AT)m−GC−

(AT)n−GC −(AT)m de acordo com o modelo. Estes mecanismos foram analisados atrav´es

da taxa de transporte que são expressões de caráter exponencial. No primeiro caso, a taxa de tunelamento é escrita dessa forma.

R =vtunexp(−βL) (3.1)

(35)

Figura 3.1: Esquema de três poss´ıveis mecanismos para transferência de carga no DNA: (a) Tunelamento coerente, (b) Tunelamento incoerente e (c) thermal hopping. O eixo vertical representa a energia E e o eixo horizontal representa a posi¸cão espacial X.

pares de base A-T, aé a distância entre pares de base, β é o coeficiente de decaimento e o vtun

parˆametro de ajuste. No segundo caso, a taxa do thermal hopping deve ser da forma.

R=vthermexp(−_kg_BG_T) (3.2)

Onde gG ´e a energia de separa¸c˜ao entre o n´ıvel de um buraco localizado no par G-C e

na parte inferior da banda de condu¸cão A-T,kB é a constante de Boltzmann e T é temperatura

em Kelvin. Portanto, o n´umero n de pares de bases A-T tem um valor cr´ıtico N0, quando este

valor é superado o thermal hopping torna-se o mecanismo de transporte eletrônico dominante, já que no tunelamento a transferência de carga decresce exponencialmente com o tamanho do DNA.

(36)

As sequências quase-periodicas têm sido usadas em um vasto campo de pesquisa prin-cipalmente na nanobiotecnologia. Basicamente, essas sequências constituem um sistema que envolvem dois ou mais blocos distintos que são empilhados por uma série de gera¸cões que obe-decem a uma regra particular. Na molécula de DNA são os nucleot´ıdeos G, C, A e T que formam os blocos da sequência quase-periódica.

Para estudar as sequências quase-periódicas do DNA é preciso definir uma sequência de substitui¸cão. Inicialmente, consideramos um conjunto com quatro nucleot´ıdeos ξ (Aqui ξ = G, C, A, T) chamado de alfabeto genético e denotemos por ξ∗ _{o conjunto de todas as palavras}

finitamente longas que podem ser escritos neste alfabeto. Agora consideramos ζ sendo uma proje¸c˜ao de ξ para ξ∗ _{especificando que} _ζ _{atua sobre uma palavra, substituindo cada letra (por}

exemplo, G) dessa palavra com a sua imagem correspondente ζ(G). Tal sequência é chamada de sequência de substitui¸cão, se for um ponto fixo de ζ, ou seja, se este permanece invariante quando cada letra na sequência é substitu´ıda por sua imagem em ζ. Em outra palavra, a sequência é obtida simplesmente aplicando infinitas vezes uma regra de substitui¸cão definida para um determinado caso [39]. Neste momento, apresentaremos as regras de constru¸cão de algumas sequências quase-periódicas que têm atra´ıdo aten¸cão de vários campos de pesquisas que são as sequências quase-periódicas de Fibonacci e de Rudin-Shapiro.

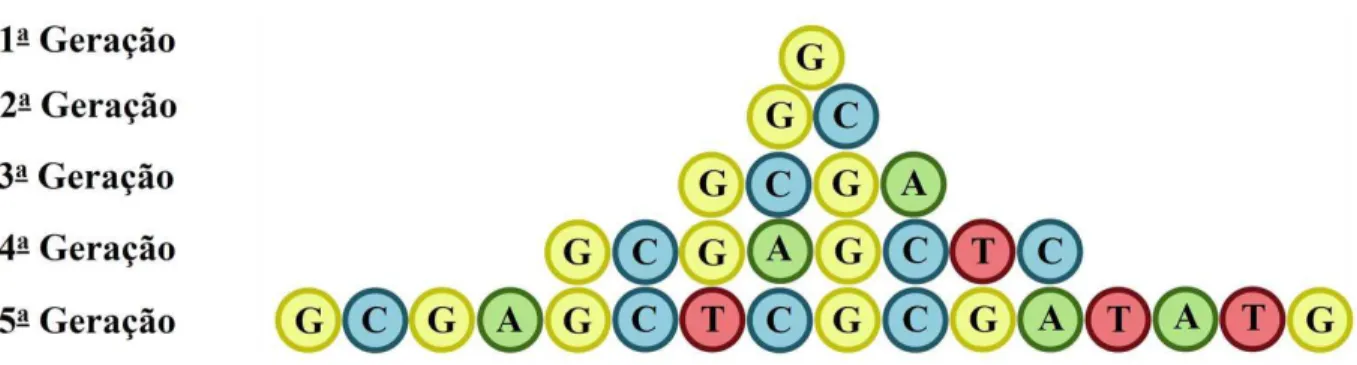
A sequência quase-periódica de Fibonacci pode ser crescida pela justaposi¸cão de dois nucleot´ıdeos G e C que obedecem a uma sequência de substitui¸cão conhecida na literatura como regra de infla¸cão. Esta regra funciona da seguinte forma: o nucleot´ıdeo G é substitu´ıdo pelos elementos GC e o nucleot´ıdeo C é substitu´ıdo por G. Escrevendo em termos simbólicos: G_→GC eC _→G (lê G vai para GC e C vai para G), ver Fig 3.2.

Figura 3.2: A sequência quase-periódica de Fibonacci para as primeiras gera¸cões, que crescem seguindo a regra de infla¸cão G_→GC e C _→G.

(37)

Fn−2 (com F0 = 0 e F1 = 1). Observe que em cada gera¸c˜ao o n´umero de guaninas G equivale

ao número deFibonacci para a mesma gera¸cão, isto é, na sexta gera¸cão deFibonacci temos que F6 = 8 o qual é o mesmo número de guaninas nesta gera¸cão. Além disso, a razão dos números

de guaninas e citosinas em cada gera¸cão tende á razão áurea definida como

xn = F_Fn+1_n = Fn+_FF_nn−1 = 1 + F_Fn−_n1 = 1 + Fn1 Fn−1

= 1 + _x1

n−1, (3.3)

como a sequência xn é limitada e monotônica crescente ela é convergente, portanto,

limxn

n→∞ =

limxn−1

n→∞ = 1 (3.4)

de onde obtemos a seguinte equa¸cão quadrática, cuja única solu¸cão positiva é denomi-nada de número áureo

L2₋_L₋_{1 = 0} _→ _φ₌ 1+√5

2 ≈1,61803. (3.5)

A sequência quase-periódica de Rudin-Shapiro também pode ser crescida, mas pela justaposi¸cão de quatro nucleot´ıdeos G, C, A e T de tal forma que a regra de substitui¸cão é dada por: G _→ GC, C _→ GA, A _→ T C e T _→ T A, ver Fig 3.3. Nesta sequência o número de nucleot´ıdeos correspondente a gera¸cão é da ordem de 2n−1_{, onde}_n _{é o n´}_{umero da gera¸cão, isto}

´e, na quinta gera¸c˜ao temos 16 nucleot´ıdeos.

Figura 3.3: A sequência quase-periódica de Rudin-Shapiro para as primeiras gera¸cões, que crescem seguindo a regra de infla¸cão G_→GC, C_→GA, A_→T C e T _→T A.

(38)

acordo com a regra que estudamos e a segunda fita segue a complementaridade dos pares de base de Watson e Crick.

3.5 Propriedades eletrˆ

onicas da mol´

ecula de DNA

Para tratar das questões relacionadas como o comportamento da condutividade do DNA, relatamos nesta se¸cão duas propriedades eletrônicas de um segmento de DNA poly(dG)-poly(dC), considerando a sua geometria planar de fita dupla com a inclusão do esqueleto a¸c´ ucar-fosfato (SP), que é representado na Fig 3.4.

(39)

O Hamiltoniano tight-binding do sistema ´e escrito em termos das bases localizadas.

H =P

n

∈n

SP |n,1i hn,1|+∈nα |n,2i hn,2|+∈nβ |n,3i hn,3|+∈nSP |n,4i hn,4|

+P

n

[V12(α→SP) [|n,1i hn,2|+|n,2i hn,1|]]

+P

n

[V23(α→β) [|n,2i hn,3|+|n,3i hn,2|]]

+P

n

[V34(β →SP) [|n,3i hn,4|+|n,4i hn,3|] +VSS(|n, Si hn, S|)]

+P

n

[V11(SP →S) (|n,1i hn−1,1|) +V44(SP →SP) (|n,4i hn±1,4|)],

(3.6)

onde_∈n

SP representa a energia de ioniza¸cão do a¸cúcar-fosfato e∈nα(α= C ou G) é a

ener-gia de ioniza¸c˜ao da respectiva base α localizado no siten. Tamb´em V12(α →SP), V23(α→β)

eV34(β→SP) s˜ao as amplitude dehopping entre primeiros vizinhos na vertical da cadeia, com

α,β= C, ou G, enquantoVSS´e o termo dehoppingno substrato. Al´em disso,V11(SP →S) = VS

e V44(SP →SP) = VSP s˜ao as amplitudes de hopping na horizontal da cadeia. Aqui, a letraS

significa o substrato e SP significa o esqueleto a¸c´ucar-fosfato.

A densidade de estado, bem como a transmissividade eletrônica são calculadas conside-rando que a molécula de DNA é colocada em contato entre dois eletrodos de platina. Além disso, a molécula é organizada numa geometria poly(dG)-poly(dC) seguindo uma estrutura quase-periódica de Fibonacci. Os espectros são então comparados com aqueles encontrados a partir de uma sequência genômica do DNA, considerando-se o primeiro segmento sequenciado do cromossomo humano 22 (Ch22).

3.5.1 Densidade de estado

A densidade de estado pode ser obtido atrav´es da fun¸c˜ao de Green

(E₋H)G(E) =I (3.7)

onde I ´e a matriz identidade eH ´e o Hamiltoniano dado por (3.6).

(40)

atrav´es da regra de infla¸c˜ao G _→ GC e C _→ G para a primeira fita de DNA. Para a segunda fita de DNA, temos bases complementares, de tal forma que sempre temos um GC ou um par de bases CG.

Para a primeira gera¸cão da sequência de FB, em que apenas a base guanina é ligada ao substrato, a fun¸cão de Green leva a:

G(E)−1

=KG+ 2Γ (1), (3.8)

onde

Γ (1) =₋LSP S[KS+LST]−1LSP S. (3.9)

AquiT é uma matriz de transferência que liga a fun¸cões de Green a dois s´ıtios vizinhos. Além disso, LS =−VSSI, I é uma matriz identidade 4×4, e KG, KC, KS, LSP S são matrizes

dadas por

KG =

     

E_{− ∈}SP −V12(G→SP) 0 0

−V12(G→SP) E− ∈G −V23(G→C) 0

0 ₋V23(G→C) E− ∈C −V34(C →SP)

0 0 ₋V34(C →SP) E− ∈SP

      (3.10)

KC =

     

E_{− ∈}SP −V12(G→SP) 0 0

−V12(G→SP) E− ∈C −V23(G→C) 0

0 ₋V23(G→C) E− ∈G −V34(C →SP)

0 0 ₋V34(C →SP) E− ∈SP

      (3.11)

KS =

     

E_{− ∈}S −VSS 0 −VSS

−VSS E− ∈S −VSS 0

0 ₋VSS E− ∈S −VSS

−VSS 0 −VSS E− ∈S

(41)

LSP S =



    

−VS 0 0 0

0 0 0 0 0 0 0 0 0 0 0 ₋VS



    

(3.13)

Repetindo o procedimento para qualquer gera¸cão de Fibonacci, observamos uma dife-ren¸ca entre a fun¸cão de Green G(E) para gera¸cões ´ımpares (sequências da primeira fita com termina¸cão G) e pares (sequências da primeira fita com termina¸cão C), ou seja,

G(E)−1 ₌_K

G+ Γ (1) + ∆ (nF B), (3.14)

para as gera¸cões ´ımpares, ondenF B é o número de nucleot´ıdeo na fita. Para as gera¸cões

pares temos

G(E)−1

=KG+ Γ (1) + Γ (nF B). (3.15)

aqui

∆ (nF B) = −LSP SP[Ki+ ∆ (nF B −1)]−1LSP SP (3.16)

cuja condi¸c˜ao inicial ´e:

∆ (1) =₋LSP S[KS+LST]−1LSP S. (3.17)

A express˜ao para Γ (nF B) pode ser encontrado de forma similar. Vamos agora voltar

nossa discuss˜ao para a determina¸c˜ao da densidade de estado (DOS), definida por:

(42)

3.5.2 Resultados

As energias_∈α,βs˜ao escolhidos a partir da energia de ioniza¸c˜ao das respectivas bases, ou

seja, _∈G = 7,77 eV (guanina) e ∈C = 8,87 eV (citosina) [22, 40]. Al´em disso, usamos a energia

do eletrodo de platina _∈S = 5,36 eV, que est´a relacionado com a fun¸c˜ao trabalho desse metal

[38], enquanto a energia do esqueleto a¸c´ucar-fosfato ´e _∈SP = 12,27 eV [41, 42]. Os potenciais

de hopping entre a base (G ou C) e o esqueleto a¸c´ucar-fosfato (SP) s˜ao V12(G→SP) =

V34(C →SP) = 1,5 eV [42], enquanto que no substrato (eletrodo de platina) ´e VSS = 12 eV

[42]. Al´em disso, o hopping entre o par de base ´e V23(G→C) = 0,90 eV [42]. O energia de

ioniza¸cão na interface DNA-eletrodo é considerado como a diferen¸ca entre o n´ıvel de Fermi da platina e doHOMO (Orbital Molecular Mais Ocupado) do a¸cúcar-fosfato que é dando porVS =

6,91 eV [42]. Finalmente, o potencial de hopping entre os esqueletos a¸c´ucar-fosfato ´e VSP =

0,02 eV [43].

Os espectros da densidade de estados (DOS) para uma molécula de DNA moldada pela sequência quase-periódica de Fibonacci, é mostrado na Fig 3.5 com fun¸cão da energia (em eV), para o número de gera¸cão de Fibonacci NF B = 12 enF B = 610. O NF B aqui significa o número

de gera¸cão da sequência, enquanto nF B corresponde ao número de pares de nucleot´ıdeos numa

dada gera¸cão da sequência. Estamos mostrando apenas o caso de paridade, mesmo porque o DOS não é sens´ıvel a paridade da sequência deFibonacci, como o seu espectro de calor espec´ıfico [44]. Para efeito de compara¸cão, estamos mostrando a densidade de estado de um trecho do segmento natural do DNA extra´ıdo do cromossomo humano Ch22 (linha tracejada), cujo os

espectros mostram uma notável concordância com aquela modelada pela sequência deFibonacci. Embora o DOS para cada gera¸cão como um todo, não mostra qualquer simetria, apresentamos para os espectros de Fibonacci e Ch22 duas regiões simétricas, localizadas em torno da energia

de 7,03 eV (pico I) e 15,35 eV (pico III), respectivamente, al´em de uma assim´etrica em torno de 9,03 eV (pico II).

Embora o pico I não tem uma correla¸cão direta com as energias de ioniza¸cão das bases (guanina e citosina), o seu valor está próximo do termo de hopping da interface eletrodo-DNA, sugerindo uma influência importante para a escolha do substrato sobre a propriedade da densidade de estado do DNA.

(43)

na gera¸c˜ao FB, bem como no trecho do cromossomo humanoCh22 seja menor que a guanina, a

sua energia de ioniza¸c˜ao _∈C seja maior faz a diferen¸ca em rela¸c˜ao ao DOS de todo o sistema.

O terceiro pico (pico III) ocorre a um valor aproximadamente igual ao dobro da energia de ioniza¸cão da guanina. Também podemos observar uma anomalia no espectro do DOS em torno de 10,6 eV, que é duas vezes o valor da energia de ioniza¸cão do eletrodo _∈S. Além disso,

o DOS em cada n´ıvel de energia aumenta com a gera¸cão de Fibonacci para os intervalos 5,36 < E < 15,98 (em unidade de eV), aproximadamente. Note que este intervalo é compreendido entre a energia de ioniza¸cão do substrato _∈S e o dobro da energia de ioniza¸cão do guanina∈G.

No entanto, em torno de 12.5 eV, observamos que o DOS ´e quase nulo para ambos os casos FB e Ch22. Esse resultado pode estar relacionado com o termo de hopping do substrato e /ou a

energia de ioniza¸cão do a¸cúcar-fosfato, que estão em torno de 12 eV.

3.5.3 Transmitˆ

ancia

Também reportamos neste cap´ıtulo a condutividade da estrutura quase-periódica do DNA poly(dG)-poly(dC). Para este sistema, o coeficiente de transmissão TN(E) é dado pela

taxa de transmissão da cadeia e está relacionada com a resistência de Landauer que é definida por [45].

TN(E) =

8 P i,j=1

P_Nij

16 2 , (3.19)

com P_Nij =X22−X21X11−1X12. Aqui X ´e a matriz 8×8, convenientemente escrita na

forma particionada com quarto matrizes quadradas Xij(i, j = 1 at´e 4) de ordem 4×4. Este ´e

definida como X =Q−1_S−1_{℘(n)S, com:}

Q=

"

e−ika_I ₀

0 e−ika_I

#

, (3.20)

S=

"

e−ika_{I e}ika_I

I I

#

, (3.21)

onde k ´e dada por k = cos−1

(E_{− ∈}S)/(2VSS) +

√

5₋1

/4

(44)

MnMn−1...M2M1, onde Mn ´e a matriz transferˆencia definida por

MN =

"

M(E) ₋I

I 0

#

, (3.22)

M(E) = (1/VSP)

     

(E_{− ∈}n

SP) −V12(α→SP) 0 0

−V12(α→SP) (E− ∈nα) −V23(α →β) 0

0 ₋V23(α→β) E− ∈nβ

−V34(β →SP)

0 0 ₋V34(β →SP) (E− ∈nSP)

      (3.23)

Na expressão acima I(0) é a matriz 4_×4 identidade(nula). Para uma dada energia E, TN(E) mede o n´ıvel de eventos espalhados no transporte de elétrons (ou buracos) na cadeia.

3.5.4 Resultados

Na Fig 3.6 mostra o espectro de transmitância, em fun¸cão da energia em unidade de eV, para a sequênciapoly(dG)-poly(dC)deFibonacci com o número pares de nucleot´ıdeos (nF B)

é igual a 610 (linha cheia). Para efeito de compara¸cão estamos mostrando também o coeficiente de transmissão de um segmento de DNA natural, uma parte do cromossomo humano Ch22

(linha tracejada), cujo espectro está novamente de acordo com aquele modelado pela sequência deFibonacci. O espectro de transmitância mostra a energia com ressonância de transmissão alta [TN (E) = 1] na região próxima a 12,9 eV, influenciado pela energia de ioniza¸cão do esqueleto

a¸cúcar-fosfato. As bandas de transmissão no espectro tornam-se mais fragmentada à medida que aumenta o tamanho da cadeia de nucleot´ıdeos (não mostrado aqui). Esta caracter´ıstica está relacionada com a natureza localizada do autoestado do elétron em cadeias desordenadas.

´

(45)

n˜ao correlacionada com algumas propriedades interessantes:

(a) Existem gaps de energias (regi˜oes proibidas) nas regi˜oes (em eV) E<6,3; 7,2 <E< 8,1; e 9,5 < E <12,15.

(b) A transmitância é máxima (próximo de um) em E = 12,9 eV.

(c) Devido `a estrutura robusta a transmiss˜ao vai a zero em grande segmento de DNA.

3.6 Conclus˜

oes

Em resumo, com o objetivo de facilitar a compreensão sobre as propriedades eletrônicas de um segmento de DNA, estudamos aqui as propriedades de transporte eletrônico das sequências de nucleot´ıdeos finitas dentro de uma abordagem tight-binding da fita dupla de DNA poly(dG)-poly(dC). Embora relevantes, temos negligenciado neste trabalho a topologia da dupla hélice e o efeito de vibra¸cão fônon em nosso modelo. Os resultados estão de acordo quando comparamos as densidades de estados (DOS) da sequência quase-periódica de FB com o cromossomo humano Ch22. Além disso, estudamos os espectros que mostram além de outras propriedades f´ısicas, que

a correla¸cão de longo alcance presente no Ch22 e na sequência FB são responsáveis pelo lento

(46)

Figura 3.5: Espectros da densidade eletrônica de estado (DOS), com fun¸cão da energia (em eV), para a décima quarta gera¸cão de Fibonacci do modelo de fita dupla do DNApoly(dG)-poly(dC), correspondente ao número de pares de nucleot´ıdeos NF B = 610 (linha cheia). Para efeito de

(47)

(48)

Cap´ıtulo

4

Uma abordagem da renormaliza¸c˜ao para

descrever o transporte de carga na mol´ecula de

DNA

4.1 Introdu¸c˜

ao

O transporte de carga em molécula de DNA atrai considerável interesse entre a f´ısica, qu´ımica e a biologia não só devido à sua relevância, como portador do código genético de todos os organismos vivos, mas também como um candidato promissor para a eletrônica molecular. Na verdade, o uso de molécula como componente eletrônico tem tomado novas dire¸cões na ciência e tecnologia em sistema de escala nanométrica, devido à sua aplica¸cão cient´ıfica e de engenharia [47, 48]. Além disso, a mobilidade de carga no DNA tem sua importância com base em contexto biológico [49], bem como sobre os contextos tecnológicos (por exemplo, o uso de DNA em sensores eletroqu´ımicos [50] e em nanotecnologias futuras [51, 52]). Na verdade, a condu¸cão eletrônica na molécula de DNA é uma investiga¸cão de fronteira em eletrônica molecular [27, 53] devido ao seu uso potencial em dispositivos de nanoeletrônica, tanto como modelo para as montagens de nanocircuitos, e como elemento de tais circuitos [54, 55].

Embora o uso da molécula de DNA em circuito nanoeletrônico é muito promissor, devido à sua automontagem e habilidade de reconhecimento molecular, suas propriedades de condutividades estão ainda sob intenso debate. Diferentes conclusões são obtidas através de

(49)

vários experimentos. No lado teórico, ambos os cálculos ab initio [56, 57, 58, 59] e modelos baseados em Hamiltonianos [60, 61, 62, 63, 64, 65] são amplamente adotados para interpre-tar as diversidades dos resultados experimentais e verificar os mecanismos de transporte de carga. A primeira pode fornecer uma descri¸cão detalhada, mas estão atualmente limitadas as moléculas relativamente curtas. O último é muito menos detalhado, embora permita trabalhar com sistemas com comprimentos maiores. No entanto, a abordagem baseada em modelo pode desempenhar um papel importante, porque agarra geralmente no fundamento f´ısico.

Modelos anteriores de transporte eletrônico em molécula de DNA assumem que os canais de transmissão são ao longo de seu eixo longitudinal. As intera¸cõesπ₋πde nucleobases do DNA, formada por uma sequência simbólica de quatro letra do alfabeto genético: guanina (G), citosina (C), adenina (A), e timina (T) fornecem o caminho para promover a migra¸cão de carga de longo alcance, que em sua vez, dão pistas importantes sobre os mecanismos e fun¸cões biológicas de transporte de carga [66, 67, 68, 69, 70]. Outras melhorias incluem a estrutura do esqueleto a¸cúcar-fosfato da molécula de DNA de forma expl´ıcita, que reduz a arquitetura do par de bases do DNA em um único site por par, o modelo é chamado de espinha de peixe [71, 72]. Mais tarde, Klotsa et al. [73] generaliza o modelo de fishbone do DNA considerando cada base como um s´ıtio distinto, fracamente acoplado por pontes de hidrogênio. Como consequência, dois ramos centrais são assim obtidos, cujos locais interligados representam os pares de bases do DNA, que são acoplados aos s´ıtios superior e inferior dos esqueletos a¸cúcares-fosfatos desconectados, dando origem ao chamado modelo (DBL) do DNA.

Neste cap´ıtulo, usamos um modelo Hamiltoniano dentro de uma abordagem da renor-maliza¸cão de uma etapa para descrever as propriedades de transporte de carga numa molécula de DNA-DBL (ver Fig. 4.1). Nossa descri¸cão da molécula de DNA leva em conta as contri-bui¸cões do sistema nucleobase, bem como as moléculas do esqueleto a¸cúcar-fosfato. Para este fim, usamos um modelo Hamiltoniano tight-binding, juntamente com o emprego de uma técnica da matriz de transferência para simplificar a álgebra. Consideramos um modelo de DNA-DBL seguindo os arranjos de base quase-periódicas de Fibonacci (FB) e um deRudin-Shapiro (RS) [39, 74], bem como a sequência de DNA da primeira sequência do cromossomo humano (Ch22)

para efeito de compara¸cão. As varia¸cões resultantes da eficiência do transporte de carga são analisadas, nessas sequências, computando numericamente as principais caracter´ısticas de seus coeficientes de transmissão de elétrons e suas curvas caracter´ısticas I-V.

(50)

Figura 4.1: Esbo¸co ilustrando o processo de renormaliza¸cão de uma etapa do mapeamento do modelo DBL da cadeia de DNA. (a) Modelo DBL-DNA para as sequências deFibonacci, Rudin-Shapiro eCh22; (b) Modelo de renormaliza¸cão da molécula de DNA-DBL após a primeira etapa

da decima¸c˜ao. .

em movimento numa geometria composta por duas cadeias interligadas de sites sanduichadas por dois eletrodos met´alicos de platina (doador DN, receptor AC), ver Fig. 4.1a, produzindo

Htotal =HDN A+Heletrodo+Hcontato (4.1)

(51)

por [39, 73, 74, 75]:

εn

α,β =∈nα,β +

v(α→SP)2

(E−∈nSP) (4.2)

Aqui _∈n

α,β (α, β = G, C, A ou T) ´e a energia de ioniza¸c˜ao (em unidades de ~) da

respectiva base α, β; v(α _→SP) ´e o termo de hopping entre a base α (G, C, A ou T) e o esqueleto a¸c´ucar-fosfato (SP), finalmente, _∈n

SP representa a energia de ioniza¸c˜ao no site n do

orbital a¸cúcar-fosfato, tendo em conta a natureza da base vizinha, bem como a presen¸ca da molécula de água e/ou contra-´ıons ligado ao esqueleto a¸cúcar-fosfato.

As energias _∈α,β s˜ao escolhidos a partir das energias de ioniza¸c˜ao de suas respectivas

bases, ou seja, _∈G = 7,77 eV (Guanina), ∈C = 8,87 eV (Citosina), ∈A = 8,25 (Adenina), e

∈T = 9,13 (Timina) [22]. N´os usamos a energia do eletrodo (platina) ∈S = 5,36 eV, que est´a

relacionado com a fun¸c˜ao trabalho desse metal [38], enquanto a energia do esqueleto a¸c´ ucar-fosfato ´e _∈SP = 11,0 eV. Tomamos os termos de hopping entre a base (G, C, A ou T) e o

esqueleto a¸cucar-fosfato (SP) como v = 0,7 eV, enquanto que o hopping entre o par de base vertical(horizontal) da cadeia é ω(α_→β) = 0,05 eV e (t(α_→α) = 0,5 eV), que estão dentro dos intervalos dos valores obtidos por cálculos de qu´ımica quântica [76]. Além disso, o hopping

do eletrodo ´e t0 = 12,0 eV [42].

Tendo em conta o procedimento de renormaliza¸c˜ao, o primeiro termo do Hamiltoniano (1) ´e descrito por

HDN A =P n

εn

α|n,1i hn,1|+εnβ|n,2i hn,2|

+P

n

ω(α_→β) [_|n,1_{i h}n,2_|+_|n,2_{i h}n,1_|] +P

n

t(α _→α) [_|n,1_{i h}n_±1,1_|] +P

n

t(β _→β) [_|n,2_{i h}n_±1,2_|]. (4.3)