Apostila de Física Experimental II
Engenharia Mecânica
AUTORES:
ALUNO MONITOR : Pedro Araújo da Costa Ward
PROFESSOR ORIENTADOR: Prof. Asso. Dra. Mirian Enriqueta Bracco
PROFESSORES COLABORADORES: Prof. Adj. Dra. Kanchan Pradeepkumar Khemchandani
Conteúdo
1. INTRODUÇÃO ... 3
1.1. Importância e conexão com a engenharia ... 3
1.2. Segurança e comportamentos no laboratório ... 6
2. INSTRUMENTOS E EQUIPAMENTOS ... 6
2.1. Paquímetro ... 8
2.2. Micrômetro ... 9
2.3. Relógio comparador ... 10
2.4. Dinamômetro ... 11
2.5. Dilatômetro linear ... 11
2.6. Calorímetro ... 12
3. MEDIDAS, INCERTEZAS E DESVIOS ... 13
3.1. Erros de medida ... 13
3.2. Algarismos significativos... 13
3.3. Arredondamento e truncamento ... 16
3.4. Operações com algarismos significativos ... 17
3.4.1. Adição e subtração... 17
3.4.2. Multiplicação e divisão ... 18
3.5. Método dos Mínimos quadrados ... 18
3.6. Incerteza nas medidas diretas ... 19
3.7. Incerteza nas medidas indiretas ... 20
3.8. Desvio ... 22
3.9. Desvio percentual ... 22
4. ROTEIROS DAS PRÁTICAS ... 23
4.1. Mesa Giratória ... 23
4.2. Hidrostática ... 26
4.3. Sistema massa-mola ... 28
4.4. Pêndulo Simples ... 30
4.5. Pêndulo Físico ... 34
4.6. Dilatação linear dos sólidos ... 36
4.7. Calorímetro e calor específico ... 38
1. INTRODUÇÃO
1.1. Importância e conexão com a engenharia
A engenharia está diretamente ligada com a disciplina de Física experimental. O engenheiro é aquele que deve buscar sempre melhoria, evolução e soluções para situações do cotidiano e problemas maiores. Para que as ideias surjam é necessário utilizar a metodologia semelhante a aquela utilizada nas aulas de laboratório, descritas a seguir.
O aluno, ao seguir o roteiro, aprende a observar uma situação e interpreta-la (nestes casos um experimento relacionado à física). Ele deve ser capaz de se fazer as seguintes perguntas, por exemplo:
O que ocorreu?
Quais fenômenos estão envolvidos? Quais grandezas e dados posso coletar? Quais são os erros?
Quais fatores que causam esses erros? O que é possível realizar para melhorar?
Durante os processos, nas aulas experimentais o aluno consegue verificar o conteúdo visto em sala de aula e entender melhor os fenômenos físicos. Além de ganhar mais experiência e familiaridade com os instrumentos e equipamentos de estudo, análise, leitura e medição. Tudo isso aplicando conhecimentos básicos de estatística com os cálculos de incertezas e desvios.
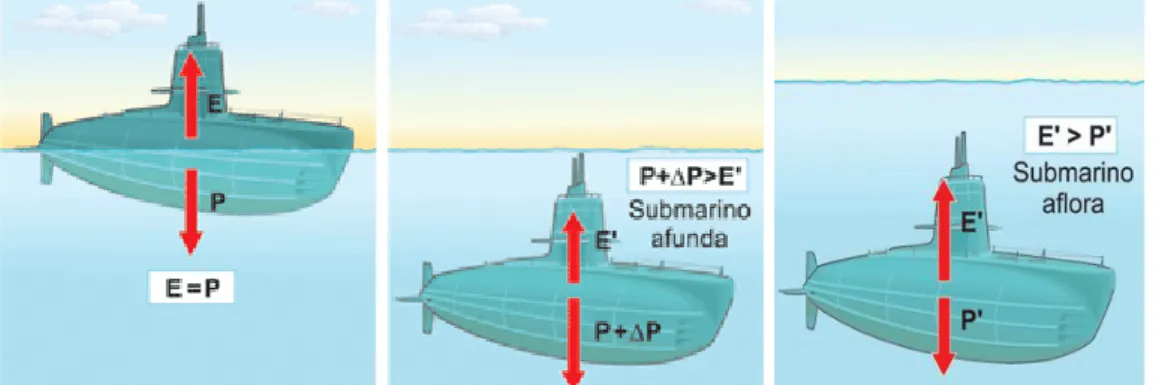
Nesta apostila o conteúdo dos roteiros tem foco principalmente nos temas de momento de inércia, fluidos, movimentos oscilatórios e troca de calor. Podemos interligar os assuntos físicos citados acima com alguns projetos da engenharia, como é o caso da confecção de um submarino. Neste caso é necessário estudar a pressão suportada pela estrutura do submarino e o princípio de Arquimedes explicando quando o mesmo afunda ou aflora.
Figura 1.1 – Esquema de movimentação de um submarino
Outro exemplo que podemos citar é o ensaio mecânico destrutivo de Impacto. Este teste é um método de avaliação da resistência e sensibilidade de materiais. Consiste em submeter um corpo de prova a uma carga praticamente instantânea, provocando a fratura. A energia absorvida no impacto é o parâmetro de avaliação da propriedade.
No ensaio de impacto um corpo de prova com entalhe é quebrado pelo impacto de um pêndulo, que cai de uma distância fixa numa velocidade pré-determinada. O teste mede a energia absorvida pelo corpo de prova fraturado.
Figura 1.2 – Exemplo de teste que necessita o conceito de pêndulos
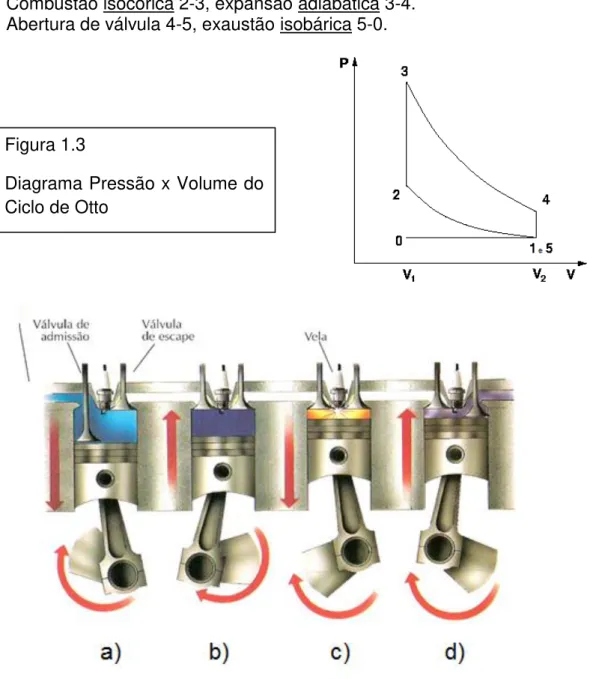
O ciclo ideal se constitui dos seguintes processos:
a) Admissão isobárica 0-1.
b) Compressão adiabática 1-2.
c) Combustão isocórica 2-3, expansão adiabática 3-4.
d) Abertura de válvula 4-5, exaustão isobárica 5-0.
Figura 1.4 – Passo a passo de um motor de combustão interna
Podemos observar com essa breve introdução a importância de se realizar experimentos. Adquirimos com eles a prática científica e abrimos a porta para futuras grandes descobertas.
Figura 1.3
1.2. Segurança e comportamentos no laboratório
O aluno deve ter uma postura profissional respeitando todas as normas de segurança estabelecidas ao laboratório e também aprenderá como manusear corretamente instrumentos e equipamentos utilizados, que serão descritos com um pouco mais de detalhes adiante.
Abaixo estão listadas as normas de segurança que deverão seguidas por todos aqueles que forem utilizar o laboratório.
Estar com o traje adequado (sapato fechado e calça comprida);
Não manusear equipamentos sem a devida autorização, sem saber como funciona ou sem conhecer sua periculosidade;
Caso ocorra alguma anormalidade durante o experimento comunicar o professor;
Não brincar, correr, comer, beber ou fumar no laboratório; Não se expor às radiações ultravioleta, infravermelha, etc.
Manter as bancadas sempre limpas e livres de materiais estranhos ao trabalho;
A organização é imprescindível, manter sempre a organização no laboratório.
2. INSTRUMENTOS E EQUIPAMENTOS
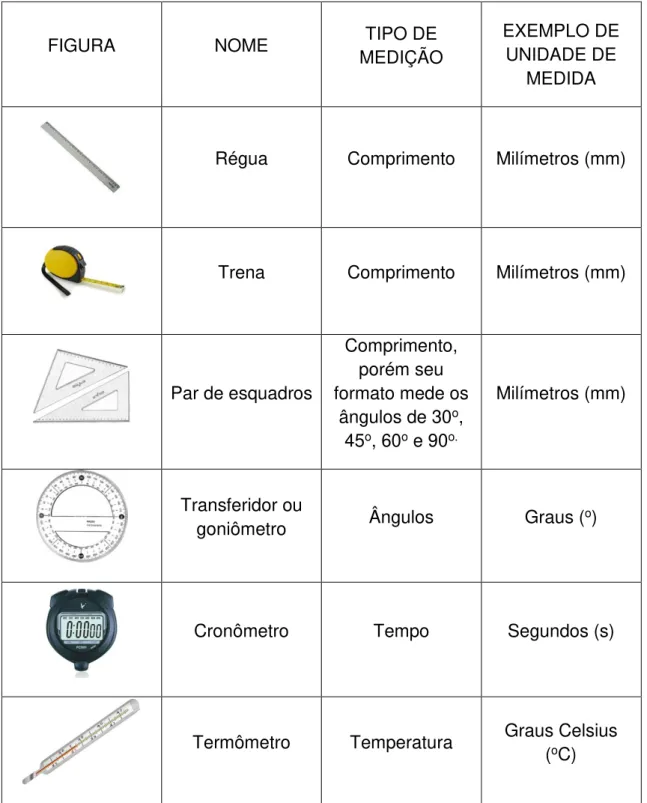
Nesta seção da apostila serão listados alguns instrumentos e equipamentos (com uma breve introdução) que serão utilizados no laboratório e que em muitas situações diferentes estão presentes no dia-a-dia de um engenheiro ou estudante de engenharia. Para começar, abaixo temos uma tabela com alguns instrumentos de medição e suas usuais especificações.
FIGURA NOME TIPO DE
MEDIÇÃO
EXEMPLO DE UNIDADE DE
MEDIDA
Régua Comprimento Milímetros (mm)
Trena Comprimento Milímetros (mm)
Par de esquadros
Comprimento, porém seu formato mede os
ângulos de 30o, 45o, 60o e 90o.
Milímetros (mm)
Transferidor ou
goniômetro Ângulos Graus (o)
Cronômetro Tempo Segundos (s)
Termômetro Temperatura Graus Celsius (oC)
2.1. Paquímetro
O paquímetro é um instrumento utilizado para medições de partes internas, externas e de ressaltos com alguns exemplos do seu uso a seguir:
Figura 2.1 - Exemplos do uso do paquímetro
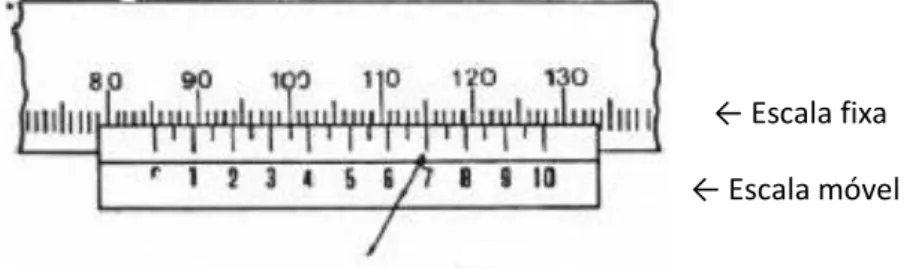
Temos a seguir um exemplo de como se faz a medição de um paquímetro de menor medida 0,05mm e escala móvel de 20 divisões:
Figura 2.3 - Como fazer a leitura de um paquímetro
1) Observamos que o zero da escala móvel se encontra junto à medida 85 mm da escala fixa.
2) E temos também, que o traço da escala móvel que coincide com algum traço qualquer da escala fixa é o de número 7, ou seja, medida de 0,70 mm na escala móvel.
3) Juntando a medida da escala fixa mais a da escala móvel temos que a figura acima está medindo um objeto de:
𝑒𝑠𝑐𝑎𝑙𝑎 𝑓𝑖𝑥𝑎 + 𝑒𝑠𝑐𝑎𝑙𝑎 𝑚ó𝑣𝑒𝑙 = (85𝑚𝑚) + (0,70𝑚𝑚) = 85,70𝑚𝑚
2.2. Micrômetro
O micrômetro é um instrumento que permite medir diretamente dimensões lineares com uma precisão maior que a do paquímetro.
← Escala fixa ← Escala móvel
Figura 2.4:
Partes de um micrômetro.
Figura 2.5:
2.3. Relógio comparador
O relógio comparador é um instrumento de precisão de grande sensibilidade. Utilizado tanto na verificação de medidas, superfícies planas, concentricidade e paralelismo, como para leituras diretas.
Figura 2.6: Partes de um relógio comparador.
Figura 2.7:
Exemplo de medição de um relógio comparador:
Precisão: 0,01 mm
2.4. Dinamômetro
Um dispositivo que pode ser utilizado para medir a força chama-se dinamômetro. Este dispositivo é dotado de: Estrutura; Mola; Gancho em uma das extremidades da mola; Graduação na estrutura.
Em uma das extremidades da mola encontra-se presa a estrutura graduada e em outra extremidade, o gancho, que se localiza fora da estrutura.
O princípio de funcionamento consiste na deformação que a mola sofre em razão da ação de uma força que é proporcional a esta força aplicada, sua intensidade é indicada na graduação existente na estrutura (dinamômetro ideal).
2.5. Dilatômetro linear
O dilatômetro linear é um aparelho que permite medir o coeficiente de dilatação dos metais de modo muito preciso, através de um relógio comparador de precisão de 0,01 mm. Nos quais estão feitos os tubos por onde se faz
passar o vapor “d água” produzida pelo gerador de vapor na elevação da
temperatura.
Figura 2.8:
Esquema básico de um dinamômetro.
Figura 2.9:
2.6. Calorímetro
A fim de estudar as trocas de calor entre dois ou mais corpos, principalmente quando um deles está no estado líquido, é conveniente ter um recipiente adequado, que permita obter, de forma direta ou indireta, o valor das quantidades de calor trocadas entre os corpos. A esse tipo de recipiente, que facilita o contato térmico entre os corpos e dificulta as trocas de energia térmica com o meio externo, damos o nome de calorímetro.
Sendo assim, geralmente podemos dizer que todo recipiente isolado termicamente do ambiente externo é um calorímetro. O calorímetro pode ser usado para a determinação do calor específico das substâncias. Geralmente despeja-se água no seu interior e, após um curto intervalo de tempo, estando o sistema em equilíbrio térmico, coloca-se um corpo que se quer estudar dentro da água, com temperatura inicial diferente do sistema água-calorímetro. A figura abaixo mostra um exemplo básico de um calorímetro.
3. MEDIDAS, INCERTEZAS E DESVIOS
Em qualquer medida de uma grandeza física há sempre presença de fatores aleatórios que introduzem erros nas medições. Cabe ao pesquisador determinar as principais fontes de erros durante a medição e reduzir ao máximo a sua importância. Por exemplo, ao realizar medição de massa com uma balança, as correntes de ar ou vibrações podem alterar o valor real da massa de um objeto. Contudo, esses dois valores específicos podem ser reduzidos ou praticamente eliminados colocando-se a balança numa mesa aprova de vibrações e protegendo-se a balança em uma caixa de vidro ou mesmo em vácuo quando se desejar alta precisão.
3.1. Erros de medida
Como todo processo de medida possui uma incerteza intrínseca, chamada comumente de erro, nunca saberemos dizer se o valor que foi medido é exatamente o verdadeiro. Para saber avaliar de que ordem é o erro, devemos notar que existem três fontes fundamentais de erro:
- Erros Grosseiros: são cometidos por imperícia do operador, como por exemplo, em erros de leitura ou pelo próprio desconhecimento do método experimental ou do uso dos instrumentos.
- Erros Sistemáticos: são cometidos de forma idêntica durante o experimento, tipicamente causados por uma limitação do método de medida, do uso de fórmulas teóricas aproximadas, má calibração ou até mesmo mal funcionamento dos instrumentos utilizados. Esse tipo de erro torna o valor da medida menos exato, embora em alguns casos possa ser bastante preciso. - Erros Estatísticos: estes são os erros mais importantes de analisar. São causados por mudanças aleatórias, não controladas, nas condições do processo de medida incluindo o operador, os instrumentos, o ambiente do experimento e o próprio sistema físico. Estes erros são inevitáveis, mas pela sua natureza aleatória é possível definir estratégias experimentais para minimizá-los e para estimar o quanto influenciam na confiabilidade do resultado numérico.
3.2. Algarismos significativos
devemos considerar para nossa medida, visto que se desprezarmos a fração contida no intervalo entre os dois valores, aproximando a medida, poderemos estar perdendo importantes informações. A fração de milímetro que deverá ser acrescentada a 14,3cm, terá de ser avaliada, pois a régua não apresenta divisões inferiores a 1 mm. Esta avaliação pode ser feita imaginando o intervalo entre as duas medidas, (14,3cm e 14,4cm) subdivido em partes iguais, de modo que a fração de milímetro acrescentada a 14,3cm poderá ser obtida com razoável aproximação. Na figura podemos avaliar a fração mencionada como sendo 5 décimos de milímetro. Assim, nossa medida poderia ser expressa como 14,35cm.
Observe agora que os algarismos 1, 4 e 3 foram obtidos diretamente da leitura da escala da régua, são os algarismos corretos. Por outro lado, o algarismo 5 foi avaliado, isto é, não temos certeza sobre o seu valor e outra pessoa poderia avaliá-lo como sendo 4 ou 6, por exemplo. Por isto, este algarismo avaliado é denominado algarismo duvidoso ou algarismo incerto.
Devemos notar que não teria sentido tentar avaliar um segundo algarismo, pois ele não seria significante.
Assim, nos resultados de uma medida devem figurar somente algarismos significativos corretos e o primeiro algarismo avaliado. Podemos definir: algarismos significativos de uma medida são seus algarismos corretos (a contar do primeiro diferente de zero) e o seu primeiro algarismo duvidoso.
Figura 1.1:
O algarismo zero só é significativo se estiver situado à direito de um algarismo significativo. Os exemplos mostrados a seguir, mostram como definir os algarismos significativos em medidas que contenham o número zero.
1) 27,40cm tem quatro algarismos significativos: 2,7,4 e 0;
2) 0,0027cm tem 2 algarismos significativos: 2 e 7, pois o zero encontra-se à esquerda do primeiro algarismo significativo, 2;
3) 27cm tem dois algarismos significativos; 4) 27,0cm tem 3 algarismos significativos.
Note a diferença entre o terceiro e o quarto exemplos: no terceiro, o algarismo 7 é duvidoso, enquanto que no quarto ele é correto, sendo duvidoso o zero.
A este ponto, perguntamos o que ocorre quando realizamos uma mudança de unidades, isto é, como explicitar a medida corretamente, sem mudar o número de algarismos significativos. Para verificar o procedimento correto, tomemos como exemplo uma medida de distância entre dois pontos de 27,5m, que tem três algarismos significativos. Podemos expressar a mesma medida em centímetros como 2750 cm. Poderia então parecer que o número de significativos aumentou de três para quatro. A forma correta de expressar a mesma medida em unidade diferente, mantendo o mesmo número de algarismos significativos é usando potência de 10. Podemos assim escrever a medida como:
27,5 × 102𝑐𝑚 𝑜𝑢 2,75 × 103𝑐𝑚
que continuam contendo três algarismos significativos.
Com respeito ao algarismo avaliado ou duvidoso, sua determinação depende da menor divisão da escala da régua. Esse limiar depende do material com que a régua é feita, das condições de uso, como por exemplo, temperatura, e do processo de fabricação.
usadas, dependendo da experiência e sensibilidade do experimentador. Deve-se lembrar que em qualquer processo de medida experimental, o mais difícil não é medir, mas avaliar a incerteza na medida obtida.
Devemos explicitar o procedimento de avaliação do algarismo duvidoso, quando apresentamos o resultado.
Esta discussão, válida para medidas de distância com uma régua, pode ser estendida para outros instrumentos.
3.3. Arredondamento e truncamento
Quando estamos tratando com um pequeno número de valores que contém mais algarismos significativos que aqueles necessários, devemos estar atentos para efetuar o procedimento correto a fim de expressarmos o resultado final com o número conveniente de algarismos significativos. Tomemos como exemplo, a medida de comprimento de 27,327 m a qual possui cinco algarismos significativos. Vejamos como expressar este resultado com diferentes aproximações.
27,33 m – expresso com quatro algarismos significativos; 27,3 m – expresso com três algarismos significativos.
No primeiro caso, o algarismo da segunda casa decimal, passou de 2 para 3; enquanto que no segundo caso, o valor do algarismo da primeira casa foi mantido.
Se no primeiro caso tivéssemos apenas cortado o algarismo 7, obteríamos 27,32 m e, teríamos realizado um truncamento. Examinando o desvio entre os valores arredondado (27,33 m) e truncado (27,32 m) e o valor original 27,327 m,
27,327 − 27,32 = 0,007𝑚 27,33 − 27,327 = 0,003𝑚
Verificamos que no segundo caso, obtemos um desvio menor. Por este motivo, ao arredondar um número, usa-se a seguinte regra:
superior a 5; quando o primeiro algarismo descartado for exatamente 5 é indiferente acrescentar ou não uma unidade ao último algarismo mantido.
3.4. Operações com algarismos significativos
3.4.1. Adição e subtração
No caso em que tratamos com um pequeno número de parcelas, podemos realizar estas operações de duas maneiras: 1o) Verificamos o termo que contém o menor número de algarismos após a vírgula, então, arredondamos todos os outros termos para que contenham o mesmo número de casas decimais. Este procedimento facilita o trabalho quando, por exemplo, realizamos as operações usando uma máquina de calcular com recursos limitados ou mesmo sem o auxílio da mesma. 2o) Consideramos todos os algarismos presentes em cada uma das parcelas e realizamos as operações.
Em ambos os casos o resultado final deve ser arredondado de forma a conter tantas casas decimais quanto aquelas da parcela de menor número de casas decimais.
Exemplo: Vamos adicionar 2327,51 ; 0,0568 e 27,689.
1o caso: Realizando os arredondamentos pertinentes e procedendo a adição.
Resultado final: 2355,27
2ocaso: Realizando as operações levando em conta todos os algarismos em cada uma das parcelas.
Resultado final: 2355,26
envolvem um grande número de operações e parcelas e decidimos arredondar cada uma das parcelas antes das operações, devemos usar no mínimo, um algarismo a mais que aquele contido na parcela com menor número de casas decimais, assegurando assim uma melhor precisão do resultado final.
3.4.2. Multiplicação e divisão
Nestes casos primeiramente, realiza-se a operação de divisão ou multiplicação levando-se em conta todos os algarismos significativos de todas as parcelas. O resultado da operação deve finalmente ser arredondado, de forma a ser expresso com tantos algarismos significativos quantos aqueles da parcela que contém o menor número de algarismos significativos. Veja o exemplo a seguir:
0,045 é a parcela com menor número de algarismos significativos (dois), portanto o resultado final será: 1,2.
3.5. Método dos Mínimos quadrados
Suponha que, em uma experiência, sejam medidos N valores xi e yi. Em física experimental, é geralmente conveniente determinar uma função teórica que represente, o mais fielmente possível, o conjunto de dados experimentais. Não podemos simplesmente unir os pontos obtidos ou traçar uma curva que
“julgamos” ser a que melhor se ajusta aos dados experimentais em questão.
Devemos usar uma técnica que independa de critérios pessoais na determinação da função representativa dos dados experimentais.
Uma técnica de ajuste de dados, de uso frequente em física, é o chamado método dos mínimos quadrados. Esta técnica é aplicável a diversos tipos de distribuição, seja ela linear, polinomial, exponencial, etc. Em nossa análise, nos restringiremos ao caso mais simples, isto é, suporemos que nossa distribuição seja caracterizada por um comportamento linear.
O método dos mínimos quadrados estabelece que a função linear y’ =
que minimiza a soma dos quadrados dos desvios ∑ (𝑦𝑁 1− 𝑦1′)2
𝑖=1 entre o valor
experimental y e o valor dado pela mesma, y’.
Fórmula para coeficientes angular e linear para o ajuste de uma reta y=mx+b:
𝑚 =𝑀𝑀𝑥𝑦
𝑥𝑥 [1] 𝑏 =
1
𝑁 (∑ 𝑦𝑖 − 𝑚
𝑁
𝑖=1
∑ 𝑥𝑖 𝑁
𝑖=1
) [2]
Onde os termos da eq. [1] são:
𝑀𝑥𝑦= ∑ 𝑥𝑖 𝑁
𝑖=1
. 𝑦𝑖 −𝑁 (∑ 𝑥1 𝑖 𝑁
𝑖=1
) (∑ 𝑦𝑖 𝑁
𝑖=1
) [3] 𝑀𝑥𝑥 = ∑ 𝑥𝑖2−𝑁 (∑ 𝑥1 𝑖 𝑁 𝑖=1 ) 2 𝑁 𝑖=1 [4]
E, além disso, fórmulas para o desvio padrão e erros associados aos coeficientes angular e linear respectivamente:
𝜎2 = 1
𝑁 − 1 ∑(𝑦𝑖− (𝑚𝑥𝑖 + 𝑏))
2
[5]
𝑁
𝑖=1
𝜀𝑚 = √ 𝜎 2
𝑀𝑥𝑥 [6] 𝜀𝑏 = √
𝜎2
𝑁𝑀𝑥𝑥∑ 𝑥𝑖 2 𝑁
𝑖=1
[7]
3.6. Incerteza nas medidas diretas
Não existem resultados experimentais sem incerteza: nunca deixe valores medidos sem a sua respectiva incerteza. Ao se fazer uma série de N medidas, os valores observados xi são utilizados para estimar o valor verdadeiro da grandeza física através do cálculo do valor médio
𝑥̅ = 1 𝑁 ∑ 𝑥𝑖
𝑁
𝑖=1
[8]
Figura 1.2:
Enquanto que a melhor estimativa para o erro estatístico é obtida do cálculo do desvio padrão da média
𝜎𝑠𝑡𝑎𝑡 = √𝑁(𝑁 − 1) ∑1 (𝑥𝑖 − 𝑥̅)2 𝑁
𝑖=1
[9]
Os experimentos de maior precisão são aqueles onde o erro estatístico é o menor possível. Contudo, um experimento bastante preciso não necessariamente corresponde a um experimento com muita exatidão: a presença de erros sistemáticos pode afastar todos os valores de xi do valor verdadeiro. Observe que na expressão [9], o erro estatístico depende inversamente do número de medidas N e, portanto, tende a ser reduzido quando N aumenta. Este comportamento pareceria indicar que podemos aumentar a precisão do experimento sem limites, simplesmente repetindo as medidas, o que é falso. Temos sempre que lembrar que a precisão da medida está limitada pela precisão dos próprios instrumentos. Portanto, precisamos também considerar o erro sistemático dos instrumentos
𝜎𝑠𝑦𝑠𝑡 = ∆𝑖𝑛𝑠𝑡 [10]
Finalmente, a incerteza em uma medida direta deve ser sempre calculada pela seguinte fórmula
𝜎 = √𝜎𝑠𝑡𝑎𝑡2 + 𝜎𝑠𝑦𝑠𝑡2 [11]
3.7. Incerteza nas medidas indiretas
Geralmente, se a medida indireta de uma grandeza física w é calculada em função de medidas diretas de outras grandezas físicas, ou seja,
𝑊(𝑥, 𝑦, 𝑧, … ) [12]
Então a incerteza σw também será determinada pelas incertezas das
demais grandezas σx, σy, σz,…
Se os erros nas variáveis x, y, z,… são completamente independentes
entre si, a incerteza na medida indireta é obtida pela equação
𝜎𝑤 = √(𝜕𝑤𝜕𝑥 ) 2
𝜎𝑥2+ (𝜕𝑤𝜕𝑦) 2
𝜎𝑦2+ (𝜕𝑤𝜕𝑧 ) 2
𝜎𝑧2+ ⋯ [13]
𝑉 = 𝜋𝑅2ℎ = 1
4 𝜋𝐷2ℎ [14]
Neste caso, iremos medir diretamente no laboratório a altura h e o diâmetro D da peça cilíndrica. Logo, expressão geral para o cálculo da incerteza na medida do volume é dada por
𝜎𝑉 = √(𝜕𝑉𝜕ℎ) 2
𝜎ℎ2+ (𝜕𝑉𝜕𝐷) 2
𝜎𝐷2 [15]
É facilmente verificado que as derivadas parciais são:
𝜕𝑉 𝜕ℎ =
1
4 𝜋𝐷2 𝑒 𝜕𝑉 𝜕𝐷 =
1
2 𝜋𝐷ℎ [16]
e, portanto, a incerteza final na determinação do volume é dada por
𝜎𝑉 = √(14 𝜋𝐷2) 2
𝜎ℎ2+ (1
2 𝜋𝐷ℎ)
2
𝜎𝐷2 [17]
Observe que se estivéssemos interessados no cálculo da densidade volumétrica dessa peça cilíndrica, teríamos que considerar uma outra medida direta, a massa. Para isso, considere a equação da densidade
𝜌 =𝑚𝑉 [18]
A partir da Eq.[13], verificamos que a incerteza será obtida através da relação
𝜎𝜌 = √(𝜕𝑚)𝜕𝜌 2
𝜎𝑚2 + (𝜕𝑉)𝜕𝜌 2
𝜎𝑉2 [19]
Onde σm é o erro sistemático da balança e σV é a incerteza no volume calculada pela Eq. [16]. Resta então determinar as derivadas parciais da densidade em função da massa e do volume,
𝜕𝜌 𝜕𝑚 =
1
𝑉 𝑒 𝜕𝜌 𝜕𝑉 = −
𝑚
𝑉2 [20]
E obter a expressão final para a incerteza no valor da densidade da peça cilíndrica medida
𝜎𝜌 = √𝜎𝑚 2
𝑉2 +
𝑚2𝜎𝑉2
3.8. Desvio
O desvio de uma medida é a diferença entre a medida e o valor médio encontrado para a série de medidas.
∆𝑥 = 𝑥𝑛− 𝑥̅ [22]
3.9. Desvio percentual
É o erro relativo expresso em percentual. Este desvio permite comparar a precisão das medidas:
∆𝑥% = 𝑥𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑜𝑥 − 𝑥̅
𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑜 × 100 [23]
4. ROTEIROS DAS PRÁTICAS
4.1. Mesa Giratória
a) Objetivos:
Determinar o Momento de Inércia, I, de uma Haste Cilíndrica.
b) Introdução Teórica:
Inércia, propriedade da matéria que faz com que ela resista a qualquer mudança em seu movimento. Esta propriedade é descrita com precisão na lei do movimento de Newton. A inércia de um objeto diante de uma translação é determinada por sua massa. Diante de uma rotação, a inércia do objeto é determinada por seu momento de inércia.
Em geral, um momento de inércia menor significa uma rotação mais fácil, deste modo, o momento de inércia de um corpo não é uma quantidade única e fixa. Se um objeto é girado em torno de eixos diferentes, também terá momentos de inércia diferentes, uma vez que a distribuição de sua massa em relação ao novo eixo é normalmente distinta do que era no anterior. A unidade SI para I é o kg m2.
c) Procedimento experimental:
1a Parte – Determinação do momento de Inércia da mesa giratória
1) Com o sistema ainda em repouso, determine a altura, H, do peso em relação ao solo.
2) Libere o sistema cronometrando o tempo gasto T, para que a altura H seja percorrida. O tempo T deve ser obtido através da média aritmética de 5 tomadas de tempo.
T1 T2 T3 T4 T5 Média
Tempo(Ti)
3) Substitua os valores obtidos na expressão e considerando g = 980 cm/s2:
Onde:
IM– Momento de Inércia da mesa; RM– Raio da mesa;
m – Massa do peso suspenso
M – Massa da roldana.
g – Aceleração da gravidade;
M H gT m R
IM M
2a Parte – Determinar o momento de inércia de uma haste cilíndrica oca
1) Coloque a haste sobre a mesa giratória, fazendo coincidir o centro de massa.
2) Mantenha a mesma altura H, e determine o novo tempo médio, T’.
T’1 T’2 T’3 T’4 T’5 Média
Tempo(T’)
3) Substitua os valores encontrados na expressão:
4) Comparar o valor obtido no item 3 com o valor teórico esperado:
𝐼
𝑡𝑒ó𝑟𝑖𝑐𝑜=
𝑚′𝐿2
12
Onde: m’ e L são respectivamente a massa e o comprimento da haste.
5) Comparar o Iteórico e Iexperimental, determinando erro percentual.
M M
al
Experiment M I
4.2. Hidrostática
a) Objetivo:
Determinar o empuxo sofrido por um corpo imerso em água.
b) Materiais utilizados:
- Cilindro metálico;
- Béquer;
- Dinamômetro.
c) Introdução Teórica:
O princípio de Arquimedes foi criado pelo filósofo, matemático, físico, engenheiro, inventor e astrônomo grego Arquimedes (287 a.C. - 212 a.C.) por ter descoberto como calcular o empuxo. Ele descobriu que todo o corpo imerso em um fluido em equilíbrio, dentro de um campo gravitacional, fica sob a ação de uma força vertical, com sentido oposto a este campo, aplicado pelo fluido, cuja intensidade é igual à intensidade do Peso do fluido que é ocupado pelo corpo.
𝐸⃗ = 𝑚𝐹𝐷. 𝑔 [26]
Onde:
𝐸⃗ - Empuxo (N);
𝑚𝐹𝐷 - Massa de fluido deslocado (kg);
𝑔− Aceleração da gravidade (m/s2).
Sabemos também que a essa massa de fluido pode ser escrita em função do volume deslocado (𝑉𝐹𝐷) e de sua densidade (𝜌𝐹):
𝑚𝐹𝐷 = 𝜌𝐹. 𝑉𝐹𝐷 [27]
Juntando-se as equações [26] e [27] obtém:
𝐸⃗ = 𝜌𝐹. 𝑉𝐹𝐷. 𝑔 [28]
Por causa desta forca de empuxo que ao imergimos algum objeto dentro de uma piscina ou bacia, por exemplo, que temos a impressão de que ele esta
mais leve. Esse peso que sentimos e’ o chamado peso aparente (𝑃⃗ 𝐴) e pode
ser definido pela diferença do peso (𝑃⃗ ) fora do fluido menos o empuxo.
d) Procedimento experimental:
1) Pese o cilindro metálico e determine o seu volume.
2) Mergulhe completamente o cilindro em água, determinando o seu peso aparente e o empuxo sofrido por ele.
3) Determine o empuxo sofrido pelo cilindro, usando o princípio de Arquimedes.
4) Determine o erro experimental entre os valores obtidos nos itens 2 e 3. 5) Faça um esquema do procedimento. Desenhe as forças envolvidas. 6) Resultados – Conclusões.
4.3. Sistema massa-mola
a) Objetivos:
Verificar os parâmetros que influem na frequência de oscilação de um Movimento Harmônico Simples (MHS).
b) Introdução Teórica:
Muitos dos movimentos oscilatórios que conhecemos surgem a partir da existência de forças restauradoras que agem sempre contra o movimento, ou a alguma força atuante, para trazer ou manter o sistema em certo estado de equilíbrio. O sistema massa-mola se enquadra nesses padrões, e como todos os sistemas que se enquadra, ela também obedecem a lei de Hooke: F =-k X, sendo a massa da mola, uma massa desprezível em relação a massa ligada a mola, e por isso sendo desconsiderada. . Vamos analisar especificamente o sistema massa-mola. O sistema consiste em um corpo com massa de valor m, presa por uma das extremidades a certa mola de fator de restauração k (também chamado constante de deformação), enquanto a outra extremidade está ligada a um ponto fixo. O estado de equilíbrio pode ser chamado de ponto 0, e sempre que tem-se uma tentativa de retirar o sistema desse ponto, atua a força restauradora, que tenta recompor o sistema a esse estado inicial. À medida que afastamos o bloco de massa m da posição de equilíbrio, a força restauradora vai aumentando (estamos tomando o valor de X crescendo positivamente à direita do ponto de equilíbrio e vice-versa), se empurrarmos o bloco de massa m para a esquerda da posição 0, uma força de sentido contrário e proporcional ao deslocamento X surgirá tentando manter o bloco na posição de equilíbrio 0. Hooke definiu a lei: "A intensidade da força elástica (Fel) é proporcioná-la deformação X".
1) Determinação estatística da constante elástica, k, da mola:
Usando três pesos diferentes, montando o esquema da figura acima, meça o deslocamento alcançado (com cada peso) a partir da posição de origem. Considere as forças atuantes no corpo suspenso na mola e faça um esquema das forças que agem no corpo. No estado de equilíbrio, escreva a lei de Newton entendendo que a tensão da mola é dada pela lei de Hooke.
Esta equação permitirá determinar experimentalmente o valor k? Como?
2) Obtenha o valor médio de k.
No pré-relatório, realize um esquema das forças na posição de equilíbrio, escreva a equação de equilíbrio de forças, e confeccione a tabela para obter o valor médio de k.
3) Monte o esquema da figura 1, com m = 20 g.
4) Faça oscilar com amplitude inicial de 2 cm, similar a Fig. 2. Meça o tempo de 10 oscilações e determine a frequência experimental, f experimental.
5) Calcular a frequência teórica, f teórico, usando a fórmula:
Como esta formula é obtida?
6) Determine o desvio percentual; Determine os erros no resultado final considerando a propagação de erros.
7) Repita os itens de 3.1 à 3.6 com amplitude inicial igual a 1 cm.
Compare resultados e conclua.
8) Repita os itens de 1) à 6) com m = 10 g.
4.4. Pêndulo Simples
a) Objetivos:
Determinar o valor da aceleração da gravidade local, utilizando um pêndulo simples.
b) Introdução Teórica:
Um pendulo simples, consta de um corpo de massa m, suspenso por um fio de massa depressível. A massa então é livre para oscilar em um plano, à esquerda e à direita de uma linha vertical que passa através do ponto em que a extremidade superior do fio está fixada.
As forças que agem sobre o corpo são: seu peso, P =mg, e a Tensão “T”
no fio. Após afastar o corpo da posição de equilíbrio, um ângulo pequeno, e soltá-lo, ele inicia um movimento oscilatório devido a componente tangencial da força P, chamada de força restauradora que leva o pendulo de volta a posição central.
Decompomos mg numa componente radial “mg cos θ” e na componente “mg sen θ” que é tangente a trajetória da partícula. Esta componente tangencial
é à força de restauração, porque sempre age em oposição ao deslocamento da partícula, de forma a trazê-la de volta à sua localização central, a posição de
equilíbrio (θ = 0) onde estaria em repouso, se não estivesse oscilando.
Escreve-se a força de restauração (F) e a tensão (T) como:
𝐹 = −𝑚𝑔 𝑠𝑒𝑛𝜃 [30] 𝑇 = 𝑚 𝑔 𝑐𝑜𝑠𝜃 [31]
Onde o sinal negativo indica que F age em oposição ao deslocamento.
Como o ângulo θ é pequeno, então sen θ será quase igual a θ em radianos. O
𝐹 ≅ −𝑚𝑔𝜃 = −𝑚𝑔𝑠𝐿 = − (𝑚𝑔𝐿 ) 𝑠 [32]
Analisando a equação da lei de hooke:
𝐹 = −𝑘𝑥 [33]
Comparando as duas, temos o deslocamento agora sendo o comprimento do arco s em lugar de x. Então, se um pendulo simples oscila com pequenas amplitudes, se comporta como um oscilador linear. Aqui a
amplitude do movimento é a amplitude angular θmax, o ângulo máximo de
oscilação. E a constante k é mg/L, a constante elástica efetiva da “mola gravitacional” que associamos ao pendulo. Então substituindo mg/L por k na
equação, do período do oscilador linear:
𝑇 = 2𝜋√𝑚𝑘 → 𝑇 = 2𝜋√𝑚𝑔𝑚 𝐿
⁄ → 𝑇 = 2𝜋√ 𝐿
𝑔 [34]
Na área de física, é chamado de período o tempo necessário para que um movimento realizado por um corpo volte a se repetir. Por exemplo, em um relógio de pêndulo, o período do pêndulo é determinado pelo tempo que este leva para realizar o movimento de ida e de volta. Nota-se que, depois deste período, o pêndulo fará o mesmo movimento novamente, ou seja, se repetirá. O período é usualmente representado pela letra T. O inverso do período é chamado de frequência.
𝑓 =1
𝑇 [35]
c) Procedimento experimental:
1. Monte o esquema da Figura abaixo usando iniciando por um comprimento da linha L = 60 cm e use a massa.
2. Faça oscilar o pêndulo e meça o tempo de 10 oscilações.
3. Complete a tabela, para outros 9 comprimentos do fio.
𝑦𝑖 = 𝑓𝑖2 𝑥𝑖 = 1 𝐿⁄ 𝑖 𝑦𝑖2 𝑥𝑖2 𝑥𝑖. 𝑦𝑖 [𝑦𝑖− (𝑚𝑥𝑖+ 𝑏)]2
∑ 𝑦𝑖 ∑ 𝑥𝑖 ∑ 𝑦𝑖2 ∑ 𝑥𝑖2 ∑ 𝑥𝑖. 𝑦𝑖 ∑[𝑦𝑖− (𝑚𝑥𝑖+ 𝑏)]2
𝑀𝑥𝑥 𝑀𝑥𝑦 𝑚 𝑏 ∈𝑚 ∈𝑏
5) Utilizando o valor encontrado pelo método de ajuste de mínimos quadrados, determine o valor experimental, g, para a aceleração da gravidade, através da formula [34] , usando [35].
Pode escrever a equação que será utilizada?
6) Faça um gráfico de (f2) versus (1/L) , dados da Tabela. Neste mesmo gráfico faça o gráfico da reta obtida pelo método de ajuste. Conclua?
7) Calcule os erros e compare com o valor obtido no observatório em Engenheiro passos, que corresponde a g = 979,789 cm/s.
8) Destaque que erros experimentais acredita que acontecem.
4.5. Pêndulo Físico
a) Objetivo:
Determinar o momento de inércia, I, de um corpo rígido em relação a um eixo qualquer, usando um Pêndulo Físico.
b) Introdução teórica:
Para os pêndulos físicos temos inicialmente o mesmo principio de funcionamento dos pêndulos simples. A força que age sobre o centro de massa do corpo é seu peso “mg”. A componente tangencial a trajetória “mg sen θ” do
peso é a força de restauração que leva o pendulo de volta a posição central. Logo, o torque restaurador será:
𝜏 = −𝑑(𝑚𝑔 𝑠𝑒𝑛𝜃) [36]
Temos também a Segunda lei de Newton para rotações que nos dá a
aceleração angular do pêndulo (α) e o momento de inércia do corpo (I):
𝜏 = 𝐼𝛼 [37]
O ângulo θ é muito pequeno e se aproxima de seu seno em radianos,
além disso, igualando as equações [36] e [37] temos:
𝐼𝛼 = −𝑑(𝑚𝑔 𝑠𝑒𝑛𝜃) ↔ 𝛼 = −𝑚𝑔𝑑𝐼 𝜃 [38]
A aceleração para o movimento harmônico simples é descrita da seguinte forma:
𝑎 = −𝜔2𝑥 [39]
Podemos obter uma nova expressão para a frequência angular (𝜔) ao observar as seguintes semelhanças entre as equações [38] e [39] onde ambas estão relacionadas à aceleração do corpo:
𝜔2=𝑚𝑔𝑑
𝐼 ↔ 𝜔 =√𝑚𝑔𝑑𝐼 [40]
Lembrando também que a frequência angular (𝜔) é descrita como:
𝜔 = 2𝜋𝑓 [41]
Igualando as equações [40] e [41] temos:
2𝜋𝑓 = √𝑚𝑔𝑑
𝐼 ↔ 𝑓 = 1
c) Procedimento experimental:
1) Determine o comprimento, L, e a massa, m, de uma haste grande. 2) Monte o esquema com o eixo de rotação na extremidade superior da
haste do item anterior.
3) Coloque o pêndulo para oscilar, meça o tempo de 10 oscilações e determine a freqüência, usando a expressão:
4) Utilizando o valor encontrado no item anterior, determine o valor experimental, I experimental, para o momento de inércia da haste, através da equação [42] *.
* Onde d é a distância entre o eixo de oscilação e o centro de massa da haste. 5) Repita 5 vezes o item 3, a fim de determinar um valor médio para a
freqüência f. Este deve ser o valor usado na expressão do item 4.
6) Calcule o erro percentual entre o valor de I obtido no item 4 e o valor teórico. Calcule I teórico usando o Teorema dos Eixos Paralelos:
tempo oscilações n
f
o
erimental
exp [43]
Iteórico = ICM + md2 [44]
𝐼𝐶𝑀=𝑚𝐿 2
3 [45]
4.6. Dilatação linear dos sólidos
a) Objetivos:
Determinar o coeficiente de dilatação linear.
b) Introdução Teórica:
A maioria dos materiais se expande quando a temperatura aumenta desde que este aumento de temperatura não produza uma mudança de fase. Vejamos se podemos entender por que isto ocorre. Os átomos de um sólido cristalino se mantêm coesos num arranjo tridimensional, chamado rede cristalina, sob ação de forças Inter atômicas semelhantes às exercidas por molas. Os átomos vibram, em torno de suas posições de equilíbrio na rede, com uma amplitude que depende da temperatura. Quando a temperatura aumenta, a amplitude média de vibração dos átomos aumenta também, e isto leva a um aumento da separação média entre eles, produzindo a dilatação.
Suponha uma barra de comprimento “L”, cuja temperatura variou de uma quantidade “∆T”. Se a variação de temperatura “∆T” não é muito grande, a variação de comprimento (dilatação) ”∆L” é proporcional ao comprimento “L” e
à variação de temperatura “∆T”. Matematicamente, isto pode ser expresso
como:
∆L = α L0∆T [46]
onde “α” é conhecido como o coeficiente linear de dilatação térmica. O valor de
“α” muda de material para material. A unidade de medida de “α” é o grau
Celsius recíproco (°C-1).
O valor de “α”, para um dado material, só é constante dentro de uma faixa de temperatura, sendo esta a razão pela qual “∆T” não pode ser muito
grande.
Nesta experiência, vamos medir o coeficiente linear de dilatação térmica
faixa de temperatura em que o experimento será realizado o valor de “α” é
constante.
Embora tenhamos nos concentrado na análise de uma única dimensão de um corpo sólido, a equação acima é válida para as outras duas dimensões também, de modo que a expansão térmica de um sólido é semelhante a uma ampliação fotográfica tridimensional.
Esta lei de dilatação linear é valida apenas em um intervalo de
temperatura muito limitado, já que “α” varia com a temperatura. Caso “∆T” seja
grande, outras potências da temperatura devem ser consideradas:
LT = L0( 1 + α1T + α2T + α3T + ... ) [47]
onde Lo e o comprimento do material a 0° e os coeficientes são determinados experimentalmente.
c)Procedimento experimental:
1) Meça o comprimento da haste metálica.
2) Zere o dilatômetro, depois de encaixar a haste e a mangueira, se não estiver já com vapor de água saindo.
3) Acenda o bico de Bunsen e observe o dilatômetro, e meça a temperatura do vapor da água saindo.
4) Anote sua leitura, ao estabilizar.
5) Com os valores anotados determine o coeficiente de dilatação linear. 6) Repita o procedimento com as outras duas hastes.
7) Calcule propagação de erros.
Observações:
a) Temperatura inicial = Temperatura ambiente b) Temperatura final dado experimental c) Alguns valores de :
4.7. Calorímetro e calor específico
a) Objetivos:
Determinar a constante do calorímetro e o calor específico de um material.
b) Fundamentação Teórica:
Quando são colocados em contato dois ou mais corpos que se encontram em diferentes temperaturas, observa-se que, após certo intervalo de tempo, ocorre o equilíbrio térmico. Durante esse processo, há uma transferência de energia térmica dos corpos de maior temperatura para os de menor temperatura. O estudo feito da troca de calor entre os corpos foi realizado em um calorímetro, que é um recipiente vedado, com a função de não deixar ter trocas de calor entre o objeto de estudo e o meio ambiente. Durante esse processo de troca de calor, a quantidade de calor (Q) transferida
é proporcional à massa (m) do corpo e a variação da temperatura (∆T).
Algebricamente temos:
𝑄 = 𝑚𝑐∆𝑇 [48]
Onde:
c =é o calor específico da substancia. m =é a massa do objeto.
∆T =é a variação de temperatura.
Vale lembrar também que podemos definir a capacidade calorífica do corpo, como sendo:
𝐶 = 𝑚𝑐 [49]
Sabendo que dentro de um calorímetro, os corpos colocados trocam calor até atingir o equilíbrio térmico e considerando as quantidades de calor trocadas pelo calorímetro, pela água e pelo corpo x.
a) Como temos um calorímetro não ideal temos que considerá-lo ao realizar o experimento. Sabendo que o calor não se perde e é transferido de um corpo para outro:
𝑄𝑟𝑒𝑐𝑒𝑏𝑖𝑑𝑜 = 𝑄𝑐𝑒𝑑𝑖𝑑𝑜
𝑄𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜+ 𝑄𝐻2𝑂 𝑓𝑟𝑖𝑎 = 𝑄𝐻2𝑂 𝑞𝑢𝑒𝑛𝑡𝑒
(𝐶 × ∆𝑇𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜) + (𝑚𝐻2𝑂 𝑓𝑟𝑖𝑎× 𝑐𝐻2𝑂× ∆𝑇𝐻2𝑂 𝑓𝑟𝑖𝑎) = (𝑚𝐻2𝑂 𝑞𝑢𝑒𝑛𝑡𝑒× 𝑐𝐻2𝑂× ∆𝑇𝐻2𝑂 𝑞𝑢𝑒𝑛𝑡𝑒)
𝐶 =(𝑚𝐻2𝑂 𝑞𝑢𝑒𝑛𝑡𝑒× 𝑐𝐻2𝑂× ∆𝑇𝐻2𝑂 𝑞𝑢𝑒𝑛𝑡𝑒) − (𝑚𝐻2𝑂 𝑓𝑟𝑖𝑎× 𝑐𝐻2𝑂× ∆𝑇𝐻2𝑂 𝑓𝑟𝑖𝑎)
Onde:
∆𝑇𝐻2𝑂 𝑓𝑟𝑖𝑎 = ∆𝑇𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜= (𝑇3− 𝑇1)
∆𝑇𝐻2𝑂 𝑞𝑢𝑒𝑛𝑡𝑒 = (𝑇3− 𝑇2)
b) Calculando o calor específico do material imerso no calorímetro, pelo mesmo princípio acima:
Onde:
∆𝑇𝐻2𝑂 𝑓𝑟𝑖𝑎 = ∆𝑇𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜= (𝑇6− 𝑇4)
∆𝑇𝑐𝑜𝑟𝑝𝑜 = (𝑇6− 𝑇5)
c) Procedimento:
1) Coloque 125 g de água no calorímetro, aguarde o equilíbrio térmico e meça a temperatura do sistema (𝑇1).
2) Coloque 100 g de água no béquer e aqueça até a ebulição (𝑇2), despeje-a no calorímetro, aguarde o equilíbrio térmico e meça a temperatura do sistema (𝑇3).
3) Determine a constante do calorímetro (𝐶), aplicando a lei zero da termodinâmica, usando a equação [50].
4) Despeje toda a água do calorímetro fora.
5) Coloque novamente 125 g de água a temperatura ambiente no calorímetro, aguarde o equilíbrio térmico e meça a temperatura do sistema (𝑇4).
6) Pese o corpo a ser colocado na água.
7) Coloque o corpo em água no béquer e aqueça-os até a ebulição (𝑇5).
𝑄𝑟𝑒𝑐𝑒𝑏𝑖𝑑𝑜 = 𝑄𝑐𝑒𝑑𝑖𝑑𝑜
𝑄𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜+ 𝑄𝐻2𝑂 𝑓𝑟𝑖𝑎 = 𝑄𝑐𝑜𝑟𝑝𝑜
(𝐶 × ∆𝑇𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜) + (𝑚𝐻2𝑂 𝑓𝑟𝑖𝑎× 𝑐𝐻2𝑂× ∆𝑇𝐻2𝑂 𝑓𝑟𝑖𝑎) = (𝑚𝑐𝑜𝑟𝑝𝑜× 𝑐𝑐𝑜𝑟𝑝𝑜× ∆𝑇𝑐𝑜𝑟𝑝𝑜)
𝑐𝑐𝑜𝑟𝑝𝑜 = (𝐶 × ∆𝑇𝑐𝑎𝑙𝑜𝑟í𝑚𝑒𝑡𝑟𝑜) + (𝑚𝑚 𝐻2𝑂 𝑓𝑟𝑖𝑎× 𝑐𝐻2𝑂× ∆𝑇𝐻2𝑂 𝑓𝑟𝑖𝑎)
Anotações:
8) Depois de entrado em ebulição, coloque o corpo no calorímetro. 9) Aguarde o equilíbrio térmico e meça a temperatura do sistema (𝑇6).
10) Calcule o calor específico do corpo (𝑐𝑐𝑜𝑟𝑝𝑜) utilizando a equação [51] e
compare-o com o valor teórico, obtenha o erro percentual.
Valores teóricos médios:
c ferro = 0,113 cal/g0C c latão = 0,094 cal/g0C c alumínio = 0,217 cal/g0C
OBS.:
1) No item 3 do procedimento, a quantidade de água pode ser qualquer, já que a água é usada unicamente para elevar a temperatura do bloco até aproximadamente 1000C.
2) Os valores dos calores específicos dados são para materiais sem mistura 3) Um valor incorreto da constante do calorímetro, determinada na prática
5. REFERÊNCIAS BIBLIOGRÁFICAS
1. http://www.cimm.com.br/portal/material_didatico/6571#.Vumx2ObW7Ks
2. http://www.infoescola.com/fisica
3. http://www.mundovestibular.com.br/articles
4. ‘’A Técnica de Ajustagem’’, Editora Hemus - 2004 - Tecnologia Mecânica.
5. http://www.industriahoje.com.br/o-que-e-um-paquimetro/
6. http://brasilescola.uol.com.br/fisica
7. J.H. Vuolo, “Fundamentos da Teoria de Erros”, São Paulo: Edgard Blucher
(1996).
8. Texto adaptado da Apostila “Laboratório de Física Experimental” da
Universidade Federal do ABC (UFABC).
9. Texto adaptado da Apostila “Laboratório de Física I” do Instituto de Física de
São Carlos da Universidade de São Paulo (IFSC-USP).
10. Texto adaptado da Apostila “Medidas diretas e propagação de erros".