Centro Universit´ario de Itajub´a
Engenharia de Produ¸c˜ao – Curso de F´ısica II Notas compiladas Adhimar
1
Ementa
• Movimento Harmˆonico Simples;
• Movimento ondulat´orio e som;
• Mecˆanica dos fluidos;
• Temperatura e Calor;
• Propriedades T´ermicas da Mat´eria;
• Primeira Lei da Termodinˆamica;
• Segunda lei da Termodinˆamica.
1.1
Bibliografia B´
asica
• HALLIDAY, DAVID; RESNICK, Robert. Fundamentos de f´ısica: Mecˆanica. 4a
ed. Rio de Janeiro: Livros T´ecnicos e Cient´ıficos, 1996. v.2. 330 p.
• TIPLER, PAUL A.. F´ısica para cientistas e engenheiros: mecˆanica, oscila¸c˜oes e ondas, termodinˆamica. 4. ed. Rio de Janeiro: Livros t´ecnicos e cient´ıficos, 2000. v.2. 651 p. ISBN 85-216-1214-1. 44
• SERWAY, RAYMOND A.. F´ısica : Para cientistas e engenheiros com f´ısica moderna. 3a
ed. Rio de janeiro: Livros T´ecnicos e Cient´ıficos, 1992. v.3. 428 p. ISBN 85-216-1074-2.
1.2
Bibliografia Complementar
• SHAMES, IRVING H.. Mecˆanica dos fluidos. S˜ao Paulo: Edgard Blucher, 1973. v.1. 192 p.
• VAN WYLEN, GORDON J.; SONNTAG, Richard E.. Fundamentos da termo-dinˆamica cl´assica. 2. ed. S˜ao Paulo: Edgard Bl¨ucher, 1976. 565 p.
• YOUNG, HUGH D.; FREEDMAN, Roger A.. F´ısica II: Termodinˆamica e ondas. 12. ed. S˜ao Paulo: Pearson, 2008. 329 p. ISBN 978-85–88639-33-1.
• LEE, JOHN F.; SEARS, Francis Weston. Termodinˆamica. Rio de Janeiro: Ao Livro T´ecnico, 1969. 667 p.
site <http://phet.colorado.edu/en/simulations/category/physics>
2
Movimento Harmˆ
onico Simples
O movimento Harmˆonico Simples - MHS ´e um movimento que descreve uma trajet´oria, e a partir de um certo instante come¸ca a repetir esta trajet´oria, ou seja, ´e mum movimento peri´odico. O MHS ´e um movimento peri´odico, e portanto o objeto passa pela mesma posi¸c˜ao depois de um per´ıodo T. No MHS definimos o per´ıodo, T, que ´e o tempo cor-respondente a um ciclo, sendo sua unidade no SI ´e o segundo e a frequˆencia, f, que ´e o n´umero de ciclos na unidade de tempo, com unidade no SI ´e o hertz. Sendo
T = 1
T. (1)
1 hertz=1 Hz=1 ciclo/s = 1 s−1
Outra grandeza ´util ´e a frequˆencia angular,ω que ´e 2π vezes a frequˆencia
ω = 2πf (2)
Um exemplo de MHS ´e um sistema Massa-Mola, apresentado na Figura 1
Figura 1: Sistema Massa-mola
Um objeto que se desloca em MHS tem a sua posi¸c˜ao descrita pela equa¸c˜ao
em que A ´e a amplitude de oscila¸c˜ao,ω ´e a frequˆencia angular de oscila¸c˜ao, (ωt+φ) ´e a fase e φ´e a constante de fase.
Quando a constante de fase assume o valorφ=−π/2 a equa¸c˜ao anterior, que descreve o movimento do corpo, tem a forma
x(t) = Asenωt (4)
No gr´afico da Figura 34 ´e mostrada a posi¸c˜ao em fun¸c˜ao do tempo para o MHS.
Figura 2: Gr´afico da posi¸c˜ao em fun¸c˜ao do tempo para o MHS
Como o movimento ´e peri´odico, teremos que as posi¸c˜oes se repetem depois de um tempo igual ao per´ıodo T , ou seja,
x(t) = x(t+T), (5)
logo,
x(t) =x(t+T) =x◦cos [ω(t+T) +φ] =x◦cos [(ωt+φ) +ωT], (6)
assim,
ωT = 2π, (7)
ou,
ω = 2π
T (8)
ou ainda,
ω = 2πν (9)
2.1
A velocidade no MHS
v(t) = dx
dt =−ωx◦sen(ωt+φ). (10)
Definido a amplitude da velocidade v◦ =ωx◦, temos
v(t) =−v◦sen(ωt+φ) (11)
2.2
A acelera¸c˜
ao no MHS
a(t) = dv
dt =−ωv◦cos (ωt+φ). (12)
Definindo a amplitude da acelera¸c˜aoa◦ =ωv◦ =ω
2
a(t) = −a◦cos [ωt+φ], (13)
ou ainda,
a(t) =−ω2
x(t). (14)
Para um sistema massa-mola que obede¸ca `a lei de Hooke e supondo que a resultante das for¸cas que atuam na massa ´e a for¸ca restauradora da mola,temos
F = ma (15)
= −mω2
x (16)
−kx = −mω2
x, (17)
assim,
k=mω2
⇒ω= r
k
m ⇒T = 2π
r
m
k (18)
2.3
Pˆ
endulo Simples
O Pˆendulo simples (Figura 3)´e composto por um objeto suspenso atrav´es de um fio de massa desprez´ıvel, e ele ´e posto a oscilar em torno de sua posi¸c˜ao de equil´ıbrio.
Figura 3: Ilustra¸c˜ao do pˆendulo simples
A for¸ca peso na dire¸c˜aox,Px´e a for¸ca de restaura¸c˜ao do movimento e componente da for¸ca peso perpendicular ao deslocamento ´e equilibrada pela tra¸c˜ao exercida pelo fico, de modo que
ou ainda,
−mgsenθ =md 2
S
dt2 (20)
em queS ´e o deslocamento medido ao longo do arco que descreve a oscila¸c˜ao, e o sinal negativo indica que a for¸ca age na dire¸c˜ao da posi¸c˜ao de equil´ıbrio.
Sabendo que
S =Lθ⇒ d 2
S dt2 =L
d2 θ
dt2, (21)
temos que
d2 θ dt2 +
g
Lsenθ= 0. (22)
Para pequenas oscila¸c˜oes do pˆendulo, podemos aproximar senθ =θ, e teremos ent˜ao
d2 θ dt2 +
g
Lθ = 0. (23)
Da Equa¸c˜ao 23, temos que a frequˆencia angular de oscila¸c˜ao do pˆendulo simples ´e
ω =
r
g
L ⇒T = 2π
q√
Lg (24)
e a solu¸c˜ao da Equa¸c˜ao 23 ser´a
θ(t) =Acos (ωt+δ). (25)
2.4
Movimento Harmˆ
onico Amortecido
Em nosso cotidiano os movimentos oscilat´orios tem dura¸c˜ao finita. Isso ocorre devido a atua¸c˜ao de for¸cas dissipativas tais como as for¸cas de atrito.
Uma for¸ca dissipativa pode ser descrita por
F =−bv, (26)
em que b ´e chamada de constante de amortecimento e v ´e a velocidade escalar. Para o sistema ilustrado na Figura 4, temos que a resultante das for¸cas que atuam no corpo de massa m ´e
X
F = ma (27)
−kx−bv = ma (28)
−kx−bdx
dt = m
d2 x
dt2 (29)
ou ainda,
d2 x dt2 +
b m
dx dt +ω
2
◦x= 0 (30)
em que ω◦ =p
k/m
Figura 4: Ilustra¸c˜ao do oscilador massa-mola amortecido.
x(t) =Cert, (31)
em que C e r s˜ao constantes a serem determinadas. Assim,
x′(t) = rCert (32)
x′′(t) = r2
Cert, (33)
logo, da Equa¸c˜ao 30, temos
r2
+ b
mr+ω 2
◦ = 0 (34)
r=− b 2m ±
s
b
2m
2
−ω2
◦ (35)
Para um movimento sub-amortecido
ω2 ◦ > b 2m 2 , (36) definimos ωA= s omega2 ◦− b 2m 2 (37) obtendo
r=− b
2m ±iωA. (38)
x(t) = e− bt
2m(A1eiωAt+A2e−iωAt) (39)
ou ainda,
x(t) = Ae−bt/2m
cos(ωAt+φ) (40)
O gr´afico da Equa¸c˜ao 40 ´e apresentado na Figura 5.
Figura 5: Gr´afico do movimento sub-amortecido.
Supondo que o movimento ´e super-amortecido,
ω2
◦ <
b
2m
2
, (41)
temos
ωB =
s
b
2m
2
+omega2
◦ (42)
obtendo obtendo
r=− b
2m ±ωA. (43)
A fun¸c˜ao x(t) ser´a
x(t) = e− bt
ou ainda,
x(t) = Ae−bt/2m
cosh(ωAt+φ) (45)
O gr´afico da Equa¸c˜ao 45 ´e apresentado na Figura 6.
3
Movimento ondulat´
orio e som
3.1
Tipos de ondas
Ondas mecˆanicas obedecem as leis de Newton, existem apenas em meio material (´agua, ar, etc.) e s˜ao familiares (som, ondas do mar, etc.).
Ondas eletromagn´eticas se propagam no v´acuo (c=299792458 m/s) alguns exemplos s˜ao a luz vis´ıvel, a luz ultravioleta, as ondas de r´adio e de televis˜ao, as micro-ondas, raios X e radares.
Ondas de mat´eria est˜ao associadas a el´etrons, pr´otons e outras part´ıculas elementares, e mesmo a ´atomos e mol´eculas.
3.2
Ondas transversais e longitudinais
Ondas transversais s˜ao aquelas em que a dire¸c˜ao de vibra¸c˜ao ´e perpendicular `a dire¸c˜ao de propaga¸c˜ao da onda (Figura 7).
Ondas Longitudinais ´e uma onda que vibra na mesma dire¸c˜ao em que se propaga (Fi-gura 7).
3.3
Comprimento de onda, frequˆ
encia, amplitude, fase e n´
umero
de onda
Seja a onda senoidal apresentada na Figura 8, se propagando no sentido positivo do exito x. Em um certo instante t o deslocamento y de um elemento da onda situado na posi¸c˜ao x ´e dado por
Figura 8: Ilustra¸c˜ao de uma onda senoidal.
y(x, t) = ymsen(kx−ωt) (46)
em que:
• ym ´e a amplitude da corda, ou ainda, o m´odulo do deslocamento m´aximo dos elementos
a partir da posi¸c˜ao de equil´ıbrio. Como ym ´e o m´odulo, ´e sempre uma grandeza positiva.
• kx−ωt ´e a fase da onda.
• λ ´e o comprimento da onda que ´e a repeti¸c˜ao da forma de onda (Figura 9). Para um instante t= 0, a Equa¸c˜ao 46 pode ser escrita da forma
y(x,0) = ymsenkx (47)
Por defini¸c˜ao, o deslocamento y ´e o mesmo nas duas extremidades do comprimento de onda, ou seja, no ponto x=x1 e x=x1+λ a amplitude y ´e a mesma. Assim
ymsenkx1 = ymsenk(x1+λ) (48)
Figura 9: Ilustra¸c˜ao de uma onda senoidal.
uma fun¸c˜ao seno repete quando seu argumento aumenta de 2π. Logo,
k = 2π
λ (50)
• k ´e o n´umero de onda, sua unidade no SI ´e o rad/m.
Per´ıodo T ´e o tempo que um elemento da onda leva para realizar uma oscila¸c˜ao completa (Figura 10).
Figura 10: Ilustra¸c˜ao de uma onda senoidal.
Fazendo x=0 na Equa¸c˜ao 46, temos
Aplicando a Equa¸c˜ao 10 `as extremidades do intervalo T (Figura 10), temos
−ymsenωt = −ymsenω(t+T) (52) = −ymsen(ωt+ωT) (53)
Esta equa¸c˜ao ´e satisfeita apenas se ωT = 2π, ou
ω = 2π
T (54)
• ω ´e a frequˆencia angular da onda, sua unidade no SI ´e o rad/s.
• f ´e a frequˆencia de um onda e ´e definida como 1/T e est´a relacionada com a frequˆencia angular atrav´es da equa¸c˜ao
f = 1
T =
ω
2π, (55)
sendo a unidade de frequˆencia no SI o Hertz (Hz) (1 Hz=1/s)
3.4
A velocidade de uma onda progressiva
Se quisermos calcular a velocidade co que uma onda se propaga devemos acompanhar um dado ponto dela, ou seja um ponto de fase constante
φ(x, t) =kx−ωt= constante. (56)
Derivando a Equa¸c˜ao 56 com rela¸c˜ao a t
kdx
dt −ω = 0 (57)
v = dx
dt = ω
k =
λ
T (58)
Exemplo
Uma onda que se propaga em uma corda ´e descrita pela equa¸c˜ao
y(x, t) = 0,00327sen(72,1x−2,72t), (59)
em que as constantes num´ericas est˜ao em unidades do SI. (a) Qual ´e a amplitude da onda? (b) Quais s˜aos o comprimento de onda, o per´ıodo e a frequˆencia? (8,71 cm, 2,31 s e 0,433 Hz) (c) Qual ´e a velocidade da onda? (0,0377 m/s) (d) Qual ´e o deslocamento y para x=22,5 cm e t=18,9 s? (1,92 mm)
3.5
Velocidade de uma onda em uma corda esticada.
TDcosθ
2−TEcos
θ
2 = 0 (60)
TDsenθ
2 +TEsen
θ
2 = F (61)
Figura 11: Ilustra¸c˜ao de uma onda para o c´alculo da velocidade.
Como a tens˜ao da esquerda ´e igual da direita, temos
2Tsenθ
2 =F. (62)
Considerando θ pequeno,temos
2Tsenθ 2 ≃2T
∆L
2R =T
∆L
R . (63)
Sabendo que,
Fc =mv2
/R, (64)
temos
T∆L
R =mv
2
/R, (65)
ou ainda,
v = s
T
µ (66)
em que µ=m/∆L´e a densidade linear da corda. Exemplo
3.6
Superposi¸c˜
ao de ondas
Suponha que duas ondas se propagam simultaneamente na mesma corda esticada. Sejam
y1(x, t) ey2(x, t) os deslocamentos. O deslocamento da corda quando as ondas se propagam
ao mesmo tempo ´e a soma alg´ebrica
y′(x, t) =y
1(x, t) +y2(x, t), (67)
Ondas superpostas somam algebricamente para produzir uma onda resultante ou onda total (Figuras 12 e 13).
Figura 12: Ilustra¸c˜ao da superposi¸c˜ao de ondas.
Figura 13: Ilustra¸c˜ao da superposi¸c˜ao de ondas.
3.7
Interferˆ
encia
3.7.1 Ondas no mesmo sentido
Vamos considerar duas ondas, sendo a primeira com constante de fase nula e a segundaφ
y1 = ymsen(kx−ωt) (68)
y2 = ymsen(kx−ωt+φ) (69)
Usando a identidade trigonom´etrica
senα+ senβ = 2sen
α+β
2
cos
α−β
2
A superposi¸c˜ao das ondas ´e
y(x, t) = y1(x, t) +y2(x, t) (71)
=
2ymcos φ 2 sen
kx−ωt+ φ 2
(72)
em que
2ymcos
φ
2
´e a amplitude da onda.
3.7.2 Ondas em sentido contr´ario
Considere duas ondas que se propagam em sentido contr´ario, dadas por
y1 = ymsen(kx−ωt) (73)
y2 = ymsen(kx+ωt) (74)
Usando a identidade trigonom´etrica 70, temos
y(x, t) = y1(x, t) +y2(x, t) (75)
= [2ymsen(kx)] cos(ωt) (76)
Esta n˜ao ´e uma onda progressiva, por´em ela oscila para cima e para baixo (Figura 20). Existem alguns pontos na corda onde a amplitude ´e m´axima. Eles s˜ao localizados quando kx assume valores m´ultiplos ´ımpares de π/2. Logo,
kx = π
2 ; 3π
2 ; 5π
2 (77)
= (2n+ 1)π 2 =
n+ 1 2
π para n= 0,1,2,3, .... (78)
e a posi¸c˜ao xpara os quais a amplitude ´e m´axima, fazendo k = 2π/λ,
xn=
n+ 1 2
λ
2 para n = 0,1,2,3, .... (79)
Por outro lado existem pontos em que a amplitude de oscila¸c˜ao ´e nula. Esses pontos s˜ao localizados quando kx´e m´ultiplo de π, ou seja,
kx= 0, π,2π, ... (80)
ou ainda,
kx=nπ (81)
para n = 0,1,2,3, ... e a posi¸c˜ao x para os quais a amplitude ´e nula
xn =nλ
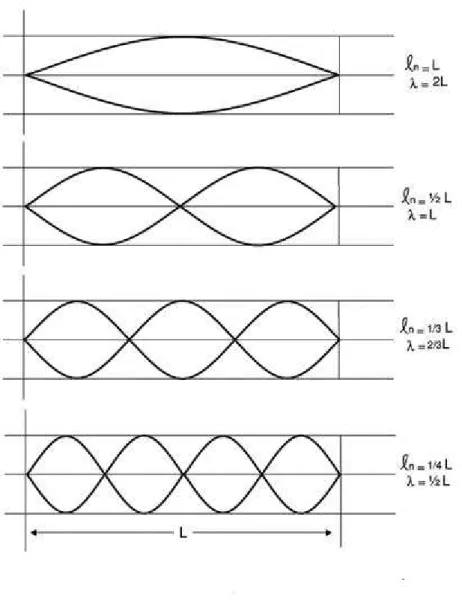
Figura 14: Ilustra¸c˜ao dos 4 primeiros harmˆonicos de uma onda estacionaria.
para n = 0,1,2,3, ...
Exemplo
Duas ondas progressivas iguais, que se propagam no mesmo sentido, est˜ao defasadas de π/2 rad. Qual ´e a amplitude da onda resultante em termos da amplitude comum ym
das duas ondas?
3.8
Ressonˆ
ancia
Ondas estacion´arias podem ser podem ser produzidas em uma corda atrav´es da reflex˜ao de ondas progressivas nas extremidades da corda. Se uma extremidade ´e fixa, deve ser a posi¸c˜ao de um n´o. Isso limita as frequˆencias poss´ıveis para as ondas estacion´arias em uma dada corda. Cada frequˆencia poss´ıvel ´e uma frequˆencia de ressonˆancia. Para uma corda de comprimento L comas extremidades fixas as frequˆencias de ressonˆancia s˜ao dadas pro
f = v
λ =n v
3.9
Velocidade do Som
Antes de obtermos a rela¸c˜ao para a velocidade do som vamos definir o m´odulo de elastidade volum´etrico, B, que ´e a propriedade que determina o quanto um elemento de um meio muda de volume quando ´e submetido a uma press˜ao,
B =− ∆P
∆V /V (84)
em queP ´e a press˜ao e ∆V /V ´e a varia¸c˜ao relativa de volume produzido por uma varia¸c˜ao de press˜ao.
Assim, temos que a velocidade do som em um meio de m´odulo de elasticidade vo-lum´etrica B e massa espec´ıfica ρ´e
v = s
B
ρ (85)
Em particular a velocidade do som no ar a 20◦ ´e de 343 m/s.
3.10
Propaga¸c˜
ao de ondas Sonoras
`A medida que uma onda sonora avan¸ca em um tubo cada elemento de volume do ar contido no tubo oscila em torno de sua posi¸c˜ao de equil´ıbrio (Figura 7.2).
Figura 15: Som de um alto-falante se propagando ao longo de um tubo.
Uma onda sonora progressiva s(x, t), se propagando no sentido positivo do eixo x, e expressa por
s(x, t) =Smcos(kx−ωt) (86)
Quando uma onda se propaga, a press˜ao do ar em qualquer posi¸c˜ao x varia senoidal-mente da forma
∆P(x, t) = ∆Pmsen(kx−ωt) (87)
em que ∆Pm ´e a varia¸c˜ao m´axima da press˜ao, que ´e dada por
∆Pm = (vρω)Sm (88)
3.11
Interferˆ
encia
Considere duas ondas sonoras iguais, S1 eS2 que se propagam no mesmo sentido, Figura
16.
Figura 16: Duas ondas sonoras iguais que se propagam no mesmo sentido.
Como elas s˜ao iguais elas est˜ao em fase e possuem o mesmo comprimento de onda. Suponha que a distˆancia at´e P ´e muito maior que distˆancia entre as fontes, de modo que podemos considerar que as ondas s˜ao aproximadamente paralelas.
Se as ondas percorrem distˆancias iguais para chegarem at´e o ponto P, estariam em fase, ou ainda, sofreriam uma interferˆencia totalmente construtiva. Por´em, na Figura 16
L1 ´e menor queL2.
A diferen¸ca de percurso pode significar que as ondas podem n˜ao estar em fase no ponto P. Sendo que a diferen¸ca de fase φ no ponto P depende da diferen¸ca
∆L|L2−L1| (89)
φ
2π =
∆L
λ (90)
φ = ∆L
λ 2π (91)
A interferˆencia ´e construtiva se φ for
φ = 0, 2π, 4π.... (92)
ou ainda,
φ=m(2π), (93)
para m = 0,1,2,3, ... Logo, a raz˜ao
∆L
λ = 0,1,2,3.... (94)
A interferˆencia ´e destrutiva se φ ´e m´ultiplo ´ımpar de π/2, ou seja,
φ = (2m+ 1)π (95)
para m = 0,01,2,3....Logo, a raz˜ao
∆L
λ = 0.5,1.5,2.5, ... (96)
Exemplo Na Figura 17, duas fontes pontuais S1 e S2, que est˜ao em fase separadas
por uma distancia D= 1,5λ, emitem ondas sonoras iguais de comprimento de onda λ. a) Qual ´e a diferen¸ca de percurso das ondas no ponto P1? Que tipo de interferˆencia ocorre
em P1? b) Quais s˜ao a diferen¸ca de percurso e o tipo de interferˆencia no ponto P2?
3.12
Batimento
Quando dois sons com frequˆencias muito pr´oximas chegam aos nossos ouvidos simultane-amente percebemos uma grande varia¸c˜ao na intensidade do som. Ele aumenta e diminui alternadamente, produzindo um batimento, que se repete com um intervalo dado pela diferen¸ca entre as duas frequˆencias originais (Figura 18).
Seja duas ondas
S1 = Smcos(omega1t) (97)
S2 = Smcos(omega2t) (98)
em que ω1 > ω2. A superposi¸c˜ao delas ´e dada por
Usando a identidade trigonom´etrica
cosα+ cosβ= 2 cos
1
2(α−β)
cos
1
2(α+β)
, (100)
temos que
S = 2Smcos
1
2(ω1−ω2)t
cos
1
2(ω1+ω2)t
. (101)
Definindo
ω′ = 1
2(ω1−ω2) (102)
ω = 1
2(ω1+ω2) (103)
podemos escrever
S(t) = [2Smcosω′t] cosωt (104)
Sendo que, um m´aximo de amplitude ocorre sempre que cosω′t ´e igual a 1 ou (-1), o
que ocorre duas vezes em cada repeti¸c˜ao da fun¸c˜ao co-seno. Logo, a frequˆencia angular de batimento ´e
ωbat = 2ω′ (105)
ou seja,
ωbat = 2ω′ = 2
1
2(ω1−ω2) = ω1−ω2 (106) como ω = 2πf, temos que fbat =f1−f2
3.13
Efeito Doppler
O efeito Doppler ´e a mudan¸ca da frequˆencia observada, quando uma fonte ou um detector est´a se movendo com rela¸c˜ao ao meio onde a onda est´a se propagando.
Vamos considerar que um detector, D, e uma fonte sonora, S, est˜ao paradas a uma distˆancia d, Figura 19
O n´umero de comprimentos de ondas na distˆancia d ´e
n = n
λ =
vt
λ (107)
A taxa na qual D intercepta os comprimentos de onda ´e a frequˆencia
f = n
t = vt λ/t =
v
λ (108)
sendo que, nessa situa¸c˜ao n˜ao ocorre o efeito Doppler.
Supondo agora, que D se mova na dire¸c˜ao da fonte S, que est´a parada. Assim,
f′ = (vt+vDt)/λ
t =
v+vD
sendo,
λ= v
f, (110)
temos
f′ =fv+vD
v (111)
em que v ´e a velocidade do Som e vD ´e a velocidade do detector.
Usando o mesmo racioc´ınio para o detector se afastando da fonte S. Temos
f′ =fv −vD
v (112)
E finalmente generalizando as equa¸c˜oes temos
f′ =fv ±vD
v (113)
em que o sinal ”+”´e para aproxima¸c˜ao do detector e -”para afastamento.
Agora para a fonte em movimento na dire¸c˜ao do detector parado. O movimento de S altera o comprimento de onda das ondas emitidas pela fonte, e portanto, a frequˆencia detectada por D.
f′ = v
λ′ =
v
vT −vST = v
T(v−vS) (114)
sendo f = 1/T, ent˜ao
f′ =f v
v−vs (115)
J´a quando a fonte se afasta
f′ =f v
v+vS (116)
Podendo considerar, para o movimento da fonte
f′ =f v
v∓vS (117)
em que o sinal ”+”significa que a fonte est´a se afastando e o -”aproximando. Para ambos os casos, de fonte e detector se movendo, temos
f′ =fv ±vD
v∓vS (118)
4
Mecˆ
anica dos fluidos (Introdu¸c˜
ao)
O que ´e um fluido?
• Um substˆancia que pode escoar.
• Assumem a forma do recipiente onde s˜ao colocados.
• L´ıquidos e gases s˜ao agrupados na mesma categoria e s˜ao chamados fluidos.
4.1
Massa espec´ıfica e Press˜
ao
A massa espec´ıfica ou densidade volum´etrica (ρ) ´e definida como a raz˜ao
ρ= ∆m
∆V (119)
e para um corpo uniforme, pode-se escrever
ρ= m
V (120)
em que m e V s˜ao a massa e o volume da amostra.
Exemplo: Calcule a massa espec´ıfica (ρ) de uma certa quantidade de l´ıquido que possui massa igual a 0,200 kg e ocupa um volume de 300 ml.
Para definir a press˜ao, considere um recipiente cheio de fluido e um ˆembolo de ´area ∆A que pode deslizar no interior do cilindro fechado (Figura ??).
Figura 20: Ilustra¸c˜ao de um cilindro cheio de fluido com um ˆembolo de ´area ∆A
Considere uma for¸ca de m´odulo ∆F ´e aplicada sobre o ˆembolo, logo a press˜ao sobre o fluido ´e
Se a for¸ca ´e uniforme em uma superf´ıcie plana de ´areaA, podemos escrevem
P = F
A (122)
em que F ´e o m´odulo da for¸ca normal sobre a superf´ıcie de ´area A. A unidade de press˜ao no SI ´e o Newton por metro quadrado que recebe o nome de Pascal (P a)
1N/m2
= 1P a (123)
1atm = 1,01×105
P a (124)
Exemplo: Qual ´e o m´odulo da for¸ca que a atmosfera exerce sobre o alto da cabe¸ca de uma pessoa, que ter uma ´area da ordem de 0,040 m2
?
4.2
Fluidos em Repouso
Considere um cilindro com ´agua em repouso (Figura 21).
Figura 21: Ilustra¸c˜ao de um cilindro com ´agua com uma amostra em repouso.
De acordo com a segunda lei de Newton, temos que
X
~
F =m~a, (125)
F2−F1−P = 0 (126)
F2 = F1+P (127)
Utilizando as Equa¸c˜oes 122 e 120, temos
P2A=P1A+ρV g (128)
sendo V =Ah em que A ´e a ´area do ˆembolo e h ´e altura dada porh =y1−y2. Assim,
P2A = P1A+ρA(y1−y2)g (129) P2 = P1+ρg(y1−y2) (130)
Usando a Equa¸c˜ao 130 para determinar a press˜ao tanto de um l´ıquido (em fun¸c˜ao da profundidade) como na atmosfera (em fun¸c˜ao da altura), fazendo y1 = 0, y2 = −h, P1 =P◦ a press˜ao atmosf´erica e P2 =P, temos
P =P◦+ρgh, (131)
que ´e a press˜ao na profundidade h. Com a Equa¸c˜ao 131 verificamos que a press˜ao em um ponto de um fluido em equil´ıbrio depende da profundidade desse ponto, mas n˜ao da dimens˜ao horizontal do fluido (Figura 22).
Figura 22: Exemplos de que a press˜ao n˜ao depende da dimens˜ao horizontal do fluido
Exemplo 1: Um mergulhador novato, praticando em uma piscina, inspira ar suficiente do tanque para expandir totalmente os pulm˜oes antes de abandonar o tanque a uma profundidade L e nadar para a superf´ıcie. Ele ignora as instru¸c˜oes e n˜ao exala o ar durante a subida. Ao chegar `a superf´ıcie, a diferen¸ca entre a press˜ao externa a que est´a submetido e a press˜ao do ar em seus pulm˜oes ´e 9,3 kPa. De que profundidade partiu? Que risco possivelmente fatal est´a correndo?
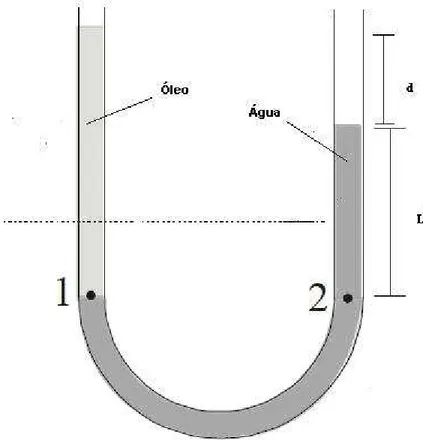
Exemplo 2:O tudo em forma de U cont´em dois l´ıquidos em equil´ıbrio est´atico: no lado direito existe ´agua de massa espec´ıficaρa = 998kg/m
3
de massa espec´ıfica desconhecida ρx. Os valores das distˆancias indicadas na Figura s˜ao L=135 mm e d=12,3 mm (Figura 23). Qual ´e a massa espec´ıfica do ´oleo?
Figura 23: Figura do Exemplo 2
4.2.1 O Barˆometro de merc´urio simples
O Barˆometro de merc´urio simples ´e um aparelho usado para medir a press˜ao da atmosfera, Figura 24.
O espa¸co acima da coluna de merc´urio cont´em apenas vapor de merc´urio cuja press˜ao ´e t˜ao baixa que pode ser desprezada. Assim,
P2 =P1+ρgh, (132)
para P2 = 0 e P1 =P◦, temos
0 = P◦ −ρgh (133)
P◦ =ρgh (134)
em que ρ ´e a densidade do merc´urio.
4.3
O princ´ıpio de Pascal
Figura 24: Barˆometro de merc´urio simples
Considere a ilustra¸c˜ao da Figura 25. Temos,
P =Pext+ρgh (135)
Ao acrescentar bolinhas de chumbo no recipiente para aumentar Pext. Como ρ, g e h
n˜ao variam, a varia¸c˜ao da press˜ao no ponto P ´e
∆P = ∆Pext (136)
Exemplo : Na Figura 26 ´e apresentada uma ilustra¸c˜ao de um macaco hidr´aulico, levando em considera¸c˜ao os dados apresentados na figura, qual ´e o m´odulo da for¸ca FA2
4.4
Princ´ıpio de Arquimedes
Quando um corpo est´a total ou parcialmente submerso em um fluido uma for¸ca de empuxo
~
FE exercida pelo fluido age sobre o corpo, Figura 27.
A for¸ca ´e dirigida para cima e tem um m´odulo igual ao peso do fluido deslocado pelo corpo.
FE =mfg (137)
em que FE ´e o m´odulo da for¸ca de empuxo e mf ´e a massa de fluido deslocada. Exemplo: Uma ˆancora de ferro de massa espec´ıfica 7870 kg/m3
Figura 25: Ilustra¸c˜ao do princ´ıpio de Pascal
4.5
Fluido Ideal
Para nosso estudo vamos considera um fluido ideal com as seguintes caracter´ısticas:
• Escoamento laminar: A velocidade do fluido em qualquer ponto fixo n˜ao varia.
• Escoamento incompress´ıvel: sua massa espec´ıfica tem valor constante
• Escoamento n˜ao viscoso: o fluido n˜ao apresenta resistˆencia ao escoamento.
• Escoamento irrotacional: n˜ao fira em torno de um eixo. 4.5.1 A equa¸c˜ao da continuidade
Considere o tubo ilustrado na Figura 28 em que o fluido se desloca da esquerda para a direita.
O tubo tem se¸c˜ao transversal A1 e A2 e velocidades v1 e v2. A massa de fluido que
cruza a ´area A1 no intervalo ∆t ´e
∆m1 =ρ∆v1 =ρ(A1v1∆t), (138)
como n˜ao existe fonte ou sorvedouros a massa de fluido que atravessa A1 atravessar´aA2
Figura 26: Ilustra¸c˜ao de uma macaco hidr´aulico.
ou ainda,
∆m1 = ∆m2 (140)
A1v1 =A2v2 (141)
Exemplo: Uma mangueira de jardim com diˆametro interno de 1,9 cm est´a ligada a um borrifador (estacion´ario) que consiste apenas em um recipiente com 24 furos de 0,13 cm de diˆametro. Se a ´agua circula na mangueira com uma velocidade de 0,91 m/s, com que velocidade deixa os furos do borrifador?
4.5.2 A equa¸c˜ao de Bernoulli
Na Figura 29 ´e apresentado um tubo atrav´es do qual um fluido ideal escoa com vaz˜ao constante.
Sejamh1,v1, eP1a altura, a velocidade e a press˜ao do fluido que entra do lado esquerdo,
e h2, v2, e P2 os valores correspondentes do fluido que sai do lado direito. Aplicando ao
fluido a lei de conserva¸c˜ao da energia temos:
P1+
1 2ρv
2
1 +ρgh1 =P2+
1 2ρv
2
2 +ρgh2 (142)
em que 1 2ρv
2
´e a energia cin´etica por unidade de volume e v ´e a velocidade. A Equa¸c˜ao 142 ainda pode ser escrita da forma
P +1 2ρv
2
Figura 27: Ilustra¸c˜ao do princ´ıpio de Arquimedes
que ´e chamada equa¸c˜ao de Bernoulli Sendoh=constante, temos
P1+
1 2ρv
2
1 =P2+
1 2ρv
2
2 (144)
ExemploA ´agua se move com velocidade de 5 m/s atrav´es de um cano com uma ´area de se¸c˜ao transversal de 4 cm2
. a ´agua desce 10 m gradualmente, enquanto a ´area do cano diminui para 8 cm2
. a) Qual ´e a velocidade do escoamento no n´ıvel mais baixo? b) Se a press˜ao no n´ıvel mais alto for 1,5×105
P a, qual ser´a a press˜ao no n´ıvel mais baixo?
Figura 29: Tubo atrav´es do qual um fluido ideal escoa com vaz˜ao constante.
5
Temperatura, Calor e Propriedades T´
ermicas da
Mat´
eria
• Os corpos s˜ao feitos de part´ıculas que est˜ao em cont´ınuo estado de vibra¸c˜ao.
• Quando um corpo se aquece, aumentam as vibra¸c˜oes das part´ıculas, e assim, aumen-tam as energias cin´eticas dessas part´ıculas.
• A soma de todas as energias cin´eticas de todas as part´ıculas do corpo chama-se energia t´ermica.
A temperatura est´a relacionada com `as nossas sensa¸c˜oes quentes e frio. ´E medida com um termˆometro, instrumento que cont´em uma substˆancia com propriedades mensur´aveis como press˜ao e comprimento.
5.1
Lei zero da Termodinˆ
amica
Se dois corpos A e B est˜ao separados em equil´ıbrio t´ermico com um terceiro corpo T, A e B est˜ao em equil´ıbrio t´ermico entre si
Quando um termˆometro e um objeto s˜ao colocados em contato eles entram em equil´ıbrio t´ermico ap´os um certo tempo. Ap´os o equil´ıbrio t´ermico ser atingido a leitura do termˆometro ´e tomado como sendo a temperatura do objeto.
5.2
Escalas de temperatura
5.2.1 A Escala Kelvin de Temperatura5.2.2 A Escala Celsius e Fahrenheit
A escala Celsius de temperatura ´e definida atrav´es da equa¸c˜ao
TC =T −273,15, (145)
com T em Kelvin. Exemplo:
Para uma temperatura de 293,15 K, temos
TC =T −273,15 = 293,15−273,15 = 20,00◦C (146)
onde se lˆe 20,00 graus Celsius.
A escala Fahrenheit, a mais comum nos Estados Unidos, possui um zero de temperatura diferente. A rela¸c˜ao entre as duas escalas Celsius e Fahrenheit ´e
TF =
9
5TC + 32 (147)
a unidade ´e o ◦F.
TC =T −273,15, (148)
Figura 30: Compara¸c˜ao entre as escalas Kelvin, Celsius e Fahrenheit de temperatura. Fonte: Halliday et. al., 2009
5.3
Dilata¸c˜
ao T´
ermica
Quando aumentamos a temperatura de um s´olido ele se dilata. A dilata¸c˜ao t´ermica desse s´olido est´a associada ao aumento da distˆancia entre os ´atomos vizinhos que o comp˜oe. Poder´ıamos dizer que a for¸ca de intera¸c˜ao el´etrica entre esses ´atomos j´a n˜ao ´e suficiente para mantˆe-los t˜ao pr´oximos um dos outros devido a agita¸c˜ao t´ermica oriunda do aumento da temperatura.
As propriedades de dilata¸c˜ao t´ermica de alguns materiais podem ter aplica¸c˜oes pr´aticas. Alguns termˆometros e termostatos utilizam a diferen¸ca na dilata¸c˜ao dos componentes de uma tira bimet´alica (Figura 31).
Figura 31: (a) Uma tira bimet´alica, formada por uma tira de lata¸c˜ao e uma tira de a¸co soldados entre si, `a temperatura T◦. (b) A tira se enverga da forma mostrada devido ao aumento de temperatura.
Fonte: Halliday et. al., 2009
5.4
Dilata¸c˜
ao Linear
`As vezes, estamos interessados em conhecer a dilata¸c˜ao do corpo em apenas uma de suas dimens˜oes; por exemplo: s´o a dila¸c˜ao no comprimento, no caso de trilhos do trem, ou o comprimento de um fio. Nesse caso falamos em dilata¸c˜ao linear. Para uma varia¸c˜ao de temperatura ∆T, uma varia¸c˜ao de ∆L de qualquer dimens˜ao linearL ´e dada por:
∆L=Lcircα∆T, (149)
em que α ´e o coeficiente de dilata¸c˜ao linear eL◦ ´e o comprimento inicial do corpo.
5.5
Dilata¸c˜
ao Superficial
A experiˆencia mostra que , para a varia¸c˜ao de temperatura ∆T, uma varia¸c˜ao de ∆S de qualquer dimens˜ao superficial S ´e dada por:
em que β ´e o coeficiente de dilata¸c˜ao superficial e S◦ ´e a ´area inicial da superf´ıcie. O coeficiente de dilata¸c˜ao superficial se relaciona com o linear atrav´es da rela¸c˜ao
β = 2α (151)
5.6
Dilata¸c˜
ao Volum´
etrica
A varia¸c˜ao ∆V do volume V de um s´olido ou de um l´ıquido ´e dada por
∆V =V◦γ∆T, (152)
em que γ = 3α´e o coeficiente de dilata¸c˜ao volum´etrica.
Exemplo: Em um dia quente em Las Vegas um caminh˜ao-tanque foi carregado com 3700 L de ´oleo diesel. Ele encontrou tempo frio ao chegar em Payson, Utah, onde a temperatura estava 23,0 K abaixo da temperatura de Las Vegas, e onde ele entregou a carga. Quantos litros foram descarregados? O coeficiente de dilata¸c˜ao volum´etrica do ´oleo disel ´e 9,50×10−4
C◦.
5.7
Calor
Quando um corpo quente ´e colocado em contato com um corpo frio, h´a transferˆencia de energia do corpo quente para o corpo frio, at´e que os corpos estejam em equil´ıbrio t´ermico. Calor ´e a energia que passa de um corpo para o outro devido a diferen¸ca de temperatura. O calor pode ser medido em Joules (J) e em calorias (cal)
1 cal=4,1868 J.
5.8
Capacidade T´
ermica
Se uma quantidade de calor Q ´e absorvida por um objeto, a varia¸c˜ao de temperatura do objeto, Tf −T i, est´a relacionada a Q atrav´es da equa¸c˜ao
Q=C(Tf −Ti) (153)
em que C ´e a capacidade t´ermica do objeto.
5.9
Calor espec´ıfico
Se dois objetos feitos do mesmo material, por exemplo a¸co, tˆem capacidades t´ermicas proporcionais a suas massas. Assim, ´e conveniente definir uma capacidade t´ermica por unidade de massa, ou calor espec´ıfico c. Se o objeto tem massa m,
Q=cm(Tf −Ti) (154)
5.10
Calor de Transforma¸c˜
ao
O calor absorvido por um material pode mudar o estado f´ısico do material, fazendo-o passar, por exemplo, do estado s´olido para o estado l´ıquido. A quantidade de energia por unidade de massa necess´aria para mudar o estado de um material ´e chamada de calor de transforma¸c˜ao. Sendo
Q=Lm
Exemplo: Que quantidade de calor deve absorver uma amostra de gelo de massa m=720 g a -10◦ C para passar ao estado l´ıquido a 15◦ C? Sendo Calor espec´ıfico do
gelo cgelo = 2220J/kg.K, o calor de fus˜ao Lf = 333kJ/kg e o calor espec´ıfico da ´agua
cagua = 4190J/kg.K.
5.11
Trabalho Associado a uma Varia¸c˜
ao de Volume
Um g´as pode trocar energia com o ambiente atrav´es do trabalho. O trabalhoW realizado por um g´as quando ao se expandir ou se contrair pode ser obtido da forma
dW = F~ ·d~s (155)
= (pA)(ds) (156)
= (p)(Ads) (157)
= pdV, (158)
em que dV ´e a varia¸c˜ao infinitesimal no volume. Dado um volume inicia Vi para um
volume final Vf ´e temos
W =
Z Vf
Vi
pdV. (159)
5.12
A Primeira Lei da Termodinˆ
amica
A primeira lei da termodinˆamica ´e uma lei de conserva¸c˜ao de energia para os processos termodinˆamicos. Ela ´e apresentada da forma:
A energia interna Eint de um sistema tende a aumentar, se acrescemos energia na
forma de calor Q, e a diminuir, se removemos energia na forma de trabalho W realizado
pelo sistema.
Assim, podemos escrever
∆Eint =Q−W (160)
ou ainda,
dEint=dQ−dW (161)
em que Eint ´e a energia interna do material
5.13
Aplica¸c˜
oes da Primeira Lei da Termodinˆ
amica
ambiente.
Q= 0
Assim,
∆Eint =−W (162)
Exemplo: Figura 32
Figura 32: Ilustra¸c˜ao de um processo adiab´atico. Fonte: CRV,2011
2. Processos a volume constante. Se o volume de um sistema ´e mantido constante, o sistema n˜ao pode realizar trabalho. Assim,
W = 0
Logo,
∆Eint=Q (163)
Assim, se o sistema recebe calor a energia interna do sistema aumenta. Por outro lado, se o sistema cede calor a energia interna do sistema diminui.
3. Processos C´ıclicos. E um processo que ap´os certas trocas d e calor e de trabalho o sistema volta ao seu estado inicial. Nesse caso,
∆Eint= 0,
logo,
Q=W (164)
4. Expans˜ao Livres. S˜ao processos adiab´aticos nos quais nenhum trabalho ´e realizado. Assim,
Q=W = 0,
logo,
∆Eint = 0 (165)
Figura 33: O est´agio inicial de um processo de expans˜ao livre. Ap´os a v´alvula ser aberta o g´as ocupa as duas cˆamaras e, depois de algum tempo atinge o estado de equil´ıbrio.
Fonte: UFSM,2011
Exemplo: Suponha que 1,00 kg de ´agua a 100◦C ´e convertido em vapor a 100◦C `a
press˜ao atmosf´erica padr˜ao (1 atm=1,01×105
Pa). O volume da ´agua varia de um valor inicial de 1,00×10−3
m3
do l´ıquido para 1,671m3
do vapor. a) Qual ´e o trabalho realizado pelo sistema durante esse processo? b) Qual a energia transferida durante o processo? (Dado: Calor de vaporiza¸c˜ao Lv = 2256kJ/kg) c) Qual ´e a varia¸c˜ao da energia interna do
6
Segunda lei da Termodinˆ
amica
6.1
Introdu¸c˜
ao `
a Teoria Cin´
etica dos Gases
A teoria cin´etica dos gases relaciona as propriedades como temperatura e press˜ao dos gases com propriedades das mol´eculas do g´as, tais como velocidade e energia cin´etica
6.1.1 O n´umero de Avogadro
Um mol de uma substˆancia cont´em NA (n´umero de Avogadro) unidades elementares, em que NA ´e uma constante f´ısica cujo valor experimental ´e
NA= 6,02×1023 mol−1
(166)
A massa molar M de uma substˆancia ´e a massa de um mol da substˆancia, e est´a relacionada com `a massa m de uma mol´ecula da substˆancia atrav´es da equa¸c˜ao
M =NAm (167)
O n´umero de mols n em uma amostra de massa Mamostra, que cont´emN mol´eculas, ´e dada por
n = N
NA =
Mamostra
M =
Mamostra
mNA (168)
6.1.2 G´as Ideal
Um g´as ideal ´e um g´as para o qual a press˜ao p, o volume V e a temperatura T est˜ao relacionados atrav´es da equa¸c˜ao
pV =nRT (169)
em quen´e o n´umero de mols do g´as eR´e a constante dos gases ideais (8,31 J/mol.K). A lei dos gases ideais tamb´em pode ser escrita da forma
pV =N kT (170)
em que k ´e a constante de Boltzmann
k = R
NA = 1,38×10
−23
J/K. (171)
Exemplo:
Um cilindro cont´em 12 L de oxigˆenio a 20◦C e 15 atm. A temperatura ´e aumentada
para 35◦C e o volume ´e reduzido para 8,5 L. Qual ´e a press˜ao final do g´as em atmosferas?
Suponha que o g´as ´e ideal.
6.2
Entropia
• Como sabemos, a 1a lei da termodinˆamica ´e uma formula¸c˜ao da conserva¸c˜ao de
• No entanto, podemos imaginar muitos processos termodinˆamicos em que a energia se conserva e que, todavia nunca ocorrem.
Por exemplo (Figura 34), um objeto com uma temperatura Ti em contato t´ermico com o meio externo, com temperatura Te. SendoTi > Te
Figura 34: Objeto a uma temperatura Ti em contato t´ermico com o meio externo.
Ap´os um intervalo de tempoTi =Te (Figura 35)
O transforma¸c˜ao inversa n˜ao viola a 1a lei da termodinˆamica,
Figura 35: Ap´os o equil´ıbrio t´ermico
Mas n˜ao vemos ela acontecer espontaneamente.
• De modo semelhante, a 1a lei n˜ao restringe a convers˜ao de calor em trabalho ou
trabalho em calor,
• embora possamos converter completamente em calor uma dada quantidade de traba-lho (Figura 36), nunca se conseguiu imaginar um meio de transformar completamente uma dada quantidade de calor em trabalho.
Figura 36: Exemplo de convers˜ao de trabalho em calor
• A entropia ´e diferente da energia no sentido de n˜ao obedecer a uma lei de conserva¸c˜ao.
• A energia de um sistema fechado permanece constante.
• Nos processos irrevers´ıveis, a entropia de um sistema fechado aumenta.
• A entropia e chamada ”seta do tempo”.
6.3
Varia¸c˜
ao de Entropia
A figura 37 mostra um g´as no estado de equil´ıbrio inicial i, confinado por uma v´alvula fechada no lado esquerdo do recipiente termicamente isolado.
A figura 38 mostra um g´as, ap´os a expans˜ao ocupando todo o recipiente atingido, depois de um certo tempo, o estado de equil´ıbrio final f.
Em um processo irrevers´ıvel, as mol´eculas do g´as jamais voltam a ocupar o estado inicial.
O diagrama p−V, da Figura 39, mostra a press˜ao e o volume do g´as no estado inicial e no final.
A press˜ao, o volume, temperatura e a energia s˜ao propriedades de estado. Al´em disso, definimos a varia¸c˜ao de entropia de um estado inicial a um final
∆S =Sf −Si = Z f
i dQ
T (172)
em que Q´e o calor cedido ou absorvido pelo sistema e T ´e a temperatura do sistema em kelvins. A unidade de entropia no SI ´e joule por kelvin.
Por´em, n˜ao ´e poss´ıvel aplicar a Equa¸c˜ao 172 em um processo irrevers´ıvel, pois:
• a press˜ao,
Figura 37: Estado inicial i
• e o volume
do g´as flutuam de forma imprevis´ıvel. Impossibilitando a realiza¸c˜ao da integra¸c˜ao da Equa¸c˜ao 172.
No entanto, a entropia ´e uma propriedade de estado, ou seja, a diferen¸ca de entropia entre os estados i e f s´o depende desses estados, e n˜ao da forma como o sistema passa de um estado para outro.
Ent˜ao, para determinar a varia¸c˜ao de entropia em um processo irrevers´ıvel que ocorre em um sistema fechado substitu´ımos esse processo por qualquer outro processo revers´ıvel que ligue os mesmos estados inicial e final e calculamos a varia¸c˜ao de entropia para esse processo revers´ıvel usando a Equa¸c˜ao 172.
Sabendo que, a temperatura de um g´as ideal n˜ao varia durante uma expans˜ao livre. Um processo que substitui convenientemente ´e uma expans˜ao isot´ermica revers´ıvel do estado i para o estado f.
Considere o sistema da Figura 40
Ap´os remover lentamente as esferas de chumbo (Figura 41).
Como o chumbo ´e removido lentamente, os estados intermedi´arios do g´as s˜ao estados de equil´ıbrio e podem ser representados em um diagrama p−V, Figura refpvr.
Aplicando a Equa¸c˜ao 172 na expans˜ao isot´ermica representado pelas Figuras 40 e 41, temos
∆S =Sf −Si = 1
T
Z f
i
dQ= Q
T , (173)
em que Q´e a energia total transferida como calor durante o processo.
tempe-Figura 38: Estado final f
ratura antes e depois do processo, a varia¸c˜ao de entropia e dada aproximadamente por
∆S =Sf −Si ≈ Q
Tmed, (174)
em que Tmed´e a temperatura m´edia do sistema, em kelvin, durante o processo.
6.4
A entropia como Fun¸c˜
ao do Estado
O fato de que a entropia seja fun¸c˜ao do estado pode ser mostrado apenas experimental-mente. Entretanto, pode-se provar que ´e uma fun¸c˜ao de estado para o caso especial no qual o g´as ideal passa por um processo revers´ıvel. Um processo revers´ıvel ´e executado
Figura 40: Estado inicial i
em uma s´erie de pequenos passos, com o g´as em um estado de equil´ıbrio ao final de cada passo. Para cada pequeno passo
• a varia¸c˜ao de energia na forma de calor ´edQ,
• o trabalho realizado pelo g´as ´e dW
• e a varia¸c˜ao de energia interna ´e dEint
Essas varia¸c˜oes est˜ao relacionadas pela 1a lei da termodinˆamica.
dEint=dQ−dW. (175)
Como os passos s˜ao revers´ıveis, com o g´as em estados de equil´ıbrio, podemos substituir
dW por pdV
dEint por nCVdT (176)
em que CV ´e o calor espec´ıfico de um g´as a volume constante
CV = Q
n∆T =
∆Eint
n∆T . (177)
Assim, obtemos
dQ=pdV +nCVdT. (178)
Usando a lei dos gases ideais, podemos substituir p por nRT /V. Dividindo ambos os membros por T e integrando de um estado inicial arbitr´ario i para um estado final arbitr´ario, temos
Z f
i dQ
T =
Z f
i
nRdV
V +
Z f
i
nCV dT
Figura 41: Estado final f
Figura 42: Diagrama p−V para a expans˜ao isot´ermica revers´ıvel.
ou ainda,
∆S =Sf −Si =nRlnVf
Vi +nCV lnTfTi. (180)
a varia¸c˜ao de entropia ∆S n˜ao depende do modo como o g´as passa do estado inicial para o estado final.
Exemplo: Suponha que 1,0 mol de nitrogˆenio esteja confinado no lado esquerdo do recipiente da Figura 40. A v´alvula ´e aberta e o volume do g´as dobrado. Qual ´e a varia¸c˜ao de entropia do g´as para esse processo irrevers´ıvel? Trate o g´as como sendo ideal.
6.5
A Segunda Lei da Termodinˆ
amica
Embora a entropia possa diminuir em uma parte do sistema fechado, sempre acorre o aumento em outra parte do sistema, de modo que a entropia do sistema jamais diminui.
∆S ≥0. (181)
Experimentalmente todos os processos s˜ao irrevers´ıveis, devido ao atrito, turbulˆencia e outros fatores.
6.6
M´
aquinas T´
ermicas
Uma m´aquina t´ermica (Figura 43) ´e um dispositivo que, opera ciclicamente, extrai energia t´ermica|Q◦| de uma fonte quente, realiza uma certa quantidade de trabalho|W| e rejeita
calor para uma fonte fria.
Figura 43: Representa¸c˜ao esquem´atica da m´aquina t´ermica.
Como a substˆancia operante efetua um ciclo, a sua energia interna, no in´ıcio e no final do ciclo ´e a mesma, sendo ent˜ao ∆U = 0. Portanto pela primeira lei
W =Qq−Qf (182)
ou seja, ´e igual `a quantidade de calor liqu´ıdo que passa pela m´aquina. Sendo que Qq eQf
s˜ao grandezas positivas.
Como a substˆancia operante efetua um ciclo, a sua energia interna, no in´ıcio e no final do ciclo ´e a mesma, sendo ent˜ao ∆U = 0. Portanto pela primeira lei
W =Qq−Qf (183)
ou seja, ´e igual `a quantidade de calor liqu´ıdo que passa pela m´aquina. Sendo que Qq eQf
s˜ao grandezas positivas.
Figura 44: Diagrama p−V para um processo c´ıclico arbitr´ario.
6.6.1 Rendimento T´ermico
O rendimento t´ermico η de uma m´aquina t´ermica ´e a raz˜ao entre o trabalho l´ıquido efetuado pela m´aquina e o calor absorvido na temperatura mais alta do ciclo
η= Wmaq
Qq =
Qq−Qf
Qq = 1−
Qf
Qq (184)
Na pr´atica, nenhuma m´aquina t´ermica converte todo o calor absorvido em trabalho. Com base nessa observa¸c˜ao a formula¸c˜ao de Kelvin-Planck da 2a lei da
termo-dinˆamica pode ser apresentada como segue:
• E imposs´ıvel construir uma m´aquina t´ermica que, operando em um ciclo, n˜ao pro-´ duza nenhum efeito al´em da absor¸c˜ao de calor de um reservat´orio e a realiza¸c˜ao de uma quantidade igual de trabalho.
6.6.2 Refrigeradores
Um refrigerador ´e uma m´aquina t´ermica que opera ao rev´es, na qual
• uma m´aquina absorve o calor Qf de um reservat´orio frio
• e rejeita calor Qq para um reservat´orio quente.
• Esse efeito s´o pode ser conseguido se houver trabalho sobre o refrigerador.
Na figura 45 temos a representa¸c˜ao esquem´atica de um refrigerador. Com isso o enunciado de Clausius da 2a lei afirma:
• O calor n˜ao flui espontaneamente de um corpo frio para um corpo quente.
Na figura 46 temos a representa¸c˜ao esquem´atica de um refrigerador, que absorve calor de um reservat´orio frio e transfere para um reservat´orio quente.
OCoeficiente de desempenho, CDD, ´e definido como
Figura 45: Esquema de um refrigerador.
Um refrigerador eficiente ´e aquele que remove a maior quantidade de calor do reservat´orio frio com a menor quantidade de trabalho.
6.7
A M´
aquina de Carnot
Em 1824, um engenheiro francˆes chamado Sadi Carnot descreveu uma m´aquina te´orica, conhecida hoje como ciclo de Carnot.
Essa m´aquina ideal estabelece um limite superior ao rendimento de todas as m´aquinas
t´ermicas.
Ou seja, nenhuma m´aquina real, operando entre reservat´orios de calor, pode ser mais eficiente que uma m´aquina de Carnot que opera entre os mesmos dois reservat´orios.
A fim de descrever o ciclo de Carnot,
• admitamos que a substˆancia operante ´e um g´as ideal contido em um cilindro com um pist˜ao m´ovel em uma extremidade.
• As paredes do cilindro e o pist˜ao s˜ao termicamente n˜ao condutores.
Os 4 est´agios do ciclo de Carnot s˜ao mostrados na Figura 47. Carnot mostrou que, para este ciclo,
|Qf|
|Qq| = Tf
Tq, (186)
logo, o rendimento t´ermico de uma m´aquina de Carnot ´e
η = 1− Tf
Figura 46: Refrigerdor
Todas as m´aquinas de Carnot que operam entre as mesmas temperaturas tˆem o mesmo rendimento.
Exemplo:
1-Uma M´aquina de Carnot opera entre as temperaturas TQ=850 K e TF=300 K. A m´aquina realiza 1200 J de trabalho em cada ciclo, que leva 0,25 s. (a) Qual ´e a eficiˆencia da m´aquina? (b) Qual ´e a potˆencia m´edia da m´aquina? (c) Qual ´e a energia|QQ|extra´ıda em forma de calor da fonte quente a cada ciclo?
Figura 47: Ciclo de Carnot
7
Exerc´ıcios
7.1
Movimento Harmˆ
onico Simples
7.1.1. O diafragma de um alto-falante est´a vibrando num movimento harmˆonico simples com frequˆencia de 440 Hz e um deslocamento m´aximo de 0,75 mm.
a)Qual ´e a frequˆencia angular deste diafragma?(440 Hz) b)Qual ´e a velocidade m´axima deste diafragma?(2,07 m/s) c)Qual ´e a acelera¸c˜ao m´axima deste diafragma?(5732,25 m/s2
)
7.1.3. Um corpo oscila com movimento harmˆonico simples cuja equa¸c˜ao ´e
x= 6,0 cos (3πt+π/3)metros. (188)
Determinar: a) o deslocamento, b) a velocidade e c) a acelera¸c˜ao, no instante t=2 s. Determinar tamb´em d) a fase, e) a frequˆencia e f) O per´ıodo do movimento.
7.1.4. Um pˆendulo simples, de 1,00 m de comprimento, realiza 100 oscila¸c˜oes comple-tas em 204 s, em certo lugar. Qual o valor da acelera¸c˜ao da gravidade nesse lo-cal?(9,5 m/s2
)
7.1.5. Qual ´e o per´ıodo de um pˆendulo simples cujo per´ıodo ´e exatamente de 1 s em um ponto onde g=9,81 m/s2
?
7.1.6. Podemos considerar que um autom´ovel esteja montado sobre quatro molas idˆenticas, no que concerne `as suas oscila¸c˜oes verticais. As molas de um certo carro est˜ao ajus-tadas de forma que as vibra¸c˜oes tenham uma frequˆencia de 3,0 Hz.
a) Qual a constante de elasticidade de cada mola, se a massa do carro ´e de 1450 kg e o peso est´a homogeneamente distribu´ıda entre elas? (1,29×105
N/m)
b) Qual ser´a a frequˆencia de vibra¸c˜ao se cinco passageiros, com m´edia de 73 kg cada um, estiverem no carro?
7.2
Movimento ondulat´
orio e som
7.2.1. Uma onda possui uma frequˆencia angular de 110 rad/s e um comprimento de onda de 1,80 m. Calcule (a) o n´umero de onda e (b) a velocidade da onda.(3,49m−1
,31,5m/s)
7.2.2. Sey(x, t) = (6,0mm)sen(kx+(600 rad/s)t+φ) descreve uma onda que se propaga em uma corda, quanto tempo um ponto da corda leva para se mover entres os deslocamentos y = 2,0mme y=−2,0mm? (1,1×10−3
s)
7.2.3. Quais s˜ao (a) a menor frequˆencia, (b) a segunda menor frequˆencia e (c) a terceira menor frequˆencia das ondas estacion´arias em um fio com 10,0 m de comprimento, 100 g de massa e uma tens˜ao de 250 N?(7,91, 15,8 e 23,7 Hz)
7.2.4. A tens˜ao em um fio preso nas duas extremidades ´e duplicada sem que o compri-mento do fio sofra uma varia¸c˜ao apreci´avel. Qual ´e a raz˜ao entre a nova e a antiga velocidade das ondas transversais que se propagam no fio?
7.2.5. Duas ondas progressivas iguais, que se propagam no mesmo sentido, est˜ao defasadas deπ/4 rad. Qual ´e a amplitude da onda resultante em termos da amplitude comum
ym das duas ondas?
7.2.6. Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequˆencia, 540 Hz, se propagam na mesma dire¸c˜ao e no mesmo sentido a 330 m/s. As fontes est˜ao em fase. Qual ´e a diferen¸ca de fase das ondas em um ponto que est´a a 4,40 m de uma fonte e a 4,00 m da outra?
7.2.7. A press˜ao de uma onda sonora progressiva ´e dada pela equa¸c˜ao ∆p= (1,5P a)sen{π[(0,900m−1
)x−(315s−1
Determine a) a amplitude, b) a frequˆencia, c) o comprimento de onda e d) a veloci-dade da onda.
7.2.8. A corda l´a de um violino est´a esticada demais. s˜ao ouvidos 4,00 batimentos por segundo quando a corda ´e tocada junto com um diapas˜ao que oscila exatamente na frequˆencia do l´a de concerto (440 Hz). Qual ´e o per´ıodo de oscila¸c˜ao da corda do violino? (2,25 ×10−3
s
7.2.9. Um guarda rodovi´ario persegue um carro que excedeu o limite de velocidade em um trecho reto de uma rodovia; os dois carros est˜ao a 160 km/h. A sirene do carro de pol´ıcia produz um som com uma frequˆencia de 500 Hz. Qual ´e o deslocamento Doppler da frequˆencia ouvida pelo motorista infrator? (0)
7.2.10. Uma ambulˆancia cuja sirene emite um som com uma frequˆencia de 1600 Hz passa por um ciclista que est´a a 2,44 m/s. Depois de ser ultrapassado, o ciclista escuta uma frequˆencia de 1590 Hz. Qual ´e a velocidade da ambulˆancia?
7.3
Mecˆ
anica dos fluidos
7.3.1. Encontre o aumento de press˜ao de um fluido em uma seringa quando uma enfer-meira aplica de 42 N ao ˆembolo da seringa de raio de 1,1 cm.
7.3.2. Um piscina tem dimens˜oes de 24m×9,0m×2,5m. Quando ela est´a cheia, qual ´e a for¸ca (devido somente a ´agua) sobre o fundo da piscina?
7.3.3. Encontre o peso total de ´agua em cima de um submarino nuclear a uma profundi-dade de 200 m, suponho que seu casco (corte da se¸c˜ao transversal) tenha a ´area de 3000 m2
.
7.3.4. Um piston de ´area menor a=0,30 m2
´e usado em uma prensa hidr´aulica. Um tudo conecta com outro piston maior de ´area A=1,50 m2
. Qual ´e a for¸ca exercida no piston de ´area a para elevar um peso de 20 kN.
7.3.5. Sobre a asa de um avi˜ao de ´area A, o ar escoa com velocidade vc e sob a asa deste
avi˜ao a velocidade do ar ´e vb. Mostre que nesta situa¸c˜ao simplificada a equa¸c˜ao de Bernoulli prediz que a for¸ca F de sustenta¸c˜ao na asa ser´a:
F = 1 2ρA(v
2 c −v
2
b). (190)
Dica: a diferen¸ca de energia potencial gravitacional ´e desprez´ıvel com rela¸c˜ao a energia cin´etica, ou seja, ρg(yc −yb)≈0.
7.3.6. Se a velocidade de escoamento, passando debaixo de uma asa ´e de 110 m/s, que velocidade de escoamento na parte de cima criar´a uma diferen¸ca de press˜ao de 900 Pa entre a superf´ıcie de cima e de baixo? Considere a densidade do ar ρ = 1,3× 10−3
g/cm3
7.3.7. As janelas de um pr´edio de escrit´orio tem dimens˜oes de 4m×5m. Em um dia de tempestade o ar passa pela janela do 53◦ andar, paralela `a janela, a uma velocidade
de 30 m/s. Calcule a for¸ca resultante aplicada na janela. A densidade do ar ´e 1,23 kg/m3
7.4
Temperatura, Calor e Propriedades T´
ermicas da Mat´
eria
7.4.1. Suponha que em uma escala linear de temperatura X , a ´agua ferva a -53,50X e secongele a -170X . Qual a temperatura de 340K na escala X ?
7.4.2. A 200◦C , uma haste mede exatamente 20,05 cm de comprimento em uma r´egua
de a¸co. Tanto a haste quanto a r´egua s˜ao colocadas em um forno a 2700◦C , onde
a haste passa a medir 20,11 cm na mesma r´egua. Qual o coeficiente de expans˜ao t´ermica para o material do qual ´e feita a haste? (Dados αaco = 11×10−5◦
C−1
).
7.4.3. Uma barra feita com liga de alum´ınio mede 10 cm a 20◦C e 10,015 cm no ponto de
ebuli¸c˜ao da ´agua. a) Qual o seu comprimento no ponte de congelamento da ´agua? b) Qual a sua temperatura, se seu comprimento ´e 10,009 cm? (a)9,9963 cm b) 68◦C)
7.4.4. O calor pode ser absorvido por uma substˆancia sem que esta mude de tempera-tura. Esta afirma¸c˜ao contradiz o conceito do calor como uma energia no processo de transferˆencia, devido a uma diferen¸ca de temperatura?
7.4.5. Uma amostra de g´as se expande a partir de uma press˜ao e um volume iniciais de 10 Pa e 1 m3
para um volume final de 2 m3
. Durante a expans˜ao a press˜ao e o volume s˜ao obtidos pela equa¸c˜ao p = aV2
, em que a = 10N/m8
. Determine o trabalho realizado pelo g´as durante a expans˜ao. (23,33 J)
7.4.6. Um g´as em uma cˆamara fechada passa pelo ciclo mostrado no diagrama p-V da Figura 48. A escala do eixo horizontal ´e definida por Vs = 4,0m3
. Calcule a energia l´ıquida adicionada ao sistema em forma de calor durante um ciclo completo.(-30J)
Figura 48: Exerc´ıcio 6. Fonte: Halliday et. al., 2009
7.4.7. Um trabalho de 200 J ´e realizado sobre um sitema, e uma quantidade de calor de 70,0 cal ´e removida do sistema. Qual ´e o valor (a) de W, (b) de Q e (c) de ∆Eint?
7.4.8. Suponha que 33,00 kg de ´agua a 100◦C ´e convertido em vapor a 100◦C `a press˜ao
atmosf´erica padr˜ao (1 atm=1,01×105
inicial de 3,30×10−3 m3
do l´ıquido para 3,652m3
do vapor. a) Qual ´e o trabalho realizado pelo sistema durante esse processo? b) Qual a energia transferida durante o processo? (Dado: Calor de vaporiza¸c˜ao Lv = 2256kJ/kg) c) Qual ´e a varia¸c˜ao da energia interna do sistema durante o processo?
7.5
Segunda lei da Termodinˆ
amica
7.5.1. Uma amostra de oxigˆenio com volume de 1000 cm3
a 40,0◦ C e 1,01×105
Pa se expande at´e um volume de 1500 cm3
a uma press˜ao de 1,06×105
Pa. Determine (a) o n´umero de mols de oxigˆenio presentes na amostra e (b) a temperatura final da amostra.(0,0388 mol e 220◦ C)
7.5.2. Uma amostra de ar, que ocupa 0,14 m3
`a press˜ao de 1,03×105
Pa, se expande isotermicamente at´e atingir apress˜ao atmosf´erica. Calcule o volume final.
7.5.3. Para fazer gelo, um freezer extrai 42 kcal de calor de um reservat´orio a -12◦ C
em cada ciclo. O coeficiente de performance do freezer ´e 5,7. A temperatura do ambiente ´e 26◦C. (a) Quanto calor, por ciclo ´e rejeitado para o ambiente? (b) Qual a
quantidade de trabalho por ciclo necess´ario para manter o freezer em funcionamento?
7.5.4. Num ciclo de Carnot, a expans˜ao isot´ermica de um g´as ideal acontece a 400 K e a compress˜ao isot´ermica a 300 K . Durante a expans˜ao, 500 cal de calor s˜ao transferidas pelo g´as. Calcule (a) o trabalho realizado pelo g´as durante a expans˜ao t´ermica, (b) o calor rejeitado pelo g´as durante a compress˜ao isot´ermica e (c) o trabalho realizado pelo g´as durante a compress˜ao isot´ermica.
7.5.5. Uma m´aquina t´ermica absorve 52,4 kJ e libera 36,2 kJ de calor em cada ciclo. Calcule (a) o rendimento e (b) o trabalho efetuado pela m´aquina em cada ciclo.
Figura 49: Exerc´ıcio 5
7.5.6. Uma m´aquina a vapor absorve calor da caldeira a 200◦ C (press˜ao de 15 atm) e
o descarrega diretamente no ar (press˜ao de 1 atm) a 100◦ C. Qual o rendimento
7.5.7. Em um refrigerador mecˆanico a cˆamara de baixa temperatura encontra-se a -13◦ C
e o g´as comprimido no compressor est´a a 27◦ C. Qual o coeficiente de eficiˆencia