Livros e Materiais Online Evandro Marquesone Apostila Final

UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ

CÂMPUS CORNÉLIO PROCÓPIO

DIRETORIA DE GRADUAÇÃO E EDUCAÇÃO PROFISSIONAL

GLEYSON DO NASCIMENTO OLIVEIRA

MARCOS VINICIUS TAVARES DA SILVA

VINÍCIUS SUTERIO

MATEMÁTICA MAIS DO QUE BÁSICA

GLEYSON DO NASCIMENTO OLIVEIRA

MARCOS VINICIUS TAVARES DA SILVA

VINÍCIUS SUTERIO

MATEMÁTICA MAIS DO QUE BÁSICA

Trabalho de participação do curso

apresentado à Universidade

Tecnológica Federal do Paraná, como parte dos pré-requisitos dos cursos de graduação, sob a orientação do

professor Evandro Estevão

Marquesone.

Sumário

APRESENTAÇÃO ... 3

1. CONJUNTOS NÚMERICOS ... 4

2. PROPORÇÃO ... 7

3. REGRA DE TRÊS SIMPLES ... 9

4. PORCENTAGEM ... 11

5. POTÊNCIA OU EXPONENCIAÇÃO ... 13

6. NOTAÇÃO CIENTÍFICA ... 14

7. FATORAÇÃO ... 15

8. RADICIAÇÃO ... 18

9. RACIONALIZAÇÃO ... 20

10. EQUAÇÕES ... 22

11. TRIGONOMETRIA ... 29

12. EXERCÍCIOS ... 36

13. GABARITO ... 63

APRESENTAÇÃO

O presente texto é resultado do Projeto Matemática Mais do Que Básica, relacionado ao edital de produção de mídias digitais, e trata de alguns assuntos em matemática básica e necessários para um bom desempenho das disciplinas oferecidas que tenham estes conteúdos como pré-requisitos exigidos. Isso porque observa-se que uma grande parcela da dificuldade nas disciplinas dos primeiros semestres, está não somente nos conteúdos respectivos, mas na matemática necessária para um bom desenvolvimento no assunto, o que na maioria das vezes não inclui os pré-requisitos destas disciplinas.

Além de alguns tópicos em matemática básica, também há alguns temas básicos para estas mesmas disciplinas. Cada capítulo é composto por um assunto, ou um grupo de assuntos relacionados, com alguns exemplos resolvidos, e ao final um grupo de questões sobre este tema. Há também uma vídeo-aula sobre cada capítulo, e um banco maior de questões ao final do material didático, com a classificação sobre o nível de dificuldade de cada questão e um gabarito com as respostas de cada problema. O aluno que acessar a página do grupo poderá acessar o material completo, composto por cada capítulo, ou ainda escolher qual capítulo deseja acessar, sendo possível nas duas ocasiões salvar o arquivo no próprio computador.

O texto didático, bem como a dinâmica do material teve como primeira influência uma apostila que o Prof. Evandro utilizou na ocasião em que era vestibulando em Maringá. Este material sobre matemática básica, foi preparado pelo Cursinho Pré-Vestibular Alternativo, e era utilizado periodicamente quando oferecido

o curso intitulado “Matemática Básica”.

Espera-se que este material auxilie os alunos que tem tais dificuldades, e que possam passar por elas e ir muito além do que possam imaginar, afinal o papel da

educação é contribuir para o “voo” de cada um.

1. CONJUNTOS NÚMERICOS

1.1. Conjunto dos números naturais: Chama-se conjunto dos numéricos naturais (N) o conjunto formado pelos números 0,1,2,3,..., assim temos:

N = {0,1,2,3,4,5,...}

1.2. Conjunto dos números inteiros: Chama-se conjunto dos números inteiros

(Z) os números que variam de -∞ até +∞, assim temos:

Z = {...,-3,-2,-1,0,1,2,3,...}

1.3. Conjunto dos números racionais: Chama-se conjunto dos números

racionais (Q) o conjunto dos números , onde a Z e b ≠ 0.

Exemplos:

i. Os números naturais e inteiros: 13; -4; 0; 9.

ii. OS decimas exatos: 0.75; -3/2; 2/5.

iii. As dizimas periódicas: 0,77777...; 1,233333....

1.4. Conjunto dos números irracionais: Chama-se o conjunto dos números irracionais (I) o conjunto dos números que não podem ser escritos pela razão de dois números, bem como todo número não-periódica.

Exemplos:

i. _√ = 1.41421...

ii. _√ = 1.73205...

iii. = 2.71828...

1.6. Subconjunto: Dentro de cada conjunto podemos representar subconjuntos contendo certos valores ou não, assim quando um subconjunto vem com um indicador, quer dizer que dentro do subconjunto são excluídos alguns valores.

i. O símbolo * exclui o zero do conjunto;

ii. O Sinal de + exclui os negativos do conjunto;

iii. O sinal de – exclui os positivos do conjunto;

1.7. Números primos: É todo número divisível por 1 e por ele mesmo. Assim temos:

NP = {1, 2, 3, 5, 7, 11, 13, 17, 19, ...}

Para se determinar se um número é primo ou não, devemos verificar se ele não é divisível por todos os números primos antecessores.

1.8. Decomposição de um número: Podemos decompor um número qualquer e reescreve-lo como um produto de fatores de números primos.

Exemplo:

i. _{= × ×}

ii. _{= ×}

1.10. Exemplos:

1 _– Calcule o MMC da expressão abaixo:

+ =

Solução:

. . , = 3,6|3

1,2|2 1,1| = 6

+ =

2 _– Calcule o MMC da expressão abaixo:

− =

Solução:

. . , = 5,3|5

1,3|3 1,1| = 15

+ =

1.11. Observações:

Exercício 1: como o 6 é divisível por 3 e por ele mesmo, adotamos ele como sendo o MMC.

2. PROPORÇÃO

Pode-se dizer que temos uma proporção quando temos uma igualdade entre duas razões, como por exemplo, tomando A, B, C e D, temos:

= =

Diante da expressão obtida para proporção, temos que:

i. a e d são chamados de extremos

ii. b e c são chamados de meios

iii. k é a constante de proporcionalidade.

2.1. Propriedades:

Para proporções temos as seguintes propriedades validas

i. Os produtos dos meios são iguais aos produtos dos extremos.

. = .

ii. Para a soma ou subtração dos numeradores e denominadores de uma

proporção, temos que k se conserva.

= = _±±

iii. Assim como a soma ou subtração dos elementos do primeiro termo da

proporção sobre o extremo do primeiro termo, mantém a proporcionalidade e igualdade com a soma ou subtração dos elementos do segundo termo sobre o extremos do mesmo.

±

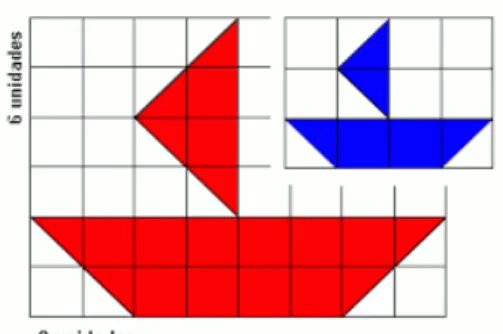
Figura 1 – Exemplo visual de proporção.

Podemos notar na figura acima a proporção do barco azul – comprimento =

4u, altura = 3u – com o barco vermelho – comprimento 8u, altura 6u. A proporção é

3. REGRA DE TRÊS SIMPLES

As grandezas podem ser diretamente ou inversamente proporcionais:

i. Diretamente Proporcionais: Quando o quociente entre elas é constante.

ii. Inversamente Proporcionais: Quando o produto entre elas é constante.

REGRA DE 3

DIRETAMENTE PROPORCIONAL

=

REGRA DE 3

INVERSAMENTE PROPORCIONAL

=

A resolução de regras de três que envolvam apenas duas grandezas é composta por três passos:

i. Reunir em cada coluna as grandezas de mesma espécie e unidade de

medida.

ii. Classificar as grandezas como diretamente ou inversamente

proporcionais.

iii. Obter a proporção correspondente e solucionar o problema.

3.1. Exemplo:

1 – Em uma obra quatro (4) operários concluem a construção em quinze (15) dias.

Quantos dias serão necessários para que vinte (20) operários concluam a mesma obra?

Solução:

Operários Dias

4 15

20 x

Primeiramente vamos organizar as setas. Para isso devemos inverter uma das informações:

Operários Dias

20 15

4 x

Multiplicando em cruz temos:

20 15

4 x

. = . . =

=

4. PORCENTAGEM

A porcentagem consiste basicamente na razão em que o denominador é 100. Os problemas de porcentagem podem ser resolvidos por regra de três.

% =

4.1. Exemplos:

1) A soma das idades do pai e do filho é de 60 anos. Sabendo que suas idades são proporcionais aos números 5 e 15. Determine as idades.

Solução:

Chamando a idade do pai de P e a do filho de F, temos:

+ � =

A partir das razões de proporcionalidade dadas, temos a seguinte relação:

=� ; : = �

Onde pode-se obter o valor de F da seguinte forma:

� + � =

Assim obtemos:

� = =

2) Os comprimentos de duas peças de linho estão na razão de 11/18. Mas o quíntuplo do comprimento de primeiro menos o triplo do segundo é igual a 2 m. Quantos metros tem cada peça?

Solução:

A relação é dada por

=

Onde a diferença entre o quíntuplo de a e triplo de b é:

− =

Isolando o valor de a na primeira relação temos que:

=

A partir disso, pode-se substituir na segunda equação da seguinte forma:

− =

Assim, obtemos:

= =

5. POTÊNCIA OU EXPONENCIAÇÃO

A operação de potenciação de um número pode ser definida como uma operação usada para indicar a multiplicação deste número por ele mesmo n vezes. Esta operação é dada da seguinte forma:

= . . . . … .⏟

�� � Onde:

a é chamado de base. n é chamado de expoente.

5.1. Propriedades:

Dentro da operação de potenciação, temos algumas propriedades:

i. =

ii. =

iii. = , ≠ iv. = , >

v. − ₌

vi. ₌ .

vii. _{. =} +

viii. ₌ − _{, ≠}

ix. . = .

x. ₌

xi. _{=⏟ . . . . … .} �� �

=⏟ …

�

∗

xii. − _{= =}

6. NOTAÇÃO CIENTÍFICA

Quando precisamos expressar um número com muitos algarismos, pode-se utilizar a notação cientifica que consiste basicamente em uma multiplicação por uma potência de base 10.

Um número escrito em notação cientifica é dado da seguinte forma:

=

Onde a é denominado mantissa e n a ordem de grandeza.

6.1. Notação cientifica padronizada:

Uma das formas mais usuais de representação para notação cientifica é a forma padronizada, onde restringe a mantissa em ser maior ou igual a 1 e menor que 10. Para que haja a transformação, deve-se apenas deslocar a vírgula.

Resumindo:

Deslocamento da vírgula para a Esquerda Eleva o expoente.

Deslocamento da vírgula para a Direita Diminui o expoente.

6.2. Exemplo:

. . = ,

. = ,

. = ,

. = ,

= , , = ,

, = ,

, = , −

, = , −

, = , −

, = , −

, = , −

7. FATORAÇÃO

A fatoração consiste basicamente em encontrar um fator comum em todas as parcelas da equação e coloca-los em evidencia da seguinte forma:

+ = +

7.1. Agrupamento

Pode-se realizar ainda o agrupamento de termos semelhantes nas parcelas, onde estes podem ser:

+ + + = + + + = + +

7.2. Quadrado da soma

O quadrado da soma de dois termos é dado por:

+ = + +

7.3. Quadrado da diferença

O quadrado da diferença é dado por:

− = − +

7.4. Diferença de Quadrados

Temos que a diferença de quadrados é dada por:

7.5. Exemplos:

1) (USP) Se x = 10-3_{, então} , , −

, é igual a:

Solução:

Resolvendo a multiplicação dada temos:

, , −

, =

,

, = ,

Onde temos que

= − _{= ,}

Sendo assim,

, , −

, =

2) (MACK) A expressão / �+ _−�−− − . / � quando simplificada é igual a:

Solução:

Colocando (1/2)x em evidencia no numerador temos:

[ − − _]

Na expressão obtida, temos que (1/2)x _{pode ser dado como 2}-x_{, sendo assim é}

possível fazer a simplificação da expressão

− −

−

Onde realizando os cálculos temos:

8. RADICIAÇÃO

A radiciação pode ser definida como a operação inversa da potenciação. Sendo assim a radiciação é dada por

√ = , , =

Onde:

n é chamado de índice. a é o radicando.

b é a raiz.

8.1. Índice do radical (n):

A partir de uma análise do índice da raiz, é possível verificar sua existência, como por exemplo:

Se n for par temos que a (o radicando) se restringe a números reais positivos. Se n for ímpar temos que a (o radicando) pode assumir valores positivos e negativos.

8.2. Propriedades:

Temos que as seguintes propriedades são validas na radiciação quando o

radicando é maior igual a 0 (a ≥ 0).

i. _{√ =} � / �_√ / _{, p N*}

ii. _{√ . = √ . √}

iii. _{√ =} √

√ , ≠

iv. _{( √ ) = √}

v. √ √ = √.

8.3. Exemplo:

9. RACIONALIZAÇÃO

A operação de racionalização consiste basicamente em multiplicar o numerador e o denominador pelo fator de racionalização, onde o numerador pode ser:

i. Monômio, sendo este da seguinte forma:

√ = √ .

√

√ =

√

ii. Binômio:

√ = √ .

√ −

√ − =

√ −

9.1. Exemplos:

1 _– Racionalize a expressão abaixo:

√

Solução:

√ = √ . √ √ =

√

2 _– Racionalize a expressão abaixo:

Solução:

Observação: Vale ressaltar quando possuímos uma operação no denominador. Quando acontece, há a necessidade de multiplicar pelo conjugado:

√ + √ = √ + √ .

√ − √

√ − √ =

. (√ − √ )

3 – Racionalize a expressão abaixo:

√ + √ √ + √ Solução:

Neste caso, possuímos um exercício mais complexo onde podemos notar as raízes exatas:

√ + √ √ + √ .

√ − √

√ − √ =

(√ . √ ) − (√ . √ ) + (√ . √ ) − (√ . √ ) (√ . √ ) − (√ . √ ) + (√ . √ ) − (√ . √ )

√ − √ + √ − √ √ − √ + √ − √

√ . − √ + √ . − √ −

10. EQUAÇÕES

10.1. Equação do 1º grau: Qualquer equação que possa ser escrita na seguinte forma:

. + =

Onde:

x é a incógnita

a e b são números reais com a ≠ 0.

Para efetuar a resolução desta equação, basta isolar a incógnita, e determinar o valor da raiz da equação, desta forma:

= −

10.2. Exemplo:

1 _– Calcule o valor de x na expressão:

. +

= . −

Solução:

. + = . −

. + − . + = . =

=

=

Exemplo:

2 – Resolva o sistema de equações abaixo:

{ . + = . − +_{+ = −}

Solução I:

Adição ou escalonamento: consiste em multiplicar ou dividir uma das equações por um valor qualquer de modo que ao somarmos as duas equações, desapareça uma das incógnitas.

Onde: _{{ − . − = −}

+ = − +

Com isso obtemos: _{= = −}

Solução II:

Substituição: consiste em isolar uma das incógnitas em uma das expressões e substituir o valor encontrado na outra expressão.

{ . + =_{+ = −}

= − −

Onde: _{. + − − =}

Solução III:

Comparação: consiste em isolar a mesma incógnita em ambas as expressões e igualar as equações.

{ . + =_{+ = −}

Onde: _{= − . = − −}

Como: ₌

Temos: _{− = − −}

Com isso obtemos: _{= = −}

De um modo mais geral, podemos falar que a equação ( _{. + =} ) é a

equação da reta, sendo que a é seu coeficiente angular, delimitando se a reta é crescente ou decrescente e b é seu coeficiente linear, isto é, onde corta o eixo y (ordenadas).

10.4. Equação do 2º grau: Qualquer equação que possa ser escrita na seguinte forma:

. + . + =

Onde:

x é a incógnita

a, b e c são números reais com a ≠ 0.

10.5. Resolução da equação de 2º grau:

Método de BHÁSKARA:

Método de GIRAD:

+ = −

. =

Vale ressaltar que para a equação de 2º grau temos: - Duas raízes repetidas: x1 = x2 b2– 4.a.c = 0

- Duas raízes simétricas: x1 = -x2 b = 0

10.6. Exemplo:

3 _– Resolva a seguinte equação:

. − . + =

Solução:

Por BHÁSKARA temos:

= − − ± √ −_. − . .

Com isso obtemos: ′ ₌ ′′₌

Por GIRAD temos:

= − −

=

Com isso temos que encontrar dois valores que somados deem e

multiplicados deem .

10.7. Dispositivo de BRIOT-RUFFINI:

Consiste em um algoritmo para que possa ser efetuada a divisão de polinômios com o intuito de reduzir o seu grau.

= +

Sendo:

P(x) = dividendo; H(x) = divisor; Q(x) = quociente; R(x) = resto.

10.8. Exemplo:

4 _– Efetue a divisão do polinômio _{= + +} por _{= +}

Solução:

Sabemos que para o divisor, a raiz de x + 1 = -1

-1 | 1 4 3

| 1 3 = RESTO

1o passo: desce o primeiro coeficiente; 2o passo: (1 x(-1)) + 4 = 3;

3o _{passo: (3 x (-1)) +3 = 0.}

Com isso obtemos o novo polinômio é x + 3 = 0. Podemos tirar prova: H(x) . Q(x) + R(x) = P(x).

(x+1) . (x+3) + 0 = x² + 4x + 3

5 _– Efetue a divisão do polinômio _{= − + − +} por

= −

Solução:

Sabemos que para o divisor, a raiz de x - 1 = 1

1 | 5 -3 2 -7 3

| 5 2 4 -3 0 = RESTO

1o passo: desce o primeiro coeficiente; 2o passo: (5 x 1) + (-3) = 2;

3o passo: (2 x 1) + 2 = 4; 4o passo: (4 x 1) + (-7) = -3; 5o passo: (1 x (-3)) + 3 = 0;

Com isso obtemos o novo polinômio é 5x³ + 2x² + 4x -3 = 0 Podemos tirar prova: H(x) . Q(x) + R(x) = P(x).

(x-1) . (5x³ + 2x² + 4x -3) + 0 = 5x4 _{- 3x³ + 2x² - 7x + 3}

6 _– Efetue a divisão do polinômio _{= − + +} por = −

Solução:

Sabemos que para o divisor, a raiz de − =

4 | 2 -7 2 1

---

| 2 1 6 25 = RESTO

1o passo: desce o primeiro coeficiente; 2o passo: (2 x (4)) – 7 = 1;

3o passo: (1 x (4)) + 2 = 6;

0

4º passo: (6 x (4)) + 1 = 25.

Com isso obtemos o novo polinômio _{+ +} com resto igual a 25.

Podemos tirar a prova:

H x . Q x + R x = P x .

11. TRIGONOMETRIA

Pode-se dividir a trigonometria em dois sub tópicos:

i. Trigonometria em um triângulo retângulo;

ii. Trigonometria em um triângulo qualquer.

Para o primeiro temos:

Figura 2 – Triângulo retângulo

11.1. Observações:

A hipotenusa é o lado do triângulo que é oposto ao ângulo de 90º; Os catetos são os outros lados do triângulo.

Ao falarmos sobre triangulo retângulo, o tópico mais importante que deve ser relevado é a aplicação do teorema de PÍTAGORAS, onde:

ℎ = +

A hipotenusa ao quadrado é igual à soma dos catetos ao quadrado. Pode-se aplicar também as funções trigonométricas:

= ℎ

= ℎ

Cateto Oposto: cateto que esta “sendo visto” pelo ângulo analisado

Cateto Adjacente: cateto que esta junto ao ângulo analisado.

Como um dos ângulos internos possui o valor de 90º a soma dos outros ângulos também possui o valor de 90º - (ângulos complementares) - pois a soma dos ângulos internos de um triangulo é 180º, com isso apresentamos os ângulos notáveis.

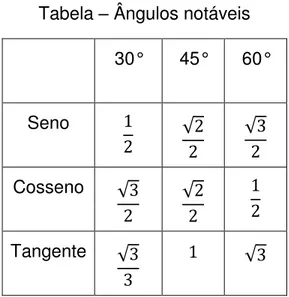
Tabela – Ângulos notáveis

30° 45° 60°

Seno _{√ √}

Cosseno _{√ √}

Tangente _{√ √}

11.2. Exemplo:

1 _– Encontre o valor de h no triangulo abaixo:

Solução:

Temos duas opções para encontrarmos h:

i.

= ( ) + ℎ

ℎ = −

ℎ = .

ℎ = √

ii.

tg = ℎ

ℎ = √

Observação.: podemos encontrar qualquer valor do triangulo a partir das

relações explicitadas acima, desde ângulos até lados – Se tivermos um lado e um

ângulo ou se tivermos dois lados.

11.3. Lei dos senos:

= = =

11.4. Exemplo:

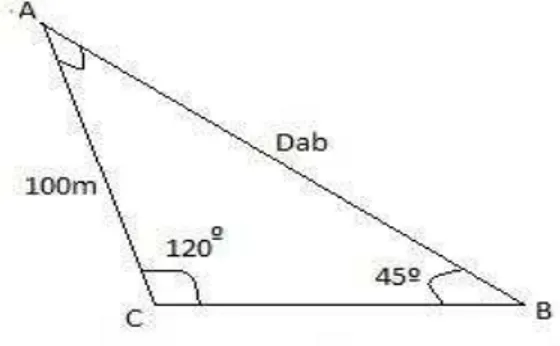
2 – Encontre o valor de dab no triangulo abaixo utilizando a lei dos senos:

Figura 5 – Exercício Lei dos senos

Solução:

= →

√ = √

√

. = .√ → √ . = . √

= . √

√ → =

. √ . √ √ . √

11.5. Lei dos cossenos:

Figura 6 – Lei dos cossenos

= + − . . .

= + − . . .

= + − . . .

Observação: A aplicação da lei dos cossenos no triangulo retângulo

° = portanto resume-se em A² = B² + C²

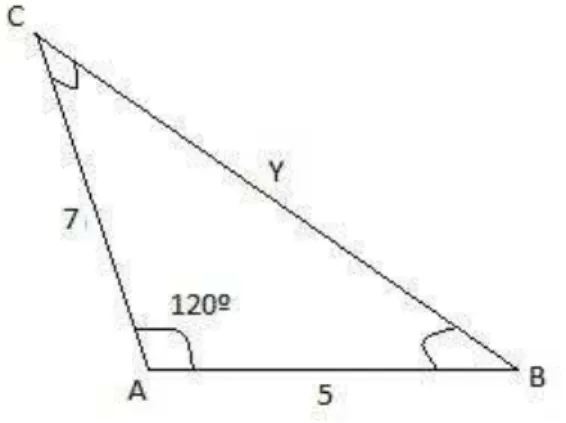
11.6. Exemplo:

3 – Encontre o valor de γ no triângulo dado:

Solução:

= + − . . .

= + − . −

= + + .

= +

= = √

11.7. Observações ciclo trigonométrico:

Vale ressaltar os ângulos comuns para que possamos trocar o sinal ao

usarmos as funções trigonométricas exemplo, o ângulo de 120o _{(segundo quadrante)}

corresponde ao de 60o _{(primeiro quadrante), portanto, seus valores em módulo são}

iguais. O seno de 60o vale √ e o de 120o vale também √ , já o cosseno de 60o vale 1 e o de 120o vale -1.

Figura 8 – Ciclo trigonométrico seno

Figura 10 – Ciclo trigonométrico tangente

Exemplo

4 – Calcule:

a) _{cos °}

Solução:

Pela definição dada, tem-se:

cos ° = cos ° − . ° = cos ° − °

cos ° − ° = cos °

Logo,

cos ° = cos ° =√

b) _cos �

Solução:

Pela definição dada, tem-se:

cos ( �) = cos ( �− �) = cos �

12. EXERCÍCIOS

Os exercícios abaixo foram classificados de acordo com os níveis de dificuldade apresentado. A classificação é dada por:

● Fácil ●● Médio ●●●Difícil

● 1) (PUC) Sejam Q e I os conjuntos dos números racionais e irracionais, respectivamente. Então, sempre é verdadeira a afirmação:

a) x _{I; y I ⇒ x + y I} b) _{x I; y I ⇒ x.y I} c) _{x Q; y I ⇒ x –y I} d) x Q; y Q ⇒ x/y Q

e) n.d.a

● 2) (EPCAR) Qual das proposições abaixo é falsa?

a) Todo número real é irracional b) Todo número natural é inteiro c) Todo número irracional é real d) Todo numero inteiro é racional e) Todo número natural é raciona

● 3) (UFMG) Seja N o conjunto dos números naturais

k = {3x/x N}, L = {5x/x N} e M = {15x/x N}. Qual a afirmativa correta?

a) k _{L = M}

● 4) (CESGRANRIO) A intersecção do conjunto de todos os inteiros múltiplos de 6

com o conjunto de todos os inteiros múltiplos de 15 é o conjunto de todos os inteiros é o conjunto de todos os inteiros múltiplos de:

a) 3 b) 6 c) 10 d) 15 e) 30

● 5) (PUC-SP) Um conjunto de M possui dez números primos, dez números pares e dez números ímpares. Qual é o menor número de elementos que M pode ter?

a) 31 b) 30 c) 28 d) 20 e) n.d.a

●● 6) (PUC-PR) O número de divisores positivos de 54.63 é:

a) 12 b) 20 c) 40 d) 60 e) 80

●● 7) (UEL) Se o número natural n = 8,27m _{admite 52 divisores positivos, o valor de}

m é:

● 8) (Santa Casa) De um aeroporto partem aviões de 10 em 10 minutos para a cidade A, de 15 em 15 minutos para a cidade B e de 40 em 40 minutos para C. Se às 12 horas partem aviões para as três cidades, a que horas haverá nova coincidência dos três horários?

a) 14 horas b) 16 horas c) 18 horas d) 20 horas e) 22 horas

● 9) (ENEM) Considere dois grupos de agentes censitários, um deles com 66

agentes e o outro, com 72. Os dois grupos serão divididos em equipes de trabalho. Essas equipes deverão ter o mesmo número de agentes, sendo que todos os agentes de cada equipe devem ser originários do mesmo grupo. Desse modo, o número máximo de agentes por equipe será:

a) 3 b) 4 c) 5 d) 6

● 10) (PUC–SP) Numa linha de produção, certo tipo de manutenção é feita na máquina A a cada 3 dias, na máquina B, a cada 4 dias, e na máquina C, a cada 6 dias. Se no dia 2 de dezembro foi feita a manutenção nas três máquinas, após quantos dias as máquinas receberão manutenção no mesmo dia.

● 11) Obter o mínimo múltiplo comum entre os números 250 e 450

● 12) (UNIPAR) Supondo que dois pilotos de formula 1 largam juntos num

determinado circuito e completam, respectivamente, cada volta em 72 e 75 segundos, responda depois de quantas voltas do mais rápido, contadas a partir da largada , ele estará uma volta na frente do outro?

a) 6 b) 9 c) 15 d) 24 e) 25

● 13) Um trabalhador gasta 3 horas para limpar um terreno circular de 5 m de raio.

Quantas horas gastará para limpar um terreno de 10 m de raio?

●● 14) (UNIPAR) Duas jarras iguais contém misturas de álcool e água nas proporções 3:7 na primeira jarra e 3:5 na segunda jarra. Juntando-se os conteúdos das jarras, obteremos uma mistura de álcool e água na proporção de:

a) 9:35 b) 3:5 c) 7:13 d) 21:35 e) 27:53

●● 15) (UNIPAR) A torneira x enche um tanque em 3 horas, enquanto que a torneira y enche o mesmo tanque em 5 horas. Estando as duas torneiras ligadas juntas, quanto tempo elas levarão para encher o tanque?

● 16) (FUVEST) São dados três números reais, a < b < c. Sabe-se que o maior deles é a soma dos outros dois e o menor é um quarto do maio. Então a, b e c são, respectivamente, proporcionais a:

a) 1, 2 e 3 b) 1, 2 e 5 c) 1, 3 e 4 d) 1, 3 e 6 e) 1, 5 e 12

● 17) (UFLA) Três pessoas montam uma sociedade, na qual cada uma delas aplica,

respectivamente, R$ 20.000,00, R$ 30.000,00 e R$ 50.000,00. O balanço anual da firma acusou um lucro de R$ 40.000,00. Supondo-se que o lucro seja dividido em partes diretamente proporcionais ao capital aplicado, cada sócio receberá, respectivamente:

a) R$ 5.000,00; R$ 10.000,00 e R$ 25.000,00 b) R$ 7.000,00; R$ 11.000,00 e R$ 22.000,00 c) R$ 8.000,00; R$ 12.000,00 e R$ 20.000,00 d) R$ 10.000,00; R$ 10.000,00 e R$ 20.000,00 e) R$ 12.000,00; R$ 13.000,00 e R$ 15.000,00

● 18) (UNIPAR) A pressão P e o volume V de um gás perfeito mantido a uma

temperatura constante satisfazem a lei de Boyle PV = K(cte). Se aumentarmos a pressão em 25%, em quantos por cento diminuirá o volume do gás.

a) 15% b) 20% c) 25% d) 30% e) 40%

● 19) (VUNESP) Em um concurso participaram 3000 pessoas e foram aprovadas

1800. A razão do número de candidatos aprovados para o total de candidatos participantes do concurso é:

a) _⁄

b) _⁄

c) _⁄

d) _⁄

● 20) (UNIPAR) Uma loja de eletrodomésticos em Umuarama vende seus produtos nas seguintes condições: (I) à vista com desconto de 20% sobre o preço de tabela ou no cheque, para 30 dias, com acréscimo de 10% sobre o preço de tabela. Um artigo que à vista sai por R$ 128,00 no cheque sairá por:

a) R$ 140,80 b) R$ 152,00 c) R$ 160,00 d) R$ 176,00 e) R$ 182,00

● 21) (ENEM) Em um curso de inglês, as turmas são montadas por meio da

distribuição das idades dos alunos. O gráfico abaixo representa a quantidade de alunos por suas idades. A porcentagem de alunos com que será formada uma turma com idade maior ou igual a 18 anos é:

a) 11% b) 20% c) 45% d) 55% e) 65%

● 22) (UEM) Quando um lado de quadrado aumenta 20%, de quantos por cento

● 23) (PUC-Rio) Em uma turma de Ciências da Computação formada de 40 rapazes e 40 moças, tem-se a seguinte estatística:

 20% dos rapazes são fumantes

 30% das moças são fumantes

Logo, a porcentagem dos que não fumam na turma é de:

a) 25% b) 50% c) 60% d) 65% e) 75%

●● 24) (PUC-Rio) Maria comprou duas bicicletas por um total de R$ 670,00. Vendeu uma das bicicletas com lucro de 10% e a outra com prejuízo de 5%. No total, ela ganhou R$ 7,00. Quais foram os preços de compra?

a) R$ 370,00 e R$ 300,00 b) R$ 270,00 e R$ 400,00 c) R$ 277,00 e R$ 400,00 d) R$ 200,00 e R$ 470,00 e) R$ 377,00 e R$ 293,00

●● 25) (UEM) Um investidor aplicou no mercado de ações 5 milhões de reais, sendo

1/5 da aplicação nas ações A e o restante nas ações B. Em uma semana, as ações A subiram 50% enquanto as ações B caíram 30%. Qual a porcentagem correspondente à perda do investidor nessa semana?

● 26) (UFMG) O preço de venda de determinado produto tem a seguinte composição: 60% referentes ao custo, 10% referentes ao lucro e 30% referentes a impostos. Em decorrência da crise econômica, houve um aumento de 10% no custo desse produto, porém, ao mesmo tempo, ocorreu uma redução de 20% no valor dos impostos. Para aumentar as vendas do produto, o fabricante decidiu, então, reduzir seu lucro à metade.

É CORRETO afirmar, portanto, que, depois de todas essas alterações, o preço do produto sofreu redução de:

● 27) (UFRN) Uma gravura de forma retangular, medindo 20 cm de largura por 35

cm de comprimento, deve ser ampliada por 1,2 m de largura. O comprimento será:

a. 0,685 m b. 6,85 m c. 2,1 m d. 1,35 m e. n.d.a

● 28) (FEI-SP) O valor da expressão B = 5.108_.4.10-3 _é:

a) 206 b) 2.106 c) 2.109 d) 20.10-4

●29) Há aproximadamente 6,01x1023 átomos de Hidrogênio em um grama, Calcule

a massa aproximada, em grama de um átomo de Hidrogênio.

● 30) (MACK) Sendo 2x _{= b, então 2}-2+3x _vale:

a) 3b2 b) b/3 c) b3_/4 d) 4b e) 2b2_/3

● 31) (E.S.A) A diferença 270,3333..._{– 16}0,75_{, é:}

a) 5 b) 6 c) -5 d) -6 e) 2

●● 32) O matemático De Morgan, que viveu no século XIX, propôs o seguinte enigma à respeito de sua idade: “Eu tinha x anos em x2”. Em que ano ele nasceu?

● 33) (UEL) Se x = 2.10-12_{, y = 50.10}-11 _{e z = 3.10}-10_{, então:}

a) x < y < z b) x < z < y c) y < x < z d) z < x < y e) z < y < x

● 34)

(

)

−

pode ser escrito como:

a) a/2 b) 2/a c) -2/a d) –a/2 e) n.d.a

● 35) √ + √ + √ + √ é igual a:

a) 9 b) 10 c) 90 d) 100 e) n.d.a

●● 36) A expressão / + _// vale:

a) + √ +

b) + √ + + c) √ + √

d) +

● 37) Racionalizando a expressão √ +√

√ obtemos:

a) _√

b) _{+ √}

c) _√

d) _√

e) n.d.a

● 38) (UEL) Racionalizando-se

√ + √ , obtém-se:

a) _√

b) _√

c) _√

d) _√

e) _√

● 39) (UNIPAR) Assinale a alternativa correta:

a) (0,99)2 _{> (0,99)}3

b) (0,99)7 _{< (0,99)}8

c) (0,99)4 > (0,99)3 d) (0,99)0,99 > (0,99)0.90 e) (0,99)-2 < 1

● 40) (UFRGS) O valor da expressão − − +₋

+

●● 41) (UFRGS) A expressão √ −√

√ − √

a) √ + √

√

b) _√

c) _√

d) _√

e) 1

●● 42) (UFRGS) Sendo n > 1, a expressão

√

−

a) √ −

−

b) √

+√

c) √

+√

d) √

e) √ −

+

●● 43) (FUVEST) Simplifique

√

a)

b) c) d)

e)

● 44) (UNIPAR) O valor de 44_.94_.49_.99 _{é igual a:}

a) 1313

● 45) (UEM) Considerando que x2 _{= 5}3_{, y}3 _{= 5}4 _{e z}6 _{= 5}, _{então o valor de n que}

satisfaz a igualdade 5n _{= (xyz)}24 _é:

●● 46) (FUVEST) Um foguete é equipado com um sistema de propulsão que lhe

confere uma velocidade continuamente crescente, de tal forma que, a partir da velocidade de 100 km/h, a cada 80 litros de combustível consumido ocorre um acréscimo de 20% em sua velocidade. Logo após o lançamento, observa-se que no combustível é de 2000 litros. Determine a velocidade do foguete no instante em que termina o combustível.

a) 100.0,225 b) 100.1,225

c) 1025

d) 1,225 e) 1225

● 47) Se os números x, y e z são tais que: = , = √ = √− então:

a) = , = = −

b) _{= ± , = ± = −}

c) _{= ± , = ±}

d) _{= ± , =}

e) n.d.a.

● 48) O número √ √ √ é igual a:

a) _√

b) _√

c) _√

d) 1 e) 4

● 49) Racionalizando a expressão √ +√

√ obtemos:

a) _√

b) _{+ √}

c) _√

d) _√

●● 50) (ITA) Racionalize a fração

√ + √

a) √ − √

−

b) _{√ + √} c) _{√ − √}

d) √ + √ − e) n.d.a

●● 51) (UNIPAR) Chama-se cosseno hiperbólico de x e seno hiperbólico de x, e

representam-se respectivamente por cosh(x) e senh(x), os nos _{cosh =}��+�−�

e _{ℎ =} ��− �−�

. Então (cosh(x))

a) 0 b) 1 c) e d) ex e) ex + e-x

● 52) (UNIPAR) O valor de x que verifica a equação −

−

=

é igual a:

b) 41/25 c) 48/25 d) 17/60 e) 5/12

● 53) (FUVEST) O dobro de um número mais a sua terça parte, mais a sua quarta

● 54) (ENEM) O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ 100 000,00 por km construído (n), acrescidos de um valor fixo de R$ 350 000,00, enquanto a segunda cobrou R$ 120 000,00 por km construído (n), acrescidos de um valor fixo de R$ 150 000,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas

uma delas poderá ser contratada.

Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?

a) 100n + 350 = 120n + 150 b) 100n + 150 = 120n + 350 c) 100(n + 350) = 120 (n + 150)

d) 100(n + 350 000) = 120(n + 150 000) e) 350(n + 100 000) = 150(n + 120 000)

● 55) (UFPR) De acordo com a Organização Mundial de Saúde, um Índice de Massa

Corporal inferior a 18,5 pode indicar que uma pessoa está em risco nutricional. Há, inclusive, um projeto de lei tramitando no Senado Federal, e uma lei já aprovada no Estado de Santa Catarina, proibindo a participação em eventos de modelos que apresentem esse índice inferior a 18,5. O Índice de Massa Corporal de uma pessoa, abreviado por IMC, é calculado através da expressão

= ℎ

em que m representa a massa da pessoa, em quilogramas, e h sua altura, em metros. Dessa forma, uma modelo que possua IMC = 18,5 e massa corporal de 55,5 kg, tem aproximadamente que altura?

●● 56) (UNEMAT) A professora Ana Maria precisa comprar 80 unidades de material para a sua aula, entre eles, lápis, canetas e cadernos. Espera comprar os lápis a R$ 1,00 cada, as canetas a R$ 2,00 e os cadernos a R$ 4,00. Arrecadou dos alunos

R$ 230,00 para esta compra.

Se o número de cadernos deve ser igual ao número de lápis e canetas juntos, a solução para esta compra será:

a) 40 lápis, 35 canetas e 5 cadernos b) 5 lápis, 35 canetas e 40 cadernos c) 10 lápis, 30 canetas e 40 cadernos d) 20 lápis, 20 canetas e 40 cadernos e) 15 lápis, 25 canetas e 40 cadernos.

● 57) Quarenta pessoas em excursão pernoitam em um hotel. Somados, os homens despendem R$ 2.400,00. O grupo de mulheres gasta a mesma quantia, embora cada uma tenha pago R$ 64,00 a menos que cada homem. Denotando por x o número de homens do grupo, uma expressão que modela esse problema e permite encontrar tal valor é:

a) 2400x = (2400 + 64x)(40 – x)

b) 2400(40 – x) = (2400 – 64x)x c) 2400x = (2400 - 64x)(40 – x)

d) 2400(40 – x) = (2600 + 64x)x

Após determinar a população brasileira em 2006 e em 2009, resolvendo um sistema linear, verifica-se que:

a) O número de brasileiros indigentes passou de 19,0 milhões, em 2006, para 13,3 milhões, em 2009.

b) 12,9 milhões de brasileiros em indigentes em 2009. c) 18,5 milhões de brasileiros eram indigentes em 2006.

d) Entre 2006 e 2009, o total de brasileiros incluídos nas faixas de pobreza e de indigência passou de 36% para 28% da população.

● 59) (UERGS) Sendo S a soma e P o produto das raízes da equação 2x2– 5x – 7 = 0, pode-se afirmar que:

a) S – P = 6 b) S + P = 2 c) S.P = 4 d) S/P = 1 e) S < P

●● 60) (FUVEST) A soma e o produto das raízes da equação de segundo grau

+ − + − =

Valem, respectivamente, 5/8 e 3/32. Então m+n é igual a:

a) 9 b) 8 c) 7 d) 6 e) 5

●● 61) (ENEM) O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605 trabalhadores com carteira assinada.

Disponível em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).

Considerando-se que y e x representam, respectivamente, as quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é

a) ₌

b) ₌

c) = +

d) _{= +}

e) _{= +}

● 62) (PUC-Rio) As duas soluções de uma equação do 2º grau são -1 e 1/3. Então a equação é:

a) _{− − =}

b) + − =

c) _{+ − =}

d) _{− − =}

e) _{− + =}

Uma jovem com IMC = 20 kg/m², 100 cm de circunferência dos quadris e 60 kg de massa corpórea resolveu averiguar seu IAC. Para se enquadrar aos níveis de normalidade de gordura corporal, a atitude adequada que essa jovem deve ter diante da nova medida é

(Use _{√ = , √ , = ,} )

a) Reduzir seu excesso de gordura em cerca de 1% b) Reduzir seu excesso de gordura em cerca de 27% c) Manter seus níveis atuais de gordura

d) Aumentar seu nível de gordura em cerca de 1% e) Aumentar seu nível de gordura em cerca de 27%

● 64) (UEL) Uma das características da sociedade moderna é a identificação cada vez mais precisa dos indivíduos. Um exemplo é o CPF (Cadastro de Pessoa Física), um registro na Receita Federal composto por 11 dígitos, sendo os dois últimos verificadores, para se evitar erros de digitação. O número do CPF tem a seguinte configuração:

−

Onde N1 a N8 são números-base e N9 define a região fiscal, por exemplo, N9 = 9

para Paraná e Santa Catarina. N10 e N11 verificam os números anteriores. O

algoritmo para obter o digito verificador N11 é calculado a partir da soma:

= + + + + + + + + +

Dividindo S10 por 11, obtém-se o resto R desta divisão. Se R = 0 ou R = 1, então N11

= 0; caso contrário N11 = 11 – R.

Considerando o número de CPF 094.610.079 – 9X, assinale a alternativa que

representa corretamente o valor de X.

●● 65) (UNICAMP) As companhias aéreas costumam estabelecer um limite de peso para a bagagem de cada passageiro, cobrando uma taxa por quilograma de excesso de peso. Quando dois passageiros compartilham a bagagem, seus limites

são considerados em conjunto.

Em um determinado voo, tanto um casal como um senhor que viajava sozinho transportaram 60 kg de bagagem e foram obrigados a pagar pelo excesso de peso. O valor que o senhor pagou correspondeu a 3,5 vezes o valor pago pelo casal. Para determinar o peso excedente das bagagens do casal (x) e do senhor que viajava sozinho (y), bem como o limite de peso que um passageiro pode transportar sem pagar qualquer taxa (z), pode-se resolver o seguinte sistema linear:

a) _{ ++ ==

, − =

b) _{ ++ ==

, − =

c) _{ ++ ==

, + =

d) _{ ++ ==

, + =

● 66) (ENEM) Há, em virtude da demanda crescente de economia de água, equipamentos e utensílios como, por exemplo, as bacias sanitárias ecológicas, que utilizam 6 litros de água por descarga em vez dos 15 litros utilizados por bacias sanitárias não ecológicas, conforme dados da Associação Brasileira de Normas

Técnicas (ABNT).

Qual será a economia diária de água obtida por meio da substituição de uma bacia sanitária não ecológica, que gasta cerca de 60 litros por dia com a descarga, por uma bacia sanitária ecológica?

●● 67) (UDESC) Se

ℎ =

−

, então o valor absoluto de h é:

a) _{+ √}

b) c) d)

√ + √

e) √ + √

● 68) (ENEM) Um dos estádios mais bonitos da Copa do Mundo na África do Sul é o Green Point, situado na cidade do cabo com capacidade para 68 000 pessoas.

CENTAURO. Ano 2, edição 8, mar/abr, 2010.

Em certa partida, o estádio estava com 95% de sua capacidade, sendo que 487 pessoas não pagaram o ingresso que custava 150 dólares cada.

A expressão que representa o valor arrecadado nesse jogo, em dólares, é:

a) _{, −}

b) _{, −}

c) _{, −}

d) ₋ 150

e) −

●● 69) (UNEMAT) Um trabalhador ganhou, em um dia, R$ 540,00, incluindo o pagamento de horas extras. O salário (sem horas extras) excede em R$ 200,00 o que o trabalhador recebeu pelas horas extras. Qual é o seu salário sem horas extras?

●● 70) (UFBA) A razão entre a soma e o produto das raízes da equação

− + = , é:

a) 14/9 b) 2/9 c) -14 d) 63/2 e) -63/2

● 71) (PUC-MG) Um avião levanta voo sob um ângulo de 30°. Então, depois que tiver percorrido 500 m, conforme indicado na figura, sua altura h em relação ao solo, em metros, será igual a:

a) 250 m b) 300 m c) 400 m d) 435 m

A altura h do mastro da bandeira, em metros, é

a) _,

b) 1 _{, √}

c) _,

d) _{, √}

e) _,

●● 73) (ITA) Um navio, navegando em linha reta, passa sucessivamente pelos pontos A, B e C. O comandante quando o navio está em A, observa um farol em L, e calcula o ângulo LÂC=30º. Após navegar 4 milhas até B, verifica o ângulo L^BC=75º. Quantas milhas separam o farol do ponto B?

a)

b) _√

c)

d) e) n.d.a

●● 74) (ENEM) As torres Puerta de Europa são duas torres inclinadas uma contra a

Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço

a) Menor que 100 m² b) Entre 100 m² e 300 m² c) Entre 300 m² e 500 m² d) Ente 500 m² e 700 m² e) Maior que 700 m²

●● 75) (ENEM) Um balão atmosférico, lançado em Bauru (343 quilômetros aa Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.

Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.

Qual a altura aproximada em que se encontrava o balão?

a) 1,8 km b) 1,9 km c) 3,1 km d) 3,7 km e) 5,5 km

●● 76) (ENEM) O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6 m e 4 m. A figura representa a situação real na qual os postes são descritos pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e o BC representam cabos de aço que serão instalados.

Qual deve ser o valor do comprimento da haste EF?

a) b)

c) _,

d)

e) _√

● 77) Aplicando o algoritmo de Briot-Ruffini, calcule o coeficiente e o resto das divisões de:

a) _{= − − −} por _{ℎ = −}

b) _{= − +} por _{ℎ = −}

●● 78) (VUNESP) Assinale a alternativa que indica o polinômio que possui os

números 0 e 1 como raízes, sendo 0 uma raiz de multiplicidade 3:

a) _{= −}

b) _{= −}

c) _{= −}

d) _{= − −}

e) _{= + −}

●● 79) (UDESC) Sejam q1(x) e r1(x), respectivamente, o quociente e o resto da

divisão de f(x) = 6x4 - 5x3 + 7x2 + 5x - 11 por g(x) = 2x2 + x -1. Dividindo q1(x) por

r1(x), encontram-se um novo quociente q2(x) e um novo resto r2(x). Analise as

proposições e classifique (V) para verdadeira ou (F) para falsa.

( ) Os polinômios g(x) e q2(x) admitem uma raiz em comum. ( ) Os termos independentes de f(x) e r2(x) possuem o mesmo valor absoluto. ( ) A soma das raízes de q1(x) é raiz de r1(x).

Assinale a alternativa correta, de cima para baixo.

a) F- V – V b) V – F – F c) V – V – F d) V – F – V e) F – V – F

●● 80) (UFRN) A respeito do polinômio = − + − , é correto afirmar:

a) É divisível por (x – 1) b) Possui uma raiz real.

c) O produto de suas raízes é igual a 2.

● 81) (UFG) Considere que no primeiro dia do Rock in Rio 2011, em um certo

momento, o público presente era de cem mil pessoas e que a Cidade do Rock, local do evento, dispunha de quatro portões por onde podiam sair, no máximo, 1250 pessoas por minuto, em cada portão.

Nestas circunstâncias, o tempo mínimo, em minutos, para esvaziar a Cidade do Rock será de:

a) 80 b) 60 c) 50 d) 40 e) 20

● 82) (UEMG)

Vendas de veículos sobem 0,61% em julho ante junho

Os emplacamentos de veículos novos no mercado brasileiro somaram 306 202 unidades em julho, ante 304 332 unidades em junho, o que representou uma ligeira alta de 0,61%, segundo informou hoje a Federação Nacional da Distribuição de Veículos Automotores (Fenabrave).

(...)

Fonte: em.com.br. Acesso em qº/8/2011.

Considerando que a alta de 0,61% na venda de veículos seja constante nos próximos meses, pode-se afirmar CORRETAMENTE que o número y de emplacamentos de veículos novos, no período de x meses, a partir de julho, é representado pela função

a) _{= , +}

b) _{= +}

c) _{= +}

● 83) (FUVEST) A equação

−

+

= −

a) Tem apenas uma raiz real

b) Tem duas raízes reais cuja soma é 1 c) Não tem nenhuma raiz real

d) Tem três raízes reais cuja soma é -1 e) Admite 4 como raiz

● 84) (UFPR) Se as raízes da equação + − = são inteiros, calcular | b |.

●● 85) (PUC) Um professor propôs a seus alunos a resolução de certa equação do

2º grau. Um dos alunos copiou errado apenas o coeficiente do termo do 1º grau e encontrou as raízes 1 e -3; outro, copiou errado apenas o termo constante, encontrando as raízes -2 e 4. A solução da equação original proposta pelo professor é:

13. GABARITO

1 – c

2 – a

3 – c

4 – e

5 – d

6 – e

7 – c

8 – a

9 – d

10 – 12 dias

11 – c

12 – e

13 – 12 horas

14 – e

15 – d

16 – c

17 – c

18 – b

19 – b

20 – d

21 – d

22 – 44 %

23 – e

24 – b

25 – c

26 – a

27 – c

28 – b

29 – 1,66 x 10-24

30 – c

31 – c

32 – b

33 – b

34 – d

35 – b

36 – c

37 – b

38 – a

39 – a

40 – e

41 – e

42 – a

43 – d

44 – c

45 – 76

46 – b

47 – a

48 – a

49 – b

50 – e

51 – b

52 – a

53 – 12

54 – a

55 – d

56 – c

57 – c

58 – c

59 – e

60 – a

61 – c

62 – c

63 – a

64 – a

65 – a

66 – b

67 – e

68 – b

69 – d

70 – a

71 – a

72 – b

73 – b

74 – e

75 – c

76 – c

77 – a) Q(x) = 2x² - 8

R(x) = -43

77 – b) q(x)=x³ + 3x²+ 4x + 12

r(x)= 41

77 – c) q(x)=5x4_-5x3_+5x2_-5x+4

r(x) = -3

78 – c

79 – b

80 – b

81 – a

82 – b

83 – a

84 – 28

REFERÊNCIAS

GIOVANNI, José R., BONJORNO, José R., Matemática Completa. 2.Ed. São

Paulo: Editora FTD, 2005.

IEZZI, Gelson, et al. Matemática. São Paulo: Atual Editora, 1997.

MEDEIROS, Valéria Z., et al. Pré-Cálculo. 2. Ed. São Paulo: Editora Cengage Learning, 2011.

TROTTA, Fernando., IMENES, Luiz M. P., JAKUBOVIC, José. Matemática

Aplicada: 2. São Paulo: Editora Moderna, 1979.

TROTTA, Fernando., IMENES, Luiz M. P., JAKUBOVIC, José. Matemática

Aplicada: 3. São Paulo: Editora Moderna, 1980.