Numerical Mathematics
Alfio Quarteroni
Riccardo Sacco
Fausto Saleri
Texts in Applied Mathematics
m
37
Springer
New York Berlin Heidelberg Barcelona Hong Kong London Milan Paris Singapore TokyoAlfio Quarteroni
MM
Riccardo Sacco
Fausto Saleri
123
Numerical Mathematics
Alfio Quarteroni
Department of Mathematics Ecole Polytechnique
MFe´de´rale de Lausanne CH-1015 Lausanne Switzerland
alfio.quarteroni@epfl.ch
Riccardo Sacco
Dipartimento di Matematica Politecnico di Milano Piazza Leonardo da Vinci 32 20133 Milan
Italy
ricsac@mate.polimi.it
Fausto Saleri
Dipartimento di Matematica,
M“F. Enriques” Università degli Studi di
MMilano Via Saldini 50 20133 Milan Italy
fausto.saleri@unimi.it
Series Editors
J.E. Marsden
Control and Dynamical Systems, 107–81 California Institute of Technology Pasadena, CA 91125
USA M. Golubitsky
Department of Mathematics University of Houston Houston, TX 77204-3476 USA
L. Sirovich
Division of Applied Mathematics Brown University
Providence, RI 02912 USA
W. J¨ager
Department of Applied Mathematics Universit ¨at Heidelberg
Im Neuenheimer Feld 294 69120 Heidelberg Germany
Library of Congress Cataloging-in-Publication Data Quarteroni, Alfio.
Numerical mathematics/Alfio Quarteroni, Riccardo Sacco, Fausto Saleri. p.Mcm. — (Texts in applied mathematics; 37)
Includes bibliographical references and index. ISBN 0-387-98959-5 (alk. paper)
1. Numerical analysis.MI. Sacco, Riccardo.MII. Saleri, Fausto.MIII. Title.MIV. Series. I. Title.MMII. Series.
QA297.Q83M2000
519.4—dc21 99-059414
© 2000 Springer-Verlag New York, Inc.
All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer-Verlag New York, Inc., 175 Fifth Avenue, New York, NY 10010, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or heraf-ter developed is forbidden.
The use of general descriptive names, trade names, trademarks, etc., in this publication, even if the former are not especially identified, is not to be taken as a sign that such names, as understood by the Trade Marks and Merchandise Marks Act, may accordingly be used freely by anyone.
ISBN 0-387-98959-5nSpringer-VerlagnNew YorknBerlinnHeidelbergMSPIN 10747955
Preface
Numerical mathematics is the branch of mathematics that proposes, de-velops, analyzes and applies methods from scientific computing to several fields including analysis, linear algebra, geometry, approximation theory, functional equations, optimization and differential equations. Other disci-plines such as physics, the natural and biological sciences, engineering, and economics and the financial sciences frequently give rise to problems that need scientific computing for their solutions.
As such, numerical mathematics is the crossroad of several disciplines of great relevance in modern applied sciences, and can become a crucial tool for their qualitative and quantitative analysis. This role is also emphasized by the continual development of computers and algorithms, which make it possible nowadays, using scientific computing, to tackle problems of such a large size that real-life phenomena can be simulated providing accurate responses at affordable computational cost.
The corresponding spread of numerical software represents an enrichment for the scientific community. However, the user has to make the correct choice of the method (or the algorithm) which best suits the problem at hand. As a matter of fact, no black-box methods or algorithms exist that can effectively and accurately solve all kinds of problems.
viii Preface
and cons. This is done using the MATLAB 1 software environment. This choice satisfies the two fundamental needs of user-friendliness and wide-spread diffusion, making it available on virtually every computer.
Every chapter is supplied with examples, exercises and applications of the discussed theory to the solution of real-life problems. The reader is thus in the ideal condition for acquiring the theoretical knowledge that is required to make the right choice among the numerical methodologies and make use of the related computer programs.
This book is primarily addressed to undergraduate students, with partic-ular focus on the degree courses in Engineering, Mathematics, Physics and Computer Science. The attention which is paid to the applications and the related development of software makes it valuable also for graduate stu-dents, researchers and users of scientific computing in the most widespread professional fields.
The content of the volume is organized into four parts and 13 chapters. Part I comprises two chapters in which we review basic linear algebra and introduce the general concepts of consistency, stability and convergence of a numerical method as well as the basic elements of computer arithmetic.
Part II is on numerical linear algebra, and is devoted to the solution of linear systems (Chapters 3 and 4) and eigenvalues and eigenvectors com-putation (Chapter 5).
We continue with Part III where we face several issues about functions and their approximation. Specifically, we are interested in the solution of nonlinear equations (Chapter 6), solution of nonlinear systems and opti-mization problems (Chapter 7), polynomial approximation (Chapter 8) and numerical integration (Chapter 9).
Part IV, which is the more demanding as a mathematical background, is concerned with approximation, integration and transforms based on orthog-onal polynomials (Chapter 10), solution of initial value problems (Chap-ter 11), boundary value problems (Chap(Chap-ter 12) and initial-boundary value problems for parabolic and hyperbolic equations (Chapter 13).
Part I provides the indispensable background. Each of the remaining Parts has a size and a content that make it well suited for a semester course.
A guideline index to the use of the numerous MATLAB Programs de-veloped in the book is reported at the end of the volume. These programs are also available at the web site address:
http://www1.mate.polimi.it/˜calnum/programs.html
For the reader’s ease, any code is accompanied by a brief description of its input/output parameters.
We express our thanks to the staff at Springer-Verlag New York for their expert guidance and assistance with editorial aspects, as well as to Dr.
Preface ix
Martin Peters from Springer-Verlag Heidelberg and Dr. Francesca Bonadei from Springer-Italia for their advice and friendly collaboration all along this project.
We gratefully thank Professors L. Gastaldi and A. Valli for their useful comments on Chapters 12 and 13.
We also wish to express our gratitude to our families for their forbearance and understanding, and dedicate this book to them.
Contents
Series Preface v
Preface vii
PART I: Getting Started
1. Foundations of Matrix Analysis 1
1.1 Vector Spaces . . . 1
1.2 Matrices . . . 3
1.3 Operations with Matrices . . . 5
1.3.1 Inverse of a Matrix . . . 6
1.3.2 Matrices and Linear Mappings . . . 7
1.3.3 Operations with Block-Partitioned Matrices . . . . 7
1.4 Trace and Determinant of a Matrix . . . 8
1.5 Rank and Kernel of a Matrix . . . 9
1.6 Special Matrices . . . 10
1.6.1 Block Diagonal Matrices . . . 10
1.6.2 Trapezoidal and Triangular Matrices . . . 11
1.6.3 Banded Matrices . . . 11
1.7 Eigenvalues and Eigenvectors . . . 12
1.8 Similarity Transformations . . . 14
1.9 The Singular Value Decomposition (SVD) . . . 16
1.10 Scalar Product and Norms in Vector Spaces . . . 17
xii Contents
1.11.1 Relation Between Norms and the
Spectral Radius of a Matrix . . . 25
1.11.2 Sequences and Series of Matrices . . . 26
1.12 Positive Definite, Diagonally Dominant and M-Matrices . 27 1.13 Exercises . . . 30
2. Principles of Numerical Mathematics 33 2.1 Well-Posedness and Condition Number of a Problem . . . 33
2.2 Stability of Numerical Methods . . . 37
2.2.1 Relations Between Stability and Convergence . . . 40
2.3 A priorianda posterioriAnalysis . . . 41
2.4 Sources of Error in Computational Models . . . 43
2.5 Machine Representation of Numbers . . . 45
2.5.1 The Positional System . . . 45
2.5.2 The Floating-Point Number System . . . 46
2.5.3 Distribution of Floating-Point Numbers . . . 49
2.5.4 IEC/IEEE Arithmetic . . . 49
2.5.5 Rounding of a Real Number in Its Machine Representation . . . 50
2.5.6 Machine Floating-Point Operations . . . 52
2.6 Exercises . . . 54
PART II: Numerical Linear Algebra 3. Direct Methods for the Solution of Linear Systems 57 3.1 Stability Analysis of Linear Systems . . . 58
3.1.1 The Condition Number of a Matrix . . . 58
3.1.2 Forwarda prioriAnalysis . . . 60
3.1.3 Backwarda prioriAnalysis . . . 63
3.1.4 A posterioriAnalysis . . . 64
3.2 Solution of Triangular Systems . . . 65
3.2.1 Implementation of Substitution Methods . . . 65
3.2.2 Rounding Error Analysis . . . 67
3.2.3 Inverse of a Triangular Matrix . . . 67
3.3 The Gaussian Elimination Method (GEM) and LU Factorization . . . 68
3.3.1 GEM as a Factorization Method . . . 72
3.3.2 The Effect of Rounding Errors . . . 76
3.3.3 Implementation of LU Factorization . . . 77
3.3.4 Compact Forms of Factorization . . . 78
3.4 Other Types of Factorization . . . 79
3.4.1 LDMT Factorization . . . . 79
3.4.2 Symmetric and Positive Definite Matrices: The Cholesky Factorization . . . 80
Contents xiii
3.5 Pivoting . . . 85
3.6 Computing the Inverse of a Matrix . . . 89
3.7 Banded Systems . . . 90
3.7.1 Tridiagonal Matrices . . . 91
3.7.2 Implementation Issues . . . 92
3.8 Block Systems . . . 93
3.8.1 Block LU Factorization . . . 94
3.8.2 Inverse of a Block-Partitioned Matrix . . . 95
3.8.3 Block Tridiagonal Systems . . . 95
3.9 Sparse Matrices . . . 97
3.9.1 The Cuthill-McKee Algorithm . . . 98
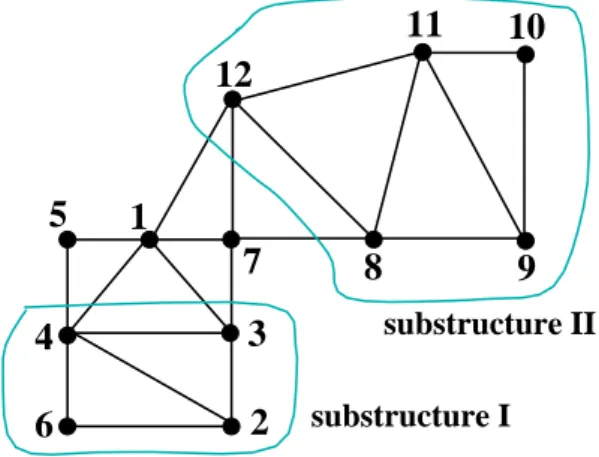
3.9.2 Decomposition into Substructures . . . 100
3.9.3 Nested Dissection . . . 103
3.10 Accuracy of the Solution Achieved Using GEM . . . 103
3.11 An Approximate Computation ofK(A) . . . 106
3.12 Improving the Accuracy of GEM . . . 109
3.12.1 Scaling . . . 110
3.12.2 Iterative Refinement . . . 111
3.13 Undetermined Systems . . . 112
3.14 Applications . . . 115
3.14.1 Nodal Analysis of a Structured Frame . . . 115
3.14.2 Regularization of a Triangular Grid . . . 118
3.15 Exercises . . . 121
4. Iterative Methods for Solving Linear Systems 123 4.1 On the Convergence of Iterative Methods . . . 123
4.2 Linear Iterative Methods . . . 126
4.2.1 Jacobi, Gauss-Seidel and Relaxation Methods . . . 127
4.2.2 Convergence Results for Jacobi and Gauss-Seidel Methods . . . 129
4.2.3 Convergence Results for the Relaxation Method . 131 4.2.4 A prioriForward Analysis . . . 132
4.2.5 Block Matrices . . . 133
4.2.6 Symmetric Form of the Gauss-Seidel and SOR Methods . . . 133
4.2.7 Implementation Issues . . . 135
4.3 Stationary and Nonstationary Iterative Methods . . . 136
4.3.1 Convergence Analysis of the Richardson Method . 137 4.3.2 Preconditioning Matrices . . . 139
4.3.3 The Gradient Method . . . 146
4.3.4 The Conjugate Gradient Method . . . 150
4.3.5 The Preconditioned Conjugate Gradient Method . 156 4.3.6 The Alternating-Direction Method . . . 158
4.4 Methods Based on Krylov Subspace Iterations . . . 159
xiv Contents
4.4.2 The GMRES Method . . . 165
4.4.3 The Lanczos Method for Symmetric Systems . . . 167
4.5 The Lanczos Method for Unsymmetric Systems . . . 168
4.6 Stopping Criteria . . . 171
4.6.1 A Stopping Test Based on the Increment . . . 172
4.6.2 A Stopping Test Based on the Residual . . . 174
4.7 Applications . . . 174
4.7.1 Analysis of an Electric Network . . . 174
4.7.2 Finite Difference Analysis of Beam Bending . . . . 177
4.8 Exercises . . . 179
5. Approximation of Eigenvalues and Eigenvectors 183 5.1 Geometrical Location of the Eigenvalues . . . 183
5.2 Stability and Conditioning Analysis . . . 186
5.2.1 A prioriEstimates . . . 186
5.2.2 A posterioriEstimates . . . 190
5.3 The Power Method . . . 192
5.3.1 Approximation of the Eigenvalue of Largest Module . . . 192
5.3.2 Inverse Iteration . . . 195
5.3.3 Implementation Issues . . . 196
5.4 The QR Iteration . . . 200
5.5 The Basic QR Iteration . . . 201
5.6 The QR Method for Matrices in Hessenberg Form . . . 203
5.6.1 Householder and Givens Transformation Matrices 204 5.6.2 Reducing a Matrix in Hessenberg Form . . . 207
5.6.3 QR Factorization of a Matrix in Hessenberg Form 209 5.6.4 The Basic QR Iteration Starting from Upper Hessenberg Form . . . 210
5.6.5 Implementation of Transformation Matrices . . . . 212
5.7 The QR Iteration with Shifting Techniques . . . 215
5.7.1 The QR Method with Single Shift . . . 215
5.7.2 The QR Method with Double Shift . . . 218
5.8 Computing the Eigenvectors and the SVD of a Matrix . . 221
5.8.1 The Hessenberg Inverse Iteration . . . 221
5.8.2 Computing the Eigenvectors from the Schur Form of a Matrix . . . 221
5.8.3 Approximate Computation of the SVD of a Matrix 222 5.9 The Generalized Eigenvalue Problem . . . 224
5.9.1 Computing the Generalized Real Schur Form . . . 225
5.9.2 Generalized Real Schur Form of Symmetric-Definite Pencils . . . 226
5.10 Methods for Eigenvalues of Symmetric Matrices . . . 227
5.10.1 The Jacobi Method . . . 227
Contents xv
5.11 The Lanczos Method . . . 233
5.12 Applications . . . 235
5.12.1 Analysis of the Buckling of a Beam . . . 236
5.12.2 Free Dynamic Vibration of a Bridge . . . 238
5.13 Exercises . . . 240
PART III: Around Functions and Functionals 6. Rootfinding for Nonlinear Equations 245 6.1 Conditioning of a Nonlinear Equation . . . 246
6.2 A Geometric Approach to Rootfinding . . . 248
6.2.1 The Bisection Method . . . 248
6.2.2 The Methods of Chord, Secant and Regula Falsi and Newton’s Method . . . 251
6.2.3 The Dekker-Brent Method . . . 256
6.3 Fixed-Point Iterations for Nonlinear Equations . . . 257
6.3.1 Convergence Results for Some Fixed-Point Methods . . . 260
6.4 Zeros of Algebraic Equations . . . 261
6.4.1 The Horner Method and Deflation . . . 262
6.4.2 The Newton-Horner Method . . . 263
6.4.3 The Muller Method . . . 267
6.5 Stopping Criteria . . . 269
6.6 Post-Processing Techniques for Iterative Methods . . . 272
6.6.1 Aitken’s Acceleration . . . 272
6.6.2 Techniques for Multiple Roots . . . 275
6.7 Applications . . . 276
6.7.1 Analysis of the State Equation for a Real Gas . . 276
6.7.2 Analysis of a Nonlinear Electrical Circuit . . . 277
6.8 Exercises . . . 279
7. Nonlinear Systems and Numerical Optimization 281 7.1 Solution of Systems of Nonlinear Equations . . . 282
7.1.1 Newton’s Method and Its Variants . . . 283
7.1.2 Modified Newton’s Methods . . . 284
7.1.3 Quasi-Newton Methods . . . 288
7.1.4 Secant-Like Methods . . . 288
7.1.5 Fixed-Point Methods . . . 290
7.2 Unconstrained Optimization . . . 294
7.2.1 Direct Search Methods . . . 295
7.2.2 Descent Methods . . . 300
7.2.3 Line Search Techniques . . . 302
7.2.4 Descent Methods for Quadratic Functions . . . 304
xvi Contents
7.2.7 Secant-Like Methods . . . 309
7.3 Constrained Optimization . . . 311
7.3.1 Kuhn-Tucker Necessary Conditions for Nonlinear Programming . . . 313
7.3.2 The Penalty Method . . . 315
7.3.3 The Method of Lagrange Multipliers . . . 317
7.4 Applications . . . 319
7.4.1 Solution of a Nonlinear System Arising from Semiconductor Device Simulation . . . 320
7.4.2 Nonlinear Regularization of a Discretization Grid . 323 7.5 Exercises . . . 325
8. Polynomial Interpolation 327 8.1 Polynomial Interpolation . . . 328
8.1.1 The Interpolation Error . . . 329
8.1.2 Drawbacks of Polynomial Interpolation on Equally Spaced Nodes and Runge’s Counterexample . . . . 330
8.1.3 Stability of Polynomial Interpolation . . . 332
8.2 Newton Form of the Interpolating Polynomial . . . 333
8.2.1 Some Properties of Newton Divided Differences . . 335
8.2.2 The Interpolation Error Using Divided Differences 337 8.3 Piecewise Lagrange Interpolation . . . 338
8.4 Hermite-Birkoff Interpolation . . . 341
8.5 Extension to the Two-Dimensional Case . . . 343
8.5.1 Polynomial Interpolation . . . 343
8.5.2 Piecewise Polynomial Interpolation . . . 344
8.6 Approximation by Splines . . . 348
8.6.1 Interpolatory Cubic Splines . . . 349
8.6.2 B-Splines . . . 353
8.7 Splines in Parametric Form . . . 357
8.7.1 B´ezier Curves and Parametric B-Splines . . . 359
8.8 Applications . . . 362
8.8.1 Finite Element Analysis of a Clamped Beam . . . 363
8.8.2 Geometric Reconstruction Based on Computer Tomographies . . . 366
8.9 Exercises . . . 368
9. Numerical Integration 371 9.1 Quadrature Formulae . . . 371
9.2 Interpolatory Quadratures . . . 373
9.2.1 The Midpoint or Rectangle Formula . . . 373
9.2.2 The Trapezoidal Formula . . . 375
9.2.3 The Cavalieri-Simpson Formula . . . 377
9.3 Newton-Cotes Formulae . . . 378
Contents xvii
9.5 Hermite Quadrature Formulae . . . 386
9.6 Richardson Extrapolation . . . 387
9.6.1 Romberg Integration . . . 389
9.7 Automatic Integration . . . 391
9.7.1 Non Adaptive Integration Algorithms . . . 392
9.7.2 Adaptive Integration Algorithms . . . 394
9.8 Singular Integrals . . . 398
9.8.1 Integrals of Functions with Finite Jump Discontinuities . . . 398
9.8.2 Integrals of Infinite Functions . . . 398
9.8.3 Integrals over Unbounded Intervals . . . 401
9.9 Multidimensional Numerical Integration . . . 402
9.9.1 The Method of Reduction Formula . . . 403
9.9.2 Two-Dimensional Composite Quadratures . . . 404
9.9.3 Monte Carlo Methods for Numerical Integration . . . 407
9.10 Applications . . . 408
9.10.1 Computation of an Ellipsoid Surface . . . 408
9.10.2 Computation of the Wind Action on a Sailboat Mast . . . 410
9.11 Exercises . . . 412
PART IV: Transforms, Differentiation and Problem Discretization 10. Orthogonal Polynomials in Approximation Theory 415 10.1 Approximation of Functions by Generalized Fourier Series 415 10.1.1 The Chebyshev Polynomials . . . 417
10.1.2 The Legendre Polynomials . . . 419
10.2 Gaussian Integration and Interpolation . . . 419
10.3 Chebyshev Integration and Interpolation . . . 424
10.4 Legendre Integration and Interpolation . . . 426
10.5 Gaussian Integration over Unbounded Intervals . . . 428
10.6 Programs for the Implementation of Gaussian Quadratures 429 10.7 Approximation of a Function in the Least-Squares Sense . 431 10.7.1 Discrete Least-Squares Approximation . . . 431
10.8 The Polynomial of Best Approximation . . . 433
10.9 Fourier Trigonometric Polynomials . . . 435
10.9.1 The Gibbs Phenomenon . . . 439
10.9.2 The Fast Fourier Transform . . . 440
10.10 Approximation of Function Derivatives . . . 442
10.10.1 Classical Finite Difference Methods . . . 442
10.10.2 Compact Finite Differences . . . 444
10.10.3 Pseudo-Spectral Derivative . . . 448
xviii Contents
10.11.1 The Fourier Transform . . . 450
10.11.2 (Physical) Linear Systems and Fourier Transform . 453 10.11.3 The Laplace Transform . . . 455
10.11.4 The Z-Transform . . . 457
10.12 The Wavelet Transform . . . 458
10.12.1 The Continuous Wavelet Transform . . . 458
10.12.2 Discrete and Orthonormal Wavelets . . . 461
10.13 Applications . . . 463
10.13.1 Numerical Computation of Blackbody Radiation . 463 10.13.2 Numerical Solution of Schr¨odinger Equation . . . . 464
10.14 Exercises . . . 467
11. Numerical Solution of Ordinary Differential Equations 469 11.1 The Cauchy Problem . . . 469
11.2 One-Step Numerical Methods . . . 472
11.3 Analysis of One-Step Methods . . . 473
11.3.1 The Zero-Stability . . . 475
11.3.2 Convergence Analysis . . . 477
11.3.3 The Absolute Stability . . . 479
11.4 Difference Equations . . . 482
11.5 Multistep Methods . . . 487
11.5.1 Adams Methods . . . 490
11.5.2 BDF Methods . . . 492
11.6 Analysis of Multistep Methods . . . 492
11.6.1 Consistency . . . 493
11.6.2 The Root Conditions . . . 494
11.6.3 Stability and Convergence Analysis for Multistep Methods . . . 495
11.6.4 Absolute Stability of Multistep Methods . . . 499
11.7 Predictor-Corrector Methods . . . 502
11.8 Runge-Kutta Methods . . . 508
11.8.1 Derivation of an Explicit RK Method . . . 511
11.8.2 Stepsize Adaptivity for RK Methods . . . 512
11.8.3 Implicit RK Methods . . . 514
11.8.4 Regions of Absolute Stability for RK Methods . . 516
11.9 Systems of ODEs . . . 517
11.10 Stiff Problems . . . 519
11.11 Applications . . . 521
11.11.1 Analysis of the Motion of a Frictionless Pendulum 522 11.11.2 Compliance of Arterial Walls . . . 523
11.12 Exercises . . . 527
12. Two-Point Boundary Value Problems 531 12.1 A Model Problem . . . 531
Contents xix
12.2.1 Stability Analysis by the Energy Method . . . 534
12.2.2 Convergence Analysis . . . 538
12.2.3 Finite Differences for Two-Point Boundary Value Problems with Variable Coefficients . . . 540
12.3 The Spectral Collocation Method . . . 542
12.4 The Galerkin Method . . . 544
12.4.1 Integral Formulation of Boundary-Value Problems 544 12.4.2 A Quick Introduction to Distributions . . . 546
12.4.3 Formulation and Properties of the Galerkin Method . . . 547
12.4.4 Analysis of the Galerkin Method . . . 548
12.4.5 The Finite Element Method . . . 550
12.4.6 Implementation Issues . . . 556
12.4.7 Spectral Methods . . . 559
12.5 Advection-Diffusion Equations . . . 560
12.5.1 Galerkin Finite Element Approximation . . . 561
12.5.2 The Relationship Between Finite Elements and Finite Differences; the Numerical Viscosity . . . . 563
12.5.3 Stabilized Finite Element Methods . . . 567
12.6 A Quick Glance to the Two-Dimensional Case . . . 572
12.7 Applications . . . 575
12.7.1 Lubrication of a Slider . . . 575
12.7.2 Vertical Distribution of Spore Concentration over Wide Regions . . . 576
12.8 Exercises . . . 578
13. Parabolic and Hyperbolic Initial Boundary Value Problems 581 13.1 The Heat Equation . . . 581
13.2 Finite Difference Approximation of the Heat Equation . . 584
13.3 Finite Element Approximation of the Heat Equation . . . 586
13.3.1 Stability Analysis of theθ-Method . . . 588
13.4 Space-Time Finite Element Methods for the Heat Equation . . . 593
13.5 Hyperbolic Equations: A Scalar Transport Problem . . . . 597
13.6 Systems of Linear Hyperbolic Equations . . . 599
13.6.1 The Wave Equation . . . 601
13.7 The Finite Difference Method for Hyperbolic Equations . . 602
13.7.1 Discretization of the Scalar Equation . . . 602
13.8 Analysis of Finite Difference Methods . . . 605
13.8.1 Consistency . . . 605
13.8.2 Stability . . . 605
13.8.3 The CFL Condition . . . 606
13.8.4 Von Neumann Stability Analysis . . . 608
xx Contents
13.9.1 Equivalent Equations . . . 614
13.10 Finite Element Approximation of Hyperbolic Equations . . 618
13.10.1 Space Discretization with Continuous and Discontinuous Finite Elements . . . 618
13.10.2 Time Discretization . . . 620
13.11 Applications . . . 623
13.11.1 Heat Conduction in a Bar . . . 623
13.11.2 A Hyperbolic Model for Blood Flow Interaction with Arterial Walls . . . 623
13.12 Exercises . . . 625
References 627
Index of MATLAB Programs 643
1
Foundations of Matrix Analysis
In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text. For most of the proofs as well as for the details, the reader is referred to [Bra75], [Nob69], [Hal58]. Further results on eigenvalues can be found in [Hou75] and [Wil65].
1.1 Vector Spaces
Definition 1.1 Avector spaceover the numeric fieldK(K=RorK=C) is a nonempty set V, whose elements are called vectorsand in which two operations are defined, calledadditionandscalar multiplication, that enjoy the following properties:
1. addition is commutative and associative;
2. there exists an element0∈ V (the zero vector or null vector) such thatv+0=vfor eachv∈V;
3. 0·v=0, 1·v=v, where 0 and 1 are respectively the zero and the unity ofK;
4. for each elementv∈V there exists its opposite, −v, inV such that
2 1. Foundations of Matrix Analysis
5. the following distributive properties hold
∀α∈K, ∀v,w∈V, α(v+w) =αv+αw,
∀α, β∈K, ∀v∈V, (α+β)v=αv+βv;
6. the following associative property holds
∀α, β∈K, ∀v∈V, (αβ)v=α(βv).
Example 1.1 Remarkable instances of vector spaces are:
- V =Rn(respectivelyV =Cn): the set of then-tuples of real (respectively complex) numbers,n≥1;
- V =Pn: the set of polynomialspn(x) =nk=0akxk with real (or complex)
coefficientsakhaving degree less than or equal ton,n≥0;
-V =Cp([a, b]): the set of real (or complex)-valued functions which are
con-tinuous on [a, b] up to theirp-th derivative, 0≤p <∞. •
Definition 1.2 We say that a nonempty partW ofV is avector subspace
ofV iffW is a vector space over K.
Example 1.2 The vector spacePnis a vector subspace ofC∞(R), which is the
space of infinite continuously differentiable functions on the real line. A trivial subspace of any vector space is the one containing only the zero vector. •
In particular, the setW of the linear combinations of a system ofpvectors ofV,{v1, . . . ,vp}, is a vector subspace ofV, called thegenerated subspace or spanof the vector system, and is denoted by
W = span{v1, . . . ,vp}
={v=α1v1+. . .+αpvp withαi∈K, i= 1, . . . , p}.
The system{v1, . . . ,vp} is called a system ofgeneratorsforW. IfW1, . . . , Wmare vector subspaces ofV, then the set
S={w: w=v1+. . .+vmwithvi∈Wi, i= 1, . . . , m}
1.2 Matrices 3
Definition 1.3 A system of vectors {v1, . . . ,vm} of a vector space V is called linearly independentif the relation
α1v1+α2v2+. . .+αmvm=0
withα1, α2, . . . , αm∈Kimplies thatα1=α2=. . .=αm= 0. Otherwise, the system will be calledlinearly dependent.
We call a basis ofV any system of linearly independent generators of V. If {u1, . . . ,un} is a basis of V, the expression v = v1u1+. . .+vnun is called the decomposition of v with respect to the basis and the scalars
v1, . . . , vn ∈ K are the components of v with respect to the given basis. Moreover, the following property holds.
Property 1.1 Let V be a vector space which admits a basis ofn vectors.
Then every system of linearly independent vectors of V has at most n
el-ements and any other basis of V has n elements. The number n is called
the dimension ofV and we writedim(V) =n.
If, instead, for any n there always exist n linearly independent vectors of
V, the vector space is called infinite dimensional.
Example 1.3 For any integerpthe spaceCp([a, b]) is infinite dimensional. The
spacesRnandCnhave dimension equal ton. The usual basis forRnis the set of
unit vectors {e1, . . . ,en}where (ei)j=δij fori, j= 1, . . . n, where δij denotes
theKronecker symbol equal to 0 ifi=j and 1 ifi=j. This choice is of course not the only one that is possible (see Exercise 2). •
1.2 Matrices
Letmandnbe two positive integers. We call amatrixhavingmrows and
n columns, or a matrixm×n, or a matrix (m, n), with elements in K, a set ofmn scalarsaij ∈K, withi= 1, . . . , mand j= 1, . . . n, represented in the following rectangular array
A =
a11 a12 . . . a1n
a21 a22 . . . a2n ..
. ... ...
am1 am2 . . . amn
. (1.1)
4 1. Foundations of Matrix Analysis
We shall abbreviate (1.1) as A = (aij) withi= 1, . . . , mandj = 1, . . . n. The index i is called row index, while j is the column index. The set (ai1, ai2, . . . , ain) is called the i-th row of A; likewise, (a1j, a2j, . . . , amj) is thej-th columnof A.
If n=m the matrix is called squared or having ordern and the set of the entries (a11, a22, . . . , ann) is called itsmain diagonal.
A matrix having one row or one column is called arow vectororcolumn
vectorrespectively. Unless otherwise specified, we shall always assume that
a vector is a column vector. In the casen=m= 1, the matrix will simply denote a scalar ofK.
Sometimes it turns out to be useful to distinguish within a matrix the set made up by specified rows and columns. This prompts us to introduce the following definition.
Definition 1.4 Let A be a matrixm×n. Let 1≤i1< i2< . . . < ik ≤m and 1≤j1< j2< . . . < jl≤ntwo sets of contiguous indexes. The matrix S(k×l) of entries spq =aipjq with p = 1, . . . , k, q = 1, . . . , l is called a
submatrixof A. Ifk=l andir=jr forr= 1, . . . , k, S is called aprincipal
submatrixof A.
Definition 1.5 A matrix A(m×n) is called block partitioned or said to
be partitioned into submatricesif
A =
A11 A12 . . . A1l A21 A22 . . . A2l
..
. ... . .. ... Ak1 Ak2 . . . Akl
,
where Aij are submatrices of A.
Among the possible partitions of A, we recall in particular the partition by columns
A = (a1, a2, . . . ,an),
aibeing thei-th column vector of A. In a similar way the partition by rows of A can be defined. To fix the notations, if A is a matrix m×n, we shall denote by
A(i1:i2, j1:j2) = (aij) i1≤i≤i2, j1≤j ≤j2
the submatrix of A of size (i2−i1+ 1)×(j2−j1+ 1) that lies between the rowsi1 andi2 and the columnsj1 andj2. Likewise, ifvis a vector of size
n, we shall denote byv(i1 :i2) the vector of size i2−i1+ 1 made up by thei1-th to thei2-th components ofv.
1.3 Operations with Matrices 5
1.3 Operations with Matrices
Let A = (aij) and B = (bij) be two matricesm×n overK. We say that
A is equal to B, if aij =bij for i= 1, . . . , m, j = 1, . . . , n. Moreover, we
define the following operations:
- matrix sum: the matrix sum is the matrix A+B = (aij+bij). The neutral
element in a matrix sum is thenull matrix, still denoted by 0 and made up only by null entries;
- matrix multiplication by a scalar: the multiplication of A by λ∈K, is a
matrixλA = (λaij);
- matrix product: the product of two matrices A and B of sizes (m, p)
and (p, n) respectively, is a matrix C(m, n) whose entries are cij = p
k=1
aikbkj, fori= 1, . . . , m,j= 1, . . . , n.
The matrix product is associative and distributive with respect to the ma-trix sum, but it is not in general commutative. The square matrices for which the property AB = BA holds, will be called commutative.
In the case of square matrices, the neutral element in the matrix product is a square matrix of order n called the unit matrix of order n or, more frequently, the identity matrix given by In = (δij). The identity matrix is, by definition, the only matrix n×n such that AIn = InA = A for all square matrices A. In the following we shall omit the subscriptnunless it is strictly necessary. The identity matrix is a special instance of adiagonal
matrixof ordern, that is, a square matrix of the type D = (diiδij). We will
use in the following the notation D = diag(d11, d22, . . . , dnn).
Finally, if A is a square matrix of ordernandpis an integer, we define Ap as the product of A with itself iterated ptimes. We let A0= I.
Let us now address the so-called elementary row operations that can be performed on a matrix. They consist of:
- multiplying the i-th row of a matrix by a scalar α; this operation is equivalent to pre-multiplying A by the matrix D = diag(1, . . . ,1, α,
1, . . . ,1), whereαoccupies thei-th position;
- exchanging the i-th and j-th rows of a matrix; this can be done by pre-multiplying A by the matrix P(i,j)of elements
p(i,j)rs =
1 ifr=s= 1, . . . , i−1, i+ 1, . . . , j−1, j+ 1, . . . n,
1 ifr=j, s=ior r=i, s=j,
0 otherwise,
6 1. Foundations of Matrix Analysis
where Ir denotes the identity matrix of order r = j−i−1 if j > i (henceforth, matrices with size equal to zero will correspond to the empty set). Matrices like (1.2) are calledelementary permutation
matrices. The product of elementary permutation matrices is called
apermutation matrix, and it performs the row exchanges associated
with each elementary permutation matrix. In practice, a permutation matrix is a reordering by rows of the identity matrix;
- adding αtimes the j-th row of a matrix to itsi-th row. This operation can also be performed by pre-multiplying A by the matrix I + N(i,j)α , where N(i,j)α is a matrix having null entries except the one in position
i, jwhose value isα.
1.3.1 Inverse of a Matrix
Definition 1.6 A square matrix A of ordernis calledinvertible(orregular
or nonsingular) if there exists a square matrix B of order n such that
A B = B A = I. B is called theinverse matrixof A and is denoted by A−1. A matrix which is not invertible is calledsingular.
If A is invertible its inverse is also invertible, with (A−1)−1= A. Moreover, if A and B are two invertible matrices of order n, their product AB is also invertible, with (A B)−1= B−1A−1. The following property holds.
Property 1.2 A square matrix is invertible iff its column vectors are lin-early independent.
Definition 1.7 We call the transpose of a matrix A∈ Rm×n the matrix
n×m, denoted by AT, that is obtained by exchanging the rows of A with
the columns of A.
Clearly, (AT)T = A, (A + B)T = AT + BT, (AB)T = BTAT and (αA)T =
αAT
∀α∈R. If A is invertible, then also (AT)−1= (A−1)T = A−T.
Definition 1.8 Let A∈Cm×n; the matrix B = AH
∈Cn×mis called the
conjugate transpose(oradjoint) of A ifbij= ¯aji, where ¯ajiis the complex
conjugate ofaji.
In analogy with the case of the real matrices, it turns out that (A+B)H = AH+ BH, (AB)H= BHAH and (αA)H= ¯αAH
∀α∈C.
1.3 Operations with Matrices 7
Definition 1.10 A matrix A∈Cn×n is calledhermitianorself-adjoint if AT = ¯A, that is, if AH = A, while it is calledunitary if AHA = AAH= I. Finally, if AAH = AHA, A is callednormal. As a consequence, a unitary matrix is one such that A−1= AH.
Of course, a unitary matrix is also normal, but it is not in general her-mitian. For instance, the matrix of the Example 1.4 is unitary, although not symmetric (if s= 0). We finally notice that the diagonal entries of an hermitian matrix must necessarily be real (see also Exercise 5).
1.3.2 Matrices and Linear Mappings
Definition 1.11 Alinear mapfrom Cn into Cm is a functionf :Cn−→ Cmsuch thatf(αx+βy) =αf(x) +βf(y),∀α, β∈Kand∀x,y∈Cn.
The following result links matrices and linear maps.
Property 1.3 Let f : Cn −→ Cm be a linear map. Then, there exists a
unique matrixAf ∈Cm×n such that
f(x) = Afx ∀x∈Cn. (1.3)
Conversely, if Af ∈ Cm×n then the function defined in (1.3) is a linear
map fromCn intoCm.
Example 1.4 An important example of a linear map is the counterclockwise
rotation by an angleϑ in the plane (x1, x2). The matrix associated with such a
map is given by
G(ϑ) =
c s
−s c
, c= cos(ϑ), s= sin(ϑ)
and it is called arotation matrix. •
1.3.3 Operations with Block-Partitioned Matrices
All the operations that have been previously introduced can be extended to the case of a block-partitioned matrix A, provided that the size of each single block is such that any single matrix operation is well-defined. Indeed, the following result can be shown (see, e.g., [Ste73]).
Property 1.4 Let AandBbe the block matrices
A =
A11 . . . A1l
..
. . .. ...
Ak1 . . . Akl
, B =
B11 . . . B1n
..
. . .. ...
Bm1 . . . Bmn
8 1. Foundations of Matrix Analysis
1.
λA =
λA11 . . . λA1l
..
. . .. ...
λAk1 . . . λAkl
, λ∈C; AT =
AT
11 . . . ATk1
..
. . .. ...
AT
1l . . . ATkl
;
2. ifk=m,l=n,mi=ki andnj =lj, then
A + B =
A11+ B11 . . . A1l+ B1l
..
. . .. ...
Ak1+ Bk1 . . . Akl+ Bkl
;
3. ifl=m,li=mi andki =ni, then, letting Cij=
m
s=1 AisBsj,
AB =
C11 . . . C1l
..
. . .. ...
Ck1 . . . Ckl
.
1.4 Trace and Determinant of a Matrix
Let us consider a square matrix A of ordern. Thetraceof a matrix is the
sum of the diagonal entries of A, that is tr(A) = n
i=1
aii.
We call thedeterminantof A the scalar defined through the following for-mula
det(A) = π∈P
sign(π)a1π1a2π2. . . anπn,
where P =π= (π1, . . . , πn)T is the set of the n! vectors that are ob-tained by permuting the index vectori= (1, . . . , n)T and sign(π) equal to 1 (respectively, −1) if an even (respectively, odd) number of exchanges is needed to obtainπ fromi.
The following properties hold
det(A) = det(AT), det(AB) = det(A)det(B), det(A−1) = 1/det(A),
det(AH) = det(A), det(αA) =αndet(A),
∀α∈K.
1.5 Rank and Kernel of a Matrix 9
of sign in the determinant. Of course, the determinant of a diagonal matrix is the product of the diagonal entries.
Denoting by Aij the matrix of order n−1 obtained from A by elimi-nating thei-th row and thej-th column, we call thecomplementary minor
associated with the entry aij the determinant of the matrix Aij. We call
the k-th principal (dominating) minor of A, dk, the determinant of the
principal submatrix of order k, Ak = A(1 : k,1 : k). If we denote by ∆ij = (−1)i+jdet(A
ij) the cofactorof the entry aij, the actual computa-tion of the determinant of A can be performed using the following recursive relation
det(A) =
a11 if n= 1,
n
j=1
∆ijaij, forn >1,
(1.4)
which is known as the Laplace rule. If A is a square invertible matrix of ordern, then
A−1= 1 det(A)C
where C is the matrix having entries ∆ji,i, j= 1, . . . , n.
As a consequence, a square matrix is invertible iff its determinant is non-vanishing. In the case of nonsingular diagonal matrices the inverse is still a diagonal matrix having entries given by the reciprocals of the diagonal entries of the matrix.
Everyorthogonal matrixis invertible, its inverse is given by AT, moreover det(A) =±1.
1.5 Rank and Kernel of a Matrix
Let A be a rectangular matrix m×n. We call the determinant of order
q (with q ≥ 1) extracted from matrix A, the determinant of any square
matrix of order q obtained from A by eliminating m−q rows and n−q
columns.
Definition 1.12 The rank of A (denoted by rank(A)) is the maximum order of the nonvanishing determinants extracted from A. A matrix has
complete or full rankif rank(A) = min(m,n).
Notice that the rank of A represents the maximum number of linearly independent column vectors of A that is, the dimension of therangeof A, defined as
10 1. Foundations of Matrix Analysis
Rigorously speaking, one should distinguish between the column rank of A and the row rank of A, the latter being the maximum number of linearly independent row vectors of A. Nevertheless, it can be shown that the row rank and column rank do actually coincide.
Thekernelof A is defined as the subspace
ker(A) ={x∈Rn : Ax=0}.
The following relations hold
1. rank(A) = rank(AT) (if A∈Cm×n, rank(A) = rank(AH)) 2. rank(A) + dim(ker(A)) =n.
In general, dim(ker(A))= dim(ker(AT)). If A is a nonsingular square ma-trix, then rank(A) =nand dim(ker(A)) = 0.
Example 1.5 Let
A =
1 1 0 1 −1 1
.
Then, rank(A) = 2, dim(ker(A)) = 1 and dim(ker(AT)) = 0. •
We finally notice that for a matrix A∈Cn×n the following properties are equivalent:
1. A is nonsingular;
2. det(A)= 0;
3. ker(A) ={0};
4. rank(A) =n;
5. A has linearly independent rows and columns.
1.6 Special Matrices
1.6.1 Block Diagonal Matrices
These are matrices of the form D = diag(D1, . . . ,Dn), where Diare square matrices with i = 1, . . . , n. Clearly, each single diagonal block can be of different size. We shall say that a block diagonal matrix has size n if n
1.6 Special Matrices 11
1.6.2 Trapezoidal and Triangular Matrices
A matrix A(m×n) is calledupper trapezoidalifaij = 0 fori > j, while it
is lower trapezoidalifaij = 0 fori < j. The name is due to the fact that,
in the case of upper trapezoidal matrices, withm < n, the nonzero entries of the matrix form a trapezoid.
Atriangular matrixis a square trapezoidal matrix of ordernof the form
L =
l11 0 . . . 0
l21 l22 . . . 0 ..
. ... ...
ln1 ln2 . . . lnn
or U =
u11 u12 . . . u1n 0 u22 . . . u2n
..
. ... ... 0 0 . . . unn
.
The matrix L is calledlower triangular while U isupper triangular. Let us recall some algebraic properties of triangular matrices that are easy to check.
- The determinant of a triangular matrix is the product of the diagonal entries;
- the inverse of a lower (respectively, upper) triangular matrix is still lower (respectively, upper) triangular;
- the product of two lower triangular (respectively, upper trapezoidal) ma-trices is still lower triangular (respectively, upper trapezodial);
- if we call unit triangular matrix a triangular matrix that has diagonal entries equal to 1, then, the product of lower (respectively, upper) unit triangular matrices is still lower (respectively, upper) unit triangular.
1.6.3 Banded Matrices
The matrices introduced in the previous section are a special instance of banded matrices. Indeed, we say that a matrix A ∈Rm×n (or in Cm×n)
has lower band p if aij = 0 when i > j+p and upper band q if aij = 0
whenj > i+q. Diagonal matrices are banded matrices for whichp=q= 0, while trapezoidal matrices havep=m−1,q= 0 (lower trapezoidal),p= 0,
q=n−1 (upper trapezoidal).
Other banded matrices of relevant interest are the tridiagonal matrices
for whichp=q= 1 and theupper bidiagonal(p= 0,q= 1) orlower bidiag-onal(p= 1,q= 0). In the following, tridiagn(b,d,c) will denote the triadi-agonal matrix of sizenhaving respectively on the lower and upper principal diagonals the vectorsb= (b1, . . . , bn−1)T andc= (c1, . . . , cn−1)T, and on
the principal diagonal the vectord= (d1, . . . , dn)T. If bi =β,di =δand
12 1. Foundations of Matrix Analysis
We also mention the so-called lower Hessenberg matrices (p = m−1,
q = 1) and upper Hessenberg matrices (p= 1, q = n−1) that have the following structure
H =
h11 h12
0
h21 h22 . .. ..
. . .. hm−1n
hm1 . . . hmn
or H =
h11 h12 . . . h1n
h21 h22 h2n . .. . .. ...
0
hmn−1 hmn .
Matrices of similar shape can obviously be set up in the block-like format.
1.7 Eigenvalues and Eigenvectors
Let A be a square matrix of ordernwith real or complex entries; the number
λ∈Cis called aneigenvalueof A if there exists a nonnull vector x∈Cn such that Ax = λx. The vector x is the eigenvector associated with the eigenvalueλand the set of the eigenvalues of A is called thespectrumof A, denoted byσ(A). We say thatxandyare respectively aright eigenvector
and aleft eigenvectorof A, associated with the eigenvalueλ, if
Ax=λx, yHA =λyH.
The eigenvalueλcorresponding to the eigenvectorxcan be determined by computing the Rayleigh quotientλ=xHAx/(xHx). The numberλis the solution of the characteristic equation
pA(λ) = det(A−λI) = 0,
where pA(λ) is thecharacteristic polynomial. Since this latter is a
polyno-mial of degreenwith respect toλ, there certainly existneigenvalues of A not necessarily distinct. The following properties can be proved
det(A) = n
i=1
λi, tr(A) = n
i=1
λi, (1.6)
and since det(AT−λI) = det((A−λI)T) = det(A−λI) one concludes that
σ(A) =σ(AT) and, in an analogous way, thatσ(AH) =σ( ¯A).
From the first relation in (1.6) it can be concluded that a matrix is singular iff it has at least one null eigenvalue, since pA(0) = det(A) = Πn
i=1λi.
Secondly, if A has real entries, pA(λ) turns out to be a real-coefficient
1.7 Eigenvalues and Eigenvectors 13
Finally, due to the Cayley-Hamilton Theorem if pA(λ) is the
charac-teristic polynomial of A, then pA(A) = 0, wherepA(A) denotes a matrix
polynomial (for the proof see, e.g., [Axe94], p. 51).
The maximum module of the eigenvalues of A is called thespectral radius
of A and is denoted by
ρ(A) = max
λ∈σ(A)|λ|. (1.7)
Characterizing the eigenvalues of a matrix as the roots of a polynomial implies in particular thatλis an eigenvalue of A∈Cn×n iff ¯λis an eigen-value of AH. An immediate consequence is thatρ(A) =ρ(AH). Moreover, ∀A∈Cn×n,∀α∈C,ρ(αA) =|α|ρ(A), andρ(Ak) = [ρ(A)]k
∀k∈N.
Finally, assume that A is a block triangular matrix
A =
A11 A12 . . . A1k 0 A22 . . . A2k
..
. . .. ... 0 . . . 0 Akk
.
As pA(λ) =pA11(λ)pA22(λ)· · ·pAkk(λ), the spectrum of A is given by the
union of the spectra of each single diagonal block. As a consequence, if A is triangular, the eigenvalues of A are its diagonal entries.
For each eigenvalue λof a matrix A the set of the eigenvectors associated with λ, together with the null vector, identifies a subspace ofCn which is called the eigenspace associated withλ and corresponds by definition to ker(A-λI). The dimension of the eigenspace is
dim [ker(A−λI)] =n−rank(A−λI),
and is called geometric multiplicity of the eigenvalue λ. It can never be greater than the algebraic multiplicity of λ, which is the multiplicity of
λas a root of the characteristic polynomial. Eigenvalues having geometric multiplicity strictly less than the algebraic one are calleddefective. A matrix having at least one defective eigenvalue is called defective.
The eigenspace associated with an eigenvalue of a matrix A is invariant with respect to A in the sense of the following definition.
Definition 1.13 A subspaceS inCn is calledinvariantwith respect to a square matrix A if AS⊂S, where AS is the transformed ofS through A.
14 1. Foundations of Matrix Analysis
1.8 Similarity Transformations
Definition 1.14 Let C be a square nonsingular matrix having the same order as the matrix A. We say that the matrices A and C−1AC aresimilar, and the transformation from A to C−1AC is called a similarity
transfor-mation. Moreover, we say that the two matrices are unitarily similarif C
is unitary.
Two similar matrices share the same spectrum and the same characteris-tic polynomial. Indeed, it is easy to check that if (λ,x) is an eigenvalue-eigenvector pair of A, (λ,C−1x) is the same for the matrix C−1AC since
(C−1AC)C−1x= C−1Ax=λC−1x.
We notice in particular that the product matrices AB and BA, with A ∈ Cn×m and B ∈ Cm×n, are not similar but satisfy the following property (see [Hac94], p.18, Theorem 2.4.6)
σ(AB)\ {0}=σ(BA)\ {0}
that is, AB and BA share the same spectrum apart from null eigenvalues so thatρ(AB) =ρ(BA).
The use of similarity transformations aims at reducing the complexity of the problem of evaluating the eigenvalues of a matrix. Indeed, if a given matrix could be transformed into a similar matrix in diagonal or triangular form, the computation of the eigenvalues would be immediate. The main result in this direction is the following theorem (for the proof, see [Dem97], Theorem 4.2).
Property 1.5 (Schur decomposition) Given A∈Cn×n, there existsU
unitary such that
U−1AU = UHAU =
λ1 b12 . . . b1n 0 λ2 b2n
..
. . .. ...
0 . . . 0 λn
= T,
whereλi are the eigenvalues of A.
It thus turns out that every matrix A is unitarily similar to an upper triangular matrix. The matrices T and U are not necessarily unique [Hac94]. The Schur decomposition theorem gives rise to several important results; among them, we recall:
1. every hermitian matrix is unitarily similar to a diagonal real ma-trix, that is, when A is hermitian every Schur decomposition of A is diagonal. In such an event, since
1.8 Similarity Transformations 15
it turns out that AU = UΛ, that is, Aui =λiui fori = 1, . . . , nso that the column vectors of U are the eigenvectors of A. Moreover, since the eigenvectors are orthogonal two by two, it turns out that an hermitian matrix has a system of orthonormal eigenvectors that generates the whole spaceCn. Finally, it can be shown that a matrix A of ordernis similar to a diagonal matrix D iff the eigenvectors of A form a basis forCn [Axe94];
2. a matrix A∈Cn×n is normal iff it is unitarily similar to a diagonal matrix. As a consequence, a normal matrix A ∈ Cn×n admits the followingspectral decomposition: A = UΛUH =ni=1λiuiuHi being U unitary and Λ diagonal [SS90];
3. let A and B be two normal and commutative matrices; then, the generic eigenvalue µi of A+B is given by the sum λi +ξi, where
λi and ξi are the eigenvalues of A and B associated with the same eigenvector.
There are, of course, nonsymmetric matrices that are similar to diagonal matrices, but these are not unitarily similar (see, e.g., Exercise 7).
The Schur decomposition can be improved as follows (for the proof see, e.g., [Str80], [God66]).
Property 1.6 (Canonical Jordan Form) Let A be any square matrix.
Then, there exists a nonsingular matrixXwhich transformsAinto a block
diagonal matrix Jsuch that
X−1AX = J = diag (Jk1(λ1),Jk2(λ2), . . . ,Jkl(λl)),
which is called canonical Jordan form, λj being the eigenvalues of A and
Jk(λ)∈Ck×k a Jordan block of the form J1(λ) =λif k= 1 and
Jk(λ) =
λ 1 0 . . . 0 0 λ 1 · · · ... ..
. . .. ... 1 0
..
. . .. λ 1
0 . . . 0 λ
, fork >1.
16 1. Foundations of Matrix Analysis
Partitioning X by columns, X = (x1, . . . ,xn), it can be seen that the
ki vectors associated with the Jordan block Jki(λi) satisfy the following
recursive relation
Axl=λixl, l= i−1
j=1
mj+ 1,
Axj =λixj+xj−1, j =l+ 1, . . . , l−1 +ki, if ki = 1.
(1.8)
The vectorsxiare calledprincipal vectorsorgeneralized eigenvectorsof A.
Example 1.6 Let us consider the following matrix
A =
7/4 3/4 −1/4 −1/4 −1/4 1/4
0 2 0 0 0 0
−1/2 −1/2 5/2 1/2 −1/2 1/2 −1/2 −1/2 −1/2 5/2 1/2 1/2 −1/4 −1/4 −1/4 −1/4 11/4 1/4 −3/2 −1/2 −1/2 1/2 1/2 7/2
.
The Jordan canonical form of A and its associated matrix X are given by
J =
2 1 0 0 0 0 0 2 0 0 0 0 0 0 3 1 0 0 0 0 0 3 1 0 0 0 0 0 3 0 0 0 0 0 0 2
, X =
1 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 1 1 1
.
Notice that two different Jordan blocks are related to the same eigenvalue (λ= 2). It is easy to check property (1.8). Consider, for example, the Jordan block associated with the eigenvalueλ2 = 3; we have
Ax3= [0 0 3 0 0 3]T = 3 [0 0 1 0 0 1]T=λ2x3,
Ax4= [0 0 1 3 0 4]T = 3 [0 0 0 1 0 1]T+ [0 0 1 0 0 1]T=λ2x4+x3,
Ax5= [0 0 0 1 3 4]T = 3 [0 0 0 0 1 1]T+ [0 0 0 1 0 1]T=λ2x5+x4.
•
1.9 The Singular Value Decomposition (SVD)
Any matrix can be reduced in diagonal form by a suitable pre and post-multiplication by unitary matrices. Precisely, the following result holds.
Property 1.7 LetA∈Cm×n. There exist two unitary matricesU∈Cm×m
andV∈Cn×n such that
UHAV = Σ = diag(σ1, . . . , σp)∈Cm×n with p= min(m, n) (1.9)
and σ1 ≥. . .≥σp ≥0. Formula(1.9) is called Singular Value
Decompo-sition or (SVD) of A and the numbers σi (or σi(A)) are called singular
1.10 Scalar Product and Norms in Vector Spaces 17
If A is a real-valued matrix, U and V will also be real-valued and in (1.9) UT must be written instead of UH. The following characterization of the singular values holds
σi(A) =λi(AHA), i= 1, . . . , n. (1.10)
Indeed, from (1.9) it follows that A = UΣVH, AH= VΣUH so that, U and V being unitary, AHA = VΣ2VH, that is, λi(AHA) =λi(Σ2) = (σi(A))2. Since AAH and AHA are hermitian matrices, the columns of U, called the
left singular vectors of A, turn out to be the eigenvectors of AAH (see
Section 1.8) and, therefore, they are not uniquely defined. The same holds for the columns of V, which are theright singular vectorsof A.
Relation (1.10) implies that if A∈Cn×nis hermitian with eigenvalues given byλ1,λ2, . . . , λn, then the singular values of A coincide with the modules of the eigenvalues of A. Indeed because AAH = A2,σ
i =
λ2
i =|λi| for
i= 1, . . . , n. As far as the rank is concerned, if
σ1≥. . .≥σr> σr+1=. . .=σp= 0,
then the rank of A is r, the kernel of A is the span of the column vectors of V,{vr+1, . . . ,vn}, and the range of A is the span of the column vectors of U, {u1, . . . ,ur}.
Definition 1.15 Suppose that A∈Cm×n has rank equal tor and that it admits a SVD of the type UHAV = Σ. The matrix A† = VΣ†UH is called
theMoore-Penrose pseudo-inversematrix, being
Σ†= diag
1
σ1
, . . . , 1 σr
,0, . . . ,0
. (1.11)
The matrix A† is also called thegeneralized inverseof A (see Exercise 13). Indeed, if rank(A) = n < m, then A† = (ATA)−1AT, while if n = m = rank(A), A†= A−1. For further properties of A†, see also Exercise 12.
1.10 Scalar Product and Norms in Vector Spaces
18 1. Foundations of Matrix Analysis
Definition 1.16 A scalar product on a vector space V defined over K
is any map (·,·) acting from V ×V into K which enjoys the following properties:
1. it is linear with respect to the vectors of V, that is
(γx+λz,y) =γ(x,y) +λ(z,y), ∀x,z∈V, ∀γ, λ∈K;
2. it ishermitian, that is, (y,x) = (x,y), ∀x,y∈V;
3. it is positive definite, that is, (x,x) > 0, ∀x = 0 (in other words, (x,x)≥0, and (x,x) = 0 if and only ifx=0).
In the case V =Cn (or Rn), an example is provided by the classical Eu-clidean scalar product given by
(x,y) =yHx= n
i=1
xiy¯i,
where ¯z denotes the complex conjugate ofz.
Moreover, for any given square matrix A of ordernand for anyx,y∈Cn the following relation holds
(Ax,y) = (x,AHy). (1.12)
In particular, since for any matrix Q∈Cn×n, (Qx,Qy) = (x,QHQy), one gets
Property 1.8 Unitary matrices preserve the Euclidean scalar product, that is, (Qx,Qy) = (x,y)for any unitary matrixQand for any pair of vectors
x andy.
Definition 1.17 LetV be a vector space over K. We say that the map · fromV into Ris a normonV if the following axioms are satisfied:
1. (i) v ≥0∀v∈V and (ii) v = 0 if and only ifv=0;
2. αv =|α| v ∀α∈K, ∀v∈V (homogeneity property);
3. v+w ≤ v + w ∀v,w∈V (triangular inequality),
where |α| denotes the absolute value of α if K = R, the module of α if
1.10 Scalar Product and Norms in Vector Spaces 19
The pair (V, · ) is called a normed space. We shall distinguish among norms by a suitable subscript at the margin of the double bar symbol. In the case the map| · |from V intoRenjoys only the properties 1(i), 2 and 3 we shall call such a map a seminorm. Finally, we shall call aunit vector
any vector ofV having unit norm.
An example of a normed space isRn, equipped for instance by thep-norm
(or H¨older norm); this latter is defined for a vector xof components{xi}
as
x p=
n
i=1 |xi|p
1/p
, for 1≤p <∞. (1.13)
Notice that the limit aspgoes to infinity of x pexists, is finite, and equals the maximum module of the components ofx. Such a limit defines in turn a norm, called theinfinity norm(ormaximum norm), given by
x ∞= max
1≤i≤n|xi|.
When p = 2, from (1.13) the standard definition of Euclidean norm is recovered
x 2= (x,x)1/2=
n
i=1 |xi|2
1/2
=xTx1/2,
for which the following property holds.
Property 1.9 (Cauchy-Schwarz inequality) For any pairx,y∈Rn,
|(x,y)|=|xTy| ≤ x 2 y 2, (1.14)
where strict equality holds iff y=αx for someα∈R.
We recall that the scalar product in Rn can be related to the p-norms introduced overRn in (1.13) by theH¨older inequality
|(x,y)| ≤ x p y q, with 1
p+
1
q = 1.
In the case where V is a finite-dimensional space the following property holds (for a sketch of the proof, see Exercise 14).
Property 1.10 Any vector norm · defined onV is a continuous function
of its argument, namely, ∀ε > 0, ∃C > 0 such that if x−x ≤ ε then
| x − x | ≤Cε, for any x,x∈V.
20 1. Foundations of Matrix Analysis
Property 1.11 Let · be a norm ofRn andA∈Rn×n be a matrix with
nlinearly independent columns. Then, the function · A2 acting fromRn
intoRdefined as
x A2 = Ax ∀x∈Rn,
is a norm of Rn.
Two vectorsx,yinV are said to beorthogonalif (x,y) = 0. This statement has an immediate geometric interpretation when V =R2 since in such a case
(x,y) = x 2 y 2cos(ϑ),
where ϑ is the angle between the vectors x and y. As a consequence, if (x,y) = 0 thenϑis a right angle and the two vectors are orthogonal in the geometric sense.
Definition 1.18 Two norms · p and · q onV are equivalentif there exist two positive constantscpq andCpq such that
cpq x q ≤ x p≤Cpq x q ∀x∈V.
In a finite-dimensional normed space all norms are equivalent. In particular, ifV =Rn it can be shown that for thep-norms, withp= 1, 2, and∞, the constantscpq andCpq take the value reported in Table 1.1.
cpq q= 1 q= 2 q=∞
p= 1 1 1 1
p= 2 n−1/2 1 1
p=∞ n−1 n−1/2 1
Cpq q= 1 q= 2 q=∞
p= 1 1 n1/2 n
p= 2 1 1 n1/2
p=∞ 1 1 1
TABLE 1.1. Equivalence constants for the main norms ofRn
In this book we shall often deal with sequences of vectors and with their
convergence. For this purpose, we recall that a sequence of vectorsx(k)
in a vector spaceV having finite dimensionn, converges to a vectorx, and we write lim
k→∞x
(k)=xif
lim k→∞x
(k)
i =xi, i= 1, . . . , n (1.15)
1.11 Matrix Norms 21
sequence of real numbers, (1.15) implies also the uniqueness of the limit, if existing, of a sequence of vectors.
We further notice that in a finite-dimensional space all the norms are topo-logically equivalent in the sense of convergence, namely, given a sequence of vectorsx(k),
|||x(k)||| →0 ⇔ x(k) →0 if k→ ∞,
where||| · ||| and · are any two vector norms. As a consequence, we can establish the following link between norms and limits.
Property 1.12 Let · be a norm in a space finite dimensional space V. Then
lim k→∞x
(k)=x
⇔ lim
k→∞ x−x
(k) = 0,
wherex∈V andx(k)is a sequence of elements ofV.
1.11 Matrix Norms
Definition 1.19 Amatrix normis a mapping · :Rm×n →Rsuch that:
1. A ≥0∀A∈Rm×n and A = 0 if and only if A = 0;
2. αA =|α| A ∀α∈R, ∀A∈Rm×n (homogeneity);
3. A + B ≤ A + B ∀A,B∈Rm×n (triangular inequality).
Unless otherwise specified we shall employ the same symbol · , to denote matrix norms and vector norms.
We can better characterize the matrix norms by introducing the concepts of compatible norm and norm induced by a vector norm.
Definition 1.20 We say that a matrix norm · iscompatibleorconsistent
with a vector norm · if
Ax ≤ A x , ∀x∈Rn. (1.16)
22 1. Foundations of Matrix Analysis
Definition 1.21 We say that a matrix norm · is sub-multiplicative if ∀A∈Rn×m,∀B∈Rm×q
AB ≤ A B . (1.17)
This property is not satisfied by any matrix norm. For example (taken from [GL89]), the norm A ∆ = max|aij| fori = 1, . . . , n, j = 1, . . . , m does not satisfy (1.17) if applied to the matrices
A = B =
1 1 1 1
,
since 2 = AB ∆> A ∆ B ∆= 1.
Notice that, given a certain sub-multiplicative matrix norm · α, there always exists a consistent vector norm. For instance, given any fixed vector
y=0inCn, it suffices to define the consistent vector norm as
x = xyH α x∈Cn.
As a consequence, in the case of sub-multiplicative matrix norms it is no longer necessary to explicitly specify the vector norm with respect to the matrix norm is consistent.
Example 1.7 The norm
AF =
n
i,j=1
|aij|2= tr(AAH) (1.18)
is a matrix norm called theFrobenius norm(orEuclidean norminCn2) and is compatible with the Euclidean vector norm · 2. Indeed,
Ax22 =
n
i=1
n
j=1
aijxj
2
≤
n
i=1
n
j=1
|aij|2 n
j=1
|xj|2
=A2Fx22.
Notice that for such a normInF =√n. •
In view of the definition of a natural norm, we recall the following theorem.
Theorem 1.1 Let · be a vector norm. The function
A = sup
x=0
Ax
x (1.19)
1.11 Matrix Norms 23
Proof.We start by noticing that (1.19) is equivalent to
A= sup
x=1
Ax. (1.20)
Indeed, one can define for anyx=0the unit vectoru=x/x, so that (1.19) becomes
A= sup
u=1
Au=Aw withw= 1.
This being taken as given, let us check that (1.19) (or, equivalently, (1.20)) is actually a norm, making direct use of Definition 1.19.
1. IfAx ≥0, then it follows thatA= sup
x=1
Ax ≥0. Moreover
A= sup
x=0
Ax
x = 0⇔ Ax= 0 ∀x=0
and Ax=0∀x=0if and only if A=0; thereforeA= 0⇔A = 0. 2. Given a scalarα,
αA= sup
x=1
αAx=|α| sup
x=1
Ax=|α| A.
3. Finally, triangular inequality holds. Indeed, by definition of supremum, if
x=0then
Ax
x ≤ A ⇒ Ax ≤ Ax,
so that, takingxwith unit norm, one gets
(A + B)x ≤ Ax+Bx ≤ A+B,
from which it follows thatA + B= sup
x=1
(A + B)x ≤ A+B.
✸ Relevant instances of induced matrix norms are the so-called p-norms de-fined as
A p= sup
x=0
Ax p
x p
The 1-norm and the infinity norm are easily computable since
A 1= max j=1,... ,n
m
i=1
|aij|, A ∞=i=1,... ,mmax
n
j=1 |aij|
and they are called the column sum normand therow sum norm, respec-tively.
Moreover, we have A 1 = AT ∞ and, if A is self-adjoint or real
sym-metric, A 1= A ∞.
24 1. Foundations of Matrix Analysis
Theorem 1.2 Letσ1(A)be the largest singular value ofA. Then
A 2=
ρ(AHA) =ρ(AAH) =σ1(A). (1.21)
In particular, ifA is hermitian (or real and symmetric), then
A 2=ρ(A), (1.22)
while, if Ais unitary, A 2= 1.
Proof.Since AHA is hermitian, there exists a unitary matrix U such that
UHAHAU = diag(µ1, . . . , µn),
whereµiare the (positive) eigenvalues of AHA. Lety= UHx, then
A2 = sup
x=0
(AHAx,x)
(x,x) = supy=0
(UHAHAUy,y)
(y,y)
= sup
y=0
n
i=1
µi|yi|2/ n
i=1
|yi|2=
max
i=1,... ,n|µi|,
from which (1.21) follows, thanks to (1.10).
If A is hermitian, the same considerations as above apply directly to A. Finally, if A is unitary
Ax22= (Ax,Ax) = (x,AHAx) =x22
so thatA2= 1. ✸
As a consequence, the computation of A 2 is much more expensive than that of A ∞ or A 1. However, if only an estimate of A 2 is required, the following relations can be profitably employed in the case of square matrices
max
i,j |aij| ≤ A 2≤nmaxi,j |aij|, 1
√
n A ∞≤ A 2≤ √n A
∞,
1
√
n A 1≤ A 2≤ √n A
1,
A 2≤
A 1 A ∞.
For other estimates of similar type we refer to Exercise 17. Moreover, if A is normal then A 2≤ A p for anynand allp≥2.
Theorem 1.3 Let||| · |||be a matrix norm induced by a vector norm · . Then