U M ESTUDO SOBRE O CONCEITO DE MÉDIA

U

M ESTUDO SOBRE O CONCEITO DE MÉDIA

COM ALUNOS DO

E

NSINO

M

ÉDIO

MESTRADO EM EDUCAÇÃO MATEMÁTICA

PUC/SP

CRISTIANE APARECIDA STELLA

U

M ESTUDO SOBRE O CONCEITO DE MÉDIA

COM ALUNOS DO

E

NSINO

M

ÉDIO

Dissertação apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para obtenção do título de MESTRE EM EDUCAÇÃO MATEMÁTICA, sob a orientação da Profa Dra Siobhan Victoria Healy.

PUC/SP

Banca Examinadora

____________________________________

____________________________________

Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta Dissertação por processos de fotocopiadoras ou eletrônicos.

D

A

A

G

G

R

R

A

A

D

D

E

E

C

C

I

I

M

M

E

E

N

N

T

T

O

O

S

S

Muitas pessoas me ajudaram na construção deste

trabalho e na realização dessa etapa da minha vida,

dando-me um pouco de conhecimento, apoio, carinho e

amizade que me foram vitais. Ao citar de modo especial

algumas delas, não significa falta de reconhecimento da

colaboração das demais. Registro aqui meus

agradecimentos àquelas pessoas ou instituições que, a

meu ver, participaram mais diretamente dessa minha

formação.

À Capes, pela oportunidade à mim conferida para

realizar esta etapa essencial à minha formação

acadêmica.

À minha orientadora Lulu Healy, sem a qual este

trabalho não seria possível, pelas incessantes horas de

auxílio, dedicação e compreensão durante a execução

desse estudo.

À prof

_{Dra Sandra Magina por todo apoio, amizade,}

incentivo, carinho e pela acolhida.

Às prof

_{Doutoras Cileda de Queiroz e Silva}

examinadora, pela aceitação, sugestões e comentários que

contribuíram para o enriquecimento deste trabalho. E, a

profa Dra Ana Paula Jahn por ter participado do exame

de qualificação.

Aos meus pais Ari e Arlete, pelo estímulo, apoio,

compreensão e paciência quanto às minhas ausências e

preocupações.

Ao meu irmão João Marcelo, pelo incentivo

responsável pelo meu ingresso no mestrado. E, ao meu

sobrinho Giovanni, pelo carinho e amizade.

Ao meu namorado Otávio, de modo especial, pelo

companheirismo, carinho, apoio e incentivo nos

momentos mais difíceis.

À minha tia Doriva, em memória, por me ter feito

acreditar no meu sonho e pela torcida para eu seguir em

frente.

À minha amiga Sandra, companheira de curso e de

estudo por sua amizade, incentivo, auxílio e socorro nos

momentos de adversidade.

Aos funcionários e alunos da Escola Prof

_Carmosina

Ao secretário Francisco que colaborou e forneceu

todo o apoio necessário.

S

S

U

U

M

M

Á

Á

R

R

I

I

O

O

LISTA DE TABELAS... X

LISTA DE FIGURAS... XI

LISTA DE QUADROS... XIII

RESUMO... XIV

ABSTRACT... XV

CAPÍTULO 1: INTRODUÇÃO

1.1 PROBLEMÁTICA E OBJETIVO ... 1

1.2 DESCRIÇÃO DA DISSERTAÇÃO ... 3

CAPÍTULO 2: MÉDIA NO CONTEXTO HISTÓRICO E ESCOLAR 2.1 INTRODUÇÃO ... 6

2.2 A PALAVRA MÉDIA NA HISTÓRIA ... 6

2.2.1 O CONCEITO DE MÉDIA NO ENSINO... 9

2.3 MÉDIA NA PERSPECTIVA MATEMÁTICA... 11

2.3.1 MEDIDAS DE POSIÇÃO ... 17

2.3.2 CONSIDERAÇÕES SOBRE O CONCEITO DE MÉDIA... 21

CAPÍTULO 3: MÉDIA NOS DOCUMENTOS OFICIAIS 3.1 INTRODUÇÃO ... 25

3.2 ANÁLISE DOS PARÂMETROS CURRICULARES NACIONAIS (PCNS) ... 26

3.3 MÉDIA NOS LIVROS DIDÁTICOS DO E.M... 33

3.4 DESCRIÇÃO DO ENEM ... 37

3.5 DESCRIÇÃO DO SAEB... 40

3.6 CONSIDERAÇÕES ... 44

4.2 OS ELEMENTOS DO CONCEITO ... 46

4.2.1 ELEMENTOS EXTENSIVOS ... 50

4.2.2 ELEMENTOS ACTUATIVOS ... 53

4.2.3 ELEMENTOS INTENSIVOS ... 54

4.2.4 ELEMENTOS OSTENSIVOS ... 57

4.2.5 ELEMENTOS VALIDATIVOS ... 63

4.3 CONSIDERAÇÕES ... 64

CAPÍTULO 5: ANÁLISE DE QUESTÕES SOBRE MÉDIA 5.1 INTRODUÇÃO ... 65

5.2 ANÁLISE DAS QUESTÕES DO ENEM 1998 A 2002 ... 66

5.2.1 ENEM 1998 ... 67

5.2.2 ENEM 1999 ... 69

5.2.3 ENEM 2000 ... 73

5.2.4 ENEM 2001 E 2002 ... 75

5.3 O TRATAMENTO DA MÉDIA NOS EXAMES DO ENEM... 76

5.4 A QUESTÃO DO SAEB ... 78

5.5 QUESTÕES DE MOKROS E RUSSELL... 80

5.6 CONSIDERAÇÕES... 88

CAPÍTULO 6: ENTREVISTAS E ANÁLISE DOS RESULTADOS 6.1 INTRODUÇÃO ... 90

6.2 ENTREVISTAS ... 91

6.3 ANÁLISE DAS RESPOSTAS ... 93

6.4 CONCLUSÃO DA ANÁLISE DAS RESPOSTAS... 129

CAPÍTULO 7: CONCLUSÃO 7.1 INTRODUÇÃO ... 135

7.2 REFLEXÕES SODRE OS RESULTADOS DA PESQUISA... 137

7.4 DIREÇÕES PARA PESQUISAS FUTURAS... 144

BIBLIOGRAFIA... 146 ANEXO 1 – MEDIDAS DE ASSIMETRIA E CURTOSE

ANEXO 2 – MEDIDAS DE VARIABILIDADE OU DISPERSÃO

ANEXO 3 – EXERCÍCIOS DO LIVRO “MATEMÁTICA NO ENSINO MÉDIO” – MÁRCIO CINTRA GOULART

L

L

I

I

S

S

T

T

A

A

D

D

E

E

T

T

A

A

B

B

E

E

L

L

A

A

S

S

TABELA 2.1 – TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIAS...

TABELA 3.1 – ANÁLISE DE ALGUNS LIVROS DIDÁTICOS...

TABELA 3.2 – NÍVEIS DE DESEMPENHO DA 8A

SÉRIE DO E.F. E DO 3O

ANO DO E.M... TABELA 5.1 - LEVANTAMENTO DO N° DE QUESTÕES QUE ENVOLVEM GRÁFICOS, TABELAS, CONCEITO DE

MÉDIA OU A PALAVRA MÉDIA...

TABELA 5.2 – PERCENTUAIS DE RESPOSTAS PARA A QUESTÃO 15...

TABELA 5.3 – PERCENTUAIS DE RESPOSTA PARA A QUESTÃO 61...

TABELA 5.4 – PERCENTUAIS DE RESPOSTA PARA A QUESTÃO 58...

TABELA 5.5 – PERCENTUAIS DE RESPOSTAS PARA A QUESTÃO 50...

TABELA 6.1 – ACERTOS E ERROS REFERENTES À QUESTÃO 1... TABELA 6.2 – ACERTOS E ERROS REFERENTES À QUESTÃO 2... TABELA 6.3 – ACERTOS E ERROS REFERENTES À QUESTÃO 3... TABELA 6.4 – ACERTOS E ERROS REFERENTES À QUESTÃO 4...

TABELA 6.5 – ACERTOS E ERROS REFRENTES À QUESTÃO 5...

TABELA 6.6 – ACERTOS E ERROS REFERENTES À QUESTÃO 6...

TABELA 6.7 – ACERTOS E ERROS REFERENTES À QUESTÃO 7...

TABELA 6.8 – ERROS REFERENTES À QUESTÃO 7...

TABELA 6.9 – VALOR MAIS ALTO REFERENTE À QUESTÃO 7... TABELA 6.10 – ACERTO/ERRO DE CADA ALUNA POR QUESTÃO...

L

L

I

I

S

S

T

T

A

A

D

D

E

E

F

F

I

I

G

G

U

U

R

R

A

A

S

S

FIGURA 2.1 – TIPOS DE VARIÁVEL...

FIGURA 2.2 – CURVA DE FREQÜÊNCIA SIMÉTRICA...

FIGURA 2.3 - CURVA DE FREQÜÊNCIA ASSIMÉTRICA À ESQUERDA...

FIGURA 2.4 - CURVA DE FREQÜÊNCIA ASSIMÉTRICA À DIREITA... FIGURA 2.5 – DEFINIÇÃO DE MÉDIA ARITMÉTICA SIMPLES...

FIGURA 2.6 – DEFINIÇÃO DE MÉDIA ARITMÉTICA SIMPLES...

FIGURA 2.7 – DEFINIÇÃO DE MÉDIA ARITMÉTICA PONDERADA...

FIGURA 5.1 – QUESTÃO 15, CADERNO DE QUESTÕES ENEM 1998...

FIGURA 5.2 – QUESTÃO 61, CADERNO DE QUESTÕES ENEM 1999...

FIGURA 5.3 – QUESTÃO 58, CADERNO DE QUESTÕES ENEM 2000...

FIGURA 5.4 – QUESTÃO 55, CADERNO DE QUESTÕES ENEM 2002...

FIGURA 5.5 – QUESTÃO 13, CADERNO DE QUESTÕES SAEB 2001... FIGURA 5.6 – QUESTÃO DA PESQ. DE POLLATSEK, LIMA E WELL (1981) – QUESTÃO 3 DA NOSSA

ENTREVISTA...

FIGURA 5.7 – QUESTÃO DA PESQ. DE MOKROS E RUSSELL (1995) – QUESTÃO 5 DA NOSSA ENTREVISTA...

FIGURA 5.8 – GRÁFICO AUXILIAR...

FIGURA 5.9 – QUESTÃO DA PESQ. DE MOKROS E RUSSELL (1995) – QUESTÃO 6 DA NOSSA ENTREVISTA...

FIGURA 5.10 – QUESTÃO DA PESQ. DE MOKROS E RUSSELL (1995) – QUESTÃO 7 DA NOSSA ENTREVISTA...

FIGURA 5.11 – POSSÍVEL RESOLUÇÃO PARA A QUESTÃO 7 DA NOSSA ENTREVISTA...

FIGURA 5.12 – QUESTÃO DA PESQ. DE MOKROS E RUSSELL (1995) – QUESTÃO 8 DA NOSSA ENTREVISTA...

FIGURA 5.13 – GRÁFICO AUXILIAR...

FIGURA 6.1 – QUESTÃO 1 DO PROTOCOLO DA ENTREVISTA...

FIGURA 6.2 – RESPOSTA DE JOANA À QUESTÃO 1...

FIGURA 6.3 – RESPOSTA DE SIMONE À QUESTÃO 1... FIGURA 6.4 – QUESTÃO 2 DO PROTOCOLO DE ENTREVISTA...

FIGURA 6.5 – QUESTÃO 3 DO PROTOCOLO DE ENTREVISTA...

FIGURA 6.6 – RESPOSTA DE JOANA À QUESTÃO 3...

FIGURA 6.7 – RESPOSTAS À QUESTÃO 3...

FIGURA 6.8 – QUESTÃO 4 DO PROTOCOLO DE ENTREVISTA...

FIGURA 6.9 – RESPOSTA DE JOANA À QUESTÃO 4...

FIGURA 6.10 – QUESTÃO 5 DO PROTOCOLO DE ENTREVISTA...

FIGURA 6.11 – RESPOSTA DAS ALUNAS AO ITEM A DA QUESTÃO 5...

FIGURA 6.12 – RESPOSTA DE JOANA AO ITEM B DA QUESTÃO 5...

FIGURA 6.13 – RESPOSTA DE JOANA AO ITEM C DA QUESTÃO 5...

FIGURA 6.14 – RESPOSTA DE JOANA À QUESTÃO 5...

FIGURA 6.15 – RESPOSTA DE KARINA À QUESTÃO 5... FIGURA 6.16 – QUESTÃO 6 DO PROTOCOLO DE ENTREVISTA... FIGURA 6.17 – RESPOSTA DE SIMONE À QUESTÃO 5...

FIGURA 6.18 – RESPOSTA DE JULIANA À QUESTÃO 6...

FIGURA 6.19 – RESPOSTA DE FERNANDA À QUESTÃO 6...

FIGURA 6.20 – RESPOSTA DE JOANA À QUESTÃO 6...

FIGURA 6.21 – RESPOSTA DE AMANDA À QUESTÃO 6...

FIGURA 6.22 – QUESTÃO 7 DO PROTOCOLO DE ENTREVISTA... FIGURA 6.23 – REPOSTAS DE SIMONE E GLACE À QUESTÃO 7... FIGURA 6.24 – REPOSTAS DE KARINA, JOANA E FERNANDA À QUESTÃO 7... FIGURA 6.25 – QUESTÃO 8 DO PROTOCOLO DE ENTREVISTA...

FIGURA 6.26 – RESPOSTA DE JOANA À QUESTÃO 8...

FIGURA 6.27 – RESPOSTA DE GLACE À QUESTÃO 8...

FIGURA 6.28 – RESPOSTA FINAL DE GLACE À QUESTÃO 8...

FIGURA 6.29 – RESPOSTAS DE SIMONE E AMANDA À QUESTÃO 8...

L

L

I

I

S

S

T

T

A

A

D

D

E

E

Q

Q

U

U

A

A

D

D

R

R

O

O

S

S

QUADRO-RESUMO 2.1 – ELEMENTOS TÍPICOS DE UMA DISTRIBUIÇÃO...

QUADRO-EXEMPLO 3.1 – DEFINIÇÃO DE MÉDIA E EXEMPLO DE EXERCÍCIO... QUADRO-EXEMPLO 4.1 – PROBLEMA 1 –BATANERO (2000)... QUADRO-EXEMPLO 4.2 – PROBLEMA 2 – BATANERO (2000)... QUADRO-EXEMPLO 4.3 – PROBLEMA 3. – BATANERO (2000)...

QUADRO-EXEMPLO 4.4 – PROBLEMA 4.. – BATANERO (2000)...

QUADRO-EXEMPLO 4.5 – PROBLEMA POLLATSEK Y COLS (1981)...

QUADRO-EXEMPLO 4.6 – PROBLEMA POLLATSEK, LIMA E WELL (1981)...

QUADRO-EXEMPLO 4.7 – QUESTÃO DA PESQ. DE RUSSELL E MOKROS (1995)...

QUADRO-EXEMPLO 4.8 - QUESTÃO DA PESQ. DE RUSSELL E MOKROS (1995)... QUADRO-EXEMPLO 4.9 – PROBLEMA DA PESQ. DE READINF E PEGG (1996)...

R

R

E

E

S

S

U

U

M

M

O

O

O objetivo deste trabalho é identificar as interpretações do conceito de média, de alunos do Ensino Médio, que seguem o currículo brasileiro. Para alcançar este objetivo pesquisamos as características do conceito de média enfatizadas no currículo de Matemática do Ensino Médio e em pesquisas que visam compreender a aprendizagem de tal conceito.

Iniciamos nossa pesquisa com algumas considerações do conceito de média sob o ponto de vista histórico e epistemológico. Em seguida, buscamos identificar os aspectos do conceito de média enfatizados em instrumentos de ensino como: documentos oficiais (PCN’s), livros didáticos do Ensino Médio, os sistemas de avaliação ENEM e SAEB. Também consideramos as abordagens ao conceito propostas em pesquisas de Educação e escolhemos, como base para nossas análises, em particular, o modelo teórico proposto por Batanero (2000).

A luz destas investigações, selecionamos algumas questões para aplicarmos nas entrevistas a alunos da 3a série do Ensino Médio, de tal forma que contemplasse os diferentes elementos do conceito e as diferentes abordagens enfatizadas nos instrumentos de ensino e nas pesquisas que foram apresentadas. Os resultados obtidos indicam que os alunos apresentaram um bom desempenho com problemas que envolvem média aritmética ponderada e em problemas de construção (problemas em que o aluno constrói a distribuição dos dados). Em contrapartida, a maioria dos alunos pesquisados tem uma interpretação algorítmica do conceito de média e apresentam dificuldade para resolver problemas que envolvem o cálculo de média quando os dados são apresentados na forma gráfica.

Tais resultados sugerem problemas no aprendizado de média que vão além do aluno, mas têm a ver com uma questão estrutural que começa nos documentos oficiais, percorre os livros didáticos, as formas de avaliação até chegar ao aluno.

A

A

B

B

S

S

T

T

R

R

A

A

C

C

T

T

The aim of this study is to identify interpretations of the concept of arithmetic mean held by High School students following the Brazilian curriculum. With this aim in mind, we investigate the characteristics of the concept of mean that are emphasised in the High School Mathematics Curriculum and in research studies related to understanding the teaching and learning processes associated with this concept.

We begin our research with some considerations about the concept of mean from historical and epistemological perspectives. We go on to attempt to identify aspects of the concept emphasised in the following teaching instruments: official documents (PCNs), textbooks, and systems of curriculum evaluation (ENEM and SAEB). We also determine different approaches to the concept that are proposed in Mathematics Education research studies, choosing as a basis for our analyses the theoretical model of Batanero (2000).

As a result of these investigations, we selected some questions to be used in interviews of students from the third year of High School, with questions chosen to take into account the different approaches associated with teaching instruments and the research studies. Analysis of the interviews indicate that, on the one hand, students perform well in relation to problems involving weighted means and in problems of construction (problems in which they construct distributions of data sets). On the other hand, most of the students interviewed see mean as algorithm and have difficulties in solving problems in which they have to calculate means on the basis of graphically presented data.

These results suggest problems in the teaching and learning of mean that go beyond the student and are associated with structural questions which have their beginning in official documents, reaching the students by means of mathematics textbooks and forms of evaluation.

IIII

IIII

1.1 P

Atualmente, a Estatística descritiva tem tido um papel primordial no

desenvolvimento da sociedade ao proporcionar ferramentas para análise, leitura,

interpretação de tabelas, dados e gráficos que aparecem com freqüência na vida

cotidiana através dos meios de informação (jornais, revistas, Internet, etc.).

No desenvolvimento pessoal, ela estimula o raciocínio crítico

fundamentado em argumentações coerentes que visam resolver determinadas

situações que envolvem fenômenos aleatórios nos quais é necessário coletar,

organizar e apresentar dados, interpretar amostras e comunicar resultados por

meio da linguagem estatística, dando significado aos conceitos e não

simplesmente utilizando um algoritmo que não tem significado para o aluno.

Segundo esta perspectiva, Batanero (2002) justifica o ensino de Estatística

pelas seguintes razões:

⇒ ⇒ ⇒

⇒ A estatística é parte da educação geral desenvolvida para futuros cidadãos

adultos que precisam adquirir a capacidade de leitura, interpretação de tabelas e

gráficos que aparecem nos meios de informação;

⇒ ⇒ ⇒

⇒ É útil para a vida posterior, já que em muitas profissões se faz necessário

alguns conhecimentos básicos do tema;

⇒ ⇒ ⇒

⇒ Seu estudo ajuda no desenvolvimento pessoal, baseado na valorização da

QUAIS SÃO AS INTERPRETAÇÕES DO CONCEITO DE MÉDIA, DE ALUNOS

DO ENSINO MÉDIO, QUE SEGUEM O CURRÍCULO BRASILEIRO? ⇒

⇒ ⇒

⇒ Ajuda a compreender as outras disciplinas do currículo, tanto da Educação

Básica quanto da posterior, onde com freqüência aparecem gráficos ou

conhecimentos estatísticos.

Estas razões citadas por Batanero (2002), além das já citadas

anteriormente, têm feito com que a Estatística se incorpore cada vez mais aos

currículos. Entretanto, apesar de ser um tema atual e fazer parte da vida

cotidiana, o interesse pelo tema Estatística, mais particularmente pelo conceito de

média aritmética, deu-se quando verificamos a pouca ênfase dada a este

conteúdo no Ensino Médio, no contexto brasileiro.

Diante deste quadro, a presente pesquisa tem como objetivo responder a

seguinte questão:

Para tanto, julgamos pertinente elaborar questões específicas para auxiliar

a responder a questão principal acima:

! !!

! QUAIS CARACTERÍSTICAS DO CONCEITO DE MÉDIA, EM GERAL, SÃO

ENFATIZADAS NO CURRÍCULO DE MATEMÁTICA DO ENSINO MÉDIO, EM DOCUMENTOS OFICIAIS E INSTRUMENTOS DE AVALIAÇÃO?

! !!

! QUAIS CARACTERÍSTICAS DESTE CONCEITO SÃO ENFATIZADAS EM

PESQUISAS QUE VISAM COMPREENDER A APRENDIZAGEM DE TAL

Para responder estas questões dividimos nosso estudo em duas partes. Na

primeira parte investigaremos o que é abordado sobre média em quatro

instrumentos relacionados ao ensino de Matemática no Brasil: os Parâmetros

Curriculares Nacionais (PCN’s), o Exame Nacional do Ensino Médio (ENEM), o

Sistema de Avaliação da Educação Básica (SAEB) e os livros didáticos.

A partir de nossa análise dos PCN’s, na qual confirmamos que o conceito

de média deve ser abordado tanto no Ensino Fundamental como no Ensino

Médio, uma vez que faz parte do bloco Tratamento da Informação, resolvemos

investigar se o que é proposto nos PCN’s é realmente “cobrado” nos Sistemas de

Avaliação de Ensino, de que forma isto é “cobrado” e que tipo de problema é

proposto.

Na segunda parte de nosso estudo nós tivemos como objetivo investigar o

que o aluno brasileiro, do Ensino Médio, entende por média, quais concepções

ele já tem a respeito deste conceito, quais estratégias ele utiliza na resolução de

problemas tradicionais (em que é pedido para obter a média por meio do uso do

algoritmo), de construção (onde é dada a média e o aluno constrói a distribuição)

e de interpretação (onde é preciso descrever, resumir, comparar e raciocinar

sobre um conjunto de dados).

Na próxima seção faremos uma breve descrição da organização de nosso

trabalho em capítulos.

1.2 D

No presente capítulo, situamos o leitor a respeito da problemática que

motivou nossa pesquisa expondo o objetivo da mesma e realizando uma breve

descrição da cada capítulo.

O capítulo 2 será dividido em duas seções: a primeira seção tratará a

palavra média no contexto histórico abordando seu significado, o contexto de

surgimento e sua evolução ao longo do tempo, incluindo o conceito de média no

ensino.

A segunda seção abordará a média como perspectiva matemática, ou seja,

o conceito de média. Para tanto, fizemos uma retrospectiva de alguns conceitos

estatísticos que julgamos importantes serem discutidos em nosso trabalho a fim

de abordarmos os elementos típicos de uma distribuição, mais particularmente, as

medidas de posição e também para situar o leitor em que parte da Estatística

nosso trabalho está focado. Entre estes conceitos estão os elementos de

interpretação de uma distribuição: variáveis, tabelas de freqüências, tipos de

curva de freqüência. Dentre as medidas de posição, o que realmente nos

interessa são as medidas de posição central, em particular a média aritmética que

é o tema central de nosso trabalho.

No capítulo 3, apresentaremos nossa análise de quatro instrumentos: os

Parâmetros Curriculares Nacionais de Ensino Fundamental e Médio no que se

refere ao bloco Tratamento da Informação, os livros didáticos mais usados nas

escolas brasileiras e que teve análise fundamentada no livro “Exame de textos:

análise de livros de Matemática para o Ensino Médio (2001)”, o ENEM (Exame

Nacional de Ensino Médio) e o SAEB (Sistema de Avaliação da Educação

No capítulo 4, trataremos dos aspectos teóricos de nossa pesquisa

apresentando, em particular, o modelo defendido por Carmen Batanero sobre os

elementos de conceitos matemáticos e suas aplicações em pesquisas existentes

relacionadas às concepções de alunos sobre a média.

No capítulo 5, usamos o modelo de Batanero para fazer uma análise das

questões do ENEM, SAEB e de um estudo sobre as concepções de média

aplicado nos Estados Unidos (Mokros e Russell, 1995). Esta análise tem dois

motivos: primeiro identificar os tipos de questões que compõem a avaliação de

competências de alunos brasileiros ligado a este conceito e, segundo para montar

uma entrevista, baseada em tarefas sobre o conceito de média a ser conduzida

com um grupo de alunos do Ensino Médio.

No capítulo 6, explicitaremos os procedimentos metodológicos a serem

utilizados em nosso trabalho. Ele compreende uma entrevista piloto e, entrevistas

realizadas com 7 alunos do 3o _{ano do Ensino Médio de uma escola pública do}

Estado de São Paulo, na presença da pesquisadora. Além disto, neste capítulo

faremos também a análise das respostas das entrevistas segundo as categorias

já definidas no capítulo 4.

No capítulo 7, faremos algumas considerações relevantes, a partir das

análises realizadas no capítulo 6 e responderemos as questões apresentadas

inicialmente ou ao longo da pesquisa, sugerindo algumas questões que poderiam

M

M

M

M

M

M

_M

_M

2.1 I

Este capítulo está dividido em duas partes. Na primeira, faremos um breve

estudo a respeito da história da palavra média: seu significado, o contexto de

surgimento e sua evolução ao longo do tempo, focando a palavra média na

história e no ensino. Na segunda, introduziremos brevemente algumas noções

estatísticas importantes para a interpretação de distribuição.

Para a seção 2.2, referente à parte histórica, utilizamos como fonte

principal o artigo de Lavoie e Gatuso (1998)1.

Na seqüência, na seção 2.3 abordaremos a questão das medidas de

tendência central, entre outras e, em particular, o conceito de média.

2.2 A

H

Nesta seção estudaremos o termo “média” e seus significados em

diferentes culturas e, em seguida o abordaremos com enfoque no ensino.

Segundo Lavoie e Gatuso (1998), a média pode ser vista como um

conceito filosófico de “generalização” e, tem também algum significado

1 _{Traduzido por nós do original “An historical exploration of the concept of average”. In Proceedings of the}

sociológico no desenvolvimento das sociedades, em específico às sociedades

industriais, onde a padronização era essencial.

Citaremos, a seguir, a palavra média em diferentes culturas, pois apesar de

cada língua ter seu próprio estilo, veremos que as dificuldades apresentadas

quanto ao conceito média são universais.

Na França, por exemplo, se usa a palavra “moyenne” para descrever o que

os ingleses chamam de “mean” e o que nós conhecemos por média. A palavra

“moyenne” deriva da raiz do indo-europeu “medhyo” no sentido de “o que está no

meio”. Pela segunda metade do século XIII, a forma do substantivo “la moyenne”

(média) já existia. Em francês, a palavra média é primeiramente utilizada como

um adjetivo e, isto reflete sua etimologia de “situado no meio”.

Desta forma, segundo Rey2_{, apud Lavoie e Gatuso (ibid), dois significados}

do termo “média” se desenvolveram: o primeiro correspondendo ao significado

inicial, ou seja, a palavra média indicava algo igualmente distante de dois

extremos (não é grande nem pequeno, está no meio) e, neste sentido era usada,

em aritmética no século XVII, para se referir a metade da soma de dois números

(como um ponto médio). O segundo significado, que apareceu na Idade Média,

onde a palavra média servia para evocar o que é “mais comum”, “mais freqüente”

ou a forma “mais típica”. Um exemplo para o segundo significado é: “a média de

mulheres pensa que”, ou seja, a média representando a massa, a maioria (o valor

modal). É interessante notar que estes dois significados representavam o que

hoje nós conhecemos, respectivamente, por mediana e moda.

No século XIX, um terceiro significado foi desenvolvido e recebeu o nome

(em inglês) de “average” e, em seguida, “on average”, que representava uma

quantidade arbitrária. Os próprios físicos já falavam sobre “média” quando se

referiam à velocidade média definida como a relação entre uma distância

percorrida e o tempo necessário para percorrê-la, significado este que veio da

astronomia. A maior confusão é feita com a expressão “na média” utilizada no

senso comum como alguma coisa aproximada.

Segundo Bakker (2003)3, os exemplos históricos até o século XIX diziam

respeito a encontrar um valor real, como por exemplo, o diâmetro da lua. Até

então, a média era utilizada com uma finalidade, entretanto, após um longo

tempo, a média começa a ser usada como um valor representativo (a partir do

século XIX).

Assim, a média aritmética não era amplamente usada até o século XIX. O

conceito, entretanto é mais antigo, pois os babilônios, por exemplo, do século VI

ao III a.C., já haviam feito muitas observações sobre a medida das variações no

movimento do sol, lua e planetas para estabelecer certos parâmetros, tais como

posição particular destes astros durante o ano. Entretanto, até então não se sabe

se a idéia de média era utilizada.

Entre os gregos, a técnica para estimar a posição do centro das

observações era empregada por Hipparchus no século II a.C. No mesmo século,

os trabalhos de Ptolomeu sugerem que a média não era uma técnica, em geral,

3 _{Traduzido por nós do original “The early History of average values and implications for Education”. In}

usada. Segundo Droesbeke e Tassi (1990)4 foi com Tycho Brahé, no fim do

século XVI, que o uso do termo média tornou-se claramente distinto, uma vez que

foi utilizado para eliminar erros sistemáticos, pois Tycho trabalhava com o recurso

das várias observações para estimar uma valor que constituía um conjunto de

dados sobre o movimento dos planetas.

De acordo com Lavoie e Gatuso (ibid), no século XVII, por exemplo, a

média já era utilizada para falar sobre a metade da soma de dois números e, no

século XVIII, os eruditos eram peritos no uso da astronomia.

No século XIX, a idéia de média que era utilizada na astronomia tornou-se

um conceito usado nas ciências sociais e, não é por acaso que a primeira menção

sobre média foi encontrada no livro “Quick at Figures”, designado especialmente

para escolas comerciais e homens de negócios. Tem-se então o aparecimento do

conceito de média, voltado para o Ensino.

2.2.1 O CONCEITO DE MÉDIA NO ENSINO

No começo do século XX, a idéia de média foi introduzida no Ensino Médio

em problemas de distância, comida, reparos, baseball, etc e, em 1935 em um livro

texto na França para a 4a série da escola elementar. Primeiro o método da adição

e da divisão era explicado em um contexto e então se tinha a preocupação em

dar um significado à média. No mesmo período, nos livros texto, os dados são

apresentados às vezes como uma lista, porém, em geral, trabalha-se ainda com

somente dois ou três valores.

4 _{Traduzido por nós do original “Histoire de la Statistique”. Jean-Jacques Droesbeke et Philippe Tassi. P.}

Apesar do método da adição e divisão dominar o tipo de apresentação em

livros textos, ocasionalmente eram observadas algumas abordagens

interessantes, tal como o que aparecia no livro “Algebra for Problem Solving”

(Freilich, Berman, Johnson5_{, 1957 apud Lavoie e Gatuso (ibid)) onde os autores}

sugeriram começar com uma média estimada e ir trabalhando com os desvios à

média assumida, encontrando a média destes desvios e adicionando isto à média

estimada para encontrar a resposta correta. É verdade que isto era o método

empregado pelas calculadoras, porém é um método também que trabalha com

uma média já determinada. Em Lavoie e Gatuso (ibid) é citado o livro texto Calcul

Nouveau (Colas, 1963)6 onde os estudantes de 5a série não só calculavam a

média, mas também encontravam o valor procurado através de uma média já

determinada, e encontravam o total de dados a partir da média e o número de

valores.

Finalmente, a média é introduzida como uma estatística entre outros

valores de medida de tendência central em um capítulo intitulado “Introduction à la

statistique” (Ouelette, Desroches, 1969)7 apud Lavoie e Gatuso (1998) de um livro

para 8a _{série. Isto trouxe as comparações entre moda, mediana e média e}

enriqueceu o conceito.

Daquele tempo, muitas coisas mudaram, segundo Lavoie e Gatuso (1998)

dados são agora, em livros atuais, apresentados como uma lista de muitas

observações, os contextos são variados e incluem mais variáveis

sócio-econômicas, os números são altos e a solução proposta é algorítmica e mais e

5 _{Freilich, J.; Berman, S.; Johnson, E. (1957) Algebra for problem solving. Boston: Houghton Mifflin}

Company.

6 _{Colas, L. (1963)}

mais símbolos foram introduzidos, mas infelizmente, as questões seguem um

estereótipo “encontre o valor médio”. A dificuldade, segundo os autores, é criada

pela diferença na apresentação dos dados: listas, grupos de dados, tabelas, etc.

Neste sentido, pensamos que o problema possa ser a forma de

apresentação dos dados ou a não recontextualização do valor encontrado na

interpretação dos dados obtidos.

Salientamos, neste breve estudo histórico do conceito de média no ensino,

a importância deste conceito pela sua aplicabilidade. Por exemplo, em geometria,

calculamos a média aritmética das coordenadas dos três vértices para

encontrarmos as coordenadas do baricentro de um triângulo (ponto de encontro

das medianas de um triângulo), ou ainda, para encontrarmos o ponto médio de

um segmento, entre outras.

A seguir, nos deteremos ao estudo desse conceito em uma perspectiva

matemática.

2.3 M

Além de ser um dos principais conceitos estatísticos de medida de

tendência central, a média tem muitas aplicações em questões práticas da vida

diária como, por exemplo, quando analisamos notas de alunos, índices de

evolução de preços, etc. Mesmo que não saibamos o conceito matemático em si

ou tão pouco interpretá-lo, podemos ter alguma idéia de como calculá-lo, mesmo

que o usemos em situações nas quais o resultado fica mais difícil de ser

interpretado, por exemplo, quando calculamos a média de idades de alguns

7 _{Ouelette R., Desroches, G. (1969)}

estudantes em uma sala de aula e chegamos ao valor médio de 37,3. Ou ainda

quando utilizamos o conceito de média em situações em que melhor seria utilizar

a mediana, como a seguir.

Há algum tempo, um telejornal realizou uma pesquisa em diversos bairros

de São Paulo para saber a aceitação popular dos administradores regionais. Na

pesquisa, uma amostra da população era convidada a dar nota de zero a dez

para o administrador. Quando o jornalista anuncia os resultados para um

administrador regional afirmou: "O senhor obteve nota 5 (o jornalista se referindo

a média) na avaliação popular, o que quer dizer que 50% dos eleitores aprovam

sua administração”.

Mas podemos ilustrar que, o jornalista não estava correto nesta

interpretação: imagine uma situação simplificada em que votem apenas três

eleitores e suas notas para o administrador são iguais a 7, 6 e 2. Neste caso, a

média do administrador é 5       + + 3 2 6 7

, mas ele obteve mais de 50% dos eleitores

atribuindo nota acima da média ao seu trabalho. Por outro lado, se as notas dos

três eleitores fossem 9, 4 e 2, a nota média também seria igual a 5       + + 3 2 4 9 ,

mas agora teríamos apenas cerca de 33% de notas acima da média. O raciocínio

do jornalista, de fato, está relacionado a outro tipo de medida de tendência

central, a mediana.

Assim, entre as várias razões que poderiam justificar o estudo da

estatística na escola, uma delas seria a relação entre o conhecimento matemático

e a vida cotidiana (por exemplo, os direitos do consumidor), pois assim a

Quanto à média como conhecimento matemático, nos deteremos à média

aritmética, porém julgamos importante fazer um apanhado sobre as medidas de

tendência já que a média aritmética é uma delas. Para tanto, percebemos que

estudos sobre distribuições de freqüências nos permitem descrever, de modo

geral, os grupos de valores que uma variável pode assumir. Assim, podemos

localizar a maior concentração de valores de uma dada distribuição, isto é, se ela

se localiza no início, no meio ou no final, ou ainda, se há uma distribuição

simétrica, ou seja, a redução dos dados através de tabelas de freqüências fornece

muito mais informações sobre o comportamento de uma variável do que a própria

série original dos dados. Essas medidas “resumem” os dados apresentando um

ou alguns valores que sejam “representativos” dos dados fornecidos.

É importante salientar que para cada elemento investigado, se associa um

resultado (ou mais de um resultado) correspondendo à realização de uma certa

variável. Por exemplo, um pesquisador está interessado em fazer um

levantamento sobre alguns aspectos sócio-econômicos dos empregados na

seção de orçamentos de uma companhia. Considerando-se a variável estado civil,

para cada empregado temos associada a realização “solteiro” ou “casado”. Assim,

variável é uma característica da unidade elementar (resultado ou observação) que

pode ter valores diferentes entre as unidades de medida.

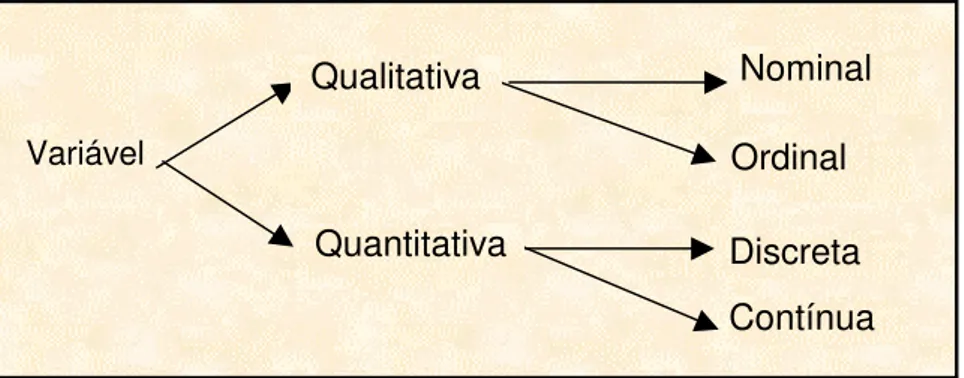
Existem dois tipos de variáveis: as qualitativas, que se subdividem em

nominal e ordinal, e as quantitativas, que podem ser do tipo discreta ou contínua,

Figura 2.1 – Tipos de variável

Quando estudamos uma variável é interessante conhecer a sua

distribuição através dos possíveis valores que ela assume. Temos várias

maneiras de representar uma distribuição de freqüência, incluindo tabelas de

freqüência, tais como a tabela 2.1 e gráficos de freqüência.

Estaturas (cm) Freqüência

150 1548 4

154 158 9

158 162 11

162 166 8

166 170 5

170 174 3

Total 40

Tabela 2.1 – Tabela de distribuição de freqüências

Entretanto, uma distribuição de freqüência pode ter outro tipo de

representação, além da tabela. Por exemplo, os gráficos, que são representações

geométricas da relação entre variáveis. Diferentes tipos de gráficos são

empregados em estatística, de acordo com o tipo de dados e a finalidade a que

ele se destina. Assim, podemos ter gráficos de barras (ou colunas), de setores, de

linhas, de áreas, entre outros. Quando é necessária uma análise mais profunda

dos dados, gráficos mais complexos são usados, tais como histogramas, curvas

de freqüência, entre outros.

8_{150 154 é um intervalo fechado à esquerda e aberto à direita, tal que 150≤x<154} Variável

Qualitativa

Quantitativa

Nominal

Ordinal

A apresentação gráfica é um complemento importante da apresentação

tabular. A principal vantagem de um gráfico sobre a tabela prende-se ao fato de

que ele permite conseguir uma visualização imediata da distribuição dos valores

observados. Os gráficos propiciam uma idéia preliminar mais satisfatória da

concentração e dispersão dos valores, uma vez que por meio deles os dados

estatísticos se apresentam em termos de grandezas visualmente interpretáveis.

Em relação a nossa área de interesse, as medidas de tendência central, é

possível, por exemplo, observar algumas relações entre as três diferentes

medidas (média, mediana e moda) olhando as curvas de freqüência, conforme

ilustrado nas figuras 2.2, 2.3 e 2.4. Em uma curva simétrica, por exemplo, as três

medidas coincidem.

Como a representação gráfica de uma distribuição de freqüências que

pode ser dada pelas curvas de freqüência, destacaremos, a seguir, a curva

simétrica e a assimétrica:

Figura 2.3 – Curva de freqüência assimétrica à esquerda - Estatística Básica, p. 250

Figura 2.4 - Curva de freqüência assimétrica à direita - Estatística Básica, p. 250

De forma geral, para ressaltar as tendências características de cada

distribuição, isoladamente ou em confronto com outras, é necessário introduzir

alguns conceitos que nos permitam exprimir por meio de números essas

tendências. Esses conceitos são denominados elementos típicos da distribuição e

- medidas de assimetria e curtose (ver Anexo 1)

- medidas de variabilidade ou dispersão (ver Anexo 2)

- medidas de posição (que incluem as medidas de tendência central)

2.3.1 MEDIDAS DE POSIÇÃO

Dentre as medidas de posição podemos ter medidas de tendência central e

medidas de ordenamento (as separatrizes), porém as mais usadas são as

medidas de tendência central, que recebem esta denominação porque os dados

observados tendem, em geral, a se agrupar em torno dos valores centrais.

As medidas de ordenamento ou separatrizes são:

- mediana

- quartis

- percentis

- decis

As medidas de tendência central são:

- mediana

- moda

- média aritmética ou média

A moda, a média aritmética e a mediana são as três medidas de tendência

central ou promédios mais utilizados para resumir o conjunto de valores

representativos do fenômeno que se pretende estudar. Outros promédios menos

usados são a média geométrica, harmônica, quadrática, cúbica e biquadrática.

Para cada um destes promédios existem dois tipos: simples e ponderada, no caso

da média cúbica, por exemplo, temos a média cúbica simples e a média cúbica

Para o presente trabalho julgamos desnecessário apresentar uma

descrição pormenorizada desses tipos de medida de tendência menos usados e,

preferimos nos deter ao estudo das principais medidas de tendência central.

Dessa forma, na seqüência apresentamos um breve estudo sobre

mediana, moda e, em especial, média que é o foco da nossa investigação.

Mediana

A mediana caracteriza uma série de valores devido à sua posição central.

No entanto, ela apresenta uma outra característica, tão importante quanto a

primeira: ela separa a série em dois grupos que apresentam o mesmo número de

valores. Assim, há medidas de posição que estão ligadas à mediana,

relativamente à característica de sua posição na série. Essas medidas - os

quartis, percentis, decis – são, juntamente com a mediana, conhecida pelo nome

genérico de separatrizes.

Sabemos que a mediana divide a distribuição em duas partes iguais quanto

ao número de elementos de cada parte. Já os quartis permitem dividir a

distribuição em quatro partes iguais quanto ao número de elementos de cada

uma; os decis em dez partes e os centis em cem partes iguais.

Em Toledo e Ovalle (1991) p. 152, podemos encontrar a seguinte definição

de mediana:

“A mediana pode ser definida como o valor que divide uma série ordenada de tal forma que pelo menos a metade ou cinqüenta por cento dos itens sejam iguais ou

maiores do que ela, e que haja pelo menos outra metade ou cinqüenta por cento de itens maiores do que ela. A mediana é considerada uma separatriz, por dividir a

distribuição ou conjunto de dados em partes iguais”

- desejamos obter o ponto que divide a distribuição em partes iguais;

- há valores extremos na distribuição.

Moda

Uma outra medida de tendência central é a moda que Toledo e Ovalle

(1991) apresenta a seguinte definição:

“Considerando um conjunto ordenado de valores, a moda será o valor predominante, o valor mais freqüente desse conjunto”.

Assim, o salário modal dos empregados de uma indústria é o salário mais

comum, isto é, o salário recebido pelo maior número de empregados dessa

indústria. A moda é utilizada, geralmente, quando desejamos obter uma medida

rápida e aproximada de posição ou quando a medida de posição deve ser o valor

mais típico da distribuição. Ela não é afetada pelos extremos, porém tem suas

desvantagens: não utiliza todos os valores da variável e a variável pode ter mais

de uma moda ou não tê-la.

Média Aritmética

A medida de tendência central mais comumente usada para descrever

resumidamente uma distribuição de freqüências é a média aritmética que pode

ser de dois tipos: simples ou ponderada.

1) Média Aritmética Simples

Figura 2.5 – Definição de média aritmética simples - Estatística Fácil, 2001, p. 80

A definição acima foi retirada de um livro freqüentemente utilizado no nível

superior. Na maioria dos livros didáticos do Ensino Médio, entretanto a definição é

apresentada com uma linguagem mais simples, sem o símbolo de somatório e

tendo os valores da variável representados por

_x

_x

_x

_x

apresentamos a definição do livro “Matemática Fundamental, 2002, p.551”:

Figura 2.6 – Definição de média aritmética simples

Após esta definição, os livros didáticos quase sempre apresentam

exemplos, tais como:

Media aritmética (x)

Média aritmética é o quociente da divisão da soma dos valores da variável pelo número deles:

x = n

x

∑

x: a média aritmética

i

x : os valores da variável

n: o número de valores

”Média aritmética (x) dos valores

_x

_x

_x

_x

valores e o seu número total n.

x =

n

x

x

x

x

Se um grupo de nove pessoas tem as idades: 12, 54, 67, 15, 84, 24, 38, 25, 33 então

a idade média do grupo (utilizando o algoritmo acima descrito) pode ser calculada

pela média aritmética:

x = 39,1

9 = + + + + + + +

Vale observar que em exemplos como este se valoriza o algoritmo e não

há uma interpretação do valor encontrado (no caso, o que significaria uma média

de idade 39,1?).

2) Média Aritmética Ponderada

A média aritmética é considerada ponderada quando os valores do

conjunto tiverem pesos diferentes. Assim, obtém-se a média aritmética ponderada

por meio do quociente entre o produto dos valores da variável pelos respectivos

pesos e a soma dos pesos. Exemplo:

Figura 2.7 – Definição de média aritmética ponderada - Estatística básica, 1991, p. 109

2.3.2 CONSIDERAÇÕES SOBRE O CONCEITO DE MÉDIA

Dentre as medidas de tendência central apresentadas anteriormente nos

deteremos aos aspectos relacionados à média aritmética, objeto do nosso estudo.

Para facilitar o desenvolvimento do nosso trabalho, adotaremos o termo média

aritmética ou simplesmente média para designarmos a média aritmética simples.

A média aritmética além de ser a medida de tendência central mais

utilizada, a aplicação de seu conceito tem como vantagem a utilização de todos

os valores da variável e a obtenção de um valor único para representá-la. Porém,

Um professor pode realizar quatro provas por ano em sua matéria, atribuindo a cada uma delas os seguintes pesos: 1, 2, 3 e 4. Se um aluno tiver recebido as notas 8, 7, 9 e 9, nessa ordem, sua nota final será a média ponderada 8,5, obtida da seguinte maneira:

Média final =

4 3 2 1 ) 4 9 ( ) 3 9 ( ) 2 7 ( ) 1 8 ( + + + + +

+ x x x x

= 8,5

10 85 10 36 27 14

tem como desvantagem o fato do resultado final (a média) ser afetado pelos

valores extremos.

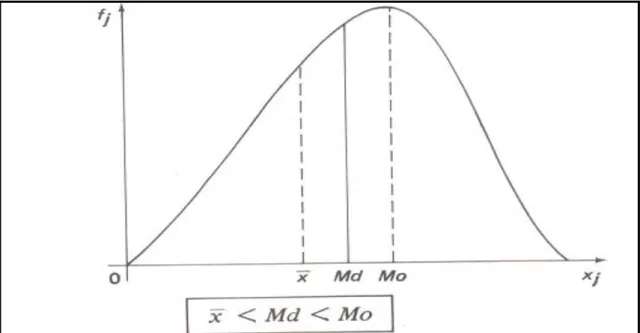
Salientamos que no caso da distribuição ser simétrica, a média, a moda e a

mediana assumem os mesmos valores, ou seja, são iguais (ver Figura 2.2).

Na figura 2.3, entretanto, por se tratar de uma distribuição assimétrica à

esquerda (assimetria negativa), a média aritmética é menor que a mediana, e esta

é menor que a moda (x<Md<Mo). E na figura 2.4, por ser uma distribuição

assimétrica à direita (assimetria positiva) há uma predominância de valores

superiores à moda (Mo<Md<x).

A seguir, apresentamos o quadro-resumo 2.1 dos elementos típicos de

uma distribuição, discutidos até então, com o objetivo de situarmos o leitor onde

Curva

Platicúrtica LeptocúrticaCurva Curva

Mesocúrtica PlaticúrticaCurva LeptocúrticaCurva Curva

Mesocúrtica

Medidas de assimetria

Curva

Simétrica SimétricaCurva Positiva Curva Simétrica Negativa Curtose Medidas de posição Medidas de tendência central Medidas de ordenamento

Média Moda Mediana Separatrizes Medidas de variabilidade ou dispersão Medidas de dispersão absoluta Medidas de dispersão relativa Desvio médio/ padrão Variância Amplitude

Vale ressaltar que as medidas de posição podem ser utilizadas em

conjunto para auxiliar a análise de dados ou, em determinadas situações, uma

pode ser mais conveniente do que a outra. Em situações em que um ou mais

valores são muito discrepantes do que o geral das observações, a média será

muito influenciada por este valor, tornando-a assim, inadequada para representar

aquele conjunto de dados. Neste caso, como a mediana não é afetada por valores

discrepantes, seu uso seria mais adequado para representar os dados. Assim

sendo, tudo depende do objetivo da análise.

De forma geral, precisamos ter o cuidado de, ao usarmos estas medidas,

não distorcermos informações e características dos dados que estamos

analisando.

Do ponto de vista didático, o que poderíamos nos perguntar é: O que

significa uma média de idade igual a 39,1? Qual o significado para esta média? O

que representa este número? Quando é que a média aritmética faz sentido? E

quando é que não faz? São perguntas como estas que nosso trabalho pretende

esclarecer, sem termos é claro, a pretensão de esgotar o assunto.

Acreditamos, enfim, que a compreensão de um conceito não se reduz

simplesmente a conhecer as definições, algoritmos e propriedades, mais que isso,

é preciso compreender o significado de tal conceito e quando é possível aplicá-lo.

Neste capítulo fizemos uma análise do conceito de média sob o aspecto

histórico, de ensino e sob uma perspectiva matemática situando o leitor onde se

encontra o foco de nosso trabalho.

No capítulo a seguir, estudaremos como o conceito de média é

apresentado em documentos oficiais, tais como PCN’s, ENEM, SAEB e livros

M

M

M

M

M

M

M

M

3.1 I

Neste capítulo faremos uma breve análise dos PCN’s (Parâmetros

Curriculares Nacionais), de alguns livros didáticos, de algumas questões do

ENEM (Exame Nacional do Ensino Médio) e de uma questão do SAEB (Sistema

Nacional de Avaliação da Educação Básica) a fim de refletirmos sobre o ensino

de estatística descritiva e especialmente, sobre como as noções relacionadas às

medidas de tendência central são tratadas no currículo atual do Brasil.

Salientamos que embora o sistema de avaliação da Educação Básica

compreenda o Censo Escolar, o ENEM, o SAEB e, o Exame Nacional de

Certificação de Competências de Jovens e Adultos (ENCCEJA), nos limitaremos

a análise de dois desses instrumentos: o ENEM e o SAEB.

Em nossa análise dos PCN’s nos detivemos a um dos quatro blocos de

conteúdos que os PCN’s apresentam, ou seja, o bloco Tratamento da Informação.

E, optamos por analisar não só os PCN’s do Ensino Médio como também os

PCN’s de 3o e 4 o ciclos do Ensino Fundamental (5a a 8a série) a fim de investigar

se o conceito de média já era sugerido nestes ciclos e estabelecer uma

comparação entre os PCN’s do Ensino Fundamental (3o _{e 4}o _{ciclos) e do Ensino}

3.2 A

P

C

N

(PCN’

)

O interesse pelo ensino de Estatística, mais particularmente pelo conceito

de média, deu-se quando percebemos, a partir de uma leitura preliminar de

alguns livros didáticos aliada a experiência pessoal, a pouca ou nenhuma ênfase

dada a este conteúdo no Ensino Médio. Com base neste fato, sentimos a

necessidade de investigar o que é abordado sobre média nos PCN’s e livros

didáticos e o que se espera de um aluno, a respeito de média, em sistemas de

avaliação como o ENEM e o SAEB.

Quanto aos PCN’s do Ensino Fundamental, os conteúdos matemáticos

estão divididos em quatro blocos, a saber: Números e Operações, Espaço e

Forma, Grandezas e Medidas e, Tratamento da Informação. Este último bloco, no

qual nos deteremos, se justifica pela necessidade de acrescentar aos outros três

blocos conteúdos que permitam ao cidadão “tratar” as informações que recebem

cotidianamente, aprendendo assim a lidar com dados estatísticos, tabelas ou

gráficos, a raciocinar utilizando idéias relativas à probabilidade e à combinatória.

Estas competências são consideradas importantes, pois na vida cotidiana,

os alunos deparam-se com dados e afirmações de caráter aleatório, como por

exemplo, situações referentes às eleições, loterias, esporte, publicidade, etc., e,

portanto encontrarão situações de incerteza nas quais deverão julgar, estimar

probabilidades, fazer previsões, tomar decisões e agir.

Nesse sentido, consideramos que os PCN’s sugerem que a introdução dos

alunos à Estatística seja feita de forma significativa1 permitindo aos alunos o

1 _{Entendemos por forma significativa, a forma na qual o aluno constrói o conceito dando sentido ao mesmo}

desenvolvimento de formas particulares de pensamento e raciocínio, visando

resolver determinadas situações que envolvem ou não fenômenos aleatórios. De

acordo com os PCN’s:

“Com relação à Estatística, a finalidade é fazer com que o aluno venha a construir procedimentos para coletar, organizar, comunicar dados, interpretar amostras e

comunicar resultados por meio da linguagem estatística, utilizando tabelas, gráficos

e representações que aparecem freqüentemente em seu dia-a-dia. Além disso,

calcular algumas medidas estatísticas como média, mediana e moda com o objetivo

de fornecer novos elementos para interpretar dados estatísticos”.

(Parâmetros Curriculares Nacionais - Matemática: Ensino de 5a a 8a série, 1998, p. 52)

O destaque ao bloco Tratamento da Informação visa evidenciar sua

importância, em função de seu uso atual na sociedade, conforme enfatizamos

anteriormente.

A seguir trataremos, em específico, do terceiro e quarto ciclos do Ensino

Fundamental (5a a 8a séries) em relação ao uso de Estatística a fim de

estabelecer um paralelo entre o que é citado sobre Estatística nos PCN’s destas

séries e os PCN’s do Ensino Médio.

No terceiro ciclo (5a e 6a série) do Ensino Fundamental, os PCN’s

estabelecem que o ensino de Matemática deve visar o desenvolvimento do

raciocínio combinatório, estatístico e probabilístico, por meio da exploração de

situações de aprendizagem que levem o aluno a:

“Coletar, organizar e analisar informações, construir e interpretar tabelas e gráficos,

formular argumentos convincentes (um argumento, de acordo com os PCN’s (p. 70)

matemáticos e se possível responder aos contra-argumentos ou réplicas que lhe

forem impostos), tendo por base a análise de dados organizados em

representações matemáticas diversas”;

(Parâmetros Curriculares Nacionais - Matemática: Ensino de 5a a 8a série, 1998, p. 65)

Desta forma, quanto ao bloco Tratamento da Informação, para este ciclo é

importante fazer com que os alunos ampliem noções já apreendidas em séries

anteriores (como coletar e organizar dados em tabelas e gráficos, estabelecer

relações entre acontecimentos, fazer algumas previsões, observar a freqüência

de ocorrência de um acontecimento), aprendendo também a formular questões

pertinentes para um conjunto de informações, a elaborar algumas conjecturas e,

comunicar informações de modo convincente e a interpretar diagramas e

fluxogramas.

No decorrer desse trabalho, especificado pelos PCN’s, espera-se o início

do estudo das medidas estatísticas, como a média aritmética, que possibilitará

uma interpretação mais “aperfeiçoada” dos dados.

Já no quarto ciclo (7a _{e 8}a _{série) do Ensino Fundamental, a proposta dos}

PCN’s não é muito diferente e estabelecem os mesmos objetivos:

desenvolvimento do raciocínio estatístico e probabilístico, por meio da exploração

de situações de aprendizagem que levem o aluno a:

“Construir tabelas de freqüência e representar graficamente dados estatísticos,

utilizando diferentes recursos, bem como elaborar conclusões a partir da leitura,

análise, interpretação de informações apresentadas em tabelas e gráficos”.

(Parâmetros Curriculares Nacionais - Matemática: Ensino de 5a _{a 8}a _{série, 1998, p.}

Embora os objetivos sejam os mesmos, ressaltamos que neste ciclo o bloco

Tratamento da Informação pode ser aprofundado, uma vez que a própria

experiência dos alunos no ciclo anterior pode ajudá-los a desenvolver pesquisas

sobre sua própria realidade e interpretá-la, utilizando-se de gráficos e algumas

medidas estatísticas. Um dos conceitos/procedimentos para este ciclo que nos

chamou a atenção é a questão da obtenção das medidas de tendência central

dos dados obtidos em uma pesquisa (média, moda e mediana), compreendendo

seus significados para fazer inferências (Parâmetros Curriculares Nacionais - Matemática:

Ensino de 5a _{a 8}a _{série, 1998, p. 62)}

Podemos salientar que os conteúdos que constituem o bloco Tratamento

da Informação propiciam estabelecer ligações entre a Matemática e os conteúdos

de outras áreas (Ciências, Meio Ambiente, Saúde, por exemplo) e com os Temas

Transversais à medida que o aluno os perceba como instrumentos essenciais

para a constituição de uma atitude crítica diante de questões sociais, políticas,

culturais, científicas da atualidade. Enfim, podemos dizer que no Ensino

Fundamental, é grande a ênfase dada ao bloco Tratamento da Informação e que

a Estatística é parte integrante da formação neste nível e de grande importância.

Além disto, nos dois ciclos já se sugere o estudo das medidas de tendência

central, entre elas a média.

Quanto aos PCN’s do Ensino Médio, eles estão divididos em três áreas:

“Linguagens, códigos e suas tecnologias”, “Ciências da natureza, Matemática e

suas tecnologias” e “Ciências Humanas e suas tecnologias”. Na segunda área,

que é a que nos interessa, apresenta-se as habilidades básicas e as

competências que se espera que sejam desenvolvidas pelos alunos em Biologia,

Por tratar de habilidades e competências, os PCN’s do E.M. parecem que

têm uma abordagem sobre Estatística mais tímida se comparada à feita no

Ensino Fundamental.

Porém salienta-se que as habilidades de descrever e analisar um grande

número de dados, realizar inferências e fazer predições com base numa amostra

de população, aplicar as idéias de probabilidade e combinatória a fenômenos

naturais e do cotidiano são aplicações da Matemática em questões do mundo real

que tiveram um crescimento muito grande e se tornaram complexas. Neste

sentido, técnicas e raciocínios estatísticos e probabilísticos são, sem dúvida,

instrumentos tanto das Ciências da Natureza quanto das Ciências Humanas. Isto

mostra como será importante uma cuidadosa abordagem dos conteúdos de

contagem, estatística e probabilidade no Ensino Médio, ampliando a interface

entre o aprendizado da Matemática e das demais ciências e áreas. Neste sentido,

algumas das finalidades do ensino de Matemática no nível médio indicam como

objetivos levar o aluno a:

•••• “aplicar seus conhecimentos matemáticos a situações diversas, utilizando-os

na interpretação da ciência, na atividade tecnológica e nas atividades cotidianas;

•••• analisar e valorizar informações provenientes de diferentes fontes, utilizando

ferramentas matemáticas para formar uma opinião própria que lhe permita

expressar-se criticamente sobre problemas da matemática, das outras áreas do

conhecimento e da atualidade;

•••• desenvolver as capacidades de raciocínio e resolução de problemas, de

comunicação, bem como o espírito crítico e criativo;

•••• expressar-se oral, escrita e graficamente em situações matemáticas e valorizar

•••• estabelecer conexões entre diferentes temas matemáticos e entre esses temas

e o conhecimento de outras áreas do currículo;

•••• reconhecer representações equivalentes de um mesmo conceito, relacionando

procedimentos associados às diferentes representações“.

(Parâmetros Curriculares Nacionais - Matemática: Ensino Médio, 1999, p. 84-85)

Diante de alguns dos objetivos propostos pelos PCN’s do Ensino Médio que

foram acima relacionados, o que nos indagamos é a que ponto o livro didático

(instrumento de apoio no trabalho do professor, uma vez que os alunos de Ensino

Médio da rede estadual não recebem livros) cumpre esses objetivos.

Diferente dos PCN’s de E.M., nos PCN’s de E.F., são citadas algumas

orientações didáticas para o 3o e 4o ciclos do Ensino Fundamental e,

particularmente em relação ao conceito de média, são propostas situações em

que haja discrepâncias bastante acentuadas entre as medidas de tendência

central para que os alunos possam refletir sobre qual é a mais significativa para

expressar a tendência da maioria. Por exemplo, nos PCN’s de E. F. temos a

seguinte situação:

“Suponha que cada um dos sete números da seqüência 1, 2, 2, 2, 3, 3, 22

represente a quantidade de salários mínimos de um funcionário de uma firma que tem sete funcionários, ou seja, um funcionário ganha 1 mínimo, três funcionários

ganham 2 mínimos, dois ganham 3 mínimos e um ganha 22 mínimos. A mediana desses valores é 2. A média desse conjunto de valores, no entanto, é 5, pois

5 7

22 3 3 2 2 2

1+ + + + + + _{= . Nesse caso os alunos poderão perceber que a mediana}

representa melhor a situação real dos dados, pois o valor 22, por ser muito superior aos outros termos, “eleva” a média.”.

Embora os PCN’s do E.F. tenham diluído os conteúdos referentes à

Estatística e ao Tratamento da Informação ao longo de todo o Ensino

Fundamental, no Ensino Médio o que se tem é uma abordagem mais tímida e

incipiente uma vez que é genérica em relação aos conteúdos.

Diante desta consideração, o que nos perguntamos é: Será que os livros

didáticos abordam os conteúdos de forma significativa? Para responder a esta

pergunta, na próxima seção consideraremos aspectos da análise de alguns livros

didáticos do Ensino Médio, feita por Lima (2001), para verificarmos se o que é

proposto nos PCN’s é realmente utilizado nestes livros, que tipo de situações são

propostas e que importância é dada às medidas de tendência central, em

3.3 M

E

M

Lima (2001) apresenta no livro “Exame de textos. Análise de livros de

Matemática para o Ensino Médio” uma análise de 12 coleções (36 volumes) dos

livros didáticos mais usados nas escolas brasileiras. Na tabela 3.1 apresentamos

na 1a coluna, o nome de cada uma das 12 coleções e seus respectivos autores e,

na 2a _{coluna se tem capítulo sobre média e em qual volume está:}

Livros e autores2 Tem capítulo sobre média

Matemática na Escola do 2o grau (Antônio dos Santos Machado Sim

(vol. 3)

Matemática, aula por aula (Benigno Barreto Filho e Cláudio Xavier da Silva)

Sim

(vol. 3)

Matemática (Edwaldo Bianchini e Herval Paccola) Sim

(vol. 3)

Matemática (Gelson Iezzi, Osvaldo Dolce e outros) Não

Coleção Matemática para o Segundo Grau (Nelson Gentil, Carlos Alberto Marcondes dos Santos e outros)

Sim (vol. 2) Coleção Matemática (José Ruy Giovanni e José Roberto Bonjorno) Sim

(vol. 3)

Matemática (Kátia Cristina Stocco Smole e Rokusaburo Kijukawa) Sim (vol. 1)

Matemática: contexto e aplicações (Luiz Roberto Dante) Sim

(vol. 3)

Coleção Matemática (Manoel Rodrigues Paiva) Não

A Matemática no Ensino Médio (Marcio Cintra Goulart) Sim

(vol. 3)

Matemática (Maria Helena Soares de Souza e Walter Spinelli) Sim

(vol. 3)

Curso Prático de Matemática (Paulo Bucchi) Sim

(vol. 3)

Tabela 3.1 – Análise de alguns livros didáticos

2 _{No livro de referê ncia “Exame de textos. Aná lise de livros de Matemá tica para o Ensino Mé dio (LIMA,}

Assim, por exemplo, na análise do livro “Matemática” dos autores Bianchini

e Paccola – volume 3, é citado que o último capítulo do livro (o décimo) é uma

introdução sucinta à estatística descritiva. Há uma seção dedicada às medidas de

tendência central (média, média ponderada, mediana) e outra sobre as medidas

de dispersão (variância e desvio padrão). Segundo Lima (2001) não há, no

entanto, maiores explicações, exercícios resolvidos ou propostos sobre a

importância de tais medidas para compreender a variabilidade dos dados.

No caso do livro “Matemática” dos autores Iezzi, Dolce, Teixeira, Machado,

Goulart, Castro e Santos Machado, Lima (ibid) relata que os autores trabalham

apenas com probabilidade e combinatória. Apesar de Lima (ibid) considerar esta

coleção uma das melhores existentes no mercado, não aborda o conceito de

média em nenhum dos três volumes.

Dada a atual importância do bloco Tratamento da Informação e a referência

às medidas de tendência central, já citadas anteriormente na análise dos PCN’s,

nos causa estranheza um livro que foi considerado um dos melhores existentes

no mercado não aborde nenhuma das medidas de tendência central, focando seu

trabalho na questão da probabilidade e análise combinatória.

Apenas duas coleções das 12 analisadas por Lima, colocaram a Estatística

no volume 2 ou 1. Uma delas é a “Coleção Matemática para o Segundo Grau”

(Nelson Gentil, Carlos Alberto Marcondes dos Santos, Antonio Carlos Grecco,

Antônio Belotto Filho e Sérgio Emílio Grecco) que, no volume 2, possui 15

capítulos e aborda os elementos introdutórios da Estatística no capítulo 13. Este

capítulo tem menos exercícios que os outros e, o autor não menciona a

possibilidade do uso de calculadoras e computadores, o que poderia tornar os