PUC/SP
TALITA CARVALHO SILVA DE ALMEIDA
A BASE DE CONHECIMENTO PARA O ENSINO DE
SÓLIDOS ARQUIMEDIANOS
DOUTORADO EM EDUCAÇÃO MATEMÁTICA
PUC/SP
BASE DE CONHECIMENTO PARA O ENSINO DE
SÓLIDOS ARQUIMEDIANOS
Tese apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para obtenção do título de
DOUTOR EM EDUCAÇÃO MATEMÁTICA, sob a orientação da Professora Doutora Maria José Ferreira da Silva.
Banca Examinadora
_____________________________________
_____________________________________
_____________________________________
_____________________________________
Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta Tese por processos de foto copiadoras ou eletrônicos.
Dedico este trabalho ao meu filho
A
GRADECIMENTOS
Agradeço primeiramente a Deus e aos meus anjos da
guarda, pela proteção, força e pela oportunidade de iniciar e
concluir mais uma etapa importante da minha vida.
À amiga e Professora Doutora Maria José Ferreira da Silva,
pela orientação, incentivo, confiança e apoio nos momentos
delicados que passei durante o percurso.
Aos membros da banca, Professores Doutores Saddo Ag
Almouloud, Barbara Lutaif Bianchini, Jesus Victoria Flores
Salazar e Gilson Bispo de Jesus, pelas sugestões valiosas e
contribuições para essa pesquisa.
Ao corpo docente do Programa de Estudos Pós-Graduados
em Educação Matemática da PUC-SP, especialmente, a
professora Doutora Cileda de Queiroz e Silva Coutinho.
A todos os funcionários do Centro de Ciências Exatas da
PUC-SP.
Aos amigos do Programa de Estudos Pós-Graduados em
Educação Matemática.
Aos meus pais amados, Henrique e Eliana, por me
Ao meu esposo Érico e ao meu filho Arthur, pelo amor e
apoio sempre.
À CAPES, pela concessão da bolsa de estudos.
A todas as pessoas que, de alguma forma, contribuíram para
realização desta pesquisa.
arquimedianos. 2015. Tese (Doutorado). Programa de Estudos Pós-Graduados em Educação Matemática. Pontifícia Universidade Católica de São Paulo. PUCSP.
R
ESUMO
O presente trabalho tem como objetivo identificar os saberes docentes mobilizados para que sólidos arquimedianos sejam ensinados. Assim, a pergunta de pesquisa foi: qual base de conhecimento para o ensino de sólidos arquimedianos na escola básica? Para responder a esta questão, recorremos a um estudo bibliográfico desenvolvido com base em material já elaborado, constituídos principalmente de artigos científicos. O referencial teórico baseou-se no Conhecimento Matemático para o Ensino, no sentido de Ball, Thames e Phelps, e no Conhecimento Tecnológico para o Ensino, no sentido de Mishra e Koehler, ambos obtidos com avanços na proposta inicial de Shulman, e colaboradores acerca da base de conhecimento para o ensino e na Teoria Antropológica do Didático de Yves Chevallard. Tais referenciais foram fundamentais para a composição de um cenário que evidenciasse quais saberes docentes estão minimamente envolvidos no processo de ensino de sólidos arquimedianos. A escolha metodológica pela pesquisa bibliográfica contribuiu para o alcance do objetivo desejado, visto que nos permitiu encontrar aspectos do conhecimento não evidenciados nos estudos de Shulman. A escolha de um procedimento matemático realizado por renascentistas como Modelo Epistemológico de Referência nos conduziu a uma Organização Matemática e uma possível Organização Didática para sólidos arquimedianos, nos ajudando a perceber que os saberes docentes são provenientes da interação de três componentes particulares de conhecimento, conhecimento matemático, conhecimento tecnológico e conhecimento didático.
A
BSTRACT
This research aims to identify the teaching knowledge mobilized for Archimedean solids are taught. Thus, the research question was: which knowledge base for the Archimedean solid education in basic school? To answer this question we resort to a bibliographical study developed based on material already prepared, consisting of books and scientific articles. The theoretical framework was based on Mathematical Knowledge for Teaching, in sense Ball, Thames and Phelps, and Technological Knowledge for Education, in sense Mishra and Koehler, both obtained with advances in the initial proposal of Shulman and colleagues about the knowledge base for teaching and the Anthropological Theory of Didactic Yves Chevallard. Such references were fundamental in the composition of a scene that showed that teaching knowledge are minimally involved in the Archimedean solids teaching process. The methodological choice for the literature contributed to the achievement of the desired goal, since it allowed us to find aspects of knowledge not evidenced in studies by Shulman. The choice of a mathematical procedure performed by Renaissance as Mathematics Reference Model Epistemological led us to an Mathematics Organization and a possible Didactic Organization for Archimedean solids helping us to realize that the teaching knowledge come from the interaction of three particular components of knowledge, mathematical knowledge, technological knowledge and didactic knowledge.
FIGURA 1.SÓLIDOS ARQUIMEDIANOS ... 41
FIGURA 2.CONHECIMENTO PEDAGÓGICO DO CONTEÚDO (CPC). ... 60
FIGURA 3.TRIÂNGULO PEDAGÓGICO ... 67
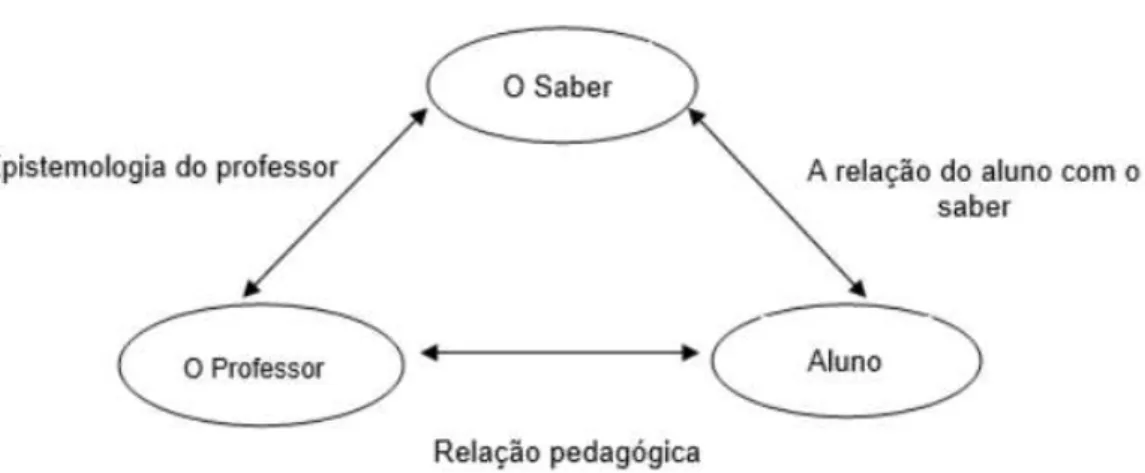
FIGURA 4.TRIÂNGULO DIDÁTICO ... 68
FIGURA 5.TETRAEDRO DIDÁTICO ... 72
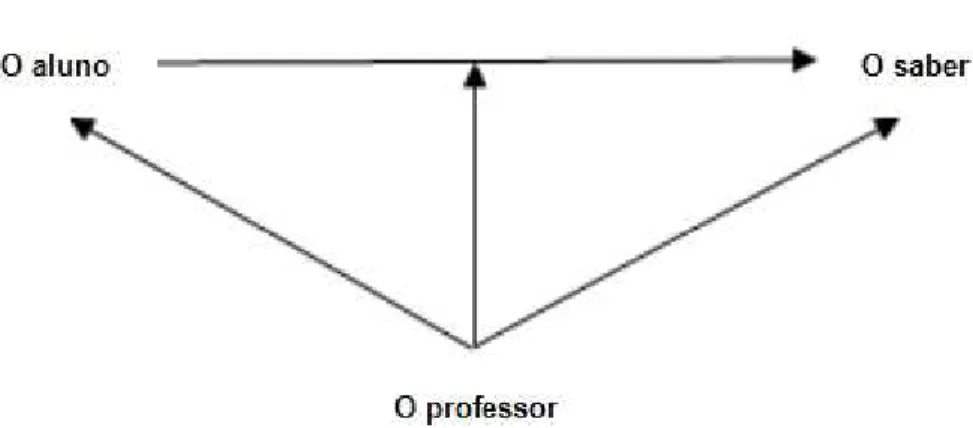
FIGURA 6.RELAÇÃO PEDAGÓGICA ... 72
FIGURA 7.RELAÇÕES DIDÁTICAS ... 73
FIGURA 8.PRIMEIRA DISCUSSÃO DO CONHECIMENTO ESPECIALIZADO ... 82
FIGURA 9.SEGUNDA DISCUSSÃO DO CONHECIMENTO ESPECIALIZADO ... 83
FIGURA 10.TERCEIRA DISCUSSÃO DO CONHECIMENTO ESPECIALIZADO ... 83
FIGURA 11.DIAGRAMA CONHECIMENTO MATEMÁTICO PARA O ENSINO ... 87
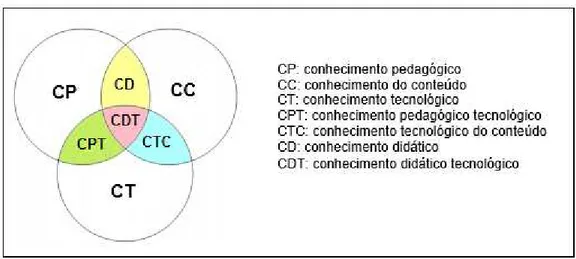
FIGURA 12.CONHECIMENTO PEDAGÓGICO TECNOLÓGICO DO CONTEÚDO ... 91
FIGURA 13.CONHECIMENTO DIDÁTICO TECNOLÓGICO ... 95
FIGURA 14.CARACTERIZAÇÃO DE UM PROBLEMA DIDÁTICO ... 104
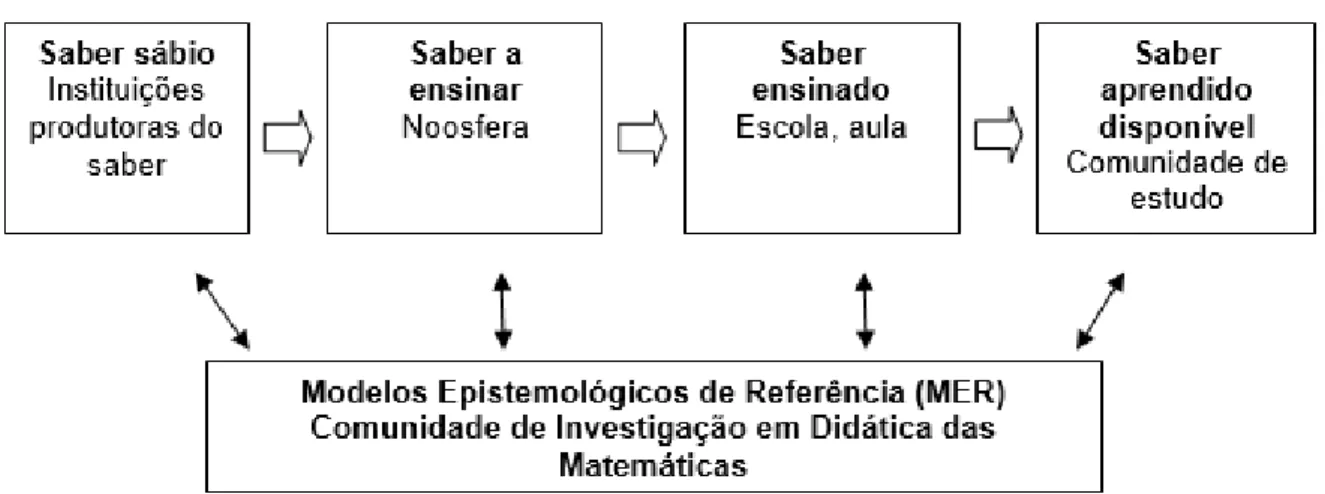
FIGURA 15.ETAPAS DA TRANSPOSIÇÃO DIDÁTICA ... 107
FIGURA 16.HEXÁGONO REGULAR A PARTIR DE UM TRIÂNGULO EQUILÁTERO ... 115
FIGURA 17.TETRAEDRO TRUNCADO, OCTAEDRO TRUNCADO E ICOSAEDRO TRUNCADO ... 116
FIGURA 18.ESCRITO DE PIERO DELLA FRANCESCA DE UM CUBOCTAEDRO ... 116
FIGURA 19.CUBO TRUNCADO E DODECAEDRO TRUNCADO ... 117
FIGURA 20.ICOSIDODECAEDRO E ROMBICUBOCTAEDRO ... 117
FIGURA 21.CUBOCTAEDRO TRUNCADO ... 118
FIGURA 22.ROMBICOSIDODECAEDRO E ICOSIDODECAEDRO TRUNCADO ... 118
FIGURA 23.SÓLIDOS ARQUIMEDIANOS OBTIDOS POR TRUNCATURAS ... 119
FIGURA 24.FACE QUADRADA OBTIDA A PARTIR DE UMA FACE DO CUBO... 121
FIGURA 25.CUBOCTAEDRO OBTIDO A PARTIR DE UM CUBO ... 122
FIGURA 26.FACE TRIANGULAR OBTIDA A PARTIR DE OUTRA FACE TRIANGULAR ... 122
FIGURA 27.CUBOCTAEDRO OBTIDO A PARTIR DO OCTAEDRO REGULAR ... 123
FIGURA 28.ICOSIDODECAEDRO OBTIDO A PARTIR DE UM ICOSAEDRO REGULAR ... 124
FIGURA 29.FACE PENTAGONAL OBTIDA A PARTIR DE UMA FACE DO DODECAEDRO REGULAR ... 124
FIGURA 30.ICOSIDODECAEDRO OBTIDO A PARTIR DO DODECAEDRO REGULAR ... 124
FIGURA 31.FACE HEXAGONAL OBTIDA A PARTIR DE FACE TRIANGULAR ... 126
FIGURA 32.FACE OCTOGONAL OBTIDA A PARTIR DE UMA FACE DO CUBO ... 127
FIGURA 33.PONTOS DE CORTE DA FACE DO CUBO ... 128
FIGURA 34.FACE DECAGONAL OBTIDA A PARTIR DA FACE DO DODECAEDRO REGULAR ... 129
FIGURA 37.BISSETRIZ DO ÂNGULO O... 131
FIGURA 38.BISSETRIZ DO ÂNGULO P4 ... 131
FIGURA 39.OBTENÇÃO DO CUBO NO CABRI 3D ... 138
FIGURA 40.PONTOS MÉDIOS DAS ARESTAS DO CUBO A PARTIR DA FERRAMENTA "PONTO MÉDIO" ... 138
FIGURA 41.PONTOS MÉDIOS DAS ARESTAS DO CUBO A PARTIR DA MEDIATRIZ ... 139
FIGURA 42.PONTOS MÉDIOS DAS ARESTAS DO CUBO A PARTIR DA CALCULADORA... 140
FIGURA 43.PONTOS MÉDIOS DO CUBO A PARTIR DA MEDIATRIZ (QUADRADO) ... 141
FIGURA 44.OBTENÇÃO DOS PONTOS MÉDIOS DAS ARESTAS DO CUBO ... 141
FIGURA 45. TETRAEDRO RETIRADO (CUBO) ... 142
FIGURA 46.OBTENÇÃO DO OCTAEDRO REGULAR NO CABRI 3D ... 143
FIGURA 47.PONTOS MÉDIOS DAS ARESTAS DO OCTAEDRO FERRAMENTA "PONTO MÉDIO" ... 143
FIGURA 48.PONTOS MÉDIOS DAS ARESTAS DO OCTAEDRO A PARTIR DA MEDIATRIZ ... 143
FIGURA 49.PONTOS MÉDIOS DAS ARESTAS DO OCTAEDRO A PARTIR DA CALCULADORA ... 144
FIGURA 50.PONTOS MÉDIOS A PARTIR DA MEDIATRIZ (TRIÂNGULO) ... 144
FIGURA 51.CONSTRUÇÃO DA BISSETRIZ (OCTAEDRO REGULAR) ... 145
FIGURA 52.TRAÇANDO A BISSETRIZ (OCTAEDRO REGULAR) ... 146
FIGURA 53.PIRÂMIDE RETIRADA (OCTAEDRO REGULAR)I ... 146
FIGURA 54.CUBOCTAEDRO OBTIDO POR TRUNCATURAS NO CUBO OU OCTAEDRO REGULAR ... 147
FIGURA 55.OBTENÇÃO DO ICOSAEDRO REGULAR NO CABRI 3D ... 147
FIGURA 56.PONTOS MÉDIOS DAS ARESTAS DO ICOSAEDRO FERRAMENTA "PONTO MÉDIO" ... 148
FIGURA 57.PONTOS MÉDIOS DAS ARESTAS DO ICOSAEDRO A PARTIR DA MEDIATRIZ ... 148
FIGURA 58.PONTOS MÉDIOS DAS ARESTAS DO CUBO A PARTIR DA CALCULADORA... 149
FIGURA 59.PONTOS MÉDIOS DAS ARESTAS DO ICOSAEDRO REGULAR DA MEDIATRIZ (TRIÂNGULO) ... 149
FIGURA 60.CONSTRUINDO A BISSETRIZ (ICOSAEDRO REGULAR) ... 149
FIGURA 61.TRAÇANDO A BISSETRIZ (ICOSAEDRO REGULAR) ... 150
FIGURA 62.PIRÂMIDE RETIRADA (ICOSAEDRO REGULAR) ... 150
FIGURA 63.OBTENÇÃO DO DODECAEDRO REGULAR NO CABRI 3D ... 151
FIGURA 64.PONTO MÉDIO DA ARESTA DO DODECAEDRO FERRAMENTA "PONTO MÉDIO" ... 151
FIGURA 65.PONTO MÉDIO DA ARESTA DO DODECAEDRO A PARTIR DA MEDIATRIZ... 152
FIGURA 66.PONTO MÉDIO DA ARESTA DO DODECAEDRO A PARTIR DA CALCULADORA ... 152
FIGURA 67.CONSTRUINDO A BISSETRIZ (DODECAEDRO REGULAR) ... 152
FIGURA 68.TRAÇANDO A BISSETRIZ (DODECAEDRO REGULAR) ... 152
FIGURA 69.OBTENÇÃO DE PONTOS MÉDIOS A PARTIR DA MEDIATRIZ (PENTÁGONO) ... 153
FIGURA 70.PIRÂMIDE RETIRADA (DODECAEDRO REGULAR) ... 153
FIGURA 71.ICOSIDODECAEDRO OBTIDO POR TRUNCATURAS NO ICOSAEDRO OU DODECAEDRO ... 154
FIGURA 72.OBTENÇÃO DO TETRAEDRO REGULAR NO CABRI 3D ... 154
FIGURA 75.DIVISÃO DA ARESTA EM TRÊS PARTES IGUAIS PELO TEOREMA DE TALES ... 156
FIGURA 76.DIVISÃO DA ARESTA DO TETRAEDRO PARTES IGUAIS (TRANSFERINDO MEDIDAS) ... 157
FIGURA 77.ARESTAS DO TETRAEDRO REGULAR DIVIDAS EM TRÊS PARTES IGUAIS ... 157
FIGURA 78.TETRAEDRO RETIRADO (TETRAEDRO REGULAR) ... 158
FIGURA 79.TETRAEDRO TRUNCADO OBTIDO POR TRUNCATURAS NO TETRAEDRO REGULAR ... 158
FIGURA 80.DIVISÃO DA ARESTA DO OCTAEDRO REGULAR USANDO O TEOREMA DE TALES ... 159
FIGURA 81.DIVISÃO DAS ARESTAS EM TRÊS PARTES DO OCTAEDRO TRANSFERINDO MEDIDAS ... 159
FIGURA 82.ARESTAS DO OCTAEDRO REGULAR DIVIDAS EM TRÊS PARTES IGUAIS ... 160
FIGURA 83.RETIRADA DA PIRÂMIDE (OCTAEDRO REGULAR II) ... 160
FIGURA 84.OCTAEDRO TRUNCADO OBTIDO POR TRUNCATURAS REALIZADAS NO OCTAEDRO REGULAR ... 160
FIGURA 85.DIVISÃO DA ARESTA DO ICOSAEDRO EM TRÊS PARTES IGUAIS USANDO O TEOREMA TALES... 161
FIGURA 86.DIVISÃO DAS ARESTAS EM TRÊS PARTES DO ICOSAEDRO TRANSFERINDO MEDIDAS ... 161
FIGURA 87.ARESTAS DO ICOSAEDRO REGULAR DIVIDAS EM TRÊS PARTES IGUAIS ... 162
FIGURA 88.RETIRADA DA PIRÂMIDE (ICOSAEDRO REGULAR II)... 162
FIGURA 89.ICOSAEDRO TRUNCADO OBTIDO A PARTIR DO CUBO ... 162
FIGURA 90.PONTO MÉDIO DA DIAGONAL DE UM FACE DO CUBO ... 164
FIGURA 91.DETERMINAÇÃO DE UM DOS PONTOS DE CORTE NA ARESTA DO CUBO ... 164
FIGURA 92.PONTOS DE CORTE PERTENCENTES A UMA FACE DO CUBO ... 164
FIGURA 93.OBTENÇÃO DE PONTOS NAS ARESTAS DO CUBO A PARTIR DA CALCULADORA ... 165
FIGURA 94.DETERMINAÇÃO DOS DOIS PONTOS EM CADA ARESTA DO CUBO ... 166
FIGURA 95.RETIRADA DO TETRAEDRO (CUBO)II. ... 166
FIGURA 96.CUBO TRUNCADO OBTIDA A PARTIR DE TRUNCATURAS NO CUBO. ... 167
FIGURA 97.PONTOS NAS ARESTAS DO DODECAEDRO REGULAR A PARTIR DA CALCULADORA ... 168
FIGURA 98.TRIÂNGULO RETÂNGULO ... 168
FIGURA 99. DIVISÃO DA ARESTA DO DODECAEDRO REGULAR EM CINCO PARTES IGUAIS ... 169
FIGURA 100.DÉCIMA PARTE DA ARESTA DO DODECAEDRO REGULAR ... 169
FIGURA 101.SEGMENTO CONSTRUÍDO ... 170
FIGURA 102.DETERMINAÇÃO DOS PONTOS DE TRUNCATURA NA ARESTA DO DODECAEDRO REGULAR. ... 170
FIGURA 103.DETERMINAÇÃO DOS PONTOS NAS ARESTAS DO DODECAEDRO REGULAR ... 171
FIGURA 104.RETIRADA DO TETRAEDRO (DODECAEDRO REGULAR)II ... 171
FIGURA 105.DODECAEDRO TRUNCADO OBTIDA A PARTIR DE TRUNCATURAS NO CUBO ... 172
S
UMÁRIO
1 INTRODUÇÃO... 15
2 ESTUDOS PRELIMINARES ... 19
2.1REFLEXÃOSOBREOENSINODEGEOMETRIA ... 19
2.1.1 O passado recente ... 21
2.1.2 A revalorização da geometria ... 27
2.1.2.1 Materiais manipulativos ... 30
2.1.2.2 Os ambientes de geometria dinâmica ... 32
2.2SÓLIDOSARQUIMEDIANOSNASPESQUISAS ... 37
2.3BASEDECONHECIMENTOPARAOENSINO:ALGUMASCONCEPÇÕES ... 48
2.3.1 Gauthier ... 49
2.3.2 Tardif ... 52
2.3.3 Shulman ... 56
2.3.4 Nossas considerações ... 61
2.4UMAFORMADIFERENTEDEINTEGRAROPEDAGÓGICOEOMATEMÁTICO ... 62
3 PROBLEMÁTICA ... 75
3.1DELIMITAÇÃODOPROBLEMA ... 75
3.2METODOLOGIAEPROCEDIMENTOSMETODOLÓGICOS ... 76
3.3REFERENCIALTEÓRICO ... 79
3.3.1 Avanços nos estudos de Shulman ... 79
3.3.1.1 Conhecimento matemático para o ensino ... 79
3.3.1.2 Conhecimento tecnológico para o ensino ... 89
3.3.2 A Teoria Antropológica do Didático ... 96
3.3.2.1 A organização praxeológica ou praxeologia ... 98
3.3.2.2 O problema didático ... 103
4 SABERES DOCENTES E SÓLIDOS ARQUIMEDIANOS ... 113
4.1TRUNCAMENTOCOMOMODELOEPISTEMOLÓGICODEREFERÊNCIA ... 114
4.2UMAORGANIZAÇÃOMATEMÁTICAPARASÓLIDOSARQUIMEDIANOS ... 120
4.3UMMODELODIDÁTICODEREFERÊNCIAPARASÓLIDOSARQUIMEDIANOS... 134
4.3.1 Estudo da Organização Didática para os sólidos arquimedianos ... 137
4.3.1 Nossas reflexões ... 172
5 CONSIDERAÇÕES FINAIS ... 177
1 INTRODUÇÃO
O interesse inicial para a realização desta pesquisa surgiu com os resultados obtidos na dissertação de mestrado realizada por esta autora. Neste estudo, partimos do pressuposto que os problemas de ensino de Geometria Espacial, em especial, do conteúdo matemático poliedros arquimedianos1, têm relação com aspectos ligados à visualização e interpretação de objetos tridimensionais e suas representações. Nessa pesquisa, foi identificado que embora existam estudos de poliedros, em geral a respeito de poliedros convexos regulares devido à simplicidade de suas formas, quase inexistem os que se dedicam a estudar os poliedros arquimedianos. Também foi constatado que alguns poliedros de Arquimedes eram estudados via planificação de suas superfícies em Desenho Geométrico, disciplina que dava suporte para que suas propriedades geométricas fossem exploradas.
Contudo, Pavanello (1993) e Rabello (2005) pontuam que, com a promulgação da Lei de Diretrizes e Bases 5692/71, a disciplina Desenho Geométrico foi substituída por Educação Artística no currículo. Rabello (2005), ainda lembra que, como o desenho geométrico tem base conceitual em matemática, não tendo em tese afinidade estrutural com a área artística, esse conhecimento de ensino passou a não ser mais abordado.
Por outro lado, tendo em vista que os poliedros arquimedianos não são facilmente representados em ambientes bidimensionais, sem o domínio de conhecimentos e habilidades oferecidos pelo Desenho Geométrico, e com o surgimento da Geometria Dinâmica2 como recurso didático que favorece não só a exploração e aquisição de conceitos geométricos, mas também apresenta vantagens em relação às construções com régua e compasso no ambiente lápis e papel, nos propusemos a revisitar alguns poliedros arquimedianos no ambiente de
1 Segundo Pappus (1878) são os sólidos descobertos por Arquimedes, em número treze, que
contém polígonos equilaterais e equiângulas, mas não similares.
2 Embora seja um termo bastante utilizado para designar softwares de geometria que permitem,
com a ajuda do mouse, movimentar uma figura construída sem que suas propriedades sejam
Geometria Dinâmica Cabri 3D, bem como estudá-los por meio de suas
construções.
Para tanto, investigamos na história processos de construções para esses poliedros e identificamos o truncamento como procedimento matemático utilizado
por artistas renascentistas para a obtenção de alguns destes a partir de poliedros platônicos. Esse procedimento evidenciou um caminho de construção, para poliedros arquimedianos, bem diferente do apresentado nos livros3 encontrados de Desenho Geométrico, a planificação de suas superfícies. Isso nos levou a considerar que embora as técnicas de representação fossem estudadas em Desenho Geométrico, não eram suficientes para um estudo matemático profundo.
Assim, pudemos constatar que a construção de arquimedianos, a partir de truncaturas realizadas nas arestas de poliedros platônicos, pode ser realizada no ambiente de Geometria Dinâmica Cabri 3D. Nesse sentido, confirmamos o Cabri
3D como habitat para o objeto matemático estudado, como também foi apontada
uma possibilidade para o ensino e aprendizagem de poliedros arquimedianos e sua inclusão na Educação Básica por meio deste ambiente computacional aliado a história como fonte geradora de conhecimento.
Tendo em vista o resultado desta pesquisa, começamos de início a pensar na possibilidade de elaborar e desenvolver, para o ensino destes poliedros, uma sequência de atividades no Cabri 3D, na medida em que tal
ambiente facilita a representação e consequentemente a visualização destes objetos matemáticos.
No entanto, com base nos estudos e nas leituras realizadas ao longo do processo de doutoramento, percebemos que nosso estudo inicial a respeito de tais poliedros contribuiu e vêm contribuindo para que novas ações sejam tomadas a respeito deste ensino. Algumas possibilidades para o ensino de arquimedianos têm sido apresentadas e desenvolvidas em pesquisas da área, o que não só
3 Nos dois livros de Desenho Geométrico encontrados a apresentação de alguns arquimedianos é
fortalece nossa investigação inicial como também aponta novos caminhos para serem investigados.
Desse modo, percebemos que enquanto algumas alternativas de ensino com os arquimedianos têm sido apontadas, questões relacionadas ao professor parecem não estar sendo investigadas nesse processo, o que contribuiu em grande parte para a escolha do tema do presente trabalho. Ao voltarmos nosso olhar para o professor, uma nova inquietação nos tomou conta. O que de fato ele precisaria saber para ensinar sólidos arquimedianos aos seus alunos? Ou ainda, que saberes precisariam estar minimamente envolvidos para que tais sólidos sejam ensinados?
Tomamos por hipótese que os saberes docentes envolvidos no processo de ensino de poliedros arquimedianos são procedentes da interação de três componentes particulares de conhecimento, que denominamos aqui de conhecimento matemático, conhecimento didático e conhecimento tecnológico. Assim, pretendendo contribuir na composição de um cenário que revele os saberes envolvidos no processo de ensino de sólidos arquimedianos, nos propomos responder à seguinte questão de pesquisa: Qual base de conhecimento para o ensino dos sólidos arquimedianos na escola básica? Para respondê-la aprofundamos nosso estudo em algumas concepções de base de conhecimento para o ensino, especialmente na concepção de base iniciada por Shulman (1986;1987) e colaboradores, e na Teoria Antropológica do Didático de Yves Chevallard.
O presente trabalho foi estruturado em cinco capítulos, tendo como o primeiro esta introdução.
No terceiro capítulo, trazemos a nossa problemática, em que destacamos nosso problema de pesquisa, nossa metodologia e os procedimentos metodológicos utilizados na pesquisa, e ainda nossos referenciais teóricos.
O quarto capítulo, relacionado à saberes docentes e sólidos arquimedianos, traz além do Modelo Epistemológico de Referência e da tecnologia escolhida para o ensino dos sólidos arquimedianos, uma Organização Matemática e uma Organização Didática para sólidos arquimedianos a partir das escolhas realizadas anteriormente.
2 ESTUDOS PRELIMINARES
Iniciamos o capítulo com uma reflexão de como a geometria no Brasil veio sendo ensinada ao longo dos anos e de pesquisas que retratam em seus estudos o objeto matemático sólidos arquimedianos. Em seguida, algumas concepções de base de conhecimento para o ensino são discutidas, bem como uma maneira diferente de integrar o "pedagógico" e o "matemático".
2.1 REFLEXÃO SOBRE O ENSINO DE GEOMETRIA
Segundo Veloso (1998), em março de 1990, um grupo reduzido de professores e investigadores universitários realizou um seminário nos Estados Unidos cujo objetivo principal centrava-se na reforma do ensino de geometria nos
colleges4 americanos. Nesse contexto, questões que tratavam do ensino de
geometria foram discutidas, bem como foram apontadas sugestões para sua revitalização. A preocupação com estas questões foi expressa nas atas das reuniões, como pode ler-se:
os Elementos de Euclides [...] juntamente com as descobertas de J. Bolyai e de N. Lobachewsky [...] têm constituído o núcleo central da geometria com que a generalidade das pessoas e dos matemáticos entram em contato, nas escolas e nos nossos institutos e universidades.
No entanto, aquele pequeno grupo de matemáticos que se consideram a si próprios geômetras veem seu tema de trabalho num contexto muito mais largo, profundo e valioso. Os geômetras sabem que [...] as ideias geométricas têm fornecido o ponto de partida para desenvolvimentos conceituais em outros ramos da matemática, que agora estão afastados das suas raízes geométricas. Além disso, profissionais fora do campo da matemática [...] estão a descobrir que as ideias geométricas têm uma utilização muito mais ampla, não só como fundamentação teórica dos seus domínios de trabalho, mas também na realização de novas tecnologias que estão a desenvolver-se nesses domínios. [...] Muitos geômetras têm visto com tristeza que estes progressos empolgantes coexistem com um currículo cristalizado de geometria nas escolas e institutos. (VELOSO, 1998, p. 17).
É com esse olhar, que surgiram recomendações para o ensino de geometria nas reuniões realizadas.
Os conceitos e objetos geométricos devem ser estudados mais de um ponto de vista experimental e indutivo do que axiomático. Deve ser dada tanta importância aos aspectos combinatórios, topológicos, analíticos e computacionais da geometria como às ideias métricas. O amplo campo de aplicações da geometria deve ser mostrado aos estudantes: aplicações ao mundo dos negócios, à biologia, à robótica, etc. Uma ampla variedade de programas de computador devem ser utilizados, tanto como ferramentas para investigações como para construção de conceitos. Deve ser exposta a valiosa história da geometria. A utilização de diagramas e modelos concretos, como o auxílio na construção conceitual da geometria, deve ser intensificada. Deve ser dada maior ênfase aos conceitos centrais da geometria, tais como, as transformações geométricas e os seus efeitos nos conjuntos de pontos, nos conceitos referentes à distância, à superfície, etc. Devem ser encorajados o pensamento e o raciocínio visuais; Devem ser trabalhados domínios nos quais seja possível fazer experimentações em matemática. (VELOSO, 1998, p. 17 e 18).
Ainda que tais recomendações estivessem destinadas aos colleges, era
esperado, pelos participantes da reunião, que sua exposição atingisse também, por meio dos universitários presentes no evento, às escolas secundárias. A divulgação dessas novas ideias implicaria, no mínimo, um repensar de como o ensino de geometria acontecia, o que já contribuiria para o declínio da cristalização de seu ensino.
Concordamos com Veloso (1998) ao sinalizar que essas recomendações muito se aproximam do pensamento contemporâneo que defende um ensino renovado de geometria. Além disso, está em consonância com outras propostas apresentadas em outras publicações, como por exemplo nas Normas do National
Council of Teachers of Mathematics (NCTM), mais especificamente no campo das
conexões da geometria com a ciência e a tecnologia atuais, ao dizer que,
por meio da utilização de modelos concretos, desenhos e programas de geometria dinâmica, os alunos poderão envolver-se ativamente com conceitos geométricos [...] formular e explorar conjecturas e poderão aprender a raciocinar cuidadosamente a respeito de noções geométricas. (NCTM, 2008, p. 44, tradução nossa).
para o ensino renovado de geometria. Não obstante, ao voltar seu olhar para as questões relacionadas ao ensino de geometria em Portugal, percebeu que discussões desse nível ainda não tinham sido feitas, o que o fez arriscar dizer que a avaliação pessimista da vitalidade e atualidade do ensino de geometria nas instituições portuguesas além de se confirmarem, se acentuariam em relação às instituições de ensino americanas.
Pelas mesmas razões do autor, que julgou importante, mesmo em nível menos ambicioso, apresentar uma reflexão do ensino passado e atual de geometria em Portugal, pretendemos, nos parágrafos seguintes desta seção, discutir brevemente como a geometria no Brasil vem sendo ensinada e em que situação nos encontramos no momento presente.
2.1.1 O passado recente
Em linhas gerais, podemos dizer que, anos antes do movimento da matemática moderna, o ensino de geometria no Brasil ocupava-se com as construções geométricas e o estudo da geometria euclidiana, no plano e no espaço.
De acordo com Zuin (2001), a partir do século XIX, as construções geométricas, feitas com régua e compasso, tornaram-se um saber escolar autônomo nos documentos oficiais brasileiros, assumindo várias denominações: Desenho, Desenho Geométrico, Desenho Linear e Linear Geométrico. Em parte, o ensino de Desenho Geométrico desvinculado da Geometria se deve a influência francesa, na medida em que eram adotados métodos e manuais didáticos franceses.
O estudo da geometria de Euclides, pautado na tradição de considerar a geometria como campo ideal, baseava-se, como apontam Mocrosky, Mondini e Estephan (2012), na apresentação dos conteúdos acompanhados pelas definições, axiomas, postulados, lemas, teoremas e colorários, seguidos de numerosos exercícios que solicitavam a demonstração pelo aluno. Esperava-se com esse estudo dedutivo, sem utilidade prática, que os alunos aprendessem a demonstrar e admirar a matemática como uma construção lógica e perfeita.
Durante a década de cinquenta, com os primeiros congressos a nível nacional, Duarte e Leme (2006) apontam que novas ideias começam a ser discutidas em benefício do currículo e do ensino de matemática, que já traziam manifestações iniciais do movimento renovador que ficou conhecido como Movimento da Matemática Moderna (MMM).
Contudo, é durante a década de sessenta que o ensino de matemática no Brasil sofre influência desse movimento internacional, o que acarretou em mudanças, principalmente nos níveis ginasial e secundário. Ferh (1971 apud SOARES, 2001, p. 46) pontua que o MMM "tinha como finalidade organizar e corrigir o ensino tradicional que se apresentava nas escolas e incluir aos programas temas da denominada Matemática Moderna".
Como no Brasil havia insatisfações quanto ao ensino de Matemática, principalmente no nível secundário, a introdução desse movimento no país apresentava-se como
uma alternativa para superar as dificuldades existentes no ensino tradicional. A Matemática contribuía para uma elitização intelectual e econômica pela constatação do baixo rendimento dos alunos; o objetivo da disciplina era o adestramento dos alunos em regras, fórmulas e cálculos sem aplicações e o currículo apresentava a Aritmética, a Álgebra, a Geometria e a trigonometria como ramos estanques e isolados da Matemática e o estudo de um só é reiniciado após o estudo completo do outro. (SOARES, 2001, p. 78).
Dieudonné, que em 1959 no Seminário de Royaumont5 criticou a forma como o ensino de geometria era conduzido, "a maneira como hoje se ensina o princípio da geometria, com séries de definições que não definem nada e de pseudo
demonstrações que não podem resistir à análise lógica" (VELOSO, 1998, p. 21).
Dieudonné, ainda acrescentou que,
julga-se desonroso não poder apresentar aos alunos uma teoria completamente dedutiva a partir dos axiomas fundamentais [...]. Pela minha parte, não vejo o que haja de mal ou desonroso partir de uma premissa que pode ser uma proposição complicada, desde que seja possível demonstrar sem erros lógicos que a proposição em questão implica uma outra; não apenas isso seria muito mais instrutivo, como mostraria à luz do dia a natureza da dedução lógica e o seu caráter relativo, muitas vezes encoberto devido à maneira como se fazem confusões com a noção metafísica de verdade. (IBID., p. 22).
O apelo à intuição nas fases iniciais do ensino de geometria também foi destacado e defendido pelo francês na mesma intervenção.
Não se pode desenvolver com proveito uma teoria sob forma axiomática enquanto o aluno não está familiarizado com as questões a que ela se aplica, trabalhando algum tempo em uma fase experimental, ou semi-experimental, fazendo constante apelo a intuição. [...] Quanto a geometria, sei que recentemente se fizeram muitas investigações e experiências nos meios pedagógicos (em particular na Bélgica) sobre os métodos permitindo ensinar geometria, por assim dizer, como um capítulo da física. Penso que estas iniciativas se devem encorajar bastante, desde que se privilegiem, não os brinquedos artificiais como os triângulos, mas as noções fundamentais, como as simetrias, translações, produtos de transformações, etc. (IBID., p. 22).
O discurso de Dieudonné também expressava, em conformidade com MMM, a preocupação em preparar os alunos para as universidades, na medida em que buscava aproximar a matemática desenvolvida na escola básica com a matemática científica. Diante desse contexto, um modelo axiomático, baseado na noção de espaço vetorial é proposto para o ensino de geometria. Para Veloso (1998), a posição tomada pelo MMM se justifica devido seus defensores, em sua
5 No Seminário de Royaumont foram lançadas as bases do Movimento da Matemática. Jean
totalidade, emanarem do meio universitário e da concepção estruturalista da natureza da matemática adotada pelo grupo dominante naquela época, grupo Bourbaki.
Um dos principais objetivos do movimento liderado pelo grupo Bourbaki era a unificação do ensino de matemática. Desse modo, era preciso que toda a Matemática fosse reconstruída sob uma base geral que reorganizasse toda a teoria conhecida até então. Essa reorganização se daria assim por meio da teoria dos conjuntos e do estudo das estruturas fundamentais da Matemática que apoiavam-se, segundo Soares (2001), na teoria de Piaget e na importância do aspecto psicológico do ensino e da aprendizagem, renegado até então.
Para a autora, como as propostas do movimento estavam em consonância com a política de modernização econômica do governo brasileiro na década de sessenta, as ideias do movimento foram amplamente aceitas no país. Naquela época vigorava no Brasil a corrente pedagógica tecnicista, que defendia a industrialização e privilegiava a formação técnica, assim alternativas para melhorar a qualidade do ensino e do currículo de matemática eram demandadas.
As consequências das ideias que esse movimento trouxe para o ensino de geometria no Brasil foram sentidas pelo novo enfoque dado à disciplina. No momento em que o ensino de matemática se fundamentou no estudo das estruturas algébricas e na teoria dos conjuntos, a abordagem euclidiana clássica até então utilizada no ensino de geometria passou a enfatizar, a "noção de figura geométrica e de intersecção de figuras como conjunto de pontos do plano, adotando-se para sua representação a linguagem da teoria dos conjuntos" (PAVANELLO, 1993, p. 7). A autora pontua que para trabalhar a geometria, segundo uma abordagem "intuitiva", os livros didáticos traziam os teoremas como postulados por meio dos quais alguns problemas podiam ser resolvidos, mas sem se preocupar em construir uma sistematização, partindo de noções primitivas e empiricamente elaboradas.
domínio deste assunto, como também acabou por fazer com que muitos deles deixassem de ensinar, sob qualquer enfoque, a geometria.
Além do mais, ao procurar aproximar a matemática escolar da Matemática pura, com ênfase no ensino das estruturas e com o uso da linguagem dos conjuntos como elemento de unificação, deixou-se de considerar que o que estava sendo proposto estava fora do alcance dos alunos e também dos professores, que eram obrigados a ensinar uma Matemática que exigia algo distante de sua formação. Assim, os problemas se agravaram.
Embora Lima (1999) considere algumas das práticas do MMM aconselháveis, as influências vindas da Europa e dos Estados Unidos, bem como o apoio do governo a essas ideias, não foram suficientes para seu sucesso. As consequências do movimento, para o ensino de matemática, em especial de geometria, foram desastrosas, pois
desde os nossos dias de colônia, estamos acostumados a seguir a moda que nos ditam os países mais desenvolvidos. E, em geral, imitamos o que é fácil, superficial e frívolo. Nossa imitação da Matemática Moderna resultou em abandono da geometria e dos cálculos numéricos, substituídos por exageros e um pseudo-formalismo vazio e desligado da realidade. (LIMA, 1999).
Esse abandono iniciado pelo MMM, foi agravado pela implantação da Lei de Diretrizes e Bases da Educação Nacional, de 11 de agosto nº 5692/71. Tal lei, ao fundir os antigos cursos primário e ginasial, institui uma escola de 1º grau, com duração de 8 anos, e uma escola de 2º grau cujo objetivo central era a profissionalização. De acordo com Pavanello (1993), essa lei dava liberdade para cada professor estruturar seu programa segundo as condições dos alunos. Como os professores do 1º grau, em geral do ensino público, limitavam-se a ensinar aritmética e noções de conjuntos, seus alunos deixaram de aprender geometria.
Educação Artística, em que são tratadas naturalmente sem qualquer perspectiva matemática. Quanto às escolas particulares, o ensino de geometria seguia acontecendo, ainda que não existisse uma formação adequada por parte dos professores.
Diante do exposto, a geometria foi na prática perdendo espaço no currículo implementado pelos professores, e muitos alunos atravessaram o ensino de matemática na escola básica tendo como únicos contatos com a geometria elementar o teorema de Pitágoras e algumas fórmulas para o cálculo de medidas de áreas e de volumes. A redução do papel da geometria no ensino de Matemática, no Brasil, ocorreu particularmente ao longo dos anos 70 e 80. Entretanto, mesmo com o fim do MMM as consequências se fazem sentir até hoje, pois muitos educadores brasileiros foram formados nessa época. Além disso, boa parte dos materiais utilizados nas escolas trazem alguns de seus vestígios, como por exemplo, "a insistência com o trabalho de conjuntos nas séries iniciais, o predomínio absoluto da Álgebra nas séries finais, a formalização precoce de conceitos e a pouca vinculação da Matemática às suas aplicações
práticas”. (BRASIL, 1998, p. 21).
Não podemos precisar quando o Movimento da Matemática Moderna chegou ao fim, porém é possível dizer que a partir de meados da década de setenta as críticas a ele se intensificaram, sinalizando caminhos e conteúdos diferentes para o ensino e a aprendizagem de Matemática. Mesmo que as propostas defendidas pelo movimento tenham se instaurado como uma alternativa para o ensino de Matemática, que há tempo vinha se desgastando, suas ideias iniciais foram alteradas ou descumpridas.
2.1.2 A revalorização da geometria
Como reação aos maus resultados do MMM, surgiu em todo o mundo um movimento em defesa do regresso aos métodos e conteúdos matemáticos anteriores à reforma, chamado de Back to Basis (Volta às Bases). Soares (2001)
assinala que alguns educadores brasileiros, como Ubiratan D'Ambrósio, não concordavam com a participação do Brasil no movimento conservador que se formava, embora acreditassem que mudanças no ensino eram necessárias, mas sem exageros ou promessas impossíveis de serem realizadas.
No sentido oposto ao novo movimento, perspectivas alternativas, que não concordavam com o retrocesso, caminhavam para a necessidade de mudanças quanto aos métodos e conteúdos do ensino de Matemática.
Podemos dizer que, em relação ao ensino de geometria, Hans Freudenthal6 (1905-1990) desempenhou grande influência. Trechos do capítulo
The case of geometry, de sua obra Mathematics as an Educational Task, trazem
algumas impressões do autor quanto à importância desse ensino.
Durante muito tempo a matemática foi sinônimo de geometria. [...] A geometria era a verdade genuína. Mas a alta estima que era atribuída à geometria foi desaparecendo. Os sistemas axiomáticos de Pasch e Hilbert revelaram muitas falhas na geometria clássica. Por outro lado, [...] eram tão complicados que o que se podia fazer era lê-los ou fazer investigação [...], mas não era possível ensinar geometria com eles. Noutros tempos, a geometria não era apenas uma poderosa peça de ciência dedutiva; era o mais antigo e divulgado exemplo de didática. [...] A estrutura da geometria tradicional não foi apenas um sucesso didático. Existem atualmente pessoas que acreditam ter a geometria falhado por não ter sido suficientemente dedutiva. Na minha opinião, a causa foi antes o fato da dedução não ser ensinada como reinvenção, como fez Sócrates, mas sim imposta ao aluno. De qualquer modo, algumas pessoas defendem e promovem atualmente a abolição da geometria. [...] Os dias da geometria tradicional estão contados, se porventura ainda existe e, algum lugar. Se existem hoje motivos para a preocupação acerca do futuro do ensino da geometria e mesmo para recear que a geometria possa desaparecer do currículo, os primeiros culpados são aqueles que, ativa ou passivamente, resistiram à inovação no ensino de
6 Matemático de origem Holandesa, que em seus primeiros anos de estudo se dedicou a
Matemática. As vozes daqueles que defendiam a renovação não foram ouvidas. O grupo mais perigoso era constituído por aqueles que acreditavam que podiam salvar a velha geometria reforçando a sua estrutura dedutiva; tarefa voltada ao fracasso, sem dúvida. Geometria não é apenas dedução. (FREUDENTHAL,1973, p. 401 e 402, tradução nossa).
Ao longo do capítulo também estão presentes observações, comentários e orientações para um estudo renovado de geometria, que para o autor, pode ser compreendida em diferentes níveis. No nível mais elevado, a geometria é parte da matemática de certo modo axiomaticamente organizada. No nível mais baixo, compreende a geometria como "o espaço em que a criança deve aprender a conhecer, explorar, conquistar, de modo por aí viver, respirar e mover-se melhor" (IBID., p. 403). Quanto aos objetivos da geometria, o autor ressalta que, "presta-se, mais do que em outros temas, para a aprendizagem da matematização da realidade e para a realização de descobertas, que sendo feitas também com os próprios olhos e mãos, são mais convincentes e surpreendentes" (IBID., p. 403).
No entanto, o autor chama atenção para o critério da utilidade que, mesmo relevante para outras áreas da matemática, falha inteiramente na geometria, pois seu uso reduziria o ensino a um pequeno grupo de teoremas como o de Pitágoras, e de algumas fórmulas para o cálculo de perímetros, e de medidas de áreas e de volumes.
Com base nos trabalhos de Dina Van Hiele e de P. J. Van Albada, Freudenthal (1973) dá orientações quanto à realização do trabalho experimental, partindo do espaço, para manipular e construir. Neste trabalho, os alunos devem proceder como os matemáticos em suas investigações, formular conjecturas e tentar justificá-las. O espaço como ponto de partida, bem como a utilização de materiais concretos diversos para a manipulação, o fazem ressaltar a
necessidade de dar tempo ao aluno para organizar as suas experiências
espaciais, o que nega a antecipação de qualquer organização, seja ela do
professor ou do material utilizado, e a conveniência de proceder a pequenas
organizações locais da geometria, para que a partir de um pequeno número de
A publicação em 1989, do documento National Council of Teachers of
Mathematics (NCTM), deu força ao movimento que se iniciava em favor da
recuperação da geometria como tema relevante da matemática escolar. Rejeitando também a situação que se encontrava o ensino de geometria após o fim do MMM, o documento vem propor, nas normas dedicadas à geometria, uma visão revigorada de seu ensino, cujos pontos principais são:
a compreensão dos objetos geométricos e suas relações, e utilização da geometria na resolução de problemas; integração da geometria em todos os temas e em todos os anos de escolaridade; abordagem da geometria por intermédio das coordenadas e das transformações geométricas; desenvolvimento de curtas sequencias de teoremas; argumentos dedutivos expressos oralmente ou por frases ou parágrafos escritos; explorações em computador de figuras bi e tridimensionais; geometria no espaço; aplicações ao mundo real e modelação. (VELOSO, 1998, p. 29).
É recomendado ainda pelo NCTM que seja dada menos atenção a geometria euclidiana como sistema axiomático completo, que a geometria analítica não seja ensinada como tema isolado e que o trabalho com demonstrações em "duas colunas"7 seja evitado. Esta tendência foi consolidada e intensificada nos adendos às Normas publicadas nos anos seguintes e nas revistas do NCTM onde vários artigos têm sido publicados a respeito de geometria e seu ensino.
Fora do contexto do NCTM, pode-se dizer que, ao longo dos anos, o movimento de revalorização da geometria para o cenário escolar vem acentuando-se, tanto em nível nacional como internacional, por meio de pesquisas, publicações de livros, novos materiais, reuniões de diversos tipos, e a criação de diversos software para o ensino de geometria, além de iniciativas e
propostas de ensino que surgem naturalmente, com qualidade e maturidade diversificadas.
Para identificar e se aproximar das propostas mais atuais que surgem no Brasil para o ensino de geometria, recorremos ao Banco de Dissertações e Teses
7 Enquanto a primeira coluna apresenta os argumentos usados na demonstração, a segunda
da Capes entre os anos 2011 e 2014. Ao considerar o descritor "geometria", fomos conduzidos a um total de 1230 trabalhos, em diversas áreas de conhecimento, dos quais 200 estão relacionados a seu ensino. Ao refinar mais a análise, percebemos que enquanto aproximadamente 14% destes retratam em seus estudos materiais manipulativos, 40% tratam de recursos computacionais.
Tendo em vista o exposto, nas seções seguintes discutimos como essas duas perspectivas de ensino tem auxiliado a revalorização da geometria no currículo escolar.
2.1.2.1 Materiais manipulativos
De acordo com Fiorentini e Miorim (1990), o uso de materiais manipuláveis8 no ensino já havia sido apontado por Comenius (1562-1671) em sua obra “Didática Magna” de 1657. Mas é no século XIX com Pestalozzi que o uso desses materiais ganha destaque. Segundo os autores, Pestalozzi defendia que a educação nasce a partir da experiência direta e das operações sobre as coisas.
No Brasil, o discurso em defesa do uso de materiais manipulativos para minimizar as dificuldades no ensino e aprendizagem de Matemática, e em especial de geometria, não é tão recente como aponta Fiorentini (1995). A ideia surge na década de vinte aliada a uma tendência no ensino de Matemática comumente conhecida de empírico-ativista, contrária ao modelo que trazia o professor como elemento central do processo de ensino. Tal concepção, ao negar o modelo tradicional de ensino, passa a considerar o aluno como elemento central e a propor métodos de ensino que privilegiam o desenvolvimento de atividades em grupos, bem como o uso de materiais didáticos que possibilitam a ação, a manipulação e a experimentação. Com efeito, com a crença de que o aluno
“aprende fazendo”, o ensino se baseia em atividades organizadas pelo o uso de jogos, experimentações ou o contato com materiais manipuláveis.
8Entendemos por materiais manipuláveis “objetos ou coisas que o aluno é capaz de sentir, tocar, manipular e movimentar. Podem ser objetos reais que têm aplicação no dia-a-dia ou podem ser
objetos que são usados para representar uma ideia”. (REYS, 1971 apud MATOS e SERRAZINA
No entanto, é na década de setenta no Brasil que essa tendência ganha mais força, principalmente, pelo fim do Movimento da Matemática Moderna e o grande incentivo de produção de materiais para o ensino de Matemática. Como assinala Nacarato (2005), as discussões já iniciadas acerca do uso de materiais manipulativos no ensino puderam ser amplamente divulgadas.
Em geometria, a justificativa decorre, em grande parte, da expectativa de que pelo suporte da materialidade, as dificuldades inerentes a representação e visualização de objetos geométricos sejam amenizadas. No início da aprendizagem, como bem aponta Pais (2000), os materiais tendem a funcionar como primeira representação, com a possibilidade de responder aos movimentos coordenados tanto pelo tato quanto pela visão. Nesse contexto, vários materiais são sugeridos, como por exemplo, o uso de modelos para sólidos geométricos, geoplano, tangran, poliminós, pentaminós, caleidoscópio e o caleidociclo.
A escolha de se trabalhar com esses materiais, principalmente por professores polivalentes, pode também estar associada a ideia de considerar a representação de objetos geométricos por um material manipulável menos complexa do que a representação obtida por um desenho. Como assinala Pais (1996), o uso do desenho mesmo em geometria plana embora seja mais simples do que em geometria espacial (já que requer, quase sempre, o recurso da técnica em perspectiva) exige o domínio de algumas informações técnicas para decodificar informações geométricas contidas nele, que geralmente não são explicitamente ensinadas nas séries iniciais.
Nesse sentido, a exploração adequada de materiais manipuláveis pode ajudar no desenvolvimento da visualização geométrica e, consequentemente, na construção de imagens mentais9, que vão sendo cada vez mais enriquecidas e
multiplicadas quanto mais operacionais elas forem. Para tanto, se torna inevitável dizer que, para a aprendizagem geométrica, boas imagens mentais fazem-se necessárias. Em contrapartida, embora o incentivo à utilização de materiais manipuláveis se faça presente, seja por meio de pesquisas ou mesmo de livros
9 Partilhamos do pensamento de Pais (2000) ao compreender que a imagem mental está
didáticos, pesquisadores têm chamado atenção quanto a sua forma de utilização. O material não pode ser utilizado como uma finalidade em si mesmo, isto é, em detrimento da aquisição de um conhecimento geométrico específico, pois é necessário refletir a respeito de seu uso e dos significados que podem ser negociados e construídos a partir deles.
Além dos materiais manipulativos outros recursos didáticos vêm sendo sugeridos para o ensino de Geometria, como o uso de meios computacionais, que embora distantes da realidade da maioria das escolas, podem muito auxiliar a compreensão de conceitos geométricos. É do que trataremos no que segue.
2.1.2.2 Os ambientes de geometria dinâmica
É bem verdade, como apontam Borba e Penteado (2003), que os computadores estão cada vez mais presentes em todos os domínios da atividade humana, o que já nos traz um forte argumento para sua inserção nos meios educacionais, bem como em todos os níveis de ensino. Mas para além disso, como propiciador de ambientes de ensino e aprendizagem, os computadores vieram tornar alguns problemas e conteúdos mais acessíveis, proporcionar novas formas de representação e domínio da informação matemática, o que nunca antes tinha sido possível.
A discussão a respeito do uso de tecnologia informática na educação se inicia no final da década de 70, e com ela surgem possibilidades de mudanças no que tange ao próprio saber estudado, bem como a superação de práticas antigas limitadas aos recursos disponibilizados até então.
Concordamos com os autores ao assinalarem que a utilização de tecnologias informáticas no ambiente educacional pode auxiliar na construção do conhecimento que privilegia não o produto-resultado em sala de aula, mas o processo, uma vez que estimula o uso de problemas abertos, de formulação de conjecturas em que a sistematização só se dá como coroamento de um processo investigativo por parte dos alunos e, muitas vezes, do próprio professor.
a geometria é o que tem experimentado as maiores e mais profundas transformações com a utilização da tecnologia informática; devido principalmente, ao desenvolvimento de
software específicos voltados para o seu processo de ensino e
aprendizagem. (ALVES e SOARES, 2003, p. 277).
Isso se torna relevante para o ensino, porque como aponta Duval (2005), entre todos os domínios do conhecimento a geometria parece ser aquele que exige a atividade cognitiva mais completa, pois solicita o gesto, a linguagem e o olhar. No entanto, adquirir domínio de conceitos geométricos não é tarefa fácil, ainda mais quando atividades de construção não fazem mais parte do dia a dia de sala de aula. Isso traz consequências danosas, principalmente, quanto ao tratamento estereotipado dado aos objetos geométricos e a apresentação de demonstrações com argumentos ordenados e prontos.
Para minimizar tais consequências, dentre os programas específicos para o ensino e aprendizagem de geometria, os mais recentes permitem que construções geométricas sejam realizadas na tela do computador, com o uso explícito das propriedades das figuras, além de ser possível manipulá-las sem alteração de suas propriedades. Chamamos os software que apresentam essa
característica de ambientes de geometria dinâmica.
Os ambientes de geometria dinâmica passaram a existir a partir de avanços nos recursos disponíveis no hardware10 de computadores pessoais, principalmente, a partir do crescimento na capacidade de memória e na velocidade de processamento de informações, além da criação do mouse como
meio de comunicação do usuário com a tela do computador.
Segundo Silva (2012), a possibilidade advinda do mouse, de objetos
serem manipulados diretamente na tela do computador, incentivou um grupo de pesquisadores franceses no desenvolvimento de uma ferramenta computacional que permitisse a exploração da teoria dos grafos. Com a criação da ferramenta
Cabri-graph, os grafos passaram a ser explorados em diferentes combinações, na
medida em que podiam ser "arrastados" com o uso do mouse pela tela do computador. Algum tempo depois, um dos pesquisadores, Jean-Marie Laborde,
propôs o desenvolvimento de uma ferramenta similar para o trabalho com a geometria euclidiana, o que facilitaria o trabalho de construção e manipulação de figuras geométricas. Assim, deu-se início ao Cabri-Géomètre, software de
geometria dinâmica que foi difundido em todos os níveis da educação francesa, e do mundo todo. Embora o Cabri-Géomètre, tenha sido um dos primeiros software
de geometria dinâmica a ser desenvolvido, outro programa conhecido como
Geometer's Sketchpad parece ter sido desenvolvido paralelamente.
De acordo com Goldenberg, Scher e Feurzeig (2008), tais software estão
sustentados por cinco princípios: o "arrastamento", relacionado ao deslocamento de um objeto na tela do computador; a pequena distância em relação à geometria euclidiana, dado a preocupação dos desenvolvedores do software
em encontrar um modelo para seu sistema mais próximo e fiel da geometria plana; a reversibilidade dos objetos geométricos, o usuário ao arrastar um objeto para qualquer posição da tela tem a possibilidade de retornar a posição inicial encontrando um objeto idêntico àquele arrastado anteriormente; a continuidade, muito complicada de ser implantada no modelo matemático dos
software; e a minimização de momentos estranhos sentido pelo usuário do
programa. Torna-se importante ressaltar que a divulgação desses ambientes, ocorrida no final da década de 80, permitiu que outros programas dessa natureza fossem desenvolvidos.
Quanto aos princípios destacados, o arrastar talvez seja o principal. Com a ajuda do mouse, é possível clicar sobre um ponto da figura geométrica
construída e depois arrastá-la pela tela do computador, alterando a configuração inicial da figura, ao mesmo tempo em que suas propriedades são conservadas. Esse recurso não só possibilita, quando as propriedades geométricas são corretamente utilizadas na construção, a percepção de invariantes, como a validação de inúmeras conjecturas, porque as representações que caracterizam os objetos geométricos são obtidas por meio de comandos definidos em uma linguagem geométrica.
propriedades da figura quando arrastada na tela do computador, e a construção, vista, como um caso geral, pois a figura construída, conserva suas propriedades quando arrastada, o que permite por meio de seus invariantes o reconhecimento de uma classe de figuras que representam o objeto geométrico.
Nesse sentido, o arraste associado a uma representação geométrica obtida via construção e não apenas com traçados desenhados, coloca em evidência a distinção entre o desenho e a figura geométrica. Isso se torna importante porque, como bem lembra Duval (2005, p.11), as figuras geométricas não podem ser obtidas à mão livre, mas sim com o auxílio de instrumentos, e é por meio de sua utilização que "alunos podem verdadeiramente tomar consciência de que as propriedades geométricas não tem somente características perceptivas". Assim, pensamos que a utilização de ambientes de geometria dinâmica pode ajudar mais facilmente os alunos na passagem do desenho para a figura geométrica, na medida em que se apresentam de maneiras distintas.
Além do mais, em ambientes de geometria dinâmica, a possibilidade de alterar a configuração inicial da figura, bem como as demais configurações que surgem, sem ter de construir a figura novamente, se torna importante para o ensino de geometria, na medida em que favorece o aparecimento de configurações outras bem diferentes dos desenhos prototípicos11 de objetos geométricos comumente estudados. Além do que, como aponta Laborde e Capponi (1994), embora um desenho revele propriedades do objeto geométrico, apenas o faz parcialmente, o que não traduz o domínio de variação dos elementos deste objeto. Desse modo,
a partir de um desenho é impossível inferir se um ponto de segmento pertence somente ao segmento ou à reta base do segmento, se duas circunferências secantes o são por hipótese ou se podem estar em uma posição relativa qualquer. [Nesse caso é] necessária uma descrição discursiva que caracterize o objeto geométrico para eliminar as ambiguidades inerentes ao desenho. (LABORDE e CAPONI, 1994, p. 53).
11 Desenhos bem conhecidos que resultam de influências ao mesmo tempo perceptivas e
Em contrapartida, com o recurso arrastar, as representações de objetos geométricos obtidas em ambientes dessa natureza possibilitam a desqualificação de interpretações não pertinentes sem que haja necessidade de tal descrição discursiva.
Outra característica, não menos importante desses ambientes, é a possibilidade de ocultar elementos da construção, por exemplo traçados auxiliares frequentes em construções mais complexas, como as dos sólidos arquimedianos. Os vários e necessários traçados podem comprometer a sua visualização, e consequentemente o entendimento da figura construída. A possibilidade de esconder o que é auxiliar para obtenção do produto final, ou o que é menos importante em determinado momento da construção, auxilia até mesmo a própria ação de construir.
Além disso, esses programas apresentam a possibilidade de observar as etapas de construção, início ao fim; as figuras construídas podem ser vistas em movimento, pelo comando "animação", o que pode auxiliar no estudo de transformações geométricas nesses ambientes, como o realizado por Salazar (2009). Outra característica de ambientes desse tipo é a construção de lugares geométricos. Para Belfort (2001), é um dos recursos mais notáveis, pois se a mesma representação fosse reproduzida com a utilização de recursos geométricos tradicionais, o mesmo procedimento teria de ser repetido tantas vezes quanto fossem necessárias para a obtenção de uma amostra de pontos de
Locus que produzisse, por interpolação, um resultado satisfatório.
Ante o exposto, podemos dizer que os ambientes de geometria dinâmica dão uma nova vida à geometria, na medida em que oferecem um sistema de representação de objetos geométricos de domínio bem mais extenso do que o sistema de representações oferecidos em lápis e papel. Além disso, com a utilização desses ambientes o termo figura ganha um novo sentido, na medida em que é compreendida a partir de uma construção bem sucedida, em que suas propriedades geométricas são consideradas, o que nos faz tomar consciência de que tais propriedades não são somente características perceptivas.
permitem sua ressignificação, no que segue visitamos as pesquisas que tratam de nosso objeto de estudo, os sólidos arquimedianos.
2.2 SÓLIDOS ARQUIMEDIANOS NAS PESQUISAS
Procuramos aqui evidenciar as pesquisas em Geometria Espacial, na área de Educação Matemática, que retratam em seus estudos os Sólidos de Arquimedes. Como nossa área de interesse está relacionada a questões de ensino e aprendizagem de tais sólidos, podemos dizer que a nível internacional não encontramos pesquisas que abordassem em seus estudos questões de seu ensino ou mesmo aprendizagem. A nível nacional, nossa busca se iniciou no Banco de Teses e Dissertações da Capes que nos conduziu a quatro dissertações que contemplam em suas investigações pelo menos um arquimediano. Tendo em vista poucos trabalhos encontrados, partimos para outras fontes, como periódicos e anais de eventos, dentre outros. Todos os trabalhos encontrados são apresentados no que segue.
Fernandes (2008) e Silva (2008)
As pesquisas de Fernandes (2008) e Silva (2008) estão relacionadas à
WebQuest “Bola de Futebol e a Matemática”, desenvolvida pelas próprias autoras
para o ensino e aprendizagem de sólidos arquimedianos, mais especificamente, do arquimediano icosaedro truncado. Na WebQuest são apresentadas tarefas que envolvem noções relativas aos Sólidos Arquimedianos, bem como competências para o trabalho geométrico, tais como: leitura e interpretação de textos, definições em matemática, princípios das construções geométricas, dentre outras. Além disso, traz a tarefa de construir um modelo do icosaedro truncado, com a utilização de papel cartão, a partir da planificação de sua superfície obtida na internet.
As autoras justificam a escolha do conteúdo matemático sólidos arquimedianos pela dificuldade de serem encontrados em livros didáticos, embora seu ensino seja sugerido em documentos oficiais para o ensino de matemática
conteúdo estar associado a diversas áreas de conhecimento como Biologia,
formato dos favos de mel de algumas abelhas, Química e Física, formato da
molécula de carbono conhecida como buckminsterfulereno C60 e a lapidação de pedras preciosas, Arquitetura e Engenharia, construções de sólidos e
planificações de suas superfícies, e Artes, como as obras de Leonardo da Vinci,
por exemplo.
Ainda que tímido, as autoras dedicaram um capítulo de seus trabalhos para o estudo do objeto matemático sólidos arquimedianos. Enquanto Fernandes (2008), em sua dissertação se preocupou em analisar o papel do professor na utilização da WebQuest, Silva (2008) investigou como a estratégia escolhida para
o ensino dos arquimedianos pode colaborar para o desenvolvimento de conteúdos matemáticos com alunos do Ensino Médio. Nesse sentido, como os objetivos de suas pesquisas não estavam relacionados com o objeto matemático em si, mas com a utilização e a interação dos alunos e professores com a
WebQuest construída, não temos como apontar efetivamente como a construção
do conhecimento matemático aconteceu.
Almeida (2010)
O estudo dos sólidos arquimedianos apresentado por Almeida (2010) mostra que esses sólidos não estão presentes no atual ensino de matemática na escola básica brasileira, ainda que, poucos deles apareçam em materiais didáticos, paradidáticos e de apoio ao professor por meio de exemplos e exercícios, em geral, associados à Relação de Euler e à convexidade, mas sem qualquer definição ou mesmo nomeação correspondente. “O icosaedro truncado é o sólido arquimediano que mais aparece, provavelmente, por ser associado à bola
de futebol”. (IBID, p. 38).
Em geral, sabemos que há perda de informações quando representamos objetos tridimensionais no plano, uma vez que representações bidimensionais de objetos espaciais quase sempre não correspondem à formação de suas imagens mentais. Há um conflito do que é visto no espaço e o que é representado no plano. (ALMEIDA, 2010, p. 58).
No entanto, a autora assevera que nem sempre foi assim, quando apresenta dois livros de Desenho Geométrico que fornecem informações a respeito de alguns dos Sólidos Arquimedianos: Primeiras Noções de Geometria
Prática de Olavo Freire, publicado em 1897 e Programa de Desenho para a primeira e segunda séries ginasiais de Benjamin de A. Carvalho, publicado em
1960. Embora o estudo dos arquimedianos, nos livros apresentados, fosse realizado via planificação de superfície, levou-a inferir que esse objeto matemático já fez parte da grade curricular de Matemática, mais especificamente na disciplina Desenho Geométrico, disciplina que segundo Zuin (2002), permaneceu oficialmente por quarenta anos consecutivos nos currículos escolares – 1931 a 1971.
Nesse sentido, a partir de Pavanello (1993) e Rabello (2005), a autora conclui que a razão do abandono da disciplina Desenho Geométrico da grade curricular de matemática e, consequentemente do ensino dos sólidos arquimedianos, está relacionada à sua substituição por Educação Artística na grade curricular do ensino público, em todas as séries do 1° e 2° graus do Ensino Básico. Para a autora, sem o domínio de conhecimentos e habilidades oferecidos pelo Desenho Geométrico, essa substituição contribuiu para que os sólidos arquimedianos não fossem mais abordados.
Considerando o exposto, a autora procurou um ambiente computacional que favorecesse a representação e visualização de objetos tridimensionais como também possibilitasse o estudo das propriedades de tais sólidos via construções geométricas. Dentre os ambientes computacionais existentes para o ensino de matemática, optou pelo ambiente de geometria dinâmica Cabri 3D. Para Almeida
Diante do exposto, e com base na Problemática Ecológica de Chevallard a autora presumiu que o Cabri 3D pudesse ser o ambiente para que o estudo dos
sólidos arquimedianos fosse retomado via construções geométricas e não por planificação de superfície como era realizado na disciplina Desenho Geométrico. Para isso, recorreu a um estudo bibliográfico para investigar na história processos de construções para esses sólidos e averiguar se tais construções poderiam ser realizadas no ambiente sugerido. A autora observou que, assim como grande parte das obras dos matemáticos gregos, os livros de Arquimedes que tratam desses sólidos estão perdidos, entretanto, encontrou no quinto livro da Coleção Matemática de Pappus (290 d.C. - 350 d.C.), grupo de oito livros que contém
notas históricas sobre o assunto, os treze sólidos semi-regulares descobertos por Arquimedes. A autora ressalta que o livro não trazia ilustrações e nem nomeação dos arquimedianos.
A retomada desse estudo matemático, segundo a autora, parece ter sido com Kepler no século XV, talvez o primeiro a sistematizá-lo e atribuir nomes a cada um deles, como mostra a Figura 1. No entanto, a autora se detém no período do Renascimento onde pôde constatar que diversos artistas e matemáticos interessados pelo estudo e representação desses sólidos, variavam seus desenhos, cortando cantos e arestas de sólidos platônicos, o que,
naturalmente, produzia alguns Sólidos Arquimedianos como resultado.
O processo mais utilizado para essa redescoberta por esses artistas, segundo a autora, é chamado de truncamento - eliminação de partes de um sólido de forma simétrica que pode ser feita a partir de seus vértices ou a partir de suas arestas. No entanto, com base em Field (1997), afirma que não há qualquer explicitação ou esquematização do estudo das relações entre Sólidos Platônicos, Sólidos Arquimedianos e os diferentes processos de construção a partir de truncaturas pelos renascentistas.
É a partir dessa constatação que Almeida (2010) evidencia em seu estudo a operação truncamento, para a obtenção de sete arquimedianos construídos a partir de truncaturas diretas em sólidos platônicos, da matemática utilizada em cada processo de construção, assim como os passos de geração no Cabri 3D de