4. TRANSFORMADA DE LAPLACE Introdução - Apostila transformada de Laplace versao atual a

(1)

Sumário

4. TRANSFORMADA DE LAPLACE ... 1

Propriedades da Transformada de Laplace ... 6

Transformada de uma função contínua definida por partes ... 7

Transformada inversa de Laplace. ... 8

A transformada de uma derivada ... 9

Resolvendo EDOs Lineares ... 11

Translação sobre o eixo s ... 17

Teorema: Teorema de translação sobre o eixo s ... 17

A forma inversa do teorema da translação em s... 18

Translação sobre o eixo t ... 25

Função degrau ou função de Heaviside... 25

A derivada de uma transformada ... 38

Transformada de Laplace e função gama ... 39

Lista de Figuras Figura 1 - Representação esquemática da transformada de Laplace _____________________________ 2 Figura 2 - Função contínua por partes (Fonte Dennis Zill) ______________________________________ 8 Figura 3 - Solução de equações diferenciais usando Transformada de Laplace ____________________ 12 Figura 4 - Gráfico do deslocamento no eixo s _______________________________________________ 18 Figura 5 - Gráfico da função degrau unitário _______________________________________________ 26 Figura 6 - Gráfico da função 𝒇𝒕 = 𝟐𝒕 − 𝟑𝒖(𝒕 − 𝟏) __________________________________________ 26 Figura 7 - Deslocamento em t ___________________________________________________________ 27 Figura 8 - a) gráfico da função f t

 

sen t

 

, b) gráfico da função f t

 

sen t u t

  

2



__ 27 Figura 9 - Gráfico da função 𝒇𝒕 = 𝟐 − 𝟑𝒖𝒕 − 𝟐 + 𝒖(𝒕 − 𝟑). __________________________________ 28 Figura 7 - Força eletromotriz ____________________________________________________________ 38 4. TRANSFORMADA DE LAPLACE Introdução E você pode está se perguntando, e o que isto tem haver com equações diferenciais? Nós podemos dizer que tudo, a transformada de Laplace torna mais fácil a resolução de equações diferenciais lineares com coeficientes constantes:  

_{ }

0 ... n n a y  a yg x (1) Em que, por exemplo, a função independente g x

 

não é contínua. Nesta aula estudaremos todo o fundamento teórico necessário de como aplicar a transformada de Laplace na resolução de equações diferenciais ordinárias.

(2)

4.1. Definição e exemplos

A transformada de Laplace foi encontrada muito antes de Laplace nos trabalhos de Euler. Nesta seção, vamos examinar um tipo especial de transformação integral chamada transformada de Laplace, a qual tem várias propriedades utilizadas na resolução de problemas lineares e valor inicial.

Antes de darmos a definição de transformada de Laplace, relembraremos o conceito de funções contínuas por partes, uma vez que esse conceito será necessário para descrevermos o conjunto em que a transformada de Laplace existe.

A transformada de Laplace transforma uma ED em uma equação algébrica. Será primeira feita uma analogia com as derivadas, podemos dizer que a transformada de Laplace é um operador, neste caso temos a derivada com operador:

  3 '  ₃ 2

dy dx

f x x f x  x (2)

A entrada neste caso da Eq. (2) temos uma função de x e trabalhamos com o operador dy

dx e com saída teremos uma derivada. Porém, no caso da transformada de Laplace teremos uma função de entrada, ao trabalhar com o operador de transformada de Laplace o resultado será outra função:

 

0 TLaplace st

f t F s e f t dt

 

 



(3)

onde st

e é denominado núcleo. É importante notar que o “s” é tratado como constante

na integração dt. Portanto, quando integra-se resulta em uma função de s. Logo notamos que a transformada é uma integral é linear, teremos a propriedade de linearidade. Todas essas transformações envolvem integrais, muitas vezes são denominadas transformadas integrais de Laplace. Será usado a transformada de Laplace para resolver ED com coeficientes constantes e sistemas dessas equações. O intervalo de interação é [0, ) . Se

 

f t for definida para t0: Ela resulta em uma simplificação dessas soluções de ED’s,

ou seja:

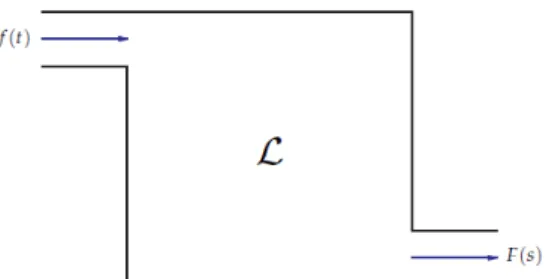
Figura 1 - Representação esquemática da transformada de Laplace

 





 





 

0

st L f t F s

L f t f t e dt F s 

 



_

 

(3)

O expoente

st

deve ser adimensional. Será para todo sonde a integral converge. Assim, quando a variável independente

t

for tempo, a dimensão de s deve ser o

inverso do tempo, isto é, frequência. Neste caso, por ser uma variável complexa, s é

frequentemente denominada “frequência complexa”.

Porque introduzir mais um método? Porém esse método trata muito bem ED’s de

coeficientes constantes e o lado direito não precisa ser contínuo, modela muito bem modelos físicos cuja força externa tem alto impacto instantânea, e também não precisa ser contínua.

Antes de qualquer cálculo precisamos recordar o que é uma integral imprópria, o que é a convergência de uma integral imprópria, ou seja:

 

0 0 lim b Definição b

g t dt g t dt









(5)

A integral definida é preciso fazer o limite, a integral converge se existe o limite, caso contrário ela diverge.

 

0

1 1 1

1 1 lim lim 0

0 st sb st b b b e e

L e dt

s s s s s

              _ _ _  _    _   _   



(6)

Neste caso precisamos testar o limite para ver se ele existe. Para s0 o limite não existe (é ilimitada). Então, precisa ser maior que zeros0, pois o expoente sbé negativo e sb 0

e quando b. Dessa forma:

 

1 1 , 0

L s

s

  (7)

Podemos da mesma maneira verificar o valor da transformada de Laplace de t

t f( ) :

 

0 0 0 0

st

L t e tdt udv uv vdu

  

 









 



(8)

' 0 0 , lim 0 , 0 st st st st b L Hopital s s

u t dv e dt

b

e e

t dt

e

s s

du dt v s e e s s             _ _  _ _      _ _     



' 2 2 0 0

1 1 1

lim 0

0 L Hopital

st st

sb sb bt b

s

e b e

dt

s se e s e s s s

       _ _              _  _ _ _  _            



(9)

 

2

1

, 0

L t s

s

  (10)

(4)

0 0 0 0

n st n

L t e t dt udv uv vdu

  

 

     

 



(11)

1 1 1

0 0

, ,

0

n st

st st st

n n n st n

u t dv e dt

e e e n

du nt v t nt dt e t dt

s s s s

                   







(12) 1

n n n

L t L t

s 

   

    (13)

Dando alguns valores para n:

 

2

2 3

2 2 1 2

2, L

n t L t

s s s S

 

 _{ }   (14)

3 2

3 4

3 3 2 3!

3, L

n t L t

s s s S

   

 _{ } _{ }  (15)

1 ! L n n n t s    

  (16)

Vamos agora calcular a transformada de uma função exponencial:

 

3 1 3 ₀ ) 3 ( 0 ) 3 ( 0 3 3            _ _  _ _ 



e e dt e dt e_s _s

e L t s t s t st

t _, ₃₀

s ou s3

E na forma geral essa transformada pode ser obtida como segue:

   





 













0 0

1 1 1

lim lim 0

0

0 , st s a

at st at

t s a b s a

b b

L e e e dt e dt

b

e e

s a s a s a s a s a

s a s a

                          _{ }  _{ }  _{ } _{ } _       



(17)

Neste caso se s a 0, ou seja, negativo não irá existir o limite. No entanto, a expressão é valida para s a 0.

Obs: neste caso se a  i também é válido, ocorre à mesma coisa, ou seja:

(5)

 







 



 

 

L af t bg t aL f t bL g t , será usada para calcular o próximo exemplo:





_

_{ }

_

 _ _ 

_

       0 0 ) 3 (

0 cos2

2 2 .

2

2 e tdt

s s t sen e dt e dt t sen e t sen L st st t s st



  

0 cos2

2

tdt e

s

st _, ₀ s 0 , 0 2 cos

lim   



 e t s

st t



            0 0 2 2 2 cos 2 tdt sen e s s t e s st st



sen t



L s s 2 4 2 2 2  

Nesse ponto, temos uma equação em L



sen2t



que aparece nos dois lados da igualdade. Resolvendo essa equação obtemos:





4 2 2 ₂   s t sen

L , s0

Podemos também resolver as transformadas de funções trigonométricas por soluções da fórmula de Euler:













_{ }

0

2 2 2 2

cosh cosh

1 1

cosh ,

2

1 1 1 1

cosh

2 2

1 2

st

kt kt kt

kt kt

s k

s k

L kt e ktdt

kt e e L e

s k

L kt L e L e s k

s k s k

s k s k s

s k s k

     _       _{ }            _ _{ } _ __                    



(18)

Obs: Cosh nunca se anula é a soma de duas exponenciais. Notamos que:





2 2 2 2

1 1 1 1

sinh

2 2

1 2

2

kt kt

L kt L e L e

s k s k

k k

s k s k

         _ _{ } _ __ _  _         (19)

Veremos a transformada de seno pela fórmula de Euler:

coskt sinkt

ikt

(6)





 

im

cos sin

ikt

função par função par ikt

e kt i kt

kt i kt



   

 

(21)

Somadas as duas expressões resultam em:





1 cos

2

ikt ikt

e e

 _ _  ₍₂₂₎

Se subtraídas tem-se:





1 sin

2

ikt ikt

e e

i

 _ _  ₍₂₃₎

Essas relações serão utilizadas para calcular as transformadas de seno e cosseno.













2 2 2 2 2 2

1 1 1 1

sin

2 2 2

1 1 2

2 2

ikt ikt ikt ikt i

L kt L e e L e L e

i i i s ik s ik

s ik s ik ik k

i s k i s k s k

 

  _ _{ } _ __  

 _  _ _ _{ } _ __ _  _

 

   

  

 

 _ _ 

  

 

(24)

Esse resultado também pode ser obtido usando a definição da transformada de Laplace, assim teremos que usar a integração por partes.



cos



1





1

2 2

1 1 1 1

2 2

ikt ikt ikt ikt

L kt L e e L e L e

s i k

s ik s ik

 

  _ _{ } _ __

 _  _ _ _{ } _ __

 



 

 _  _

 

 

s i k  

2 2 2 2

s

s k s k

(25)

Propriedades da Transformada de Laplace

A transformada de Laplace é uma transformação linear. Ou seja, dadas as funções f t

 

e g t

 

contínuas por partes para t0 e de ordem exponencial e a uma constante, segue que:

   







 



 

 







 



L f t g t L f t L g t L af t aL f t

  



(7)

   







   



 





 

 

0

0 0

, st

st st

L f t g t e f t g t dt

e f t dt e g t dt L f t L g t

 

 

 

  

 



e

 







 



 





 





0

. st

st

L af t e af t dt

a e af t dt aL f t

 





Essa propriedade é muito útil, pois usando a linearidade da transformada, não precisamos calcular a transformada de toda função:

Exemplo: Calcule a transformada de Laplace da função _{( )}₄ 3 ₅ ₇ 2t f t  t   cos te . Se calcularmos pela definição, temos que resolver a integral:







3 2



0

4 5

( ) st 7 t

L f t e t cos t e dt

 





  

Contudo, usando a propriedade de linearidade da transformada esse cálculo é significativamente reduzido quando se conhece a transformada das funções que aparecem na expressão de f . Dessa maneira, temos:





 

3

  



 

2

4 2

4 +5L 1 +L cos 7 +L

3! 1 1

4 5 , 2

4 (

9 )

2

t

L f t L t t e

s

s s s s



    

 

Transformada de uma função contínua definida por partes

 

f(t)

L , para

  

   

3 ,

2

3 0 , 0 ) (

t t t

f

(8)

Figura 2 - Função contínua por partes (Fonte Dennis Zill)

 

_

_

  _

_



 

_

_

 

 

3 3

0

0 ( ) 0 2

)

(t e f t dt e dt e dt

f

L st st st

s e s

e st 3s

3

2 2

0

  

  

 , s0.

Transformada inversa de Laplace.

Se F s

 

for a transformada de Laplace da função f t

 

, então definimos f t

 

como a transformada inversa de Laplace de F s

 

e denotamos por L1



F s

 



. Assim, enunciamos o seguinte:

Seja kum número real. Então,

A transformada inversa de Laplace também possui as mesmas propriedades da transformada de Laplace.

Teorema: Sejam _{F s}

 

e _{G s}

 

as transformadas das funções _{f t}

 

e _{g t}

 

,

respectivamente, e a; b constantes, então:

 







 





 



1

1 1 1

1) L é uma transformação linear ;

L aF s bG s aL F s bL G s



 _ _  _ 









 

1

2) at .

L F s a e f t

 







 



1

3) tF s , 0.

(9)

Teorema. Seja L f t



 



F s

 

, então:

   



 



1 n ₁ n _n 1

n d

L F s t L F s

ds

  _{ } 

 

 

Exemplo: Calcule 1 2

3 5 L

s

  

 _ 

 . Observe que 2 2

3 3 5

5 5 5

s   s  . Assim,

1 1

2 2

3 3 5 3

5

5 5 5 5

L L senh t

s s

      _

 _   _ 

  _ _

Exemplo: Usando frações parcias

Calcule







1 1

3 1

L

s s

  

 _ _ 

 

 . Podemos calcular essa transformada começando por decompor a expressão racional



s3



1s1



como soma de duas funções racionais, cuja

a transformada é conhecida. Para isso, a técnica de frações parciais, será muito útil. Vamos recordá-la um pouco. A idéia é achar constantes A e B tais que:



3



1 1

 

3

 

1



A B

s s  s  s

Multiplicando ambos os lados da igualdade acima por



s3



s1



e igualando os coeficientes de mesma potência em s, obtemos 1; 1

4 4

A B  .Assim,









 











3

1 1 1 1 1 1 1 1 1 1 1

3 1 4 3 4 1 4 3 4 1 4 4

t t

e e

L L L L

s s s s s s



  _   _ _   _   _ _

 _ _   _ _   _   _ 

       

       

A transformada de uma derivada

Antes de resolvermos equações diferenciais precisaremos obter expressões para, por exemplo, a transformada das derivadas. Assim, nesta seção, estudaremos a transformada de derivadas. Observe que se '

(10)

 





 

_{ }

 

     

 

   

 

' ' ' 0 0 0 0 0 0

lim lim 0

0

sb cb sb

b s c sb

dv _st _st

st u b

st st bt st

b b

e f b Me e

L f t e f b Me

b se s c é igual a

u e du se dt

L f t e f t dt uv vdu

dv f t dt v f t

e f t s e f t dt e f b e f s e f t dt

f sL                                _{ }            



 



f t



sF s

 

F

 

0

(26)

 

f(t) F(s)

L 

 

'( ) ( ) (0) F s sF t f

L  

Onde F s

 

L f t



 



(no cálculo acima assumimos que estf t

 

0 quando t). Usamos da Eq. (26) e procedendo de maneira análoga, obtemos:

 





 





 

'' 2 '

''' 3 2 '

0 0

L f t s F s sf f

L f t s F s s f s sf f

  

   

(27)

Teorema: Se _{, ,...,}' n 1

f f f  forem contínuas em [0, ) e de ordem exponencial, e se  n

 

f t for contínua por partes em [0, ) , então:

 



n



n

 

n 1

 

n 2 '

 

₀ _... n 1

 

₀

L f t s F s s  f s s  f   f  (28) Onde F s

 

L f t



 



.

O exemplo a seguir representa a transformada caso a '

f é contínua por partes, ou seja:

 

1 1

 

' ' 0 0 lim lim i i t b n st st b b i t

e f t dt e f t dt





 





 



_



(29)

Novamente preciso fazer a integral por partes, onde a ideia é particionar a integral

 

  1 1 1 i i st t st t e f t

e f t 

       0 2 0 2 st st

e f t e f t

 _ _

 

  __ est1f t 1 __ est2f t 2  

    3 3 1 1 ... st

stn stn

n n

e f t e f t e f t

      _       

 

1 1 0 i i i t n st i i _t

se f t dt

                 _{ }           





(30)

Os limites pela esquerda e pela direita f t 1 e f t 1 são iguais por isso podem ser

(11)

 

       

 

  1 1 0

0 ₀ 0

0 0 1 0 0 i i i i i st tnb

st stn sb

n t t n _t st st i t i _t

s e f t dt e f t e f t f e f b

e f t se f t dt

     _               _  _ _ _                                   



_

(31)

Teremos a mesma reposta, porém, é preciso dividir o intervalo. Assim, temos o seguinte teorema para f t

 

contínua por partes

 

1

   

1 1

0 st

f e _f t  f t _ esta medindo a descontinuidade no t₁ é o salto que a função dá e assim posso escrever todas as somas, considerando que t0 ou posso ter finitos pontos:

 

   

 

   

 







 



 

1 2

1 1 2 2

' 1 0 ... L 0 i i st st j t st i i

f e f t f t e f t f t

f t sL f t f e j t

              _ _  _  _ _  _       



(32)

Resolvendo EDOs Lineares

Fica evidente com base no resultado geral dado no teorema anterior que

      n n dt y d

L depende de Y(S)L

 

y(t) e das 𝑛 − 1 derivadas de y(t) calculadas em 𝑡 =

0. Essa propriedade torna a transformada de Laplace idealmente adequada para a resolução de problemas lineares de valor inicial nos quais a equação tem coeficientes constantes.

 

_{ }

1

1 1 0

1 '

0 1 1

...

0 , 0 ,..., 0 ,

n n

n n n n

n

d y d y

a a a y g t

dt dt

y y y y y y

            (33)

onde ,a_i i0,1,...,ney₀,y₁,...,yn₁ são constantes. Pela linearidade, a transformada de Laplace dessa combinação linear é uma combinação linear de transformadas de Laplace:

 

 

1

1 1 ... 0

n n

n n n n

d y d y

a L a L a L y L g t

dt dt               

    (34)

(12)

 

_{ }

 

_{ }

 

1 1

2

1 2

1

0

0 ... 0

...

n

n n

n

n n

n

a s Y s s y y

a Y s G s

 



 



    

 

 _ _{ } 

 

  

(35)

Onde L

 

y(t) Y(S) e L

 

g(t) G(S). Em outras palavras, a transformada de Laplace de uma equação diferencial linear com coeficientes constantes torna-se uma equação algébrica Y(S). Se resolvermos a equação geral transformada para determinar o símbolo Y(S), obtemos primeiramente P(S)Y(S)Q(S)G(S)e então escrevemos:

) (

) ( ) (

S P

S G S P

S Q S

Y  

Onde 1 ₀

1

)

(S a S a S a

P n n

n

n  

 

 é um polinômio em sde grau menor ou igual a 1



n , que consiste nos vários produtos dos coeficientes a_i, i0,1,...,n e das condições iniciais prescritas y₀,y₁,...,y_n_₁, e G(S)é a transformada de Laplace de g(t).

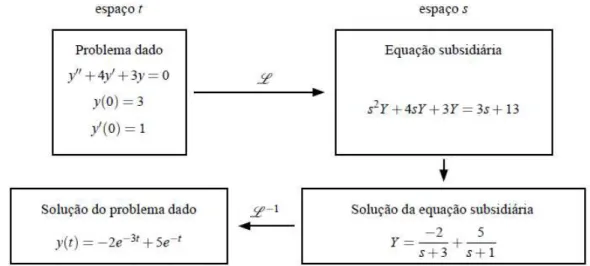
Figura 3 - Solução de equações diferenciais usando Transformada de Laplace

Exemplo 1: Dada uma ED usar a transformada de Laplace, em uma equação simples, neste caso temos um método fácil de resolver pela equação característica:

 

'' '

'

6 0

0 2

0 1

x t x t x t x

x

   

  

 _{ }



(13)

 





 

 

 

 

   

 





 

_

_

'' ' '' ' 2 ' 2 2 2 6 0 6 0

0 0 0 6 0

6 2 1 2 0

6 2 3

2 3

6 x t x t x t

L x t L x t L x t

s X s sx x sX s x X s

s X s sX s X s s

X s s s s

s X s s s                          

Preciso saber quem é o x t

 

, devido a unicidade teremos a inversa, ela esta bem definida, ou seja, será feiro a inversa. Primeiramente precisamos tentar decompor o denominador para encontrar formas que já existam de forma direta as transformadas.

 

_

_

_

_

_{ }

_









2

2 3 2 3

2 3 3 2

6

2 3 2 3

2 7 3

5 7 ;A

2 3 3 5 5

s s A B

X s

s s s s

s s

A s B s s

A B B B A B                             _ _{ } 

O que resulta em:

 

_

₂2 3

_

_

2

_

3

_

3

_

1

_

7

_

1

_

2 3 5 3 5 2

6

s s

X s

s s s s

s s             Ou seja,

 

_

_

_

_

 

1 1 3 2

3 1 7 1

5 3 5 2

3 7

5 5

t t

x t L L

s s

x t e e

            _ _ _ _            

Neste caso não faz sentido resolver o PVI com transformada de Laplace, com poucas linhas seria resolvido pelo método de coeficientes constantes, porém foi utilizado por fins didáticos.

Exemplo 2: Dada uma ED usar a transformada de Laplace para resolver:

 

''' 6 '' 11 ' 6 1

'' 0 0 ' 0 0

0 0

y t y t y t y t

(14)

Essa resolução por fins didáticos será realizada por etapas: Etapa 1: Aplicação da transformada de Laplace

 



 





 



 

 

 

''' 6 '' 11 ' 6 1

L y_ t _ L y t  L y t  L y t L

 

   

 

3 2 ₀ _{' 0} _{'' 0} ₆ 2 ₀ _{' 0}

1

11 0 6

s Y s s y sy y s Y s sy y

sY s y Y s

s

        

   

  

 

 

 

_

₃ ₂1

_

_

_

1

_

_

1 2 3

6 11 6

Y s

s s s s

 

  

Etapa 2: Expansão por frações parciais

 

_

_{ }

_

1 2 3

A B C D

Y s

s s s s

   

  

1 1 1 1

; ; ;

6 2 2 6

A B  C D 

 

1

_

1

_

_

1

_

_

1

_

6 2 1 2 2 6 3

Y s

s s s s

   

  

Etapa 3: Aplicar a transformada inversa de Laplace

 

1 1 1 1 1

_

1

_

1 1

_

1

_

1 1

_

1

_

6 2 1 2 2 6 3

y t L L L L

s s s s

           

 _{ } _ _ _ _ _ _

  

  _ _ _ _ _ _

 

1 1 1 2 1 3

6 2 2 6

t t t

y t   e  e  e

Exemplo 3: Dada uma Edo resolva usando a TL, este caso para a transformada inversa teremos que usar a translação em s.

 

'' ' 2

'

3 2 4

0 3

0 5

t

y t y t y t e

y y

   



  

 _

(15)

(16)

Neste caso teremos que usar o teorema da inversa da translação em s, dado pela Eq.(36), ou seja:











 



 





1 1

1 1 2

2 2

1 1

2

at s s a

t s s a

L F s a L F s e f t

L L e t

s s

 

 

 

 

  

  _ _

 _{ } _

   

  

 

 

Exercícios

1 - Resolva a Ed com condições iniciais:

   

 

'' sin 2 t

) ' 0 1

0 2

y t y t a y

y

 

 

 

 _



   

 

0 ''' 0 0 b) '' 0 0

' 0 1

0 0

IV

y t y t y

y y y

  



 

 _



 _



 _

(17)

 

'' 4 sin 3

) ' 0 0

0 0

x t x t t

c x x

 

 

 

 _



d) Ache a solução do P.V.I.

 

'' ₄ _3, ₀ _0, ' ₀ ₀

y  y y  y 

Solução:

 

3 3cos 2 4 4

y t   t

Translação sobre o eixo s

O cálculo de transformadas tais como

 

5 3

t e

L t e L



e2tcos4t



é direto desde que conheçamos

 

3

L t e L



cos4t



. Em geral quando conhecemos a transformada de Laplace de uma função _𝑓, L

 

f(t) F(s), é possível computar a transformada de Laplace de um múltiplo exponencial de 𝑓, isto é, L



eatf(t)



, sem nenhum esforço.

Teorema: Teorema de translação sobre o eixo s

Se L f t



 



F s

 

e a for um número real qualquer, então:

 



at







L e f t F sa

Demonstração:

Pela definição de transformada, temos que:

 





 

_{ }

_

_

0 0

s a t at st at

L e f t e e f t dt e f t dt F s a

 

  









 

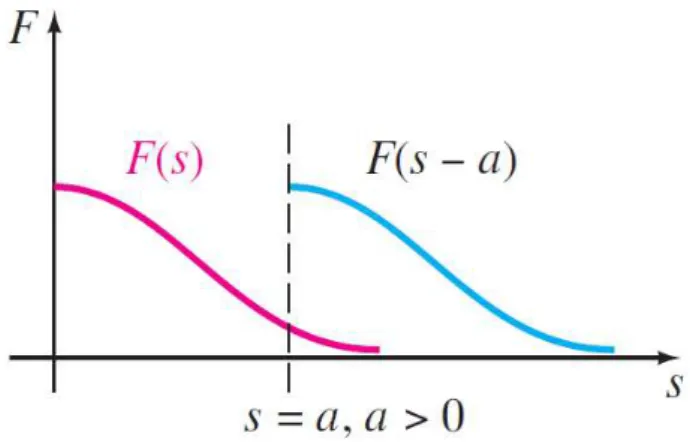
Se considerarmos _𝑠 uma variável real, o gráfico de _{𝐹(𝑠 − 𝑎)} será o gráfico de

(18)

Figura 4 - Gráfico do deslocamento no eixo s

Para enfatizar, é às vezes proveitoso usar o simbolismo:

 



at





 



s s a L e f t L f t _{ }

Exemplo 1: Calcule a transformada

 

5 3t L e t .

   

5 3 3

_

_

4 5

6 5 t

s s L e t L t

s  

 



Exemplo 2: Calcule a transformada



2t_{cos 4}



L e t .













2

2 2

2

cos 4 cos 4

2 16

t

s s

s

L e t L t

s 

 



 

 

A forma inversa do teorema da translação em s

As transformações geralmente precisam ser ajustadas pelas frações parcias e a transformada inversa resulta em:











 



 

1 1 at

s s a

L F s a L F s _{ } e f t (36)

Exemplo 3: Calcule a transformada inversa 1 2

2 3

4 20 s L

s s

   

 _ _ 

 . Aqui tentaremos usar a

(19)





















2 2 2 2 2

2 2 7

2 3 2 3

4 20 ₄ ₁₆ ₄ ₁₆

2 2

2 7 4

1 ₄ ₁₆ 4 ₄ ₁₆

s

s s

s s _s _s

s s s    _  _ _   _ _ _ _  _     _    _ _   _ _     

Como, pela propriedade de translação, temos que:









1 2 2 2 cos 4 2 16 t s

L e t

s              e





1 2 2 4 4 2 16 t

L e sen t

s            

Fica fácil ver que:

1 2 4

2

2 3 7

2 4 4

4 20 4

t t

s

L e sen t e sen t

s s

     _

 _ _ 

 

Exercícios

a) Calcule a transformada inversa de





1 2 2 5 3 s L s         

 : usando frações parciais teremos:





1 3 3

2 2 5 2 11 3 t t s

L e e t

s      _       

b) Calcule a transformada inversa de 1 2 5 2 3 4 6 s L s s   _     _ _     

 

3t_{cos 2} 3t ₂ e t e sen t

 

















2 2 1 1 2 2

2 10 2 10

)

2 5 1 ₁ ₄ ₁

s s s s

c L L

s s s _s _s

   _            _ _ _       _ _ Solução:

(20)

 

'' 2 ' 5 8 )

0 2; ' 0 12

t

y y y e

d

y y



    

 

 



Aplicando a transformada de Laplace tem-se:

Chegamos ao mesmo resultado do exemplo c.

Exemplo 5: Usar a transformada de Laplace para resolver o PVI

 

' 2 3

'

'' 6 9

0 2, 0 17

t

y t y y t t e

y y

  

 

Decompondo em frações parciais,

(21)

Exemplo 6:

 

'

'' 6 34 0

0 3, 0 1

x t x x t

x x

  

 

Exemplo 7:

 

'

'' 6 34 30sin 2

0 0, 0 0

x t x x t t

x x

  

(22)

(23)

Exemplo 8: Ache a solução do PVI usando as transformadas de Laplace:

 

'' ' 2

'

4 13 2 3 cos

0 0

0 1

t

y y y t e t

y y



    

  

 _{ }



Tomando a transformada de Laplace de ambos os lados desta equação e aplicando as condições iniciais dadas, obtemos:

 









2

2 2

3 2

2

1 4 13

2 9

s

s F s sF s F s

s _s



    

  ,

onde F s

 

L y t

 

 

. Assim,

 

_

_









2

2 2 2 ₂

3 2

1 2

4 13 4 13 ₄ ₁₃

s F s

s s s s s _s _s



  

    _ _

Agora, devemos achar a transformada inversa de cada termo da soma acima, comecemos pelo primeiro termo.





_

_

2

1 1 1 3

4 13 2 9 3 ₂ ₉

s  s  s    _s   Logo,

1 2

2

1 1

3

4 13 3

t

L e sen t

s s

     

 _ _ 

 

Para o segundo membro da soma, usamos frações parciais:





2 2

2

4 13 4 13

A B Cs D

s s s s

s s s



  

 

Resolvendo a igualdade acima, obtemos 8 ; 2 , 8 , 6

169 13 169 169

A  B C  D .

Portanto,













2 2

2

2 8 1 2 1 1 8 6

169 13 169 4 13

4 13

8 1 2 1 1 2 10 3

169 13 169 ₂ ₉ 3 169 ₂ ₉

s

s s s s

s s s

s

s s _s _s



   

 



    



   

,

(24)





1 2 2

2 2

2 8 2 8 10

cos3 3

169 13 169 507

4 13

t t

L t e t e sen t

s s s

     _ _  _ 

 

 

 

 

E, finalmente a terceira soma pode ser vista como:







₂



2 2





2

3 2 3 1 1 3

2 4 13 2

4 13 2 9

s d d

ds s s ds

s s s

   _ _ _ _   _ _          _   _

Portanto, pelo Teorema 11.6 e pelo item 2 do Teorema 11.5, segue que :









1 2

2 2

3 2 1

3 2

4 13

t s

L te sen t

s s               Portanto,

 

2 2 2 2

2 2 2

1 8 2 8 10 1

3 cos3 3 3

3 169 13 169 507 2

179 8 1 2 8

3 cos3 3

507 169 2 13 169

t t t t

t t t

y t e sen t t e t e sen t te sen t

y t e sen t e t te sen t t

   

  

      

     

Exercícios

1 - Resolva as Edo’s com condições iniciais:

 

'' 4 ' 6 1

) ' 0 0

0 0

t

y t y t y t e

a y y           _  2 2

1 1 1 2

( ) cos 2 2

6 3 2 3 2

t t t

y t   e  e t e sen t

 

2

'' 4 ' 4

b) ' 0 0

0 0

y t y t y t t

y y         _ 

   

 

0 ' '' sin )

0 0, 0 0

x t x t F t

(25)

 

_{ }

_{   }

 

_{ }

4

3

2 '' 4

)

0 '' 0 ' 0 0 0

t

y t y t y t te

d

y y y y

 _ _ _

 

   



 

'

'' 6 34 0

)

0 3, 0 1

x t x x t

e

x x

   

 

 



 

'

'' 6 34 30sin 2

)

0 0, 0 0

x t x x t t

f

x x

   

 

 



Resposta:

 

5



_{2cos 2} ₅ ₂



2 3



_5cos5 ₂ ₅



29 29

t

x t   t sen t  e t sen t

g) Ache a solução do PVI usando as transformadas de Laplace:

 

'' ' 2

'

4 13 2 3 cos

0 0

0 1

t

y y y t e t

y y



    

  

 _{ }



Solução:

 

179 2 ₃ 8 2 _cos3 1 2 ₃ 2 8

507 169 2 13 169

t t t

y t   e sen t  e t te sen t  t

Translação sobre o eixo t

Nas engenharias são frequentemente encontradas funções que pode ser “ligadas” e “desligadas”. Por exemplo, uma força externa agindo sobre um sistema mecânico ou

uma voltagem sendo aplicada a um circuito elétrico que pode ser desligada a certo período. Essa função é muito importante porque ela descreve funções descontínuas, ou contínuas por partes mais simples. Para trabalhar com esse tipo de processos vamos introduzir a função de Heaviside.

Função degrau ou função de Heaviside

Definição: uma função é contínua por partes em I se existe uma partição de I

0; i

(26)

limites laterais lim

 

i

tp f t e tlimp_i f t

 

são finitos.

É conveniente então definir uma função especial que seja número 0 (desligada) até um determinado tempo _{𝑡 = 𝑎} e número 1 (ligada) após esse tempo.





 

0 0

1 a

se t a

u t a u t

se t a

  

  _{ }



 (37)

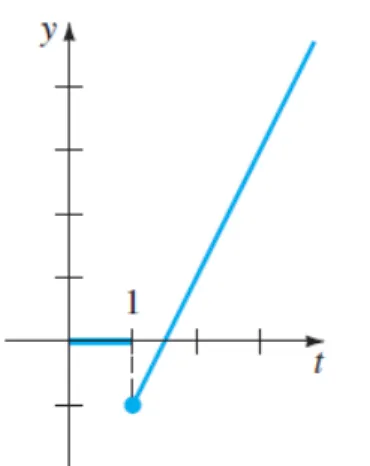
Como Laplace trabalha com t>0 o gráfico da função de Heaviside é:

Figura 5 - Gráfico da função degrau unitário

Quando uma função _𝑓 for multiplicada por _{𝑢(𝑡 − 𝑎)}, a função degrau unitário

“desliga” uma parte do gráfico dessa função. Por exemplo, considere a função

𝑓(𝑡) = 2𝑡 − 3. Para desligar a parte do gráfico de _𝑓 sobre o intervalo _{0 ≤ 𝑡 < 1}, simplesmente tomamos o produto _{(2𝑡 − 3)𝑢(𝑡 − 1)}. Em geral, o gráfico de

𝑓(𝑡)𝑢(𝑡 − 1)é “desligado” para 0 ≤ 𝑡 < 𝑎 e “ligado” para 𝑡 ≥ 𝑎.

Figura 6 - Gráfico da função _{𝒇(𝒕) = (𝟐𝒕 − 𝟑)𝒖(𝒕 − 𝟏)}

Em um outro ponto de vista podemos afirmar que quando multiplicamos uma

(27)

Figura 7 - Deslocamento em t

Exemplo 1:

 

  

2



0 0

_{ }

2 ,



2



0 0

_{ }

2

sen 2 sen 2

se t se t

f t sen t u t uma vez que u t

t se t t se t

 

   

 

 

  _  _

 

 

 

Representação gráfica:

Figura 8 - a) gráfico da função f t

 

sen t

 

, b) gráfico da função

 

  

2



f t sen t u t 

A função degrau unitário Eq. (37) também pode ser usada para descrever funções definidas por partes em uma forma compacta. Por exemplo, se considerarmos os intervalos _{0 ≤ 𝑡 < 2}, _{2 ≤ 𝑡 < 3} e _{𝑡 ≥ 3} e os valores correspondentes de _{𝑢(𝑡 − 2)} e

(28)

Figura 9 - Gráfico da função _{𝒇(𝒕) = 𝟐 − 𝟑𝒖(𝒕 − 𝟐) + 𝒖(𝒕 − 𝟑)}.

Da mesma forma, uma função definida por partes do tipo:

  

   

a t t h

a t t

g t f

), (

0 ), ( ) (

É idêntica a _{𝑓(𝑡) = 𝑔(𝑡) − 𝑔(𝑡)𝑢(𝑡 − 𝑎) + ℎ(𝑡)𝑢(𝑡 − 𝑎)} Analogamente, uma função do tipo:

    

  

  

b t

b t a

a t t

g t f

0

, 0

), (

, 0 ) (

Pode ser escrita como: _{𝑓(𝑡) = 𝑔(𝑡)[𝑢(𝑡 − 𝑎) − 𝑢(𝑡 − 𝑏)]}

Uma forma alternativa e descomplicada de escrever a função de Heaviside é multiplicar a parte da _𝑓(𝑡) pelas funções de Heavise que representam a região onde está é ligada ou desligada. Por exemplo a figura 9 representa um gráfico de uma função com três partes.

    

  

  



3 3 2

2 0

, 0

, 1

, 2 ) (

t t t t

f .

A _𝑓(𝑡) é composta pela seguinte soma:

𝑓(𝑡) = 2[𝑢(𝑡 − 0) − 𝑢(𝑡 − 2)] − 1[𝑢(𝑡 − 2) − 𝑢(𝑡 − 3)] + 0[𝑢(𝑡 − 3)]

Desta forma _{𝑓(𝑡) = 2 − 3𝑢(𝑡 − 2) + 𝑢(𝑡 − 3)}

Com base nesse conceito, podemos ter outras aplicações práticas; observe abaixo:

(29)

Imagine que você tenha que restringir o intervalo da sua função; podemos usar a função pulso; basta multiplicar a função pela função pulso.

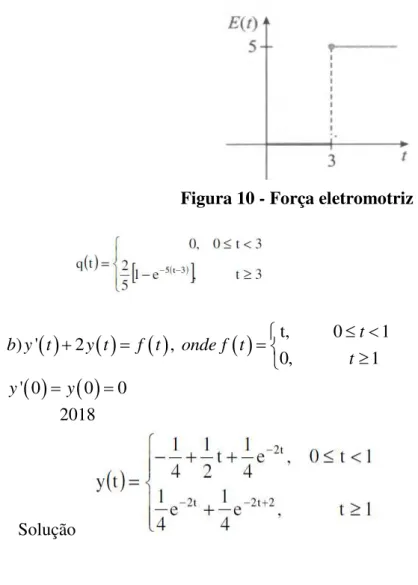
Exemplo 2: A voltagem em um circuito é dada por uma função definida por partes:

 

20 , 0 5 0, 5

t se t E t

se t

  

  _

 (38)

Lembrando que é essa função que precisamos definir, então teremos que a função degrau é



5



0, 0 5

1, 5

se t

u t

se t

  

   _

 podemos expressar a Eq. (38) como:

Resp: E t

 

20t20t u t



5



Considere uma função genérica _{𝑦 = 𝑓(𝑡)} definida para _{𝑡 ≥ 0}. A função definida por partes

  

 

  

 

a t a t f

a t a

t u a t f

), (

0 , 0 )

( ) (

desempenha um papel significativo

Veremos agora como calcular a transformada de Laplace desse tipo de função: Segundo teorema da Translação

Se _{𝐹(𝑠) = 𝐿{𝑓(𝑡)} 𝑒 𝑎 > 0}, então







f t a u(t a)



e F(s)

(30)

Observe abaixo a demonstração do teorema em que colocamos a função f (t) = f (t - a) u (t - a) e achamos a transformada de Laplace (lembrando que u (t - a) é igual a 1

para t ≥ a, e criamos uma variável x = t - a para isolar "t" e integramos em função de x):

Prova:

Pela propriedade aditiva das integrais,



f t a u t a



e f t a u t a dt

L ₍ ₎ ₍ ₎ st ₍ ₎ ₍ ₎

0  

 





 

Pode ser escrita como soma de duas integrais:



f t a u t a



e f t a u t a dt e f t a u t a dt e f t a dt

L st

a t para um a

st a

t para zero a _st

) ( )

( ) ( )

( ) (

0 _

_ 0

_ _

0       

 



_

 

  

  

4 4 3 4 4 4 2 1 4

4 3 4 4 4 2 1

Agora se fizermos na última integral _{𝑣 = 𝑡 − 𝑎}, _{𝑑𝑣 = 𝑑𝑡}, então:



( ) ( )



( ) ( )

 

( )

0 0

) (

t f L e dv v f e e dv v f e a

t u a t f

L   



 sva  as



 sv  sv

Exemplo 4: Calcule as transformadas de Laplace: a) _{𝑓(𝑡) = (𝑡 − 2)}3_{𝑢(𝑡 − 2)}

b) 𝑓(𝑡) = 𝑠𝑒𝑛ℎ(2𝑡 − 4)𝑢(𝑡 − 2)

c) _{𝑓(𝑡 − 𝑎) = 1} d)

(31)

RESOLUÇÃO:

a) Observe que a forma de deslocamento da função e do degrau unitário são iguais, (t - 2). Basta aplicar diretamente a fórmula (usamos a tabela de transformada de Laplace, item 19).

b) Temos que manipular matematicamente a função para colocar a função senh (2t - 4) na mesma forma de deslocamento u (t - 2). Usamos o item 6 da tabela de transformada de Laplace.

c) Basta substituir na fórmula f(t - a) = 1. Usamos a tabela de transformada de Laplace item 1.

d) Observe que o gráfico é uma função por partes para explicar como definimos a função por partes de forma compacta dividirei o gráfico em 3 funções (f1(t) = 2, f2(t) =

(32)

Para montar o intervalo com funções definidas por partes, basta somar as funções usando afunção pulso nos respectivos intervalos. Obtemos a função:

f(t) = f1(t) [u (t - a) - u (t - b)] + f2(t) [u (t - a) - u (t - b)]

Substituindo os valores das funções, obtemos (u(t), para t ≥ 0, é igual a 1): f(t) = 2 [u (t - 0) - u (t - 2) + -1 [u (t - 2) - u (t - 3)] ---> f(t) = 2 u(t) - 2 u (t - 2) + (-1) u (t - 2) - (-1) u (t - 3) --->

f(t) = 2 - 2 u (t - 2) - 1 u (t - 2) + 1 u (t - 3) ---> f(t) = 2 - 3 u (t - 2) + u (t - 3)

Calculando a transformada de Laplace (Obtive a transformada inversa consultando a tabela de transformada de Laplace):

(33)

Achamos a função; Temos que colocar a função (2t - 3) na mesma forma de deslocamento u(t - 1). Observe que podemos escrever -3 como - 3 = -2 - 1. Observe abaixo a resolução; usamos atabela de transformada de Laplace itens 1 e 2.

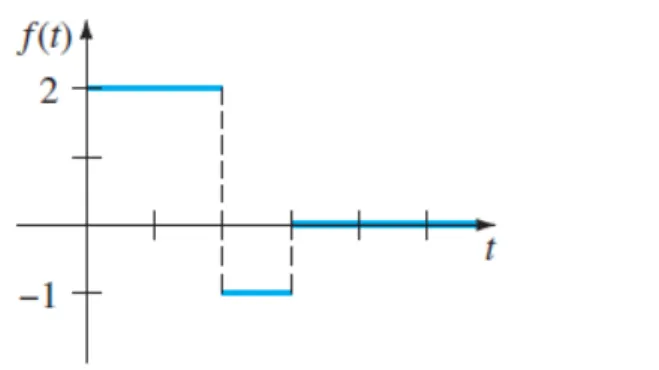
Exemplo 5: A figura é representada pela seguinte equação

 

2 3



2

 

3



f t   u t u t , ou seja:

 

         

 

0, 0

- - - ,

0, t a f t g t g t u t a h t u t a g t a t b

t b   



  _  

 _



(34)

Obs: precisa ser cuidado quem é o a da função degrau com o da função a ser transformada.

Ela é muito importante porque outras funções descontínuas ou contínuas por partes podem ser descritas pela função degrau. De maneira geral podemos fazer a transformada dessas funções de forma alternativa, ou seja: